pH dependent conformational dynamics of Beta-secretase 1: a molecular dynamics study

Abstract

Beta-secretase 1 (BACE-1) is an aspartyl protease implicated in the overproduction of β-amyloid fibrils responsible for Alzheimer’s disease. The process of β-amyloid genesis is known to be pH dependent, with an activity peak between solution pH of 3.5 and 5.5. We have studied the pH dependent dynamics of BACE-1 to better understand the pH dependent mechanism. We have implemented support for graphics processor unit (GPU) accelerated constant pH molecular dynamics within the AMBER molecular dynamics software package and employed this to determine the relative population of different aspartyl dyad protonation states in the pH range of greatest β-amyloid production, followed by conventional molecular dynamics to explore the differences among the various Aspartyl dyad protonation states. We observed a difference in dynamics between double protonated, mono-protonated, and double deprotonated states over the known pH range of higher activity. These differences include Tyr 71-Aspartyl dyad proximity and active water lifetime. This work indicates that Tyr 71 stabilizes catalytic water in the Aspartyl dyad active site, enabling BACE-1 activity.

Introduction:

Alzheimer’s Disease (AD) is characterized by a degradation of cognitive function and memory loss.¹ These phenotypes are thought to be caused by the overaccumulation of a cytotoxic form of amyloid-beta peptide, Aβ−42.^2,3 Aβ−42 is one of a variety of amyloid beta peptides that are produced via the amyloidogenic pathway.⁴ When amyloid precursor protein (APP) is first cleaved by β-secretase (BACE-1) rather than α-secretase, Aβ−42 is formed preferentially over other non-oligomerizing amyloid-beta peptides.^5,6 This, coupled with BACE-1 mice knockout studies in which Aβ−42 production was abolished with no other apparent phenotypic changes,^7,8 have led to BACE-1 being an extremely promising protein target in the fight against AD.^9,10

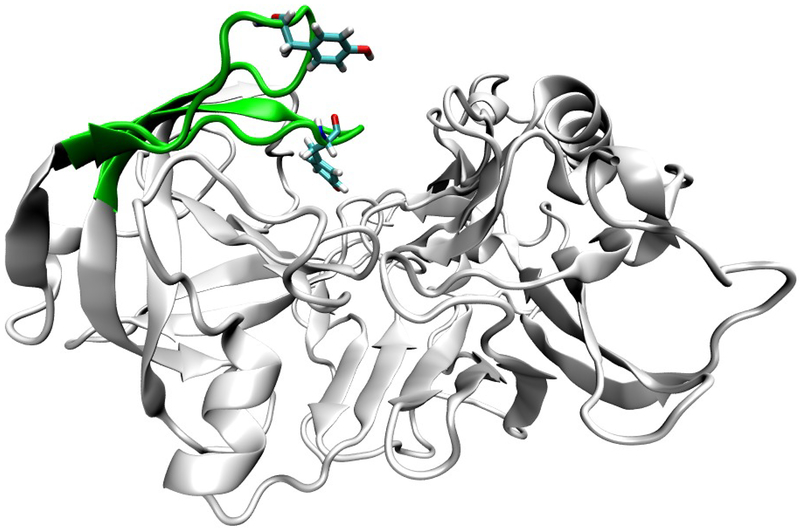
BACE-1 is a 501 amino acid transmembrane aspartyl protease.^11,12 As a member of the aspartyl protease family, it has the characteristic aspartyl dyad at the center of its active site.¹³ BACE-1 activity has a well-known pH dependence, with activity declining sharply below pH 3.5 and above pH 5.5.¹⁴ BACE-1 is thought to act by some variant of a general acid-base mechanism, possibly involving a bridging catalytic water.^15,16 In the case of BACE-1, the aspartyl dyad (Asp dyad) acts as the general acid and general base. Asp 32, with an experimental pK_a of 5.2,¹⁶ would be the general acid, while Asp 228 (experimental pK_a of 3.5)¹⁶ would be the general base. The exact role of water and in turn how solution pH regulates BACE-1 activity are still subjects of study.^14,16–18 Toulokhonova et al. proposed a mechanism in which a bridging water allows for the formation of a tetrahedral intermediate and with an unknown pH dependent conformational change as the rate limiting step.¹⁶ Shimizu et al. proposed that at acidic pH water is prevented from entering the active site and catalyzing peptide cleavage while at basic pH activity is prevented by a conformational change of BACE-1.¹⁴ Both hypotheses involved the motion of a β-hairpin loop consisting of residues Tyr68 through Glu77, more commonly referred to as the “flap” region. Molecular dynamics and crystallography studies have demonstrated the flap region’s flexibility, shown below in figure 1.^14,19–21

Figure 1:

example flap motion in BACE-1

Previous work by Kim et al.¹⁷ as well as Ellis and Shen¹⁸ both using constant pH molecular dynamics has shown that the flap region dynamics are vastly different at different pHs. Of relevance to the question of mechanism, pH control, and the role of water in BACE-1 catalysis, Ellis and Shen demonstrated that Tyr 71 can hydrogen bond to BACE-1 inhibitors resulting in openings small enough to potentially occlude water.¹⁸ It is possible that the flap is capable of occluding water without the presence of inhibitor, in which case water would be a major limiting factor in catalysis. By calculating how much water is present in the active site at different pHs, and how long said water remains in the active site, we can determine whether water is limiting to BACE-1 activity. From this information, we may be able to ascertain whether a conformational change is responsible for BACE-1 pH dependence, or whether BACE-1 pH dependence is due entirely to the electrostatic environment of the active site.

To explore water residence times across a range of solution pHs, we have employed two variations of molecular dynamics simulations (MD): conventional MD (cMD) and constant pH MD (CpH-MD). MD simulations allow the direct observation of protein sized systems as they propagate forward in time. This enables us to observe and account for all the binding poses and conformational changes that can occur. However, cMD requires a constant protonation state that is set prior to the simulation. For BACE-1, which has a known pH dependence, ignoring changes in protonation state would potentially miss very relevant information. CpH-MD can be used to probe the effect of the surrounding environment on the pK_a of a given residue by accounting for the effect of conformational flexibility on pK_a.²² By accounting explicitly for the possibility of multiple protonation states, we can vastly improve our understanding of pH dependent conformational changes and the associated changes in electrostatic environment. Previous studies have attempted to use constant pH^17,18 or other forms of molecular dynamics^19,23–27 to study BACE-1 dynamics. To our knowledge, this is the first study to use explicit solvent CpH-MD to quantitatively examine the effect of pH on water lifetimes in BACE-1, and to attempt to correlate this with a conformational change in the protein towards the understanding of the source of the pH dependence of BACE-1 activity.

Materials and Methods

Calculating pK_as using CpH-REMD

In CpH-MD, protonation states of the residues of interest are allowed to change over the molecular dynamics simulations, sampling from a semi-grand canonical ensemble.²⁸ In the particular variety of CpH-MD employed in this work, modified from the method of Mongan et al.²² and implemented on CPUs within the AMBER molecular dynamics suite^29–31 by Swails et al.³² and subsequently extended to GPUs^33–35 as part of this work, dynamics propagate from an initial set of protonation states using explicit solvent conventional MD. In this method, dynamics are interrupted, and for each residue being titrated a change of protonation state is attempted sequentially. Protonation state changes are attempted using generalized Born implicit solvent. Acceptance is decided by the following Monte Carlo (MC) criteria (1):²²

$${\text{ΔG}}_{\text{trans}}{\text{=k}}_{\text{b}}\text{T}\left({\text{pH-pK}}_{\text{a,ref}}\right)\text{ln}\left(\text{10}\right){\text{+ΔG}}_{\text{elec}}{\text{-ΔG}}_{\text{elec, ref}}$$ (1)

where k_b is the Boltzmann constant, T is the temperature in Kelvin, pH is the solvent pH, pK_a,ref is an experimentally measured pK_a value for a simpler form of the amino acid, with the sequence acetyl–amino acid–methyl amine, and $\text{Δ}{\text{G}}_{\text{elec, ref}}$ is the precomputed free energy of changing the protonation state of the reference compound. $\text{Δ}{\text{G}}_{\text{elec}}$ is the calculated free energy of changing the pronation state at the current simulation condition using generalized Born. Following titration, the water molecules must be allowed to relax before protein dynamics can continue. This is accomplished by holding the solute position constant and running dynamics on the water molecules. Replica exchange was employed along the pH coordinate. After every cycle described above, adjacent replicas attempt to exchange solution pH per the following MC criteria (2):³⁶

$${\text{P}}_{\text{i}\to \text{j}}\text{=min}\left\{\text{1,exp}\left[\text{ln10}\left({\text{N}}_{\text{i}}{\text{-N}}_{\text{j}}\right)\left({\text{pH}}_{\text{i}}{\text{-pH}}_{\text{j}}\right)\right]\right\}$$ (2)

Where N_i and N_j are the number of titratable residues that are currently protonated in replica i and j, respectively, and pH_i and pH_j are solvent pH in replica i and j, respectively. The result of such a simulation is a protonation fraction for each residue at each pH. These values can then be fit to the Hill equation (3) to generate predicted pK_a values:

$$\text{fraction protonated}\left(\text{pH}\right)\text{= }\frac{\text{1}}{\left({\text{1+10}}^{\left(\text{n*(pKa-pH}\right)\text{)}}\right)}$$ (3)

Where n is the cooperativity coefficient, fraction protonated is the percentage of time a residue spent in the protonated state at a given pH, and pH is the solvent pH.

Conventional MD for dynamics

While it is possible to use CpH-MD to study dynamics, as even in explicit solvent it satisfies the weaker detailed balance criteria,³⁷ the solvent relaxation time requirement makes extracting time dependent information, e.g. water residence or flap motion, from CpH-MD very difficult in practice. Conventional MD (cMD) is useful for generating such time dependent quantitative information but requires a set protonation state. By using CpH-MD to calculate the relative populations of each set of protonation states at each pH, and then running cMD on each of these sets of protonation states that are present at our pH range of interest, we can calculate residence times and flap motion for the states of interest. To test the differences at, below, and above the pH range of high activity, we first need to determine the different protonation states present within pH 3.5 – 5.5, below 3.5, and above 5.5. Then we can run conventional MD to extract flap-dyad distance and residence time, and correlate this with how frequently each protonation state occurs below, above, and within the pH range of interest.

Choice of titratable residues

PROPKA³⁸ was used to determine the predicted pK_a of all potentially titratable residues at pH 3.5 and pH 5.5. From this, all residues with a predicted difference in pK_a between pH 3.5 and pH 5.5 of greater than 0.5 pK_a units were selected to be titratable in our CpHMD simulations.

System preparation and generation of production coordinates

The X-ray crystallographic structures of BACE-1 in complex with the inhibitor N-[(1S,1R)-ben- zyl-3-(cyclopropylamino)-2-hydroxypropyl]-5-[methyl(methylsulfonyl)amino-N’-[(1R)- 1-phenylethyl]isophthalamide (PDB ID 2B8L)³⁹ was used to build the starting structure for all simulations. The apo structure of BACE-1 was generated by removing the bound inhibitor from the refined 2B8L structure. The mutations that were added to the protein for crystallographic purposes were corrected to the original sequence.³⁹ Residues from Gly158 to Ser169 were not resolved in this structure. This loop was constructed using homology modeling from the Structure Prediction Wizard module of Schrödinger’s Prime program.^40–42 First, the FASTA sequence of the protein including the missing loop region was obtained from UniProt.⁴³ Then, utilizing the homologs found by the BLAST search algorithm⁴⁴ a chimera model containing the missing loop region was built. Finally, the homology-modeled loop region was energy-refined for relaxation using the Refine Loops panel of the Prime program.⁴²

The leap module in AMBER 16²⁹ was used to parameterize Apo BACE-1. the AMBER ff14SB forcefield⁴⁵ was used for protein parameters. TheTIP3P⁴⁶ model was used for water. 18 sodium and eight chlorine TIP3P ions with Joung and Cheatham parameters^47,48 were added to generate a neutralized system with a 0.1M ion concentration. A 0.1M concentration was needed to match the ion concentration that the GB pK_a,ref and ΔG_elec,ref were parameterized for. A cubic periodic box was used with a minimum distance of 10 Å between any box edge and any solute atom. Disulfide bonds were added manually in leap between Cys 155 and Cys 359, Cys 217 and Cys 382, and Cys 269 and Cys 319. Residues Asp 32, Asp106, Asp138, Asp223, Asp 228, Glu116, Glu265, Glu339, His45 and Tyr 71 were selected for titration. Initial protonation states were selected by using PROPKA.^38,49 A modified prmtop and cpin file with generalized Born (GB) parameters GB^OBC,I from Onufriev, Bashford and Case^50,51 were generated using cpinutils.py in AMBERTools16.³⁰

Minimization was carried out over four steps. First, 2000 cycles of steepest descent were performed with a restraint weight of 5 kcal/(mol*Ų) on all non-hydrogen atoms. Second, 5000 cycles of steepest descent were performed with a restraint weight of 5 kcal/(mol*Ų) on all non-hydrogen protein atoms. Third, 5000 cycles of steepest descent were performed with a restraint weight of 5 kcal/(mol*Ų) on all atoms except for carbons and nitrogens. Fourth, 25000 cycles of steepest descent were performed with no restraint. Following minimization, the system was heated gradually to 300K over 250 ps using a Langevin thermostat with a collision frequency of 2.0 ps⁻¹. All protein atoms were restrained with a weight of 5 kcal/(mol*Ų). The system was then pressure equilibrated to 1 atm over 2 ns with a Langevin thermostat set to 300 K with collision frequency of 5.0 ps⁻¹ and a Berendsen barostat with a pressure relaxation time of 1.0 ps. Finally, the system was run under NVT conditions for 100 ns of equilibration with a Langevin thermostat, collision frequency of 2.0 ps⁻¹ and a target temperature of 300 K. Particle Mesh Ewald⁵² was used for long range electrostatic forces, with direct force calculation truncated after 8.0Å.

Constant pH REMD

CpH REMD simulations were run using our GPU implementation of CpH-MD in pmemd.cuda.MPI within AMBER 16.²⁹ The only modification beyond the code released as part of AMBER 16 was to allow for coupled titrations for residues which were separated by more than 2Å such as in this case where the bridging water caused Asp 32 and Asp 228 to be separated by on average 5Å. 18 total pH replicates were run, spanning from −6 to 12 by single pH units. Each of three replicates was run for 60 ns of dynamics (excluding solvent relaxation). Simulations were run with NVT at a target temperature of 300K using the Langevin thermostat with a collision frequency of 2.0 ps⁻¹. Dynamics was propagated for 200 fs, at which point titration was attempted on all titratable residues. In the case of a successful titration on any of the residues, 200 fs of solvent relaxation was performed. Following solvent relaxation, replica exchange was attempted. Explicit solvent was used for the dynamics (icnstph=2), while generalized Born implicit solvent was used for the titration attempts, with igb=2 which corresponds to GB^OBC,I.⁵¹ A salt concentration of 0.1M was used to match the parametrization of the reference pK_a values. Protonation state population data was recorded after every set of titration attempts. Energies and coordinates were recorded every 10 ps.

Production MD on four protonation states

System preparation for cMD was identical to CpH-REMD, except that instead of generating a modified prmtop and cpin file, the initial prmtop was modified to have the desired protonation states for each of the four combinations of Asp dyad protonation. The four protonation states were Asp 32 protonated, Asp 228 deprotonated; Asp 32 deprotonated, Asp 32 protonated; both Asp 32 and Asp 228 protonated; and both Asp 32 and Asp 228 deprotonated. Prmtop modification was accomplished using ParmEd in AMBERTools17³⁰. For each protonation state, three replicate cMD simulations were run for 800 ns with identical NVT conditions to CpH-REMD simulations, for a total of 12 cMD simulations. Energies and coordinates were recorded every 10 ps.

Data analysis

Cphstats in AMBER was used to reconstruct trajectories by pH following replica exchange, as well as calculated protonation fractions of all residues at each pH. This data was fit to the Hill equation (3) using Gnuplot.⁵³ Cpptraj in AMBERTools³⁰ was used to calculate the dyad-Tyr 71 distance over the course of the cMD trajectories as well as generate water-dyad distances for residence times. The center of mass of the aspartyl dyad titratable protons was used for the dyad location when measuring water-dyad and Tyr 71-dyad distances. Trajectories were visualized in VMD version 1.9.3a6.⁵⁴

Calculating hydration numbers and water residence time

Hydration numbers and residence times were calculated using an in-house python script. Water molecules were considered to be within the first hydration shell of the aspartyl dyad if their oxygen atom was within 3.5Å from the center of mass of the aspartyl dyad titratable protons. Only the closest 10 water molecules were considered for computational simplicity. There was no noticeable effect of including the 11^th closest water molecule on the hydration number compared to just the 10 closest water molecules (SI Table 1).

Results and Discussions:

Calculation of pK_as

Constant pH MD was used to generate ensemble averages of protonation fractions from pH −6 through pH 12 in units of single pH units for 10 residues. Residues titrated included the aspartyl dyad, the Tyr 71, and seven others which were hypothesized to vary significantly over the active pH range. The predicted pK_a values are shown in table 1.

Table 1:

predicted pK_a values for titrated residues. Uncertainties are derived from the fit to the Hill equation.

Residue	Calculated pKa
Asp 32	3.16 ± 0.08
Asp 106	3.35 ± 0.01
Asp 138	2.53 ± 0.02
Asp 223	3.50 ± 0.002
Asp 228	−1.17 ± 0.08
Glu 116	3.26 ± 0.04
Glu 265	5.30 ± 0.004
Glu 339	4.04 ± 0.02
His 45	7.26 ±0.01
Tyr 71	11.80 ±0.001

The pK_a of the aspartyl dyads are of note. The experimentally calculated values of Asp 32 and Asp 228 are 5.2 and 3.5 respectively.¹⁶ Our macroscopic pK_as were correctly ordered, but differ by 2.1 and 4.6, respectively. This variation is likely due to the bridging water which is removed during the implicit solvent titration attempts. The other key titratable residues had pK_a values near their normal ranges. The pK_a of tyrosine 71 was a bit elevated from the typical value of 9.1. Because the calculated pK_as of Asp 32 and Asp 228 appear to be artifactually perturbed by the missing water molecule, we used the experimental values of those residues, together with the calculated values of the other residues, to guide the chosen protonation states for the cMD simulations.

Protonation states relevant to the dyad motion and hydration

To understand the Asp flap dynamics over time at different pHs, we first needed to determine which protonation states were likely to be present at each pH. Of the titratable residues, only the Asp dyad and Tyr 71 were found to influence the dyad motion. However, Tyr 71 had a calculated pK_a of 11.8, far above that of the Asp dyad, and did not change protonation state below the upper bound of pH range of high activity (pH 5.5). Therefore, we assumed Tyr 71 would be monoprotonated in all cases. As such, there were only four combinations of protonation states whose dynamics were of interest. These were Asp 32 protonated Asp 228 deprotonated (32p 228 d), Asp 32 deprotonated Asp 228 protonated (32d 228p), both Asp protonated (32p 228p), and both Asp deprotonated (32d 228d). Among the two monoprotonated states (32p 228d and 32d 228p), 32p 228d will occur more often than 32d 228p based on ordering of the pK_as of the aspartyl dyad in table 1 above.

Tyr flap – Asp dyad distance as an explanation for different catalytic activity between protonation states

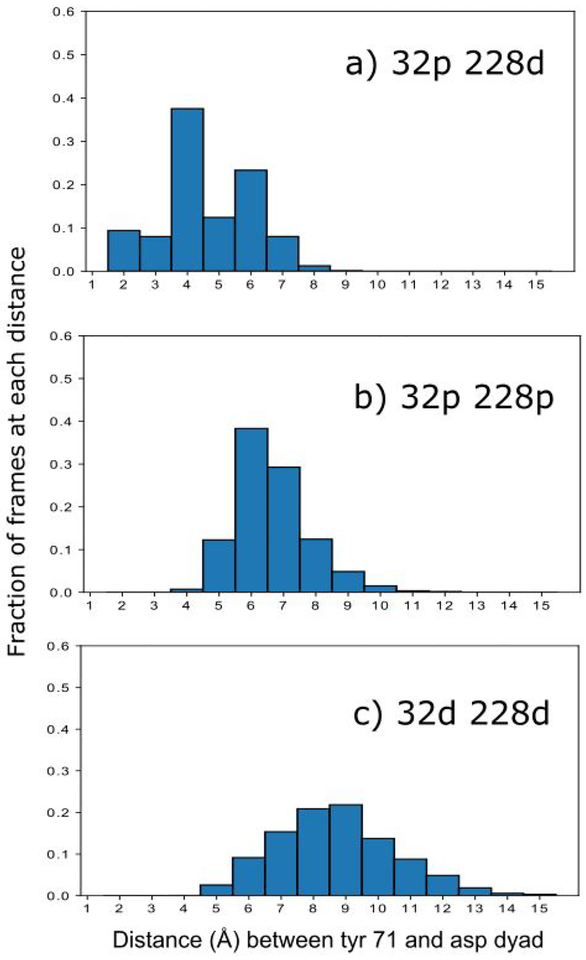
We examined the distance of the Tyr 71 flap to Asp dyad to test for a source of the differences in catalytic activity state to state. One hypothesis is that water could be excluded from the active site or prevented from leaving the active site if the flap moves close enough to the dyad. The relative amount of time spent with a given distance between Tyr 71 and the Asp dyad for the more prevalent monoprotonated state (32p 228d), the doubly protonated state and the doubly deprotonated state is shown in Fig 2.

Figure 2:

fraction of time that the Tyr 71 to Asp dyad distance is a given number of angstroms for: a) the more prevalent monoprotonated state (32p 228d), b) the doubly protonated state (32p 228p) and c) the doubly deprotonated state (32d 228d). This distance is calculated as the Tyr 71 hydroxyl hydrogen to the center of mass of the four aspartyl dyad oxygens.

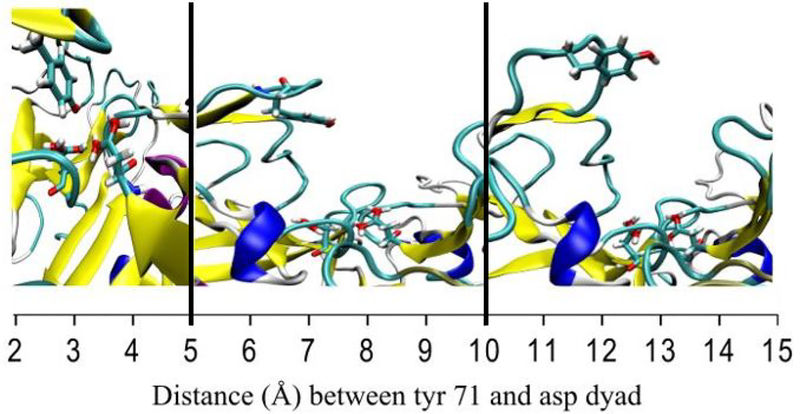
Figure 2 demonstrates that in the catalytically active state, Tyr 71 spends a much larger fraction of the time within 5Å of the aspartyl dyad. It is possible, given that we know the monoprotonated state is the catalytically active state, that the Tyr-dyad interaction is necessary to stabilize the catalytic water. To illustrate that Tyr 71 is interacting with the dyad, representative frames taken for three different ranges of Tyr-dyad distance (2Å-5Å, 5Å −10Å, and 10Å - 15Å) are shown in figure 3 below.

Figure 3:

Representative frames for each of the three distance regimes. Left: representative frame for 2Å-5Å Tyr-dyad distance. Center: representative frame for 5Å-10Å Tyr-dyad distance. Right: representative frame for 10Å-15Å Tyr-dyad distance. The black vertical lines indicate the boundaries between different representative frames.

In the closest distance regime, which only occurs in the monoprotonated states, Tyr 71 is directly interacting with the Asp dyad. At the further distances, based on the representative frames, there is no clear interaction between the dyad and Tyr 71.

Differences in water residence between different protonation states.

In the hypothesized general acid base mechanism for BACE-1, a bridging water facilitates a proton transfer allowing for cleavage of substrate.^15,16 It is unclear the role pH plays in this catalysis, and why the activity of BACE-1 drops so quickly below pH 3.5 and above pH 5.5. It has been hypothesized that water may be a limiting factor in catalysis outside of the pH range of high activity.¹⁸ It is also possible that Tyr 71, by being closer to the Asp dyad in the monoprotonated states (figure 3), stabilizes the catalytic water molecule. To examine these hypotheses, we have calculated the residence time of water for the more prevalent monoprotonated state (32p 228d), the doubly protonated state and the doubly deprotonated state. To examine the effect of having Tyr 71 very close to the dyad on water dynamics, we have also calculated these values for frames for which Tyr 71 was within five Å of the Asp dyad. This is all shown in table 2 below:

Table 2:

hydration number, active water lifetime, residence time and distance of Asp dyad to closest water for monoprotonated (32p 228d), doubly protonated (32p 228p) and doubly deprotonated (32d 228d) states as well as monoprotonated state frames in which Tyr 71 was within five Å of the Asp dyad (32p 228d*). Active water lifetime is defined as the continuous length of time the water closest to the dyad remains the closest water. Residency is defined as being within 3.5 A of the Asp dyad, which is defined as the oxygen of the water molecule to the center of mass of the four total titratable protons of Asp 32 and Asp 228. Distance of dyad to closest water is defined as the distance between the center of mass of the water molecule and the center of mass of the oxygens and hydrogens on the Asp dyad.

State	Number of water present in first hydration shell	Active water lifetime (ns)	Residence time for all water (ns)	Distance of dyad to closest water (Å)
32p 228d	2.57 ± 1.4	0.16 ± 0.17	1.25 ± 0.15	1.92 ± 0.16
32p 228p	4.35 ± 1.8	0.07 ± 0.08	0.87 ± 0.09	1.72 ± 0.08
32d 228d	6.16 ± 1.7	0.03 ± 0.05	1.56 ± 0.18	1.86 ± 0.08
32p 228d*	2.00 ± 1.0	0.29 ± 0.12	1.49 ± 0.10	1.90 ± 0.09

Based on the number of water present in the first hydration shell, combined with the lack of discrepancy between distance of water to dyad, there is clearly water present in all three states. The only statistically significant difference between 32p 228d and the two non-active states (32p 228p and 32d 228d) initially appears to be the residence time for all waters. However, subsampling for just the frames in which Tyr 71 is within five Å of the Asp dyad, the active water lifetime, or how long a single water molecule on average remains engaged with the Asp dyad, is significantly longer for the catalytically active state than either of the non-active states. This supports the hypothesis that Tyr 71, when it is close to the dyad, is stabilizing the water for catalysis.

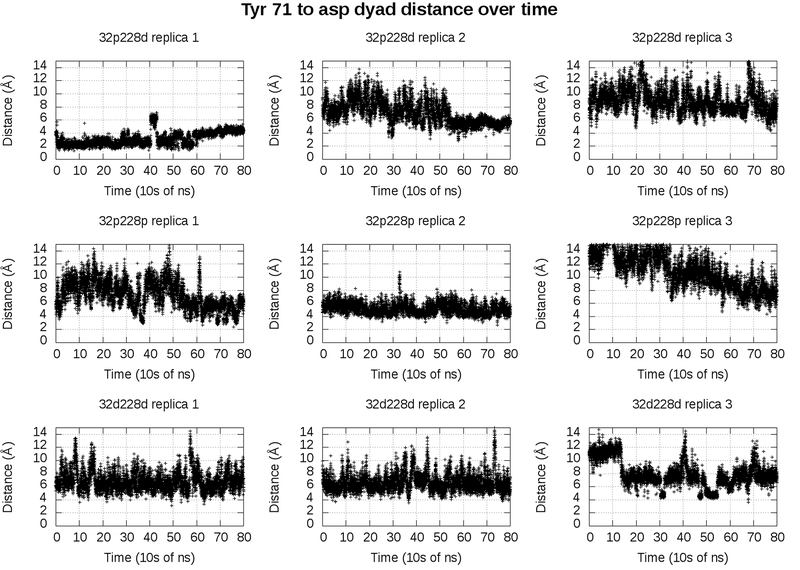
This strategy of subsampling frames in which Tyr 71 is within 5 Å of the Asp dyad is only valid if the two different distances represent two different metastable states. If this is the case, the frames in which Tyr is within five Å of the Asp dyad will occur consecutively in the trajectory. If they do not, then the apparent difference in distances is likely due to random variance, and the mean of all frames combined is the more relevant value. Figure 4 shows the Tyr-dyad distance over time in our catalytically active state and our two catalytically inactive states.

Figure 4:

Distance of Tyr 71 to the Asp dyad in 32p 228d (top), 32p 228p (middle), and 32d228d (bottom). Replica 1, replica 2 and replica 3 each represent a different 800 ns trajectory. Distance is defined as hydrogen of the Tyr 71 side chain to the center of mass of the carboxylate oxygen atoms of the Asp dyad side chains.

In both replica 1 and replica 2 of the catalytically active state (figure 4, top left and top center), there are stretches of over hundreds of nanoseconds consecutively in which Tyr 71 is within five Å of the Asp dyad. This validates our subsampling approach, as it appears that BACE-1 has two dominant configurations in the catalytically active state. In one of these states, the state in which the Tyr-dyad distance is less than five Å, Tyr 71 appears to stabilize the water.

Conclusions:

Based on our CpH simulations and knowledge of the experimental pK_as, 32p 228d should be the most prevalent at the pH of greatest in vivo activity. In this 32p 228d state, the water that is in the active site remains proximal to the active site for longer. It is beyond the scope of this work to attempt to measure the kinetics and timescale of the proton transfer, but it is possible that the water is not able to stay long enough in the fully protonated or fully deprotonated states for transfer to occur. The stabilization of water in 32p 228d appears to be due to a conformational change in which the Tyr 71 flap moves very close to and interacts with the aspartyl dyad. This conformational change was not observed in the non-catalytically active protonation states. This indicates that the extra time which water can spend engaged with the dyad due to this anchoring by Tyr 71 allows for optimal proton transfer. Given these results as well as previous studies which indicate the importance of Tyr 71 in BACE-1^17,18,21, focus on inhibitors that are capable of disrupting the Tyr 71-Asp dyad interaction will likely aid in combating AD via BACE-1 inhibition.