Forming a Moon with an Earth-like composition via a Giant Impact

Abstract

In the giant impact theory, the Moon forms from debris ejected into an Earth-orbiting disk by the collision of a large planet with the early Earth. Prior impact simulations predict that much of the disk material originates from the impacting planet. However, the Earth and Moon have essentially identical oxygen isotope compositions. This has been a challenge for the impact theory, because the impactor’s composition would have likely differed from that of the Earth. Here we simulate impacts involving larger impactors than previously considered. We show these can produce a disk with the same composition as the planet’s mantle, consistent with Earth-Moon compositional similarities. Such impacts require subsequent removal of angular momentum from the Earth-Moon system through a resonance with the Sun as recently proposed.

The oblique, low-velocity impact of a roughly Mars-mass planet with the Earth can produce an iron-depleted disk with sufficient mass and angular momentum to later produce our iron-poor Moon, while also leaving the Earth-Moon system with roughly its current angular momentum (1-3). A common result of simulations of such impacts is that the disk forms primarily from material originating from the impactor’s mantle. The silicate Earth and the Moon share compositional similarities, including in the isotopes of oxygen (4), chromium (5), and titanium (6). These would be consistent with prior simulations if the composition of the impactor’s mantle was comparable to that of the Earth’s mantle. It had been suggested that this similarity would be expected for a low-velocity impactor with an orbit similar to that of the Earth (4, 7-8). However, recent work (9) finds this is improbable given the degree of radial mixing expected during the final stages of terrestrial planet formation (10). Explaining the Earth-Moon compositional similarities would then require post-impact mixing between the vaporized components of the Earth and the disk before the Moon forms (9), a potentially restrictive requirement (11).

A recent development is the work of Cuk and Stewart (12-13), who find that the angular momentum of the Earth-Moon system could have been decreased by about a factor of two after the Moon-forming impact due to the evection resonance with the Sun. This would allow for a broader range of Moon-forming impacts than previously considered, including those involving larger impactors.

Prior works (1-3, 14) focus primarily on impactors that contain substantially less mass than that of the target, with impactor masses M_imp ∼ 0.1 to 0.2M_T, where M_T ≈ M_⊕ is the total colliding mass and M_⊕ is the Earth’s mass. If the target and impactor have different isotopic compositions, creating a final disk and planet with similar compositions then requires that the disk be formed overwhelmingly from material derived from the target’s mantle. However, gravitational torques that produce massive disks tend to place substantial quantities of impactor material into orbit (2-3).

Here we consider a larger impactor that is comparable in mass to that of the target itself. A final disk and planet with the same composition are then produced if the impactor contributes equally to both, which for large impactors is possible even if the disk contains substantial impactor-derived material because the impactor also adds substantial mass to the planet. For example, in the limiting case of an impactor whose mass equals that of the target and in the absence of any pre-impact rotation, the collision is completely symmetric, and the final planet and any disk that is produced will be composed of equal parts impactor and target-derived material and can thus have the same silicate compositions even if the original impactor and target did not.

We describe the impactor and target as differentiated objects with iron cores and overlying silicate mantles (16). We simulated impacts using smooth particle hydrodynamics (SPH; Fig. 1) as in (1-3, 15-16), representing the impactor and target with 300,000 SPH particles. Each particle was assigned a composition (either iron for core particles or dunite for mantle particles) and a corresponding equation of state (17-18), and its evolution was tracked with time as it evolved due to gravity, pressure forces, and shock dissipation.

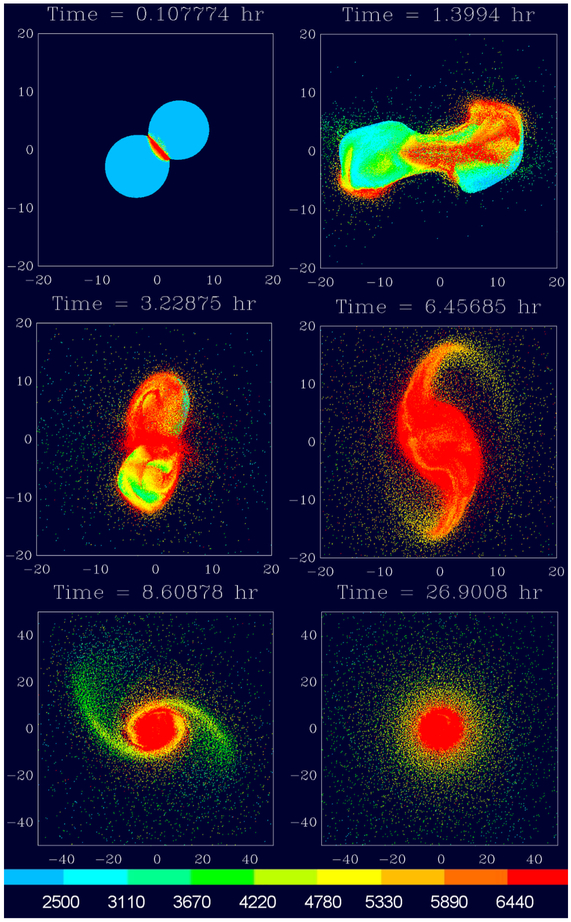
Figure 1.

An SPH simulation of a moderately oblique, low-velocity (v_∞ = 4 km/sec) collision between an impactor and target with similar masses (run 31 from Table 1). Color scales with particle temperature in Kelvin, per color bar, with red indicating temperatures > 6440 K. All particles in the 3D simulation are overplotted. Time is shown in hours, and distances are shown in units of 10³ km. After the initial impact, the planets re-collided, merged, and spun rapidly. Their iron cores migrated to the center, while the merged structure developed a bar-type mode and spiral arms (24). The arms wrapped up and finally dispersed to form a disk containing about 3 lunar masses whose silicate composition differed from that of the final planet by less than 1%. Due to the near symmetry of the collision, impactor and target material are distributed approximately proportionately throughout the final disk, so that the disk’s δf_T value does not vary appreciably with distance from the planet.

We simulate a given impact for approximately 1 day of simulated time. We use an iterative procedure (1-3, 16) to determine whether each particle at the end of the simulation is in the planet, in bound orbit around the planet (i.e., in the disk), or escaping. Given the calculated disk mass, M_D, and angular momentum, L_D, we estimate the mass of the moon that would later form from the disk, M_M using a conservation of mass and angular momentum argument (19-20). Assuming that the disk will later accumulate into a single Moon at an orbital distance of about 3.8R_⊕, where R_⊕ is the Earth’s radius, (19-20)

$$\frac{M_M}{M_D}\approx 1.9\left(\frac{L_D}{M_D\sqrt{2.9G{M}_{\oplus }{R}_{\oplus }}}\right)-1.1-1.9\left(\frac{M_{esc}}{M_D}\right)$$ (1)

where M_esc is the mass that escapes from the disk as the Moon accretes. To estimate M_M, we use eqn. (1) and make the favorable assumption that M_esc = 0.

We track the origin (impactor vs. target) of the particles in the final planet and the disk. To quantify the compositional difference between the silicate portions of the disk and planet, we define a deviation percentage

$$\delta f_T\equiv [F_{D,tar}∕F_{P,tar}-1]\times 100,$$ (2)

where F_D,tar and F_P,tar are the mass fractions of the silicate portions of the disk and the planet derived from the target’s mantle (21). Identical disk-planet compositions have δf_T = 0, whereas a disk that contains fractionally more (less) impactor-derived silicate than the final planet has δf_T < 0 (δf_T > 0).

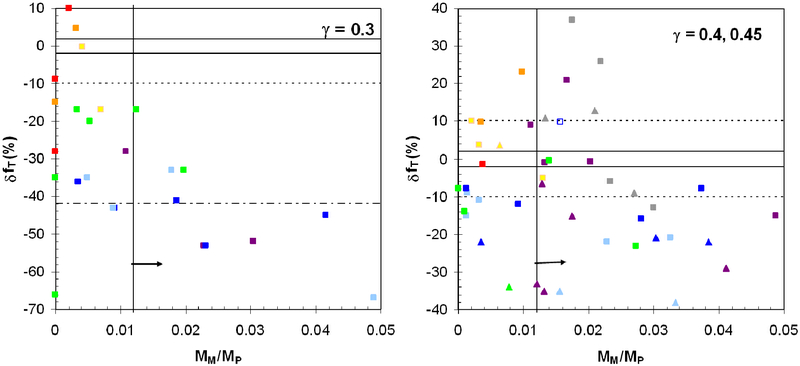
Prior impact simulations (1-3, 14, 16) that consider γ ≡ M_imp/M_T ≈ 0.1 to 0.2 produce disks with – 90% ≤ δf_T ≤ −35% for cases with M_M > M_L, where M_L is the Moon’s mass. Figures 1, 2, and Table 1 show results with larger impactors having γ = 0.3, 0.4 and 0.45. As the relative size of the impactor (γ) is increased, there is generally a closer compositional match between the final disk and the planet. For γ = 0.4, some disks have both sufficient mass and angular momentum to yield the Moon and nearly identical silicate compositions to that of the final planet; others even contain proportionally more silicate from the target than from the impactor (δf_T > 0). We expect successful cases such as those in Fig. 1 and Table 1 could be identified across the 0.4 ≤ γ ≤ 0.5 range.

Figure 2.

Compositional difference between the disk and final planet (δf_T, eqn. 2) produced by simulations with γ = 0.3 (left) and γ = 0.4 (right, triangles) and 0.45 (right, squares) versus the predicted mass of the moon that would accrete from each disk (M_M, eqn. 1) scaled to the final planet’s mass (M_P). Note the change in y-axis scales between the two plots. Grey, purple, dark blue, light blue, green, yellow, orange, and red points correspond to v_imp/v_esc = 1.0, 1.1, 1.2, 1.3, 1.4, 1.6, 1.8, and 2.0, respectively. The open square is run 60* from Table 1 that includes pre-impact rotation. Forming an appropriate mass Moon mass requires M_M/M_P > 0.012, the region to the right of the vertical solid line. Constraints on δf_T needed to satisfy Earth-Moon compositional similarities are shown by horizontal lines for oxygen (solid), titanium (dotted), and chromium (dot-dashed), assuming a Mars-composition impactor.

Table 1: Properties of candidate impacts.

All cases had a total colliding mass M_T = 1.04M_⊕. Shown are the impactor-to-total mass ratio (γ), scaled impact parameter (b), impact velocity relative to the escape velocity (v_imp/v_esc), relative velocity at infinity (v_∞), disk mass in lunar masses (M_D/M_L), disk angular momentum in units of that of the current Earth-Moon system (L_EM = 3.5 × 10⁴¹ g cm² s⁻¹), fraction of the disk mass in iron (M_FE/M_D), final bound system angular momentum in units of L_EM, the post-impact rotational period of the planet in hours (T), the predicted mass of the moon in lunar masses that would accrete from the disk (M_M/M_L), and the percent compositional deviation of the disk from the final planet (δf_T). Run 60* had a target with a 3 hour rotational day prior to the impact, with the pre-impact spin vector anti-aligned to the impact angular momentum vector. The values of T found here are consistent with successful evection models presented in (12), in which the resonance removes angular momentum from the Earth-Moon system until a value comparable to L_EM is achieved.

run	γ	b	vimp/vesc	v∞ (km/sec)	MD/ML	LD/LEM	MFE/MD	LF/LEM	T (hr)	MM/ML	δfT
1	0.40	0.60	1.0	0.0	2.94	0.51	0.01	2.32	2.2	2.17	−9%
3	0.40	0.55	1.0	0.0	1.74	0.29	0.02	2.18	2.2	1.10	11%
4	0.40	0.55	1.1	4.0	2.72	0.42	0.05	2.39	2.0	1.41	−15%
6	0.40	0.50	1.0	0.0	2.16	0.39	0.02	1.96	2.6	1.71	13%
7	0.40	0.50	1.1	4.0	1.93	0.30	0.05	2.17	2.2	1.05	−6.6%
11	0.45	0.35	1.6	10.9	2.30	0.31	0.06	1.89	2.0	0.96	−5%
14	0.45	0.40	1.1	4.0	1.87	0.30	0.03	1.77	2.7	1.09	−1%
17	0.45	0.40	1.4	8.6	2.88	0.39	0.03	2.22	2.0	1.09	−0.3%
31	0.45	0.55	1.1	4.0	3.03	0.47	0.02	2.45	2.0	1.64	−0.8%
32	0.45	0.55	1.2	5.8	5.06	0.78	0.03	2.52	2.1	2.89	−8%
35	0.45	0.60	1.0	0.0	2.84	0.47	0.01	2.37	2.1	1.88	−6%
39	0.45	0.65	1.0	0.0	3.63	0.60	0.00	2.61	2.0	2.40	−13%
40	0.45	0.65	1.1	4.0	5.46	0.90	0.01	2.63	2.1	3.75	−15%
43	0.45	0.70	1.0	0.0	5.58	0.97	0.00	2.71	2.2	4.39	−15%
60*	0.45	0.55	1.2	5.7	2.39	0.37	0.05	2.15	2.2	1.26	+10%

One can roughly estimate how small ∣δf_T ∣ needs to be for consistency with observed geochemical similarities between the silicate Earth and the Moon. The impactor and target’s original compositions are, of course, unknown. However results of planet accretion simulations (10), in combination with the assumption that planetary embryo composition varied linearly with heliocentric distance, have been used to estimate that the average deviation of a large impactor’s composition from that of the final planet was about half the observed compositional difference between Earth and Mars. We nominally adopt a “Mars-like” composition for our impactor, and use a simple mass balance argument (21, 16) to estimate the required values for δf_T. The most restrictive constraint is from oxygen (4), which requires ∣δf_T ∣ < 2% assuming a Mars-like impactor; accounting for the titanium (6) and chromium (5) similarities between the Earth and Moon requires ∣δf_T∣ < 10% and ∣δf_T∣ < 42%, respectively. There is considerable uncertainty in these estimates due to both uncertainties in the compositional measurements and probable scatter in impactor compositions (16). For example, the relatively broad distribution of impactor compositions found by (9) implies that the impactor could have been substantially more similar compositionally to the Earth than Mars, which would relax the oxygen constraint to ∣δf_T∣ less than about 10 to 15% (16).

Table 1 lists impacts that produce an iron-poor moon of at least a lunar mass and ∣δf_T∣ < 15% as our most promising candidates. Several disk-planet pairs are compositionally similar enough (δf_T ∼ 0%) to explain the Earth-Moon oxygen similarity even assuming a Mars-like impactor. The candidate impacts span a relatively broad range of impact parameters, with 0.35 ≤ b ≤ 0.7 (where b = sin ξ, ξ is the impact angle, and b = 1 is a grazing impact). For randomly oriented impacts (22), about 40% of all impacts would have b in this range. The impact velocity, v_imp, is a function of the mutual escape velocity of the colliding objects, v_esc, and their relative velocity at large separation, v_∞, with $v_{imp}^2=v_{esc}^2+v_{\infty }^2$. The impacts in Table 1 have 1.0 ≤ v_imp/v_esc ≤ 1.6, corresponding to 0 ≤ v_∞(km s⁻¹) ≤ 11. These v_∞ values are in good agreement with terrestrial accretion simulations (23), which find 〈v_∞〉 ≈4 to 5 km s⁻¹, with a typical range from 1 to 10 km s⁻¹ for large impactors with M_imp > 0.1M_⊕. Similar models (22, 16) have found that the ratio of the mass of the largest impactor to collide with a planet (M_lgst) to the final planet’s mass (M_P) is 〈M_lgst M_p〉 ≈ 0.3 ± 0.08 for planets with M_P > 0.5M_⊕, with approximately 20% of such planets experiencing a final collision with γ ≥ 0.4.

Our impactors and targets are not rotating prior to collision. Planetary embryos would have been rotating with randomly oriented spin axes due to prior impacts (22). When the orientation of a pre-impact spin axis differs substantially from the angular momentum vector of the impact, the resulting disk mass and angular momentum are broadly similar to cases without pre-impact rotation (3). However, it is also possible to find similar outcomes for the extreme case of perfect alignment between the pre-impact rotational axis and the impact angular momentum vector (e.g., Table 1, run 60*).

The impacts here differ greatly from the canonical Moon-forming impact with γ ∼ 0.1 to 0.15 (1-2). Here the Moon-forming collision involves two planetary embryos of comparable mass, similar in some respects to the collision invoked for the origin of Pluto-Charon (24). Compared to disks produced by the canonical impact, the disks here are hotter [those in Table 1 contain between 50 and 90% of their mass in vapor, vs. 10 to 30% vapor in the canonical case, (2)] and typically more massive. Recent work (25) suggests that eqn. (1) overestimates M_M for a given disk M_D and L_D, implying that more massive initial disks may be needed to form a lunar mass Moon.

The impacts here can remove the need for an improbable compositional match between the impactor and target or for post-impact equilibration between the planet and disk (16). However, they all produce a planet-disk system whose angular momentum is substantially higher than that in the current Earth and Moon (L_EM). They thus require that the system angular momentum is decreased by about a factor of 2 to 2.5 after the Moon forms due to capture into the evection resonance with the Sun as proposed by (12-13). Cuk and Stewart (13) find that reducing the system angular momentum to a value consistent with L_EM requires a specific (and relatively narrow) range for the ratio of the tidal parameters for the Moon, (k₂/Q)_M (where k₂ is the degree 2 Love number and Q is the tidal quality factor), compared to those in the Earth, (k₂/Q)_⊕, at the time of the resonance. It is also possible that the duration of occupancy of the Moon in the evection resonance as the Moon’s orbit contracts may vary with the specifics of the tidal model considered, a potential sensitivity which has not yet been assessed.