Phase-plane geometries in coupled enzyme assays

Abstract

The determination of a substrate or enzyme activity by coupling one enzymatic reaction with another easily detectable (indicator) reaction is a common practice in the biochemical sciences. Usually, the kinetics of enzyme reactions is simplified with singular perturbation analysis to derive rate or time course expressions valid under the quasi-steady-state and reactant stationary state assumptions. In this paper, the dynamical behavior of coupled enzyme catalyzed reaction mechanisms is studied by analysis of the phaseplane. We analyze two types of time-dependent slow manifolds – Sisyphus and Laelaps manifolds – that occur in the asymptotically autonomous vector fields that arise from enzyme coupled reactions. Projection onto slow manifolds yields various reduced models, and we present a geometric interpretation of the slow/fast dynamics that occur in the phase–planes of these reactions.

1. Introduction

Biochemical reactions inside cells are generally catalyzed by enzymes, which accelerate the conversion of substrates into products under physiologi-cal conditions. Most of the complex chemical processes occurring inside cells or organisms that are necessary for the maintenance of life are catalyzed by enzymes. Consequently, the experimental measurement of enzyme activity through in vitro assays plays a substantial role in understanding the dy-namics of biochemical processes inside cells [1]. Often however, the activity of numerous enzymes cannot be observed experimentally through direct ob-servation of their reaction. Instead, these non-observable enzyme catalyzed reactions must be observed indirectly by coupling it to another enzyme cat-alyzed reaction that is used to indicate the progress of the non-observable reaction. The observable enzyme catalyzed reaction is known as the indicator or monitor reaction [2]. The non-observable enzyme catalyzed reaction can be of varying complexity; it may contain linear inhibition or exhibit enzyme degradation [3]. Regardless of the nature of the non-observable reaction, there are two general mechanisms employed to couple enzyme reactions: the coupled auxiliary enzyme reaction mechanism [4], and zymogen activation coupled to its enzyme catalyzed reaction [5].

To set the stage, and explain how the coupling mechanisms between a non-observable and an indicator reaction operate, let us assume (for simplicity) that the non-observable reaction follows the Michaelis–Menten (MM) singleenzyme, single-substrate mechanism of action [6]

$$E_1+S_1\underset{k_{-1}}{\overset{k_1}{\rightleftharpoons }}{C}_1\stackrel{k_2}{\to }{E}_1+S_2,$$ (1)

from which we need to indirectly measure the activity of E₁ through means of an indicator reaction (S₁ denotes the substrate of the non-observable reaction, C₁ denotes the complex, and S₂ is the substrate generated in the non-observable reaction). In the coupled auxiliary enzyme reaction mechanism, the product of the non-observable reaction (S₂) is catalyzed by an auxiliary enzyme, E₂, in the indicator reaction [4]:

$$E_2+S_2\underset{k_{-3}}{\overset{k_3}{\rightleftharpoons }}{C}_2\stackrel{k_4}{\to }{E}_2+P.$$ (2)

In the above mechanism, k₁,k₋₁,k₃,k₋₃,k₂ and k₄ are rate constants. The coupled auxiliary enzyme reaction is by far the most common type of coupled assay, and there are many examples reported in the literature (see, Tables II and III in [3] and Table 4.5 in [2]). One specific example is the phosphoryla- tion of glucose to glucose-6 phosphate. The primary reaction is catalyzed by hexokinase, and is non-observable in typical steady-state kinetic experiments. Therefore, to investigate the hexokinase activity, its reaction is coupled to the catalytic conversion of glucose-6 phosphate into 6-P gluconolactone with the enzyme glucose 6-P dehydrogenase, which serves as the indicator reaction.

A less common coupled assay is the zymogen activation coupled to its enzyme catalyzed reaction. In a zymogen activation reaction coupled to its enzyme reaction, the product of the non-observable reaction is the indicator enzyme, E₂, which binds with the auxiliary substrate, S₂, to form a product [5]:

$$E_1+S_1\underset{k_{-1}}{\overset{k_1}{\rightleftharpoons }}{C}_1\stackrel{k_2}{\to }{E}_1+E_2,$$ (3)

$$E_2+S_2\underset{k_{-3}}{\overset{k_3}{\rightleftharpoons }}{C}_2\stackrel{k_4}{\to }{E}_2+P.$$ (4)

Reactions of the form (3)-(4) often occur in vivo. For example, the phys- iologic response to a vascular lesion entails a number of enzymatic steps that lead to clot formation. These enzymatic steps are a cascade of enzyme catalyzed reactions that follow a sequence of zymogen activation steps as de-scribed above [7]. In the laboratory, the activity of thrombin, one of the blood coagulation enzymes, has been studied with a zymogen activation coupled to an enzyme catalyzed reaction assay. Thrombin catalyzes the activation of protein P, which is non-observable using steady-state kinetic laboratory assays. However, the formation of p-nitroaniline from substrate S2266 is cat-alyzed by activated protein P, and is observable through steady-state kinetic progress curve experiments. By coupling the two reactions, thrombin func-tion is studied with a zymogen activation coupled to its enzyme catalyzed reaction [8].

As mentioned, the overall aim of an assay is to measure the enzyme activity of a specific reaction. When the reaction can be observed experimentally, the MM equation, (5), is usually employed to measure the enzyme kinetics:

$$\frac{dp}{dt}=\frac{V_1{s}_1}{K_{M_1}+s_1}.$$ (5)

In (5), V₁ is the limiting rate of the primary reaction, and $K_{M_1}$ is its Michaelis constant [9, 10]. The Michaelis constant is defined operationally as the con-centration of the substrate at which the rate of the reaction is half of the limiting rate; that is, dp/dt = 0.5V₁. The enzyme specificity is character-ized by the specificity constant, which is the result of dividing k₂ by $K_{M_1}$ [11, 12, 13]. The kinetic constants (V₁ and $K_{M_1}$) are generally estimated through initial rate or time course experiments [14, 2] by mathematically solving an inverse problem [15, 16]. In the case of coupled enzyme assays, the caveat with this procedure is that the primary reaction is not experimentally observable. Thus, V₁ and $K_{M_1}$ need to be estimated through means of indirect measures of data recorded from the indicator reaction. From a theo-retical point of view, the demand is obvious: a mathematical theory must be developed that is capable of accurately describing the relationship between the non-observable reaction and the indicator reaction. Most enzyme kinetic analyses developed to study coupled enzyme assays assume that the coupled enzyme reactions follow first-order kinetics [17, 18, 19, 20, 21]. The limiting fact with this assumption is that first order models are typically only valid during the lag time of the reaction, which is effectively the length of time it takes before measurable formation rates of P become experimentally detectable. If the indicator reaction is fast, then first order models are only valid over very small timescales; this limits the duration of time over which useful (in the context of the inverse problem) experimental measurements can be made.

In order to develop experimental protocols that yield an accurate quantification of enzyme activity in a non–observable reaction, a mathematical model must be developed, conditions for its validity must be established, and timescales that characterize the lengths of transient and steady–state regimes must be approximated. Qualitatively, the most useful tool that can be employed to study the mathematical structure of a chemical reaction is phase–plane analysis; in contrast, the most influential quantitative tool is the combination of scaling and asymptotic analysis [22]. The single–enzyme, single–substrate MM reaction is well understood in terms of scaling and asymptotic analyses [23, 24, 25], and the geometric picture of the phase– plane dynamics is also well defined [26]. While scaling/asymptotic analysis has recently been applied to coupled enzyme reactions [5, 4], a clear picture of the phase–plane geometry is lacking. The phase–plane description of a reaction is useful in that it illustrates the reaction visually as a two-dimensional play whose characters are trajectories, attracting manifolds, and fixed points. The overall goal of this paper is to describe the previously mentioned coupled reaction mechanisms geometrically, and illustrate what certain results from scaling analysis say about what is happening in the phase–plane. The unique feature of the phase-plane descriptions of the reaction mechanisms discussed in this work is that the indicator reaction (in both reactions) is described by an asymptotically autonomous vector field [27]. Consequently, while the phase–plane analysis of the single–enzyme, single–substrate MM reaction presents a phase-plane with fixed points and manifolds that are stationary, the phase–planes of the indicator reactions studied in this paper are best analyzed by moving nullcline analysis. In the sections that follow, we illustrate the geometric interpretation of the quasi-steady-state assumption (QSSA), and the reactant-stationary assumption (RSA) of the indicator re-actions utilized in the auxiliary enzyme assay and zymogen activation assay.

2. Analysis of the coupled auxiliary enzyme reaction mechanism

We start our analysis with the coupled auxiliary enzyme reaction mec-hanism represented by the chemical equations (1)–(2), which consists of a single-substrate, single-enzyme non-observable reaction followed by another single-substrate, single-enzyme observable reaction (indicator reaction). In this mechanism, the product of the non-observable reaction becomes the substrate of the indicator reaction. By applying the law of mass action to (1)–(2), we obtain a nonlinear system of differential equations with three conservation laws [4]. We begin our analysis by scaling the mass action equations.

2.1. Scaling of the coupled auxiliary enzyme reaction

After eliminating redundant expressions using the conserved quantities $s_1^0,e_1^0$, and $e_2^0$, the mass action equations that model the coupled auxiliary enzyme mechanism are:

$${\dot{s}}_1=-k_1\left(e_1^0-c_1\right)s_1+k_{-1}{c}_1,$$ (6a)

$${\dot{c}}_1=k_1\left(e_1^0-c_1\right)s_1-\left(k_{-1}+k_2\right)c_1,$$ (6b)

$${\dot{s}}_2=-k_3\left(e_2^0-c_2\right)s_2+k_{-3}{c}_2+k_2{c}_1,$$ (6c)

$${\dot{c}}_2=k_3\left(e_2^0-c_2\right)s_2-\left(k_{-3}+k_4\right)c_2.$$ (6d)

The lowercase letters in (6) denote the concentrations of the uppercase letters in (1)–(2). Notice equations (6a)-(6b) are autonomous and independent of s₂ and c₂. In this regard, the first catalyzed reaction drives the second catalyzed reaction; thus, the indicator reaction can be viewed as a non-autonomous system with forcing term k₂c₁(t). Moreover, since lim_t→∞ c₁ = 0, the vector field that governs the flow of the indicator reaction is asymptotically autonomous [27].

The complete catalyzed coupled auxiliary enzyme reaction (6) can be characterized by three timescales ($t_{c_1},t_{s_1}$, and $t_{s_2}$) [4]:

$$t_{c_1}\equiv \frac{1}{k_1\left(K_{M_1}+s_1^0\right)},t_{s_1}\equiv \frac{K_{M_1}+s_1^0}{V_1},t_{s_2}\equiv \frac{K_{M_2}+s_1^0}{V_2}.$$ (7)

In (7), $K_{M_1}$ and $K_{M_2}$ denote the Michaelis constants

$$K_{M_1}\equiv \frac{k_{-1}+k_2}{k_1},K_{M_2}\equiv \frac{k_{-3}+k_4}{k_3},$$ (8)

V₁ and V₂ are the limiting rates

$$V_1\equiv k_2{e}_1^0,V_2\equiv k_4{e}_2^0,$$ (9)

and $s_2^{\max }$ denotes the maximum concentration of unbound s₂. The timescales $t_{c_1}$ and $t_{s_1}$ define, respectively, the temporal order of magnitude of the initial fast transient and the approximate length of non-observable reaction [23]. Likewise, $t_{s_2}$ is a rough estimate of the indicator reaction’s depletion timescale when it is sufficiently slow. We cautiously note that $t_{s_2}$ has no direct physical interpretation when the indicator reaction is fast; however, $t_{s_2}$ is useful in terms of scaling analysis, and we will illustrate this utility in the upcoming sections.

The slow/fast dynamics of autonomous vector fields is typically the result of disparate timescales that admit the existence of a slow invariant manifold. In the non-autonomous context, slow manifolds are generally referred to as slow integral manifolds. For simplicity, we will use the term “slow manifold” to describe both slow manifolds (the autonomous version) and slow integral manifolds (the non-autonomous version). To establish the presence of slow manifolds, we rescale the mass action equations with respect to the dimensionless variables

$$T=\frac{t}{t_{s_1}},{\overline{s}}_1=\frac{s_1}{s_1^0},{\overline{c}}_1=\frac{\left(K_{M_1}+s_1^0\right)}{e_1^0{s}_1^0}{c}_1,$$ (10a)

$$\tau =\frac{t}{t_{s_2}},{\overline{s}}_2=\frac{s_2}{s_2^{\max }},{\overline{c}}_2=\frac{\left(K_{M_2}+s_2^{\max }\right)}{e_2^0{s}_2^{\max }}{c}_2.$$ (10b)

In dimensionless form, the mass action equations (6) that govern the non-observable reaction are:

$$\frac{d{\overline{s}}_1}{dT}=\left(1+{\sigma }_1\right)\left(1+{\kappa }_1\right)\left[\left(\frac{{\sigma }_1}{1+{\sigma }_1}{\overline{c}}_1-1\right){\overline{s}}_1+\frac{{\alpha }_1}{1+{\sigma }_1}{\overline{c}}_1\right],$$ (11a)

$$\epsilon \frac{d{\overline{c}}_1}{dT}=\left(1+{\sigma }_1\right)\left(1+{\kappa }_1\right)\left[\left(1-\frac{{\sigma }_1}{1+{\sigma }_1}{\overline{c}}_1\right){\overline{s}}_1-\frac{1}{1+{\sigma }_1}{\overline{c}}_1\right].$$ (11b)

The dimensionless equations that describe the indicator reaction are:

$$\frac{d{\overline{s}}_2}{d\tau }=\left(1+{\sigma }_2\right)\left(1+{\kappa }_2\right)\left[\left(\frac{{\tilde{\sigma }}_2}{1+{\tilde{\sigma }}_2}{\overline{c}}_2-1\right){\overline{s}}_2+\frac{{\alpha }_2}{1+{\tilde{\sigma }}_2}{\overline{c}}_2\right]+\mathrm{\Lambda }{\delta }_s{\overline{c}}_1,$$ (12a)

$${\lambda }^{\max }\frac{d{\overline{c}}_2}{d\tau }=\left(1+{\sigma }_2\right)\left(1+{\kappa }_2\right)\left[\left(1-\frac{{\tilde{\sigma }}_2}{1+{\tilde{\sigma }}_2}{\overline{c}}_2\right){\overline{s}}_2-\frac{1}{1+{\tilde{\sigma }}_2}{\overline{c}}_2\right].$$ (12b)

The variables ${\tilde{\sigma }}_2$, σ₁, σ₂, κ₁, and κ₂ are given by,

$${\tilde{\sigma }}_2\equiv \frac{s_2^{\text{max}}}{K_{M_2}},{\sigma }_1\equiv \frac{s_1^0}{K_{M_1}},{\sigma }_2\equiv \frac{s_1^0}{K_{M_2}},{\kappa }_1\equiv \frac{k_{-1}}{k_2},{\kappa }_2\equiv \frac{k_{-3}}{k_4},$$ (13)

and the constants α₁ and α₂ are dependent on κ₁ and κ₂:

$${\alpha }_1={\kappa }_1/\left(1+{\kappa }_1\right),{\alpha }_2={\kappa }_2/\left(1+{\kappa }_2\right).$$ (14)

The additional constants, ε and λ^max, are dependent on the initial enzyme and maximum substrate concentrations, as well the Michaelis constants

$$\epsilon =\frac{e_1^0}{K_{M_1}+s_1^0},{\lambda }^{\max }=\frac{e_2^0}{K_{M_2}+s_2^{\max }}.$$ (15)

The remaining constants, Λ and δ_S, are ratios:

$$\mathrm{\Lambda }=\frac{s_1^0}{s_2^{\max }},{\delta }_s=\frac{t_{s_2}}{t_{s_1}}.$$ (16)

Scaling the indicator reaction with respect to $\tau =t/t_{s_2}$ is no accident. This is because, as mentioned previously, $t_{s_2}$ gives a very good estimate of the completion timescale corresponding to the indicator reaction when the non-observable reaction is extremely fast in comparison. Moreover, the ratio δ_S should give a good indication of how well the indicator reaction “keeps up” with the non-observable reaction. Since the completion of the indicator reaction cannot occur before the completion of the non-observable reaction, it stands to reason that if δ_S ≪ 1, then the completion of the indicator reaction will occur at roughly the same time as the non-observable reaction [4].

The ratio Λ will be very large if the indicator reaction is fast, since s₂ should quickly bind with e₂ and form product. Consequently, the maximum concentration of unbound s₂ should be much less than the initial non-observable substrate $s_1^0$. In contrast, if the indicator reaction is slow (i.e., if $t_{s_2}\gg t_{s_1}$), then Λ ≈ 1.

If ε, λ^max ≪ 1, then there exist slow manifolds ${\mathcal{M}}_{\epsilon },{\mathcal{M}}_{\lambda }$, such that

$${\dot{s}}_1\simeq -\frac{V_1}{K_{M_1}+s_1}{s}_1,$$ (17a)

$${\dot{s}}_2\simeq -\frac{V_2}{K_{M_2}+s_2}{s}_2+k_2{c}_1,$$ (17b)

are good zeroth order approximations to the mass action equations on the T and τ timescales, respectively. Moreover, after the initial fast transient of the non-observable reaction, equation (17b) becomes

$${\dot{s}}_2\simeq -\frac{V_2}{K_{M_2}+s_2}{s}_2+\frac{V_1}{K_{M_1}+s_1}{s}_1.$$ (18)

The validity of (17a) is well-established [28], and we will not go into the details of this here. Further reduction of (18) is possible when the speeds of the non-observable and indicator reaction significantly differ, and in the subsequent sections we will convey the geometric interpretation of the reduced models that arise from (18) when the indicator reaction is very fast or, in contrast, very slow.

2.2. The coupled auxiliary enzyme reaction exhibits a Sisyphus manifold

Under appropriate conditions, the phase-plane of the indicator reaction exhibits what we call a Sisyphus manifold. What we see computationally is the solution starting on the c₂-nullcline (when experimental initial conditions are prescribed) and essentially moving up and down the c₂-nullcline. Since the c₂-nullcline resembles a hill, we refer to the slow manifold ${\mathcal{M}}_{\lambda }$ (that lies close to the c₂-nullcline) as the Sisyphus manifold, after the Greek mytho-logical king who was sentenced for eternity to push a stone up a hill only to have it roll back down as it neared the top (see FIGURE 1 and MOVIE 1 in the Supplementary Material).

Figure 1: Phase–plane illustration of the Sisyphus manifold for the reaction mechanism (1)–(2).

The numerical solution of the mass action equations (6) (thick black curve that is barely visible) moves up, then down, the c₂-nullcline (dashed red curve) in the phase-plane for the coupled auxiliary enzyme reaction mechanism. Movement is illustrated dynamically in Movie 1 available in the Supplementary Material. The dimensionless units used in the numerical integration of 6) are: $s_1^0=1000,e_1^0=1,e_2^0=1$, k₁ = 1, k₂ = 10, k_-1 = 1, k₃ = 1, k₄ = 10, k_-3 = 1. The concentrations of substrate and complex have been scaled by their numerically-obtained maximum values.

We invoke moving nullcline analysis to geometrically illustrate why solutions roll up and then slide down the c₂-nullcline. Starting with some basic notation, we will denote the respective s₂ and c₂ nullclines as

$$\left\{\left(s_2,c_2\right)\in {ℝ}^2:c_2-\frac{k_3{e}_2^0{s}_2-k_2{c}_1}{k_3{s}_2+k_{-3}}=0\right\}\equiv {\mathcal{N}}_{s_2}^t,$$ (19a)

$$\left\{\left(s_2,c_2\right)\in {ℝ}^2:c_2-\frac{e_2^0}{K_{M_2}+s_2}{s}_2=0\right\}\equiv {\mathcal{N}}_{c_2},$$ (19b)

where the superscript “t” in (19a) denotes the time-dependency of the s₂-nullcline. If we consider snapshots of the s₂–c₂ phase–plane at different points in time (i.e., let t = t_n), we see that the intersection of the nullclines, x^*(t_n),

$${\mathit{x}}^{*}\left(t_n\right)={\mathcal{N}}_{c_2}{\displaystyle \bigcap {\mathcal{N}}_{s_2}^{t=t_n}},$$ (20)

slides, like a bead on a wire, up and down the c₂-nullcline. Algebraically, the coordinates of the intersection “x^*(t)” are

$$s_2^{*}=\frac{K_{M_2}}{V_2-k_2{c}_1}{k}_2{c}_1,c_2^{*}=\frac{k_2{c}_1}{k_4}.$$ (21)

An important observation can be made from (21): as the indicator reaction becomes extremely fast (with respect to the speed of the non-observable reaction), the maximum distance from x^* to the origin becomes negligibly small:

$$S_2^{*},C_2^{*}\approx (0,0).$$ (22)

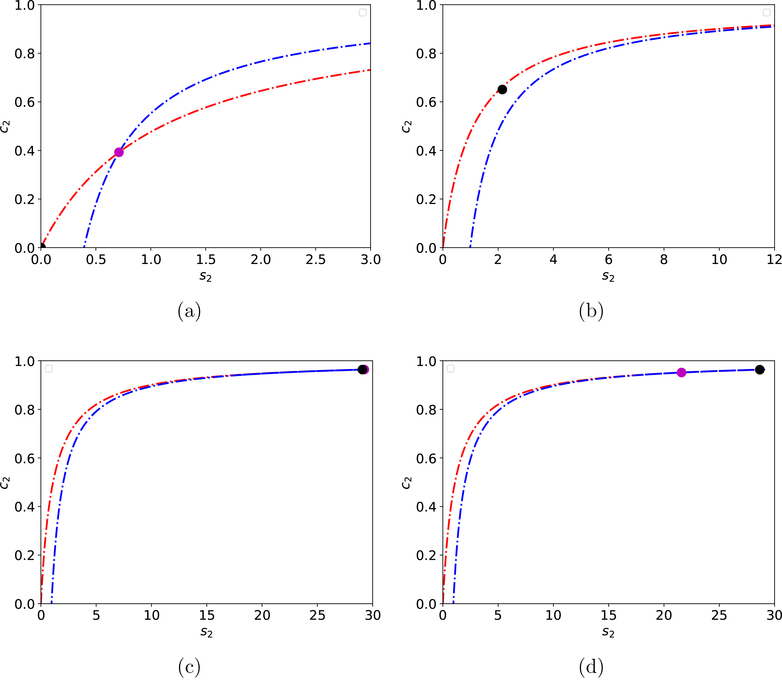
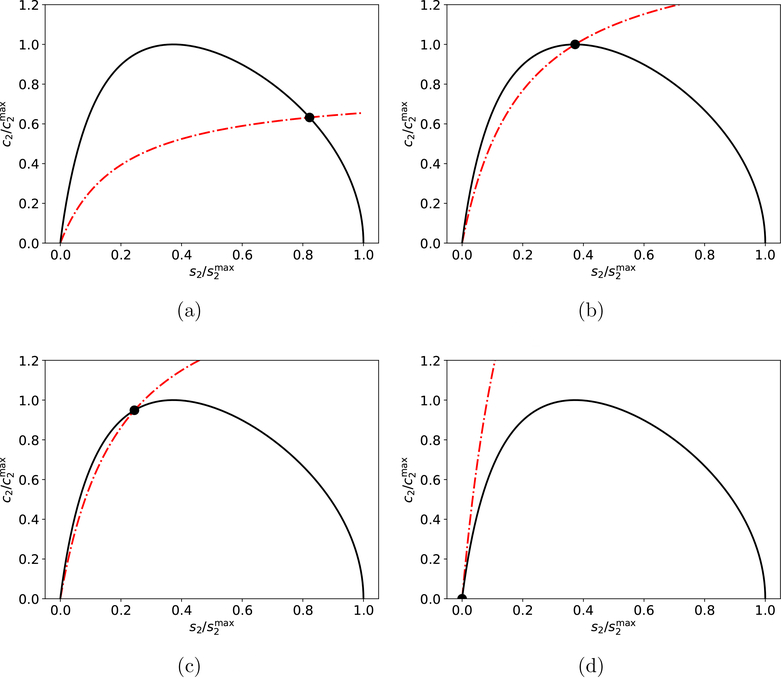
What phase-space trajectories do is follow x^* and, under appropriate conditions (to be defined), the phase-plane trajectory will follow x^* along a path that is extremely close to the c₂-nullcline. This typically occurs in three stages: (1) the trajectory chases the fixed point up the c₂-nullcline, (2) the trajectory “catches” x^*, at which time both s₂ and c₂ reach their maximum values and, (3) the trajectory follows x^* back down the c₂-nullcline (see FIGURES 2a–2d for another visualization of the Sisyphus manifold). Since the relative speed of the indicator reaction determines how far x^* can travel away from the origin, it follows that $s_2^{\max }$ will be much less than $s_1^0$ when the indicator reaction is fast.

Figure 2: Phase–plane illustration of the mechanism responsible for the Sisyphus manifold for the reaction mechanism (1)–(2).

The numerical solution of (6) (black dot) follows the intersection, x^∗ (purple dot) of the nullclines, along a path that can be approximated by the c₂-nullcline (dashed/dotted red curves in panels (a)–(d)). Eventually, the solution catches x^∗ (panel (c)) and then chases x^∗ back down the c₂-nullcline (d). The s₂–nullcline is the dashed/dotted blue curve in (a)–(d). In the panels (a)–(d), the initial conditions and parameter values are: $e_1^0=1,s_1^0=1000$, k₁ = 1, k₂ = 10 and k_-1 = 1. $s_2^0=0,e_2^0=1$, k₃ = 10, k₄ = 10 and k_-3 = 1.

2.3. Analysis of slow and fast coupled auxiliary indicator reactions

We now want to consider the cases when the indicator is very fast (or very slow) in comparison to the non-observable reaction. We again emphasize that the completion of the indicator reaction cannot occur before the completion of the non-observable reaction for the coupled auxiliary enzyme reaction mechanism. Thus, a fast indicator is taken to be synonymous with a small maximum displacement of x^*.

2.3.1. Analysis of extremely fast indicator reactions

The first form of the indicator reaction we will consider is the case when k₃ and k₄ are very large (in comparison to k₁ and k₂), and the indicator reaction is incredibly fast. What phase-space trajectories do in the case of the coupled auxiliary enzyme reaction is chase x^*. Given the limits computed in (22), we expect the phase plane trajectory to “catch” x^* very quickly when the indicator reaction is fast. This means that the coordinates given in (21) will serve as a very good approximation to the mass action equations over measurable timescales. In fact, we can simplify the expression even further in the limiting case: if the phase–plane trajectory slides down the c₂–nullcline at a distance from x^* that is negligibly small, then

$$\dot{p}=k_4{c}_2\simeq k_4\cdot \frac{k_2{c}_1}{k_4}\simeq \frac{V_1}{K_{M_1}+s_1}{s}_1,t_{c_1}\lesssim t.$$ (23)

Equation (23) holds provided ε ≪ 1 and the non-observable reaction is in a QSS for the duration of the reaction. Therefore, the rate expression for the product formation is equivalent to the rate expression for the single-enzyme, single-substrate reaction when the indicator reaction is extremely fast. Notice that it is not necessary that λ ≪ 1 in order to impose the QSSA, and the restriction that $e_2^0$ be less than $s_1^0$ is not required: the QSSA will be valid as long as the phase–plane trajectory closely adheres to x^*, and this will occur provided the indicator reaction is sufficiently fast, even if the initial auxiliary enzyme concentration ($e_2^0$) is large.

Quantitatively, s₂ (during its accumulation to $s_2^{\max }$) is expressible in terms of a Lambert-W function (when the indicator reaction is fast, see [4] for details),

$$s_2=s_2^{\max }\left(1+\mathrm{\Omega }W\left[-{\mathrm{\Omega }}^{-1}\exp \left(-{\mathrm{\Omega }}^{-1}-\varphi t\right)\right]\right),\varphi \equiv \frac{{\left(V_2-\gamma \right)}^2}{V_2{K}_{M_2}}$$ (24)

where Ω ≡ (V₂/V₁) · (1 + σ₁)/σ₁ and $\gamma \equiv s_1^0/t_{s_1}$. If Ω⁻¹ ≪ 1, then (24) is asymptotic to

$$s_2\simeq s_2^{\max }\left[1-\exp \left(-{\mathrm{\Omega }}^{-1}-\varphi t\right)\right],$$ (25)

and the characteristic timescale that arises from (25) is

$$t_{s_2}^{\chi }=\frac{K_{M_2}+s_2^{\text{max}}}{V_2}.$$ (26)

Under the condition that the indicator reaction is fast, it is straightforward to show that

$$s_2^{\max }=\frac{K_{M_2}{k}_2{c}_1^{\max }}{V_2-k_2{c}_1^{\max }},c_1^{\max }=\epsilon s_1^0.$$ (27)

Geometrically, the maximum values defined in (27) follow from the fact that the non-observable reaction is in QSS when the phase–plane trajec-tory catches x^*; thus, c₁ will be on the order of its maximum value when the trajectory reaches x^*.

If the QSSA is valid when s₂ and c₂ reach their threshold concentrations, what role does λ^max ≪ 1 play in establishing the validity of the QSSA? Rescaling the mass action equations with respect to $T^{\chi }=t/t_{s_2}^{\chi }$ yields

$${\lambda }^{\max }\frac{d{\overline{c}}_2}{d{T}^{\chi }}=\left(1+{\kappa }_2\right)\left(1+{\tilde{\sigma }}_2\right)\left[\left(1-\frac{{\tilde{\sigma }}_2}{1+{\tilde{\sigma }}_2}{\overline{c}}_2\right){\overline{s}}_2-\frac{1}{1+{\tilde{\sigma }}_2}{\overline{c}}_2\right].$$ (28)

Thus, if λ^max ≪ 1, then the approach to x^* will occur (approximately) along the c₂-nullcline in the phase-plane. However, if λ^max is order unity, then the trajectory will move (although not initially along the c₂-nullcline) until it catches x^*, at which time the indicator reaction will remain in a QSS. Thus, if λ^max is large enough, a transient window occurs before QSS can be imposed, which is interpreted (geometrically) as the approach to x^* in the phase-plane. In either case, we have an inner solution that approximates the approach to x^*, and an outer solution that closely follows x^* as it rolls back to the origin:

$$s_2\simeq s_2^{\max }\left[1-\exp \left(-{\mathrm{\Omega }}^{-1}-\varphi t\right)\right],t\lesssim t_{s_2}^{\chi }$$ (29a)

$$s_2\simeq \frac{K_{M_2}{c}_1}{V_2-k_2{c}_1},t_{s_2}^{\chi }\lesssim t.$$ (29b)

To ensure that initial conditions are met, it again follows that if V₂ ≫ V₁, then (29a) is

$$s_2\simeq s_2^{\max }\left[1-\exp \left(-V_{2}t/K_{M_2}\right)\right].$$ (30)

Together, equations (29a) and (29b) comprise a composite solution, $s_2^{\text{comp}}$:

$$s_2^{\text{comp}}=-\frac{K_{M_2}{\dot{s}}_1^{\epsilon }}{V_2+{\dot{s}}_1^{\epsilon }}-s_2^{\text{max}}\exp \left(-V_{2}t/K_{M_2}\right),{\dot{s}}_1^{\epsilon }\equiv -\frac{V_1}{K_{M_1}+s_1}{s}_1.$$ (31)

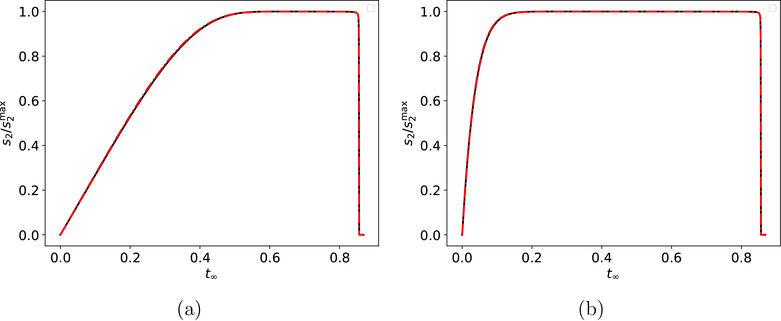
The validity of (31) is easily verified numerically (see FIGURES 3a–3b), and is the appropriate composite solution to employ when $t_{c_1}\ll t_{s_2}^{\chi }\ll t_{s_1}$.

Figure 3: The validity of the composite solution for fast indicator reactions in the reaction mechanism (1)–(2).

The solid black curve (barely visible) is the numerical solution to the mass action equations (6), and the dashed/dotted red curve is the numerical solution to the composite solution (31). In panel (a), the initial conditions (without units) are: $e_1^0=1,s_1^0=1000$, k₁ = 1, k₂ = 1 and k_-1 = 1. $s_2^0=0$, k₃ = 1, = 0, k4 = 100 and k₋₃ = 1. In panel (b), the initial conditions (without units) are: $e_1^0=1,s_1^0=1000$, k₁ = 1, k₂ = 1 and k_-1 = 1. $s_2^0=0$, k₃ = 10, k₄ = 100 and k_-3 = 1 The substrate concentrations in (a) and (b) has been scaled by their maximum values, and time has been mapped to the t_∞ scale: t_∞(t) = 1 − 1/ln(t + e).

2.3.2. Analysis of slow indicator reactions

The indicator reaction will be slow in comparison to the non-observable reaction if $t_{s_2}\gg t_{s_1}$. Consequently we take δ_S ≫ 1 in the slow regime. Since $t_{s_1}$ is now fast relative to $t_{s_2}$, we rescale the indicator reaction mass action equations with respect to T:

$$\frac{d{\overline{s}}_2}{dT}=\frac{\left(1+{\sigma }_2\right)\left(1+{\kappa }_2\right)}{{\delta }_s}\left[\left(\frac{{\sigma }_2}{1+{\sigma }_2}{\overline{c}}_2-1\right){\overline{s}}_2+\frac{{\alpha }_2}{1+{\sigma }_2}{\overline{c}}_2\right]+{\overline{c}}_1$$ (32a)

$$\lambda \frac{d{\overline{c}}_2}{dT}=\frac{\left(1+{\sigma }_2\right)\left(1+{\kappa }_2\right)}{{\delta }_s}\left[\left(1-\frac{{\sigma }_2}{1+{\sigma }_2}{\overline{c}}_2\right){\overline{s}}_2-\frac{1}{1+{\sigma }_2}{\overline{c}}_2\right]$$ (32b)

In (32b), $\lambda \equiv e_2^0/\left(s_1^0+K_{M_2}\right)$, since $s_2^{\max }\approx s_1^0$ when the indicator reaction is slow.Looking carefully at the scaled equations, we see that if the QSSA holds, or δ_S ≫ (1 + σ₂)(1 + κ₂), then

$$d{s}_2\simeq -d{s}_1,t\lesssim t_{s_1}.$$ (33)

If λ ≪ 1, then the QSSA assumption can be imposed when $t_{s_1}\lesssim t$, in which case we have an inner solution, (34a), and an outer solution, (34b):

$${\dot{s}}_2\simeq \frac{V_1}{K_{M_1}+s_1}{s}_1,t_{c_1}\le t\le t_{s_1},$$ (34a)

$${\dot{s}}_2\simeq -\frac{V_2}{K_{M_2}+s_2}{s}_2,t_{s_1}<t.$$ (34b)

Together, equations (34a)–(34b) constitute a composite solution, “$s_2^{uni}$”, in the form of the Schnell–Mendoza equation [29]:

$$s_2^{uni}\simeq K_{M_2}W\left[{\sigma }_2\exp \left({\sigma }_2-{\eta }_{2}t\right)\right]-K_{M_1}W\left[{\sigma }_1\exp \left({\sigma }_1-{\eta }_{1}t\right)\right],$$ (35)

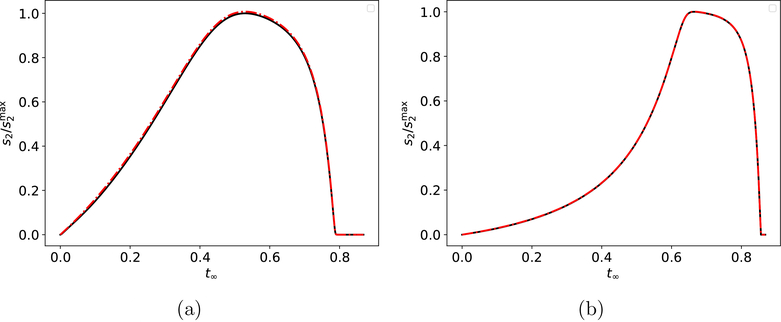
and the validity of (35) is easily verified numerically (see Figures 4a–4b).

Figure 4: The validity of the composite solution for slow indicator reactions in the reaction mechanism (1)–(2).

The solid black curve (barely visible) is the numerical solution to the mass action equation (6), and the dashed/dotted red curve is the numerical solution to the composite solution (35). In panel (a), the initial conditions (without units) are: $e_1^0=1,e_2^0=1,s_1^0=100$, k₁ = 1, k₂ = 100 and k_-1 = 1. $s_2^0=0$, k₃ = 1, = 0, k₂ = 1 and k₋₃ = 1. In panel (b), the initial conditions (without units) are: $e_1^0=1,e_2^0=1,s_1^0=1000$, k₁ = 1, k₂ = 100 and k_-1 = 1. $s_2^0=0$, k₃ = 1, k₂ = 1 and k_-3 = 1 The substrate concentrations in (a) and (b) has been scaled by their maximum values, and time has been mapped to the t_∞ scale: t_∞(t) = 1 − 1/ln(t + e).

3. Zymogen activation coupled to its enzyme catalyzed reaction

We now turn our attention to the zymogen activation coupled to its enzyme catalyzed reaction described by the chemical equations (3)–(4). In this type of reaction [30, 31, 32, 33] the product of the non-observable reaction is the indicator enzyme E2 [5]. Following the same format utilized in the analysis of the coupled auxiliary enzyme reaction mechanism, we begin by scaling the mass action equations obtained by applying the law of mass action to (3)–(4).

3.1. Scaling of zymogen activation coupled to its enzyme catalyzed reaction

The mass action equations that govern this reaction are:

$${\dot{s}}_1=-k_1\left(s_1^0-c_1\right)e_1+k_{-1}{c}_1,$$ (36a)

$${\dot{c}}_1=k_1\left(e_1^0-c_1\right)s_1-\left(k_{-1}+k_2\right)c_1,$$ (36b)

$${\dot{s}}_2=-k_3\left(e_2^A-c_2\right)s_2+k_{-3}{c}_2,$$ (36c)

$${\dot{c}}_2=k_3\left(e_2^A-c_2\right)s_2-\left(k_{-3}+k_4\right)c_2,$$ (36d)

where $e_2^A$ denotes the concentration of activated E₂ and is given by

$$e_2^A=s_1^0-s_1-c_1,$$ (37)

with $s_1^0$ denoting the initial non-observable S₁ concentration. Thus, the indicator reaction is described by a non-autonomous set of equations with $e_2^A(t)$ as its forcing term. As with the coupled auxiliary enzyme reaction, the basic analysis of the zymogen activation assay can be carried out with three timescales: $t_{c_1},t_{s_1}$ and $t_{s_2}^a$. The timescales $t_{c_1}$ and $t_{s_1}$ are identical to those defined earlier in the coupled auxiliary enzyme reaction. The additional timescale,

$$t_{s_2}^a=\frac{K_{M_2}+s_2^0}{k_4\langle e_2^A\rangle },$$ (38)

is the depletion timescale of the indicator reaction (see [5] for details regarding the validity of these timescales). The quantity $\langle e_2^A\rangle$ is the average amount of enzyme produced by the non-observable reaction over the duration of the indicator reaction. Rescaling the indicator reactions with respect to $t_{s_1}$ yields

$$\frac{d{\tilde{s}}_2}{dT}=\frac{\max e_2^A}{\langle e_2^A\rangle }\frac{(1+\beta )\left(1+{\kappa }_2\right)}{\varpi }\left[\left(\frac{\beta }{1+\beta }{\tilde{c}}_2-{\tilde{e}}_2^A\right){\tilde{s}}_2+\frac{{\alpha }_2}{1+\beta }{\tilde{c}}_2\right],$$ (39a)

$$\mu \frac{d{\tilde{c}}_2}{dT}=\frac{\max e_2^A}{\langle e_2^A\rangle }\frac{(1+\beta )\left(1+{\kappa }_2\right)}{\varpi }\left[\left({\tilde{e}}_2^A-\frac{\beta }{1+\beta }{\tilde{c}}_2\right){\tilde{s}}_2-\frac{1}{1+\beta }{\tilde{c}}_2\right],$$ (39b)

where μ, β, ${\delta }_s^a$, ${\tilde{s}}_2$, max $e_2^A$, ${\tilde{e}}_2^A$ and ${\tilde{c}}_2$ are given by:

$$\varpi \equiv t_{s_2}^a/t_{s_1},\beta \equiv \frac{s_2^0}{K_{M_2}},\mu \equiv \frac{\max e_2^A}{K_{M_2}+s_2^0},{\tilde{e}}_2^A=e_2^A/\max e_2^A,$$ (40a)

$${\tilde{s}}_2\equiv \frac{s_2}{s_2^0},{\tilde{c}}_2\equiv \frac{\left(K_{M_2}+s_2^0\right)}{s_2^0\max e_2^A}{c}_2,\max e_2^A\equiv \underset{t\le t_{s_2}^a}{\max }{e}_2^A.$$ (40b)

The phase–plane description of the zymogen activation assay is markedly different than that of the auxiliary enzyme assay. For example, the condition μ ≪ 1 establishes the presence of a slow manifold when the indicator reaction is fast. However, unlike the auxiliary enzyme reaction, the s2 and c2–nullclines of (39a)–(39b) only intersect at the origin. This means that when ϖ ≪ 1, and the depletion timescale of the indicator reaction is much smaller than $t_{s_1}$, that

$$0\simeq \frac{\max e_2^A}{\langle e_2^A\rangle }(1+\beta )\left(1+{\kappa }_2\right)\left[\left(\frac{\beta }{1+\beta }{\tilde{c}}_2-{\tilde{e}}_2^A\right){\tilde{s}}_2+\frac{{\alpha }_2}{1+\beta }{\tilde{c}}_2\right],$$ (41a)

$$0\simeq \frac{\max e_2^A}{\langle e_2^A\rangle }(1+\beta )\left(1+{\kappa }_2\right)\left[\left({\tilde{e}}_2^A-\frac{\beta }{1+\beta }{\tilde{c}}_2\right){\tilde{s}}_2-\frac{1}{1+\beta }{\tilde{c}}_2\right],$$ (41b)

should still be interpreted to mean that the solution (39a)-(39b) to lies at the intersection of both the c₂ and s₂–nullclines when $t_{s_2}^a\lesssim t$; however, since the intersection of the nullclines occurs at the origin, the biochemical interpretation is that the indicator reaction has completed. Another subtle difference between the phase–plane dynamics of the auxiliary enzyme assay and the zymogen activation assay is that both the s₂ and c₂–nullclines move in the phase–plane of the zymogen activation reaction, whereas only the s₂–nullcline moves in the phase–plane of the auxiliary enzyme reaction.

In the subsections that follow, we will again invoke moving nullcline analysis to study the phase–plane dynamics of the zymogen activation assay. We will consider the limiting cases when ϖ ≪ 1 and ϖ ≫ 1, and illustrate the geometric interpretation of the RSA and QSSA for the zymogen activation assay through moving nullcline analysis.

3.2. The zymogen activation coupled to its enzyme catalyzed reaction exhibits a Laelaps manifold

In the case of the zymogen activation coupled to its enzyme catalyzed reaction, the time-dependent slow manifold propagates (swings) through the phase–plane as long as the non-observable reaction is producing E₂. In this scenario, the c₂–nullcline swings through the phase-plane almost like a (curved) windshield wiper rotating counterclockwise. The phase-plane solution to the indicator reaction initially follows behind the swinging c₂–nullcline until it eventually catches it, at which time c₂ reaches its maximum value. After the solution catches the c₂–nullcline it slides down the c₂–nullcline as it approaches the origin (see, MOVIE 2 in Supplementary Materials). We refer to this manifold as a Laelaps manifold after the Greek mythological dog that always caught what she was hunting. Analogously, the solution to the mass action equations “hunts” the moving the c₂–nullcline (see FIGURES 5a–5d).

Figure 5: Visualization of the Laelaps manifold in the phase–plane of the reaction mechanism (3)–(4).

The solid black curve is the numerical solution to the mass action equations (36). The solid black dot is the numerical solution to (36) at various points in time; the dashed/dotted red curve is the corresponding location of the c₂–nullcline. Initially, the solution lags just behind the c₂–nullcline (panel (a)). Eventually, the solution catches the c₂–nullcline (panel (b)), and then lies just above for the duration of the reaction (panel(c)). Panel (d) is the location of the c₂–nullcline upon completion of the indicator reaction. A dynamical representation of the Laelaps manifold is shown in Movie 2 (Supplementary Materials). The constants (without units) used in the numerical simulation are: $e_1^0=1,s_1^0=100$, k₁ = 1, k₂ = 1 and k₋₁ = 1. $s_2^0=1000$, k₃ = 1, k₄ = 100 and k₋₃ = 100. The substrate (s₂) and complex (c₂) concentrations have been scaled by their maximum values.

3.3. Analysis of slow and fast zymogen activation coupled to its enzyme cat 221 alyzed reaction

In this section we again consider the extreme cases when the indicator reaction is very fast or very slow in comparison to the non-observable reaction for the zymogen activation coupled to its enzyme catalyzed reaction. As mentioned, the major difference between the zymogen activation coupled to its enzyme catalyzed reaction and the coupled auxiliary reaction mechanism is that, while the indicator reaction for the coupled auxiliary enzyme assay cannot complete before the non-observable reaction, the completion of the secondary reaction can occur before or after the completion of the primary reaction.

3.3.1. Analysis of fast indicator reactions

If the indicator reaction is extremely fast, then ϖ ≪ 1. If μ ≪ 1, then the leading order approximation is

$$c_2\simeq \frac{e_2^A}{K_{M_2}+s_2}{s}_2,$$ (42)

and the depletion of substrate is given in terms of a Lambert-W function (again, see [5] for details regarding this particular solution):

$$s_2=K_{M_2}W\left[\beta \exp \left(\beta \frac{k_4\nu t^2}{2K_{M_2}}\right)\right],\nu \equiv \epsilon k_2{s}_1^0.$$ (43)

Notice that for fast indicator reactions, it is not necessary that $s_2^0\gg s_1^0$, as the amount of activated enzyme concentration e₂ produced by the nonobservable reaction will be small if the duration of the indicator reaction is short in comparison to the completion timescale ($t_{s_1}$)of the non-observable reaction.

It is straightforward to determine the approximate time at which the phase-plane trajectory catches the moving c₂–nullcline when β ≪ 1. If β ≪ 1, then (43) is approximately

$$s_2\approx s_2^0\exp \left(-\frac{k_4\nu t^2}{2K_{M_2}}\right).$$ (44)

If the QSSA is valid, then it follows that

$$c_2\simeq -\frac{1}{k_4}{\dot{s}}_2.$$ (45)

Thus, ${\dot{c}}_2\simeq -{\ddot{s}}_2/k_4$, and ${\dot{c}}_2$ vanishes when ${\ddot{s}}_2$ vanishes:

$$\frac{1}{k_4}{\ddot{s}}_2=0.$$ (46)

Inserting (44) into (46) and subsequently solving for t yields the catch time, t_c:

$$t_c=\sqrt{\frac{K_{M_2}}{{\widehat{V}}_2}\cdot t_{s_1},}{\widehat{V}}_2\equiv k_4{s}_1^0.$$ (47)

Thus, the phase-plane trajectory will “catch” the c₂-nullcline when t ≈ t_c, provided the indicator reaction is extremely fast and β ≪ 1 (see FIGURES 6a-6b).

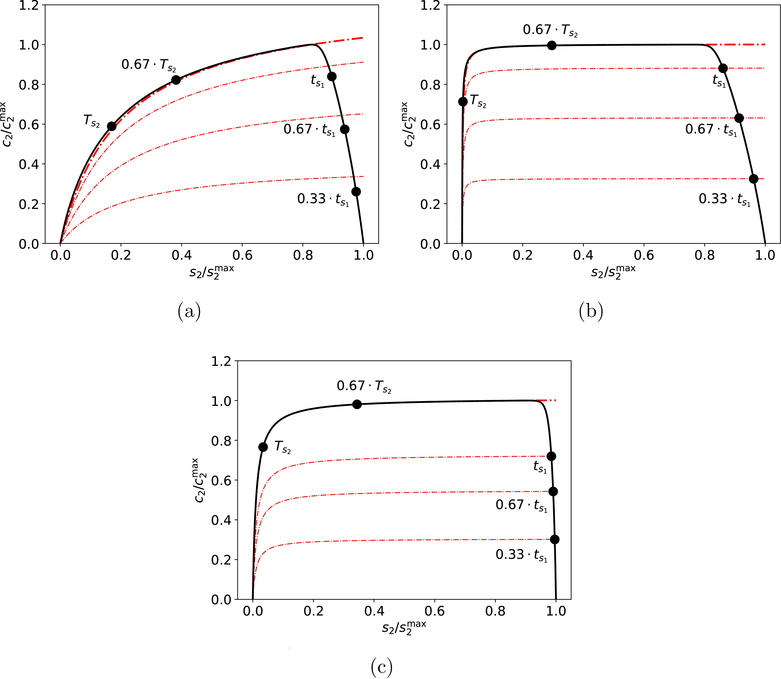
Figure 6: The “catch time,” t_c, for fast indicator reactions when β ≪ 1 in the reaction mechanism (3)–(4).

Panel (a): The solid black curve is the numerical solution to the mass action equations (36). The solid black dots correspond to the location of the phase-plane trajectory at times: t = 0.33 · t_c, 0.67 · t_c, t_c, 1.33 · t_c and 1.67 · t_c The thick, dashed/dotted red curve is the c₂-nullcline at time t = t_c, and the thin, dashed/dotted red curves are the locations of the c₂-nullcline at the additional time points: t = 0.33 · t_c, 0.67 · t_c, 1.33 · t_c and 1.67 · t_c. Notice the phae-plane trajectory lies just below the c₂ nullcline for t < t_c and just above it for t > t_c. Panel (b): The evolution of c₂ in the concentration/time plane. The black dashed line corresponds to = t_c, and clearly indicates the time at which c₂ reaches its threshold value and intercept the c₂-nullcline. The constants and initial conditions (both without units) used in (a) and (b) are: $e_1^0=1$, $s_1^0=100$, k₁ = 1, k₂ = 1 and k₋₁ = 1. $s_2^0=1$, k₃ = 1, k₄ = 100 and k₋₃ = 1. The substrate concentrations in (a) and (b) has been scaled by their maximum values, and time has been mapped to the t_∞ scale: t_∞(t) = 1 − 1/ln(t + e).

3.4. Analysis of slow indicator reactions

The average available enzyme approaches $s_1^0$ as the indicator reaction begins to slow down, and for sufficiently slow indicator reactions we take

$$T_{s_2}=\frac{K_{M_2}+s_2^0}{{\widehat{V}}_2}$$ (48)

to be the appropriate depletion timescale [5]. Applying the previous scaling laws, we obtain

$$\frac{d{\tilde{s}}_2}{dT}=\frac{(1+\beta )\left(1+{\kappa }_2\right)}{\varpi }\left[\left(\frac{\beta }{1+\beta }{\tilde{c}}_2-{\tilde{e}}_2^A\right){\tilde{s}}_2+\frac{{\alpha }_2}{1+\beta }{\tilde{c}}_2\right],$$ (49a)

$$\mu \frac{d{\tilde{c}}_2}{dT}=\frac{(1+\beta )\left(1+{\kappa }_2\right)}{\varpi }\left[\left({\tilde{e}}_2^A-\frac{\beta }{1+\beta }{\tilde{c}}_2\right){\tilde{s}}_2-\frac{1}{1+\beta }{\tilde{c}}_2\right],$$ (49b)

where μ and 𝜛 are now given by

$$\mu \equiv \frac{s_1^0}{K_{M_2}+s_2^0},\varpi \equiv \frac{T_{s_2}}{t_{s_1}}.$$ (50)

By inspection of (49a)–(49b), it is clear that if

$$\varpi \gg (1+\beta )\left(1+{\kappa }_2\right),$$ (51)

then s₂ will be a slow variable for the duration of the non-observable reaction [5]. In fact, (51) is a RSA for slow indicator reactions. Furthermore, if μ ≪ 1, then we can assume a QSS with respect to the $T_{s_2}$ timescale:

$$c_2\simeq \frac{s_1^0}{K_{M_2}+s_2}{s}_2,t_{s_1}\lesssim t.$$ (52)

Combining (52) with (51) yields

$$s_2=s_2^0,t\lesssim t_{s_1}$$ (53a)

$$s_2=K_{M_2}W\left[\beta \exp \left(\beta -{\eta }_{2}t\right)\right],t_{s_1}\lesssim t,$$ (53b)

which will hold provided μ ≪ 1

Next, we want to determine if the QSSA is valid when $t\lesssim t_{s_1}$. Notice from (49a) that the QSSA will not hold for $t\lesssim t_{s_1}$ unless

$$\mu \varpi \ll \left(1+{\beta }_2\right)\left(1+{\kappa }_2\right).$$ (54)

If we demand that (54) hold, then it follows that

$$\frac{t^{*}}{t_{s_1}}\ll 1,t^{*}\equiv \frac{1}{k_3\left(K_{M_2}+s_2^0\right)}.$$ (55)

Geometrically, the invalidity of the QSSA over the $t_{s_1}$ timescale is due to the fact that the c₂-nullcline propagates through the phase-plane at a speed that is much faster than the speed at which the solution trajectory propagates (see FIGURES 7a–7c for a phase–plane illustration).

Figure 7: The QSSA and the RSA on the $t_{s_1}$ timescale for slow indicator reactions in the reaction mechanism (3)–(4).

In (a)–(c), the solid black curve is the numerical solution to the mass action equations (36). The solid black dots are the locations of the trajectory at times t = 0.33 · $t_{s_1}$, 0.67 · $t_{s_1}$, $t_{s_1}$, 0.67 · $T_{s_2}$ and 0.67 · $T_{s_2}$. The thin, dashed red curves are corresponding snapshots of c₂-nullcline at these time points. The thick, dashed red curve is the stationary c₂-nullcline: $c_2=s_1^0{s}_2/\left(K_{M_2}+s_2\right)$. In panel (a), both the RSA and QSSA fail over the the $t_{s_1}$ timescale. Constants (without units) used in (a) are: k₁ = 10, k₂ = 100, k₋₁ = 1, $s_1^0=100,e_1^0=1,s_2^0=1000$, k₃ = 0.01, k₄ = 1, k_-3 = 1. In panel (b), the QSSA holds over $t_{s_1}$ but the RSA fails. Constants (without units) used in (b) are: k₁ = 10, k₂ = 100, k₋₁ = 1, $s_1^0=100,e_1^0=1,s_2^0=1000$, k₃ = 1, k₄= 1, k₋₃ = 1. In panel (c), both the RSA and QSSA hold over the $t_{s_1}$ timescale. Constants (without units) used in (c) are: k₁ = 10, k₂ = 100, k_-1 = 1, $s_1^0=100,e_1^0=1,s_2^0=10000$, k₃ = 0.1, k₄ = 1, k₋₃ = 10. s₂ and c₂ have been scaled by their maximum values.

As a final remark, we point out the subtle relationship between the RSA (51) and the QSSA (54). If the QSSA holds for $t\lesssim t_{s_1}$, then

$${\dot{s}}_2\ge -\frac{{\widehat{V}}_2}{K_{M_2}+s_2^0}{s}_2^0.$$ (56)

If we demand that max $\left|{\dot{s}}_2\right|\cdot t_{s_1}\ll s_2^0$, with

$$\max \left|{\dot{s}}_2\right|=\frac{{\widehat{V}}_2}{K_{M_2}+s_2^0}{s}_2^0,$$ (57)

then it follows that the depletion of s₂ over the $t_{s_1}$ timescale will be negligible as long as $t_{s_1}\ll T_{s_2}$. Thus, (51) is sufficient but not necessary for the validity of the RSA. In short, the separation $t^{*}\ll t_{s_1}\ll T_{s_2}$ will ensure that both the QSSA and the RSA are valid for $t\lesssim t_{s_1}$.

4. Discussion

In this work, two types of coupled enzyme reaction mechanisms – the coupled auxiliary enzyme mechanism and zymogen activation coupled to its enzyme catalyzed reaction – have been studied through scaling analysis. The main contribution of this paper is the geometric understanding of how scaling laws and how singularly perturbed problems can be analyzed when multiple timescales contribute to the phase-plane dynamics in biochemical systems.

In the case of the indicator reaction of the coupled auxiliary enzyme reaction mechanism, we have shown that if the indicator reaction has adequate speed, then the mass action equations can be approximated by the intersection of the nullclines, x^*. Thus, the QSSA is a natural consequence of the phase–plane geometry, and the requirement that the initial substrate concentration ($s_1^0$) be in excess of the initial auxiliary enzyme concentration ($e_2^0$) is not necessary for the validity of the QSSA, provided the indicator reaction has sufficient speed. Moreover, for extremely fast indicator reactions, the rate expression for product formation reduces to

$$\dot{p}\simeq \frac{V_1}{K_{M_1}+s_1}{s}_1,$$

from which $K_{M_1}$ and V₁ could be estimated by analyzing progress curves generated by the indicator reaction. In contrast, we have shown that when the indicator reaction is extremely slow, the substrate concentration, s₂, admits a composite solution comprised of two Schnell-Mendoza equations.

Additionally, the analysis of the zymogen activation coupled to its enzyme catalyzed reaction has been interpreted in the phase–plane via moving nullcline analysis. Specifically, we have illustrated that the invalidity of the QSSA occurs when the c₂-nullcline propagates through the s₂–c₂ phase–plane at a speed that temporarily exceeds the speed of the solution.

We hope that the applied mathematics and chemical kinetics communities will continue to investigate these types of reactions, as we feel there are still interesting and novel results to uncover.

Highlights.

• A singular perturbation analysis of coupled enzyme catalyzed reactions is performed.

• The catalyzed reactions consist of a non-observable reaction as well as an indicator reaction. We show that the indicator reaction has a natural lag time.

• A geometric description of slow/fast coupled reactions is formulated based on the motion of slow manifolds relative to the motion of the solution trajectories.

• Conditions for the validity of the reduced equations are derived and inter- preted both geometrically and biochemically.