Patient-specific simulation of transcatheter aortic valve replacement: impact of deployment options on paravalvular leakage

Abstract

Transcatheter aortic valve replacement (TAVR) has emerged as an effective alternative to conventional surgical valve replacement in high-risk patients afflicted by severe aortic stenosis. Despite newer-generation devices enhancements, post-procedural complications such as paravalvular leakage (PVL) and related thromboembolic events have been hindering TAVR expansion into lower-risk patients. Computational methods can be used to build and simulate patient-specific deployment of transcatheter aortic valves (TAVs) and help predict the occurrence and degree of PVL. In this study finite element analysis and computational fluid dynamics were used to investigate the influence of procedural parameters on post-deployment hemodynamics on three retrospective clinical cases affected by PVL. Specifically, TAV implantation depth and balloon inflation volume effects on stent anchorage, degree of paravalvular regurgitation and thrombogenic potential were analyzed for cases in which Edwards SAPIEN and Medtronic CoreValve were employed. CFD results were in good agreement with corresponding echocardiography data measured in patients in terms of the PVL jets locations and overall PVL degree. Furthermore, parametric analyses demonstrated that positioning and balloon over-expansion may have a direct impact on the post-deployment TAVR performance, achieving as high as 47% in PVL volume reduction. While the model predicted very well clinical data, further validation on a larger cohort of patients is needed to verify the level of the model’s predictions in various patient-specific conditions. This study demonstrated that rigorous and realistic patient-specific numerical models could potentially serve as a valuable tool to assist physicians in pre-operative TAVR planning and TAV selection to ultimately reduce the risk of clinical complications.

1. Introduction

Calcific aortic stenosis (AS) is an active disease process in which the aortic valve (AV) leaflets progressively experience morphological changes due inflammation, atherosclerosis and calcium deposition reactions. This in turn alters the valve’s function resulting in narrowed opening of the leaflets during systole, abnormal hemodynamics and increased left ventricular (LV) mechanical stress (Kanwar et al. 2018). Surgical aortic valve replacement (SAVR) is considered the gold-standard treatment for severe AS; however, clinical attention has shifted toward the less-invasive transcatheter aortic valve replacement (TAVR) approach. PARTNER trials have demonstrated TAVR superiority in short- and medium-term mortality (Smith et al. 2011), and this new revolutionary treatment has been remarkably establishing in the last decade and growing in safety and efficacy. TAVR represents the only life-saving solution for extreme- and high-surgical risk patients who cannot endure the invasiveness of an open-heart surgery due to the presence of significant comorbidities (Pilgrim and Windecker 2015). Given its promises, TAVR was recently approved to treat intermediate-risk patients who can therefore benefit from shorter hospitalization and recovery (Leon et al. 2016).

Despite this early successful growth, intra- and post-procedural clinical complications have been casting doubts and undermining its potential expansion to lower-risk patients. Among the most important drawbacks, post-deployment paravalvular leakage (PVL), cardiac conduction abnormalities (Bagur et al. 2012; Van der Boon et al. 2012) and coronary artery occlusion (Ribeiro et al. 2013) have shown to increase mortality and rate of re-intervention. Additionally, the altered hemodynamics due to PVL, where narrow gaps are subjected to large pressure (distolic) gradients, may lead platelets to be exposed to high flow shear stress. This may trigger their activation and formation of microemboli, which are then ejected upon subsequent systole and may get trapped and/or deposited in the sinus region where typical low-shear re-circulations zones are found. Therefore, PVL can be linked to thrombus deposition around the TAV and/or dissemination of thromboemboli in the circulation, thereby increasing the risk of stroke. Although thromboembolism is less common than hypo-attenuated leaflet thickening, it is still a phenomenon that is common enough for being clinically addressed (Scotten and Siegel 2014).

The presence of PVL after TAVR was associated with higher late mortality, cardiac death and repeated hospitalization even in the presence of trace regurgitation (Maisano et al. 2015). This effect was proportional to the severity of the regurgitation, with mild PVL resulting in doubling the mortality rate after 1 year (Genereux et al. 2013). Data from the PARTNER trial showed an occurrence of 66% for trace/mild regurgitation and moderate/severe in 12% (Kodali et al. 2012), in the absence of post-deployment PVL corrective measures. However, its progression may be unpredictable, as it has shown to increase at 2 years by ≥ 1 grade in 22.4% of patients, to remain unchanged in 46.2% and to improve by ≥ 1 grade in 31.5% (Webb et al. 2009). Additionally, patients receiving self-expandable Medtronic CoreValve experienced higher PVL frequency and worsened severity than cases with balloon-expandable Edwards SAPIEN following the procedure (Gilbert et al. 2018). However, new devices enhancements involving low profile delivery system, an external skirt to improve TAV sealing and more precise valve positioning, are reducing the rate of PVL at least on the short term (Still et al. 2018).

The presence and degree of post-TAVR PVL are clinically assessed and quantified by several imaging modalities, with echocardiography remaining the most frequently employed. More specifically, transesophageal echocardiography, cineangiography and hemodynamic measurements are utilized intra-procedurally, whereas transthoracic echocardiography is generally used for the assessment and follow-up of PVL after TAVR (Pibarot et al. 2015). Specifically, continuous-wave echo is used to assess the overall hemo-dynamic performance of the valve, but spatial localization of the leakage is not possible. Therefore, aortic regurgitation is quantified as the ratio of reverse flow to the forward flow, as often measured and calculated experimentally (Hatoum et al. 2018). A semi-quantitative description of the jets via pulsed-wave color doppler is used to localize and assess the severity of the PVL jets.

However, the quantification of PVL after TAVR still lacks standardization and remains challenging, since it is often qualitative and different grading scheme are adopted (trace, mild, moderate and severe) (Abdelghani et al. 2016; Pibarot et al. 2015). Several interventional alternatives to reduce paravalvular regurgitation are employed, such as post-implantation balloon dilation, re-positioning, snaring maneuvers and valve in valve (ViV) (Eggebrecht et al. 2012), with increasing risk of vascular complication. During the procedure, positioning the TAV with respect to the patient’s aortic annulus is crucial and was directly associated with TAV hemodynamic performance and rate of re-intervention (Dvir et al. 2012). Additionally, balloon overinflation is often employed to reduce PVL degree. It has been shown that post-ballooning reduces regurgitation in a majority of patients by at least one degree (Nombela-Franco et al. 2012; Takagi et al. 2011). However, post-dilation effect on survival remains uncertain since it was also associated with a higher incidence of cerebrovascular events (Nombela-Franco et al. 2012). In conclusion, minimizing the amount and the incidence of residual PVL post-TAVR is necessary to improve long-term clinical outcomes.

Computational models have been employed to study the interaction between TAVR stent and aortic native tissue and predict post-procedural device performance from a structural dynamics standpoint (Bianchi et al. 2016; McGee et al. 2018; Morganti et al. 2016; Sturla et al. 2016; Wang et al. 2014). Recent studies quantified the interaction between the device and the implantation site, as a surrogate measure of PVL, by measuring the gap between the stent (Bosi et al. 2018; Morganti et al. 2014) or the skirt (Schultz et al. 2016) from the native tissue in patient-specific and idealized aortic root (AR) anatomies (Chang et al. 2018). Similarly, a max-flow algorithm was proposed (Bosmans et al. 2016), which creates a one-dimensional connected graph to represent the flow network based on the size of the gap between the stent and AR. Results showed good correlation with cases of absent regurgitation, but models suffered from inaccuracy for patients with PVL. In a more extensive work (De Jaegere et al. 2016) modeling predictability was tested on a set of 60 cases of Medtronic CoreValve deployment and validated the results with angiography and echocardiography measurements; yet no description of the reconstruction of the patients anatomy and of the modeling assumptions was provided. Finally, a recent study (Mao et al. 2018) investigated the effect of CoreValve orientation and modeling assumptions, such as skirt shape and stent thickness, on post-deployment hemodynamics. Post-TAVR thrombus formation was only considered for leaflets thrombosis after ViV. Blood stasis was assessed and quantified in idealized models of ViV with intra-annular and supra-annular TAV positions (Vahidkhah and Azadani 2017).

Therefore, a comprehensive analysis of the effect of procedural parameters on patient-specific post-TAVR hemo-dynamics is lacking. This work aims to offer a methodology to assess the effect of TAV implantation depth and balloon overinflation on stent anchorage, post-deployment PVL and risk of thrombus formation. The ultimate goal of this study is to understand the effect of the interventional cardiologist’s choice on post-procedural complications and to help in reducing their impact based on patient-specific data.

2. Methods

2.1. Anatomy reconstruction

A set of three cases of patients at Stony Brook University Hospital who experienced post-procedural mild-to-moderate regurgitation was selected. Pre-TAVR contrast-enhanced CTA scans of the patients were then collected under approval of the local institutional review board. Images of the AR were imported as DICOM, with variable voxel spacing from 0.586 × 0.586 × 0.5 mm to 0.659 × 0.659 × 0.5 mm, acquired at 75% of the R–R interval when the attenuation is the highest across the cardiac cycle. To study the performance of different type and size of TAVs, patients with varying annulus sizes who received both SAPIEN (first generation) and CoreValve were chosen, as detailed in Table 1.

Table 1.

Elucidation of TAV types and comparison of annular measurements between clinical data and model

TAV type	TAV size (mm)	Annulus dav CTA- derived (mm)	Annulus dav model (mm)	Annulus dav Δ (%)
Edwards SAPIEN (PVL01)	26	23.5	24.1	+2.5
Edwards SAPIEN (PVL02)	23	22.2	22.9	+3.2
Medtronic CoreValve (PVL03)	29	24.3	24.3	0

The AR lumen and calcification region were segmented in 3D by the open source software ITK-SNAP 3.6 (Yushkevich et al. 2006). Range thresholding (average thresholds were 50–650 HU for the lumen and > 600 HU for the calcifications, allowing continuous extraction) and automatic region competition snake algorithms were employed. AR region was included until mid-ascending aorta, coronary ostia and left ventricle outflow tract (LVOT). Additionally, the coordinates of AV landmarks were manually extracted to drive the reconstruction of the leaflets (Morganti et al. 2014). The surface bodies were then imported in ANSYS SpaceClaim for subsequent processing. Global smoothing was required in order to remove step-like-shaped features derived from the low-resolution images (Fig. 1a), and the volume loss was kept under 10%. A non-uniform rational basis spline (NURBS)-based surface was then created from the faceted AR sinus (Fig. 1b) and the AV landmarks projected on it. The height of the leaflets and that of the coaptation were based on a previously suggested parametric model (Haj-Ali et al. 2012). The surface of the leaflets is constructed based on two splines, one defining the free edge and one defining the “symmetry” line of the leaflet itself. In order to consider the difference in wall thickness between the thick aortic sinus and the thin leaflets, a variable-thickness algorithm was implemented. A schematic is provided in Fig. 1. The resulting leaflets are inserted in the sinus (t_s = 1.56 mm) and have a 150-μm-thick free edge (Mensel et al. 2014). The average diameter (area-derived) of the aortic annulus was also compared to the clinical CT-based measurements, and good agreement was found for all cases (Table 1).

Fig. 1.

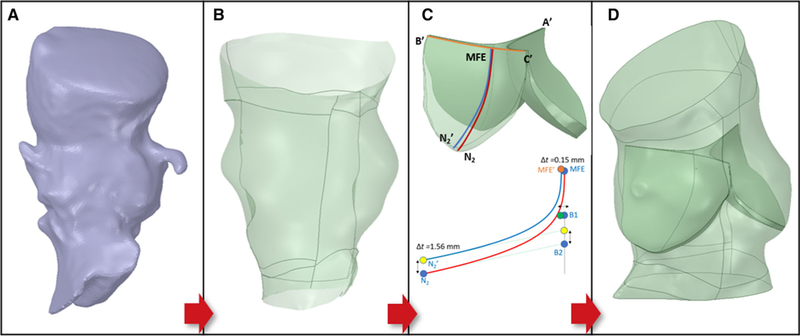
Representative AR patient-specific reconstruction (PVL01). a STL AR model from segmentation; b NURBS-based surface of the AR c) (Top) Variable-thickness AV with highlighted landmarks and construction splines (B’C’: free edge spline (orange); N₂MFE and N2MFE’: symmetry splines); (Bottom) Algorithm implemented for variable thickness showing the construction of the symmetry spline and location of its control points (B1 and B2) and attachment landmarks (N2) for the bottom surface (red) and top surface (blue) of each leaflet. MFE: middle free edge as midpoint of the free edge spline; d Native AV inserted in the AR sinus

The sinus was then extruded in Abaqus CAE, whereas calcifications deposits were processed in MATLAB before being assembled into the AR. As described in Bianchi et al. (Bianchi et al. 2016), calcifications were embedded into the soft tissue to better mimic the stenotic morphology (Fig. 2). The AR was finally re-meshed with tetrahedral elements in Ansys Fluent Meshing to assure mesh continuity at the interface between sinus and leaflets and between calcifications and surrounding soft tissue and appropriate quality (skewness <0.9) for finite element (FE) modeling was enforced. The mesh size was approximately 1.4 million for the SAPIEN cases and 2.5 million for the CoreValve case, since a larger portion of ascending aorta was needed for the deployment.

Fig. 2.

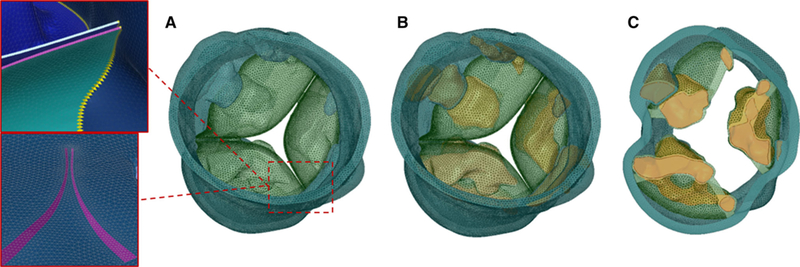
Meshed AR for PVL02. a Tetrahedra-based AR with AV leaflets (green) and AR sinus (teal). Zoom-ins of the mesh show conform mesh at the interface between AV leaflets and sinus wall. b AR mesh with embedded calcific deposits (orange) and c cross section with a plane parallel to the annulus showing the calcifications confinement into the AR wall

2.2. TAV crimping and balloon inflation

TAVs were modeled and meshed with hexahedra-based structured mesh, and the crimping process was simulated through an explicit analysis in Abaqus, by enforcing radial displacement boundary conditions (BCs) to the nodes of a coaxial cylindrical sheath. The following constitutive laws for the stents material were employed: stainless steel modeled with bilinear elasto-plastic material (ρ = 7760 kg/m³, E =193 GPa, σ_Y (0.2%) = 340 MPa, σ _U (48%) = 670 MPa, v =0.29) (Tzamtzis et al. 2013) for the SAPIEN and superelastic Nitinol alloy (14 constants user material VUMAT available in Abaqus) (Morganti et al. 2016) for the CoreValve (Fig. 3). The balloon was modeled with quadrilateral shell elements as linear elastic (ρ = 1100 kg/m³, E =600 MPa, v = 0.45, α_R =8000) (Tzamtzis et al. 2013) and deflated in a similar fashion, by a cylindrical sheath. TAV prosthetic leaflets were not included in the models, as described previously.

Fig. 3.

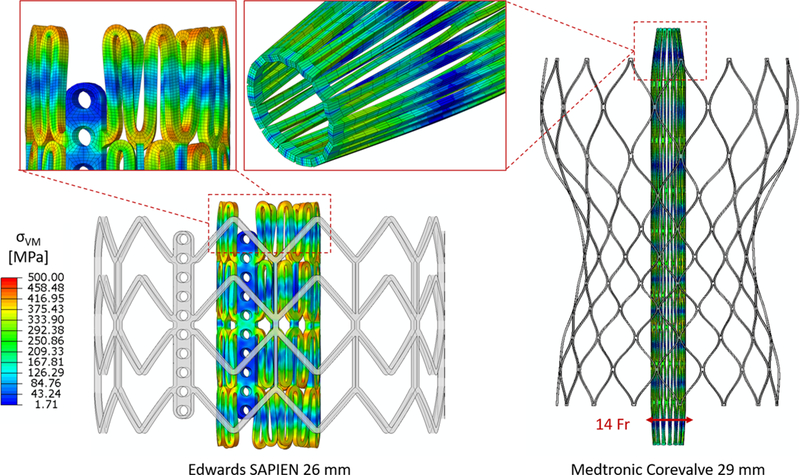
Stent crimping showing initial undeformed configuration and von Mises stresses on the final crimped configuration for the two types of TAVs. Zoom-ins of the top of the stents are provided with the hexahedra-based mesh. Longitudinal elongation of the stent upon crimping is visible

For the balloon inflation two approaches were followed: a pressure-based inflation with 4 atm, value extracted from compliance tests performed on delivery systems upon reaching nominal diameter, and a fluid-cavity-based approach which allows a more realistic volume-controlled inflation. Specifically, the diameter-pressure curves and final diameters were quantitatively compared, and a maximum difference of 2% was observed. The fluid-cavity-based model was solved in almost half the time of the pressure-based model (approximately 6 vs 11 h on 96 cores), and the former was employed for the deployment models in order to implement the over-expansion. Clinically, stent over-expansion is achieved by injecting a controlled quantity of extra volume; therefore, the fluid-cavity model more faithfully replicates the deployment and the interventionalist’s decision.

2.3. TAV deployment in patient-specific anatomies

The AR soft tissue was modeled using dedicated hyperelastic models (for each leaflet and the sinus tissue) calibrated with animal data available in the literature (Martin et al. 2011; Martin and Sun 2012), whereas the calcification deposits were modeled as homogenous linear elastic material (E = 12.6 MPa, v = 0.3) (Wang et al. 2014). AV leaflets were pre-opened with a cone-shaped catheter to simulate the effect of the insertion of the delivery system across the AV.

The deployment and recoil of the TAV in the patient-specific AR were simulated in Abaqus Explicit for four procedural scenarios for the SAPIEN cases (S26 and S23): midway positioning (center of the stent on the annulus plane) and aortic positioning (with only 30% of the stent in the LVOT), each with both nominal and overinflation. For the CoreValve case (C29), midway (bottom of the stent 5 mm below the annulus), aortic (3 mm below the annulus) and ventricular (7 mm below) positions were simulated (Petronio et al. 2015). Table 2 summarizes the configurations analyzed in relationship with the procedural parameters, i.e., midway-nominal (MN), midway-overinflation (MO), aortic-nominal (AN), aortic-overinflation (AO). The deployment of the CoreValve was simulated by axially displacing the cylindrical sheath thus releasing the stent inside the AR. For both types of valves, a recoil phase after the deployment was modeled. The top of the AR was constrained in its translational degrees of freedom (DOFs). Frictional hard contact (Mummert et al. 2013) for the TAV interacting with the native tissue and scaled penalty contact for the stent–balloon interaction were implemented. Mass scaling was employed for every model, and the ratio between kinetic energy and internal energy was kept under 5% (Chung et al. 1998), so that inertial forces would not have a significant effect on the model dynamics. The prosthetic leaflets were excluded from the analysis since it was demonstrated (Bailey et al. 2015) that they have negligible impact (< 1% in nodal discrepancy) on the post-deployment stent deformation; therefore, the extra computational cost derived from a more complex interaction to be computed is not justified. Total contact area and force were computed in the two phases and compared across all the configurations (Bianchi et al. 2016).

Table 2.

Summary of the procedural configurations simulated based on the implantation depth and balloon inflation parameters. A total of 11 configurations were investigated. S26 Edwards SAPIEN 26 mm, S23 Edwards SAPIEN 23 mm, C29 CoreValve 29 mm, MN midway-nomissnal, MO midway-overinflation, AN aortic-nominal, AO aortic-overinflation

Self-expandable		Midway C29_M	Aortic C29_A	Ventricular C29_V
Balloon expandable	Nominal	S26_MN/S23_MN	S26_AN/S23_AN
	Overinflation	S26_MO/S23_MO	S26_AO/S23_AO

2.4. Fluid domain extraction and TAV leaflets mapping

The AR deformed anatomy and the stent were exported from the last timepoint of the recoil phase for each configuration. The inner surface of the AR was extracted and closed in Ansys SpaceClaim. The displacement field of the stent nodes was calculated in reference to the original (pre-crimped) configuration, and it was applied to the TAV model equipped with skirt and prosthetic leaflets. This was performed in a quasi-static explicit dynamic analysis to map the TAV leaflets into the deformed deployed configuration (Fig. 4a, b and e, f), while constraining their nodes on the suture line in all DOFs. The SAPIEN leaflets made of glutaraldehyde-treated bovine pericardium were modeled with isotropic hyperplastic material with Ogden third-degree material model (Martin and Sun 2015), the Dacron cuff with linear elastic material (ρ = 1120 kg/m³, E =500 MPa, v = 0.3), and the metal clips connecting the leaflets to the stent with stainless steel material. Porcine pericardium material of the CoreValve leaflets and cuff was assumed as linear elastic (ρ = 1120 kg/m³, E =7.5 MPa, v = 0.45) (Capelli et al. 2012). Subsequently, the mapped leaflets were closed with a physiological pressure drop in a similar quasi-static analysis to model their diastolic configuration (Fig. 4c, d, g, h). TAV leaflets were meshed with quadrilateral shell elements in which the nodes on the suture line were shared with the triangular (SAPIEN) and quadrilateral (CoreValve) membrane element inner cuff, thus avoiding computationally expansive tie definitions. The fluid domain of the AR with the deployed TAV was then extracted in Ansys Fluent Meshing using collective shrinkwrap function while retaining the patient-specific AR and TAV features. The model was initially meshed with tetrahedra elements with dedicated size functions (stent and leaflets free edge: 0.1 mm; prosthetic leaflets/cuff: 0.3 mm; top/bottom root and coronary outlets: 0.5 mm; root/native AV/AV attachments: 0.35 mm) (Fig. 5). The meshed inlet and outlet surfaces were then imported in MATLAB and extruded to a length of three equivalent diameters (triangular prisms-based sweep mesh) to apply the BCs far away from the region of interest (ROI) and to thereby ensure no flow interference on the PVL. A mesh sensitivity analysis was conducted by coarsening and refining the size the element size on the root region (TAV and free edges are locked for geometrical constraints) by a factor of two. Max velocity magnitude, pressure gradient and regurgitant flow rate differed by less than 5% and the coarse mesh model over-estimated the fluid volume in the region were calcified leaflets are tangent to the sinus wall. A schematic of the fluid domain extraction process is provided in the supplementary material (Figure S1).

Fig. 4.

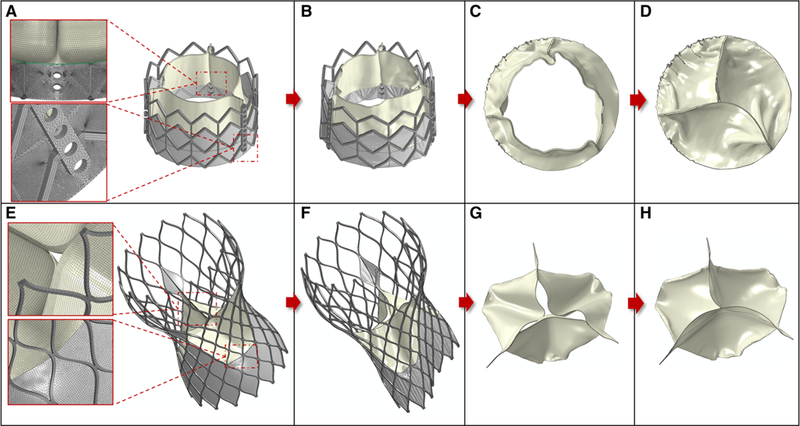
TAV leafletsmapping (first and second column) and closure (third and fourth column) for the Edwards SAPIEN 26 mm (top row) and Medtronic CoreValve 29 mm (bottom row). Zoomins of the mesh are showed at the node-to-node connection between leaflets cuff (green line) and stent cuff (a), and at the central top of the CoreValve leaflets (e) in their initial expanded configuration

Fig. 5.

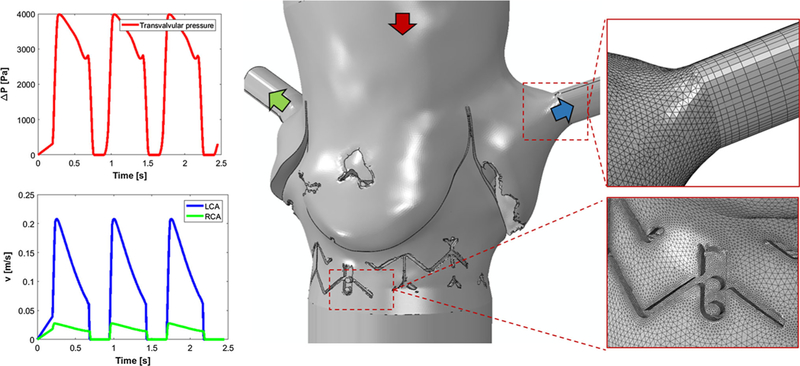
Fluid domain model for patient PVL01. Insets of the mesh in the sinus-coronary outlets connection showing axially-varying sweep mesh for the coronary outlets and mesh refinement in the proximity of the stent. BCs are applied as pressure drop at the top inlet (red) and as velocity outlets at the coronaries (LCA left-coronary artery, RCA: right-coronary artery)

2.5. Flow analyses

For each configuration investigated, a transient analysis was performed in Ansys Fluent. Inflow BCs were applied at the aortic inlet as scaled pressure drop (De Jaegere et al. 2016) to account for the increase in LV pressure due to the aortic regurgitation. Flow BCs were imposed at the coronary outlets (Pappano and Wier 2013), and simulations were solved for three successive cycles via computational fluid dynamics (CFD) (Fig. 5). Blood was modeled as two-phase Newtonian fluid with viscosity of 3.5 cP and density of 1065 kg/m³. The platelets were assumed as neutrally buoyant spherical particles with 3 μm diameter and the particle-fluid interactions, such as drag, lift and Basset forces, are accounted for (Girdhar et al. 2012). Specifically, these particles were seeded inside the fluid domain through an injection plane placed on the aortic side of the TAV leaflets. Particles were distributed in the region close to the wall which covers the paravalvular area where PVL gaps are expected to form (Fig. 11). Blood was modeled as Newtonian fluid, and the flow was assumed to be laminar. As the calculation of Reynolds number is not trivial due the geometrical features and distribution of the paravalvular gaps, a comparative analysis on one arbitrary model was performed to see whether or not a turbulence flow model is necessary. For this purpose, we employed SST k-ω turbulence model to solve unsteady Reynolds averaged Navier-Stokes equations, due to its advantages in handling both near-wall and freestream regions in the transition range over other two-equations models (Aftab et al. 2016). Difference in total regurgitant volume was approximately 0.3%; therefore, a laminar flow model was employed for all the cases.

Fig. 11.

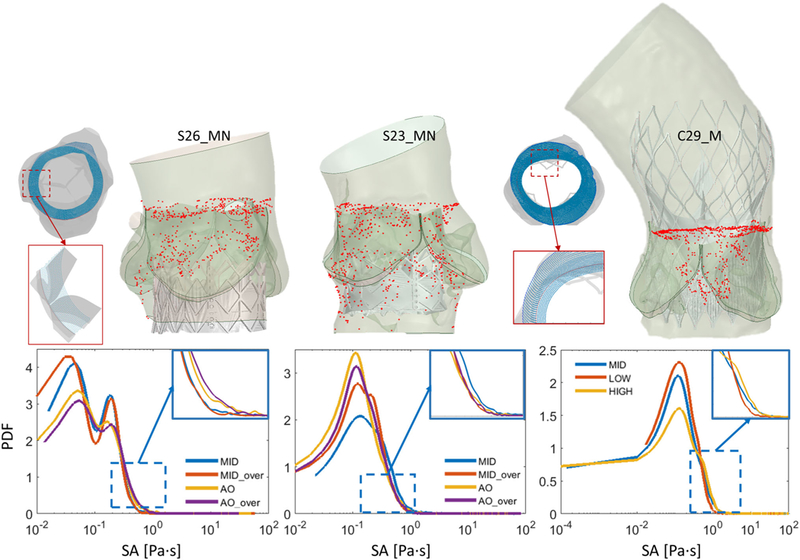
(Top) Top view of the particles injection seeding for a SAPIEN and a CoreValve case. Zoom-in showing particle distribution on the injection plane along the sinus wall (PVL01 and PVL02) and stent profile (PVL03). Snapshots of the particle tracking during the flowanalyses showing convection of the platelets across the paravalvular gaps for three midway cases (S26_MN, S23_MN, C29_MN). (Bottom) PDFs of SA calculated for each configuration across the three cases with zoom-ins highlighting the difference between SA distributions toward higher SA range

The flow stress loading history along the platelet Lagrangian flow trajectories through the gaps, with the stress accumulation (SA), was computed by incorporating the combined effect of flow stress and exposure time. This approach was extensively described and utilized in investigating thromboresistance in cardiovascular devices (Chiu et al. 2014; Marom and Bluestein 2016). The stress tensor extracted from each simulation along the corresponding trajectories was rendered into an average scalar stress value (σ) and the SA calculated as follows:

$$\text{SA}=\sigma \cdot t_{\text{exp}}=\underset{t_0}{\overset{t_{\text{exp}}}{\int }}\sigma (t)\text{d}t\approx \sum _{i=1}^N{\sigma }_i\cdot \Delta t$$

where σ_i is the scalar stress value at time step i, extracted from the total stress tensor, and Δt is the corresponding time step size between successive time steps (Xenos et al. 2010). The SA values (in Pa·s) were then collapsed into a probability density functions (PDF) to statistically represent the distribution of the SA of all trajectories (the “thrombogenic footprint”), and to facilitate the comparison among all the configurations. The comparisons were focused on two ranges of the PDF—the main mode (bulk flow) and the tail region (trajectories at the higher and riskier SA range, therefore more prone to platelets activity) (Xenos et al. 2010). Simulation timestep was set to Δt=0.005 s after a time step sensitivity analysis was performed. Volumetric flow rate was computed at the LV side of the ROI and utilized to calculate the effective regurgitant orifice area (EROA) and integrated over the diastole duration to compute the total regurgitant volume in one cardiac cycle. EROA (cm²) calculation was adapted from the effective systolic opening area, commonly utilized to test hydrodynamic performance of heart valves and prescribed in the ISO-5840, as follows:

$$\text{EROA}=\frac{Q_{\text{RMS}}}{51.6\cdot \sqrt{\Delta P/\rho }}$$

where Q_RMS (ml/s) is the root mean square of the volumetric flow in diastole, ΔP (mmHg) is the transvalvular pressure difference, and ρ (g/cm³) is the density of the blood.

3. Results

3.1. Anchorage assessment

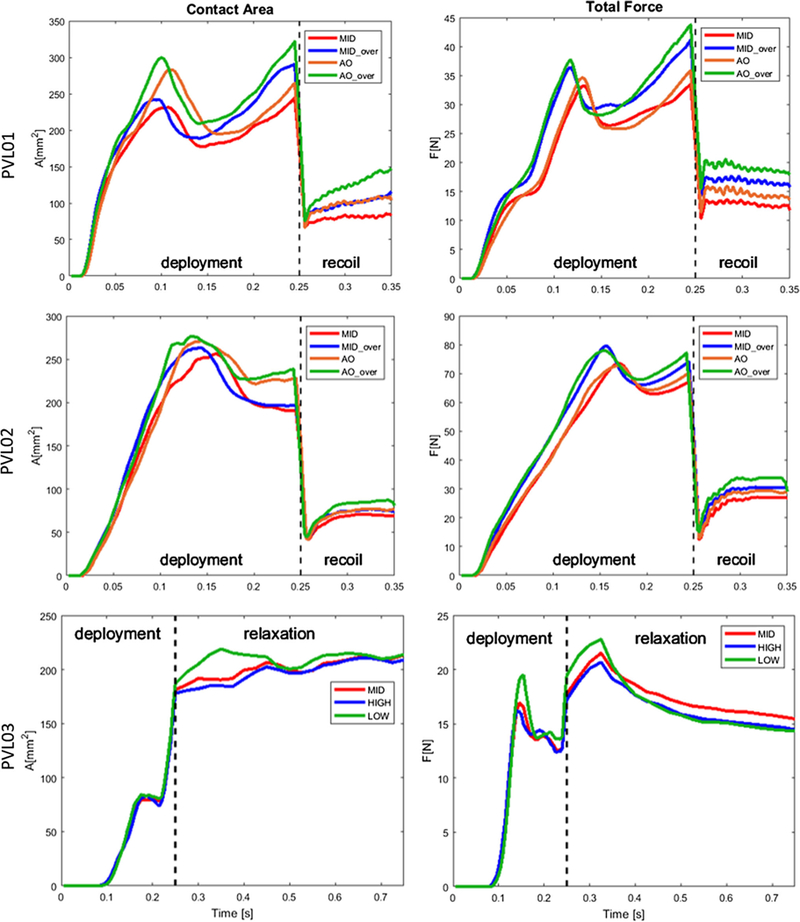
Four configurations for the SAPIEN cases (PVL01 and PVL02) and three for the CoreValve case (PVL03) were analyzed and compared in terms of native tissue stresses, total contact area, and total contact forces exerted from the TAV device. The total contact area was calculated and averaged based on the triangular elements on the surface of the AR so that they are independent on the model mesh density (Bianchi et al. 2016). In the first two cases contact area and force drops occurred at the beginning of the recoil phase, when the contact with the balloon was disabled. Total contact area and total contact force plots for each case are shown in Fig. 6. In the two SAPIEN cases, the aortic over-expanded configuration led to the highest contact area at the end of the recoil (A_S26__AO = 147.4 and A_S23__AO = 80.7 mm²), whereas comparable values were obtained for the CoreValve case (A_C29__M = 213.4, A_C29__A = 208.8, A_C29__V = 213.9 mm²) at the end of the relaxation phase. The total contact forces were the highest in the over-expanded cases, in the aortic (F_S26__AO = 17.9 N) and in the midway (F_S23__MO = 30.5 N) configuration for the 26 mm and 23 mm SAPIEN cases, respectively. The 23 mm SAPIEN resulted in lower contact area and higher contact force, which is a result of a more localized interaction with the soft tissue and a consequence of the larger calcification distribution in situ. In fact, calcification volumes calculation reveals that PVL02 had significantly larger calcification deposits (V_PVL02 = 1561 mm³) than the other two cases (V_PVL01 = 524, V_PVL03 = 689 mm³), and they extend into the LVOT leading to reduced stent expansion and potential larger paravalvular gaps. The CoreValve case resulted in larger contact area since it has longer structure that extends on the ascending aorta wall in its distal part, not just to the AV leaflets. In all the configurations, the CoreValve stent did not experience complete distal anchorage, with larger contact on the outer curvature of the aorta and poor contact on the inner side, mainly due to the presence of a massive calcific deposit above the right-coronary ostia (Fig. 7).

Fig. 6.

Stent anchorage calculated for the three cases, presented in terms of total contact area (left column) and total contact force (right column). In PVL01 and PVL02, anchorage is calculated during balloon deployment and stent recoil phases, whereas in PVL03 the simulation was divided in catheter retraction (deployment) and stent relaxation

Fig. 7.

Contact area distribution on the inner sinus and ventricular side of the AV leaflets for the three cases at the end of the stent recoil/relaxation phase. Bottom view for PVL01 and PVL02 showing more circular distribution of the contact area (top and mid row). Frontal/top view for PVL03 showing concentration of contact area on bulky calcific deposit in the non-coronary leaflet (bottom row)

3.2. PVL degree assessment

The resulted 11 FE AR geometries in the recoiled state, which were investigated to assess anchorage, were then extracted and used to build the post-deployment flow analyses. A turbulent analysis was conducted for S26_MN and no noticeable differences with the laminar model were observed in terms of flow distribution and magnitudes.

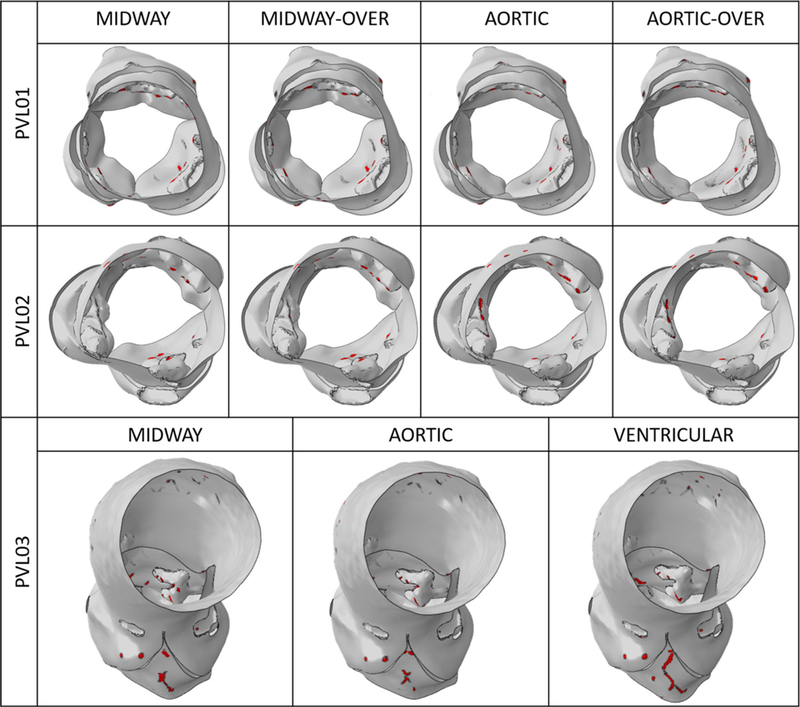
Figure 8 shows the diastolic flow in all the configurations on planes where the regurgitant jets are visible, in the instance of maximum transvalvular pressure difference (75 ms after the beginning of diastole). PVL01 showed the presence of a supra-skirtal large jet around the right-coronary cusp across all four configurations, mainly developing in proximity to the near TAV commissure. Upon 1-ml balloon over-expansion the degree of regurgitation in the same jets slightly reduces, as visible in S26_MO, at the expense of a more pronounced central regurgitation orifice. On the other hand, aortic positioning resulted in a more noticeable regurgitation with higher peak velocity in the same region of the stent. Compared to the midway configuration, aortic positioning (S26_AN, S26_AO) resulted in larger flow recirculation at the bottom of the stent (in the LVOT) which prolonged until the end of diastole. Additionally, balloon over-expansion did not offer a significant PVL reduction. PVL02 was the case with largest paravalvular regurgitation.A large posterior jet on the left-coronary cusp in proximity to the non-coronary cusp and a smaller jet on the opposite cusp were observed. The location of the posterior jet is in close proximity to a large sub-annular calcific deposit which caused sub-optimal stent expansion and anchorage to the AR. Comparably to PVL01, midway configurations (S23_MN, S23_MO) resulted in higher PVL reduction compared to aortic positioning (S23_AN, S23_AO), where significant macroscopic regurgitation around large portion of the stent was observed. Given the higher flow rate across the PVL gaps, the flow starts to accelerate on the aortic side of the AV leaflets and is entrained through the posterior paravalvular gaps. In S23_AN, S23_AO, blood accelerates below the stent being directed from the near bulky calcification. In PVL03, a posterior jet in the commissural region between left and non-coronary cusp was observed, in proximity to two bulky calcific deposits at the base of the AV leaflets. The aortic configuration (C29_A) resulted in the highest PVL reduction, whereas the ventricular one (C29_V) resulted in PVL worsening, with peak velocity approaching 4 m/s and noticeable flow acceleration at the top the AV. Additionally, in C29_V the jet tends to expand circumferentially toward the non-coronary leaflet, as shown from the velocity vectors in Fig. 8. For each case, time-dependent volumetric flow rate (Fig. 9) and EROA (Fig. 10, left) were calculated below the TAV at the bottom boundary of the ROI. Volumetric flow rate was then integrated over the diastolic time to calculate the total regurgitant volume (Fig. 10, right) per cardiac cycle. These values confirmed the above observations. In PVL01 implantation depth mattered more than the balloon inflation volume, with 32.0% in PVL reduction from S26_MN to S26_AN (and 38.9% from S26_MO to S26_AO) against 10.0% in volume change from S26_MO to S26_MN (and 5.2% from S26_AO to S26_AN). The impact of the procedural parameters was remarkably reduced for PVL02, with 6.2% volume reduction from S23_MO to S26_MN and only 1.3% reduction from S23_AN to S23_MN. Finally, for PVL03 the severity of PVL decreases by 22.1% and increases by 46.7% by positioning the TAV more downstream and upstream, respectively (Fig. 10, right). Location of PVL was qualitatively compared to clinical measurement to validate the models’ predictions. In all the three clinical cases, a nominal balloon inflation was performed and a midway TAV positioning was attempted. Excellent agreement on the location was found, as summarized in Table 3, where the effect of the procedural parameters on PVL grading is also presented (Pibarot et al. 2015).

Fig. 8.

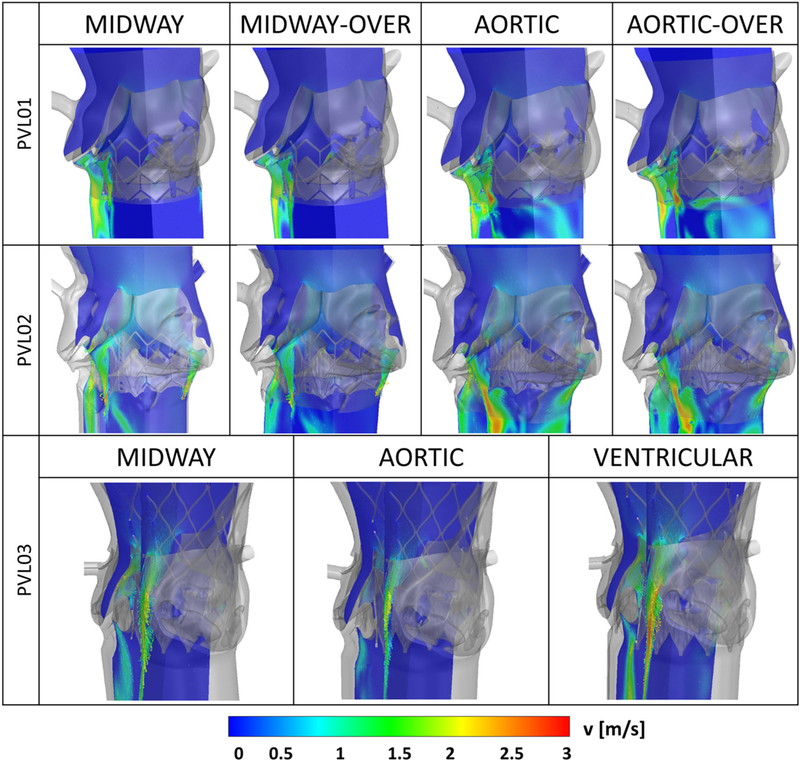
Velocity magnitude contours and vectors on longitudinal planes showing paravalvular regurgitant jets for each parametric configuration analyzed, for the SAPIEN cases (top and mid row) and the CoreValve case (bottom row)

Fig. 9.

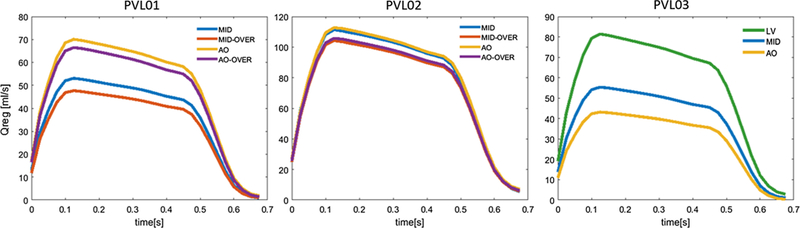
Transient volumetric flow rate calculated on the ventricular boundary of the ROI during diastole for the three cases. Configurations are depicted in different colors. The waveforms resemble the pressure-based BC applied across the TAV

Fig. 10.

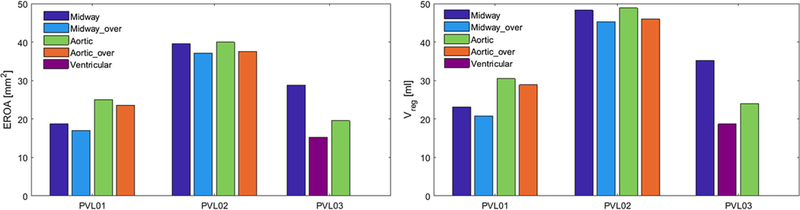
EROA (left) and total regurgitant volume (right) calculated for each analyzed configuration for the three cases

Table 3.

PVL outcome for each case and comparison between clinical measurements and model prediction, in terms of severity and location of PVL

Clinical report	Configuration	Model PVL degree	Model PVL location
PVL01
Mild-to-moderate anterior	S26_MN	Mild to moderate	RCL (anterior)
	S26_MO	Mild to moderate	RCL (anterior)
	S26_AN	Mild	RCL (anterior)
	S26_AO	Mild	RCL (anterior)
PVL02
Moderate posterior	S23_MN	Moderate-to-severe	LCL + NCL (posterior)
	S23_MO	Moderate	LCL + NCL (posterior)
	S23_AN	Moderate-to-severe	LCL + NCL (posterior)
	S23_AO	Moderate-to-severe	LCL + NCL (posterior)
PVL03
Moderate posterior+ trivial anterior	C29_M	Mild to moderate	LCL/NCL (posterior)
	C29_A	Mild	LCL/NCL (posterior
	C29_V	Moderate	LCL/NCL (posterior) RCL (anterior)

RCL right-coronary leaflet; LCL left-coronary leaflet; NCL non-coronary leaflet

3.3. Thrombogenic potential assessment

Approximately 6000 particles representing platelets were seeded on a plane located above the TAV leaflets at the beginning of diastole for each configuration. Specifically, for the PVL03 configurations, particles were seeded with higher density along the profile of the stent struts, in such a way as to cover the projected area of the paravalvular gaps. For the other two cases, particles were seeded with uniform density along the sinus inner wall (Fig. 11, top). PDFs of three cases are presented in Fig. 11, showing the distribution of SA for each configuration analyzed. In PVL01, PDFs present a bi-modal shape with the second mode being attenuated for the two aortic configurations. In PVL02, all the curves are slightly shifted toward higher SA due to the larger regurgitation volumes. Specifically, S23_MN led to the highest thrombogenic potential, as shown from its lower peak and slight translation toward higher SA range. Interestingly, the aortic configurations (S23_AN, S23_AO) experienced higher main-mode peak and the best performance in terms of thrombogenic potential. In PVL03, all the curves share similar patterns, with the aortic configuration leading to the highest SA, a possible consequence of the paravalvular gaps narrowing.

4. Discussion

In this study, the influence of procedural TAVR deployment parameters on the degree of post-deployment PVL was investigated using computational biomechanics tools. Specifically, the aim was to determine the effect of TAV implantation depth and balloon inflation volume on stent anchorage, degree of paravalvular regurgitation, and the resultant thrombogenic potential. As these effects are tightly coupled to the complex interaction between the TAV and the anatomy of the surrounding diseased tissue, those need to be considered on a case by case basis. Therefore, FE and CFD methods were employed in three patient-specific anatomies. This set of clinal cases was chosen since these patients endured non-trivial PVL after TAVR. The post-deployment echo data were utilized to verify the accuracy and the predictability of the models in terms of PVL degree and jet location.

Given their paramount role during the deployment, the interaction between calcifications with the surrounding soft tissue needs to be incorporated. In this work, these deposits were embedded in the AR wall, allowing a more accurate replication of the pathological tissue than before (Bosi et al. 2018; McGee et al. 2018; Morganti et al. 2016; Wang et al. 2014).

The stent anchorage was the first device performance index which was investigated for the three clinical cases. In the two SAPIEN cases, positioning the stent downstream and over-inflating the balloon led to the highest anchorage forces and largest contact area. The peak occurred when maximum expansion was reached, before dropping during balloon retraction. It is important to notice that contact during the balloon deployment is not predictive of the anchorage after the recoil, as shown in Fig. 6. For example, S26_MO and S26_AN had identical final contact area despite the fact that the over-expanded configuration had higher peak value at the end of the deployment. Additionally, contact tends to steadily increase in the recoil phase suggesting a progressive relaxation of the soft tissue over the stent after being stretched upon balloon expansion. The self-expanding CoreValve in PVL03 shows different dynamics, with the contact area rapidly rising due to the unsheathing of the stent and a following slower adaptation in the relaxation phase. Contact area also experiences a transient plateau at about two-third of the deployment phase, due to the additional time required for the distal part of the stent to uncover and get in contact with the sinotubular junction region of the aortic wall.

Regurgitation was addressed in previous studies by calculating the paravalvular gap size, but without an accurate and direct flow quantification (Bosi et al. 2018; Bosmans et al. 2016; Morganti et al. 2014; Schultz et al. 2016). Our CFD regurgitation results revealed the relative influence of implantation depth and balloon inflation volumes on post-TAVR degree of PVL in the three cases investigated. Their effects are highly dependent on the patient-specific anatomy and calcification distribution, as demonstrated by the difference in regurgitation volume between PVL01 and PVL02 (Fig. 9). The latter case experienced larger regurgitation volume (threefold increase) which can be explained by the overall larger AR calcification mass and the presence of bulky deposits in the annular region extending toward the ventricular cavity, which prevents stent adequate apposition. Specifically, the bulky calcification located in the left-coronary leaflet is responsible for the incomplete stent deployment and apposition on the side of the AR (where the largest PVL jet occurs); additionally, another large deposit located more distally on the opposite non-coronary cusp locks the top strut of the stent in a position which prevents further opening. This explains the limited impact of the procedural parameters on the post-deployment PVL. This patient was diagnosed with moderate PVL and implantation depth resulted to have negligible influence on the post-deployment state. To note, this patient received a 23 mm TAV which provided a 3.6% annulus oversizing (which basically nullifies according to the model annular dimension), rather than the larger stent (26 mm) which would provide a riskier but potentially more effective 14% oversizing. Clinically, it is generally accepted to reduce oversizing in highly calcified anatomies to reduce the risk of AR rupture (Barbanti et al. 2013; Pasic et al. 2015). Given the flow analyses results, a 26-mm TAV implantation could have been an alternative valuable strategy. Inversely, PVL01 showed that implantation depth had a large effect on PVL degree. Interestingly, the configuration which resulted in lower PVL (S26_MO) did not coincide with the highest anchorage one (S26_AO) resulting from the FE models, suggesting that contact area and pressure exerted from the TAV cannot be correlated with the degree of post-deployment PVL. The main jet originated between the stent struts above the skirt in all configurations, with the aortic configuration leading to an additional jet in the middle of the RCL which merged with the first one at the LV side of the skirt. This developed a larger regurgitation and more pronounced re-circulation area on the opposite side (below the LCL). The flow in this region of the domain was more chaotic toward the end of the diastole, when the transvalvular pressure decreases, as compared to the midway configurations. In the self-expanding case (PVL03) implantation depth was the only parameter at play and it did have a visible effect on the PVL. Ventricular positioning led to the most severe PVL, and it was the only configuration in which the anterior jet became more apparent. In all the cases, the CoreValve stent properly sealed in the left–right-coronary leaflets commissures, but it resulted in less stent apposition on the opposite side (toward to non-coronary leaflet), which is mainly caused by an arc-shape calcification spanning across the entire leaflet. This also led to an apparent inward deformation on the ventricular side of the TAV stent which was not resolved upon different positioning. Positioning in self-expanding valves remains a crucial point since delivery systems allow partial retrievability of the valve; therefore, a more precise implantation depth is achievable.

PVL results from Fig. 10 (right) were ranked based on the unifying 5-class grading scheme (Pibarot et al. 2015) so that a semi-quantitative comparison with the patient-specific echo reports would be possible. Excellent agreement was found in terms of PVL jets location, but a quantitative comparison cannot be rigorously done since PVL clinical score was assigned upon visual inspection of the ultrasound images. No specific information was provided on the prosthesis placement; therefore, it was assumed that physicians attempted to implant the prosthesis in the midway location employing nominal inflation. Based on these considerations, a better outcome, in terms of PVL degree, could have been achieved for PVL01 and PVL03 by over-expanding the stent and by positioning the TAV more distally, respectively.

Even though there is no statistically significant correlation being described and demonstrated, moderate PVL could be associated with abnormal flow patterns over the leaflets and in the left main coronary artery that could lead to TAV thrombosis and accelerated progression of atherosclerosis (Couture et al. 2017). Furthermore, the thrombus formation that we hypothesize and which could be more directly related to PVL is thrombus embolism. This could be explained by the local PVL flow, characterized by high (diastolic) pressure gradients, and the narrow gaps, thus leading the platelets to be exposed to high flow shear stress. Despite its currently limited clinical occurrence, this phenomenon is common enough to be addressed clinically (Scotten and Siegel 2014).

Therefore, to better investigate the relationship between PVL and platelet activation, the thrombogenic potential of each procedural configuration was assessed by calculating the SA along particles trajectories in the PVL region. All the PDFs of PVL01 show comparable patterns, with aortic over-inflated configuration (S26_AO) more shifted toward the right (higher SA). This can be explained by the higher velocity observed in the PVL jets that leads to higher flow shear stress. Higher SA values were observed for PVL02, in accordance with the overall larger regurgitation volumes. Comparably, in PVL03, PDFs differ in the main-mode peak, with the aortic configuration (C29_A) having a slight shift toward the right as a consequence of partial closure of the paravalvular gap. PVL02 and PVL03 PDFs show comparable patterns, having both modes in the range of SA between 10^–2 and 1 Pas and the majority of the PDFs in the |1.25–2.25 Pas range. PVL3 configurations, however, resulted in absolute lower SA as for the longer left tail, which is absent in PVL02 configurations. The information extracted from the PDFs clearly informs that the PVL variation affects the potential for platelet activation. For example, in PVL03, the reduction in PVL degree for C29_A led to slightly higher thrombogenic potential, as platelets experienced higher shear flowing through smaller paravalvular gaps. A similar relationship was observed for PVL01. On the other hand, when the regurgitation volume is considerably larger (PVL02), such cause–effect relation between PVL reduction and susceptibility to platelet activation reflects a more-complicated interaction.

The presented computational approach has demonstrated capability to predict TAVR complications; however, some limitations need to be considered. To robustly validate the model, a larger set of clinical cases needs to be investigated, inclusive of successful cases of TAVR (absence of PVL) or mixed scenarios (implantation of a different TAV type than the one employed clinically), but the validity of the results stands due to their comparative nature. It should be emphasized that most of these comparisons were done between cases where only clinical parameters were changed while the anatomy and device were not. Moreover, it has been demonstrated TAV rotational orientation may have an impact on procedural outcome (Bailey et al. 2016); however, since this is currently not an option controllable by the interventionalist in the catheterization laboratory, such parameter was not included into the analysis. Furthermore, to adequately capture the real post-TAVR hemodynamics a patient-specific fluid–structure interaction model needs to be built and run on the full cardiac cycle. Nevertheless, given the high computational cost involved, derived from the necessity to have refined mesh to capture patient-specific anatomical features, these analyses may become prohibitive, as they ultimately need to be clinically applicable.

5. Conclusions

In conclusion, we have developed a computational approach by employing FE and CFD techniques to investigate post-TAVR hemodynamics in retrospective clinical cases affected by PVL. The models offered quantitative information on TAV stent anchorage and paravalvular regurgitation volumes, and these results were qualitatively compared to correspondent clinical measurements. The effect of implantation depth and balloon inflation volume on post-procedural complications provided useful insights on how the physician’s choice would impact the procedural outcome. Positioning was shown to influence PVL up to 47% in specific cases, thus leading to remarkably different post-procedural outcomes. Further investigation on a larger cohort of patients is needed to verify the accuracy of the models. This study demonstrated that rigorous and realistic patient-specific numerical models could potentially serve as a valuable tool to assist in pre-operative TAVR planning and TAV selection to ultimately reduce the risk of clinical complications.