Segmenting the Brain Surface from CT Images with Artifacts Using Locally-Oriented Appearance and Dictionary Learning

Abstract

Accurate segmentation of the brain surface in post-surgical CT images is critical for image-guided neurosurgical procedures in epilepsy patients. Following surgical implantation of intra-cranial electrodes, surgeons require accurate registration of the post-implantation CT images to pre-implantation functional and structural MR imaging to guide surgical resection of epileptic tissue. One way to perform the registration is via surface matching. The key challenge in this setup is the CT segmentation, where extraction of the cortical surface is difficult due to missing parts of the skull and artifacts introduced from the electrodes. In this paper, we present a dictionary learning-based method to segment the brain surface in post-surgical CT images of epilepsy patients following surgical implantation of electrodes. We propose learning a model of locally-oriented appearance that captures both the normal tissue and the artifacts found along this brain surface boundary. Utilizing a database of clinical epilepsy imaging data to train and test our approach, we demonstrate that our method using locally-oriented image appearance both more accurately extracts the brain surface and better localizes electrodes on the post-operative brain surface compared to standard, non-oriented appearance modeling. Additionally, we compare our method to a standard atlas-based segmentation approach and to a U-Net-based deep convolutional neural network segmentation method.

I. INTRODUCTION

SEGMENTATION of clinical images is a challenging medical image analysis task. This task is particularly difficult for patients who have undergone surgical procedures, where images are often of imperfect quality, subject to artifacts, and can be missing normal anatomical features. Such challenges arise in image-guided planning of neurosurgical procedures in epilepsy patients. Epilepsy is a neurological disorder in which seizures temporarily disrupt brain function. Surgical resection of ictal tissue, e.g. tissue involved in the generation of the seizures, can be an effective method to reduce or eliminate seizures for certain patients who do not respond favorably to medication [1]. In one method, and the current “gold-standard” to localize ictal tissue in different regions of the brain suspected to be causing the seizures, clinicians monitor brain activity through a diagnostic procedure that includes a craniotomy and surgical implantation of both intracranial electrodes on the brain surface and depth electrodes within the brain [2]. However, before performing a resection, surgeons must localize the electrode locations corresponding to functionally eloquent brain tissue, e.g. motor, sensory, and language regions, which may be identified by pre-operative imaging such as anatomical magnetic resonance (MR) imaging (MRI) and functional imaging modalities such as functional MRI (fMRI), PET, and SPECT [3], [4]. Accurate registration of this pre-operative multi-modal imaging to the electrode locations is, therefore, critical for surgical planning.

A variety of methods to localize the implanted electrodes within the pre-implantation imaging data have been proposed. Intra-operative digital photography may be used to identify the implanted surface electrodes, which may then be manually localized with respect to the pre-op MRI brain surface [5], [6]. Alternatively, the electrodes can easily be identified in a post-implantation computed tomography (CT) image. Surface electrodes identified in the post-op CT can then be projected to the nearest point on the pre-op MRI brain surface after rigid registration [7]. However, this localization strategy neither accounts for non-rigid tissue deformations nor does it allow for localization of sub-dural electrodes. These sub-dural electrode displacements can be estimated, for example, using a kernel-based averaging of the surface electrode displacements [8]. In some cases, but not everywhere, post-op MRI is available. Here, intensity-based registration methods may be used to register the post-op CT with the post-op MRI. Rigid registration between the two post-op modalities [9] suffices, in this case, because negligible levels of non-rigid deformation occur between the two image acquisitions. Nevertheless, surgeons ultimately want to integrate the electrode information into the surgical plan, which requires visualizing the electrodes within the pre-implantation imaging space.

Therefore, the current best method to co-register the implanted electrodes and the pre-implantation imaging involves two registration steps. First, the post-op CT is rigidly registered to the post-op MRI, and, second, to compensate for the non-rigid post-surgical deformations, the post-op MRI is non-rigidly registered to the pre-op MRI image. Even though the post-op MRI contains multiple imaging artifacts as a result of the implanted electrodes and image quality is relatively poor compared to the pre-op MRI, accurate non-rigid registration of the pre-op and post-op MRIs is still possible. The soft tissue contrast properties of MRI provides detailed anatomical structures that are critical for accurate image registration. Once these two registration steps are complete, the electrodes may then be transformed to the pre-implantation imaging space to facilitate co-visualization and localization of the electrodes with respect to this multi-modal data. Unfortunately, the post-implantation MRI acquisitions present a number of challenges: (i) it is inconvenient for the patient, who has implanted electrode wiring protruding from their skull, (ii) a potential source of infection for the patient as they are transported to and from the scanner, (iii) an additional expense, and (iv) may not be available at all institutions. In previous work, we presented a method to directly register the post-op CT to the pre-op MRI using a non-rigid statistical deformation model to constrain the intensity-based registration [10]. However, intensity-based non-rigid registration methods are ill-suited to register the pre-op MRI and post-op CT due to (i) poor soft tissue contrast in the CT imaging presenting minimal anatomical structures within the brain, (ii) a lack of anatomical correspondences, such as removal of the skull during surgery, between the two acquisitions, (iii) the presence of imaging artifacts and intensity inhomogeneities caused by implanted electrodes, and (iv) non-rigid brain surface deformations that can oftentimes be larger than 1 cm [11].

Surface-based registration methods offer an alternative to intensity-based methods for co-registering the post-implantation CT and the pre-implantation MRI. Numerous surface-based, non-rigid registration methods exist [12], [13], [14]. In this work, the key challenge is not the surface matching and registration itself, but rather the extraction of the cortical surface from the images. Well-tested methods exist to extract the brain surface from pre-op MRIs [15]. Segmenting the brain surface from post-op CT images, on the other hand, is challenging due to (i) large portions of the skull being removed for the craniotomy, (ii) imaging artifacts caused by the implanted electrodes, (iii) the most likely non-Gaussian, appearance of the brain surface, and (iv) the variability in the location of the craniotomy across patients, which can confound global models of appearance [16].

In this work, we present a segmentation method using locally-oriented image patches to segment the cortical brain surface in post-op CT imaging. This manuscript significantly expands upon our previous conference publication [17]. As previously shown, a standard surface-based registration method between two reliable sets of surfaces provides a superior registration compared to intensity registration [17]. We therefore focus this work solely on the segmentation aspect of the project. In this paper, we include rigorous validation experiments and provide extensive experiments to justify method parameter choices, as well as compare our approach to both standard atlas-based segmentation and to a U-Net-based deep convolutional neural network segmentation of the same data. In Sec. II, we detail our methods for locally-oriented image patch appearance learning and segmentation (Fig. 1). As an alternative to using image intensity information to determine the local orientation of image patches [18], we instead use the local geometry of our estimated surface segmentation to orient the patches. From these patches, we learn a sparse representation of the brain cortical surface appearance using a dictionary-learning framework to model textural appearance both inside and outside the surface bound-aries [19]. In contrast to the work of Huang et al. [19], which uses image patches canonically aligned with the image axes, our approach uses locally-oriented image patches along the evolving segmentation surface. By orienting the image patches with respect to local surface geometry, this oriented appearance model is invariant to rotational changes in the surface. Furthermore, rather than creating unique intra-subject appearance models for each subject, our approach builds an inter-subject appearance dictionary using a population of clinical training data. In Sec. III, we present experimental results demonstrating accurate segmentation of the cortical surface from post-implantation CT images and additionally compare our results to standard atlas-based segmentation. Finally, Sec. IV concludes with a discussion of our results and presents future research directions.

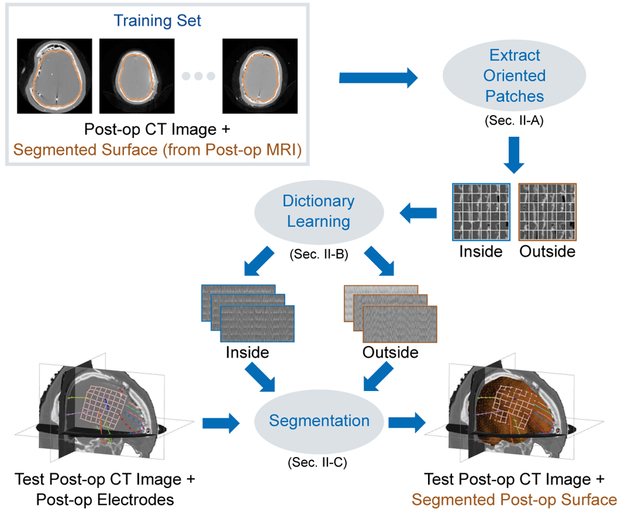
Fig. 1.

In order to segment the cortical brain surface in post-surgical CT images in epilepsy patients, we learn a model of the brain surface’s appearance. Instead of using image patches oriented along the image axes, we use the local surface geometry of the segmentation surface to orient the appearance patches. From a training set of post-op CT images with ground-truth brain segmentation surfaces (from registered post-op MRI), our approach learns two dictionary-based models of image appearance, one inside the brain surface and one outside. These learned models are then used to accurately segment the cortical surface in test post-op CT images. The resulting post-op CT segmentation can then be registered to a pre-op MRI segmentation surface using surface-based registration methods in order to localize and visualize post-implantation electrodes with multi-modal pre-implantation imaging to guide surgical procedures.

II. METHODS

To train our model of brain surface appearance in post-surgical CT images, we make use of a database of N neurosurgical epilepsy patients. This database contains the set of images $\mathcal{I}=\{I_{\text{MR},i}^1,I_{\text{MR},i}^2,I_{\text{CT},i}^2\mid i=1,\dots ,N\}$, where $I_{m,i}^t$ denotes pre-op images acquired at time t = 1 and post-op images acquired at time t = 2 using imaging modality m ∈ {MR, CT} for patient i. For each patient, we perform the following preprocessing steps as currently done in practice. (i) We create brain surfaces $S_i^1$ and $S_i^2$ from the pre-op and post-op MR images, respectively, by extracting isosurfaces of the brain masks generated by the Brain Extraction Tool (BET) [15]. A trained expert manually refines the segmented brain masks, if necessary. (ii) Next, we rigidly register $I_{\text{CT},i}^2$ to $I_{\text{MR},i}^2$ using the normalized mutual information (NMI) similarity metric [20] to estimate the transformation T_CT→MR,i. Sec. II-A begins by introducing locally-oriented image patches, which we use to train a model of cortical surface appearance in Sec. II-B. We then use this model to perform segmentation of the cortical surface in post-op CT images in Sec II-C. We note that the post-op MRI $I_{\text{MR},i}^2$ and its surface $S_i^2$ are used only in the training phase and not in the testing phase. Fig. 1 illustrates and summarizes our training and segmentation framework.

A. Locally-Oriented Image Patches

For a 3D image I : ${\mathrm{\Omega }}_I\subset {\mathbb{R}}^3\mapsto \mathbb{R}$ mapping points from the spatial domain Ω_I to image intensity values, we define an orientable local image patch Φ centered about u ∈ Ω_I as a set of intensity values:

$$\mathrm{\Phi }(I,\mathbf{u})=\{I(\mathbf{u}+\mathbf{R}\mathbf{t})\mid \mathrm{\forall }\mathbf{t}\in \mathrm{\Theta }\},$$ (1)

where, $\mathbf{R}\in {\mathbb{R}}^{3\times 3}$ is a rotation matrix defining orthonormal basis vectors and Φ is the set of d image intensity values sampled at patch template points $\mathrm{\Theta }=\{{\mathbf{t}}_i\mid {\mathbf{t}}_i\in {\mathbb{R}}^3,i=1,\dots ,d\}$. Typically in image processing applications, image patches are statically aligned with the image axes such that R uses the identity matrix as the canonical basis, i.e. R = I, while Φ consists of a grid of isotropically spaced sample points centered about the patch origin. As an example, a 5 × 5 × 5 isotropic image patch Φ centered at image location u would be specified by a set of d =125 sampling point locations Θ that define grid point locations relative to the patch origin u. We refer to this patch format as standard image patches.

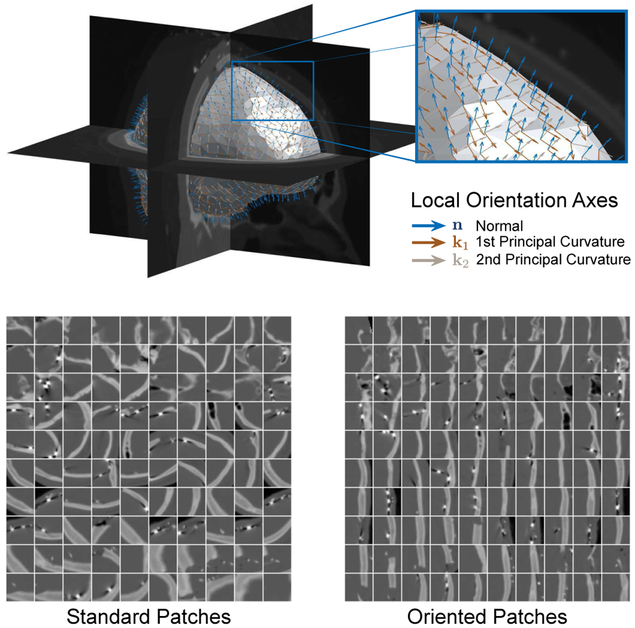
In this work, we use data-driven oriented image patches, where the orientation of the patch R is determined by local surface geometry. For each point on the surface of interest u ∈ S, the local, outward-facing surface normal $\mathbf{n}\in {\mathbb{R}}^3$ and the directions of principal curvature ${\mathbf{k}}_1,{\mathbf{k}}_2\in {\mathbb{R}}^3$ [21] define an orthonormal basis R = [n∣k₁ ∣k₂] that orients the patch Φ(u) in (1) to the local geometry by rotating the Θ sampling point locations. To illustrate the effect of local surface geometry orientation on image patches, Fig. 2 compares image patches using either standard or oriented sampling at corresponding points along a surface u ∈ S. Orienting image patches in this way allows for texture appearance along the surface to be invariant to changes both in location along the surface S and to rotations of the underlying image data.

Fig. 2.

Examples of local surface geometry oriented axes and their resulting locally-oriented image patches. We compare the oriented patches to their corresponding canonical image patches oriented along the image axes. The segmentation surface S and the local surface geometry define a local orthonormal basis for the oriented image patch specified by the normal direction n and directions of principal curvature k₁, k₂. For illustration purposes, we show a large patch size of 33 × 33 × 33 and display the central slice.

B. Training the Cortical Surface Appearance Model

In order to learn a model of brain boundary appearance in the post-op CT image, we must provide a ground-truth segmentation of the cortical surface in this image. Here, we make use of the post-op MRI brain segmentations $S_i^2$ (created using BET [15] with manual refinement be a trained technologist) available at our institution to identify the brain cortical surface in the CT. For each subject i, we map the segmented post-op MRI brain surface to the post-op CT image space using the rigid transformation T_CT→MR,i such that $S_i^{2^{\prime }}=T_{\text{CT}\to \text{MR},i}^{-1}\circ S_i^2$, where ○ is the transformation operator. To model the image appearance both inside and outside the brain surface, we create two sparse representation models (dictionaries) D_in and D_out, respectively [19]. We train these models by extracting two sets of overlapping local image patches from each subject’s post-op CT images:

$$\begin{gathered} {\mathcal{P}}_{\text{in}}=\bigcup _{i=1}^N\left\{\mathrm{\Phi }(I_{\text{CT},i}^2,\mathbf{u}-\alpha \mathbf{n})\mid \mathrm{\forall }\mathbf{u}\in S_i^{2^{\prime }}\right\}, \\ {\mathcal{P}}_{\text{out}}=\bigcup _{i=1}^N\left\{\mathrm{\Phi }(I_{\text{CT},i}^2,\mathbf{u}+\alpha \mathbf{n})\mid \mathrm{\forall }\mathbf{u}\in S_i^{2^{\prime }}\right\}, \end{gathered}$$

where P_c denotes the sets for appearance classes c = {in, out} either inside or outside the surface boundary for all N subjects, and n is the outward facing local surface normal at u. Both to expand the area defined as being either outside or inside the cortical boundary and to account for possible errors in the surface segmentation, we extract patches from a narrow band region 0 < α ≤ 3.0mm around the surfaces $S_i^{2^{\prime }}$. Using all N subjects in the training set, these two dictionaries capture the varieties of textural appearance found within the narrow band regions near the brain surface boundary across the training population. As in Sec. II-A, we orient the image patches according to the local surface geometry at u.

For each image patch in ${\mathcal{P}}_c$, we transform the patch data into an appearance vector ${\mathbf{p}}_c\in {\mathbb{R}}^d$ by concatenating the patch intensity values, where d is the sample dimensionality determined by the chosen patch sampling template Θ in Sec. II-A. We normalize the p_c appearance vectors by subtracting the mean class intensity value (over all patches in the class) and then scaling to have unit length. Then, we model the distribution of p_c’s from all N training images using an overcomplete dictionary ${\mathbf{D}}_c\in {\mathbb{R}}^{d\times n}$ such that p_c ≈ D_cγ [22], where n is the number of dictionary atoms and γ is the sparse dictionary weighting coefficients. Fig. 3 shows two example dictionaries learned using either standard or oriented patches.

Fig. 3.

Example dictionary atoms learned using either standard or locally-oriented image patches. For illustration purposes here, we display the central slice through 33 × 33 × 33 atoms for dictionaries using n = 100 atoms with a sparsity constraint Γ₀ = 4.

Given a novel, normalized appearance vector sample p, we use the learned dictionaries D_c to reconstruct this sample by solving the sparse coding problem:

$$\underset{\gamma }{\text{min}}\Vert \mathbf{p}-{\mathbf{D}}_c\gamma {\Vert }_2^2\text{s.t.}\Vert \gamma {\Vert }_0\le {\mathrm{\Gamma }}_0,$$

where ${\mathrm{\Gamma }}_0\in \mathbb{N}$ is a target sparsity constraint. We solve this problem using an orthogonal matching pursuit (OMP) algorithm[23]. Next, we define the residual error

$$R_c(\mathbf{p})=\Vert \mathbf{p}-{\mathbf{D}}_c\gamma {\Vert }_2$$ (2)

for both the inside and the outside region classes. Here, the residual values R_c(p) are bounded 0 ≤ R_c(p) ≤ 1 because the appearance vectors are normalized to have unit length. In this case, values of R_c(p) = 0 correspond to perfect appearance sample reconstruction, which indicates strong membership to class c, and residual values of R_c(p) = 1 indicate that p could not be reconstructed well by D_c, which indicates poor membership to class c. Intuitively, if an image patch sample is from inside the cortical surface boundary then R_in(p) < R_out(p). Our approach to appearance modeling differs from that presented by Huang et al. [19] in that we perform appearance modeling individually for each level k = 1, …, K in a multi-resolution Gaussian image pyramid, which means that we train K dictionary pairs $\{{\mathbf{D}}_{\text{in}}^k,{\mathbf{D}}_{\text{out}}^k\}$ instead of concatenating appearances from multiple scales into a single multi-scale appearance vector.

C. Post-Implantation CT Brain Surface Segmentation

To segment a post-implantation CT not included in the training set $I_{\text{CT}}^2\notin \mathcal{I}$, we first register a template brain to this image to provide an initial brain surface segmentation estimate ${\widehat{S}}_{\text{init}}$ (Sec. II-C1) and then use our locally-oriented brain appearance model to accurately segment the brain surface $\widehat{S}$ (Sec. II-C2). Post-op MR imaging is not used in the segmentation phase.

1). Initial CT Surface Estimate:

Rather than relying on the pre-op MRI brain mask segmentation, which may contain segmentation errors, as the initial post-op CT segmentation estimate, we instead make use of the MNI Colin 27 average brain volume [24] brain mask S_MNI as a template, which has been manually segmented. To estimate the initial brain surface ${\widehat{S}}_{\text{init}}$ using the MNI template, we perform the following steps: (i) register the MNI brain surface S_MNI to the pre-op MR brain segmentation $S_{\text{MR}}^1$ using standard affine RPM surface registration [25], which gives the transformation T_MNI→MR; (ii) register the pre-op MRI $I_{\text{MR}}^1$ to $I_{\text{CT}}^2$ using standard intensity-based rigid registration by maximizing the normalized mutual information [20], which gives the transformation T_MR→CT; and (iii) transform the segmented MNI brain mask to post-op CT imaging space $I_{\text{CT}}^2$, i.e. ${\widehat{S}}_{\text{init}}=T_{\text{MR}\to \text{CT}}\circ T_{\text{MNI}\to \text{MR}}\circ S_{\text{MNI}}$. We use this surface as the initial estimate for our post-op CT cortical surface segmentation method detailed below.

2). Brain Surface Segmentation:

For all points on the segmentation surface $\mathbf{u}\in \widehat{S}$, we extract the locally-oriented image patch Φ(u), transform this patch into an appearance vector $\mathbf{p}\in {\mathbb{R}}^d$ (normalized), compute appearance model residuals from (2), and then compute the difference between these values as

$$D(\mathbf{p})=R_{\text{out}}(\mathbf{p})-R_{\text{in}}(\mathbf{p}).$$

If u lies within the true boundary of the cortical surface in the CT image then, intuitively, D(p) > 0. On the other hand, if u is outside the true boundary then D(p) < 0. Thus, the cortical surface boundary is located at the point u where D(p) = 0, i.e. the point belongs equally to the inside and outside classes. To find the cortical surface in $I_{\text{CT}}^2$, we minimize the following objective function

$$\widehat{S}=\underset{S}{\text{min}}{\int }_S\Vert D{\Vert }_2^{2}dS.$$

We solve this optimization problem by iteratively updating the surface in a greedy manner, where at each iteration t, we update the surface points

$${\mathrm{u}}_{t+1}={\mathrm{u}}_t+\sigma D({\mathrm{p}}_t){\mathrm{n}}_t+{\mathrm{r}}_t,\mathrm{\forall }{\mathrm{u}}_t\in {\widehat{S}}_t,$$

where n_t is the local surface normal at ${\mathbf{u}}_t,\sigma \in {\mathbb{R}}_{>0}$ is a scale term determined by the image resolution, and r_t is a regularization update vector that maintains surface smoothness with respect to the local surface curvature as done by BET [15]. The algorithm converges as the updated surface estimate approaches the true boundary of the cortical surface and ∥σD(p_t)n_t∥ tends to zero. From (2), −1 ≤ D(p) ≤ 1, which means that updates in the direction of the surface normal n_t are bounded to have maximum magnitude σ. In our multiresolution Gaussian image pyramid representation of $I_{\text{CT}}^2$, we update the segmentation surface estimate by starting at the lowest level of resolution and proceeding for a fixed number of iterations before switching to the next higher resolution level. This way, the algorithm first updates the surface with large changes to the surface at low resolutions and then successively refines the results at high levels of resolution until convergence.

III. RESULTS

From a clinical database of epilepsy patients who had electrodes surgically implanted at Yale New Haven Hospital, we selected 18 patients with pre-op and post-op T1-weighted MR images, and post-op CT images to validate our segmentation approach. The set of images had heterogeneous voxel spacings (isotropic spacings in the axial plane) and dimensions. The pre-op MRIs had voxel spacing in the range 0.49-1.00 × 0.49-1.00 × 1.00-1.50 mm with dimensions 256-512 × 256-512 × 96-192 voxels, post-op MRIs had voxel spacing in the range 0.94-1.06 × 0.94-1.06 × 1.00-1.50 mm with dimensions 192-256 × 192-256 × 96-192 voxels, and post-op CT had voxel spacing in the range 0.39-0.70 × 0.39-0.70 × 1.25-2.00 mm with dimensions 512 × 512× 119-173 voxels. Ten patients had lateral craniotomies on the right side of the skull and the remaining eight had left-side craniotomies. On average, each patient had a total of 197 electrodes implanted (both sub-dural and intra-cranial), and each had an 80 × 80 mm grid of electrodes (8 × 8 electrodes) at the craniotomy location. All images and electrode data were fully anonymized.

Following the clinical routine practiced at our institution, a trained technician used BET [15] to segment both the pre-op and the post-op MRIs, and, if necessary, manually corrected the brain masks using a painting tool. All images were resampled to have 1mm³ isotropic resolution, and all images had different volume dimensions. All surfaces S used in this work were parameterized as triangulated meshes. The 18 post-op brain surfaces $S_i^2$ used for training in Sec. II-B had 2685±188 vertices (Mean±SD) and the template MNI brain surface used as the initial segmentation estimate $\widehat{S}$ in Sec. II-C had 2354 vertexes. We performed leave-one-out cross-validation, where we trained dictionaries using N =17 subjects and then tested our segmentation method on the left-out subject. We utilized a MATLAB implementation of K-SVD [23] to learn the appearance dictionaries, and implemented our segmentation method in C++ as part of BioImage Suite [26]. All CPU computations were run on a 4 GHz Intel Core i7 iMac with 16 GB of RAM.

First, Sec. III-A details our methods for evaluating the performance of CT segmentation. We then compare segmentation performance using locally-oriented patches to standard patches in Sec. III-B, and test the algorithms sensitivity to the initial surface alignment in Sec. III-C. Additionally, we study the effects of patch size and shape in Sec. III-D and Sec. III-E, respectively. We also compare our segmentation method to a standard, atlas-based segmentation method in Sec. III-F as well as to a U-Net-based deep neural network segmentation method in Sec III-G.

A. Evaluation Methods

To quantitatively assess cortical surface segmentation performance, we used the rigidly registered post-op MRI surface $S^{2^{\prime }}$ as a gold-standard to evaluate surface segmentation estimates $\widehat{S}$ For two surfaces A and B, we measure segmentation accuracy using the following metrics: (i) Dice overlap

$$\text{DICE}(A,B)=\frac{2V_A\cap V_B}{V_A+V_B},$$

where V_S is the volume enclosed by surface S; (ii) Hausdorff Distance

$$\text{HD}(A,B)=\text{max}\left\{\underset{\mathrm{a}\in A}{\text{max}}d(\mathbf{a},B),\underset{\mathrm{b}\in B}{\text{max}}d(\mathbf{b},A)\right\};$$

(iii) Modified Hausdorff Distance (MHD), which uses the 95th percentile of d(a, B) instead of using the maximum value as in HD and is less sensitive to outliers; and (iv) Mean Absolute Distance

$$\text{MAD}(A,B)=\frac{1}{2}\left\{\frac{1}{N_A}\sum _{\mathrm{a}\in A}d(\mathbf{a},B)+\frac{1}{N_B}\sum _{\mathrm{b}\in B}d(\mathbf{b},A)\right\},$$

where d(a, B) = min_b∈B ∥b – a∥₂. In addition to these metrics, we specifically quantify segmentation errors at a subset of surface electrode locations. Here, we use only intracranial cortical electrodes, extracting the largest 8×8 electrode grids (64 total electrodes per patient) from each patient’s set of electrodes, and omit the depth electrodes because their location is far from the cortical boundary. These grids are of particular interest as they lie on the brain surface closest to the craniotomy location where the largest amount of brain deformation is expected to occur [27]. Given identified electrode locations x_e ∈ E ⊂ Ω_I for each subject, we define the Mean Electrode to Surface Distance (MESD)

$$\text{MESD}(E,S)=\frac{1}{N_E}\sum _{{\mathrm{x}}_e\in E}d({\mathrm{x}}_e,S)$$

to be a measure of the distribution of electrode distances from the given surface estimate $\widehat{S}$ Intra-cranial cortical electrodes are expected to lie on the surface of the brain, and the MESD metric quantifies how close the electrodes are to the surface $\widehat{S}$ Electrode localization is accurate and trivial, thus high MESD values indicate poor segmentation estimates rather than electrode localization errors. Poor segmentation results would result in electrodes that appear to be floating above the surface or sunk within, with high MESD values indicating that the distribution of electrodes is far from the estimated surface.

B. Oriented Patches

For each test image $I_{\text{CT}}^2$ in our leave-one-out study, we tested how our proposed cortical boundary learning (Sec. II-B) and segmentation (Sec. II-C) performed using oriented local image patches (Sec. II-A) and compared our segmentation results to those found using standard, non-orientated local image patches, e.g. R = I in (1) We adopted a multi-resolution Gaussian image pyramid with K = 3 levels for each segmentation. We set the image patches Φ(u) to be a 5 × 5 × 5 isotropic grid by creating a point sampling template Θ centered around each surface vertex u ∈ S. Appearance samples vectors p, therefore, had total dimensionality d = 125. For each resolution level k, we adjusted Θ’s sample point spacing to make image patches at higher scales effectively have larger physical size, e.g. Θ had spacing 1, 2, 4mm for k = 1, 2, 3, respectively. For each level k, we extracted patch samples from a narrow band region at every surface vertex point in the N training CT images to train the inside and outside dictionaries in Sec. II-B. This sampling technique resulted in patch samples totaling three times the number of training surface vertexes for each class. To segment $I_{\text{CT}}^2$, we fixed the number of surface update iterations to t = 150 for each resolution level k (Sec. II-C). The choice of t = 150 was based on empirical observations of the segmentations where the average absolute surface displacement between successive iterations converged after a little more than 100 iterations on average in our experiments. We evaluated segmentation performance using different dictionary parameters by creating dictionaries of sizes n = {256, 512, 1024} and using sparsity constraints Γ₀ = {2, 4, 8} for a total of 9 parameter permutations.

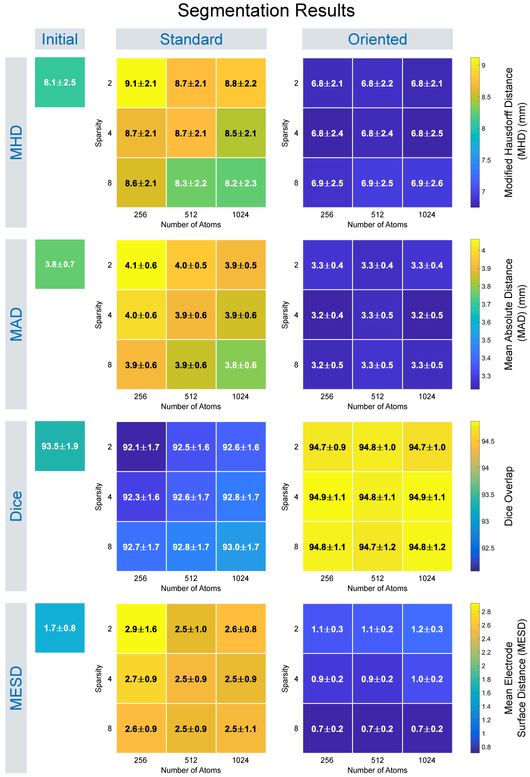
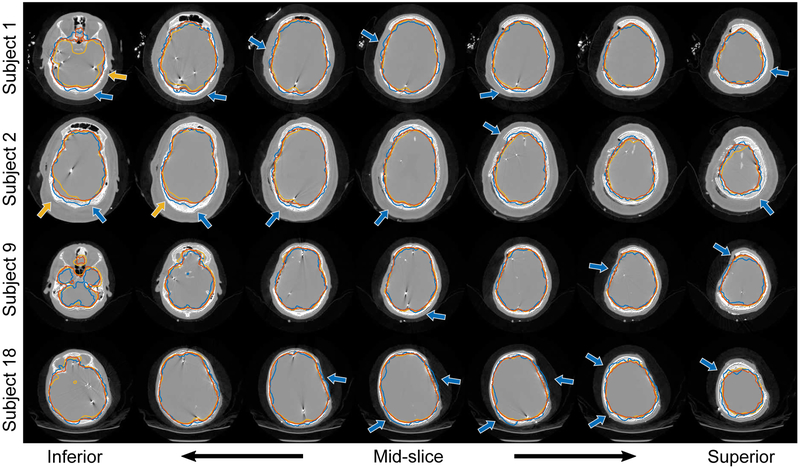
For each test, we computed the surface evaluation measures between the segmentation surface estimate $\widehat{S}$ and the reference surface $S^{2^{\prime }}$ and report segmentation results for the following methods: (i) segmentation as the initial, affine registered MNI template surface, i.e. no segmentation updates; (ii) segmentation using standard image patch orientation; and (iii) segmentation using locally-oriented image patches. We summarize the distribution of these results over all dictionary parameters in Fig. 4 (we omit HD results as they were similar to MHD). To assess significance, we performed a two-sided Wilcoxon signed rank test, where we concatenated the results across all dictionary size and sparsity constraint parameters into a single sample and then performed paired significance testing. Segmentation using locally-oriented patches significantly reduced MHD, MAD, and MESD compared to segmentation using standard patches, and significantly improved Dice overlap (p ≤ 10⁻²³). Overall, results using locally-oriented image patches were relatively stable across different dictionary parameter choices. Using a dictionary of size n = 256 and sparsity Γ₀ = 4 offered good performance across evaluation metrics. Segmentation results using standard patches, on the other hand, improved as both dictionary size and sparsity increased. In many cases though, using standard patch orientation resulted in segmentation results that were worse than the initial surface estimate (found by affinely registering the MNI template to the test subject). As confirmed by the MESD values, Fig. 5 illustrates an example subject, that our method more accurately identifies the surface on which the electrodes lie by comparing these three surface estimates with respect to the implanted electrodes identified in the CT images. Fig. 6 illustrates results from four subjects using both the standard and the locally-oriented patch segmentation approaches. Qualitatively, the use of oriented image patches appeared to segment the cortical surface more accurately than when using standard, non-oriented patches. The standard patch method had particular trouble segmenting the cortical surface in regions where the skull was removed, often leaking outside the brain volume at the site of the craniotomy.

Fig. 4.

The distribution of segmentation evaluation quality measures for leave-one-out experimental results comparing cortical surface segmentation using our dictionary-based segmentation method with locally-oriented image patches and segmentation using standard images patches, as well as the initial surface estimate. Results are shown for learned dictionary appearance models using 5 × 5 × 5 patches with different numbers of atoms and sparsity constraints, with values expressed as Mean±SD.

Fig. 5.

Visualizing the segmented cortical brain surface estimate with respect to implanted electrodes. For the initial segmentation that uses affine registration (left), the surface electrodes appear embedded within the brain. Segmentation using standard patch orientation (middle) only partially corrects the surface whereas segmentation using locally-oriented patches (right) accurately segments the cortical surface, and the electrodes appear to be correctly localized on the brain surface.

Fig. 6.

Cortical surface segmentation results using (i) locally-oriented image patches aligned to the surface’s local geometry (orange contour), (ii) the standard, local image patches aligned with the image axes (blue contour), and (iii) the ground-truth segmentations (yellow contour). Axial slices are shown for each subject progressing from the bottom of the head (left) up to the top (right). Blue arrows highlight areas where our approach using oriented patches better identified the cortical surface compared to standard patch alignment, which are particularly pronounced in areas around the location of the craniotomy. Yellow arrows highlight areas where our approach appears to more correctly segment that brain surface compared to the ground-truth. All results shown were computed using 5 × 5 × 5 patches and dictionary size n = 256 with sparsity constraint Γ₀ = 4.

The running time for the segmentation using oriented patches is higher than when using standard patches due to computing the principal curvatures at each step. For example, using 5 × 5 × 5 patches with dictionary size n = 256 and sparsity Γ₀ = 4 results in running times (Mean±SD) of 83.6 ± 1.9 seconds and 56.6 ± 0.7 seconds for segmentation using oriented patches and standard patches, respectively. Our segmentation method also includes 19.7 ± 2.5 seconds for the registrations used to estimate the initial surface (Sec. II-C1), which results in total computational time of 103.3 ± 2.7 seconds for the entire segmentation pipeline using oriented patches.

C. Sensitivity to Initial Alignment

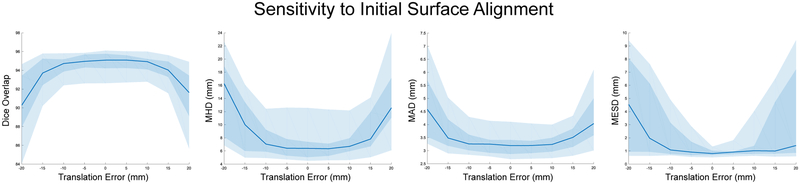
We tested the sensitivity of the segmentation algorithm to errors in the initial surface alignment ${\widehat{S}}_{\text{init}}$ (Sec. II-C1). To simulate initial misalignments, we translated the surface ${\widehat{S}}_{\text{init}}$ along the x-axis in ±5 mm increments with a maximum translation of ±20 mm. Using these translated initial surfaces, we then ran our oriented segmentation algorithm with a dictionary size n = 256 and sparsity constraint Γ₀ = 4. Fig. 7 plots the results for our evaluation metrics. In terms of overall accuracy, quantified by the Dice, MHD, and MAD metrics, the segmentation algorithm is relatively robust within ±10 mm. Segmentation results at the area of the craniotomy surface electrodes, measured by our MESD metric, indicate that the median MESD values are also robust within ±10 mm; however, we observe increasing variability of MESD values as measured by larger interquartile range values as initial surface misalignment distance increases.

Fig. 7.

The sensitivity of our model to synthetic errors in the initial surface alignment as evaluated by the Dice overlap, MHD, MAD, and MESD metrics. Each plot shows the median value as a blue line with both the middle 50% (interquartile range between the 25th and 75th percentiles) as a dark blue shaded region and the middle 90% (between the 5th and 95th percentiles) as a light blue shaded region. All results used 5 × 5 × 5 patches and dictionary size n = 256 with sparsity constraint Γ₀ = 4.

D. Patch Size

We investigated the effect of patch size on the algorithm’s segmentation performance. For these experiments we fixed the dictionary size n = 256 and sparsity Γ₀ = 4. We compared segmentation performance using oriented patches with isotropic grids of size 3 × 3 × 3, 5 × 5 × 5 (the results from Sec. III-B), and 7 × 7 × 7, which had appearance dimensionality of d = 27, 125, 343, respectively. Table I shows the patch size segmentation experiment results. Using a two-sided Wilcoxon signed rank test to assess segmentation significance (p ≥ 0.05), we found no significant differences (see Supplemental Fig. S1 for tables of p-values available in the supplementary files/multimedia tab) between the different patch sizes with the exception of MESD values for isotropic grids of size 5 and 7.

TABLE I.

Segmentation evaluation quality measures for cortical surface segmentation using our proposed method with different patch sizes and shapes. All results shown were computed using dictionary size n = 256 with sparsity constraint Γ₀ = 4. All values are expressed as Mean±SD and d indicates total patch dimensionality. Please refer to Supplemental Fig. S1 for statistical significance testing p-values available in the supplementary files/multimedia tab.

Patch Shape	Patch Limits	d	Dice (%)	HD (mm)	MHD (mm)	MAD (mm)	MESD (mm)
Cube Patches	3 × 3 × 3	27	94.79 ± 1.19	14.25 ± 3.75	7.10 ± 2.68	3.25 ± 0.47	0.96 ± 0.40
	5 × 5 × 5	125	94.87 ± 1.05	13.62 ± 4.41	6.75 ± 2.39	3.23 ± 0.43	0.87 ± 0.24
	7 × 7 × 7	343	94.85 ± 1.12	14.34 ± 4.07	6.85 ± 2.41	3.24 ± 0.45	1.09 ± 0.38
Spherical Patches	5 × 5 × 5	33	94.85 ± 1.22	14.21 ± 3.83	7.05 ± 2.63	3.28 ± 0.49	0.83 ± 0.36
	7 × 7 × 7	123	94.87 ± 1.03	13.78 ± 4.70	6.72 ± 2.36	3.22 ± 0.42	0.85 ± 0.19
	9 × 9 × 9	257	94.91 ± 0.98	13.75 ± 4.18	6.68 ± 2.34	3.21 ± 0.40	0.96 ± 0.24

E. Patch Shape

We also tested the shape of the patch with respect to the algorithm’s segmentation performance. Similar to the patch size tests, we set the dictionary size to n = 256 and sparsity to Γ₀ = 4. Rather than using standard, cube-shaped patches, we experimented with a spherical patch that was sampled along an isotropic, rectilinear grid. We tested using patches with maximum size 5 × 5 × 5, 7 × 7 × 7, and 9 × 9 × 9, where only points within the central sphere were used to create the patch sampling template. These spherical patches had appearance dimensionality d = 33, 123, 257, respectively. Table I shows the patch shape segmentation experiment results. Using a two-sided Wilcoxon signed rank test to assess segmentation significance (p ≤ 0.05), we found no significant differences (see Supplemental Fig. S1 for tables of p-values available in the supplementary files/multimedia tab) between the different spherical patch sizes with the exception of MHD values for patches of size 5 and 9 and MESD values using patch size of 9.

To assess significance between the cube and spherical patches, we performed another two-sided Wilcoxon signed rank test (p ≤ 0.05), where we concatenated both the cube and the spherical patch results across all sizes into two samples and then performed paired significance testing. Here, paired significance testing is appropriate because the spherical patch dimensionality of the paired samples roughly corresponds to the dimensionality of the cube patches. There were no significant differences between cube and spherical patch shapes in terms of Dice, HD, MHD, and MAD. In terms of MESD, our algorithm using spherical patches performed significantly better than cube-shaped patches (p = 0.002).

F. Atlas-based Segmentation

We compared our segmentation approach to standard multiatlas-based segmentation [28]. Atlas-based registration consisted of the following steps: (i) we non-rigidly registered each post-op CT image $I_{\text{CT},i}^2$ in the training set to the test image $I_{\text{CT}}^2$ with intensity-based registration using an FFD transformation model [29] with 15mm isotropic B-spline control point spacing and maximizing their NMI; (ii) using these transformations, we transformed the post-op CT brain surface masks $S_i^{2^{\prime }}$ (computed in Sec. II-B) to the test image; and (iii) to segment the brain in $I_{\text{CT}}^2$ image space, we performed a majority vote classification of voxels being inside the transformed brain surface masks. While atlas-based segmentation performed comparably to our dictionary-based segmentation approach in terms of HD, MHD, MAD, and Dice, the method performed particularly poorly in the location of the craniotomy where the electrode grids were placed, which resulted in MESD values significantly higher than all other results (Table II and Supplemental Fig. S2 shows significance testing results available in the supplementary files/multimedia tab).

TABLE II.

Segmentation evaluation quality measures comparing our dictionary-based approach to cortical surface segmentation to the initial surface estimate, atlas-based segmentation and a deep convolutional neural network (CNN). Results using our method used 5 × 5 × 5 patches and dictionary size n = 256 with sparsity constraint Γ₀ = 4. Values are expressed as Mean±SD. Please refer to Supplemental Fig. S2 for statistical significance testing p-values available in the supplementary files/multimedia tab.

Method	Patch Limits	Dice (%)	HD (mm)	MHD (mm)	MAD (mm)	MESD (mm)
Initial Estimate	Image Size	93.47 ± 1.86	14.38 ± 3.97	8.09 ± 2.50	3.76 ± 0.68	1.66 ± 0.84
Atlas-based	Image Size	94.21 ± 1.77	13.18 ± 4.38	6.81 ± 2.46	3.20 ± 0.70	2.51 ± 1.06
Deep CNN	64 × 64 × 64	95.00 ± 1.18	14.59 ± 4.76	7.00 ± 2.71	2.94 ± 0.44	1.11 ± 0.61
Oriented Dictionary	5 × 5 × 5	94.87 ± 1.05	13.62 ± 4.41	6.75 ± 2.39	3.23 ± 0.43	0.87 ± 0.24

Since we performed atlas-based segmenation in each test subject’s image space, the 15mm FFDs had variable grid sizes, with mean grid size 19 × 19 × 12 across all test subjects. These grids parameterized FFD transformations with (Mean±SD) 13, 708 ± 3674 degrees of freedom in three dimensions. All registrations utilized the C++ implementation of FFD registration included as part of the BioImage Suite software package [26], and the registration process required (Mean±SD) 108.2 ± 33.2 seconds using the same computer workstation as our dictionary learning method. For our leave-one-out testing, atlas-based registration for each subject required a total of 17 non-linear registrations, which on average resulted in total processing time of approximately 30 minutes per test subject.

G. Deep Learning Segmentation

Additionally, we compared segmentation results to a deep learning-based approach. Deep convolutional neural networks (CNNs), especially fully-convolutional networks (FCN) [30] can segment whole image patches at a time. The U-Net [31], one particular FCN architecture, and its 3D derivatives [32], have become particularly popular in medical image analysis. Here, we utilize the U-Net architecture to perform patch-based, or semantic, segmentation. We train our segmentation model with respect to a common reference space in order to take advantage of the brain’s geometry providing contextual clues to the segmentation algorithm. Here, we rigidly register all images I_CT,i in the training set to the MNI Colin 27 brain reference space. For registration, we maximize the NMI similarity metric between the two images and reslice the masks using this transformation estimate. As a result, all image pairs (I_CT,i, M_CT,i) are resampled to have 1 mm³ isotropic resolution and dimensions 181 × 217 × 181. We use a patch-based training and segmentation approach, where we set the patch size to 64 × 64 × 64 voxels. Due to GPU memory limitations, our network implementation uses 3 max-pooling operation layers (compared to four for standard U-Net) for a total of 18 convolutional layers. To train the networks, we used mini-batches of size 4 (due to memory requirements on our GPU) that consisted of randomly extracted overlapping patches from the images, which we augmented by randomly flipping patches left and right. We used a fixed learning rate of 0.0001 and evaluated stopping based on convergence of both the training data and testing data segmentation results.

We performed a 6-fold cross validation study (N = 15 subjects used for training in each fold). Using each fold’s trained CNN to segment a novel test image I_CT not included in the training set, we first rigidly register this image to the MNI Colin template space using NMI, and we denote this transformation T_MNI. Segmentation is performed by uniformly sampling the test CT image with overlapping patches at a stride length equal to half the patch dimensions. Once all patches have been segmented by the deep network, we perform a weighted combination of the segmented patches results, where the voxels are weighted according to their distance from the patch center. The resulting segmentation volumes are then thresholded at 0.5 and we remove any extraneous segmentation regions that are smaller than 1 million voxels in volume using a cluster thresholding algorithm. We then apply a median filter of size 3 to these results to smooth the segmentation. Finally, the post-processed segmentation result is resliced back to the original post-op CT image space using the inverse transformation $T_{\text{MNI}}^{-1}$ with nearest neighbor interpolation. We implemented the U-Net models in Python using TensorFlow and trained all models on an NVIDIA GTX 1080 Ti GPU with 11 GB RAM. Prediction times for this network were (Mean±SD) 19.4 ± 0.2 seconds. However, this method required spatial normalization to the MNI brain using image registration, which added 3.2 ± 0.3 seconds to the computation time. This resulted in total segmentation times of 22.6 ± 0.3 seconds for the entire deep learning pipeline.

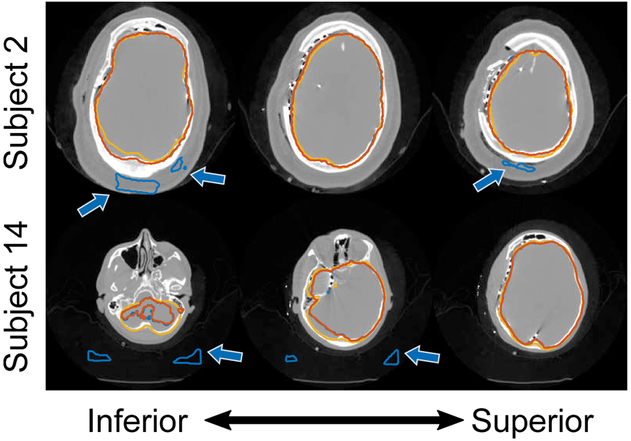
We report segmentation results in Table II. Using a two-sided Wilcoxon signed rank test to assess significant differences (p ≤ 0.05) between this deep learning approach and our oriented patch dictionary-learning method (using 5×5×5 cube patches and dictionary size n = 256 with sparsity constraint Γ₀ = 4), we found no significant difference in segmentation performance across all but the MAD metrics (see Supplemental Fig. S2 for tables of p-values available in the supplementary files/multimedia tab). Our deep CNN did perform significantly better than the atlas-based segmentation method in terms of Dice, MAD, and MESD. The post-processing steps were necessary because 5 of 18 (28%) cases had segmentation artifacts at the exterior skull boundary or at locations outside the head (Fig. 8). The pre-processed segmentation results had Dice values (Mean±SD) 93.96 ± 2.95, which were significantly different than the post-processed segmentation Dice results 95.00 ± 1.18 (p < 0.05).

Fig. 8.

Example cortical surface segmentation results using a deep convolutional neural network (DCNN) where predictions were poor. Segmentation contours show (i) the initial DCNN segmentation (blue contour), (ii) the segmentation result after post-processing (orange contour), and (iii) the ground-truth segmentation (yellow contour). Axial slices are shown for each subject progressing from the bottom of the head (left) up to the top (right). Arrows highlight areas where the DCNN produced incorrect segmentation results.

IV. DISCUSSION AND CONCLUSION

The segmentation method proposed in this paper can be used to solve an actual clinical problem using imperfect clinical data. Our method using locally-oriented image appearance models accurately extracts the brain surface from post-electrode implantation CT images containing many artifacts, distortions, and missing anatomical features. In creating a dictionary-based model of the brain boundary’s appearance that uses image patches oriented according to the local surface geometry, we realize an appearance model that is invariant to changes in image orientation. This contrasts with standard appearance models that utilize image patches statically aligned with the image axes. The resulting oriented appearance model, when combined with our proposed surface estimation method, significantly improves segmentation performance over standard image patch-based models that do not take local surface geometry into account (Sec. III-B).

For our application to post-implant CT registration, our experiments indicate that the choices of dictionary size n and sparsity constraint Γ₀ have limited effect on the segmentation results when using oriented patches. Our choice of a small dictionary size n = 256 and low sparsity constraint Γ₀ has practical benefits in terms of reduced computational performance compared to using larger dictionaries or higher sparsity without sacrificing segmentation accuracy. Segmentation performance using standard patches, on the other hand, improves as both the dictionary size and sparsity increases, which also increases computational time. This result is intuitive because dictionaries of increasing size and sparsity should be able to better reconstruct anatomical appearances from a wider variety of anatomical orientations. It is also important to point out that the standard patch segmentation technique resulted in segmentations that were worse than the initial segmentation estimate over all metrics, which may indicate that the appearance models learned by the dictionaries were highly sensitive to the orientation of the training data and do not generalize well to novel images with arbitrary orientations. Our comparison deep learning segmentation method (Sec. III-G) faces a similar criticism in that segmentation results are not invariant to arbitrary anatomical orientations. In this case, the DCNN required that all images be aligned to a common reference space with a rigid registration step prior to both training and segmentation.

By creating local orientation axes for each image patch, the image appearance model is invariant to anatomical orientation. This invariance leads to appearance modeling that generalizes across the population. Furthermore, this invariance to orientation eliminates the need for registration of the training data to a common reference space. The local patch-based nature of the appearance model also provides invariance to the location of features along the surface, which contrasts with appearance models that use the whole image or entire anatomy. The atlas-based segmentation method failed to accurately segment the cortical surface at the location of the craniotomy because the location of this surgical site is specific to each patient and we do not have enough training data to cover all possible locations. Similar to our approach and in contrast with the atlas-based method, the deep learning algorithm used local anatomical information to better segment the brain at the craniotomy site, in this case accurate segmentation was made possible by the convolutional implementation, patch-based training methodology, and use of right-left flips to augment the size of the training data.

A major drawback of deep learning is that it requires a large amount of training data for results to generalize well. While we did not find significant differences between our approach and the DCNN in terms of segmentation performance at the craniotomy (as measured by MESD), there was a trend to slightly worse and more variable results using the DCNN most likely due to the network over-training to the spatial relationship of implanted electrodes. Furthermore, post-processing (cluster thresholding and median filtering) was necessary and played a large role in resolving segmentation errors caused by imaging artifacts due to the presence of electrodes and wiring around the skull. Our modeling approach has further advantages over DCNN-based methods: (i) our use of locally-oriented patches is also invariant to rotations of the data as evidenced by not having the requirement to spatially normalize each subject to a template space, which contrasts with the CNN that is invariant to translations but not rotations; (ii) the learned model parameters are easily interpretable, i.e. the dictionary atoms display the learned appearance features, which contrasts with the difficulty in interpreting the learned features in the CNN’s hidden layers; (iii) our approach evolves the segmentation surface according to local image appearance patches that are intrinsically tied to the whole brain shape surface during segmentation, whereas the DCNN, even though it builds a hierarchical representation of anatomical features, uses convolution kernels that ultimately operate locally and also the final segmentation applies relatively locally [33]. This results in the DCNN incorrectly segmenting areas outside the skull (Fig. 8) most likely because they are symmetrically similar to regions inside the skull boundary on the opposite side of the head and thus appear locally similar in appearance to the classifier; and (iv) our model is of much lower dimensionality, e.g. a dictionary with n = 256 atoms and 5³ image patches at 3 scales requires a total of 96,000 parameters whereas our tested U-Net DCNN had over 22 million parameters. While our DCNN experiments were not exhaustive, we used a highly popular network architecture (U-Net) used by the medical imaging community. Overall, in medical imaging datasets that have low sample sizes such as ours, non-deep learning methods like dictionary learning may still have a useful role to play, especially in applications such as surgery that require a high level of trust in the algorithmic results.

Our sensitivity experiments (Sec. III-C) demonstrate that our approach is robust to errors within ±10 mm in the initial segmentation surface estimate (Sec. II-C1). These results can be explained by our choice of α in Sec. II-B and our chosen patch size (5 × 5 × 5). The purpose of the α parameter is twofold. First, it allows for possible errors in the ground-truth surface segmentations (Fig. 6) that were used for training the appearance models. Second, along with the patch size, it defines the capture range for the algorithm’s surface evolution, i.e. how far off the initial segmentation can be and the surface still converges to the true surface boundary. We chose the maximum value of α = 3 mm to roughly correspond to the MAD values of the initial surface alignment (Table II) at the final image resolution level (1mm³ voxel spacing). Larger α values might lead to a lack of specificity in the definition of the surface band region. On the other hand, larger α values may extend the capture range, i.e. how far off the initial segmentation can be and the result still converges to the true surface boundary. At the lowest image resolution level k = 3, where voxel spacing is 4mm³, the 5 × 5 × 5 patch size at 4 mm spacing between sampling points extends 8 mm in each direction from the patch center that when added to α provides a capture range of 11 mm. These results explain why our algorithm was robust to initial surface misalignments within ±10 mm.

Our experiments with patch size and shape showed that larger patches do not necessarily offer better segmentation performance. While larger patches allow for greater spatial context to be represented, increasing patch size (either as a cube or as a sphere) increases appearance vector dimensionality, which may have the adverse effect of making discrimination between classes more challenging (in the L₂ sense). For roughly that same dimensionality d, the sphere allows for a larger patch field of view than the cube, while discounting information furthest from the patch center, e.g. compare a 7 × 7 × 7 sphere (d = 123) to a 5 × 5 × 5 cube (d = 125). Other than at the site of the craniotomy (as measured by MESD), spherical patches do not appear to perform significantly better than cube patches when comparing patch shapes of roughly the same dimensionality.

We also note our choice to use the MNI Colin 27 brain [24] mask surface as the initial surface for the segmentation. While this choice necessitates registering a single subject template brain to the post-op CT image as a starting point for the segmentation, we found that low-dimensional affine registration using the NMI similarity metric is stable for multi-modal inter-subject MRI-CT alignment. We make this choice because the pre-op MRI segmentation is unreliable using methods such as BET [15] due to the missing skull anatomy and the artifacts present in imaging due to the implanted electrodes, and rather than having a noisy surface estimate, we prefer to start with a trusted brain shape. Even though post-op MRI brain segmentation may be manually refined by a trained technician (as done for our training data in Sec. II-B), our use of the MNI brain eliminates the need for the post-op MRI imaging for our segmentation. For our algorithm, post-op MRI imaging is only necessary for creating our training data.

One of the limitations of our method is that we rely on K-SVD for dictionary learning and orthogonal matching pursuit (OMP) to approximately solve the sparse reconstruction problem. Numerous methods for sparse representation and dictionary learning have been proposed [34], and alternative methods to OMP for solving non-convex optimization problems exist [35], [36]. However, full recovery of the appearance signal may not be necessary for this problem. These methods might also impose an unwarranted computational burden. Our results indicate that K-SVD and OMP perform well in this segmentation task.

In the future, the accurate post-op CT brain segmentations provided by our method can be used to non-rigidly register pre-op MR and post-op CT imaging in epilepsy patients. In our previous paper [17], we demonstrated that having an accurate CT brain surface segmentation could be used to directly register these images forgoing the use of the currently acquired post-op MRI. Given a segmentation of the pre-op MR and post-op CT brain surfaces, a variety of registration methods could be applied to align the data: (i) point-based surface registration [12], [14] and as we previously showed [17]; (ii) distance map registration; or (iii) a combination of surface points and intensity-based registration [13]. Additionally, any of these registration methods could incorporate a biomechanical model [37], [38] to constrain the registration transformation. Our method could also be combined with statistical models of brain shape [39] and brain deformation [10] to better constrain the surface estimation process. While our segmentation method does not incorporate any prior information regarding the shape of the brain surface other than the initial surface segmentation, using locally-oriented appearance implicitly encodes the brain geometry at a local level. In this case, our model learned contextual information about the patch appearance based on local brain geometry. The locally-oriented patch segmentation approach presented in this paper could be applied to other anatomical structures of interest whose appearance has a highly non-Gaussian distribution, for example images with post-surgical appearance changes caused by scar tissue or implants. Furthermore, as structural boundaries often change orientation while keeping the same intensity pattern, the proposed rotationally-invariant technique is more broadly applicable beyond the current application.