Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Nov 26;18(12):7969–7976. doi: 10.1021/acs.nanolett.8b03937

Strain-Tunable Quantum Integrated Photonics

Ali W Elshaari †,*, Efe Büyüközer ‡, Iman Esmaeil Zadeh §, Thomas Lettner †, Peng Zhao ∥, Eva Schöll †, Samuel Gyger †, Michael E Reimer ⊥, Dan Dalacu #, Philip J Poole #, Klaus D Jöns †, Val Zwiller †
PMCID: PMC6477803  PMID: 30474987

Abstract

graphic file with name nl-2018-039374_0006.jpg

Semiconductor quantum dots are crucial parts of the photonic quantum technology toolbox because they show excellent single-photon emission properties in addition to their potential as solid-state qubits. Recently, there has been an increasing effort to deterministically integrate single semiconductor quantum dots into complex photonic circuits. Despite rapid progress in the field, it remains challenging to manipulate the optical properties of waveguide-integrated quantum emitters in a deterministic, reversible, and nonintrusive manner. Here we demonstrate a new class of hybrid quantum photonic circuits combining III–V semiconductors, silicon nitride, and piezoelectric crystals. Using a combination of bottom-up, top-down, and nanomanipulation techniques, we realize strain tuning of a selected, waveguide-integrated, quantum emitter and a planar integrated optical resonator. Our findings are an important step toward realizing reconfigurable quantum-integrated photonics, with full control over the quantum sources and the photonic circuit.

Keywords: Nanowires, strain tuning, quantum dot, quantum integrated photonics, ring resonator, single photon

Photons and quantum optical technology have been the main testing grounds for fundamental ideas of quantum science. This can be traced back to the first quantum entanglement experiment using photons in an atomic cascade and ground breaking experiments in quantum teleportation and communication using parametric down conversion processes.1,2 Photons are robust and versatile candidates for flying qubits with several coding schemes successfully implemented relying on polarization,3 time domain,4,5 spatial domain,6 frequency domain,7 and even a combination of more than one.8,9 Although there are alternative approaches currently under investigation to harness different quantum phenomena, the use of photons to communicate the results is inevitable, which makes the photonic approach even more attractive.10 Nevertheless, the slow progress of quantum information processing and sensing implementations using quantum states of light can be traced to a scalability issue: Implementing quantum optics experiments beyond the single-photon level brings about large increases in required resources, calling for an integrated approach following the footsteps of the microelectronics industry.

At the heart of quantum integrated photonics lies the quantum emitter. Quantum dots (QDs), in particular, are very promising sources for on-chip quantum technology because they can provide near-ideal single-photon emission11−14 and entangled photon pair generation15 with the possibility for electrical control,16,17 in addition to their potential usage as solid-state spin qubits.18−20 The downside of this versatile potential is the random nature of their position and emission properties, which imposes serious difficulties to scale up the quantum network.21 Additionally, the quality of the optical circuits using a III–V platform is low compared with that of silicon, where waveguide losses are orders of magnitude lower.22 This is partially due to the highly optimized nanofabrication recipes adapted directly from the microelectronics industry. Additional sources of loss come from the fact that even passive routing elements can still contain thousands of randomly positioned unwanted emitters causing absorption. Hybrid integration techniques, combining selected III–V quantum emitters and silicon-based photonics, are particularly interesting, as they potentially offer the best of both platforms.23−28

Another major challenge with quantum integrated photonics is tuning the emission wavelength of circuit-integrated quantum sources. Controlling the emission properties of bulk quantum emitters is a rapidly advancing field. Several techniques have been investigated, such as strain tuning with piezoelectric materials15,29 and MEMS structures,30,31 electric-field tuning,32 and thermal tuning.33 Among these approaches, strain tuning is particularly attractive because it allows for advanced control of a quantum emitter in a reversible manner, without visible degradation of the optical properties. Recent progress in strain tuning of QDs includes tuning the emission energy,29,34−36 eliminating the fine structure splitting,15,37 and rotating the dipole orientation of a bulk QD.38 The major drawback of strain tuning is that it involves wafer-bonding techniques to transfer the strain from a piezoelectric crystal to the circuit layer, making it very challenging to realize large-scale planar photonic circuits, with single selected quantum emitters.39

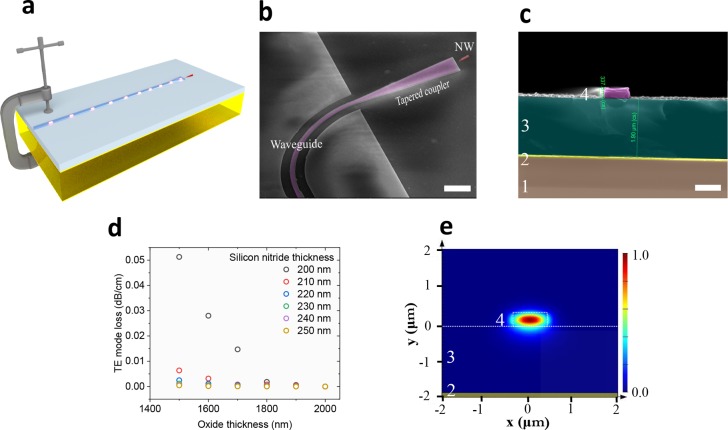
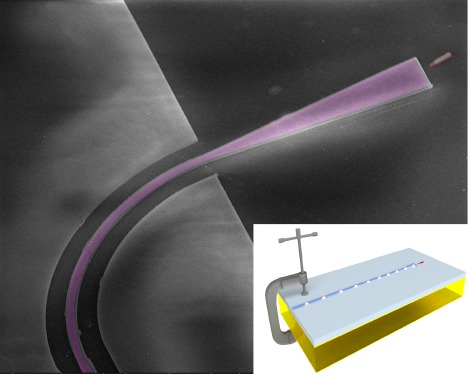
In this work, we present a novel hybrid quantum photonic platform through fabricating silicon nitride photonic waveguides with preselected III–V single nanowire QDs directly on a piezoelectric crystal substrate for strain tuning. An artistic representation of the device and a scanning electron microscope image of the fabricated chip are shown in Figure 1a,b, respectively. The nanowire quantum emitter is shown in red, whereas the silicon nitride waveguide is shown in purple. Figure 1c presents a cross section of the photonic waveguide fabricated directly on the piezoelectric crystal. Starting from the bottom, we find lead magnesium niobate–lead titanate (PMN–PT) crystal labeled “1”, 20 nm/80 nm thick chromium/gold contact labeled “2”, 2 μm thick silicon oxide labeled “3”, and finally 230 nm silicon nitride labeled “4”. Biaxial strain exerted within the underlying PMN–PT piezoelectric substrate will be transferred toward the top silicon nitride waveguide and the quantum emitter. Reducing the thickness of the intermediate oxide layer will maximize the strain transfer but comes with the trade-off of potential loss due to plasmonic coupling to the gold contact. Figure 1d shows numerical eigenmode simulations of the fundamental TE mode loss as a function of the silicon nitride core and the oxide cladding thicknesses, respectively. For each silicon nitride thickness value, the propagation loss increases rapidly below a certain height of the oxide layer. Thicker silicon nitride can be implemented to further reduce the height of silicon oxide; however, using this strategy, the undesired confinement of the higher order modes becomes more probable. On the basis of the simulation, we designed the waveguides to have silicon nitride and oxide thicknesses of 230 nm and 2 μm, respectively, which enables single-mode operation while maintaining low silicon oxide thickness for strain transfer. Figure 1e shows a 2D simulation of the x component of the fundamental transverse electric-field mode in the waveguide, with no visible coupling to the gold contact placed 2 μm below the waveguide.

Figure 1.

Figure 1

Open in a new tab

(a) Artistic representation of a waveguide-coupled nanowire single-photon source, directly fabricated on a strain-tunable substrate. (b) Scanning electron microscope image of an InP nanowire QD, shown in red, coupled to a silicon nitride waveguide, shown in purple, all directly fabricated on the PMN–PT substrate. (c) Scanning electron microscope image of the waveguide cross section. The different layers from bottom to top are PMN–PT crystal (labeled “1”), 20 nm of chromium and 80 nm of gold (labeled “2”), 2 μm of silicon oxide (labeled “3”), and 230 nm of silicon nitride (labeled “4”). (d) Numerical simulations of the fundamental TE mode loss as a function of the silicon oxide cladding thickness and the silicon nitride core thickness. (e) Electric-field profile of the fundamental TE mode showing no significant plasmonic coupling to the bottom gold contact; the silicon nitride thickness is 230 nm and the silicon oxide thickness is 2 μm. The scale bars in panels b and c are 2 and 1 μm, respectively.

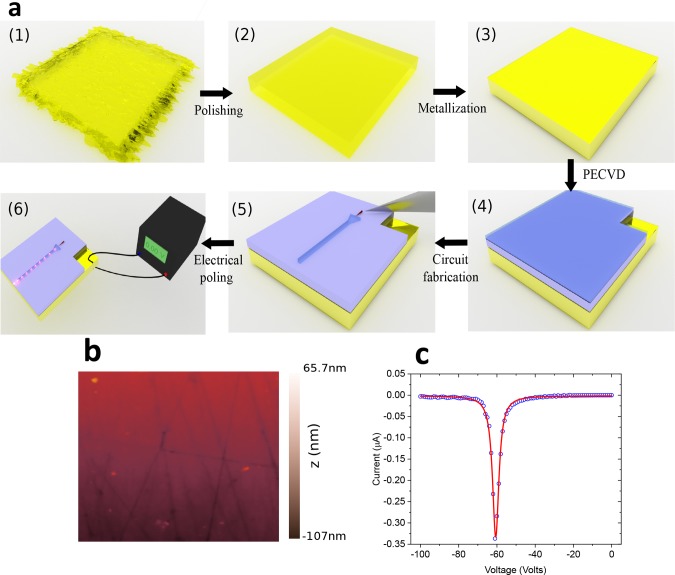
The details of the fabrication process are shown in Figure 2a. We start with a single crystal, 300 μm thick, PMN–PT substrate. As artistically shown in step 1, the surface suffers from micrometer-scale trenches produced during the sawing process of the crystal ingot. In step 2, we perform an extensive polishing routine to remove the trenches and reduce the surface roughness. Figure 2b shows an atomic force microscope scan of 5 μm × 5 μm, with a root mean square (RMS) roughness of 22.5 nm. The roughness becomes even less pronounced as we deposit more layers on the PMN–PT substrate, which tend to fill in the gaps and flatten the surface. In step 3, we evaporate 20 nm of chromium, then 80 nm of gold as the electrical contact. The same bimetallic layer evaporation procedure is implemented on the backside of the chip. For the photonic circuit, silicon oxide and silicon nitride were selected as the bottom cladding and the waveguide core, respectively. There are several advantages for selecting this combination of materials for realizing the photonic components. First, the refractive index contrast between the core and the cladding, Δn ≈ 0.50 in the near-infrared, provides strong optical confinement. Second, the deposited nature enables tuning the refractive indices by controlling the deposition parameters. Third, the platform is compatible with superconducting single-photon detector integration40 and overall well-suited for backend microelectronics fabrication processes.41 In step 4, we use plasma-enhanced chemical vapor to deposit the silicon oxide and silicon nitride in selected regions of the substrate. The process has a low thermal budget, making it compliant with the InAsP/InP nanowire QD23 and PMN–PT crystal. First, 2 μm of silicon oxide is deposited using a SiH4/N2:N2O (710 sccm:425 sccm) gas mixture at a temperature of 300 °C, pressure of 800 mTorr, and RF power of 24 W. Second, we deposit 230 nm of silicon nitride using SiH4/N2:NH3(800 sccm:16 sccm) gas mixture at a temperature of 300 °C, pressure of 650 mTorr, and RF power of 24 W. Ellipsometry data show no absorption in the films near the QD emission at ∼880 nm; for the same wavelength, the real parts of the refractive index of the silicon nitride and silicon oxide are 1.94 and 1.46, respectively. In step 5, we perform electron beam lithography to pattern the circuit using electron-beam resist CSAR 62 (AR-P 6200). After developing the structures, the pattern is transferred to the silicon nitride layer using CHF3:Ar (20 sccm:10 sccm) reactive ion etching under pressure of 7 mTorr and radio frequency power of 50 W. Finally, we transfer preselected high-quality nanowire QDs using a nanomanipulator.23,24 The setup consists of a tungsten tip mounted on an x–y–z movable stage imaged by a high-resolution optical microscope. The nanowire is detached at its base from the growth chip, then transferred to a PMN–PT substrate with <500 nm position accuracy and <2° rotation precision. In step 6, we pole the PMN–PT substrate at room temperature. The process involves applying an electric field above a certain threshold voltage to align different polarization domains in the crystal, then cooling it to cryogenic temperatures to freeze the domains. After the crystal gains macroscope polarization from poling, a change in the applied electric field will modify the internal charges separation that will, in turn, strain the crystal. Figure 2c shows the poling curve of the piezoelectric-substrate at room temperature. It is important to note that despite the extensive processing steps described previously including several thin-film depositions, 50 keV electron beam lithography, and plasma exposure during reactive ion etching, the piezoelectric substrate shows typical poling behavior, with no visible degradation in the strain-tuning characteristics compared with unprocessed samples.

Figure 2.

Figure 2

Open in a new tab

(a) Process flow for fabricating the device: (1) Raw PMN–PT substrate with rough surface, which is initially not suitable for fabricating photonic circuits due to the deep trenches formed during ingot sawing. (2) Polished PMN–PT chip. (3) Metal evaporation to form top and bottom contacts. (4) Deposition of silicon oxide and silicon nitride using plasma-enhanced chemical vapor. 1 mm2 of the gold surface is left exposed for subsequent electrical bonding. (5) Electron beam lithography and reactive ion etching to form different photonic elements, then deterministic placement of a selected nanowire quantum dot using nanomanipulation technique. (6) Poling of the piezo using a high-voltage source, then optical and electrical testing. (b) Atomic force microscope image of the polished piezo surface with an RMS roughness of 22.5 nm. (c) Electrical poling curve of the processed piezoelectric chip at room temperature. Despite extensive processing steps, including electron-beam lithography, thin-film deposition, and reactive ion etching, no visible degradation in the piezoelectric behavior of the crystal is seen.

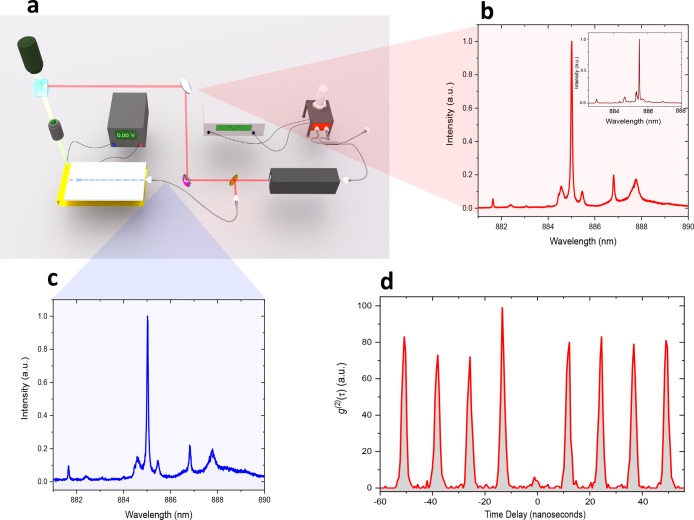
The experimental setup is shown in Figure 3a. The hybrid photonic circuit is placed in a closed-cycle cryostat at a temperature of 5.8 K; laser excitation and QD signal collection can be done either in free space using a top objective (NA = 0.81, working distance 700 μm) or through the waveguide using a focusing optical fiber with a working distance of 13 μm. The QD is excited nonresonantly at 795 nm with a 3 ps pulsed laser having an average power of 1.12 μW. The QD emission is directed to a 0.75 m focal length monochromator, equipped with a 1800 lines/mm grating. The monochromator is either terminated by a charge-coupled device camera or fiber-coupled to two superconducting single-photon detectors with efficiencies of 50 and 64%, timing jitter of 20 and 30 ps, and dark count rates of 0.01–0.01+0.02 and 0.02–0.02 s–1, respectively, to perform photon correlation measurements.12Figure 3b,c shows the collected QD emission spectra via free space and through the photonic waveguide, respectively. The results show successful coupling of a quantum emitter emission to our newly developed waveguide on the PMN–PT crystal. The inset of Figure 3b presents the emission spectrum of the same QD on the growth chip, which was deterministically selected based on its emission characteristics before transfer, to be integrated in a controlled fashion to the PMN–PT substrate. For details of the efficiency of the QD coupling to the guided mode, please refer to Supporting Information S1. In Figure 3d, we verify the nonclassical nature of the quantum emitter by performing an autocorrelation measurement. The result shows uncorrected zero-delay multiphoton probability of g(2)(0) = 0.1 ± 0.04 under nonresonant excitation conditions, well below the classical limit.

Figure 3.

Figure 3

Open in a new tab

(a) Experimental setup for the piezo-tunable hybrid quantum photonic circuit. The setup allows for both in-plane (via the waveguide using tapered optical fiber) and out-of-plane laser excitation and collection; additional details of the setup are available in the main text. The collected emission from the nanowire QD is coupled to a monochromator, then either detected by charge-coupled devices camera or fiber-coupled to two superconducting single-photon detectors and a correlation module. The QD is nonresonantly excited with 3 ps pulsed laser operating at 795 nm wavelength. (b,c) Out-of-plane (free space) and through the waveguide (via optical fiber) collected emission spectrum of the QD, respectively. The inset in panel b shows the same QD emission at the growth chip before transfer. (d) Second-order correlation measurement of the QD line at ∼885 nm; the uncorrected zero-delay multiphoton probability is g(2)(0) = 0.1 ± 0.04, showing the nonclassical nature of the deterministically integrated quantum emitter.

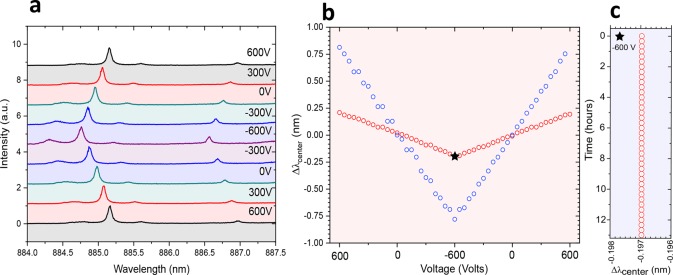
The tunability of the devices was tested by applying voltage to the piezoelectric substrate while recording the QD emission collected through the waveguide using the focusing optical fiber. Strain generated in the PMN–PT crystal is transferred to the oxide surface through the different deposited layers and then to the nanowire QD by the van der Waals forces between the nanowire and the oxide.35 Negative (positive) voltage corresponds to in plane compression (expansion) of the photonic substrate and the quantum emitter. We tune the piezo voltage between −600 and 600 V in steps of 5 V to apply biaxial strain on the quantum emitter. The QD emission spectrum at selected voltage values is displayed in Figure 4a. The tuning range of the QD emission was measured to be 0.39 nm; the emission is blue (red) shifted for negative (positive) voltages. In Figure 4b, the red circles show the QD emission wavelength as a function of the voltage applied to the piezo. We clearly see a linear relation between the two. Next, we increase the efficiency of the strain transfer to the nanowire QD by increasing the rigidness of the nanowire–substrate interface, which was predominantly due to van der Waals forces when the nanowire is placed on the surface of the oxide. To achieve this, we encapsulate the nanowire by depositing 20 nm of silicon nitride and 200 nm of silicon oxide. Figure 4b, blue circles, shows the emission wavelength shift of the same encapsulated nanowire QD as a function of piezo voltage. We measure a tuning range of 1.6 nm (2.53 meV), a four-fold increase as compared with the case with no encapsulation. As a figure of merit of the tuning efficiency, we extract the tuning rate to be 0.325 pm/V before encapsulation and 1.33 pm/V after encapsulation. Note that these values can be further enhanced by modifying the design of the photonic circuit and reducing the thickness of the PMN–PT substrate. More data of another working device is provided in Supporting Information S2. It is important to compare the achieved tuning range of 2.53 meV with the typical inhomogeneous distribution of the nanowire QDs. The standard deviation of the nanowires emission in the growth sample is 5.7 meV.35 To tune two nanowire QDs in the sample to the same wavelength, a combination of preselection and optimized encapsulation, to increase the strain tuning of nanowires, can be employed. While the tuning in a controlled and reversible manner is crucial in operating quantum photonic circuits, an equally important aspect is the stability of operation over time.29 In Figure 4c, we study the emission wavelength stability of the waveguide-integrated QD by fixing the applied voltage to the piezo at −600 V (marked with a star in Figure 4b) while measuring the spectrum every 1 min for 13 h. The emission wavelength shows excellent stability, with no measurable shift within the setup resolution of 25 μeV.

Figure 4.

Figure 4

Open in a new tab

(a) Emission spectra of the nanowire QD collected from the waveguide as a function of the applied voltage to the piezoelectric substrate. Negative voltages correspond to compressive biaxial strain, resulting in lowering the emission energy of the QD. We achieve a total shift in the QD emission of 0.39 nm by changing the applied voltage to the piezoelectric substrate by 1.2 kV. (b) Red circles show the trace of a single fitted peak of the QD emission as a function of the applied voltage; we see a clear linear and recoverable behavior for the QD tuning. The strain transfer between the nanowire QD and the substrate is mainly due to van der Waals forces between the two. The tunability can be enhanced by increasing the surface area of the interaction region between the two and anchoring the nanowire rigidly to the substrate. To achieve this, we deposited 20 nm of silicon nitride and 200 nm of silicon oxide using plasma-enhanced chemical vapor; the tuning results are shown in blue circles in panel b. After deposition, we achieve a four-fold increase in the strain transfer; the total shift of the QD emission after encapsulation is 1.6 nm. (c) Emission stability test. The piezo voltage was fixed at −600 V while measuring the spectrum every 1 min for 13 h. The emission wavelength shows excellent stability, with no measurable shift within the experimental setup resolution of 25 μeV.

In addition to tuning the quantum emitter itself, it is also of paramount importance to reconfigure photonic integrated circuits to enable a broad range of functionalities6 such as filtering, routing, and fine-tuning of coupling and interference conditions between remote emitters.42 In particular, ring resonators play an important role in quantum integrated photonics,43 with recent demonstrations of their usage for single-photon filtering and Purcell enhancement of quantum emitters.23,28 Typically, the tuning mechanism of integrated resonators involves thermal tuning,44 which suffers from several disadvantages such as power consumption, cross talk, and incompatibility with superconducting single-photon detectors. Recently, strain tuning have been demonstrated in integrated photonic circuits,45,46 which can overcome the discussed limitations of thermal-tuning. 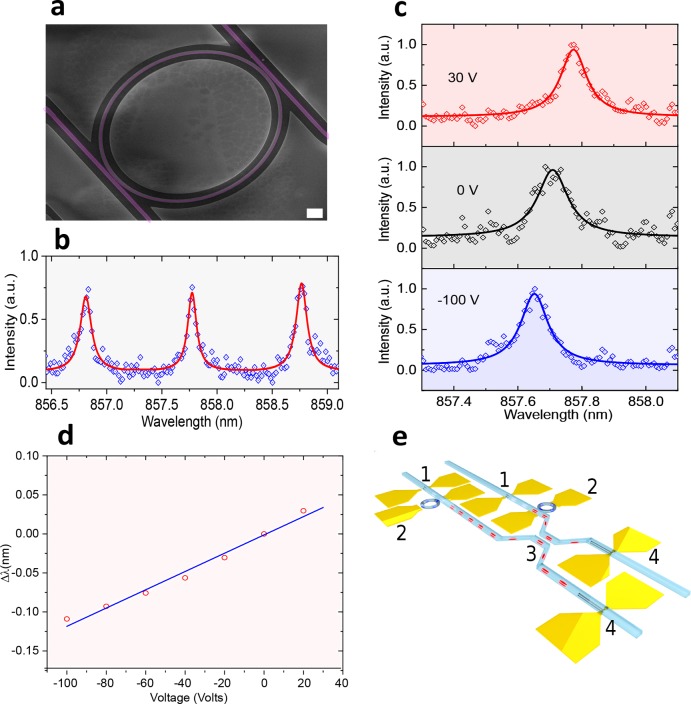To demonstrate the potential of our piezo-electric photonic platform, we realize the reconfiguration of a ring resonator filter. Figure 5a shows a scanning electron microscope of the fabricated device; the drop port transmission of the ring is shown in Figure 5b. We initially pole the piezo at ∼−90 V, then monitor the resonance peak of the ring filter as a function of the piezo voltage. Figure 5c shows the wavelength shift of a single resonance peak at different piezo voltages; 30 (top), 0 (middle), and −100 V (bottom). Figure 5d shows the cavity drop port transmission peak as a function of voltage. Here, we clearly see a linear relation between the two 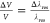Inline graphic.47 The detailed description of strain in PMN–PT is a multidimensional tensor relation that takes into account external stresses and the direction of the applied electric field. In our case, where there is no additional external in situ stress and with the electric field applied only in one principal direction, the nonzero piezoelectric coefficient is linearly proportional to the electric field across the piezoelectric substrate. The resulting strain modifies the optical length of the cavity, which will, in turn, change the resonance condition. The presented device shows a tuning rate of 0.96 pm/V, applied across the 300 μm thick piezoelectric substrate, allowing for very precise resonance tuning. We conclude by summing up the importance of reconfiguring integrated photonic circuits in an envisioned hybrid circuit to demonstrate two-photon interference, schematically shown in Figure 5e. The depicted circuit shows two nanowire quantum emitters, which usually emit at different wavelengths, that are strain-tuned to the same wavelength. The top contacts for strain-tuning are patterned to apply strain locally and independently to several quantum emitters on the chip. To reduce cross talk between strained regions, the contacts can be placed further apart or through micromachining48 of the piezo using femtosecond laser pulses. Next, single or multiple filtering stages, depicted here by a pair of ring resonators similar to the one we have experimentally demonstrated, are strain-tuned to transmit specific optical transitions of the quantum emitters. Finally, a pair of superconducting single-photon detectors are integrated with a beam splitter to study on-chip quantum interference between remote emitters. The on-chip two-photon interference of remote sources presents the main building block for more complex quantum networks on chip, combining the generation, manipulation, and detection of qubits/photons on a single platform. For the emitted photons to be indistinguishable, lifetime-limited emission from remote emitters needs to be achieved. It is worth noting here that strain tuning may not be the only method for controlling quantum emitters’ properties in future hybrid quantum circuits. Strain tuning can be complemented by other methods such as electric-field tuning11 to add more versatile functionalities, for example, controlling the electric charges in a QD, which is an important milestone for solid-state qubit realization in integrated circuits.50

Figure 5.

Figure 5

Open in a new tab

(a) Scanning electron microscope image of silicon nitride ring resonator fabricated on a piezoelectric substrate, the scale bar is 2 μm. (b) Drop port transmission of the ring resonator with free spectral range of 0.96 nm. (c) Single resonance peak at different applied voltages to the PMPT–PT substrate: 30, 0, and −100 V for top, middle, and bottom panels, respectively. Negative voltages correspond to compressive biaxial strain, resulting in blue-shifting the resonance of the optical cavity. (d) Trace of the drop port transmission peak as a function of voltage. (e) Envisioned applications of strain-tunable hybrid quantum photonic circuit. The depicted circuit shows two nanowire quantum emitters (labeled “1”) strain-tuned to the same wavelength, then a filtering stage consisting of a pair of ring resonators (labeled “2”) that are strain-tuned to transmit specific optical transitions of the nanowire QD. Finally, a pair of superconducting nanowire single-photon detectors (labeled “4”) is integrated with a beam splitter (labeled “3”) to study on-chip quantum interference between remote emitters.

In summary, we have realized a novel hybrid quantum photonic platform combining silicon nitride photonics, III–V quantum emitters, and piezoelectric substrates, all seamlessly integrated using a combination of bottom-up, top-down, and nanomanipulation techniques. The fabrication method enables the possibility of performing 3D integration to realize more complex large-scale architectures. Furthermore, the nanowires are all site selected so a fully automated process for nanowire transfer can be realized for large-scale integration. The integrated quantum emitters show a tuning range of 0.39 and 1.6 nm for air-cladding and dielectric-cladding, respectively. The piezoelectric substrate demonstrates excellent strain-tuning characteristics, despite extensive fabrication steps to realize the hybrid platform. Additionally, the fact that the photonic waveguide core and cladding are directly deposited on the piezoelectric substrates, with no wafer bonding involved, delivers the required wavelength stability, making the platform very attractive for precise locking to atomic vapors in the future.51−53 In addition, we presented tuning of a ring resonator filter as a proof-of-concept for reconfigurable photonic integrated circuits. The resonator and the quantum emitter show comparable tuning rates of 0.96 and 1.33 pm/V, respectively. Our strain-tuning method of waveguide-integrated sources is a crucial step toward on-chip optical quantum processing, as it provides, in addition to preselecting the quantum emitter, the needed fine-tuning to compensate for spectral mismatch between multiple sources on the same chip. Our method is versatile and can be adapted for integration with other quantum emitters such as 2D materials54 and diamond,55,56 and it can be also realized with other photonic platforms such as silicon carbide or aluminum nitride, with the possibility of integration with superconducting single-photon detectors,57 enabling the generation, manipulation, and detection of photons on a single platform for quantum simulation, quantum computation, lab-on-chip, and quantum sensing.

Acknowledgments

A.W.E acknowledges support from the Swedish Research Council (Vetenskapsrådet) Starting Grant (ref: 2016-03905) and MARIE SKŁODOWSKA-CURIE Individual Fellowship under REA grant agreement no. 749971 (HyQuIP). V.Z. acknowledge the support of the ERC grant (ERC-2012-StG) and VR grant for international recruitment of leading researchers (ref: 2013-7152). I.E.Z. acknowledges the support of NWO LIFT-HTSM for Physics 2016-2017, project nr 680-91-202 and support from Single Quantum B.V. (SQ). K.D.J. acknowledges funding from the MARIE SKŁODOWSKA-CURIE Individual Fellowship under REA grant agreement no. 661416 (SiPhoN) and funding from European Union’s Horizon 2020 research and innovation programme under grant agreement No. 820423 (S2QUIP).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.8b03937.

  • Details of efficiency (S1) and data for another functional device (S2) (PDF)

Author Contributions

A.W.E proposed the idea and conceived the experiment. A.W.E, E.B., P.Z., T.L., and I.E.Z. processed the samples. K.D.J. designed and built the optical setup with help from T.L. and E.S. A.W.E. carried out the experiments with the contribution from E.B., P.Z., T.L., K.D.J., E.S., and S.G. The data were analyzed by A.W.E. D.D. and P.J.P. fabricated the nanowire quantum dot. V.Z. led and supervised the project. A.W.E. wrote the manuscript with input from all authors.

The authors declare no competing financial interest.

Supplementary Material

nl8b03937_si_001.pdf (202KB, pdf)

References

  1. Bouwmeester D.; Pan J.-W.; Mattle K.; Eibl M.; Weinfurter H.; Zeilinger A. Nature 1997, 390 (6660), 575–579. 10.1038/37539. [DOI] [Google Scholar]
  2. Aspect A.; Dalibard J.; Roger G. Phys. Rev. Lett. 1982, 49 (25), 1804. 10.1103/PhysRevLett.49.1804. [DOI] [Google Scholar]
  3. Akopian N.; Lindner N. H.; Poem E.; Berlatzky Y.; Avron J.; Gershoni D.; Gerardot B. D.; Petroff P. M. Phys. Rev. Lett. 2006, 96 (13), 130501. 10.1103/PhysRevLett.96.130501. [DOI] [PubMed] [Google Scholar]
  4. Wakabayashi R.; Fujiwara M.; Yoshino K.-i.; Nambu Y.; Sasaki M.; Aoki T. Opt. Express 2015, 23 (2), 1103–1103. 10.1364/OE.23.001103. [DOI] [PubMed] [Google Scholar]
  5. Jayakumar H.; Predojević A.; Kauten T.; Huber T.; Solomon G. S.; Weihs G. Nat. Commun. 2014, 5, 4251. 10.1038/ncomms5251. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Wang J.; Paesani S.; Ding Y.; Santagati R.; Skrzypczyk P.; Salavrakos A.; Tura J.; Augusiak R.; Mančinska L.; Bacco D.; Bonneau D.; Silverstone J. W.; Gong Q.; Acín A.; Rottwitt K.; Oxenløwe L. K.; O’Brien J. L.; Laing A.; Thompson M. G. Science 2018, 360 (6386), 285–291. 10.1126/science.aar7053. [DOI] [PubMed] [Google Scholar]
  7. Kobayashi T.; Ikuta R.; Yasui S.; Miki S.; Yamashita T.; Terai H.; Yamamoto T.; Koashi M.; Imoto N. Nat. Photonics 2016, 10 (7), 441–444. 10.1038/nphoton.2016.74. [DOI] [Google Scholar]
  8. Barreiro J. T.; Langford N. K.; Peters N. A.; Kwiat P. G. Phys. Rev. Lett. 2005, 95 (26), 260501. 10.1103/PhysRevLett.95.260501. [DOI] [PubMed] [Google Scholar]
  9. Prilmüller M.; Huber T.; Müller M.; Michler P.; Weihs G.; Predojević A. Phys. Rev. Lett. 2018, 121 (11), 110503. 10.1103/PhysRevLett.121.110503. [DOI] [PubMed] [Google Scholar]
  10. O’Brien J. L.; Furusawa A.; Vučković J. Nat. Photonics 2009, 3 (12), 687–695. 10.1038/nphoton.2009.229. [DOI] [Google Scholar]
  11. Somaschi N.; Giesz V.; De Santis L.; Loredo J. C.; Almeida M. P.; Hornecker G.; Portalupi S. L.; Grange T.; Antón C.; Demory J.; Gómez C.; Sagnes I.; Lanzillotti-Kimura N. D.; Lemaítre A.; Auffeves A.; White A. G.; Lanco L.; Senellart P. Nat. Photonics 2016, 10, 340. 10.1038/nphoton.2016.23. [DOI] [Google Scholar]
  12. Schweickert L.; Jöns K. D.; Zeuner K. D.; Covre da Silva S. F.; Huang H.; Lettner T.; Reindl M.; Zichi J.; Trotta R.; Rastelli A.; Zwiller V. Appl. Phys. Lett. 2018, 112 (9), 093106. 10.1063/1.5020038. [DOI] [Google Scholar]
  13. Senellart P.; Solomon G.; White A. Nat. Nanotechnol. 2017, 12, 1026. 10.1038/nnano.2017.218. [DOI] [PubMed] [Google Scholar]
  14. Ding X.; He Y.; Duan Z. C.; Gregersen N.; Chen M. C.; Unsleber S.; Maier S.; Schneider C.; Kamp M.; Höfling S.; Lu C.-Y.; Pan J.-W. Phys. Rev. Lett. 2016, 116 (2), 020401. 10.1103/PhysRevLett.116.020401. [DOI] [PubMed] [Google Scholar]
  15. Huber D.; Reindl M.; Covre da Silva S. F.; Schimpf C.; Martín-Sánchez J.; Huang H.; Piredda G.; Edlinger J.; Rastelli A.; Trotta R. Phys. Rev. Lett. 2018, 121 (3), 033902. 10.1103/PhysRevLett.121.033902. [DOI] [PubMed] [Google Scholar]
  16. Yuan Z.; Kardynal B. E.; Stevenson R. M.; Shields A. J.; Lobo C. J.; Cooper K.; Beattie N. S.; Ritchie D. A.; Pepper M. Science 2002, 295 (5552), 102–105. 10.1126/science.1066790. [DOI] [PubMed] [Google Scholar]
  17. Varnava C.; Stevenson R. M.; Nilsson J.; Skiba-Szymanska J.; Dzurňák B.; Lucamarini M.; Penty R. V.; Farrer I.; Ritchie D. A.; Shields A. J. Npj Quantum Information 2016, 2, 16006. 10.1038/npjqi.2016.6. [DOI] [Google Scholar]
  18. Kuhlmann A. V.; Houel J.; Ludwig A.; Greuter L.; Reuter D.; Wieck A. D.; Poggio M.; Warburton R. Nat. Phys. 2013, 9, 570. 10.1038/nphys2688. [DOI] [Google Scholar]
  19. De Greve K.; Yu L.; McMahon P. L.; Pelc J. S.; Natarajan C. M.; Kim N. Y.; Abe E.; Maier S.; Schneider C.; Kamp M.; Höfling S.; Hadfield R. H.; Forchel A.; Fejer M. M.; Yamamoto Y. Nature 2012, 491, 421. 10.1038/nature11577. [DOI] [PubMed] [Google Scholar]
  20. Gao W. B.; Fallahi P.; Togan E.; Miguel-Sanchez J.; Imamoglu A. Nature 2012, 491, 426. 10.1038/nature11573. [DOI] [PubMed] [Google Scholar]
  21. Lodahl P.; Mahmoodian S.; Stobbe S. Rev. Mod. Phys. 2015, 87 (2), 347–400. 10.1103/RevModPhys.87.347. [DOI] [Google Scholar]
  22. Tien M.-C.; Bauters J. F.; Heck M. J. R.; Blumenthal D. J.; Bowers J. E. Opt. Express 2010, 18 (23), 23562–23568. 10.1364/OE.18.023562. [DOI] [PubMed] [Google Scholar]
  23. Elshaari A. W.; Zadeh I. E.; Fognini A.; Reimer M. E.; Dalacu D.; Poole P. J.; Zwiller V.; Jöns K. D. Nat. Commun. 2017, 8, 379. 10.1038/s41467-017-00486-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Zadeh I. E.; Elshaari A. W.; Jöns K. D.; Fognini A.; Dalacu D.; Poole P. J.; Reimer M. E.; Zwiller V. Nano Lett. 2016, 16 (4), 2289–2294. 10.1021/acs.nanolett.5b04709. [DOI] [PubMed] [Google Scholar]
  25. Kim J.-H.; Aghaeimeibodi S.; Richardson C. J. K.; Leavitt R. P.; Englund D.; Waks E. Nano Lett. 2017, 17 (12), 7394–7400. 10.1021/acs.nanolett.7b03220. [DOI] [PubMed] [Google Scholar]
  26. Ellis D. J. P.; Bennett A. J.; Dangel C.; Lee J. P.; Griffiths J. P.; Mitchell T. A.; Paraiso T.-K.; Spencer P.; Ritchie D. A.; Shields A. J. Appl. Phys. Lett. 2018, 112 (21), 211104. 10.1063/1.5028339. [DOI] [Google Scholar]
  27. Katsumi R.; Ota Y.; Kakuda M.; Iwamoto S.; Arakawa Y. Optica 2018, 5 (6), 691–694. 10.1364/OPTICA.5.000691. [DOI] [Google Scholar]
  28. Davanco M.; Liu J.; Sapienza L.; Zhang C.-Z.; De Miranda Cardoso J. V.; Verma V.; Mirin R.; Nam S. W.; Liu L.; Srinivasan K. Nat. Commun. 2017, 8 (1), 889. 10.1038/s41467-017-00987-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Zeuner K. D.; Paul M.; Lettner T.; Reuterskiöld Hedlund C. R.; Schweickert L.; Steinhauer S.; Yang L.; Zichi J.; Hammar M.; Jöns K. D.; Zwiller V. Appl. Phys. Lett. 2018, 112 (17), 173102. 10.1063/1.5021483. [DOI] [Google Scholar]
  30. Petruzzella M.; Birindelli S.; Pagliano F. M.; Pellegrino D.; Zobenica Z.; Li L. H.; Linfield E. H.; Fiore A. APL Photonics 2018, 3 (10), 106103. 10.1063/1.5039961. [DOI] [Google Scholar]
  31. Bishop Z. K.; Foster A. P.; Royall B.; Bentham C.; Clarke E.; Skolnick M. S.; Wilson L. R. Opt. Lett. 2018, 43 (9), 2142–2145. 10.1364/OL.43.002142. [DOI] [PubMed] [Google Scholar]
  32. Sköld N.; Boyer de la Giroday A.; Bennett A. J.; Farrer I.; Ritchie D. A.; Shields A. J. Phys. Rev. Lett. 2013, 110 (1), 016804. 10.1103/PhysRevLett.110.016804. [DOI] [PubMed] [Google Scholar]
  33. Faraon A.; Englund D.; Fushman I.; Vučković J.; Stoltz N.; Petroff P. Appl. Phys. Lett. 2007, 90 (21), 213110. 10.1063/1.2742789. [DOI] [Google Scholar]
  34. Kremer P. E.; Dada A. C.; Kumar P.; Ma Y.; Kumar S.; Clarke E.; Gerardot B. D. Phys. Rev. B  2014, 90 (20), 201408. 10.1103/PhysRevB.90.201408. [DOI] [Google Scholar]
  35. Chen Y.; Zadeh I. E.; Jöns K. D.; Fognini A.; Reimer M. E.; Zhang J.; Dalacu D.; Poole P. J.; Ding F.; Zwiller V.; Schmidt O. G. Appl. Phys. Lett. 2016, 108 (18), 182103. 10.1063/1.4948762. [DOI] [Google Scholar]
  36. Jöns K. D.; Hafenbrak R.; Singh R.; Ding F.; Plumhof J. D.; Rastelli A.; Schmidt O. G.; Bester G.; Michler P. Phys. Rev. Lett. 2011, 107 (21), 217402. 10.1103/PhysRevLett.107.217402. [DOI] [PubMed] [Google Scholar]
  37. Trotta R.; Martín-Sánchez J.; Wildmann J. S.; Piredda G.; Reindl M.; Schimpf C.; Zallo E.; Stroj S.; Edlinger J.; Rastelli A. Nat. Commun. 2016, 7, 10375. 10.1038/ncomms10375. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Yuan X.; Weyhausen-Brinkmann F.; Martín-Sánchez J.; Piredda G.; Křápek V.; Huo Y.; Huang H.; Schimpf C.; Schmidt O. G.; Edlinger J.; Bester G.; Trotta R.; Rastelli A. Nat. Commun. 2018, 9 (1), 3058. 10.1038/s41467-018-05499-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Trotta R.; Atkinson P.; Plumhof J. D.; Zallo E.; Rezaev R. O.; Kumar S.; Baunack S.; Schröter J. R.; Rastelli A.; Schmidt O. G. Adv. Mater. 2012, 24 (20), 2668–2672. 10.1002/adma.201200537. [DOI] [PubMed] [Google Scholar]
  40. Schuck C.; Pernice W. H. P.; Tang H. X. Appl. Phys. Lett. 2013, 102 (5), 051101. 10.1063/1.4788931. [DOI] [Google Scholar]
  41. Romero-García S.; Merget F.; Zhong F.; Finkelstein H.; Witzens J. Opt. Express 2013, 21 (12), 14036–14046. 10.1364/OE.21.014036. [DOI] [PubMed] [Google Scholar]
  42. Qiang X.; Zhou X.; Wang J.; Wilkes C. M.; Loke T.; O’Gara S.; Kling L.; Marshall G. D.; Santagati R.; Ralph T. C.; Wang J. B.; O’Brien J. L.; Thompson M. G.; Matthews J. C. F. Nat. Photonics 2018, 12 (9), 534–539. 10.1038/s41566-018-0236-y. [DOI] [Google Scholar]
  43. Hach E. E.; Preble S. F.; Elshaari A. W.; Alsing P. M.; Fanto M. L. Phys. Rev. A 2014, 89 (4), 043805. 10.1103/PhysRevA.89.043805. [DOI] [Google Scholar]
  44. Elshaari A. W.; Zadeh I. E.; Jöns K. D.; Zwiller V. IEEE Photonics J. 2016, 8 (3), 1–9. 10.1109/JPHOT.2016.2561622. [DOI] [Google Scholar]
  45. Sebbag Y.; Goykhman I.; Desiatov B.; Nachmias T.; Yoshaei O.; Kabla M.; Meltzer S. E.; Levy U. Appl. Phys. Lett. 2012, 100 (14), 141107. 10.1063/1.3701587. [DOI] [Google Scholar]
  46. Jin W.; Polcawich R. G.; Morton P. A.; Bowers J. E. Opt. Express 2018, 26 (3), 3174–3187. 10.1364/OE.26.003174. [DOI] [PubMed] [Google Scholar]
  47. Preble S. F.; Xu Q.; Lipson M. Nat. Photonics 2007, 1 (5), 293–296. 10.1038/nphoton.2007.72. [DOI] [Google Scholar]
  48. Martín-Sánchez J.; Trotta R.; Mariscal A.; Serna R.; Piredda G.; Stroj S.; Edlinger J.; Schimpf C.; Aberl J.; Lettner T.; Wildmann J.; Huang H.; Yuan X.; Ziss D.; Stangl J.; Rastelli A. Semicond. Sci. Technol. 2018, 33 (1), 013001. 10.1088/1361-6641/aa9b53. [DOI] [Google Scholar]
  49. Bennett A. J.; Pooley M. A.; Cao Y.; Sköld N.; Farrer I.; Ritchie D. A.; Shields A. J. Nat. Commun. 2013, 4, 1522. 10.1038/ncomms2519. [DOI] [PubMed] [Google Scholar]
  50. Kumar S.; Trotta R.; Zallo E.; Plumhof J. D.; Atkinson P.; Rastelli A.; Schmidt O. G. Appl. Phys. Lett. 2011, 99 (16), 161118. 10.1063/1.3653804. [DOI] [Google Scholar]
  51. Akopian N.; Wang L.; Rastelli A.; Schmidt O. G.; Zwiller V. Nat. Photonics 2011, 5, 230. 10.1038/nphoton.2011.16. [DOI] [Google Scholar]
  52. Schweickert L.; Jöns K. D.; Namazi M.; Cui G.; Lettner T.; Zeuner K. D.; Scavuzzo Montaña L.; Filipe Covre da Silva S.; Reindl M.; Huang H.; Trotta R.; Rastelli A.; Zwiller V.; Figueroa E.. 2018, arXiv:1808.05921. arXiv.org e-Print archive. https://arxiv.org/abs/1808.05921.
  53. Branny A.; Kumar S.; Proux R.; Gerardot B. D. Nat. Commun. 2017, 8, 15053. 10.1038/ncomms15053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Meesala S.; Sohn Y.-I.; Pingault B.; Shao L.; Atikian H. A.; Holzgrafe J.; Gündoğan M.; Stavrakas C.; Sipahigil A.; Chia C.; Evans R.; Burek M. J.; Zhang M.; Wu L.; Pacheco J. L.; Abraham J.; Bielejec E.; Lukin M. D.; Atatüre M.; Lončar M. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 97 (20), 205444. 10.1103/PhysRevB.97.205444. [DOI] [Google Scholar]
  55. Lee K. W.; Lee D.; Ovartchaiyapong P.; Minguzzi J.; Maze J. R.; Bleszynski Jayich A. C. Phys. Rev. Appl. 2016, 6 (3), 034005. 10.1103/PhysRevApplied.6.034005. [DOI] [Google Scholar]
  56. Gourgues R.; Esmaeil Zadeh I.; Elshaari A. W.; Bulgarini G.; Los J. W. N.; Zichi J.; Dalacu D.; Poole P. J.; Dorenbos S. N.; Zwiller V.. 2018, arXiv:1811.03979. arXiv.org e-Print archive. https://arxiv.org/abs/1811.03979.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl8b03937_si_001.pdf (202KB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES