A clinical trial design using the concept of proportional time using the generalized gamma ratio distribution

Abstract

Traditional methods of sample size and power calculations in clinical trials with a time-to-event end point are based on the logrank test (and its variations), Cox proportional hazards (PH) assumption, or comparison of means of 2 exponential distributions. Of these, sample size calculation based on PH assumption is likely the most common and allows adjusting for the effect of one or more covariates. However, when designing a trial, there are situations when the assumption of PH may not be appropriate. Additionally, when it is known that there is a rapid decline in the survival curve for a control group, such as from previously conducted observational studies, a design based on the PH assumption may confer only a minor statistical improvement for the treatment group that is neither clinically nor practically meaningful. For such scenarios, a clinical trial design that focuses on improvement in patient longevity is proposed, based on the concept of proportional time using the generalized gamma ratio distribution. Simulations are conducted to evaluate the performance of the proportional time method and to identify the situations in which such a design will be beneficial as compared to the standard design using a PH assumption, piecewise exponential hazards assumption, and specific cases of a cure rate model. A practical example in which hemorrhagic stroke patients are randomized to 1 of 2 arms in a putative clinical trial demonstrates the usefulness of this approach by drastically reducing the number of patients needed for study enrollment.

1 |. INTRODUCTION

Sample size and power calculations are an integral part of a clinical trial design. Numerous clinical trial designs have been developed over the last half-century to compare 2 treatment arms where the outcome of interest is a continuous variable. In a typical situation, biomedical researchers approach a statistician asking him or her to calculate the number of patients that they need to enroll in the 2 arms to have acceptably high power (eg, 80%) to be able to detect a clinically meaningful treatment effect (should it truly be present) at a given level of significance (eg, 5%). This gives rise to the notion of “effect size,” the magnitude of which is sometimes known to the researchers on the basis of factors such as topic-related experience or pilot data, often guided by published literature. In situations where such information is not readily available, a statistician can still perform sample size–power calculations on the basis of the concept of “standardized” effect size, wherein the effect size is defined by how large a clinically important effect is in terms of standard deviation(s) relative to the mean. Further, sample size–power calculations can be performed for both one-sided (eg, as for a superiority trial) or two-sided trials, for hypothesized noninferiority or bioequivalence of the new treatment as compared to the standard treatment, or for different allocation ratios (that is, the ratio of the sample sizes in the 2 arms). Sample size calculations can then be adjusted for the effect of other covariates, repeated measures, and study attrition rates.

In clinical trials using a survival end point (time-to-event data), the traditional methods of sample size–power calculations aim to calculate the number of events that each treatment arm is hypothesized to experience. The total sample size is then adjusted for the assumed rate of censoring (ie, the number of observations who will not experience the event of interest). Popular software packages such as GPower, PASS, and nQuery allow the user to conduct sample size–power calculations using the following traditional approaches: (1) Logrank test: nonparametric (see Machin et al,¹ Lakatos,² Lachin and Foulkes³); (2) Cox regression: semiparametric (see Schoenfeld,⁴ Hsieh and Lavori⁵); and (3) Exponentially distributed failure times: parametric (see Bernstein and Lagakos⁶).

Of these approaches, the sample size calculation method proposed by Schoenfeld using Cox regression (Cox⁷) is used most commonly and is often used in phase II and phase III clinical trials. This method is based on the assumption of the proportionality of hazards (PH) between the 2 treatment groups with the magnitude of this proportionality remaining constant throughout the observation window. That is, the individual hazards in the 2 treatment arms may increase, decrease, or remain constant, but the hazard ratio Δ_HR always remains constant and is used as a measure of effect size. A typical scenario involves a researcher providing the statistician information about a clinically relevant Δ_HR (a Δ_HR less than 1 implies risk reduction, with the new treatment being more effective than standard treatment) and asking him or her to do the sample size calculation for a given value of power, significance level, allocation ratio, and standard deviation of a covariate.

Some authors such as Royston and Parmar⁸ and Zhao et al⁹ have discussed the PH assumption being too restrictive and, as a result, have proposed alternate methods of sample size calculation such as restricted median survival time or model-free approaches on the basis of event rates. However, such approaches have yet to find widespread acceptance compared to the traditional approaches discussed above. Nevertheless, in the context of our proposed method, it is important to confront the limitations of the Cox approach from the perspective of both the validity of the PH assumption (that is, whether this assumption can be met with certainty) as well as the practical difficulties faced by researchers in adopting this approach. In Section 2 of our manuscript, we discuss these limitations motivated primarily by challenges faced in designing a clinical trial for a specific scenario. Section 3 lays the foundation for our proposed method, and the proposed method is explained in Section 4. Results for our motivating example as well as for other simulated scenarios (including comparisons with the PH approach) are presented in Section 5, followed by a discussion in Section 6.

2 |. MOTIVATING EXAMPLE

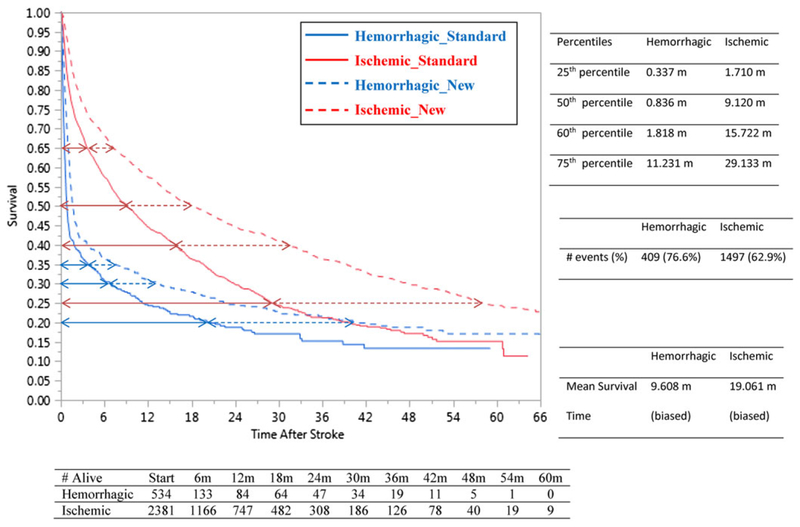
A large cohort (n = 69 371) of patients with end stage renal disease receiving maintenance dialysis was constructed by linking data from the United States Renal Data System, comprised largely of persons insured by Medicare, to Medicaid claims data to create a cohort of “dually eligible” (Medicare-Medicaid) individuals. This was done to permit observation of both medication exposures (via Medicaid) and clinical outcomes (via Medicare billing data claims data). The primary clinical entity of interest in this example was stroke (both hemorrhagic and ischemic). The research team developed clinical algorithms that allowed identification of hemorrhagic and ischemic stroke events from Medicare claims data, as described in Wetmore et al.^10,11 Follow-up for this cohort began upon full observability in the database (specifically, dialysis initiation plus 90 d, as is standard with analyses of United States Renal Data System data since in many cases, Medicare coverage is not secured until 3 mo has elapsed). Patients were then followed until death (the outcome of interest) and were right-censored in the case that they lost their Medicare or Medicaid coverage (rare), received a kidney transplant (rare), or became unobservable when follow-up ended at the last time point in the data (common). As would be expected in any study, additional exclusion criteria based on clinical considerations were applied to construct this cohort. Both hemorrhagic (n = 534) and ischemic (n = 2391) strokes were hypothesized to confer substantial risk for mortality in dialysis patients, with various patient-level factors and comorbidities affecting the risk of mortality; the effect of hemorrhagic strokes would be expected to be substantially greater than ischemic strokes. Kaplan Meier (KM) curves for the 2 stroke types are shown in Figure 1 (solid blue for hemorrhagic and solid red for ischemic) accompanied by the summary statistics.

FIGURE 1.

Kaplan Meier curves for the 2 stroke types for standard arm and proposed new treatment arm

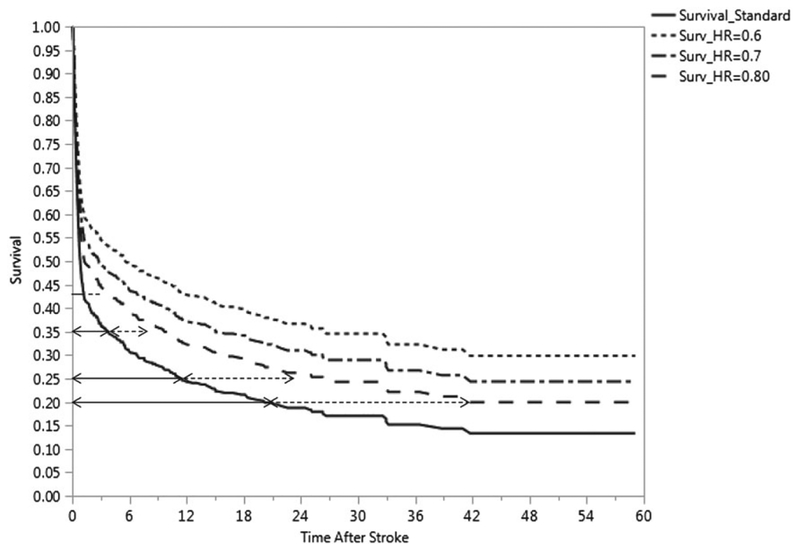
As can be seen in the case of hemorrhagic strokes (from the solid blue arc-shaped survival curve in Figure 1), fully 60% of the deaths occur by 1.8 months, indicating poor longevity for the most afflicted patients. If a new treatment were to become available for hemorrhagic stroke, it would be important that it demonstrates superiority to any existing treatment regimens by conferring substantial improvements in longevity. On the basis of the large sample size of the observational study, investigators could be fairly confident that the survival curve for the standard-of-care treatment arm would closely mimic the KM curve for hemorrhagic strokes shown in Figure 1. However, it would be extremely difficult for investigators to quantify a hypothesized improvement (that is, effect size) of the new treatment over the standard treatment in terms of Δ_HR, the hazard ratio, due to a variety of reasons. First, there is no real reason to believe that the PH assumption will necessarily hold true for such a proposed trial and, based on the clinical expertise of researchers in the field of stroke and cardiovascular research (see Phadnis et al¹²), nonproportionality of hazards is a realistic assumption. Second, sample size calculations using the PH assumption (even if it were to hold true) could be criticized because an effect size justification based on Δ_HR is rather arbitrary. That is, prior to the trial actually being conducted, it cannot be absolutely clear to the researchers whether the manner in which a Δ_HR of, say, 0.75 or 0.60 or 0.50 affects the overall improvement in longevity associated with the novel intervention is a realistic expectation. To illustrate the dangers, the projected survival curves for the treatment group shown in Figure 2 (with Δ_HR = 0.70, 0.60) using the PH assumption do not reflect the improvement in longevity hypothesized by the investigators. Third, no general consensus is available in published literature on Cohen-type qualitative definitions of “small, moderate, or large” for Δ_HR. As such, one can imagine a phase III clinical trial with large sample sizes that declares small risk reductions as being statistically significant without discussing its corresponding effect on any clinically meaningful improvement in longevity.

FIGURE 2.

Survival curves for Δ_HR = 0.8, 0.7, 0.6 in comparison to the standard treatment group (for hemorrhagic stroke)

In case of our planned clinical trial, we hypothesize that the new treatment called “NewTrt” may be superior to the standard treatment regimen if it can double the longevity for 60% of the deaths (40th percentile on the solid blue KM curve in Figure 1) from 1.8 to 3.6 months. NewTrt might, for example, be administered immediately upon onset of confirmation of a hemorrhagic stroke by cerebral imaging in the hospital emergency department, NewTrt might have its effect by preserving brain tissue from hypoxemia, or by reducing the effect of cerebral edema on vascular reactivity, or by reducing oxygen free radical damage (any number of realistic mechanisms could be posited). The proposed definition of improvement is a more realistic expectation given the steep arc-shaped KM curve in Figure 1 and is also strongly motivated by practical considerations. That is, for most patients (and their families) for whom life expectancy would otherwise be less than 2 months when receiving standard-of-care treatment, a potent motivation for enrolling in the study is the direct and straightforward interpretation of the prospect of the doubling of lifespan should the patient be randomized to the NewTrt treatment arm (of note, the risk reduction by 50% does not directly translate to doubling the lifespan unless there are exponentially distributed failure times). Furthermore, the solid blue KM curve in Figure 1 also shows that 75% of the deaths occur by ≈11 months and that 85% of the deaths occur by ≈33 months. While the doubling of lifespan for this 25th and 15th survival percentile would be a prodigious clinical achievement, researchers would likely be gratified if NewTrt increases the longevity by a factor of 1.5 or even 1.4. The dotted blue curve in Figure 1 demonstrates a hypothetical scenario in which longevity due to NewTrt is doubled for any given survival percentile of patients experiencing a hemorrhagic stroke. As can be seen from the example, the hypothesized superiority of NewTrt over the standard-of-care treatment is better defined by an effect size that incorporates a multiplicative factor on time rather than the hazard.

In the next 2 sections, we describe how this goal can be realized.

3 |. METHODS: BACKGROUND DETAILS

3.1 |. Using a three-parameter generalized gamma distribution

As the main research question is motivated by improvement in longevity of the new treatment group, compared to the standard treatment group, by a multiplicative factor of time, we cannot ignore the shape of the hazard function for the 2 treatment arms. Table 1 compares the fit of commonly used parametric distributions for the observational study data for hemorrhagic stroke patients.

TABLE 1.

Model comparisons for hemorrhagic stroke observational study data

Distribution	AICc	−2 Loglikelihood	BIC
Generalized gamma	1668.812	1662.766	1681.608
Lognormal	1815.855	1811.832	1824.393
Log-logistic	1832.544	1828.521	1841.082
Weibull	1952.095	1948.072	1960.633
Exponential	2511.168	2509.160	2515.441

Abbreviations: AIC, Akaike information criterion; BIC, Bayesian information criterion.

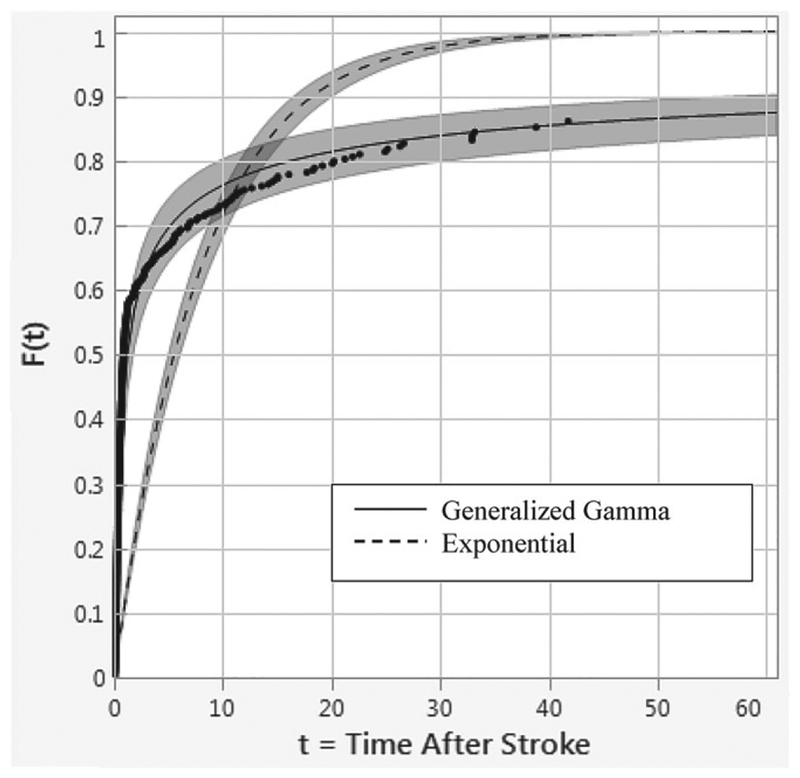
We note that the generalized gamma (GG) distribution provides the best fit (AICc = 1668.81, BIC = 1681.61) whereas the exponential distribution provides the worst fit (AICc = 2511.17, BIC = 2515.44) for this data (see Figure 3). If we ignore the information (for the standard treatment arm) provided by the observational study, and instead naively use the assumption of exponentially distributed survival times in the 2 arms (noting that many commercial statistics software have only this option for parametric distributions), then our sample size calculation based on a hypothesized improvement of doubling the mean survival time would yield a total sample size of N = 54 (27 in each arm). To understand why this is incorrect, we need to briefly discuss the specifics of the GG distribution as discussed below.

FIGURE 3.

Distribution fits for the generalized gamma vs exponential for hemorrhagic stroke mortality data

The GG distribution (Stacy and Mihram¹³) is a three-parameter family of distributions with a probability density function:

$$f(t)=\frac{\beta }{\Gamma (k).\theta }{\left(\frac{t}{\theta }\right)}^{k\beta -1}{e}^{-{\left(\frac{t}{\theta }\right)}^{\beta }},$$ (1)

where β > 0 and k > 0 are the shape parameters, θ > 0 is the scale parameter, and Γ(k) is the gamma function defined as $\Gamma (\text{k})={\int }_0^{\infty }{x}^{k-1}{e}^{-x}dx$.

For model fitting purposes, a reparametrization is used to avoid convergence problems using location parameter μ, scale parameter σ, and shape parameter λ that generalizes the two-parameter gamma distribution. The general notation used to specify the distribution is GG(μ, σ, λ). It is given by the density function:

$$f_{GG}(t)=\frac{\left|\lambda \right|}{\sigma t\Gamma \left({\lambda }^{-2}\right)}{\left[{\lambda }^{-2}{\left\{\text{exp}(-\mu )t\right\}}^{\lambda /\sigma }\right]}^{{\lambda }^{-2}}\text{exp}\left[-{\lambda }^{-2}{\left\{\text{exp}(-\mu )t\right\}}^{\lambda /\sigma }\right],$$ (2)

where σ > 0, μ ∈ (−∞, ∞), λ ∈ (−∞, ∞), and $\Gamma (\text{x})={\int }_0^{\infty }{m}^{x-1}{e}^{-m}dm$ is the gamma function of x.

The parameters of (1) and (2) are related in the following way:

$$\begin{gathered} \mu =\text{ln}(\theta )+\frac{1}{\beta }\text{ln}\left({\lambda }^{-2}\right), \\ \sigma =\frac{1}{\beta \sqrt{k}}, \\ \lambda =\frac{1}{\sqrt{k}}=\beta \sigma . \end{gathered}$$ (3)

A complete taxonomy of the various hazard functions for the GG family has been articulately explained in Cox et al,¹⁴ and the relevant aspects are discussed in the following subsections. Briefly, the GG family allows the flexibility of modeling different shapes of hazard functions such as increasing from 0 to ∞, increasing from a constant to ∞, decreasing from ∞ to 0, decreasing from ∞ to a constant, arc-shaped hazards, and bathtub-shaped hazards. Another important feature of this family is that many popular parametric distributions are special case members of this family. Thus, λ = σ gives the two-parameter gamma $\left(\mathcal{G}\right)$ distribution; μ = 0; σ = 1 gives the standard gamma distribution for fixed values of λ; λ = 1 gives the Weibull distribution; λ = σ = 1 gives the exponential distribution; λ = 0 gives the lognormal distribution; λ = − 1 gives the inverse Weibull distribution; λ = − σ gives the inverse gamma distribution; λ = 1/σ gives the ammag distribution; λ = − 1/σ gives the inverse ammag distribution; and a lognormal distribution with σ′= 1.82σ approximates the log-logistic distribution (Cox et al¹³). Maximum likelihood estimation using standard statistics software can be used to obtain estimates of the 3 parameters of the GG distribution with parsimonious reductions resulting in fitting of well- known parametric distributions.

3.2 |. Quantiles of the GG distribution

Cox et al¹⁴ discuss that for a GG(μ, σ, λ) distribution,

$$\begin{gathered} \text{log}\left\{t_{GG(\mu ,\sigma ,\lambda )}(p)\right\}=\mu +\sigma \cdot \text{log}\left\{t_{GG(0,1,\lambda )}(p)\right\}, \\ =\mu +\sigma \cdot g_{\lambda }(p). \end{gathered}$$ (4)

Here, g_λ(p) is the logarithm of the p-th quantile from the GG(0, 1, λ) distribution. The location parameter μ acts as a time multiplier and governs the values of the median for fixed values of σ and λ, resulting in an accelerated failure time (AFT) model. The scale parameter σ determines the interquartile ratio for fixed values of λ and independently of μ. The shape parameter λ determines the GG(0, 1, λ) distribution. Together, σ and λ describe the type of hazard function for the GG(μ, σ, λ) distribution. See Wei¹⁵ for operational details of a standard AFT model.

3.3 |. The concept of relative time with proportional time as a special case

The time by which p% of the population experience an event can lead to a statistic called “relative times RT(p),” which can be used to compare survival profiles of patients in different treatment arms (new treatment versus standard treatment). Thus,

$$RT(p)=\frac{t_1(p)}{t_0(p)}=\frac{S_1{}^{-1}(1-p)}{S_0{}^{-1}(1-p)},$$ (5)

where $S_i^{-1}(1-p)$ is the inverse survival function for group i (i = 0,1).

The interpretation of RT(p) is that the time required for p% of individuals in the stroke group to experience death is RT(p) times the time required for p% of individuals in the no stroke group to experience death. Thus, if (μ₀, σ₀, λ₀) and (μ₁, σ₁, λ₁) denote 2 different sets of GG parameter values, then

$$RT(p)=\text{exp}\left\{\left({\mu }_1-{\mu }_0\right)+{\sigma }_1\cdot g_{{\lambda }_1}(p)-{\sigma }_0\cdot g_{{\lambda }_0}(p)\right\}.$$ (6)

The manner in which covariates affect RT(p) can be summarized as

1. If λ₁ = λ₀ and σ₁ = σ₀, then we have a conventional AFT model resulting in non-PH, but proportional RT or simply “proportional times (PT) assumption”; that is, covariates affect μ only. Thus,

   $$RT(p)=\text{exp}\left({\mu }_1-{\mu }_0\right)={\mathrm{\Delta }}_{\text{PT}}\equiv \text{PT assumption}.$$ (7)

2. If only λ₁ = λ₀, then we have a model that results in non-PH and nonproportional RT(p); that is, covariates affect both μ and σ.

3. Full generalization is obtained by having covariates affect all 3 parameters.

4. Reduced parsimonious models result in the fitting of family members of the GG distribution.

As is evident from our discussion above, sample size calculations performed using the assumption of exponentially distributed times for the 2 treatment arms is only a restrictive special case that conveniently ignores information available to us from the previously performed observational study.

In the next section, we show how sample size calculations can be performed under the PT assumption.

4 |. METHODS: SAMPLE SIZE CALCULATIONS

4.1 |. Development of a test statistic

Combining Equations 3 and 7, we can show that

$$RT(p)=\text{exp}\left({\mu }_1-{\mu }_0\right)=\text{exp}\left\{\text{ln}\left({\theta }_1\right)+\frac{1}{\beta }\text{ln}\left({\lambda }^{-2}\right)-\text{ln}\left({\theta }_0\right)-\frac{1}{\beta }\text{ln}\left({\lambda }^{-2}\right)\right\}=\frac{{\theta }_1}{{\theta }_0}.$$ (8)

Denoting the maximum likelihood estimate (MLE) of θ_i as ${\widehat{\theta }}_i$ for i = 0 (standard) and i = 1 (new), Bernsetin and Lagakos⁶ have shown that for an exponential distribution

$$\frac{{\widehat{\theta }}_1}{{\widehat{\theta }}_0}~\frac{{\theta }_1}{{\theta }_0}{F}_{n_0,n_1},$$ (9)

where n₀ and n₁ are the number of events for the standard and new treatment arm, respectively.

Following a similar framework, in case of a GG distribution, we show (see Appendix A) that the test statistic, which is a ratio of the MLEs for the two treatment arms, follows a four-parameter GG ratio (GGR) distribution.

$$\frac{{\widehat{\theta }}_1}{{\widehat{\theta }}_0}~GGR\left(\frac{n_0}{n_1}{\left[\frac{{\theta }_1}{{\theta }_0}\right]}^{\beta },n_{0}k,n_{1}k,\beta \right),$$ (10)

For new treatment to standard treatment allocation ratio r = n₁/n₀ we get

$$\frac{{\widehat{\theta }}_1}{{\widehat{\theta }}_0}~GGR\left(\frac{1}{r}{\left[\frac{{\theta }_1}{{\theta }_0}\right]}^{\beta },\frac{n_{1}k}{r},n_{1}k,\beta \right),$$ (11)

Under the null hypothesis H₀: θ₀ = θ₁ we get

$$\frac{{\widehat{\theta }}_1}{{\widehat{\theta }}_0}~GGR\left(\frac{1}{r},\frac{n_{1}k}{r},n_{1}k,\beta \right).$$ (12)

Thus, for calculating number of events based on the PT assumption, we can replace β and k by their MLEs obtained from the large observational study. Then number of events(s) can be calculated for a given magnitude of PT (effect size), power, alpha, and allocation ratio (See Appendix A for the iterative logic used in the sample size calculation using the GGR distribution).

4.2 |. Calculating total sample size

In a clinical trial with accrual time a and follow-up time f, we can calculate the proportion of patients that will die in each treatment arm using Simpson′s rule as shown below:

$$d_i=1-\frac{1}{6}\left\{S_i(f)+4S_i(f+0.5a)+S_i(f+a)\right\}.$$ (13)

If information is available about the survival curve S₀ for the standard treatment arm (as in our case, from a large observational study), d₀ can be calculated easily. Then using the value of Δ_PT under the alternate hypothesis, the survival curve S₁ for the new treatment arm is tractable and, hence, d₁ can be calculated. If p_i is the probability of being assigned to treatment arm i, the proportion of patients that will die during the clinical trial can be calculated as

$$d={\sum }_{i=0}^1{p}_i{d}_i=\frac{n_0}{N}\left(d_0+r{d}_1\right),$$ (14)

where N = n₀ + n₁ is the total number of events in the 2 treatment arms.

The total sample size N_total = N/d can be simply obtained by dividing N by d. Alternatively, N_total can be calculated simply by dividing N by the anticipated event rate.

4.3 |. Variance inflation factor adjustment for an additional covariate

Our sample size calculations based on PT are applicable to an AFT model. In this case, we assume that treatment assignment has correlation ρ with an additional covariate and that this additional covariate affects only the location parameter of the GG distribution; the total sample size can be adjusted using a variance inflation factor of (1 − ρ²)⁻¹. This follows from the discussion by Hsieh and Lavori,⁵ where such adjustment can be performed in a regression model. In our case, the difference in the location parameters between the new treatment arm and standard treatment arm μ₁ − μ₀ can be represented by α₁X₁ in a regressing setting where X₁ = 0, 1 represents the 2 treatment arms and α₁ is the regressing coefficient of X₁. Hsieh and Lavori⁵ discuss that in a regression model, the variance of the estimate a₁ of the parameter α₁is inversely related to the variance of the corresponding covariate X₁ and that increasing the scale of X by a factor c increases the variance of X₁ by c² and decreases the variance of a₁ by c². Thus, if ρ² is the proportion of variance explained by the regression of X₁ on an additional covariate X₂, then the conditional variance of X₁∣X₂ is smaller than the marginal variance of X₁ by a factor of 1 − ρ². This increases the variance of a₁ estimated from the regression model by a factor of (1 − ρ²)⁻¹. Thus, to preserve power, we can use this variance inflation factor to calculate the adjusted sample size using the formula N_adjusted = N_total/(1 − ρ²).

5 |. RESULTS

5.1 |. Sample size (analytical) calculations for our example

From our observational study data, we obtained (using SAS 9.4) the following MLEs and corresponding 95% confidence intervals: $\widehat{\sigma }=1.4140(1.2719-1.5561)$, $\widehat{\lambda }=-1.9929(-2.3175\text{ to }-1.6683)$. This yields $\widehat{k}=0.2518$ and $\widehat{\beta }=1.4094$. Then for 80% power and 5% level of significance, using a relation between the GGR distribution and the F distribution (see Appendix A), we get the following results: (1) For r = 0.5, n₀ = 84, n₁ = 42, N = 126; (2) for r = 1, n₀ = n₁ = 54, N = 108; and (3) for r = 2, n₀ = 39, n₁ = 78, N = 117.

For r = 1, Table 2 shows sample size calculations for different values of accrual time a, follow-up time f, and correlation ρ with an additional covariate.

TABLE 2.

Sample size for our example (r = 1) for varying values of a and f

	ρ = 0	ρ = 0.4
a = 12 months, f = 12 months	Ntotal = 144	Nadjusted = 172
a = 24 months, f = 12 months	Ntotal = 140	Nadjusted = 168
a = 12 months, f = 24 months	Ntotal = 136	Nadjusted = 162
a = 24 months, f = 24 months	Ntotal = 132	Nadjusted = 158

From Figure 2, we see that the survival curve for the new treatment arm with Δ_HR = 0.80 (corresponding to a 20% risk reduction) comes closest (visually) to our anticipated survival curve for the new treatment arm with Δ_PT = 2. If the statistician were to render the calculations for the number of events that would be needed to have 80% power at the 5% significance level to detect 20% reduction in risk, he or she would end up with N = 498 (verified using PASS statistical software), and this would be drastically different from the N = 108 that we obtained using Δ_PT = 2. Thus, in our motivating example, ignoring the shape of the survival curve obtained from the previous observational study could have significant drain on resources, as it would be very difficult to enroll 498 patients for a trial where the survival rates for most patients are low to begin with. In the next subsection, we compare the 2 approaches to gain a better understanding of the advantages and limitations of the 2 approaches.

5.2 |. Comparisons with PH approach—an overview

To compare the PT approach with the PH approach, we first performed analytical calculations for number of events N that would be required to detect Δ_PT = 2 with 80% power at the 5% level of significance. The left-hand side of Table 3 shows these calculations for r = 1 assuming a one-sided hypothesis. Note that as per Equation 3, specifying λ and β automatically fixes the value of σ. The right-hand side of Table 3 shows corresponding calculations for N using the PH approach for varying values of Δ_HR again keeping r = 1.

TABLE 3.

Comparing PT versus PH approaches

# Events N for PT assumption (80% power, α = 0.05 one-sided, ΔPT = 2, r = 1)											# Events N for PH assumption (80% power, α = 0.05 one-sided, r = 1)
		β											N
		4	3	2	1.5	1	0.75	0.5	0.25	0.1		0.85	938
	0.10	-	-	-	-	-	-	-	10	52		0.8	498
	0.25	-	-	-	-	-	-	14	52	322		0.75	300
	0.50	-	-	-	-	14	24	52	208	1288		0.7	196
	0.75	-	-	-	14	30	54	118	466	2898		0.65	134
|λ|	1.00	-	-	14	24	52	94	208	826	5150	ΔHR	0.6	96
	1.50	10	16	32	56	120	210	466	1858	11586		0.55	70
	2.00	16	28	56	96	212	372	828	3300	20596		0.5	52
	2.50	26	44	88	150	332	582	1294	5158	-		0.45	40
	3.00	38	64	128	218	478	838	1864	7426	-		0.4	30

N is rounded up to an even number to avoid fractional values for n₀ and n₁.

A “-” indicates that N is either too small or too large to be considered practically meaningful.

This table shows N for a one-sided hypothesis. Similar calculations can be done for a two-sided hypothesis.

This table is constructed for Δ_PT = 2. For Δ_PT > 2, N will decrease and vice versa.

From Table 3, we see that when λ = β = σ = 1, we obtain N = 52. This represents a special case corresponding to the exponential distribution for which Δ_PT = 2 implies Δ_HR = 0.5 and the calculation for N matches what we get using the PH approach. When we only have the restriction λ = 1, we are confronting the special case scenario of a Weibull distribution. The Weibull distribution has the property of fulfilling both the PT and PH assumptions; hence, our calculations for N should match. For example, if we look at λ = 1, β = 0.5 (Weibull with decreasing hazard with σ = 2), then using the PT assumption Δ_PT = 2, we calculate N = 208. Using the relation ln(Δ_PT) = − ln(Δ_HR). σ specific to the Weibull, we calculate Δ_HR = 0.707 and this matches the N = 208 we obtain using the PH assumption.

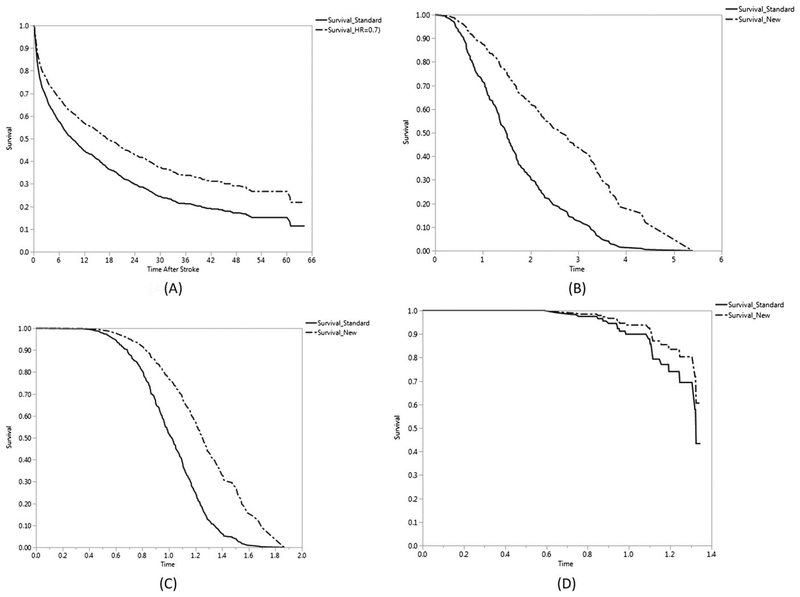
For cases where λ ≠ 1, the comparisons between the 2 approaches are not straightforward. For example, consider the survival curve (solid red color) for ischemic strokes (see Figure 1) arising from the observational study as representative of the standard treatment arm and hypothesize that NewTrt will double longevity (Δ_PT =2). Then from the observational study data, we calculate $\widehat{\sigma }=1.8831(95\%\text{ CI},1.8035-1.9625)$ and $\widehat{\lambda }=-0.2002(95\%\text{ CI},-0.4263-0.0259]$ as the MLEs. Next, using our PT approach of Equation 10, we arrive at N = 184 using r = 1 with 80% power at the 5% significance level. Note how the 95% CI for λ includes 0, and hence, the lognormal distribution will be a good fit for this data. Using the sample-size method of Hale¹⁶ for the lognormal distribution would have resulted in N = 178. If we were to adopt the PH approach and use Δ_HR = 0.7 (a commonly used effect size in many time-to-event based trials), as per Table 3, we would need N = 196 as the required number of events. From Figure 4A, for this particular case, we see that Δ_HR = 0.7 does indeed generate a survival curve for the new treatment arm that “visually” comes somewhat close to what would have been obtained using Δ_PT =2 (note that although Δ_HR = 0.675, yielding N = 162 would be obtained by using $S_1(0.5)=S_0{(0.5)}^{{\mathrm{\Delta }}_{\text{HR}}}$ and would be an even better approximation it would be difficult for a researcher come up with this magnitude of Δ_HR for effect size). Thus, it appears that either approach would work adequately for performing the sample size calculations for a hypothesized new treatment for ischemic stroke patients; Δ_PT = 2, however, would have a more direct clinical interpretation than Δ_HR = 0.7.

FIGURE 4.

Survival curves for comparing standard treatment arm to new treatment arm A, ischemic stroke observational study with Δ_HR = 0.7, B, hypothetical data GG (μ = 0, λ = 0.832, σ = 0.416) with Δ_HR = 0.4, C, hypothetical data GG (μ = 0, λ = 0.832, σ = 0.208) with Δ_HR = 0.4, D, hypothetical data GG (μ = 0, λ = 0.832, σ = 0.166) with Δ_HR = 0.6

For situations where N in Table 3 is large and Δ_PT = 2, we generated KM curves using appropriate values for the parameters of the GG distribution and found that these large values of N were due the survival curve of the standard treatment arm being even more steep than the one shown for hemorrhagic stroke patients in Figure 1. Thus, in these situations, for a majority of the patients, “doubling” of longevity does not offer a significant benefit. Small effect sizes require large N, meaning that to get smaller N, we would have to define the effect size in terms of larger values of Δ_PT (for example, 3, 4, or even larger). When the survival curve for the standard treatment arm is very steep, then using the PH approach also results in very large N for commonly values of Δ_HR such as 0.7, 0.6 or 0.5. Here also, to reduce N, we would then need to define large effect sizes, thereby implying small values of Δ_HR such as 0.3 or 0.2.

5.3 |. Evaluation of the PT method when the PH assumption is true

Since the PH method is widely used in designing a clinical trial, it is important to consider the situations where the PH assumption holds true in the population (that is, when Δ_HR is constant). We calculate the sample size N obtained for 80% power and 5% significance level using this assumption and then assess how well the proposed PT approach performs. Note that no direct formula is available to convert N between the 2 approaches; thus, to perform these comparisons, we undertook the following tasks. (1) Generate baseline survival curve representing the standard treatment arm by simulating data from a known parametric distribution. This baseline distribution can be from the GG family (so as to include well-known parametric distributions as special cases) or some other distribution such as the log-logistic or the exponentiated Weibull distribution (see Mudholkar and Srivastava¹⁷ and Cox and Matheson¹⁸). (2) Assuming that the PH assumption to be true (Δ_HR defines the effect size), generate the survival curve for the new treatment arm. Calculate the sample size required for achieving 80% power at the 5% level of significance for a one-sided test. (3) Using careful visual inspection, calculate an approximate value for Δ_PT using the survival curves for the 2 treatment arms. Thus, Δ_PT can be approximated at either the median survival time or the average of the 25th, 50th, and 75th survival quartiles, or, if the situation permits, the average of survival deciles. (4) Assess, if using this value of Δ_PT, power comparable to 80% is achieved for a given value of sample size. Results are displayed in Table 4A.

TABLE 4A.

Performance of PT method using 10 000 simulations (r = 1 in all cases, one-sided test) when the proportional hazards assumption is true

Baseline Distribution (Control Group)	n/ΔHR/Power	Approximated ${\widehat{\mathrm{\Delta }}}_{\text{PT}}$	% Empirical Power
Exponential	12/0.35/0.8	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=2.857$	78.90
λ = 1, σ = 1 d = 1	16/0.35/0.9	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=2.857$	88.95
Generalized gammaa	15/0.40/0.8	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.501$	82.47
λ = 0.832, σ = 0.416 d = 1	21/0.40/0.9	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.501$	92.23
Generalized gammaa	15/0.40/0.8	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.215$	80.28
λ = 0.832, σ = 0.208 d = 1	21/0.40/0.9	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.215$	90.48
Inverse gamma	20/0.45/0.8	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.889$	78.89
λ = −0.8, σ = 0.8 d = 1	27/0.45/0.9	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.889$	88.95
Log-logisticc	26/0.50/0.8	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=3.251$	79.26
μlocation = 1.08, Sscale = 0.9882 d = 1	36/0.50/0.9	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=3.251$	88.85
Exponentiated Weibullc	35/0.55/0.8	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=2.075$	79.30
λ = 1, σ = 2, αshape = 2 d = 1	48/0.55/0.9	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=2.075$	88.86
Generalized gammaa	48/0.6/0.8	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.090$	80.30
λ = 0.832, σ = 0.166 d = 0.25	66/0.6/0.9	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.090$	90.41
Generalized gammab	54/0.62/0.8	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=2$	80.62
λ = −1.992, σ = 1.414 d = 0.766	75/0.62/0.9	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=2$	90.28
2-parameter gamma	97/0.70/0.8	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=2.050$	79.48
λ = 2, σ = 2 d = 1	135/0.70/0.9	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=2.050$	89.40
Ammag	150/0.75/0.8	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.776$	79.76
λ = 0.5, σ = 2 d = 1	207/0.75/0.9	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.776$	90.33
Inverse Weibull	299/0.80/0.8	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.450$	79.59
λ = −1, σ = 1.667 d = 1	344/0.80/0.9	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.450$	89.38
Inverse Ammag	469/0.85/0.8	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.115$	80.20
λ = −0.817, σ = 1.225 d = 1	649/0.85/0.9	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.115$	89.99
Standard gamma	1114/0.9/0.8	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.427$	79.82
λ = 1.5, σ = 1 d = 1	1543/0.9/0.9	${\widehat{\mathrm{\Delta }}}_{\text{PT}}=1.427$	90.17

^aThese simulations represent the scenarios presented in Figure 4B–D.

^bThis scenario represents the motivating example discussed in the text.

^cBaseline distribution is not from the generalized gamma family.

For example, say that the survival times in a standard treatment arm follow a GG (μ = 0, λ = 0.832, σ = 0.416) distribution and that the hazards in the 2 treatment arms are truly proportional, with Δ_HR = 0.4 being the effect size of clinical interest. Then, as per Table 3, for 80% power at the 5% significance level, we need to accrue N = 30 events in the study. Figure 4B shows the “true” KM curves (considering that all simulated observations are events) for the 2 treatment arms for this study. Thus, a 60% hypothesized (and clinically meaningful) risk reduction requires that the 2 treatment arms experience only 15 events each for the study to have 80% power. Now, suppose that we were to define the effect size in terms of Δ_PT instead of Δ_HR. Since no direct conversion is available, we can take an approximate approach. We observe that at the 75th and 25th percentile of survival, the ratio RT(p) using Equation 5 is approximately 1.45, whereas at the 50th percentile (median) of survival, the ratio RT(p) is about 1.5. Thus, Δ_PT can be averaged out to be (1.45 + 1.5 + 1.45)/3 = 1.5. Then by using our proposed method, for N = 30—that is 15 events in each treatment arm—the empirical power obtained from 10 000 simulations is 82.47%. Thus, in this scenario, even if the PH assumption were to hold true, designing a trial using the PT assumption would give comparable performance. Figure 4C represents a similar situation with the survival times in a standard treatment arm following a GG (μ = 0, λ = 0.832, σ = 0.208) distribution with Δ_HR = 0.4 yielding N = 30 (15 in each arm). In this case, calculating Δ_PT at each survival decile yields an average of Δ_PT= 1.215, resulting in empirical power of 80.28% for N = 30 using our proposed method. In Figure 4D, we consider a more extreme case with survival times in a standard treatment arm following a GG (μ = 0, λ = 0.832, σ = 0.166) distribution with 25% event rate. In this case, Δ_HR = 0.6 would require enrollment of a total of N = 96 patients (48 in each arm). Here, too, an averaged estimate of Δ_PT= 1.09 yields 80.30% power with N = 96 patients using the PT assumption. Other simulation scenarios in Table 4A yield similar results, even when other baseline distributions for the standard treatment arm are used.

5.4 |. Performance evaluations of PT method using simulations

We also performed simulations to assess the overall performance of our approach. Table 4B displays the results of power calculations for 10 000 simulations done for the various scenarios explained above with r = 1. Data were simulated from the GG distribution, and the SAS procedure PROC LIFEREG was used to obtain MLEs of the GG parameters and hence calculate ${\widehat{\Delta }}_{\text{PT}}$, the estimate of PT. This allowed us to calculate the bias, mean square error, and coverage probability, in addition to evaluating the power under both the null (type I error) and the alternate hypothesis. In all of our simulations, we found that there was a small positive bias in estimating Δ_PT but that it was always less than 5%. The empirical type I error rate was close to the nominal type I error rate of 5%, and it never exceeded 6.67% even for small sample sizes. We chose sample sizes so as to be able to compare simulated value of power with the analytical calculations displayed in Table 3. As can be seen from Table 4B, power obtained through simulations either matched the analytical calculations given in Table 3 or was marginally below it. In most situations where the power was slightly below 80%, the addition of 2 or 4 subjects (1 or 2 in each group) resulted in the achievement of power above the 80% threshold value. The approximate Wald coverage probability was lower than the nominal value of 95% in some simulations. However, it should be noted that PROC LIFEREG assumes an approximate normal distribution for the location parameters μ_i and that this may explain the somewhat lower values for coverage. (Note that since our test statistic follows a GGR distribution, the μ_i follows a log-GGR distribution of which the log-GG is a special case and the normal distribution is in turn a special case of the log-GG distribution.) Overall, it appears that there is a good match between the analytical and simulated results.

TABLE 4B.

Performance evaluation of proportional time (PT) method using 10 000 simulations (r = 1 in all cases) when the PT assumption is true

Simulation Scenario: PT Assumption is True		$\overline{{\widehat{\mathrm{\Delta }}}_{\text{PT}}}$	SE ($\overline{{\widehat{\mathrm{\Delta }}}_{\text{PT}}}$)	Bias (${\widehat{\mathrm{\Delta }}}_{\text{PT}}$)	% Bias (${\widehat{\mathrm{\Delta }}}_{\text{PT}}$)	MSE	% Wald Coverage	% Power
Exponential	ΔPT = 1	1.0393	0.0031	0.0393	3.930	0.0972	92.24	5.77
λ = σ = 1	ΔPT = 1.5	1.5589	0.0046	0.0589	3.930	0.2151	92.24	41.46
n = 26, N = 52	ΔPT = 2	2.0786	0.0062	0.0786	3.930	0.3889	92.24	78.47
Weibull	ΔPT = 1	1.0386	0.0029	0.0386	3.860	0.0871	94.86	4.68
λ = 1, σ = 2	ΔPT = 1.5	1.5579	0.0044	0.0579	3.860	0.1959	94.86	49.48
n = 104, N = 208	ΔPT = 2	2.0772	0.0059	0.0772	3.860	0.3482	94.86	79.86
Weibull	ΔPT = 1	1.0453	0.0033	0.0453	4.530	0.1131	87.78	6.15
λ = 1, σ = 0.8	ΔPT = 1.5	1.5679	0.0050	0.0679	4.530	0.2545	87.78	49.46
n = 17, N = 34	ΔPT = 2	2.0906	0.0067	0.0906	4.530	0.4524	87.78	78.47
Standard gamma	ΔPT = 1	1.0420	0.0030	0.0420	4.020	0.0931	84.74	5.88
λ = 2, σ = 1	ΔPT = 1.5	1.5603	0.0044	0.0603	4.020	0.2094	84.74	49.78
n = 30, N = 60	ΔPT = 2	2.0804	0.0060	0.0804	4.020	0.3723	84.74	81.93
2-parameter gamma	ΔPT = 1	1.0469	0.0030	0.0469	4.693	0.0932	93.42	5.64
λ = σ = 2	ΔPT = 1.5	1.5704	0.0045	0.0704	4.693	0.2097	93.42	49.62
n = 107, N = 214	ΔPT = 2	2.0939	0.0060	0.0939	4.693	0.3728	93.42	81.00
Lognormalab	ΔPT = 1	1.0414	0.0030	0.0414	4.135	0.0922	94.42	5.52
λ = −0.2, σ = 1.883	ΔPT = 1.5	1.5620	0.0044	0.0620	4.135	0.2075	94.42	49.46
n = 92, N = 184	ΔPT = 2	2.0827	0.0060	0.0827	4.135	0.3689	94.42	80.23
Ammag	ΔPT = 1	1.0382	0.0029	0.0382	3.820	0.0856	94.72	5.07
λ = 0.5, σ = 2	ΔPT = 1.5	1.5595	0.0044	0.0595	3.820	0.2015	94.72	49.46
n = 104, N = 208	ΔPT = 2	2.0794	0.0059	0.0794	3.820	0.3583	94.72	80.03
Inverse gamma	ΔPT = 1	1.0444	0.0031	0.0444	4.435	0.0979	89.91	6.41
λ = −0.8, σ = 0.8	ΔPT = 1.5	1.5665	0.0046	0.0666	4.435	0.2202	89.91	49.77
n = 18, N = 36	ΔPT = 2	2.0887	0.0062	0.0887	4.435	0.3915	89.91	81.48
Inverse Weibull	ΔPT = 1	1.0366	0.0029	0.0366	3.660	0.0887	94.24	5.10
λ = −1, σ = 1.667	ΔPT = 1.5	1.5599	0.0044	0.0599	3.660	0.1996	94.24	41.58
n = 72, N = 144	ΔPT = 2	2.0732	0.0059	0.0732	3.660	0.3548	94.24	79.66
Inverse ammag	ΔPT = 1	1.0424	0.0031	0.0424	4.240	0.0960	93.56	5.44
λ = −0.817, σ = 1.225	ΔPT = 1.5	1.5636	0.0046	0.0636	4.240	0.2486	93.56	49.45
n = 39, N = 78	ΔPT = 2	2.0848	0.0061	0.0848	4.240	0.3839	93.56	79.52
Generalized gammac	ΔPT = 1	1.0469	0.0030	0.0469	4.693	0.0942	91.66	5.37
λ = −1.992, σ = 1.414	ΔPT = 1.5	1.5704	0.0045	0.0704	4.693	0.2118	91.66	49.60
n = 54, N = 108	ΔPT = 2	2.0939	0.0061	0.0939	4.693	0.3766	91.66	80.62

^aLognormal has λ = 0, but here, we have taken λ = − 0.2 to reflect the scenario discussed in the text.

^bThis simulation scenario is visually represented in Figure 4A.

^cThis scenario represents the motivating example discussed in the text.

5.5 |. Comparisons with a cure rate model and piecewise exponential model

When the PH assumption is not valid, a researcher may opt for conducting the sample size calculations using alternative methods that do not require this assumption to hold. For example, a researcher may perform the sample size calculations using the cure rate (CR) model or the piecewise exponential (PE) model to account for the nonproportionality of hazards in the 2 treatment arms, provided such approaches are appropriate. To evaluate the robustness of our PT method, we compared it to the CR and PE model using simulations. Table 5 displays the simulation results where the data are simulated using the PT assumption and sample sizes are obtained. These are compared to sample sizes that would have been obtained had the CR or PE methods been used. Analogously, Table 6 displays the simulation results where the CR model is assumed to be true and where sample sizes calculated are therefore assumed to be correct. These are then compared to sample sizes that would have been obtained had the PT or PE methods been used. It should be noted that direct comparisons between these 3 approaches are not always possible owing to the different assumptions under which these methods operate. We therefore sought to evaluate the robustness of our method only under those situations where such comparisons are possible.

TABLE 5.

Sample size comparisons for proportional time (PT) approach (true) versus piecewise exponential model (PEM) and cure rate (CR) model

PT model (ΔPT assumed true)		Piecewise Exponential PE model		Cure Rate Mixture CRM model (EL = Exponential-Logit, WL = Weibul-Logit, CL = Cox-Logit)
Simulation Scenarios	Power/NTotal	Calculation Parameters	Power/NTotal	Calculation Parameters	Power/NTotal
λ = −1.9930	0.8/ 142	mstd = 9	0.8/ NLR = 408,	π0 = π1 = 0.1335,	0.8/ NWLR = 258, NSLR = 238
σ = 1.414		mnew = 9	NG = 220, NTW = 282	λ0 = 0.3641,
a = 12, f = 36	0.9/ 194	a = 12	0.9/ NLR = 564,	ω = −0.6931,	0.9/ NWLR = 356, NSLR = 330
d = 0.77, ΔPT = 2		f = 36	NG = 304, NTW = 390	a = 12, f = 36, EL
λ = −0.2	0.8/ 232	mstd = 15	0.8/ NLR = 230,	π0 = π1 = 0.1988,	0.8/ NWLR = 360, NSLR = 378
σ = 1.8830		mnew = 11	NG = 212, NTW = 218	λ0 = 0.1456,
a = 12, f = 48	0.9/ 324	a = 12	0.9/ NLR = 316,	ω = −0.6931,	0.9/ NWLR = 498, NSLR = 524
d = 0.63, ΔPT = 2		f = 48	NG = 306, NTW = 300	a = 12, f = 48, EL
λ = 1.5,	0.8/ 48	mstd = 15	0.8/ NLR = 62,	π0 = π1 = 0.0001,	0.8/ NWLR = 76, NSLR = 72
σ = 0.85		mnew = 11	NG = 92, NTW = 74	λ0= 1.1985,
a = 1, f = 2.5	0.9/ 62	a = 1	0.9/ NLR = 86,	ω = −0.6066,	0.9/ NWLR = 104, NSLR = 98
d = 1, ΔPT = 2		f = 2.5	NG = 128, NTW = 102	a = 1, f = 2.5, CL
λ = 2	0.8/ 232	mstd = 9	0.8/ NLR = 304,	π0 = π1 = 0.0001,	0.8/ NWLR = 622, NSLR = 618
σ = 2		mnew = 11	NG = 932, NTW = 544	λ0 = 0.6274,
a = 2, f = 8	0.9/ 312	a = 2	0.9/ NLR = 422,	ω = −0.2006,	0.9/ NWLR = 862, NSLR = 856
d = 1, ΔPT = 1.1		f = 8	NG = 1290, NTW = 754	a = 2, f = 8, CL
λ = 0.9717	0.8; 70	mstd = 9	0.8/ NLR = 80,	π0 = π1 = 0.0547	0.8/ NWLR = 90, NSLR = 76
σ = 0.1606		mnew = 8	NG = 72, NTW =	λ0 = 0.2567, β = 3.8956
a = 0, f = 1.5	0.9; 96	a = 0	740.9/ NLR = 110,	ω = −0.7431	0.9/ NWLR = 126, NSLR = 104
d = 0.80		f = 1.5	NG = 98, NTW = 102	a = 0, f = 1.5, WL
λ = 0.5559	0.8; 134	mstd = 4	0.8/ NLR = 138,	π0 = π1 = 0.0464,	0.8/ NWLR = 155, NSLR = 147
σ = 2.0396		mnew = 7	NG = 144, NTW = 134	λ0= 1.3645, β = 1.8475	0.9/ NWLR = 214, NSLR = 203
a = 6, f = 15	0.9; 186	a = 6	0.9/ NLR = 190,	ω = −0.6010,
d = 0.5, ΔPT = 2.5		f = 18	NG = 198, NTW = 184	a = 6, f = 15, WL

For PE model: N_LR, N_G, and N_TW represent the sample size calculations using the Logrank, Gehan, and Taroneware options; m_std and m_new represent the number of intervals for the standard and new treatment groups, respectively, such that the shape of the survival curve for the 2 groups is approximated as much as possible.

For CR model (following Xiong and Wu¹⁹), N_WLR and N_SLR are the sample sizes calculated using the weighted logrank and the standard logrank test, respectively; π₀ and π₁ are the cured proportions in the standard and new treatment arms, respectively; λ₀ is the constant hazard rate in the standard treatment arm; and ω is the log hazards ratio comparing the new treatment to the standard treatment arm.

TABLE 6.

Comparing sample sizes for cure-rate model (true) versus proportional time (PT) and piecewise exponential model (PEM), for one-sided hypothesis, r = 1

Cure Rate Mixture CR model assumed true			Proportional Time PT model		Piecewise Exponential PE model
Simulation Scenarios	δ−1/γ	Power/NWLR; NSLR	Calculation Parameters	Power/Ntotal	Calculation Parameters	Power/Ntotal
Exponential-logit mixture	1.3/0.0	0.8/	λ = 0.01	0.8/562	mstd = 9	0.8/ NLR = 566,
		944; 1020	σ = 1.5539		mnew = 15	NG = 460, NTW = 458
		0.9/	a = 12, f = 36	0.9/776	a = 12	0.9/ NLR = 784,
		1306; 1412	d = 0.874, ΔPT = 1.418		f = 36	NG = 638, NTW = 636
π0 = 0.1	1.5/0.0	0.8/	λ = 0.01	0.8/366	mstd = 9	0.8/ NLR = 346,
λ0 = 0.1		380; 428	σ = 1.5539		mnew = 15	NG = 274, NTW = 282
a = 12		0.9/	a = 12, f = 36	0.9/504	a = 12	0.9/ NLR = 480,
f = 36		526; 592	d = 0.868, ΔPT = 1.545		f = 36	NG = 378, NTW = 388
β = 1	1.8/0.0	0.8/	λ = 0.01	0.8/190	mstd = 9	0.8/ NLR = 188,
		174; 204	σ = 1.5539		mnew = 13	NG = 142, NTW = 150
		0.9/	a = 12, f = 36	0.9/262	a = 12	0.9/ NLR = 258,
		240; 282	d = 0.859, ΔPT= 1.836		f = 36	NG = 198, NTW = 206
	2/0.0	0.8/	λ = 0.01	0.8/124	mstd = 9	0.8/ NLR = 110,
		122; 148	σ = 1.5539		mnew = 12	NG = 84, NTW = 90
		0.9/	a = 12, f = 36	0.9/172	a = 12	0.9/ NLR = 152,
		180; 204	d = 0.847, ΔPT = 2.143		f = 36	NG = 116, NTW = 124
Weibull-logit mixture	1.3/0.0	0.8/	λ = 0.2903	0.8/906	mstd = 14	0.8/ NLR = 898,
		1030; 1096	σ = 0.7705		mnew = 14	NG = 692, NTW = 732
		0.9/	a = 2, f = 6	0.9/1256	a = 2	0.9/ NLR = 1244,
		1426; 1518	d =, ΔPT= 1.145		f = 6	NG = 960, NTW = 1014
π0 = 0.1	1.5/0.0	0.8/	λ = 0.2903	0.8/372	mstd = 14	0.8/ NLR = 344,
λ0 = 0.1		418; 460	σ = 0.7705		mnew = 14	NG = 290, NTW = 292
a = 12		0.9/	a = 2, f = 6	0.9/516	a = 2	0.9/ NLR = 476,
f = 36		578; 636	d = 0.875, ΔPT= 1.237		f = 6	NG = 400, NTW = 402
β = 2	1.8/0.0	0.8/	λ = 0.2903	0.8/192	mstd = 14	0.8/ NLR = 188,
		192; 220	σ = 0.7705		mnew = 14	NG = 138, NTW = 146
		0.9/	a = 2, f = 6	0.9/266	a = 2	0.9/ NLR = 260,
		264; 304	d = 0.870, ΔPT= 1.347		f = 6	NG = 190, NTW = 202
	2.0/0.0	0.8/	λ = 0.2903	0.8/134	mstd = 14	0.8/ NLR = 134,
		134; 157	σ = 0.7705		mnew = 13	NG = 98, NTW = 104
		0.9/	a = 2, f = 6	0.9/184	a = 2	0.9/ NLR = 184,
		186; 218	d = 0.862, ΔPT = 1.432		f = 6	NG = 136, NTW = 146

See footnote below Table 5 for explanation of the notation used in this table. Additionally, δ⁻¹ represents the hazard ratio comparing the standard treatment to the new treatment and γ = 0 represents no change in cure rate between the 2 treatment arms.

Briefly, a CR model assumes that the failure time T* is given by T* = vT + (1 − v)∞, where T is the failure time for uncured patients and v = 0, 1 is an indicator of whether a patient will eventually not experience or experience treatment failure. Thus, the overall survival distribution S*(t) = π + (1 − π)S(t) is a mixture model of a CR π = P(v = 0) and the conditional survival distribution S(t) of patients who will experience failure. Xiong and Wu¹⁹ have performed sample size calculations under the CR model using a weighted log-rank test and compared their results to the sample size calculation done using the standard log-rank test by Wang et al.²⁰ They have considered 3 scenarios: (a) New treatment has reduced hazards as compared to standard treatment and resulted in an improved CR; (b) new treatment does not have reduced hazards as compared to standard treatment but resulted in an improved CR; (c) new treatment has reduced hazards as compared to standard treatment, but no improvement in CR resulted. Our PT approach cannot be compared directly to (a) and (b) when the CR model is assumed to be true. Specifically, in (a), it is not clear as to how to calculate Δ_PT as it ranges from a value greater than 1 to ∞ as we move along the time axis. In (b), the survival curves may cross until the CR is realized, and our PT approach is not intended for this scenario since we are interested specifically in performing sample size calculations aimed at improving longevity using a multiplicative factor of time. Therefore, in both Tables 5 and 6, we have compared our PT approach to (c). The footnote below Table 5 briefly explains the notations used in these 2 tables, the detailed explanations for which can be found in Xiong and Wu.¹⁹ In Table 5, we see that when the PT assumption is true and the CR model is used, all situations require larger sample sizes to design the trial. In Table 6, it can be seen that when the CR assumption is true and when the hazard ratio between the 2 treatment arms is large, our PT method yields equivalent sample sizes once the appropriate values of the shape parameters of the GG distribution are estimated. In the case of hazard ratios of small magnitude, our PT methods yield sample sizes smaller than those obtained by the CR method. However, these comparisons are not direct one-to-one comparisons, as both models are working under different assumptions. Xiong and Wu¹⁹ note that they have found optimal weighted logrank tests for sample size calculation only for (b) and that more work needs to be done in scenarios (a) and (b). Thus, merely obtaining smaller sample sizes should not be seen as one method being superior, as the CR model can also handle scenarios (a) and (b). Rather, the comparisons should be seen to complement each other by helping the researcher make informative choices.

Another approach to approximating the survival curves when the PH assumption does not hold true is to assume a PE model. Operational details of this model are briefly discussed in Hougaard.²¹ In this case, the observation time is partitioned into J successive intervals with cut points 0 = ε₀ < ε₁ < … ε_J < ∞ and the j-th interval [ε_{J − 1}, ε_J) extends from the j-1th boundary (inclusive) to the j-th boundary (noninclusive). In each interval of time, the baseline hazard of the standard treatment arm is assumed to be constant so that h₀(t) = h_j for t in [ε_{J − 1}, ε_J). This allows modeling of the baseline hazard using J parameters h₁, h₂, …, h_j one in each interval representing the hazard of the reference group. Using careful selection of cut points, it is then possible to approximate, with reasonable accuracy, any shape of the baseline hazard. Another selection of cut points for the new treatment arm allows approximation of the hazard shape in the new treatment arm. Thus, the PE model can be used to approximate survival curves when the PH assumption is not true and, therefore, to calculate sample sizes prior to designing a clinical trial. Lakatos² and Lakatos²² discuss sample size calculations using the PE model using Markov processes; these calculations can be performed using standard statistics software. It should be noted that judicious selection of cut points is needed to achieve sample sizes of reasonable magnitude; not doing so may considerably inflate the sample sizes.

Table 5 shows the results where the PT assumption is true and the sample sizes obtained by using the PE model are compared to those obtained by the PT model when varying values of accrual and follow-up time are used. In all scenarios, we see that the PE method renders comparable sample sizes. However, the choice of the weighing function (standard logrank, Gehan, or Taroneware) seems to play a key role in obtaining sample sizes comparable to those of the PT approach. Likewise, results presented in Table 6 where the CR model is assumed to be true are quite informative in comparing what sample sizes would have been obtained had the researcher used the PE or the PT approach. This comparison represents a realistic scenario whereby it is known to the researchers that a small proportion of the patients are likely to get cured in both treatment arms, and in anticipating nonproportionality of hazards, they might want perform the sample size calculations using the PE method. From Table 6, it can be said that, in general, the PE method gives smaller sample sizes than the CR method and the PT method but that the choice of the weights seems to influence the calculations. However, the unequal number of intervals for the 2 treatment arms was selected by us after carefully studying the shape of the survival functions. This means that unlike the CR and PT methods, where knowledge of only a few parameters is required to calculate the sample sizes, careful selection of cut points is needed to use the PE method. In real-life scenarios, a researcher may not be comfortable using only the weights that yield smaller sample sizes, meaning that knowledge of comparisons displayed in Table 6 is informative in making sample size decision.

Overall, from Table 5 and Table 6, it appears that our PT approach is reasonably robust provided that the shape parameters of the GG distribution for the standard treatment arm are estimated with reasonable accuracy. In the next section, we discuss some real-life implications of choosing our method to do the sample size calculations.

6 |. DISCUSSION

In our work, we have attempted to show how a statistician can incorporate information available from a previously conducted observational study into designing a clinical trial for time-to-event data. Similarly, one could also use information from large-scale clinical trials. Investigators experienced in their field of study often have an intuitive idea as to what is a clinically meaningful improvement for a new proposed treatment compared to standard treatment regimen, meaning that availability of observational study data can only help a statistician in translating a researcher′s definition of improvement into a statistically relevant definition of effect size. In areas where survival of patients receiving a standard treatment regimen is quite modest (or even poor), researchers are intuitively interested in how much additional longevity will be conferred by a new proposed treatment rather than in a hypothesized percentage risk reduction. Our proposed method of sample size calculation aims to fulfil this requirement, as it allows researchers to converse directly in terms of improved lifetimes when enrolling patients for a new study. From the point of view of potential participants also, an effect size for improved longevity defined in terms of a multiple of time is easy to interpret.

Our proposed method, therefore, is not in opposition to traditional PH, PE, or CR methods for sample size calculation; rather, it provides an opportunity to use it when there is good reason to believe that the proportionality of hazards assumption may not be valid and that improvement in longevity by a multiplicative factor is the primary aim of a researcher′s proposed intervention. For example, in the field of oncology, there is considerable interest in the development of newer treatment regimens and vaccines that improve patient lifetime. A detailed search on National Institute of Health (NIH) and National Cancer Institute (NCI) websites suggests that many ongoing phase II and phase III clinical trials discuss doubling of survival time as the hypothesis of main interest. When successful, published papers often report improvement in median survival times (and sometimes improvement in 25th and 75th percentiles of survival time) as the measurement scale for evaluating treatment efficacy and effectiveness. In such trials, percentage reduction in risk is not of immediate interest and many a times not reported at all, but knowing by what factor of time lifetime has increased is considered very important. A search on the internet with keywords such as “doubling survival time,” “improvement in longevity,” and “treatment increases survival time” shows numerous results both of ongoing trials as well as published articles and official news briefings for successful trials.

The oncology literature readily provides examples in which the extension of life was the desired trial endpoint and, therefore, constitute examples where our approach might have considerable utility. For example, the monoclonal antibody blinatumomab is considered superior to standard chemotherapy since it resulted in a twofold increase in overall survival in patients with relapsed or refractory B-cell precursor acute lymphoblastic leukemia (See Kantarjian et al²³). Another example is that of treatment fasudil, a rho kinase inhibitor, which has been shown to double the lifespan of mice with pancreatic cancer (see Vennin et al²⁴); where this drug to be trialed in humans, lifespan improvement would likely constitute the end point of interest. There are many other such studies where the research is driven by a hypothesis that requires a multiple-of-time–based definition of effect size such as research in new treatment options for metastatic renal cell carcinoma (see Zarrabi et al²⁵). Similarly, research in human ageing is preceded by animal studies mostly using mouse models where significant advancements have been made using techniques that target calorie and methionine restrictions, telomerase enhancements, metabolic enzyme alterations, growth hormone knockout and insulin signaling manipulations, and reducing the activity of mitochondria associated genes. The Palo Alto Longevity Prize²⁶ is an international $1 million life science competition dedicated to ending ageing with the specific aim of restoring the human body′s homeostatic capacity to promote an extended and healthy lifespan. Their mission statement commits $500 000 to the first team of researchers that will demonstrate improvement in mean lifespan of a wild-type mammalian cohort by 50% relative to what is expected naturally (that is, a multiplicative factor of 1.5 in the context of the PT model) at the 5% significance level. Should success be found in the near future for a large cohort study, it is then not farfetched to imagine a PT-based early phase clinical trial come into play that uses information from the large cohort study.

Therefore, there is intuitive clinical appeal in designing a clinical trial based on an effect size that is defined in terms of improvement in survival time. Current methods of sample size calculation do so only in the case of exponentially distributed times (which is only a special case of the GG distribution); hence, we suggest that sample size calculations should be performed using PT assumption when efforts are focused on extending it to the more generalizable RT(p) assumption.

In our simulations, we have found our proposed PT approach to be relatively robust even when the PH assumption represent the true model. Likewise, it is also comparable to the CR model under the conditions discussed in Section 5. While the CR model is indeed pertinent to areas of biomedical research where a proportion of patients are said to be cured, it operates under the theoretical assumption of infinite longevity for such cured patients; obviously, this may not always be justifiable. In contrast, the PT method makes no such assumption and can model the shape of the survival curve as long as it is within the ambit of the GG family of distributions. Available software fits a parametric CR model with the hazard part modeled by an exponential, Weibull, lognormal, or log-logistic distribution, while the CR is modeled by a logit, probit, or complementary log-log link. This means that for sample size calculations, the CR method often requires a priori knowledge of 3 parameters (2 for the hazard component and 1 for the CR component, as shown in Table 5) plus an effect size defined in terms of a hazard ratio. In this sense, it is similar to the PT method where, once again, a priori knowledge of 3 parameters is required along with a time-based definition of effect size. More research is needed to investigate the possibility of combining the 2 approaches.

The PE method relies on careful selection of the intervals and shares the aspect of requiring some prior knowledge with the PT method. It is somewhat tedious in that some trial and error is needed to obtain the appropriate choice of intervals. Additionally, comparable sample sizes will be obtained only when such intervals are constructed for both treatment arms. Thus, in practice, this method can be used when an a priori hypothesis is well formulated. It can therefore be argued that the CR and PT methods provide a faster (and more parsimonious) alternative, as then the shape of the survival curve for the new treatment arm follows from knowledge of at most 3 parameters plus a well-defined effect size.

One limitation of our approach is that it depends on reliable information made available from a large observational study or large clinical trial. The MLEs of λ and σ obtained from the observational study data are used as the parameters that generate the survival curve for the standard treatment arm. If the previous research did not have large sample sizes, then λ and σ would have wide confidence intervals and it would be difficult to rely on their point estimates. For example, a very wide 95% confidence interval for λ that included 0 and 1 would imply that the choice between a lognormal distribution (PH assumption is not met) and a Weibull distribution (PH assumption is met) for the standard treatment arm could not be made in a reliable manner. In our motivating example, even with a sample size of 534 (76.6% event rate), the 95% CI for λ is (−2.3175 to −1.6683)—which is still somewhat wide but not of alarming concern (as per the schematic representation of hazard functions given in Cox et al¹⁴—there will be no qualitative difference in the shape of the hazard function whether we take $\widehat{\lambda }=-1.9929$ or any other value that falls in this CI). Still, reasonably large sample sizes are desirable if we are to depend on observational study data for reliable estimates of λ. However, any sample size calculation method relies on clinically relevant definitions of effect size, and we suggest that when such information is present, it should be used to have better study designs.

In view of the limitations mentioned above, researchers should rely on practical considerations while designing a clinical trial. If absolutely no prior knowledge is available about the shape parameters, a safe choice is to assume λ = σ = 1, in which case, the trial will be designed using the assumption of exponentially distributed times. In fact, it can be argued that all such trials that have assumed exponentially distributed survival times are a special case of our PT method, and it may be that in at least some of these studies, some information was available about the shape parameters but that it was ignored. Likewise, documentation of the Weibull++ software by Reliasoft²⁷ recommends that for obtaining stable estimate of the shape parameter β of a Weibull distribution, (1) a sample size of 10 is needed when using the criterion of average relative bias less than 20% and (2) a sample size of 31 is needed when the criterion of average coefficient of variation is less than 0.15. This means that when information is available from a phase I or II study with 31 observations, it could be used to design a future phase II or III study by assuming λ = 1 and using the point estimate of β to design a clinical trial. This would result in the same sample size as would result from a PH assumption. Thus, even with the lack of knowledge of λ, our method cannot practically perform any worse than does the PH method. However, in cases where information about the point estimate of λ is available from moderately sized prior studies, our sample size formula can be used to design future trials. Examples of future work in this area are to investigate situations where information about the GG parameters is available only through multiple small sample studies (instead of one large observational study), to extend our approach to the more general RT(p) assumption, to investigate stability criteria for the shape parameter λ, and to explore Bayesian options to further this approach.

APPENDIX A

A. |. The probability density function of a GGR distribution is

$$f_Z(z)=\frac{\left|\beta \right|{\delta }^{a_0}}{\mathcal{B}\left(a_0,a_1\right)}{\left(1+\delta z^{\beta }\right)}^{-\left(a_0+a_1\right)}{z}^{\beta a_0-1},$$

where z>0, $\delta ={\left(\frac{{\theta }_1}{{\theta }_0}\right)}^{\beta }$ and $\mathcal{B}(.,.)$ is the beta function.

Let T₁, T₂, … , T_n be i.i.d random variables that follow the GG distribution given in Equation 1. We can show the MLE of θ to be

$$\widehat{\theta }={\left(\frac{\sum _{j=1}^n{t}_j^{\beta }}{nk}\right)}^{\frac{1}{\beta }}.$$

Now when T ~ GG(k, β, θ), a known result is that $T^{\beta }~\mathcal{G}\left(k,{\theta }^{\beta }\right)$. Using the relationships between a GG distribution and a $\mathcal{G}$ distribution, it is then easy to show that $\frac{{\sum }_{j=1}^n{T}_j^{\beta }}{nk}~\mathcal{G}\left(nk,\frac{{\theta }^{\beta }}{nk}\right)$ and hence $\widehat{\theta }~GG\left(nk,\frac{\theta }{\sqrt[\beta ]{nk}},\beta \right)$.

Let i = 0 and i = 1 index the standard treatment arm and the new treatment arm, respectively. Then we have ${\widehat{\theta }}_0~GG\left(n_{0}k,\frac{{\theta }_0}{\sqrt[\beta ]{n_{0}k}},\beta \right)$ and ${\widehat{\theta }}_1~GG\left(n_{1}k,\frac{{\theta }_1}{\sqrt[\beta ]{n_{1}k}},\beta \right)$, respectively. Then following the in Coelho and Mexia²⁸ for the ratio of 2 GG distributed variables, we get the result given in Equation 10. Under the null hypothesis H₀: θ₀ = θ₁ we get Equation 12. The relationship between a random variable that follows the F distribution and a GGR distribution can be summarized as

$$\text{If }X~F_{2n_{0}k,2n_{1}k}\text{ and if }Q=\frac{X^{1/\beta }}{{\theta }_0/{\theta }_1}\text{ then Q}~GGR\left(\frac{n_0}{n_1}{\left[\frac{{\theta }_1}{{\theta }_0}\right]}^{\beta },n_{0}k,n_{1}k,\beta \right).$$

Under the null hypothesis H₀: θ₀ = θ₁, we simply have Q = X^1/β and this makes the sample size calculations easy. Following iterative logic can be used to do the sample size calculations:

• Step 1. For a starting value of n₀ and n₁ (or n₁ and allocation ratio r), shape parameters k and β, and type I error rate α, find the critical value from the GGR distribution under the null hypothesis H₀: θ₀ = θ₁. This may be denoted as $Q_{critical}=gg{r}_{1-\alpha ,\frac{1}{r},\frac{n_{1}k}{r},n_{1}k,\beta }$, the (1 − α)^th quantile from the $GG{R}_{1-\alpha ,\frac{1}{r},\frac{n_{1}k}{r},n_{1}k,\beta }$ distribution.

• Step 2. Under the alternative hypothesis, we have $\text{Q}~GGR\left(\frac{1}{r}{\left[\frac{{\theta }_1}{{\theta }_0}\right]}^{\beta },\frac{n_{1}k}{r},n_{1}k,\beta \right)$. Therefore, for a PT effect size of interest Δ_PT and type II error rate τ, Power (using sample sizes n₀ and n₁) can be calculated as

  $$Power=1-\tau =P\left(Q>Q_{critial}|Q~GG{R}_{\frac{{\mathrm{\Delta }}_{\text{PT}}^{\beta }}{r},\frac{n_{1}k}{r},n_{1}k,\beta }\right).$$

• Step 3. If this value of power exceeds a desired value, say 0.8, decrease the values of n₀ and n₁, and repeat the 2 steps mentioned above. Similarly, if this value of power is lower than a desired value, say 80%, increase the values of n₀ and n₁, and repeat the 2 steps mentioned above. Continue this step till you find n₀ and n₁ that yield power greater than or equal to 80% such that the same calculation done with sample sizes n₀ − 1 and n₁ − 1 will give less than 80% power. For two-sided hypothesis, α/2 can be used in place of α.

• Step 4. For small sample sizes, simulation may be used to confirm the above mentioned analytic calculations.