The 1962 He³ Scale of Temperatures III. Evaluation and Status

Abstract

In this third paper the 1962 He³ Scale of Temperatures is evaluated both as to its precision and its deviations from the thermodynamic Kelvin Scale. Various thermodynamic quantities of He³ consistent with the 1962 He³ Scale are derived and listed. The correction to an observed vapor pressure for small amounts of He⁴ is discussed and tabulated. A description is given of the method of multiple variable least squares analysis used for deriving the final scale equation and for re-analysis of isotherm data. Finally the present status of the 1962 He³ Scale is discussed along with some considerations for the future.

1. An Evaluation of the 1962 He³ Scale

1.1. Fit of the Input 1961 L.A.S.L. Vapor-Pressure Data

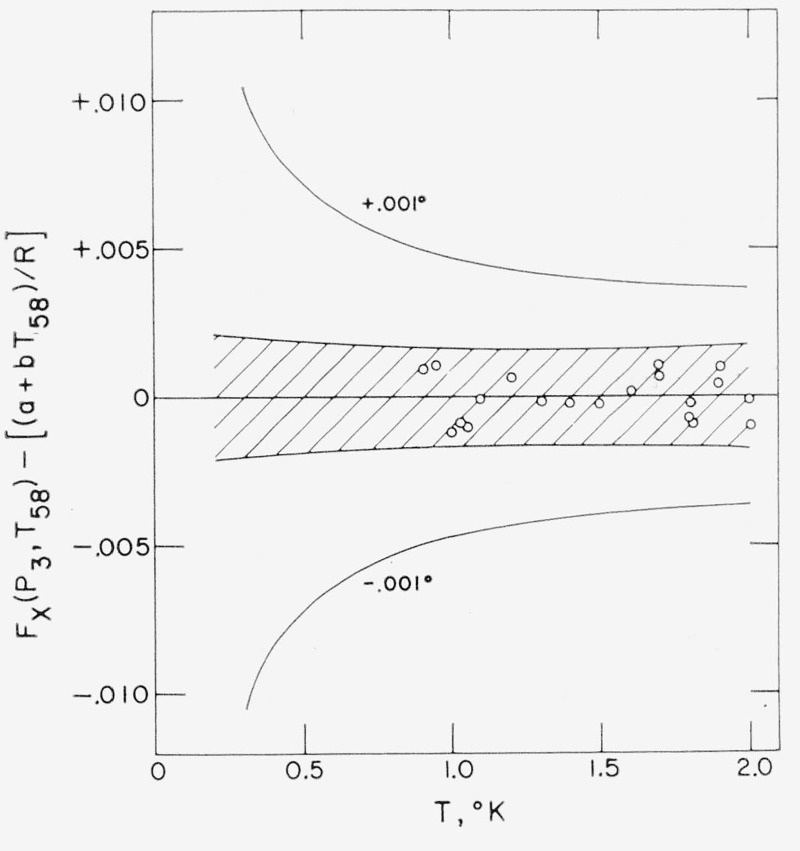
One factor in evaluating the 1962 He³ Scale is the fit of the input vapor-pressure data of Part I [46] to the Scale. Figure 1 and table 1 of Part II [6] show the deviations of the observed data from the final scale as T₆₂(P₃) — T₅₈(P₄). The symbol T₆₂ is the temperature on the 1962 He³ Scale corresponding to a He³ vapor pressure, P₃, while T₅₈ is the temperature on the 1958 He⁴ Scale [2] corresponding to the experimentally determined isothermal He⁴ vapor pressure, P₄. The standard deviation of the data from the scale is 0.25 mdeg and the maximum deviation over the full range is 0.6 mdeg. The data may not scatter completely randomly. For example, the data points just below 2 °K are all below the 1958 He⁴ Scale and the points just above 2 °K are all above the 1958 He⁴ Scale. Hence, if one wished to obtain the vapor pressure of He³ which is most probably isothermal with a given He⁴ vapor pressure, a slightly better value (in terms of consistency with the observed data) may be obtained by drawing a smooth curve through these data points or by using direct interpolation equations as discussed in Part I. However, the overall fit of the Scale to the input data is very satisfactory in comparison with the errors of measurement of the two vapor pressures.

Figure 1.— Deviations from the ETE Scale, eq (1).

The circles are deviations from the fitted equation of the function F_x(P₃, T₅₈) calculated from eq (2) for each input (P₃, T₅₈) data point. The central cross-hatched area is the 95 percent prediction interval [53] for a prediction of F_x(P₃, T) from eq (1) as calculated from the ± values for a and b given in eqs (3) and (4). The outermost solid curves represent a change in F_x(P₃, T) corresponding to a 1 mdeg change in temperature and are calculated as 0.001 T(dln P₃/dT)_sat.

Table 1. Effect of possible systematic or random errors on the ETE scale, eq (1).

Systematic or random changes in the constants a and b of eqs (3) and (4) and of temperatures on the ETE scale below 1 °K are listed for the following arbitrary, but plausible, cases:

Case 1. the fit of the input (P₃, T₅₈) data expressed as the 95 percent confidence limit [53] for the prediction of a value of ln P at any single temperature (see fig. 1);

Case 2. random errors of ±3 percent in f_x (C_sat);

Case 3. random errors of ±3 percent in ϵ, eq (4a) of Part II;

Case 4. a systematic error of −3 percent in all C_sat values, and hence in f_x(C_sat);

Case 5. a systematic error of +3 percent in all values of ϵ;

Case 6. the difference between the empirical function, f_x(V_L), and the numerically integrated values of the thermodynamic term, $f\left(V_L\right)={\int }_0^T{V}_L{(dP/dT)}_{\mathrm{sat}}dT$; and

Case 7. the increase of all values of input temperatures between 0.9 and 2.0 °K by adding 0.002 deg to each T₅₈.

Case	Δa	Δb	ΔT
			1.0 °K	0.8 °K	0.6 °K	0.4 °K	0.2 °K
	J/mole	J/mole deg	mdeg	mdeq	mdeq	mdeg	mdeq
1-	±0.006	±0.004	±0.4	±0.3	±0.3	±0.2	±0.1
2-	-	-	0. 0	±0.1	±0.2	±0.4	±0.4
3-	-	-	±0. 2	±0.1	0.0	0.0	0.0
4-	0. 069	−0.060	0.2	0.5	0.8	1.0	1.0
5-	0. 073	−0.076	0.2	0.4	0.5	0.6	0.5
6-	-	-	−0.1	−0.1	−0.1	0.0	0.0
7-	0.094	−0.026	-	1.7	1.5	1.2	0.7

1.2. Fit of the Experimental Thermodynamic Equation (ETE) Scale

Below 0.9 °K the 1962 He³ Scale was evaluated by examining its fit to the ETE Scale described in Part II. The ETE Scale is defined by a linear equation fitted to an empirical function, F_x(P₃, T), of He³ vapor pressure and temperature,

$$F_x\left(P_3,T\right)=(a+bT)/R.$$ (1)

As shown by the full line curve in figure 1 of Part II, temperatures calculated from eq (1) are in good agreement with the 1962 He³ Scale; nowhere below 2 °K do the scales differ by more than 0.4 mdeg. the 1962 He³ Scale, defined by eq (9b) of Part II, is therefore in effect an ETE scale from 0.2 to 2° and an empirical scale above 2 °K.

The effect of possible errors in the various terms of the equation for the ETE scale, over the temperature range from 0.2 to 1.0 °K, should also be considered in evaluating the 1962 He³ Scale. The ETE scale was obtained from a least squares fit of the He³-He⁴ vapor-pressure intercomparisons between 0.9 and 2.0 °K to eq (1). The function F_x(P₃, T) is calculated for each experimental P₃,T₅₈-observation; deviations of this “observed” value of F_x(P₃,T) from the fitted value, [(a+bT₅₈)/R], from eq (1) are shown as circles in figure 1. The function F_x (Ρ₃, Τ) is derived in Part II and in ref. [10] as

$$\begin{gathered} F_x\left(P_3,T\right)=T[(5/2)\ln T-\ln P_3+i_0 \\ +f_x\left(V_L\right)-f_x\left(C_{sat}\right)+ϵ] \end{gathered}$$ (2)

where i₀ is the chemical constant including the nuclear spin degeneracy; f_x(V_L) is an empirical power series representing the theoretical and exact integral term,

$$f\left(V_L\right)\equiv (1/RT){\int }_0^T{V}_L{\left(d{P}_3/dT\right)}_{\text{sat}}dT$$

involving the molar liquid volume, V_L; f_x(C_sat) is an equation for the theoretical and exact double integral term of eq (3a) of Part II, $f\left(C_{\text{sat}}\right)\equiv (1/RT){\int }_1^{T}dT\prime {\int }_1^{T\prime }\left(C_{\text{sat}}/T\prime \prime \right)dT\prime \prime$, based on an empirical power series fitted between 0.2 and 2.0 °K to data for (C_sat, the specific heat of the saturated liquid; and ϵ is the gas imperfection term, eq (4a) of Part II.

The least squares values for the coefficients a and b of eq (1), and their equivalent expressions from eqs (6) and (7) of Part II are

$$a=L_0-{\int }_0^1{C}_{\text{sat}}dT=17.4459\pm 0.0058\text{joule}{\text{mole}}^{-1}$$ (3)

and

$$b=S_L\left(1.0°\right)=9.0098\pm 0.0038\text{joule}{\text{mole}}^{-1}{\text{deg}}^{-1}.$$ (4)

The plus-or-minus values for a and b were found from the fit of the data points to the straight line, a+bT. Mood [53] has given an equation for the prediction interval for a single prediction of F_x(P₃, T) from eq (1) for any value of T. The ETE Scale is just the set of P₃ values obtained by solving eq (2) for In P₃ at any given temperature using the predicted value of F_x(P₃,T). Hence a prediction interval for F_x(P₃, T) can be expressed as an equivalent prediction interval in P₃ by neglecting the contribution of possible errors in the other terms on the right hand side of eq (2).

The 95 percent prediction interval for a single prediction of F_x(P₃, T) [with a 95 percent probability of containing the statistically “true” value of F_x(P₃,T)] is shown as the central cross-hatched area in figure 1. The outermost curves in this figure show the change in F_x(P₃, T) corresponding to a one millidegree change in temperature. The same prediction intervals have been converted to equivalent temperature scale errors as listed in table 1.

The effects of random errors of ±3 percent in f_x (C_sat) and ϵ on individual temperatures below 1° are also shown in table 1.

Systematic errors in f_x(C_sat), 𝜖 and in f_x(V_L) would be compensated between 0.9° and 2.0° by the least squares process of fitting the (P₃, T₅₈) data to eq (1). The scale below 1° would be skewed by such errors as is shown in table 1 for assumed 3 percent systematic errors in all values of C_sat or ϵ. Table 1 also shows the systematic errors below 1° resulting from use of the approximate empirical function, f_x(V_L), instead of the graphically integrated values of the true thermodynamic function, f(V_L) [see table 4 of Part II].

Table 4. Thermodynamic properties of He³ and vapor pressures of He⁴ consistent with the 1962 He³ Scale.

T	P3	P4(T58)	$\left(\frac{dl\mathrm{n}{P}_3}{dT}\right)$	${\left(\frac{dln{P}_X}{dX}\right)}_T$ at X = 1 (see note†)	Csat	SL	Virial coeff		VG	VL	L
							B	C
°K	microns Hg at 0 °C and std. g		deg−1		J/deg mole	J/deg mole	cm3/mole	cm6/mole2	cm3/mole	cm3/mole	J/mole
0				0		0				36.8346	20.56
0.2	0.0121		73.32	0. 23	2.728	3.703	−1350	6409	103×107	36.7809	24.39
0.4	28.115		21.04	0.47	3.146	5.731	−672.5	4532	887×103	36.7203	27.97
0.6	544.49	0.2812	10.57	0. 70	3.477	7.071	−446.7	3700	68274	36.7197	31.42
0.8	2892.5	11.445	6.650	0. 88	3.812	8.117	−333.8	3204	16909	36.7849	34.61
1.0	8842.4	120.00	4.721	0. 92	4.222	9.010	−266.0	2866	6776.6	36.9073	37.51
1.2	20163	625.02	3.613	0. 92	4.753	9.824	−220.9	2616	3476. 7	37.0897	40.08
1.4	38516	2155.4	2.908	0.91	5.414	10.605	−188.6	2422	2060. 7	37.3517	42.29
1.6	65467	5689.9	2.425	0.89	6.201	11.378	−164.4	2266	1338.9	37.7151	44.07
1.8	102516	12466	2.077	0. 88	7.079	12.159	−145.6	2136	925.5	38.201	45.34
2.0	151112	23767	1.815	0. 86	7.983	12.951	−130.6	2027	667.8	38.854	45.99
2.2	212673	40466	1.611	0. 810			−118.2	1932	496.6	39.680	45.91
2.4	288613	63304	1.448	0. 781			—108.0	1850	376. 7	40. 734	44.94
2.6	380383	93733	1.317	0. 754			−99.3	1777	288.8	42.124	42.84
2.8	489549	132952	1.210	0. 728			−91.8	1713	221. 0	44.049	39.11
3.0	617907	182073	1.122	0. 705			−85.4	1655	163.1	46.818	32.25

^†Here × is the He³ mole fmcLioll.

The He⁴ IlIole fraction, (1–×), is used to make the impurity correction.

Another possible source of systematic error is a smooth deviation of the 1958 He⁴ Scale from the thermodynamic Kelvin Scale. The effect on the ETE scale of adding 2 mdeg to each scale input temperature is listed in table 1.

The overall effect on the 1962 He³ Scale of random errors in the specific heat of liquid He³, the virial coefficient equations, and the 1958 He⁴ Scale might amount to as much as three millidegrees. Durieux [54] has analyzed the 1962 He³ Scale for the effects of possible errors and has reached similar conclusions.

1.3. Fit of the Argonne Laboratory Vapor-Pressure Data

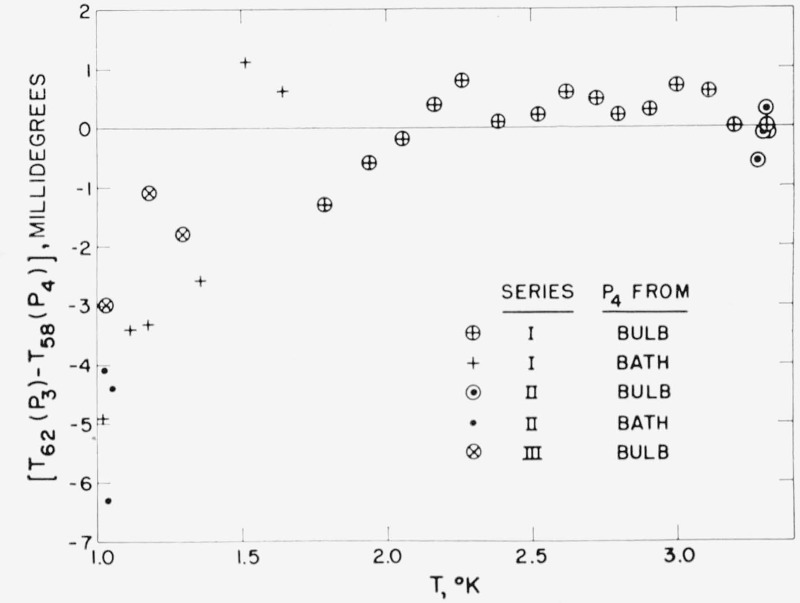
The He³-He⁴ vapor-pressure intercomparisons of Abraham, Osborne, and Weinstock [5] have been used in deriving all previous He³ temperature scales, but these were rejected for the 1962 He³ Scale because of apparent thermodynamic inconsistency (see refs. [10 and 45]) with recent precise measurements of the latent heat of vaporization of He³ by the same workers [4, 55]. The fit of the AOW vapor-pressure data to the 1962 He³ Scale is shown in figure 2. Above 1.9° the agreement is within 0.5 mdeg. Below 1.5° the AOW data deviate systematically from the 1962 Scale indicating either that their He³ vapor pressures were lower or that their He⁴ pressures were higher than the data of Sydoriak and Sherman (Part I). For encircled points in figure 2, a He⁴ vapor pressure bulb was fastened to the He³ bulb. The He⁴ pressure may have been high because of insufficient correction for effects due to the refluxing superfluid film. For the uncircled crosses and dots, the He⁴ bath pressure was measured in the pumping line in a warm part of the apparatus. The corrected He⁴ pressures as published may have been high because the effluent gas was significantly colder than the tip of the pressure-sensing tube, thus increasing the actual thermomolecular pressure difference.

Figure 2.— The deviation in millidegrees of the 1950 Abraham, Osborne, and Weinstock [5] (P₃, P₄) data from the 1962 He³ Scale: T₆₂(P₃) − T₅₈(P₄).

The uncircled crosses and small dots are data points below the λ-point for which the He⁴ cryostat bath pressure was published as P₄. For the encircled points a He⁴ vapor pressure bulb was fastened to the He³ bulb.

1.4. Fit of Heat-of-Vaporization Data

Heat-of-vaporization, L, data may be used to test the thermodynamic consistency of the temperature scale. The equations used may be either

$$L=T\left(S_G-S_L\right)$$ (5)

with the vapor entropy, S_G, calculated from the Sackur-Tetrode equation, or

$$L=T\left(V_C-V_L\right){(dP/dT)}_{\text{sat}}$$ (6)

from the Clausius-Clapeyron equation. The use of these equations for testing He⁴ scales of temperature has been discussed extensively; see van Dijk and Durieux [25], Durieux [15], Berman and Mate [56], and Keller [43].

The liquid entropy at 1.0 °K (or any other temperature) may be calculated from eq (5) and data for C_sat as

$$S_L\left(1.0°\right)=S_G(T)-(L/T)-{\int }_{1\cdot 0}^T\left(C_{\text{sat}}/T\prime \right)dT\prime .$$ (7)

The Argonne (WAO) heat-of-vaporization measurements [4] were undertaken in order to determine the entropy of liquid He³ in this way.

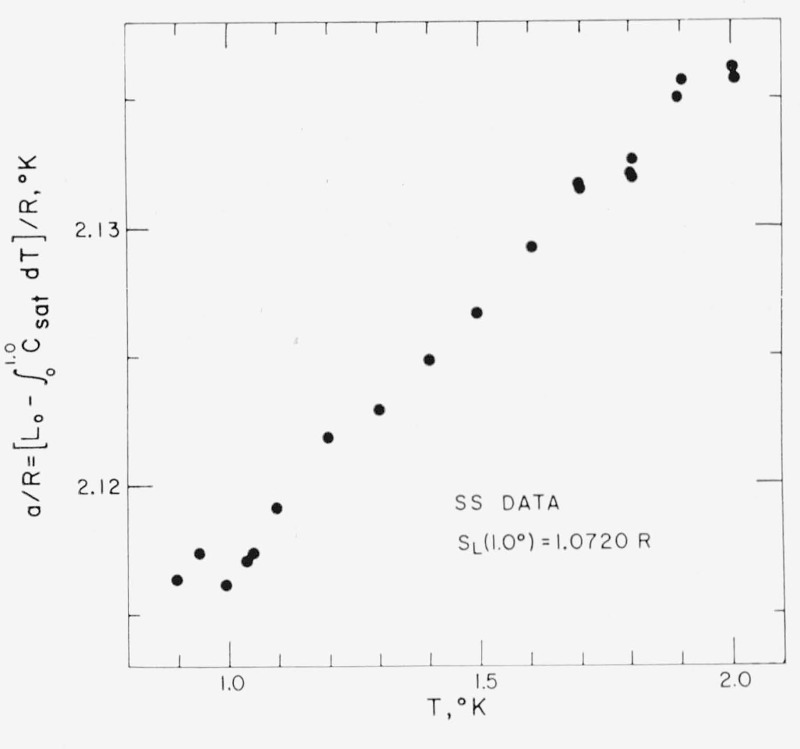
At one stage of the derivation of the 1962 He³ Scale, it was proposed [10] to use all the WAO heat-of-vaporization data and eq (7) to get an average value for S_L(1.0°), which is just the coefficient, b, in eqs (1) and (4). Then, values of (a/R) = F_x(P₃, T) − (bT/R) from eq (1) were computed for every vapor-pressure datum point between 0.9 and 2.0 °K. This two-step method failed to converge on a stable, consistent pair of constants a and b, and led to the decision to undertake the new L.A.S.L. intercomparisons of the vapor pressures of He³ and He⁴. Analysis of the new intercomparisons [45] by this same two-step method also failed to yield a consistent set of a and b values, although these data showed much less scatter, as shown in figure 3. The heat-of-vaporization data were not used to determine the 1962 He³ Scale; instead a and b values were obtained by a least squares fit of the He³ vapor-pressure data to eq (1) using for T the T₅₈ values that corresponded to the He⁴ vapor pressures observed concurrently with the He³ vapor pressures.

Figure 3.— Demonstration of the remaining thermodynamic inconsistency between eqs (1) and (7) involving the He³ latent-heat data, (L, P₃), of Weinstock, Abraham, and Osborne [4], [55]; the (P₃, P₄) intercomparisons of Sydoriak and Sherman [46]; and the 1958 He⁴ Scale [2], T₅₈(P₄).

The indicated value of S_L(1.0°) is the average of nine values calculated from eq (7) for the WAO (L,P₃) data and is about 1 percent lower than the 1962 He³ Scale value for that entropy, eq (4). The solid circles are the individual values of the theoretical constant, (a/R), in eq (1) calculated for each (P₃, T₅₈) data point as F_x(P₃, T₅₈) — [S_L(1.0°) T₅₈/R] using the indicated average value of S_L(1.0°).

The 1958 WAO heat-of-vaporization data may be used to test the 1962 He³ Scale in the manner explained by Durieux [15]. In terms of an apparent heat of vaporization, L_a (defined as the heat necessary to evolve a mole of gas outside of a calorimeter), eq (6) becomes

$$\begin{gathered} L_a=T{V}_G{\left(dP/dT\right)}_{\text{sat}} \\ =-R\left(1+B/V_G+C/V_G^2\right){\left[d\ln P/d(1/T)\right]}_{\text{sat}} \\ =R{T}^{2}Z{\left(d\ln P/dT\right)}_{\text{sat}} \end{gathered}$$ (8)

where the compressibility coefficient, $Z\equiv \left(P{V}_G/RT\right)=\left(1+B/V_G+C/V_G^2\right)$ from the density virial form of the equation of state.

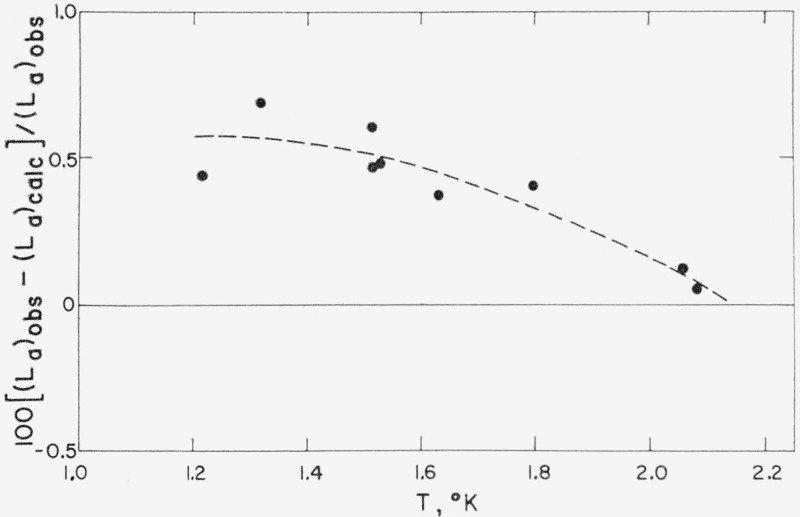
As shown in figure 4, the observed values of L_a average about 0.5 percent higher than the values calculated from the 1962 He³ Scale using eq (8), a deviation considerably in excess of the estimated 0.1 percent accuracy [55] of the L_a measurements. Durieux [15] calculates that the L_a values of Berman and Mate [56] for He⁴ average 0.76 percent higher than the values calculated from the 1958 He⁴ Scale between 2.2 and 3.0 °K. These differences may be due in part to a deviation of the 1962 He³ and 1958 He⁴ Scales from the true thermodynamic temperature scale. An estimate of such a difference may be obtained by neglecting the variation of (d ln P/dT)_sat and Z in eq (8). In this case δT/T ≈ (1/2)(δL_a)/L_a. From the dashed curve drawn through the He³ data of figure 4 this estimate of δΤ varies from 3 mdeg at 1.2 °K to 1 mdeg at 2.0 °K, a not unreasonable range of deviations. For the He⁴ data, this approximation yields values from 8 mdeg at 2.2 °K up to 11 mdeg at 3.0 °K which are much larger than appears reasonable for the departure of the 1958 He⁴ Scale from the thermodynamic scale. An error in the temperature scale also would cause both (d ln P/dT)_sat and Z to change.

Figure 4.—

Deviations of the values of L_a, the apparent latent heat of vaporization (see sec. 1.4), observed by Weinstock, Abraham, and Osborne [4, 55] from values of L_a calculated for the 1962 He³ Scale from eq (8) using eqs (10) and (11).

1.5. Fit of Gas Thermometer, Isotherm, and Acoustic Interferometer Measurements

In principle, gas thermometer, isotherm and acoustic interferometer measurements of the absolute temperature associated with a He⁴ vapor pressure may be used to check the 1962 He³ Scale by directly interpolating the He⁴ vapor pressure to an isothermal He³ vapor pressure. The direct interpolation equations and table described in Part I are usable for this interpolation of He⁴ vapor pressures. Since the 1962 He³ Scale has been made to agree so closely with the 1958 He⁴ Scale, at least in terms of the (P₃, P₄) data of Part I, little really significant new information would be expected from this kind of comparison.

Van Dijk [57] has critically reanalyzed all published gas thermometer and isotherm measurements and compared them with the 1958 He⁴ Scale. The majority of these measurements between 1.5 and 3.3 °K seem to indicate that the thermodynamic temperature may be several millidegrees higher than T₅₈, although the data scatter over a range of about ±10 mdeg from T₅₈.

Two preliminary acoustic interferometer results of Cataland and Plumb [58] indicate thermodynamic temperatures that are 3 ± 2 mdeg higher than T₅₈ at 2.0 and 2.2 °K.

The isotherm measurements of Keller [11, 12] are generally conceded to be the most accurate in the liquid helium temperature range, and are the only data for gaseous He³. During the derivation of the 1962 He³ Scale, the isotherm data of Keller were reanalyzed [10, 48] by Deming’s method [47] of least squares adjustment with errors in more than one measured variable (see appendix A). For the isotherm measurements the observed pressures for each data point were corrected or normalized to a calculated value which would have been observed if the cell volume were at the normalized temperature for the set of data points. This normalized temperature, T_N,₅₈, was taken as the temperature on the 1958 He⁴ Scale corresponding to ${\overline{P}}_4$, the average He⁴ vapor pressure for the set of data. The values of ${\overline{P}}_4$ and T_N, ₅₈ are listed in tables 2 and 3. The method of normalization was essentially the same as that described in detail by Keller [11].

Table 2. Summary of reanalysis of Keller’s gaseous He³ isotherms [12].

The isotherm designations, the data points, and the method of normalization for each isotherm are the same as those used by Keller. ${\overline{P}}_4$ is the average He⁴ vapor pressure for each isotherm and ${\overline{P}}_3$ is_the average He³ vapor pressure for the α isotherm. $T_{58}({\overline{P}}_4)$ is the normalized temperature for each isotherm and is the 1958 He⁴ Scale temperature corresponding to ${\overline{P}}_4$. $P_3({\overline{P}}_4)$ is the directly interpolated He³ vapor pressure corresponding to ${\overline{P}}_4$, using the direct interpolation equations described in Part I, and $T_{62}[P_3({\overline{P}}_4)]$ is the 1962 He³ Scale temperature corresponding to $P_3({\overline{P}}_4)$. The values of T_iso, B, and C listed under the heading “Three-constant fit” were obtained by solving eq (9) using Deming’s method of least squares adjustment with errors in two measured variables (see appendix A). The standard errors and the weighted variance are calculated in accordance with the statistical formulas given by Deming [47]. The two constant fit values of T_iso and B were obtained by solving eq (9) assuming C=0. For the For the γ, δ, and ϵ isotherms the variance of the three-constant fit is lower and the values of C are greater than the magnitude of their statistically assigned errors. Therefore the three constant fit solutions were used for fitting He³ virial coefficient equations, eqs (10) and (11), and for the temperature differences shown in figure 2 of Part II.

Isotherm	Units	γ	δ	α	ϵ	β
No.of points		18	18	11	10	8
${\overline{P}}_4$	mm Hg	489.52	178. 09	36.16	13.070	3.782
T58(${\overline{P}}_4$)	mdeg	3779.1	2985.3	2154.2	1813.4	1510.3
P3(${\overline{P}}_4$)	mm Hg		607. 70	197.43	105.33	52.21
${\overline{P}}_3$	mm Hg			197.62
T62[P3(${\overline{P}}_4$)]	mdeg		2985. 2±0.2	2154.4±0.2	1813.1±0.2	1510.2±0.2
T62(${\overline{P}}_3$)	mdeg			2.1550
THREE-CONSTANT FIT
Tiso-	mdeg	3782.3 ±2.2	2992.4±1.6	2153.7±1.0	1816.4±0.8	1510.4±2.5
B-	cm3/mole	−65.50±0.86	−86.31 ±0.52	−118.81 ±1.35	−145. 08±1.61	−162.15±10. 7
C-	cm6/mole2	1192 ±306	1746±136	548±822	2611 ±1289	−11,069±16, 390
Variance		7.0	13.8	6.1	0. 86	4.8
(T58–Tiso)	mdeg	−3.3±2.2	−7.1±1.6	0.5±1.0	−3. 0±0.8	−0.1 ±2. 5
(T62–Tiso)-	mdeg		−7.2±1.8	0.7±1.2	−3.2±1.0	−0.2±2.7
(T62(${\overline{P}}_3$)–Tiso)	mdeg			1.3±1. 0
TWO-CONSTANT FIT
Tiso-	mdeg	3774.4±1.3	2974.4±2.8	2153.2±0.6	1814. 9±0.4	1512.0±0. 7
B-	cm3/mole	−62.18±0.19	−79.66±0.33	−117.92 ±0.26	−141.87 ±0.29	−169.30±1.15
Variance-		13.2	156	5.7	1.20	4.4

Table 3. Summary of reanalysis of Keller’s gaseous He⁴ isotherms [11].

The various Quantities have the same meaning as in table 2. The three constant fits gave a statistically better fit for only one isotherm, so the results of the two constant fits have been accepted as being more meaningful and have been used for figure 2 of Part II.

Isotherm	Units	A	B	C	D	E
No. of points		12	14	12	17	9
${\overline{P}}_4$	mm Hg	588.55	291.31	147.55	52.758	35.541
T58(${\overline{P}}_4$)	mdeg	3954.2	3339.2	2864.0	2315.1	2147.3
P3(${\overline{P}}_4$)	mm Hg			528.42	254.50	195.21
T62[P3(${\overline{P}}_4$)]	mdeg			2864.0 ± 0.2	2315.0 ± 0.2	2147.6 ± 0.2
TWO-CONSTANT FIT
Tiso	mdeg	3953.7 ± 2.1	3338.4 ± 2.1	2863.5 ± 0.9	2316.7 ± 2.3	2148.9 ± 0.9
B	cm3/mole	−83.97±0.66	−103.60±0.78	−124.16±0.63	− 153.38±4.21	−176.04±2.04
Variance		8.7	17.8	3.6	23.4	1.69
(T58 – Tiso)	mdeg	−1. 5±2.1	0.8±2.1	0.5±0.9	−1.6±2.3	−1.6±0.9
(T62 – Tiso)	mdeg			0.5±1.1	−1.7±2. 5	−1.3±1.1
THREE-CONSTANT FIT
Tiso	mdeg	3953.8±4.3	3335.3±3. 7	2860.9±1.5	2311.9±6.1	2146. 5±2.8
B	cm3/mole	−82.16±3.52	−99.80±3.78	−118.47±2.86	−132.1 ±25.7	−162.6±15.8
C	cm6/mole2	−1452±2773	−3133 ±3042	−6741 ±3331	− 50,490±60,020	−38, 900±45,160
Variance		9.4	17.7	2.8	23.9	1.75

For the isotherm measurements the quantity minimized by the least squares adjustment was Σ[W_p(P₀−P_c)²+W_n(N₀−N_c)²] where the independently observed variables are P₀, the normalized helium gas pressure, and N₀, the molar density. The fitted function was

$$F\left(P_c,N_c\right)=P_c-N_{c}RT\left(1+B{N}_c+C{N}_c^2\right)=0$$ (9)

where B and C are the second and third virial coefficients, T is the isotherm temperature for a normalized set of data, and P_c and N_c are the calculated or adjusted values of P and N. The individual weights, W_p and W_n, were calculated from Keller’s assignment of errors in the various observed quantities.

The results of the reanalysis of Keller’s gaseous He³ data [12] were fitted to empirical equations for the He³ second and third virial coefficients. These equations are

$$B=(4.942-270.976/T){\text{cm}}^3/\text{mole}$$ (10)

and

$$C=(2866/\sqrt{T}){\text{cm}}^6/{\text{mole}}^2.$$ (11)

The deviations of both He³ and He⁴ isotherm temperatures from the 1962 He³ and 1958 He⁴ Scales are shown in figure 2 of Part II. Keller used a He⁴ vapor-pressure thermometer for all but one of his isotherms, but his observed P₄’s have been interpolated to P₃’s by use of the direct interpolation equations of Part I. The weighted average of the isotherm temperatures is 1.50 ± 1.0 mdeg above the corresponding T₅₈ values and 1.52 ± 1.2 mdeg above the T₆₂ values. For one isotherm He³ containing about 0.25 percent He^4, was condensed in the vapor-pressure bulb. The corrected average pressure for pure He³ was 197.62 ± 0.02 mm Hg (T₆₂ = 2.1550 °K) at an isotherm temperature of 2.1537 ± 0.0010 °K. It was concluded that nothing would be gained by trying to base a He³ scale more directly on these isotherm temperatures since the 1958 He⁴ Scale is based on these data. Moreover, the 1962 He³ Scale, as it has been set up to agree with the 1958 He⁴ Scale, adequately expresses the experimental He³—He⁴ vapor-pressure relation for most practical purposes.

2. Thermodynamic Properties of He³ Consistent with the 1962 He³ Scale

Two temperatures which are frequently given in discussing helium vapor pressure scales are the boiling point and the critical point. The boiling point of He³ on the 1962 He³ Scale, at a vapor pressure of 760 mm Hg at 0 °C and standard gravity, is 3.1905 °K. The temperature at the critical point for He³ was measured by Sydoriak and Sherman [46] by observing the He⁴ vapor pressure. This measured critical temperature on the 1958 He⁴ Scale was 3.3240 ± 0.0018 °K at a He³ critical pressure, P_c, of 873.0± 1.5 mm Hg. The calculated critical temperature on the 1962 He³ Scale is the temperature given by eq (9b) of Part II [6] corresponding to P_c and is 3.3246 ± 0.0017 °K. This close agreement with the directly measured temperature is quite gratifying and somewhat unexpected since the scale-defining equation was fitted over the full range of the vapor-pressure intercomparisons.

Table 4 gives a number of quantities which are consistent with the 1962 He³ Scale, including, for comparison, values of He⁴ vapor pressures from the 1958 He⁴ Scale. The concentration derivative of In Ρ_X, (d ln P_X/dX)_{T, X = 1}, where X is the mole fraction of He³ and P_X is the corresponding mixture vapor pressure, is useful for correcting for the He⁴ impurity in a He³ vapor-pressure thermometer. This correction is discussed in section 3.

The table values for C_sat, the specific heat of the saturated liquid, were calculated from the empirical equation, eq (3b) of Part II, fitted to specific-heat data for the derivation of the 1962 He³ Scale. The calculated values agree with the experimental data to ±1 percent; the deviations are given in table 2 of Part II. Values for S_L, the entropy of the saturated liquid, were calculated from the relation

$$S_L(T)=S_L\left(1.0°\right)+{\int }_{1.0}^T\left(C_{\text{sat}}/T\prime \right)dT\prime$$ (12)

using the above-mentioned C_sat equation and the 1962 He³ Scale value of S_L( 1.0°), given in eq (4).

Values for the second and third virial coefficient were calculated from eqs (10) and (11) while V_G, the molar volume of the saturated vapor, was calculated from the equation given for Z in eq (8). These calculated values of V_G agree to within 1 percent with the smoothed fit to the experimental data of Kerr [59] up to 2.8 °K. The values of V_L, the molar volume of the saturated liquid, are taken from the table of Kerr and Taylor [60]. The values of L, the heat of vaporization, are calculated from eq (6).

The heat of vaporization at absolute zero, L₀, can be obtained from the fitted constant, a, of eq (3) if the specific heat integral is evaluated. The specific heat of liquid He³ under a pressure of a few centimeters of mercury has been measured by Anderson, Wheatley, and coworkers [61] down to a temperature of 0.015 °K. Their empirical equation for C_p, the specific heat at a constant pressure of 0.12 atm, is (C_p/R) = 2.89T−7.80T²+7.09T³ for 0<T<0.3°. Integration of this equation yields ${\int }_0^{0.2}{C}_{\text{sat}}dT\approx {\int }_0^{0.2}{C}_{p}dT=0.331\pm 0.013\text{J}/\text{mole}$. This value is in excellent agreement with the value 0.333 ± 0.010 J/mole obtained by graphical integration of the smooth curve through recent specific heat data given by Strongin, Zimmerman, and Fairbank [62]. From the empirical equation for C_sat used for the T₆₂ scale, ${\int }_{0.2}^{1.0}{C}_{\text{sat}}dT=2.784\pm 0.056J/\text{mole}$. Our corresponding value of L₀ is 20.56 ± 0.07 J/mole.

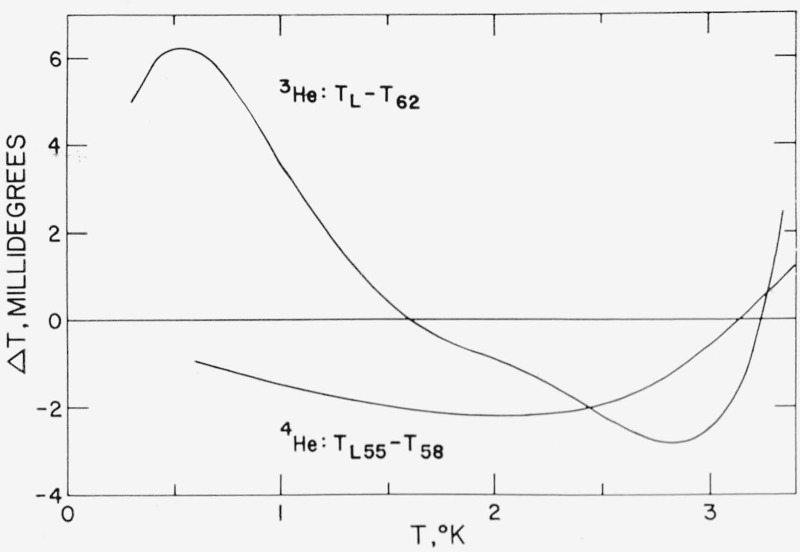
The entropy of the saturated liquid can be assumed to be approximately equal to ${\int }_0^T\left(C_p/T\prime \right)dT\prime$ from the 0.12 atm C_p equation of Anderson et al. [61] given above. From this approximation S_L(0.23 °K) is 4.05 ± 0.17 J/mole deg. Strongin et al. [62] also have computed the entropy from their extrapolation of specific heat data to 0 °K. Their value for the entropy at 0.23 °K is 3.97 ± 0.17 J/mole deg. These values are in good agreement with the value 4.02 ± 0.25 J/mole deg obtained by Weinstock, Abraham and Osborne [4], who used eq (5) to calculate S_L(1.5°) from their three separate latent heat measurements at that temperature. The equivalent of eq (12) was used by WAO to compute other entropies in the range of the then available specific heat data. The value of S_L(0.23°) consistent with the 1962 He³ Scale, calculated from eq (12), is S_L,(0.23°) = 4.09 ± 0.10 J/mole deg, estimating a ±2 percent limit of error for the specific heat integral term. The good agreement among these values is gratifying but it may be fortuitous. For example, the He³ temperature scale used by Weinstock et al. [4] to assign temperatures to observed He³ vapor pressures was the T_L Scale, eq (9) of ref. [9]. The deviations of the T_L Scale from the 1962 He³ Scale are shown in figure 5 and range from +6 to −3 mdeg. At 1.5 °K, however, the two scales are in good agreement as to the temperature. Thus the value of T used in computing both S_G and L/T in eq (7) would give essentially the same value for liquid entropy at T ≈ 1.5 °K on the T_L and 1962 He³ Scales. If, however, a value of L calculated from eq (6) is used in eq (7) instead of a WAO experimental value of L, significantly different values are obtained for S_L depending upon which of the two scales, T_L or 1962 He³, is used for the calculation of (dP₃/dT)_sat since there is a difference of about 0.4 percent in these derivatives on the two scales as inferred from the slope of the ∆T curve in figure 5 (see, for example, ref. [63]).

Figure 5.— Graphs of differences between old and new He³ and He⁴ temperature scales.

The He³ curve, T_L(P₃)—T₆₂(P₃), is a graph of the difference between the T_L Scale [9] and the 1962 He³ Scale. The He⁴ curve is the difference between the T_L55 Scale [25] and the 1958 He⁴ Scale given in table 6 of ref [2], It was intended in their derivations that the T_L Scale would reproduce the T_L55 Scale, and that the 1962 He³ Scale would reproduce the 1958 He⁴ Scale. The difference between the two curves is explained principally by the new (P₃,P₄) intercomparison data of Sydoriak and Sherman [46] used in deriving the 1962 He³ Scale.

3. Corrections to the Measured Pressure of a He³ Vapor-Pressure Thermometer for the He⁴ Impurity

Sydoriak and Sherman have discussed in Part I corrections to be applied to an observed pressure as measured in the laboratory in order to obtain the vapor pressure at the surface of liquid He³. The correction for a small He⁴ impurity will be discussed in more detail here.

The presence of He⁴ in liquid He³ thermometers lowers the vapor pressure below that of pure He³. Much of the He³ available for purchase up to the present has contained significant quantities of He⁴; even the He³ used for the 1962 He³ Scale input data measurements [46] contained about 0.04 percent He⁴. Specially purified He³ containing less than 0.01 percent is being made available for purchase through the Division of Research of the United States Atomic Energy Commission [64].

The correction for small amounts of He⁴ may be calculated from the approximate relation

$$P_3-P_x\approx (1-X){\left(d{P}_x/dX\right)}_{T,X=1}$$ (13)

where P_x is the observed vapor pressure for mole fraction, X, of He³. Although very little data has been published for the vapor pressures of dilute solutions of He⁴ in He³, the liquid phase diagrams of Sydoriak and Roberts [32] and Esel’son and Berezniak [38] indicate that (dP_x/dX)_T is probably a constant for X≥0.9 and hence eq (13) may be valid for concentrations of up to 10 percent He⁴.

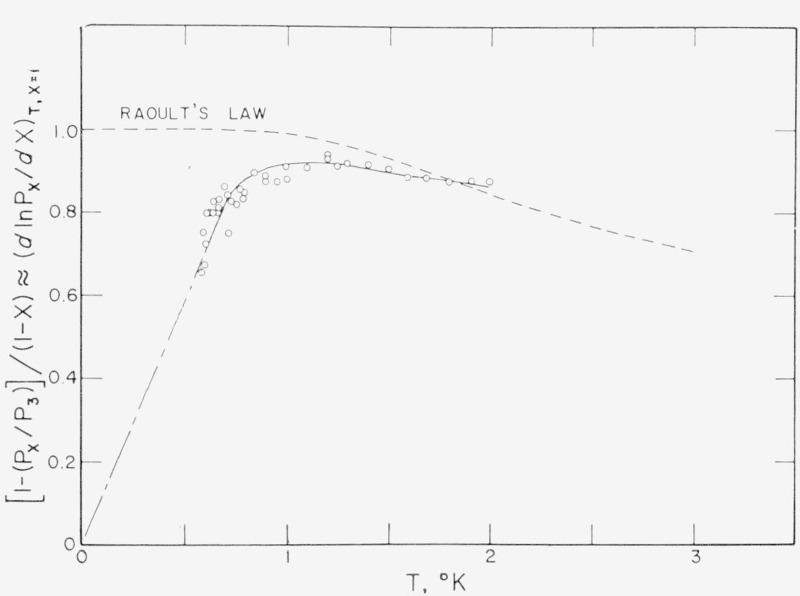
Smooth values of this derivative in reduced form,

$$\begin{gathered} {\left(d\ln P_x/dX\right)}_{T,X=1}=\left(1/P_3\right){\left(d{P}_x/dX\right)}_{T,X=1} \\ \approx \left[1-\left(\frac{P_x}{P_3}\right)\right]/(1-X), \end{gathered}$$ (14)

are listed in table 4 and are compared with the raw data of Sydoriak and Roberts [32] in figure 6. Between 0.6 and 2.0 °K the table 4 entries and the solid curve in figure 6 were calculated from eq (14) using the X = 0.9 values from the smoothed table of ref. [32]. Below 0.6 °K the derivative has been assumed to go linearly to zero at 0 °K mainly because such an extrapolation is consistent with the data below 1 °K, as shown in figure 6. Actually for all practical purposes this derivative may be zero below about 0.2 °K since at these temperatures liquid He³—He⁴ mixtures with very small amounts of He⁴ undergo phase separation [65] and, when this happens, the vapor pressure becomes independent of further decreases in X. Above 2.0 °K, the table 4 values were calculated from Raoult’s law,

$${\left(d\ln P_x/dX\right)}_{T,X=1}=1-\left(P_4/P_3\right),$$ (15)

shown as the dashed curve in figure 6. That law is in fairly good agreement with all existing vapor-pressure data for X ≥ 0.89 and T ≥ 1.7 °K.

Figure 6.— The correction factor for He⁴ impurity.

The circles are the data points of Sydoriak and Roberts [32] for He³ mole fraction, X, of 0.897. The solid curve from 0.6 to 2.0 °K is drawn through the smoothed table values of ref. [32] for X=0.9. The long and short dashed curve is an arbitrary extrapolation to 0 ° K. The dashed curve is Raoult’s Law, eq (15).

The concentration of He⁴ in the saturated vapor will be much less than that of the liquid. This fact can cause fractionation and may require further correction in precise thermometry if much of the He³ in the thermometer system is not condensed.

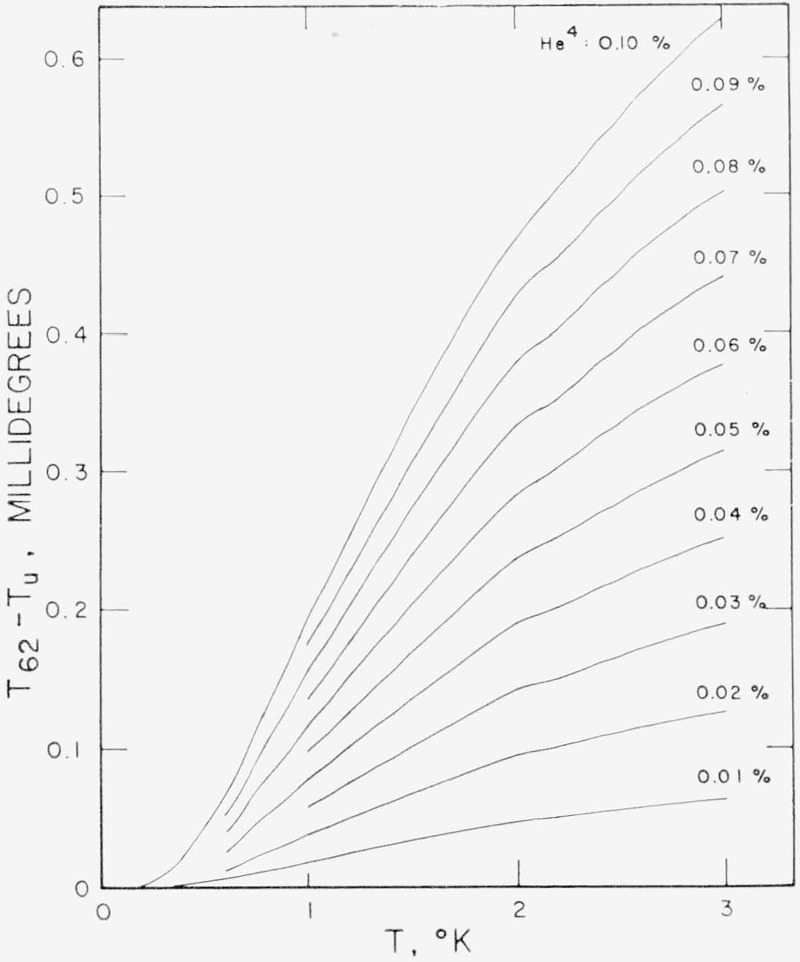
The correction to a temperature measurement made with a He³ sample containing 0.1 percent He⁴ in the liquid phase ranges from 0.02 mdeg at 0.4 °K to 0.71 mdeg at 3.2 °K. For most purposes the correction may be calculated from the approximate relation

$$P_3-P_x\approx (1-X)P_x{\left(d\ln P_x/dX\right)}_{T,X=1}.$$ (16)

The derivative below 2 °K may be interpolated from a curve through the values listed in table 4 or from figure 6. Above 2 °K the derivative can be easily calculated from eq (15). A careful experimental determination of the correction above 2 °K would improve the accuracy of this correction. Figure 7 may be used to read the temperature correction directly for known He⁴ concentrations in the liquid.

Figure 7.— Correction for He⁴ impurity, (T₆₂ —T_u), to be added to the uncorrected temperatures, T_u, calculated from the observed vapor pressure and the 1962 He³ Scale.

The correction is calculated as T₆₂—T_u=(1—X) (dlnP_x/dX)_T,X=1/(dlnP₃/dT) based on eqs (13) and (14) and using the derivative values listed in table 4. The curves can be used for ten times the indicated percent of He⁴ in the liquid if the ordinate is multiplied by ten.

4. Status of the 1962 He³ Scale of Temperatures

The 1962 He³ Scale was presented [66] at the Eighth International Conference on Low Temperature Physics in London, September 17–21, 1962. During the next week the new scale was discussed in detail by the Advisory Committee on Thermometry of the International Committee on Weights and Measures. A scale proposal along with ref. [54] has been published along with the minutes of the meeting of the Advisory Committee in Sèvres, France, September 26 and 27, 1962. Quoting from the draft of those minutes [67]:

“Il a estimé que l’Échelle ³He 1962 doit également être recommandée pour l’usage général, avec la désignation T₆₂.

“Les deux échelles T₅₈ (l’Échelle ⁴He 1958) et T₆₂ peuvent être utilisées concurremment dans le domaine où elles sont valables. Cependant, quand il s’agit de l’adoption de cette nouvelle échelle ³He comme partie de l’E.Ι.Ρ.Τ., on doit prendre soin d’éviter toute ambiguité dans le domaine de recouvrement avec l’échelle ⁴He.” 3

The recommendation by the Advisory Committee of the 1962 He³ Scale was approved in October 1962, by the International Committee on Weights and Measures meeting in Sevres. The International Committee requested the United States and Russian Governments to take steps to make high-purity He³ available internationally for vapor-pressure thermometry, and to prepare and distribute known mixtures of He³ and He⁴ for the calibration of or the checking of the calibration of apparatus for measuring the isotopic purity of He³.

The status of the 1962 He³ Scale and proposed changes in the International Practical Temperature Scale have been discussed by Stimson [68] and Brickwedde [69].

5. Practical Lower Limits for He³ and He⁴ Vapor-Pressure Thermometry

Practical lower limits for helium vapor-pressure thermometry are determined by the desired precision of temperature determination, the accuracy with which the vapor pressure can be measured, and by how small or how well known the temperature difference is between the thermometric fluid and the object of the measurement.

Below about 2.2 °K, He³ can much more easily be made isothermal with an object the temperature of which is being measured than can He⁴, for the reasons discussed in Part I. A major factor in fixing a practical lower limit for He³ thermometry is the time necessary to achieve an equilibrium thermomolecular ratio, P_c/P_w, of cold pressure, P_c, to warm pressure, P_w, and more importantly, of sufficient data to permit accurate calculation of that ratio.

To measure temperatures from 0.3 to 0.25 °K to a millidegree precision using He³, vapor pressures from 1.9 to 0.24 μ would have to be measured to 4 or 5 percent accuracy. This accuracy in the pressure system is relatively easy to achieve. However, the error in P_c/P_w may amount to several percent because of marked quantum effects in the gas viscosity and because no He³ measurements have been made of the empirical thermal transpiration coefficients postulated by Weber [70]. The He³ thermomolecular pressure measurements made by Roberts and Sydoriak [37] showed that for a cold temperature of 2 °K observed He³ P_c/P_w ratios from 1.0 to 0.5 agreed within 1 percent with ratios calculated for He⁴ using the Weber-Schmidt equation [71].

Roberts and Sydoriak also discuss the possible effect of the low-temperature viscosity on pressure ratios in the tubing at liquid helium temperatures. For warm and cold temperatures, T_w and T_c, below 5 °K and pressure ratios close to 1, eq (5) of ref. [37] is (P_c/P_w)²= 1 — 0.005642 $\left(T_w^2-T_c^2\right)/{\left(R{p}_w\right)}^2$ where R is the tubing radius in centimeters and p_w is in microns of mercury. In order to be reasonably sure that the calculated thermomolecular ratio is within 4 or 5 percent of the true ratio for He³ it is suggested that the calculated (p_c/p_w) be kept greater than 0.5 in the rest of the pressure sensing tube. For the stepped pressure sensing tube used by Sydoriak and Sherman with dimensions shown in figure 4 of Part I [46], this suggests a practical lower limit of $R{p}_c=0.155\text{cm}$ microns or a vapor pressure of 1.16 μ (T₆₂ = 0.287°).

The practical lower limit for He⁴ vapor-pressure thermometry is strongly dependent on numerous details of the particular technique and apparatus used. In many cases experimental temperatures are determined from the vapor pressure of the bath in which the experimental apparatus is immersed. For bath temperatures and with proper corrections for pressure drops associated with film reflux and/or motion of effluent vapor from the bath, temperatures may be determined down to about 1 °K. Figure 1 of Part I shows errors due to film reflux pressure drops for typical sizes of pressure sensing tubing. However, for temperatures determined by thermal contact with a closed-bulb He⁴ vapor-pressure thermometer the practical lower limit is raised to just below the λ point, because of the large and variable temperature discontinuity at the bulb wall associated with recondensation of the refluxing film. Figure 1 of Part I also shows this “correction” for a variety of conditions.,

If the bulb wall is a poor thermal conductor, a still higher limit is imposed due to the effects of the density maximum at about 2.18 °K, discussed by Chase, Maxwell, and coworkers [72].

In the case of precision measurements using He³ thermometry, the publication of only a few pertinent details, such as the diameters and temperatures of any stepped junctions in the pressure sensing tube, will enable future correction of data as improved thermal transpiration corrections become possible.

6. Conclusion and Considerations for the Future

These papers on the development of the 1962 He³ Temperature Scale have emphasized marked differences between liquid He³ and He⁴. One is in the low-temperature variation of the liquid entropy. The quantum mechanical exchange forces in liquid He³ lead to appreciable correlation of the nuclear spins in the liquid at temperatures as high as 1 °K. The difficulty in fitting the entropy curve with a simple analytical expression has led to difficulty in attaching theoretical significance to certain terms in empirical vapor-pressure equations at temperatures below the temperature of fitted data.

The superfluid transition of liquid He⁴ makes accurate isothermal intercomparisons of He³ and He⁴ vapor pressures difficult below the He⁴ λ-point. The 1961 intercomparison data of Sydoriak and Sherman [46], however, are considered to be valid to a few tenths of a millidegree. The 1962 He³ Scale, which is based on these intercomparisons, is believed to be in agreement with the 1958 He⁴ Scale to within two or three tenths of a millidegree over the full range of the intercomparison data, from 0.9 °K to the critical point, 3.324 °K. A lower limit for practical He³ vapor-pressure thermometry is 0.25 °K corresponding to a He³ vapor pressure of 0.24 μ Hg.

A number of independent measurements, including measurements of the latent heats of vaporization of He³ and He⁴, precise isotherm measurements, and preliminary acoustical interferometer measurements, indicate that both the 1962 He³ Scale and the 1958 He⁴ Scale may be 2 or 3 mdeg lower than true thermodynamic temperatures between 1 and 3.3 °K When more accurate data on the thermodynamic properties of He³ and He⁴ are available, together with better determinations of absolute thermodynamic temperatures, the precise intercomparison data will allow both the He³ and the He⁴ scales to be adjusted consistently and simultaneously. He³ and He⁴ scales, thermodynamically consistent between 1 and 3 °K, may be extended by precision para magnetic salt thermometry above 3 °K using He⁴ and below 1 °K using He³. Also, the scales may be extended downward by thermodynamic calculations using coefficients evaluated between 1 and 3 °K as in the development of the 1962 He³ Scale and the T_L55 He⁴ Scale [25]. Further measurements on He³ that would be helpful in improving the Scale are measurements of the vapor pressure and thermo-molecular pressure ratio down to temperatures of 0.25 °K, more accurate specific heat measurements on the liquid below 2 °K, and specific heat, latem heat, and high-precision vapor-density measurements above 2 °K.

7. Appendix A. Method of Multiple Variable Least Squares Analysis

In the usual least squares adjustment of experimental data the implicit assumption is made that only one measured quantity, often called the dependent variable, is in error. This dependent variable is measured as a function of one or more independent variables. The usual procedures for the adjusting of sets of observations to an empirical or theoretical equation assume no error in the independent variables. Frequently, however, the “independent variable” is also determined by a physical measurement and is just as subject to error as the dependent variable.

Deming [47] has discussed a method of adjustment of sets of observations of two or more variables when all variables are subject to error. His method is essentially equivalent to statistical weighting of the data. The method has been coded by P. McWilliams of the Los Alamos laboratory for use with the Gaussian method of iterative least squares analysis adapted by Moore and Zeigler [73] for high-speed computers. We will give a simple example of the method of analysis with exaggerated scatter and uncertainty.

7.1. Simple Example

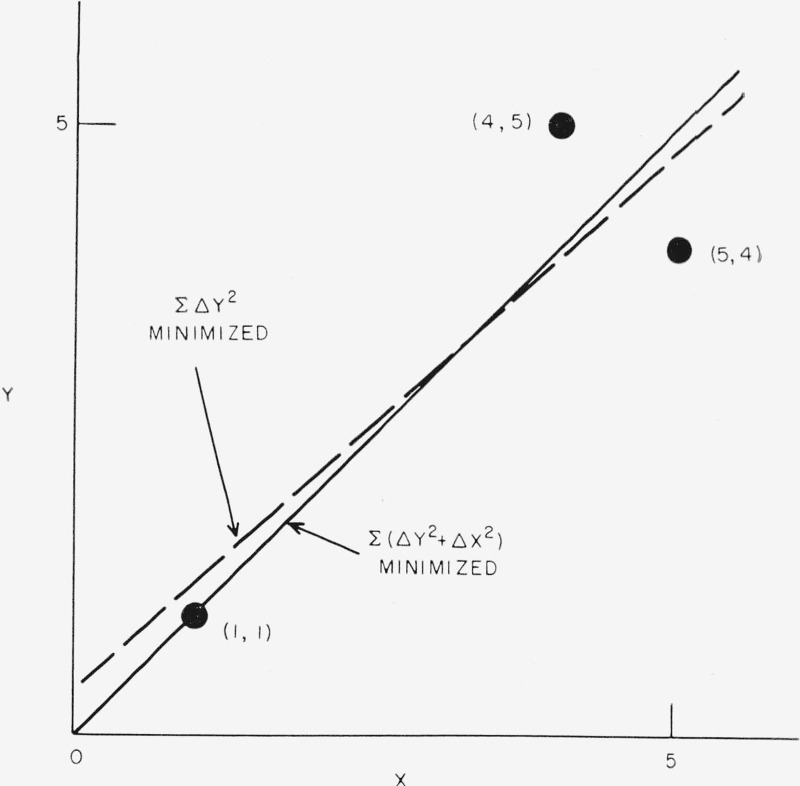
As a simple illustration consider fitting the best straight line to the following three points:

$$\begin{array}{cc}X& Y\\ 1\pm 1& 1\pm 1\\ 4\pm 1& 5\pm 1\\ 5\pm 1& 4\pm 1\end{array}$$

The dashed line in figure 8 shows the fit of the usual least squares solution of Y=a+bX assuming that only Y is in error and equally weighting the points. The solid line, Y=X, is the solution assuming that the X and Y values are all equally subject to equal absolute errors. The general case of fitting to a straight line is discussed in detail by Deming. For our special case of equal weighting, the two solutions go through the centroid but have different slopes.

Figure 8.— Simple example of the least squares fit of a straight line to the three observed points shown as dots.

The dashed line is the usual least squares solution of Y=a+bX which minimizes Σ(Y₀—Y_c)². The solid line is the solution assuming both X and Y are subject to equal absolute errors.

Actually the quantity which is minimized by the least squares solution is

$$S=\sum _{i=1}^M[w_{y,i}{\left(Y_{o,i}-Y_{c,i}\right)}^2+w_{x,i}{\left(X_{o,i}-X_{c,i}\right)}^2]$$ (17)

where the subscript o indicates the observed value; subscript c indicates the calculated or adjusted value; and w_y, _i and w_{x, i} are the weights of the ith of M sets of observations. Thus in figure 8 the solid line is identified as minimizing

$$S=\sum [{(\mathrm{\Delta }Y)}^2+{(\mathrm{\Delta }X)}^2]$$

since all the individual weights are equal. ∆Y is defined as (Y₀—Y_c) and ∆X = (X₀—X_c).

The geometrical relation between ∆Y and ∆X that is assumed in Deming’s method of solution is illustrated in figure 18 of ref. [47]. The relation for each point depends on the individual weights for that point.

If w_x=w_y, this condition requires that the line from the observed point, (X,Y₀), to the calculated point, (X_c, Y_c), be perpendicular to the calculated curve.

7.2. General Discussion of Method

In many cases the least squares problem can be expressed as minimizing eq (17) subject to M equations:

$$F\left(X_{c,i},Y_{c,i}\right)=0.$$ (18)

As an example consider a case in which three coefficients, a, b, and c, are to be fitted by least squares to the relation Y = f(X, a, b, c). We take

$$F(X,Y)=Y-f(X,a,b,c).$$ (19)

Using his geometrical relation between ΔY and ΔX, and using the Gaussian method of linearization of the problem by a truncated Taylor’s Series expansion of the function, Deming derives a typical least squares solution “normal” equation as

$$\begin{gathered} \mathrm{\Delta }a\sum _{i=1}^M{W}_i{F}_{a,i}^2+\mathrm{\Delta }b\sum _{i=1}^M{W}_i{F}_{a,i}{F}_{c,i} \\ +\mathrm{\Delta }c\sum _{i=1}^M{W}_i{F}_{a,i}{F}_{c,i}=\sum _{i=1}^M{W}_i{F}_{a,i}{F}_{o,i}. \end{gathered}$$ (20)

In this equation, the subscripts a,b, and c designate the partial derivatives of F with respect to the respective coefficients; Δα=α₁—a_c, the difference between the initial value, α₁, and the calculated or adjusted value, a_c; F_{0, i}=F(X_{0, i}, Y_{0, i}, α₁, b₁, c₁); and the weights are

$$W_i={(F_{x,i}^2/w_{x,i}+F_{y,i}^2/w_{y,i})}^{-1}.$$ (21)

F_x,i and F_y,i are the partial derivatives of F with respect to X and F, respectively. Where a set of observations, Χ_{0, i} and Y_0,i, can be assigned respective standard deviations 𝜎_χ,i and 𝜎_y,i, we take the weights as:

$$w_{x,i}=1/{\sigma }_{x,i}^2;w_{y,i}=1/{\sigma }_{y,i}^2.$$ (22)

If variations in X and Y are independent, substitution of eq (22) in eq (21) yields

$$W_i=1/{\sigma }_{F,i}^2$$ (23)

and hence the method is equivalent to statistical weighting of the individual sets of observations.

Using the Gaussian method, several iterations using the successively improved values of the coefficients may be used. The partial derivatives are usually evaluated using the observed values of X and Y in each iteration.

As pointed out by Deming, an advantage of the method is that the solution is unequivocal; i.e., the coefficients are independent of variations in the way of writing the equation. Thus a straight line can be written as either Y=a+bX or X=−a/b+Y/b and correspondingly F would be (Y—a—bX) or (X+a/b—Y/b). The values of a and b and the adjusted points will be the same to within higher powers of the residuals, ∆X and ∆Y.

The least squares code used computes standard deviations of the fitted parameters based on the fit of the observed points to the calculated points. The code also permits computation of standard deviations of points calculated at interpolated or extrapolated points as well as at data points.