Abstract
The significance of flu prediction is that the appropriate preventive and control measures can be taken by relevant departments after assessing predicted data; thus, morbidity and mortality can be reduced. In this paper, three flu prediction models, based on twitter and US Centers for Disease Control’s (CDC’s) Influenza-Like Illness (ILI) data, are proposed (models 1-3) to verify the factors that affect the spread of the flu. In this work, an Improved Particle Swarm Optimization algorithm to optimize the parameters of Support Vector Regression (IPSO-SVR) was proposed. The IPSO-SVR was trained by the independent and dependent variables of the three models (models 1-3) as input and output. The trained IPSO-SVR method was used to predict the regional unweighted percentage ILI (%ILI) events in the US. The prediction results of each model are analyzed and compared. The results show that the IPSO-SVR method (model 3) demonstrates excellent performance in real-time prediction of ILIs, and further highlights the benefits of using real-time twitter data, thus providing an effective means for the prevention and control of flu.
Introduction
Influenza (flu) is a stealthy killer that threatens human health with its widespread contagion [1, 2]. The flu refers to a viral acute respiratory infection caused by the common flu virus. If the flu is not effectively controlled, it can cause wide-ranging flu outbreaks that pose a threat to social stability and development. The World Health Organization (WHO) asserts that about 3 to 5 million serious illnesses are reported worldwide each year and about 250,000-650,000 of those result in death [3]. If we can predict a flu trend in some areas before the outbreak of flu, and take effective measures to mitigate the contagion ahead of time, we can control the spread of disease and reduce the loss of life to a certain extent.
To prevent and control flu pandemic, the current worldwide Flu Surveillance System (FSS) relies on the collaboration of medical institutions (at all levels), e.g., centers for disease control and prevention and sentinel hospitals. The worldwide FSS monitors the flu weekly, via accurate reporting, and releases the information to regional centers [4]. In the US, the CDC releases weekly health data at the national and state level to determine when and where flu outbreak reaches the US to measure the impact of the epidemic on the whole country [5].
With the development of the information technology field, new efficient data sources are continuously produced by a variety of reporting agencies. In the US, about 90 million adults search for health information [6], such as disease and medicine, on the internet every year. When a flu outbreak occurs, people often learn about the outbreak (and how to deal with it) via search engines like Baidu or Google [7, 8]. Therefore, internet search data has become an ideal data source for flu surveillance [9–12]. Google analyzed the data from its own search engine and found that there was a relationship between the number of people who searched for flu-related subjects and the number of people who had flu symptoms [13]. In 2008, Google launched the Google Flu Trend (GFT), based on aggregated Google search data that estimated the current global flu transmission in near real time [14, 15]. Although some success was achieved, a February 2013 Nature magazine article pointed out that, compared with data from CDC, the GFT overestimated the peak number of ILI in the US [16]. Millions of engineers and users are constantly changing search engine algorithms [17–22], but ultimately, the GFT was shut down in August 2015.
Many other data sources are actively searching for a precise way to perform correlation analysis with flu data [23, 24], particularly by companies (sources) who sell over-the-counter (OTC) medication that reduce the symptoms of the flu such as fever, body ache, coughing and sneezing [25]. Much of the literature on disease surveillance using social media has focused on tracking influenza with twitter [26–28]. Twitter is a popular social network. There are over 600 million users as of January 2014, generating over 780 million tweets daily [29]. Twitter data is appealing as a data source because the application can access millions of public short messages instantly every day. The twitter application has become a viable option for disseminating and tracking information. Although twitter, as a social network, appears to be targeted to a young generation, the demographic breakdown of the social network reveals that users of the twitter application are diverse in terms of age. The social network is not only for young people, but also for middle aged and the technology savvy older population [30].
Previous work has drawn upon novel web data-based twitter application messaging models to detect influenza rates in real time, to infer health status or measure the spread of a disease in a population. For instance, Paul et al. [31] uses ILI data available at the time of the forecast show that models incorporating data derived from twitter can reduce forecasting error. Kim et al. [32] proposed an adaptive algorithm for real-time prediction of influenza infection and actual disease activity using the Hangeul Twitter. Hu et al. [33] proposed an improved artificial tree algorithm to optimize the parameters of BP neural networks (IAT-BPNN) that can predict the CDC’s %ILI of US. Signorini et al. [34] applied content analysis and regression models to measure and monitor public concern about the levels of disease during the H1N1 pandemic in the US. The CDC used the twitter application to post tips for preventing flu to help slow the spread of H1N1 influenza in 2009. The twitter’s account grew from 2,500 followers to 370,000 followers during the 2009 outbreak [35]. Lampos [36] analyzed twitter messages using regression models in the UK and the US, respectively. Broniatowski et al. [37] argued that the twitter social network produces an open data collection and the interests in flu and the number of real flu cases are separable in twitter flu data.
The biggest advantage of these methods, compared to traditional methods, is the immediate feedback: Twitter message and/or query log analyses are available almost immediately. This is extremely important to prevent influenza, as early detection can reduce the impact of flu outbreaks. Although many studies targeting flu prediction using twitter data have been presented, most of these methods simply use linear regression algorithm to predict %ILI. These methods do not consider geographical to their models, for example, they do not consider regional correlation in their flu-spread model. In this study, we improve the short-term predictions of flu activity by using inter-regional ILI correlation, and propose a non-linear methodology based on machine learning algorithms capable of providing real-time (“nowcast”) and forecast estimates of %ILI by leveraging twitter application and CDC data.
Machine learning (ML) is a type of artificial intelligence method that has reemerged to analyze large data typically called “big data.” ML applications are becoming increasingly widespread as the amount of available information increases exponentially. For example, we can apply ML algorithms to improve hospital-based expert systems [38], bibliographic classification [39, 40], automatic target tracking algorithms [41], the implementation of computer-based GO games [42] and the optimization of driverless car algorithms [43]. In fact, we can apply ML methods to model almost any aspect of human life so that we may develop innovative technological tools that can improve living conditions.
SVR is a type of ML method developed from pattern recognition and computational learning that stems from statistics; it is a theoretical tool with excellent performance that can 1) guarantee the global optimum of an algorithm and 2) adopt a kernel function method that avoids complex operations and solves the problem of high-dimensionality [44]. In the present study, we propose an improved PSO to optimize the parameters of SVR. The independent and dependent variables of models 1-3 are used as input and output of IPSO-SVR for predicting the CDC’s unweighted %ILI of US. The aim of the present study is to evaluate the application of this ML approach applied to flu prediction. Although these models have not been used for national or regional %ILI predictions in the past, they can be reference models against which new methods can be tested.
Important novelty of our work is: the impact of flu transmission between geographical regions are analyzed and verifies whether the CDC ILI are complementary to the twitter data; we develop a correction to the existing PSO algorithm that optimizes a penalty parameter C and kernel function parameter σ of an SVR-based model that improves the prediction for %ILI. The resulting model, in turn, can be employed to forecast influenza epidemics in the US, which may help to facilitate vaccination-strategy development and antiviral distribution.
Models
Historical twitter data mapped onto ILI contains a lot of information about flu epidemic from previous years, which has important significance for future flu trend-based predictions. Therefore, we develop model 1 by historical twitter data on ILI. The flu is an acute infectious disease with the ability to spread in physical space. Population regions that are geographically near each other will likely experience highly correlated patterns of flu cases. Therefore, we construct an empirical network model (model 2) using twitter data to verify the regional impact of flu transmission. In traditional flu prediction model development, the data becomes more accurate after rigorous scientific experimentation. Various forecasting methods have their own advantages and disadvantages. Therefore, we construct a combination model (model 3) by introducing CDC ILI data to model 2. Model 3 verifies whether the twitter data is complementary to CDC ILI data. Model 3 also determines whether the twitter data contains new information that is not provided by the historical CDC ILI data. The specific formulas of models 1-3 are
- Model 1:
(1) - Model 2:
(2) - Model 3:
(3)
In all models, the Xi,t−k represents twitter data in the i-th region for week t − k, ωi,j is weighting factor that establishes the relationship between regions i and j the correlation coefficient of the CDC ILI data in region i and j represents the relationship weight. ILIi,t−l characterizes the CDC ILI data of the i-th region for the last l weeks, p, q are the lagged order coefficients (the experimental results show that the prediction effect of the model is best when p = q = 3) and the coefficients αk, βk, δj, γk, μl and σj are the parameters of the model. The variables εt, θt and τt are the residual terms for each model, while N is the number of regions (in this case N = 10).
Methods
Support vector regression
Support Vector Machine (SVM) was first proposed by Vapnik et al. in 1995 [45], and is a ML method based on Vapnik-Chervonenkis (VC) dimension theory and the principle of structural risk minimization. It was first applied to classical classification problems and showing promise in solving nonlinear and high dimensional problems, then the method was applied to common regression problems [46, 47]. An SVM applied to nonlinear regression is called Support Vector Regression (SVR). In this paper, the ε-SVR methodology is adopted and its specific form is as follows [48, 49]:
We are given training data
| (4) |
where xi ∈ Rn is the input vector, yi ∈ R is the corresponding output and k is the sample size.
The nonlinear SVR maps the input (data) vectors into a high-dimensional feature space H via a nonlinear mapping Φ and then performs linear regression in this space. The specific function can be expressed as
| (5) |
where ω is the weight vector of the hyperplane and b is the bias term.
In fact, SVR solves optimization problem (6) under constraint conditions (7).
| (6) |
with constraint
| (7) |
where ξi and ξi* are the relaxation variables, which represents the upper and lower limits of the training error under the error constraint (∣yi − [ωT ⋅ Φ(x) + b] ∣< ε). The error term ε is the maximum error allowed by the regression step, limits the number of support vector solutions and prevents over-generalization. Larger ε values imply less support vectors. The constant C > 0 controls the penalty for any sample that exceeds the error ε.
Expressions (6) and (7) represent a Convex Quadratic Optimization (CQO) problem. To solve the CQO problem, we express a Lagrange function
| (8) |
where , are the Lagrange multipliers. Then, we find the minimization of function L with respect to ω, b, ξi and ; the maximization of L with respect to and ; the maximization function of the dual form is obtained by substituting it into the Lagrange function:
| (9) |
According to the KKT conditions, the following equations and constraints can be established
| (10) |
where the kernel function K(xi, xj) = Φ(xi)TΦ(xj). This formulation describes the inner product of the high dimensional eigenspace. In this paper, we select the Radial Basis Kernel Function (RBKF) as a kernel function that is characterized by
| (11) |
After solving, αi and are substituted into (10). Finally, the regression function is expressed by:
| (12) |
The influence of parameters
The performance of SVR is associated with the appropriate choice of parameter values. The parameter size has a considerable influence on SVR algorithm learning and generalization ability [50]. Therefore, determining the optimal support vector parameters is an important problem. The main parameters of the SVR model based on RBKF are penalty parameter C and kernel function parameter σ. The penalty parameter C is a trade-off parameter between the control error minimization and confidence interval maximization. The larger the C, the greater the penalty for the training error, which results in over-fitting; the smaller the C, the smaller the penalty for the empirical error, leading to a learning machine that is simpler but with higher (experience-based) risk. The kernel function parameter σ is related to the input space range and width of the learning sample; the larger the sample input space is, the greater the value. Conversely, the smaller the sample input space is, the smaller the value. Because the parameter search scope is sizable, and the parameter numbers are large, the optimal parameter is difficult to find. Thus, we optimized the parameters of SVR.
Improved support vector regression
Support vector regression based on K-fold cross validation algorithm
Cross Validation (CV) is a random grouping of original data to some degree. One group is used as the test set and the others as the training set. Firstly, the training set is used to train the model, and the model is verified via the test set [51, 52]. The common CV methods are the Hold-Out Method, K-fold Cross Validation (K-CV) and Leave-One-Out Cross Validation (LOO-CV). In this paper, C and σ are optimized by the K-CV method under the training set. The SVR algorithm, after the K-CV parameter-optimization step is complete, is called K-CV-SVR. Its basic six steps are delineated in the pseudo-code that follows.
Step 1: Data preprocessing step. Reads in the sample set and preprocesses it.
Step 2: The sample set S is divided (equally) into K disjoint subsets, denoted as {S1, S2, ⋯, SK}.
-
Step 3: Take an element of the sample set (Si) as a test set without repetition. The remaining K−1 elements are used as the training set. The following subroutine is performed.
for C = 2−8: 28, σ = 2−8: 28
for i = 1: K
Let Si be the test sample Stest
Let S1 ⋃⋯⋃ Si−1 ⋃ Si+1 ⋃⋯⋃ SK be the training sample Strain
Use Strain to train SVR
Input the Stest into the trained SVR model to determine the test error
Step 4: After the previous step, for each parameter pair {C, σ}, the K test errors and K models can be obtained. The average of the squared error sum of the K model test set is called the MSE.
Step 5: When all possible parameter {C, σ} are traversed, we select the parameters that minimize the MSE to be the optimal parameter {Cbest, σbest}.
Step 6: Using the training sample set, the SVR model with parameters {Cbest, σbest} is established, and the network is trained to complete the prediction.
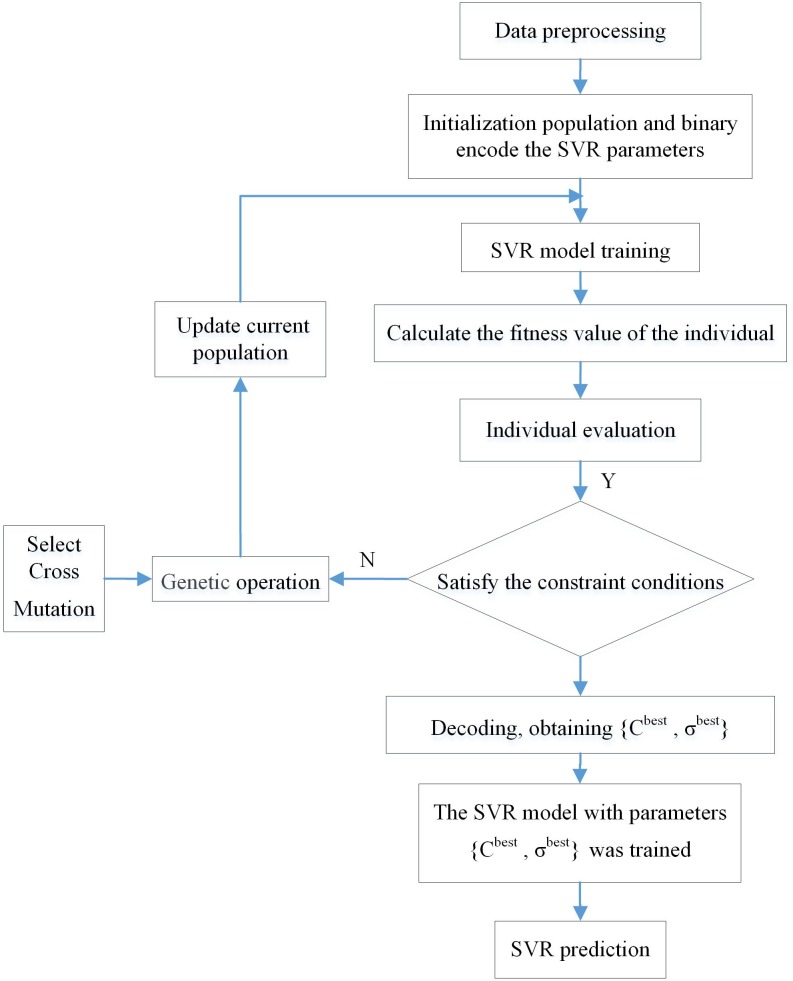
The specific process of the GA-SVR algorithm is shown in Fig 1.
Fig 1. Flow chart of SVR algorithm based on K-CV.
Support vector regression based on genetic algorithm
The Genetic Algorithms (GA) were proposed and developed by professor Holland of the University of Michigan in 1962. It is a search algorithm that is based on the biological evolutionary process of the survival of the fittest in nature [53]. The basic process is as follows: First, we randomly generate a population of a certain size for the problem to be solved, the adaptive value of each individual is calculated and the fitness assessment was performed for all individuals in the group. Second, by selecting, crossing, and mutating a group of individuals, a set of individuals more adaptable to the environment is produced. Finally, based on the new generation, the three operations that select, cross and mutate are carried out. After several generations of evolution, until the set termination conditions are satisfied, the optimal solution to the problem is found [54]. The nine basic steps of the genetic algorithm applied to SVR parameter optimization (GA-SVR) are delineated in the steps that follow.
Step 1: Data preprocessing. To avoid a large magnitude difference between the various factors, the input sample is normalized.
Step 2: Initialization of the population. The penalty parameter C and the kernel function parameter σ are initialized and binary coding is performed. The initial population P(t) of the genetic algorithm is constructed. The parameters of the GA are set, such as the initial population size of the GA, the maximum genetic algebra T, crossover rate and mutation rate. A set of chromosomes that represent the SVR parameter values are randomly generated and each chromosome is composed of {C, σ}.
- Step 3: Individual evaluation. Regression training was performed for each individual generated by the population. The reciprocal of the mean square error (found during training) is used as the objective function value, i.e., the individual fitness. The fitness function value of each individual is calculated, and the calculation formula is:
where m is the number of network output nodes, yi is the expected output of the i-th node of the SVR and is the prediction output of the i-th node.(13) Step 4: Select operation. Individual fitness is based on roulette method, the chromosomes with higher fitness values were selected from the current population to replicate.
Step 5: Cross operation. Two individuals in the population were selected as the parent body, a new generation of chromosomes were obtained via a cross operation associated with some probability. A single point-cross method is used here.
Step 6: Mutation operation. Randomly select individuals in a population and change some genes in individuals with certain probabilities. This results in a new set of individuals.
Step 7: Termination conditions. If t ≤ T, then go to step. If t > T or if the optimal individual continues to be less than a constant, then the algorithm is automatically terminated and the output is the optimal value.
Step 8: Optimal decoding. This step outputs the optimal parameter {Cbest, σbest} of the SVR.
Step 9: Using the training set, the SVR model with parameters {Cbest, σbest} are established. The network is now trained and the test sample is placed back into the training set. Thus, SVR achieves the predicted results.
The specific process of the GA-SVR algorithm is shown in Fig 2.
Fig 2. SVR parameter optimization based on GA.
Support vector regression based on improved particle swarm optimization
Particle Swarm Optimization (PSO) algorithm is an optimization algorithm based on swarm intelligence theory, which was first proposed by Kennedy and Eberhart in 1995 [55]. It is a global optimization algorithm that simulates bird-predator behavior and achieves the goal of optimization via a collective cooperation among birds. The solution of each optimization problem in the PSO is considered a bird in the search space called the “particle”. Each particle is associated with its own position and speed, which is dynamically adjusted according to its “flight experience” and the influence of other particles in the set [56, 57]. The PSO is an optimal solution search method for a particle that follows the current optimal method to find (determine) a particle in the solution space. To measure the superiority of each particle solution, a fitness value function is defined. In this paper, the mean square error is taken as the fitness function, which can directly reflect the performance of SVR regression.
The basic principle of the PSO algorithm is described using mathematical terminology. Suppose that in an n-dimensional solution space, the population X = (X1, X2, ⋯, Xm) is composed of m particles, where Xi = (xi1, xi2, ⋯, xin) is the current coordinate position of the i-th particle, Vi = (vi1, vi2, ⋯, vin) is the current velocity of the i-th particle, Pibest is the current best position of i-th particle and Pgbest is the best location of the whole particle swarm. According to the basic principle of the optimal particle, each particle Xi, i = 1, 2, ⋯, m will update its velocity and position according to velocity adjustment Eq (14) and position adjustment Eq (15).
| (14) |
| (15) |
where ω is the inertia weight, t is the current evolutionary algebra, r1 and r2 are random numbers distributed between [0, 1]; c1 and c2 are the accelerated constants that are usually evaluated between (0, 2]; Vi(t) is the original velocity of the particle and Vi(t + 1) is the new velocity of the particle.
To reduce the possibility of particles leaving the search space during evolution, the flight velocity Vi of a particle is usually limited to a certain range, namely Vi ∈ [−Vmax, Vmax].
| (16) |
The adjustment of equation Pibest and Pgbest are show in Eqs (17) and (18), where f(x) is the fitness function.
| (17) |
| (18) |
| (19) |
where m is the number of particles, yi is the actual value and is the predictive value.
The inertia weight ω is mainly used to balance the global search capability and local development capability of particles in Eq (14). A larger inertia weight results in overly rapid particle velocity and deviation from the search area of the optimal solution. A smaller inertia weight gives the particle stronger local search ability, but takes a longer time to find the global optimal solution. Therefore, careful selection of inertia weight is important to obtain good performance. In this paper, the inertia weight ω is taken as
| (20) |
where ωmax is the maximum inertia weight; ωmin is the minimum inertia weight; t is the current iteration number; Tmax is the maximum iteration number. In order to be distinguished from PSO, PSO with the inertia weight (20) is named as IPSO.
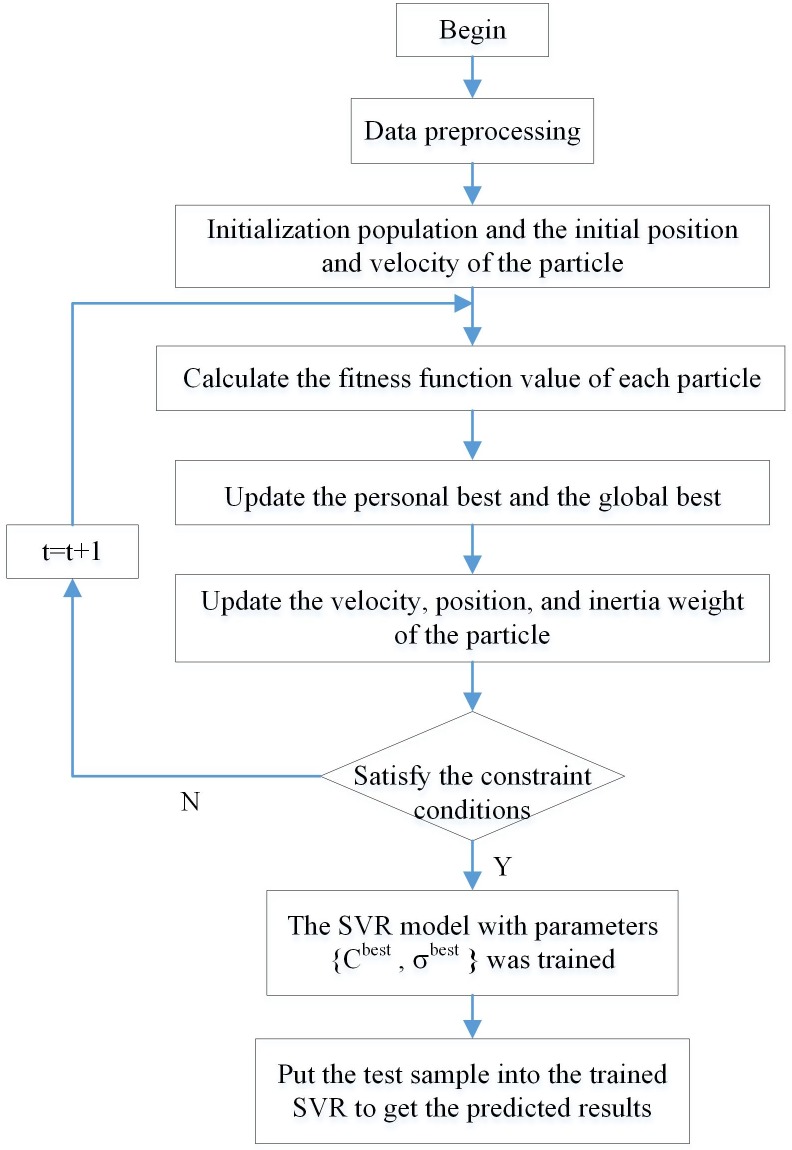
The algorithm for the IPSO-optimized SVR parameter is called IPSO-SVR and its basic steps are as follows
Step 1: Data preprocessing. Read in the sample set and preprocess it.
Step 2: PSO initialization. A particle is composed of a penalty parameter C and a kernel function parameter σ. We initialize the particle swarm {C, σ}, determine the population size of PSO, randomly generate the initial position and velocity of the particle, set the maximum number iterations Tmax of the algorithm and the range of velocity [−Vmax, Vmax].
Step 3: We calculate the fitness function value of each particle. The prediction error of the current position of each particle is obtained by using the SVR corresponding to each particle vector to predict the learning sample. The fitness function value of each particle is calculated by using Eq (19).
Step 4: Update the personal best Pibest of particle. The fitness of each particle is evaluated. If the fitness value of the current iteration is better than the personal best Pibest, then Pibest is replaced by the current fitness value; otherwise, the original value is retained.
Step 5: We update the global best of the population. If the fitness value of a particle is better than the current global best Pgbest, then Pgbest is updated; otherwise, the original value is retained.
Step 6: We update the velocity, position and inertia weight of the particle according to Eqs (14), (15), and (20).
Step 7: Termination conditions. Either the current number of iterations t = Tmax or fitness values is less than (the provided) precision ε. If ε is satisfied, then the optimization step is complete, the optimal parameter {Cbest, σbest} is obtained and the algorithm moves on to step 8. Otherwise, let t = t + 1, and the algorithm returns to step 3.
Step 8: We implement the training sample set, the SVR model with parameters {Cbest, σbest} are determined. The network is trained and the test sample is placed back into the trained SVR to get the predicted results.
The specific process of the IPSO-SVR algorithm is shown in Fig 3.
Fig 3. The SVR algorithm based on IPSO.
Experimental
The data source
Influenza-like cases are a main indicator for the condition monitoring of flu, both domestically and overseas. These cases refer to a specific set of symptoms provided by specific outpatient cases of sentinel hospitals. The symptoms are fever with a temperature equal to or greater than 38 °C, a cough or a sore throat. These cases often lack diagnosis based on laboratory findings. The source of flu data in this article mainly consists of official data from the 10 regional flu outbreaks in the US and the twitter data for the same period. In [58], the 10 regions defined by Health and Human Services (HHS) can be easily identified. The software used to simulate the prediction model is MATLAB (R2014a). The official data used in this study was acquired from the historical ILI weekly (https://gis.cdc.gov/grasp/fluview/fluportaldashboard.html) data set which was published by the Center for Disease Control and Prevention S1 Table. Twitter data refers to data in [33], it is derived from flu data provided by the prototype of flu-surveillance system that was established by Wang et al. [26]. In this paper, we collected 55 weeks of data in 10 regions of the US from the 41st week of 2016 to the 43rd week of 2017. ILI data from the 41st week of 2016 to the 38th week of 2017 was selected as the training set to use for model building. ILI data from the 39th week to 43rd week of 2017 was selected as the test set to use for model validation.
The data processing
The vectors in the original data sample use various orders of magnitude and the order of magnitude varies from sample to sample. To avoid the outliers based on data ranges, the data was normalized. The Mapminmax MATLAB function was used to normalize the sample to be constrained within the [0, 1] interval. The disadvantage of dimensional inconsistency to model was eliminated and the operation efficiency of the model was improved. The normalized formula is
| (21) |
where is the normalized data, Xt is the original input data and Xmax,Xmin are the largest and smallest value in the historical data, respectively.
After predicting the output, a reverse normalization process is performed and the actual predicted ILI were obtained. The reverse normalization formula is
| (22) |
Experimental results and analysis
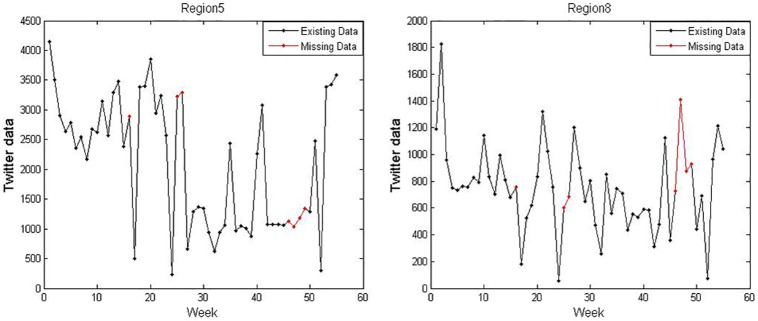
In this study, the twitter data for regions 1-10 misses the 16th, 25th-26th, and 46th-49th data. We use the SVR for prediction to revise these missing data. We perform twenty times and take the corresponding prediction of the missing data with the minimum MAPE. For example, the twitter data of regions 5 and 8 are shown in Fig 4. The red dots in Fig 4 represent our predictions.
Fig 4. The twitter data of regions 5 and 8.
To evaluate the prediction performance of the various prediction models, each model was evaluated by the Mean Square Error (MSE), Relative-Mean-Square Error (RMSE), Mean Absolute Percentage Error (MAPE) and calculation time.
| (23) |
| (24) |
| (25) |
In these evaluation methods, n is the number of samples; yt is the actual value of period t; and is the predicted value of period t.
In this work, we predict %ILI using CV-SVR, GA-SVR, PSO-SVR, and IPSO-SVR methods. The independent variable of models 1-3 were used as feature inputs of these ML methods and the dependent variable was used as the output. We compared the prediction results generated by the IPSO-SVR with CV-SVR, GA-SVR, and PSO-SVR methods (which are based on models 1-3). The prediction results are shown in Tables 1–3, and calculation times are shown in Table 4.
Table 1. Evaluation index results of model 1 for 10 regions of US.
| Region | Error | CV-SVR | GA-SVR | PSO-SVR | IPSO-SVR |
|---|---|---|---|---|---|
| 1 | MSE | 1.2247 | 1.1309 | 0.8836 | 0.8075 |
| RMSE | 1.7433 | 1.6070 | 1.3214 | 1.2458 | |
| MAPE | 1.0936 | 1.0626 | 1.0069 | 0.8252 | |
| 2 | MSE | 0.5515 | 0.7651 | 0.5810 | 0.5447 |
| RMSE | 0.1952 | 0.2730 | 0.1904 | 0.1794 | |
| MAPE | 0.3949 | 0.4827 | 0.3181 | 0.3215 | |
| 3 | MSE | 2.7369 | 2.7564 | 0.7368 | 0.7378 |
| RMSE | 1.8162 | 1.8549 | 0.5134 | 0.5139 | |
| MAPE | 1.1778 | 1.1505 | 0.5987 | 0.5989 | |
| 4 | MSE | 7.2071 | 9.4694 | 11.1045 | 11.7234 |
| RMSE | 2.7272 | 3.5422 | 4.2457 | 4.6025 | |
| MAPE | 1.5791 | 1.8344 | 2.0160 | 2.0881 | |
| 5 | MSE | 1.6050 | 1.7586 | 0.2454 | 0.2272 |
| RMSE | 1.2276 | 1.3436 | 0.1861 | 0.1724 | |
| MAPE | 0.9989 | 1.0861 | 0.3537 | 0.3425 | |
| 6 | MSE | 0.0759 | 2.1083 | 0.0638 | 0.0582 |
| RMSE | 0.0172 | 0.5241 | 0.0132 | 0.0118 | |
| MAPE | 0.1164 | 0.6709 | 0.0983 | 0.0883 | |
| 7 | MSE | 2.4362 | 2.5517 | 2.0060 | 1.6671 |
| RMSE | 2.4432 | 2.4943 | 2.0476 | 1.6982 | |
| MAPE | 1.4827 | 1.4981 | 1.3379 | 1.2257 | |
| 8 | MSE | 0.2397 | 0.2608 | 0.1347 | 0.1330 |
| RMSE | 1.0788 | 1.0961 | 0.5915 | 0.5821 | |
| MAPE | 0.8556 | 0.8319 | 0.5967 | 0.5833 | |
| 9 | MSE | 0.0367 | 0.0806 | 0.0249 | 0.0248 |
| RMSE | 0.0147 | 0.0332 | 0.0100 | 0.0099 | |
| MAPE | 0.1041 | 0.1609 | 0.0814 | 0.0812 | |
| 10 | MSE | 0.8944 | 0.8979 | 0.8503 | 0.8401 |
| RMSE | 0.8648 | 0.8689 | 0.8350 | 0.8225 | |
| MAPE | 0.7786 | 0.7806 | 0.7175 | 0.7082 |
Table 3. Evaluation index results of model 3 for 10 regions of US.
| Region | Error | CV-SVR | GA-SVR | PSO-SVR | IPSO-SVR |
|---|---|---|---|---|---|
| 1 | MSE | 0.0127 | 0.0217 | 0.0211 | 0.0123 |
| RMSE | 0.0225 | 0.0419 | 0.0388 | 0.0221 | |
| MAPE | 0.1329 | 0.1880 | 0.1659 | 0.1203 | |
| 2 | MSE | 0.0125 | 0.0132 | 0.0126 | 0.0111 |
| RMSE | 0.0044 | 0.0051 | 0.0046 | 0.0042 | |
| MAPE | 0.0596 | 0.0617 | 0.0580 | 0.0575 | |
| 3 | MSE | 0.0285 | 0.0279 | 0.0238 | 0.0163 |
| RMSE | 0.0225 | 0.0220 | 0.0189 | 0.0130 | |
| MAPE | 0.1489 | 0.1473 | 0.1361 | 0.1124 | |
| 4 | MSE | 0.0314 | 0.0355 | 0.0315 | 0.0205 |
| RMSE | 0.0098 | 0.0111 | 0.0098 | 0.0076 | |
| MAPE | 0.0795 | 0.0797 | 0.0726 | 0.0724 | |
| 5 | MSE | 0.0106 | 0.0108 | 0.0086 | 0.0082 |
| RMSE | 0.0086 | 0.0087 | 0.0068 | 0.0065 | |
| MAPE | 0.0666 | 0.0664 | 0.0603 | 0.0583 | |
| 6 | MSE | 0.0212 | 0.0204 | 0.0225 | 0.0237 |
| RMSE | 0.0050 | 0.0049 | 0.0055 | 0.0058 | |
| MAPE | 0.0578 | 0.0577 | 0.0610 | 0.0622 | |
| 7 | MSE | 0.0143 | 0.0270 | 0.0598 | 0.0598 |
| RMSE | 0.0200 | 0.0314 | 0.0645 | 0.0645 | |
| MAPE | 0.0979 | 0.1444 | 0.1969 | 0.1971 | |
| 8 | MSE | 0.0381 | 0.0314 | 0.0523 | 0.0248 |
| RMSE | 0.0692 | 0.0562 | 0.0976 | 0.0458 | |
| MAPE | 0.2460 | 0.2177 | 0.2910 | 0.1893 | |
| 9 | MSE | 0.0498 | 0.0504 | 0.0472 | 0.0426 |
| RMSE | 0.0194 | 0.0199 | 0.0185 | 0.0164 | |
| MAPE | 0.1159 | 0.1226 | 0.1155 | 0.0987 | |
| 10 | MSE | 0.0433 | 0.0432 | 0.0464 | 0.0421 |
| RMSE | 0.0485 | 0.0484 | 0.0508 | 0.0406 | |
| MAPE | 0.1495 | 0.1697 | 0.1596 | 0.1463 |
Table 4. Comparison of the calculation time for each algorithm (in models 1-3).
| Model | CV-SVR | GA-SVR | PSO-SVR | IPSO-SVR |
|---|---|---|---|---|
| Model 1 | 242s | 31s | 25s | 20s |
| Model 2 | 244s | 32s | 27s | 26s |
| Model 3 | 213s | 54s | 26s | 25s |
Table 2. Evaluation index results of model 2 for 10 regions of US.
| Region | Error | CV-SVR | GA-SVR | PSO-SVR | IPSO-SVR |
|---|---|---|---|---|---|
| 1 | MSE | 0.3803 | 0.3811 | 0.5575 | 0.3612 |
| RMSE | 0.6677 | 0.6683 | 0.9634 | 0.6356 | |
| MAPE | 0.6940 | 0.6884 | 0.8843 | 0.6841 | |
| 2 | MSE | 1.4038 | 0.8164 | 2.0968 | 1.9606 |
| RMSE | 0.5899 | 0.3746 | 1.0149 | 0.8310 | |
| MAPE | 0.6131 | 0.5070 | 0.7272 | 0.7451 | |
| 3 | MSE | 1.8137 | 1.7965 | 1.6740 | 1.6977 |
| RMSE | 1.3737 | 1.3615 | 1.2818 | 1.3016 | |
| MAPE | 0.9777 | 0.9760 | 0.9518 | 0.9526 | |
| 4 | MSE | 1.8745 | 1.9831 | 1.7528 | 1.3208 |
| RMSE | 0.6592 | 0.7418 | 0.6787 | 0.4623 | |
| MAPE | 0.7639 | 0.7279 | 0.7023 | 0.5795 | |
| 5 | MSE | 0.8477 | 0.8379 | 1.1876 | 0.8092 |
| RMSE | 0.6482 | 0.6413 | 0.9080 | 0.6207 | |
| MAPE | 0.7482 | 0.7528 | 0.9035 | 0.7327 | |
| 6 | MSE | 0.8563 | 0.8644 | 0.8550 | 0.8459 |
| RMSE | 0.2144 | 0.2213 | 0.2128 | 0.1884 | |
| MAPE | 0.4013 | 0.3915 | 0.4032 | 0.3781 | |
| 7 | MSE | 0.4899 | 0.4960 | 0.6058 | 0.4313 |
| RMSE | 0.5341 | 0.5409 | 0.5221 | 0.4841 | |
| MAPE | 0.6587 | 0.6853 | 0.6517 | 0.6073 | |
| 8 | MSE | 0.7583 | 0.3963 | 0.7538 | 0.6458 |
| RMSE | 2.1670 | 1.1701 | 2.3610 | 1.7764 | |
| MAPE | 1.1702 | 0.8843 | 1.1066 | 1.0388 | |
| 9 | MSE | 0.2956 | 0.1221 | 0.3401 | 0.3395 |
| RMSE | 0.1200 | 0.0588 | 0.1387 | 0.1369 | |
| MAPE | 0.2853 | 0.2198 | 0.3271 | 0.3035 | |
| 10 | MSE | 0.1334 | 0.1097 | 0.7560 | 0.2935 |
| RMSE | 0.1074 | 0.1554 | 0.8328 | 0.3150 | |
| MAPE | 0.2836 | 0.3134 | 0.6261 | 0.5104 |
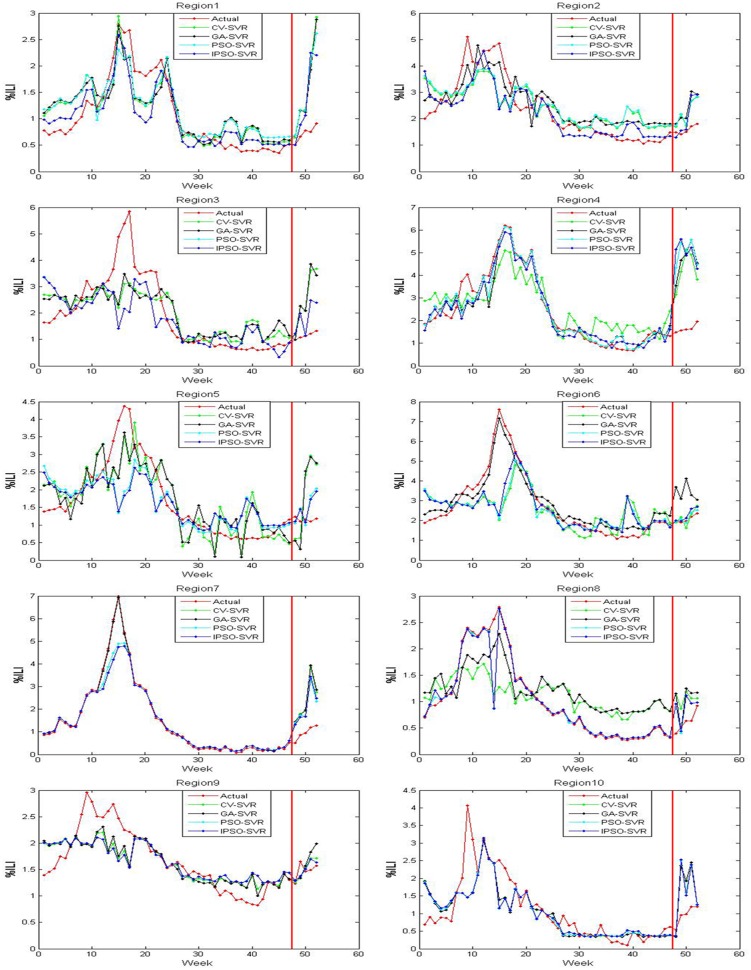
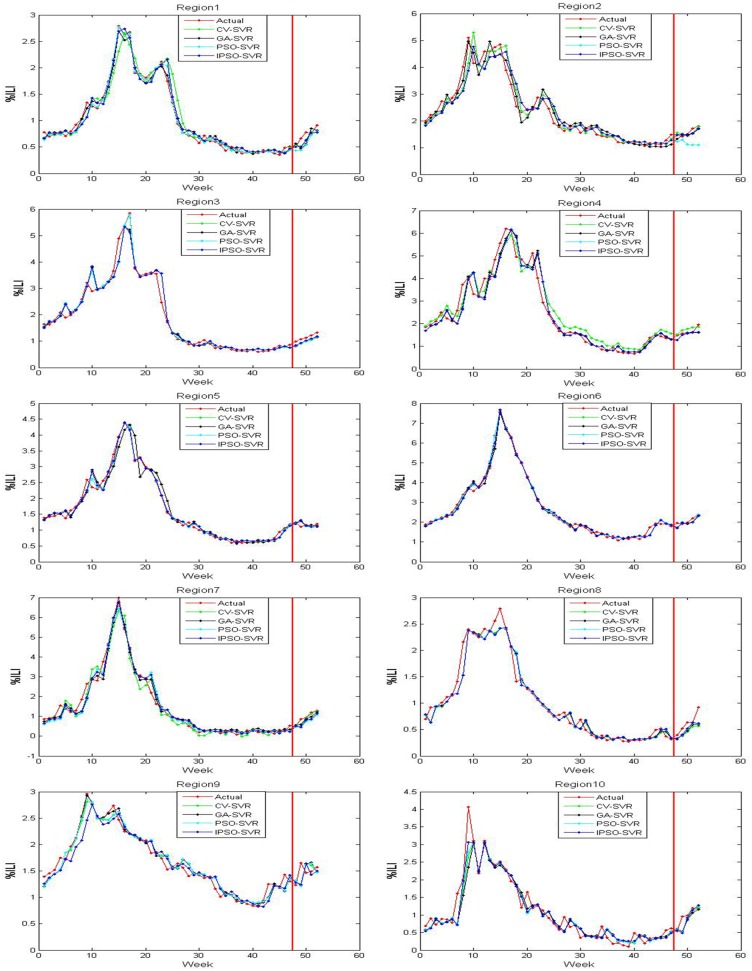
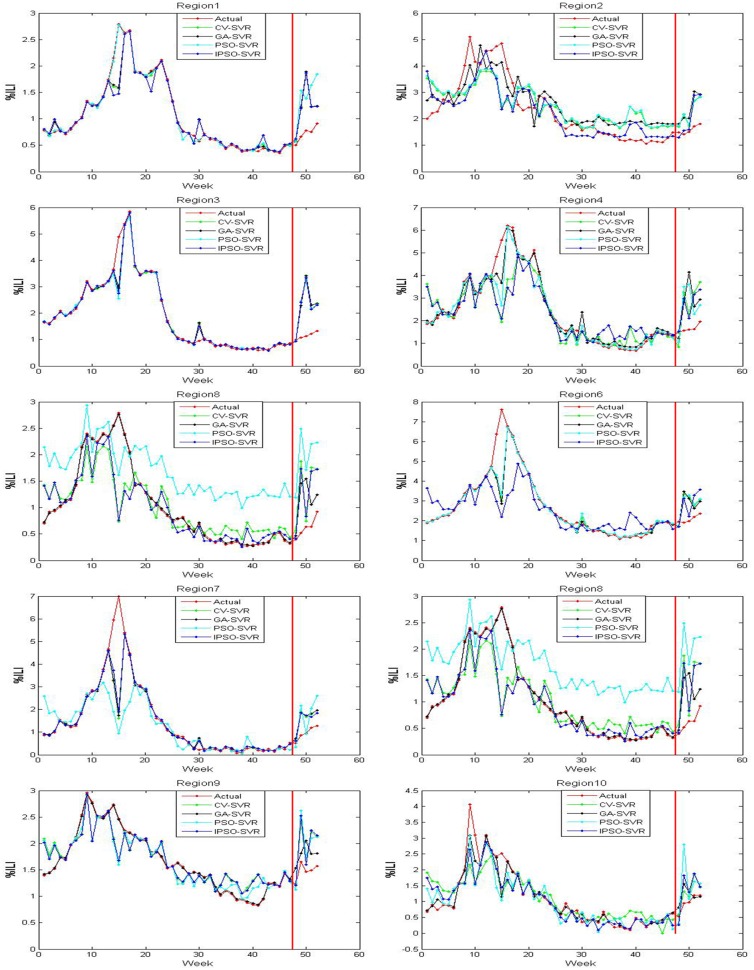
The actual value and predicted value of models 1-3 on the trained and tested samples of ten regions are shown in Figs 5–7, where the red line perpendicular to the horizontal axis in every subfigure divides the whole plate into two parts: the left part is the actual outputs and predicted outputs of the training samples on models 1-3, and right part is the actual outputs and the predicted outputs of the test samples on models 1-3. From Figs 5–7, we can see that the output of model 3 are the closest to the actual output in the training samples and test samples. The output of model 2 are close to the actual output in the training samples, but there are differences between the predicted output of model 2 and the actual output in the test samples. There are many discrepancies between the estimates using model 1 and the actual CDC values in the training samples and test samples.
Fig 5. The trained and tested results of model 1 for 10 regions.
Fig 7. The trained and tested results of model 3 for 10 regions.
Fig 6. The trained and tested results of model 2 for 10 regions.
Tables 1–3 shows the MSE, RMSE, and MAPE on the test samples of ten regions for models 1-3, respectively. By comparing the MSE, RMSE, and MAPE results of models 1 and 2, we find that model 2 has higher ILI prediction capabilities for most regions; this is because the MSE, RMSE and MAPE values are smaller. These results suggest that the flu epidemic other regions has an impact on the current region, which means that the spread of flu is also affected by an inter-regional spread of flu. Therefore, the %ILI prediction should not only consider the role of the current regional flu data, but should also consider the impact of flu transmission in extended regional areas. Similarly, compared to the MSE, RMSE, and MAPE results of model 2 with model 3, we found that the prediction effect of the model 3 was better than the model 2 over all 10 regions. The results show that the twitter data complements with CDC ILI data, that is, the twitter data may contain new information that CDC data does not have. This information reflects the variation trend of the previous period of the flu that typically lasts 1-2 weeks.
By comparing the IPSO-SVR, PSO-SVR, GA-SVR, and CV-SVR prediction results of model 1, we find that the prediction effect of the IPSO-SVR, in most regions (1-2 and 5-9) showed more robustness than the other three methods. By comparing the IPSO-SVR, PSO-SVR, GA-SVR, and CV-SVR prediction results of model 2, we find that the prediction effect of the IPSO-SVR was better than other three methods in most regions (1 and 4-7). By comparing the IPSO-SVR, PSO-SVR, GA-SVR, and CV-SVR prediction results of model 3, we find that the prediction effect of the IPSO-SVR, in most regions (1-5 and 8-9) showed more robustness than the other three methods. By comparing the IPSO-SVR, PSO-SVR, GA-SVR and CV-SVR, the calculation time to find a result (based on models 1-3), we find that IPSO-SVR has the shortest calculation time than the other three algorithms.
Several comparison can be made to illustrate that the IPSO-SVR prediction results of model 3 are the best of the three models since its MSE, RMSE and MAPE values are the smallest, and the run-time of the IPSO-SVR method is the shortest. Meanwhile, the prediction results were compared to the results of the BP neural network influenza prediction model based on improved artificial tree algorithm in reference [33]. We can show that the IPSO-SVR prediction results of model 3 are better than the prediction results of the IAT-BPNN model in most regions (1-3, 5-6, and 8-10) under review. The precision is higher, better and more reflects the ground truth of flu transmission. Results show that in flu prediction, the IPSO-SVR algorithm can predict %ILI more effectively, while showing that the method of using IPSO to optimize the SVR parameters is feasible and effective, and that the techniques not only provide new methods to further the development of flu prediction, but also have important reference value for the further applications of SVR.
Conclusions
In this paper, we proposed three flu prediction models that use US-based twitter and CDC data. Then, we proposed an improved PSO to optimize the parameters of SVR. The independent and dependent variables of models 1-3 are used as input and output of the IPSO-SVR for predicting the CDC’ unweighted %ILI of US. Comparing the prediction results of IPSO-SVR, PSO-SVR, GA-SVR, and CV-SVR for models 1-3. The experimental results show that 1) flu outbreaks in adjacent areas also have an impact on the current spread of flu in a region; 2) the twitter data complements with CDC ILI data; 3) the IPSO-SVR prediction results of model 3 was better than the prediction results of IAT-BPNN model; 4) the IPSO-SVR prediction results of model 3 for %ILI are not only suitable for ten regions defined by HHS, but also generates an optimization algorithm that can be applied to optimize the SVR parameters, which used to solve the other predict problem.
Supporting information
Distribution of ILIs from week 41st in 2016 to week 43rd in 2017 in ten regions of the United States.
(XLSX)
Data Availability
The CDC data for this manuscript are attached in supplementary files. The twitter data underlying the results presented in the study is owned by a third party and authors do not have permission to share the data. The owner of the original data has published articles before (DOI: 10.1007/s10916-016-0545-y), which includes the specific methods of data sources and the detailed implementation process of the experiment, and the data are available from the author. I confirm that did not have any special access privileges that others would not have.
Funding Statement
Research Project Supported by National Nature Science Foundation of China (Grant No. 61774137) and Shanxi Natural Science Foundation (Grant No. 201701D121012, 201801D121026 and 201701D221121) and Shanxi Scholarship Council of China (Grant No.2016-088) and North University of China Postgraduate Scientific and Technological Innovation Project (Grant No.20181549). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Zhai HN. The analysis of relationship between influenza and atmospheric ambient and the establishment of influenza-like-illness rates forecasting model. China University of Geosciences, Wuhan, China, 2009. [Google Scholar]
- 2. Ou CQ, Deng ZH, Yang L, Chen PY. Prediction of Influenza-like Illness Using Auto-regression Model. Chinese Journal of Health Statistics. 2007. December;24(6):569–571. [Google Scholar]
- 3.WHO, Seasonal Influenza. Available online: http://www.who.int/mediacentre/factsheets/fs211/zh/ (accessed on 23 January 2018).
- 4. Zhong HJ, Yang F. Introduction of influenza surveillance at domestic and foreign. South China Prev. Med. 2010. June;36(3): 66–68. [Google Scholar]
- 5. Ren YH, Yao JY, Yan L, Huang XX, Zhang YP, Yan SY, et al. Research on influenza surveillance systems in China and abroad. Dis. Surveillance. 2010. October;25(10):833–838. [Google Scholar]
- 6.Online health search. Available online: http://www.pewinternet.org/2006/10/29/online-health-search-2006/ (accessed on 15 March 2018).
- 7. Dong XC, Li L, Xu WT, Zhang Y, Zhang ZL, Zhao Z. Correlation between Baidu index of specific keywords and influenza epidemics. CHN. J. Public Health. 2016. December;32(11):1543–1546. [Google Scholar]
- 8. Yuan Q, Nsoesie EO, Lv B, Peng G, Chunara R, Brownstein JS. Monitoring influenza epidemics in china with search query from baidu. Plos One. 2013. May;8(5):e64323 10.1371/journal.pone.0064323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Pi G, Zhang J, Li W, Yang S, Luo G, Deng C, et al. Monitoring seasonal influenza epidemics by using internet search data with an ensemble penalized regression model. Sci. Rep. 2017. April;7:46469 10.1038/srep46469 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Domnich A, Panatto D, Signori A, Lai PL, Gasparini R, Amicizia D. Age-Related Differences in the Accuracy of Web Query-Based Predictions of Influenza-Like Illness. Plos One. 2015. May;10(5):e0127754 10.1371/journal.pone.0127754 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Alessa A, Faezipour M. A review of influenza detection and prediction through social networking sites. Theor. Biol. Med. Model. 2018;15(1):2 10.1186/s12976-017-0074-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Liang F, Guan P, Wu W, Huang DS. Forecasting influenza epidemics by integrating internet search queries and traditional surveillance data with the support vector machine regression model in Liaoning, from 2011 to 2015. PeerJ. 2018. June;6:1–14. 10.7717/peerj.5134 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Ginsberg J, Mohebbi MH, Pate RS, Brammer L, Smolinski MS, Brilliant L. Detecting influenza epidemics using search engine query data. Nature. 2009;457(7232):1012 10.1038/nature07634 [DOI] [PubMed] [Google Scholar]
- 14. Zou XH, Zhu WF, Yang L, Shu YL. Google Flu Trends-the initial application of big data in public health. CHN. J. Prev. Med. 2005. June;49(6):581–584. [PubMed] [Google Scholar]
- 15. Yang S, Santillana M, Kou SC. Accurate estimation of influenza epidemics using Google search data via ARGO. P. Natl. Acad. Sci. USA. 2015. August;112(47):14473–11478. 10.1073/pnas.1515373112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Butler D. When Google got flu wrong. Nature. 2013. February;494(7436):155–156. 10.1038/494155a [DOI] [PubMed] [Google Scholar]
- 17. Davidson MW, Haim DA, Radin JM. Using Networks to Combine “Big Data” and Traditional Surveillance to Improve Influenza Predictions. Sci Rep. 2015. January;5:8154 10.1038/srep08154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Martin LJ, Xu B, Yasui Y. Improving Google Flu Trends estimates for the United States through transformation. Plos One. 2014. December;9(12):e109209 10.1371/journal.pone.0109209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Leonenko VN, Ivanov SV. Prediction of influenza peaks in Russian cities: Comparing the accuracy of two SEIR models. Math. Biosci. Eng. 2018;15(1):209–232. 10.3934/mbe.2018009 [DOI] [PubMed] [Google Scholar]
- 20. Petukhova T, Ojkic D, Mcewen B, Deardon R, Poljak Z. Assessment of autoregressive integrated moving average (ARIMA), generalized linear autoregressive moving average (GLARMA), and random forest (RF) time series regression models for predicting influenza A virus frequency in swine in Ontario, Canada. Plos One. 2018. June;13(6):e0198313 10.1371/journal.pone.0198313 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Dukic VM, Lopes HF, Polson N. Tracking flu epidemics using Google Flu Trends and particle learning. SSRN Electron. J. 2009. November;1–31. 10.2139/ssrn.1513705 [DOI] [Google Scholar]
- 22. Doornik JA. Improving the timeliness of data on influenza-like illnesses using Google search data. Working Paper. 2009. September;1–21. [Google Scholar]
- 23. Huang JM. Detection and prediction algorithm for flu based of social network. East China Normal University, Shanghai, China, 2015. [Google Scholar]
- 24. Santillana M, Nsoesie EO, Mekaru SR, Scales D, Brownstein JS. Using clinicians’ search query data to monitor influenza epidemics. Clin. Infect. Dis. Off. Publ. Infect. Dis. Soc. Am. 2015. November;59(10):1146–1150. 10.1093/cid/ciu647 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Magruder SF. Evaluation of over-the-counter pharmaceutical sales as a possible early warning indicator of human disease. J. Hopkins Apl. Tech. D. 2003. October; 24(4):349–353. [Google Scholar]
- 26. Wang F, Wang HY, Xu K, Raymond R, Chon J, Fuller S, et al. Regional level influenza study with Geo-Tagged Twitter data. J. Med. Syst. syst. 2016. July;40(8):1–8. 10.1007/s10916-016-0545-y [DOI] [PubMed] [Google Scholar]
- 27.Culotta A. Towards detecting influenza epidemics by analyzing Twitter messages. 1st Workshop on social Media Analytics (Soma’ 10), Washington, DC, USA, 25 July 2010; Melvile, P., Leskovec, J.; Publisher: New York, NY, USA, 2010.
- 28.Aramaki E, Maskawa S, Morita Mizuki. Twitter catches the flu: Detecting influenza epidemics using Twitter. Proceedings of the 2011 Conference on Empirical Methods in Natural Language Processing, Edinburgh, Scotland, UK, 27-31 July 2011. https://www.researchgate.net/publication/221012847
- 29.Statistic Brain Research Institute. Available online: http://www.pewinternet.org/2006/10/29/online-health-search-2006/ (accessed on 23 Feb 2018).
- 30.Suh B, Hong L, Pirolli P, Chi EH. Wang to be retweeted? Large scale analytics on factors impacting retweet in twitter network. 2010 IEEE Second International Conference On Social Computing, Minneapolis, MN, USA, Sep 2010. 10.1109/SocialCom.2010.33 [DOI]
- 31. Paul MJ, Dredze M, Broniatowski D. Twitter improves influenza forecasting. PLOS Currents Outbreaks. 2014. October; 6 10.1371/currents.outbreaks.90b9ed0f59bae4ccaa683a39865d9117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Kim E-K, Seok JH, Oh JS, Lee HW, Kim KH. Use of Hangeul Twitter to track and predict human influenza infection. Plos One. 2013. July; 8(7): e69305 10.1371/journal.pone.0069305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Hu HP, Wang HY, Wang F, Langley D, Avram A, Liu MX. Prediction of influenza-like illness based on the improved artificial tree algorithm and artificial neural network. Sci. Rep-UK. 2018. March;8(1):4895 10.1038/s41598-018-23075-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Signorini A, Segre AM, Polgreen PM. The use of twitter to track levels of disease activity and public concern in the U.S. during the influenza a H1N1 pandemic. Plos One. 2011. May; 6(5):e19467 10.1371/journal.pone.0019467 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Currie D. Public health leaders using social media to convey emergencies: New tools a boon. Nations Health. 2009. August;39(6):1–10. [Google Scholar]
- 36.Lampos V, Cristianini N. Tracking the flu pandemic by monitoring the social web. Proceedings of the 2nd international Workshop on Cognitive Information Processing (CIP), Elba, Italy, June 2010. 10.1109/CIP.2010.5604088 [DOI]
- 37. Broniatowski DA, Paul MJ, Dredze M. Twitter: Big data opportunities. Science. 2014. July;345(6193):148 10.1126/science.345.6193.148-a [DOI] [PubMed] [Google Scholar]
- 38.Van Dyne MM, Woolery LK, Gryzmala-Busse J, Tsatsoulis C. Using machine learning and expert systems to predict preterm delivery in pregnant women. Proceedings of the tenth Conference on Artificial Intelligence for Applications (CAIA), San Antonio, TX, USA, March 1994.
- 39. Wang H, Yan M, Su XY. Research on automatic classification for Chinese bibliography based on machine learning. Journal of Library Science in China. 2010. November;36(6):28–39. [Google Scholar]
- 40. Chen LF, Zhou N, Li D. Study on machine learning based automatic text categorization model. New Technol. Lib. Inform. Serv. 2005. June;36(6):23–27. [Google Scholar]
- 41. Qian DL, Li WJ, Yuan CF, Lu Q, Wu ML. Applying Machine Learning to Chinese Entity Detection and Tracking. Comput. Linguist. Text Process. 2007. January;4394:154–165. [Google Scholar]
- 42.Ramon J, Blockeel H. A survey of the application of machine learning to the game of go. First International Conference on Baduk, Myong-ji, Korea, 11 May 2001.
- 43. Navarro PJ, Fernández C, Borraz R, Alonso D. A Machine Learning Approach to Pedestrian Detection for Autonomous Vehicles Using High-Definition 3D Range Data. Sensors, 2017. January;17(1):18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Wu CH, Ho JM, Lee DT. Travel-time prediction with support vector regression. IEEE T. Intell. Transp. 2004. May;5(4):276–281. 10.1109/TITS.2004.837813 [DOI] [Google Scholar]
- 45. Vapnik VN. The Nature of Statistical Learning Theory. IEEE T. Neural Networ. 1997. November;38(4):1564–1564, 10.1109/TNN.1997.641482 [DOI] [Google Scholar]
- 46. Uddin MR, Sharma A, Farid DM, Rahman MM, Dehzangi A, Shatabda S. EvoStruct-Sub: An accurate Gram-positive protein subcellular localization predictor using evolutionary and structural features. J. Theor. Biol. 2018;443:138–146, 10.1016/j.jtbi.2018.02.002 [DOI] [PubMed] [Google Scholar]
- 47. Niu XX, Yang CL, Yang HC, Wang HC, Wang YY. Investigation of ANN and SVM based on limited samples for performance and emissions prediction of a CRDI-assisted marine diesel engine. Appl. Therm. Eng. 2017. January;111:1353–1364, 10.1016/j.applthermaleng.2016.10.042 [DOI] [Google Scholar]
- 48.Li YM, Gong SG, Liddell H. Support vector regression and classification based multi-view face detection and recognition. Proceeding Fourth IEEE International Conference on Automatic Face and Gesture Recongnition (Cat. No. PR00580), Grenoble, France, France, Mar 2000.
- 49. Clarke SM, Griebsch JH, Simpson TW. Analysis of Support Vector Regression for Approximation of Complex Engineering Analyses. J. Mech. Design. 2004. August;127(6):1077–1087. 10.1115/1.1897403 [DOI] [Google Scholar]
- 50. Lin SL, Liu Z. Parameter selection in SVM with RBF kernel function. J. Zhejiang Univ. Technol. 2007. April;35(2):163–167. [Google Scholar]
- 51. Wang Y, Li J. Credible Intervals for Precision and Recall Based on a K-Fold Cross-Validated Beta Distribution. Neural Comput. 2016. August;28(8):1694–1722. 10.1162/NECO_a_00857 [DOI] [PubMed] [Google Scholar]
- 52.Nematzadeh Z, Ibrahim R, Selamat A. Comparative studies on breast cancer classifications with k-fold cross validations using machine learning techniques. 2015 10th Asian Control Conference (ASCC), Kota Kinabalu, Malaysia, Jun 2015. 10.1109/ASCC.2015.7244654 [DOI]
- 53. Saitoh F. High-speed Image Matching by Extracting Block Areas and Pixels Using Two-stage Genetic Algorithm. J. Japan Soc. Precis. Eng. 2001. June;67(6):987–991. [Google Scholar]
- 54. Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE T. Evolut. Comput. 2002. August;6(2):182–197. 10.1109/4235.996017 [DOI] [Google Scholar]
- 55.Kennedy J, Eberhart R. Particle swarm optimization. Proceedings of ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, Australia, Dec 1995. 10.1109/ICNN.1995.488968 [DOI]
- 56.Sridhar M, Rama Mohan Babu G. Hybrid Particle Swarm Optimization scheduling for cloud computing. 2015 IEEE International Advance Computing Conference (IACC), Banglore, India, June 2015.
- 57. Yang K, Pan M, Luo Y, Chen KX, Zhao YS, Zhou XL. A time-series analysis of urbanization-induced impervious surface area extent in the Dianchi Lake watershed from 1988-2017. Int. J. Remote Sens. 2018. September; 1–20. 10.1080/01431161.2018.1516312 [DOI] [Google Scholar]
- 58.Regional Offices. Available online: https://www.hhs.gov/about/agencies/iea/regional-offices/index.html (accessed on 2 March 2019).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Distribution of ILIs from week 41st in 2016 to week 43rd in 2017 in ten regions of the United States.
(XLSX)
Data Availability Statement
The CDC data for this manuscript are attached in supplementary files. The twitter data underlying the results presented in the study is owned by a third party and authors do not have permission to share the data. The owner of the original data has published articles before (DOI: 10.1007/s10916-016-0545-y), which includes the specific methods of data sources and the detailed implementation process of the experiment, and the data are available from the author. I confirm that did not have any special access privileges that others would not have.