Long-term trajectory of kidney function in autosomal dominant polycystic kidney disease

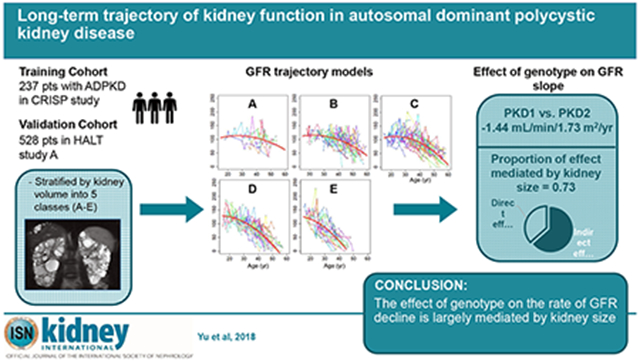
Abstract

Autosomal dominant polycystic kidney disease (ADPKD) is characterized by cyst and kidney growth, which is hypothesized to cause loss of functioning renal mass and eventually end-stage kidney disease. However, the time course of decline in glomerular filtration rate (GFR) is poorly defined. The Consortium for Radiologic Imaging Studies of Polycystic Kidney Disease study is a 14-year observational cohort study of 241 adults with ADPKD. As an estimate of the rate of kidney growth, participants were stratified into 5 subclasses based on baseline age and MRI measurements of total kidney volume (TKV) according to the method of Irazabal. GFR trajectories spanning over four decades of life were reconstructed and fitted using mixed polynomial models, which were validated using data from the HALT-PKD study. GFR trajectories were nonlinear, with a period of relative stability in most participants, followed by accelerating decline. The shape and slope of these trajectories were strongly associated with baseline Irazabal class. Patients with PKD1 mutations had a steeper GFR decline than patients with PKD2 mutations or with no detected mutation, largely mediated by the effect of genotype on Irazabal class. Thus, GFR decline in ADPKD is nonlinear, and its trajectory throughout adulthood can be predicted from a single measurement of kidney volume. These models can be used for clinical prognostication, clinical trial design, and patient selection for clinical interventions. Our findings support a causal link between growth in kidney volume and GFR decline, adding support for the use of TKV as a surrogate endpoint in clinical trials.

Graphical Abstract

INTRODUCTION

Autosomal dominant polycystic kidney disease (ADPKD) is a lifelong hereditary disease. Kidney cysts develop beginning in utero¹ and grow exponentially throughout life,² leading eventually to ESRD. However, the decline in GFR generally occurs late in adulthood, usually in the 4th or 5th decade of life,^3,4 suggesting that there is preserved, or even increased^5,6 GFR for the first 2-3 decades of life. Once kidney function starts to deteriorate, GFR has been observed to decline rapidly and uniformly at a rate that has consistently been found to be 4-6 mL/min/yr.^3,4,7 However, to date, there have been no studies that have successfully characterized the trajectory of GFR over the entire adult lifespan of ADPKD patients.

Although several longitudinal studies in ADPKD have been published,^2,4,8–14 the duration of follow-up, which ranged from 14 months to 8 years, is exceedingly short relative to the natural history of the disease (40 to 60 years or more). GFR data sampled within such a narrow window of time identifies short-term fluctuations and patterns but is not very informative of long-term trends. Indeed it is inevitable that these short-term GFR trajectories would be largely indistinguishable from a straight line (Fig. S1A), and hence most such studies have modeled short-term GFR with linear methods. If one could pool GFR data from multiple patients observed at different ages, it should in theory be possible to reconstruct the GFR trajectory of an idealized patient over a much longer time horizon (Fig. S1B). However, because there is considerable interindividual variability in the rate of disease progression, aggregate data from an unselected population is rather uninformative.

These limitations suggest the need for a method to stratify patients into subgroups by rate of progression of disease such that, within each subgroup, patients would follow similar GFR trajectories that cluster together, while different subgroups would exhibit distinctly different trajectories (Fig. S1C). Total kidney volume (TKV) or height-adjusted TKV (htTKV) has been shown to be a good predictor of subsequent GFR decline.^2,10 When TKV is considered in isolation it serves primarily as a marker of the stage of disease that has been attained. However, when TKV is factored for age, it becomes informative of the rapidity of PKD disease progression. Specifically, Irazabal et al. showed that using htTKV determined at a single point in time, and knowing the age of the patient at that time, one could extrapolate the rate at which that patient’s kidneys must have grown and hence classify patients into one of 5 risk classes.¹³ They found that the Irazabal class was a good predictor of short-term GFR decline, modeled as a linear slope over 6 years of follow-up.

In this study, we re-analyzed data from the CRISP and HALT studies to test the hypothesis that the rate of kidney growth, represented by the Irazabal class, is a predictor of the long-term shape and slope of the GFR trajectory over the lifetime of adults with ADPKD.

RESULTS

Using baseline age and htTKV, we classified patients in the CRISP cohort (Table 1) according to the method of Irazabal.¹³ Fig. 1 shows, as expected, that this classification was quite effective at stratifying the population into subgroups with distinct rates of kidney growth. To test the hypothesis that patients within each subgroup that share similar rates of kidney growth will also share similar GFR trajectories over the course of adulthood, GFR trajectories were plotted for the entire population (Fig. S2) or separately for each subgroup (Fig. 2). These show that the GFR trajectories for patients within each subgroup tend to cluster together. Between subgroups there appears to be a trend for the GFR to decline earlier and/or faster with increasing Irazabal class (from A to E). This trend is evident in a summary plot in which the data are binned into 5 year intervals (Fig. 3).

Table 1.

Comparison of CRISP and HALT Study A cohorts by baseline characteristics

	CRISP	HALT Study A
Total no. patients	237	528
Age (yr)	32.3 ± 8.8	36.3 ± 8.3
Sex (% male)	39.7%	51.9%
Race
Caucasian	86.5%	92.2%
African-American	11.4%	2.7%
Height (cm)	172.0 ± 11.0	174.0 ± 10.3
BMI (kg/m2)	25.8 ± 5.2	27.1 ± 5.2
Office SBP (mm Hg)	123.1 ± 13.1	126.8 ± 13.9
Office DBP (mm Hg)	79.4 ± 10.5	80.1 ± 11.1
htTKV (ml/m)	616±371	685 ± 394
eGFR*	92.4± 22.9	91.6 ± 17.6
PKD genotype
PKD1	78.7%	76.2%
PKD2	14.0%	15.1%
NMD	7.2%	8.7%
Mutation type†
Truncating PKD1	58.6%	51.5%
Non-truncating PKD1	27.6%	30.5%
Truncating PKD2	10.48%	14.4%
Non-truncating PKD2	3.3%	3.6%

^*By CKD EPI formula (mL/min/1.73 m²)

^†In patients with detectable PKD1 or PKD2 mutations

htTKV, height-adjusted total kidney volume; eGFR, estimated GFR from serum creatinine by CKD-Epi equation; NMD, no mutation detected

Fig. 1.

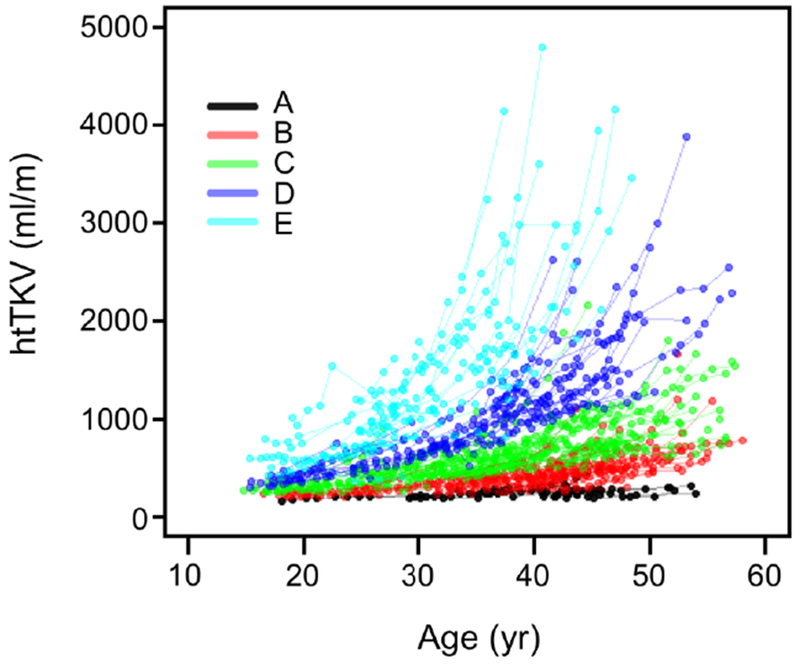
Kidney growth in the CRISP cohort, stratified by Irazabal class. Based on baseline age and htTKV, patients were assigned to one of 5 Irazabal classes (A-E, color-coded as shown). htTKV values determined over the course of the study are plotted, with each line representing an individual patient.

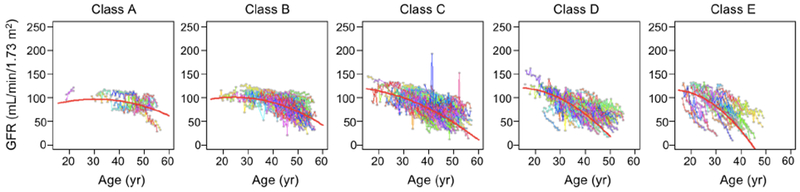
Fig. 2.

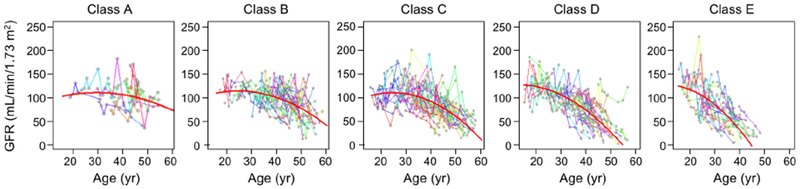
Trajectories of measured GFR fitted to patients in each Irazabal class (A-E) in the CRISP study. Individual patient data are represented by gray dots connected by straight lines in different colors. The red curved lines represent the best fit to a polynomial mixed model.

Fig. 3.

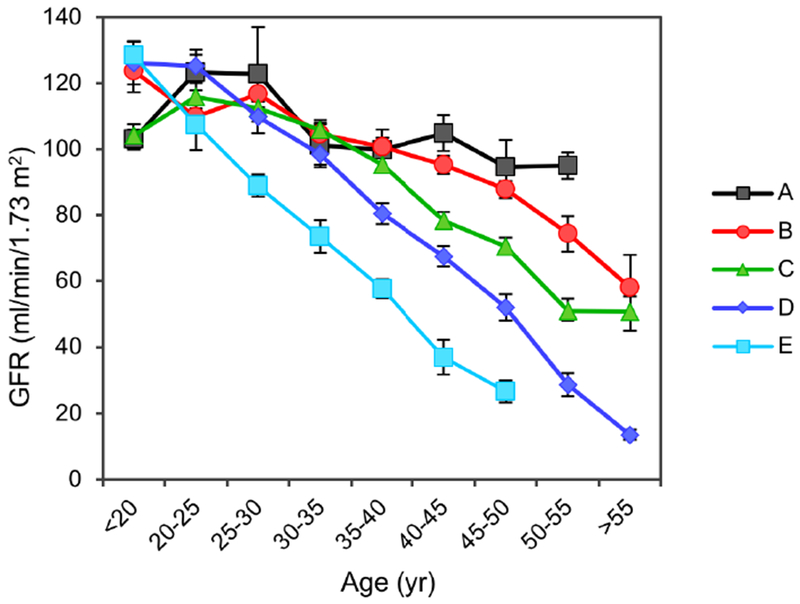
Summary plot of GFR trajectories from the CRISP cohort, divided by Irazabal class, without imposing an arbitrary model. Data points represent mean (± S.E.) GFR for each 5-year range of age.

Because the data within each class depict a curvilinear decline in GFR, we modeled the data with a polynomial model with linear and quadratic terms (red curves in Fig. 2) and a nested linear model without quadratic age term. The quadratic term of age was highly significant (P<0.001) based on the Wald test. A likelihood ratio test between the two nested models yielded a highly significant P-value (P<0.0001) indicating a nonlinear shape of GFR trajectory. The overall model fit was statistically significant (P<0.001), with increasing proportion of variability explained with the higher risk class (Table S1). The model coefficients are listed in Table S2. We also fitted the polynomial model to creatinine-based eGFR trajectories and found very similar results (Fig. S3).

The polynomial model was next used to predict the GFR and GFR slope expected at defined age cut-offs (Table 2). The 95% confidence intervals for most of these estimates are ≤ 20 mL/min/1.73 m², with the exception of Class A. The model predicts that patients with Class E, on average, reach ESRD before age 50 yr. The model also predicts a terminal slope of GFR once it falls below ~45 mL/min/1.73 m² (i.e. CKD stage 3b) that is consistently about −5 to −6 mL/min/1.73 m²/yr.

Table 2.

Predicted GFR values, slopes and paired differences between predicted and observed GFR at different ages using polynomial model

Age (yr)		20-30	30-40	40-50	50-60
Class A	GFR	109 (95-123)	110 (99-121)	97 (83-110)	69 (49-90)
	Slope	0.77	−0.63	−2.03	−3.42
	Diff (SE)	−2.19 (5.56)	−2.27 (11.00)	−4.84 (5.26)	12.19 (2.33)
Class B	GFR	113 (106-120)	108 (103-113)	89 (82-96)	56 (45-67)
	Slope	0.21	−1.19	−2.58	−3.98
	Diff (SE)	6.51 (5.96)	5.77 (3.55)	5.83 (3.88)	−0.06 (7.24)
Class C	GFR	113 (107-119)	101 (96-106)	75 (68-82)	35 (24-45)
	Slope	−0.52	−1.92	−3.32	−4.71
	Diff (SE)	2.39 (5.38)	9.27 (3.98)	8.84 (3.77)	6.42 (5.19)
Class D	GFR	119 (112-125)	92 (87-98)	51 (44-59)	−3.23 (−15.73-9.26)
	Slope	−1.97	−3.37	−4.77	−6.16
	Diff (SE)	4.40 (5.71)	7.00 (4.25)	6.34 (5.26)	21.13 (5.59)
Class E	GFR	103 (97-110)	64 (57-71)	10 (0-21)	0
	Slope	−3.25	−4.65	−6.05
	Diff (SE)	−0.93 (4.94)	1.99 (5.65)	20.27 (6.92)

Units of GFR are mL/min/1.73 m² (95% CI); slopes are mL/min/1.73 m² per year

Diff (SE) are calculated based on the midpoint of age intervals.

Diff = observed GFR - predicted GFR; positive means underestimated

To assess the goodness of fit of the model, we first quantified the model performance by calculating the 1000-fold bootstrapping mean paired differences between the predicted and observed GFR values using the same CRISP data (Table 2). Subjects were divided into groups based on age (<30 yr, 30-40 yr, 40-50 yr and >50 yr) and Irazabal class (A-E). Most paired differences were low (<10 mL/min/1.73 m²) indicating goodness of fit of the polynomial model. For older patients, the paired differences increased, likely due to small sample size (n=4 for >50 yr and class A) and the large variation in patients’ GFR values (Fig. 2).

To validate the model, we used data for patients from HALT PKD Study A. The characteristics of this cohort are similar to the CRISP population, though the patients were slightly older, more often male, and had larger htTKV (Table 1). Fig. 4 shows that the predicted polynomial curve derived from the CRISP cohort provides an accurate representation of the observed data for HALT patients. In later ages (especially for Class D and E), model predictions underestimated the validation data, which may be due to longer follow-up in the CRISP data. The model performance was quantified by determining the mean paired differences between the predicted and observed eGFR values using the coefficients from the CRISP model applied to the HALT A data (Table S3).For two-thirds of the age by Irazabal class categories, the mean differences were < 6 mL/min/1.73 m². For older patients in the higher Irazabal classes (>40 yr for class C and D, >30 yr for class E), the large variability in observed eGFR greatly limited the ability of any model to accurately predict results. Predictions from a polynomial mixed model fit specifically to the HALT A data yielded very similar curves to the CRISP model (data not shown).

Fig. 4.

Validation of the polynomial trajectory model in patients from the HALT study. Individual patient data from HALT Study A are represented by straight lines in different colors. The predicted eGFR trajectory for each Irazabal class, using the model developed with the CRISP cohort, is depicted by the superimposed red curved lines.

Our model can be used to test other variables for their ability to predict the shape and slope of GFR trajectory over the course of adult life in ADPKD patients. As proof of concept, we tested the predictive ability of gene type, defined as the identity of the PKD gene that is mutated. It is well known that patients with PKD1 mutations have faster progression of CKD and reach ESRD earlier in life, compared to patients with PKD2 mutations, or those in which no mutation can be detected (NMD).^15–18 Consistent with this, when gene type was included as a predictor variable in the polynomial trajectory model (Model 1 in Table 3, Fig. 5A), patients with PKD1 mutations were found to have a faster decline in GFR (difference in linear slope of −1.44 mL/min/1.73 m² per year, 95% CI −1.92 to −0.96, P < 0.001) compared to patients with PKD2 mutations or NMD.

Table 3.

Effect of gene type on GFR in polynomial models with and without adjustment for Irazabal class

Variable	Model 1			Model 2
	Coefficient	95% CI	P value	Coefficient	95% CI	P value
Age	2.08	1.02, 3.14	<0.001	5.27	4.05, 6.49	<0.001
Age2	−0.0466	−0.0590, −0.0342	<0.001	−0.0618	−0.0741, −0.0495	<0.001
Gene	40.6	20.6, 60.7	<0.001	25.3	5.77, 44.9	0.011
Gene × age	−1.44	−1.92, −0.96	<0.001	−0.61	−1.08, −0.13	0.012
Class				19.4	12.5, 26.3	<0.001
Class × age				−0.89	−1.07, −0.71	<0.001
Intercept	87.7	62.2, 113.1	<0.001	20.0	−11.8, 51.9	0.218

Outcome is measured GFR in mL/min/1.73 m²

Age is in years

Gene, gene type: PKD1 vs. PKD2 or NMD

Class, Irazabal class: 1A through 1E, coded as 1-5, respectively

Fig. 5.

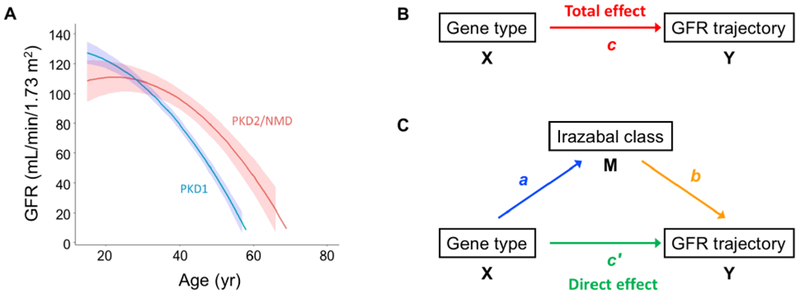
Effect of gene type and test of mediation model. A. Trajectories of GFR estimated from modeling the entire CRISP cohort, using gene type as a predictor variable (Model 1 in Table 3). B. Diagram of unmediated model. C. Diagram of mediated model. X, causal variable; Y, outcome variable; M, mediator variable. Path a represents the association between X and M, and path b the association between M and Y. Path c represents the association between X and Y (total effect), and path c’ represents the association between X and Y after controlling for M (direct effect). The effect mediated by Irazabal class (c-c’), is called the indirect effect and is equal to the product of the coefficients, ab.

Finally, we used this model to determine the mechanism for the gene type effect. There is ample experimental evidence in animal models to suggest that cyst growth can directly cause renal insufficiency. However, the causal link between kidney/cyst growth and decline in GFR in patients with ADPKD has been called into question.¹⁹ To determine whether the effect of gene type on the GFR trajectory is mediated by differences in the rate of kidney growth (as represented by Irazabal class), we performed mediation analysis by the method of Baron and Kenny ²⁰. The four criteria of Baron and Kenny²⁰ were tested as follows (see Fig. 5B, C for nomenclature of the paths):

1. Gene type is associated with GFR trajectory (path c in Fig. 5B)

   This represents the total effect of gene type on GFR. As shown above and in Model 1 in Table 3, the coefficient for [gene × age], c, was −1.44 mL/min/1.73 m² per year.

2. Gene type is associated with Irazabal class (path a in Fig. 5C)

   The proportion of patients with PKD1 mutations increased progressively with more severe Irazabal class (Table S4). The chi-square statistic for this trend is 46.1 (P < 0.0001). For the purpose of the Sobel test, we also fitted a simple linear regression model using Irazabal class as a continuous outcome variable and gene type as a predictor. Results of linear regression agreed with the chi-square test. The coefficient for [gene] is a = 1.19 (95% CI −0.86 to 1.52, P <0.001, Standard error S_a = 0.17), indicating that patients with PKD1 mutations would have 1.19 higher Irazabal class on average, compared to PKD2 or NMD patients.

3. Irazabal class is associated with GFR trajectory after adjusting for gene type (path b in Fig. 5C)

   For the purpose of the mediation analysis, we modeled the whole population using Irazabal class as an ordinal variable and gene type as a covariate, with GFR as the outcome (Model 2 in Table 3, Fig. 6). As expected, Irazabal class is a strong predictor of GFR slope, with a coefficient b = −0.89 (95% CI −1.07 to −0.71, P < 0.001, Standard error S_b = 0.09), indicating that for patients with the same gene type, GFR is predicted to decline faster by 0.89 mL/min/1.73 m² per year, for each consecutive step up in class from A to E.

4. The association of gene type with GFR trajectory is reduced after controlling for Irazabal class (path c’ in Fig. 5C)

   This represents the direct effect of gene type on GFR. The same model as in step 3 (Model 2 in Table 3, Fig. 6) was applied. After adjusting for Irazabal class, the association between gene type and GFR trajectory was reduced albeit still significant. The coefficient for [gene × age] is c’ = −0.61 mL/min/1.73 m² per year (95% CI −1.08 to −0.13, P = 0.01), indicating that within the same Irazabal class, the GFR of patients with PKD1 mutations declined faster by a linear rate of 0.61 mL/min/1.73 m² per year, compared to PKD2 or NMD patients.

Fig. 6.

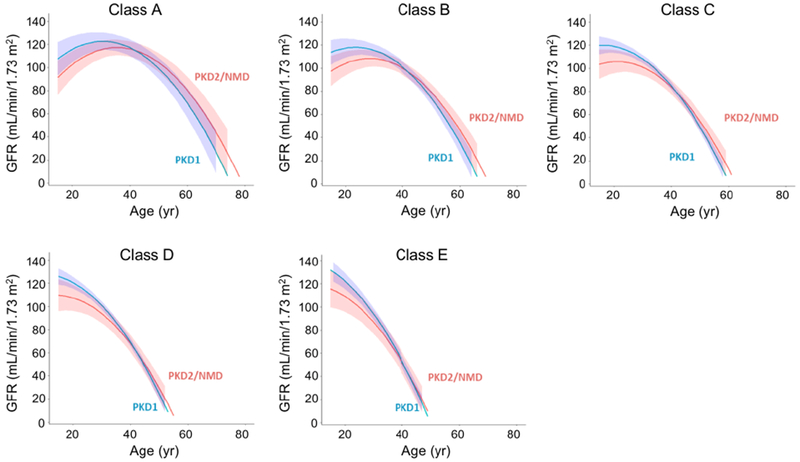
Trajectories of GFR estimated from modeling the entire CRISP cohort, using both gene type and Irazabal class as predictor variables (Model 2 in Table 3).

Our results show that the criteria of Baron and Kenny were fulfilled. The association of gene type with GFR trajectory was reduced after controlling for Irazabal class. The direct effect of gene type was estimated to be −0.61 mL/min/1.73 m² per year, whereas the indirect effect (that which is mediated by Irazabal class, ab) was −1.06 mL/min/1.73 m² per year. A bootstrap Sobel test based on 1000 bootstrap samples of size 235 yielded a p-value less than 0.001. We found similar results when we subclassified the gene type by mutation severity (Table S5, S6). These results indicate that Irazabal class mediates, in part, the causal effect of gene type on GFR trajectory. The proportion of the total effect that is mediated by Irazabal class²¹ was estimated to be 0.73.

DISCUSSION

The basis for this study was the longstanding conjecture that GFR stays constant during childhood and early adulthood due to compensatory glomerular hyperfiltration followed, once the limit of compensation is exceeded, by a constant, rapid decline.²² In this study, we devised a method to reconstruct the long-term trajectory of GFR over the adult lifetime of patients with ADPKD. We found that Irazabal class is a powerful predictor of GFR trajectory. We showed that the GFR trajectory is curvilinear, except in very slow progressors (Class A), in which the GFR appears well preserved at least until the 5th decade of life, and in very fast progressors (Class E), in whom the GFR is already declining even at the earliest observable time point in early adulthood. We confirmed that gene type is a strong predictor of GFR trajectory, with patients with PKD1 mutations having faster GFR decline than those with PKD2 mutations or no mutation detected, and formally showed that this effect is largely mediated by its influence on the rate of kidney growth, represented here by Irazabal class.

Our findings extend the findings of a previous study that showed the utility of Irazabal class as a prognostic biomarker of short-term GFR decline¹³, now demonstrating its association with long-term GFR trends. It is likely that Irazabal class performs better at predicting the overall pattern of disease progression over the lifetime of patients, while kidney volume markers such as htTKV perform better at predicting short-term changes in GFR from a baseline time point, because of a fundamental distinction between these two biomarkers. Irazabal class reflects the rate of disease progression for that patient, while kidney volume is a measure of how far the disease has already progressed at a specific moment in time. Nevertheless, the prognostic accuracy of the current model for individual patients remains poor. The inclusion of additional prognostic factors into a multivariable model would likely improve its accuracy.

The shape of the GFR trajectory that we describe is consistent with what had previously been conceptualized,^22,23 resembling a course of relatively preserved GFR through childhood and early adult life, perhaps due to compensatory glomerular hyperfiltration, followed by a period of rapid, pseudolinear decline. Variations in the rate of disease progression in patients of differing Irazabal class appear to manifest predominantly as variations in the age at which rapid decline begins. By contrast, the rate of decline, once this rapid phase ensues, is fairly constant from patient to patient and averages 5-6 mL/min/1.73 m² per year (Fig. 3 and Table 2). This is fairly close to previous estimates^3,4,7 and confirms the observation that ADPKD kidneys decline faster than CKD from other etiologies.⁷

Our models hint at an early period of hyperfiltration and suggest that the decline in GFR in fast progressors may be preceded by greater hyperfiltration than in slow progressors, but we have insufficient data from childhood and adolescence to observe this directly. Previous studies in children had observed abnormally high GFRs, suggesting that a period of hyperfiltration precedes, and perhaps contributes to, the subsequent progressive decline in GFR later in life, ^5,6 but no study so far has been able to track the trajectory of GFR continuously from childhood to adulthood.

We have used mediation analysis to address the question of whether cyst and kidney growth is in the pathogenic pathway leading to loss of kidney function (i.e. GFR) and CKD. There is considerable evidence, particularly from animal models, showing that cyst growth causes local and distant kidney injury, for example by obstructing tubules and compromising vascular blood flow, leading to nephron loss.^22,24 However, it is also conceivable that PKD mutations could activate signaling pathways that directly lead to inflammation, immune infiltration, fibrosis, nephron injury and loss, independently of cyst growth. A causal link between cyst growth (which is tracks closely with growth in TKV) and loss of GFR has been called into question¹⁹ because several clinical trials have shown an apparent dissociation between improvement in the rate of change of TKV and GFR, most notably in the everolimus trial.²⁵ In part on the basis of this evidence, drug regulatory agencies such as the U.S. Food and Drug Administration have refused to accept TKV as a validated surrogate endpoint for approval of drugs for the treatment of ADPKD.

To address this we tested the hypothesis that the association between gene type and GFR trajectory (or more specifically GFR slope) is mediated by kidney size relative to age (represented by Irazabal class). Gene type is associated with GFR slope and risk of CKD and the direction of the causal relationship is known a priori. This allowed us to use the method of Baron and Kenny and bootstrapping Sobel test to demonstrate mediation and show that the effect size is large. The proportion of the total effect of gene type that is mediated by Irazabal class is 0.73. Our findings support the assertion that PKD mutations cause loss of GFR predominantly by affecting kidney size.

Our study has many strengths. CRISP is the longest prospectively studied cohort with TKV data determined rigorously by MRI, and GFR measured by iothalamate clearance. So although we reconstructed trajectories from multiple patients to span 4 decades of adult life, the median duration of individual patient trajectories was itself remarkably long at 13.0 years. GFR was determined both by iothalamate clearance and by creatinine-based eGFR estimation, and we were able to corroborate the results of one with the other. Our model predictions match quite well with the observed data in our validation cohort from the HALT study, except in the oldest patients with rapidly progressive disease that have not yet reached ESRD. Finally, our study is the first to use mediation analysis to demonstrate statistically a causal link between changes in TKV and GFR in patients with ADPKD.

The main limitation of the study is that trajectories were reconstructed indirectly from multiple patients rather than by direct observation of individual patients over their entire adult life. Unfortunately the latter is not currently feasible given the follow-up duration of existing patient cohorts, and so the method we devised to stratify the patients represents the best approach to date to visualize ADPKD GFR trajectories. A further limitation is that for rapid progressors who are older but have not yet reached ESRD (>40 yr for class C and D, >30 yr for class E), the model accuracy is quite limited.

In conclusion, the long-term trajectory of GFR in ADPKD follows a curvilinear pattern with accelerating decline in later life. The size of kidneys as a function of age, as determined by Irazabal class, is a strong predictor of the shape and slope of this trajectory. Predictions of GFR using this model can be used now for prognostication at a population level and hopefully refined in the future for individual patient prediction. These models will also facilitate design and planning of clinical trials, and selection of patient populations for therapy. Our finding that the effect of PKD gene type on GFR slope is mediated by the kidney volume factored for age consolidates the causal link between TKV growth and GFR decline, adding support for the use of TKV as a surrogate endpoint in clinical trials.

METHODS

Patient population

The development cohort was derived from 241 patients with ADPKD, aged 15 to 46 years with a creatinine clearance of at least 70 ml/min, that were enrolled in the CRISP study between 2001 and 2002 and followed through September 2015 (Table 1).^2,26 The validation cohort was drawn from 558 patients in HALT PKD Study A, a randomized controlled trial of the effects of intensive blood pressure control and dual renin-angiotensin system blockade.²⁷ TKV was determined from coronal T1- and T2-weighted MRI using a stereologic method,^26,28,29 and corrected for height (htTKV, ml/m). Patients that had atypical imaging characteristics for ADPKD were excluded. The rest (237 in CRISP, 521 in HALT) were classified according to their kidney size for their age into subclass A-E by the method of Irazabal.¹³ GFR was measured by iothalamate clearance in CRISP, and estimated from serum creatinine using the CKD-EPI equation in both studies. Both cohorts were classified for PKD1 and PKD2 mutations by genotyping as described previously.¹⁸ The NMD group contains a single GANAB and DNAJB11 patient. The studies were approved by the institutional review board at each site.

Fitting to GFR trajectory models

The models were developed by fitting GFR trajectories of patients from CRISP to a polynomial model with linear and quadratic terms, using a mixed models framework with a random effect for the subject and fixed effects for all covariates. The likelihood ratio was used to test whether overall model fit was different from chance. To test the association of gene type and Irazabal class with GFR trajectory, polynomial mixed models were fitted to the entire cohort of 237 patients, and gene type and Irazabal class were included as predictor variables. Irazabal class was treated as a continuous variable (1 for Class A, 2 for Class B, 3 for Class C, 4 for Class D and 5 for Class E). Each predictor variable was modeled as a main effect and an interaction with age². Likelihood ratio test was also performed for model comparison between linear and polynomial models. To assess the goodness of fit, the model was then used to predict the CRISP data. The CRISP subjects were first divided into groups based on age and Irazabal class. Then, the estimated paired difference between the predicted and observed GFR values for each subject was calculated using bootstrap analysis with 1000-fold replacement.

For the validation analysis, the models fit to CRISP with eGFR data as the outcome were used to calculate predictions for the subjects from the HALT A data. To describe the resulting prognostic accuracy, the HALT subjects were divided into groups based on age and Irazabal class, and the estimated paired difference between the predicted eGFR values and observed values from HALT data for each subject, was calculated using bootstrap analysis with 1000-fold replacement.

Mediation analysis

To test whether the effect of gene type on GFR trajectory was mediated by Irazabal class, the four-step procedure of Baron and Kenny was used.²⁰ In the mediation model, the causal variable, X, was gene type. The outcome of interest, Y, was GFR trajectory, which we defined as the GFR slope as a linear function of age (i.e. the coefficients for [age] and [predictor variable × age] interaction terms). Irazabal class was the mediating variable, M. Age² was included as per the polynomial model, but because [gene × age²] and [class × age²] were not statistically significant according to the likelihood ratio test, the coefficients for these quadratic interaction terms were not used for mediation analysis. We reported the direct effect (c’), indirect effect (ab) and the proportion of the total effect mediated by Irazabal class. The proportion was estimated as 1 - (direct effect) / (total effect), or 1 - c’ / c²¹ To test the significance of indirect effect of mediator Irazabal class, a bootstrapping Sobel test was performed. Please see Supplemental Material for additional details of the method.

Supplementary Material

1

Fig. S1. Strategy for visualization of ADPKD GFR trajectories. A. The gray dotted line depicts a theoretical trajectory of GFR over the adult lifetime of an ADPKD patient. A single longitudinal period of observation, even one with as long follow-up as CRISP (13 years, red line), is inadequate to capture the shape and course of the trajectory over the entire natural history of the disease. B. An extended trajectory could be reconstructed by stitching together short, individual GFR trajectories derived from multiple individuals studied at different ages (3 colored lines). C. Because of interindividual variability in the rate of disease progression, represented here by three trajectories with different courses (dotted lines), aggregate data for the whole population is difficult to interpret. If patients can be stratified by a biomarker associated with the rate of disease progression, then the GFR data within each strata or subgroup would be expected to cluster together (red, blue and green lines) and could be used to reconstruct extended trajectories representative of the disease course for each subgroup.

8

Table S3. Paired differences between the predicted eGFR values based on the CRISP model and the observed data in the HALT validation cohort

9

Table S4. Distribution of gene type among Irazabal classes in the CRISP cohort

10

Table S5. Effect of gene mutation, classified into four categories, on GFR in polynomial models with and without adjustment for Irazabal class

11

Table S6. Distribution of gene mutations among Irazabal classes in the CRISP cohort

2

Fig. S2. Trajectories of GFR plotted against age for the entire eligible cohort in CRISP (n=237). Each line in a single color represents an individual patient, and the gray dots represent actual GFR data points.

3

Fig. S3. Trajectories of eGFR from the CRISP cohort, determined by the creatinine-based CKD-Epi equation, subgrouped by Irazabal class and fit to polynomial models.

4

Supplementary Methods

5

Supplementary References

6

Table S1. Goodness of fit of polynomial GFR trajectory model

7

Table S2. Coefficients for the polynomial model