On-chip cell mechanophenotyping using phase modulated surface acoustic wave

Abstract

A surface acoustic wave (SAW) microfluidic chip was designed to measure the compressibility of cells and to differentiate cell mechanophenotypes. Polystyrene microbeads and poly(methylmethacrylate) (PMMA) microbeads were first tested in order to calibrate and validate the acoustic field. We observed the prefocused microbeads being pushed into the new pressure node upon phase shift. The captured trajectory matched well with the equation describing acoustic radiation force. The compressibility of polystyrene microbeads and that of PMMA microbeads was calculated, respectively, by fitting the trajectory from the experiment and that simulated by the equation across a range of compressibility values. Following, A549 human alveolar basal epithelial cells (A549 cells), human airway smooth muscle (HASM) cells, and MCF-7 breast cancer cells were tested using the same procedure. The compressibility of each cell from the three cell types was measured also by fitting trajectories between the experiment and that from the equation; the size was measured by image analysis. A549 cells were more compressible than HASM and MCF-7 cells; HASM cells could be further distinguished from MCF-7 cells by cell size. In addition, MCF-7 cells were treated by colchicine and 2-methoxyestradiol to disrupt the cell microtubules and were found to be more compressible. Computer simulation was also carried out to investigate the effect of cell compressibility and cell size due to acoustic radiation force to examine the sensitivity of the measurement. The SAW microfluidic method is capable of differentiating cell types or cells under different conditions based on the cell compressibility and the cell size.

I. INTRODUCTION

Cell mechanobiology is an approach to describe how the mechanical properties of cells affect or reflect biological activities, such as understanding cell function or identifying the impacts of human disease at the cellular level.^1–3 Cell mechanophenotyping is one of the key aspects of cell mechanobiology. The mechanical properties of cells have been used to examine and differentiate cells from healthy donors or patients, and different cell types.^4–6 For example, the abnormalities in the mechanical properties of red blood cells were impacted by sickle cell anemia⁷ and malaria.^8,9 Moreover, circulated tumor cells in the process of metastasis showed distinct mechanophenotype compared with those in the primary tumor.^10–12 These studies highlighted the importance of the mechanical properties of cells, which could be exploited in single-cell bioassay for diagnostic applications.

Conventional methods for measuring the mechanical properties of single cell have been well established, such as atomic force microscopy (AFM), optical tweezer, and micropipette aspiration.^13–19 However, these methods are limited by high equipment cost, time-consuming protocol, and low throughput. For example, micropipette aspiration requires a well-trained experimenter to look into the eyepieces of microscope, operate multiple devices until the micropipette tip contacts the cell membrane, adjust the suction pressure, record a stack of images, and postprocess data, which makes it difficult to use.²⁰

In contrast, several emerging microfluidic techniques have been proposed that are low in cost with higher throughput for measuring the mechanical properties of cells. Such techniques include microfluidic devices that deform the cells by either mechanical constraint or hydrodynamic stress, i.e., passive microfluidics, while few studies have incorporated an active external field into the microfluidic devices to increase the potential, versatility, and functionality, i.e., active microfluidics.^21–24 Acoustophoretic microfluidics is one of the active methods combining the application of an acoustic field with microfluidics. A commonly used acoustophoretic microfluidic method is the bulk acoustic wave (BAW), generated using a piezo-ceramic transducer (PZT), that travels across the bulk volume of the material (such as silicon or glass) from the PZT side to the other side comprising the fluid domain. BAW has been used to measure the cell’s bulk modulus and compressibility,^25–27 enrich cell subpopulations,²⁸ and separate different cell types.^29,30 Recently, a size-independent BAW device was built based on inhomogeneous fluid with acoustic contrast gradient and measured the mechanophenotypes of cell lines and leukocytes.³¹ However, a key limitation with BAW is the reliance on the resonation from the microfluidic channel sidewalls, which restricts the allowable width of the channel to a multiple of λ/2 (where λ is the wavelength) and the microfluidic channel material must be acoustic-reflective (for example, silicon or glass).^29,32 Furthermore, the restrictions on the width of the channel limit the geometry of the channel, the position and modality of the pressure node, and, therefore, the flexibility of the design. The restrictions on the microfluidic channel material prohibit the usage of the acoustically absorbent polydimethylsiloxane (PDMS), which is widely used in microfluidic applications because of its transparency and ease to fabricate.³³

In order to overcome this limitation, a different method to generate and propagate acoustic wave was introduced, i.e., surface acoustic wave (SAW), where acoustic wave propagates along the surface of the piezoelectric substrate immediately adjacent to the fluid domain.^33–35 SAW does not constrain the material or the geometry of the microfluidic channel, because the acoustic field is formed on the piezoelectric substrate independently of the microfluidic channel. The independent formation of acoustic field in SAW applications results in higher flexibility to shape and adapt the acoustic field, such as tunable frequency and versatile pressure nodal position, thereby improving the performance to manipulate particles and examine the property of particles.^36–38 To date, most of the surface acoustic wave (SAW) microfluidic applications focused on droplet manipulation,³⁹ particle focusing,⁴⁰ cell patterning or manipulation,^37,41–43 and size-based separation of particles or cells.^38,44–46 However, few studies have incorporated the compressibility measurement of cells into SAW microfluidics.^33,47

In this study, a SAW microfluidic device was developed to measure the compressibility of cells and also to differentiate cell mechanophenotype based on the compressibility and the cell size. Microbeads of known mechanical properties were used to calibrate the device and measure compressibility. It was further used to characterize A549 human alveolar basal epithelial cells (A549 cells), human airway smooth muscle (HASM) cells (HASM cells), and MCF-7 breast cancer cells based on the compressibility and the cell size. In addition, MCF-7 cells treated by colchicine and 2-methoxyestradiol, respectively, that destroyed the microtubules were tested and compared with the non-treated MCF-7 cells in terms of cell compressibility and cell size.

II. METHOD

A. Fabrication and experimental setup

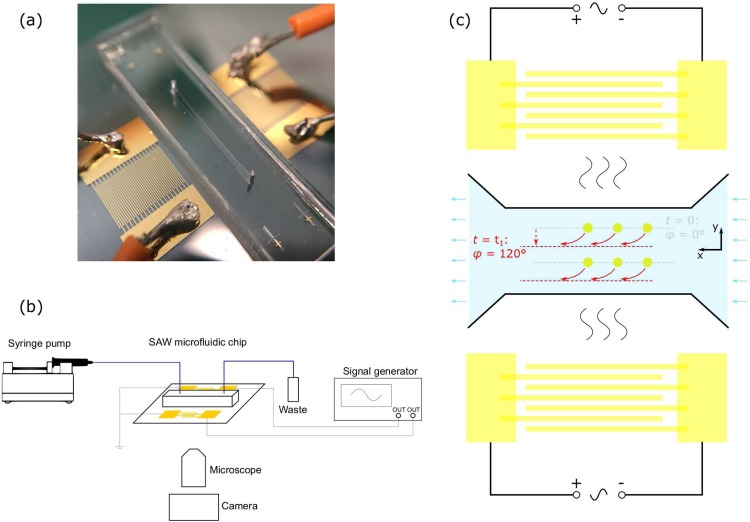
The fabrication process of the microfluidic chip is demonstrated in the supplementary material. The microfluidic chip is built from two identical interdigital transducers (IDTs) on the LiNbO₃ substrate, with a polydimethylsiloxane (PDMS) microchannel located between the two IDTs. The width of the microchannel is 450 μm and the height is 40 μm. The IDTs have an aperture of 4 mm and fingers of 75 μm in width and 75 μm in spacing between neighboring fingers. Thus, the fingers of IDT have a period of 300 μm, resulting in a resonant frequency of 12.8 MHz. The frequency was chosen to ensure relatively large wavelength and therefore long travel distance of particles. The experimental setup is shown in Fig. 1(b). A signal generator (DG-4102, RIGOL) inputs two MHz-frequency sinusoidal signals to the two IDTs. The SAW microfluidic chip is placed on a microscope (IX51, Olympus) with a digital monochrome camera (BM-141GE, JAI cameras). A syringe pump (Legato 180, KD Scientific) is used to inject the sample into the SAW microfluidic chip.

FIG. 1.

(a) Image of the SAW microfluidic chip with two identical interdigital transducers (IDTs) on the LiNbO₃ substrate and a polydimethylsiloxane (PDMS) microchannel between the two IDTs. (b) Schematic of the experimental setup. (c) Schematic of the SAW microfluidic chip and its working mechanism. When t = 0, two input signals are synchronized (relative phase φ = 0), and particles are initially prefocused at the pressure node (gray line). When t = t₁, the phase of one IDT is shifted by 120° (relative phase φ = 120°), and the pressure node is immediately translated to a new nodal line (red line), and all the prefocused particles are moved to the new nodal line.

B. Methodology for measuring compressibility

Upon applying two synchronized sinusoidal signals of the same frequency on the IDTs (i.e., the relative phase φ = 0), a standing acoustic wave is generated and therefore pressure interference is formed inside the fluid domain. Consideration should be given to the difference between the BAW half-wavelength resonator and our device. In our study, PDMS was used instead of silicon or glass. The reflection at the interface of PDMS and liquid can be considered as negligible, as it has been reported that the calculated reflection coefficient of PDMS/water is 4%.⁴⁸

The acoustic radiation force pushes and prefocuses particles inside the fluid domain toward the pressure node [gray line in Fig. 1(c)]. Once the particles appear in the center of the field of view, the phase of one IDT is shifted by 120° (i.e., the relative phase φ = 120°) so that the pressure node is immediately translated to a new nodal line [red line in Fig. 1(c)]. All the prefocused particles are moved to the new nodal line, where the motion of the particles inside the microfluidic channel is driven by both acoustic radiation force F_r and Stokes drag force F_drag. The governing equation is

$$F_r+F_{drag}=ma,$$ (1)

where F_r denotes the acoustic radiation force in a vector form, F_drag denotes the Stokes drag force in a vector form, m denotes the mass of the particle, and a denotes the acceleration in a vector form.

The equation describing the acoustic radiation force on a compressible sphere as applied to progressive or standing acoustic waves was proposed by Yosioka and Kawasima,⁴⁹ where the magnitude of acoustic radiation force F_r in the standing acoustic field is defined as

$$F_r=F_r(y)=-\frac{\pi {\displaystyle \frac{\alpha P_I{\rho }_s{c}_s}{A_w}{V}_p{\beta }_m}}{2\lambda }\times \left(\frac{5{\rho }_P-2{\rho }_m}{2{\rho }_P+{\rho }_m}-\frac{{\beta }_P}{{\beta }_m}\right)\times \sin (2ky),$$ (2)

where ρ_P, β_P, and V_P denote the density, the compressibility, and the volume of the particle, respectively; ρ_m and β_m denote the density and the compressibility of the medium, repectively; ρ_s and c_s denote the density and the acoustic velocity within the substrate, respectively; y denotes the distance away from the pressure node and y = 0 coincides with the pressure node; λ and k denote the wavelength and the wavenumber of acoustic wave, respectively; P_I denotes the input power to the IDT; A_w denotes the working area of IDT; and α denotes the energy coefficient.

Assuming that the particles are of spherical shape, the well-known Stokes drag force is applied to calculate the interaction between fluids and particles

$$F_{drag}=-6\mu \pi R{v}_{rel},$$ (3)

where μ denotes the dynamic viscosity; R denotes the radius of the particle; and v_rel denotes the particle velocity relative to that of the flow.

The motion of particles toward the new pressure nodal line was captured via the camera, and the video data were analyzed by Motion Studio (Integrated Design Tool Inc.) tracking the trajectory within the image sequence. A custom Matlab (R2017a, MathWorks) program was written to simulate the trajectory by solving Eqs. (1)–(3) and compare it with the captured trajectory. To calibrate and validate the acoustic field, the SAW microfluidic chip was first tested by polystyrene microbeads with a diameter of 3 μm (Sigma-Aldrich), polystyrene microbeads with a diameter of 10 μm (Magsphere), and PMMA microbeads with a diameter of 10 μm (PolyAn). This is made possible because of the known physical properties of the microbeads, which are summarized in the supplementary material. The energy coefficient α in Eq. (2), i.e., the only unknown parameter, was calibrated when the error between the experimental and theoretical trajectory reached the minimum (see the supplementary material). Once calibrated, the theoretical trajectory was simulated and compared with the experimental trajectory.

Following, A549 human alveolar basal epithelial cells (A549 cells), human airway smooth muscle (HASM) cells, and MCF-7 breast cancer cells were tested using the same procedure. In order to calculate the compressibility of these cells based on Eq. (2), it would require the density value of these cells. Unfortunately, there are no published data of single-cell density of the cell types in this study. However, there are few studies that have examined single-cell density such as Anderson et al., who measured the density of Chinese hamster ovary (CHO) epithelial cells during different cell cycles using buoyant balance in solution with density gradient and concluded that the average density was 1051 ± 3 kg m⁻³.⁵⁰ Bryan et al. measured the single-cell density of H1650 human lung cancer cells and L1210 mouse lymphoblastic leukemia cells using suspended microchannel resonator (SMR) and obtained values ranging from 1040 kg m⁻³ to 1070 kg m⁻³.⁵¹ In this study, we assumed a constant cell density of 1050 kg m⁻³. The compressibility of cell β_p was therefore the only unknown parameter that could be calculated by fitting the theoretical trajectory with the experimental trajectory.

Finally, MCF-7 cell’s compressibility was measured when treated with drugs that disrupt the cell’s microtubules, which are responsible for maintaining the cell’s mechanical structure and compressibility.^52–55 Microtubule-disruptors, colchicine⁵⁶ and 2-methoxyestradiol,⁵⁷ were added to MCF-7 cells, respectively, to alter the condition of cells. The treated group and the nontreated control group were tested using the same procedure.

C. Cell culture

1. A549 cell and MCF-7 cell

The type II alveolar epithelium-derived adenocarcinoma cell line A549 [American Type Culture Collection (ATCC), VA] was cultured in complete DMEM medium [containing 10% (v/v) HIFCS, 2 mM l-glutamine, 1% (v/v) nonessential amino acids, 1% (v/v) sodium pyruvate, 0.2% (v/v) sodium bicarbonate, 15 mM HEPES, 100 IU/ml penicillin, and 50 μg/ml streptomycin]. MCF-7 human breast adenocarcinoma cell line was cultured in complete DMEM medium [containing 10% (v/v) HIFCS, 15 mM HEPES, 1% (v/v) l-glutamine, 1% (v/v) nonessential amino acids, 1% (v/v) sodium pyruvate, 100 IU/ml penicillin, and 50 μg/ml streptomycin]. Both cell lines were kept at 37 °C in a humidified atmosphere containing 5% CO₂. The cells were passaged twice weekly by washing confluent cell monolayers twice with PBS and then incubated with trypsin (0.12% w/v) for 5 min or until cells were in suspension.

2. Human airway smooth muscle (HASM) cell

The human airway smooth muscle cells were generated from the bronchi resected from heart-lung transplant recipients that were provided by the Alfred Hospital and the Royal Melbourne Hospital (Melbourne, Victoria, Australia). The dissected airway smooth muscle was incubated with filtered elastase (Worthington Elastase, 1 mg ml⁻¹) for approximately 3 h, followed by incubation with collagenase (Worthington Collagenase Type II, 1 mg ml⁻¹) at 37 °C overnight. The cells were isolated from centrifugation (5 min, 1000 × g, 4 °C), washed with phosphate buffered saline (PBS), and resuspended in complete DMEM medium. The resultant cell suspension was transferred into a sterile 25 cm² culture flask and allowed to grow to confluency (approximately 7–10 days) in a 37 °C incubator with 5% CO₂.

3. Drug treatment

Both colchicine and 2-methoxyestradiol were used at 10 μM. After adding the drugs, cells were left in the 37 °C incubator with 5% CO₂ for 3 h, washed with PBS, trypsinized, and suspended in solution prior to the experiment. The cell solution was in the concentration of around 400 000/ml, allowing around 5 cells in the field of view at one time.

III. RESULTS

A. Microbead focusing and compressibility measurement

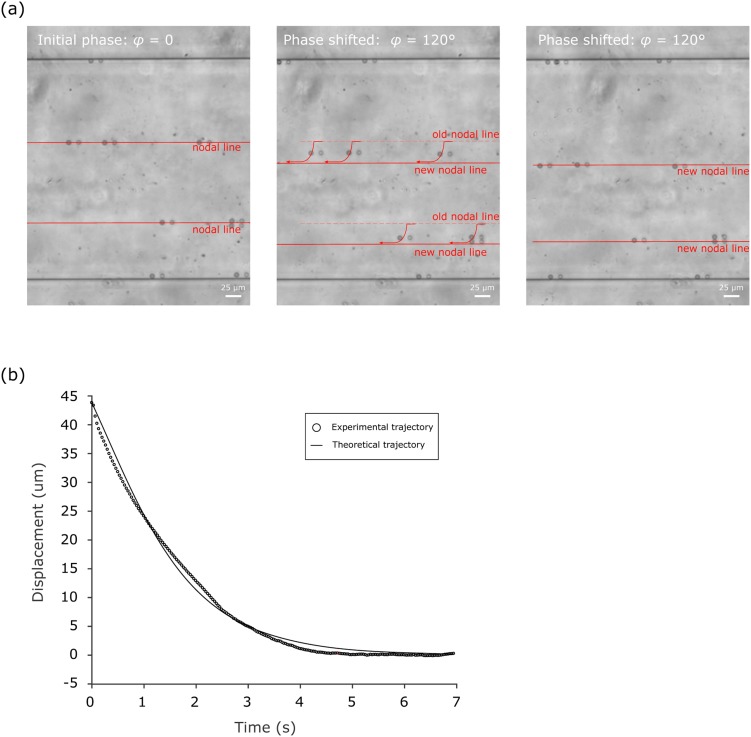
To observe the SAW phenomenon and to validate the SAW device, polystyrene microbeads with a diameter of 10 μm were injected into the SAW microfluidic chip. The signal generator produced a sinusoidal waveform with a frequency of 12.8 MHz and an amplitude of 12V_p-p that were then transmitted to the two IDTs. The polystyrene microbeads were first prefocused, and once the relative phase φ was shifted from 0° to 120°, the microbeads moved to the new nodal line due to the phase modulation [Fig. 2(a)]. These observations validate the existence of the standing acoustic wave and its capability of phase modulation in the SAW microfluidic chip, which moved the microbeads toward the new pressure node.

FIG. 2.

(a) Image of 10-μm polystyrene microbeads inside the SAW microfluidic chip moving from the old pressure nodal line to the new pressure nodal line, upon phase shifting from φ = 0 to φ = 120°. (b) Experimental trajectory and theoretical trajectory of the microbead moving toward the pressure node.

The trajectory on which microbeads were pushed toward the new pressure node, represented in displacement vs time, was imported into Matlab and compared with the theoretical trajectory. Since the acoustic radiation force F_r is along the y-direction [Fig. 1(c)], only the lateral displacement (i.e., displacement along the y-direction) vs time was considered, while the motion along the x-direction is constant and similar to the fluid flow. Once the energy coefficient α was calibrated (see the supplementary material), we compared all the experimental trajectories with their corresponding theoretical trajectories and found that they were closely matched with a fitting residual error of 1.22 μm (defined as the root mean square of the difference between the experimental displacement and the simulated displacement). The relative error, the ratio of the fitting residual error to the total displacement, was 2.8%, indicating a good reliability of the measuring methodology [Fig. 2(b)].

To demonstrate the ability to measure compressibility using SAW, the experiments were repeated with polystyrene microbeads of 3 μm in diameter, polystyrene microbeads of 10 μm in diameter, and poly(methylmethacrylate) (PMMA) microbeads of 10 μm in diameter. Assuming that the compressibility of microbeads was unknown, we calculated the compressibility of each group of microbeads in order to examine the accuracy. The measured compressibilities are 2.12 ± 0.21 × 10⁻¹⁰ Pa⁻¹ (n = 40) for 3-μm polystyrene microbeads, 2.23 ± 0.28 × 10⁻¹⁰ Pa⁻¹ (n = 27) for 10-μm polystyrene microbeads, and 1.68 ± 0.21 × 10⁻¹⁰ Pa⁻¹ (n = 20) for 10-μm PMMA microbeads. They are, respectively, consistent with the polystyrene compressibility 2.16 × 10⁻¹⁰ Pa⁻¹ used in the calibration,³⁸ the polystyrene compressibility reported from the literature ranging from 2.1 to 2.4 × 10⁻¹⁰ Pa⁻¹,^25,58 and the PMMA compressibility reported from the literature, that is 1.73 × 10⁻¹⁰ Pa⁻¹.⁵⁹

B. Compressibility measurement of different cell types

To establish the compressibility from cells and distinguish the mechanophenotypes of different cell types, A549 human alveolar basal epithelial cells (A549 cells), human airway smooth muscle cells (HASM cells), and MCF-7 breast cancer cells were tested in the SAW microfluidic chip. A549 and HASM were chosen due to their similarity in sizes and their locations being found in the human respiratory system. MCF-7 cells were selected because they are larger than A549 and HASM in size. Both the setup and procedure were similar to the microbead experiment, except that cells instead of microbeads were used. The cells were injected by the syringe pump, and prefocused at the initial pressure node by two signals with a frequency of 12.8 MHz, an amplitude of 20V_p-p (for A549 and HASM cells) or 12V_p-p (for MCF-7 cells) and zero relative phase (φ = 0). Once cells appeared in the center of the field of view, the relative phase of acoustic wave was shifted to φ = 120°. We observed that the cell was pushed from the initial pressure node to the new pressure node by the acoustic radiation force [Fig. 3(a)].

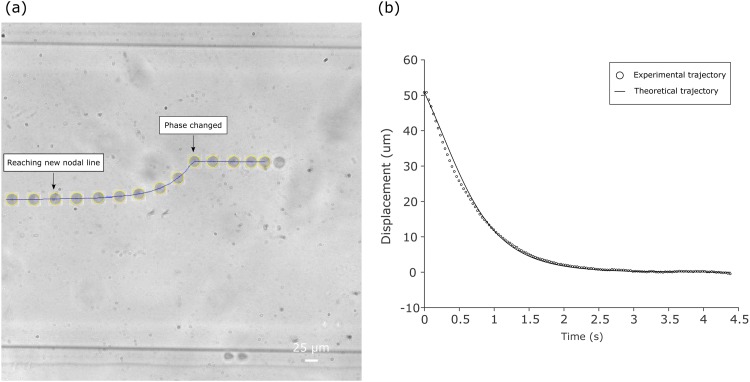
FIG. 3.

(a) Overlapped image at different time while the cell was pushed toward the new pressure node upon phase shifting. (b) Experimental trajectory and theoretical trajectory of the cell moving toward the pressure node.

Once the trajectory traveling to the pressure node and the size of the cell were captured and recognized, respectively, we fitted the theoretical trajectories with the experimental trajectories using cell compressibility as the fitting parameter. The theoretical trajectories matched well with the experimental trajectories for each cell types. The fitting residual error was 1.43 μm for A549 cells, 1.26 μm for HASM cells, and 1.10 μm for MCF-7 cells; the relative error was 2.6% for A549 cells, 2.3% for HASM cells, and 2.0% for MCF-7 cells.

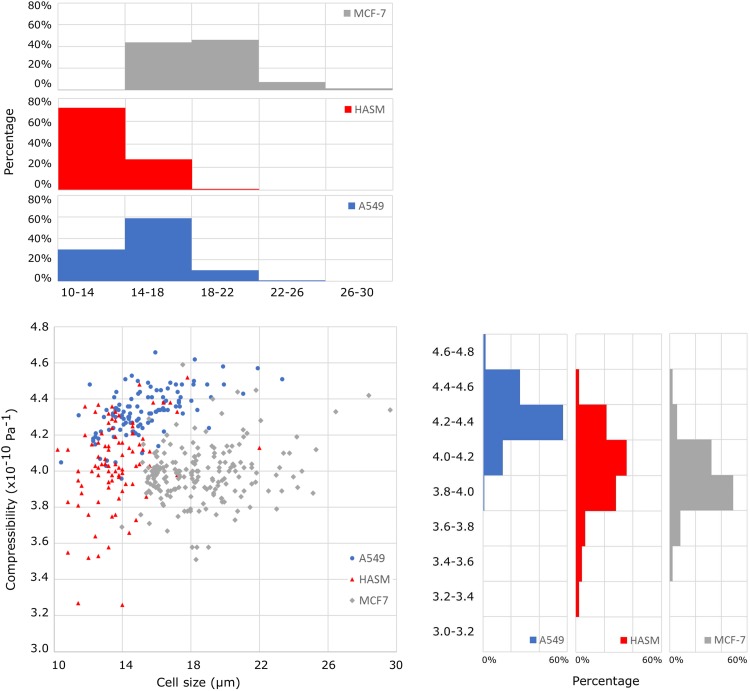
The compressibility and size of each cell were also obtained from these experiments. The measured compressibility was A549: 4.33 ± 0.13 × 10⁻¹⁰ Pa⁻¹ (n = 114), HASM: 4.04 ± 0.24 × 10⁻¹⁰ Pa⁻¹ (n = 93), and MCF-7: 3.99 ± 0.16 × 10⁻¹⁰ Pa⁻¹ (n = 191). The cell size was A549: 15.2 ± 2.2 μm (n = 114), HASM: 13.6 ± 1.7 μm (n = 93), and MCF-7: 18.7 ± 2.8 μm (n = 191). By comparing these values, A549 and HASM cells were similar in size but distinguished by compressibility (p < 0.001, Student's unpaired t-test), while HASM and MCF-7 cells were similar in compressibility but distinguished by size (p < 0.001). The SAW microfluidic chip was able to distinguish the cell types based on either compressibility or cell size or both. The relationship between compressibility and cell size (Fig. 4) also demonstrates that the three cell types are further differentiated when setting compressibility and cell size as two metrics of cell mechanophenotype. Each cell type populates different regions of the graph and the distributions of compressibility or cell size are differed among cell types. For example, A549 cells are broadly distributed in terms of cell size but narrowly in terms of compressibility; the converse pattern was observed for HASM cells. These distinctions cannot be appreciated when only considering compressibility. Therefore, the combination of the measured compressibility and cell size sheds additional light on the mechanophenotypic difference among the three cell types.

FIG. 4.

Compressibility vs cell size for A549, HASM, and MCF-7 cells. The compressibility is measured for A549: 4.33 ± 0.13 × 10⁻¹⁰ Pa⁻¹ (n = 114), for HASM: 4.04 ± 0.24 × 10⁻¹⁰ Pa⁻¹ (n = 93), and for MCF-7: 3.99 ± 0.16 × 10⁻¹⁰ Pa⁻¹ (n = 191); the cell size is measured for A549: 15.2 ± 2.2 μm (n = 114), for HASM: 13.6 ± 1.7 μm (n = 93), and for MCF-7: 18.7 ± 2.8 μm (n = 191).

C. Compressibility measurement of cells under different conditions

To establish the capability of distinguishing the mechanophenotypes of the same cell type but under different conditions, MCF-7 cells were treated with colchicine and 2-methoxyestradiol, which are known to disrupt microtubules in the cells.^56,57 Both treated group and the corresponding control group were tested in the SAW microfluidic chip using the same procedure, where two signals with a frequency of 12.8 MHz and an amplitude of 12V_p-p were phase-shifted in order to move the cells and measure the compressibility from the motion.

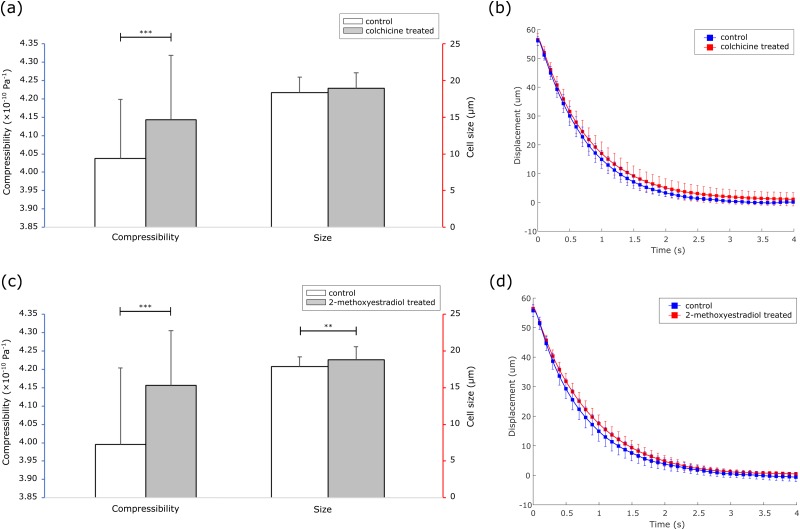
Colchicine treatment increased the cell compressibility from 4.04 ± 0.16 × 10⁻¹⁰ Pa⁻¹ (n = 62) to 4.14 ± 0.18 × 10⁻¹⁰ Pa⁻¹ (n = 75) (p < 0.001), but it did not affect the cell size when comparing the control and the colchicine treated groups, 18.4 ± 2.1 μm (n = 62) vs 18.9 ± 2.2 μm (n = 75) (p = 0.13) [Fig. 5(a)]. 2-Methoxyestradiol treatment increased the cell compressibility from 3.99 ± 0.21 × 10⁻¹⁰ Pa⁻¹ (n = 66) to 4.16 ± 0.15 × 10⁻¹⁰ Pa⁻¹ (n = 74) (p < 0.001), and it also increased the cell size from 17.9 ± 1.3 μm (n = 66) to 18.8 ± 1.8 μm (n = 74) (p < 0.01) [Fig. 5(c)]. The increase in compressibility agrees with the assumption that cells become more compressible after destroying microtubules and demonstrates the capability of the SAW microfluidic chip in detecting the changes in cell conditions.

FIG. 5.

(a) Compressibility and size of MCF-7 cells before and after colchicine treatment. (b) Average trajectory of control and colchicine treated groups, represented as displacement vs time. (c) Compressibility and size of MCF-7 cells before and after 2-methoxyestradiol treatment. (d) Average trajectory of control and 2-methoxyestradiol treated groups, represented as displacement vs time. Please note that ** denotes p < 0.01 and *** denotes p < 0.001, using two-tailed t-test.

By plotting displacement vs time with the average displacement as each data point, we noted that the treated groups for both drugs moved slower than its control group because of higher compressibility [Figs. 5(b) and 5(d)]. The travel time, which is the time that each cell took to travel to the pressure node, of control and colchicine treated groups were 2.7 ± 0.4 s (n = 62) and 3.3 ± 0.5 s (n = 75), while the travel time of control and 2-methoxyestradiol treated groups were 2.8 ± 0.4 s (n = 66) and 3.1 ± 0.4 s (n = 74). The slope of the trajectories of both control groups was, respectively, steeper than that of the corresponding treated group, indicating that the acoustic radiation force was reduced after drugs destroyed the microtubules in the cells.

D. Theoretical sensitivity study of cell compressibility and cell size

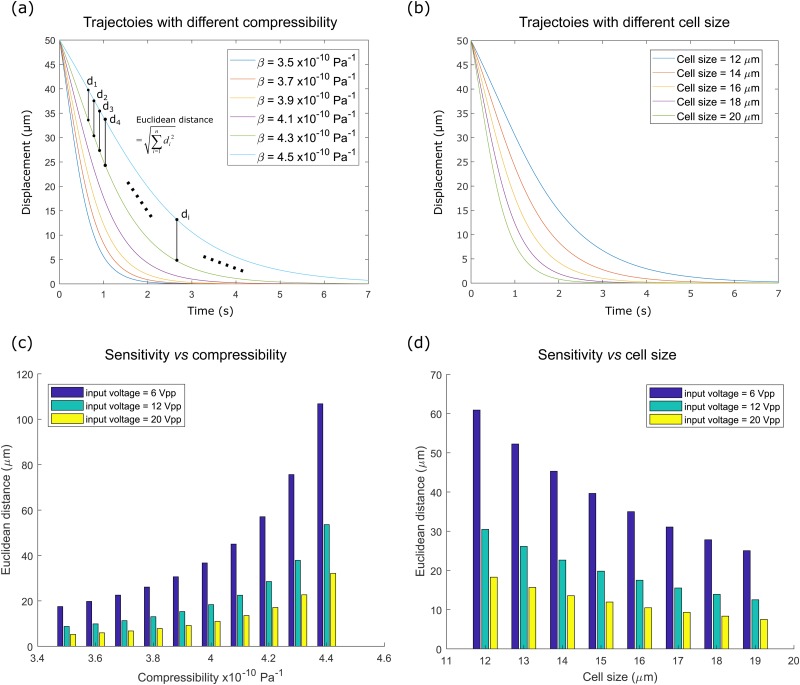
In order to better understand the effects of cell compressibility and cell size on the trajectory of the cell toward the pressure node, a theoretical sensitivity study was conducted by solving Eqs. (1)–(3) under different cell compressibility or cell size. The effects of compressibility were analyzed by substituting all the experimentally measured parameters except compressibility β_p. A range of compressibility values from 3.5 × 10⁻¹⁰ Pa⁻¹ to 4.5 × 10⁻¹⁰ Pa⁻¹ were defined and used to calculate the corresponding cell trajectories [Fig. 6(a)]. Each trajectory contains a series of 2-dimensional data, i.e., lateral position vs time (y, t). The simulated sampling rate was set as 30 points/s, consistent with the frame rate of camera in the experiment. Here, in order to evaluate the difference between two trajectories containing two series of 2-dimensional data, we introduced Euclidean distance of trajectories, which is commonly used in motion tracking and trajectory similarity testing.⁶⁰ Euclidean distance between trajectory R and trajectory S each containing n datapoints is defined as

$$Eu(R,S)=\sqrt{{\sum }_{i=1}^n[{(r_{i,x}-s_{i,x})}^2+{(r_{i,y}-s_{i,y})}^2],}$$ (4)

where r_i,x and r_i,y denote the x and y coordinates of the ith point of trajectory R; s_i,x and s_i,y denote the x and y coordinates of the ith point of trajectory S. Since only the lateral displacement is considered, the x components can be neglected. Euclidean distance involves the summation of position difference at every point of the trajectory and interprets trajectory difference [Fig. 6(a)].

FIG. 6.

(a) A group of simulated trajectories of different compressibilities ranging from 3.5 × 10⁻¹⁰ Pa⁻¹ to 4.5 × 10⁻¹⁰ Pa⁻¹. d_i denotes the distance of the ith points of the two trajectories. Euclidean distance of trajectories is defined as the root-sum-square distance of every corresponding point from the two trajectories. (b) A group of simulated trajectories of different cell sizes ranging from 12 μm to 20 μm. (c) Sensitivity test vs compressibility under different voltages. Sensitivity was represented as the Euclidean distance between two trajectories with an increment of compressibility Δβ, i.e., Eu(R(β), R(β + Δβ)). The increment of compressibility Δβ was set as 0.1 × 10⁻¹⁰ Pa⁻¹. (d) Sensitivity test vs cell size under different voltages. Sensitivity was represented as the Euclidean distance between two trajectories with an increment of cell size Δd, i.e., Eu(R(d), R(d + Δd)). The increment of compressibility Δd was set as 1 μm.

Sensitivity was represented as the Euclidean distance between two trajectories with an increment of compressibility Δβ, i.e., Eu(R(β), R(β + Δβ)). The increment of compressibility Δβ was set as 0.1 × 10⁻¹⁰ Pa⁻¹. As the input voltage determines the intensity of the acoustic field and thereby influences the cell trajectory, the sensitivity analysis was again repeated but under different input voltages ranging from 6V_p-p to 20V_p-p. The results demonstrate that the Euclidean distance and therefore sensitivity increase with an increase in compressibility [Fig. 6(c)]. It indicates that when differentiating two objects with higher compressibility, the trajectory difference between these two objects grows and vice versa. In the comparison using different input voltages, a reduction in the input voltage increases the Euclidean distance between two trajectories and makes the trajectory differences more pronounced.

The sensitivity study on the cell size was conducted by simulating a group of trajectories for cells of different sizes [Fig. 6(b)]. Similar to the compressibility analysis, cell size was introduced as the variable instead, ranging from 12 μm to 20 μm. Sensitivity was represented as the Euclidean distance between two trajectories with an increment of cell size Δd, i.e., Eu(R(d), R(d + Δd)). The increment of cell size Δd was set as 1 μm. The analysis was repeated again with input voltages ranging from 6V_p-p to 20V_p-p. The Euclidean distance and therefore sensitivity decrease with an increase in cell size, while reducing voltage still increases sensitivity [Fig. 6(d)].

IV. DISCUSSION

In our study, the mechanophenotypes of the three different cell types were characterized using a SAW microfluidic device. Compared with conventional techniques such as atomic force microscopy and optical tweezer, the experimental procedure of the SAW microfluidic device is simpler and lower in cost. However, it will still require capturing video data and postprocessing the data, which can be time-consuming. This could be improved by automatic control and real-time data processing.

The vertical position of microbeads or cells inside microfluidic channel was not measured in this study. It has been reported in previous works that the acoustic radiation force is mainly induced by horizontal time-averaged pressure field and independent of the vertical position.⁶¹ However, the acoustic streaming, which is another effect in addition to acoustic radiation force, relates to the vertical position.^41,62 These studies also showed that acoustic streaming is strengthened by an increase of the channel depth from 40 μm to 100 μm⁶² or by an increase of the applied power from 200 mW to 1500 mW,⁴¹ which increase Stoke drag force induced by acoustic streaming and move the particles vertically. In our study, the channel depth was fixed as 40 μm and we anticipate that there is minimal acoustic streaming effect.⁶² Furthermore, we did not observe any vertical movement of microbeads or cells during the exposure to acoustic waves (videos in the supplementary material). We also anticipate that any acoustic streaming would move the particles vertically and had minimal impact on the horizontal acoustic radiation force, hence not affecting the compressibility measurements.

Though the heating effect was not measured in our study, temperature measurement can be found in a similar 13-MHz SAW mixer device in the work by Luong et al.⁶³ In their report, temperature increase was observed only when the applied voltage was above 35 V; while the voltage in our study was below 20 V. Hence, we anticipate that heating effect was negligible in our study.

The concentration of cell solution was chosen to allow around 5 cells in the field of view at any one time, minimizing the potential scattering disturbance from the cell to the surrounding acoustic field. In addition, the particle-to-particle effect was theoretically neglected in most acoustofluidic studies.⁶⁴ As a proof, we used microbeads of concentrations varying from 400 000/ml to 3 000 000/ml in our study, and however did not observe any obvious effect of the particle concentration on the trajectory.

A. Validation of the measured cell compressibility

The existing applications to measure the compressibility of cells have been mainly established based on BAW microfluidic methods, by similarly tracking the cell trajectory toward the pressure node in the center of the microfluidic channel.^25–27 However, BAW is limited by its reliance on the resonation from the microfluidic channel sidewalls, hence restricting the channel’s material and geometry. It further constrains the modality of pressure node, the choice of material, and therefore the flexibility of design.^29,32 In order to alleviate the limitation of BAW, one study managed to decouple the acoustic resonation and fluidic domain, by placing an additional PDMS layer to fill in part of the silicon microfluidic channel, which only impacted fluidic domain and had no effect on acoustic resonation.⁶⁵ However, it resulted in more complex fabrication protocol, involving precise laser cutting and complex PDMS casting.

In this study, instead of forming a standing wave by resonation between acoustic-reflective channel walls, SAW generates acoustic waves by IDTs on the piezoelectric substrate and overcomes the limitations of BAW to some extent. The measured compressibility of MCF-7 cells, 3.99 ± 0.16 × 10⁻¹⁰ Pa⁻¹, agrees with those in the literature using BAW, 3.8–4.22 × 10⁻¹⁰ Pa⁻¹.^25,27 Although there are no published data on the compressibility value of A549 and HASM cells, the measured values in this study are comparable to other cell types reported in the literature using BAW: 3.77 ± 0.09 × 10⁻¹⁰Pa⁻¹ for MCF-12A breast cells²⁵ and 4.3 ± 0.2 × 10⁻¹⁰ Pa⁻¹ for HEPG2 liver cancer cells.²⁷

In addition to compressibility measurement using BAW, Pasternak et al. used scanning acoustic microscopy to measure the bulk modulus, the inverse of compressibility, of MCF-7 cells at different cell cycle, which gave values of bulk modulus ranging from 2.40 GPa to 2.45 GPa, equivalent to compressibility of 4.08–4.17 × 10⁻¹⁰ Pa⁻¹.⁶⁶ Nijenhuis et al. measured bulk modulus of NIH3T3 mouse fibroblasts in response to drug treatment using scanning acoustic microscopy, which gave values around 2.6 GPa, equivalent to compressibility of 3.85 × 10⁻¹⁰ Pa⁻¹.⁵³ Cushing et al. used ultrasound on neutrally buoyant samples of a variety of cell types and obtained compressibility ranging from 334 TPa⁻¹ = 3.34 × 10⁻¹⁰ Pa⁻¹ to 404 TPa⁻¹ = 4.04 × 10⁻¹⁰Pa⁻¹.⁵⁹ These values are also comparable to the measured values in this study.

B. Effects of cell compressibility, cell size, and input voltage on the cell trajectory

In our study, we found that the cell trajectory was impacted by both the compressibility and the size of the cell. The results show that the SAW microfluidic method is better at differentiating cells of higher compressibility or smaller size. In addition, a reduction in input voltage increases the differences in cell trajectory and hence increases the sensitivity of the device. It provides an experimental insight that reducing the input voltage would be a reasonable practice to improve the sensitivity of differentiating the cells with different compressibility or size. However, if the input voltage is too low, the effect of acoustic radiation force may become so small that the motion toward pressure node becomes too slow to be observed.⁶⁷

In addition, the measure of cell size can affect the measure of cell compressibility, as the two factors concurrently influence the cell trajectory. We have measured the cell size by analyzing every frame of the video and averaging the measured sizes among the frames. The measured sizes of cells were recorded to have a relative error of around 0.6%, which would cause an approximately 0.3% relative error of the measured compressibility as pointed out by the work by Hartono et al.²⁵ Thus, this error could be considered as negligible. In addition, we did not observe any dependency of measured compressibility on cell size in Fig. 4. Hence, we believe that the compressibility was measured independently of the cell size.

C. Mechanophenotyping based on both cell compressibility and cell size

Some studies characterized the mechanophenotypes of cells by examining cell compressibility as the only factor.^25,26 Other studies differentiated or separated microbeads or cells based only on their size and consequently were only effective at large size difference with a diameter ratio from 3.33 to 14.46.^44,45,68 In this study, both compressibility difference and size difference could be concurrently measured. It was possible to measure the compressibility difference of the A549 and HASM cells with similar sizes (i.e., with a diameter ratio of 1.12) and that of non-treated and treated MCF-7 cells. At the same time, it was also possible to differentiate the size differences of HASM and MCF-7 cells. These further distinctions would not be appreciated if only one of the two factors were considered. Hence, further insights into cell mechanophenotype could be achieved using a combined metric consisting of cell compressibility and cell size.

V. CONCLUSION

This study presented a surface acoustic wave (SAW) microfluidic device to measure the compressibility of cells and differentiate cell mechanophenotype. The device was first validated using microbeads of known properties and then used to characterize the properties of A549, HASM, and MCF-7 cells based on compressibility and cell size. In the following, MCF-7 cells with or without colchicine treatment and 2-methoxyestradiol treatment were tested. A sensitivity analysis was conducted to understand the effects of cell compressibility, cell size, and input voltage to the device. Using a combined metric of cell compressibility and cell size, the device was successful in differentiating different cell types and cells under different conditions. Future work may exploit the trajectory difference between cells induced by compressibility and cell size, with multiple microfluidic channels, to achieve cell separation based on their mechanophenotype.

SUPPLEMENTARY MATERIAL

See the supplementary material for details on microfluidic chip fabrication, values used in simulation, and calibration using microbeads. The supplementary videos include recordings of microbeads or cells moving upon phase shift in the experiment.