Graphical abstract
Keywords: Hadfield steel, Resource savings, Lifetime prediction, Regression trees, Multi-layer perceptrons, Artificial intelligence
Highlights
-
•
Dataset of plates lifetime were obtained by 3 casting methods and chemical composition.
-
•
A two-steps model for prediction of the full lifetime of plates of Hadfield steel was proposed.
-
•
The prediction model combines regression trees with multilayer perceptron (MLP)
-
•
MLP provides accurate weaŕs models considering the chemical composition.
-
•
Regression trees provide visual information about dataset structure to build MLP.
Abstract
Highly tensile manganese steel is in great demand owing to its high tensile strength under shock loads. All workpieces are produced through casting, because it is highly difficult to machine. The probabilistic aspects of its casting, its variable composition, and the different casting techniques must all be considered for the optimisation of its mechanical properties. A hybrid strategy is therefore proposed which combines decision trees and artificial neural networks (ANNs) for accurate and reliable prediction models for ore crushing plate lifetimes. The strategic blend of these two high-accuracy prediction models is used to generate simple decision trees which can reveal the main dataset features, thereby facilitating decision-making. Following a complexity analysis of a dataset with 450 different plates, the best model consisted of 9 different multilayer perceptrons, the inputs of which were only the Fe and Mn plate compositions. The model recorded a low root mean square error (RMSE) of only 0.0614 h for the lifetime of the plate: a very accurate result considering their varied lifetimes of between 746 and 6902 h in the dataset. Finally, the use of these models under real industrial conditions is presented in a heat map, namely a 2D representation of the main manufacturing process inputs with a colour scale which shows the predicted output, i.e. the expected lifetime of the manufactured plates. Thus, the hybrid strategy extracts core training dataset information in high-accuracy prediction models. This novel strategy merges the different capabilities of two families of machine-learning algorithms. It provides a high-accuracy industrial tool for the prediction of the full lifetime of highly tensile manganese steel plates. The results yielded a precision prediction of (RMSE of 0.061 h) for the full lifetime of (light, medium, and heavy) crusher plates manufactured with the three (experimental, classic, and highly efficient (new)) casting methods.
Introduction
Highly tensile manganese steel, also known as Hadfield steel, named after its first manufacturer, consisting of 11.5–15.0% of Mn and 0.9–1.4% of C demonstrates high tensile strength under shock loads, such as in tank track operation, tractors and other soil-removal machines, bucket tooth bars for limestone, ore crusher jaws, and railroad track switches on wheel sets. The aforementioned properties are due to the interaction of steel with a softer material and the absence of scuffing on the impact surface of the steel workpiece, thus causing fatigue-induced rather than abrasive wear. As a consequence of the difficulties associated with cutting this alloy, highly tensile manganese-steel workpieces are typically produced via casting.
Extensive research on improvements in this type of steel reflects the active industrial interest in its mechanical properties. Siafakas et al. [1] conducted a quantitative analysis of the amount, size, and number of particles which precipitate in situ in titanium- and aluminium-treated Hadfield steel during casting. In certain research works, heat treatment has been suggested as a means of increasing the micro-hardness of the cast Hadfield steel matrix [2], [3], [4]. Moreover, in several studies [5], [6], [7], the factors which can affect the increased wear resistance of high-manganese steel have been examined.
Wear resistance appears to be the focus of most research efforts owing to the fact that it can extend the workpiece lifetime. There are works dedicated to the study of wear resistance in high-speed pounding (HSP) of Hadfield steel to produce a thick nanocrystalline surface layer with gradient nanostructure [8]. Abbasi et al. [9] studied the abrasive wear behaviour of Al-alloyed Hadfield steel under both high- and low-stress wear conditions in comparison with that of non-Al alloyed Hadfield steel. Kolokoltsev et al. [10] studied the resistance of Hadfield steel cooled at different rates. El-Fawkhry et al. and Kalandyk et al. [11], [12] both discussed the results of austenitic matrix modification in high-manganese steel castings. Smith et al. [13] studied the materials produced through the addition of minor amounts of other carbide-forming and solid-solution strengthening elements and through the heat treatment of the as-cast components under pressure. Tęcza and Głownia and Głownia et al. [14], [15] studied the composite structure of high-manganese steel using vanadium carbides following melting and solidification. Najafabadi et al. [16] studied the wear resistance of cast Hadfield steel after adding Ti elements. Zhong et al. [17] studied the effect of the composite structure of (Fe, Cr)7C3-Fe on its wear resistance and concluded that it was 1.34 times higher than that of the Hadfield steel. Finally, Zhang et al. [18] examined a composite coating of WC/Hadfield steel produced via centrifugal casting to improve its impact wear resistance.
However, all aforementioned methods complicate the technology of manufacturing workpieces using Hadfield steel and cause it to be more expensive. Moreover, insufficient attention has been paid to the issue of resource conservation, with the exception of the studies by Erdakov et al. [19], [20], [21], [22], who proposed a new highly efficient gating and feeding system and defined its optimum parameters for casting using green sand moulds. With the optimum parameters, the new technology requires neither heavy heads nor labour-intensive operations with the casting form both before and after pouring to achieve the optimum angle; thereby decreasesing the cost of producing plates and leading to considerable savings on metal in the gating system and machine heads (15–20%).
As we approach the fourth technological revolution in the setting of global competition, the analysis of all existing data from the casting process becomes increasingly relevant in terms of identifying the best strategies which will optimise the mechanical characteristics, particularly the wear resistance of components which are cast using this steel type, thus creating a competitive advantage. Previously unknown and hidden trends can be useful, and comprehensible patterns found at the intersection of databases, statistics, and machine-learning techniques. The size of the database (big data or data of a specific experiment) is not essential; the importance lies in the identification of hidden patterns, which would be impossible to establish with direct visual analysis or by calculating simple statistical features.
Casting is an inherently probabilistic process; the quality of a cast is primarily attributed to the chemical composition of the alloy and the nature of its solidification. The objective of finding hidden patterns in the array of technological data from the production and operation of steel plates used at crushing stations appears relevant to the investigation of the reasons which cause their wear. Therefore, the objective of this study is to extend the total lifetime of (light, medium, and heavy) Hadfield steel plates for ore processing equipment by revealing new trends using machine-learning techniques to model their wear limits.
The solutions of complex industrial manufacturing processes, as presented in this study, typically follow two separate strategies. In the first one, the use of analytical models is proposed based on experimental data; in certain cases, this strategy is supported by physical models or simulations of the manufacturing process and is fine-tuned with the experimental data acquired under laboratory conditions. This approach has already been discussed in the introduction for the prediction of the lifetime of ore crushing plates. In the second approach, machine-learning techniques are employed to build prediction models from massive datasets; this approach could become a suitable tool for decision making.
Each approach has its advantages and disadvantages. The analytical models are typically based on homogeneous and simplified manufacturing processes, first, because they use data for fine-tuning collected under restricted laboratory conditions (to reduce experimental costs); second, because they are meant to consider only variables of the same nature in the manufacturing process, e.g. cutting conditions and chemical composition. However, they rarely mix variables of distinctly different natures, because the analytical and physics-based models are not designed for such tasks. The most common machine-learning approaches, such as artificial neural networks, belong to the black-box category of these techniques, i.e. they provide no equation which shows the relationship between inputs and outputs. The only manner in which the information contained in those models can be extracted is to query the predicted output for a certain combination of inputs and the prediction model will provide an estimated value. Hence, if useful information would be extracted from these models, they would require either a 2D or a 3D representation of their predictions [23], [24], [25]. This approach has been successfully validated for several industrial tasks, for example, in predicting surface roughness [26], [27], [28], surface quality [29], and cutting-tool wear [30], [31], among others. Furthermore, the datasets required to train these models should be as big and diverse as possible. However, industrial data are limited to real-life scenarios, given the reluctance of the industry to finance tests which go beyond the specification of manufacturing conditions. Nevertheless, such tests are essential in the training process of machine-learning techniques. Moreover, part of the information in the datasets, rather than relating to the manufacturing problem, is related to the experimental design method itself (e.g. if in a certain cutting process we test a range of cutting tools, each having an additional tooth and an extra 5 mm diameter in addition to those of the preceding one, as per the specifications of the manufacturer, then the machine-learning model will conclude that the number of teeth and the diameter of the tool are two completely correlated inputs, playing the same role in the cutting process).
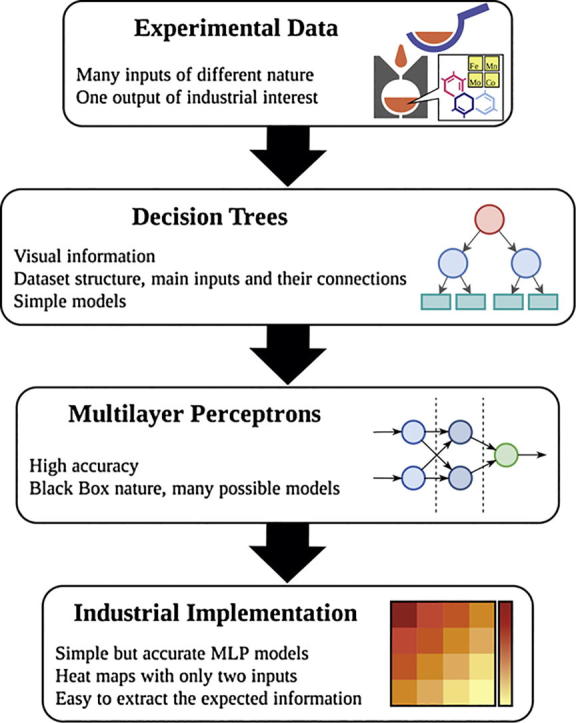
Although the most common machine-learning techniques belong to the black-box category, there are certain machine-learning techniques, such as decision trees, that provide visual information on the process. However, these techniques are often simpler than artificial neural networks (ANNs) and might not perform equally well in very complex processes, although they are free from the complexity and tediousness of fine-tuning the ANN model parameters. In this study, we propose a hybrid strategy to overcome this limitation, which combines decision trees for extraction of the main information included in the training dataset with ANNs for high-accuracy prediction models. This strategy combines the greatest advantages of both machine-learning techniques: to understand the main features of the dataset, it generates rapid, visual, and simple decision trees, thereby facilitating decision-making on inputs for simple, yet accurate, ANN models.
The modelling process was divided into three stages. First, a visual pre-analysis was performed using reduced error pruning (REP) trees, which advised splitting the dataset into nine subsets and considering only eight chemical components as inputs for the prediction model. Then, the 9 independent prediction models (one for each subset) for 13 different multilayer perceptron (MLP) structures (the most promising combinations of chemical components) were trained and the most accurate models were identified. The test of only some of the possible combinations of chemical composition of the ore plates in the MLPs is an industrial requirement (to reduce the modelling effort). Meanwhile, the efficient selection of the features used in the training stage of the MLPs is an interesting challenge owing to the high number of possible combinations. Then, the complexity of the MLP structure was considered to select the best prediction model from an industrial perspective. Finally, the identification of a high-accuracy prediction model may be insufficient for its successful implementation under real industrial conclusions. Therefore, the best of all the proposed models was used to build a heat map of direct industrial use, namely a 2D representation of the main inputs of the manufacturing process with a colour scale showing the predicted output, i.e. the wear limit of the manufactured plates.
This strategy is able to deal with data of different natures, the chemical composition of the plates, and the manufacturing process of the plates in our case study. Moreover, the strategy produces models which are optimised in terms of accuracy, with a reduced number of inputs; the reduction of the number of inputs is an additional industrial requirement in order for such models to be implemented in factories, because they will reduce the costs of analysis (i.e. if a percentage of only 2 rather than 16 chemical components should be evaluated in a workpiece, then the analytical process will cost less).
Research material and methods
Before developing a model for the prediction of the lifetime of crushing plates and prior to conducting an experiment, it is necessary to determine the properties of the materials that are used, the parameters of the cast products, as well as the casting and investigation methods.
Plate manufacturing and casting methods
In this research, the following materials and research methods were used. The chemical composition (%) of Hadfield steel is listed in Table 1. Hadfield steel contains 84.3–87.3% iron (Fe), 11.5–15.0% magnesium (Mn), 0.9–1.4% carbon (C), 0.3–1.0% silicon (Si), and 0–3% impurities. The physical and mechanical properties of Hadfield steel in its austenite form are the following: a density (ρ) of 7890 kg/m3, a Brinell hardness HB of 186–229, and a strength, σ, of 654–830 MPa; mechanical properties: ductile alloy. The physical and the mechanical properties of ferro-chromium industrial-type ores with high-melt impurities are the following: a density (ρ) of 2235 kg/m3, a Brinell hardness (HB) of 438–662, and a strength, σ, of 307–522 MPa. mechanical properties: fragile ore mineral.
Table 1.
Chemical composition (%) of Hadfield steel.
| Fe | Mn | C | Si | Impurities |
|---|---|---|---|---|
| 84.3–87.3 | 11.5–15.0 | 0.9–1.4 | 0.3–1.0 | 0–3 |
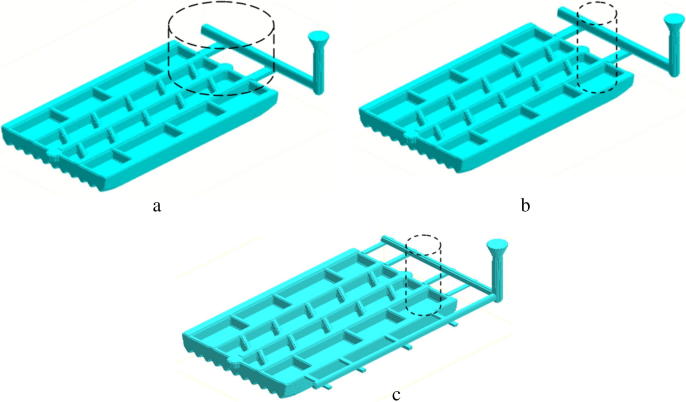
The gating and feeding system parameter variation methods are categorised into classic, experimental, and high-efficiency (new) (Fig. 1).
Fig. 1.
Designs of a feeding and gating system (head locations shown as dotted lines): a–classic horizontal form at 25° after pouring, b–experimental, and c–high-efficiency (new).
The classic method involved a massive head for the supply of molten metal through the gating system. After pouring the molten metal into the mould, the form was horizontally rotated at 25° (Fig. 1a). In the experimental method, a significantly reduced head was used in the corner of the plate. The supply of molten metal was not through the gating system to the head; molten metal entered from the end of the plate and there was no rotation of the form after pouring (Fig. 1b). The new, highly efficient method permitted the molten metal to enter from the end and the side of the plate. The supply of molten metal through the gating system was switched to both the end and the side of the plate. Moreover, the form was not turned after pouring (Fig. 1b).
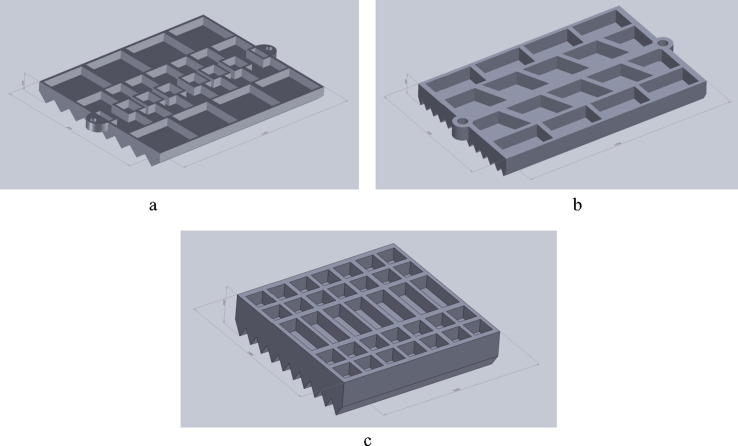
The tests were conducted on cast plates with the following designs (Fig. 2a–c): a – ‘light’, b – a ‘medium’, and c – a ‘heavy’ design.
Fig. 2.
Mechanical 3D drawing of stationary plate: a – a ‘light’ design, length: 1165 m, width: 950 mm, and height: 106 mm; b – a ‘medium’ design, length: 1500 m, width: 950 mm, and height: 149 mm; and c – a ‘heavy’ design, length: 1080 m, width: 1045 mm, and height: 249 mm.
Each plate has a matching one with negligible variation in weight, average wall thickness, and design. These plates are widely used in ferroalloy crushing stations, have a relatively simple design, and their production is fraught with several thermal stress, shrinkage, and drop defects.
The plates are conventionally classified into ‘light’, ‘medium’, and ‘heavy’; this categorisation identifies the effect of the plate geometrics (primarily that of the average wall thickness) on the severity of production-related defects.
To determine the chemical composition of the alloy, spectral analysis was performed on a modern ISKROLINE 300 static-emission spectrometer with a concentration measuring range of 0.0001–0.1%.
The measurement of the steel temperature as it crystallised in the mould was performed by applying tungsten-rhenium thermocouples (VR 5/20) which were connected to EPR-08mz, an automatic electronic potentiometer. The melt temperature was measured in degrees Celsius.
Experimental
The experimental investigations were conducted from February 2013, to December 2016, in an operational foundry shop of the Katav–Ivanovsk Foundry, which is part of the Chelyabinsk Electrometallurgical Integrated Plant (ChEMK, Russia). During the experimental investigations, approximately 50 meltings of Hadfield steel were conducted and 450 crusher plates, 150 of each type (light, medium, and heavy), were obtained using the three different methods (classic, experimental, and high-efficiency).
Each melting produced nine forms, in which cavities existed for three types of plates with three variants of gating and feeding systems. An additional sample was produced with each cast plate for the chemical analysis of the alloy. All samples and plates were labelled by melt number.
Before installation in the crushing station, the plates were weighed. Then, the ore grinding time was recorded with a stopwatch throughout the three crushing divisions (SMD-109A, SMD-110A, and B9-2H) in parallel mode. The complete abrasion of the plate edges was determined by visual inspection; after weighing the worn plate, if its weight loss had reached a limit value (marginal mass loss: light plate = 90 kg, medium plate = 170 kg, and heavy plate = 240 kg), the time on the stopwatch was considered to be the total plate lifetime.
One-off forms of the plates were made via the cold-box-amine process. The average wall thickness of the plates was: 50 mm for the light plate, 70 mm for the medium plate, and 85 mm for the heavy plate. Mould filling was performed in 7, 8, and 9 min for the light, medium, and heavy plates, respectively. The area of the narrow sections of the gating systems was as follows: 23.00 cm2 for the light plate, 28.00 cm2 for the medium, and 33 cm2 for the massive plate. The temperature of the molten steel poured into the mould was 1570 °C for the light plate, 1540 °C for the medium plate, and 1520 °C for the heavy plate. The volume economy achieved for the experimental and high-efficiency casting methods was as follows: 7500 cm3 for the light plate, 15,000 cm3 for the medium plate, and 41,000 cm3 for the massive plate. The volume was three times greater using the classic casting method.
The control of the chemical composition of the marked steel samples was carried out on sixteen elements: Fe, C, Si, Mn, P, S, Mo, Ni, Al, Co, Cu, Nb, Ti, V, and W. The pouring temperature of the steel lied within 1520–1570 °C. The hardness coefficients of the chrome ore and the prill shape were determined to be f = 0.1 × 317 = 30.1 and SC = (193 × 240)/29 = 1597, respectively.
Modelling
Dataset description
From an industrial perspective, there is a clear output for the wear-limit experiments which should be considered in the dataset, namely the total time during which the plates remain in the crushing station before they pass a limit (time). The dataset included up to 11 inputs of two clearly different natures: the first group of inputs described the chemical composition of the plates in mass percentages, whereas the second group had two characteristics which described the casting process of the plates. In the first group, the percentages of iron (Fe), carbon (C), silicon (Si), manganese (Mn), phosphorus (P), sulphur (S), chromium (Cr), molybdenum (Mo), nickel (Ni), aluminium (Al), cobalt (Co), copper (Cu), neodymium (Nb), titanium (Ti), vanadium (V), and tungsten (W) were all recorded. In the second group, the casting method (Method) and the type of cast plate (Type) which have been previously described in Section 2 were recorded. All inputs of the first group are continuous variables, whereas the inputs of the second group are nominal and can each take three different values. As outlined in the introduction, these inputs were selected because they are the main indicators available to the process engineer regarding the quality and source of the plate, as well as the different casting methods through which it was formed. The dataset included 450 different plate compositions cast in a balanced proportion with the nine different casting conditions. Table 2 summarises the inputs and the output, their units, and the range of values in the dataset; the output variable, time, is shown in bold. The dataset is included as supplementary material for further research.
Table 2.
Dataset variables and their variation range.
| Variable | Abbreviation | Range | Units |
|---|---|---|---|
| Iron | Fe | 85.357–87.172 | % |
| Carbon | C | 0.818–1.032 | % |
| Silicon | Si | 0.410–0.636 | % |
| Manganese | Mn | 11.098–12.832 | % |
| Phosphorus | P | 0.028–0.056 | % |
| Sulfur | S | 0.012–0.032 | % |
| Chromium | Cr | 0.029–0.262 | % |
| Molybdenum | Mo | 0.008–0.016 | % |
| Nickel | Ni | 0.075–0.125 | % |
| Aluminium | Al | 0.007–0.011 | % |
| Cobalt | Co | 0.015–0.021 | % |
| Copper | Cu | 0.085–0.099 | % |
| Neodymium | Nb | 0.004–0.007 | % |
| Titanium | Ti | 0.001–0.004 | % |
| Vanadium | V | 0.016–0.023 | % |
| Tungsten | W | 0.043–0.063 | % |
| Casting method | Method | High-efficiency, experimental, classic | None |
| Type of cast plate | Type | Light, medium, heavy | None |
| Total lifetime | time | 746.368–6902.709 | h |
Because the total time during which the plates remain in the crushing station before they reach their breakage limit is a continuous output, its prediction is a regression problem.
Machine-learning techniques
One of the main purposes of machine-learning techniques is to solve classification and regression problems. If the output can only receive a discrete number of values or classes, the task is referred to as classification; however, if the output is a continuous value, the problem must be solved with a regression.
Regression trees [32] are a popular and effective machine-learning approach for the solution of regression problems. In our research, Reduced Error Prunning (REP) trees were used; more specifically, their implementation is referred to as REPTree [33]. A regression tree is a decision tree, the predicted outcome of which is a continuous value. This type of predictive model consists of a set of three different types of nodes: one root node, the internal nodes or branches, and the terminal nodes or leaves. Root and internal nodes serve to make decisions depending on one of the input attributes. Alternatively, each terminal node provides a prediction by means of a linear model of the inputs. To summarise, regression trees consist of a series of decisions made from the top of the tree to the bottom, where a leaf node is reached [34]; then, a continuous outcome is predicted.
ANNs, known for their capabilities as universal approximators [36], are a powerful non-linear family of techniques which draw their inspiration from neuroscience [35]. A neural network is a collection of nodes, also referred to as neurons [37], which perform simple operations, i.e. typically, a sum of the weighted inputs followed by the application of an activation function to that sum. The neurons are distributed in multiple layers, where, with the exception of the input and the output layers of the network, the neuronal outputs of one layer will be the inputs for the neurons in the following layer. Each neuron input is associated with a weight which has to be fitted during the network training process, typically through back-propagation algorithms [38], such as the stochastic gradient descent [39].
The use of ANNs to solve regression problems could even be described as a trend in machine learning [40]. ANNs have the capability of outperforming other techniques, such as, for example, the aforementioned regression trees. There are several types of ANNs, e.g. feedforward, radial basis functions (RBFs), and recurrent neural networks (RNN). Each type addresses a very specific type of problem. In this study, an MLP, which is part of the family of feedforward networks, was applied to predict the lifetime of steel plates. MLPs had a large impact within the research community [41]. A perceptron [42] is a linear classifier, i.e. a straight line can be used to divide input data into two categories (e.g. true and false). Through the combination of several perceptrons in an MLP architecture, non-linear classification, or regression problems can be addressed by distinguishing data which are not linearly separable [43].
Methodology
The Waikato Environment for Knowledge Analysis (WEKA) software tool [44] was used to build the machine-learning models and to conduct the experiments. Its implementation of the algorithms will be described in Section 3.2. All attributes of the data set, except for the target value, were normalised in a pre-processing step which improved the training process for experimentation with the models.
A -fold cross-validation technique was selected for the evaluation step. In cross-validation, the data were randomly split into subsets or folds. When using this technique, the under-evaluation predictive model was trained times; at each training stage, one fold was used as the test data and the remaining folds as training data. Each fold can only be used once for testing because the data used during validation will not have been used in the training stage, thus providing a better generalisation of the model [45]. A well-generalised model is capable of predicting target values from new input data [34]. The repetition of cross-validation in several operations can ensure that statistical value is attached to the average error of the prediction models. In this research, a 10-fold cross-validation technique repeated 10 times (10 × 10 cross-validation) was employed; therefore, each result was an average of 100 runs [46].
The performance of a machine-learning model was assessed through the use of evaluation metrics. Two of the best overall measures in regression are the root-mean-square error (RMSE) and the mean absolute error (MAE) [47]. In this study, both were selected for the evaluation of the effectiveness of the models; although certain authors have stated that the RMSE is not a good choice for determining the average model performance [48], others have postulated that the RMSE is more appropriate than the MAE in some specific cases [49]. In our case, the hourly units of both RMSE and MAE were the same as the predicted target attribute. Obviously, the lower the value of the RMSE and MAE is, the better the model is. The following expressions were used to determine the RMSE and MAE:
where, represents the number of instances of the test subset, refers to the instance when it is used for the current prediction, is the predicted value, and is the actual value of the output variable.
Results and discussion
The results of the prediction models generated from the experimental dataset will be presented in this section. First, the modelling results following different analyses will be discussed in detail. Then, the industrial implementations of the best model will be outlined.
Modelling results
The modelling process, as presented in the Introduction, was divided into three stages. First a visual pre-analysis was performed using REPTrees. Then, the conclusion of the pre-analysis was used to split the dataset into nine subsets and to build nine independent prediction models, one for each subset; different MLP configurations were trained and the results of their performance were discussed. Finally, the complexity of the MLP structure was considered to select the best prediction model from an industrial perspective.
Visual pre-analysis using REPTrees
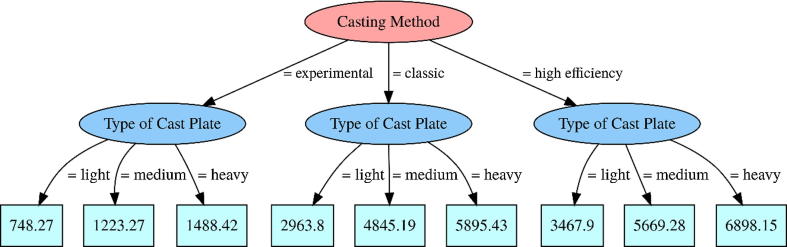
Typically, data from industrial sources include certain major features which can be linked to the nature of the industrial problem, as well as the experimental design; however, these features will not necessarily be apparent to the programmer who is responsible for building the prediction model. If these features are not taken into account, the models can be very inaccurate. Therefore, in this research, a regression model using a REPTree was first trained to take this possibility into account. The REPTree parameter values were the default options in WEKA. The most useful information which can be obtained from the resulting model is the tree structure that it generates, as shown in Fig. 3, where only two out of eighteen features were used by the tree. These features coincide with the group which describes the casting process of the plates. Therefore, we can intuitively expect that the influence of the chemical composition on the wear-limit resistance of the steel plates will be different for the nine leaves: one for each pair of Type of Cast Plate–Casting Method. Therefore, the dataset can be split into nine subsets with different behaviours. If we analyse the model accuracy, the model achieved an RMSE value of 1.81 h and a MAE value of 1.51 h. These errors, although apparently very good considering the standard deviation of 2125.52 h of the full data set, are quite the opposite: if we look closely at the data which correspond to each subset of each leaf of the tree, their standard deviations were between 1.13 and 2.24; hence, the obtained error value was not acceptable.
Fig. 3.
Reduced-error pruning tree (REPTree) obtained for a period of the plates (in hours) prediction using the full dataset.
Upon completion of this pre-analysis, an ANN model was built with the aim of improving the accuracy of the REPTree model. The reason for this strategy is attributed to the fact that regression trees are one of the simplest machine-learning approaches, whereas ANNs are typically more precise at predicting complex processes, such as the plate wear limit. Therefore, the most well-known ANN structure, the MLP, was selected for this task. After performing a parameter tuning process, the best performance was achieved with the WEKA default options with the exceptions of the following.
-
•
The number of neurons in the hidden layer: the same as the number of attributes (18).
-
•
The learning rate: 0.5.
-
•
The momentum: 0.1.
-
•
The training time (number of epochs): 10,000.
The RMSE of the model, considering the full dataset, was 0.874 h and its MAE was 0.657 h, which clearly outperformed the REPTree model. Additionally, the training time of this model (25.03 s) was significantly higher than that of the REPTree (0.0011 s). Both training times were obtained with a workstation equipped with an Intel Core i7 6700 3.4-GHz processor, 16 GB RAM, and an NVIDIA Titan Xp GPU.
Subset modelling
The analysis of the REPTree allowed us to conclude that nine different subsets were present in the dataset and that two of the inputs were sufficient to define them: casting method and type of cast plate. Thus, having divided the dataset into nine subsets, a REPTree for each subset with a WEKA default parameter configuration was built. Table 3 lists the performance of the REPTree models for each subset in terms of the RMSE and the MAE, as well as the chemical elements which were selected by the REPTree algorithm to build each regression tree. According to the MAE value (within the range of 0.165–0.442 h), in all nine cases, the generated models outperformed the REPTree considering the full dataset (a MAE value of 1.51 h); the best MLP model (with a MAE value of 0.657 h) was built using the full dataset (Section 4.1.1).
Table 3.
Types of cast plate and casting method tree models, indicating the chemical elements selected by each regression tree and their performance indicators (RMSE and MAE).
| Cast Plate Type | Casting Method | Alloy elements chosen by regression tree |
RMSE (h) | MAE (h) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fe | Mn | Mo | S | V | P | Nb | Co | ||||
| Light | Experimental | ✓ | ✓ | 0.3347 | 0.1650 | ||||||
| Classic | ✓ | ✓ | ✓ | ✓ | 0.3511 | 0.1650 | |||||
| High-efficiency | ✓ | ✓ | ✓ | ✓ | 0.3288 | 0.1692 | |||||
| Medium | Experimental | ✓ | ✓ | 0.3931 | 0.2013 | ||||||
| Classic | ✓ | ✓ | ✓ | 1.0276 | 0.3631 | ||||||
| High-efficiency | ✓ | ✓ | ✓ | 0.6477 | 0.2851 | ||||||
| Heavy | Experimental | ✓ | ✓ | 0.4775 | 0.2433 | ||||||
| Classic | ✓ | ✓ | ✓ | ✓ | 0.6137 | 0.2918 | |||||
| High-efficiency | ✓ | ✓ | ✓ | ✓ | 1.2155 | 0.4416 | |||||
Moreover, the resulting trees yielded information on the importance of each chemical element. Eight out of sixteen characteristics (Cr, W, Cu, Ti, Si, C, Ni, and Al) were not used by any tree; therefore, it may be stated that those features will be of no use for the prediction of plate lifetime. The trees also showed that Fe was the most significant element, because it was present in eight out of the nine possible models, followed by Mn (6/9), Mo and S (4/9), V and P (2/9), and finally, Nb and Co, which were selected only by one tree. Finally, only one of the combinations appears twice; therefore, the REPTree identified eight different combinations of features for the nine subsets. As listed in Table 3, four of these combinations require four chemical features of the plates, two combinations require only three features, and in the remaining three cases is a combination of only two chemical features sufficient to build the REPTree model.
MLPs were used in a second stage to build one model for each subset. The MLP parameters were the same as in the MLP presented in Section 4.1.1, with the exception of the training time, which was 1500 h in this case. Shorter training times were needed because each subset was nine times smaller than the full data set, and a smaller number of features was also used. In this case, different MLPs were built considering only some of the features. Although this strategy might reduce the scope of the prediction model in its industrial implementation (because fewer chemical components are measured), it presents an interesting challenge: the selection of the features to be used in the MLPs owing to the high number of possible feature combinations.
First, the eight different combinations of chemical components obtained with the regression trees (Table 3) were used to build the MLP models for each data subset. Table 4 summarises the performance indicators, the RMSE and MAE, of the 72 MLPs (9 subsets × 8 combinations of chemical components). The most accurate models are highlighted in bold in Table 4. According to the RMSE, the best combination was Fe + Mn + Mo + Co in all subsets (9/9). However, in the case of the MAE value, the agreement was not particularly clear because two combinations yielded the best result for half of the subsets, namely the aforementioned combination (Fe + Mn + Mo + Co) (4/9 subsets) and the combination Fe + Mn (4/9 subsets). Both combinations achieved the best accuracy for the remaining subset.
Table 4.
MLP model performance comparison using alloy chemical-element combinations chosen by regression trees (The most accurate models are highlighted in bold).
| Type Cast Plate | Casting Method | Alloy elements chosen by regression tree |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fe + S |
Fe + S + V |
Fe + Mo + Mn |
Fe + Mn |
Fe + Mn + Mo + Co |
Fe + S + Mn + Mo |
Mn + Mo + V + P |
Fe + S + P + Nb |
||||||||||
| RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | ||
| Light | Experimental | 0.0460 | 0.0319 | 0.0446 | 0.0309 | 0.0407 | 0.0271 | 0.0417 | 0.0261 | 0.0368 | 0.0254 | 0.0444 | 0.0308 | 0.0744 | 0.0482 | 0.0482 | 0.0303 |
| Classic | 0.0439 | 0.0313 | 0.0418 | 0.0292 | 0.0369 | 0.0243 | 0.0370 | 0.0233 | 0.0360 | 0.0241 | 0.0430 | 0.0297 | 0.0756 | 0.0476 | 0.0432 | 0.0270 | |
| High-Efficiency | 0.0432 | 0.0302 | 0.0429 | 0.0295 | 0.0348 | 0.0231 | 0.0359 | 0.0226 | 0.0318 | 0.0221 | 0.0391 | 0.0277 | 0.0677 | 0.0452 | 0.0408 | 0.0256 | |
| Medium | First Experimental | 0.0711 | 0.0495 | 0.0632 | 0.0440 | 0.0615 | 0.0395 | 0.0623 | 0.0382 | 0.0598 | 0.0399 | 0.0620 | 0.0426 | 0.1212 | 0.0765 | 0.0709 | 0.0438 |
| Classic | 0.0727 | 0.0517 | 0.0674 | 0.0478 | 0.0652 | 0.0430 | 0.0655 | 0.0408 | 0.0573 | 0.0401 | 0.0689 | 0.0473 | 0.1173 | 0.0761 | 0.0730 | 0.0449 | |
| Optimal | 0.0744 | 0.0522 | 0.0744 | 0.0525 | 0.0650 | 0.0434 | 0.0675 | 0.0424 | 0.0585 | 0.0405 | 0.0729 | 0.0499 | 0.1182 | 0.0767 | 0.0775 | 0.0491 | |
| Heavy | Experimental | 0.0882 | 0.0619 | 0.0856 | 0.0593 | 0.0808 | 0.0540 | 0.0831 | 0.0522 | 0.0802 | 0.0542 | 0.0866 | 0.0617 | 0.1523 | 0.0987 | 0.0948 | 0.0599 |
| Classic | 0.0899 | 0.0632 | 0.0867 | 0.0614 | 0.0778 | 0.0522 | 0.0759 | 0.0483 | 0.0699 | 0.0483 | 0.0828 | 0.0581 | 0.1398 | 0.0924 | 0.0918 | 0.0580 | |
| High-Efficiency | 0.0919 | 0.0651 | 0.0864 | 0.0614 | 0.0807 | 0.0544 | 0.0835 | 0.0531 | 0.0786 | 0.0545 | 0.0952 | 0.0673 | 0.1460 | 0.0978 | 0.0956 | 0.0627 | |
| Average (simulates full data set) | 0.0690 | 0.0486 | 0.0659 | 0.0462 | 0.0604 | 0.0401 | 0.0614 | 0.0386 | 0.0565 | 0.0388 | 0.0661 | 0.0461 | 0.1125 | 0.0732 | 0.0706 | 0.0446 | |
In a second step, owing to the similar performance of a combination of four elements (Fe + Mn + Mo + Co) and a combination of two (Fe + Mn), it was decided that all the possible combinations of two components extracted from the best combination thus far, i.e. Fe + Mn + Mo + Co, be tested. The objective was to establish whether a simpler model of higher accuracy could be obtained. If such a model exists, it would be of industrial interest because it would imply a simpler measurement of plate composition. As there are 6 possible combinations of 4 components combined in groups of 2 components, 54 new MLP models (9 subsets × 6 chemical component combinations) were built, although 9 of them had been previously built for tests (Fe + Mn) and have already been included in Table 4. The accuracy of these 54 MLP models is listed in Table 5. The most accurate models are highlighted in bold in Table 5.
Table 5.
MLP model performance comparison using all alloy chemical element combinations of two elements obtained from the combination with the best performance (Fe + Mn + Mo + Co) (The most accurate models are highlighted in bold).
| Type Cast Plate | Casting Method | Alloy elements chosen by regression tree |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fe + Mn + Mo + Co |
Fe + Mn |
Fe + Mo |
Fe + Co |
Mn + Mo |
Mn + Co |
Mo + Co |
|||||||||
| RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | ||
| Light | Experimental | 0.0368 | 0.0254 | 0.0417 | 0.0261 | 0.0443 | 0.0305 | 0.0520 | 0.0364 | 0.0880 | 0.0671 | 0.1339 | 0.0992 | 0.2001 | 0.1499 |
| Classic | 0.0360 | 0.0241 | 0.0370 | 0.0233 | 0.0402 | 0.0274 | 0.0473 | 0.0335 | 0.0765 | 0.0585 | 0.1316 | 0.0952 | 0.1913 | 0.1409 | |
| High-Efficiency | 0.0318 | 0.0221 | 0.0359 | 0.0226 | 0.0418 | 0.0281 | 0.0466 | 0.0325 | 0.0849 | 0.0647 | 0.1289 | 0.0951 | 0.1883 | 0.1353 | |
| Medium | Experimental | 0.0598 | 0.0399 | 0.0623 | 0.0382 | 0.0686 | 0.0456 | 0.0809 | 0.0557 | 0.1327 | 0.0967 | 0.2258 | 0.1664 | 0.3330 | 0.2534 |
| Classic | 0.0573 | 0.0401 | 0.0655 | 0.0408 | 0.0703 | 0.0486 | 0.0864 | 0.0622 | 0.1341 | 0.1025 | 0.2372 | 0.1713 | 0.3617 | 0.2805 | |
| High-Efficiency | 0.0585 | 0.0405 | 0.0675 | 0.0424 | 0.0739 | 0.0505 | 0.0832 | 0.0586 | 0.1416 | 0.1035 | 0.2317 | 0.1684 | 0.3248 | 0.2431 | |
| Heavy | Experimental | 0.0802 | 0.0542 | 0.0831 | 0.0522 | 0.0877 | 0.0597 | 0.1037 | 0.0727 | 0.1625 | 0.1197 | 0.2750 | 0.2006 | 0.3759 | 0.2740 |
| Classic | 0.0699 | 0.0483 | 0.0759 | 0.0483 | 0.0881 | 0.0600 | 0.0998 | 0.0700 | 0.1593 | 0.1201 | 0.2713 | 0.2017 | 0.4033 | 0.3076 | |
| High-Efficiency | 0.0786 | 0.0545 | 0.0835 | 0.0531 | 0.0881 | 0.0608 | 0.1041 | 0.0751 | 0.1673 | 0.1277 | 0.2727 | 0.1990 | 0.4143 | 0.3137 | |
| Average (simulates full data set) | 0.0565 | 0.0388 | 0.0614 | 0.0386 | 0.0670 | 0.0457 | 0.0782 | 0.0552 | 0.1274 | 0.0956 | 0.2120 | 0.1552 | 0.3103 | 0.2332 | |
In Table 5, two levels of accuracy may be observed; the first three models—(Fe + Mn + Mo + Co), (Fe + Mn), and (Fe + Mo)—have a clearly higher level of accuracy than the remaining models. Although the more complex model, i.e. (Fe + Mn + Mo + Co), once again achieved the best performance, its differences with the (Fe + Mn) and the (Fe + Mo) models were not significant.
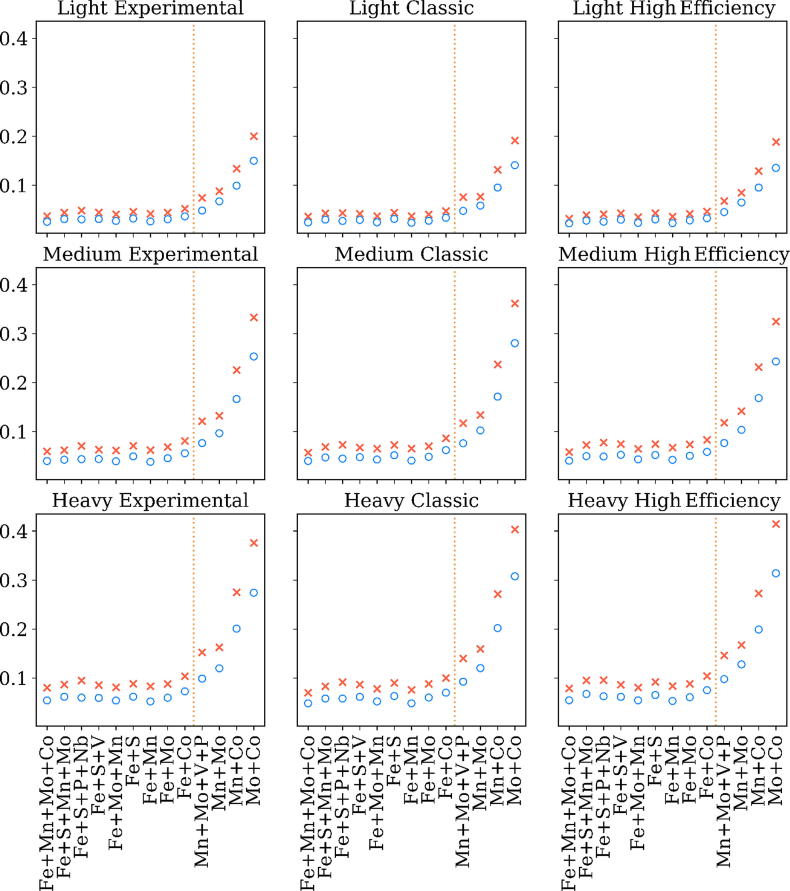
From Table 5, the proportion of iron is expected to significantly affect the process of wear. The 13 tested combinations of features for the 9 subsets in terms of their RMSE and MAE were compiled in Fig. 4 to verify this expectation. Fig. 4 shows small differences in the performance of the combinations which contain Fe and greater differences in the performance of the combinations which do not contain Fe (separated by a vertical line in each graph). In fact, a common pattern can be identified in the performance of the nine models (a curve which grows smoothly to the right). This pattern justifies the division of the original data set into nine subsets because the pattern clarifies that the features related to the casting process of the steel plates functioned independently from the features related to the chemical composition used in the prediction of the plate lifetime.
Fig. 4.
MLP model performance comparison. Crosses (X) represent RMSE values, whereas circles (O) represent MAE values. The models presented at the left of each graph have Fe as an input, unlike the models on the right.
Model complexity
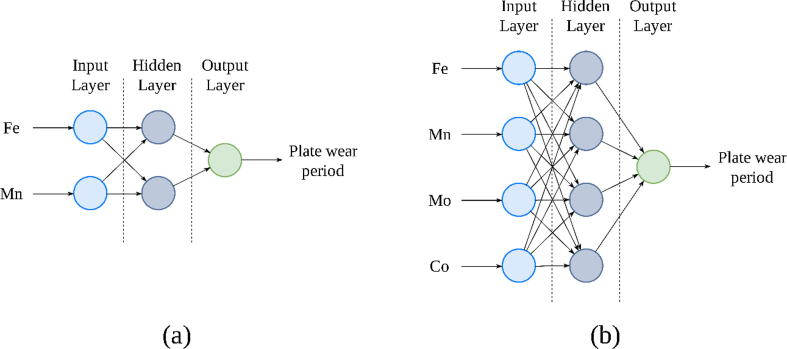
As previously mentioned, in terms of performance, the best model is the Fe + Mn + Mo + Co MLP; nevertheless, other aspects can also be considered, such as the complexity of the model which is generated. Fig. 5 shows the MLP topologies of the best model built in Section 4.1.2 with the lowest number of possible inputs (two) and the best model regardless of the number of inputs. The Fe + Mn MLP is composed of only five neurons; therefore, it only has to learn six weights. The Fe + Mn + Mo + Co MLP is more complex; it is composed of 9 neurons and has to learn 20 weights. Hence, a longer training time is needed. The Fe + Mn MLP model was selected as the best option for the plate-lifetime prediction owing to the similar performance of both models and the fact that the first one required fewer inputs and shorter training times.
Fig. 5.
Topologies of MLP models built using Fe + Mn feature combination (a), and Fe + Mn + Mo + Co feature combination (b).
In Table 6, the above assertion is clearly demonstrated. The table presents the performance of the different models built during this research, as well as the training times which are required by the computer to build each model. The RMSE and the MAE for the nine models built by subsets are the corresponding averages of the nine models, whereas in the case of the training time, it is the sum of the nine training times.
Table 6.
Performance comparison of tree and MLP models considering the entire data set and the nine subsets in terms of model accuracy and training time.
| REPTree full data set, all features | MLP full data set, all features | REPTree 9 subsets, all features | Fe + Mn MLP 9 subsets, 2 features | Fe + Mn + Mo + Co MLP 9 subsets, 4 features | |
|---|---|---|---|---|---|
| RMSE (h) | 1.8134 | 0.8739 | 0.5989 | 0.0614 | 0.0565 |
| MAE (h) | 1.5059 | 0.6574 | 0.2584 | 0.0386 | 0.0388 |
| Training Time (s) | 0.0011 | 25.0294 | 0.0009 | 0.1413 | 0.2085 |
As previously described, the accuracy of each model summarised in Table 6 indicates a drastic improvement between nine-subset models and full-dataset models (e.g. the RMSE dropped from 1.8134 h with the full dataset to 0.5989 h with the nine subsets and the REPTree model). Second, the training times were shorter as well, particularly in the case of the MLP models. In this case, the decrease was approximately 99% of the training time of the entire dataset owing to the greater simplicity of the new models.
Industrial implementation
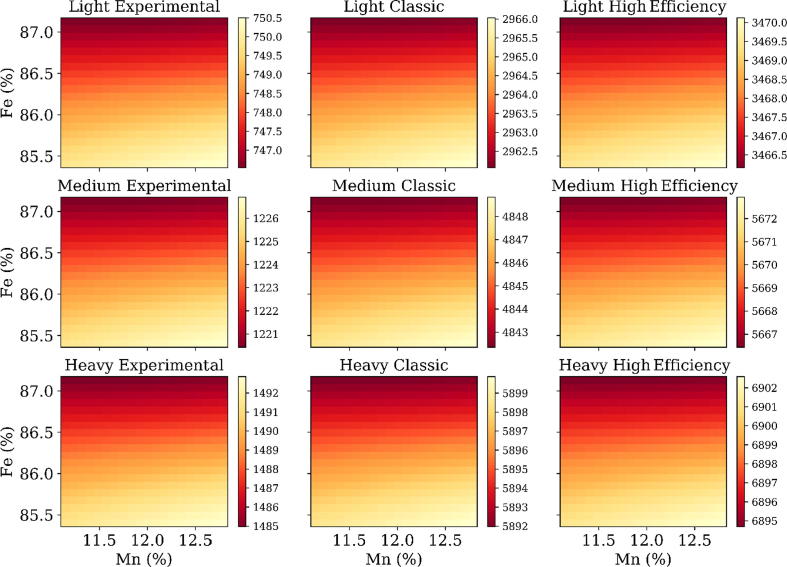
The identification and training of a high-accuracy prediction model might not be sufficient for its successful implementation under real industrial conclusions. Manufacturing industries expect visual tools with which quick and direct decisions can be taken on the best manufacturing conclusions for a certain quality requirement. Therefore, the best model in terms of low-complexity and high-accuracy—developed in the previous section (nine Fe + Mn MLPs, one for each pair of casting method–type of cast plate)—will now be used to build nine different heat maps. A heat map is a 2D representation of two inputs, where the colour of each pixel represents a value of a certain output. In this case study, there is one industrial quality requirement, namely the plate lifetime, whereas there are four inputs which mainly affect the output: the casting method, the type of cast plate, and the percentages of iron and manganese in the chemical composition of the plate. The influence of the first two inputs is great, whereas the influence of the second two is smaller. Hence, it is more suitable to build nine heat maps, one for each combination of the two first inputs, and to use the X and Y axis to represent the respective percentages of manganese and iron. Fig. 6 illustrates the nine heat maps. It is important to notice that the colour scale of each graph differs, whereas the X and the Y axes are the same, thus facilitating a simultaneous overview of the nine graphs.
Fig. 6.
Heat maps generated with the nine Fe + Mn MLPs prediction models for the plate lifetime.
This figure can be consulted in two steps. First, it is necessary to identify the proper lifetime range which is expected for a certain plate and to select the graph in the figure which includes this range. After this first step, the proper casting method and the type of cast plate will have already been fixed. Then, the desired plate-lifetime parameters may be found by searching the selected graph for the combination range of iron and manganese. As an example of the use of the information in Fig. 6, if a plate were to be manufactured with an expected lifetime of 2964.0 h, the graph in the middle column in the first row should be selected; therefore, the plate should be manufactured using the Light–Classic combination. The iron percentage should remain within the range of 85.8–86.5%, whereas the manganese percentage should remain within the range of 11.7–12.3%, as reflected by the medium-grey colour scale of this graph, to achieve the desired plate lifetime.
Conclusions
A hybrid model has been developed to measure the influence of the chemical composition of Hadfield steel on the lifetime of (light, medium, and heavy) crusher plates produced via three different casting methods. A regression analysis established a considerable influence of Fe, Mn, Mo, and Co. Moreover, Fe and Mn had a significant effect because they formed manganese austenite, which is capable of cold-work strengthening during abrasive impacts. The effect of Mo on the wear limit in steel can be explained by carbide and nitrite-forming effects during the crystallisation of the alloy. Cobalt is inherently wear-resistant and hard, which positively affects the lifetime of steel crusher plates.
The proposed hybrid strategy for the modelling of the lifetime of a plate could be divided into three steps. First, decision trees were used for the extraction of the main information included in the training dataset. These trees allowed us to conclude from the experimental data that the type of cast plate and the casting method were the most influencing factors. Therefore, the dataset could be divided into nine subsets, one for each paired type of cast plate and casting method, to model the influence of the chemical composition of the plates with greater accuracy. Second, ANNs were proposed for the development of high-accuracy prediction models after comparing their performance with those of other machine-learning techniques. A detailed discussion on the best ANNs structure was presented, taking into account the most relevant inputs. The results have shown that an ANN based only on the Fe, Mn, Mo, and Co proportions would provide the most accurate model, as well as a combination of two (Fe + Mn). Hence, the decision was made to test all the possible combinations of both components extracted from the best combination thus far, i.e. Fe + Mn + Mo + Co (RMSE of 0.056 h). Finally, a better option was proposed from an analysis of the complexity of the machine-learning model: an ANN which only processes the Fe and Mn proportion; this model would have a slightly lower accuracy (RMSE of 0.061 h); however, its complexity would be significantly lower, which would simplify its tuning process and shorten its training time.
Finally, the identification of a high-accuracy prediction model might not be sufficient for its successful implementation under real industrial conclusions. Therefore, the best model (nine Fe + Mn MLPs, one for each pair of casting method and type of cast plate) was reproduced on a heat map, i.e. a 2D representation of the main inputs of the manufacturing process with a colour scale to represent the value of the predicted output, namely the lifetime of the manufactured plates. Considering the nature of the dataset, the most suitable heat map in this case was divided into nine submaps, one for each combination of plate type and casting method; the X and Y axes showed the value of the Fe and Mn proportions in the plate. A quick visual analysis of this heat map provides useful and immediate information to the process engineer for the selection of the best manufacturing technology and chemical composition of the plate, depending on the wear-limit requirements of any workpiece.
Future research will be focused on the effect that a higher dispersion in the composition of the plates can have on the accuracy of the machine-learning model. This extension of the dataset, from a medium dataset to big data, can also affect the proposed methodology, and specific machine-learning models for big data might be tested, such as deep neural networks. Proposals for future work include a study of the micro-alloying of Hadfield steel and its effect on the wear-limit resistance of crushing plates with minimum ratios of iron (85.357%) and manganese (12.832%), which correspond to the maximum full lifetime of a crusher plate, in accordance with the previously presented diagrams.
Conflict of interest
The authors have declared no conflict of interest.
Compliance with Ethics Requirements
This article does not contain any studies with human or animal subjects.
Acknowledgments
The work was supported by Act 211 of the Government of the Russian Federation, Russia (contract № 02.A03.21.0011), by the project TIN2015-67534-P of the Ministerio de Economía Competitividad of the Spanish Government, Spain, and the project BU085P17 of the Junta de Castilla y León (both projects co-financed through European-Union FEDER funds) and by the Consejería de Educación of the Junta de Castilla y León and the European Social Fund with the EDU/1100/2017 pre-doctoral fellowships. The research was conducted within the South-Ural State University, Chelyabinsk city, Russia, Project 5-100 from 2016 to 2020, aiming to increase the competitiveness of leading Russian universities among global research and educational centres. The authors gratefully acknowledge the support of NVIDIA Corporation and its donation of the Titan Xp GPU used in this research, as well as Dr. Alvar Arnaiz from the University of Burgos for his kind-spirited and useful advice.
Footnotes
Peer review under responsibility of Cairo University.
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jare.2019.03.008.
Appendix A. Supplementary material
The following are the Supplementary data to this article:
References
- 1.Siafakas D., Matsushita T., Lauenstein Å., Ekerot S., Jarfors A.E.W. A particle population analysis in Ti- and Al- deoxidized Hadfield steels. Int J Cast Metal Res. 2018;31(3):125–134. [Google Scholar]
- 2.Agunsoye J.O., Talabi S.I., Bello O. Wear characteristics of heat-treated Hadfield austenitic manganese steel for engineering application. Adv Prod Eng Manag. 2015;10(2):97–107. [Google Scholar]
- 3.Parzych S. The effect of heat treatment on microstructure and mechanical properties of cast bainitic steel used for frogs in railway crossovers. Arch Metall Mater. 2017;62(4):2147–2151. [Google Scholar]
- 4.Tęcza G., Zapała R. Changes in impact strength and abrasive wear resistance of cast high manganese steel due to the formation of primary titanium carbides. Arch Found Eng. 2018;18(1):119–122. [Google Scholar]
- 5.Luo K., Bai B. Microstructure, mechanical properties and high stress abrasive wear behavior of air-cooled MnCrB cast steels. Mater Des. 2010;31(5):2510–2516. [Google Scholar]
- 6.Vdovin K.N., Feoktistov N.A., Gorlenko D.A., Chernov V.P., Khrenov I.B. Influence of alloying and thermal treatment on abrasive and impact-abrasive wear resistance of castings produced from high-manganese steel. Izvestiya Vysshikh Uchebnykh Zavedenij. Chernaya Metallurgiya. 2017;60(11):904–909. [Google Scholar]
- 7.Vdovin K.N., Feoktistov N.A., Gorlenko D.A., Chernov V.P., Khrenov I.B. Influence of alloying and heat treatment on the abrasive and impact-abrasive wear resistance of high-manganese steel. Steel Transl. 2017;47(11):705–709. [Google Scholar]
- 8.Feng X.Y., Zhang F.C., Yang Z.N., Zhang M. Wear behaviour of nanocrystallised Hadfield steel. Wear. 2013;305(1–2):299–304. [Google Scholar]
- 9.Abbasi M., Kheirandish S., Kharrazi Y., Hejazi J. On the comparison of the abrasive wear behavior of aluminum alloyed and standard Hadfield steels. Wear. 2010;268(1):202–207. [Google Scholar]
- 10.Kolokoltsev V.M., Vdovin K.N., Gorlenko D.A., Gulin A.E. Calculation of stacking fault energy and its influence on abrasive wear resistance of Hadfield cast steel cooled at different rates. CIS Iron Steel Rev. 2016;11:35–40. [Google Scholar]
- 11.El-Fawkhry M.K., Fathy A.M., Eissa M.M., El-Faramway H. Eliminating heat treatment of Hadfield steel in stress abrasion wear applications. Int J Metalcast. 2014;8(1):29–36. [Google Scholar]
- 12.Kalandyk B., Tęcza G., Zapała R., Sobula S. Cast high-manganese steel-the effect of microstructure on abrasive wear behaviour in Miller test. Arch Found Eng. 2015;15(2):35–38. [Google Scholar]
- 13.Smith R.W., DeMonte A., Mackay W.B.F. Development of high-manganese steels for heavy duty cast-to-shape applications. J Mater Process Technol. 2004;153–154(1–3):589–595. [Google Scholar]
- 14.Tęcza G., Głownia J. Resistance to abrasive wear and volume fraction of carbides in cast high-manganese austenitic steel with composite structure. Arch Found Eng. 2015;15(4):129–133. [Google Scholar]
- 15.Głownia J., Tȩcza G., Asłanowicz M., Ościłowski A. Tools cast from the steel of composite structure. Arch Found Eng. 2013;58(3):803–808. [Google Scholar]
- 16.Najafabadi V.N., Amini K., Alamdarlo M.B. Investigating the effect of titanium addition on the wear resistance of Hadfield steel. Metall Res Technol. 2014;111(6):375–382. [Google Scholar]
- 17.Zhong L., Wu T., Guo S., Li J. Microstructure and mechanical properties of (Fe, Cr)7C3-Fe/Hadfield steel composites. J Compos Mater. 2015;49(20):2433–2440. [Google Scholar]
- 18.Zhang G.-S., Xing J.-D., Gao Y.-M. Impact wear resistance of WC/Hadfield steel composite and its interfacial characteristics. Wear. 2006;260(7–8):728–734. [Google Scholar]
- 19.Erdakov I.N., Tkachev V.M., Novokreshchenov V.V. Increase of wear resistance of steel plates for crushing stations. J Frict Wear. 2014;35(6):739–745. [Google Scholar]
- 20.Erdakov I.N., Karpinskii A.V., Novokreshchenov V.V. Analysis of pore formation and impeded shrinkage of an alloy in the system ProCast. Metallurgist. 2014;58(2–4):243–249. [Google Scholar]
- 21.Erdakov I.N. Computerized study of intense deformed state of grinding plate of high-manganese steel. Solid State Phenom. 2018;284:563–567. [Google Scholar]
- 22.Erdakov I.N., Ivanov V.A., Pashnyov V.A., Fekolin P.V., Davydov V., Walter R., Pimenov D.Yu. Studies of highly filled composite based on two-component organic binder stress state in thermal stress. Procedia Manuf. 2018;22:325–330. [Google Scholar]
- 23.Bustillo A., Grzenda M., Macukow B. Interpreting tree-based prediction models and their data in machining processes. Integr Comput-Aid Eng. 2016;23(4):349–367. [Google Scholar]
- 24.Pimenov D.Yu., Bustillo A., Mikolajczyk T. Artificial intelligence for automatic prediction of required surface roughness by monitoring wear on face mill teeth. J Intell Manuf. 2017;29(5):1045–1061. [Google Scholar]
- 25.Bustillo A., Pimenov D.Yu., Matuszewski M., Mikolajczyk T. Using artificial intelligence models for the prediction of surface wear based on surface isotropy levels. Robot Comput Integr Manuf. 2018;53:215–227. [Google Scholar]
- 26.Markopoulos A.P., Manolakos D.E., Vaxevanidis N.M. Artificial neural network models for the prediction of surface roughness in electrical discharge machining. J Intell Manuf. 2008;19(3):283–292. [Google Scholar]
- 27.Grzenda M., Bustillo A. Semi-supervised roughness prediction with partly unlabeled vibration data streams. J Intell Manuf. 2018 Article in press:1-13. [Google Scholar]
- 28.Raju M., Gupta M.K., Bhanot N., Sharma V.S. A hybrid PSO–BFO evolutionary algorithm for optimization of fused deposition modelling process parameters. J Intellig Manuf. 2018 Article in press:1-16. [Google Scholar]
- 29.Simunovic K., Simunovic G., Saric T. Predicting the surface quality of face milled aluminium alloy using a multiple regression model and numerical optimization. Meas Sci Rev. 2013;13(5):265–272. [Google Scholar]
- 30.Mikołajczyk T., Nowicki K., Bustillo A., Pimenov D.Yu. Predicting tool life in turning operations using neural networks and image processing. Mech Syst Sign Process. 2018;104:503–513. [Google Scholar]
- 31.Mikołajczyk T., Nowicki K., Kłodowski A., Pimenov D.Yu. Neural network approach for automatic image analysis of cutting edge wear. Mech Syst Sign Process. 2017;88:100–110. [Google Scholar]
- 32.Breiman L., Friedman J.H., Olshen R.A., Stone C.J. Classification and regression trees (Book) Classif Regress Trees. 2017:1–358. [Google Scholar]
- 33.Witten I.H., Frank E., Hall M.A., Pal C.J. Data Mining: Practical Machine Learning Tools and Techniques. 2016. Data Mining: Practical Machine Learning Tools and Techniques (Book) pp. 1–621. [Google Scholar]
- 34.Rodríguez J.J., Quintana G., Bustillo A., Ciurana J. A decision-making tool based on decision trees for roughness prediction in face milling. Int J Comput Integr Manuf. 2017;30(9):943–957. [Google Scholar]
- 35.Kuhn M., Johnson K. Springer, New York; New York, NY: 2013. Applied predictive modeling (Book). Applied Predictive Modeling; pp. 1–600. [Google Scholar]
- 36.Hornik K., Stinchcombe M., White H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989;2(5):359–366. [Google Scholar]
- 37.McCulloch W.S., Pitts W. A logical calculus of the ideas immanent in nervous activity. Bull Mathem Biophys. 1943;5(4):115–133. [PubMed] [Google Scholar]
- 38.Rumelhart D.E., Hinton G.E., Williams R.J. Readings in Cognitive Science: A Perspective from Psychology and Artificial Intelligence. 2013. Learning Internal Representations by Error Propagation (Book Chapter) pp. 399–421. [Google Scholar]
- 39.LeCun YA, Bottou L, Orr GB, Müller K-R. Efficient backprop. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 7700 LECTURE NO. 2012:9–48.
- 40.Gurevich P, Stuke H. Learning uncertainty in regression tasks by artificial neural networks; Jul. 2017.
- 41.Collobert R., Bengio S. Proceedings, Twenty-First International Conference on Machine Learning, ICML 2004. 2004. Links between Perceptrons, MLPs and SVMs; pp. 177–184. [Google Scholar]
- 42.Rosenblatt F. The perceptron: a probabilistic model for information storage and organization in the brain. Psychol Rev. 1958;65(6):386–408. doi: 10.1037/h0042519. [DOI] [PubMed] [Google Scholar]
- 43.Leonard J.A., Kramer M.A. Radial basis function networks for classifying process faults. IEEE Control Syst. 1991;11(3):31–38. [Google Scholar]
- 44.Hall M., Frank E., Holmes G., Pfahringer B., Reutemann P., Witten I.H. The WEKA data mining software: an update. ACM SIGKDD Explor Newsletter. 2009;11:10–18. [Google Scholar]
- 45.Bustillo A., Ukar E., Rodriguez J.J., Lamikiz A. Modelling of process parameters in laser polishing of steel components using ensembles of regression trees. Int J Comput Integr Manuf. 2011;24(8):735–747. [Google Scholar]
- 46.Cho S., Binsaeid S., Asfour S. Design of multisensor fusion-based tool condition monitoring system in end milling. Int J Adv Manuf Technol. 2010;46(5–8):681–694. [Google Scholar]
- 47.Willmott C.J. Some comments on the evaluation of model performance. Bul Amer Meteorol Soc. 1982;63(11):1309–1313. [Google Scholar]
- 48.Willmott C.J., Matsuura K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim Res. 2005;30(1):79–82. [Google Scholar]
- 49.Chai T., Draxler R.R. Root mean square error (RMSE) or mean absolute error (MAE)? – Arguments against avoiding RMSE in the literature. Geosci Model Dev Discuss. 2014;7(1):1525–1534. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.