Abstract
First-principles evolutionary algorithms are employed to shed light on the phase stability of Al–Nb intermetallics. While the tetragonal Al3Nb and AlNb2 structures are correctly identified as stable, the experimentally reported Laves phase of AlNb3 yields soft phonon modes implying its dynamical instability at 0 K. The soft phonon modes do not disappear even upon elevating the temperature in the simulation up to 1500 K. X-Ray diffraction patterns recorded for our powder-metallurgically produced arc cathodes, however, clearly show that the AlNb3 phase exists. We propose that AlNb3 is dynamically stabilised by ordered antisite defects at the Al sublattice, leading also to a shift of the Nb content from 75 to ∼81 at.%. Unlike the defect-free AlNb3, the antisite-stabilised variant hence falls into the compositional range consistent with our CALPHAD-based phase diagram as well as with the previous reports.
Keywords: ab initio, CALPHAD, phase stability, phonons, point defects, AlNb3
1. Introduction
Intermetallics containing Al—the most abundant metal in the Earth’s solid crust—and transition metals (TMs) exhibit resistance to oxidation and corrosion, considerable hardness, low density, and high melting points [1,2]. Owing to their low diffusivity in Al, TMs perfectly meet the requirements for long-term strengthening of aluminides at elevated temperatures, which is an important prerequisite for applications in high-performance automobiles, railway cars, airplanes, spacecrafts or light ships. Among transition metals, Nb is a promising alloying element to improve wear resistance and strength of Al compounds [3]. The difference in crystal structure (bcc-Nb, fcc-Al) together with the largely disparate melting points (2743 and 942 K for Nb and Al, respectively), nevertheless, makes niobium aluminide compounds challenging to prepare as bulk. In terms of thin films, physical vapour deposition (PVD) techniques, such as magnetron sputter deposition or cathodic arc deposition (CAD), allow for synthesis of materials from the vapour phase [4]. Using such plasma-based deposition processes, phases not accessible by bulk methods, e.g., metastable phases, can be synthesised. However, the plasma properties and hence the thin film growth conditions are largely affected by the presence of the cathode surface, which is in a direct contact with plasma. In particular, in the case of CAD the formation of intermetallic phases on the cathode surface due to the exposure to the plasma affects the plasma properties, such as ion charge states and energies [5,6,7].
The published Al–Nb phase diagrams [3,8,9,10,11,12] show three single-phase fields corresponding to intermetallic phases: the body-centred tetragonal (bct) ε-Al3Nb (I4/mmm, #139, DO22), the tetragonal σ-AlNb2 (P42/mnm, #136), and the cubic δ-AlNb3 (Pm3n, #223, A15) phase. According to Jorda et al. [3], the -phase is promising as a superconductor with transition temperature [13]. Wen et al. [14] have recently correlated superconducting properties of δ-AlNb3 with kinetic mechanism of its phase formation. The authors further stated that deviations from the exact 1:3 Al-to-Nb stoichiometry leads to a significant decrease of . Intriguingly, the reported compositional window for δ-AlNb3 does not contain the nominal composition [12]. He et al. [15] have recently pointed out further discrepancies regarding the homogeneity ranges and melting points of Al–Nb compounds reported in the literature and proposed a new thermodynamic description of the system. Still, also their phase diagram calculated for temperatures 500–2500 K features for AlNb3 stability range xNb = 0.79–0.84, which is a somewhat surprising span for a phase with nominally .
Applying ab initio and CALPHAD calculations, we aim to clarify the (meta)stability and stoichiometry of -AlNb3 as well as to extend the existing phase diagrams to lower temperatures. According to our DFT predictions, Al3Nb and AlNb2 are the only stable phases at 0 K, while the lowest-energy -AlNb3 crystallographic variant still appears above the convex hull line (connecting all stable structures in the Al–Nb system). Moreover, phonon spectrum of -AlNb3 shows imaginary phonon frequencies from 0 up to 1500 K, which disproves any temperature-induced dynamical stabilisation. Yet this phase is present in both our CALPHAD-based phase diagram and XRD patterns recorded for powder-metallurgically produced arc cathodes. We show that the stability of AlNb3 is conditioned by the presence of point defects, which further allow to reach the experimentally reported higher Nb contents.
2. Modelling and Experimental Details
The phase diagram of Al–Nb binary system was constructed using CALculation of PHAse Diagram (CALPHAD) method [16]. Thermodynamic description proposed by Witusiewicz et al. [12] was adopted, whereas the parameters for pure Al were slightly modified. Importantly, as Gibbs free energies for the stable and metastable structures of the pure elements were taken from the SGTE database [17], the calculated phase diagram is valid only above 298.15 K.
To access even lower temperatures, Density Functional Theory (DFT) calculations were performed using the Vienna Ab-initio Simulation Package (VASP) [18,19] together with plane-wave projector augmented wave (PAW) pseudopotentials [20] and the Perdew-Burke-Ernzerhof generalized gradient approximation [21] for the exchange and correlation effects. The plane-wave cutoff energy of 600 eV and the k-vector sampling of the Brillouin zone ensured a total energy accuracy of 10−3 eV/at. or better. The binary Al3Nb, AlNb2, and AlNb3, were assumed to adopt the bct DO22 (I4/mmm, #139, ), tetragonal D8b (P42/mnm, #136, ), and cubic A15-type (Pm3n, #223, ) structure, respectively. Equilibrium lattice parameters were determined by fitting the energy vs. volume data with the Birch-Murnaghan equation of state [22]. Additional structural candidates for low-energy Al–Nb intermetallics were predicted employing first-principles evolutionary algorithms as implemented in the USPEX (Universal Structure Predictor: Evolutionary Xtallography) code [23,24,25]. In order to reveal Al1−xNbx structures with different Nb contents, we performed two USPEX runs in a variable-composition mode with 4–16 and 16–32 atoms in the simulation cell, respectively, with 150 individuals in the initial generation and 80 in the subsequent ones. To compare relative chemical stability of the predicted compounds, energy of formation, , was calculated according to
| (1) |
where is the total energy of the simulation cell, and are the number of atoms and the chemical potential, respectively, of a species . The total energies per atom of fcc-Al and bcc-Nb were conventionally adopted for the and chemical potentials, respectively. To identify the stable compounds, the convex hull was constructed by connecting the local minima in the vs. composition plot. At compositions with a potentially stable or nearly stable structures (i.e., lying on or closely above the convex hull), fixed-composition USPEX runs were performed with variable number of formula units from 1 up to 10. Furthermore, point defects (vacancies and antisites) were distributed in the δ-AlNb3 in either ordered, or disordered manner. The former configuration will be described later (Figure 5 and the corresponding discussion), while the latter was achieved by employing the Special Quasi-random Structure (SQS) method [26]. To verify whether or not the proposed structures satisfy conditions for dynamical stability, phonon dispersion curves throughout the Brillouin zone and phonon density of states were analysed employing the finite-displacement approach as implemented in the PHONOPY package [27]. Furthermore, we employed the self-consistent ab initio lattice dynamical method (SCAILD) [28] which allows to simulate temperature dependent phonon dispersion curves and densities of states. Elastic properties for selected structural candidates were evaluated by applying the stress-strain method [29,30], which yields the fourth-rank elastic tensor from the Hooke’s law, based on the predefined strains and the computed stresses. Using the Voigt’s notation, the obtained fourth-rank elastic tensors were projected onto 6 × 6 elastic matrices, imposing the symmetry of the equilibrium simulation cells [31]. The polycrystalline bulk, B, shear, E, and Young’s moduli, E, were evaluated using the standard formulae, see e.g., Supplemental material for Ref. [32].
On the experimental side, the AlNb3 cathode was produced by powder-metallurgical methods and purchased from Plansee Composite Materials GmbH in Lechbruck am See, Germany. The phases prevalent in the cathode were structurally characterised by means of X-ray diffraction (XRD) using a Bruker-AXS D8 Advance. diffractometer equipped with Cu-Kα radiation and parallel optics. The diffractogram was recorded at 2 angles ranging from 10 to 120° with a step size of 0.035° and a dwell time of 2s per step. For the determination of the lattice parameters by means of a Rietveld refinement, we applied the commercial software package TOPAS supplied by Bruker AXS, USA. Furthermore, the elemental composition of the cathode was measured by energy-dispersive X-ray spectroscopy (EDX) using an Oxford Instruments INCA EDX system which was attached to a Zeiss EVO 50 scanning electron microscope (SEM).
3. Results and Discussion
3.1. Al–Nb Phase Diagram down to 0 K
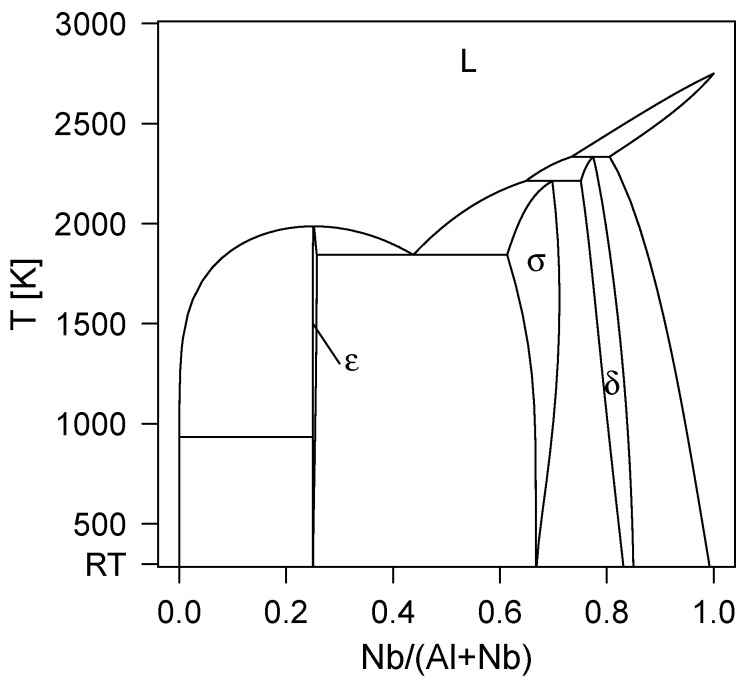
In accordance to the previous thermodynamic assessments of Al–Nb system [9,11,12,15], our CALPHAD-based phase diagram, Figure 1, shows ε-Al3Nb, σ-AlNb2, and δ-AlNb3 as stable phases. The stability range of δ-AlNb3 turns out to be peculiar in the same way as for the previous CALPHAD models, i.e., does not contain the nominal composition, but actually goes far beyond that—up to about 82–84 at.% of Nb—when temperature decreases down to room temperature, 298.15 K.
Figure 1.
CALPHAD-based phase diagram of the binary Al–Nb system from room temperature (RT) up to 3000 K showing the ε-Al3Nb, σ-AlNb2, and δ-AlNb3 phase.
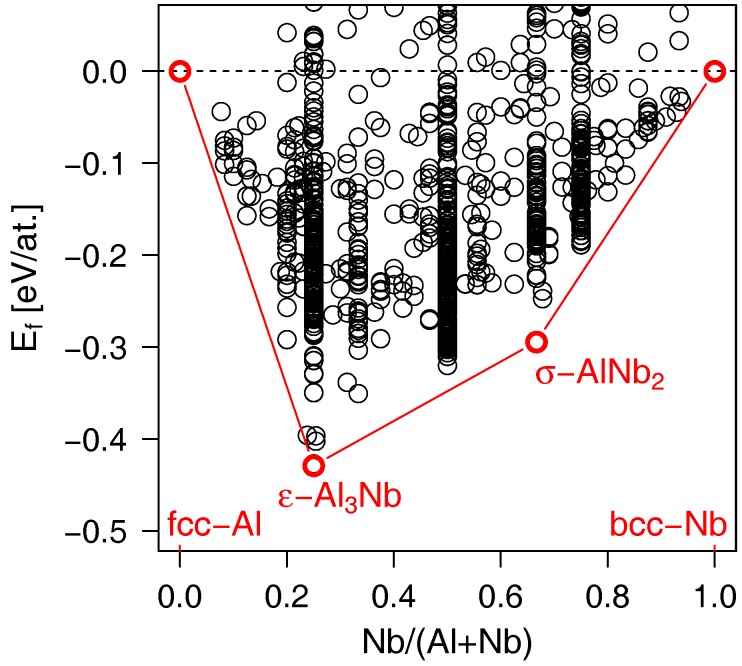
In order to investigate phase stability at even lower temperatures, in particular, to probe the extreme 0 K case, we employed ab initio calculations. No assumption on either stoichiometries, or crystal structures of the stable Al–Nb intermetallics was made. Instead, various Al1−xNbx structural candidates were generated by the evolutionary algorithm USPEX and subsequenty relaxed by DFT. The measure of their chemical stability was quantified by calculating formation energy, , which is presented in Figure 2 as a function of the Nb content. To identify the stable compounds, a convex hull is constructed by connecting the local minima in the vs. composition data. The structures lying above the convex hull line and yielding negative values are deemed metastable. As expected, the tetragonal ε-Al3Nb and σ-AlNb2 phases have been correctly reproduced and found on the convex hull (i.e., stable). Nonetheless, the cubic δ-AlNb3—yielding the lowest out of all the predicted polymorphs at the composition—appears about ∼0.03 eV/at. above the convex hull. Such finding disagrees with the previous calculations by Colinet et al. [10] employing the linear-muffin-tin-orbital (LMTO) method in the full potential (FP) approach and reporting δ-AlNb3 on the convex hull line, i.e., as a stable phase, exactly at . Unfortunately, we were unable to reproduce their convex hull irrespectively of various GGA-DFT or LDA-DFT flavours of Al and Nb pseudopotentials used in the simulation.
Figure 2.
Energy of formation, , of various Al1−xNbx structures predicted by first-principles evolutionary algorithm USPEX as a function of the Nb content. The convex hull line (red) connects the stable phases.
Contradictory to the published as well as our own (Figure 1) phase diagrams, no stable compound (i.e., lying on the convex hull) is predicted within the critical compositional window xNb = 0.79–0.84. Here we note that evolutionary algorithms do not guarantee finding the ground state structure, since the search space is infinite in principle, but a finite (user-controlled) number of generations is produced. Naturally, USPEX performs the best for small systems. If a unit cell is so large that it exceeds the (user-controlled) maximum number of atoms allowed in the simulation box, it can never be found. For that reason, additional variable-composition evolutionary search was carried out in the xNb = 0.7–0.9 range with 32–64 atoms in the unit cell, which was, however, computationally demanding and converged very slowly. Being aware of the above limitations, so far we could not disprove the existence of δ-AlNb3 or any other Al1−xNbx structural variant lying within the critical xNb = 0.79–0.84 compositional window.
3.2. Experimental Observation of AlNb3
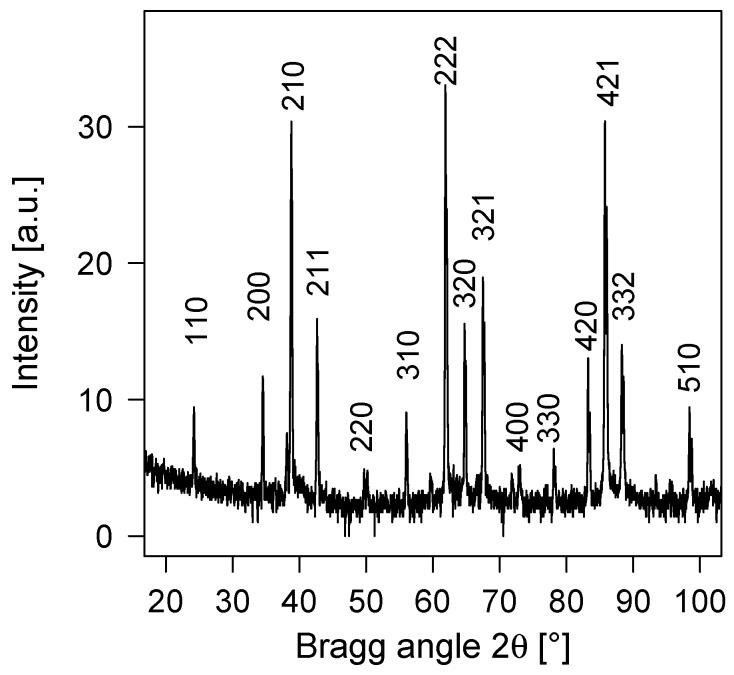
In parallel to the initial calculations, we analysed a cathode with nominal composition available in our laboratory. The resulting X-ray diffractogram recorded in the Bragg-Brentano geometry, is shown in Figure 3. The peaks were labelled using our own DFT-optimised -AlNb3 (lying above the convex hull, cf. Figure 2), thus clearly demonstrating existence of this phase in experiment. The lattice constant determined through Rietveld refinement, Å, is in a good agreement with the DFT calculated value ( Å). The small offset is a well-known overestimation of the lattice constants by the GGA-DFT method. According to the elemental composition obtained by EDX, the chemistry of our sample is Al0.22Nb0.78, i.e., the sample shows a slight Nb overstoichiometry (as compared to the nominal 75 at.% of Nb). Therefore, the experiment (Figure 3) and the phase diagram (Figure 1) are consistent with each other, pointing towards stability of the AlNb3 phase, however, our DFT calculations so far suggest the opposite. To clarify this intriguing disagreement, we now turn our attention to possible stabilisation mechanisms of the -phase.
Figure 3.
Indexed XRD pattern recorded for AlNb3 cathodes.
3.3. Stabilisation Mechanism of δ-AlNb3
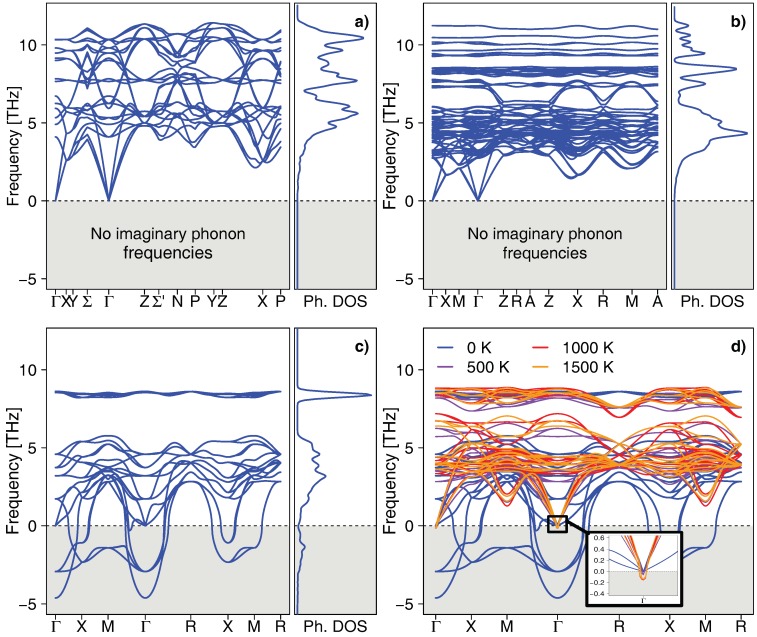
To shed light on the (meta)stability of the AlNb3 phase, lattice dynamics calculations were carried out. Figure 4 clearly demonstrates that while ε-Al3Nb and σ-AlNb2 satisfy conditions for dynamical stability, i.e., all their phonon frequencies are real, the δ-AlNb3 polymorph yields imaginary phonon modes (plotted as modes with negative frequencies) at, e.g., the , X, and M points. Consequently, the atomic displacements corresponding to these soft phonon modes reduce the potential energy in the vicinity of the equilibrium atomic positions. Following some of these modes (not shown here), however, did not shift all the optical phonon branches from the imaginary to real frequencies, i.e., did not lead to a vibrationally stable structure. Additionally, evaluating phonon density of states (DOS) and phonon bandstructure of δ-AlNb3 under compression/tension by setting the cubic lattice parameter below/above the equilibrium value (not shown here) also did not lead to any stabilisation effect.
Figure 4.
Phonon bandstructure and phonon DOS of the -Al3Nb (a), -AlNb2 (b), and -AlNb3 phase (c) at 0 K. The paths in the first Brilloiun zone were chosen based on the crystal symmetry considerations, as proposed by Setyawan and Curtarolo [34]. (d) Phonon bandstructure of -AlNb3 at elevated temperatures.
Despite the lack of dynamical stability at 0 K, the soft phonon modes might still disappear at higher temperatures, particularly when bearing in mind that the formation energy of δ-AlNb3 is only ≈0.03 eV/at. above the convex hull line (cf. Figure 2). Such temperature-induced stabilisation has been previously demonstrated, e.g., for the B2-NiTi phase [33] using the self-consistent ab initio lattice dynamical approach. We therefore employ the same approach also for the -phase of AlNb3, exploring temperatures from 0 up to 1500 K. Figure 4d indicates that despite reducing the imaginary phonon modes noticeably, the effect of elevated temperature is not sufficient to stabilise δ-AlNb3 due to the remaining instabilities at the point. In contrast to the 0 K case, elevated temperature leads to a significant reduction of the gap of forbidden frequencies at ≈6–8 THz. Bandstructure in this particular frequency range, however, does not saturate but changes significantly at each temperature considered (500, 1000, and 1500 K).
3.4. Antisites Leading to the Off-Stoichiometry
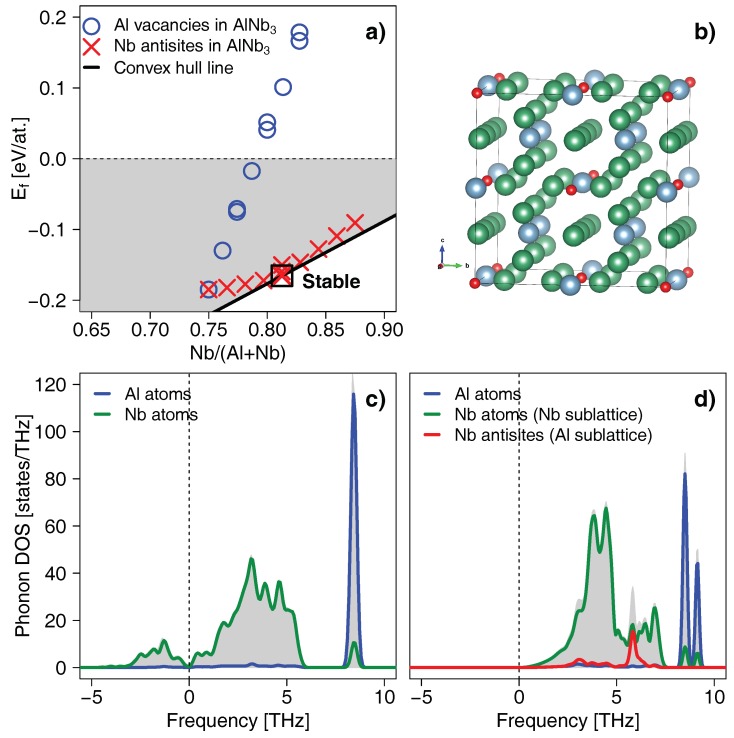
Excluding pressure and temperature induced dynamical stabilisation of the δ-AlNb3 phase, we further investigate the impact of point defects, which have been identified as key contributors to the stabilisation of numerous nitride [35,36,37], oxide [38], and carbide [39,40] systems. Since we wish to slightly alter composition to reach the experimental stability range of the -phase, the desirable defects are those which change stoichiometry. Conveniently, Al vacancies and Nb antisites (i.e., Nb atoms occupying some of the Al lattice sites) allow to shift the Nb content above the nominal 75 at.%. Figure 5a presents formation energies of the defected δ-AlNb3 phase as a function of the Nb content. Clearly, vacancies on the Al sublattice lead to a massive increase of , hence destabilise the structure. Unlike that, increases only slightly upon populating some of the Al sites by Nb, i.e., by introducing antisite defects, and falls exactly on the convex hull line when the Nb content reaches 81.5 at.%. Our DFT calculations further suggest that the Nb antisite defects tend to order, as the disordered configurations (with antisites generated randomly according to the SQS method, cf. the Methodology section) result in slightly higher formation energies (about ∼0.01 eV/at.). The ordered distribution of Nb antisites in -Al0.19Nb0.81 can be described in a way that the Al sublattice forms an fcc-like structure (the structural model is presented in Figure 5b). Such ordered configuration yields lattice parameter of 5.215 Å, which exceeds the 5.196 Å of the defect-free AlNb3. Nevertheless, both these values can be regarded as in agreement with the experimentally estimated lattice parameter of 5.188 Å. Importantly, the corresponding phonon DOS of the ordered -Al0.19Nb0.81 does no longer show imaginary phonon frequencies, which clearly underpins the fact that of this phase falls on the convex hull (Figure 5a). This structural variant is thus dynamically stable. Noteworthy, the relatively large spread of structural parameters, 5.196–5.251 Å, predicted for various antisite distributions from ordered to disordered, overlaps with the 5.196 Å of the defect-free δ-AlNb3. Since the energetic difference of ∼0.01 eV/at. between the ordered the disordered structures becomes negligible at higher temperatures, the defect-free and antisite-containing -phase can be easily exchangeable in experiments.
Figure 5.
(a) Formation energy of the -AlNb3 phase containing Al vacancies (circles) or Nb antisites (crosses) as a function of the Nb content. The black solid line shows the convex hull, while the shaded area denotes region for the chemically stable compounds. (b) The -Al0.19Nb0.81 structural variant with ordered Nb antisites lying on the convex hull. The blue, green, and red spheres denote Al, Nb, and Nb antisite atoms, respectively. The phonon DOS of the defect-free -AlNb3 (c) compared to that of the -Al0.19Nb0.81 with ordered Nb antisites (d). The grey shaded area represents the total phonon DOS, while the solid lines show the partial contribution from Al and Nb atoms.
3.5. Convex Hull at Finite Temperatures
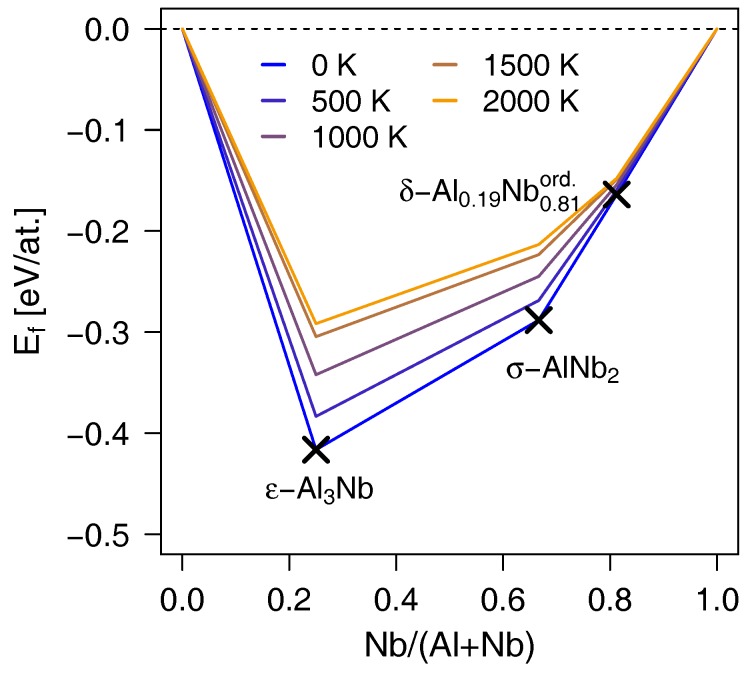
To verify if the proposed -Al0.19Nb0.81 is stable also at higher temperatures, we calculated Helmholtz free energies of the structures forming the convex hull as a function of temperature, T, from 0 up to 2000 K. As the ordered -Al0.19Nb0.81 variant posseses higher symmetry and hence, is computationally easier to handle than the disordered polymorphs, it was considered for investigations of high temperature stability. Nonetheless, we note that Helmholtz free energies of the disordered configurations would have additional contribution form the mixing entropy, helping to stabilise them with respect to the ordered phase. Figure 6 displays the calculated temperature evolution of the Al–Nb convex hull. Interestingly, chemical stability of the -Al0.19Nb0.81 structure is only little affected by T, in contrast to the -Al3Nb and -AlNb2. This small dependence of the Helmholtz free energy on temperature causes that -Al0.19Nb0.81 always falls on the convex hull line and not above it. Hence, despite the overall shape of the convex hull changes noticeably, the stable compounds do not differ from the 0 K case and the antisite-stabilised structure is predicted to form also at higher temperatures.
Figure 6.
Energetics of the stable Al–Nb intermetallics—forming the convex hull—as a function of temperature.
3.6. Mechanical Properties of Stable Phases
Table 1 summarises structural and elastic data calculated for the stable Al1−xNbx phases, including the newly proposed antisite-stabilised ordered -Al0.19Nb0.81. We note that vibrational instability of the -AlNb3 phase at 0 K is related to optical phonons (cf. Figure 4), therefore, cannot be revealed by evaluating elastic constants. Indeed, elastic constants for both -Al0.19Nb0.81 (Table 1) and -AlNb3 (not shown here) satisfy conditions for mechanical stability [41]. Comparing elastic response of all the three stable Al1−xNbx intermetallic phases, i.e., for , our calculations suggest that an increase of x leads to a slight increase of B (from 134 to 165 GPa), whereas both G and E decrease (from 102 to 62 GPa and from 242 to 166 GPa, respectively). While the ratio / obtained for -Al3Nb indicates that the (111) crystallographic direction is stiffer as compared to (100), this is not true for -AlNb2 and -Al0.19Nb0.81 yielding / value of 1.16 and 1.36, respectively. Furthermore, both and values, conventionally employed as relative empirical estimates of ductility [42,43], are predicted to increase with Nb content. We therefore envision that the order of ductility is Al3Nb < AlNb2 < Al0.19Nb0.81.
Table 1.
Lattice parameters of -Al3Nb, -AlNb2, and the ordered -Al0.19Nb0.81 together with the corresponding elastic constants ( in GPa), the polycrystalline bulk (B in GPa), shear (G in GPa) and Youngs’s moduli (E in GPa). The and the Poisson’s ratio () represent ductility estimates, while the / ratio between the Young’s moduli in the (100) and (111) direction relates to elastic isotropy.
| a | c | C 11 | C 12 | C 13 | C 33 | C 44 | B | G | E | B/G | ν | E100/E111 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ϵ-Al3Nb | 3.851 | 8.644 | 248 | 96 | 46 | 267 | 99 | 132 | 102 | 242 | 1.23 | 0.18 | 0.82 |
| σ-AlNb2 | 5.188 | 9.978 | 278 | 98 | 100 | 284 | 74 | 159 | 81 | 208 | 1.96 | 0.28 | 1.16 |
| δ-Al0.19Nb0.81 | 5.215 | 268 | 114 | 54 | 165 | 62 | 166 | 2.62 | 0.33 | 1.36 |
4. Conclusions
Stability of Al1−xNbx intermetallics was re-assessed combining theoretical (CALPHAD, DFT, evolutionary algorithms) and experimental (XRD, EDX) approaches. In agreement with previous reports, our phase diagram (extended down to room temperature) showed -Al3Nb, -AlNb2, and -AlNb3 as stable, yielding a peculiar compositional window xNb = 0.79–0.84 for the AlNb3 phase. First-principles evolutionary algorithms at 0 K, however, only uncovered the -Al3Nb and -AlNb2 intermetallics as stable. The -AlNb3—clearly present in both our phase diagram and XRD patterns recorderd for Al0.25Nb0.75 arc cathode—was found dynamically unstable (featuring imaginary phonon frequencies in the first Brillouin zone). We propose that AlNb3 can be stabilised by populating 25% of Al lattice sites with Nb, i.e., by antisite defects formation. Importantly, the resulting off-stoichimetric -Al0.19Nb0.81 configuration satisfies conditions for dynamical stability, lies on the convex hull line from 0 K up to 2000 K, and falls within the experimental compositional window. Such structural model of -AlNb3 allows to explain a long-standing discrepancy between first principles-based predictions on one hand and experimental observations and thermodynamic assessments on the other hand, and hence brings new and more accurate insights into understanding structural stability of the Al–Nb system.
Acknowledgments
N.K. acknowledges the DOC fellowship from the Austrian Academy of Sciences. Access to computing and storage facilities owned by parties and projects contributing to the National Grid Infrastructure MetaCentrum provided under the programme “Projects of Large Research, Development, and Innovations Infrastructures” (CESNET LM2015042), is greatly appreciated. Additional computational resources were provided by the Vienna Scientific Cluster (VSC). The authors are grateful to Gerhard Hawranek (Montanuniversität Leoben, Austria) for performing the SEM investigations.
Author Contributions
Conceptualization, N.K., D.H., R.F. and P.H.M.; methodology, D.H.; validation, N.K., P.E., S.Z. and S.L.; formal analysis, N.K., P.E., S.Z. and S.L.; investigation, N.K., P.E., S.Z. and S.L.; resources, P.H.M., R.F. and Y.D.; data curation, N.K., P.E. and S.Z.; writing—original draft preparation, N.K.; writing—review and editing, P.E., D.H., R.F., Y.D. and P.H.M.; visualization, N.K.; supervision, D.H. and P.H.M.; project administration, D.H.; funding acquisition, D.H., R.F. and Y.D.
Funding
This research was funded by the Austrian Science Fund (FWF, Project No. P27867-N36) and by the National Natural Science Foundation of China (Grant No. 51531009).
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Bilić A., Gale J.D., Gibson M.A., Wilson N., McGregor K. Prediction of novel alloy phases of Al with Sc or Ta. Sci. Rep. 2015;5:9909. doi: 10.1038/srep09909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Almeida A., Petrov P., Nogueira I., Vilar R. Structure and properties of Al–Nb alloys produced by laser surface alloying. Mater. Sci. Eng. 2001;303:273–280. doi: 10.1016/S0921-5093(00)01838-4. [DOI] [Google Scholar]
- 3.Jorda J., Flükiger R., Muller J. A new metallurgical investigation of the Niobium-Aluminium system. J. Less Common Met. 1980;75:227–239. doi: 10.1016/0022-5088(80)90120-4. [DOI] [Google Scholar]
- 4.Ohring M. Materials Science of Thin Films—Deposition and Structure. 2nd ed. Academic Press; San Diego, CA, USA: 2002. [Google Scholar]
- 5.Franz R., Mendez Martin F., Hawranek G., Polcik P. Erosion behavior of composite Al-Cr cathodes in cathodic arc plasmas in inert and reactive atmospheres. J. Vac. Sci. Technol. 2016;34:021304. doi: 10.1116/1.4941409. [DOI] [Google Scholar]
- 6.Zöhrer S., Anders A., Franz R. Time-resolved ion energy and charge state distributions in pulsed cathodic arc plasmas of Nb-Al cathodes in high vacuum. Plasma Sources Sci. Technol. 2018;27:055007. doi: 10.1088/1361-6595/aabdc7. [DOI] [Google Scholar]
- 7.Zöhrer S., Anders A., Franz R. Influence of Ar gas pressure on ion energy and charge state distributions in pulsed cathodic arc plasmas from Nb–Al cathodes studied with high time resolution. J. Phys. D Appl. Phys. 2019;52:055201. doi: 10.1088/1361-6463/aaeecc. [DOI] [Google Scholar]
- 8.Massalski T., Okamoto H., Subramanian P.R., Kacprzak L. Binary Alloy Phase Diagrams. ASM International; Russell Township, OH, USA: 1990. p. 843. [Google Scholar]
- 9.Servant C., Ansara I. Thermodynamic assessment of the Al-Nb system. J. Chim. Phys. 1997;94:869–888. doi: 10.1051/jcp/1997940869. [DOI] [Google Scholar]
- 10.Colinet C., Pasturel A., Manh D.N., Pettifor D.G., Miodownik P. Phase-stability study of the Al-Nb system. Phys. Rev. B. 1997;56:552. doi: 10.1103/PhysRevB.56.552. [DOI] [Google Scholar]
- 11.Zhu Z., Du Y., Zhang L., Chen H., Xu H., Tang C. Experimental identification of the degenerated equilibrium and thermodynamic modeling in the Al–Nb system. J. Alloys Compd. 2008;460:632–638. doi: 10.1016/j.jallcom.2007.06.033. [DOI] [Google Scholar]
- 12.Witusiewicz V., Bondar A., Hecht U., Velikanova T.Y. The Al–B–Nb–Ti system: IV. Experimental study and thermodynamic re-evaluation of the binary Al–Nb and ternary Al–Nb–Ti systems. J. Alloys Compd. 2009;472:133–161. doi: 10.1016/j.jallcom.2008.05.008. [DOI] [Google Scholar]
- 13.Willens R.H., Geballe T.H., Gossard A.C., Maita J.P., Menth A., Hull G.W., Soden R.R. Superconductivity of Nb3Al. Solid State Commun. 1969;7:837–841. doi: 10.1016/0038-1098(69)90773-X. [DOI] [Google Scholar]
- 14.Wen X., Li X., Zhao H., Ma Z., Yu L., Li C., Liu C., Guo Q., Liu Y. The phase formation mechanism of Nb3Al prepared by mechanical alloying and subsequent sintering and its effect on superconducting properties. Intermetallics. 2018;103:33–39. doi: 10.1016/j.intermet.2018.10.001. [DOI] [Google Scholar]
- 15.He C., Stein F., Palm M. Thermodynamic description of the systems Co–Nb, Al–Nb and Co–Al–Nb. J. Alloys Compd. 2015;637:361–375. doi: 10.1016/j.jallcom.2015.02.182. [DOI] [Google Scholar]
- 16.Ågren J. Calculation of phase diagrams: Calphad. Curr. Opin. Solid State Mater. Sci. 1996;1:355–360. doi: 10.1016/S1359-0286(96)80025-8. [DOI] [Google Scholar]
- 17.Dinsdale A. SGTE data for pure elements. Calphad. 1991;15:317–425. doi: 10.1016/0364-5916(91)90030-N. [DOI] [Google Scholar]
- 18.Kresse G., Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. 1996;54:11169–11186. doi: 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- 19.Kresse G., Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B. 1999;59:1758–1775. doi: 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
- 20.Kohn W., Sham L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965;140:A1133–A1138. doi: 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
- 21.Perdew J.P., Burke K., Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 22.Birch F. Finite elastic strain of cubic crystals. Phys. Rev. 1947;71:809. doi: 10.1103/PhysRev.71.809. [DOI] [Google Scholar]
- 23.Oganov A.R., Glass C.W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006;124:244704. doi: 10.1063/1.2210932. [DOI] [PubMed] [Google Scholar]
- 24.Lyakhov A.O., Oganov A.R., Stokes H.T., Zhu Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 2013;184:1172–1182. doi: 10.1016/j.cpc.2012.12.009. [DOI] [Google Scholar]
- 25.Oganov A.R., Lyakhov A.O., Valle M. How Evolutionary Crystal Structure Prediction Works and Why. Accounts Chem. Res. 2011;44:227–237. doi: 10.1021/ar1001318. [DOI] [PubMed] [Google Scholar]
- 26.Wei S.H., Ferreira L., Bernard J.E., Zunger A. Electronic properties of random alloys: Special quasirandom structures. Phys. Rev. B. 1990;42:9622. doi: 10.1103/PhysRevB.42.9622. [DOI] [PubMed] [Google Scholar]
- 27.Togo A., Oba F., Tanaka I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B. 2008;78:134106. doi: 10.1103/PhysRevB.78.134106. [DOI] [Google Scholar]
- 28.Souvatzis P., Eriksson O., Katsnelson M., Rudin S. The self-consistent ab initio lattice dynamical method. Comput. Mater. Sci. 2009;44:888–894. doi: 10.1016/j.commatsci.2008.06.016. [DOI] [Google Scholar]
- 29.Le Page Y., Saxe P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. Phys. Rev. B. 2002;65:104104. doi: 10.1103/PhysRevB.65.104104. [DOI] [Google Scholar]
- 30.Le Page Y., Saxe P. Symmetry-general least-squares extraction of elastic coefficients from ab initio total energy calculations. Phys. Rev. B. 2001;63:174103. doi: 10.1103/PhysRevB.63.174103. [DOI] [Google Scholar]
- 31.Moakher M., Norris A.N. The closest elastic tensor of arbitrary symmetry to an elasticity tensor of lower symmetry. J. Elast. 2006;85:215–263. doi: 10.1007/s10659-006-9082-0. [DOI] [Google Scholar]
- 32.Tasnádi F., Odén M., Abrikosov I.A. Ab initio elastic tensor of cubic Ti0.5Al0.5N alloys: Dependence of elastic constants on size and shape of the supercell model and their convergence. Phys. Rev. B. 2012;85:144112. doi: 10.1103/PhysRevB.85.144112. [DOI] [Google Scholar]
- 33.Souvatzis P., Legut D., Eriksson O., Katsnelson M.I. Ab initio study of interacting lattice vibrations and stabilization of the β phase in Ni-Ti shape-memory alloy. Phys. Rev. B Condens. Matter Mater. Phys. 2010;81:092201. doi: 10.1103/PhysRevB.81.092201. [DOI] [Google Scholar]
- 34.Setyawan W., Curtarolo S. High-throughput electronic band structure calculations: Challenges and tools. Comput. Mater. Sci. 2010;49:299–312. doi: 10.1016/j.commatsci.2010.05.010. [DOI] [Google Scholar]
- 35.Koutná N., Holec D., Svoboda O., Klimashin F.F., Mayrhofer P.H. Point defects stabilise cubic Mo-N and Ta-N. J. Phys. D Appl. Phys. 2016;49:375303. doi: 10.1088/0022-3727/49/37/375303. [DOI] [Google Scholar]
- 36.Balasubramanian K., Khare S., Gall D. Vacancy-induced mechanical stabilization of cubic tungsten nitride. Phys. Rev. B. 2016;94:174111. doi: 10.1103/PhysRevB.94.174111. [DOI] [Google Scholar]
- 37.Balasubramanian K., Khare S.V., Gall D. Energetics of point defects in rocksalt structure transition metal nitrides: Thermodynamic reasons for deviations from stoichiometry. Acta Mater. 2018;159:77–88. doi: 10.1016/j.actamat.2018.07.074. [DOI] [Google Scholar]
- 38.Koller C., Koutná N., Ramm J., Kolozsvári S., Paulitsch J., Holec D., Mayrhofer P. First principles studies on the impact of point defects on the phase stability of (AlxCr1−x)2O3 solid solutions. AIP Adv. 2016;6:025002. doi: 10.1063/1.4941573. [DOI] [Google Scholar]
- 39.Lasfargues H., Glechner T., Koller C., Paneta V., Primetzhofer D., Kolozsvári S., Holec D., Riedl H., Mayrhofer P. Non-reactively sputtered ultra-high temperature Hf-C and Ta-C coatings. Surf. Coat. Technol. 2017;309:436–444. doi: 10.1016/j.surfcoat.2016.11.073. [DOI] [Google Scholar]
- 40.Riedl H., Glechner T., Wojcik T., Koutná N., Kolozsvári S., Paneta V., Holec D., Primetzhofer D., Mayrhofer P.H. Influence of carbon deficiency on phase formation and thermal stability of super-hard TaCy thin films. Scr. Mater. 2018;149:150–154. doi: 10.1016/j.scriptamat.2018.02.030. [DOI] [Google Scholar]
- 41.Mouhat F., Coudert F.X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B. 2014;90:224104. doi: 10.1103/PhysRevB.90.224104. [DOI] [Google Scholar]
- 42.Pugh S. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954;45:823–843. doi: 10.1080/14786440808520496. [DOI] [Google Scholar]
- 43.Frantsevich I. Reference Book. Naukova Dumka; Kyiv, Ukraine: 1982. Elastic constants and elastic moduli of metals and insulators. [Google Scholar]