Mathematical thinking in children with Developmental Language Disorder: The roles of pattern skills and verbal working memory

Abstract

Previous research suggests that children with language disorders often have difficulties in mathematical tasks. In the current study, we investigated two relevant factors – working memory and pattern skills – that may underlie children’s poor mathematics performance. Children with developmental language disorder (DLD, n = 18, ages 6 to 13) and age-matched typically-developing children (n = 18) completed three math tasks that tapped calculation skill and knowledge of concepts. Children also completed a visual pattern extension task and a verbal working memory task. There were four key findings: (1) children with DLD exhibited poorer mathematical knowledge than typically-developing children, both in calculation and on key math concepts, (2) children with DLD performed similarly to typically-developing children on the visual pattern extension task, (3) children with DLD had lower verbal working memory scores than typically-developing children, and these differences in working memory accounted in part for their poorer calculation performance, and (4) children’s pattern extension scores predicted their arithmetic calculation scores, but not their concept scores.

Language disorders are relatively common in childhood and can result in substantial difficulties in educational contexts. It has been estimated that up to 7% of children have a developmental language disorder of unknown etiology (Norbury et al., 2016). The term developmental language disorder (DLD) is used to describe deficits in language abilities that are not associated with a known biomedical etiology (Bishop, Snowling, Thompson, Greenhalgh & the CATALISE-2 Consortium, 2017). In this research, we focus on children with DLD who also have nonverbal intelligence in the typical range.

A growing body of evidence indicates that children with developmental language disorders often display deficits in mathematical thinking. These deficits appear both in calculation skill, which is the ability to operate on numbers or sets (e.g., Donlan, Cowan, Newton, & Lloyd, 2007; Fazio, 1996, 1999; Koponen, Monomen, Räsänen, & Ahonen, 2006), and in conceptual knowledge, which is understanding of mathematical principles (e.g., Alt, Arizmendi, & Beal, 2014). Moreover, evidence suggests that children with more severe language impairments show greater deficits in mathematical thinking (Cowan, Donlan, Newton, & Lloyd, 2005; Durkin, Mok, & Conti-Ramsden, 2013). These findings raise the question of what factors underlie poor mathematics performance in children with DLD. In this paper, we focus on the potential roles of two factors: working memory, which is a cognitive system involved in the temporary maintenance and active processing of relevant information, and pattern skills, which are skills for recognizing commonalities in sequences and using them to make predictions.

Some researchers have argued that deficits in language processing are secondary to limitations in verbal working memory (for a review see Montgomery, Magimairaj, & Finney, 2010). One account is that, relative to their typically-developing peers, children with DLD have reduced verbal working memory capacity, which refers to the amount of verbal information that can be actively maintained. Reduced capacity may lead to problems tracking incoming information, and may contribute, not only to poor language skills, but also to poor mathematics performance in children with DLD. For example, calculating 9 + 6 requires children to maintain some information in mind (e.g., the initial quantity, 9) while tracking and processing new information (e.g., the addition operation and the second addend, 6). A young child with DLD may successfully count up to 9 by using her fingers and then attempt to count 6 more, but she may lose track of the initial quantity due to capacity limitations and consequently make an error.

A large body of research with typically-developing children has highlighted the critical role of working memory in mathematical reasoning (for reviews, see Peng, Namkung, Barnes, & Sun, 2016; Raghubar, Barnes & Hecht, 2010). Many studies have documented associations between working memory and general mathematics achievement (e.g., De Smedt et al., 2009; Gathercole, Pickering, Knight, & Stegmann, 2004). For example, one cross-sectional study of children ages 7 to 14 reported moderate correlations (rs = .4-.5) between children’s verbal working memory capacity and their level of achievement on a standardized mathematics test (Gathercole et al., 2004).

Fewer studies have focused on working memory as a predictor of specific mathematical skills or concepts. However, some evidence suggests that working memory is correlated with calculation skills (Berg, 2008; Fuchs et al., 2005). For example, Berg (2008) found that verbal working memory capacity was a unique predictor of 8- to 12-year-old children’s ability to perform arithmetic computations (e.g., 16 + 7), even after controlling for age, reading ability, and processing speed. Theoretically, working memory is thought to support calculation skill because calculation often requires both storing and operating on information (e.g., to solve 9 + 6, one must hold the quantities in mind while performing a counting operation; Berg, 2008).

Limited evidence suggests that working memory may also be correlated with knowledge of specific mathematics concepts. For example, Fuchs et al. (2005) assessed 6-year-olds with mathematics difficulty and found an association between verbal working memory capacity and performance on a broad measure of first-grade mathematics concepts, including numeration and measurement. Hansen et al. (2015) worked with older children (~10 years old) and found that verbal working memory was associated with understanding of specific fraction concepts (e.g., Which picture shows that ¾ is the same as 6/8?). Working memory is thought to support knowledge of concepts by facilitating children’s ability to connect new knowledge with prior knowledge and to make connections across problems (Purpura & Ganley, 2014). However, working memory may not relate to all mathematics concepts. For example, in a sample of 4- to 6-year-olds, verbal working memory was related to some early number concepts (e.g., cardinality and set comparison), but not others (e.g., counting, story problems; Purpura & Ganley, 2014).

Although working memory is implicated in the development of mathematical reasoning, it is not the only individual difference factor that has been identified as relevant. A growing body of research has focused on the role of pattern skills in mathematics performance (see Burgoyne, Witteveen, Tolan, Malone, Hulme, 2017). Pattern skills involve recognizing and identifying commonalities in sequences in such a way that one can extend the sequences and make predictions. A growing body of research suggests that pattern skills are associated with mathematics achievement in typically-developing children. For example, in a longitudinal study, children’s skills with repeating patterns (e.g., red-blue-red-blue) at age 5 predicted their mathematics achievement at age 11 (ß = .18), even after controlling for other mathematics, language, and cognitive skills (Rittle-Johnson et al., 2017). Further, interventions designed to improve pattern skills in children ages 5 to 6 can also lead to improvements in children’s mathematics performance (e.g., Kidd et al., 2014; Papic et al., 2011).

As with working memory, fewer studies have focused on pattern skills as a predictor of specific mathematics skills or concepts. Kidd et al. (2014) found that a patterning intervention for struggling 6-year-olds led to improved scores on several different mathematics measures, including the Key Math 3 test of computation as well as the Woodcock Johnson Math Concepts test. Theoretically, pattern skills may support calculation skill because many calculation strategies are based on knowledge of the counting system (e.g., Thevenot, Barrouillet, Castel, & Ulttenhove, 2016), which contains many patterns that can support calculation performance (see Mimeau, Coleman & Donlan, 2016). For example, the digits 0 through 9 occur in the same order in the ones place in every decade. Similarly, repeatedly adding two yields a sequence of numbers with a predictable pattern of digits in the ones place. Key aspects of conceptual knowledge of mathematics may also be supported by noticing patterns (White, Alexander, & Daugherty, 1998). For example, adding and subtracting the same number always yields the original quantity, and noticing this pattern may support students’ understanding of the concept of inverse operations. Thus, there is reason to believe that pattern skills might be involved in acquiring both calculation skill and knowledge of concepts, but empirical evidence on this issue is limited.

This body of work suggests that deficits in pattern skills might also contribute to poor mathematics performance in children with language disorders. Given the association between pattern skills and mathematics performance in typically-developing children (see Burgoyne et al., 2017), it seems warranted to ask whether this is association also holds for children with DLD. Previous research indicates that children with language disorders often display deficits on measures of implicit statistical learning, which involves the tracking of patterns in auditory or visual input (e.g., one syllable often predicts the next syllable; Evans, Saffran, & Robe-Torres, 2009). However, it remains unknown how children with DLD would perform on an explicit patterning task, relative to age-matched, typically-developing children.

In the present study, we investigate the performance of children with DLD and typically-developing children on a task that is widely used in the literature on pattern skills: visual pattern extension. In visual pattern extension tasks, people are asked to decide “what comes next” in a sequence of items that follows a predictable rule. We further investigate whether verbal working memory capacity and pattern skills play a role in calculation skill and in knowledge of mathematics concepts. We selected two concepts that children acquire during the elementary school years and that are foundational in early mathematics (Crooks & Alibali, 2014): (1) understanding of mathematical equivalence, which is the idea that the two sides of an equation represent the same quantity; and (2) understanding of the inversion principle for addition and subtraction, which is the idea that adding and subtracting the same value results in no net change (e.g., a + b − b = a). The age of acquisition for these concepts varies depending on children’s educational experiences, but many children display knowledge of inversion for addition and subtraction between 5 and 7 years (see, e.g., Canobi, 2005; Prather & Alibali, 2009), and understanding of mathematical equivalence between 7 and 10 years (McNeil, 2007).

In the present study, we address four research questions: (1) Do children with DLD differ from age-matched typically-developing children in calculation skills and conceptual knowledge of mathematics? (2) Do children with DLD differ from age-matched typically-developing children in pattern extension skills? (3) Do children with DLD differ from age-matched typically-developing children in verbal working memory capacity? (4) To what extent do pattern skills and verbal working memory predict performance on mathematics problems in children with DLD and age-matched typically-developing children? Based on the work reviewed above, we expected that children with DLD would demonstrate poorer calculation skills, less conceptual knowledge and reduced verbal working memory capacity, relative to age-matched typically-developing children. Given limited prior work on explicit patterning tasks in children with DLD, we did not advance a specific predication about group differences in pattern extension performance. Finally, based on past empirical and theoretical work on relations between pattern skills and mathematics performance in children with typical development, we predicted that relations among pattern skills, verbal working memory, and mathematics performance would be similar across groups.

Method

Participants

Participants were 36 children spanning ages 6 to 13 (M age = 10.2, SD = 1.8). The sample included 18 children with DLD (8 females) and 18 children with typical language abilities (12 females). The children were recruited from the greater Madison, Wisconsin, metropolitan area. Each child’s parent or guardian consented for their child to participate, and each participant also provided assent. All the children had participated in a previous study investigating cognitive processing in school-aged children with and without language disorders. As part of the previous study, children were evaluated for expressive and receptive language, verbal working memory, and nonverbal IQ by a certified speech-language pathologist. All children met the following inclusion criteria: (1) nonverbal intelligence scores at or above 85 on the Leiter International Performance Scale (Roid & Miller, 1997), (2) passed a pure-tone hearing screening, (3) no oral or speech motor disabilities, and (4) from monolingual, English-speaking homes. In the present study, given our focus on mathematics and pattern skills, we chose to study children with normal nonverbal intelligence, so as to ensure that low intelligence was not responsible for children’s difficulties with the experimental tasks.

All children identified as having DLD performed at least 1.00 SD below the mean on both Expressive Language Scores and Receptive Language Scores on the Clinical Evaluation of Language Fundamentals-3 (CELF-3, Semel, Wiig, & Secord, 1995a). The CELF-3 is a comprehensive language assessment instrument that has been widely used in the study of developmental language disorders (see, e.g., Chow & Wehby, 2018). All children in the typically-developing group performed above 1.00 SD below the mean on Expressive Language Scores on the CELF-3 and on one subtest of the Receptive Language Scale (Concepts and Directions) that was given as a receptive language screener. In considering whether the CELF-3 accurately identifies children with language disorders, we reviewed information from the test manual about how identification of children with language disorders based on the CELF-3 (using a cutoff of 1 SD below the mean) aligns with identifications made by children’s school systems (Semel, Wiig & Secord, 1995b). Based on the data provided in the test manual, we calculated the specificity of the CELF-3 to be .85, and its sensitivity to be .57. However, we note that this estimate of sensitivity is likely to be a severe underestimate because (as noted in the manual), some children who were identified as language disordered by the schools but not by the CELF-3 were presumably identified on the basis of abilities that are not evaluated on the CELF-3 (such as phonology, pragmatics, and written skills), and some children had presumably received speech therapy and would no longer qualify as having a language disorder if retested in their schools (Semel, et al., 1995b, p. 64).

Approximately six months after the previous study, children were invited to return to the lab for the current study, which was approved by the Social and Behavioral Sciences Institutional Review Board at the University of Wisconsin-Madison (Protocol #05–02-22). The same speech-language pathologist who had done the testing for the previous study generated lists of potential participants in the target age range with and without DLD, based on the language and IQ scores that had been obtained at the time of the prior study. Children were recruited for this study from these lists. To construct the sample for this study, for each participant who was identified as having DLD, a typically-developing child who matched closely in age and IQ was selected for the typically-developing group. Note that the typically-developing group in this study is a subset of the sample reported in Fyfe, Evans, Matz, Hunt, and Alibali (2017).

The DLD group (n = 18) and the typically-developing group (n = 18) did not differ in age, t(34) = .62, p = .54, or nonverbal IQ, t(34) = .82, p = .42. Means are reported in Table 1. The racial/ethnic composition of the sample was 56% White, 39% African American, and 6% Hispanic/Latino. Participants’ mothers had completed an average of 14.6 years of schooling (SD= 2.6). Full information on the participants is presented in Appendix A.

Table 1:

Participant group comparisons on key variables

	DLD Group (n = 18)		TD Group (n = 18)
	M (SD)	Range	M (SD)	Range
Participant Variables
Age (in years)	10.4 (1.8)	6.9–13.3	10.0 (1.9)	7.1–13.1
Nonverbal IQ	97.3 (5.8)	89.0–109.0	98.8 (5.6)	87.0–109.0
Verbal Working Memory*	37.0 (12.6)	4.8–57.1	57.5 (18.0)	33.3–100.0
Expressive Language Scores*	70.2 (10.5)	50.0–84.0	108.2 (11.9)	88.0–139.0
Receptive Language Scores	65.8 (13.4)	50.0–84.0	--	--
Years of Mother’s Education	14.3 (1.9)	12.0–18.0	14.8 (3.2)	12.0–21.0
% Female	44.0 (51.1)	--	67.0 (48.5)	--
% White	44.0 (51.1)	--	67.0 (48.5)	--
Pattern Task Performance
% Correct on all 24 trials	78 (23)	25–100	87 (13)	58–100
% Correct on Same-Same trials	85 (24)	13–100	96 (7)	75–100
% Correct on Same-Different trials	85 (27)	13–100	95 (11)	63–100
% Correct on Different-Different trials	63 (26)	13–100	69 (28)	25–100
Mathematics Performance
% Correct on Calculation*	69 (33)	0–100	88 (23)	22–100
% Correct on Concepts*	12 (23)	0–92	39 (34)	0–92

Note. DLD = developmental language disorders group. TD = typically-developing group.

^*significant group differences, ps < .05. Participants in the TD group were administered only one receptive language subtest as a screener, so they did not have composite Receptive Language Scores.

Materials

Working Memory.

As a measure of verbal working memory, all children completed the Competing Language Processing Task (CLPT, Gaulin & Campbell, 1994). This task requires children to verify the truth of sentences while holding the last word of each sentence in working memory for later recall. Children listened to a series of sentences (ranging from one to six sentences), made yes/no judgments after each one, and then were asked to report the last word of each sentence in the series. Scores were the percentage of words recalled correctly. This task was originally validated for children between 6 and 12 years of age (Gaulin & Campbell, 1994), and has been used successfully with children that span the age range of the current sample (6 to 13; e.g., Poll et al., 2013). Although limited psychometric data is available for the CLPT, it correlates positively with other measures of working memory (e.g., digit span, Gaulin & Campbell, 1994), it is widely used in research on individuals with language disorders, and some research has shown that it is an unbiased or “culture-fair” test (Campbell, Dollaghan, Needleman & Janosky, 1997).

Mathematics Tasks.

Children were asked to solve fifteen math problems presented one at a time on laminated sheets (see Appendix B for the list of items). On each problem, each child was asked to solve the problem and write the answer in the blank using a dry-erase pen. After writing each answer, the child was asked to explain the strategy he or she used to arrive at that answer (“How did you get that?”). Three problems were standard arithmetic problems, which presented four addends in an operations-equals-answer format (e.g., 2 + 4 + 5 + 2 =__). Six were inversion problems, in which the same number was added to and subtracted from a target number (e.g., 4 + 7 − 7 =__). Six were equivalence problems, which are equations with operations on both sides of the equal sign (e.g., 3 + 4 + 6 = 3 +__). Reliability for each type of problem was good; for arithmetic problems, Cronbach’s α = .73, for inversion problems, α = .90, and for equivalence problems, α = .99.

Pattern Extension Task.

The pattern extension task required children to predict what comes next in a pattern on 24 trials. On each trial, seven elements formed the pattern and were followed by a blank to indicate the continuation of the pattern. The seven elements were presented in solid black, and they varied in shape (circle or square) and size (big or small). Below the pattern, four elements were enclosed in a black border and represented the four possible choices for which item could come next (i.e., big square, small square, big circle, small circle). On each trial, each child was asked to point to the one that “comes next” in the pattern. After making a selection, the child was asked to explain his or her strategy (“How did you get that?”).

Two patterns were embedded in the sequence on each trial: one for shape and one for size. These patterns varied by unit length (two or three) and unit type (AAB, ABA, ABB, or AB). Based on these variations, there were three pattern types: (1) Same-Same, in which the unit length and unit type were the same for shape and size, (2) Same-Different, in which the unit length was the same for shape and size, but the unit type was different, and (3) Different-Different, in which the unit length and unit type were different for shape and size. For examples, see Figure 1. Reliability for the pattern extension task was good; Cronbach’s α = .88.

Figure 1.

Three pattern types for the pattern extension task

Note. Same-Same = same unit length for shape and size, same unit type for shape and size; Same-Different = same unit length for shape and size, different unit type for shape and size; Different-Different = different unit length for shape and size, different unit type for shape and size.

Coding

Mathematics Tasks.

On the standard arithmetic problems and the inversion problems, children’s solutions were coded as correct if their written answers were exactly correct. For inversion problems, we also coded whether children used the inversion shortcut (i.e., noticed that adding and subtracting the same number results in no net change) based on their solution times. This solution-time measure is based on the assumption that when children use the shortcut, they solve the problems very quickly, because the shortcut does not require slow, error-prone calculation processes. In line with previous research (Siegler & Stern, 1998), answers that were correct and took fewer than 5 seconds from presentation to solution were coded as solved via the inversion shortcut. Using this coding method, solutions that were coded as using the shortcut took 3.4 seconds on average (SD = 0.7); this was similar in the DLD group (M = 3.5, SD = 0.7) and in the typically-developing (TD) group (M = 3.3, SD = 0.7), t(47) = 0.77, p = .45. Solutions that were not coded as using the shortcut took 15.5 seconds on average (SD = 12.8); this was also similar in the DLD group (M = 16.7, SD = 13.0) and the TD group (M = 14.0, SD = 12.4), t(163) = 1.34, p = .18.¹

For equivalence problems, we coded whether children’s strategies were correct based on their verbal explanations, using a system that was developed in previous research (Perry, Church, & Goldin-Meadow, 1988). Explanations coded as correct conveyed one of three conceptually-correct strategies: making both sides of the equal sign sum to the same total (equalize), adding the numbers on the left side of the equal sign and subtracting the number on the right (add-subtract), or ignoring the numbers that were the same on both sides and adding the remaining addends on the left side (grouping). Children’s verbal explanations were coded in terms of the strategies they described, even when those strategies did not correspond with their written solutions. Discrepancies were rare (only 3 across 216 trials). A second rater coded 30% of explanations and agreement was high (.96). All disagreements were resolved by discussion between coders.

Given our interest in the relation between pattern skills and mathematics performance, we created two summary math scores. First, we created a calculation score by summing the number of problems solved correctly on the three standard arithmetic problems and the six inversion problems. Correctness on these problems is determined by the accuracy of the solution; correct solutions can be obtained via correct calculation. Second, we created a concepts score by summing the number of inversion problems out of six solved with the shortcut strategy and the number of equivalence problems out of six solved with a conceptually correct strategy; these strategies demonstrate conceptual understanding of inversion and equivalence, respectively. Reliability of the composite measures was good; calculation α = .84, and concepts α = .92.

Pattern Extension Task.

On the pattern extension task, each response was coded as correct if the child correctly selected the element that would come next in the pattern. Children’s verbal explanations were coded into one of eight categories using a system developed in previous research (Fyfe et al., 2017). The codes, their descriptions, and examples are presented in Table 2. A second rater coded 30% of explanations and agreement was high (.89).

Table 2:

Frequency of explanation use on the pattern task by group

Explanation Type	Description and Example	DLD	TD	Total
Match	Matches a previous instance (“the big square here matches the big square here, and after it was a little circle”)	26	20	23
Labels Both	Labels items in order by shape and size (“big square, little circle, little circle”)	12a	30	21
Labels One	Labels items in order by shape or size (“square, circle, circle”)	14	14	14
Names Both	Names sizes and shapes of elements (“big squares and little circles”)	3	4	3
Names One	Names sizes or shapes of elements (“squares and circles”)	6	5	5
Pattern Word	Mentions the word pattern with nothing else (“I just followed the pattern”)	7	3	5
Vague	Attempts an explanation, but is unclear (“by looking behind”)	13	16	15
No Verbal Response	No verbal answer or gives statement of uncertainty (“I don’t know”)	19	8	14

^aNote. = percent use was significantly lower for the DLD group than for the TD group, p < .05. DLD = developmental language disorders group, TD = typically-developing group.

Procedure

Children participated individually in a single session in a laboratory space. Children first completed a hearing screening, followed by the pattern extension task and then the mathematics tasks.

Results

In the following sections, we address our four primary research questions. The first three sections report comparisons between the DLD and typically-developing (TD) groups on the mathematics tasks, the pattern extension task, and the verbal working memory test. In the final section, we examine whether pattern skills and verbal working memory relate to mathematics performance.

Performance on the Math Tasks

Standard arithmetic problems.

Average scores on the three standard arithmetic problems were 67% (SD = 41%) in the DLD group and 89% (SD = 23%) in the TD group. Figure 2 presents a scatterplot of performance by group and age. The distribution was skewed, with more than half of the children in each group scoring 100%. Given this high performance, we used logistic regression to predict the log of the odds of scoring 100% as a function of participant group and age. There was a main effect of participant group, B = −2.07, p = .03, OR = 7.93; fewer children in the DLD group (50%) than in the TD group (78%) scored 100% on the arithmetic problems. Performance also improved with age, B = 0.77, p = .01, OR = 2.17.

Figure 2.

Performance on standard arithmetic problems by participant group and age

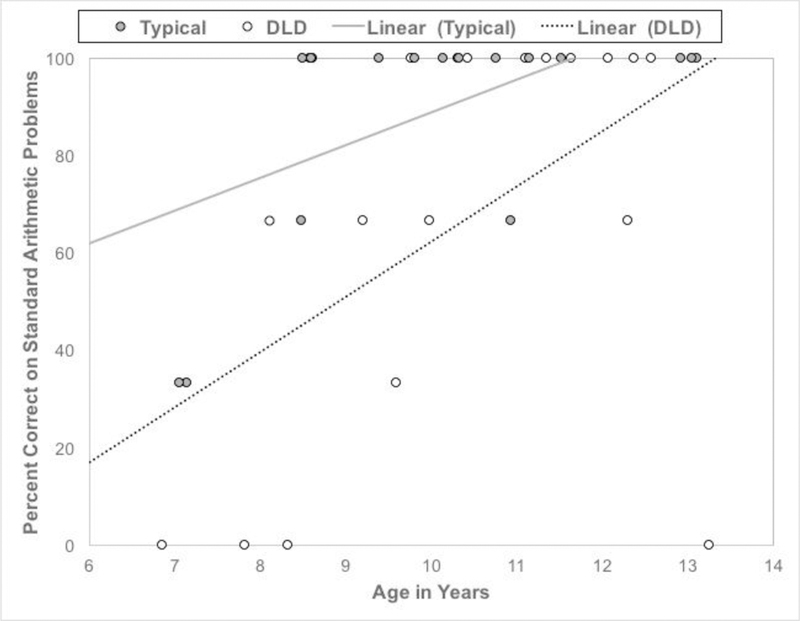
Note. DLD = developmental language disorders group. Linear (Typical) and Linear (DLD) display the linear regression line of age predicting percent correct within each group.

Inversion problems.

Average scores on the six inversion problems were 69% (SD = 39%) in the DLD group and 87% (SD = 27%) in the TD group. We were interested in whether children used the conceptually-based “inversion shortcut,” rather than calculating the correct answer. The percentage of trials on which the shortcut was used was 14% (SD = 24%) in the DLD group and 33% (SD = 32%) in the TD group. Figure 3 presents a scatterplot of shortcut use by group and age. The distribution was skewed; 50% of children never used the shortcut and the remaining 50% were relatively evenly distributed across other possible scores; on average, children used the shortcut on 24% of trials. Given this distribution, we used logistic regression to predict the log of the odds of using the shortcut on more trials than average, as a function of participant group and age. There was a main effect of participant group, B = −2.38, p < .01, OR = 10.81; fewer children in the DLD group (17%) than in the TD group (61%) used the shortcut on more trials than average. There was no effect of age, B = 0.36, p = .14, OR = 1.43.

Figure 3.

Shortcut use on inversion problems by participant group and age

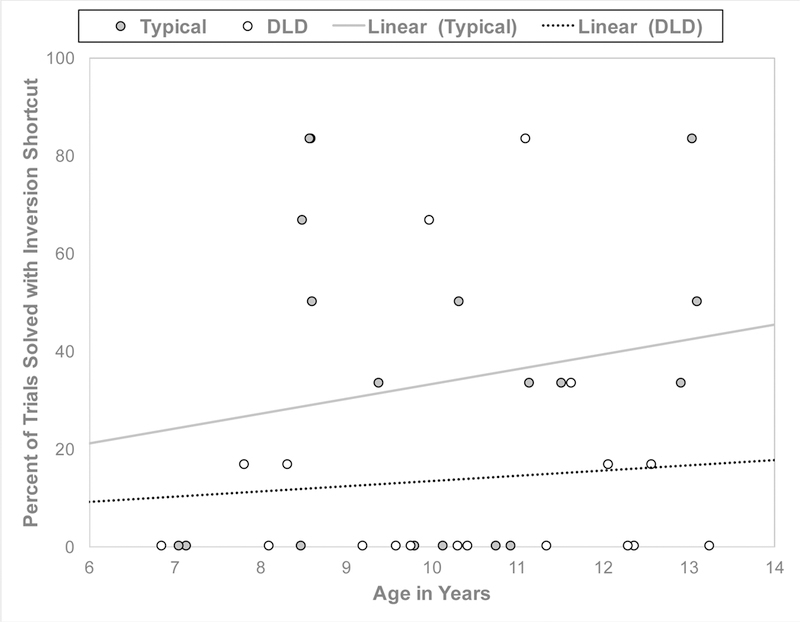
Note. DLD = developmental language disorders group. Linear (Typical) and Linear (DLD) display the linear regression line of age predicting shortcut use within each group.

Equivalence problems.

For the six equivalence problems, the percentage of trials on which a conceptually correct strategy was used was 9% (SD = 28%) in the DLD group and 44% (SD = 50%) in the TD group. Figure 4 presents a scatterplot of performance by group and age. The distribution was bimodal; 70% of children never used a conceptually correct strategy and 22% of children always used a conceptually correct strategy. We used logistic regression to predict the log of the odds of scoring above 0% as a function of participant group and age. There was a main effect of participant group, B = −3.04, p = .01, OR = 20.80; fewer children in the DLD group (11%) than in the TD group (50%) scored above 0% (i.e., solved at least one problem correctly). Performance also improved with age, B = 0.77, p = .02, OR = 2.17.

Figure 4.

Performance on equivalence problems by participant group and age

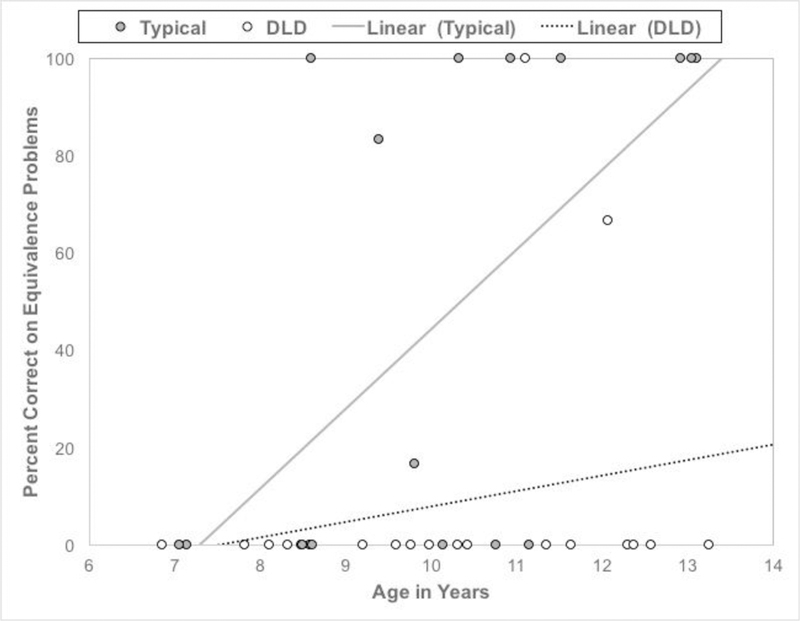
Note. DLD = developmental language disorders group. Linear (Typical) and Linear (DLD) displays the linear regression line of age predicting percent correct within each group.

In sum, children’s performance varied as a function of task, participant group and age. For children in both groups, success tended to be higher on the calculation tasks (solving standard arithmetic and inversion problems correctly) than on conceptual tasks (using conceptually-based strategies on inversion and equivalence problems). However, across all of the math tasks, children in the DLD group performed more poorly than children in the TD group, and older children tended to perform better than younger ones.

Performance on the pattern extension task

For the pattern extension task, across all 24 trials, the average percent correct was 78% (SD = 23%) in the DLD group and 87% (SD = 13%) in the TD group. To examine group differences, we conducted a 2 × 3 mixed ANOVA with participant group (DLD vs. TD) as a between-subjects factor and pattern type (same-same, same-different, and different-different) as a within-subjects factor. Summary data are presented in Table 1. There was a main effect of pattern type, F(2, 68) = 34.83, p < .01, η_p² = .51. Scores were lower on different-different trials (M = 66%, SD = 27%), relative to same-same trials (M = 91%, SD = 18%), F(1, 34) = 39.44, p < .01, and relative to same-different trials (M = 90%, SD = 21%), F(1, 34) = 41.11, p < .01. However, there was no main effect of participant group, F(1, 34) = 2.24, p = .14, η_p² = .06, nor did participant group interact with pattern type, F(2, 68) = 0.48, p = .62, η_p² = .01.

Given the overall high level of performance, we also examined the percent of children who achieved success on each trial type. With 8 items and 4 answer choices for each item, the probability of answering 5 or more items correctly due to chance alone is less than 5%; therefore, we classified children who answered 5 or more items of a given type correctly as successful on that item type. On same-same trials, 89% of children in the DLD group were successful (16 out of 18) compared to 100% of children in the TD group (18 out of 18). On same-different trials, 83% of children in the DLD group were successful (15 out of 18) compared to 100% of children in the TD group (18 out of 18). On different-different trials, 67% of children in the DLD group were successful (12 out of 18) compared to 72% of children in the TD group (13 out of 18). Fisher’s exact tests of independence revealed no significant differences between the groups on same-same trials, p =.49, same-different trials, p = .23, and different-different trials, p = 1.00.

On each trial, children were also asked to explain their selections. As shown in Table 2, children’s explanations fell into one of eight categories. The most common explanation types (35% of all trials) were (a) to label the items in order by naming either their shape or size (Labels One) or (b) to label the items in order by naming both shape and size (Labels Both). The next most common explanation (23% of all trials) was to relate the final item to a matching item that occurred earlier in the pattern (Match). The success rates for these three common explanations were high, ranging from 91% to 94%, and these success rates did not differ significantly for children in the DLD and the TD groups (Labels One: 85% vs. 94%; Labels Both: 90% vs. 94%; Match: 93% vs. 94%). This means that if a child provided one of these three explanations on an item, they were highly likely to get that item correct.

There was one group difference in explanation use. Children in the DLD group provided the labels-both explanation on fewer trials than children in the TD group, t(34) = 2.28, p = .03 (see Table 2). There were also differences in which explanation types correlated with success. In the DLD group, the correlation between percent correct and use of the labels-both explanation was low and non-significant, r(16) = .23, p = .35, but the correlation between percent correct and use of the match explanation was moderate and significant, r(16) = .49, p = .04. In contrast, in the TD group, the correlation between percent correct and use of the labels-both explanation was moderate, though not significant, r(16) = .44, p = .06, and the correlation between percent correct and use of the match explanation was low and not significant, r(16) = .14, p = .57.

In sum, children were quite successful on the pattern extension task, and accuracy did not vary as a function of participant group. There were only three children who had strikingly poor pattern extension performance (the only three children to score lower than 50% correct) and all three were in the DLD group (participants D01, D09 and D18 in Appendix A). These three children varied widely in age (6.9, 10.3, and 13.3 years of age), Expressive Language Scores (61, 65 and 78), Receptive Language scores (50, 65 and 82), NVIQ scores (91, 95, 107), and verbal working memory scores (5, 36, and 45).

Performance on the working memory task

Average scores on the working memory task were 37.0 (SD = 12.6) in the DLD group and 57.5 (SD = 18.0) in the TD group. To examine group differences, we conducted a linear regression with participant group and age as predictors. As expected, there was a main effect of participant group, B = −22.87, p < .01, with children in the DLD group scoring lower than those in the TD group. Working memory scores also improved with age, B = 6.13, p < .01.

Relations between pattern extension scores, working memory, and mathematics

Finally, we assessed the relations between pattern extension, working memory, and mathematics performance. To do so, we examined participant group, age, IQ, working memory, and pattern extension scores as predictors of mathematics performance. Table 3 presents simple correlations among these variables for each participant group. As described in the method section, we created two summary math scores, one to reflect children’s calculation skill and another to reflect their knowledge of concepts (equivalence and inversion). Figures C1 and C2 in Appendix C present scatterplots of calculation and concept scores by age and participant group.

Table 3:

Correlations among key variables within each participant group

FOR TD GROUP	1	2	3	4	5	6
1. Age	--
2. IQ	.23	--
3. Working Memory	.85*	.36	--
4. Pattern Extension Score	.50*	.13	.41	--
5. Calculation Score	.44	.08	.33	.71*	--
6. Math Concepts Score	.54*	.07	.34	.45	.49*	--
FOR DLD GROUP	1	2	3	4	5	6
1. Age	--
2. IQ	−.28	--
3. Working Memory	.58*	.02	--
4. Pattern Extension Score	−.03	.11	.25	--
5. Calculation Score	.33	.06	.58*	.51*	--
6. Math Concepts Score	.17	.52*	.27	.29	.40	--

Note. TD = typically-developing; DLD = developmental language disorders.

^*p < .05.

We conducted two hierarchical regression analyses: one to predict calculation scores and one to predict concept scores. In each regression, participant group was entered in the first step. Next, age and nonverbal IQ were entered as covariates in the second step. Working memory scores were entered in the third step, and pattern extension scores were entered in the fourth step.

First, we used hierarchical regression to predict calculation scores. As shown in Table 4, Step 1 (participant group only) was significant, F(1, 34) = 4.12, p = .05; children in the DLD group had lower calculation scores (M = 69%, SD = 33%) than children in the TD group (M = 88%, SD = 23%). Step 2 (with age and IQ added) was also significant, F(3, 32) = 3.23, p = .04, but did not result in significant change in R² over the initial step (R² change = .12, p = .09). Participant group and age were significant predictors of calculation scores, though IQ was not. Step 3 (with working memory scores added) was also significant, F(4, 31) = 2.93, p = .04, but again did not result in significant change in R² over the previous step (R² change = .04, p = .19). The effect of participant group was no longer significant with working memory in the model, and no other variables were significant predictors. Step 4 (with pattern extension scores added) was significant, F(5, 30) = 5.40, p < .01, and resulted in significant change in R² over the previous step (R² change = .20, p < .01). Pattern scores significantly predicted calculation scores over and above participant group, age, IQ, and working memory, p < .01. No other variables were significant (see Table 4). This model accounted for 47% of the variance in calculation scores.

Table 4:

Hierarchical regression predicting calculation scores

Variable	B	SE B	ß	ΔR2	F for ΔR2
Predicting Calculation
Step 1				.11	4.12*
Intercept	87.65	6.66
DLD vs. TD Group	−19.14	9.42	−.33*
Step 2				.12	2.59
Intercept	88.44	6.42
DLD vs. TD Group	−20.70	9.15	−.36*
Age	5.58	2.49	.35*
IQ	0.38	0.81	.07
Step 3				.04	1.80
Intercept	81.62	8.12
DLD vs. TD Group	−7.08	13.59	−.12
Age	1.74	3.77	.11
IQ	−0.01	0.85	−.00
Working Memory	0.62	0.46	.39
Step 4				.20	11.36**
Intercept	81.61	7.03
DLD vs. TD Group	−7.05	11.76	−.12
Age	2.48	3.28	.16
IQ	−0.10	0.74	−.02
Working Memory	0.30	0.41	.19
Pattern Extension Score	0.76	0.22	.48**

Note. TD = typically-developing; DLD = developmental language disorders.

^*p < .05

^**p < .01.

To explore the possibility that working memory and/or pattern skill accounted for the observed group differences in calculation scores, we conducted a mediation test using the bootstrapping technique recommended by Preacher and Hayes (2008), which yields a 95% bias-corrected confidence interval around the indirect effect. We included participant group as the independent variable, calculation score as the dependent variable, and working memory and pattern skill as potential mediators. Working memory significantly mediated the effect of participant group on calculation scores, indirect effect B = −15.87, 95% CI [−35.90, −5.04], as suggested by the fact that the effect of participant group was no longer significant when working memory scores were included in the model (comparison of Steps 2 and 3 in Table 4). Differences in pattern skill did not mediate the effect of participant group on calculation scores, indirect effect B = −8.01, 95% CI [−24.54, 0.49], which is not surprising since there were not significant group differences on pattern extension scores. Instead, as shown by the correlations in Table 3, pattern skill was associated with calculation scores in both the DLD and the TD groups, and it explained unique variance in calculation scores over and above the effects of participant group and working memory (see Table 4).

Next, we used hierarchical regression to predict concept scores. As shown in Table 5, Step 1 (with participant group) was significant, F(1, 34) = 7.94, p < .01; children in the DLD group had lower concept scores (M = 12%, SD = 23%) than children in the TD group (M = 39%, SD = 33%). Step 2 (with age and IQ added) was also significant, F(3, 32) = 6.13, p < .01, and resulted in significant change in R² over the previous step (R² change = .18, p = .02). Participant group and age were significant predictors, though IQ was not. Step 3 (with working memory scores added) was also significant, F(4, 31) = 4.49, p < .01, but did not result in significant change in R² over the previous step (R² change = .002, p = .79). The effect of participant group remained significant in this model. The effect of age was marginal (p < .10), and the effects of IQ and working memory were not significant (see Table 5). Step 4 (with pattern extension scores added) was significant, F(5, 30) = 4.34, p < .01, but again did not result in significant change in R2 over the previous model (R² change = .05, p = .11). Pattern extension scores did not predict concept scores over and above participant group, age, IQ, and working memory, p = .11. Instead, participant group remained the only significant predictor (see Table 5). This model accounted for 42% of the variance in concept scores.

Table 5:

Hierarchical regression predicting concept scores

Variable	B	SE B	ß	ΔR2	F for ΔR2
Predicting Concepts
Step 1				.19	7.94**
Intercept	38.89	6.86
DLD vs. TD Group	−27.32	9.70	−.44**
Step 2				.18	4.43*
Intercept	39.04	6.30
DLD vs. TD Group	−27.60	8.98	−.44**
Age	6.12	2.44	.36*
IQ	1.34	0.80	.24
Step 3				.002	0.08
Intercept	40.44	8.19
DLD vs. TD Group	−30.41	13.70	−.48*
Age	6.91	3.80	.40
IQ	1.42	0.86	.25
Working Memory	−0.13	0.47	−.08
Step 4				.05	2.75
Intercept	40.44	7.97
DLD vs. TD Group	−30.40	13.33	−.48*
Age	7.32	3.71	.43
IQ	1.37	0.84	.25
Working Memory	−0.31	0.47	−.18
Pattern Extension Score	0.42	0.25	.25

Note. TD = typically-developing; DLD = developmental language disorders.

^*p < .05

^**p < .01.

We again conducted a formal mediation test using the bootstrapping technique (Preacher & Hayes, 2008). We included participant group as the independent variable, concept scores as the dependent variable, and working memory and pattern skill as the mediators. Neither working memory, indirect effect B = −12.12, 95% CI [−27.43, 1.02], nor pattern skill, indirect effect B = - 4.74, 95% CI [−14.31, 0.02], significantly mediated the effect of participant group on concept scores. Thus, there is no evidence that group differences in working memory or pattern skill account for the group differences in concept scores.

Discussion

This study examined mathematics performance, pattern skills, and verbal working memory in children with developmental language disorders (ages 6 to 13) and age-matched typically-developing children. There were four key findings. First, children in the DLD group exhibited poorer mathematics skills than did children in the typically-developing group. This was true for both calculation skill and conceptual knowledge of equivalence and inversion. Second, children in the DLD group and the TD group exhibited similarly successful performance on the pattern extension task. Thus, the children with DLD did not have deficits in the ability to identify and extend predictable sequences in visual patterns, at least those of the sort we studied. Third, children in the DLD group had lower verbal working memory scores than children in the typically-developing group, and these group differences in working memory accounted in part for group differences in calculation skill. Fourth, in both the DLD and TD groups, pattern extension scores predicted calculation scores, but not concepts scores. Below we outline the contributions of this work and discuss limitations and future directions.

First, the current study provides insight into the development of mathematics knowledge in children with developmental language disorders. Consistent with previous research (Alt et al., 2014; e.g., Donlan et al., 2007; Fazio, 1996; 1999; Koponen et al., 2006; Mainela-Arnold et al., 2011), children in the DLD group exhibited poorer calculation skills and less conceptual knowledge than children in the age-matched TD group. Specifically, children with developmental language disorders were less likely to solve arithmetic problems correctly, less likely to use a correct strategy to solve equivalence problems, and less likely to use the inversion shortcut on inversion problems. These differences suggest that mathematics difficulties among children with DLD may be widespread and not limited to a few, particular types of mathematics knowledge.

Second, the current study provides insight into the development of pattern skills in children with developmental language disorders. Although pattern extension tasks are commonly used to assess pattern skills in typically-developing children (e.g., Clements et al., 2008; Rittle-Johnson et al., 2013; Warren & Cooper, 2006), to our knowledge, this study is the first to systematically study pattern extension performance in children with developmental language disorders. Here, children in the DLD group exhibited high success rates on the pattern extension task (solving nearly 80% of all trials correctly) that were similar to the success rates of children in the typically-developing group. Further, the relative performance of children in the DLD group on the three pattern types also aligned with that of children in the TD group. In both groups, performance was similar on the same-same and same-different trials but was much poorer on different-different trials, on which children had to discern patterns of different types for the shape and size dimensions.

The one difference that emerged on pattern extension was in children’s explanations. Children in the DLD group provided the labels-both-dimensions explanation on fewer trials than children in the TD group. This may be due to children with developmental language disorders relying on less verbally-demanding strategies to solve the task. Indeed, within the DLD group, use of the verbally-demanding labels-both-dimensions explanation was not related to success on the pattern task, but use of the more visually-based matching explanation was positively related to performance. Thus, there are multiple effective strategies for pattern extension, and children’s use of these strategies varied by participant group.

Third, the current results contribute to a growing body of literature focusing on relations between patterning, working memory, and mathematics (e.g., Fyfe, Rittle-Johnson, & Farran, 2018; Kidd et al., 2014; Lee et al., 2011; Miller et al., 2016; Rittle-Johnson et al., 2017). Importantly, group differences in calculation scores were mediated by differences in verbal working memory, but group differences in concepts scores were not. This suggests that some, but not all aspects of the poorer mathematics performance displayed by children with developmental language disorders can be explained by the fact that they tend to have lower verbal working memory capacity. One possibility is that, due to their limited working memory capacity, children with developmental language disorders sometimes have difficulties maintaining information or tracking incoming information, which hinders the development of calculation skill. Working memory is involved in processing incoming information and actively maintaining relevant information (Miyake & Shah, 1999), and calculation often requires learners to hold some information in mind (e.g., the initial quantity) while updating and processing new information (e.g., the operations and the remaining quantities), which taxes working memory. Thus, if children with developmental language disorders have difficulties processing new and maintaining information in working memory, this may explain why they also have difficulties in calculation.

The current results also provide empirical support for a link between pattern skills and calculation. Whereas participant group and working memory scores explained overlapping variance in children’s calculation (indicated by mediation of the group effect by working memory scores), pattern skills explained unique variance in calculation. Moreover, this pattern- mathematics relation emerged, over and above the effects of participant group, age, nonverbal IQ, and working memory. In both groups, pattern extension scores were predictive of children’s calculation skill, but not their knowledge of key math concepts (equivalence and inversion).

Why might pattern skills relate to calculation, but not to knowledge of concepts? We suspect that the difference may be attributed to how calculation skill and knowledge of the specific concepts studied here are acquired. Calculation skill tends to develop over a long period of time and may require identifying stable, generalizable patterns in the number sequence (e.g., noticing that the digits 0 through 9 repeat in each decade). In contrast, success on equivalence and inversion problems may involve acquiring one critical “chunk” of conceptual knowledge in each case (e.g., learning that the equal sign means “the same as”, or learning that addition and subtraction are inverse operations). These critical “chunks” of knowledge may be acquired in a short period of time, rather than incrementally over a longer period of time, as evidenced by the bimodal distributions in children’s performance (e.g., children tended to either “have” each relevant chunk or not have it). Thus, pattern skill may predict calculation skill because it supports the ability to identify generalizable rules in the number sequence over a long period of time, but it may not facilitate children’s acquisition of a single, specific chunk of conceptual knowledge at a particular time.

Future work is needed to evaluate the relations between pattern skill and different aspects of conceptual knowledge of mathematics. Some aspects of conceptual knowledge of mathematics seem to be acquired gradually; for example, the relations to operands principle for addition—that is, the principle that increasing the size of one addend increases the size of the sum—is rarely explicitly taught, but children seem to acquire it through experience with arithmetic (see Prather & Alibali, 2009). For acquiring concepts that involve discerning relations across examples, like the relation to operands principle, pattern skill may be essential.

Several limitations of the current study suggest additional directions for future research. First, we assessed a relatively small number of children spanning a large age range, with a truncated range of nonverbal IQ scores (all above 85). Future research that focuses on relations among cognitive skills (such as working memory, pattern skills, and mathematics) should include larger, more diverse samples to examine the generalizability of the results. Indeed, a recent review of the literature on children’s pattern skills highlights the need for “large-scale correlational studies” with many participants and many measures (Burgoyne et al., 2017, p. 242).

In addition to limiting the generalizability of results, the small sample size may have limited our power to detect group differences, particularly on the novel pattern extension task. On the one hand, the mean pattern scores were descriptively higher in the TD group than in the DLD group, and the effect size was non-trivial. On the other hand, the study was sufficiently powered to detect group differences on the math tasks, and the differences in pattern scores were not statistically significant across multiple metrics (e.g., percent correct across trials and percent of successful children). By and large, the current results suggest that the groups were largely indistinguishable on their pattern skills, apart from the 3 children in the DLD group who performed poorly. Future research should continue to examine pattern skills in children with a range of language competencies.

Second, due to time limitations during data collection, we included only a few items for each of the mathematical tasks, and this may have contributed to the skewed distributions of scores (i.e., near ceiling performance on standard arithmetic problems and near floor performance on equivalence and inversion problems). Such skewed distributions make it difficult to detect group differences because all participants perform either very well or very poorly; yet, differences between children in the DLD and TD groups were still evident in the current study. In some cases, the skewed distributions reveal important characteristics of the knowledge being assessed; for example, it is commonly observed that children’s performance on mathematical equivalence tasks is bimodally distributed, with some children “getting it” and others not (e.g., McNeil, 2007). Nevertheless, there is a clear need for research that assesses group differences using larger numbers of items, so as to tap continuous changes in mathematics knowledge.

Finally, our study focused on only a small number of predictors of children’s mathematics knowledge. We included predictors related to language skills, working memory, pattern skills, age, and nonverbal IQ; yet, our models only accounted for only 47% of the variance in calculation and 42% of the variance in concepts. Future research should continue to investigate the many diverse factors that contribute to the development of children’s mathematics knowledge.

In sum, the present findings are important in four ways. First, we have shown that children with developmental language disorders perform similarly to age-matched typically-developing children on a pattern extension task—and that children in the two participant groups may succeed by relying on different strategies. Second, we replicate and extend past findings showing that children with developmental language disorders have difficulties both with calculation and with mathematics concepts. Third, we have provided suggestive evidence that difficulties with calculation, but not concepts, may be attributed, at least in part, to deficits in verbal working memory. Finally, we have demonstrated that pattern skills are related to calculation skills, but not to conceptual knowledge of inversion and mathematical equivalence, and that these relations hold even after controlling for age, nonverbal IQ, and working memory. Future work should further evaluate the relations between mathematics, pattern skills, and working memory, so as to better understand mathematical reasoning and performance in children with typical development and children with language disorders.

Highlights.

• Children with DLD exhibited poorer math knowledge than their TD peers.

• Children with DLD performed similarly to TD children on a pattern extension task.

• Children with DLD had lower verbal working memory scores than their TD peers.

• Children’s pattern extension scores predicted their arithmetic calculation scores.

Author Statement:

Emily Fyfe: Formal Analysis, Writing-Original, Visualization

Lauren Matz: Conceptualization, Methodology, Investigation, Funding Kayla Hunt: Conceptualization, Methodology, Investigation

Martha Alibali: Conceptualization, Methodology, Resources, Writing – Reviewing and Editing, Supervision, Administration, Funding

	Emily Fyfe	Lauren Matz	Kayla Hunt	Martha Alibali
Conceptualization		x	x	x
Methodology		x	x	x
Software
Validation
Formal Analysis	x
Investigation		x	x
Resources				x
Data Curation
Writing - original	x
Writing - revised				x
Visualization	x
Supervision				x
Administration				x
Funding		x		x