Abstract
We review, systematize and discuss models of diffusion in neuronal tissue, by putting them into an overarching physical context of coarse-graining over an increasing diffusion length scale. From this perspective, we view research on quantifying brain microstructure as occurring along the three major avenues. The first avenue focusses on the transient, or time-dependent, effects in diffusion. These effects signify the gradual coarse-graining of tissue structure, which occurs qualitatively differently in different brain tissue compartments. We show that the transient effects contain information about the relevant length scales for neuronal tissue, such as the packing correlation length for neuronal fibers, as well as the degree of structural disorder along the neurites. The second avenue corresponds to the long-time limit, when the observed signal can be approximated as a sum of multiple non-exchanging anisotropic Gaussian components. Here the challenge lies in parameter estimation and in resolving its hidden degeneracies. The third avenue employs multiple diffusion encoding techniques, able to access information not contained in the conventional diffusion propagator. We conclude with our outlook on the future directions which can open exciting possibilities for designing quantitative markers of tissue physiology and pathology, based on methods of studying mesoscopic transport in disordered systems.
1. DIFFUSION MRI THROUGH A BIRD’S EYE
One of the most astonishing things about the world in which we live is that there seems to be interesting physics at all scales. To do physics amid this remarkable richness, it is convenient to be able to isolate a set of phenomena from all the rest, so that we can describe it without having to understand everything. Fortunately, this is often possible. We can divide the parameter space of the world into different regions, in each of which there is a different appropriate description of the important physics. Such an appropriate description of the important physics is an “effective theory”
H. Georgi, Effective Field Theory [1]
Diffusion MRI (dMRI) is a macroscopic physical measurement of the voxel-averaged stochasticmotion of nuclear-spin-carrying molecules (typically water). This measurement occurs in a structurally complex tissue microenvironment such as the brain. Diffusion in complex media has been studied for about a century in a variety of fields, and is part of a broad class of transport phenomena in disordered systems.
Our goal in this review article is to place biophysical dMRI modeling into a broader physical context. Our overarching theme will be that of coarse-graining and effective theory, which will allow us to present and discuss neuronal tissue models of diffusion from a unifying perspective.
1.1. Mesoscopic Bloch-Torrey equation as an effective theory
One of the key 20th century advances in understanding the physics of complex systems was achieved by the development of effective theory, a paradigm to describe dynamics that involves only a handful of the so-called relevant degrees of freedom, or relevant parameters, thereby ignoring myriads of other, “irrelevant” ones [2–4]. This way of thinking was spurred by attempts to describe systems with an ever greater number of degrees of freedom, and a subsequent realization that it is plain impossible to keep track of all of them at once.
The more complex the system, the more the challenge of building an adequate theory shifts towards identifying which (few) parameters to keep, and which ones (almost all!) to ignore. Over time, selecting relevant parameters and formulating an adequate effective theory has become synonymous with the notion of understanding the system’s behavior.
Having NMR as an example, the quantum-mechanical couplings of a very complex multi-spin Hamiltonian, together with all molecular degrees of freedom describing rotations, vibrations and translations, relevant at the nm and ps level, average out to produce effective parameters such as the relaxation rate constants R1 and R2, and the diffusion coefficient D, at least for the most common NMR measurements. The parameters R1 and R2 emerge in Bloembergen–Purcell–Pound theory and enter the Bloch equations describing the semiclassical evolution of macroscopic magnetization [5, 6]. Reducing a myriad of variables describing molecular microenvironment to just a few relevant parameters has been a major scientific achievement of the 1940s–1960s NMR, and has formed the basis of effective theory of nuclear magnetization in liquids.
The step from NMR in uniform liquids to biological tissues has brought along a new challenge, which our community is only beginning to fully embrace. This challenge is associated with the above effective parameters R1(r), R2(r) and D(r) acquiring spatial dependence at the scale ~ 0.1 – 10 µm, set by the cellular architecture, much coarser than molecular dimensions. These spatial variations become relevant at the corresponding ~ 1 – 1000 ms time scales of dMRI, — much slower than the ps time scales on which the local relaxation rate constants and the diffusion coefficient emerge.
From the physics standpoint, the spatial variations of R1(r), R2(r) and D(r) (with the latter including boundary conditions associated with cell membranes), occur at the mesoscopic scale, Fig. 1. The term “mesoscopic” originated in condensed matter physics some decades ago [7], signifying focussing on the intermediate scales (“meso”), in-between elementary (say, atomic or molecular), and macroscopic (associated with the sample size or the measurement resolution). By design, this term is relative, depending on which spatio-temporal scales are deemed small and large.
FIG. 1.
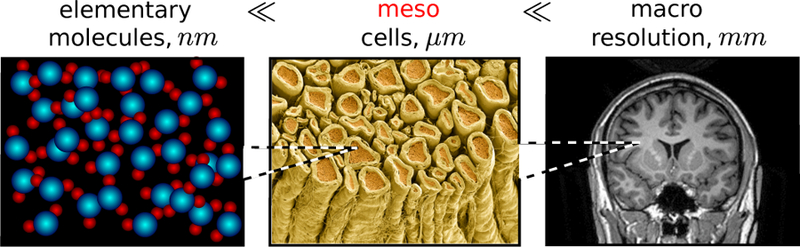
The mesoscopic scale in brain dMRI, as an intermediate scale between the elementary (molecular) and the macroscopic (resolution).
For dMRI, the mesoscopic scale corresponds to tissue heterogeneities at the scale defined by the MRI-controlled diffusion length, , which is the root mean squared molecular displacement for times t ~ 1 – 1000 ms. In the dMRI literature, it is commonly referred to as the microstructure scale. This scale is commensurate with immense structural complexity of tissue architecture.
At the mesoscale, quantum degrees of freedom become irrelevant (at least for the dMRI purposes), and the dynamics of transverse magnetization m(t, r) (a two dimensional vector, represented by a complex number) can be captured by the mesoscopic Bloch-Torrey equation
| (1.1) |
Here Ω(t,r) is the Larmor frequency offset that may include externally applied diffusion-sensitizing Larmor frequency gradients g(t), Ω(t, r) = Ω(r) + g(t)r, and the static Ω(r) arises from the intrinsic mesoscopic magnetic structure of tissues due to paramagnetic ions such as iron, myelin susceptibility in the white matter, or due to added contrast agent. While we focus on the transverse magnetization in what follows, the full version of the above equation includes the longitudinal magnetization components with m being a three-dimensional vector. Further extension can incorporate multicomponent m to describe the interplay between different proton pools, e.g., to describe magnetization transfer [8, 9].
The mesoscopic Bloch-Torrey equation (1.1) is an adequate effective description at the µm level, commensurate with typical diffusion length scales probed with dMRI. It is a mesoscopic equation in the sense that it involves scales in-between the quantum-mechanical molecular dynamics on the nm scale and the measurable signal in mm-sized MRI voxels. While the averaging up to the mesoscopic scale is already performed in its r-dependent parameters, it is our task to perform the remaining averaging over a macroscopic voxel V inherent to the observed (complex-valued) signal , for which the µm-level spatially varying R1(r), R2(r), and diffusive properties produce the observable deviations from mono-exponential relaxation and Gaussian diffusion. It is because of this averaging that addressing the mesoscopic tissue complexity requires bringing the tools and intuition from condensed matter and statistical physics, in contrast to the quantum-mechanical description at the molecular level [5, 6] and classical electrodynamics-based considerations used in designing MR hardware.
The overarching goals of “microstructural”, or “mesoscopic” MRI modeling are
To identify the relevant tissue-specific parameters, which contribute to R1(r), R2(r), D(r), Ω(r), and survive in the voxel-averaged signal (i.e., to build an appropriate effective theory for the macroscopic signal);
To suggest optimal ways to probe them (i.e., to solve the corresponding parameter estimation problem).
Notice that to keep our terminology reasonably rigorous, we separated modeling into theory and parameter estimation (sometimes called “fitting”); hence our title. These two facets of modeling require very different tools and ways of thinking, as we will see below in Sections 2 and 3, respectively.
1.2. Coarse-graining and emergent phenomena
Equation (1.1) is an example of an effective theory — i.e., an approximate description that emerges by averaging out the dynamics at the smaller spatial and temporal scales. It illustrates a general principle: pretty much every dynamical equation in physics is an effective theory (governed by an effective Hamiltonian or an effective action), i.e., it has emerged by identifying “collective” phenomena involving many-particle interactions at a more elementary level [1–4].
Over the past century, physicists have come to realize that, at each level of complexity, the effective theory and its relevant parameters can look very different [2], giving rise to the hierarchy of scales and of the corresponding emergent phenomena, from the most microscopic to the most macroscopic. Interactions between quarks and gluons give rise to protons and neutrons, so that their charge and mass can be viewed as effective parameters emerging by averaging over the quark/gluon degrees of freedom. Interactions between protons and neutrons forms a nucleus; interactions between nuclei and electrons give rise to all of chemistry, whereby the details of interactions between protons and neutrons inside nuclei become irrelevant. Interactions between molecules, coarse-grained over nm scale, give rise to hydrodynamics, statistical mechanics and eventually, to biology, and so on.
It is remarkable that, for instance, there is not a hint of classical hydrodynamics at the level of the Schro¨dinger and Dirac equations describing the atomic structure; the large-scale hydrodynamic description emerges after a highly nontrivial averaging over the corresponding quantum degrees of freedom of many molecules. Refined methods such as renormalization [3, 4] were crafted specifically to single out relevant parameters from the rest upon iterativecoarse-graining [10, 11], which is a procedure that averages the dynamics over finer-scale degrees of freedom to derive approximate effective dynamics at the coarser scales involving a minimal number of parameters. This way of thinking reveals a fascinating hierarchy of natural phenomena [2].
For quantifying tissue microstructure by measuring diffusion, transverse relaxation or magnetization transfer with MRI, the mesoscopic Bloch-Torrey equation (1.1) contains all relevant physical processes. This effective theory is as fundamental for the mesoscopic MRI, as the Schro¨dinger equation is for the non-relativistic quantum mechanics, or the Navier-Stokes equation is for the classical hydrodynamics. It is always the starting point for developing biophysical models relating the NMR signal to the mesoscopic tissue architecture.
1.3. Diffusion as coarse-graining
Diffusion in heterogeneous media is a beautiful and simple example of coarse-graining. It can be thought of as a gradual “forgetting”, or homogenizing over the increasing diffusion length. To illustrate this concept, consider a two-dimensional model example of a two-scale mesoscopic structure, represented by randomly placed impermeable disks of two different radii, embedded into an NMR-visible space with diffusion coefficient D0, Fig. 2. To be specific, let us assign sizes, typical to cell dimensions: the small disks have radius rsmall = 1 µm and the large ones are 20 times larger. In a (hypothetical) tissue, this could describe diffusion in the extra-axonal space transverse to a fiber tract, hindered by two types of axons. Here we consider diffusion as a physical phenomenon; its relation to dMRI is discussed below in Sec. 1.4.
FIG. 2. Diffusion as coarse-graining.

An example of a medium where the mesoscopic structure is created by randomly placing black disks of two different radii, rsmall = 1 μm and rlarge = 20 μm, top left panel. To obtain snapshots of the medium as effectively seen by the diffusing molecules at different time scales, we used a Gaussian filter with width L/2, where , and ignored the time dependence of D(t) in the definition of diffusion length, using a typical value D = 1 μm2/ms for the illustration purposes (cf. Sec. 2.4 below).
At time t → 0, each water molecule only senses its own immediate environment; all molecules see the same “intrinsic” diffusion coefficient D|t=0 = D0, which is of the order ~ 1 µm2/ms. (For pure water at 37°C, D0 = 3 µm2/ms.)
As time increases (top row of Fig. 2), molecules get restricted by the walls of both small and large disks. As small disks have much higher net surface area than the large ones, the hindrance occurs mostly due to the small ones. Hence, the decrease of the resulting voxel-averaged diffusion coefficient would happen on the scale of a few ms, mostly dominated by the geometry of the small disks at the scale ~ 1 µm.
At (bottom row), when the diffusion length L(t) strongly exceeds the small disk size, the effect of the small disks has become coarse-grained (while the effect of the large disks is not). Now, we can view the medium in-between the large disks as a homogeneous “effective medium”, with some effective diffusion coefficient Dsmall < D0 given by the macroscopic (“tortuosity”) limit of a medium with the small disks only. It is important to note that if we did not have access to shorter times and could only resolve the diffusion times corresponding to the lower row of panels, there would be no way to identify the presence of the small disks — their effect has been homogenized,1 and their numerous parameters (e.g., size, coordinates) have become “irrelevant”, with their only role in renormalizing D0 down to Dsmall.
Hence, from time on, we can adopt the coarse-grained description which only involves the large disks, immersed in a uniform medium with diffusion constant Dsmall. The corresponding Eq. (1.1) would have the effective D(r) varying at the scale associated with large disks, with D(r) ≃ Dsmall outside them, and the short-distance spatial harmonics of D(r) filtered out as it is obvious from Fig. 2; in Section 2, we will rigorously justify and use this intuitive picture. The measured diffusion coefficient would further decrease with t at the scale of a few hundred ms, corresponding to being hindered by the large disks — the remaining restrictions.
Eventually, at even longer , the effect of the large disks also becomes coarse-grained, and the whole sample looks as if it were homogeneous with some macroscopic diffusion coefficient D∞, such that 0 < D∞ < Dsmall < D0. From this t onwards, one cannot distinguish this sample from a uniform medium with diffusion constant D∞.
Our example shows that the hallmark of coarse-graining over larger-and larger-scale mesoscopic structure is the time-dependence of the overall diffusion coefficient. In the view of this time dependence, it will be convenient to work with the instantaneous diffusion coefficient,
| (1.2) |
defined as the rate of change of the mean squared molecular displacement in a particular direction . (For simplicity, we assumed that our sample in Fig. 2 is statistically isotropic. For anisotropic samples, the diffusion tensor components will acquire the time dependence.)
The average in the definition (1.2) is actually a double average: (i) over the Brownian paths in the vicinity (of size ~ L(t)) of any given initial point r0 ≡ r(t)|t=0, yielding the local coarse-grained diffusivity value D(r0); and (ii) over the ensemble of random walkers (spins) originating from all possible initial points r0. Because of the ensemble average, the measured diffusion characteristics, such as Eq. (1.2), describe a macroscopic sample as a whole. They do not belong to any given Brownian path, but rather emerge as a result of averaging (i) over all possible Brownian paths that could be taken by a given molecule, and (ii) over the initial positions of all molecules in a sample.
Upon taking into account increasing length scales, the effective voxel-averaged Dinst(t) flows towards the tortuosity limit D∞, starting, as in our example, from the “microscopic” D0 > D∞. We used the term “to flow” because the above picture mimics the renormalization group flow [3, 4] according to which the gradual evolution of a physically important parameter, such an elementary particle charge or an effective mass, occurs as a function of the coarse-graining length scale, from the high-energy = short-distance scale, down to the low-energy parameters relevant for the macroscopic description.2
Looking back, there was nothing special about requiring the disks to be impermeable (the black regions could have corresponded to some medium with diffusion coefficient D1 ≠ D0); we could have used objects of a non-disk shape, and/or with non-sharp boundaries. Generally, as long as the random walkers can, in the limit t → ∞, reach any point in a given “compartment”, the above coarse-graining picture applies to this compartment. If a voxel contains multiple non-exchanging compartments, it applies to them separately, with the net signal given by a sum of their contributions.
A similar physical picture qualitatively applies to the effects of spatially varying transverse relaxation rate constant R2(r) — e.g., if the black and white regions in Fig. 2 instead represented different local molecular-level R2 values, and spins were able to diffuse everywhere. The above argument would then lead to an effective R2(r) entering Eq. (1.1) for times t exceeding the corresponding coarse-graining time scale. For instance, for t ≳ 100 ms, the effect of small disks would homogenize to produce a uniform R2,small rate constant in-between the large disks, and so on, leading to the time-dependent overall observed “rate constant” R2(t) from a voxel (clearly, not a constant — hence, quotation marks), asymptotically approaching the macroscopic limit R2|t→∞ at very long t. Likewise, if the mesoscopic structure in Fig. 2 represented spatially varying susceptibility χ(r), inducing the corresponding Ω(r), the resulting voxel-wise “rate constant” would also become time-dependent. In this case, it will increase with t, approaching the macroscopic value as a result of the gradual coarse-graining [12].
We note that all the above mentioned quantities — Dsmall and R2,small; D∞ and R2|t→∞; — are nonuniversal, i.e., they depend on the numerous structural details, such as packing geometry (e.g., periodic versus random arrangement); they would change if the disks were instead squares, etc. Certainly, these quantities are not given by a simple averaging of the microscopic D(r) or R2(r) over the sample. However, the initial values Dinst(0) and R2(0) are given by the sample-averaged D(r) and R2(r), correspondingly, since at t → 0 (practically, at times just exceeding the ps time scale necessary for the local D(r) and R2(r) to emerge), each spin senses only its immediate environment.
The picture of gradual coarse-graining over an increasing diffusion length has a number of important consequences:
The mesoscopic Bloch-Torrey equation (1.1) can be fully determined only after the relevant spatio-temporal scales are specified, since its parameters R2(r), Ω(r) and D(r) are effective and, hence, scale-dependent.
Generally, the observed voxel-averaged diffusion coefficient and the effective relaxation “rate constant” would depend on time t because of the presence of the mesoscopic structure (such as Dinst(t) decaying from D|t=0 down to D∞ in our example of Fig. 2). This time t can be set by the measurement sequence, and varying it provides a unique window into the tissue architecture at the scale of the corresponding diffusion length L(t).
This brings us to the fundamental challenge of interpreting such time dependencies in terms of the mesoscopic structural complexity. Practically, we must figure out which features in the effective R2(r), Ω(r) and D(r) remain observable after the voxel-wise averaging as a result of a macroscopic acquisition (cf. Section 2). This is the overarching task — and justification — for the theoretical efforts in our community.
If a measurement is too slow to track the transient processes, we are left (in each non-exchanging compartment) with the t → ∞macroscopic Bloch-Torrey equation, i.e., Eq. (1.1) with uniform effective parameters D(r) → D∞, R2(r) → R2(t)|t→∞, Ω(r) → 〈Ω(r)〉. Its solution becomes trivial — mono-exponential relaxation and Gaussian diffusion (cf. Section 3); i.e., coarsegraining leads to the universal t → ∞ dynamics, albeit with nonuniversal macroscopic parameters such as D∞. The mesoscopic information is now lost, as the signal is indistinguishable from that in a uniform medium. Effective macroscopic parameters are in general different from the intrinsic mesoscopic ones; for instance, D∞ can be notably lower than the intrinsic water or axoplasmic diffusion coefficient.
1.4. dMRI signal as the diffusion propagator; qt Imaging
So far we managed to get away with looking at a single equation (1.1) and wave hands based on drawing parallels with concepts developed in physics. It is now time to introduce basic notations; the content of this subsection should be familiar to anyone actively working in dMRI.
In what follows, for simplicity we will confine ourselves only to the mesoscopic structure as related to diffusion, and will assume the relaxation effects to be trivial (at least in each tissue compartment), setting R2(r) → R2, and a uniform voxel-wise Larmor frequency, Ω(r) → 〈Ω〉. (The nontrivial R2(r) and Ω(r) modify apparent diffusion metrics [13–16]; this is beyond the scope of our review.) This allows us to factorize the magnetization , where ψ(t, r) is not subjected to the relaxation and frequency shift and obeys the following equation
| (1.3) |
We focus here on the most easily interpretable measurement with very narrow (i.e., short) gradient pulses.3 As we now discuss, serendipitously, this measurement accesses the propagator of the mesoscopic diffusion equation, which (cf. Sec. 1.3) describes evolution of particle density ρ(t, r)
| (1.4) |
The fundamental solution of Eq. (1.4), or diffusion propagator , satisfies this equation
| (1.5) |
with the point-like and instant source at r = r0. The source term corresponds to the solution with zero particle density for t < 0 and with the initial condition δ(r r0) instantly appearing at t = 0. The solution is thus proportional to the unit step function, θ|t>0 = 1 and θ|t<0 = 0, such that ∂tθ(t) = δ(t).
The propagator t;r,r0 is a fundamental quantity describing the diffusion process around the point r0, with a meaning of the probability distribution function (PDF) of molecular displacements r – r0 over time t. (This PDF can be sampled using Monte Carlo simulations by releasing random walkers all at once from the point r0.) Of course, since the local tissue structure is different around each initial point r0, the propagator depends on the points r0 and r separately.
The fundamental connection between the diffusion process (1.4) and the NMR measurement stems from the gradient-dependent phase of ψ(t, r) as described by Eq. (1.3). In the limit of narrow pulses g(τ) = q [δ(τ – t) – δ(τ )] and the initial condition as in Eq. (1.5), the magnetization ψ(t, r) differs from by the position-dependent phase acquired during the gradient application. The diffusion-weighted signal, which is a net magnetization in a voxel,
| (1.6) |
becomes equivalent to a spatial Fourier transform of the voxel-averaged propagator
| (1.7) |
In Eq. (1.6) we divided by the voxel volume V, such that the unweighted signal (the right-hand side) is normalized to unity. A thorough discussion can be found e.g., in ref. [27].
Note that exact “local” propagator is not translation invariant, i.e., it depends on the absolute coordinates rt, r0 (and time t). The voxel-averaging in Eq. (1.6) automatically restores translation invariance, which means that the measured propagator tt is parameterized by the two variables: the spatial displacement r ≡ rt – r0 and the diffusion time interval t (equivalently, by q and t).
Hence, the parameter space of dMRI fundamentally consists of q and t, Fig. 3 (here we dropped the directionality in q to not overload the picture). Literally speaking, mapping the diffusion propagator in the space of q and t can be referred to as qt Imaging.4 For multiple diffusion encoding, which maps a more complex object than the diffusion propagator (Section 4), the parameter space in principle depends on the multiple q and t intervals.
FIG. 3.
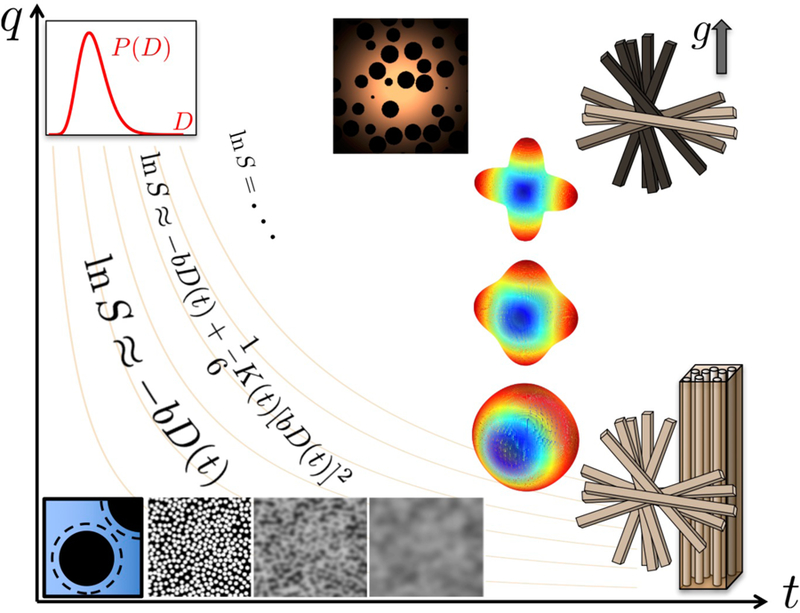
The parameter space of dMRI is at least twodimensional: By increasing q one accesses the progressively higher-order diffusion cumulants, Sec. 1.8, whereas the dependence along the t-axis reflects their epvolution over an increasing diffusion length scale , Eq. (1.12). The b-value alone does not uniquely describe the measurement, unless diffusion in all tissue compartments is Gaussian; contour lines of b = q2t are schematically drawn in beige. Large-q limits: Top-left is high-resolution limit L(t) ≪ lc, qlc ≫ 1, Sec. 1.5(i); middle is the , limit of probing the pore correlation function, Sec. 1.6. The hierarchy of dMRI models (pictures), cf. Fig. 4, as well as the cumulant representation with different number of terms, cf. Fig. 5, are superimposed. The decrease of the signal from axonal bundles parallel to the increasing gradient is shown by their darkening (top right). In Section 2 we move along the t-axis at low q, and in Section 3 we move along the q-axis at asymptotically long t. Section 4 is devoted to effects beyond this diagram, contained in voxelaveraged products of propagators at different t and q.
The so-called b-value [30] has historically become the often single-quoted measurement parameter. However, it only defines the measurement if diffusion is Gaussian in every compartment, in which case the diffusion propagator
| (1.8) |
in each compartment is determined solely by the parameter combination q2t. Schematically, the contour lines of constant b are outlined in Fig. 3. In general, for anisotropic tissues such as brain white matter, Gaussian diffusion in each compartment is described by the diffusion tensor, bD → bijDij, where the b-matrix [31] bij = qiqj t.
The Gaussian limit (1.8), and its more general anisotropic Gaussian limit, are hallmarks of “full” coarse-graining, which occurs in the t → ∞ limit, cf. Fig. 2. In this case, no matter how structurally complex the tissue, it can be modeled as a sum of (anisotropic) Gaussian signals. Section 3 will be devoted to the picture of multiple Gaussian compartments (the Standard Model), cf. the column of pictures at long t in Fig. 3.
1.5. Hierarchy of diffusion models based on coarse-graining: The three regimes
From the unifying coarse-graining point of view, we can now categorize biophysical models of diffusion, Fig. 4, into the fol lowing three regimes. In either of the regimes, the theoretical treatment simplifies. The regimes can be arranged according to the increasing diffusion length L(t) relative to characteristic mesoscopic tissue length scales:
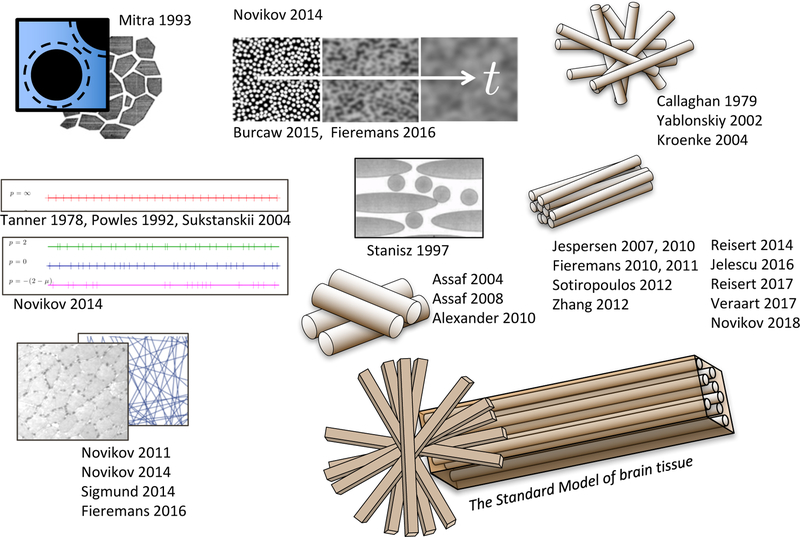
FIG. 4. Models are pictures….
Here they are drawn with coarse-graining occurring, roughly, from left to right. References: Mitra 1993 [32], universal short-t limit; Novikov 2014 [33], universal long-t behavior; Burcaw 2015 [23] and Fieremans 2016 [34], long-t behavior transverse and along WM fibers; Tanner 1978 [49], Powles 1992 [50], Sukstanskii 2004 [35], periodic 1-dimensional lattice; Novikov 2011 [51], random permeable barriers in any dimension, and its application to myofibers (Sigmund 2014 [52] and Fieremans 2016 [53]); Callaghan 1979 [54], first model of diffusion inside random narrow cylinders; Yablonskiy 2002 [55], diffusion in finite-diameter cylinders modeling lung alveoli; Stanisz 1997 [56], first model for WM fiber tracts made of ellipsoids; Assaf 2004 [57], CHARMED; Assaf 2008 [58], AxCaliber; Alexander 2010 [59], ActiveAx; Kroenke 2004 [36], NAA diffusion inside neurites. The widely adopted t → ∞ picture of narrow “sticks” for the neurites, embeded in the extra-neurite space (the Standard Model): Jespersen 2007 [37], Jespersen 2010 [38], Fieremans 2010 [39], Fieremans 2011 (WMTI) [40], Sotiropoulos 2012 (Ball and rackets) [41], Zhang 2012 (NODDI) [42], Reisert 2014 (MesoFT) [43], Jelescu 2016 (NODDIDA) [44], Reisert 2017 [45], Veraart 2017 (TEdDI) [48], Novikov 2018 (LEMONADE [46], RotInv [47]).
No coarse-graining has yet occurred. If the local D(r) varies in space over the correlation length scale lc, then for L(t) ≪ lc and qlc ≫ 1, each molecule senses its own, locally homogeneous D(r). In this high-resolution limit [27], the signal is a Laplace transform of the histogram (D) of all the local values D(r). A more relevant to biology situation occurs when instead of smooth D(r) variations, there are sharp barriers. The relevant parameter is then the net surface-to-volume ratio S/V of all barriers (e.g., cell walls). For times such that L(t)S/V ≪ 1, one observes the S/V universal short-time limit of the diffusion coefficient [32].
Coarse-graining over the structural disorder [33] results in the power-law approach t−ϑ of the instantaneous diffusion coefficient Dinst(t) towards the t → ∞ limit D∞. Here, the power-law exponent ϑ is connected to the large-scale behavior of the density correlation function of the hindrances to diffusion, and to the spatial dimensionality, yielding qualitatively distinct behavior along [33, 34] and transverse [23, 34] to the neurites in the brain. In Section 2 we argue, following ref. [33], that the more heterogeneous, or “disordered”, the sample is, the slower the approach (the smaller the exponent ϑ). Conversely, in ordered media, such as in the model of perfectly ordered membranes [33, 35], the approach of Dinst(t) towards D∞ is exponentially fast.
Complete coarse-graining. Diffusion in each non-confining tissue compartment has approached its t → ∞ Gaussian (tortuosity) limit, as discussed above (cf. also a more detailed discussion in Sec. 1.9 below). If there is no exchange between compartments, we obtain the most common, “multi-exponential” model. For neuronal tissue, the compartments are anisotropic due to the presence of effectively one-dimensional neurites. In Section 3, we introduce the “Standard Model” of neuronal tissue that accounts for the neurites with associated extra-neurite space, and with an orientation dispersion (Fig. 8). While known under a plethora of names and acronyms [36–48], from the physics stand-point, this is practically the same model, with differences in the parameterization of the neurite orientation distribution function and variations in the descriptions of the extracellular space, as well as in the model parameter estimation procedures and employed parameter constraints.
FIG. 8. The Standard Model of diffusion in neuronal tissue, Eq. (3.4).
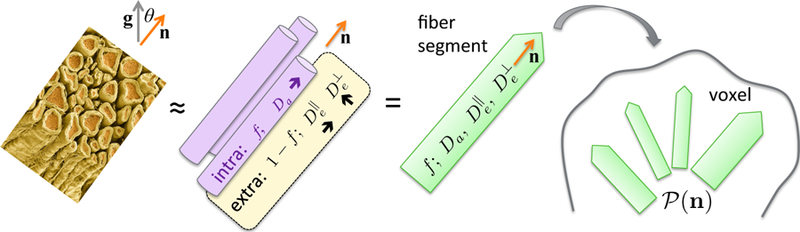
In the t → ∞ regime (iii), elementary fiber segments (fascicles), consisting of intra- and extra-neurite compartments, are described by at least 4 independent parameters: f, Da, and . CSF can be further added as the third compartment, cf. Eq. (3.5). Within a macroscopic voxel, such segments contribute to the directional dMRI signal according to their ODF .
The crossover between regimes (i) and (ii) occurs when the diffusion length, L(t), is commensurate with the characteristic length scale of the structural disorder. The instantaneous diffusion coefficient Dinst(t) decreases with time within this crossover; while no general results are available there, it can be studied using numerical simulations.
1.6. How to become sensitive to short length scales?
Working in the t → ∞ limit (iii) can only give us compartment volume fractions and their diffusion coefficients. Coarse-graining has already occurred and apparently washed out all traces of other microstructural parameters.
Determining characteristic µm-level length scale(s) lc, such as the correlation length of the arrangement of tissue building blocks (e.g., disk radii in Fig. 2), is in principle possible using deviations from the Gaussian signal shape. In the spirit of Fig. 3, varying either t or q can yield the sensitivity of the diffusion signal (propagator) to the length scale, via the diffusion length [cf. Eq. (1.12) below], and via 1/q, respectively. However, as we now discuss, these theoretically distinct ways are not that different in practice, because attaining q ~ 1/lc at times t ≫ tc practically requires sensing the signal contributions that are small at least as some positive power of the small ratio tc/t ≪ 1, where .
Varying t amounts to literally observing the diffusive dynamics for short times, when the coarse-graining has not yet fully occurred, such as during the regimes (i) and (ii) above. In our example in Sec. 1.3, to identify the presence of the small disks, one could try, e.g., detecting time dependence in Dinst(t) or in D(t) at . The random permeable barrier model [51, 53], a candidate for diffusion transverse to myofibers and for one-dimensional hindrances along the neurites [33], allows one to trace the effect of coarse-graining in Dinst(t) or in D(t) across all the regimes (i) – (iii).
Varying q, by employing strong narrow gradients (with width δ ≪ tc so that q is well-defined [17–19, 21, 23–26]), can in principle allow one to unravel the coarse-graining, i.e., to observe features at q ~ 1/lc even when t ≫ tc.5 However, the price to pay for accessing such fine structures is the suppression of the signal. To give an example [68], consider diffusion in a porous medium with connected pores and isolated grains, cf. Fig. 3 (center-top drawing). For long diffusion times, the pore structure is effectively coarse-grained (similar to diffusion in-between the small grains in Fig. 2). While having the overall Gaussian-like envelope with D ≈ D∞, the diffusion propagator (up to an overall normalization) replicates the pore shape on the fine scale of the order of lc, Fig. 3, with the density correlation function Γ(r) of the pore space arising due to voxel averaging. Correspondingly, in q-space,
| (1.9) |
where the first term originates from sample-averaged , the pore water fraction, and represents the average spin density spread, while the product becomes a convolution (the second term) of this envelope with the correlation function in q-space (i.e., the pore space power spectrum) Γ(q). The longer the time, the sharper is the Gaussian propagator in q-space, and the less is the blurring of the pore correlation function induced by the convolution. However, longer times result in a stronger power-law suppression of this nontrivial convolution term, whose magnitude can be estimated as ~ [lc/L(t)]d in d dimensions. This estimate comes from noting that we are essentially averaging the pore density fluctuations over the “diffusion volume” Ld(t); for the short-range disorder in the grain placement, these fluctuations, ~ 1 at the scale ~ lc, become uncorrelated at the scales much beyond lc.
When a tissue consists of non-exchangeable compartments of different nature, one can tune the experiment to focus on one or the other. Consider an example of a tissue consisting of a non-confining compartment (e.g., the extra-cellular space), and a fully confining, i.e., restricted one (e.g., cells of size a). The diffusional coarse-graining in the latter stops at the time ta ~ a2/D. The whole medium possesses two relevant scales, L(t) and a, which are markedly different for long times when L(t) ≫ a. An experimentalist working in this limit has a choice of selecting the wave number q of diffusion measurements (the strength of diffusion weighting). The choice q ∼ 1/a (diffusion diffraction [69]) enables measuring the size of the restricted compartment, but strongly suppresses the signal from the permeable one. The choice q ~ 1/L(t) enables observation of diffusion dynamics in the permeable compartment. The signal from the restricted compartment remains unsuppressed, such that both the signal attenuation ln S ~ (qa)2 ≪ 1 and the diffusivity D(t) ~ a2/t ≪ 1 become negligible; one can then formally treat such a compartment as Gaussian with its diffusion coefficient D → 0. This leads to the picture of zero-radius “sticks” in the brain (neurites with zero diffusivity in the transverse direction), cf. Sec. 3.1 below.
1.7. Models versus representations
Models are pictures (Fig. 4), exemplifying a rough sketch of physical reality, specified by their assumptions meant to simplify nature’s complexity. This simplification relies on averaging over the irrelevant degrees of freedom, and keeping only a handful of relevant parameters describing the corresponding effective theory. Model assumptions are therefore a claim for the relevant parameters. They are more important than mathematical expressions, as they prescribe a parsimonious way to think about the complexity. Model validation is thereby validation of our frame of thinking.
A representation could be defined as a model-independent mathematical expression used to store, to compress, or to compare measurements. It can be realized as a function with a few adjustable parameters or a set of coefficients for a decomposition in a basis (cf. Fig. 5 for a few most commonly used representations in dMRI). In contrast to models, representations are as general as possible, and have very little assumptions. As there are infinite ways to represent a continuous function, the choice of representation is often dictated by convenience or tradition. Practically, not all representations are equivalent because one only uses a few basis functions rather than an infinite set; from this standpoint, sparser representations are more favorable. By construction, representations do not carry any particular physical meaning and hence do not immediately invoke any picture of physical reality; one can say that representations are formulas.
FIG. 5. …while representations are formulas.
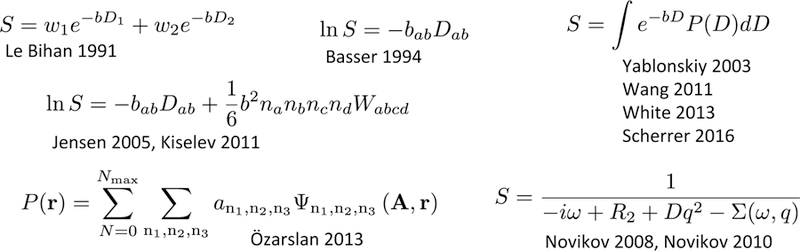
References: Le Bihan 1991 [60], first biexponential representation of dMRI signal from brain; Basser 1994 [31], diffusion tensor imaging (DTI); Jensen 2005 [61], diffusion kurtosis imaging (DKI); Kiselev 2011 [18], cumulant expansion; Novikov 2008 and 2010 [27, 62], effective medium theory (transverse relaxation and diffusion, correspondingly); Özarslan 2013 [63], expansion in harmonic oscillator basis; Yablonskiy 2003 [64], inverse Laplace transform (multi-exponential representation). Anisotropic multi-exponential representations: Wang 2011 [65], diffusion basis spectrum imaging (DBSI); White 2013 [66], restriction spectrum imaging (RSI); Scherrer 2016 [67], distribution of anisotropic microstructural environments in diffusion-compartment imaging (DIAMOND).
A detailed discussion on the choices between modeling and representing can be found in ref. [70]. In this Review, we mostly focus on models; however, there exists one fundamentally important representation that we will cover now.
1.8. The cumulant expansion as a default representation
The ubiquitous nature of Gaussian diffusion, at least for sufficiently long times, has prompted a Taylor expansion [18, 71]:
| (1.10) |
in the powers of q, describing the deviation from the Gaussian form (1.8). The summation over the repeated coordinate indices i, j, … = 1…3 is implied throughout; is the mean diffusivity used for normalization. The symmetric tensor Wijkl is called the diffusional kurtosis tensor, while the kurtosis in a given direction, , is defined as [71].
The propagator expansion (1.10) stems from the corresponding cumulant expansion in probability theory noticed almost a century ago by Fisher and Wishart [72, 73]. For diffusion, only even orders in this series are nonzero due to the time-reversal symmetry in the absence of the bulk flow. Typically, the Taylor series (1.10) converges within a finite radius in q which is model-dependent [74, 75].
A general diffusion propagator will have all even cumulant terms Dij(t), Wijkl(t), … nonzero and diffusion time-dependent [18, 27]. Experimentally we often access only a few first terms, especially when using low diffusion weighting on clinical systems. (We assume the narrow-pulse limit throughout. In Sec. 2.2 we discuss in detail how the lowest order of the ideal cumulant series (1.10) is modified by the arbitrary gradient shape).
Upon coarse-graining, for a given tissue compartment the higher-order terms Wijkl, … flow to zero, such that the signal approaches the Gaussian form (1.8) as t→ ∞. In this limit, the higher-order cumulant terms of the net diffusion propagator can originate only from the partial contributions from different tissue compartments (since a sum of Gaussians is non-Gaussian).
For any t, the series (1.10) generates the cumulants (see e.g., refs. [18, 72, 73] for definition) of the PDF of molecular displacements6 (1.6), via taking derivatives at q = 0, such as
| (1.11) |
Based on such averages, it is conventional to define the cumulative diffusion coefficient
| (1.12) |
or, more generally, the cumulative diffusion tensor
| (1.13) |
(a symmetric 3 × 3 matrix with 6 independent parameters in 3 dimensions). These objects are defined in terms of the average rate of change of the mean-squared molecular displacement over the whole interval [0, t] (in contrast to the instantaneous rate of change (1.2) above).
The linear estimation problem for Dij(t), referred to as the diffusion tensor imaging (DTI), has been solved by Basser et al. [31]. It requires7 a diffusion measurement along at least 6 non-collinear gradient directions in addition to at least one more, e.g., the b = 0 (unweighted) image.
Likewise, the linear estimation problem for both the diffusion and kurtosis tensors, via the expansion up to ~ q4 ~ b2, called diffusion kurtosis imaging (DKI), has been introduced by Jensen et al. [61, 76]. It involves the 4th order cumulant related to Wijkl(t). The number of parameters are now 6 + 15 = 21, hence one needs at least two b ≠ 0 shells in the q-space, and at least 15 non-collinear directions. The weights for unbiased estimation of diffusion and kurtosis tensors for non-Gaussian MRI noise were found recently [77].
A general method to calculate the number of parameters for a given order lc of the cumulant series (1.10) in 3 dimensions is based on the SO(3) representation theory (known in physics as theory of angular momentum in quantum mechanics). A term ~qlc of even rank lc is a fully symmetric tensor, which can be represented as a sum of the so-called symmetric trace-free (STF) tensors of ranks lc, lc 2, …, 2, 0 [78]. Each set of 2l + 1 STF tensors of rank l realizes an irreducible rep resentation of the SO(3) group of rotations, equivalent to a set of 2l + 1 spherical harmonics Ylm [78]. Hence, the total number nc of nonequivalent components in the rank-lc cumulant tensor is
| (1.14) |
so that nc = 6 for DTI (lc = 2) and nc = 15 for DKI (lc = 4).
Suppose we truncate the cumulant series (1.10) at an (even) term of rank lc = lmax. Hence we determine all the parameters of cumulant tensors (diffusion, kurtosis, …) of ranks 2, 4, …, lmax. The total number of independent parameters in the truncated series
| (1.15) |
corresponding to Nc = 6, 21, 49, … for lmax = 2, 4, 6, … Hence, DTI yields 6 parameters, DKI yields 21, etc. (Here we did not include the proton density S|b=0 in our counting.)
The cumulants Dij, Wijkl, … of the signal obtained via Taylor-expanding its logarithm in the (even) powers of qi, or equivalently, in the powers of b, correspond to the cumulants of the genuine PDF of molecular displacements r = rt – r0 only in the narrow pulse limit, and in the absence of the mesoscopic magnetic structure (uniform R2 and Ω). When the finite gradient pulse duration δ is comparable to the time scale of the transient processes, the measurement acts as a low-pass filter with a cutoff frequency ∼ 1/δ [17–26].
1.9. Normal or anomalous diffusion?
For finite t, the diffusion propagator in a heterogeneous medium is never Gaussian. The existence of domains with slightly different “local” D(r) at a given coarse-graining scale necessarily yields the time-dependent Dinst(t), as well as the higher-order terms in q, such as q4, in the Taylor expansion of ln G(0)(t, q) [27, 33]. Upon coarse-graining, these terms gradually flow to zero, and Dinst(t) D∞, such that diffusion becomes Gaussian asymptotically as t → ∞ in each separate non-confining tissue compartment. This was the picture of Sec. 1.3, cf. Fig. 2. In particular, we implied that the diffusion coefficient decreases, as a result of the coarse-graining, towards its finite tortuosity asymptote Dinst(t) t→∞ ≡ D∞ >0 How reliable is this picture? What does it take to destroy it?
Existence of finite D∞ is equivalent to mean squared displacement growing linearly with time for sufficiently long t, — this is a direct consequence of the definition (1.2). One says that diffusion asymptotically becomes “normal”, i.e., the PDF of molecular displacements over a sufficiently large t approaches normal (Gaussian) distribution, cf. Eq. (1.8) with D → D∞. Of course, if there are two or more non-exchanging tissue compartments, the total distribution will be non-Gaussian (as a sum of Gaussians with different D∞), but this non-Gaussianity is in a sense trivial; the total D∞ would still exist (given by a weighted average for the corresponding compartment values) [39], and the scaling at large t would hold.
There exists a radical alternative, when for t → ∞, with exponent α ƒ= 1 — the so-called anomalous diffusion [79]. According to the definition (1.2), D∞ = 0 for α < 1 (sub-diffusive behavior), and D∞ = for α > 1 (super-diffusive behavior). In other words, observation of anomalous diffusion is equivalent to stating that the macroscopic diffusion coefficient D∞ does not exist. (The trivial case D(t) ∼ a2/t for a confining compartment of size a is not considered anomalous; , α = 0.)
The absence of D∞ in a non-confining medium is always a drastic claim: it is potentially exciting yet should be thoroughly validated, because the underlying physical assumptions yielding α ≠ 1 are generally quite peculiar and exceptional, as we discuss below. In neuronal tissue, one always observes finite D∞ in non-confining compartments (e.g., in the extra-cellular space), Section 2, hence diffusion is empirically never anomalous [23, 33, 34] for brain dMRI.8
From the point of coarse-graining, anomalous diffusion means that the sample never quite looks homogeneous — for example, a fractal has a self-similar structure, which implies similar statistics of static structural fluctuations at every length scale. In other words, when the coarse-graining over some scale has taken place, a larger scale looks statistically similar, so that the already averaged structural features are never forgotten, since they are reproduced again and again. In contrast, the structure in Fig. 2 implies that this memory is forgotten for each of the two length scales, correspondingly on the two well-defined time scales.
Tissues empirically do not look self-similar; usually, when we look at a histological slide without a scale bar, we can still roughly say at which resolution the sample is imaged because usually cell size is well defined (for a given tissue type) — otherwise, medical students would not pass their pathology exams. For instance, when we look at cross-sections of white matter tracts, the majority of axons are of the order of ~ 1 µm in diameter [80–84], and the section does not look the same when magnified by factors of 10, 100, or 0.1, 0.01, etc. A more quantitative statement can be made by studying large-distance scaling behavior of the density-density correlation function of the tissue structure; recent investigation [23] confirms that the structural fluctuations in white matter tracts are short-range (and not diverging at large length scales).
When can anomalous diffusion arise? In a broader context, this fundamental question has been extensively studied for the Fokker-Planck equation
| (1.16) |
where in addition to the “diffusive” flow j(t, r ) = D(r)∂ ψ(t, r) (Fick’s law), one considers mesoscopic random flow b ecause o f s ome s tationary l ocal “ velocity”, or “force” field v (r) ( imagine a ctive s treams, s uch a s vortices or currents in an ocean [85]). Equation (1.16) arises as a conservation law ∂tψ= −∂r · j, where the total flow
It turns out that the presence of the random flow term v(r) with short-range spatial correlations can drastically change the dynamics in dimensions d ≤ 2 and drive the system away from the Gaussian diffusion. In dimension d = 1, random force field c auses s ub-diffusive b ehavior , a famous result by Sinai [86]. In d = 2 dimensions, superdiffusive behavior occurs when the flow v (r) i s solenoidal, div v(r) = 0, and sub-diffusive if it is potential, curl v(r) = 0 [85, 87–89].
In the absence of the random forces, v 0, small fluctuations in D(r) do not destroy the “trivial” Gaussian fixed point in dimensions d > 0 [90, 91] (cf. footnote 2). In other words, for the spatial short-range disorder in D(r) to become relevant (i.e., to increase under the renormalization group flow), and for the anomalous diffusion to take over, the spatial dimension should formally be d = 0. What this tells is that it is very difficult, without the flow term, to break the Gaussian fixed point of the finite D∞, at least starting from the weak disorder in D(r). Extremely strong disorder, which is specially tuned, can induce the percolation transition [92] D∞ → 0; another possibility for destroying finite D∞ is to create the disorder in the mesoscopic D(r) with anomalously divergent spatial fluctuations [93, 94]. To the best of our knowledge, neuronal microstructure is compatible neither with a percolation transition, nor with diverging structural fluctuations [23].
Another class of phenomena where anomalous diffusion takes place corresponds to systems with slow dynamics, originating from a broad distribution of time scales, such that the waiting time distribution p(τ) ~ 1/τ1+µ between “hops” of random walkers has a power-law tail whose first moment diverges, 0 < µ < 1. Such broad distributions can emerge, e.g., in highly disordered amorphous solids, where escape times τ from various “traps” for electrons are distributed as a power law, first postulated by Scher and Montroll [95]. For the traps, the long tail in p(τ ) can arise due to an exponentially strong dependence of the activation rate on the energy barrier E at temperature T, such that a relatively flat distrubution can result in the Le´vy-like . Hopping with traps may lead to anomalous transport [96] and fluorescence [97]. Anomalously slow dynamics also occurs in viscoelastic systems where elementary components are strongly coupled (Rouse polymer chain [98] of monomers tied to each other by elastic springs and undergoing Langevin dynamics). The simulated dynamics of single protein molecules [99] and of colloidal tracers restricted by crowded dynamical environments such as an F-actin network [100] can exhibit such a broad distribution of time scales [101]. While an active area of investigation, the anomalously slow dynamics is always characterized by strong disorder (e.g., broadly distributed traps) and/or interactions among the random walkers (e.g., parts of a polymer).
To recap, coarse-graining over an increasing diffusion length L(t) provides a physical picture for time-dependent diffusion in mesoscopically disordered samples. This picture implies gradual “forgetting” of the memory about the structural heterogeneities. In an overwhelming majority of systems, the macroscopic dynamics is characterized by a Gaussian fixed point, the absence of long-term memory, and an asymptotically normal diffusion. In short, diffusion is almost always non-Gaussian, but almost never anomalous. In the brain, it is not anomalous specifically because the density fluctuations of brain structural units do not diverge at large scales, traps for water molecules with broad distribution of escape times do not seem to exist, and the “active” flow effects (microstreaming, axonal transport) are negligible [102].
1.10. dMRI methods beyond the scope of this review
Before proceeding to review brain dMRI models, we would like to mention what we have left out, because of limited relevance to brain dMRI as of today, and/or due to exhaustive coverage elsewhere.
On the methodological front, the leitmotif of the review is the language of coarse-graining, Fig. 2. It is most intuitive for modeling structurally disordered systems, typical for biology, cf. modeling the time-dependent diffusion in Section 2, based on including all the restrictions into the spatially varying D(r) in Eq. (1.1). This took precedent to approaches to fully confining or periodic geometries, conventionally solved by formulating Eq. (1.1) as the Laplace equation with boundary conditions, thoroughly reviewed in ref. [103] in the context of diffusion in porous media.
We also left out the physics of the localization regime, where diffusion in a strong constant gradient suppresses the signal everywhere except next to pore walls, within the gradient-dependent dephasing length Lg = (D0/g)1/3, which leads to signal decay [104–106]. This is an example where effects of non-narrow pulses lead to decoupling of the gradient magnitude g and the gradient pulse width δ in the narrow-pulse combination q = gδ. The “edge enhancement” also amplifies the role of the permeability of the walls [107]. Brain structures seem to be too small for the edge effects to be relevant, but such phenomena can become important in body dMRI.
Playing with δ, e.g., using short-wide pulse combinations, we or one can map the Fourier transform of the shape of the confining pore [108, 109], which again requires prohibitively strong gradients for the narrow axons and dendrites in the brain, but is applicable in porous media NMR. The relevance of pulse width δ would add an extra dimension to the phase diagram in Fig. 3.
Detailed review of practical aspects of dMRI measurements and biological applications are beyond our scope here. The reader is referred to the review [110] for implementation details of dMRI measurements, recent reviews of dMRI in white matter [111] and in cancer [112], as well as to other articles in this Special Issue.
2. TIME-DEPENDENT DIFFUSION IN NEURONAL TISSUE
Everything should be made as simple as possible, but not simpler
Albert Einstein
The intuition of Sec. 1.3 suggests that the time-dependence of the diffusion coefficient defined as either Eq. (1.2) or Eq. (1.12), is a hallmark of the mesoscopic structure, and the associated time scale can be translated into the corresponding mesoscopic length scale. Identifying µm-level tissue length scales is the ultimate test of our ability to “quantify microstructure” — after all, how else would we know that we are indeed sensitive to the micro-structure? The focus of this Section is on determining tissue properties on such length scales.
Fundamentally, observation of the time dependent over-all D(t) is significant because it tells that diffusion is non-Gaussian in at least one of the tissue compartments. Indeed, at the lowest order of the cumulant expansion (1.10) of the signal S = ∑ fiSi, contributions from non-exchanging tissue compartments Si add up, such that the total diffusion coefficient is a weighted average:
| (2.1) |
An overall time-dependent D(t) necessarily means that at least one of Di depends on t. In turn, the time-dependent Di(t) must necessarily lead to a nonzero kurtosis and higher-order cumulants [27] in the ith compartment, arising from the same mesoscopic heterogeneity which has not yet been fully coarse-grained — and, hence, may still be possible to quantify. Conversely, if diffusion is Gaussian in all tissue compartments, all Di = const, and the overall diffusion coefficient is time-independent. The overall kurtosis is then a nonzero constant just because a sum of Gaussians is not a Gaussian.9
We begin this Section by reviewing experimental data on the time-dependent diffusion coefficient and kurtosis in brain, and then discuss the two physically distinct regimes of time-dependence, according to the hierarchy of Sec. 1.5: the short-time regime (i), and the long-time regime (ii) approaching the asymptotically Gaussian diffusion in each non-exchanging compartment.
Certainly, we are almost never in a pure limit experimentally — rather, we are typically in some crossover, e.g., in-between the regimes (i) and (ii). However, it is still important to understand the behavior of the system in certain limits where it can be modeled with more confidence. Performing experiments in such limits provides a way to validate models through observing definitive functional dependencies on the measurement parameters [70]; thus-identified relevant degrees of freedom for tissues can then be incorporated into more complex theories of the crossover behavior relevant to a broader range of dMRI studies, and for clinical translation.
2.1. Time dependent diffusion in the brain: Is there an effect?
Empirically, observing time-dependence of diffusion in brain tissue has been challenging because this effect occurs at time scales associated with diffusion across length scales featuring neurites (i.e., axons and dendrites). Typically, their diameters as well as the heterogeneities along them (e.g., spines, beads) are of 1 µm size, hence, the corresponding diffusion times are expected to be of the order of a few ms. Such short times are quite difficult to access, especially on human systems. Besides, the time-dependence is generally slow — which is theoretically expected due to its power-law character [33], as discussed below in Sec. 2.4 — therefore requiring a sufficiently broad range of times to detect.
Time-dependence of the cumulative D(t), Eq. (1.12), in brain tissue has been demonstrated using pulse gradient spin echo (PGSE) in several ex vivo studies for a range of diffusion times encompassing 20 250 ms [56, 114–116]. In vivo, time-dependent diffusion in both longitudinal and transverse directions was also observed in rat corpus callosum at t ranging from 9 to 24 ms [117], though another study yielded no change in the mean diffusivity of healthy and ischemic feline brain with respect to t between 20 − 2000 ms [118].
In the human brain, it has been unclear for quite some time whether in vivo time-dependent diffusion properties can be observed. While several in vivo studies report no observable change over a broad range of diffusion times [119, 120], Horsfield et al. [121] reported time-dependent diffusion in several white matter regions at times ranging from 40 to 800 ms. Very recently, in vivo pronounced time-dependence in the longitudinal diffusivity and less pronounced time-dependence in the transverse diffusivity has been reported in several WM tracts of healthy human volunteers for relatively long diffusion times, t = 45 600 ms, on a standard clinical scanner using stimulated echo acquisition mode (STEAM)-DTI [34]. Subsequently, a similar effect in the transverse direction to WM tracts was observed with STEAM-DTI in the range t = 48 − 195 ms [122].
Oscillating gradient spin echo (OGSE) diffusion-weighted sequences are able to probe shorter diffusion time scales compared to conventional PGSE, and have clearly demonstrated time-dependent diffusion in the brain, including the observation of time-dependent diffusivities in vivo in normal and ischemic rat brain cortex [123], as well as ex vivo in rat WM tracts [124]. By combining OGSE and PGSE, Pyatigorskaya et al. [125] observed time-dependent diffusion coefficient and a non-monotonic time-dependent kurtosis (with a maximum value K ≈ 0.6 at t ≈ 10 ms) in healthy rat brain cortex at 17.2 T, and Wu and Zhang [126, 127] recently observed time-dependence in mouse cortex and hippocampus. In humans, Baron and Beaulieu [128] found eight major WM tracts and two deep gray matter areas to exhibit time-dependent diffusion using OGSE and PGSE, and Van et al. [129] reported a similar effect with OGSE in human corpus callosum. Furthermore, works using double diffusion encoding (cf. Section 4) indirectly point at the time-dependent nature of diffusion in brain tissue.
Overall, while it is common to assume that diffusivities are approximately diffusion time-independent for t ≳ 10 ms, the experimental data described above clearly demonstrates time-dependent diffusion both at short and long times. In what follows, we describe the underlying theory for both limits and discuss the corresponding biophysical interpretation and potential for applications.
2.2. The second-order cumulant
2.2.1. Gaussian phase approximation
In Sec. 1.4, we derived a general relation (1.6) between the dMRI signal and the diffusion propagator in the narrow-pulse limit. For gradient pulses g(t) of arbitrary shape, there is no such simple relation; the signal S[g(t)] is a functional of g(t) (i.e., a mapping of a function to a number). To obtain an explicit dependence of S on g(t), one treats the gradient term in Eq. (1.3) perturbatively in g(t), generalizing the cumulant series (1.10). Here, we will stay at the level of , the so-called Gaussian phase approximation (GPA), and describe the family of diffusion coefficients which define the second-order cumulant and carry the same information content, yet can be accessible using different techniques, Fig. 6.
FIG. 6.
General relations between the basic diffusion metrics:, , Dinst(t) and D(t), and the signal attenuation up to .
The GPA approximates the dMRI signal [17–19]
| (2.2) |
up to the second cumulant of the accumulated phase
| (2.3) |
where we introduced the time-dependent wave vector
| (2.4) |
such that the Larmor frequency gradient g is given by its time derivative, g = ∂tq. The first-order cumulant in the absence of the net flow. The balanced gradient condition sets q(t)|t>T ≡ 0 at the end t = T of the gradient train interval. Eq. (2.4) generalizes the definition of q for narrow-pulse gradients, where q remained constant during an interval 0 < t < T, cf. the propagator Eq. (1.6) with t = T. Writing as a double integral, and averaging over the Brownian paths, we obtain
| (2.5) |
where we from now on dropped the explicit vector notation of q and v (the corresponding tensor indices can be easily restored; one can think about isotropic media for simplicity).
We can see that the diffusion process at the level is fully characterized by the autocorrelation function of molecular velocity, an even function of t1 – t2 in stationary media due to time translation invariance and time reversal symmetry of the Brownian motion.
For uniform media, , which can be thought of as one of the equivalent definitions of the diffusion constant D0. Technically, there is no such thing in nature as a zero-width δ(t1 – t2); we can use this approximation for simple liquids since the correlation time for forgetting the memory about the molecular collisions is of the order ~ 1 – 10 ps, orders of magnitude below our ms-level time scales. We can say that diffusion in simple liquids is thereby Markovian (has no memory) on the relevant NMR time scales. This leads to the standard expression –ln S = bD0 with , generalizing Eq. (1.8).
2.2.2. The dispersive diffusivity
For general mesoscopic media, microstructure introduces Xtemporal correlations in positions and velocities of random walkers. For instance, if a walker just hit a wall, then its velocity will correlate negatively with the velocity just before the hit (since reflection and moving away from the wall is preferred), and this memory will last during the time depending on the wall geometry and the presence of other restrictions. To characterize such correlations, let us introduce the retarded velocity autocorrelation function [27]
| (2.6) |
where θ(t) is the unit step function, cf. Sec. 1.4. In terms of , Eq. (2.5) reads
| (2.7) |
where the double integration can be extended over all real values of t, since q(t) is nonzero only on a finite interval.
The time translation invariance of allows us to rewrite the double intergral in the t-domain as a single integral in the ω-domain, by introducing the Fourier transform of , the dispersive diffusivity10 [27, 131]
| (2.8) |
Eq. (2.7) can now be written in terms of the Fourier-transformed , as11
| (2.9) |
Here, only contributes, as , odd in ω, yields zero after being integrated with an even function |qω|2. Equivalently, does not contain extra information as it can be restored using the Kramers-Kronig relations [134].
The representation (2.9) underscores that, knowing the velocity autocorrelator , one can evaluate the diffusionweighted signal to for any gradient waveform g(t). Conversely, by selecting a particular form of q(t) according to its Fourier representation qω, one effectively allocates particular weights to different Fourier harmonics contributing to the measured signal (2.9).
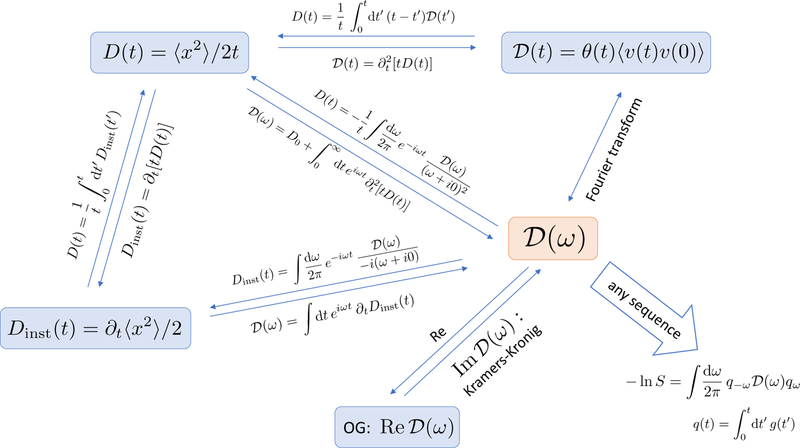
The dispersive diffusivity (2.6) and (2.8), and the cumulative (1.12) and instantaneous (1.2) diffusion coefficients, are related to each other via non-local transformations in the time domain
| (2.10) |
| (2.11) |
and in the frequency domain12 [19, 27, 131], Fig. 6:
| (2.12) |
| (2.13) |
Conversely, the dispersive diffusivity can be found either by a Fourier transform (2.8) of the retarded velocity autocorrelator , Eq. (2.6), or from the time-dependent diffusion coefficient (1.12), measured by ideal narrow-pulse gradients, via
| (2.14) |
where D0 ≡ D(t)|t=0 (cf. Eq. (D3) in Appendix D of ref. [27]). These relations are summarized in Fig. 6.
We underscore that the three diffusion metrics: the dispersive diffusivity ; the retarded velocity autocorrelator ; and the time-dependent diffusion coefficient contain the same amount of information about the medium, and thus can be expressed via each other [27]. However, the practical feasibility of their measurement may differ greatly. Generally speaking, long times are most conveniently accessed using pulse-gradient or stimulated echo-based methods [135], while short times are best measured in the frequency domain using oscillating gradients.
2.2.3. Oscillating gradients
The oscillating gradient (OG) method, typically with a refocussing pulse in the middle of the periodic gradient train (OGSE), was pioneered by Gross and Kosfeld in 1969 [136], and was first utilized to measure properties of biological tissue (muscle) by Tanner in 1979 [137] and applied to porous media later on [138, 139]. This sequence is useful for accessing short diffusion times, since the diffusion weighting accumulates over N oscillation periods, b = Nb1 [123, 131], cf. Eq. (B5) in Appendix B. In this way, the (short) diffusion time 2 π/ω gets decoupled from the (long) duration T = N · 2 π/ω of the total gradient train. It can be shown [27, 131], that in the limit of large number N ≫ 1 of oscillations, OGSE measures the real part of the dispersive diffusivity (2.8). In Appendix B, we derive the 2nd-order cumulant expression in terms of for OGSE with finite N.
To compare pulse gradient with oscillating gradient methods, a practical question arises: What is the diffusion time in terms of the OGSE frequency (and vice-versa)? How can we plot results of both types of measurements in the same axes?
Unfortunately, in the view of relations (2.10) – (2.14), there is no universal answer to the above question. The relation between D(t) and Dinst(t) on the one hand, and on the other, is mediated by the Fourier transform, which is non-local in ω. In other words, the conversion between ω and t depends on the functional form of either diffusivity — i.e., on the tissue properties. Without understanding the system’s physics (embodied by the functional form of the diffusivity), we are limited to the relations between macroscopic properties:
| (2.15) |
Below, as we describe different models, we will demonstrate examples of such conversion for different functional forms of and D(t), e.g., Eqs. (2.18) and (2.36).
2.3. The short-time limit, regime (i): Net surface area of restrictions
2.3.1. Theory
The qualitative picture of the S/V limit [68] was given in Sec. 1.5(i). Quantitatively, the short-t expansion of the diffusion coefficient (1.12) proceeds in powers of L(t)S/V, where is the diffusion length:
| (2.16) |
and S/V is the surface-to-volume ratio of the restrictions in d spatial dimensions. Identifying the term practically involves very short diffusion times. Even for a red blood cell suspension, this limit was barely observable in the time domain [140]; for the brain, with structural features even smaller than the red blood cell size, getting to this limit using PGSE is practically impossible due to very low b-values for short t.
Hence, regime (i) is best accessed using OGSE. The corresponding functional form of for Eq. (2.16) was recently derived in the N → ∞ limit [131]
| (2.17) |
For a finite total number N of oscillations, Eq. (2.17) is modified, see Appendix C, by a correction factor c, Eq. (C5), in front of the term. This factor approaches its N → ∞ limit c → ∞ rather fast, c –1 ~ 1/N, such that c–1 < 0:05 as long as N ≥ 4 for the cos, and N ≥ 10 for the sin waveforms.
From directly comparing Eqs. (2.16) and (2.17), the relation between OGSE frequency v = ω/2π and diffusion time t = Δ (in the narrow-pulse PGSE limit) is as follows [131]:
| (2.18) |
We note that Eq. (2.18) differs from the empirical relation (see, e.g., ref. [123])
| (2.19) |
which in fact is almost always incorrect [cf. Eq. (2.36) below]. Relation (2.19) originates from matching the b-value between one OGSE period and PGSE of the same duration. Since the whole notion of the b-value stems from Gaussian (i.e., time-independent) diffusion, it is not surprising that merely matching the diffusion attenuation between PGSE and OGSE for the constant D falls below the accuracy needed to define the diffusion time for the nontrivial, time-dependent case.13
2.3.2. Applications
Probing the short-time limit either in the time domain (Eq. (2.16)) or the frequency domain (Eq. (2.17)) potentially allows for decoupling the geometric effects of the surface-to-volume ratio S/V and the free diffusivity D0. Recently this limit has been demonstrated in phantoms using both PGSE [142] as well as OGSE [143]. For in vivo brain measurement, OGSE provides the most practically feasible method, with the dependency as the signature functional form (2.17) of this regime. In the healthy brain, this signature has so far never been observed, since presumably the achievable oscillation frequencies are still too low as compared to those needed to identify the effect of the restrictions from neurite walls with typical radius of curvature ~ 1 μm, requiring diffusion times much below 1 ms (i.e., frequencies v ≫ 1 kHz).
The search for the regime has prompted using brain tumors with roughly spherical cells of larger size (about 10 µm), such that the required frequency range can be potentially accessible. Recently, the functional form was observed by Reynaud et al. [144] in a mouse glioma model in the frequency range up to ω/2π = 225 Hz, which for the first time enabled the separation between the geometric (S/V) and “pure” diffusive (D0) tumor features. Further combining the OGSE and PGSE methods has lead to the POMACE [145] and IMPULSED [146] methods for quantifying cell size and extra-cellular water fraction, cf. topical review [112].
2.4. Approaching the long time limit, regime (ii): Structural correlations via gradual coarse-graining
2.4.1. Theory
Over time, random walkers probe the spatial organization of the sample’s microstructure, which makes the time-dependence of the diffusion metrics intricately tied to an increasingly large number of structural characteristics. Technically, finding D(t) or analytically in a realistic complex sample is nearly impossible as it amounts to including the contributions from the spatial correlations of the local diffusion coefficient D(r) and of the positions of all restrictions up to an infinitely high order.
The intuition based on coarse-graining, Sec. 1.3, turns out to be helpful in solving this problem in the long time regime [33], when the diffusion coefficient (1.2) gradually approaches its macroscopic (tortuosity) value (2.15). As mentioned in Sec. 1.3, in the limit t → ∞, any non-confining tissue compartment effectively looks completely uniform.
Let us step back just a bit from t → ∞ and consider t long enough (yet finite) for the sample to look almost homogeneous from the point of the diffusing molecules, Fig. 2,—no matter how heterogeneous it is in reality (e.g., at the cellular scale). In this limit, the problem of finding the diffusion propagator maps onto a much simpler problem of finding the diffusion propagator in a weakly heterogeneous medium (which is the corresponding effective theory), characterized by the diffusion equation (1.4) with
| (2.20) |
This problem admits a perturbative solution [27, 33], with Eq. (2.20) defining a small parameter, as long as the macroscopic (tortuosity) limit (2.15) exists, 0 < D∞ < ∞ (i.e., diffusion is not anomalous, which is practically always the case for dMRI in tissues, cf. Sec. 1.9). The lowest order in δD(r) vanishes, and the second order in the parameter (2.20) yields
| (2.21) |
in d spatial dimensions.
The last term in Eq. (2.21) involves the variance of the slowly-varying D(r) at a given coarse-graining length scale defined by the diffusion length L(t). This variance decreases as a result of self-averaging, i.e., when different diffusing molecules on average begin to experience more and more similar mesoscopic structure with an increasing L(t), such that any sample begins to approximate the ensemble of different disorder realizations of D(r) more and more precisely. The always positive “fluctuation correction” to D∞ (the last term) elucidates why the diffusion coefficient can only decrease with t; observation of its increase with diffusion time is a red flag for imaging artifacts.
To be more rigorous, Eq. (2.21) can be expressed as [33]
| (2.22) |
in terms of the power spectrum of the underlying effective coarse-grained over the diffusion length L(t0) corresponding to some sufficiently long time scale t0, for which the relative deviation (2.20) from D∞ is sufficiently small. The correlation function
| (2.23) |
embodies the fluctuation correction in Eq. (2.21). We can see that diffusion indeed acts as a Gaussian filter (cf. Fig. 2 in Sec. 1.3), with a filter width , over the effective medium defined via the correlation function of the weakly heterogeneous D(r).
Hence, for sufficiently long t, Eqs. w(2.21) and (2.22) become asymptotically exact with L(t) → ∞, no matter how strongly heterogeneous the “true” (microscopic) D(r) is. From the renormalization group flow standpoint, we can say that the time-dependent corrections (last terms of Eqs. (2.21) and (2.22)) to the asymptotically Gaussian propagator become irrelevant as a result of integrating out the fluctuations of the locally varying D(r) over larger and larger scales. Likewise, the kurtosis and higher-order cumulants in this compartment will decay to zero, as governed by similar fluctuation terms.
How to relate the time-dependence (2.21) and (2.22) to the mesoscopic structure? Here, one realizes [33] that the coarsegrained D(r)|L(t) depends on the similarly coarse-grained local density n(r)|L(t) of mesoscopic restrictions to diffusion (e.g., the disks in Fig. 2). Hence, the variance of D(r)|L(t) entering Eq. (2.21) is proportional to a typical density fluctuation of the restrictions in a volume of size Ld(t) in d dimensions (this becomes valid when the deviations from the mean sample density become small). This proportionality, asymptotically exact at small k (i.e., after coarse-graining over large distances, cf. Eq. (2.22) for long t), leads to the proportionality
| (2.24) |
between the correlation functions (power spectra) of D(r) and of the underlying structure n(r),
| (2.25) |
The structural correlation function can behave qualitatively distinctly at large distances, i.e., small k:
| (2.26) |
The structural exponent p in Eq. (2.26) defines the structural universality class to which a sample belongs, according to its large-scale structural fluctuations embodied by its correlation function (2.25). The greater the exponent p, the more suppressed are the structural fluctuations at large distances (low k); conversely, negative p signify strong disorder, where the fluctuations are stronger than Poissonian (for which p = 0). Hence, p characterizes global structural complexity, taking discrete values robust to local perturbations. This enables the classification of mesoscopic disorder [33], and its relation to the Brownian dynamics, as we now explain.
From Eq. (2.22) it directly follows that the time-dependent instantaneous diffusion coefficient (1.2) approaches the finite bulk diffusion constant D∞ as a power law
| (2.27) |
with the dynamical exponent [33]:
| (2.28) |
related to the statistics of large scale structural fluctuations via the structural exponent p, and to the spatial dimensionality d.
To illustrate the above general relations, consider Poissonian disorder (uncorrelated restrictions, e.g., completely randomly placed disks in Fig. 2). Their density fluctuation within the “diffusion volume” Ld scales as the inverse volume, according to the central limit theorem. Equivalently, Γ(k) → const ~ k0 as k → 0, i.e., the exponent p = 0. As a result, when restrictions are uncorrelated (or, more generally, short-range disordered, i.e., have finite correlation length in their placement), the instantaneous diffusion coefficient approaches its macroscopic limit as
| (2.29) |
in d dimensions, i.e., ϑ = (0 + d)/2. This is the intuitive picture behind the formal results [147, 148].
The approach described in ref. [33] generalizes this picture onto any universality class of structural disorder and enables identifying relevant structural fluctuations b y m easuring the dynamical exponent (2.28). This exponent manifests itself in the power law tail of the molecular velocity autocorrelation function (2.6)
| (2.30) |
and in the dispersive diffusivity,14 Eq. (2.8),
| (2.31) |
whose real part is accessible with OGSE, Sec. 2.2.3.
Relation (2.28) provides a way to determine the exponent p (or the effective dimensionality d) and, thereby, the structural universality class, using any type of macroscopic time-dependent diffusion measurement. Local properties, contributing to biological variability, affect the non-universal co-efficients, e.g., the values of D∞ and the prefactor of t−ϑ in Eq. (2.27), but not the exponent ϑ. The latter exponent is universal, i.e., is independent of microscopic details, and is robust with respect to variations between samples of a similar nature. From the point of dMRI in biological tissues, the exponent (2.28) is robust with respect to biological variability.
We can also see that the stronger the fluctuations (the smaller the exponent p), the smaller is the dynamical exponent ϑ, i.e., the slower is the approach to D∞. Physically, this happens because it takes longer for the coarse-graining to self-average the sample’s structural fluctuations. Conversely, if a sample is regular (a periodic lattice, formally equivalent to p → ∞), the approach of D∞ will happen exponentially fast (i.e., faster than any finite inverse power law) [33].
The above approach exemplifies the power of an effective theory way of thinking, where, to make fairly general statements about the relation between the diffusive dynamics and the structural disorder, we did not have to solve the full non-perturbative problem (starting from the microscopic restrictions n(r)), but instead ended up solving a relatively simple problem of finding lowest-order corrections [27, 33] to Gaussian diffusion in a weakly heterogeneous medium.
Note that the undefined constants in Eqs. (2.27) and (2.31) are different. It is possible to find a more precise correspondence between the time-dependent terms in Dinst(t) and by using Eq. (2.12) followed by contour integration in the complex plane of ω, yielding
| (2.32) |
(here Γ(ϑ) is Euler’s Γ-function; cf. also ref. [33], compare Supplementary Eqs. [S17] and [S18].)
The above “conversion” between PGSE and OGSE works for Dinst(t). However, the cumulative D(t) follows the behavior (2.27) only for ϑ < 1; for ϑ ≥ 1, the PGSE D(t) expansion at long t will begin with the 1/t term, due to the integral in inverting the relation (2.10),
| (2.33) |
converging at short t for the t−ϑ term with ϑ > 1 in Dinst(t). Therefore, the structure-specific dynamical exponent (2.28) is masked in PGSE if it exceeds unity; to reveal it, one has to use Dinst(t), which amounts to differentiating noisy experimental data [33, 142]. The borderline case ϑ = 1 has been considered in detail in ref. [23]; the PGSE diffusion coefficient has a (ln t)/t tail due to the logarithmically divergent integral in Eq. (2.33),
| (2.34) |
whereas the OGSE counterpart is given by
| (2.35) |
Here is the time to diffuse across the correlation length of the corresponding disordered environment (e.g., correlation length of the disordered axonal packing [23] in the case p = 0 and d = 2 considered below in Sec. 2.4.2). When the pulse duration δ exceeds tc, it starts to play the role of a cutoff time for the power-law tail [23–26].
Finally, we give one more illustration of the absence of any universal relation between PGSE diffusion time and OGSE frequency ω = 2πν addressed in Sec. 2.2.3. The PGSE-OGSE correspondence, empirically, means that the constants in the tail t−ϑ in D(t), and in the ωϑ tail of Eq. (2.31) are equal. According to Eqs. (2.32) and (2.33),
| (2.36) |
This relation is neither obvious, nor has it anything to do with the empirical Eq. (2.19). For example, for ϑ = 1/2 (random permeable barrier model [51] or short-range disorder in d = 1 relevant for the neurites, Sec. 2.4.2 below), we obtain t = (4/π2)/ν. And besides, Eq. (2.36) only applies for ϑ < 1; for media characterized by larger ϑ, the power-law PGSE and OGSE tails will not match.
2.4.2. Validation and applications
Probing the diffusivity time-dependence at long times potentially allows for identifying the disorder universality class of the mesoscopic structure, which then helps to parsimoniously model the relevant features of tissue architecture and extract the corresponding tissue length scale(s) and other parameters.
Validation with Monte Carlo simulations:
Equation (2.28) was verified in d = 1 MC simulations using different placements of identical permeable barriers, according to periodic, short-range, hyperuniform, and strong disorder classes [33]. The same relation for the p = –1 universality class of random permeable membranes in d = 2 was verified in ref. [51]. The borderline “log” case of ϑ = 1 for p = 0 in d = 2 dimensions, Eq. (2.34), was verified in ref. [23] in the t-domain. In ref. [149], the same universality class was considered in the ω-domain, verifying Eq. (2.35) and revealing the dependence of the prefactor A on the degree of disorder in fiber packing. Subsequently, the scaling (2.28) was verified with MC along synthetic model neurites, dimension d = 1, featuring realistic spines, leaflets and beads placed randomly according to the Poissonian statistics, p = 0 [150]. The deviation from the ϑ = 1/2 power law at the longest t may be attributed to the periodic boundary conditions for a relatively short sample. In the same setting, Eq. (2.17) transverse to the neurites was verified for the sub-ms times, regime (i).
A more empirical approach [151] was employed for diffusion of cell-specific metabolites up to t = 2 s that was measured by diffusion-weighted MR spectroscopy in vivo. Due to the broad time range, the D(t)-dependence was more pronounced, in comparison to the earlier measurements [152] for the narrower t-ranges. Distinct tissue morphologies were recognized by comparing with large-scale MC simulations for particles diffusing in many synthetic cells generated as tree-like structures, by varying statistics of the number of processes, branches, and segment lengths. While the simulations matched the measurements, the relevant structural degrees of freedom and the associated functional forms of the t-dependence were not unequivocally identified.
Validation in phantoms:
The exponent (2.28) corresponding to the short-time disorder, p = 0, has been demonstrated in d = 2 dimensions in an anisotropic fiber phantom mimicking the extra-axonal space [23] (ϑ = 1, leading to the ln t singularity in the PGSE D(t), Eq. (2.34)), as well as more recently in a d = 1-dimensional phantom [142] for which ϑ = 1/2 for p = 0 and ϑ = 3/2 for hyperuniform placement of permeable membranes (p = 2).
Cortical GM was probed with OGSE in rat [123] and mouse [126, 127], Fig. 7. It was suggested [33], that the apparent ωϑ behavior with ϑ = 1/2 can be explained by the dominance of the effectively d = 1-dimensional diffusion along the narrow neurites with the short-range disorder (e.g., spines, beads, varicosities) along them [153–155]. The varicosities are known [156, 157] to become more pronounced in ischemia, which is consistent with the increase in the structural disorder-induced coefficient in front of the ω-dependent term in Eq. (2.31). Conversely, assuming short-range disorder (e.g., in the varicosity placement), the power law exponent ϑ = 1/2 then validates the effectively d = 1-dimensional diffusion along the so-called “sticks” (narrow channels used to model the intra-neurite space), cf. Sec. 3.1 below.
FIG. 7.
OGSE measurements in cortical GM: circles are data from average of 5 rats [123] and squares from 6 neonatal mice at 24 hours after unilateral hypoxic ischemic injury [126]. Red: normal rat brain and contralateral side of mouse brain. Blue: globally ischemic rat and ipsilateral side of hypoxia-ischemia injured mouse brain. PGSE data not shown. Dashed lines are fits from Fig. 4 of ref. [33], dotted lines are ω1/2 fits (shown as guide to the eye; power-law exponent fit for mouse data was not robust due to narrow frequency range). Note that while the absolute (ω) values differ between rat and mouse, the general features are similar: data is well described with ω1/2 behavior for normal and ischemic GM (except, possibly, the ischemic mouse, where major structural changes may have occurred in 24h); and the coefficient in front of ω (the slope) increases in ischemia, consistent with short-range structural disorder increase along the neurites (e.g., due to beading).
Human WM was probed in vivo in both the longitudinal [34] and transverse directions [34, 122]. The time-dependence of longitudinal diffusivity suggests restrictions are present along axons, which, similar to the GM case above, augments the commonly used “hollow tube” model for diffusion inside and outside neurites (cf. Sec. 3.1). The “hollow tube” filled with some effective Gaussian medium with diffusion coefficient D∞ becomes an effective theory technically valid only in the t → ∞ regime (iii); for finite t, non-Gaussian effects (time-dependent D(t) and higher-order cumulants) will be present.
Recent quantitative analysis [34] based on Eq. (2.27) for d = 1, revealed that this time-dependence is compatible with short-range disorder in the placement of restrictions along axons. Intriguingly, the corresponding correlation lengths of about 3 − 7 µm are similar to those reported in the literature for varicosities along axons [153–155], suggesting them as potential sources for the reduction of the longitudinal diffusivity with time. Varicosities are often found to be rich in mitochondria and could therefore form obstacles for the diffusion along the fibers, or they could act as temporary traps for the longitudinal diffusion. Additional potential sources of the short range disorder could be axonal undulations [141, 158], or functional gap junctions unevenly spaced between 20 and 60 μm along the myelin sheath in sciatic nerve [159].
Note an interesting observation that the reduction in the diffusivity in acute stroke patients occurs predominantly along the axons when measured at the frequency ω/2π = 50 Hz, while the decrease in both the longitudinal and transverse directions directions is observable for the diffusion time 40 ms [160]. Originally explained by axonal beading, this effect has to be taken into account in more general models of the diffusion response to tissue damage.
2.4.3. Axonal diameter mapping
Quantifying µm-level structure of neuronal tracts in vivo has been brought to the forefront of neuroscience research primarily due to the axonal diameter mapping (ADM) concept, developed within the CHARMED and AxCaliber frameworks ([57, 58, 161]) and their extensions [59, 162]. Their common theme is the focus on the intra-axonal compartment (assuming no exchange) as the source of the diameter sensitivity, while typically approximating axons as impermeable cylinders, and building on exact solutions [17, 21, 103, 138]. Water diffusion in the extra-axonal space in all of the above approaches is approximated as Gaussian (time-independent).
Large overestimation of axonal diameters, by factors 3–15 in humans, cf., e.g., refs. [59, 163], provoked a debate [164– 166] about the feasibility of the method. It has been since recognized that ADM may be confounded by two issues.
The first ADM issue is the smallness of the signal attenuation for typical, i.e., thin axons. The attenuation inside a cylinder up to (GPA) is given by van Gelderen’s formula [118] that depends on the PGSE sequence timings ∆ and δ. However, in the practically relevant case δ ≫ r2/D0, the dependence on ∆ drops out, hence the diffusion time is not actually being used to probe the cylinder diameter. This is the Neuman’s limit [21], in which the attenuation
| (2.37) |
is proportional to the total time 2δ the gradients are on. The proportionality to the time 2δ can be understood in terms of the mapping onto the transverse relaxation in the diffusion-narrowing regime, where ∼ (gr)2 · r2/D0 is the effective rate constant [26]. The above attenuation was evaluated for typical values of the Larmor frequency gradient g = 0:0107 (μm · ms)–1 corresponding to 40 mT/m; free axoplasmic15 D0 = 2:4 μm2/ms; pulse duration δ = 10 ms, and a typical inner diameter 2r = 1 μm [80–84].16
Likewise, the OGSE attenuation in the relevant ωr2/D0 ≫ 1 limit [cf. Eqs. (B5) and (B7) in Appendix B]
| (2.38) |
becomes independent of the OGSE frequency ω and of the OGSE initial phase ϕ, since b ~ T/ω2 and . The analogy with Eq. (2.37) becomes obvious if we realize that, following the mapping onto the transverse relaxation in the presence of an (oscillating) gradient g = g0 cos(ωt – ϕ), what matters is the total time 2δ → T the gradients are on (here T = N · 2π/ω is the total OGSE train duration), and the time-averaged gradient power . In other words, in the low-frequency limit, OGSE is just the Neuman’s limit (2.37) albeit with the reduced average gradient amplitude, since the gradients are not at their peak value all the time. This yields that OGSE is not beneficial to map small compartment sizes, and does not provide any independent parameter combination, in the limit ωr2/D0 ≪ 1 (cf. Appendix B). Obviously, the most optimal setting is to keep the diffusion gradient at its maximum all the time , cf. Eq. (2.37). Practical resolution limits for axonal radii depending on the SNR and fiber geometry were considered for both pulse-gradient and OGSE sequences [175–177].
The second ADM issue is potentially more significant. Had the above smallness been the only problem, we would just not see any dependencies of intra-axonal signal on experimental parameters. Yet the fits of ADM model to data do show definitive trends in the estimated “apparent diameters” —for instance, with the gradient strength [163]—suggesting some unaccounted physical phenomenon. This has prompted taking into account the coarse-graining outside [23] randomly packed axons. The (ln t)/t term (2.34) from the extra-axonal space appears to completely overwhelm the weak attenuation (2.37) in simulations [23] and in the recent D(t) measurements transverse to human WM fiber tracts [34, 122]. This reveals an exciting unexpected mesoscopic effect: The structural disorder in axonal packing within a WM fiber bundle completely changes the interpretation of ADM at low to moderate diffusion weightings. Furthermore, recently observed logarithmic dependence on the pulse duration δ in human WM [26], cf. Eq. (2.34), instead of the linear one, Eq. (2.37), and validated in a fiber phantom [25], confirms the mesoscopic extra-axonal origin of the “apparent” ADM effects.
The decreasing apparent diameter trend with increasing gradient strength [163] is consistent with eventual suppression, as , of the extra-axonal contribution; however, since the transverse (cf. Section 3), very large b-values are needed to fully suppress this effect [178]. However, when sufficiently strong gradients are used in animal settings, the GPA results of van Gelderen [118] and Neuman [21] should be corrected. Unfortunately, no analytical solution exists beyond GPA for finite δ. Lee et al. [26] estimated that the GPA will break down when for axons of radius r. This may become relevant for large axons: e.g., for r = 3 µm and D0 = 2 µm2/ms, the critical gradient g∗ corresponds to 277 mT/m. Furthermore, the next-order correction to the right-hand side of Eq. (2.37) will be of the same sign as the main effect, scaling as , implying that strong gradients cause extra attenuation relative to what GPA predicts. If the GPA is used instead of the exact solution, the GPA-derived radii will be overestimated, which may explain some residual overestimation of axonal radii in a recent animal study with gradients as large as 1.3 T/m [178].
We note that an even stronger dominance of the extraaxonal contribution occurs in the OGSE domain, since the fully confined water (within an impermeable cylinder transverse to its axis) yields a regular, ω2 contribution to (Appendix B), whereas the extra-axonal water would contribute linearly, as |ω|, cf. Eq. (2.31) with ϑ = 1. The linear term will dominate at low ω, in agreement with the linear dispersion observed transverse to fibers with OGSE by Portnoy et al. [179] and analyzed in ref. [23]. Such linearity has been also observed in rat spinal cord by Xu et al. [124, 172].
The predominance of the |ω| scaling means that using OGSE is not optimal for probing inner axonal diameters — not just numerically as discussed after Eq. (2.38), but parametrically! However, the |ω| scaling makes OGSE parametrically better for probing the extra-axonal space geometry. We warn that the gradient waveform optimization which does not account for the mesoscopic effects in the extra-axonal space may sometimes give unfair preference to OGSE [175–177].
Overall, the above mesoscopic effects, measured in vivo on both animal and human scanners, may enable a novel kind of structural contrast at the micrometer scale (e.g., axonal loss and demyelination), and open up exciting possibilities of monitoring subtle changes of structural arrangements within GM and neuronal tracts in disease, aging, and development.
2.5. Mesoscopic fluctuations
When ADM is feasible (e.g., spinal cord, due to much larger r), Neuman’s r4 scaling (2.37), together with volume-weighting ∼ r2, gives a large weight to a small number of axons with largest diameters, effectively measuring [23]
| (2.39) |
where the averages are taken over the voxel-wise axonal distribution. Hence, the metric (2.39) may become susceptible to the mesoscopic fluctuations governed by the tail of the distribution (practically, for sufficiently small voxels in which such fluctuations can be pronounced). Additionally, sampling fluctuations confound the comparison of dMRI measurements with histology, — where the metric derived based on, e.g., Eq. (2.39) can be strongly sample-dependent, especially if small fields of view are utilized.
This general phenomenon of rare structural configurations determining the measurement outcome has parallels with similar effects found in hopping conduction in disordered semiconductors, kinetics of reaction-diffusion systems, and other phenomena in disordered media [92, 180, 181]. In our case, an incidentally large number of thick axons may significantly skew the intra-axonal attenuation for a particular voxel. This could lead to strongly enhanced variations (relative to those expected based on the measurement noise alone) in the corresponding parametric maps.
The issue of the mesoscopic flucutations is fundamental, and the separation of the effects of biological variabiilty from the randomness in measurement outcomes due to the thermal noise requires model-independent ways of estimating local noise level [182, 183], as well as precisely quantifying the tails of the corresponding distributions of biophysical tissue parameters (e.g., of the axonal diameter distribution [80–84]).
3. THE t → ∞ LIMIT, REGIME (III): MULTIPLE GAUSSIAN COMPARTMENTS
All science is either physics or stamp collecting
Ernest Rutherford
The flamboyant century-old quote of a founder of the atomic age could be excusable, as scientific disciplines other than physics in his days were mostly collecting empirical information. Today, with so much more knowledge about the world and the associated abundance of data, Rutherford’s quote could as well sound “All science is either physics or fitting”. While the purpose of physics remains to identify relevant parameters and to produce an explanation (an effective theory), and its instance for a particular measurement — a model [70], the complexity of models and the amount of data have turned parameter estimation into a field on its own, if not into a multitude of fields, employing a wealth of approaches, known under different names and incorporating advanced tools of statistics, machine learning and artificial intelligence. Within MRI, modern parameter estimation approaches are tied to the idea of undersampling, typically of the k-space data, which spurred the applications of compressed sensing [184, 185] and MR fingerprinting [186].
Tissue microstructure mapping presents its own set of parameter estimation challenges. As we will illustrate in this Section, while from the physics standpoint, the dMRI models in the t → ∞ regime become trivial (a sum of Gaussians = exponentials in b), their number of parameters, and the inherent degeneracy of the fitting landscape in face of the typically low SNR of dMRI acquisitions, have turned parameter estimation into an active area of investigation. In other words, the problem remains largely unsolved — even with a densely sampled q-space, and fully sampled k-space. So far, arguably, most intellectual efforts in the regime (iii) (as defined in Sec. 1.5) have been spent on the “fitting” rather than on the “physics”. This Section is hence primarily about the parameter estimation aspect of modeling (cf. Sec. 1.1).
Below, after introducing the stick compartment in Sec. 3.1, we formulate the overarching Standard Model of diffusion in neuronal tissue as a sum of anisotropic Gaussian compartments (Sec. 3.2, Figs. 4 and 8), and then discuss challenges of its parameter estimation, Sec, 3.3, focussing on its degeneracies. We subsequently review works involving constraints on the Standard Model parameters (Sec. 3.4), followed by the unconstrained, rotationally-invariant methods (Sec. 3.5), and conclude this Section with a summary of unresolved issues (Sec. 3.6).
3.1. Neurites as “sticks”
3.1.1. Theory and assumptions
In this Section, we assume that the t → ∞ regime (iii) has been practically achieved, and neglect the time-dependent power-law “tails” describing the approach of the diffusion coefficient to its tortuosity limit, discussed in Section 2.17
Full coarse-graining in the intra-neurite space then leads to the most anisotropic Gaussian compartment possible — the so-called “stick” compartment — first introduced by Kroenke et al. [36] and Jespersen et al. [37] in 2004–2007. Its main features are:
A stick is a cylinder whose radius r is negligible compared with the “free” diffusion length at given t. Equivalently, the transverse diffusion coefficient inside neurites for typical t 100 ms is negligible compared to D0 ≈ 2.4 µm2/ms,18 and hence can be set to zero,. In other words, the measurement is insensitive to neurite radii (cf. discussion in Sec. 2.4.2).
The longitudinal diffusion inside a neurite becomes Gaussian, with the macroscopic (tortuosity) asymptote Da. Of course, Da, being the effective coarse-grained parameter, can be notably reduced relatively to the intrinsic axoplasmic diffusion coefficient D0, cf. Section 2. The parameter Da takes into account all restrictions, such as varicosities (beads) and undulations, along the (average) neurite direction. Hence, it can have important biophysical and diagnostic value in the cases when the structure along neurites changes, e.g., in acute stroke [156, 157, 160] and in Alzheimer’s disease [187].
Exchange between intra- and extra-neurite water can be neglected, at least at the time scales t used in clinical dMRI. Measuring exchange times in vivo is very difficult, making this assumption hard to validate. The consensus so far has been that this assumption holds for WM tracts, where sticks represent (myelinated) axons (and possibly some glial processes). The filter-exchange study in [188] supports the presence of two compartments in healthy brain WM with the exchange time of about 1 s, consistent with assuming negligible exchange on the clinical t ~ 100 ms time scale. At which t this assumption might break for glial cells, dendrites in GM, or for unmyelinated axons, is a subject of investigation. It was hypothesized [189] that transcytolemmal water exchange in astrocytes is fast, since inhibition of aquaporin-4 significantly reduced the diffusion coefficient already for t < 25 ms, without modifying tissue histology. However, recent work [190] of measuring T1 in the presence of fast extra-cellular flow for cultures of astrocytes and neurons grown on beads puts the intracellular residence time around 570 and 750 ms, correspondingly. Likewise, MR relaxation measurement [191] in the live rat brain organotypic cortical cultures yields the net cellular water efflux rate 2.02 s−1, with a significant fraction (~34 – 45%) of this exchange rate attributed to active transcytolemmal exchange related to the Na+-K+-ATPase activity.
From the modeling standpoint, the stick compartment is the defining feature of dMRI inherent to the neuronal tissue, as compared to all other kinds of soft tissues. It is chiefly responsible for the anisotropy of the diffusion propagator in the brain (at least, in the white matter), and in spinal cord (where finite axonal radii can be detected, see footnote 16).
The diffusion propagator for a stick pointing in the unit direction , measured in the unit gradient direction ,
| (3.1) |
is determined by , where θ is the angle between and . The signal is not suppressed for and decays fast with b when . Hence, when bDa ≫ 1, the stick dMRI response (3.1) becomes a thin “pancake”, non-negligible when nearly transverse to , whose angular thickness scales as [168, 192, 193]. Both estimates follow from setting the argument of the exponential to unity.
3.1.2. Validation of the picture of sticks
An extensive review of dMRI validation studies is beyond the scope of this article. However, given the essential role sticks play in dMRI models, we mention the following two kinds of results.
First, metabolites, such as N-Acetylaspartic acid (NAA), intrinsic to the intra-neurite space, can be used to identify the stick compartment, as reviewed by Ackerman and Neil [152]. A seminal NAA study was performed by Kroenke, Ackerman and Yablonskiy [36], who demonstrated a very good agreement between the dMRI signal from large voxels in rat brain averaged over three gradient orientations, at diffusion times t = 50 − 100 ms, and the isotropically averaged stick signal,
| (3.2) |
where erf is the error function. Taking a large voxel, which presumably has all neurite orientations, and subsequently averaging over 3 directions, maps the signal to that from a completely random stick arrangement, first considered by Callaghan [54] in 1979, and subsequently by Yablonskiy et al. [55] in 2002 for 3He diffusion in the lung, resulting in Eq. (3.2) (Fig. 4). The agreement with the theory (3.2) was very good in the whole range [36]. Recent directional NAA imaging by Ronen et al. [194], quantifying the dMRI signal anisotropy, agrees well with the structure tensor [195] derived from the axonal histology in the corpus callosum.
Second, for the water dMRI, identifying a distinct functional form inherent to the stick compartment can also validate the pictures of sticks at sufficiently large b, when the extra-neurite signal becomes exponentially suppressed (because the extra-neurite diffusion coefficient is nonzero in any direction), while the intra-neurite signal is only suppressed as a very slowly decaying power-law ~ b−1/2, scaling as the width of the pancake-shaped stick response function (3.1), cf. Eq. (3.2) and refs. [168, 192, 193]. The recently observed [168, 193] power-law water signal attenuation in human WM in vivo, isotropically averaged over multiple gradient directions ,
| (3.3) |
with exponent α = 1/2, provides a unique signature of axons as sticks for water dMRI. The isotropic average (cf. Sec. 3.5.1 below) of the signal makes it equivalent to that from isotropic set of sticks, cf. Eq. (3.2) above, with erf approaching 1 at large b.
Either detectable axonal diameter values, or a notable exchange rate between intra- and extra-axonal water, would destroy the very particular stick-related b−1/2 scaling (3.3). In particular, the analysis in ref. [168] shows that, had the axonal diameters been notably higher than their histological estimates of ~1 µm [80, 81, 83], as the ADM results often show (cf. Sec. 2.4.2), the power law exponent α would differ from 1/2 for b ≤ 10 ms/µm2. Hence, human dMRI measurements are practically insensitive to axonal diameters even with gradients of 80 mT/m employed, confirming the first stick assumption in Sec. 3.1. The human measurement [168] also revealed that the immobile water fraction, not decaying with b for any direction, is below detection limit. The same conclusion was made independently using isotropic diffusion weighting [196]. Small and slightly negative γ, of about 1%, is a signature of the breakdown of zero-radius stick picture relevant at very high b [168].
A low, but measurable transverse intra-axonal diffusivity, even in vanishingly thin axons, can emerge from deviations of their form from perfectly straight sticks [141, 158]. Measurement with suppression of extra-axonal signal in the human brain suggests for the diffusion time about 120 ms, which was obtained as the difference between the trace of intra-axonal diffusion tensor and the longitudinal diffusivity, Da [141].
3.2. The Standard Model of diffusion in neuronal tissue
3.2.1. Theory
With the intra-neurite diffusion modeled as a collection of sticks, and the isotropically fully restricted water out of the picture, how should we model the remaining water? The answer depends on the coarse-graining length scale.
If the diffusion time is as large as needed for water molecules to sample a statistically representative part of the extra-neurite space (ENS) within a voxel, then diffusion in this space should become Gaussian and be described by the overall ENS diffusion tensor, , where the b-matrix bij = qiqjt ≡ bgigj depends on the components of the unit diffusion gradient , cf. Eqs. (1.8) and (1.10). The ENS tensor DENS would then by definition describe all ENS water, including cerebrospinal fluid (CSF) that could, e.g., contribute if a voxel contains part of a ventricle.
Practically, such very long-time limit is never realized for a macroscopic voxel. For typical diffusion times t = 50 – 100 ms, the corresponding diffusion length L(t) ~ 10 μm defines the coarse-graining window, where the diffusion properties locally become (almost) Gaussian. At this scale, the neuronal tissue, at least in the WM, looks as a highly aligned fiber segment (fascicle)19, Fig. 8, the leftmost image. Because the fibers are locally coherent at the scale L(t), the local ENS tensor can differ at the different positions r within a voxel if they are separated by distance much exceeding L(t) (for instance, if a voxel contains fiber crossings).20 This local microscopic anisotropy of ENS suggests that, strictly speaking, the ENS diffusion is never Gaussian — but is rather a sum of local anisotropic Gaussian contributions, which are highly aligned with the corresponding local stick arrangements.
These coarse-graining considerations lead to the general picture of anisotropic compartments, Fig. 8. The signal measured in the unit direction , is a convolution21
| (3.4) |
between the fiber orientation distribution function (ODF) normalized to , and the response kernel from a perfectly aligned fiber segment (fascicle) pointing in the direction . The kernel depends on the relative angle θ, (cf. Eq. (3.1). The general representation (3.4) gave rise to a number of methods for deconvolving the fiber ODF from the dMRI signal for a given |q| = q shell in q-space, using different empirical forms of the kernel [198–204].
Following the coarse-graining arguments above, the kernel’s functional form
| (3.5) |
is a sum of exponential (in b) contributions from the aligned intra- neurite and extra-neurite spaces, respectively modeled by a stick compartment, by the axially symmetric Gaussian compartment with transverse and longitudinal diffusivities and and the principal direction along the stick, and the CSF compartment, cf. refs. [45–47] and Fig. 8.
The myelin water compartment is typically neglected due to its short T2 time [205] as compared to the echo times TE employed in clinical dMRI. We emphasize that the fractions f and 1 – f are the relative signal fractions, and not the absolute water volume fractions, due to neglecting myelin water, as well as due to generally different T2 values for the intra-and extra-neurite compartments [48, 206]. The isotropic CSF compartment has DCSF ≈ 3 μm2/ms. Because of the ODF normalization , the CSF term can be included in the kernel or added separately to signal (3.4); we choose to include it in the kernel (3.5), as it makes the formulation (3.4) more elegant. In what follows, we will describe in depth the two-compartment kernel (3.5) with fCSF ≡ 0.
The overarching model (3.4) and (3.5) includes nearly all previously used models [36–48] (at least in the WM) as particular cases, also described in taxonomy studies in refs. [207, 208] where some of the “models” are actually representations, in the sense of Sec. 1.7. In other words, the numerous models (and acronyms), corresponding to the right part of Fig. 4 in Section 1, describe the same physics, and hence they are really the same model.
Because of the overall popularity and inclusiveness of the above picture, here we suggest to call the model (3.4)–(3.5) the Standard Model (SM)22.
We note that a major limitation of the SM kernel (3.5) is using the same scalar parameter values for different fiber tracts passing through a voxel (noted, e.g., in refs. [209, 210]), which prompted assigning different (albeit constant) fiber responses to different tracts to deconvolve the ODF [211–213], as an alternative.
3.2.2. Specificity and relevance of SM parameters
Over the past decade, it has become clear that the scalar parameters f, Da, and , and the spherical tensor parameters (the spherical harmonics coefficients of the ODF ), carry distinct biophysical significance. Deconvolving the voxel-wise fiber ODF, instead of relying on the empirical directions obtained by Fourier-transforming the dMRI signal from the q to r space, in principle provides a more adequate starting point for fiber tractography, an essential tool for mapping structural brain connectivity and for presurgical planning [214–218].
Furthermore, as illustrated further in Sec. 3.4.1, the ability to estimate scalar parameters of the kernel (3.5) would make dMRI measurements specific — rather than just sensitive — to μm-level manifestations of disease processes, such as demyelination [219–221], axonal/dendritic loss [221–224] (f), beading [225], inflammation and oedema (fCSF, as well as, potentially, mostly Da for cytotoxic and mostly , for vasogenic oedema [226]). Combining f with the extraaxonal volume fraction derived either from tortuosity modeling based on [219, 220] or from the myelin volume fraction via relaxometry, would ultimately allow one to determine axonal g-ratio [227]. Since the precise nature and pathological changes in microarchitecture of restrictions leading to the scalar parameter values are unknown, ideally, to become specific to pathology, one needs to estimate f, fCSF, Da, and separately.
The first attempt to estimate the parameters and to validate the 2-compartment SM was performed by Jespersen et al. [38] using direct fitting to an extensive ex vivo data set covering bothWMand GM, while parametrizing the ODF using spherical harmonics Ylm up to l ≤ 4. (The ENS diffusion in this work was described by the overall tensor, whose 6 components were estimated.) Data was acquired on a 16.4 T magnet using 16 shells with 0 ≤ b ≤ 15 ms/μm2 and 144 directions, with acquisition taking over 15 hours. The fraction f correlated well with AMG staining for the neurites, and the ODF directionality agreed with the histology. Further quantitative comparison of the predictions to histology was carried out in [228], where the neurite ODF was determined from Golgi stained cortical neurons in immature ferret brains.
While “brute-force” fitting of ~ 20 parameters could work for an extensive data set [38], clinical dMRI data is far noisier, with much less q-space coverage. Hence, because of the high dimensionality of parameter space and the unfavorable fitting landscape [44], SM parameter estimation for Eqs. (3.4)–(3.5) from realistic noisy clinical dMRI data has emerged as an overarching challenge (Sec. 3.3), which has until recently been addressed by introducing parameter constraints, as discussed further in Sec. 3.4. The open challenge of parameter estimation also means that the literature [36–48] differs largely in the ways SM parameters have been constrained.
3.3. The challenge: SM parameter estimation
3.3.1. SM parameter count
To quantify the problem’s complexity, we find here how many parameters Np the model (3.4) should have — and, hence, how many we have to estimate from (noisy) dMRI data. We follow here the treatment in ref. [47].
The answer depends on the maximal power lmax of the diffusion weighting to which an acquisition is sensitive, at a given SNR (by the time-reversal symmetry of diffusion, only even lmax are considered). This can be seen either from the cumulant expansion (1.10) of , or, equivalently [18], from the Taylor expansion of the signal (3.4)
| (3.6) |
in the fully symmetric moments . These moments are proportional to angular averages over the ODF , as it is evident from expanding the exponential terms containing ξ = nigi in kernel (3.5), such that subsequent terms have the form , , etc. The maximal (even) order l of the product always appears with the corresponding power bl/2 of the diffusion weighting.
The symmetric tensors , after subtracting all possible traces, can be turned into the corresponding symmetric trace-free tensors (STF) of rank l [78], which are equivalent to the set Ylm of the spherical harmonics (SH) discussed in Sec. 1.8 above. In other words, the ODF averages correspond to the SH coefficients plm of the ODF,
| (3.7) |
In particular, the highest-order cumulant or the moment still practically resolvable from the signal, sets the maximal order lmax for the even-order SH expansion (3.7). The correspondence between lmax in Eq. (3.7) and the maximal order in expansion (3.6) embodies the perturbative radial-angular connection in the q-space [47].
We note here an obvious corollary from the radial-angular connection in q-space: Oversampling the directions within the low-b shells does not improve angular resolution in estimating — in other words, optimal q-space coverage should match the sensitivity to the power of the shell radius with the minimal number nc(lmax) of directions per shell. Naive sampling, say, 256 directions at b ≈ 1 ms/μm2 would not in principle yield better angular ODF resolution than, say, ~ 10 averages of 25 directions. Indeed, the clinical dMRI signal at this b-value can be fully described using (DTI, lmax = 2), or, at best, (DKI, lmax = 4) cumulant terms, corresponding to being sensitive to the ODF expansion coefficients plm up to l = 2 or l = 4 (containing 5 or 14 parameters). There is no way to determine, say, p6m and beyond, if the diffusion weighting is too weak for the b3 terms to be discernible at a given SNR.
Coming back to counting the SM parameters, the (minimum) Ns = 4 scalar parameters from the kernel (3.5) in the absence of CSF (or Ns = 5 if the CSF compartment is added), are complemented by the nc(lmax) – 1 = lmax(lmax + 3)/2 tensor parameters plm, where nc(l) is the number of the evenorder spherical harmonics coefficients up to the order l given by Eq. (1.14) in Sec. 1.8, and we subtracted one parameter because is set by the ODF normalization. This yields the total SM parameter count
| (3.8) |
such that Np = 9, 18, 31, 48, … for lmax = 2, 4, 6, 8, … already for the two-compartment kernel (3.5), without including S(0) and fCSF in the count.
Equation (3.8) reveals that the model complexity grows fast, as , if we are to account for the rich orientational content of realistic fiber ODFs in the brain. For an achievable lmax ~ 4 – 8, the dMRI signal in principle “contains” a few dozen parameters, none of which are known a priori.
3.3.2. How many parameters are necessary?
We can now contrast the SM parameter count (3.8) with the number Nc(lmax) [Eq. (1.15) in Sec. 1.8] of independent parameters “contained” in the cumulant or moment series truncated at l = lmax. Since Nc(l) ~ l3 grows faster with l than Np(l) ~ l2, the moments/cumulants estimated from the signal should, beyond some l, contain more than enough information to determine all the corresponding SM parameters. Direct comparison of Eqs. (1.15) and (3.8) yields that
| (3.9) |
for both 2- and 3-compartmental SM. This naive counting would let one believe that, having mastered sufficiently precise DKI parameter estimation (lmax = 4), we would be able to find all the scalar SM parameters, as well as estimate arbitrary fiber ODF up to p4m, Eq. (3.7).
This intuition, however, is deceptive, as the information content is not evenly distributed among all the Nc(lmax) components. It turns out that the minimal order lmax for which the moments/cumulants contain enough information to determine all SM parameters is lmax = 6, while at the lmax = 4 level, there exists a one-dimensional manifold (for Ns = 4), which can look as a single curve, or as two disjoint continuous “branches”, or families, of scalar parameters, which exactly match the signal’s moment tensors and (equivalently, the diffusion and kurtosis tensors) [46, 47]. The two families of solutions, or the two parts of the above one-dimensional curve (“bi-modality”) technically emerge as the two branches of a square root in a solution for a quadratic equation. In what follows, we illustrate this effect with a toy model of parallel fibers [39, 40] and then show that increasing the model complexity does not cure the problem.
3.3.3. A toy model of bi-modality: Parallel fibers
Let us now see how two branches appear as solutions of a quadratic equation involving directional diffusion and kurtosis values for a very simple ODF of perfectly aligned fibers, for the 2-compartment SM case. Here we follow the cumulant-series DKI approach as in ref. [39]; an equivalent formulation in terms of the moments, cf. Eq. (3.6), can be found in ref. [47]. A similar approach was used to estimate white matter tract integrity (WMTI) metrics from DKI [40] and subsequently adapted [229] to enable their estimation with reduced data requirements using axially symmetric DKI [230].
Staying at the level (DKI), the overall radial and axial components of the diffusion tensor, estimated from an ideally measured signal (the left-hand side), correspond to the following combinations of the scalar parameters (the right- hand side):
| (3.10) |
| (3.11) |
and for kurtosis components [39, 40]
| (3.12) |
| (3.13) |
“Transverse” parameters f and are uniquely determined from K⊥ and D⊥:
| (3.14) |
However, there are two possible solutions in the parallel direction. The duality arises from choosing [40, 47] the ζ = ± branch of the square root in Eq. (3.13),
| (3.15) |
Here , where . Note that, since the ground truth is unknown, our choice for the branch ζ may differ from the correct one.
From Eqs. (3.11) and (3.15), we find that, not surprisingly, the correct choice of ζ yields the true values Da and . However, if the sign choice is wrong, then the “apparent” diffusivities do not agree with the true ones:
| (3.16) |
| (3.17) |
Note, that in this case, as expected, , i.e., the difference has the same absolute value and the wrong sign. In particular, for f = 1/2, the diffusivities are swapped, — i.e we mistake for Da and vice-versa. Yet the above “apparent” values can seem completely biophysically plausible, especially if f ≈ 0.5. From the above derivation it is evident that the bi-modality of the parameter estimation originates from having two tissue compartments, and that the branch choice is certainly not obvious based on the parameter values estimated at low b.
3.3.4. Bi-modality beyond parallel fibers. Flat directions in the fitting landscape
The simplest nontrivial model revealing general degeneracies in parameter estimation, NODDIDA (Neurite Orientation Dispersion and Density Imaging with Diffusivities Assessment) [44], is a two-compartment SM variant (Ns = 4) that assumes a 1-parameter Watson ODF shape [42] and sets fCSF 0. In this model, unconstrained nonlinear fitting has revealed two families (trenches) of biophysically plausible solutions to fit optimization already in the relatively small, (4+1)-dimensional, parameter space, and flat directions along them [44].
Hence, NODDIDA exemplifies the two-fold nature of the parameter estimation challenge. Beyond the existence of multiple parameter branches (a “discrete” degeneracy, as in the toy model above), each of them represents a shallow “trench” (a “continuous” degeneracy) in the parameter landscape of nonlinear fitting.
The flatness, or continuous degeneracy, can be formulated as having the number of estimated parameters exceeding the number of relations between the parameters obtainable from the data. In its simplest form, this problem exists already for the simplest single-directional fitting with a biexponential function [75]. A normalized biexponential has 3 parameters; however, if b is low enough so that we are practically only sensitive to the terms ~b and b2 — i.e., when the DKI representation works well — we can only estimate 2 combinations of 3 model parameters, and will have a flat direction in the corresponding 3-dimensional fitting parameter landscape. (This problem persists in the presence of exchange, as discussed in ref. [231].)
The expansion (3.6) of the 2-compartment SM with any ODF into moments has been analytically and numerically shown to possess a similar kind of degeneracy. This frame-work, called LEMONADE (Linearly Estimated Moments provide Orientations of Neurites And their Diffusivities Exactly) [46, 47], exactly relates the moment tensors M (l) to SM parameters. It turns out that, at the level, there are only 4 independent equations, which relate rotationally invariant combinations of moments M (2) and M (4) to 5 SM parameters — the 4 scalar ones: f, Da, , , and the ODF invariant p2 (that characterizes the ODF anisotropy, defined in Sec. 3.5 below). Hence, the existence of the flat trenches in nonlinear fitting of NODDIDA is actually completely general; both the discrete bi-modality and the continuous trenches follow from the exact relations [46, 47] between the moments and the SM parameters, and will be present for any fiber ODF. Hence, it is only capturing the moment M (6) that can lift both kinds of degeneracies — as we mentioned briefly after Eq. (3.9) above — which is practically quite difficult to become sensitive to.
As for the “discrete” degeneracy, the works [39, 40, 44, 46, 47] have collectively raised the fundamental question: Which “branch” of parameters should be chosen, out of at least two biophysically plausible ones? In ref. [47], the discrete branch choice was formulated in terms of the the ratio β between ground truth compartment diffusivities falling or not falling within the interval
| (3.18) |
determined by the discriminant of a quadratic equation. Note that this condition involves all three compartment diffusivities, rather than just the two axial ones as in Sec. 3.3.3. Of course, only one branch corresponds to the truth; other(s) should be discarded. Obviously, selecting the wrong branch can radically change biophysical and diagnostic implications of the estimated parameters. Yet, branch choice is nontrivial, since often times, both parameter sets look equally biophysically plausible [40, 47], and it is very difficult to have a precise enough idea about the ground truth values, especially of whose precision crucially affects β. In Sec. 3.6, we will comment on the branch selection.
3.4. SM parameter estimation using constraints
Due to the challenge explained above (Sec. 3.3) of fitting the SM to noisy dMRI data, especially those acquired in clinical setting, most attempts of SM parameter estimation so far are based on superimposing additional constraints on both the scalar SM parameters, as well as the fiber ODF, to improve robustness of the fitted SM parameters.
An overview of employed models used so far is given in Figure 4. In what follows we consider two representative modeling approaches that have been popular because of their robustness, which potentially allows for clinical translation, and try to explain the quantitative differences in parameter estimates between them in the light of each model’s assumptions and consequent biases.
3.4.1. White Matter Tract Integrity metrics (WMTI)
WMTI, as proposed by Fieremans et al. [39, 40], extracts the 2-compartment SM parameters by relating the DKI components to scalar parameters in the aligned-fiber framework [39], already explained above (Sec. 3.3.3). Subsequently, the perfectly aligned approximation was somewhat relaxed by allowing for some dispersion within the fiber bundle, as described by an intra-axonal diffusion tensor, while the diffusion in the extra-axonal space is still modeled as an overall Gaussian compartment [40]. While the advantage of using DKI eliminated the need for direct nonlinear fitting to the diffusion signal, two different biophysically plausible solutions still exist similar to the two branches as described above (Sec. 3.3.3). In WMTI, the branch was chosen as based on the available data [40]. Parameter histograms corresponding to this choice, yielded f ≈ 0.5, Da ≈ 1.2 µm2/ms and in human corpus callosum.
Since no specific model is assumed for the tortuosity , as and are fitted separately, along with Da and f, it was suggested the WMTI parameters could be used to disentangle between acute damage such as neurite beading, as reflected in Da [233], and chronic damage including different types of demyelination and axonal loss, reflected in changes in the tortuosity, and f [219, 220]. As an in vivo validation, the age-related changes in the WMTI metrics were studied during the first two years of healthy brain development [232] (Figure 9), showing significant nonlinear increases in f, and , related to increased myelination and axonal density, while no changes in the longitudinal compartment diffusivities, Da and , as expected. Ex vivo animal validation studies provided reasonably accurate estimates of f in a mouse model of hypomyelination [234] and de-, and remyelination [221, 235]. Furthermore, mouse validation studies demonstrated that Da decreased during acute inflammation, while the axonal water fraction f decreased during the chronic phase of cuprizone intoxication [236], whereby and f were found to be respectively more sensitive to global and patchy demyelination [221]. These validation studies suggest increased specificity of the WMTI parameters to microstructural changes as compared to empirical diffusion metrics.
FIG. 9.
Comparison of NODDI (Sec. 3.4.2) and WMTI (Sec. 3.4.1) parameter evolution with age in human corpus callosum splenium [232]. A qualitatively (but not quantitatively) similar trend of continued increase in the intra-axonal water fraction fintra ≡ f was observed for both models, consistent with on-going myelination. WMTI displays a trend of increased fiber alignment (expressed by the orientation dispersion , derived from the intra-axonal diffusion tensor ), which could be a manifestation of continued pruning in the first year of life, while NODDI does not. The CSF fraction is set, fiso ≡ fCSF = 0, in WMTI.
However, while the WMTI metrics correlate as expected with the concentration of (purely intra-axonal) NAA under the assumption [237], it should be noted that the measured values of Da with low b dMRI protocols in the range of 1.0 – 1.2 µm2/ms are significantly lower compared to recently reported values for Da measured in the range of 1.9 – 2.4 µm2/ms using advanced diffusion protocols providing additional information by varying TE [48], diffusion time [170], or using double diffusion encoding [238], cf. Sec. 4, planar [141], isotropic [239], or very strong multidirectional (linear) [168] diffusion encoding. Further research is warranted to understand whether the discrepancy is due to a wrong choice of branch (, cf. Sec. 3.6 below, which would affect primarily estimates of D and , but not so much of f or ), or, alternatively, due to a potential bias when estimating cumulants dMRI data over a to large b-range [240] (affecting estimates for all model parameters).
We also note that branch selection (3.18) for the unconstrained problem (3.4)–(3.5) is qualitatively similar but quantitatively different from that in the WMTI highly-aligned tracts case [39, 40], cf. the toy model of Sec. 3.3.3. While qualitatively, the “wrong branch” in both the full model (3.4)–(3.5) and WMTI [40] corresponds, roughly, to swapping of intra- and extra-neurite parameters, there is no exact correspondence with the full model that includes dispersion; for instance, f and are also different between the branches. The difference between WMTI and the full model comes from the fact that in the toy model (WMTI prototype), the perfectly-aligned fiber constraint p2 = p4 = 1 has been implemented, together with effectively mixing the LEMONADE equations with moments M(4),2m and M(4),4m. Therefore, the branch choice based on is sufficiently different from that of Eq. (3.18). An intermediate case between the two including dispersion was obtained in [44, 170], by constraining the ODF to the Watson distribution, effectively mitigating the degeneracy by parameterizing all pl in terms of the Watson distribution concentration parameter κ.
3.4.2. Neurite Orientation Dispersion and Density Imaging (NODDI)
NODDI, proposed by Zhang et al. [42], is a 3-compartment SM that assumes a Gaussian-like (Watson) ODF shape characterized by one [42] or two [241] parameters. In addition, the three diffusivities are effectively fixed, in the following way:
Da = 1.7 µm2/ms
Mean-field tortuosity model [242],.
The estimated parameters are f and fCSF, as well as the ODF parameters (one or two parameters, depending on the Watson [42] or Bingham [241] distribution used).
Using high resolution ex vivo imaging, it was recently showed that Bingham-NODDI is able to capture the cortical fibers known to exhibit fanning/bending in human neocortex [243]. It was also shown that NODDI-derived dispersion agrees with histology measures in post-mortem normal and demyelinating lesions in spinal cord samples [244]. Furthermore, recent work from Schilling et al. [245] shows a strong overall correlation between the fiber orientation dispersion index (ODI) derived from NODDI versus derived from histology based on 3D confocal z-stacks in areas to the size of an MRI voxel in adult squirrel monkey brains.
However, the same study [245] also showed a small, but systematic overestimation of the true histology-based ODI, as well as a correlation of NODDI-derived ODI with the estimates f and fCSF. Furthermore, recent extensive human measurements up to b ≤ 10 ms/µm2 [47] also suggest that the above three parameter constraints generally do not hold, and therefore may bias the estimates of the fractions and fiber dispersion.
While both NODDI and WMTI rely on the same overarching SM, they have different constraints, particularly in terms of the compartment diffusivities (fixed in NODDI, fitted in WMTI), the ODF (Watson in NODDI, single bundle in WMTI), and number of compartments (3 in NODDI, 2 in WMTI). The effect of these different constraints have been evaluated by studying changes in the model parameters through normal human early development [232] (Figure 9). In this work, qualitatively similar trends were observed in f, in full agreement with expected on-going myelination, fiber classification and asynchrony of development. The quantitative estimates, however, are model-dependent, exhibiting biases and limitations related to the models’ assumptions. Similarly, changes during the first two years in fiber dispersion in the splenium corpus callosum were qualitatively different between NODDI and WMTl. This illustration clearly calls for extreme caution when interpreting modeling studies based on limited clinical dMRI data, where accuracy is typically sacrificed in favor of precision. Indeed, both WMTI and NODDI have made assumptions that allowed for a robust, rather than accurate estimation of the SM model parameters that are not fixed according to each model. This prompts both for improved SM parameter estimation methods (discussed next in Sec. 3.5), as well as for “orthogonal” and more comprehensive validation methods to gain better understanding of the relevant tissue features of modeling (discussed in Sec. 3.6), prior to applying them to clinical dMRI data.
3.5. ODF factorization and rotational invariants
Let us now introduce the recently proposed family of approaches to SM parameter estimation that do not rely on specifying the ODF shape, by factoring it out in a rotationally invariant way. This will enable separation of estimating the scalar and the tensor (ODF) parameters. Of course, all the degeneracies of the parameter estimation will persist — and in fact, factorization has been used as a tool to prove that the above discussed degeneracies are completely general [47].
Much like convolutions become products in the Fourier domain, the convolution (3.4) between the individual fiber response and the ODF becomes a product in the “spherical Fourier” domain (i.e., the SH basis) [197]:
| (3.19) |
where Kl(b) is the projection of the kernel onto the Legendre polynomial (–1)l/2Pl(ξ) [37, 45, 47].
Since any rotation transforms SH components Slm and plm according to a unitary transformation belonging to the (2l + 1)−dimensional irreducible representation of SO(3) group labeled by “angular momentum” l, 2-norms and (defined likewise) are conserved under rotations, i.e., are rotational invariants. It is thus convenient to introduce23 rotational invariants and , where normalization is chosen so that 0 ≤ pl ≤ 1. Hence, equations (3.19) for the (l, m) SH components give rise to the corresponding equations for the rotational invariants [45, 47],
| (3.20) |
where we denoted by x the dependence on the kernel’s scalar parameters to be estimated. The invariant p0≡1 is trivial (ODF normalization); the remaining ODF invariants pl, one for each l, characterize its anisotropy irrespective of the chosen basis.
3.5.1. Isotropic l = 0 invariant K0(b)
The l = 0 invariant for Eq. (3.20) has been independently introduced as “powder averaging” and “spherical mean” [248– 253]. The ODF factorization in this case simply follows from swapping the order of integrations over and :
since is independent of fiber direction due to the “translational invariance” on a unit sphere, and the ODF is normalized to . The last identity above gives the projection of kernel (3.5) onto the l = 0 Legendre polynomial P0(ξ) ≡ 1, where ξ = cos θ in our case; for a stick compartment, this projection yields Eq. (3.2) above.
3.5.2. Rotational invariants Kl(b) for l = 2, 4, …
Equation (3.20) formally yields an infinite family of rotational invariants Kl(b) [45, 47], one for every l = 2, 4, However, it turns out that by far the most useful is the next-order, l = 2 invariant, since the projections of onto the Legendre polynomials with l > 2, giving the compartment contributions to Kl(b, x), are too slowly varying [37] and thereby adversely affecting the sensitivity to the estimated parameters x.
We also note that including the l > 0 invariants in system (3.20) is only possible for anisotropic ODFs, with pl > 0. Physically, it is expected since the less symmetric the system, the more inequivalent ways it enables for probing it.24 In the brain, the ODF is at least somewhat anisotropic; its lowest-order invariant p2 is generally nonzero even in GM.
Parameter estimation based on the ODF factorization via the rotational invariants amounts to inverting the nonlinear relations (3.20) with respect to model parameters x and pl. Such inversion has so far been technically implemented in four distinct ways:
Analytically inverting relations between their Taylor expansions — i.e., expressing model parameters in terms of the moments of the signal (LEMONADE) [46]. At typical bD ~ 1, the biases in estimating the moments cause notable bias in the model parameters.
Using the LEMONADE output as initialization for the RotInv solution of Eqs. (3.20) via nonlinear fitting using the gradient-descent optimization of the corresponding objective function [47]. This notably increases the accuracy of LEMONADE.
The prevalence method [47]: To avoid the branch selection issue, initialize the fit objective function for Eq. (3.20) with a large number (~ 20 – 100) ofrandom starting points within the plausible parameter range (e.g., 0 < f, p2 < 1, and 0 < D < 3 for all diffusivities), observe that the fit outcomes cluster around a few sets in the parameter space, and select the mean of the largest cluster (after excluding outcomes outside the bounds). The method works best for large b, say, , since increasing b broadens the basin of attraction of the true minimum [44].
Machine learning framework: Generate distributions of the invariants based on the prior distributions of x, and numerically invert these relations based on the training set [45]. The invertibility of these relations requires the resolution of the bi-modality problem (section 3.3). In particular, the constraint of close traces of intra- and extra-axonal tensors, , was applied according to results obtained using isotropic diffusion weighting [196]. While it is the fastest data processing method, it is sensitive to the way the training data are generated.
Overall, our current experience tells that, no matter the implementation, the sensitivity to different scalar parameters varies dramatically (e.g., f is obtained reasonably well while the sensitivity to and is much worse) [45, 47]; with decreasing SNR, methods (a)–(c) yield noisier parameter maps while method (d) yields “too clean” maps completely dominated by the mean values of parameter priors; branch multimodality manifests itself in the need for the branch selection (3.18) in all these approaches.
It is yet difficult to evaluate accuracy of these methods in vivo because of lack of understanding of what the ground truth is, and because all these methods are strongly dependent on the branch selection/initialization/priors.
The lack of precision (due to the “continuous” degeneracy of shallow trenches) generally exists due to the multicompartmental nature of the kernel (3.5) [47]. One can say that any standard (directional) dMRI measurement effectively under-samples the scalar part of the model (3.4), not providing enough relations between the scalar parameters (cf. Sec. 3.3.4 above), and over-samples the tensor (ODF) part. In other words, the system’s true complexity lies within the kernel’s parameters hidden in functions Kl(b, x), Eq. (3.20) — while the ODF is in some sense “on the surface”.
This prompts the need for “orthogonal” measurement schemes [48, 141, 196, 253, 255–258] which probe the scalar parameters in different combinations than entering the kernel projections Kl(b, x), as we are now going to discuss.
3.6. Open questions: Precision and branch selection
Estimating precise maps of ground truth values, as well as the branch selection (3.18), remains an essential problem for quantifying neuronal microstructure, and is currently an active topic of research. Recent experiments using advanced dMRI protocols have been either employing very strong diffusion gradients (e.g., on unique Connectome scanners with gradients up to 300 mT/m) [168], or adding “orthogonal” acquisitions such as extra-neurite water suppression by strong unidirectional gradients [257] or planar diffusion weighting [141], isotropic diffusion weighting [239, 253, 255, 256, 258, 259], and varying other parameters, such as the echo time [48] and the diffusion time [170, 260].
The choice of the branch, and an independent estimation of the compartment diffusivities Da and is of particular interest. Isotropic weighting (spherical tensor encoding) yields
| (3.21) |
which seems to produce relations due to an empirically small iso-weighted kurtosis of signal (3.21) [196, 258]. While this can be interpreted as favoring one of the branches, this relation cannot be used as a global constraint: Szczepankiewicz et al. [255] show it failing in thalamus (note however that thalamus is a GM/WM mixture). Another possibility for using orthogonal measurements to resolve the parameter estimation degeneracy is the application of double diffusion encoding (DDE), see Sec. 4, with promising preliminary results [238]. In rat spinal cord, DDE seems to indicate the branch-merging case [257]. Note that such assumption is made in NODDI (section 3.4.2), albeit this model fixes (rather than fits) the compartment diffusivities to equal values. This assumption does not seem to universally hold in the human brain [47]. As the ultimate goal of bio-physical modeling is to study pathological and other changes (e.g., aging and development), it is imperative to estimate the compartment diffusivities independently, because changes in one of them may indicate the earliest sign of a pathological or other process of interest.
Overall, the Standard Model presents a microcosm of parameter estimation challenges: a relatively low SNR in clinical dMRI coupled with both discrete and continuous degeneracies, require careful validation and prompt employing the widest possible arsenal of measurements, to probe parameters from as many vantage points as possible. Achieving compartmental specificity, crucial in studying pathological and other processes, remains a difficult but worthy goal.
4. MULTIPLE DIFFUSION ENCODINGS
The whole is greater than the sum of its parts
Aristotle
4.1. MDE basics
Multiple diffusion encoding (MDE) generalizes the Stejskal-Tanner (Sec. 1.4) pulse sequence design by adding one or more extra diffusion weighting blocks, as illustrated in Fig. 10 for the case of double diffusion encoding (DDE) [132, 261–263]. Figure 10 also defines the main pulse sequence parameters for DDE, which in addition to the familiar pulse-gradient parameters of each block, includes a mixing time τ.
FIG. 10.
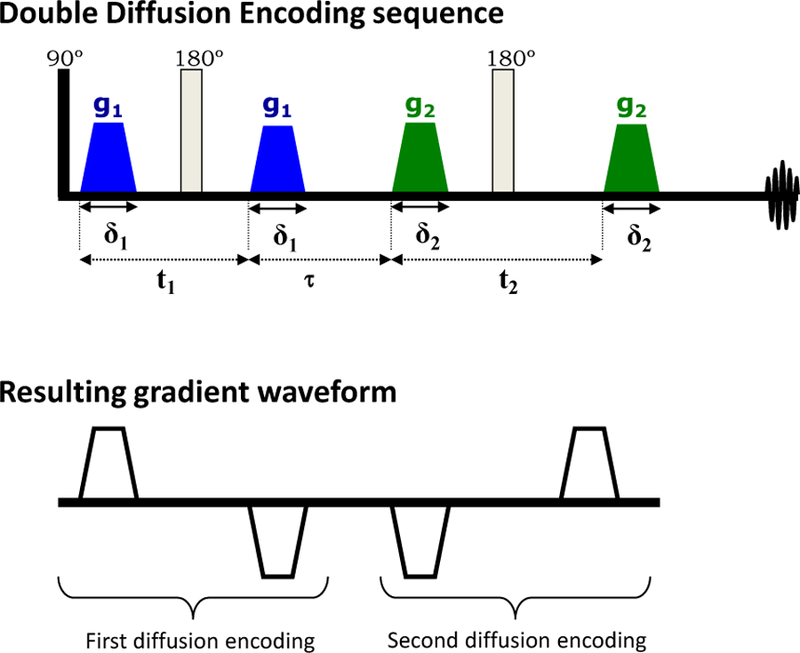
(a) Example of a DDE sequence within the framework of a double spin echo. (b) The resulting gradient waveform obtained by multiplying each gradient by , where nπ is the number of π pulses following the given gradient. In the text, we assume narrowpulse approximation, such that δi → 0, with the Larmor frequency gradients gi sufficiently large to yield finite qi = giδi (no summation over i).
In the following, we will restrict our attention to the narrow pulse limit. Generally, each diffusion weighting block is characterized by an independent diffusion wave vector qn and diffusion time25 tn, and the mixing times define delays between blocks. Thus, a rich set of experimentally controllable parameters can in principle enable qualitatively different ways of probing the microstructure, as compared with the conventional, single diffusion encoded (SDE) sequences.
The fundamental question of the information content of MDE signal SN relative to a set of independently acquired SDEs S1 can be formulated using an example of the DDE signal S2 (here we ignore the trivial factors, assuming the unweighted signal to be normalized to unity):
| (4.1) |
Technically, the above question is as follows: When does the convolution of the local propagators (1.5) defined in Sec. 1.4 contain more information than the product of the voxel-averaged translation-invariant SDE propagators (1.7)?
Let us first outline the three cases when Eq. (4.1) holds, i.e., there is no extra information in MDE relative to SDE.
Microscopic translation invariance: If depends only on the relative displacement, the above equality holds for any Gt,r. Of course, this is true for the Gaussian diffusion, when Gt,q is described by Eq. (1.8), but the statement is much broader, since its proof (by change of integration variables r1 = r1b – r1a and r2 = r2b – r2a) involves only the translation invariance requirement. Practically, this means that the time scales involved in Eq. (4.1) exceed the time needed for the coarse-graining to restore sample’s translation invariance, whether this implies the Gaussian fixed point (1.8) or its anomalous counterpart, cf. Sec. 1.9.
Long mixing time limit of a single pore: If all spins are confined in the same pore of volume V, and τ exceeds the time to diffuse across the pore size, the “mixing” propagator approaches a constant, and Eq. (4.1) again factorizes, irrespective of the (non-translation-invariant) functional form of .
Weak diffusion weighting: Equality (4.1) holds for any at the level of [264], cf. Sec. 4.2 below. For this statement to hold, it is only required that the cumulant expansion (1.10) has a nonzero convergence radius. (This common property breaks down for a diffusion propagator of a stretched-exponential form, whose assumptions contradict experimental evidence [70].)
Generally, the above requirements do not hold — tissues are microscopically not translation-invariant, a voxel can contain multiple pores of various shapes (cf. Sec. 4.3 below), and diffusion weighting can be strong, so that the terms are relevant. This justifies using MDE to obtain extra information.
To get a feel for the difference between DDE and SDE, it is instructive to consider the long mixing time limit τ →∞ in a system of disconnected pores. The average over Brownian paths splits into two parts: an average over paths within a single pore, followed by an average (denoted by an overbar) over pores α = 1; …, with volume fractions wα = Vα/V adding to unity. For example, for the SDE signal (1.6):
For DDE, spin displacements in each of the diffusion-weighting blocks become independent of one another within each pore in the limit τ → ∞ if r2a and r1b in Eq. (4.1) are from the same pore α with volume Vα, while the probability to hop between pores is zero: if r2a and r1b belong to different pores α ≠ β. This effective Kroeneker δαβ eliminates the cross-terms between different pores that are present in the right-hand side of Eq. (4.1):
| (4.2) |
Here the subscript “paths in α” was replaced with α for brevity. On the other hand, for the product of two SDE’s we have
| (4.3) |
The physical meaning of the above equations is as follows: it is not possible in general to split the coherent averaging of the product (4.2) over pores into the product of the averages (4.3).
The coherent disorder averaging of the propagators in equation (4.4) is also the reason that the effective medium theory [27, 33] for the disorder-averaged SDE propagator (1.6) has to be further augmented to incorporate the coarse-graining effects for MDE, relevant at finite τ.
4.2. Equivalence between MDE and SDE at
Historically, DDE was noted to provide a method for determination of compartment dimensions [263] at low diffusion weighting in the limit of zero mixing time and long diffusion times. Taylor-expanding Eq. (4.2) in this limit, Mitra et al. [263] showed that in a system of identical pores
| (4.4) |
where θ is the angle between the directions and of the diffusion wave vectors, and is the pore mean squared radius of gyration (rcm is pore center-of-mass), a measure of pore size.
Hence, a measure of the pore size can be determined from the signal dependence on diffusion wave vector angle in isotropic systems, or more simply from the signal difference between parallel and antiparallel diffusion wave vectors.
Equation (4.4) has since been generalized to take into account, e.g., partial volume, multiple concatenations, pulse sequence timings (e.g., finite gradient width) for various geometries [265–271]. This has later been demonstrated by several groups in model systems and biological samples ex vivo [272–278], and in vivo in humans [277, 279–281].
However, it was recently realized [264] that this property, i.e., the sensitivity (4.4) to pore gyration radius, is a general feature of any diffusion-weighted signal at the level, and hence it does not rely on information beyond that already contained in the SDE signal, which in the same regime behaves as [282]:
| (4.5) |
More generally, it was shown [264] that up to order ,
| (4.6) |
where Dij(t) is the cumulative diffusion tensor, Eq. (1.13). This explicitly demonstrates that the signal is fully characterized by the time-dependent diffusion tensor, a quantity which is obtainable from the SDE acquired at a few diffusion times.
This statement is valid for any diffusion sequence up to second order in the diffusion wave vector [264, 283], and is a consequence of the existence of the cumulant series, whose lowest order can be completely reproduced by knowing the diffusion tensor for all t or, equivalently, for all ω [18, 131],
| (4.7) |
where q(t) is the time integral of the arbitrary-shaped applied gradient, v is the molecular velocity, v = ∂tr, and no bulk flow is assumed as usual. The (symmetric) autocorrelation function is constructed out of its retarded counterpart
| (4.8) |
defined by generalizing Eqs. (2.6) and (2.14) to the anisotropic case.
The function (4.8) is generally nonlocal in t [18, 19, 27, 33, 123, 131, 284, 285]. Figure 11 illustrates how this nonlocality, integrated in Eq. (4.7), gives rise to the cross-term (second line of Eq. (4.6)); this term disappears in the Gaussian diffusion limit, when is infinitely narrow, and the function (4.8) is concentrated along the diagonal. Hence, the cross-term directly probes the time-dependence of the diffusion coefficient in Eq. (4.6), cf. Section 2.
FIG. 11.
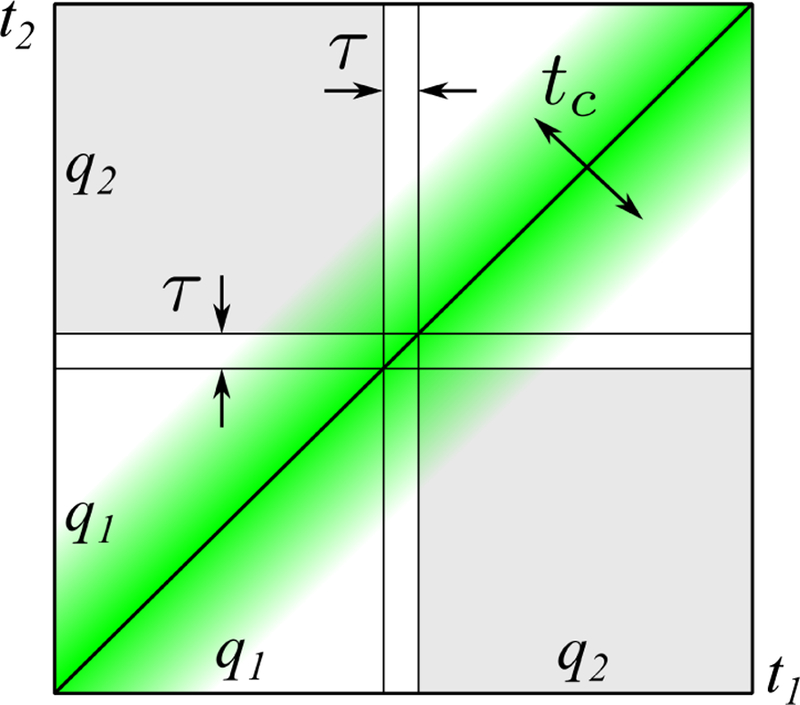
Two-dimensional temporal integration involved in the second-order cumulant, Eq. (4.7) leading to Eq. (4.6) for the DDE measurement. Labels q1 and q2 indicate the time interval in which q(t) equals to q1 and q2, respectively; for simplicity, the vector indices are not shown. The green shaded area along the diagonal symbolizes , Eq. (4.8), where it significantly deviates from 0, with the width of this region set by the correlation time tc. The nontrivial cross-term q1iq2j in Eq. (4.6) arises from the off-diagonal quadrants. As this contribution is weighted with the velocity autocorrelation function, it tends to zero when the mixing time, τ (indicated by the thin lines along each dimension) becomes larger than the correlation time, τ ≫ tc. In particular, no non-trivial cross-term is present for Gaussian diffusion, for which tc → 0.
4.3. Extra information relative to SDE at and beyond. Microscopic anisotropy
At larger values of the diffusion weighting, double diffusion encoding was shown from the beginning to have the ability to characterize microscopic anisotropy (μA) in systems which are macroscopically isotropic, Fig. 12, see panel (c). Thus, in an early application of the sequence by Cory et al. [262], DDE was used to quantitatively measure the eccentricity of yeast cells, which was shown to be directly related to the difference in signals acquired with parallel and perpendicular diffusion wave vectors. This has since been explored by many authors, e.g., in phantoms [286, 287], ex vivo tissues [288, 289], and in vivo [277, 290, 291].
FIG. 12.
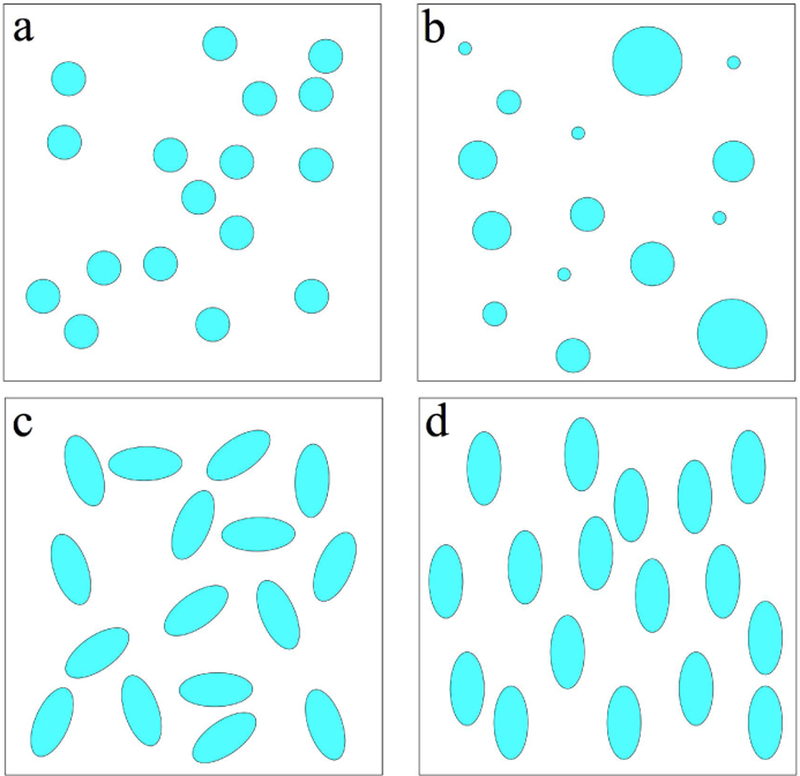
Examples of model systems considered in the text. In (a), a system of identical spherical pores is shown, whereas, in (b), the pores have a distribution of sizes. In (c), an approximately isotropic distribution of ellipsoidal pores is sketched and, in (d), the pores are coherently oriented. Systems (a)–(c) are macroscopically isotropic, system (d) is not. Systems (c) and (d) are microscopically anisotropic. Ensemble heterogeneity is only seen in systems (b) (size) and (c) (orientation). Here, spins contributing to the signal are assumed to only reside within the pores.
The basic sensitivity to anisotropic pores can be understood already from Eq. (4.2) in the long diffusion time and long mixing time limit
| (4.9) |
where χα(q) is the Fourier transform of the pore structure function, defined as χα(q) ≡ 1/Vα inside a pore and 0 otherwise [292].
For spherical pores, the structure function is isotropic, hence χα(q) does not depend on the direction of q. For anisotropic pores, say ellipsoids, the anisotropic structure functions χα(q) in Eq. (4.9) ensure that the result depends on the directions of q1 and q2. This is because diffusion in the two directions is generally correlated when pores are nonspherical.
If the overall system is macroscopically isotropic, i.e., the orientations of the individual pores are randomly distributed (Fig. 12c), the signal will be unaffected by rotations of the sample or of the laboratory system of reference, but the dependence on the relative angles between q1 and q2 will survive the pore averaging in Eq. (4.9). Mathematically speaking, this is because the two terms in the product |χα(q1)|2|χα(q2)|2 are not independent for a given pore, and hence the average of the product is different from the product of averages.
A convenient measure of the eccentricity of the pore space (microscopic anisotropy) can therefore be found from the difference of DDE signals acquired with parallel and perpendicular wave vectors q1 and q2. In the presence of macroscopic and microscopic anisotropy, the signal will depend on the orientations of both q1 and q2, and microscopic diffusion anisotropy can no longer be extracted simply from the difference between parallel and perpendicular diffusion wave vectors. The rotationally invariant way to circumvent this (cf. Sec. 3.5 above) is to powder average the signal, analogously to how the K0 invariant was introduced in Sec. 3.5.1 (although, technically, the averaging here is over the SO(3) group instead of a 2-sphere), and practical recipes for doing this were proposed in refs. [288, 293, 294]. Microscopic diffusion anisotropy can then be defined as the difference between (log of) the powder averaged signals acquired with parallel and perpendicular diffusion wave vectors [288].
| (4.10) |
where W is the kurtosis tensor as defined in [61] from the cumulant expansion (1.10) of the SDE propagator, whereas Z is a rank-4 tensor, unique to DDE, defined as
| (4.11) |
The tensors refer to the microscopic t-dependent diffusion tensors characterizing diffusion within the pores, and the SDE-measured overall diffusion tensor Dij(t) entering the first line of Eq. (4.10) is an average over all pores,.
The new tensor Z, Eq. (4.11), accessible with DDE (and inaccessible with SDE), is proportional to the covariance tensor of microscopic diffusion tensors. Microscopic diffusion anisotropy, defined as the difference between log of the powder averaged signals acquired with parallel and perpendicular diffusion wave vectors, can then be expressed as (see [288])
| (4.12) |
In the last equality, the set denote the eigenvalues of Dα, and
| (4.13) |
With the above definition, 3 tr (Dα)2 – (trDα)2 = 9 var {σα} in Eq. (4.12). The anisotropy metric ε has dimensions of [length]4. These somewhat awkward dimensions have a historical root in DDE eccentricity measurements [262]. While ε ≥ 0, in practice it is often estimated from the difference of signals, which can become negative due to noise.
As an example, for randomly oriented (and identical) axially symmetric domains, such as fibers with (timedependent) diffusivities D||(t) and D┴(t), microscopic diffusion anisotropy becomes
| (4.14) |
If the domains are different, the corresponding Eq. (4.14) should be further averaged over them, cf. the term in Eq. (4.12). Microscopic diffusion anisotropy hence depends explicitly on diffusion time, but tends to the geometric measures of pore shape anisotropy as the diffusion time increases, since for any confined region of size a, D(t) ~ a2/t, and t asymptotically drops out from Eq. (4.14). From the time dependence of the microscopic diffusion anisotropy, non-Gaussian effects of the individual compartments can be revealed by the time dependence of the compartmental (microscopic) diffusion tensors.
Practically, the anisotropy metric (4.12) can be estimated from knowledge of the full Z tensor, or by the difference of the powder averaged log signals with parallel and perpendicular diffusion wave vectors. It has an advantage of being additive (cf. the pore average in Eq. (4.12)): if several distinct types of pore populations are present in the sample (e.g., a distribution of D┴ and D|| in Eq. 4.14), ε simply becomes the volume-weighted mean over the corresponding ε from each of the populations. This is an advantage since it eases the interpretation; however, the disadvantage is the dependence on size of the pore in addition to its anisotropy. This has the additional consequence that ε is strongly biased by the larger pores: Since wα ~ a3 and εα ~ a4 for a pore of size a, the population averaged eccentricity scales as , heavily preferring the tail of the pore size distribution, — and hence susceptible to the mesoscopic fluctuations introduced in Sec. 2.5 above, cf. Eq. (2.39).
To factor out the pore sizes, normalized dimensionless measures of microscopic diffusion anisotropy were introduced [288, 293, 296], such as the microscopic fractional anisotropy, μFA:
| (4.15) |
In the previous example with axially symmetric domains, microscopic fractional anisotropy
| (4.16) |
whereas fractional anisotropy FA is modulated also by the fiber orientation distribution function [288, 297], and only recovers μFA when the fibers are all coherently aligned. Another metric which has been suggested to be of biological importance [253, 255], is the variance in isotropic diffusivity,
| (4.17) |
which can also be inferred from the Z tensor [133, 298]. When diffusion within the individual pores is Gaussian, other methods such as the so-called magic angle spinning of the qvector (q-MAS) [299] can also be used to estimate the diffusion tensor covariance [133, 300].
4.4. Concluding remarks on MDE
As we can see, MDE can potentially provide unique extra information relative to SDE. However, this information content only starts at the level of , Eq. (4.10) (in addition to the standard SDE terms), and hence to claim the true novelty of the information, it has to be properly identified relative to the SDE measurements with similar scan parameters (timings and gradients). Clarifying the advantages of MDE is practically essential in the view of much reduced SNR due to a notable increase of the echo time needed for the multiple gradients to play out.
Overall, the main advantage of MDE so far seems to lie in its ability to detect and quantify microscopic diffusion anisotropy. In particular, the advantage of the DDE metrics of microscopic diffusion anisotropy (e.g., Eq. (4.12)) is that they do not rely on concrete assumptions regarding pore shapes.
Of course, if a detailed model of microstructure is available, e.g., of the Standard Model form (Section 3), microscopic diffusion anisotropy is directly accessible in terms of model parameters (which can in principle be determined using SDE). However, even in this case, MDE adds value by providing an “orthogonal” way of being sensitive to model parameters — and, like in the SM case above, Sec. 3.6, it can provide rotationally invariant independent relations between parameters, which can help lift the parameter estimation degeneracies [238].
So far, the existing MDE models have been calculated in the limit of either Gaussian diffusion in all compartments, or in the ti → ∞ limit (e.g., closed pores). Importantly, the transient effects, cf. Section 2, have not yet been properly accounted for in the MDE framework. In particular, the structural disorder-induced power-law tails in Dinst(t), or, equivalently, in , such as the ones originating due to disordered axonal packing in the extra-axonal space [23, 34], will contribute to the “irreducible” MDE effects (that go beyond the product of a few SDE signals). Taking such transient processes into account seems a priori as crucial for the interpretation of MDE measurements, as it has been for the SDE — e.g., in the context of recent re-interpretation of the axonal diameter mapping results (cf. Sec. 2.4.2 above). The relevant coarse-graining formalism of the effective medium theory [23, 27, 33] seems perfectly suitable for the task — but it has not yet been developed.
5. OUTLOOK AND OPEN QUESTIONS
There is nothing more practical than a good theory
L. Boltzmann
5.1. To model or not to model?
We are writing this Review at a transformational moment, when our field of quantitative dMRI is experiencing a revolution due to unprecedented quality of hardware and novel acquisition methods, enabling us to observe very subtle physical effects, even in human subjects and potentially in patients.
Interpreting these effects in terms of the tissue microarchitecture is highly nontrivial; it is safe to say that the theoretical challenge has been so far greatly underappreciated. This, however, may swing the pendulum the other way, towards an “anti-modeling” point of view: Since, according to a widespread refrain, “biology is so much more complicated that anything physicists have ever studied”, there is little hope for the quantitative understanding of such effects, and the best we can do is to stay at the level of “representations” (cf. Sec. 1.7) and to draw empirical correlations between parameters of such representations (e.g. mean diffusivity or fractional anisotropy) and the clinical disease scores.
One of the messages of our Review is that the whole history of Physics in the 20th century offers the case for optimism. The quote from a nuclear physicist (before Section 1) has been a universal refrain for our sustained ability to understand nature’s complexity, step-by-step, from the origins of elementary particles to the vast scopes of the Universe. The essence of the effective theory way of thinking is that one certainly does not need to understand everything about the world in order to understand some corner of its parameter space really well. We certainly can quantify tissue microarchitecture without uncovering the origins of the human conscience or mapping full details of the brain’s biochemical machinery. Too often, “biology is way more complex than all your models” has been merely an excuse not to develop better models.
We reject this excuse [70]. We believe that having appropriate theoretical description of diffusion in tissues at the mesoscopic scale is not a luxury at this point — rather, this is an indispensable scientific method of investigation into pathological processes 2–3 orders of magnitude below nominally achievable resolution of MRI in any foreseeable future — or, in fact, ever, since the MRI resolution is stringently bounded by physical and physiological limitations that have been largely reached by now. The parallels with superresolution microscopy [301] are quite obvious; that discipline took a century to develop, based on employing models and prior information. Our task is harder but, arguably, can lead to even more impactful advances.
With that in mind, let us outline 10 exciting unresolved problems, focussing on which, to the best of our understanding, will propel our field forward.
5.2. Ten problems for mesoscopic dMRI
Apparent vs. genuine diffusion metrics: What are the confounding effects of mesoscopically varying R1(r), R2(r), and Ω(r) in the mesoscopic Bloch-Torrey equation (1.1) on the observed diffusion metrics, in the spirit of refs. [13–16]? Can we develop a multi-modal mesoscopic imaging framework able to self-consistently quantify all these mesoscopic quantities and disentangle their effects in the apparent diffusion coefficients and higher-order metrics?
Relation between time-dependent D┴(t) and its tortuosity limit D∞, and the geometric parameters of realistic axonal packings: As the time dependence of the diffusion transverse to fiber tracts is dominated by the extra-axonal water (Section 2), the natural question is what structural changes (e.g. demyelination, axonal loss) can affect this time dependence, as well as D∞. This is a difficult yet clinically impactful inverse problem [219], whose approximate solution, relying on the ideas of coarse-graining and renormalization, has so far only been obtained in the t → ∞ limit [220].
Origin of structural disorder along the neurites: What causes the time dependence along the fibers or in the gray matter? Is it varicosities, beads, synaptic boutons, undulations, or something else? Which of these structural units’ changes in pathology can be detectable?
Parameter estimation challenge for the Standard Model: How many Gaussian compartments do we have to include? For increasing the precision, it looks like we need orthogonal measurements, such as MDE (e.g., isotropic diffusion weighting), and varying echo time. What is an optimal clinically feasible measurement protocol?
Time-dependent rotationally-invariant framework: Combining the ideas of Sections 2 and 3 can lead to describing each fiber fascile in terms of the non-Gaussian propagators (inside and outside the neurites) with the corresponding time-dependent diffusion, kurtosis, etc, cumulant tensors; such fascicles then naturally combine into the SM-like signal based on the fiber ODF in a voxel. This difficult parameter estimation problem may offer an all-encompassing description of the diffusion signal measurable with dMRI in the brain.
Permeability/exchange time for the neurites: How well we can approximate compartments as nonexchanging? At which time scales this assumption breaks? The answer most likely will be different for gray and white matter, and for different brain regions and the degree of myelination.
Standard Model for GM: Can we apply SM as introduced in Section 3 to gray matter in vivo at clinical diffusion times, or should we modify the compartments? Do we have to include exchange, and if yes, then at which level of complexity (e.g., Kärger model or beyond)?
EMT for MDE: Development of the effective medium theory framework [27] for the “disorder-averaging” involved in the multiple diffusion encoding signal (Section 4). Which physical effects, from the EMT standpoint, are best captured using MDE, or are completely absent in the SDE?
Signal vs. noise: As the saying goes, “noise is signal”. The fundamental question is to separate the thermal noise, imaging artifacts, as well as the genuine differences between parameters in voxels belonging to the same region of interest. Random matrix theory-based approaches [182, 183] offer an exciting prospect.
Mesoscopic fluctuations and biological variability: How different are the mesoscopic tissue parameters within a given region of interest? Their differences provide the “natural” minimal width for the parameter distributions within an ROI, in the limit of infinite SNR. Sometimes, relatively small differences in the mesoscopic parameters can translate into large differences of the dMRI metrics; the heavy sensitivity of the signal from water inside axons to the tail of the axonal diameter distribution [23] (Secs. 2.5, 4.3) can lead to the mesoscopic fluctuations for a sufficiently small voxel, akin to a similar phenomenon noted earlier within condensed matter physics [7]. Studying these fluctuations can provide fundamental insights on the optimality and robustness of the organization of neuronal tissue microarchitecture, as well as offer practical limits on our detection capabilities.
ACKNOWLEDGMENTS
It is a pleasure to thank our numerous colleagues and members of our research groups for stimulating discussions and collaborations which are reflected in our Review. In particular, we thank Christian Beaulieu and Gene Kim for discussions on experimental issues, and DanWu and Jiangyang Zhang for sharing their OGSE data displayed in Fig. 7. We also thank Joseph Ackerman, Ivana Drobnjak, Ileana Jelescu, Markus Nilsson, Marco Palombo and Alex Sukstanskii for their thoughtful and constructive comments on the manuscript.
Photo credit to Tom Deerinck and Mark Ellisman (National Center for Microscopy and Imaging Research) for the histology image illustrating a fiber fascicle in Figs. 1 and 8.
E.F. and D.S.N. were supported by the National Institute of Neurological Disorders and Stroke of the NIH under award number R01NS088040. SNJ was supported by the Danish Ministry of Science, Technology and Innovations University Investment Grant (MINDLab, Grant no. 0601–01354B), and the Lundbeck Foundation R83-A7548.
Appendix A: Causality and analytical properties in the frequency domain
As stated after Eq. (1.4), the diffusion propagator is the density of particles released at a point r0 at the moment t = 0. While the diffusion equation is often formulated for positive times only, t > 0, with an explicit initial condition, writing Eq. (1.4) for all times t is more convenient due to reasons that will become clear below. Being the response to an instant point source of particles, the diffusion propagator helps finding the particle density for an arbitrary source f (t, r) (“particle injection”), using the linearity of diffusion equation,
| (A1) |
The solution takes the form of a t- and r-convolution,
| (A2) |
which is straightforward to prove by acting with the bracketed operator from Eq. (A1) on under the integral. This solution explains the notion of causality that implies that the response ρ(t, r) follows the source, f (t0, r0), and it cannot precede it. This means that for t < t0. This is guaranteed by the proportionality of to the step function θ(t), as stated after Eq. (1.5). Synonymous to causality is the notion that is a retarded propagator, which implies that any perturbation, f, of the system propagates into the future, which is opposed to the formally possible advanced propagator for which perturbations propagate into the past.
Likewise, quantities D(t), Dinst(t) and , entering Eqs. (2.10)–(2.14), are retarded, since they are identically zero for t < 0. In particular, the retarded velocity autocorrelator (2.6) has a physical meaning of a response of the current (sometimes called flux) J(t, r) of diffusing particles to that of a lump of particle density ρ(t, r) (the generalized Fick’s law), cf. ref. [27],
| (A3) |
Equivalently, in the Fourier domain, the convolution becomes a multiplication, cf. Eq. (2.8):
| (A4) |
In physics, the above retarded response functions are known as particular cases of the general linear response theory and the fluctuation-dissipation theorem [134, 302].
Our main goal in this Appendix is to investigate how causality, i.e., the retarded character of any response function that identically vanishes for t < 0, manifests itself in the frequency domain. We will now show that causality imposes a strict constraint on the analytical properties of its Fourier transform in the complex plane of ω. Namely, a retarded response must be an analytic function, i.e., it must have no singularities (e.g., poles or branch points), in the upper half-plane Im ω ≥ 0, Fig. 13 [134].
FIG. 13.
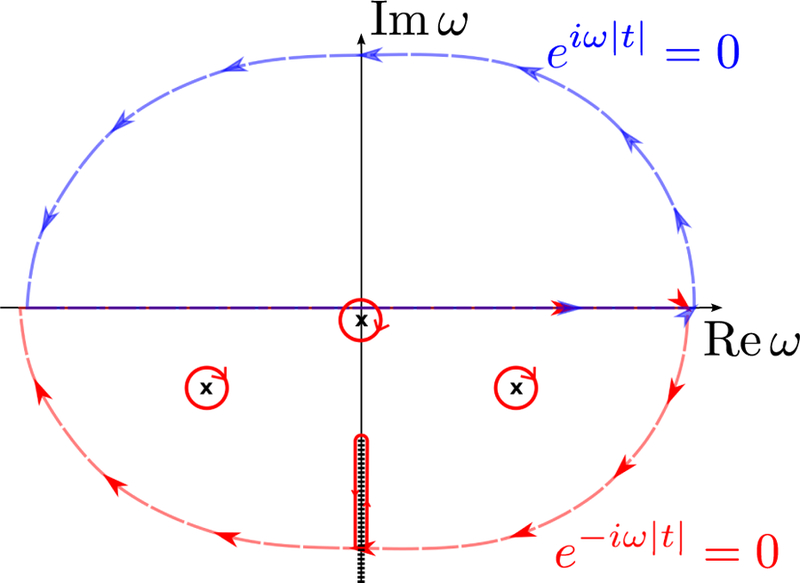
Analytical structure of a causal (retarded) response function on the complex plane of ω. When calculating the inverse Fourier transform such as Eq. (A5), the original integration contour over the real axis can be closed in the infinite semicircle with Im ω > 0 (light blue dashed line) when t < 0, according to the Jordan’s lemma. Causality then requires that no singularities are present in the upper half of the complex plane, in which case the integration contour can be shrunk to a point. For t > 0, the contour can be closed where Im ω < 0 (light red dashed line). This contour can be shrunk to encircle the singularities of the transformed function (red solid lines).
To show that, consider the inverse Fourier transform back to the time domain (having as an example):
| (A5) |
and demand that the resulting for t < 0.
The integration in Eq. (A5) is performed along the Re ω axis of the complex plane of ω (i.e., over all the frequencies). Because of the Fourier exponential, one has to close the integration contour along an infinite semi-circle on which e–iωt → 0 (Jordan’s lemma),26 and then shrink this contour to single out contributions of all singularities, according to Cauchy’s theorem. Equivalently, we can view the Fourier integration as proceeding along the equator of the Riemann sphere (topologically equivalent to the complex plane with an added point at infinity); in this case, the fact that the Re ω axis corresponds to a closed contour is more obvious. Cauchy theorem again applies, and the Jordan lemma dictates in which hemisphere — top or bottom — of the Riemann sphere the contour should be shrunk from the equator to encompass the singularities.
For negative times, t < 0, e–iωt diverges when Im ω → –∞, and vanishes when Im ω → +∞, which dictates closing the integration contour in the upper half of the ω plane, 26 In Fig. 13. For causality to hold, there must be no singularities in the upper half-plane, in which case the integration contour is constricted to a point, yielding . All singularities of must then be present in the lower half of the ω plane, where the contour is closed for t > 0. The presence of singularities is necessary, since a function without any singularities on a Riemann sphere is a constant.
Let us illustrate the above general considerations by analyzing the analytical structure of the retarded propagator of a uniform diffusion equation. Eq. (1.5) with a constant D(r) = D0 takes the form
| (A6) |
where we selected r0 = 0 due to translation invariance. The above equation in the Fourier domain becomes algebraic, as the differential operators ∂t → –iω and ∂r → iq become diagonal:
with the solution of a Lorentzian form
| (A7) |
This solution preserves causality, since its only singularity, at ω = –iD0q2, resides in the lower half-plane of ω. For t > 0, closing the integration contour in the lower half of the complex plane and using the residue theorem gives the Gaussian propagator in the qt representation, Eq. (1.8).
The above consideration shows that causality is tightly related to the integration in the time domain. We now inspect this relation closely, first without explicit reference to diffusion propagator, and then applying it to Eqs. (2.12) and (2.13). While the differentiation in the time domain of any function f(t) corresponds to the multiplication with –iω in the Fourier domain, , the inverse of the differential operator — i.e., the factor 1/(–iω) — corresponds to an indefinite integration (the antiderivative) in the time domain. However, infinitesimal shifts of the pole at ω = 0 result in different integration limits of definite time integrals. Considering both possible shift directions, the same integration technique as above gives the Fourier transformation:
| (A8) |
where θ(t) is the unit step function, and ε → +0. For an arbitrary function f(ω), which is integrable on the real axis of ω, the product f(ω)=(–iω±ε) is Fourier-transformed according to the convolution theorem,
| (A9) |
| (A10) |
Note that differentiating both Eqs. (A9) and (A10) with respect to t yields back f(t). Eqs. (A9) and (A10) show that while the addition of ε is unimportant for the Fourier transform of derivatives, it is crucial for inverting differential operators. Shifting the pole of f(ω)/(–iω) downwards from the real axis results in the causal integration (A9), for which the resulted integral up to any time moment t depends on the integrand in the past, t′ < t. The opposite shift results in the dependence on the future, t′ < t. (The results differ by , and coincide if f|ω=0 = 0, when f (ω)/ω is not singular.) Obviously, the first choice is adequate for the majority of solutions to equations describing the time evolution of physical quantities such as Eq. (1.5), or Eqs. (2.12) and (2.13). The notation ε with ε → +0 is often abbreviated to simply +0 as it is done in Eqs. (2.12) and (2.13).
Appendix B: OG with a finite number of pulses
Consider the OG gradient wave form g(t) = g0cos(ω0t − ϕ) with arbitrary initial phase ϕ and N oscillations, such that the total gradient duration T = N · 2π/ω0. The corresponding
| (B1) |
results in qω = g(ω)/(−iω), such that the wave form acts as the following “filter” for D(ω) in Eq. (2.9):
| (B2) |
As qω and Eq. (B2) are not singular when ω → 0 and ω → ±ω0, we do not need to specify how the zeroes of denominators in Eq. (B2) are shifted. Hence, one can directly substitute Eq. (B2) into Eq. (2.9) and integrate with any along the real axis.
However, to reveal the analytical structure, we find it useful to shift the frequency poles inside the square brackets by an infinitesimal positive imaginary part below the real axis, ω → ω + i0 in all the denominators, cf. Appendix A. As is also analytic in the upper half-plane of the complex ω, Appendix A, the whole integrand in Eq. (2.9) remains analytic there. Hence, in the prefactor 1 − cos ωT, the terms 1 and can be dropped for T > 0, as they identically vanish when closing the contour in the upper half plane — we now see that their role was merely to maintain the T → −T symmetry of Eq. (2.9) with q−ωqω from Eq. (B2), which is forgone by this procedure. Hence, , yielding the causal expression
| (B3) |
which starts to mimic the functional form of Eq. (2.13) — and that’s the goal! Dropping 1 and made the integrand in Eq. (B3) singular; however, the prescription how to go around its poles regularizes the result, which we obtain by a transformation into a sum of simple fractions. This yields the general relation between the intrinsic and OG with N = ω0T/2π pulses:
| (B4) |
We can now see that the singularities in Eq. (B4) occur separately at ω = ±ω0, and at ω = 0 for finite ϕ (when the gradient is not a pure cos wave form). Hence, we expect the response of on these two frequencies. This response has the contributions of three distinct physical origins. The first two terms (in the braces) in Eq. (B4) yield the “pure OG” effect, that of the cos wave form with ϕ = 0 in the limit N → ∞. The second term describes the ω = 0 singularity due to the finite time-average component in q(t), sin ϕ present for ϕ ≠ 0, which is similar to the PG measurement. Not surprisingly, it yields the bPG D(t) ∝ D(T) sin2ϕ contribution via the exact relation (2.13), i.e., the narrow-pulse D(t) with the diffusion time t = T weighted by the PG b-value contribution , which vanishes for the cos wave form (cf. Eq. (7) in ref. [131]). Finally, the last term, representing a finite OG-linewidth effect, is small as 1/N, as we will now show.
While the remaining calculations can be done using the correspondence of in the limit T → ∞ with the delta-function, we proceed via a more transparent transformation to the time domain. We use the relations
valid for any retarded response functions and related by the Fourier transformation (derived based on the property that a convolution in ω is a product in t, similar to how Eq. (A9) was derived). We can see that causality means that only t < T are integrated over, as expected. As a result, we transform Eq. (B4) into
| (B5) |
where the b-value is calculated [131, 303] assuming constant , such that [27]. We can see that the total b = b|ϕ=0 + bPG is a sum of the pure OG and the pure PG contributions, since sin ω0t is orthogonal to a constant.
In the N ≫ 1 limit of a clear separation of time scales 2π/ω0 ≪ T, we can extend the upper integration limit T → ∞; using in the first term of Eq. (B5), we can separate the main contribution and the ~ 1/N correction:
| (B6) |
Here, the term ∝ D(T ) is exact due to Eq. (2.13), while setting ω = ω0 in in the other two terms is precise up to ~ ω0/N. We can see that the first term in the square brackets of Eq. (B6) is a leading effect (it is not small when N → ∞); it gives the balance of the ω = ω0 and ω = 0 contributions with the “filter” weights defined by the phase ϕ in agreement with the general property of the second-order cumulant term, discussed after Eq. (2.9). The second term, , is suppressed as ~1/N. In the limit N → ∞, the imaginary part of does not contribute to the OG measurement [27].
There exists a case in which the 1/N term is comparable with the first one, namely, of a closed pore with a characteristic size ~a in the limit of low frequencies (long-times), ω0a2/D0 ≪ 1. In this limit, D(T) ~a2/T happens to be parametrically as small as the second term. More precisely, the second term~1/2πN of Eq. (B6) exactly cancels the 2D(T) sin2 ϕ contribution to the first term, and the net result is determined by . This was first noticed by Sukstanskii [303] via the time-domain calculation for a one-dimensional impermeable box. Such behavior, however, is completely general. Indeed, for a pore of arbitrary shape, the dispersive diffusivity is a sum over the eigenmodes of the Laplace operator,
| (B7) |
with Ck and βk determined by the pore geometry [17, 103]; to the order , , D(T) = µa2/T, where the dimensionless parameter , and so both the D(T) and the contributions to Eq. (B6) cancel each other exactly. The remaining quantity , the leading effect, vanishes very fast (quadratically) in the low-frequency limit [17, 23, 103, 138, 177, 304–306] (this scaling was first observed by Stepisnik et al. [306] in porous media). For the relevant case of a cylinder of radius a, and the sum [21]. The estimate (B7) tells that OG (with any phase ϕ) is less efficient than PGSE in creating adequate diffusion weighting if one wants to measure sizes of small fully confining compartments, cf. text after Eq. (2.38).
Appendix C: Probing the S/V limit with finite-N OG
Let us now use the general finite-N relation (B4) for the S/V model (2.16); this setup is practically relevant to study cell density in brain tumors [144, 145]. The intrinsic in this limit can be obtained performing Fourier transform of the outcome of Eq. (2.14) [131]:
| (C1) |
with the regularization θ(t)δ(t) = limη→+0 θ(t)δ(t − η) (Appendix D of ref. [27]). Substituting Eq. (C1) into Eq. (B5), using
| (C2) |
where the Fresnel integrals are defined in a standard way,
| (C3) |
we obtain
where b is given in Eq. (B6), and the finite-N correction factor
Here, the 1/ω2 term in Eq. (B4) yields the exact D(T ) according to Eq. (2.13) as discussed in Appendix B. In the “ideal OG” limit N → ∞, using , we obtain c(ϕ, N ) 1 for any ϕ, such that Eq. (C4) yields Eq. (7) of ref. [131]. When, additionally, ϕ = 0, we obtain , cf. Eq. (2.17) in the main text.
We emphasize that performing the calculation in the frequency domain allows us to separate the time scales and identify the contributions to Eq. (C4) of two distinct physical origins. The D(T ) term is completely general — i.e., the applicability of Eqs. (C4)–(C5) only requires the period of the oscillation to be short enough so that the model (C1) applies; the whole gradient train T can be long and (practically, always) falls out of the short-time S/V limit. Often times, at that point one can set D(T) ≈ D∞. As discussed in Appendix B, the D(T) term appears because at finite ϕ, the OG wave form can be thought of as a pure cos wave form and a PG with diffusion time t = T [131]. Hence, Eq. (C4) allows one to probe the S/V ratio by keeping the period short, yet the total gradient train as long as needed, to accumulate the diffusion weighting b ∝ N, Eq. (B6).
If, additionally, the whole OG train T falls into the short-time limit, under a more stringent condition , then D(T ) is given by Eq. (2.16). In this limit, Eq. (C4) yields
| (C6) |
where the re-defined correction factor corresponds to Eq. (14) of ref. [303], where the problem of finite-N correction in the S/V limit was first considered. It was noted there, that nominally diverges for N → ∞ as . It is clear that this divergence occurs due to the scaling from D(T), and it eventually gets cut off when N becomes so large than D(T) falls out of the validity regime of Eq. (2.16). Hence, this spurious divergence is a result of defining in ref. [303] by forcing Eq. (C6) to mimic the form of Eq. (2.16), instead of separating the physics at the two time scales, 2π/ω0 and T. The separation of scales identified in Eq. (C4) based on the general expression (B4) extends the validity of OG in the S/V limit far beyond the claim of ref. [303], “the high-frequency regime can be achieved only when the total diffusion time is smaller than the characteristic diffusion time” (implying ), onto the practically relevant domain , for any ϕ. Note that for pure cos gradient, , due to the absence of the ω = 0 singularity in Eq. (B4), and Eq. (C6) agrees with Eqs. (C4) and (C5).
Footnotes
An experienced reader can recall the possibility to apply strong gradients q ∼ 1/rsmall to detect the small disks. This, however, practically requires sensitivity to short t ∼ 1/(Dsmall q2), cf. Sec. 1.6 below.
We also note that the renormalization group flow can have fixed points, i.e., microscopic parameter sets for which the effective parameters do not change with the increasing coarse-graining scale. Approaching the asymptotically normal diffusion with a finite D∞ is a Gaussian fixed point, which is what happens for most structural arrangements; one can say that diffusion is most tissues is a continuous family of Gaussian fixed points (for each realization of microscopic tissue architecture). An example of a non- Gaussian fixed point is the so-called anomalous diffusion, cf. Sec. 1.9.
The focus on narrow pulses helps one to gain physical intuition. Finite pulse-width δ for relatively weak gradients has an effect of a low-pass filter, filtering out the frequencies , acting on the narrow-pulse solution [17–19], cf. models of restricted [20–22] and hindered [23–26] diffusion relevant for the brain. For strong gradients, long pulses lead to the localization regime, Sec. 1.10. Arbitrarily-shaped pulses in the Gaussian phase approximation will be considered in Sec. 2.2.
cu-tie imaging, or qtI (noun): A noninvasive medical imaging technique for spatio-temporal mapping of the diffusion propagator in soft tissues to quantify tissue structure below the nominal MRI resolution. Of course, it is nothing but the familiar q-space imaging [17, 28, 29] sampled at various t, but don’t we all need a new acronym once in a while?
In the language of emergent phenomena, Sec. 1.2, this would be analogous, e.g., to using neutron scattering (with large wave vectors ) to resolve atomic structure of the fluid, for which the coarse-grained (large t and r ≫ 1/q) continuous description is classical hydrodynamics.
Since Gt,r is written in terms of the relative displacements r = rt – r0, we re-denote δxi(t) → xi(t) in Eq. (1.12) to simplify the notation, and drop the dependence on the initial position in the view of the translational invariance property (1.7).
DTI, contrary to a widespread misconception, does not assume Gaussian diffusion, as it merely provides the lowest-order cumulant term Dij, and tells nothing about the higher-order terms in the series (1.10). DTI applicability is thus dictated by the kurtosis term W to have negligible bias on the estimated Dij, and the employed b-range is practically set by balancing the bias when b is too large and precision loss when b is too small.
We are not reviewing the MRI literature on anomalous diffusion, since our goal here is to discuss models which are relevant to observable diffusion effects in neuronal tissue. A curious reader can find occasional claims of anomalous diffusion, or dMRI signal as a stretched-exponential. We are not aware of examples of a constructive derivation of the non-Gaussian fixed point [3, 4] starting from the stationary mesoscopic disorder with properties relevant to the brain. Hence, these claims can merely be viewed as postulates “proven” by fitting in a finite range of t or q. If the model’s functional form contradicts the physics of the signal, the estimated parameters will depend on the range of t and q, thereby characterizing the particular measurement scheme, rather than the tissue [70].
This argument can also be extended onto the regime of slow exchange between compartments, since Eq. (2.1) turns out to be valid in that regime in the long-t limit, following the coarse-graining argument [39] for generalizing the Kärger model [113] to media with mesoscopic disorder. If the overall D = const (i.e., the full coarse-graining is achieved in each of the compartments), and the overall kurtosis K(t) still depends on t, this t-dependence arises due to exchange [39, 61].
The real part, , corresponds to the quantity called “D(ω)” in the NMR literature [130].
For anisotropic media, and for arbitrary q-space trajectories [132, 133], the integrands in Eqs. (2.7)–(2.9) are , vi(t)vj(0) and respectively (with the sums over repeated indices)
The addition of i0 in the denominators preserves causality (retarded response character) of integrated quantities, see Appendix A for details.
The often quoted relation t = Δ –δ/3 for the diffusion time of a finite-width PGSE is a myth for the same reasons. One can only say that the measurement gives D(t) with t ≈ Δ (with the accuracy of this approximation controlled by δ). More rigorously, the effect of finite pulse width δ creates a low-pass filter [17, 19] on , whose effect is again modeldependent, see, e.g., Eq. (24) in ref. [23], as well as refs. [24–26, 141], for the examples of this filter effect on the models of relevant for brain.
The dispersive terms reads iω ln(–iω) for the special case of ϑ = 1, hence will depend on ω as |ω|, cf. ref. [23].
This value is based on the observation [167] that axoplasmic diffusion coefficient in squid giant axon is 20% below the water diffusion coefficient at the same temperature, and is consistent with the recent estimate of Da ≈ 1.9 – 2:4 μm2/ms along axons in human WM at t = 50 ms obtained by suppressing extra-axonal compartment using either high b [168] or planar diffusion encoding [141], which sets a lower bound for D0. Another large axon study in excised lamprey spinal cord [169] reported a similar deviation of about 25% for the longitudinal diffusion coefficient from the free water diffusion coefficient. A somewhat larger value was reported in excised pig spinal cord [170]. Alternatively, using NAA as an intracellular reporter molecule, the ratio for the in vivo measured parallel diffusion coefficient in the corpus callosum relative to its diffusion coefficient in dilute aqeous solutions, ranges from 0.4 up to 0.46 [36], corresponding to estimates of water Da ~ 1.2 – 1.8 μm2/ms.
Here we consider brain; axons are about factor of 5 thicker in the spinal cord, and the ADM prospects are much better there [124, 171–174], due to the r4 scaling in Eq. (2.37); see, however, the need for beyond-GPA corrections discussed below.
Mathematically speaking, a power-law approach, being scale-invariant, means that the t → ∞ regime is never fully achieved — there is no time scale that tells us where we can neglect the residual non-Gaussian effects in each compartment. However, practically, their detection limit is set by a finite SNR.
See footnote 15 in Section 2
cf. footnote 17; effectively, we neglect D(t) – D∞ within each fascicle.
This picture might be not as definite in GM, where the dendrites are more intertwined, and the concept of the overall ENS tensor may be better justified [37, 38]. But then, much less is known about diffusion in GM overall, and the precise knowledge of in vivo neurite residence times is still lacking. Therefore, here we mostly discuss SM in the context of WM, leaving GM modeling as one of the unresolved problems in Sec. 5.2.
The name is suggested by the tongue-in-cheek analogies with the Standard Model in particle physics. In both communities, SM represents the consensus knowledge about the subject, satisfactorily describes (almost) everything, has been out there for a while, and yet one really hopes that there is exciting physics beyond it — which is far more difficult to access. Our community has a doubtless advantage in that investigations beyond SM are much cheaper (cf. Section 2) than building particle accelerators.
The idea to operate with a single “energy” L2 norm per each “frequency” band l of SH has been previously applied, e.g., to the problem of shape matching in computer graphics [246] and recently for dMRI data harmonization [247].
This intuition underlies theory of quantum-mechanical excitations of nonspherical nuclei [254], where analogs of our rotational invariants are the corresponding irreducible tensor operators underpinning the Wigner-Eckart theorem.
Set by the corresponding interval Δn between the fronts of the gradient pulses, Fig. 10. For finite pulse width δn, see footnote 13 in Section 2.
In Eq. (A5), the sign in the exponential e–iωt is chosen in the tradition of physics; the opposite sign would invoke the interchanging of the upper and lower halves of the ω plane.
References
- [1].Georgi Howard, “Effective field theory,” Annual review of nuclear and particle science 43, 209–252 (1993). [Google Scholar]
- [2].Anderson Philip W, “More is different,” Science 177, 393–396 (1972). [DOI] [PubMed] [Google Scholar]
- [3].Wilson Kenneth G, “The renormalization group and critical phenomena,” Reviews of Modern Physics 55, 583 (1983). [Google Scholar]
- [4].Cardy John, Scaling and renormalization in statistical physics, Vol. 5 (Cambridge university press, 1996). [Google Scholar]
- [5].Bloembergen N, Purcell EM, and Pound RV, “Relaxation Effects in Nuclear Magnetic Resonance Absorption,” Physical Review 73, 679–712 (1948). [Google Scholar]
- [6].Abragam A, Principles of Nuclear Magnetism (Oxford University Press, New York, 1961). [Google Scholar]
- [7].Imry Yoseph, Introduction to mesoscopic physics (Oxford University Press, New York, 1997). [Google Scholar]
- [8].Mark Henkelman R., Huang Xuemei, Xiang Qing-San, Stanisz GJ, Swanson Scott D., and Bronskill Michael J., “Quantitative interpretation of magnetization transfer,” Magnetic Resonance in Medicine 29, 759–766 (1993). [DOI] [PubMed] [Google Scholar]
- [9].Henkelman RM, Stanisz GJ, and Graham SJ, “Magnetization transfer in MRI: a review,” NMR in Biomedicine 14, 57–64 (2001). [DOI] [PubMed] [Google Scholar]
- [10].Migdal AA, “Phase transitions in gauge and spin-lattice systems,” Soviet Physics JETP 42, 743–746 (1976). [Google Scholar]
- [11].Kadanoff Leo P, “Notes on Migdal’s recursion formulas,” Annals of Physics 100, 359–394 (1976). [Google Scholar]
- [12].Kiselev Valerij G. and Novikov Dmitry S., “Transverse NMR relaxation in biological tissues,” NeuroImage (2018), 10.1016/j.neuroimage.2018.06.002. [DOI] [PMC free article] [PubMed]
- [13].Zhong Jianhui, Kennan Richard P., and Gore John C., “Effects of susceptibility variations on NMR measurements of diffusion,” Journal of Magnetic Resonance 95, 267–280 (1991). [Google Scholar]
- [14].Kiselev VG, “Effect of magnetic field gradients induced by microvasculature on NMR measurements of molecular self-diffusion in biological tissues,” Journal of Magnetic Resonance 170, 228–235 (2004). [DOI] [PubMed] [Google Scholar]
- [15].Andre´ Pampel, Jochimsen Thies H., and Mo¨ller Harald E., “BOLD background gradient contributions in diffusion-weighted fMRI - Comparison of spin-echo and twice-refocused spin-echo sequences,” NMR in Biomedicine 23, 610–618 (2010). [DOI] [PubMed] [Google Scholar]
- [16].Novikov Dmitry S., Reisert Marco, and Kiselev Valerij G., “Effects of mesoscopic susceptibility and transverse relaxation on diffusion NMR,” Journal of Magnetic Resonance (2018). [DOI] [PubMed]
- [17].Callaghan Paul T., Principles of nuclear magnetic resonance microscopy (Clarendon Press, 1993). [Google Scholar]
- [18].Kiselev Valerij G., “The Cumulant Expansion: An Overarching Mathematical Framework For Understanding Diffusion NMR,” in Diffusion MRI: Theory, methods and applications (2010).
- [19].Kiselev Valerij G, “Fundamentals of diffusion MRI physics,” NMR in Biomedicine 30, e3602 (2017). [DOI] [PubMed] [Google Scholar]
- [20].Murday JS and Cotts RM, “Self-Diffusion Coefficient of Liquid Lithium,” The Journal of Chemical Physics 48, 4938 (1968). [Google Scholar]
- [21].Neuman CH, “Spin echo of spins diffusing in a bounded medium,” Journal of Chemical Physics 60, 4508–4511 (1974). [Google Scholar]
- [22].van Gelderen P, DesPres D, van Zijl PC, and Moonen CT, “Evaluation of restricted diffusion in cylinders. Phosphocreatine in rabbit leg muscle” (1994). [DOI] [PubMed]
- [23].Burcaw Lauren M, Fieremans Els, and Novikov Dmitry S., “Mesoscopic structure of neuronal tracts from time-dependent diffusion,” NeuroImage 114, 18–37 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Lee Hong-Hsi, Burcaw Lauren M, Veraart Jelle, Fieremans Els, and Novikov Dmitry S., “Low-Pass Filter Effect of Finite Gradient Duration on Time-Dependent Diffusion in the Human Brain,” Proceedings of the International Society of Magnetic Resonance in Medicine 23, p. 2777 (2015). [Google Scholar]
- [25].Lee Hong-Hsi, Lemberskiy Gregory, Fieremans Els, and Novikov Dmitry S., “Estimation of Fiber Packing Correlation Length by Varying Diffusion Gradient Pulse Duration,” Proceedings of the International Society of Magnetic Resonance in Medicine 24, p. 2021 (2016). [Google Scholar]
- [26].Lee Hong-Hsi, Fieremans Els, and Novikov Dmitry S., “What dominates the time dependence of diffusion transverse to axons: Intra- or extra-axonal water?” NeuroImage (2017), 10.1016/j.neuroimage.2017.12.038. [DOI] [PMC free article] [PubMed]
- [27].Novikov Dmitry S. and Kiselev Valerij G, “Effective medium theory of a diffusion-weighted signal,” NMR Biomed 23, 682–697 (2010). [DOI] [PubMed] [Google Scholar]
- [28].Callaghan PT, Eccles CD, and Xia Y, “NMR microscopy of dynamic displacements: k-space and q-space imaging,” Journal of Physics E: Scientific Instruments 21, 820–822 (1988). [Google Scholar]
- [29].Cory DG and Garroway AN, “Measurement of translational displacement probabilities by NMR: an indicator of compart-mentation,” Magn Reson Med 14, 435–444 (1990). [DOI] [PubMed] [Google Scholar]
- [30].Bihan D Le, Breton E, Lallemand D, Grenier P, Cabanis E, and Laval-Jeantet M, “MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders.” Radiology 161, 401–7 (1986). [DOI] [PubMed] [Google Scholar]
- [31].Basser PJ, Mattiello J, and LeBihan D, “Estimation of the Effective Self-Diffusion Tensor from the NMR Spin-Echo,” Journal of Magnetic Resonance Series B 103, 247–254 (1994). [DOI] [PubMed] [Google Scholar]
- [32].Mitra Partha P., Sen Pabitra N., and Schwartz Lawrence M., “Short-time behavior of the diffusion coefficient as a geometrical probe of porous media,” Physical Review B 47, 8565–8574 (1993). [DOI] [PubMed] [Google Scholar]
- [33].Novikov Dmitry S, Jensen Jens H, Helpern Joseph A, and Fieremans Els, “Revealing mesoscopic structural universality with diffusion.” Proceedings of the National Academy of Sciences of the United States of America 111, 5088–93 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Fieremans Els, Burcaw Lauren M, Lee Hong-Hsi, Lemberskiy Gregory, Veraart Jelle, and Novikov Dmitry S., “In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter,” NeuroImage 129, 414–427 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Sukstanskii AL, Yablonskiy DA, and Ackerman JJH, “Effects of permeable boundaries on the diffusion-attenuated MR signal: insights from a one-dimensional model,” Journal of Magnetic Resonance 170, 56–66 (2004). [DOI] [PubMed] [Google Scholar]
- [36].Kroenke Christopher D, Ackerman Joseph J H, and Yablonskiy Dmitriy A, “On the nature of the NAA diffusion attenuated MR signal in the central nervous system,” Magnetic Resonance in Medicine 52, 1052–1059 (2004). [DOI] [PubMed] [Google Scholar]
- [37].Jespersen Sune N, Kroenke Christopher D, Ostergaard Leif, Ackerman Joseph J H, and Yablonskiy Dmitriy A, “Modeling dendrite density from magnetic resonance diffusion measurements,” Neuroimage 34, 1473–1486 (2007). [DOI] [PubMed] [Google Scholar]
- [38].Jespersen Sune N, Bjarkam Carsten R, Nyengaard Jens R, Chakravarty M Mallar, Hansen Brian, Vosegaard Thomas, Ostergaard Leif, Yablonskiy Dmitriy, Nielsen Niels Chr., and Vestergaard-Poulsen Peter, “Neurite density from magnetic resonance diffusion measurements at ultrahigh field: Comparison with light microscopy and electron microscopy,” Neuroimage 49, 205–216 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Fieremans Els, Novikov Dmitry S., Jensen Jens H, and Helpern Joseph A, “Monte Carlo study of a two-compartment exchange model of diffusion,” NMR in Biomedicine 23, 711–724 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Fieremans Els, Jensen Jens H, and Helpern Joseph A, “White matter characterization with diffusional kurtosis imaging,” Neuroimage 58, 177–188 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Sotiropoulos Stamatios N, Behrens Timothy E J, and Jbabdi Saad, “Ball and rackets: inferring fiber fanning from diffusion-weighted MRI,” NeuroImage 60, 1412–1425 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Zhang Hui, Schneider Torben, Wheeler-Kingshott Claudia A, and Alexander Daniel C, “NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain,” Neuroimage 61, 1000–1016 (2012). [DOI] [PubMed] [Google Scholar]
- [43].Reisert Marco, Kiselev Valerij G, Dihtal Bibek, Kellner Elias, and Novikov Dmitry S., “MesoFT: unifying diffusion modelling and fiber tracking,” in Medical Image Computing and Computer-Assisted Intervention–MICCAI 2014 (Springer, 2014) pp. 201–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Jelescu Ileana O, Veraart Jelle, Fieremans Els, and Novikov Dmitry S., “Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue,” NMR in Biomedicine 29, 33–47 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Reisert Marco, Kellner Elias, Dhital Bibek, Hennig Jurgen, and Kiselev Valerij G., “Disentangling micro from mesostructure by diffusion MRI: A Bayesian approach,” NeuroImage 147, 964–975 (2017). [DOI] [PubMed] [Google Scholar]
- [46].Novikov Dmitry S., Jelescu Ileana O, and Fieremans Els, “From diffusion signal moments to neurite diffusivities, volume fraction and orientation distribution: An exact solution,” Proceedings of the International Society of Magnetic Resonance in Medicine 23, p. 469 (2015). [Google Scholar]
- [47].Novikov Dmitry S., Veraart Jelle, Jelescu Ileana O., and Fieremans Els, “Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI,” NeuroImage 174, 518–538 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Veraart Jelle, Novikov Dmitry S., and Fieremans Els, “TE dependent Diffusion Imaging (TEdDI) distinguishes between compartmental T2 relaxation times,” NeuroImage (2017), 10.1016/j.neuroimage.2017.09.030. [DOI] [PMC free article] [PubMed]
- [49].Tanner JE, “Transient diffusion in a system partitioned by permeable barriers. Application to NMR measurements with a pulsed field gradient,” The Journal of Chemical Physics 69, 1748–1754 (1978). [Google Scholar]
- [50].Powles JG, Mallett MJD, Rickayzen G, and Evans W. a. B., “Exact Analytic Solutions for Diffusion Impeded by an Infinite Array of Partially Permeable Barriers,” Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 436, 391–403 (1992). [Google Scholar]
- [51].Novikov Dmitry S., Fieremans Els, Jensen Jens H, and Helpern Joseph A, “Random walks with barriers,” Nature Physics 7, 508–514 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Sigmund Eric E., Novikov Dmitry S., Sui Dabang, Ukpebor Obehi, Baete Steven, Babb James S., Liu Kecheng, Feiweier Thorsten, Kwon Jane, McGorty KellyAnne, Bencardino Jenny, and Fieremans Els, “Time-dependent diffusion in skeletal muscle with the random permeable barrier model (RPBM): application to normal controls and chronic exertional compartment syndrome patients,” NMR in Biomedicine 27, 519–528 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Fieremans Els, Lemberskiy Gregory, Veraart Jelle, Sigmund Eric E., Gyftopoulos Soterios, and Novikov Dmitry S., “In vivo measurement of membrane permeability and myofiber size in human muscle using time-dependent diffusion tensor imaging and the random permeable barrier model,” NMR in Biomedicine 30, e3612 (2017). [DOI] [PubMed] [Google Scholar]
- [54].Callaghan PT, Jolley KW, and Lelievre J, “Diffusion of water in the endosperm tissue of wheat grains as studied by pulsed field gradient nuclear magnetic resonance.” Biophysical journal 28, 133–41 (1979). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Yablonskiy Dmitriy A, Sukstanskii Alexander L, Leawoods Jason C, Gierada David S, Larry Bretthorst G, Lefrak Stephen S, Cooper Joel D, and Conradi Mark S, “Quantitative in vivo assessment of lung microstructure at the alveolar level with hyperpolarized 3He diffusion MRI,” Proceedings of the National Academy of Sciences 99, 3111–3116 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Stanisz GJ, Szafer A, Wright GA, and Henkelman RM, “An Analyitical Model of Restricted Diffusion in Bovine Optic Nerve,” Magnetic Resonance in Medicine 37, 103–111 (1997). [DOI] [PubMed] [Google Scholar]
- [57].Assaf Y, Freidlin RZ, Rohde GK, and Basser PJ, “New modeling and experimental framework to characterize hindered and restricted water diffusion in brain white matter,” Magnetic Resonance In Medicine 52, 965–978 (2004). [DOI] [PubMed] [Google Scholar]
- [58].Assaf Yaniv, Blumenfeld-Katzir Tamar, Yovel Yossi, and Basser Peter J., “Axcaliber: A method for measuring axon diameter distribution from diffusion MRI,” Magnetic Resonance in Medicine 59, 1347–1354 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Alexander DC, Hubbard PL, Hall MG, Moore EA, Ptito M, Parker GJM, and Dyrby TB, “Orientationally invariant indices of axon diameter and density from diffusion MRI,” Neuroimage 52, 1374–1389 (2010). [DOI] [PubMed] [Google Scholar]
- [60].Bihan D Le, Moonen CT, van Zijl PC, Pekar J, and DesPres D, “Measuring random microscopic motion of water in tissues with MR imaging: a cat brain study,” J Comput Assist Tomogr 15, 19–25 (1991). [DOI] [PubMed] [Google Scholar]
- [61].Jensen Jens H, Helpern Joseph A, Ramani Anita, Lu Hanzhang, and Kaczynski Kyle, “Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging,” Magn Reson Med 53, 1432–1440 (2005). [DOI] [PubMed] [Google Scholar]
- [62].Novikov Dmitry S. and Kiselev VG, “Transverse {NMR} relaxation in magnetically heterogeneous media,” J Magn Reson 195, 33–39 (2008). [DOI] [PubMed] [Google Scholar]
- [63].Özarslan Evren, Guan Koay Cheng, Shepherd Timothy M, Komlosh Michal E, \.Irfano\u glu Okan M, Pierpaoli Carlo, and Basser Peter J, “Mean apparent propagator (MAP) MRI: a novel diffusion imaging method for mapping tissue microstructure,” Neuroimage 78, 16–32 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Yablonskiy Dmitriy A, Bretthorst G Larry, and Ackerman Joseph J H, “Statistical model for diffusion attenuated MR signal,” Magn Reson Med 50, 664–669 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Wang Yong, Wang Qing, Haldar Justin P, Yeh Fang-Cheng, Xie Mingqiang, Sun Peng, Tu Tsang-Wei, Trinkaus Kathryn, Klein Robyn S, Cross Anne H, and Others, “Quantification of increased cellularity during inflammatory demyelination,” Brain 134, 3590–3601 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].White Nathan S, Leergaard Trygve B, D’Arceuil Helen, Bjaalie Jan G, and Dale Anders M, “Probing tissue microstructure with restriction spectrum imaging: histological and theoretical validation,” Human brain mapping 34, 327–346 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Scherrer Benoit, Schwartzman Armin, Taquet Maxime, Sahin Mustafa, Prabhu Sanjay P, and Warfield Simon K, “Characterizing brain tissue by assessment of the distribution of anisotropic microstructural environments in diffusion-compartment imaging (DIAMOND),” Magn Reson Med 76, 963–977 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Mitra Partha P., Sen Pabitra N., Schwartz Lawrence M., and Doussal Pierre Le, “Diffusion propagator as a probe of the structure of porous media,” Physical Review Letters 68, 3555–3558 (1992). [DOI] [PubMed] [Google Scholar]
- [69].Callaghan Paul T., Coy A, MacGowan D, Packer KJ, and Zelaya FO, “Diffraction-like effects in NMR diffusion studies of fluids in porous solids,” (1991).
- [70].Novikov Dmitry S., Kiselev Valerij G., and Jespersen Sune N., “On modeling,” Magnetic Resonance in Medicine 79, 3172–3193 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Jensen Jens H, Helpern Joseph A, Ramani Anita, Lu Hanzhang, and Kaczynski Kyle, “Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging,” Magn Reson Med 53, 1432–1440 (2005). [DOI] [PubMed] [Google Scholar]
- [72].Fisher RA and Wishart J, “The derivation of the pattern formulae of two-way partitions from those of simpler patterns,” Proc. London Math. Soc (1) s2–33, 195–208 (1932). [Google Scholar]
- [73].van Kampen NG, Stochastic Processes in Physics and Chemistry, 1st ed. (Elsevier, Oxford, 1981). [Google Scholar]
- [74].Frøhlich AF, Ostergaard L, and Kiselev VG, “Effect of Impermeable Boundaries on Diffusion-Attenuated {MR} Signal,” J. Magn. Reson 179, 223–233 (2006). [DOI] [PubMed] [Google Scholar]
- [75].Kiselev Valerij G and Il’yasov Kamil A, “Is the “biexponential diffusion” biexponential?” Magn Reson Med 57, 464–469 (2007). [DOI] [PubMed] [Google Scholar]
- [76].Jensen Jens H and Helpern Joseph A, “MRI quantification of non-Gaussian water diffusion by kurtosis analysis,” NMR Biomed 23, 698–710 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Veraart Jelle, Rajan Jeny, Peeters Ronald R, Leemans Alexander, Sunaert Stefan, and Sijbers Jan, “Comprehensive framework for accurate diffusion MRI parameter estimation,” Magn Reson Med 70, 972–984 (2013). [DOI] [PubMed] [Google Scholar]
- [78].Thorne Kip S, “Multipole expansions of gravitational radiation,” Reviews of Modern Physics 52, 299–339 (1980). [Google Scholar]
- [79].Bouchaud J-P and Georges A, “Anomalous diffusion in disordered media - statistical mechanisms, models and physical applications,” Physics Reports - Review Section of Physics Letters 195, 127–293 (1990). [Google Scholar]
- [80].Lamantia AS and Rakic P, “Cytological And Quantitative Characteristics Of 4 Cerebral Commissures In The Rhesus-Monkey,” Journal of Comparative Neurology 291, 520–537 (1990). [DOI] [PubMed] [Google Scholar]
- [81].Aboitiz F, Scheibel AB, Fisher RS, and Zaidel E, “Fiber composition of the human corpus callosum,” Brain Research 598, 143–153 (1992). [DOI] [PubMed] [Google Scholar]
- [82].Tang Y, Nyengaard JR, Pakkenberg B, and Gundersen HJG, “Age-induced white matter changes in the human brain: a stereological investigation,” Neurobiol Aging 18, 609–615 (1997). [DOI] [PubMed] [Google Scholar]
- [83].Caminiti Roberto, Ghaziri Hassan, Galuske Ralf, Hof Patrick R, and Innocenti Giorgio M, “Evolution amplified processing with temporally dispersed slow neuronal connectivity in primates,” Proceedings of the National Academy of Sciences 106, 19551–19556 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [84].Liewald Daniel, Miller Robert, Logothetis Nikos, Joachim Wagner Hans, and Schüz Almut, “Distribution of axon diameters in cortical white matter: an electron-microscopic study on three human brains and a macaque,” Biological Cybernetics 108, 541–557 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85].Kravtsov VE, Lerner IV, and Yudson VI, “Random walks in media with constrained disorder,” Journal of Physics A: Mathematical and General 18, L703 (1985). [Google Scholar]
- [86].Sinai YG, “The limiting behavior of a one-dimensional random walk in a random medium,” Theory Probab. Appl 27, 256–268 (1982). [Google Scholar]
- [87].Fisher Daniel S, “Random walks in random environments,” Physical Review A 30, 960 (1984). [Google Scholar]
- [88].Aronovitz JA and Nelson David R, “Anomalous diffusion in steady fluid flow through a porous medium,” (1984).
- [89].Fisher Daniel S., Friedan Daniel, Qiu Zongan, Shenker Scott J., and Shenker Stephen H., “Random walks in two-dimensional random environments with constrained drift forces,” (1985). [DOI] [PubMed]
- [90].Tsai Yan-Chr and Shapir Yonathan, “On the scale-invariant distribution of the diffusion coefficient for classical particles diffusing in disordered media,” Journal of Physics A: Mathematical and General 26, 39 (1993). [Google Scholar]
- [91].Lerner Igor V., “Distributions of the diffusion coefficient for the quantum and classical diffusion in disordered media,” Nuclear Physics, Section A 560, 274–292 (1993), arXiv:9402028 [cond-mat]. [Google Scholar]
- [92].Shklovskii BI and Efros AL, Electronic properties of doped semiconductors (Springer, Heidelberg, 1984). [Google Scholar]
- [93].Havlin S, Schwartz M, Selinger RB, Bunde A, and Stanley HE, “Universality classes for diffusion in the presence of correlated spatial disorder,” Physical Review A 40, 1717–1719 (1989). [DOI] [PubMed] [Google Scholar]
- [94].Havlin S and Ben-Avraham D, “Diffusion in disordered media,” Advances In Physics 51, 187–292 (2002). [Google Scholar]
- [95].Scher Harvey and Montroll Elliott W, “Anomalous transittime dispersion in amorphous solids,” Physical Review B 12, 2455–2477 (1975). [Google Scholar]
- [96].Novikov Dmitry S., Drndic M, Levitov LS, Kastner MA, Jarosz MV, and Bawendi MG, “Levy statistics and anomalous transport in quantum-dot arrays,” Physical Review B - Condensed Matter and Materials Physics 72, 1–7 (2005). [Google Scholar]
- [97].Wang Siying, Querner Claudia, Dadosh Tali, Crouch Catherine H, Novikov Dmitry S., and Drndic Marija, “Collective fluorescence enhancement in nanoparticle clusters.” Nature Communications 2, 364 (2011). [DOI] [PubMed] [Google Scholar]
- [98].Rouse Prince E., “A Theory of the Linear Viscoelastic Properties of Dilute Solutions of Coiling Polymers,” The Journal of Chemical Physics 21, 1272–1280 (1953). [Google Scholar]
- [99].Hu Xiaohu, Hong Liang, Dean Smith Micholas, Neusius Thomas, Cheng Xiaolin, and Smith JeremyC., “The dynamics of single protein molecules is non-equilibrium and self-similar over thirteen decades in time,” Nature Physics 12, 171–174 (2016). [Google Scholar]
- [100].Wong IY, Gardel ML, Reichman DR, Weeks Eric R., Valentine MT, Bausch AR, and Weitz DA, “Anomalous Diffusion Probes Microstructure Dynamics of Entangled F-Actin Networks,” Physical Review Letters 92, 178101 (2004). [DOI] [PubMed] [Google Scholar]
- [101].Metzler Ralf, Jeon Jae-Hyung, Cherstvy Andrey G, and Barkai Eli, “Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking.” Physical chemistry chemical physics : PCCP 16, 24128–64 (2014). [DOI] [PubMed] [Google Scholar]
- [102].Mussel Matan, Inzelberg Lilah, and Nevo Uri, “Insignificance of active flow for neural diffusion weighted imaging: A negative result,” Magnetic Resonance in Medicine, DOI: 10.1002/mrm.26375 (2016). [DOI] [PubMed]
- [103].Grebenkov Denis S, “NMR survey of reflected Brownian motion,” Rev. Mod. Phys 79, 1077–1137 (2007). [Google Scholar]
- [104].Stoller SD, Happer W, and Dyson FJ, “Transverse spin relaxation in inhomogeneous magnetic fields,” (1991). [DOI] [PubMed]
- [105].de Swiet Thomas M. and Sen Pabitra N., “Decay of nuclear magnetization by bounded diffusion in a constant field gradient,” The Journal of Chemical Physics 100, 5597 (1994). [Google Scholar]
- [106].Hurlimann MD, Helmer KG, Deswiet TM, and Sen PN, “Spin Echoes in a Constant Gradient and in the Presence of Simple Restriction,” Journal of Magnetic Resonance, Series A 113, 260–264 (1995). [Google Scholar]
- [107].Grebenkov Denis S., “Exploring diffusion across permeable barriers at high gradients. II. Localization regime,” Journal of Magnetic Resonance 248, 164–176 (2014). [DOI] [PubMed] [Google Scholar]
- [108].Bernd Laun Frederik, Anselm Kuder Tristan, Semmler Wolfhard, and Stieltjes Bram, “Determination of the defining boundary in nuclear magnetic resonance diffusion experiments,” Physical Review Letters 107, 2–5 (2011). [DOI] [PubMed] [Google Scholar]
- [109].Anselm Kuder Tristan and Bernd Laun Frederik, “NMR-based diffusion pore imaging by double wave vector measurements,” Magnetic Resonance in Medicine 70, 836–841 (2013). [DOI] [PubMed] [Google Scholar]
- [110].Alexander Daniel C., Dyrby Tim B., Nilsson Markus, and Zhang Hui, “Imaging brain microstructure with diffusion MRI: practicality and applications,” NMR in Biomedicine (2018), 10.1002/NBM.3841. [DOI] [PubMed]
- [111].Jelescu Ileana O. and Budde Matthew D., “Design and Validation of Diffusion MRI Models of White Matter,” Frontiers in Physics 5 (2017), 10.3389/fphy.2017.00061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [112].Reynaud Olivier, “Time-Dependent Diffusion MRI in Cancer: Tissue Modeling and Applications,” Frontiers in Physics 5, 1–16 (2017). [Google Scholar]
- [113].Kärger Jörg, “NMR self-diffusion studies in heterogeneous systems,” Advances in Colloid and Interface Science 23, 129–148 (1985). [Google Scholar]
- [114].Beaulieu Christian and Allen Peter S, “An in vitro evaluation of the effects of local magnetic-susceptibility-induced gradients on anisotropic water diffusion in nerve,” Magnetic resonance in medicine 36, 39–44 (1996). [DOI] [PubMed] [Google Scholar]
- [115].Assaf Yaniv and Cohen Yoram, “Assignment of the water slow-diffusing component in the central nervous system using q-space diffusion MRS: Implications for fiber tract imaging,” Magnetic resonance in medicine 43, 191–199 (2000). [DOI] [PubMed] [Google Scholar]
- [116].Bar-Shir A, Avram L, Özarslan E, Basser PJ, and Cohen Y, “The effect of the diffusion time and pulse gradient duration ratio on the diffraction pattern and the structural information estimated from q-space diffusion MR: Experiments and simulations,” Journal of Magnetic Resonance 194, 230–236 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [117].Kunz Nicolas, Sizonenko Ste´phane V., Hüppi Petra S., Gruetter Rolf, and Van de Looij Yohan, “Investigation of field and diffusion time dependence of the diffusion-weighted signal at ultrahigh magnetic fields,” NMR in Biomedicine 26, 1251–1257 (2013). [DOI] [PubMed] [Google Scholar]
- [118].van Gelderen Peter, de Vleeschouwer Marloes H M, DesPres Daryl, Pekar James, van Zijl Peter, and Moonen Chrit T W, “Water diffusion and acute stroke,” Magnetic resonance in medicine 31, 154–163 (1994). [DOI] [PubMed] [Google Scholar]
- [119].Clark Chris A, Hedehus Maj, and Moseley Michael E, “Diffusion time dependence of the apparent diffusion tensor in healthy human brain and white matter disease,” Magnetic resonance in medicine 45, 1126–1129 (2001). [DOI] [PubMed] [Google Scholar]
- [120].Nilsson Markus, Jimmy Lätt Emil Nordh, Wirestam Ronnie, Strahlberg Freddy, and Brockstedt Sara, “On the effects of a varied diffusion time in vivo: is the diffusion in white matter restricted?” Magnetic resonance imaging 27, 176–187 (2009). [DOI] [PubMed] [Google Scholar]
- [121].Horsfield Mark A, Barker Gareth J, and McDonald W Ian, “Self-diffusion in CNS tissue by volume-selective proton NMR,” Magnetic resonance in medicine 31, 637–644 (1994). [DOI] [PubMed] [Google Scholar]
- [122].De Santis Silvia, Jones Derek K., and Roebroeck Alard, “Including diffusion time dependence in the extra-axonal space improves in vivo estimates of axonal diameter and density in human white matter,” NeuroImage 130, 91–103 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [123].Does MD, Parsons EC, and Gore JC, “Oscillating Gradient Measurements of Water Diffusion in Normal and Globally Ischemic Rat Brain,” Magnetic Resonance In Medicine 49, 206–215 (2003). [DOI] [PubMed] [Google Scholar]
- [124].Xu Junzhong, Li Hua, Harkins Kevin D., Jiang Xiaoyu, Xie Jingping, Kang Hakmook, Does Mark D., and Gore John C., “Mapping mean axon diameter and axonal volume fraction by MRI using temporal diffusion spectroscopy,” NeuroImage 103, 10–19 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [125].Pyatigorskaya Nadya, Bihan Denis, Reynaud Olivier, and Ciobanu Luisa, “Relationship between the diffusion time and the diffusion MRI signal observed at 17.2 tesla in the healthy rat brain cortex,” Magnetic resonance in medicine 72, 492–500 (2014). [DOI] [PubMed] [Google Scholar]
- [126].Wu Dan, Martin Lee J., Northington Frances J., and Zhang Jiangyang, “Oscillating gradient diffusion MRI reveals unique microstructural information in normal and hypoxiaischemia injured mouse brains,” Magnetic Resonance in Medicine 72, 1366–1374 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [127].Wu Dan and Zhang Jiangyang, “The Effect of Microcirculatory Flow on Oscillating Gradient Diffusion MRI and Diffusion Encoding with Dual-Frequency Orthogonal Gradients (DEFOG),” Magnetic Resonance in Medicine 77, 1583–1592 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [128].Baron Corey A and Beaulieu Christian, “Oscillating gradient spin-echo (OGSE) diffusion tensor imaging of the human brain,” Magnetic resonance in medicine 72, 726–736 (2014). [DOI] [PubMed] [Google Scholar]
- [129].Van Anh T., Holdsworth Samantha J., and Bammer Roland, “In vivo investigation of restricted diffusion in the human brain with optimized oscillating diffusion gradient encoding,” Magnetic Resonance in Medicine 71, 83–94 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [130].Stepivsnik J, “Analysis of NMR self-diffusion measurements by a density matrix calculation,” Physica B+C 104, 350–364 (1981). [Google Scholar]
- [131].Novikov Dmitry S. and Kiselev Valerij G., “Surface-to-volume ratio with oscillating gradients,” Journal of Magnetic Resonance 210, 141–145 (2011). [DOI] [PubMed] [Google Scholar]
- [132].Shemesh N, Jespersen SN, Alexander DC, Cohen Y, Drobnjak I, Dyrby TB, Finsterbusch J, Koch MA, Kuder T, Laun F, Lawrenz M, Lundell H, Mitra PP, Nilsson M, Ozarslan E, Topgaard D, and Westin CF, “Conventions and nomenclature for double diffusion encoding nmr and mri,” Magn Reson Med 75, 82–7 (2016). [DOI] [PubMed] [Google Scholar]
- [133].Topgaard Daniel, “Multidimensional diffusion mri,” J Magn Reson 275, 98–113 (2017). [DOI] [PubMed] [Google Scholar]
- [134].Landau LD and Lifshitz EM, Statistical Physics, Part I (Course of Theoretical Physics, Vol. 5) (Pergamon Press, Oxford, 1969). [Google Scholar]
- [135].Merboldt KD, Hanicke W, and Frahm J, “Self-diffusion NMR Imaging Using Stimulated Echoes,” Journal Magnetic Resonance 64, 479–486 (1985). [Google Scholar]
- [136].Gross B and Kosfeld R, “Anwendung der spin-echo-methode der messung der selbstdiffusion,” Messtechnik 77, 171—177 (1969). [Google Scholar]
- [137].Tanner JE, “Self diffusion of water in frog muscle,” Biophysical Journal 28, 107–116 (1979). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [138].Stepisnik J, “Time-dependent self-diffusion by NMR spinecho,” Physica B 183, 343–350 (1993). [Google Scholar]
- [139].Callaghan Paul T. and Stepisnik Janez, “Frequency-Domain Analysis of Spin Motion Using Modulated-Gradient NMR,” Journal of Magnetic Resonance, Series A 117, 118–122 (1995). [Google Scholar]
- [140].Latour LL, Svoboda K, Mitra PP, and Sotak CH, “Time-Dependent Diffusion of Water in a Biological Model System,” Proceedings of the National Academy of Sciences of the United States of America 91, 1229–1233 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [141].Dhital Bibek, Reisert Marco, Kellner Elias, and Kiselev Valerij G, “Intra-axonal Diffusivity in Brain White Matter,” preprint, 1–9 (2017), arXiv:1712.04565v1. [DOI] [PubMed]
- [142].Papaioannou Antonios, Novikov Dmitry S., Fieremans Els, and Boutis Gregory S., “Observation of structural universality in disordered systems using bulk diffusion measurement,” Physical Review E 96, 061101 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [143].Lemberskiy Gregory, Baete Steven H., Cloos Martijn A., Novikov Dmitry S., and Fieremans Els, “Validation of surface-to-volume ratio measurements derived from oscillating gradient spin echo on a clinical scanner using anisotropic fiber phantoms,” NMR in Biomedicine 30, e3708 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [144].Reynaud Olivier, Veronica Winters Kerryanne, Hoang Dung Minh, Zaim Wadghiri Youssef, Novikov Dmitry S., and Kim Sungheon Gene, “Surface-to-volume ratio mapping of tumor microstructure using oscillating gradient diffusion weighted imaging,” Magnetic Resonance in Medicine 76, 237–247 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [145].Reynaud Olivier, Veronica Winters Kerryanne, Hoang Dung Minh, Zaim Wadghiri Youssef, Novikov Dmitry S., and Kim Sungheon Gene, “Pulsed and oscillating gradient MRI for assessment of cell size and extracellular space (POMACE) in mouse gliomas,” NMR in Biomedicine 29, 1350–63 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [146].Jiang Xiaoyu, Li Hua, Xie Jingping, Mckinley Eliot T, Zhao Ping, Gore John C, and Xu Junzhong, “In Vivo Imaging of Cancer Cell Size and Cellularity Using Temporal Diffusion Spectroscopy,” Magnenetic Resonance in Medicine 164, 156–164 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [147].Ernst MH, Machta J, Dorfman JR, and van Beijeren H, “Long-time tails in stationary random media. 1. {Theory},” Journal of Statistical Physics 34, 477–495 (1984). [Google Scholar]
- [148].Visscher PB, “Universality in disordered diffusive systems - exact fixed-points in 1,2, and 3 dimensions,” Physical Review B 29, 5472–5485 (1984). [Google Scholar]
- [149].Ginsburger Kevin, Poupon Fabrice, Beaujoin Justine, Estournet Delphine, Matuschke Felix, Mangin Jean-Franc¸ois, Axer Markus, and Poupon Cyril, “Improving the Realism of White Matter Numerical Phantoms: A Step toward a Better Understanding of the Influence of Structural Disorders in Diffusion MRI,” Frontiers in Physics 6, 12 (2018). [Google Scholar]
- [150].Palombo Marco, Ligneul Clemence, Hernandez-Garzon Edwin, and Valette Julien, “Can we detect the effect of spines and leaflets on the diffusion of brain intracellular metabolites?” NeuroImage (2017), 10.1016/j.neuroimage.2017.05.003. [DOI] [PubMed]
- [151].Palombo Marco, Ligneul Clemence, Najac Chloé, Le Douce Juliette, Flament Julien, Escartin Carole, Hantraye Philippe, Brouillet Emmanuel, Bonvento Gilles, and Valette Julien, “New paradigm to assess brain cell morphology by diffusion-weighted MR spectroscopy in vivo,” Proceedings of the National Academy of Sciences 113, 201504327 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [152].Ackerman Joseph J H and Neil Jeffrey J, “The use of MR-detectable reporter molecules and ions to evaluate diffusion in normal and ischemic brain,” NMR Biomed 23, 725–733 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [153].Shepherd Gordon M G, Raastad Morten, and Andersen Per, “General and variable features of varicosity spacing along un-myelinated axons in the hippocampus and cerebellum,” Proceedings of the National Academy of Sciences 99, 6340–6345 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [154].Shepherd Gordon M G, and Raastad Morten, “Axonal varicosity distributions along parallel fibers: a new angle on a cerebellar circuit,” The Cerebellum 2, 110–113 (2003). [DOI] [PubMed] [Google Scholar]
- [155].Debanne Dominique, Campanac Emilie, Bialowas Andrzej, Carlier Edmond, and Alcaraz Giséle, “Axon Physiology,” Physiological Reviews 91, 555–602 (2011). [DOI] [PubMed] [Google Scholar]
- [156].Zhang Shengxiang, Boyd Jamie, Delaney Kerry, and Murphy Timothy H, “Rapid reversible changes in dendritic spine structure in vivo gated by the degree of ischemia,” J Neurosci 25, 5333–5338 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [157].Li Ping and Murphy Timothy H, “Two-photon imaging during prolonged middle cerebral artery occlusion in mice reveals recovery of dendritic structure after reperfusion,” J Neurosci 28, 11970–11979 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [158].Nilsson Markus, Lätt Jimmy, Stahlberg Freddy, van Westen Danielle, and Hagslätt Hakan, “The importance of axonal undulation in diffusion {MR} measurements: a Monte Carlo simulation study,” NMR in Biomedicine 25, 795–805 (2012). [DOI] [PubMed] [Google Scholar]
- [159].Schain Aaron J, Hill Robert A, and Grutzendler Jaime, “Label-free in vivo imaging of myelinated axons in health and disease with spectral confocal reflectance microscopy,” Nat Med 20, 443–449 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [160].llan Baron Corey A, Kate Mahesh, Gioia Laura, Butcher Kenneth, Emery Derek, Budde Matthew, and Beaulieu Christian, “Reduction of Diffusion-Weighted Imaging Contrast of Acute Ischemic Stroke at Short Diffusion Times,” Stroke; a journal of cerebral circulation 46, 2136–2141 (2015). [DOI] [PubMed] [Google Scholar]
- [161].Barazany D, Basser PJ, and Assaf Y, “In vivo measurement of axon diameter distribution in the corpus callosum of rat brain,” Brain 132, 1210–1220 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [162].Zhang H, Hubbard PL, Parker GJM, and Alexander DC, “Axon diameter mapping in the presence of orientation dispersion with diffusion MRI,” Neuroimage 56, 1301–1315 (2011). [DOI] [PubMed] [Google Scholar]
- [163].Huang Susie Y, Nummenmaa Aapo, Witzel Thomas, Duval Tanguy, Cohen-Adad Julien, Wald Lawrence L, and McNab Jennifer A, “The impact of gradient strength on in vivo diffusion MRI estimates of axon diameter,” Neuroimage 106, 464–472 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [164].Horowitz Assaf, Barazany Daniel, Tavor Ido, Bernstein Moran, Yovel Galit, and Assaf Yaniv, “In vivo correlation between axon diameter and conduction velocity in the human brain,” Brain Structure and Function 220, 1777–1788 (2015). [DOI] [PubMed] [Google Scholar]
- [165].Innocenti GM, Caminiti R, and Aboitiz F, “Comments on the paper by Horowitz et al.(2014),” Brain structure and function 220, 1789–1790 (2015). [DOI] [PubMed] [Google Scholar]
- [166].Horowitz Assaf, Barazany Daniel, Tavor Ido, Yovel Galit, and Assaf Yaniv, “Response to the comments on the paper by Horowitz et al. (2014),” Brain Structure and Function 220, 1791–1792 (2015). [DOI] [PubMed] [Google Scholar]
- [167].Beaulieu C, “The basis of anisotropic water diffusion in the nervous system - a technical review,” NMR in Biomedicine 15, 435–455 (2002). [DOI] [PubMed] [Google Scholar]
- [168].Veraart Jelle, Fieremans Els, and Novikov Dmitry S., “Universal power-law scaling of water diffusion in human brain defines what we see with MRI,” preprint arXiv:1609.09145 (2016), arXiv:1609.09145.
- [169].Takahashi Masaya, Hackney David B, Zhang Guixin, Wehrli Suzanne L, Wright Alex C, O’Brien William T, Uematsu Hidemasa, Wehrli Felix W, and Selzer Michael E, “Magnetic Resonance Microimaging of Intraaxonal Water Diffusion in Live Excised Lamprey Spinal Cord,” Proceedings of the National Academy of Sciences of the United States of America 99, 16192–16196 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [170].Nørhøj Jespersen Sune, Lynge Olesen Jonas, Hansen Brian, and Shemesh Noam, “Diffusion time dependence of microstructural parameters in fixed spinal cord,” NeuroImage (2017), 10.1016/j.neuroimage.2017.08.039, arXiv:1705.03630. [DOI] [PMC free article] [PubMed]
- [171].Komlosh ME, Özarslan E, Lizak MJ, Horkayne-Szakaly I, Freidlin RZ, Horkay F, and Basser PJ, “Mapping average axon diameters in porcine spinal cord white matter and rat corpus callosum using d-PFG MRI,” NeuroImage 78, 210–216 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [172].Xu Junzhong, Li Hua, Li Ke, Harkins Kevin D., Jiang Xiaoyu, Xie Jingping, Kang Hakmook, Dortch Richard D., Anderson Adam W., Does Mark D., and Gore John C., “Fast and simplified mapping of mean axon diameter using temporal diffusion spectroscopy,” NMR in Biomedicine 29, 400–410 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [173].Duval Tanguy, McNab Jennifer A., Setsompop Kawin, Witzel Thomas, Schneider Torben, Huang Susie Yi, Keil Boris, Klawiter Eric C., Wald Lawrence L., and Cohen-Adad Julien, “In vivo mapping of human spinal cord microstructure at 300mT/m,” NeuroImage 118, 494–507 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [174].Benjamini Dan, Komlosh Michal E., Holtzclaw Lynne A., Nevo Uri, and Basser Peter J., “White matter microstructure from nonparametric axon diameter distribution mapping,” NeuroImage 135, 333–344 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [175].Drobnjak Ivana, Siow Bernard, and Alexander Daniel C, “Optimizing gradient waveforms for microstructure sensitivity in diffusion-weighted MR,” Journal of Magnetic Resonance 206, 41–51 (2010). [DOI] [PubMed] [Google Scholar]
- [176].Drobnjak Ivana, Zhang Hui, Ianu Andrada, Kaden Enrico, and Alexander Daniel C., “PGSE, OGSE, and sensitivity to axon diameter in diffusion MRI: Insight from a simulation study,” Magnetic Resonance in Medicine 75, 688–700 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [177].Nilsson Markus, Westin Carl-fredrik, Drobnjak Ivana, and Daniel T, “Resolution limit of cylinder diameter estimation by diffusion MRI : The impact of gradient waveform and orientation dispersion,” NMR Biomed, 1–13 (2017). [DOI] [PMC free article] [PubMed]
- [178].Sepehrband Farshid, Alexander Daniel C, Kurniawan Nyoman D, Reutens David C, and Yang Zhengyi, “Towards higher sensitivity and stability of axon diameter estimation with diffusion-weighted MRI,” NMR Biomed 29, 293–308 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [179].Portnoy S, Flint JJ, Blackband SJ, and Stanisz GJ, “Oscillating and Pulsed Gradient Diffusion Magnetic resonance Microscopy Over an Extended b-Value Range: Implications for the Characterization of Tissue Microstructure,” Magnetic Resonance in Medicine 69, 1131–1145 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [180].Lifshitz IM, “Energy Spectrum of Disordered Systems,” Advances In Physics 13, 483–536 (1964). [Google Scholar]
- [181].Mott Nevill F and Davies Edward A, Electronic processes in non-crystalline materials (Oxford University Press, New York, 1971). [Google Scholar]
- [182].Veraart Jelle, Fieremans Els, and Novikov Dmitry S., “Diffusion {MRI} noise mapping using random matrix theory,” Magnetic resonance in medicine 76, 1582–1593 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [183].Veraart Jelle, Fieremans Els, and Novikov Dmitry S., “Diffusion MRI noise mapping using random matrix theory,” Magnetic resonance in medicine 76, 1582–1593 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [184].Candes Emmanuel J, Romberg Justin K, and Tao Terence, “Stable signal recovery from incomplete and inaccurate measurements,” Communications on Pure and Applied Mathematics 59, 1207–1223 (2006). [Google Scholar]
- [185].Lustig Michael, Donoho David, and Pauly John M, “Sparse MRI: The application of compressed sensing for rapid MR imaging,” Magnetic Resonance in Medicine 58, 1182–1195 (2007). [DOI] [PubMed] [Google Scholar]
- [186].Ma Dan, Gulani Vikas, Seiberlich Nicole, Liu Kecheng, Sunshine Jeffrey L, Duerk Jeffrey L, and Griswold Mark A, “Magnetic resonance fingerprinting,” Nature 495, 187–192 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [187].Ikonomovic Milos D, Abrahamson Eric E, Isanski Barbara A, Wuu Joanne, Mufson Elliott J, and DeKosky Steven T, “Superior frontal cortex cholinergic axon density in mild cognitive impairment and early Alzheimer disease,” Arch Neurol 64, 1312–1317 (2007). [DOI] [PubMed] [Google Scholar]
- [188].Lampinen Björn, Szczepankiewicz Filip, van Westen Danielle, Englund Elisabet, Sundgren Pia C, Lätt Jimmy, Strahlberg Freddy, and Nilsson Markus, “Optimal experimental design for filter exchange imaging: Apparent exchange rate measurements in the healthy brain and in intracranial tumors,” Magn Reson Med 77, 1104–1114 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [189].Badaut Jérôme, Ashwal Stephen, Adami Arash, Tone Beatriz, Recker Rebecca, Spagnoli David, Ternon Be´atrice, and Obenaus Andre, “Brain Water Mobility Decreases after Astrocytic Aquaporin-4 Inhibition Using RNA Interference,” Journal of Cerebral Blood Flow and Metabolism 31, 819–831 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [190].Yang Donghan M, Huettner James E, Bretthorst G Larry, Neil Jeffrey J, Garbow Joel R, and Ackerman Joseph J.H., “Intracellular water preexchange lifetime in neurons and astrocytes,” Magnetic Resonance in Medicine 00 (2017), 10.1002/mrm.26781. [DOI] [PMC free article] [PubMed]
- [191].Bai Ruiliang, Springer Charles S., Plenz Dietmar, and Basser Peter J., “Fast, Na+/K+ pump driven, steady-state transcytolemmal water exchange in neuronal tissue: A study of rat brain cortical cultures,” Magnetic Resonance in Medicine 79, 3207–3217 (2018). [DOI] [PubMed] [Google Scholar]
- [192].Jensen Jens H., Glenn G. Russell, and Helpern Joseph A., “Fiber ball imaging,” NeuroImage 124, 824–833 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [193].McKinnon Emilie T, Jensen Jens H, Glenn G Russell, and Helpern Joseph A, “Dependence on b-value of the direction-averaged diffusion-weighted imaging signal in brain,” Magnetic resonance imaging 36, 121–127 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [194].Ronen Itamar, Budde Matthew, Ercan Ece, Annese Jacopo, Techawiboonwong Aranee, and Webb Andrew, “Microstructural organization of axons in the human corpus callosum quantified by diffusion-weighted magnetic resonance spectroscopy of N-acetylaspartate and post-mortem histology,” Brain Struct Funct 219, 1773–1785 (2014). [DOI] [PubMed] [Google Scholar]
- [195].Budde Matthew D and Frank Joseph A, “Examining brain microstructure using structure tensor analysis of histological sections,” NeuroImage 63, 1–10 (2012). [DOI] [PubMed] [Google Scholar]
- [196].Dhital Bibek, Kellner Elias, Kiselev Valerij G., and Reisert Marco, “The absence of restricted water pool in brain white matter,” NeuroImage (2017), 10.1016/j.neuroimage.2017.10.051. [DOI] [PubMed]
- [197].Healy Dennis M., Hendriks Harrie, and Pt Kim Peter T., “Spherical deconvolution,” Journal of Multivariate Analysis 67, 1–22 (1998). [Google Scholar]
- [198].Donald Tournier J., Calamante Fernando, Gadian David G., and Connelly Alan, “Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution,” NeuroImage 23, 1176–1185 (2004). [DOI] [PubMed] [Google Scholar]
- [199].Anderson Adam W., “Measurement of fiber orientation distributions using high angular resolution diffusion imaging,” Magnetic Resonance in Medicine 54, 1194–1206 (2005). [DOI] [PubMed] [Google Scholar]
- [200].Tournier J-Donald, Calamante Fernando, and Connelly Alan, “Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution,” Neuroimage 35, 1459–1472 (2007). [DOI] [PubMed] [Google Scholar]
- [201].Dell’Acqua F, Rizzo G, Scifo P, Clarke RA, Scotti G, and Fazio F, “A Model-Based Deconvolution Approach to Solve Fiber Crossing in Diffusion-Weighted MR Imaging,” (2007). [DOI] [PubMed]
- [202].Jian B and Vemuri BC, “A Unified Computational Frame-work for Deconvolution to Reconstruct Multiple Fibers From Diffusion Weighted MRI,” (2007). [DOI] [PMC free article] [PubMed]
- [203].Kaden Enrico, Kno¨sche Thomas R., and Anwander Alfred, “Parametric spherical deconvolution: Inferring anatomical connectivity using diffusion MR imaging,” NeuroImage 37, 474–488 (2007). [DOI] [PubMed] [Google Scholar]
- [204].White Nathan S. and Dale Anders M., “Optimal diffusion MRI acquisition for fiber orientation density estimation: An analytic approach,” Human Brain Mapping 30, 3696–3703 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [205].Mackay Alex, Whittall Kenneth, Adler Julian, Li David, Paty Donald, and Graeb Douglas, “In vivo visualization of myelin water in brain by magnetic resonance,” Magnetic Resonance in Medicine 31, 673–677 (1994). [DOI] [PubMed] [Google Scholar]
- [206].Dortch Richard D., Harkins Kevin D., Juttukonda Meher R., Gore John C., and Does Mark D., “Characterizing inter-compartmental water exchange in myelinated tissue using relaxation exchange spectroscopy,” Magnetic Resonance in Medicine 70, 1450–1459 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [207].Panagiotaki Eleftheria, Schneider Torben, Siow Bernard, Hall Matt G, Lythgoe Mark F, and Alexander Daniel C, “Compartment models of the diffusion MR signal in brain white matter: a taxonomy and comparison,” Neuroimage 59, 2241–2254 (2012). [DOI] [PubMed] [Google Scholar]
- [208].Ferizi Uran, Schneider Torben, Witzel Thomas, Wald Lawrence L, Zhang Hui, Wheeler-Kingshott Claudia A M, and Alexander Daniel C, “White matter compartment models for in vivo diffusion MRI at 300mT/m,” Neuroimage 118, 468–483 (2015). [DOI] [PubMed] [Google Scholar]
- [209].Assaf Yaniv and Basser Peter J., “Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain,” NeuroImage 27, 48–58 (2005). [DOI] [PubMed] [Google Scholar]
- [210].De Santis Silvia, Barazany Daniel, Jones Derek K., and Assaf Yaniv, “Resolving relaxometry and diffusion properties within the same voxel in the presence of crossing fibres by combining inversion recovery and diffusion-weighted acquisitions,” Magnetic Resonance in Medicine 75, 372–380 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [211].Sherbondy Anthony J., Rowe Matthew C., and Alexander Daniel C., “MicroTrack: An algorithm for concurrent projectome and microstructure estimation,” Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 6361 LNCS, 183–190 (2010). [DOI] [PubMed] [Google Scholar]
- [212].Tournier Jacques-Donald JD, Mori Susumu, and Leemans Alexander, “Diffusion tensor imaging and beyond.” Magnetic Resonance in Medicine 65, 1532–56 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [213].Girard Gabriel, Daducci Alessandro, Petit Laurent, Thiran Jean-Philippe, Whittingstall Kevin, Deriche Rachid, Wassermann Demian, and Descoteaux Maxime, “AxTract: Toward microstructure informed tractography,” Human Brain Mapping 38, 5485–5500 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [214].J Behrens TE, Johansen Berg H., Jbabdi S, S Rushworth MF, and Woolrich MW, “Probabilistic diffusion tractography with multiple fibre orientations: What can we gain?” NeuroImage 34, 144–155 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [215].Descoteaux Maxime, Deriche Rachid, Knösche Thomas R., and Anwander Alfred, “Deterministic and probabilistic tractography based on complex fibre orientation distributions,” IEEE Transactions on Medical Imaging 28, 269–286 (2009). [DOI] [PubMed] [Google Scholar]
- [216].Farquharson Shawna, Tournier J-Donald, Calamante Fernando, Fabinyi Gavin, Schneider-Kolsky Michal, Jackson Graeme D, and Connelly Alan, “White matter fiber tractography: why we need to move beyond DTI.” Journal of neuro-surgery 118, 1367–77 (2013). [DOI] [PubMed] [Google Scholar]
- [217].Sotiropoulos Stamatios N., Jbabdi Saad, Xu Junqian, Andersson Jesper L., Moeller Steen, Auerbach Edward J., Glasser Matthew F., Hernandez Moises, Sapiro Guillermo, Jenkinson Mark, Feinberg David A., Yacoub Essa, Lenglet Christophe, Van Essen David C., Ugurbil Kamil, and Behrens Timothy E.J., “Advances in diffusion MRI acquisition and processing in the Human Connectome Project,” NeuroImage 80, 125–143 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [218].Wilkins Bryce, Lee Namgyun, Gajawelli Niharika, Law Meng, and Lepore Natasha, “Fiber estimation and tractography in diffusion MRI: Development of simulated brain images and comparison of multi-fiber analysis methods at clinical b-values,” NeuroImage 109, 341–356 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [219].Fieremans Els, Jensen Jens H, Helpern Joseph A, Kim Sungheon, Grossman Robert I, Inglese Matilde, and Novikov Dmitry S., “Diffusion Distinguishes Between Axonal Loss and Demyelination in Brain White Matter,” Proceedings of the International Society of Magnetic Resonance in Medicine 20, p.714 (2012). [Google Scholar]
- [220].Novikov Dmitry S. and Fieremans Els, “Relating Extracellular Diffusivity to Cell Size Distribution and Packing Density as Applied to White Matter,” Proceedings of the International Society of Magnetic Resonance in Medicine 20, p.1829 (2012). [Google Scholar]
- [221].Jelescu Ileana O, Magdalena Zurek, Winters Kerryanne V, Veraart Jelle, Rajaratnam Anjali, Kim Nathanael S, Babb James S, Shepherd Timothy M, Novikov Dmitry S., Kim Sungheon G, and Fieremans Els, “In vivo quantification of demyelination and recovery using compartment-specific diffusion MRI metrics validated by electron microscopy,” Neuroimage 132, 104–114 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [222].Raza Khan Ahmad, Chuhutin Andrey, Wiborg Ove, Kroenke Christopher D, Nyengaard Jens R, Hansen Brian, and Nørhøj Jespersen Sune, “Biophysical modeling of high field diffusion MRI demonstrates micro-structural aberration in chronic mild stress rat brain,” NeuroImage (2016), 10.1016/j.neuroimage.2016.07.001. [DOI] [PMC free article] [PubMed]
- [223].Raza Khan Ahmad, Chuhutin Andrey, Wiborg Ove, Kroenke Christopher D, Nyengaard Jens R, Hansen Brian, and Nørhøj Jespersen Sune, “Summary of high field diffusion MRI and microscopy data demonstrate microstructural aberration in chronic mild stress rat brain,” Data in brief 8, 934 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [224].Vestergaard-Poulsen Peter, Wegener Gregers, Hansen Brian, Bjarkam Carsten R, Blackband Stephen J, Christian Nielsen Niels, and Jespersen Sune N, “Diffusion-weighted MRI and quantitative biophysical modeling of hippocampal neurite loss in chronic stress,” PLoS One 6, e20653 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [225].Budde Matthew D and Frank Joseph A, “Neurite beading is sufficient to decrease the apparent diffusion coef fi cient after ischemic stroke,” Proc Natl Acad Sci U S A 107, 14472–14477 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [226].Unterberg AW, Stover J, Kress B, and Kiening KL, “Edema and brain trauma,” Neuroscience 129, 1021–1029 (2004). [DOI] [PubMed] [Google Scholar]
- [227].Stikov Nikola, Campbell Jennifer S W, Stroh Thomas, Lavelée Mariette, Frey Stephen, Novek Jennifer, Nuara Stephen, Ho Ming-Kai, Bedell Barry J, Dougherty Robert F, Leppert Ilana R, Boudreau Mathieu, Narayanan Sridar, Duval Tanguy, Cohen-Adad Julien, Picard Paul-Alexandre, Gasecka Alicja, Côté Daniel, and Pike G Bruce, “In vivo histology of the myelin g-ratio with magnetic resonance imaging,” Neuroimage 118, 397–405 (2015). [DOI] [PubMed] [Google Scholar]
- [228].Nørhøj Jespersen Sune, “Equivalence of double and single wave vector diffusion contrast at low diffusion weighting,” NMR Biomed 25, 813–818 (2012). [DOI] [PubMed] [Google Scholar]
- [229].Hansen Brian, Khan Ahmad R., Shemesh Noam, Lund Torben E., Sangill Ryan, Eskildsen Simon F., Ostergaard Leif, and Jespersen Sune N., “White matter biomarkers from fast protocols using axially symmetric diffusion kurtosis imaging,” NMR in Biomedicine 30, e3741 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [230].Hansen Brian, Shemesh Noam, and Nørhøj Jespersen Sune, “Fast imaging of mean, axial and radial diffusion kurtosis,” NeuroImage 142, 381–393 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [231].Nguyen Hang Tuan, Grebenkov Denis, Van Nguyen Dang, Poupon Cyril, Le Bihan Denis, and Li Jing-Rebecca, “Parameter estimation using macroscopic diffusion MRI signal models,” Physics in Medicine and Biology 60, 3389–3413 (2015). [DOI] [PubMed] [Google Scholar]
- [232].Jelescu Ileana O, Veraart Jelle, Adisetiyo Vitria, Milla Sarah S, Novikov Dmitry S., and Fieremans Els, “One diffusion acquisition and different white matter models: How does microstructure change in human early development based on WMTI and NODDI?” NeuroImage 107, 242–256 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [233].Hui Edward S, Fieremans Els, Jensen Jens H, Tabesh Ali, Feng Wuwei, Bonilha Leonardo, Spampinato Maria V, Adams Robert, and Helpern Joseph A, “Stroke assessment with diffusional kurtosis imaging,” Stroke 43, 2968–2973 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [234].Kelm Nathaniel D, West Kathryn L, Carson Robert P, Gochberg Daniel F, Ess Kevin C, and Does Mark D, “Evaluation of diffusion kurtosis imaging in ex vivo hypomyelinated mouse brains,” NeuroImage 124, Part, 612–626 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [235].Falangola Maria F, Guilfoyle David N, Tabesh Ali, Hui Edward S, Nie Xingju, Jensen Jens H, Gerum Scott V, Hu Caixia, LaFrancois John, Collins Heather R, and Helpern Joseph A, “Histological correlation of diffusional kurtosis and white matter modeling metrics in cuprizone-induced corpus callosum demyelination,” NMR in Biomedicine 27, 948–957 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [236].Guglielmetti C, Veraart J, Roelant E, Mai Z, Daans J, Van Audekerke J, Naeyaert M, Vanhoutte G, Delgado y Palacios R, Praet J, Fieremans E, Ponsaerts P, Sijbers J, Van der Linden A, and Verhoye M, “Diffusion kurtosis imaging probes cortical alterations and white matter pathology following cuprizone induced demyelination and spontaneous remyelination,” NeuroImage 125, 363–377 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [237].Grossman Elan J, Kirov Ivan I, Gonen Oded, Novikov Dmitry S., Davitz Matthew S, Lui Yvonne W, Grossman Robert I, Inglese Matilde, and Fieremans Els, “N-acetyl-aspartate levels correlate with intra-axonal compartment parameters from diffusion MRI,” NeuroImage 118, 334–343 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [238].Coelho Santiago, Beltrachini Leandro, Pozo1 Jose M., and Frangi Alejandro F., “Double diffusion encoding vs single diffusion encoding parameter estimation of biophysical models in diffusion weighted mri,” in Proc. Int. Soc. Magn. Reson. Med, Vol. 25 (2017) p. 3383. [Google Scholar]
- [239].Fieremans Els, Veraart Jelle, Ades-Aron Benjamin, Szczepankiewicz Filip, Nilsson Markus, and Novikov Dmitry S, “Effect of combining linear with spherical tensor encoding on estimating brain microstructural parameters,” Proc. 26th Annual Meeting ISMRM, Paris, France (2018). [Google Scholar]
- [240].Chuhutin Andrey, Hansen Brian, and Nørhøj Jespersen Sune, “Precision and accuracy of diffusion kurtosis estimation and the influence of b-value selection,” NMR in Biomedicine 30, 1–14 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [241].Tariq Maira, Schneider Torben, Alexander Daniel C, Gandini Wheeler-Kingshott Claudia A, and Zhang Hui, “Bingham–NODDI: Mapping anisotropic orientation dispersion of neurites using diffusion MRI,” NeuroImage (2016). [DOI] [PubMed]
- [242].Szafer A, Zhong J, and Gore JC, “Theoretical model for water diffusion in tissues,” Magn Reson Med 33, 697–712 (1995). [DOI] [PubMed] [Google Scholar]
- [243].Tariq Maria, Kleinnijenhuis Michiel, van Cappellen van Walsum Anne-Marie, and Zhang Hui, “Validation of NODDI estimation of dispersion anisotropy in V1 of the human neo-cortex,” Proceedings of the International Society of Magnetic Resonance in Medicine 23, p. 0477 (2015). [Google Scholar]
- [244].Grussu Francesco, Schneider Torben, Tur Carmen, Yates Richard L., Tachrount Mohamed, Ianu Andrada, Yiannakas Marios C., Newcombe Jia, Zhang Hui, Alexander Daniel C., DeLuca Gabriele C., and Gandini Wheeler-Kingshott Claudia A. M., “Neurite dispersion: a new marker of multiple sclerosis spinal cord pathology?” Annals of Clinical and Translational Neurology 4, 663–679 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [245].Schilling Kurt G., Janve Vaibhav, Gao Yurui, Stepniewska Iwona, Landman Bennett A., and Anderson Adam W., “Histological validation of diffusion MRI fiber orientation distributions and dispersion,” NeuroImage 165, 200–221 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [246].Kazhdan Michael, Funkhouser Thomas, and Rusinkiewicz Szymon, “Rotation invariant spherical harmonic representation of 3 d shape descriptors,” in Symposium on geometry processing, Vol. 6 (2003) pp. 156–164. [Google Scholar]
- [247].Mirzaalian H, Ning L, Savadjiev P, Pasternak O, Bouix S, Michailovich O, Grant G, Marx CE, Morey RA, Flashman LA, George MS, Mcallister TW, Andaluz N, Shutter L, Coimbra R, Zafonte RD, Coleman MJ, Kubicki M, Westin CF, Stein MB, Shenton ME, and Rathi Y, “Inter-site and inter-scanner diffusion MRI data harmonization,” NeuroImage 135, 311–323 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [248].Nørhøj Jespersen Sune, Lundell Henrik, Kaae Sønderby Casper, and Dyrby Tim B., “Orientationally invariant metrics of apparent compartment eccentricity from double pulsed field gradient diffusion experiments,” NMR in Biomedicine 26, 1647–1662 (2013). [DOI] [PubMed] [Google Scholar]
- [249].Lasic Samo, Szczepankiewicz Filip, Eriksson Stefanie, Nilsson Markus, and Topgaard Daniel, “Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector,” Frontiers in Physics 2, 1–14 (2014). [Google Scholar]
- [250].Kaden Enrico, Kruggel Frithjof, and Alexander Daniel C, “Quantitative mapping of the per-axon diffusion coefficients in brain white matter,” Magnetic Resonance in Medicine 75, 1752–1763 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [251].Hansen Brian, Ellegaard Lund Torben, Sangill Ryan, and Jespersen Sune Nørhøj, “Neurite density from an isotropic diffusion model,” Proceedings of the International Society of Magnetic Resonance in Medicine 23, p. 3043 (2015). [Google Scholar]
- [252].Kaden Enrico, Kelm Nathaniel D, Carson Robert P, Does Mark D, and Alexander Daniel C, “Multi-compartment microscopic diffusion imaging,” NeuroImage 139, 346–359 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [253].Szczepankiewicz Filip, van Westen Danielle, Englund Elisabet, Westin Carl-Fredrik, Strahlberg Freddy, Lätt Jimmy, Sundgren Pia C, and Nilsson Markus, “The link between diffusion MRI and tumor heterogeneity: Mapping cell eccentricity and density by diffusional variance decomposition (DI-VIDE),” NeuroImage 142, 522–532 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [254].Bohr A and Mottelson Ben R, Nuclear Structure, Vol. II: Nuclear Deformations (World Scientific, 1998). [Google Scholar]
- [255].Szczepankiewicz Filip, Lasivc Samo, van Westen Danielle, Sundgren Pia C., Englund Elisabet, Fredrik Westin Carl, Strahlberg Freddy, Lätt Jimmy, Topgaard Daniel, and Nilsson Markus, “Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: Applications in healthy volunteers and in brain tumors,” NeuroImage 104, 241–252 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [256].de Almeida Martins Joao P and Topgaard Daniel, “Two-Dimensional Correlation of Isotropic and Directional Diffusion Using NMR,” Phys. Rev. Lett 116, 87601 (2016). [DOI] [PubMed] [Google Scholar]
- [257].Skinner Nathan P, Kurpad Shekar N, Schmit Brian D, Muftuler L Tugan, and Budde Matthew D, “Rapid In Vivo Detection of Rat Spinal Cord Injury With Double-Diffusion-Encoded Magnetic Resonance Spectroscopy,” Magnenetic Resonance in Medicine 77, 1639–1649 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [258].Lampinen Bjorn, Szczepankiewicz Filip, Martensson Johan, van Westen Danielle, Sundgren Pia C., and Nilsson Markus, “Neurite density imaging versus imaging of microscopic anisotropy in diffusion MRI: A model comparison using spherical tensor encoding,” NeuroImage 147, 517–531 (2017). [DOI] [PubMed] [Google Scholar]
- [259].Dhital Bibek, Kellner Elias, Reisert Marco, and Kiselev Valerij G, “Isotropic diffusion weighting provides insight on diffusion compartments in human brain white matter in vivo,” Proceedings of the International Society of Magnetic Resonance in Medicine 23, p. 2788 (2015). [Google Scholar]
- [260].Lee Hong-Hsi, Fieremans Els, and Novikov Dmitry S, “LEMONADE(t): Exact relation of time-dependent diffusion signal moments to neuronal microstructure,” Proc Intl Soc Mag Reson Med, p.884 (2018).
- [261].Cheng Y and Cory DG, “Multiple scattering by nmr,” J. Am. Chem. Soc 121, 7935–7936 (1999). [Google Scholar]
- [262].Cory DG, Garroway AN, and Miller JB, “Applications of spin transport as a probe of local geometry,” Polym. Prep. Am. Chem. Soc. Div. Polym. Chem 31, 149 (1990). [Google Scholar]
- [263].Mitra PP, Latour LL, Kleinberg RL, and Sotak CH, “Pulsed-field-gradient nmr measurements of restricted diffusion and the return-to-the-origin probability,” J. Magn. Reson. Series A 114, 47–58 (1995). [Google Scholar]
- [264].Nørhøj Jespersen Sune, “Equivalence of double and single wave vector diffusion contrast at low diffusion weighting,” NMR Biomed 25, 813–818 (2012). [DOI] [PubMed] [Google Scholar]
- [265].Finsterbusch J, “Extension of the double-wave-vector diffusion-weighting experiment to multiple concatenations,” J. Magn. Reson 198, 174–182 (2009). [DOI] [PubMed] [Google Scholar]
- [266].Finsterbusch J, “Numerical simulations of short-mixing-time double-wave-vector diffusion-weighting experiments with multiple concatenations on whole-body mr systems,” Journal of Magnetic Resonance 207, 274–282 (2010). [DOI] [PubMed] [Google Scholar]
- [267].Nørhøj Jespersen Sune and Buhl Niels, “The displacement correlation tensor: microstructure, ensemble anisotropy and curving fibers.” Journal of magnetic resonance (San Diego, Calif. : 1997) 208, 34–43 (2011). [DOI] [PubMed] [Google Scholar]
- [268].Koch Martin A and Finsterbusch Jürgen, “Numerical simulation of double-wave vector experiments investigating diffusion in randomly oriented ellipsoidal pores.” Magnetic resonance in medicine 62, 247–254 (2009). [DOI] [PubMed] [Google Scholar]
- [269].Ozarslan E and Basser PJ, “Microscopic anisotropy revealed by nmr double pulsed field gradient experiments with arbitrary timing parameters,” J Chem Phys 128, 154511 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [270].Ozarslan E, Shemesh N, and Basser PJ, “A general frame-work to quantify the effect of restricted diffusion on the nmr signal with applications to double pulsed field gradient nmr experiments,” J Chem Phys 130, 104702 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [271].Shemesh Noam, Ozarslan Evren, Basser Peter J, and Cohen Yoram, “Measuring small compartmental dimensions with low-q angular double-pgse nmr: The effect of experimental parameters on signal decay.” Journal of magnetic resonance (San Diego, Calif. : 1997) 198, 15–23 (2009). [DOI] [PubMed] [Google Scholar]
- [272].Koch MA and Finsterbusch J, “Compartment size estimation with double wave vector diffusion-weighted imaging,” Magn. Reson. Med 60, 90–101 (2008). [DOI] [PubMed] [Google Scholar]
- [273].Komlosh ME, Özarslan E, Lizak MJ, Horkay F, Schram V, Shemesh N, Cohen Y, and Basser PJ, “Pore diameter mapping using double pulsed-field gradient mri and its validation using a novel glass capillary array phantom,” J Magn Reson 208, 128–35 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [274].Ozarslan E, Komlosh ME, Lizak MJ, Horkay F, and Basser PJ, “Double pulsed field gradient (double-pfg) mr imaging (mri) as a means to measure the size of plant cells,” Magn Reson Chem 49 Suppl 1, S79–84 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [275].Shemesh N, Ozarslan E, Basser PJ, and Cohen Y, “Accurate noninvasive measurement of cell size and compartment shape anisotropy in yeast cells using double-pulsed field gradient mr,” NMR Biomed 25, 236–46 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [276].Shemesh N, Özarslan E, Bar-Shir A, Basser PJ, and Cohen Y, “Observation of restricted diffusion in the presence of a free diffusion compartment: single-and double-pfg experiments,” J. Magn. Reson 200, 214–225 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [277].Lawrenz Marco and Finsterbusch Ju¨rgen, “Double-wave-vector diffusion-weighted imaging reveals microscopic diffusion anisotropy in the living human brain,” Magn Reson Med 69, 1072–82 (2013). [DOI] [PubMed] [Google Scholar]
- [278].Weber T, Ziener CH, Kampf T, Herold V, Bauer WR, and Jakob PM, “Measurement of apparent cell radii using a multiple wave vector diffusion experiment,” Magn. Reson. Med 61, 1001–1006 (2009). [DOI] [PubMed] [Google Scholar]
- [279].Avram AV, Ozarslan E, Sarlls JE, and Basser PJ, “In vivo detection of microscopic anisotropy using quadruple pulsed-field gradient (qpfg) diffusion mri on a clinical scanner,” Neuroimage 64, 229–39 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [280].Koch MA and Finsterbusch J, “Towards compartment size estimation in vivo based on double wave vector diffusion weighting,” NMR Biomed 24, 1422–32 (2011). [DOI] [PubMed] [Google Scholar]
- [281].Lawrenz M and Finsterbusch J, “Mapping measures of microscopic diffusion anisotropy in human brain white matter in vivo with double-wave-vector diffusion-weighted imaging,” Magn Reson Med 73, 773–83 (2015). [DOI] [PubMed] [Google Scholar]
- [282].Jespersen SN, “Comment on “measuring small compartments with relatively weak gradients by angular double-pulsed-field-gradient nmr” by morozov bar, sochen, and cohen,” Magn Reson Imaging 31, 1643–4 (2013). [DOI] [PubMed] [Google Scholar]
- [283].Jensen JH, “Sufficiency of diffusion tensor in characterizing the diffusion mri signal to leading order in diffusion weighting,” NMR Biomed 27, 1005–7 (2014). [DOI] [PubMed] [Google Scholar]
- [284].Frøhlich AF, Ostergaard L, and Kiselev VG, “Effect of Impermeable Interfaces on Apparent Diffusion Coefficient in Heterogeneous Media,” App. Magn. Reson 29, 123–137 (2005). [Google Scholar]
- [285].Frøhlich Astrid F, Jespersen Sune N, Ostergaard Leif, and Kiselev Valerij G, “The effect of impermeable boundaries of arbitrary geometry on the apparent diffusion coefficient,” Journal of Magnetic Resonance 194, 128–135 (2008). [DOI] [PubMed] [Google Scholar]
- [286].Shemesh N, Ozarslan E, Adiri T, Basser PJ, and Cohen Y, “Noninvasive bipolar double-pulsed-field-gradient nmr reveals signatures for pore size and shape in polydisperse, randomly oriented, inhomogeneous porous media,” J Chem Phys 133, 044705 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [287].Shemesh Noam, Adiri Tal, and Cohen Yoram, “Probing microscopic architecture of opaque heterogeneous systems using double-pulsed-field-gradient nmr,” Journal of the American Chemical Society 133, 6028–6035 (2011). [DOI] [PubMed] [Google Scholar]
- [288].Jespersen SN, Lundell H, Sonderby CK, and Dyrby TB, “Orientationally invariant metrics of apparent compartment eccentricity from double pulsed field gradient diffusion experiments,” NMR Biomed 26, 1647–62 (2013). [DOI] [PubMed] [Google Scholar]
- [289].Shemesh Noam and Cohen Yoram, “Microscopic and compartment shape anisotropies in gray and white matter revealed by angular bipolar double-PFG MR,” Magnetic resonance in medicine 65, 1216–1227 (2011). [DOI] [PubMed] [Google Scholar]
- [290].Shemesh N, Barazany D, Sadan O, Bar L, Zur Y, Barhum Y, Sochen N, Offen D, Assaf Y, and Cohen Y, “Mapping apparent eccentricity and residual ensemble anisotropy in the gray matter using angular double-pulsed-field-gradient mri,” Magn Reson Med 68, 794–806 (2012). [DOI] [PubMed] [Google Scholar]
- [291].Yang Grant, Tian Qiyuan, Leuze Christoph, Winter-mark Max, and McNab Jennifer A, “Double diffusion encoding mri for the clinic.” Magnetic resonance in medicine (2017), 10.1002/mrm.27043. [DOI] [PMC free article] [PubMed]
- [292].Mitra PP, “Multiple wave-vector extensions of the nmr pulsed-field-gradient spin-echo diffusion measurement,” Phys. Rev. B 51, 15074–15078 (1995). [DOI] [PubMed] [Google Scholar]
- [293].Lawrenz M, Koch MA, and Finsterbusch J, “A tensor model and measures of microscopic anisotropy for double-wave-vector diffusion-weighting experiments with long mixing times,” J Magn Reson 202, 43–56 (2010). [DOI] [PubMed] [Google Scholar]
- [294].Lundell H, Dyrby TB, Hubbard PL, Zhou Feng-Lei, Parker GJ, and Jespersen SN, “Validation of double diffusion schemes of microscopic fractional anisotropy,” in Proc. Int. Soc. Magn. Reson. Med, Vol. 23 (2015) p. 155. [Google Scholar]
- [295].Özarslan E, “Compartment shape anisotropy (csa) revealed by double pulsed field gradient mr,” J. Magn. Reson 199, 56–67 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [296].Jespersen Sune N., Lundell Henrik, Sonderby Casper K., and Dyrby Tim B., “Commentary on “Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientation of order parameter by diffusion MRI with magic-angle spinning of the q-vector” Frontiers in Physics 2, 28 (2014). [Google Scholar]
- [297].Jespersen SN, Leigland LA, Cornea A, and Kroenke CD, “Determination of axonal and dendritic orientation distributions within the developing cerebral cortex by diffusion tensor imaging,” Ieee Transactions on Medical Imaging 31, 16–32 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [298].Jespersen Sune N., “White matter biomarkers from diffusion MRI,” Journal of Magnetic Resonance 291, 127–140 (2018). [DOI] [PubMed] [Google Scholar]
- [299].Eriksson Stefanie, Lasic Samo, and Topgaard Daniel, “Isotropic diffusion weighting in pgse nmr by magic-angle spinning of the q-vector.” Journal of magnetic resonance (San Diego, Calif. : 1997) 226, 13–18 (2013). [DOI] [PubMed] [Google Scholar]
- [300].Westin Carl-Fredrik, Knutsson Hans, Pasternak Ofer, Szczepankiewicz Filip, Özarslan Evren, Danielle van Westen Cecilia Mattisson, Bogren Mats, Lauren J O’Donnell Marek Kubicki, Topgaard Daniel, and Nilsson Markus, “Q-space trajectory imaging for multidimensional diffusion mri of the human brain.” NeuroImage 135, 345–362 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [301].Betzig Eric, “Nobel Lecture: Single molecules, cells, and super-resolution optics,” Reviews of Modern Physics 87, 1153 (2015). [DOI] [PubMed] [Google Scholar]
- [302].Kubo R, “The fluctuation-dissipation theorem,” Rep. Prog. Phys 29, 255–284 (1966). [Google Scholar]
- [303].Sukstanskii Alexander L, “Exact analytical results for {ADC} with oscillating diffusion sensitizing gradients,” Journal of Magnetic Resonance 234, 135–140 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [304].Dunn Keh-Jim and Bergman David J, “Self diffusion of nuclear spins in a porous medium with a periodic microstructure,” The Journal of Chemical Physics 102, 3041–3054 (1995). [Google Scholar]
- [305].Xu Junzhong, Does Mark D., and Gore John C., “Quantitative characterization of tissue microstructure with temporal diffusion spectroscopy,” Journal of Magnetic Resonance 200, 189–197 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [306].Stepisnik Janez, Lasic Samo, Mohoric Ales, Sersa Igor, and Sepe Ana, “Velocity autocorrelation spectra of fluid in porous media measured by the CPMG sequence and constant magnetic field gradient,” Magnetic Resonance Imaging 25, 517–520 (2007). [DOI] [PubMed] [Google Scholar]