The Comparative Advantage of Medicare Advantage

Abstract

We ascertain the degree of service-level selection in Medicare Advantage (MA) using individual level data on the 100 most frequent HCC’s or combination of HCC’s from two national insurers in 2012–2013. We find differences in the distribution of beneficiaries across HCC’s between TM and MA, principally in the smaller share of MA enrollees with no coded HCC, consistent with greater coding intensity in MA. Among those with an HCC code, absolute differences between MA and TM shares of beneficiaries are small, consistent with little service-level selection.

Variation in HCC margins does not predict differences between an HCC’s share of MA and TM enrollees, although one cannot a priori sign a relationship between margin and service-level selection. Margins are negatively associated with the importance of post-acute care in the HCC. Margins among common chronic disease classes amenable to medical management and typically managed by primary care physicians are larger than among diseases typically managed by specialists. These margin differences by disease are robust against a test for coding effects and suggest that the average technical efficiency of MA relative to TM may vary by diagnosis. If so, service-level selection on the basis of relative technical efficiency could be welfare enhancing.

As is well known, competitive insurance markets can be inefficient from sorting by individuals on either price or covered benefits in the case of fixed contracts and also, in the case of endogenous contracts, from service-level selection by insurers, meaning differential shadow prices for individuals with different conditions (Rothschild and Stiglitz 1976; Cutler and Reber 1998; Frank, et al. 2000; Breyer, et al. 2012).¹ To mitigate inefficiency from service-level selection, policy uses tools such as risk adjustment, mandates, subsidies, and reinsurance (Layton, et al. 2015; Geruso and McGuire 2016; Layton, et al. 2016; Azevedo and Gottlieb 2017; Geruso and Layton 2017; McGuire and van Kleef 2017). Risk adjustment addresses service-level selection by attempting to make individuals who vary in their expected spending equally profitable to the insurer, thereby limiting the insurer’s incentives to structure the insurance contract to attract certain beneficiaries and not others (Geruso and Layton 2017).²

Medicare’s initial risk adjustment scheme mostly relied upon age and sex and was notably unsuccessful in preventing favorable sorting of beneficiaries into MA (Congressional Budget Office 1997).³ About a decade ago Medicare introduced two reforms to reduce the favorable sorting into MA. It added diagnoses as a risk adjuster to the demographic risk adjusters it had previously employed, a method it termed Hierarchical Coexisting Conditions (HCC’s), and it required beneficiaries to remain in their chosen plan for several months, i.e., a lock-in period, whereas previously there had been no lock-in.⁴ These reforms markedly reduced the favorable sorting into MA (Newhouse, et al. 2013; Newhouse and McGuire 2014; Newhouse, et al. 2015).⁵ There remains the question of whether service-level selection exists within Medicare Advantage (MA), and that is the question we address in this paper. Note that such selection could be socially efficient if MA plans differentially attract beneficiaries with conditions that they are technically efficient in treating relative to TM. We thus go beyond the economics literature cited above in not assuming either the same cost function in MA and TM or alternatively a uniform reduction in cost across all MA beneficiaries relative to TM.⁶

Under the current MA risk adjustment method, payments to insurers for an individual beneficiary are proportional to the relative weight the risk adjustment scheme assigns to that beneficiary (Pope, et al. 2004). The relative weight is based on predicted TM spending from a regression of individual level TM spending on a number of demographic characteristics and a beneficiary’s diagnosis or diagnoses.⁷ As a result, an MA plan’s revenue for one type of beneficiary relative to another approximately equals the ratio of how much TM spends on each type of beneficiary. The variation in plan margins across HCC’s is therefore in part a measure of the average technical efficiency of MA relative to TM for the various HCC’s or combinations of HCC’s.

In an earlier paper (Newhouse et al., 2013) we used actual revenue and medical cost data from one insurer for 48 unique HCC’s or combination of HCC’s to explore selection across HCC’s or combination of HCC’s and differences in insurer margins across HCC’s. We had four main findings:

1. We saw negligible differences in the distribution of MA enrollees and TM enrollees across the 48 HCC’s in the sample, or no evidence of service-level selection. We also found no relationship between the observed margin and the difference in MA and TM enrollee shares.

2. This was so despite large differences in margins by HCC; the range of margins from the most to the least profitable was 160 percentage points.

3. We could not calculate standard errors for the estimated margins because we were not given individual level data, only aggregate revenue and cost for each of the 48 HCC’s. As a result, we could not determine how much of the variation in margins across HCC’s to attribute to sampling error.

4. Nevertheless, there was a pattern in the data; certain types of HCC’s were relatively more profitable on average, which suggested that not all the observed variation was attributable to sampling error. In particular, common chronic diseases typically managed by primary care physicians (PCP’s) and for which successful medical management might prevent a potentially expensive acute episode were relatively more profitable; examples included diabetes, chronic obstructive pulmonary disease (COPD), and chronic heart failure (CHF). At the other extreme, chronic diseases often managed by specialists tended to be markedly less profitable than those typically managed by PCP’s; examples included cancers of various sites and rheumatoid arthritis. We interpreted these findings as suggesting that MA had greater relative technical efficiency in the HCC categories with higher margins.

This paper revisits both the theoretical and empirical work of the earlier paper with better data that permit several improvements. Most importantly, we now have data on revenue and cost at the individual member level so that we can estimate sampling error. Second, we use data from two insurers rather than one, and the data are somewhat more recent, coming from calendar years 2012 and 2013.⁸ Third, in this work we have data on roughly twice as many HCC’s or combinations of HCC’s as in the earlier work, namely the 100 most frequent HCC’s or combination of HCC’s from each insurer for each year. Although there is substantial overlap, the top 100 HCC’s are not necessarily the same 100 HCC’s for each insurer in each year. Fourth, in the earlier work we only had data for those with at least one coded HCC; in these data we also know those not coded with an HCC, who are by far the largest group in our sample. Finally, in these results we control for geography.

We have three main findings:

1. 1) We now find some evidence of service-level selection across HCC’s, though the main difference in the distribution of the MA and TM samples across HCC’s is a markedly lower MA share with no coded HCC, consistent with more intensive diagnosis coding in MA. The differences in shares among those with a coded HCC or combination of HCC’s are small in absolute value.

2. 2) There is substantial variation in margins across HCC’s, even after accounting for sampling error. We again find that common chronic diseases usually managed by PCP’s have higher margins than chronic conditions typically managed by specialists, consistent with MA plans’ having greater average technical efficiency for those conditions. We carry out one test of whether our finding of differential margins by HCC is robust to coding effects and find that it is.

3. 3) In our earlier paper we assumed that MA plans would attempt to select beneficiaries in high margin HCC’s and interpreted the observed lack of selection as it being too costly for plans to do so. In the next section of this paper we show that this assumption is theoretically incorrect; one cannot sign a priori a relationship between the profit margins we observe and a plan’s incentive to attract beneficiaries in a given HCC without making restrictive assumptions. Fundamentally this is because a plan’s incentive to select beneficiaries with a specific HCC is a function of revenue and cost conditions at the margin and the various HCC profit margins we observe give information on average revenue and cost.

As a condition of obtaining the data, we agreed to keep the names of the two insurers and their actual margins confidential. We have done so by subtracting the same arbitrary constant from each calculated margin shown below.

The paper is organized as follows. In the next section we discuss whether one can sign a relationship between the margin in an HCC and the difference in the shares of beneficiaries in the HCC in MA and TM. Following that we turn to our empirical work. We describe our data, methods, and results and conclude with a discussion.

Profit Margins and Selection Incentives in Medicare Advantage

The margin is the gap between price and cost, measured in absolute or percentage terms, as in the case of the Lerner Index of market power. Although the relative price for an HCC in the MA market is set by regulation and so is regarded as fixed by the MA plan, coding intensity notwithstanding, the level of spending to treat a disease or groups of disease is partly chosen by the plan’s actions, for example its network, formulary, and cost sharing choices, which determine its profit margins in equilibrium. As a result, observed margins are endogenous.

It may seem intuitively appealing that a test of across-HCC or service-level selection by MA plans is whether there is a positive association between the margin in an HCC and the MA share in that HCC relative to TM. Indeed, Newhouse et al. (2013) assumed this was the case since it is what one would expect if MA plans specialized in disease categories in which they had a production advantage, and Newhouse, et al. (2013) interpreted larger profit margins in certain HCC’s as indicating production efficiency in MA relative to TM. Selection incentives, however, relate to conditions at the margin, and the observed profit margins across HCC’s relate to the average beneficiary in each HCC. There is thus no necessary link between observed profit margins and selection incentives.

In particular, a number of factors in addition to production efficiency affect the relationship between profit margins and the share of plan enrollees in MA relative to TM. Consider the simple case of one profit-maximizing MA plan competing against a passive TM alternative for beneficiaries in various diagnosis groups. The MA plan decides how much to spend on each group to maximize profit given the set level of payment for the group. Payment to the plan might be high in relation to the plan’s costs for services if the MA plan is technically efficient relative to TM for a particular diagnosis group.

But relative technical efficiency is not the only factor at play. The MA plan in this hypothetical example has market power and a monopolist maximizes profit by restricting output. Here with a fixed price, the MA plan restricts output (spends less) according to the elasticity of enrollment demand in a group with respect to the level of service spending. This elasticity of demand could differ across HCC groups in unknown ways, leading to no signed correlation between margin and share.

Yet another factor is adverse or favorable selection within a group. If the MA plan suffers adverse selection within a group, higher enrollment would lead to lower average cost, as in the standard Einav-Finkelstein model of a health insurance market (Einav, et al. 2010; Einav and Finkelstein 2011). On the other hand, if the MA plan enjoys favorable selection within a group in relation to TM, the average cost of members goes up with higher enrollment, implying lower margins with higher enrollment. Although there now appears to be only a small amount of favorable selection overall in MA (Newhouse, et al. 2013, 2015), selection patterns could differ across disease groups.

Finally, the model of one MA plan competing against TM does not represent our data. The plans we study are two national plans that compete not just against TM but also against each other and against other national plans and local plans that may be more or less efficient than our plans in some disease areas and so contribute to any pattern of favorable or adverse selection into the plans we study.

In short, one cannot derive predictions about the relationship between profit margins and the relative share of MA to TM enrollees by HCC without making additional assumptions that seem overly restrictive to us. We can get somewhat further, however, by looking at characteristics of certain disease groups and asking why MA plan cost functions relative to TM cost functions might differ across HCC’s. As a preliminary remark, enrollment in MA tends to persist; about 90 percent of MA enrollees remain enrolled in the same plan the following year (Medicare Payment Advisory Commission 2015).⁹ Because of this persistence, MA insurers have a financial incentive to increase the likelihood that their members with chronic diseases comply with prescribed medications, are examined at frequencies that treatment guidelines specify, whereas TM does not offer the same financial incentive.¹⁰ MA insurers, for example, may encourage members to purchase Part D by keeping premiums low, and they have an incentive to optimize the use of drugs to reduce medical costs, an incentive not present in TM. MA plans also have an incentive to discourage low-value care. At a given level of enrollment, therefore, cost functions of MA plans for a variety of chronic disease HCC’s may lie below those of TM. By contrast, in the case of chronic conditions for which treatment is considered non-discretionary or customarily follows a certain protocol, cost functions in MA and TM may be more similar.

One aspect of medical management that MA plans can implement is more judicious use of post-acute care, a key driver of geographic variation in TM cost (Newhouse and Garber 2013). We test whether the intensity of post-acute care in an HCC relates to the observed margin.¹¹ We use the proportion of TM spending on post-acute care in an HCC as a measure of post-acute intensity.

Cost functions may also differ for certain HCC’s if, relative to other HCC’s, they are disproportionately treated by specialists or at hospitals with greater market power, since MA plans negotiate price whereas TM sets a take-it-or-leave-it price. Cancer in particular is often managed by an oncologist or a hematologist and may be treated at a specialty cancer hospital. Such hospitals are much less numerous than general hospitals and thus may have greater market power.¹²

Not only specialty hospitals, but also specialist physicians are likely to have more market power than the more numerous PCP’s. In commercial insurance fees relative to TM are higher for both medical and surgical specialists than fees for PCP’s, consistent with greater market power of specialists (White, et al. 2013; Baker, et al. 2014; Austin and Baker 2015; Cooper, et al. 2015; Clemens and Gottlieb 2017). Although MA fees for all physicians are less than commercial fees – otherwise MA plans would have difficulty competing with TM – a differential between MA specialist fees and MA primary care physician fees relative to TM may hold as well; indeed, White, et al. (2013) show this is the case in the 13 markets they studied.¹³

The foregoing highlighted production efficiency and possibly input prices as sources of difference in MA and TM margins and cost functions, but margin functions may also differ across HCC’s because of differential coding intensity between MA and TM. Because payment under the MA risk adjustment system relies on diagnoses coded on encounter forms, MA insurers have an incentive to code all diagnoses. TM gives hospitals a similar coding incentive, since their payment also depends on coded diagnoses. TM payment to physicians, however, does not depend on diagnosis, although Medicare asks physicians to record diagnoses on the claims form. Presumably because physician reimbursement is unaffected by coding intensity, physician claims in TM are incomplete with respect to diagnosis, and coding intensity is greater in MA (Medicare Payment Advisory Commission 1998; Kronick and Welch 2014; Geruso and Layton 2015). To adjust for greater coding intensity, CMS has made annual downward adjustments in overall MA plan payment since 2010.¹⁴ Before 2014, the period from which our data come, these adjustments were uniform across HCC’s.¹⁵

MA plans may use various mechanisms to maximize coding. One is the use of Health Risk Assessments carried out during a home health visit. Information from such Assessments can be used to assign HCC’s. This mechanism is not used in TM. Another is to contact a physician to verify that a beneficiary still has a specific diagnosis or may have a more complex version of the same diagnosis.

CMS uses prospective risk adjustment, meaning that the diagnoses used to assign HCC’s are those from the prior year. Not all MA patients with HCC’s assigned from Health Risk Assessments or calls to physicians have medical claims in the prior year. Such patients would thus appear in the no-HCC group in TM but would have an HCC coded in MA. If these MA patients who are assigned an HCC in MA but not in TM are of lower cost in the current year than other patients in the HCC group to which they are assigned, margins in that HCC group would increase. Such an increase, however, would be unrelated to relative technical efficiency. We test the sensitivity of our results to omitting those with an HCC but no medical claim in the prior year.

Data

As mentioned above, the data we analyze come from two national insurers and include the revenues they received as well as the medical and drug cost they paid on behalf of their MA membership for 2012 and 2013 for the 100 most frequent HCC’s or combination of HCC’s for each insurer and year. The profit margins we calculate are gross margins that exclude the insurers’ administrative cost and profit. The denominator of the margin is thus simply the medical and drug cost the plans paid. The numerator includes all revenue the plans received on behalf of an individual enrollee, including the plans’ bid, any premium the enrollee paid for the medical or the drug plan, and any risk adjustment revenue less medical and drug cost.¹⁶ The first two elements of the revenue are the same for each enrollee in a county. As a result, the variation in margins across HCC’s that we observe is dominated by two elements: the relative weight for that HCC in the risk adjustment scheme, which is approximately proportional to TM spending for that HCC, and the MA insurer’s medical and drug cost for that HCC.¹⁷ Thus, HCC’s with higher margins could indicate greater technical efficiency in MA relative to TM. We assigned HCC’s using the v12 model, which was in effect in 2012 and 2013.

MA enrollees may be individual or group, the latter coming from an employer with retiree health benefits where MA is available to all qualified retirees from that employer. In the case of group enrollees, drug cost and revenue are not always available because the employer may contract with another insurer or a pharmacy benefit manager for the drug benefit. Our main results therefore rely on only individual MA members, who constitute the large majority of the sample (and the large majority of all MA enrollees). For the individual members we include all medical and drug revenue and cost. In an appendix we show results including group members; these are shown with just medical costs for the entire sample (individual plus group) and also for medical and drug costs for the subset of members for whom we have drug cost. The inclusion of group MA members does not change our conclusions.

The data we have do not include enrollment dates, so persons in our sample may participate for only part of a year or for a full year. Thus, we effectively assume persons enrolled for part of a year are distributed at random across HCC’s. Any bias from violations of this assumption should be small given the large persistence of enrollment from year to year described above.¹⁸ We did, however, exclude the 0.2% of persons who switched plans within the same insurer within a year.¹⁹ We also excluded MA beneficiaries who were under 66 (9% in our sample), who are largely the disabled, as well as institutionalized beneficiaries (1%) because selection mechanisms and cost functions may differ for those groups. We also excluded new Medicare enrollees (4%), because HCC’s are not available for them (prior year claims are lacking) and therefore CMS uses only demographic variables to risk adjust payment for them.

Statistical Methods

We began by testing for the degree of service-level HCC selection. To do so we compared the distribution of MA enrollees across HCC’s or combinations of HCC’s with the distribution of TM enrollees across the same HCC’s or combination of HCC’s.²⁰ We corrected for the geographic distribution differences between MA and TM enrollment using inverse probability weights applied at the age, gender, and Hospital Referral Region (HRR) level; that is, we weighted the proportion of the MA sample in HCC_i to resemble the age, gender, and geographic distribution of the TM sample using the weight $[{\sum }_{i}T{M}_{ijkmn}/{\sum }_{ijkmn}T{M}_{ijkmn}]/[{\sum }_{i}M{A}_{ijkmn}/{\sum }_{ijkmn}M{A}_{ijkmn}],$ where i indexes the HCC, j indexes the beneficiary, k indexes the HRR, m indexes age, and n indexes gender.

We then turned to estimating margins by HCC and first determined the similarity of margins across the two insurers and two years. To do so we computed a correlation matrix of the margins for the two firms and two years.²¹

To gain precision at the HCC level our next step was to pool the data from both plans and years and estimate margins and their associated standard errors for each HCC or combination of HCC’s. Margins at the individual level, however, are very skewed because some individuals in HCC’s with high reimbursement have little spending in a year. As a result, estimated standard errors were large, even with substantial trimming. Consequently, we proceeded indirectly by first estimating cost for each HCC or combination of HCC’s and then using predicted cost to estimate a margin. More specifically, we estimated adjusted cost from a mixed model with a random effect for each HCC or combination of HCC’s:

$$Cos{t}_{ij}= X_{ij}\beta +\hspace{0.17em}{u}_i+\hspace{0.17em}{e}_{ij}$$ (1)

Where $Cos{t}_{ij}$ is the cost for the j^th individual with the i^th HCC or combination of HCC’s, $u_i$ is a random variance component, and $e_{ij}$ is a randomly distributed error term; u and e are assumed to be distributed N(0, σ_u²) and N(0, σ_e²), respectively, and uncorrelated with each other. The X vector includes indicator variables for age (in 5 year bins with a top group of 85+), gender, age*gender, the original reason for Medicare eligibility (disability, end stage renal disease, or age), Medicaid status, and indicator variables for Hospital Referral Region (HRR), year, and insurer.

We next calculated a predicted cost for each HCC or combination of HCC’s as $X_{ij}\widehat{\beta }+ u_i$, where $\widehat{\beta }$ is the estimate of β and then calculated an adjusted average margin for HCC_i as:

$$[ {\sum }_{j}Revenu{e}_{ij}/{\sum }_{j}Predicted Cos{t}_{ij}]-1$$ (2)

Standard errors for margins calculated using equations (1) and (2) were bootstrapped using 100 replications of the process just described; that is, we re-estimated equation (1) 100 times and used the results to calculate (2). Because we control for geography at the level of the HRR, our method of estimation suppresses across-county variation in revenue within HRR, but that should be modest relative to the variation at the individual level in medical and drug cost in the denominator. As a result, our estimated standard errors have a downward bias that is probably small.

The HCC model that CMS uses for risk adjustment is mainly additive in disease groups or HCC’s with few HCC*HCC interactions (Pope, et al. 2004). In Newhouse, et al. (2013) we found that margins varied with the number of HCC’s. This could stem from too few disease-disease interaction terms in the CMS-HCC model, from efficiency differences as the number of HCC’s increases, or from differential coding intensity across HCC’s. We have repeated that test with these newer data.

As mentioned above, to test for the importance of coding we exploit MA plans’ ability to code diagnoses that are ascertained on Health Risk Assessments (HRA’s) during home health visits. MedPAC has raised concern about diagnoses found in HRA’s that were not followed up by any physician claim (Medicare Payment Advisory Commission 2016). Because the HCC’s established by such visits are thought to be an important source of the additional coding intensity in MA, we compare margins using all the claims with those computed by excluding beneficiaries with an HCC code in 2012 but no medical claim in 2011 and similarly for the pair of years 2012 and 2013. For this group we infer the HCC code in 2012 came from an in-home visit in 2011 and similarly for 2013 and 2012. We can therefore test the robustness of our results to omitting this group.

In Appendix A we describe another test of coding effects that we carried out using results from Kronick and Welch (2014). The results of that test, however, left us unable to distinguish coding effects from production efficiencies.

Results

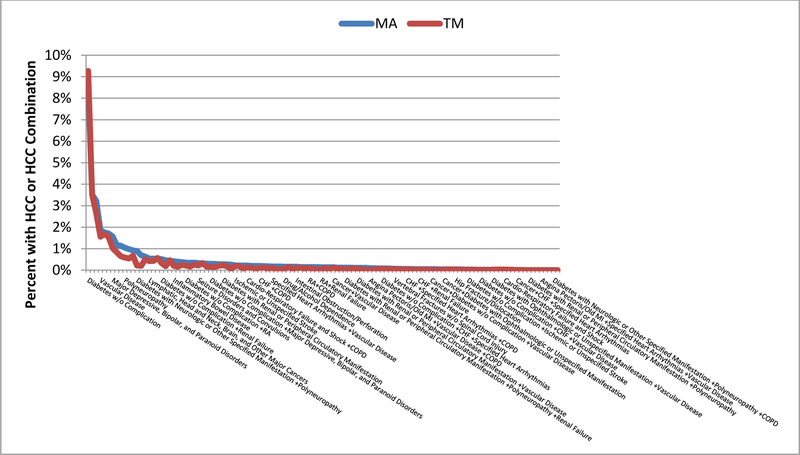
Figure 1 shows differences in the distributions of MA and TM beneficiaries across HCC’s and combinations of HCC’s. Although not shown in Figure 1 to avoid compressing the scale, by far the largest difference between the two distributions is the group with no coded HCC; 65 percent of the TM group has no coded HCC but only 52 percent of the MA group has no coded HCC, consistent with more intensive coding in MA (Kronick and Welch 2014).

Figure 1.

Distribution of TM and MA Enrollees by HCC

*The MA distribution has been reweighted using inverse probability weights to reflect the age, gender, and geographic distribution of the TM sample. More specifically the weight for a TM or MA beneficiary i in HCC j in HRR k in age group m (65–69,70–74,75–79,80+) and gender group n is: $[{\sum }_{i}T{M}_{ijkmn}/{\sum }_{ijkmn}T{M}_{ijkmn}]/[{\sum }_{i}M{A}_{ijkmn}/{\sum }_{ijkmn}M{A}_{ijkmn}],$. To avoid distorting the chart, the proportions for those with No HCCs are not shown. In TM that proportion is 65% versus 52% in MA.

As one can see in Figure 1, among coded HCC’s the absolute differences in percentage shares are small. Other than the 13 percentage point difference in the no coded HCC group, a majority of remaining differences are less than 0.1 percentage point and almost 90 percent are less than 0.25 percentage points (Table 1).

Table 1.

Frequency of Absolute Differences in MA and TM Shares by HCC or Combination of HCC’s

Range of Absolute Difference (percentage points)	Number of HCC’s or Combination of HCC’s
13*	1
0.50–0.70	4
0.25–0.49	8
0.15–0.24	8
0.10–0.14	18
<0.10	68

^*This row is the no coded HCC group.

We now turn to profit margins at the HCC level. Table 2 shows the correlation matrix of unadjusted margins for each insurer-year, weighted by the proportion of spending in each HCC or combination of HCC’s. The n shown is the number of common HCC’s for that pair of insurer-years. Within year, the correlation coefficients between the two firms are 0.43 in 2012 and 0.44 in 2013 for the 87 and 91 HCC’s or combination of HCC’s that are common across the two insurers in those years, respectively. Within insurer the weighted correlation coefficients are 0.83 and 0.72 across the two years. The larger correlations within insurer reflect the stability of enrollees in each plan over time, but that all the correlations are below 1.0 indicates the magnitude of random error from the right-skewness of health care spending. To improve precision, the remainder of our results pool across the two insurers and two years.

Table 2a.

Correlation Coefficients of Unadjusted Margins Between Insurers and Years, Weighted

		Insurer 1 2012	Insurer 1 2013	Insurer 2 2012	Insurer 2 2013
Insurer 1 2012	correlation	1
	n	100
Insurer 1 2013	correlation	0.83	1
	n	96	100
Insurer 2 2012	correlation	0.43	0.48	1
	n	87	87	100
Insurer 2 2013	correlation	0.34	0.44	0.72	1
	n	91	91	92	100

Appendix Table B1 gives margins for all 117 HCC’s or combinations of HCC’s in our data, but to simplify presentation for the reader Table 3 gives the margins (minus an arbitrary constant) for just the HCC’s with the ten largest and ten smallest margins.²² Margins with 95% confidence intervals that exclude zero are bolded.

Table 3.

The Ten HCC’s with the Most Positive and Most Negative Margins Minus an Arbitrary Constant Using Pooled Results for the Non-Group Business of Both Insurers for Both Years^*

HCC1	HCC2	HCC3	Adjusted Margin	Unadjusted Margin
The Ten Most Positive HCC’s or Combinations
Disorders of Immunity			0.582	0.864
Diabetes with Renal or Peripheral Circulatory Manifestation	Polyneuropathy	Vascular Disease /Renal Failure**	0.487	0.497
Congestive Heart Failure	Renal Failure		0.343	0.252
Diabetes with Neurologic or Other Specified Manifestation	Polyneuropathy	Chronic Obstructive Pulmonary Disease	0.332	0.251
Diabetes without Complication	Congestive Heart Failure	Chronic Obstructive Pulmonary Disease	0.284	0.115
Major Depressive, Bipolar, and Paranoid Disorders	Vascular Disease		0.241	0.279
Diabetes with Renal or Peripheral Circulatory Manifestation	Polyneuropathy	Vascular Disease	0.222	0.169
Diabetes with Renal or Peripheral Circulatory Manifestation	Polyneuropathy	Renal Failure	0.212	0.263
Vascular Disease	Chronic Obstructive Pulmonary Disease	Renal Failure	0.186	0.247
Diabetes with Renal or Peripheral Circulatory Manifestation	Vascular Disease	Renal Failure	0.176	0.188
The Ten Most Negative HCC’s or Combinations
Hip Fracture/Dislocation			−0.501	−0.541
Congestive Heart Failure	Vascular Disease	Chronic Obstructive Pulmonary Disease	−0.503	−0.630
Diabetes with Ophthalmologic or Unspecified Manifestation	Vascular Disease		−0.506	−0.577
Angina Pectoris/Old Myocardial Infarction	Specified Heart Arrhythmias	Vascular Disease	−0.518	−0.578
Breast, Prostate, Colorectal and Other Cancers and Tumors	Angina Pectoris/Old Myocardial Infarction		−0.525	−0.558
Inflammatory Bowel Disease			−0.565	−0.560
Congestive Heart Failure	Angina Pectoris/Old Myocardial Infarction	Vascular Disease	−0.600	−0.705
Diabetes without Complication	Congestive Heart Failure	Vascular Disease	−0.601	−0.693
Lung, Upper Digestive Tract, and Other Severe Cancers			−0.643	−0.672
Congestive Heart Failure	Angina Pectoris/Old Myocardial Infarction	Specified Heart Arrhythmias/Vascular Disease**	−0.703	−0.792

^*Margin is Revenue from HCC_i/Medical and Drug Cost of HCC_i - 1. An arbitrary constant has been subtracted from each value to preserve confidentiality.

^**For these two rows only, there were four conditions that were coded; to save adding a column, we show both the third and fourth comorbidity in one cell.

Like the results in Newhouse, et al. (2013), the margins of the various HCC’s or combination of HCC’s span a wide range.²³ The range of the unadjusted (raw) margins is 166 percentage points from the most profitable HCC, disorders of immunity, to the least profitable, a combination of congestive heart failure with comorbidities of angina pectoris/old myocardial infarction, heart arrhythmias, and vascular disease. Using the adjusted margins, the range is somewhat less but still large, 129 percentage points. Overall, the adjustments do not much change the estimated margins; the Pearson correlation coefficient between the adjusted and unadjusted margins is 0.98. The modest effect of the adjustments implies the standard errors of the adjusted margins are mainly driven by the error variance rather than the variance explained by the covariates in the X vector.

The results shown in Table 3 and Appendix Table B1 are for the insurers’ individual MA business. In Appendix Table B2 we show the results including their group MA business, with drug claims for that portion of the group business for which there are data and with medical claims only for the entire sample.²⁴ Our conclusions are not materially changed by including data from the group MA plans.

We found in Newhouse, et al. (2013) that diabetes, chronic heart failure (CHF), and chronic obstructive pulmonary disease (COPD), diseases capable of medical management and typically managed by PCP’s, had notably higher margins than diseases typically managed by specialists such as cancer and rheumatoid arthritis.²⁵ In the earlier paper we simply assumed the type of physician that managed the various conditions; Table 4 confirms that the earlier assumption about which type of physician managed which disease was correct. Using the 20% random sample of TM Part B, it shows the percent of all Part B charges and the percent of all outpatient charges generated by primary care providers in 2012 and 2013 for six diagnoses.²⁶ We have added inflammatory bowel disease to the group of diseases typically managed by specialists used in the earlier paper; this disease was not in the earlier sample of 48 HCC’s. One can reject the hypothesis of no difference between the proportion of the charges allowed from PCP’s for each of the three diseases usually managed by primary care providers and each of the three managed by specialists at the 0.001 level.

Table 4.

Percentage of Allowed Charges Attributed to Primary Care Providers, by Disease and Year^*

	All	Outpatient
2012
Diabetes	59.8%	70.5%
Chronic Heart Failure	48.9%	56.4%
Chronic Obstructive Pulmonary Disease	58.4%	62.2%
Cancer	4.5%	8.8%
Inflammatory Bowel Disease	18.6%	30.4%
Rheumatoid Arthritis	14.1%	19.8%
2013
Diabetes	57.7%	69.5%
Chronic Heart Failure	48.4%	54.7%
Chronic Obstructive Pulmonary Disease	58.1%	61.3%
Cancer	4.7%	9.4%
Inflammatory Bowel Disease	18.2%	30.7%
Rheumatoid Arthritis	13.2%	19.3%

^*This analysis used the 20% Part B Medicare carrier office and outpatient hospital claims files with a place of service code of 11 or 22. Primary care providers have specialty codes of internal medicine, family medicine, general practice, and geriatrics. Specialty providers are all non-primary care physician specialties; we excluded allied health providers such as nurse practitioners and physician assistants.

That the three diseases typically managed by PCP’s and capable of medical management have higher margins than those commonly managed by specialists can be seen in Table 5, which summarizes the results in Appendix Table B1 for the diseases shown in Table 4. For example, of the 117 HCC’s or combinations of HCC’s shown in Appendix Table B1, 39 involve diabetes. Table 5 shows that those 39 diabetes HCC’s, when weighted by their frequency of occurrence, are 7.3 percentage points (= −0.268 - (−0.341)) more profitable than the weighted average of all HCC’s.²⁷ The 21 HCC’s that involve COPD are 6.1 percentage points more profitable than the weighted average, and the 19 that involve CHF are 13.9 percentage points more profitable. As in the earlier work, the 17 various cancer HCC’s as well as rheumatoid arthritis are less profitable than average, 6 and 5 percentage points respectively. Inflammatory bowel disease is much less profitable than average.

Table 5.

Margins by Disease minus a Constant

	Number of HCC groups	Weighted Mean Margin Minus a Constant*	SE of Weighted Mean Margin	Difference from Weighted Mean	Standard Error of Difference from Weighted Mean	2-sided p-value for difference
Overall	117	−0.341	0.013	--	--	--
Diabetes	39	−0.268	0.029	0.073	0.031	0.025
COPD	20	−0.280	0.027	0.061	0.030	0.051
CHF	19	−0.202	0.042	0.139	0.044	0.005
Cancer	17	−0.401	0.020	−0.060	0.024	0.017
Rheumatoid Arthritis	1	−0.393	0.019	−0.052	0.023	0.026
Inflammatory Bowel Disease	1	−0.565	0.069	−0.224	0.071	0.002
Severe Mental Illness**	5	−0.169	0.066	0.172	0.067	0.058
No HCC	1	−0.421	0.005	−0.080	0.014	<0.001

^*Margins are weighted by the proportion of individuals in the HCC’s or combination of HCC’s shown in Table B1.

^**Major Depressive, Bipolar, and Paranoid Disorders.

Taken as a group, the three diseases managed by PCP’s and capable of medical management have a 13.7 percentage point higher profit margins than the group of three diseases commonly managed by specialists (Table 6). Interestingly, given the well-known results of Frank, Glazer, and McGuire showing incentives for service-level selection against mental health services in a Medicaid population (Frank, et al. 2000), the five HCC combinations involving Major Depressive, Bipolar, and Paranoid Disorders are among the most profitable conditions, 17 percentage points more than average (p = 0.06).

Table 6.

Margins of Diseases Typically Managed by PCP’s versus Specialists

	Number of HCC groups	Weighted Mean Margin - Constant*	SE of Weighted Mean Margin	Difference	SE of Difference	2-sided p-value for difference
Diabetes, COPD, CHF	67	−0.268	0.020
Cancer, Rheumatoid Arthritis, IBD	19	−0.405	0.018	0.137	0.027	<0.0001

MA plans do appear to achieve savings by reducing spending on post-acute care. Table 7 shows TM diagnoses with greater proportions of spending on post-acute care have higher margins in MA.

Table 7.

Relationship between Margins and % of TM Parts A and B Charges from Post-Acute Care^*

	Coefficient	SE	p-value	95%	CI
% Post-Acute	0.0391	0.0058	<0.0001	0.0277	0.0505
Intercept	−0.3380	0.0595	<0.0001	−0.4558	−0.2202

^*Post-Acute Care is defined as the proportion of all TM Parts A and B charges that are from Skilled Nursing Facilities, home health, Inpatient Rehabilitation Facilities, and Long-Term Care Hospitals. These results are weighted by the number of beneficiaries in the HCC. This relationship is robust if the observations are not weighted and also if beneficiaries with an HCC but no medical claim are deleted from the sample.

As discussed above, one cannot sign the relationship between the margin and an HCC share. Empirically, however, we found no association between the MA share and the margin. When we regressed the difference between the MA and TM share in an HCC or combination of HCC’s on the margin for that HCC or combination of HCC’s, the estimated effect size is effectively zero and is not significant at the 5% level (Table 8). More specifically, a 1 percentage point increase in the margin in a given HCC is estimated to result in only a 0.0043 percentage point increase in the MA share, with the limits of the 95 percent confidence interval equal to −0.006 and +0.014 percentage points.

Table 8.

Over-or Underrepresentation in the MA Plans as a Function of Adjusted Margin^*

Outcome	Adjusted R2		Coefficient	Standard Error	95% Confidence Interval
MA Share – TM Share*	−0.0024	Margin	0.0043	0.0050	(−0.0057,0.0142)
		Constant	−0.1084	0.1497	(−0.4049, 0.1881)

^*MA Share – TM Share is the reweighted proportion of members in each HCC group in the MA Plans (pooled for both insurers for both years) less the corresponding TM proportion (pooled for both years). See the footnote to Figure 1 for the weight.

Our earlier results suggested that margins were higher on those with fewer comorbidities. The current results show the opposite; margins rise with the number of comorbidities and by a substantial amount (Table 9). This result could stem from having data from an additional plan. It is consistent both with MA production efficiencies among those with more comorbidities (though any such efficiencies did not appear in the earlier data) and also with more intensive coding in MA.

Table 9.

Predicted Margins, by Number of Comorbidities^*

Number of HCC’s	Difference from Reference Category	Standard error
0	Reference Category	--
1	0.130	0.122
2	0.207	0.121
3	0.310	0.123
4	0.437	0.161

^*Differences generated from adjusted predictions, meaning a prediction was generated from each set of covariates and then averaged.

Table 10 shows results when deleting the 5 percent of MA beneficiaries with HCC’s in the following year but with no medical claim in the prior calendar year.²⁸ Comparing Tables 5 and 10, one can see that margins for diabetes, COPF, CHF, cancer, inflammatory bowel disease, and rheumatoid arthritis change only by around a percentage point.²⁹ The point estimate of the overall weighted margin falls 1.1 percentage points, which is the expected direction if the Health Risk Assessments are profitable, but the change is within sampling error.

Table 10.

Predicted Margins Minus a Constant, Medical Claims only

	Number of HCC groups	Weighted Mean Margin Minus a Constant*	SE of Weighted Mean Margin	Difference from Weighted Mean	Standard Error of Difference from Weighted Mean	2-sided p-value for difference
Overall	117	−0.352	0.013	--	--	--
Diabetes	39	−0.279	0.029	−0.073	0.031	0.023
COPD	20	−0.293	0.027	−0.059	0.030	0.060
CHF	19	−0.217	0.040	0.135	0.042	0.004
Cancer	17	−0.409	0.020	−0.056	0.024	0.025
Rheumatoid Arthritis	1	−0.402	0.019	−0.049	0.023	0.036
Inflammatory Bowel Disease	1	−0.565	0.063	−0.213	0.065	0.001
Severe Mental Illness**	5	−0.156	0.070	0.196	0.071	0.048
No HCC	1	−0.424	0.005	−0.072	0.014	<0.001
Margin Difference Between Group of PCP and Group of Specialist Diseases
Diabetes, COPD, CHF	67	−0.280	0.020
Cancer, Rheumatoid Arthritis, Inflammatory Bowel Disease	19	−0.412	0.018	0.133	0.027	<0.0001

^*Margins are weighted by the proportion of individuals in the HCC’s or combination of HCC’s shown in Table B1.

^**Major Depressive, Bipolar, and Paranoid Disorders.

Discussion

We reject the hypothesis that the distribution of beneficiaries across HCC’s or combination of HCC’s is the same between MA and TM. But by far the largest difference in the two distributions in absolute terms is the 13 percentage point greater proportion of MA beneficiaries with an HCC code; the difference in shares among those with a coded HCC are small, with close to 90 percent of them less than 0.25 percentage points and the largest 0.70 percentage points. The larger proportion with an HCC code in MA almost certainly reflects greater coding intensity, and the modest differences in shares among those with specific HCC codes is consistent with little service-level selection.

We have shown that our earlier result of differences in average profitability across HCC’s is not attributable to sampling error. Even allowing for sampling error, substantial differences in margins across various HCC’s or combinations of HCC’s remain. Although intuitively it may seem as if high margins should motivate plans to engage in service-level selection efforts, we have shown that the relationship between margins and the relative share of MA and TM enrollees in an HCC cannot be signed without additional assumptions since the observed profit margin in an HCC is an average and incentives for selection depend on conditions at the margin. Empirically there appears to be little relationship between profit margins and shares.

We replicated a result from the earlier data that common chronic diseases that are typically managed by PCP’s such as diabetes, COPD, and CHF are more profitable in MA than chronic conditions typically managed by specialists such as cancer, rheumatoid arthritis, and inflammatory bowel diseases. This pattern is suggestive of production efficiencies in MA in diabetes, COPD, and CHF relative to cancer, rheumatoid arthritis, and inflammatory bowel disease, although we cannot rule out other explanations. Furthermore, the differences in margins among these six conditions are not much affected by excluding claims from beneficiaries who had an HCC established through an in-home Health Risk Appraisal but had no subsequent medical claim. We also showed that HCC’s with a higher proportion of spending on post-acute care in TM have higher margins in MA, consistent with efficiency from better medical management in MA or with more favorable selection in those HCCs. Further progress on assessing relative production efficiencies across HCC’s is likely to require more detailed clinical data. Finally, that 20 percent of MA beneficiaries had an HCC code from an in home visit and no subsequent medical claim indicates that subsequent research comparing MA and TM that uses HCC codes or risk scores derived from claims data needs to consider potential biases from coding effects.

Table 2b.

Correlation Coefficients of Adjusted Margins Between Insurers and Years, Weighted

		Insurer 1 2012	Insurer 1 2013	Insurer 2 2012	Insurer 2 2013
Insurer 1 2012	correlation	1
	n	100
Insurer 1 2013	correlation	0.87	1
	n	96	100
Insurer 2 2012	correlation	0.57	0.60	1
	n	87	87	100
Insurer 2 2013	correlation	0.49	0.57	0.77	1
	n	91	91	92	100