Abstract
Background
Cardiovascular disease and chronic kidney disease share several common risk factors. The Framingham risk score is hypothesized to predict chronic kidney disease development. We determined if the Framingham risk scoring system can correctly predict incident chronic kidney disease in the general population.
Methods
This study included 9,080 subjects who participated in the Korean Genome and Epidemiology Study between 2001 and 2014 and had normal renal function. The subjects were classified into low- (< 10%), intermediate- (10–20%), and high- (> 20%) risk groups based on baseline Framingham risk scores. The primary endpoint was de novo chronic kidney disease development (estimated glomerular filtration rate [eGFR], < 60 mL/min/1.73 m2).
Results
During a mean follow-up duration of 8.9 ± 4.3 years, 312 (5.3%), 217 (10.8%), and 205 (16.9%) subjects developed chronic kidney disease in the low, intermediate, and high risk groups, respectively (P < 0.001). Multivariable analysis after adjustment for confounding factors showed the hazard ratios for the high- and intermediate risk groups were 2.674 (95% confidence interval [CI], 2.197–3.255) and 1.734 (95% CI, 1.447–2.078), respectively. This association was consistently observed irrespective of proteinuria, age, sex, obesity, or hypertension. The predictive power of this scoring system was lower than that of renal parameters, such as eGFR and proteinuria, but increased when both were included in the prediction model.
Conclusion
The Framingham risk score predicted incident chronic kidney disease and enhanced risk stratification in conjunction with traditional renal parameters in the general population with normal renal function.
Keywords: Chronic kidney disease, Framingham risk score, Korean Genome and Epidemiology Study, Proteinuria
Introduction
The prevalence of chronic kidney disease (CKD) has markedly increased over the past 10 years, and CKD has become a public health problem worldwide [1]. Because CKD is progressive and causes declining kidney function, it is critical to establish a confirmative risk stratification strategy and correct reversible risk factors. CKD can jeopardize patient health, work performance, and well-being, particularly when kidney function is seriously decreased [2].
Many well-known traditional risk factors predispose patients to CKD, including diabetes mellitus and hypertension. Many researchers have attempted to find novel biomarkers and predictive values for CKD [3]. However, these biomarkers are generally assessed only for research purposes and are not easily adopted in clinical practice. Currently, there is no widely accepted instrument that comprehensively integrates risk factors associated with incident CKD development. The ideal model should accurately predict future events, be easily implemented, and universally generalize to diverse populations.
The Framingham Heart Study started in 1948 and included 5,209 adults from Framingham, Massachusetts, USA [4]. This long-term cohort study has greatly contributed to the identification of cardiovascular disease (CVD) risk factors and facilitated the development of useful clinical tools to predict absolute CVD risk [5]. The Framingham prediction algorithms have been widely adopted to assess absolute risk and guide the intensity of risk factor interventions. The Framingham risk score has been validated by many studies and is the most commonly used algorithm in clinical practice. The original score was intended for use in non-diabetic patients aged 30 to 74 years with no coronary heart disease or intermittent claudication history. In 2008, it was revised and became the Framingham general CVD risk score [6].
Interestingly, CKD and CVD share common traditional risk factors, such as smoking, obesity, hypertension, diabetes mellitus, and dyslipidemia [7–9]. Furthermore, major adverse cardiac and cerebrovascular events occur more frequently in patients with estimated glomerular filtration rate (eGFR) < 60 mL/min/1.73 m2 than in those with normal renal function [10]. Conversely, uremic toxin, which accumulates in CKD, is strongly associated with adverse cardiovascular events and reducing uremic toxin may confer renal and cardiovascular protection [11]. Because the Framingham risk score is well validated for cardiovascular risk stratification, we aimed to determine whether it can perform equally well and correctly predict incident CKD in the general population.
Methods
Study population
We used data from the Korean Genome and Epidemiology Study, which is a population-based prospective cohort study performed to assess the prevalence, incidence, and risk factors for chronic degenerative disorders, such as hypertension, diabetes mellitus, and CVD. Two representative communities comprised this cohort: Anseong (rural) and Ansan cohorts (urban). Each cohort consisted of Korean males and females aged 40 to 69 years with a homogeneous ethnic background.
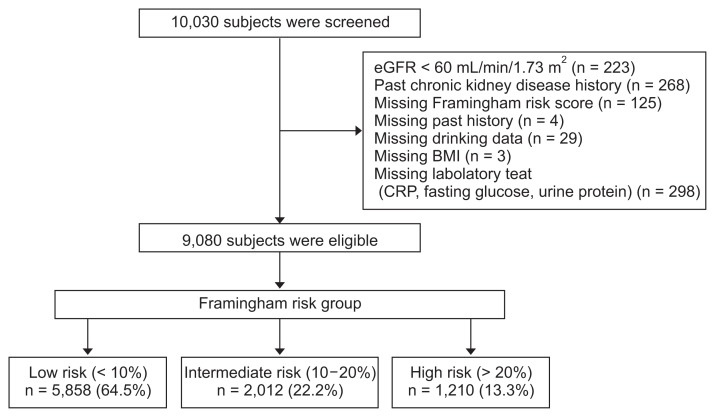
The baseline survey was performed from 2001 to 2002 in a cohort of 10,030 adults who were repeatedly examined at 2-year intervals. Of this sample, 950 individuals were excluded for the following reasons: baseline eGFR of < 60 mL/min/1.73 m2 (n = 223); underlying kidney disease (n = 268); missing Framingham risk score (n = 125); missing past history (n = 4); missing alcohol consumption data (n = 29); missing body mass index (BMI) data (n = 3); and missing laboratory test data (n = 298). A total of 9,080 participants were finally included in the current study sample (Fig. 1).
Figure 1. Flow diagram of study cohort.
BMI, body mass index; CRP, C-reactive protein; eGFR, estimated glomerular filtration rate; HDL, high density lipoprotein.
This study was conducted according to the Declaration of Helsinki guidelines. All subjects were fully informed of the study content and provided written informed consent for data use. The study was approved by the Institutional Review Board of Yonsei University Health System Clinical Trial Center (IRB no. 4-2016-0100).
Clinical and laboratory measurements
All participants underwent comprehensive health examinations and interviews according to the site visit schedule. The health examination included an anthropometric index evaluation and biological specimen collection. Participants completed interviewer-administered questionnaires including questions on age, current smoking, alcohol intake (at least once per month), marital status, and educational level. BMI was calculated as follows: weight (kg)/height (m2). Waist circumference was measured along a horizontal plane midway between the inferior margin of the ribs and superior border of the iliac crest. Participants also completed interviewer-administered questionnaires regarding their medical histories including medication use, family disease history, and lifestyle factors, such as smoking status and alcohol intake. Blood pressure was measured using mercury sphygmomanometers (Baumanometer-Standby; W. A. Baum Co., Inc., Copiague, NY, USA). All subjects were instructed to relax in the sitting position for at least 10 min before blood pressure measurement. The mean of two blood pressure readings was used for analyses.
After at least 8 hours of fasting, blood, and urine samples were collected and delivered to a central laboratory (Seoul Clinical Laboratories, Seoul, Korea) within 24 hours of sampling. Plasma was separated by centrifugation (2,000 revolution per minute, 20 minutes at 4°C), and biochemical measurements were conducted immediately. The plasma concentrations of glucose, total cholesterol, triglycerides, and high-density lipoprotein-cholesterol (HDL-C) were measured enzymatically using a 747 Chemistry Analyzer (Hitachi, Tokyo, Japan). The low-density lipoprotein-cholesterol (LDL-C) concentration was calculated using Friedewald’s equation [12]. The serum creatinine concentration was measured using Jaffe’s method with a Hitachi Automatic Analyzer 7600 (Hitachi). Urinalysis was performed using fresh urine samples and measured semiquantitatively using the urine dipstick test (URISCAN Pro II; YD Diagnostics Corp., Yongin, Korea) with the findings reported using six grades: absent, trace, 1+, 2+, 3+, and 4+. Proteinuria was defined as presence of protein ≥ 1+. Because creatinine was not measured using an isotope dilution mass spectrometry-traceable method, we adjusted creatinine levels using a conversion equation [13]. The eGFR was then calculated using the CKD-Epidemiology Collaboration equation: eGFR (mL/min/1.73 m2) = 141 × min (serum creatinine [sCr]/κ, 1)α × max (sCr/κ, 1)−1.209 × 0.993age (yr) × 1.018 (if women) × 1.159 (if black), where κ is 0.7 for women and 0.9 for men; α is −0.329 for women and −0.411 for men; min indicates the minimum of sCr/κ or 1; and max indicates the maximum of sCr/κ or 1. This equation can more precisely estimate kidney function in people with eGFR ≥ 60 mL/min/1.73 m2[14].
The Framingham risk score
Framingham general CVD risk scores were calculated for the total study population based on the following characteristics: age, smoking history (current, past, or never), diabetes mellitus (absence or presence), systolic blood pressure (mmHg), HDL-C concentration (mg/dL), and total cholesterol concentration (mg/dL). The Framingham risk score ranges from −3 to 21+ and indicates 10-year risk of developing CVD. The subjects were classified into three risk groups according to their scores: low (< 13 in women, < 11 in men; risk, < 10%), intermediate (13–17 in women, 11–14 in men; risk, 10–20%), and high (> 17 in women, > 14 in men; risk, > 20%) [6].
Study endpoint
The primary outcome was de novo CKD development, defined as the development of CKD stage 3, which is eGFR of < 60 mL/min/1.73 m2 for at least two consecutive measurements during follow-up. The first of these measurements was designated to be the study endpoint. Secondary outcomes included decline in an eGFR ≥ 40 mL/min/1.73 m2 from the baseline value during follow-up, annual decline in eGFR, and development of proteinuria ≥ 1+. Proteinuria was analyzed only in subjects with proteinuria < 1+.
Statistical analysis
Statistical analyses were performed using IBM SPSS for Windows version 23.0 (IBM Corp., Armonk, NY, USA). Continuous variables were presented as means ± standard deviations or medians (interquartile ranges) and categorical variables as frequencies and percentages. Patient characteristics were compared using one-way analysis of variance for continuous variables and chi-square tests for categorical variables. The Kruskal–Wallis test was used for data with skewed distributions. The cumulative incidence of CKD stage 3 in the three risk groups was assessed using Kaplan–Meier plots. Survival time was defined as the time between enrollment and first renal outcome onset. There were 887 (9.8%) patients who were lost to follow-up, and these were censored at the last examination date. To detect independent associations between Framingham risk score and incident stage 3, we constructed stepwise multivariable Cox proportional hazard models. Model 1 represents crude risk without adjustment. Model 2 was adjusted for residence (Ansan or Anseong), educational level, income, coronary artery disease history, and alcohol intake (non-drinker, ex-drinker, or current drinker). We constructed model 3 after adjustments for renal parameters, including eGFR and proteinuria. Finally, we constructed model 4 after including fasting glucose, albumin, triglyceride, C-reactive protein (CRP), and LDL-C concentrations. Results were expressed as hazard ratios (HRs) with 95% confidence intervals (CIs). The rate of renal function decline per year was assessed using the slope of eGFR obtained from a generalized linear mixed model. We used receiver-operating characteristic (ROC) curve analysis and C-index estimation to compare the accuracies of the Framingham risk score and of other individual traditional risk factors. Finally, to provide an unbiased evaluation of the cohort dataset, we conducted internal validation for the final model using a 10-fold cross-validation technique. The original data set was randomly partitioned into 10 equally-sized subsamples (n = 908). Of the 10 subsamples, a single sample acted as the test data set for the prediction model, and the remaining 9 subsamples were treated as training data sets. The cross-validation technique was then repeated 10 times, with each of the 10 subsamples used exactly once as the validation data. The average of the 10 iterations was calculated to assess the reliability for the model. Then, we performed ROC and C-statistics analyses. P values less than 0.05 were considered statistically significant.
Results
Baseline patient characteristics
The baseline patient characteristics according to the Framingham risk groups are shown in Table 1. The mean age was 51.8 ± 8.7 years, and 4,412 (48.6%) subjects were male. Of the 9,080 subjects, there were 5,850 (64.4%), 2,012 (22.2%), and 1,210 (13.3%) subjects in the low (< 10%), intermediate (10–20%), and high (> 20%) risk groups, respectively. The high- and intermediate risk group subjects were older and had lower eGFR than the low risk group subjects. Not surprisingly, there were more subjects with hypertension and smokers in the high risk group; they also had higher total cholesterol, triglyceride, LDL-C, and CRP concentrations than the low risk group subjects. The proportion of subjects with lower income and educational levels was also higher in the high risk group.
Table 1.
Baseline characteristics of patients classified by Framingham risk score
| Variable | Total (n = 9,080) | Low risk (n =5,858) | Intermediate risk (n = 2,012) | High risk (n = 1,210) | P value |
|---|---|---|---|---|---|
| Demographic data | |||||
| Age (yr) | 51.8 ± 8.7 | 48.8 ± 7.6 | 55.2 ± 8.3 | 60.5 ± 6.5 | < 0.001 |
| Sex, male | 4,412 (48.6) | 1,961 (33.5) | 1,440 (71.6) | 1,011 (83.6) | < 0.001 |
| Monthly wage, < $1,090 | 3,062 (33.7) | 1,607 (27.4) | 827 (41.1) | 628 (51.9) | < 0.001 |
| Married | 8,958 (98.7) | 5,776 (98.6) | 1,982 (98.5) | 1,200 (99.2) | 0.233 |
| Education ≥ 9 yr | 1,270 (14.0) | 836 (14.3) | 303 (15.1) | 131 (10.8) | 0.002 |
| SBP (mmHg) | 121.1 ± 18.2 | 114.8 ± 14.3 | 128.9 ± 18.4 | 138.2 ± 18.8 | < 0.001 |
| DBP (mmHg) | 80.2 ± 11.4 | 77.0 ± 10.2 | 85.0 ± 11.3 | 87.7 ± 10.7 | < 0.001 |
| eGFR (mL/min/1.73 m2) | 92.9 ± 13.2 | 94.9 ± 13.0 | 90.1 ± 12.7 | 87.6 ± 12.2 | 0.009 |
| Body mass index (kg/m2) | 24.5 ± 3.1 | 24.5 ± 3.1 | 24.8 ± 3.2 | 24.4 ± 3.2 | 0.099 |
| Smoking status | < 0.001 | ||||
| Never | 5,268 (58.0) | 4,249 (72.5) | 767 (38.1) | 252 (20.8) | |
| Former | 1,426 (15.7) | 839 (14.3) | 393 (19.5) | 194 (16.0) | |
| Current | 2,386 (26.3) | 770 (13.1) | 852 (42.4) | 764 (63.1) | |
| Alcohol status | < 0.001 | ||||
| Never | 4,121 (45.4) | 3,066 (52.3) | 716 (35.6) | 339 (28.0) | |
| Former | 578 (6.4) | 262 (4.5) | 180 (8.9) | 136 (11.2) | |
| Current | 4,381 (48.2) | 2,530 (43.2) | 1,116 (55.5) | 735 (60.7) | |
| Comorbidities | |||||
| Hypertension | 1,253 (13.8) | 375 (6.4) | 444 (22.1) | 434 (35.9) | < 0.001 |
| Diabetes mellitus | 369 (4.1) | 85 (1.5) | 119 (5.9) | 165 (13.6) | < 0.001 |
| Coronary artery disease | 64 (0.7) | 24 (0.4) | 25 (1.2) | 15 (1.2) | < 0.001 |
| Myocardial infarction | 70 (0.8) | 31 (0.5) | 19 (0.9) | 20 (1.7) | < 0.001 |
| Cerebrovascular accident | 92 (1.0) | 24 (0.4) | 38 (1.9) | 30 (2.5) | < 0.001 |
| Laboratory parameters | |||||
| Fasting glucose (mg/dL) | 92.3 ± 22.6 | 89.2 ± 15.5 | 95.3 ± 26.0 | 102.7 ± 37.1 | < 0.001 |
| BUN (mg/dL) | 14.2 ± 3.6 | 14.0 ± 3.5 | 14.7 ± 3.6 | 14.8 ± 3.8 | < 0.001 |
| Creatinine (mg/dL) | 0.83 ± 0.17 | 0.81 ± 0.16 | 0.88 ± 0.17 | 0.89 ± 0.16 | < 0.001 |
| Hemoglobin (g/dL) | 13.6 ± 1.6 | 13.2 ± 1.6 | 14.2 ± 1.4 | 14.4 ± 1.3 | < 0.001 |
| Total cholesterol (mg/dL) | 191.2 ± 35.5 | 187.5 ± 33.4 | 198.0 ± 37.1 | 197.5 ± 40.1 | < 0.001 |
| HDL-C (mg/dL) | 49.7 ± 11.9 | 51.2 ± 11.9 | 47.4 ± 11.6 | 46.3 ± 10.9 | < 0.001 |
| Triglyceride (mg/dL) | 151.4 ± 108.4 | 133.1 ± 90.4 | 177.5 ± 124.9 | 196.2 ± 133.9 | < 0.001 |
| cLDL-C (mg/dL) | 114.6 ± 32.8 | 113.1 ± 30.6 | 118.2 ± 35.1 | 115.6 ± 38.1 | < 0.001 |
| CRP (mg/dL) | 0.14 (0.07–0.36) | 0.13 (0.06–0.22) | 0.17 (0.08–0.29) | 0.17 (0.09–0.33) | < 0.001 |
| Albumin (g/dL) | 4.2 ± 0.3 | 4.2 ± 0.3 | 4.3 ± 0.3 | 4.2 ± 0.3 | 0.002 |
| Urine protein ≥ 1+ | 190 (2.1) | 97 (1.7) | 46 (2.3) | 47 (3.9) | < 0.001 |
Data are presented as mean ± standard deviation or number (%), if variable showed skewed deviation, presented as median ± interquartile range.
BUN, blood urea nitrogen; cLDL-C, calculated low density lipoprotein-cholesterol; CRP, C-reactive protein; DBP, diastolic blood pressure; eGFR, estimated glomerular filtration rate; HDL-C, high density lipoprotein-cholesterol; SBP, systolic blood pressure.
Incident CKD risk according to Framingham risk score groups
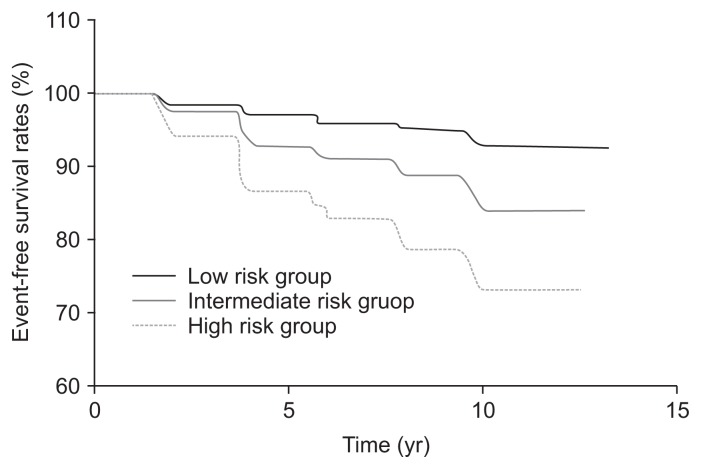
A total of 734 (8.1%) renal events occurred during a mean follow-up duration of 8.9 ± 4.3 years. There were 312 (5.3%), 217 (10.8%), and 205 (16.9%) subjects who developed CKD stage 3 in the low, intermediate, and high risk groups, respectively (P < 0.001) (Table 2). The Kaplan–Meier curve for incident CKD stage 3 according to Framingham risk score group is shown in Fig. 2. The number of cumulative renal events was significantly higher in the high risk group than in the low risk group. The intermediate risk group also had a higher number of cumulative renal events than the low risk group. As expected, more cardiovascular events occurred in the high risk group (Table 2).
Table 2.
Renal and cardiovascular outcomes classified by Framingham risk score
| Total | Framingham risk score groups | |||
|---|---|---|---|---|
|
| ||||
| Low risk | Intermediate risk | High risk | ||
| No. of participants | 9,080 | 5,858 | 2,012 | 1,210 |
| Person-year | 80,521.1 | 53,193.2 | 17,415.6 | 9,912.3 |
| eGFR < 60 mL/min/1.73 m2 | ||||
| Events | 734 | 312 | 217 | 205 |
| Events/1,000 person-year | 9.3 | 5.9 | 12.8 | 21.8 |
| Cardiovascular events | ||||
| Events | 246 | 111 | 75 | 60 |
| Events/1,000 person-year | 3.1 | 2.1 | 4.4 | 6.3 |
Data are presented as number person-year or incidence rate per 1,000 person-year.
eGFR, estimated glomerular filtration rate.
Figure 2. Kaplan–Meier curve for incident chronic kidney disease development according to Framingham risk score.
Next, we constructed stepwise multivariable Cox models to confirm this association. The association was similar in multivariable analysis after adjustment for demographic factors, including residence (Ansan or Anseong), socioeconomic status, alcohol status, and coronary artery disease history. Further adjustments for eGFR and proteinuria yielded the same results. In model 4, with further adjustments for fasting glucose, albumin, triglyceride, CRP, and LDL-C concentrations, the high risk group had a 2.7-fold increased risk of incident CKD stage 3 risk compared with the low risk group (HR, 2.674; 95% CI, 2.197–3.255; P < 0.001). In this fully adjusted model, the intermediate risk group had a 1.7-fold increased CKD stage 3 risk (HR, 1.734; 95% CI, 1.447–2.078; P < 0.001) (Table 3). The increased risk of CKD stage 3 development associated with high Framingham risk score was also found in the secondary analysis, in which decline in an eGFR ≥ 40 mL/min/1.73 m2 from the baseline value was the secondary outcome (Supplementary Table 1). When we compared renal function decline among Framingham risk score groups, eGFR declined faster in the highest score group than in the lowest and middle score groups (Supplementary Table 2).
Table 3.
Multivariate Cox regression analysis of incidental chronic kidney disease in patients according to Framingham risk score
| Model 1 | Model 2 | Model 3 | Model 4 | |||||
|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|||||
| HR (95% CI) | P | HR (95% CI) | P | HR (95% CI) | P | HR (95% CI) | P | |
| Low risk | 1 (reference) | 1 (reference) | 1 (reference) | 1 (reference) | ||||
| Intermediate risk | 2.252 (1.893–2.678) | < 0.001 | 2.454 (2.053–2.933) | < 0.001 | 1.837 (1.538–2.193) | < 0.001 | 1.734 (1.447–2.078) | < 0.001 |
| High risk | 4.239 (3.553–5.057) | < 0.001 | 4.704 (3.899–5.674) | < 0.001 | 3.157 (2.621–3.803) | < 0.001 | 2.674 (2.197–3.255) | < 0.001 |
Model 1, crude hazard ratio (HR) without adjustment; Model 2, adjusted for residence (Ansan or Anseong), education status, income, history of coronary artery disease, alcohol intake (non-drinker, ex-drinker, or current drinker); Model 3, model 2 + eGFR and proteinuria; Model 4, model 3 + fasting glucose, albumin, triglyceride, C-reactive protein, and calculated low density lipoprotein.
CI, confidence interval; eGFR, estimated glomerular filtration rate.
Relationship between Framingham risk scores and new-onset proteinuria
We further analyzed if the Framingham risk score predicted new development of proteinuria during follow-up in subjects without baseline proteinuria. The results showed that higher Framingham risk scores were associated with increased risk of proteinuria development (Supplementary Table 3).
Predictive value of the Framingham risk score and other risk factors
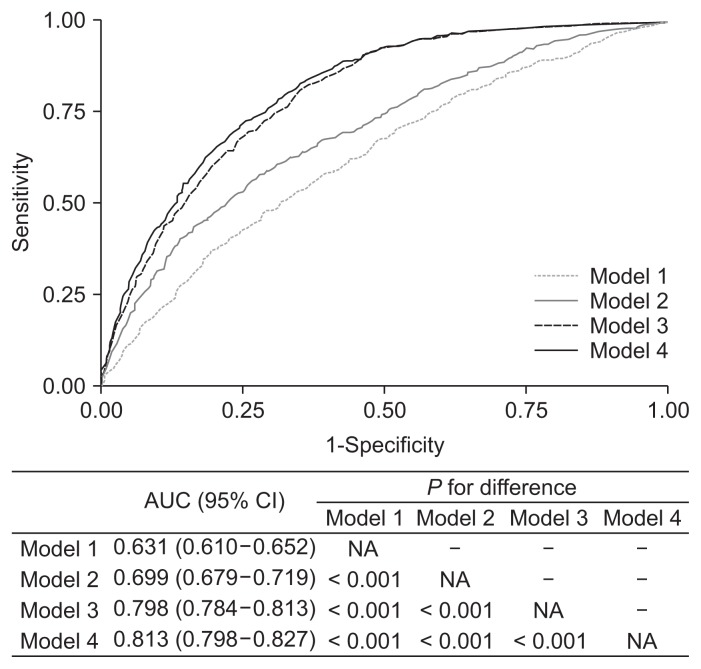
We performed ROC curve analyses to compare the value of the Framingham risk score for predicting CKD stage 3 incidence to that of other traditional risk factors. The area under the curve (AUC) for the Framingham risk score-added model (model 2) was 0.699 (95% CI, 0.679–0.719) as compared to 0.631 (95% CI, 0.610–0.652; P < 0.001) for the baseline model (model 1) (Fig. 3). However, the AUC for the renal parameter-added model (model 3) was significantly higher than that for the Framingham risk score-added model. Inclusion of the Framingham risk score with renal parameters yielded the highest AUC (0.813; 95% CI, 0.798–0.827).
Figure 3. Receiver operating characteristics curve for 4 models predicting incident chronic kidney disease.
Model 1, sex, body mass index, education level, income, fasting glucose, and serum albumin; Model 2, model 1 + Framingham risk score; Model 3, model 1 + eGFR + proteinuria; Model 4, model 1 + eGFR + proteinuria + Framingham risk score.
AUC, area under the curve; CI, confidence interval; eGFR, estimated glomerular filtration rate; NA, not applicable.
We then compared the predictive power of the Framingham risk score with that of Harrell’s C index for three multivariable Cox regression models (Table 4). Considering the ROC analysis results, the predictive power of the Framingham risk score was lower than that of the renal parameters. However, adding the Framingham risk score to the renal parameters significantly improved predictive ability compared to a model using renal parameters alone (model 4; C-statistic, 0.839; 95% CI, 0.825–0.853; P < 0.001). These findings suggest that the predictive value of the risk stratification model for future CKD stage 3 can increase when the Framingham risk score is considered in addition to kidney function and proteinuria. To finalize the model, internal validity was assessed using a 10-fold cross-validation procedure. This technique provides an estimate of the performance of the model when applied to test subsets. Following 10-fold cross-validation, the mean C-statistic across folds was 0.837 (95% CI, 0.797–0.867), and the mean AUC across folds was 0.810 (95% CI, 0.796–0.825) (Supplementary Table 4 and Supplementary Fig. 1).
Table 4.
C-statistics for prediction of incident chronic kidney disease using multivariate Cox regression models
| Model | C-statistics (95% CI) | P for difference of C-statistics compared with models | |||
|---|---|---|---|---|---|
|
| |||||
| Model 1 | Model 2 | Model 3 | Model 4 | ||
| Model 1 | 0.652 (0.631–0.674) | NA | – | – | – |
| Model 2 | 0.729 (0.709–0.749) | < 0.001 | NA | – | – |
| Model 3 | 0.819 (0.804–0.833) | < 0.001 | < 0.001 | NA | – |
| Model 4 | 0.839 (0.825–0.853) | < 0.001 | < 0.001 | < 0.001 | NA |
Model 1, sex, body mass index, education level, income, fasting glucose, and serum albumin; Model 2, model 1 + the Framingham risk score; Model 3, model 1 + eGFR and proteinuria; Model 4; model 1 + eGFR, proteinuria, and the Framingham risk score.
CI, confidence interval; eGFR, estimated glomerular filtration rate; NA, not applicable.
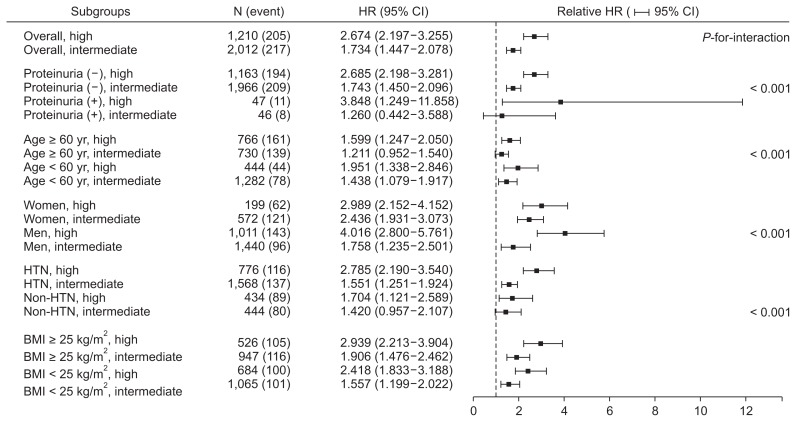
To clarify the robust association between the Framing-ham risk score and CKD stage 3 development, subgroup analysis was performed in subgroups stratified by proteinuria (≥ 1+ or no), age (< 60 or ≥ 60 years), sex (male or female), hypertension (yes or no), and BMI (< 25 or ≥ 25 kg/m2). There were no significant interactions between the Framingham risk score and subgroup parameters (Fig. 4). Thus, increased risk of incident CKD stage 3 in the high risk group was consistently observed irrespective of proteinuria, age, sex, obesity, or hypertension.
Figure 4. Forest plot for subgroup analysis.
BMI, body mass index; CI, confidence interval; HR, hazard ratio; HTN, hypertension; N, number.
Supplementary materials are presented online (available at https://doi.org/10.23876/j.krcp.18.0118).
Discussion
In this study, the Framingham risk score effectively predicted incident CKD stage 3 in the general population. Its predictive power was lower than that of renal parameters, such as eGFR and proteinuria, but increased when both were included in the prediction model. Thus, the Framingham risk score considered together with traditional renal risk factors can improve risk stratification for CKD stage 3 development in healthy individuals without kidney disease.
CVD and CKD are major public health problems worldwide [15–18]. Lifelong CKD risk is substantial and CKD symptoms or signs are almost always absent until 90% of kidney function is lost [19]. Because established CKD is irreversible, there is growing emphasis on the importance of early detection and intervention for high risk individuals. There are many common risk factors between CVD and CKD. Given the paucity of risk assessment tools for CKD development, high risk individual identification using well-known validated scoring systems would be helpful.
To date, only three studies have proposed risk prediction models for incident CKD. In a combined cohort study of 14,155 middle-aged adults from the Atherosclerosis Risk in Communities (ARIC) Study and Cardiovascular Health Study, Kshirsagar et al [20] developed a simple algorithm including eight variables: age, sex, anemia, hypertension, diabetes mellitus, peripheral vascular disease, and histories of CVD and heart failure. The incident CKD risk increased with the risk score, indicating that this algorithm is helpful for CKD prevention in healthy individuals without kidney diseases [20]. Chien et al [21] also constructed a risk prediction system using a Chinese cohort, which included age, BMI, diastolic blood pressure, diabetes mellitus, stroke, proteinuria, and uric acid, postprandial glucose, and hemoglobin A1c concentrations. Their risk model was also useful for predicting CKD [21]. Finally, O’Seaghdha et al [22] developed a prediction model using the Framingham cohort that incorporated five variables: age, diabetes mellitus, hypertension, eGFR, and albuminuria. This model was further validated in the ARIC cohort.
Our findings are consistent with those of all previous studies [20–22]. This was not surprising, because the variables used to construct models overlapped among studies. Age, hypertension, and diabetes mellitus are representative risk factors for CKD, and were incorporated in all studies including the present study. However, there are discrepancies in the predictive power of the models. The prediction model developed by Kshirsagar et al [20] had moderate discriminatory power (AUC, 0.70). Conversely, the models in two subsequent studies [21,22] had higher AUCs (0.765) or C-statistics (0.813) than did the model proposed by Kshirsagar et al [20]. This difference is presumably because Kshirsagar et al [20] did not include renal parameters, whereas the other studies incorporated proteinuria or eGFR. Proteinuria and initial kidney function were the strongest CKD predictors in the present study, although the subjects had a baseline eGFR of ≥ 60 mL/min/1.73 m2. This relationship was clearly reflected in our findings. The Framingham risk score added to the clinical model was 0.699, which was similar to that in the study by Kshirsagar et al [20]. When we included both the Framingham risk score and renal parameters, the AUC and C-statistics for the model were the highest among all models. These results are numerically similar to those for the Chinese and Framingham cohorts [21,22].
Based on our findings, the present study has a number of clinical implications. First, the Framingham risk score itself can help stratify healthy middle-aged individuals at high risk for incident CKD. However, the predictive value of this scoring system is not greater than that of traditional renal parameters. This does not mean that its use in clinical practice is limited. The Framingham scoring system can be implemented in conjunction with proteinuria and eGFR for further risk stratification for future CKD. However, our findings also suggest that measurements of creatinine and proteinuria should be included in medical check-ups because these two parameters are the strongest predictors of CKD development. Second, this strategy can determine the estimated risks of CVD and CKD simultaneously, and thus may help guide clinical decision-making and counseling to obtain better outcomes. For example, early primary prevention strategies can be targeted to individuals at high CVD and CKD risks, including timely medical treatment initiation, adherence to lifestyle modification encouragement, sustained awareness of exposure to nephrotoxic drugs, and early cardiologist or nephrologist referral for screening programs.
There are several limitations to the present study that should be discussed. First, we included only Korean individuals aged 40 to 69 years; thus, our findings may not be generalized to other ethnic or more elderly populations. Notably, previous studies that developed and tested risk score models for CKD in Chinese, European, and African-American populations have shown similar results [20–22]. All of these studies incorporated similar variables to create prediction models. Given the high AUC and C-statistics of the models in all studies, the use of this strategy appears valid in diverse populations. Second, we did not measure other novel biomarkers and used only conventional factors. It is uncertain whether novel biomarkers can improve risk stratification relative to conventional factors. Previous studies suggest that improvements in CVD predictions using some biomarkers were marginal [23,24]. Therefore, measurements of these biomarkers may not be cost-effective. In contrast, our strategy is inexpensive, well-validated, easily applicable, and can assess both CKD and CVD risks. The AUC in our model including the Framingham risk score, proteinuria, and eGFR was 0.813, and adding additional biomarkers to this model is unlikely to significantly increase the AUC. Third, we used dipstick tests of proteinuria but did not directly measure albuminuria. Albuminuria is a well-known risk factor for end-stage kidney disease and also predicts future CVD. Nevertheless, dipstick proteinuria was associated with increased incident CKD stage 3 risk (HR, 2.706; 95% CI, 2.224–3.292; P < 0.001). The Framingham risk score was predictive only in people without proteinuria, but not in those with proteinuria. This finding was unexpected, as the Framingham risk score and proteinuria are both good markers of vascular injury. However, many people at risk for CVD can have CKD even without proteinuria. In addition, our cohort included only 190 (2.1%) subjects with proteinuria, which may have resulted in lack of statistical power although there was a trend toward increased risk for CKD stage 3. Further analyses with a more adequate sample size could answer this issue in the future. Additionally, we did not assess hyperglycemia severity or blood pressure in this study. Although there are debates regarding optimal glycemic and blood pressure control, these are both very important factors in preventing CVD and CKD. Further studies to develop more comprehensive models encompassing these factors are warranted [25,26].
In conclusion, the Framingham risk score effectively predicted incident CKD stage 3 development in the general population with normal renal function. The predictive value for future CKD stage 3 development was further enhanced when this scoring system was considered in concert with proteinuria and eGFR. The Framingham risk score, together with traditional renal risk factors, can easily be used in the primary care setting to stratify healthy individuals at high risk for CKD stage 3.
Supplementary Data
Supplementary Table 1.
eGFR decline ≥ 40 mL/min/1.73 m2 from baseline outcomes among groups classified by Framingham risk score with multivariate Cox regression analysis
| Total | Framingham risk score groups | |||
|---|---|---|---|---|
|
| ||||
| Low risk | Intermediate risk | High risk | ||
| ≥ 40 eGFR decline | ||||
| Events | 679 | 450 | 133 | 96 |
| Events/1,000 person-year | 9.9 | 8.6 | 7.7 | 9.9 |
| Model 1 | HR (95% CI) | 1 [reference] | 0.917 (0.756–1.113) | 1.280 (1.026–1.595) |
| P | 0.379 | 0.028 | ||
| Model 2 | HR (95% CI) | 1 [reference] | 0.958 (0.786–1.168) | 1.313 (1.044–1.651) |
| P | 0.674 | 0.020 | ||
| Model 3 | HR (95% CI) | 1 [reference] | 1.356 (1.106–1.662) | 2.182 (1.717–2.772) |
| P | 0.003 | < 0.001 | ||
| Model 4 | HR (95% CI) | 1 [reference] | 1.222 (0.989–1.509) | 1.727 (1.341–2.224) |
| P | 0.063 | < 0.001 | ||
Data are presented as number person-year or incidence rate per 1,000 person-year.
Model 1, crude hazard ratio (HR) without adjustment; Model 2, adjusted for residence (Ansan or Anseong), education status, income, history of coronary artery disease, alcohol intake (non-drinker, ex-drinker, or current drinker); Model 3, model 2 + eGFR and proteinuria; Model 4, model 3 + fasting glucose, albumin, triglyceride, C-reactive protein, and calculated low density lipoprotein.
CI, confidence interval; eGFR, estimated glomerular filtration rate.
Supplementary Table 2.
Linear mixed model of annual eGFR decline according to Framingham risk group
| Framingham risk score groups | Slope of eGFR decline (95% CI) | P for-difference between groups | ||
|---|---|---|---|---|
|
| ||||
| Low risk | Intermediate risk | High risk | ||
| Low risk | −0.545 (−0.573 to −0.517) | – | ||
| Intermediate risk | −0.638 (−0.690 to −0.585) | 0.002 | – | |
| High risk | −0.861 (−0.940 to −0.781) | < 0.001 | < 0.001 | – |
Estimated glomerular filtration rate (eGFR) decline: biannual eGFR decline rate (mL/min/1.73 m2/year).
Supplementary Table 3.
Multivariate Cox regression analysis for the development of incident proteinuria (≥ 1+) according to Framingham risk score groups
| Model 1 | Model 2 | Model 3 | Model 4 | |||||
|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|||||
| HR (95% CI) | P | HR (95% CI) | P | HR (95% CI) | P | HR (95% CI) | P | |
| Low risk | 1 [reference] | 1 [reference] | 1 [reference] | 1 [reference] | ||||
| Intermediate risk | 3.730 (2.451–5.674) | 3.225 (2.099–4.956) | 3.148 (2.040–4.857) | < 0.001 | 3.020 (1.935–4.714) | < 0.001 | ||
| High risk | 5.598 (3.600–8.704) | 4.359 (2.741–6.300) | 4.200 (2.618–6.739) | < 0.001 | 3.346 (2.028–5.521) | < 0.001 | ||
Model 1, crude hazard ratio (HR) without adjustment; Model 2, adjusted for residence (Ansan or Anseong), education status, income, history of coronary artery disease, alcohol intake (non-drinker, ex-drinker, or current drinker); Model 3, model 2 + eGFR and proteinuria; Model 4, model 3 + fasting glucose, albumin, triglyceride, C-reactive protein, and calculated low density lipoprotein.
CI, confidence interval; eGFR, estimated glomerular filtration rate.
Supplementary Table 4.
Mean C-statistics for prediction of incident chronic kidney disease using 10-fold cross validation
| Model | C-statistics (95% CI) | P for difference of C-statistics compared with models | |||
|---|---|---|---|---|---|
|
| |||||
| Model 1 | Model 2 | Model 3 | Model 4 | ||
| Model 1 | 0.643 (0.612–0.690) | NA | – | – | – |
| Model 2 | 0.728 (0.663–0.811) | < 0.001 | NA | – | – |
| Model 3 | 0.817 (0.765–0.854) | < 0.001 | < 0.001 | NA | – |
| Model 4 | 0.837 (0.797–0.867) | < 0.001 | < 0.001 | < 0.001 | NA |
Model 1, sex, body mass index, education level, income, fasting glucose, and serum albumin; Model 2, model 1 + Framingham risk score; Model 3, model 1 + eGFR and proteinuria; Model 4, model 1 + eGFR, proteinuria, and the Framingham risk score.
CI, confidence interval; eGFR, estimated glomerular filtration rate; NA, not applicable.
Model 1, sex, body mass index, education level, income, fasting glucose, and serum albumin; Model 2, model 1 + Framingham risk score; Model 3, model 1 + eGFR + proteinuria; Model 4, model 1 + eGFR + proteinuria + Framingham risk score.
AUC, area under the curve; CI, confidence interval; eGFR, estimated glomerular filtration rate.
Acknowledgments
Data used in this study were obtained from the Korean Genome and Epidemiology Study (KoGES; 4851-302), National Research Institute of Health, Centers for Disease Control and Prevention, Ministry for Health and Welfare, Republic of Korea. Therefore, we acknowledge and appreciate the labor of all staff members working on the KoGES.
Footnotes
Conflicts of interest
All authors have no conflicts of interest to declare.
References
- 1.Hill NR, Fatoba ST, Oke JL, et al. Global prevalence of chronic kidney disease - a systematic review and meta-analysis. PLoS One. 2016;11:e0158765. doi: 10.1371/journal.pone.0158765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Levey AS, Eckardt KU, Tsukamoto Y, et al. Definition and classification of chronic kidney disease: a position statement from kidney disease: Improving Global Outcomes (KDIGO) Kidney Int. 2005;67:2089–2100. doi: 10.1111/j.1523-1755.2005.00365.x. [DOI] [PubMed] [Google Scholar]
- 3.Fassett RG, Venuthurupalli SK, Gobe GC, Coombes JS, Cooper MA, Hoy WE. Biomarkers in chronic kidney disease: a review. Kidney Int. 2011;80:806–821. doi: 10.1038/ki.2011.198. [DOI] [PubMed] [Google Scholar]
- 4.Wilson PW, D’Agostino RB, Levy D, Belanger AM, Silber-shatz H, Kannel WB. Prediction of coronary heart disease using risk factor categories. Circulation. 1998;97:1837–1847. doi: 10.1161/01.CIR.97.18.1837. [DOI] [PubMed] [Google Scholar]
- 5.Dawber TR, Meadors GF, Moore FE., Jr Epidemiological approaches to heart disease: the Framingham study. Am J Public Health Nations Health. 1951;41:279–281. doi: 10.2105/AJPH.41.3.279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.D’Agostino RB, Sr, Vasan RS, Pencina MJ, et al. General cardiovascular risk profile for use in primary care: the Framingham heart study. Circulation. 2008;117:743–753. doi: 10.1161/CIRCULATIONAHA.107.699579. [DOI] [PubMed] [Google Scholar]
- 7.Cupples LA, D’Agostino RB. Some risk factors related to the annual incidence of cardiovascular disease and death using pooled repeated biennial measurements: Framingham heart study, 30 year followup. In: Kannel WB, Wolf PA, Garrison RJ, editors. The Framingham study: an epidemiological investigation of cardiovascular disease. Bethesda: National Heart, Lung and Blood Institute; 1987. [Google Scholar]
- 8.Haroun MK, Jaar BG, Hoffman SC, Comstock GW, Klag MJ, Coresh J. Risk factors for chronic kidney disease: a prospective study of 23,534 men and women in Washington County, Maryland. J Am Soc Nephrol. 2003;14:2934–2941. doi: 10.1097/01.ASN.0000095249.99803.85. [DOI] [PubMed] [Google Scholar]
- 9.Tanner RM, Brown TM, Muntner P. Epidemiology of obesity, the metabolic syndrome, and chronic kidney disease. Curr Hypertens Rep. 2012;14:152–159. doi: 10.1007/s11906-012-0254-y. [DOI] [PubMed] [Google Scholar]
- 10.Shin JH, Kang KW, Kim JG, Lee SJ. Concurrent renal dysfunction with ischemic heart disease is an important determinant for cardiac and cerebrovascular mortality in patients on chronic digoxin therapy for atrial fibrillation. Kidney Res Clin Pract. 2018;37:130–137. doi: 10.23876/j.krcp.2018.37.2.130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cha Rh, Kang SW, Park CW, et al. Sustained uremic toxin control improves renal and cardiovascular outcomes in patients with advanced renal dysfunction: post-hoc analysis of the Kremezin study against renal disease progression in Korea. Kidney Res Clin Pract. 2017;36:68–78. doi: 10.23876/j.krcp.2017.36.1.68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Friedewald WT, Levy RI, Fredrickson DS. Estimation of the concentration of low-density lipoprotein cholesterol in plasma, without use of the preparative ultracentrifuge. Clin Chem. 1972;18:499–502. [PubMed] [Google Scholar]
- 13.ClinCalc.com. IDMS to conventional serum creatinine [Internet] ClinCalc LLC; [cited 2008 Jun 12]. Available from: https://clincalc.Com/kinetics/idms.Aspx. [Google Scholar]
- 14.Levey AS, Stevens LA, Schmid CH, et al. CKD-EPI (Chronic Kidney Disease Epidemiology Collaboration) A new equation to estimate glomerular filtration rate. Ann Intern Med. 2009;150:604–612. doi: 10.7326/0003-4819-150-9-200905050-00006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jee SH, Appel LJ, Suh I, Whelton PK, Kim IS. Prevalence of cardiovascular risk factors in South Korean adults: results from the Korea Medical Insurance Corporation (KMIC) study. Ann Epidemiol. 1998;8:14–21. doi: 10.1016/S1047-2797(97)00131-2. [DOI] [PubMed] [Google Scholar]
- 16.Ji E, Kim YS. Prevalence of chronic kidney disease defined by using CKD-EPI equation and albumin-to-creatinine ratio in the Korean adult population. Korean J Intern Med. 2016;31:1120–1130. doi: 10.3904/kjim.2015.193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lopez AD, Mathers CD, Ezzati M, Jamison DT, Murray CJ. Global and regional burden of disease and risk factors, 2001: systematic analysis of population health data. Lancet. 2006;367:1747–1757. doi: 10.1016/S0140-6736(06)68770-9. [DOI] [PubMed] [Google Scholar]
- 18.Zhang QL, Rothenbacher D. Prevalence of chronic kidney disease in population-based studies: systematic review. BMC Public Health. 2008;8:117. doi: 10.1186/1471-2458-8-117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lee MJ, Kim S, Park I, Kim H, Shin GT. Comparison of estimated glomerular filtration rate equations at the time of hemodialysis initiation. Kidney Res Clin Pract. 2015;34:207–211. doi: 10.1016/j.krcp.2015.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kshirsagar AV, Bang H, Bomback AS, et al. A simple algorithm to predict incident kidney disease. Arch Intern Med. 2008;168:2466–2473. doi: 10.1001/archinte.168.22.2466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chien KL, Lin HJ, Lee BC, Hsu HC, Lee YT, Chen MF. A prediction model for the risk of incident chronic kidney disease. Am J Med. 2010;123:836–846.e2. doi: 10.1016/j.amjmed.2010.05.010. [DOI] [PubMed] [Google Scholar]
- 22.O’Seaghdha CM, Lyass A, Massaro JM, et al. A risk score for chronic kidney disease in the general population. Am J Med. 2012;125:270–277. doi: 10.1016/j.amjmed.2011.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kavousi M, Elias-Smale S, Rutten JH, et al. Evaluation of newer risk markers for coronary heart disease risk classification: a cohort study. Ann Intern Med. 2012;156:438–444. doi: 10.7326/0003-4819-156-6-201203200-00006. [DOI] [PubMed] [Google Scholar]
- 24.Havekes B, van Manen JG, Krediet RT, Boeschoten EW, Vandenbroucke JP, Dekker FW NECOSAD Study Group. Serum troponin T concentration as a predictor of mortality in hemodialysis and peritoneal dialysis patients. Am J Kidney Dis. 2006;47:823–829. doi: 10.1053/j.ajkd.2006.01.019. [DOI] [PubMed] [Google Scholar]
- 25.Ismail-Beigi F, Moghissi E, Tiktin M, Hirsch IB, Inzucchi SE, Genuth S. Individualizing glycemic targets in type 2 diabetes mellitus: implications of recent clinical trials. Ann Intern Med. 2011;154:554–559. doi: 10.7326/0003-4819-154-8-201104190-00007. [DOI] [PubMed] [Google Scholar]
- 26.Upadhyay A, Earley A, Haynes SM, Uhlig K. Systematic review: blood pressure target in chronic kidney disease and proteinuria as an effect modifier. Ann Intern Med. 2011;154:541–548. doi: 10.7326/0003-4819-154-8-201104190-00335. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Table 1.
eGFR decline ≥ 40 mL/min/1.73 m2 from baseline outcomes among groups classified by Framingham risk score with multivariate Cox regression analysis
| Total | Framingham risk score groups | |||
|---|---|---|---|---|
|
| ||||
| Low risk | Intermediate risk | High risk | ||
| ≥ 40 eGFR decline | ||||
| Events | 679 | 450 | 133 | 96 |
| Events/1,000 person-year | 9.9 | 8.6 | 7.7 | 9.9 |
| Model 1 | HR (95% CI) | 1 [reference] | 0.917 (0.756–1.113) | 1.280 (1.026–1.595) |
| P | 0.379 | 0.028 | ||
| Model 2 | HR (95% CI) | 1 [reference] | 0.958 (0.786–1.168) | 1.313 (1.044–1.651) |
| P | 0.674 | 0.020 | ||
| Model 3 | HR (95% CI) | 1 [reference] | 1.356 (1.106–1.662) | 2.182 (1.717–2.772) |
| P | 0.003 | < 0.001 | ||
| Model 4 | HR (95% CI) | 1 [reference] | 1.222 (0.989–1.509) | 1.727 (1.341–2.224) |
| P | 0.063 | < 0.001 | ||
Data are presented as number person-year or incidence rate per 1,000 person-year.
Model 1, crude hazard ratio (HR) without adjustment; Model 2, adjusted for residence (Ansan or Anseong), education status, income, history of coronary artery disease, alcohol intake (non-drinker, ex-drinker, or current drinker); Model 3, model 2 + eGFR and proteinuria; Model 4, model 3 + fasting glucose, albumin, triglyceride, C-reactive protein, and calculated low density lipoprotein.
CI, confidence interval; eGFR, estimated glomerular filtration rate.
Supplementary Table 2.
Linear mixed model of annual eGFR decline according to Framingham risk group
| Framingham risk score groups | Slope of eGFR decline (95% CI) | P for-difference between groups | ||
|---|---|---|---|---|
|
| ||||
| Low risk | Intermediate risk | High risk | ||
| Low risk | −0.545 (−0.573 to −0.517) | – | ||
| Intermediate risk | −0.638 (−0.690 to −0.585) | 0.002 | – | |
| High risk | −0.861 (−0.940 to −0.781) | < 0.001 | < 0.001 | – |
Estimated glomerular filtration rate (eGFR) decline: biannual eGFR decline rate (mL/min/1.73 m2/year).
Supplementary Table 3.
Multivariate Cox regression analysis for the development of incident proteinuria (≥ 1+) according to Framingham risk score groups
| Model 1 | Model 2 | Model 3 | Model 4 | |||||
|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|||||
| HR (95% CI) | P | HR (95% CI) | P | HR (95% CI) | P | HR (95% CI) | P | |
| Low risk | 1 [reference] | 1 [reference] | 1 [reference] | 1 [reference] | ||||
| Intermediate risk | 3.730 (2.451–5.674) | 3.225 (2.099–4.956) | 3.148 (2.040–4.857) | < 0.001 | 3.020 (1.935–4.714) | < 0.001 | ||
| High risk | 5.598 (3.600–8.704) | 4.359 (2.741–6.300) | 4.200 (2.618–6.739) | < 0.001 | 3.346 (2.028–5.521) | < 0.001 | ||
Model 1, crude hazard ratio (HR) without adjustment; Model 2, adjusted for residence (Ansan or Anseong), education status, income, history of coronary artery disease, alcohol intake (non-drinker, ex-drinker, or current drinker); Model 3, model 2 + eGFR and proteinuria; Model 4, model 3 + fasting glucose, albumin, triglyceride, C-reactive protein, and calculated low density lipoprotein.
CI, confidence interval; eGFR, estimated glomerular filtration rate.
Supplementary Table 4.
Mean C-statistics for prediction of incident chronic kidney disease using 10-fold cross validation
| Model | C-statistics (95% CI) | P for difference of C-statistics compared with models | |||
|---|---|---|---|---|---|
|
| |||||
| Model 1 | Model 2 | Model 3 | Model 4 | ||
| Model 1 | 0.643 (0.612–0.690) | NA | – | – | – |
| Model 2 | 0.728 (0.663–0.811) | < 0.001 | NA | – | – |
| Model 3 | 0.817 (0.765–0.854) | < 0.001 | < 0.001 | NA | – |
| Model 4 | 0.837 (0.797–0.867) | < 0.001 | < 0.001 | < 0.001 | NA |
Model 1, sex, body mass index, education level, income, fasting glucose, and serum albumin; Model 2, model 1 + Framingham risk score; Model 3, model 1 + eGFR and proteinuria; Model 4, model 1 + eGFR, proteinuria, and the Framingham risk score.
CI, confidence interval; eGFR, estimated glomerular filtration rate; NA, not applicable.
Model 1, sex, body mass index, education level, income, fasting glucose, and serum albumin; Model 2, model 1 + Framingham risk score; Model 3, model 1 + eGFR + proteinuria; Model 4, model 1 + eGFR + proteinuria + Framingham risk score.
AUC, area under the curve; CI, confidence interval; eGFR, estimated glomerular filtration rate.