SUMMARY
The brain strengthens memories through consolidation, defined as resistance to interference (stabilization) or performance improvements between the end of a practice session and the beginning of the next (offline gains) [1]. Typically, consolidation has been measured hours or days after the completion of training [2], but the same concept may apply to periods of rest that occur interspersed in a series of practice bouts within the same session. Here, we took an unprecedented close look at the within-seconds time-course of early human procedural learning over alternating short periods of practice and rest that constitute a typical online training session. We found that performance did not markedly change over short periods of practice. On the other hand, performance improvements in between practice periods, when subjects were at rest, were significant and accounted for early procedural learning. These offline improvements were more prominent in early training trials when the learning curve was steep, and no performance decrements during preceding practice periods were present. At the neural level, simultaneous magnetoencephalographic recordings showed an anatomically defined signature of this phenomenon. Beta-band brain oscillatory activity in a predominantly contralateral frontoparietal network predicted rest period performance improvements. Consistent with its role in sensorimotor engagement [3], modulation of beta activity may reflect replay of task processes during rest periods. We report a rapid form of offline consolidation that substantially contributes to early skill learning and may extend the concept of consolidation to a time-scale in the order of seconds, rather than the hours or days traditionally accepted.
Keywords: consolidation, human motor learning, skill learning, procedural memory, offline learning, magnetoencephalography, beta activity, reactivation
eTOC Blurb
Bönstrup et al. take an unprecedented close look at the time course of online motor skill learning. They find that relevant performance improvements occur during short periods of rest. Frontoparietal beta oscillatory activity predicts those micro-offline gains. This rapid form of consolidation substantially contributes to early skill learning.
RESULTS
Early online learning was evidenced during short rest periods
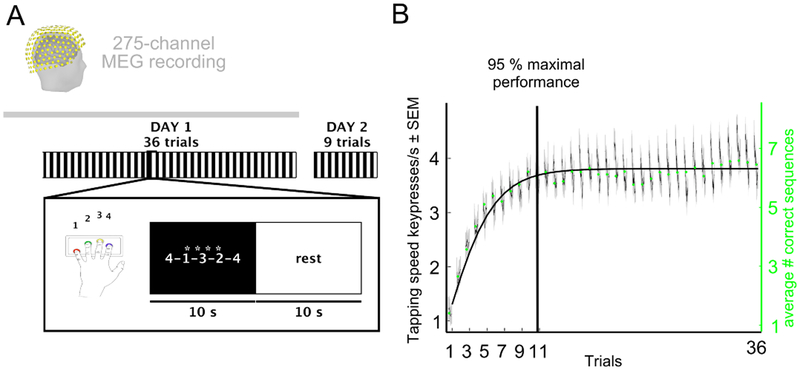
Initial training on a new motor skill consists of short periods of active practice alternating with short periods of rest, a pattern that results in significant early learning [4]. Here, we studied the relative contribution of practice and rest to early learning. 27 healthy humans practiced a well-characterized motor skill task comprised of a series of sequential key presses [5, 6] which is widely used in the study of procedural memory formation [7, 8]. They trained over 36 trials consisting of 10 seconds practice (reduced duration, [5, 9]) and 10 seconds rest periods for a total of 12 min (Day 1 in Figure 1A). In each practice period, participants were asked to repetitively tap a 5-item sequence indicated on the screen as fast and accurately as possible using their left, non-dominant hand. Participants returned the following day for a test session. Performance was measured as the tapping speed (keypresses/s) for correctly performed sequences [10]. We defined early learning as the window of practice trials required to reach 95% of the total Day 1 learning. Modelling the group average learning curve showed that this performance level was achieved by trial 11 (Figure 1B).
Figure 1. Motor skill task and performance curve.
A, Task: Participants learned the motor skill task [5, 6] over 36 trials (inset shows a single trial) consisting of alternating practice and rest periods of 10s duration for a total of 12 min. In each practice period, participants were asked to repetitively tap the sequence indicated on the screen as fast and accurately as possible using their left, non-dominant hand. The next day, performance was tested over 9 trials. Brain oscillatory activity was recorded with magnetoencephalography (MEG) for 5 min before (resting-state baseline) and during the task on Day 1. B, Skill was measured as the average inter-tap interval within correct sequences (tapping speed measured in keypresses/s) [10]. The average number of currect sequences per trial is given as green dots. The performance curve of Day 1 (mean + s.e.m.) and the modelled group average performance (overlaid) showed that 95% of learning occurred within the first 11 trials (vertical line, early learning) before reaching maximal performance. See also Figure S1 for supplemental behavioral data and Figure S2 for individual data.
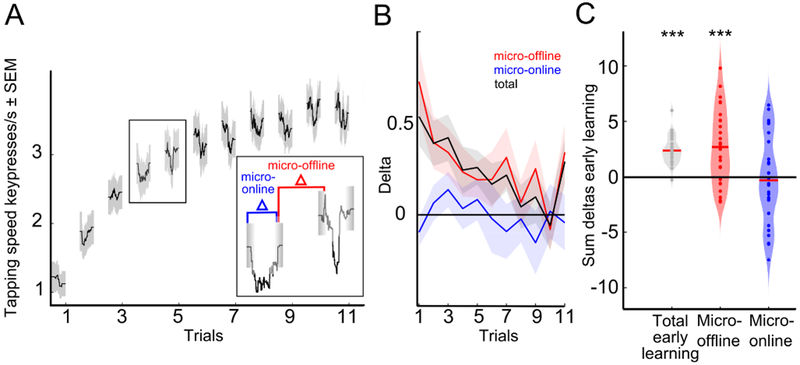
During early learning, performance improved rapidly within the first few minutes of practice (Figure 1B) before reaching performance ceiling [6, 10]. Observation of the learning curve at a high temporal within-trial resolution unveiled clear performance increments between practice periods (Figure 2A). We then proceeded to dissect learning into performance improvements occurring during the practice and rest periods. Micro-online learning was defined as the difference in tapping speed (keypresses/s) between the beginning and end of each practice period. Micro-offline learning was defined as the difference in tapping speed between the end of each practice period and the beginning of the next one (Figure 2A, STAR Methods). During practice periods, performance either slightly increased, decreased or stagnated. Whereas during rest periods, we detected micro-offline gains that closely tracked total learning at a trial-by-trial basis. Micro-offline gains were maximal in early trials when performance during practice periods neither improved nor worsened (Figure 2B).
Figure 2. Early online learning was evidenced during short rest periods.
A, Microscale early learning reveals performance increments over rest periods. Micro-online changes were calculated as the difference in tapping speed (keypresses/s) of the first and last correct sequence within a practice period (blue in inset) and micro-offline changes as the difference between the last correct sequence within a practice period compared to the first of the next practice period (red in inset). B, Trial-wise early learning. Each line depicts performance changes (micro-offline in red, micro-online in blue, total in black) per trial (mean + s.e.m.). Total learning is closely accounted for by micro-offline gains (black and red lines) whereas micro-online performance changes fluctuate around 0. Note the presence of large micro-offline gains and total early learning in the initial trials in the absence of micro-online performance decrements. Subsequently, within-practice performance decrements manifested gradually as learning slowed down. C, Data points in the violin plot depict the sum of changes in performance over early learning trials in each participant. Note that total early learning is accounted for by performance improvements during rest periods, but not during practice periods (two-tailed one-sample t test for each learning partition, ***P < 0.001, FDR-corrected for multiple comparisons). See also Figure S1.
Total early learning was calculated as the sum of single-trial performance changes and amounted to 2.37 ± 0.24 keypresses/s (mean ± s.e.m., two-tailed one-sample t test, T = 9.76, P < 0.001). To assess the micro-online and micro-offline contribution to early learning, we summed performance differences in each participant over all 11 practice or 10 rest periods. Comparing each contribution to total early learning, we found that all early learning was accounted for by performance increases during rest periods rather than during practice periods (Figure 2C). Indeed, on average, micro-online changes were nil (−0.32 ± 0.75 keypresses/s, T = −0.41, P = 0.68) whereas micro-offline gains were substantial (2.69 ± 0.63 keypresses/s; T = 4.19, P < 0.001, Figure 2B,C).
We probed the robustness of these findings by defining micro-scale learning in alternative ways: (a), tapping speed of correct sequences in the first and last two seconds of each practice period, (b), tapping speed of correct sequences of the first and last second of each practice period, (c), the difference in the intersect at the beginning and the end of a least-squares fit line to the performance of each practice period. All measurements rendered comparable results: early learning was evidenced during rest periods rather than during practice periods (see also Figure S1C-F). Performance measurements allowing within-practice period temporal resolution of errors could conceivably provide additional information.
Learning over all Day 1 trials (2.73 ± 0.22 keypresses/s, mean ± s.e.m., two-tailed one-sample t test, T = 12.15, P < 0.001) was larger than overnight improvement from the end of training on Day 1 to test on Day 2 (0.73 ± 0.10 keypresses/s, T = 6.92, P < 0.001) consistent with previous reports [6]. Overnight offline learning did not correlate with micro-offline gains during early learning (linear model, P = 0.83) suggesting different mechanisms at play. Accuracy was comparably high during early (trials 1–11: 0.89 ± 0.02 mean ± s.e.m.) and late (trials 12–36: 0.90 ± 0.01) learning trials (Figure S1B).
Micro-offline learning occurs in a state of low beta power
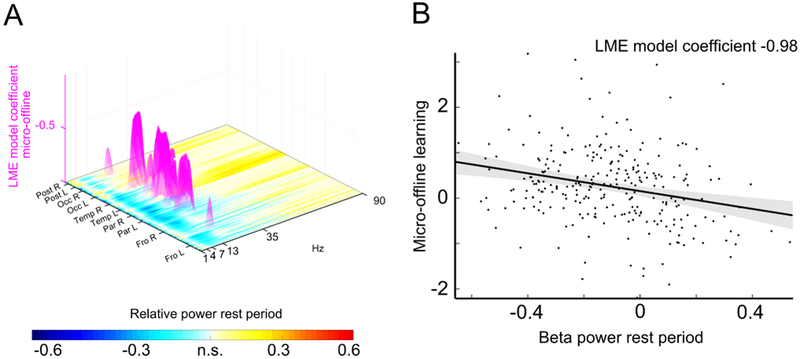
How could learning manifest itself within 10 s rest periods? To gain insight into the systems-level possible mechanisms supporting this rapid form of offline learning, we recorded magnetoencephalographic activity during the task and in a resting-state baseline (Figure 1A). We spectrally decomposed trial-by-trial brain activity projected on the entire cortical sheet spanning rhythms that support cognitive and motor function [11]. At each location (548 edges on a cortical grid) and frequency (1–90 Hz, Fig 3A), a linear mixed-effects (LME) model was estimated using oscillatory activity to predict micro-online and micro-offline learning. Micro-offline learning was inversely predicted by beta-band (16–22 Hz) brain oscillatory activity during rest periods in a predominantly contralateral frontoparietal network (Figure 3,4, Table S1).
Figure 3. Micro-offline learning occurs in a state of low beta power.
A, Brain oscillatory activity during rest periods predictive of micro-offline learning. The horizontal plane depicts the relative power during rest periods compared to resting-state baseline across spectra (x-axis, 1–90 Hz) and cortex (y-axis, 548 locations clustered at frontal (Fro), parietal (Par), temporal (Temp), occipital (Occ) and cerebellar (Post) lobes). Warm yellow colors depict significant power increases during rest periods compared to resting-state baseline, cold blue colors significant power decreases (two-tailed one-sample t tests, n = 27). The z-axis depicts the strength of the inverse relationship between oscillatory power and micro-offline learning (linear-mixed effects (LME) model coefficient, n = 10 trials × 27 participants) at the significant frequencies and locations (magenta). All P<0.05im, FDR-corrected for multiple comparisons. Note that only beta oscillatory activity at 16–22 Hz in frontoparietal areas was predictive of micro-offline learning. B, Inverse relationship between frontoparietal beta oscillatory activity during rest periods and micro-offline learning (n = 10 trials x 27 participants). See also Figure S3 for predictive oscillatory activity for micro-scale learning. See also Table S1.
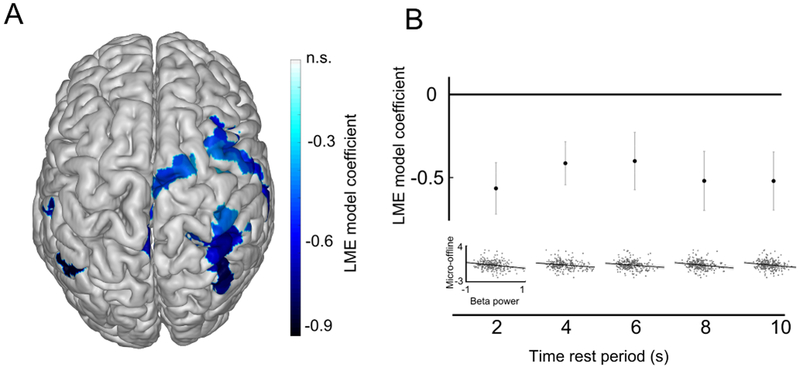
Figure 4. Topography and timecourse of predictive beta oscillatory activity for micro-offline learning.
A, Topography of the predominantly contralateral beta oscillatory activity during rest periods predictive of micro-offline learning indicated by the LME model coefficient (Table S1). B, Frontoparietal beta activity predicted micro-offline gains throughout the duration of early learning rest periods (averaged in each of 5 consecutive 2s segments, LME model coefficient ± s.e.m., n = 10 trials × 27 participants).
This inverse relationship was confirmed by modelling micro-offline learning within participant (mean ± s.e.m. model coefficient −1.23 ± 2.41, n = 27 model coefficients, T = −2.7, P = 0.01, two-tailed one-sample t test) and within trial (−0.90 ± 0.89, n = 10 model coefficients, T = −3.2, P = 0.01). The correlation between micro-offline learning and beta power during rest periods was not driven by performance improvements during early learning. First, including trial-by-trial performance in the predictive model as an additional factor (LME model with micro-offline learning as the dependent variable, beta power during rest periods and performance as fixed effects, and participants as random effect, n = 10 trials × 27 participants) did not improve the model fit (likelihood ratio test, P = 0.55). Second, the linear partial correlation coefficient between micro-offline learning and beta power during rest periods were virtually identical with and without partialing out performance (linear partial correlation coefficient ρ = −0.25; n = 10 trials × 27 participants, P = 3.8×10−5 and linear correlation coefficient ρ = −0.26; n = 10 trials × 27 participants, P = 2.4×10−5 respectively). Neither exclusion of the first second of the rest period (i.e., the beta rhythm amplitude rebound [12], which may include beta amplitude increase as a physiologic stop signal) from analysis (Figure S3A) nor inclusion of performance as an additional predictive factor (Text S1) modified this result. In order to test if beta rhythm amplitude predicted micro-offline gains during specific segments of the 10s-long rest period, we estimated the same model for 5 consecutive 2s-long segments of the rest period. The inverse prediction was stable across the entire rest period (Figure 4B). Throughout early learning, the beta rhythm power during rest periods was lower than during resting-state baseline (−0.1 ± 0.02 mean ± s.e.m, two-tailed one-sample t test, T = −4.6, P = 0.001, n = 10 trials).
The beta rhythm emerges as transient high-power ‘events’ instead of as a sustained signal [13]. Functionally relevant differences in time-averaged power can reflect changes in event characteristics like number, amplitude or duration. We investigated the predictive value of beta event characteristics on micro-offline learning. Beta event characteristics (number, maximum amplitude, duration) all inversely predicted micro-offline learning similarly to trial average beta power (LME, n = 10 trials x 27 participants, P < 0.05, Figure S4). Neither theta, alpha or gamma rhythms during rest or any rhythm during practice periods predicted micro-offline learning (Figure S3C,E). No brain oscillatory activity during practice or rest periods predicted micro-online learning (Figure S3B,D), learning over all Day 1 trials or overnight improvement from the end of training on Day 1 to test on Day 2.
DISCUSSION
The main finding of this study was that performance improvements during online procedural motor learning develop during rest instead of during practice periods. Early trials showed strongest micro-offline and total learning in the absence of preceding within-practice performance decrements. Downregulation of predominantly contralateral beta oscillatory activity during rest periods was identified as an intrinsic neural signature that predicted micro-offline gains.
Consolidation, measured as offline performance gains, has been tested at different time intervals following the end of a practice session [14, 15]. Here we studied early performance improvements over periods of rest that occur within a series of practice bouts within the same session when naïve subjects practice for the first time a new motor skill. Our results documented a substantial contribution of micro-offline performance improvements to early learning during these seconds-duration rest periods in the absence of within-practice performance decrements (Figure 2B). The sum of these improvements in performance during rest periods was four times larger than overnight offline learning (difference in performance between the end of training in Day 1 and test on Day 2), accounted for virtually all early procedural learning (Figure 2C) and represented approximately 95% of overall Day 1 learning for this task (Figure 1B). Thus, micro-offline gains made a sizable contribution to early motor skill learning and to what is often referred to as initial online learning when acquiring a new motor skill [4].
The findings that micro-offline gains in this period were substantial and largest at trials with no discernible evidence of within practice performance decrements (Figure 2B) are consistent with the interpretation that early learning micro-offline gains may represent a rapid form of consolidation. In these early trials, micro-offline gains could conceivably result from unmasking of inhibitory effects like low-level fatigue or reactive inhibition [16]. However, previous work on rapid improvements after a few minutes of rest in the rotor pursuit task [17], have been interpreted as reflecting “the need for rest on the part of the organism in order to consolidate the memory trace” [18] rather than recovery from inhibitory effects [19]. After performance maximum was reached (i.e. following trial 11), within-practice performance decrements robustly expressed, likely signaling either fatigue or reactive inhibition (Figure S1G) [9, 20]. Optimal rest/practice period duration for this rapid consolidation remain to be determined.
Classically studied offline improvements in skill over extended periods of time that manifest after the end of a training session contrast with micro-offline improvements that occur early within a training session. Accordingly, we found no correlation between micro-online or micro-offline learning and overnight behavioral gains. Overnight improvements in motor skill have been linked to a topological shift of task-related neural activity from cortical to subcortical regions [10, 21] supported by a dynamic interaction between declarative (hippocampus) and procedural (striatum) memory systems [10, 22, 23]. On the other hand, the brief time window of this rapid form of consolidation points to short-term plasticity [24] rather than long-term potentiation or structural reorganization relevant for longer forms of consolidation [2].
Our finding that frontoparietal beta (16–22 Hz) oscillatory activity during rest periods predicted micro-offline learning is consistent with the involvement of the dorsal frontoparietal network in encoding offline representations of movement kinematics [16]. Recently, the beta rhythm was found to play a role in structuring short-term activity-dependent plasticity [25] qualifying it as a possible neural signature for this fast form of consolidation. A reduction of the beta rhythm amplitude is present during brain states that mediate movement preparation, execution and imagery as well as somatosensation [3]. Thus, a low amplitude beta rhythm reflects a state of sensorimotor engagement. It is possible that beta-related activity during rest periods may contribute to micro-offline learning through reactivation of previous practice-related activity [26, 27] or memory replay [28]. Memory replay has been documented in humans [20], during awake-states [29, 30], at hippocampal [31] as well as neocortical sites [32, 33] and develop at a far faster rate than the pattern of activity during memory formation [34] either in forward or reverse order [30]. This idea is consistent with observations suggesting that the reactivations involved in reconsolidation ultimately strengthen memories after an initial period of vulnerability [4, 5, 8]. GABAergic signaling, a key determinant of plasticity related to early learning [35, 36] and beta oscillations [37, 38], could possibly contribute to micro-offline gains as well. Identification of this oscillatory signature of micro-offline learning will allow future experiments to address the question of causality.
In summary, we report a rapid form of offline consolidation that contribute substantially to early skill learning. These results support the idea that the brain opportunistically consolidates previous memories whenever it is not actively learning [39], and they extend the concept of memory consolidation to a time-scale on the order of seconds, rather than the hours or days traditionally accepted.
STAR METHODS
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Marlene Bönstrup (marlene.boenstrup@nih.gov).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Participants
33 naive right-handed healthy participants with a normal neurological examination gave their written informed consent to participate in the project, which was approved by the Combined Neuroscience Institutional Review Board of the National Institutes of Health (NIH). The sample size was estimated based on our prior data using the same task [5, 40]. Five participants didn’t follow instructions correctly. Technical problems occurred in one recording. Full data sets were analyzed from 27 participants (17 female, mean ± SEM age 26.3 ± 0.83). Active musicians were excluded from participation [5]. Of those, 25 participants (16 female, mean ± SEM age 26.6 ± 0.87) completed the Day 2 session.
METHOD DETAILS
Task
Participants learned a procedural motor skill task on Day 1 [5, 41, 42]. They used the non-dominant, left hand to perform a sequence of five keypresses (4–1-3–2-4) as quickly and accurately as possible in response to instructions displayed on a monitor. Keypresses were applied on a four-key response pad (Cedrus LS-LINE) with the pinky finger corresponding to button # 1, the ring finger to # 2, middle finger to # 3 and index finger to # 4 (Figure 1A). The monitor displayed the sequence continuously and provided feedback in the form of a star appearing immediately after each keypress regardless of correctness. Keypress timing (ms) was recorded for behavioral data analysis. 36 trials were performed during Day 1 training and 9 trials were performed during Day 2 testing. Each trial consisted of a 10-s practice period followed by a 10-s rest period [20, 40]. Participants were instructed to focus on the visually presented five-item sequence (during practice periods) or on five “X” symbols displayed on the monitor (during rest periods). Thus, a single trial included a practice period followed by a rest period. Each participant was tested at a similar time of day on Days 1 and 2 (± 2 hours). Stimuli were programmed, presented and responses recorded with E-Prime 2.
Behavioral Data Analysis
Tapping speed was quantified as the average of the time intervals between adjacent keypresses within correct sequences [10] divided by 1000 (keypresses/s). Performance within each trial was calculated as the mean tapping speed of all correctly performed sequences (including correct sequences the participant has not completed by the end of the trial [42, 43]. Accuracy was quantified as 1 minus the number of erroneous relative to correct keypresses in each trial [6, 43].
Early learning
The end of early learning was reached when 95% of the total Day 1 learning was achieved. We chose 95% of maximal performance because it corresponds to the significance level, alpha, of 5%. It was calculated using a modelling approach in which the group average performance curve of mean tapping speed per trial, B(t), was fitted using an exponential function L(t):
where k1 and k2 control the learning plateau, k3 controls the learning steepness, and t ∈ [1, +∞) represents trial. Parameters k1–3 were estimated by gradient descent, with the objective function defined as the root mean square error between B and L functions:
From this function, we estimated the end of early learning as the trial τ after 95% of the total learning had occurred. In practice, this value can be estimated as:
identifying the end of early learning at the group level by trial 11 (vertical line Figure 1B).
Microscale learning
We developed a novel approach to study trial by trial early learning, dissecting performance improvements occurring during practice (micro-online) and during rest (micro-offline) periods. Micro-online learning was defined as the difference in tapping speed between the first and the last correct sequence of a practice period. Micro-offline learning was the difference in tapping speed of the last correct sequence of a practice period and the first correct sequence of the next practice period (Figure 2A). The tapping speed of incomplete sequences was averaged with the previous complete sequence (excluding incomplete sequences from analysis elicited a comparable result, Figure S1F). In the case of only one correctly performed sequence, the speed of that sequence served as the first and last tapping speed of each trial. To derive the micro-online and micro-offline contribution to early learning we calculated the sum over all early learning trials at the participant level. The performance curve of Day 1 and the modelled group average performance showed that 95% of learning occurred within the first 11 trials (Fig 1B). Thus, 11 values (practice periods) were summed for micro-online, and 10 values (rest periods) were summed for micro-offline learning. Early learning was derived as the sum of all micro-online and micro-offline values (Figure 2B). Total learning during Day 1 over all 36 trials (online learning) was calculated as the difference between the mean tapping speed of the last and the first trial. Overnight improvement from the end of training on Day 1 to test on Day 2 was calculated as the difference between the average tapping speed of the last 9 trials of Day 1 (trials 28–36) and the 9 test trials of Day 2, as previously done [5, 41].
Magnetic Resonance Imaging
Structural MRI scanning was performed on a 3T MRI scanner (GE Excite HDxt and Siemens Skyra) with a standard head coil. T1-weighted high-resolution (1×1×1 mm, MPRAGE sequence) anatomical images were acquired for each participant to allow for spatial coregistration with the MEG sensors and individual head model computation.
Magnetoencephalography
MEG was recorded simultaneously with early learning during Day 1, starting 5 min before the task (resting-state baseline) and for the duration of the 12 min training. MEG data were recorded using a CTF 275 MEG system composed of a whole head array of 271 (four broken sensors) radial 1st order gradiometer/SQUID channels housed in a magnetically shielded room (Vacuumschmelze, Germany) at a sampling frequency of 600 Hz. Synthetic 3rd gradient balancing was used to remove background noise online. To measure head position, three electromagnetic head coils were attached to the participant’s head at the nasion, left and right pre-auricular point. The head coil positions relative to the MEG dewar were recorded at the beginning and the end of the MEG recording [44]. The task script sent synchronizing triggers via a parallel port to the MEG data acquisition computer, which were written to the MEG data file for subsequent analysis. The fiducial positions (nasion, left and right pre-auricular) of the headcoils were coregistered with the individual MRI after the MEG recording using the Brainsight Neuronavigation System (BrainSight, Rogue Research).
MEG Data Analysis
MEG data was analyzed using the FieldTrip package [45] and the MEG&EEG toolbox of Hamburg [46] on Matlab 2017b.
Preprocessing
The continuous MEG data were band-pass filtered from 1 to 150 Hz and band-stop filtered at 60 ± 1 Hz to remove line noise using the default filter settings in the FieldTrip preprocessing functions. The artifact removal process was twofold: Fist, eyeblink, eye movement and heart beat artifacts were removed by rejection of independent components, obtained via logisitic infomax independent component analysis [47]. Second, the entire recording was visually inspected and segments containing other artifacts like movements were visually identified and marked for rejection.
Source space time frequency reconstruction
Individual forward models consisting of 548 cortical locations and the corresponding lead field matrices were derived as follows: Based on a template anatomical brain image provided by the FieldTrip package, a regularly spaced (14 mm) three-dimensional grid of locations within the brain volume and constrained to the cortex, as defined by the AAL atlas [48], was created. This template grid was warped onto each individual MRI to give a three-dimensional grid of the same 548 cortical locations in the individual head space (source model). The choice of the spacing was a trade-off between minimizing computational load while spatially sampling the entire cortical sheet and corresponds to the reported spatial resolution of MEG [11]. Individual volume conduction models, describing how currents that are generated in the brain are propagated through the tissue to externally measurable magnetic fields, were constructed based on single-shell headmodels [49] derived from brain volume segmentation of individual MRI. Sensor positions in the MEG helmet were aligned to the individual head space by warping the MEG head coil positions (mean of pre and post recording) to the fiducials of the MRI and applying the same transformation matrix to all 271 MEG sensors. Based on the individual source and volume conduction models and the sensor positions, the lead field matrix describing the propagation of source activity from each cortical location on the grid to each MEG sensor was calculated.
Inverse solution: We reconstructed source activity using low-resolution brain electromagnetic tomography (ELORETA) which solves the inverse solution by spatial smoothness constraints [50]. For each of the 548 cortical locations two orthogonal (assuming the radial dimension is silent), real-valued spatial filters were computed that filter activity from each MEG sensor to the location of interest. The two filters were then linearly combined to a single filter in the direction of maximal variance after multiplication with the covariance matrix of the artifact free data. Using this filter, MEG time series were projected into source space to give a source space time series at each cortical location.
Spectro-temporal representations of the projected data were obtained by transforming the source space time series using Morlet wavelets at frequencies 1–90 Hz with a cycle number of 5. This procedure was done separately for the 5 min resting-state baseline and the 12 min task-related MEG recordings. To reduce inter-participant variability, each task-related time series was normalized with the corresponding average resting-state baseline power by subtraction and division following typical event-related desynchronization analysis [51]. Spectral power during practice and rest periods where averaged over the 10s duration.
Beta event identification and characterization (Figure S4) was performed in analogy to the methodology described in [52]. Periods of high beta activity were identified in the normalized beta band (16–22 Hz) time series during rest periods by thresholding the timeseries at the 90th percentile of individual average beta power. This threshold was empirically derived as the peak correlation coefficient (Pearson’s) between average rest period beta power and the percent area above threshold in the non-averaged beta time series, across various thresholds (percentiles). Each suprathreshold period with a local maxima was defined as a beta event and the maximal amplitude, duration (full-width-at-half-maximum) and number of events per rest period were quantified for each participant, rest period and voxel within the cluster of predictive beta oscillatory activity for micro-offline learning (Figure 3A) and then averaged within the frontal and parietal cortex (Table S1).
Visualization
Performance curve: The within-trials time-resolved representation of tapping speed for illustration of the performance curve in Figure 1B was derived as follows: For each participant, the tapping speed at each of the 10,000 milliseconds constituting one practice period was defined as the average inter-tap interval of the sequence the participant was executing at that moment. The duration of the execution of each sequence was defined as the time between the first keypress of that sequence (or the beginning of the practice period) and the first keypress of the next (or the end of the practice period). The participants’ timeseries were averaged at each millisecond to give the performance curve in Figure 1B. Topographic plots: For the topographic display of brain regions with predictive oscillatory activity (Figure 4A), the cortical grid consisting of 548 locations was interpolated onto a finer grained cortical surface of 8196 locations (provided by the FieldTrip toolbox) and spatially smoothed.
QUANTIFICATION AND STATISTICAL ANALYSIS
Behavioral data
Early learning including micro-online, micro-offline and total early learning, as well as online learning on Day 1 and overnight improvement from the end of training on Day 1 to test on Day 2 were tested for significance using two-tailed one-sample t test. P values were corrected across all behavioral data statistical tests using the Benjamini & Hochberg procedure for controlling the false discovery rate (FDR) [53].
Predictive model for microscale learning
To study the relationship between early learning and brain oscillatory activity patterns we used a linear mixed-effects modelling approach. At each cortical location and oscillatory frequency, microscale learning values were modeled as the response variable by the average spectral power as the predictor variable. Thereby, micro-online and micro-offline, as well as spectral power during practice and rest periods were modeled separately. Spectral power was modeled as a fixed effect and individual participants ID as a random effect and the fitting method used was maximum likelihood. The number of observations were 11 (micro-online) or 10 (micro-offline) trials (early learning) for each of the 27 participants (n = 297 or 270). We additionally modelled micro-offline a) within each participant, with spectral power of 10 resting periods as the predictor variable, and b) within each trial, with spectral power of 27 participants as the predictor variable. In both approaches, a linear model was used and the 27 (a) and 10 (b) model coefficients were tested for significance using two-tailed one-sample t tests. To correct for multiple comparisons across the large number of locations (548), we applied the Benjamini & Hochberg procedure [53].
DATA AND SOFTWARE AVAILABILITY
MEG and behavioral data are available upon request by contracting the Lead Contact, Marlene Bönstrup (marlene.boenstrup@nih.gov).
Supplementary Material
HIGHLIGHTS.
Temporal microscale of motor skill learning reveals strong gains during rest periods
Online motor skill learning may rely largely on gains during short periods of rest
Frontoparietal beta oscillatory activity predicts these micro-offline gains
This rapid form of consolidation substantially contributes to early skill learning
ACKNOWLEDGEMENTS
We thank Kareem Zaghloul and Steven Wise for their feedback on this work. This work was supported by the German National Academy of Sciences Leopoldina (Fellowship Program grant number LPDS 2016–01, to M.B.) and by the Intramural Research Program of the National Institute of Neurological Disorders and Stroke.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- 1.Robertson EM, Pascual-Leone A, and Miall RC (2004). Current concepts in procedural consolidation. Nat Rev Neurosci 5, 576–582. [DOI] [PubMed] [Google Scholar]
- 2.Squire LR, Genzel L, Wixted JT, and Morris RG (2015). Memory consolidation. Cold Spring Harb Perspect Biol 7, a021766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Engel AK, and Fries P (2010). Beta-band oscillations--signalling the status quo? Curr Opin Neurobiol 20, 156–165. [DOI] [PubMed] [Google Scholar]
- 4.Dayan E, and Cohen LG (2011). Neuroplasticity subserving motor skill learning. Neuron 72, 443–454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Censor N, Horovitz SG, and Cohen LG (2014). Interference with existing memories alters offline intrinsic functional brain connectivity. Neuron 81, 69–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Walker MP, Brakefield T, Morgan A, Hobson JA, and Stickgold R (2002). Practice with sleep makes perfect: sleep-dependent motor skill learning. Neuron 35, 205–211. [DOI] [PubMed] [Google Scholar]
- 7.Krakauer JW, and Shadmehr R (2006). Consolidation of motor memory. Trends Neurosci 29, 58–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Censor N, Sagi D, and Cohen LG (2012). Common mechanisms of human perceptual and motor learning. Nat Rev Neurosci 13, 658–664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pan SC, and Rickard TC (2015). Sleep and motor learning: Is there room for consolidation? Psychol Bull 141, 812–834. [DOI] [PubMed] [Google Scholar]
- 10.Vahdat S, Fogel S, Benali H, and Doyon J (2017). Network-wide reorganization of procedural memory during NREM sleep revealed by fMRI. Elife 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Baillet S (2017). Magnetoencephalography for brain electrophysiology and imaging. Nat Neurosci 20, 327–339. [DOI] [PubMed] [Google Scholar]
- 12.Kilavik BE, Zaepffel M, Brovelli A, MacKay WA, and Riehle A (2013). The ups and downs of beta oscillations in sensorimotor cortex. Exp Neurol 245, 15–26. [DOI] [PubMed] [Google Scholar]
- 13.Jones SR (2016). When brain rhythms aren’t ‘rhythmic’: implication for their mechanisms and meaning. Curr Opin Neurobiol 40, 72–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hotermans C, Peigneux P, Maertens de Noordhout A, Moonen G, and Maquet P (2006). Early boost and slow consolidation in motor skill learning. Learn Mem 13, 580–583. [DOI] [PubMed] [Google Scholar]
- 15.Doyon J, Korman M, Morin A, Dostie V, Hadj Tahar A, Benali H, Karni A, Ungerleider LG, and Carrier J (2009). Contribution of night and day sleep vs. simple passage of time to the consolidation of motor sequence and visuomotor adaptation learning. Exp Brain Res 195, 15–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ptak R, Schnider A, and Fellrath J (2017). The Dorsal Frontoparietal Network: A Core System for Emulated Action. Trends Cogn Sci 21, 589–599. [DOI] [PubMed] [Google Scholar]
- 17.Eysenck HJ (1965). A Three-Factor Theory of Reminiscence. Br J Psychol 56, 163–182. [DOI] [PubMed] [Google Scholar]
- 18.Eysenck HJ (1964). An Experimental Test of the “Inhibition” and “Consolidation” Theories of Reminiscence. Life Sci (1962) 3, 175–188. [DOI] [PubMed] [Google Scholar]
- 19.Rachman S, and Grassi J (1965). Reminiscence, Inhibition and Consolidation. Br J Psychol 56, 157–162. [DOI] [PubMed] [Google Scholar]
- 20.Rickard TC, Cai DJ, Rieth CA, Jones J, and Ard MC (2008). Sleep does not enhance motor sequence learning. J Exp Psychol Learn Mem Cogn 34, 834–842. [DOI] [PubMed] [Google Scholar]
- 21.Orban P, Peigneux P, Lungu O, Albouy G, Breton E, Laberenne F, Benali H, Maquet P, and Doyon J (2010). The multifaceted nature of the relationship between performance and brain activity in motor sequence learning. Neuroimage 49, 694–702. [DOI] [PubMed] [Google Scholar]
- 22.Albouy G, Fogel S, Pottiez H, Nguyen VA, Ray L, Lungu O, Carrier J, Robertson E, and Doyon J (2013). Daytime sleep enhances consolidation of the spatial but not motoric representation of motor sequence memory. PLoS One 8, e52805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Albouy G, King BR, Maquet P, and Doyon J (2013). Hippocampus and striatum: dynamics and interaction during acquisition and sleep-related motor sequence memory consolidation. Hippocampus 23, 985–1004. [DOI] [PubMed] [Google Scholar]
- 24.Fioravante D, and Regehr WG (2011). Short-term forms of presynaptic plasticity. Curr Opin Neurobiol 21, 269–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zanos S, Rembado I, Chen D, and Fetz EE (2018). Phase-Locked Stimulation during Cortical Beta Oscillations Produces Bidirectional Synaptic Plasticity in Awake Monkeys. Curr Biol. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Maquet P, Laureys S, Peigneux P, Fuchs S, Petiau C, Phillips C, Aerts J, Del Fiore G, Degueldre C, Meulemans T, et al. (2000). Experience-dependent changes in cerebral activation during human REM sleep. Nat Neurosci 3, 831–836. [DOI] [PubMed] [Google Scholar]
- 27.Ramanathan DS, Gulati T, and Ganguly K (2015). Sleep-Dependent Reactivation of Ensembles in Motor Cortex Promotes Skill Consolidation. PLoS Biol 13, e1002263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cohen N, Pell L, Edelson MG, Ben-Yakov A, Pine A, and Dudai Y (2015). Peri-encoding predictors of memory encoding and consolidation. Neurosci Biobehav Rev 50, 128–142. [DOI] [PubMed] [Google Scholar]
- 29.Tambini A, Ketz N, and Davachi L (2010). Enhanced brain correlations during rest are related to memory for recent experiences. Neuron 65, 280–290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Foster DJ, and Wilson MA (2006). Reverse replay of behavioural sequences in hippocampal place cells during the awake state. Nature 440, 680–683. [DOI] [PubMed] [Google Scholar]
- 31.Tambini A, and Davachi L (2013). Persistence of hippocampal multivoxel patterns into postencoding rest is related to memory. Proc Natl Acad Sci U S A 110, 19591–19596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yang G, Lai CS, Cichon J, Ma L, Li W, and Gan WB (2014). Sleep promotes branch-specific formation of dendritic spines after learning. Science 344, 1173–1178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Brodt S, Pohlchen D, Flanagin VL, Glasauer S, Gais S, and Schonauer M (2016). Rapid and independent memory formation in the parietal cortex. Proc Natl Acad Sci U S A 113, 13251–13256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Euston DR, Tatsuno M, and McNaughton BL (2007). Fast-forward playback of recent memory sequences in prefrontal cortex during sleep. Science 318, 1147–1150. [DOI] [PubMed] [Google Scholar]
- 35.Chen SX, Kim AN, Peters AJ, and Komiyama T (2015). Subtype-specific plasticity of inhibitory circuits in motor cortex during motor learning. Nat Neurosci 18, 1109–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Benali A, Weiler E, Benali Y, Dinse HR, and Eysel UT (2008). Excitation and inhibition jointly regulate cortical reorganization in adult rats. J Neurosci 28, 12284–12293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Yamawaki N, Stanford IM, Hall SD, and Woodhall GL (2008). Pharmacologically induced and stimulus evoked rhythmic neuronal oscillatory activity in the primary motor cortex in vitro. Neuroscience 151, 386–395. [DOI] [PubMed] [Google Scholar]
- 38.Nutt D, Wilson S, Lingford-Hughes A, Myers J, Papadopoulos A, and Muthukumaraswamy S (2015). Differences between magnetoencephalographic (MEG) spectral profiles of drugs acting on GABA at synaptic and extrasynaptic sites: a study in healthy volunteers. Neuropharmacology 88, 155–163. [DOI] [PubMed] [Google Scholar]
- 39.Mednick SC, Cai DJ, Shuman T, Anagnostaras S, and Wixted JT (2011). An opportunistic theory of cellular and systems consolidation. Trends Neurosci 34, 504–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Censor N, Dayan E, and Cohen LG (2014). Cortico-subcortical neuronal circuitry associated with reconsolidation of human procedural memories. Cortex 58, 281–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Censor N, Dimyan MA, and Cohen LG (2010). Modification of existing human motor memories is enabled by primary cortical processing during memory reactivation. Curr Biol 20, 1545–1549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Walker MP, Brakefield T, Hobson JA, and Stickgold R (2003). Dissociable stages of human memory consolidation and reconsolidation. Nature 425, 616–620. [DOI] [PubMed] [Google Scholar]
- 43.Hardwicke TE, Taqi M, and Shanks DR (2016). Postretrieval new learning does not reliably induce human memory updating via reconsolidation. Proc Natl Acad Sci U S A 113, 5206–5211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.de Munck JC, van Houdt PJ, Verdaasdonk RM, and Ossenblok PP (2012). A semi-automatic method to determine electrode positions and labels from gel artifacts in EEG/fMRI-studies. Neuroimage 59, 399–403. [DOI] [PubMed] [Google Scholar]
- 45.Oostenveld R, Fries P, Maris E, and Schoffelen JM (2011). FieldTrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput Intell Neurosci 2011, 156869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Nolte G (2018). https://www.nitrc.org/projects/meth/
- 47.Bell AJ, and Sejnowski TJ (1995). An information-maximization approach to blind separation and blind deconvolution. Neural Comput 7, 1129–1159. [DOI] [PubMed] [Google Scholar]
- 48.Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, and Joliot M (2002). Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 15, 273–289. [DOI] [PubMed] [Google Scholar]
- 49.Nolte G (2003). The magnetic lead field theorem in the quasi-static approximation and its use for magnetoencephalography forward calculation in realistic volume conductors. Phys Med Biol 48, 3637–3652. [DOI] [PubMed] [Google Scholar]
- 50.Pascual-Marqui RD, Lehmann D, Koukkou M, Kochi K, Anderer P, Saletu B, Tanaka H, Hirata K, John ER, Prichep L, et al. (2011). Assessing interactions in the brain with exact low-resolution electromagnetic tomography. Philos Trans A Math Phys Eng Sci 369, 3768–3784. [DOI] [PubMed] [Google Scholar]
- 51.Pfurtscheller G, and Lopes da Silva FH (1999). Event-related EEG/MEG synchronization and desynchronization: basic principles. Clin Neurophysiol 110, 1842–1857. [DOI] [PubMed] [Google Scholar]
- 52.Shin H, Law R, Tsutsui S, Moore CI, and Jones SR (2017). The rate of transient beta frequency events predicts behavior across tasks and species. Elife 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Benjamini Y, and Hochberg Y (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the royal statistical society. Series B (Methodological), 289–300. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
MEG and behavioral data are available upon request by contracting the Lead Contact, Marlene Bönstrup (marlene.boenstrup@nih.gov).