Abstract
According to the latest research, lncRNAs (long non-coding RNAs) play a broad and important role in various biological processes by interacting with proteins. However, identifying whether proteins interact with a specific lncRNA through biological experimental methods is difficult, costly, and time-consuming. Thus, many bioinformatics computational methods have been proposed to predict lncRNA-protein interactions. In this paper, we proposed a novel approach called Long non-coding RNA-Protein Interaction Prediction based on Improved Bipartite Network Recommender Algorithm (LPI-IBNRA). In the proposed method, we implemented a two-round resource allocation and eliminated the second-order correlations appropriately on the bipartite network. Experimental results illustrate that LPI-IBNRA outperforms five previous methods, with the AUC values of 0.8932 in leave-one-out cross validation (LOOCV) and 0.8819 ± 0.0052 in 10-fold cross validation, respectively. In addition, case studies on four lncRNAs were carried out to show the predictive power of LPI-IBNRA.
Keywords: lncRNA, protein, interaction prediction, bipartite network, second-order correlation elimination
1. Introduction
LncRNA, a class of ncRNAs (non-coding RNAs) of more than 200 nucleotides, that do not encode proteins, has gained increasing scientific interest in recent years (Jorge et al., 2012; Hajjari et al., 2016). Only 2% of RNAs in the human transcriptome can encode proteins while others, called ncRNAs, cannot. Note that most ncRNAs are lncRNAs. Compared to other ncRNAs, lncRNAs are longer and have complex secondary or higher-order structures (Bonasio and Shiekhattar, 2014), and their genes often have independent regulatory elements such as promoters and enhancers (Ulitsky and Bartel, 2013). There is increasing evidence that lncRNAs are related to the regulation of gene expression levels such as epigenetic regulation, transcriptional regulation, and multiple levels of post-transcriptional regulation (Sarah and Jeff, 2013), but only a few functions and mechanisms of lncRNA have been studied (Maarabouni et al., 2008; Lee et al., 2016). Moreover, interactions of lncRNAs with other molecules also have become hot spots in oncology research over the past years. The studies found that an important way for lncRNAs to function is by interacting with proteins (Khalil and Rinn, 2011). LncRNAs play a broad and important regulatory role in various processes such as tumorigenesis, cancer progression and metastasis by interacting with proteins. Thus, the prediction and identification of lncRNA-protein interactions can further reveal lncRNA-related functions and is beneficial for the study on the pathogenesis of complex diseases at the molecular level (Faghihi et al., 2008; Chen and Yan, 2013; Cui et al., 2013; Li et al., 2013; Chen et al., 2016a,c, 2017b, 2018c).
Numerous biological experimental methods were exploited to confirm protein-related RNAs (Ule et al., 2005; Galgano and Gerber, 2011; Zambelli and Pavesi, 2015). However, such experimental methods are laborious, time-consuming, and costly (Huang et al., 2012). Recently, various computational methods have been proposed to address the challenges in bioinformatics (He et al., 2018a,b; Zou et al., 2018), such as lncRNA-protein (Hu et al., 2017; Shen et al., 2019a,b), miRNA-disease (Chen and Huang, 2017; Chen et al., 2018a,b,d,e,f; Jiang et al., 2018a,b; Xie et al., 2018), drug-target (Chen et al., 2016b; Wang et al., 2017; Wu et al., 2018) and microbe-disease associations predictions (Chen et al., 2017a; Peng et al., 2018). The methods for inferring lncRNA-protein associations can roughly be classified into two types: the machine learning methods and the network-based methods. The so-called machine learning methods usually use the biological features of lncRNAs and proteins, and then employ a supervised classifier to identify whether proteins have potential interactions with a specific lncRNA (Zhan et al., 2018). For example, Bellucci et al. (2011) proposed to utilize secondary structure, hydrogen bonding and van der Waals contributions for feature integration, which has a beneficial effect for inferring the binding propensity of protein and ncRNA. Protein and lncRNA sequence information is utilized in Muppirala et al. (2011), with the employment of a support vector machine (SVM) and random forest (RF). Suresh et al. (2015) proposed an SVM-based method named RPI-Pred, which uses high-order 3D structural features and sequences of the lncRNA and protein. Hu et al. (2018) developed a method called HLPI-Ensembl, adopting the ensemble strategy based on extreme gradient boosting (XGB), SVM and RF. However, the main drawback of these methods is the insufficiency of negative samples of lncRNA-protein interactions. The lack of negative samples may cause the unstable performance of the supervised classifier. Moreover, selecting appropriate features to predict lncRNA-protein interactions is not an easy task.
Apart from the aforementioned methods, there are other approaches for potential lncRNA-protein interaction prediction, with the employment of network analysis algorithms. For instance, Li et al. (2015) presented a method called LPIHN, which constructs a heterogeneous network, and implements a random walk with restart on the heterogeneous network. In order to improve prediction performance, some recent network-based methods use recommender algorithms to infer lncRNA-protein interactions. For example, Ge et al. (2016) proposed a method called LPBNI, which only uses known lncRNA-protein interactions and implements the two-step propagation on a bipartite network. Zhao et al. (2018b) introduced an approach based on the bipartite network called LPI-BNPRA, which infers lncRNA-protein interactions by constructing bias ratings for lncRNAs and proteins, using agglomerative hierarchical clustering. By implementing two-round resource allocation on bipartite networks, these approaches achieved impressive results. But predictive validity of these investigations remains insufficient due to the existence of high-order correlations, which might have a negative effect on the lncRNA-protein interaction prediction. For example, the proteins directly correlated by the same lncRNA, could also be indirectly correlated by other media proteins, resulting in correlation redundancy. Properly eliminating the redundancy induced by the second-order correlation might further enhance the accuracy of the prediction. This inspired us to develop an effective network-based recommender algorithm for lncRNA-protein interaction prediction.
Motivated by the effectiveness of high-order correlation elimination in the study of Qiu et al. (2014), we propose a novel method named LPI-IBNRA for inferring new lncRNA-protein interactions. LPI-IBNRA uses known lncRNA-protein and protein-protein interactions, and lncRNA expression similarity, and then eliminates second-order correlations on the bipartite network appropriately to enhance the prediction accuracy. Compared with previous machine learning methods, our method does not require negative samples. Compared with many existing network-based methods (Ge et al., 2016; Zhao et al., 2018b), our method yields comparable or even better results due to second-order correlation elimination. Both 10-fold cross validation and LOOCV were carried out to assess the prediction ability of the proposed method. Experimental results illustrated that LPI-IBNRA outperformed five other methods by achieving higher AUC values. In addition, case studies on four lncRNAs further demonstrated the predictive power of LPI-IBNRA. Therefore, we conclude that LPI-IBNRA is feasible and effective for inferring potential lncRNA-protein interactions.
2. Materials and Methods
2.1. Human LncRNA-Protein Interactions
The known ncRNA-protein interaction dataset was downloaded from the NPInter v2.0 database (Yuan et al., 2014). We limited the organism to “Homo sapiens” and the type of ncRNAs to “NONCODE”, in order to filter ncRNAs and their interacting proteins. The lncRNAs were further filtered from these ncRNAs, through a human lncRNA dataset from the NONCODE 4.0 database (Xie et al., 2014). We deleted duplicate interactions. Considering the sample requirement of LOOCV, we removed the lncRNAs and proteins that have only one interaction. We then obtained 4796 distinct experimentally confirmed lncRNA-protein interactions, containing 26 proteins and 1105 lncRNAs. We denoted np as the number of known proteins, nl as the number of known lncRNAs, and matrix I ∈ ℝnp*nl as the adjacency matrix of protein-lncRNA interactions. The interaction between protein pi and lncRNA lj could be denoted as follows:
| (1) |
2.2. Protein-Protein Interaction Score Matrix and Similarity Matrix
Protein-protein interactions (PPI) were obtained from the STRING 9.1 database (Franceschini et al., 2013), which included weighted protein-protein interactions through co-expression data, genomic context predictions, automated text mining, and high-throughput lab experiments. We then deleted the redundant PPI data, and obtained 214 PPI data, and the corresponding interaction scores based on the known lncRNA-protein dataset. The symmetric matrix AP was denoted as an interaction score matrix based on PPI data, where AP(pi, pj) is the interaction score between proteins pi and pj. AP could then be standardized as follows:
| (2) |
where R(pi) is the sum of the elements in i-row of AP.
Considering the hypothesis that similar proteins tend to exhibit a similar interaction and non-interaction pattern with lncRNAs (Zheng et al., 2017), we calculated the protein similarity with the utilization of Gaussian kernel interaction profiles. We denoted X(pi) as the ith row vector of matrix I, in which the nonzero values occur at the indices where the corresponding lncRNA have one interaction with a protein pi. Then the similarity between proteins pi and pj based on Gaussian kernel interaction profiles could be calculated as follows:
| (3) |
where the adjustment coefficient βp for the kernel bandwidth is defined as follows:
| (4) |
2.3. LncRNA-LncRNA Similarity Matrix
LncRNA expression profiles were downloaded from the NONCODE 4.0 database (Xie et al., 2014). After removing the superfluous data, we obtained the expression profiles of 1,105 lncRNAs in 24 human tissues or cell types. Then the Pearson correlation coefficient (PPC) was applied for the calculation of lncRNA expression similarity between each pair of lncRNA expression profiles (Wang et al., 2010; Ganegoda et al., 2013; Tang et al., 2014). We denoted E(i) = {ei1, ei2, …, ei24} and E(j) = {ej1, ej2, …, ej24} as the expression profiles of li and lj. The expression similarity AL(li, lj) between lncRNAs li and lj was calculated as follows:
| (5) |
where AL(li, lj) denotes the absolute value of PCC between li and lj, cov(E(i), E(j)) is the covariance between E(i) and E(j), σE(i) and σE(j) are standard deviations of E(i) and E(j), respectively.
We denoted X(pi) as the ith column vector of matrix I, in which the nonzero values occur at the indices where the corresponding protein has one interaction with the lncRNA li. Similar to the aforementioned protein case, the Gaussian interaction profile kernel similarity for lncRNAs could be computed as follows:
| (6) |
where
| (7) |
2.4. Integrated Similarity Matrix for Proteins and LncRNAs
Note that the Gaussian interaction profile kernel similarity is an association information-based measurement, which can be utilized to complement protein-protein interactions and lncRNA expression similarity. Motivated by the study of Chen (2015), we constructed the integrated protein similarity matrix SimP and integrated the lncRNA similarity matrix SimL as follows:
| (8) |
| (9) |
2.5. LPI-IBNRA
The flow chart of LPI-IBNRA is shown in Figure 1. At first, we denoted SP ∈ ℝnp*nl as the resource score matrix based on protein similarity, SL ∈ ℝnp*nl as the one based on lncRNA similarity. These two matrices were computed as follows:
Figure 1.
The flowchart of LPI-IBNRA method.
| (10) |
| (11) |
where represents the score between protein pi and lncRNA lj based on protein similarity, and represents the score between protein pi and lncRNA lj based on lncRNA similarity.
Then the integrated resource score matrix was initialized as the weighted sum of SP and SL as follows:
| (12) |
where parameter γ ∈ [0, 1] is a scalar controlling the relative contributions of protein similarity and lncRNA similarity in Sini. Following the general setting, we set the parameter γ = 0.5 in this paper, making SP and SL equally weighted.
The final score matrix can be obtained by updating the Sini column by column. In other words, the calculation process can be partitioned into nl runs, each of which corresponds to a specific lncRNA. Thus, at the beginning of the kth run, the score for protein pi interacting with the given lncRNA lk can be initialized as follows:
| (13) |
Then the 1st-round of our allocation model is to allocate the score of the lncRNA lk from the protein pi, which can be calculated as follows:
| (14) |
where is obtained by a summing operation over all initial scores from lncRNAs interacting with protein pi.
The score of lncRNA lk can be obtained by summing scores over all proteins connected with lk:
| (15) |
In the 2nd-round, resource scores were allocated in a similar way as the first round. The score allocated from the lncRNA lk to the protein pi was calculated as follows:
| (16) |
where is the sum of initial scores from all proteins interacting with lncRNA lk.
The score of protein pi was allocated from all lncRNAs that interacted with pi as follows:
| (17) |
As described from Equation (13) to (17), we first initialized the score of protein pi from the given lncRNA lk and then updated it by a two-round resource allocation. An example is given in Figure 2. We defined as the final resource score matrix, which can be represented as follows:
Figure 2.
The basic idea of LPI-IBNRA. First, two resource score matrices which are computed based on protein similarity and lncRNA similarity, respectively, are combined to construct the initial integrated resource score network. Secondly, each protein gains its initial score from a specific lncRNA. Next, in two-round resource allocation, the score is allocated from proteins to lncRNAs, and then propagated back to proteins. Finally, the weight matrix is optimized by second-order correlation eliminations to obtain the final scores of proteins.
| (18) |
S can also be computed in a vectorized form as:
| (19) |
where is a column vector of Sfin, is a column vector of Sini, and W ∈ ℝnp*np is the weight matrix. Then Equation (17) can also be represented as:
| (20) |
where
| (21) |
In the lncRNA-protein interaction network, the proteins interacting with the same lncRNA are considered to be directly correlated, i.e., having the low-order correlation, while higher-order correlations between these proteins might also arise from indirect associations. Such high-order correlations might have a negative effect on the lncRNA-protein interaction prediction. Based on the studies of Zhou et al. (2009) and Liu et al. (2010), we eliminated second-order correlations in an appropriate way to further enhance the accuracy of the prediction:
| (22) |
where the parameter α ∈ (−1, 0). The final score matrix for inferring potential lncRNA-protein interactions can then be calculated as follows:
| (23) |
After the calculations, we can recommend proteins to the given lncRNA lk in descending order by the kth column of .
2.6. Performance Evaluation
We evaluated the classification performance of the proposed LPI-IBNRA method by applying two types of classification schemes, i.e., LOOCV and 10-fold cross validation. The performance of LPI-IBNRA was evaluated in terms of several widely-used indicators, including precision (PRE), sensitivity (SEN), accuracy (ACC), F1 score, and Matthews correlation coefficient (MCC), expressed as follows:
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
where TP, TN, FP, and FN count the number of true positives, true negatives, false positives, and false negatives, respectively.
As a popular method for performance evaluation, the receiver operating characteristic (ROC) curve was also utilized in our experiments. The area under the ROC curve (AUC) = 1 indicates perfect performance, while AUC = 0.5 indicates random performance. The precision-recall curve (PR curve) and the area under the PR curve (AUPR) are also used to reduce the negative influence of false positive data on the method performance. The larger the AUC and AUPR is, the better performance the evaluated method has.
3. Results
3.1. Comparison With Other Methods
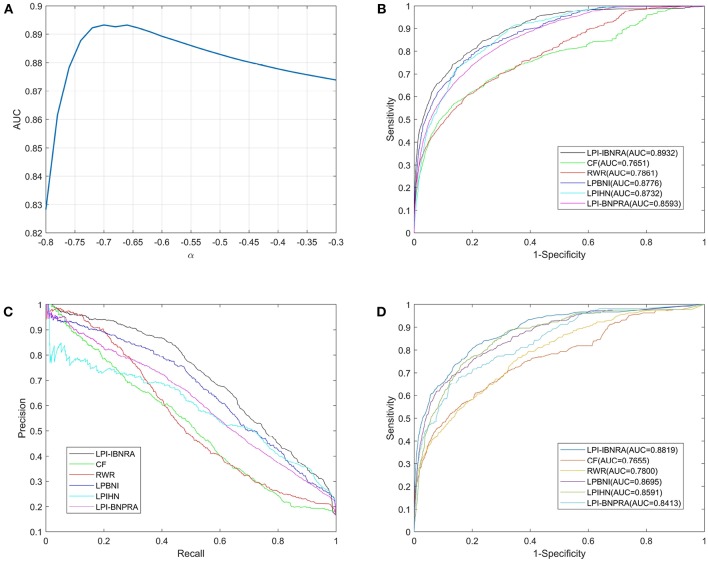
We used the aforementioned 4,796 known human lncRNA-protein interactions to carry out the above-mentioned two cross validation schemes. In each LOOCV trial, each known lncRNA-protein interaction was used as a test sample while the rest were used as training samples. To analyze the influence of parameter α on the performance of LPI-IBNRA, we applied LOOCV for the selection of parameter α. As shown in Figure 3A, the performance of LPI-IBNRA drops a lot when α is smaller than –0.70. When α is larger than –0.70, the performance of LPI-IBNRA decreases slightly. Thus, the parameter α is set to –0.70 due to the optimal performance.
Figure 3.
(A)The AUC values of LPI-IBNRA method with different values of α. (B) ROC curves of lncRNA-protein interaction predictions by all compared methods in LOOCV. (C) Precision-recall curves of all compared methods. (D) ROC curves of lncRNA-protein interaction predictions by all compared methods in 10-fold cross validation.
Five previous approaches were used for comparison in the experiments, including collaborative filtering (CF), random walk with restart (RWR), LPBNI, LPIHN, and LPI-BNPRA. LPBNI, LPIHN, and LPI-BNPRA are network-based methods that infer potential lncRNA-protein interactions, while CF and RWR have been used as benchmark methods in Ge et al. (2016) and Wen et al. (2017). RWR is often utilized as a powerful tool for network-based methods to forecast association (Zhao et al., 2018a,c; Zhu et al., 2018), while CF is a well-known recommender algorithm which can infer the information from similar neighborhoods (Fu et al., 2014; Zeng et al., 2017). In our experiments, RWR was implemented to make predictions based on the protein-protein similarity network, while a simple version of the CF algorithm was adopted to calculate the prediction scores between lncRNAs and proteins.
Here, we reproduced these methods on the same dataset by ourselves. See Figures 3B,C and Table 1 for the results of LOOCV. We can see from Figure 3B that our proposed method achieved an AUC of 0.8932, which exhibited a considerable improvement over the five previous methods (i.e., 12.81% for CF, 10.71% for RWR, 1.56% for LPBNI, 2.00% for LPIHN and 3.39% for LPI-BNPRA). In addition, the comparison of these methods, in terms of precision vs. recall, is presented in Figure 3C. It can be seen that LPI-IBNRA almost achieved a higher precision than the other methods at every recall value. Moreover, LPI-IBNRA outperformed the other methods in terms of AUPR, PRE, SEN, ACC, F1 score and MCC, which is presented in Table 1. As shown in Figure 3D, in 10-fold cross validation, LPI-IBNRA achieved an AUC of 0.8819 ± 0.0052 and was superior to the comparison methods, including CF (0.7655 ± 0.0069), RWR (0.7800 ± 0.0076), LPBNI (0.8695 ± 0.0047), LPIHN (0.8591 ± 0.0044), and LPI-BNPRA (0.8413 ± 0.0351).
Table 1.
Performance evaluation of all compared methods in LOOCV in terms of several widely-used indicators.
| Methods | AUC | AUPR | PRE | SEN | ACC | F1-score | MCC |
|---|---|---|---|---|---|---|---|
| LPI-IBNRA | 0.8932 | 0.7098 | 0.8778 | 0.3580 | 0.8845 | 0.5273 | 0.5152 |
| CF | 0.7651 | 0.5249 | 0.7941 | 0.1922 | 0.8568 | 0.3225 | 0.3452 |
| RWR | 0.7861 | 0.5500 | 0.8316 | 0.2460 | 0.8658 | 0.3949 | 0.4063 |
| LPBNI | 0.8776 | 0.6624 | 0.8526 | 0.2882 | 0.8729 | 0.4474 | 0.4496 |
| LPIHN | 0.8732 | 0.5892 | 0.7518 | 0.1522 | 0.8501 | 0.2642 | 0.2933 |
| LPI-BNPRA | 0.8593 | 0.6148 | 0.8200 | 0.2271 | 0.8627 | 0.3701 | 0.3855 |
The aforementioned results indicate that in both LOOCV and 10-fold cross evaluation, LPI-IBNRA outperforms other methods in terms of the AUC values. The outstanding performance of LPI-IBNRA demonstrates its stable and satisfying abilities in inferring potential lncRNA-protein interactions. The superior performance of the proposed method could be attributed to second-order correlation elimination, which is more suitable for our task and can lead to better prediction performance.
3.2. Case Studies
In addition, four case studies have been carried out to further evaluate the effectiveness of LPI-IBNRA. The interactions in our benchmark dataset were obtained in NPInter v2.0 which was established in 2013. NPInter was then upgraded to NPInter v3.0 in 2016 (Hao et al., 2016), which includes newly discovered lncRNA-protein interactions. Thus, we predicted novel lncRNA-protein interactions based on known interactions in the benchmark dataset, then confirmed our predictions in NPInter v3.0. For each lncRNA, the proteins ranked within the top 5 were considered as potential proteins that interact with the given lncRNA. Case studies were carried out on four lncRNAs, including lncRNA DLEU2, CRHR1-1T1, LRRC75A-AS1 and SNHG5.
Table 2 shows the prediction results and whether there were confirmations for these lncRNAs. It indicates that five (DLEU2), five (CRHR1-1T1), five (LRRC75A-AS1), and four (SNHG5) out of the top five predicted lncRNA-interacted proteins, were confirmed by NPInter v3.0. The rankings of these lncRNA-protein interactions in other benchmark method predictions are also listed in Table 2. It can be observed that several novel interactions did not have high rankings in the predictions of other methods, and these interactions are likely to be ignored by these methods. Therefore, LPI-IBNRA has great potential to predict new lncRNA-protein interactions.
Table 2.
The top five ranked proteins for lncRNA DLEU2, CRHR1-1T1, LRRC75A-AS1, and SNHG5.
| LncRNA | Protein | Confirmed? | Rank | CF | RWR | LPBNI | LPIHN | LPI-BNPRA |
|---|---|---|---|---|---|---|---|---|
| DLEU2 | ENSP00000290341 | Confirmed | 1 | 7 | 1 | 1 | 3 | 1 |
| DLEU2 | ENSP00000258729 | Confirmed | 2 | 17 | 2 | 2 | 1 | 6 |
| DLEU2 | ENSP00000381031 | Confirmed | 3 | 1 | 6 | 3 | 5 | 7 |
| DLEU2 | ENSP00000371634 | Confirmed | 4 | 16 | 3 | 6 | 2 | 8 |
| DLEU2 | ENSP00000254108 | Confirmed | 5 | 10 | 4 | 4 | 4 | 2 |
| CRHR1-IT1 | ENSP00000254108 | Confirmed | 1 | 11 | 4 | 3 | 2 | 2 |
| CRHR1-IT1 | ENSP00000240185 | Confirmed | 2 | 2 | 9 | 2 | 11 | 7 |
| CRHR1-IT1 | ENSP00000350028 | Confirmed | 3 | 1 | 10 | 8 | 12 | 10 |
| CRHR1-IT1 | ENSP00000381031 | Confirmed | 4 | 12 | 11 | 9 | 5 | 8 |
| CRHR1-IT1 | ENSP00000220592 | Confirmed | 5 | 5 | 1 | 4 | 10 | 6 |
| LRRC75A-AS1 | ENSP00000385269 | Confirmed | 1 | 6 | 1 | 1 | 1 | 1 |
| LRRC75A-AS1 | ENSP00000254108 | Confirmed | 2 | 7 | 2 | 2 | 2 | 2 |
| LRRC75A-AS1 | ENSP00000381031 | Confirmed | 3 | 8 | 4 | 3 | 6 | 3 |
| LRRC75A-AS1 | ENSP00000350028 | Confirmed | 4 | 9 | 6 | 7 | 12 | 9 |
| LRRC75A-AS1 | ENSP00000258962 | Confirmed | 5 | 1 | 10 | 5 | 16 | 5 |
| SNHG5 | ENSP00000290341 | Confirmed | 1 | 1 | 1 | 1 | 4 | 1 |
| SNHG5 | ENSP00000350028 | Confirmed | 2 | 2 | 10 | 4 | 6 | 3 |
| SNHG5 | ENSP00000240185 | Confirmed | 3 | 7 | 11 | 3 | 13 | 4 |
| SNHG5 | ENSP00000254108 | 4 | 3 | 2 | 2 | 1 | 2 | |
| SNHG5 | ENSP00000381031 | Confirmed | 5 | 4 | 8 | 5 | 10 | 6 |
4. Discussion and Conclusion
In this article, we proposed a novel method LPI-IBNRA for predicting lncRNA-protein interactions, based on the known lncRNA-protein interactions, lncRNA expression similarity and protein-protein interactions. We integrated the known interactions and similarity as the initial resource scores for a two-round resource allocation of a bipartite network recommendation. Furthermore, we optimized the weight matrix by eliminating second-order correlations appropriately, to obtain the final result of lncRNA-protein interaction prediction. We finally acquired gratifying and reliable prediction performance in LOOCV, 10-fold cross evaluation and case studies. Thus, we believe that LPI-IBNRA can make reliable predictions and might guide future experimental studies on lncRNA-protein interactions.
LPI-IBNRA has the following improvements over several previous methods in predicting lncRNA-protein interactions. First, with the employment of the bipartite network recommender algorithm, we utilized the known lncRNA-protein interactions to construct a bipartite network between lncRNAs and proteins, and then allocated the resource scores via interaction edges between lncRNA nodes and protein nodes. Therefore, the negative sample set is not required in our methods. Second, we assigned weights to each edge on the bipartite network, which is distinct from most former bipartite network methods. Thus, the resource scores would not be evenly distributed during the resource allocation process. Finally, we eliminated second-order correlations on the bipartite network appropriately, to enhance prediction accuracy.
Although impressive results have been achieved, there is still much room for improvement in our method. At first, though known lncRNA-protein interactions have been more than before, it is still very difficult for the proposed method to obtain adequate results based on the prediction. Moreover, as the resource allocation of the bipartite network recommendation algorithm is based on known lncRNA-protein interactions, LPI-IBNRA is not suitable to predict interactions of lncRNAs without any known interacted protein.
Author Contributions
GX designed the experiments. CW and ZF performed the experiments. GX, CW, YS, ZF, and JL conceived the project and analyzed the data. CW and YS wrote the manuscript and all authors contributed to the writing.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
Funding. This work was supported by the National Natural Science Foundation of China (618002072), the Natural Science Foundation of Guangdong Province (2018A030313389), and the Science and Technology Plan Project of Guangdong Province (2017A040405050, 2016B030306004, 2015B010129014).
References
- Bellucci M., Agostini F., Masin M., Tartaglia G. G. (2011). Predicting protein associations with long noncoding rnas. Nat. Methods 8, 444–445. 10.1038/nmeth.1611 [DOI] [PubMed] [Google Scholar]
- Bonasio R., Shiekhattar R. (2014). Regulation of transcription by long noncoding rnas. Ann. Rev. Genet. 48, 433–455. 10.1146/annurev-genet-120213-092323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X. (2015). Katzlda: katz measure for the lncrna-disease association prediction. Sci. Rep. 5:16840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X., Guan N. N., Sun Y. Z., Li J. Q., Qu J. (2018a). Microrna-small molecule association identification: from experimental results to computational models. Brief. Bioinformat. bby098. 10.1093/bib/bby098 [DOI] [PubMed] [Google Scholar]
- Chen X., Huang L. (2017). Lrsslmda: laplacian regularized sparse subspace learning for mirna-disease association prediction. PLoS Comput. Biol. 13:e1005912. 10.1371/journal.pcbi.1005912 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X., Huang L., Xie D., Zhao Q. (2018b). Egbmmda: extreme gradient boosting machine for mirna-disease association prediction. Cell Death Disease 9:3. 10.1038/s41419-017-0003-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X., Huang Y. A., You Z. H., Yan G. Y., Wang X. S. (2017a). A novel approach based on katz measure to predict associations of human microbiota with non-infectious diseases. Bioinformatics 33, 733–739. 10.1093/bioinformatics/btw715 [DOI] [PubMed] [Google Scholar]
- Chen X., Sun Y. Z., Guan N., Qu J., Li J. Q. (2018c). Computational models for lncrna function prediction and functional similarity calculation. Brief. Fun. Genom. 18, 58–82. 10.1093/bfgp/ely031 [DOI] [PubMed] [Google Scholar]
- Chen X., Sun Y. Z., Liu H., Zhang L., Li J. Q., Meng J. (2017b). Rna methylation and diseases: experimental results, databases, web servers and computational models. Brief. Bioinform. bbx142. 10.1093/bib/bbx142 [DOI] [PubMed] [Google Scholar]
- Chen X., Wang L., Qu J., Guan N. N., Li J. Q. (2018d). Predicting miRNA-disease association based on inductive matrix completion. Bioinformatics 34, 4256–4265. 10.1093/bioinformatics/bty503 [DOI] [PubMed] [Google Scholar]
- Chen X., Xie D., Wang L., Zhao Q., Liu H. (2018e). Bnpmda: bipartite network projection for mirna-disease association prediction. Bioinformatics 34, 3178–3186. 10.1093/bioinformatics/bty333 [DOI] [PubMed] [Google Scholar]
- Chen X., Yan C. G. C., Zhang X., You Z. (2016a). Long non-coding rnas and complex diseases: from experimental results to computational models. Brief. Bioinform. 18, 558–576. 10.1093/bib/bbw060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X., Yan C. C., Zhang X., Zhang X., Dai F., Yin J., et al. (2016b). Drug-target interaction prediction: databases, web servers and computational models. Brief. Bioinform. 17, 696–712. 10.1093/bib/bbv066 [DOI] [PubMed] [Google Scholar]
- Chen X., Yan G. Y. (2013). Novel human lncrna-disease association inference based on lncrna expression profiles. Bioinformatics 29, 2617–2624. 10.1093/bioinformatics/btt426 [DOI] [PubMed] [Google Scholar]
- Chen X., Yin J., Qu J., Huang L. (2018f). Mdhgi: matrix decomposition and heterogeneous graph inference for mirna-disease association prediction. PLoS Comput. Biol. 14:e1006418. 10.1371/journal.pcbi.1006418 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X., You Z. H., Yan G. Y., Gong D. W. (2016c). Irwrlda: improved random walk with restart for lncrna-disease association prediction. Oncotarget 7, 57919–57931. 10.18632/oncotarget.11141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui Z., Ren S., Lu J., Wang F., Xu W. D., Sun Y., et al. (2013). The prostate cancer-up-regulated long noncoding rna plncrna-1 modulates apoptosis and proliferation through reciprocal regulation of androgen receptor. Urol. Oncol. Sem. Original Investig. 31, 1117–1123. 10.1016/j.urolonc.2011.11.030 [DOI] [PubMed] [Google Scholar]
- Faghihi M. A., Modarresi F., Khalil A. M., Wood D. E., Sahagan B. G., Morgan T. E., et al. (2008). Expression of a noncoding rna is elevated in alzheimer's disease and drives rapid feed-forward regulation of β-secretase. Nat. Med. 14, 723–730. 10.1038/nm1784 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franceschini A., Szklarczyk D., Frankild S., Kuhn M., Simonovic M., Roth A., et al. (2013). String v9.1: protein-protein interaction networks, with increased coverage and integration. Nucleic Acids Res. 41, D808–D815. 10.1093/nar/gks1094 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Y., Liu Q., Cui Z. (2014). A collaborative recommend algorithm based on bipartite community. Sci. World J. 2014, 1–14. 10.1155/2014/295931 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galgano A., Gerber A. P. (2011). Rna-binding protein immunopurification-microarray (rip-chip) analysis to profile localized rnas. Methods Mol. Biol. 714, 369–385. 10.1007/978-1-61779-005-8-23 [DOI] [PubMed] [Google Scholar]
- Ganegoda G. U., Wang J. X., Wu F. X., Li M. (2013). Prioritization of candidate genes based on disease similarity and protein's proximity in ppi networks, in IEEE International Conference on Bioinformatics and Biomedicine, Shanghai, 103–108. [Google Scholar]
- Ge M., Li A., Wang M. (2016). A bipartite network-based method for prediction of long non-coding rna-protein interactions. Genom. Proteom. Bioinform. 14, 62–71. 10.1016/j.gpb.2016.01.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hajjari M., Mowla S. J., Faghihi M. A. (2016). Editorial: molecular function and regulation of non-coding rnas in multifactorial diseases. Front. Genet. 7:9. 10.3389/fgene.2016.00009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hao Y., Wu W., Li H., Yuan J., Luo J., Zhao Y., et al. (2016). Npinter v3.0: an upgraded database of noncoding rna-associated interactions. Database 2016:baw057. 10.1093/database/baw057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- He W., Jia C., Duan Y., Zou Q. (2018a). 70propred: a predictor for discovering sigma70 promoters based on combining multiple features. BMC Syst. Biol. 12:44. 10.1186/s12918-018-0570-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- He W., Ju Y., Zeng X., Liu X., Zou Q. (2018b). Sc-ncdnapred: a sequence-based predictor for identifying non-coding dna in saccharomyces cerevisiae. Front. Microbiol. 9:2174. 10.3389/fmicb.2018.02174 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu H., Zhang L., Ai H., Zhang H., Fan Y. T., Zhao Q., et al. (2018). Hlpi-ensemble: prediction of human lncrna-protein interactions based on ensemble strategy. RNA Biol. 15, 797–806. 10.1080/15476286.2018.1457935 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu H., Zhu C., Ai H., Zhang L., Zhao J., Zhao Q., et al. (2017). Lpi-etslp: lncrna-protein interaction prediction using eigenvalue transformation-based semi-supervised link prediction. Mol. Biosyst. 13, 1781–1787. 10.1039/C7MB00290D [DOI] [PubMed] [Google Scholar]
- Huang Y. Y., Yang X. F., Li H. T., Ji X. F., Cheng H. L., Zhao Y. J., et al. (2012). Protein-rna interaction interface prediction and design. Acta Phys. Chim. Sin. 28, 2390–2400. 10.3866/PKU.WHXB201209111 [DOI] [Google Scholar]
- Jiang L., Ding Y., Tang J., Guo F. (2018a). Mda-skf: similarity kernel fusion for accurately discovering mirna-disease association. Front. Genet. 9:618. 10.3389/fgene.2018.00618 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang L., Xiao Y., Ding Y., Tang J., Guo F. (2018b). Fkl-spa-laprls: an accurate method for identifying human microrna-disease association. BMC Genom. 19:911. 10.1186/s12864-018-5273-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorge N. A., Ferreira C. G., Passetti F. (2012). Bioinformatics of cancer ncrna in high throughput sequencing: present state and challenges. Front. Genet. 3:287. 10.3389/fgene.2012.00287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khalil A. M., Rinn J. L. (2011). Rna-protein interactions in human health and disease. Sem. Cell Dev. Biol. 22, 359–365. 10.1016/j.semcdb.2011.02.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S., Kopp F., Chang T. C., Sataluri A., Chen B., Sivakumar S., et al. (2016). Noncoding rna norad regulates genomic stability by sequestering pumilio proteins. Cell 164, 69–80. 10.1016/j.cell.2015.12.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li A., Ge M., Zhang Y., Peng C., Wang M. H. (2015). Predicting long noncoding rna and protein interactions using heterogeneous network model. Biomed Res. Int. 2015, 1–11. 10.1155/2015/671950 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J., Xuan Z., Liu C. N. (2013). Long non-coding rnas and complex human diseases. Int. J. Mol. Sci. 14, 18790–18808. 10.3390/ijms140918790 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J. G., Zhou T., Che H. A., Wang B. H., Zhang Y. C. (2010). Effects of high-order correlations on personalized recommendations for bipartite networks. Phys. A Statis. Mech. Appl. 389, 881–886. 10.1016/j.physa.2009.10.027 [DOI] [Google Scholar]
- Maarabouni M., Pickard M., Hedge V. L., Farzaneh F., Williams G. (2008). Gas5, a non-protein-coding rna, controls apoptosis and is downregulated in breast cancer. Oncogene 28, 195–208. 10.1038/onc.2008.373 [DOI] [PubMed] [Google Scholar]
- Muppirala U. K., Honavar V. G., Drena D. (2011). Predicting rna-protein interactions using only sequence information. BMC Bioinform. 12:489. 10.1186/1471-2105-12-489 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng L. H., Yin J., Zhou L. Q., Liu M. X., Zhao Y. (2018). Human microbe-disease association prediction based on adaptive boosting. Front. Microbiol. 9:2440. 10.3389/fmicb.2018.02440 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiu T., Han T. Y., Zhong L. X., Zhang Z. K., Chen G. (2014). Redundant correlation effect on personalized recommendation. Comput. Phys. Commun. 185, 489–494. 10.1016/j.cpc.2013.10.003 [DOI] [Google Scholar]
- Sarah G., Jeff C. (2013). Rna in unexpected places: long non-coding rna functions in diverse cellular contexts. Nat. Rev. Mol. Cell Biol. 14, 699–712. 10.1038/nrm3679 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen C., Ding Y. J., Tang J. J., Guo F. (2019a). Multivariate information fusion with fast kernel learning to kernel ridge regression in predicting lncrna-protein interactions. Front. Genet. 9:716. 10.3389/fgene.2018.00716 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen C., Ding Y. J., Tang J. J., Jiang L. M., Guo F. (2019b). Lpi-ktaslp: prediction of lncrna-protein interaction by semi-supervised link learning with multivariate information. IEEE Access 7, 13486–13496. 10.1109/ACCESS.2019.2894225 [DOI] [Google Scholar]
- Suresh V., Liu L., Adjeroh D., Zhou X. B. (2015). Rpi-pred: predicting ncrna-protein interaction using sequence and structural information. Nucleic Acids Res. 43, 1370–1379. 10.1093/nar/gkv020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang X., Wang J., Zhong J., Pan Y. (2014). Predicting essential proteins based on weighted degree centrality. IEEE/ACM Trans. Comput. Biol. Bioinform. 11, 407–418. 10.1109/TCBB.2013.2295318 [DOI] [PubMed] [Google Scholar]
- Ule J., Jensen K., Mele A., Darnell R. B. (2005). Clip: a method for identifying protein-rna interaction sites in living cells. Methods 37, 376–386. 10.1016/j.ymeth.2005.07.018 [DOI] [PubMed] [Google Scholar]
- Ulitsky I., Bartel D. P. (2013). Lincrnas: genomics, evolution, and mechanisms. Cell 154, 26–46. 10.1016/j.cell.2013.06.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang F. J., Zheng Z. G., Guo J. F., Ding X. F. (2010). Correlation and quantitation of microrna aberrant expression in tissues and sera from patients with breast tumor. Gynecol. Oncol. 119, 586–593. 10.1016/j.ygyno.2010.07.021 [DOI] [PubMed] [Google Scholar]
- Wang L., You Z. H., Chen X., Xia S. X., Liu F., Yan X., et al. (2017). A computational-based method for predicting drug-target interactions by using stacked autoencoder deep neural network. J. Comput. Biol. 25, 361–373. 10.1089/cmb.2017.0135 [DOI] [PubMed] [Google Scholar]
- Wen Z., Qu Q. L., Zhang Y. Q., Wei W., Wen Z., Qu Q. L., et al. (2017). The linear neighborhood propagation method for predicting long non-coding rna-protein interactions. Neurocomputing 273, 526–534. 10.1016/j.neucom.2017.07.065 [DOI] [Google Scholar]
- Wu Z. R., Li W. H., Liu G. X., Tang Y. (2018). Network-based methods for prediction of drug-target interactions. Front. Pharmacol. 9:1134. 10.3389/fphar.2018.01134 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie C. Y., Yuan J., Li H., Li M., Zhao G. G., Bu D. C., et al. (2014). Noncodev4: exploring the world of long non-coding rna genes. Nucleic Acids Res. 42, 98–103. 10.1093/nar/gkt1222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie D., Zhao Q., Liu H. S., Wang F., Yan G. Y., Chen X. (2018). Sscmda: spy and super cluster strategy for mirna-disease association prediction. Oncotarget 9, 1826–1842. 10.18632/oncotarget.22812 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan J., Wu W., Xie C. Y., Zhao G. G., Zhao Y., Chen R. S. (2014). Npinter v2.0: an updated database of ncrna interactions. Nucleic Acids Res. 42, D104–D108. 10.1093/nar/gkt1057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zambelli F., Pavesi G. (2015). Rip-seq data analysis to determine rna-protein associations. Methods Mol. Biol. 1269, 293–303. 10.1007/978-1-4939-2291-8-18 [DOI] [PubMed] [Google Scholar]
- Zeng X. X., Ding N. X., Rodríguezpatón A., Zou Q. (2017). Probability-based collaborative filtering model for predicting gene-disease associations. BMC Med. Genom. 10:76. 10.1186/s12920-017-0313-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhan Z. H., You Z. H., Li L. P., Zhou Y., Yi H. C. (2018). Accurate prediction of ncrna-protein interactions from the integration of sequence and evolutionary information. Front. Genet. 9:458. 10.3389/fgene.2018.00458 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Q., Liang D., Hu H., Ren G. F., Liu H. S. (2018a). Rwlpap: Random walk for lncrna-protein associations prediction. Protein Peptide Lett. 25, 830–837. 10.2174/0929866525666180905104904 [DOI] [PubMed] [Google Scholar]
- Zhao Q., Yu H. F., Ming Z., Hu H., Ren G. F., Liu H. S. (2018b). The bipartite network projection-recommended algorithm for predicting long non-coding rna-protein interactions. Mol. Therapy Nucleic Acids 13, 464–471. 10.1016/j.omtn.2018.09.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Q., Zhang Y., Hu H., Ren G. F., Zhang W., Liu H. S. (2018c). Irwnrlpi: integrating random walk and neighborhood regularized logistic matrix factorization for lncrna-protein interaction prediction. Front. Genet. 9:239. 10.3389/fgene.2018.00239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng X. X., Wang Y., Tian K., Zhou J. G., Guan J. H., Luo L., et al. (2017). Fusing multiple protein-protein similarity networks to effectively predict lncrna-protein interactions. BMC Bioinform. 18:420. 10.1186/s12859-017-1819-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou T., Su R. Q., Liu R. R., Jiang L. L., Wang B. H., Zhang Y. C. (2009). Ultra accurate personalized recommendation via eliminating redundant correlations. Phys. Soc. arXiv:0805.4127. 10.1088/1367-2630/11/12/123008 [DOI] [Google Scholar]
- Zhu L. C., Su F. C., Xu Y. C., Zou Q. (2018). Network-based method for mining novel hpv infection related genes using random walk with restart algorithm. BBA Mol. Basis Dis. 1864, 2376–2383. 10.1016/j.bbadis.2017.11.021 [DOI] [PubMed] [Google Scholar]
- Zou Q., Qu K. Y., Luo Y. M., Yin D. H., Ju Y., Tang H. (2018). Predicting diabetes mellitus with machine learning techniques. Front. Genet. 9:515. 10.3389/fgene.2018.00515 [DOI] [PMC free article] [PubMed] [Google Scholar]