A longitudinal human phantom reliability study of multi-center T1-weighted, DTI, and resting state fMRI data

Abstract

Multi-center MRI studies can enhance power, generalizability, and discovery for clinical neuroimaging research in brain disorders. Here, we sought to establish the utility of a clustering algorithm as an alternative to more traditional intra-class correlation coefficient approaches in a longitudinal multi-center human phantom study. We completed annual reliability scans on Travelling human phantoms’. Acquisitions across sites were harmonized prospectively. Twenty-seven MRI sessions were available across four participants, scanned on five scanners, across three years. For each scan, three metrics were extracted: cortical thickness (CT), white matter fractional anisotropy (FA), and resting state functional connectivity (FC). For each metric, hierarchical clustering (Ward’s method) was performed. The cluster solutions were compared to participant and scanner using the adjusted Rand index (ARI). For all metrics, data clustered by participant rather than by scanner (ARI > 0.8 comparing clusters to participants, ARI < 0.2 comparing clusters to scanners). These results demonstrate that hierarchical clustering can reliably identify structural and functional scans from different participants imaged on different scanners across time. With increasing interest in data-driven approaches in psychiatric and neurologic brain imaging studies, our findings provide a framework for multi-center analytic approaches aiming to identify subgroups of participants based on brain structure or function.

1. Introduction

The collaborative NIMH-funded multi-center study, ‘Social Processes Initiative in Neurobiology of the Schizophrenia(s)’ (SPINS) aims to identify neural circuitry related to social cognitive impairments in nearly 500 people who are healthy or who have a schizophrenia spectrum disorder (SSD). This study is being conducted as a part of the NIMH’s Research Domain Criteria (RDoC) initiative. SSDs have been associated with changes across several structural and functional neuroimaging metrics, including deficits in white matter identified via cortical thickness (Schultz et al., 2010; Wheeler et al., 2015), diffusion imaging (Voineskos et al., 2010), and resting state functional connectivity (Rotarska-Jagiela et al., 2010; Zhou et al., 2007). The SPINS study adopted a multi-modal data acquisition approach to best characterize these structural and functional neuroimaging metrics and measure how they relate to social cognitive processes.

Multi-center data collection allows for larger sample sizes, enabling discovery-based research (Clementz et al. 2016; Drysdale et al. 2017; Van Essen et al. 2013; Insel et al. 2010; Cannon et al. 2017) with more generalizable results (Baker, 2016). All multi-center studies face challenges with data harmonization and quality control (Brown et al., 2011; Fortin et al., 2017; Glover et al., 2012; Huang et al., 2012; Mirzaalian et al., 2016; Simmons et al., 2011; Wonderlick et al., 2009). Each of the three sites within the present study had different MRI scanners, but scan acquisition parameters were harmonized as much as possible across sites prior to study initiation to minimize site-based variability, and a phantom-based quality assurance (QA) protocol was developed to track scanner changes over time (Chavez et al., 2018). We also collected data on a group of individuals, ‘travelling human phantoms’, who visited all sites annually, to assess the reliability of brain imaging metrics across scanners and time.

Here, we compare the travelling human phantom data on key neuroimaging outcome metrics to study the influence of site-specific scanner effects over a period of three years. We hypothesized that participant-level variability of outcome metrics is greater than scanner-level variability both cross-sectionally and over time. We tested this assumption via cluster analysis (Finn et al., 2015; Shen et al., 2017). Previous studies aimed at characterizing inter-site reliability or differences have focused on factors such as intraclass correlation (ICC) of various metrics across sites (Jovicich et al. 2013, 2016; Forsyth et al. 2014; Whelan et al. 2016) or across-session reproducibility (Jovicich et al. 2014; Pfefferbaum et al. 2003; Choe et al. 2015; Kristo et al. 2014; Noble et al. 2017). The North American Prodrome Longitudinal Study (NAPLS) is an excellent example, scanning eight subjects twice each at eight scanners, and having examined the generalizability of the results across various imaging modalities and pipelines (Gee et al. 2015; Forsyth et al. 2014). The purpose of these analyses in traveling subjects or multi-scanner studies is often to determine if combining data across scanners is acceptable (as in e.g., Cannon et al. 2017; Deprez et al. 2018) or to determine the specific effects of doing so on a particular measure (Helmer et al. 2016). While these metrics can be highly informative, they may also present an incomplete picture. For example, while ICCs of repeated resting fMRI data are often quite low (Anderson et al., 2011; Birn et al., 2013; Noble et al., 2017; Patriat et al., 2013), individual scans across time can be reliable enough to be identifying within an individual (Finn et al., 2015), and ICCs may be greater for more global, connectomic measures (Noble et al., 2017), suggesting that ICC scores vary by measure and method, and low ICCs may obscure the true reliability of the measures within as opposed to between participants.

We chose an approach that examines neuroimaging outcome metrics across sites, time, and participants simultaneously. Rather than determining simply whether the scanner data are suitably harmonized (in the spirit of Glover et al. 2012), or as an estimate of the power gain from a multi-site study, our approach treats the outcome metrics as a classification problem and attempts to group the scans by participant (in the ‘fingerprinting’ spirit of Finn et al., 2015) using neuroimaging data across multiple sites and time-points. Our structural and functional metrics of interest were: cortical thickness (CT) from structural T1, fractional anisotropy (FA) from diffusion weighted (DTI) scans, and functional connectivity (FC) from resting fMRI. We used hierarchical clustering to evaluate classification accuracy across time and site. This study had two purposes: 1) to demonstrate that MRI metrics would be individually identifying even across scanners, supporting the collapsing of data across sites, and 2) to demonstrate that hierarchical clustering applied to MRI metrics would identify similar scans, even in the case of a small sample with many variables. We hypothesized that scan metrics would cluster together by individual participant rather than by site. As an additional exploration of scanner influences on our neuroimaging metrics, scanner-based differences were examined in each neuroimaging metric, and scan-to-scan reliability was assessed using ICC.

2. Methods

2.1. MRI scanners

Data were collected at three sites starting in 2014. The Centre for Addiction and Mental Health (CMH) in Toronto used a General Electric 750w Discovery 3T MRI throughout the study. Maryland Psychiatric Research Center started data collection using a Siemens Tim Trio 3T MRI (this MRI will be referred to as MRC) in 2014-15, and then upgraded to a Siemens PRISMA 3T MRI in 2016 (referred to as MRP). Zucker Hillside Hospital in New York started data collection using a General Electric 750 Signa 3T MRI in 2014 and 2015 (referred to as ZHH), and then upgraded to a Siemens PRISMA 3T MRI in 2016 (referred to as ZHP). Scans were labeled by site tag and scanning year. As scans were collected annually, we used the following terminology: ‘Year1’ is study initiation (fall of 2014), ‘Year2’ is the fall of 2015, and ‘Year3’ is the fall of 2016. Thus, for example, CMH_Year1 was a scan at the CMH scanner at study initiation, MRC_Year2 was a scan at the beginning of the second year on the original scanner at the MRC site, and ZHP_Year3 was a scan at beginning of the third year on that site’s upgraded scanner. Scans were performed at CMH for years one, two and three, on the ZHH and MRC scanner for years one and two, and at ZHP and MRP scanners for year three only. See Table 1 for study scanning flow.

Table 1.

Participant characteristics and scanning schedule.

	Sex	Age	Year 1 CMH	MRC	ZHH	Year 2 CMH	MRC	ZHH	Year 3 CMH	MRP	ZHP	total #
P1	M	52	x	x	x	x	x	x				6
P2	M	59	x	x	x	x	x	x	x	x	x	9
P3	M	36	x	x	x	x	x	x	x	x	x	9
P4	M	39							x	x	x	3

Note. Age is age at Year 1.

2.2. Participants (human phantoms)

Data were collected from four healthy male adult participants aged 34 to 59. No participant had a history of psychiatric or neurological problems, including concussion, or other serious medical conditions. Participant 1 (P1) had six total scans, one at each site for Year1 and Year2. This participant was unavailable for Year3. P2 and P3 completed all nine possible scans. P4 was introduced in Year3, and completed three scans (CMH, ZHP, and MRP). See Table 1 for a schematic of participant characteristics and study scanning flow. The study had REB or IRB approval at all three sites, and all participants gave informed consent.

2.3. MRI scan parameters

Scanning parameters were matched as closely as possible across all scanners, within the limitations of the scanner hardware. A complete list of all scan parameters by site is included in Supplemental Table 1. T1 anatomical scans were manufacturer-specific fast gradient echo sequences (MPRAGE for the Siemens scanners and BRAVO for GE scanners; TR = 2300 ms, 0.9 mm isotropic, no gap, interleaved ascending acquisition order, with TE from 2.78-3ms, as determined by the scanner-specific hardware). As is standard practice at that site to increase scan SNR (Kochunov et al., 2006), at MRC and MRP three T1 scans were acquired and subsequently averaged into a single image prior to any preprocessing. DTI scans used an axial EPI dual spin echo sequence (60 gradient directions, b = 1000, five baseline scans with b = 0 (or six in the case of the PRISMA scanners at MRP and ZHP), TR = 8800 ms, with the exception of ZHH where TR = 17700 ms; TE = 85 ms; FOV = 256 mm; in-plane matrix size was 128 × 128, 2.0 mm isotropic voxels). Resting fMRI scans used an EPI sequence (number of volumes acquired was 212, TR = 2000 ms, TE = 30.0 ms, FOV = 20 cm, 40 slices of 4 mm thickness, interleaved ascending acquisition order). The resting MRI scan lasted seven minutes, and participants were instructed to close their eyes, remain awake, and let their mind wander.

2.4. MRI analyses

2.4.1. Cortical thickness (CT) analysis

T1 scans were processed using FreeSurfer (Fischl, 2012) (version 5.3.0). In accordance with the ENIGMA protocol (http://enigma.usc.edu/protocols/imaging-protocols), average CT was extracted for 68 ROIs from the Desikan-Killiany atlas (Desikan et al., 2006).

2.4.2. Fractional anisotropy (FA) analysis

DTI data for the three sites were processed using the ENIGMA-DTI analysis pipeline (Jahanshad et al., 2013) (http://enigma.ini.usc.edu/ongoing/dti-working-group/), which includes quality control and quality assurance steps. The ENIGMA pipeline runs a variant of tract-based spatial statistics (Smith et al., 2006), in which the data is warped via a non-linear transform (FNIRT) to a specific template and FA values are extracted from a set of ROIs, and was implemented using FSL v 5.0.9 (Jenkinson et al., 2012). The DTI data were corrected for motion and eddy current distortions, a diffusion tensor was fitted for each voxel, and FA maps were generated using FSL. Next, individual FA maps were warped to an ENIGMA-DTI template and projected onto the ENIGMA-DTI skeleton that represents the middle of the tract of major white matter structures. ENIGMA-DTI per-tract average values were calculated for 63 ROIs from the Johns Hopkins University White Matter Atlas (Mori et al., 2005) by averaging values along tract regions of interest in both hemispheres.

2.4.3. Functional connectivity (FC) fMRI analysis

The first four TRs were removed from each fMRI series followed by slice timing correction. AFNI (Cox, 1996) (v.2014.09.22) was used to deoblique each image, perform motion correction, and perform brain masking. Time series outliers were removed via L1 regression (using AFNI’s 3dDespike) and each run was scaled to have a global mean signal of 1000. Framewise displacement (FD) was calculated during motion correction, as was a measure of instantaneous global signal fluctuation (DVARS, the root mean square of in-brain intensity changes per TR) (Power et al., 2012). If FD or DVARS exceeded 0.3mm/TR or 3%, respectively, for a given TR, that TR, the one preceding it, and the one following it were replaced with a linear interpolate between the surviving TRs. A nuisance regression model was generated for each subject to remove potential noise components, with the following regressors: second order Legendre polynomial, the six head motion parameters, the mean white matter signal (WM), the mean cerebrospinal fluid signal (CSF), the global mean brain signal, the derivative, squares, and squares of the derivatives of these signals, and finally the first three principal components of the WM and CSF (aCompCor) (Muschelli et al., 2014). In this way, we accounted for the tissue-specific regressors, head motion parameters (Satterthwaite et al., 2013), and the regression of the global mean signal, which while introducing artefactual negative correlations is also known to increase the correspondence of electrophysiological and hemodynamic signals (Keller et al., 2013). Time series were then low-passed using a bi-directional Butterworth filter and a cut-off frequency of 0.1 Hz (Carp, 2013). The registration transformation between each subject’s T2*-weighted (EPI BOLD) volumes and their T1-weighted volume were calculated between the 3Ddespike and nuisance regression steps described above using linear registration (6 degrees of freedom; FSL FLIRT). The linear (12 DOF) and non-linear transform between the T1-weighted volume and MNI atlas were also calculated using FNIRT. These transformations were finally concatenated and applied to the low-pass filtered T2*-weighted volumes to warp the fMRI data into MNI space in one step. Resting functional connectivity was calculated from the average time series within 268 ROIs (Shen et al., 2013). This atlas was selected as it was recently shown to be of sufficient resolution to allow for identifying individuals using their resting state functional connectivity alone (Finn et al., 2015). Pairwise correlations were calculated for each ROI, resulting in 35778 unique connections.

2.5. Statistical analysis

2.5.1. Evaluating cross scanner differences

A Mixed Effect Model was used to test for differences in our neuroimaging metrics across scanners. The model used scanner nested within year and subject, as well as year nested within subject as random effects. Scanner also entered the model as fixed effect since we were interested in its overall effect.

2.5.2. Hierarchical clustering

A matrix was created for each modality (CT, FA, and FC), with scanning sessions as rows and the neuroimaging metric as columns. All modalities were analyzed similarly. Euclidean distance (the sum of the squared difference between all data points) was calculated between each pair of scanning sessions for each metric. Note that as Euclidean distance is related to the scale/range and number of points in the input data, it cannot be compared across metrics. Hierarchical clustering was performed using Ward’s minimum variance method (Ward, 1963). During each stage of the bottom-up agglomerative hierarchical clustering procedure, total within-cluster variance is minimized by identifying a new cluster pair/linkage that leads to the minimum increase in total within-cluster variance. Ward’s linkage works under the assumption that the initial distances between each pair of data is proportional to the Euclidean distance. Given that the clustering approach groups similar data sets together, it can be considered a classifier, with the classification being accurate when scans from individuals are correctly grouped together.

2.5.3. Evaluating cluster accuracy

As we had specific a priori cluster labels to compare (travelling human phantom ID or scanner), we compared a range of cluster solutions to these a priori labels using the adjusted Rand index (ARI; (Hubert and Arabie, 1985; Rand, 1971), which was calculated via a MATLAB function (https://github.com/areslp/matlab/blob/master/code_cospectral/RandIndex.m; accessed April 2017). The ARI is the probability that any pair of data points share a label across two input solutions (e.g. if data points A and B share a label in two cluster solutions, they are a “match”), adjusted for the random chance probability for matched labels given the number of pairs. ARI values approximating zero indicate no overlap or random overlap, and an ARI of one indicates perfect matching of labels. Note that for a set of unmatched labels (e.g. comparing four participant IDs to a solution of five clusters) the ARI will by definition be below one, because it is not possible for all labels to match, though an ARI can still be calculated.

‘Ground truth’ labels for each of the 27 scans were created for comparison to cluster metrics. These ground truth labels included participant ID (collapsed across scanner and year; k = 4), scanner (collapsed across participant ID and year; k = 5), and year (collapsed across participant ID and scanner; k = 3). Additionally, as we were interested to examine scanner-based effects in the data, we created an additional label of participant by site, collapsed across years (k = 16; e.g. P1 at CMH, P1 at MRC, P2 at CMH, etc.). For completeness, labels were also created for scanner by year and participant ID by year. For each imaging metric, the resulting linkage tree (dendrogram) was divided into separate solutions ranging from two to 20 clusters. Cluster membership was compared to these ground truth labels using the ARI, thus allowing a quantitative comparison of the accuracy of each cluster solution against a ground truth of a priori labels.

In order to formally assess if the ARI differed from chance, a null distribution was created using a permutation approach. Each label was randomized across 1000 iterations and compared to the cluster solutions from two to 20 clusters, thus representing a distribution of ARI in the null case (e.g. when labels were random but with the same frequency as the true labels). ARI values which fell above 99% of this null distribution were considered significant (i.e. the cluster solution grouped by label more so than would be expected by chance). The evaluation of ARI relative to these labels allowed us to quantify if scans clustered by any of these labels, and to what extent.

2.5.4. Intraclass correlation coefficient (ICC) calculation

To facilitate comparison to other studies, ICC was calculated according to the methods of Shrout and Fleiss (1979), using a two-way mixed single measures model; ICC(3,1) as defined in the Shrout and Fleiss notation. ICC was calculated for the three metrics for each participant (collapsing across scanners and year), and for scanners (collapsing across participants and years).

3. Results

3.1. Scanner differences by metric

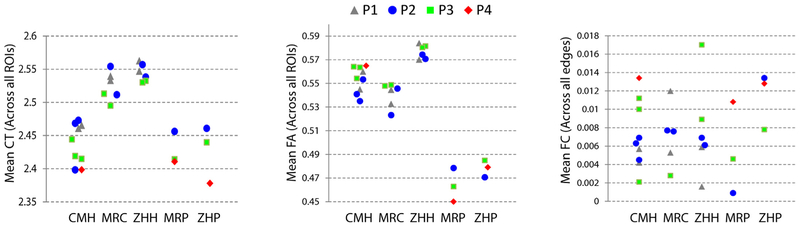
Mean CT, FA, and FC values for each scan, separated by scanner, are presented in Fig. 1. The mixed effects model revealed significant differences across scanners for mean CT, F(4,14) = 28.5, p < 0.0001, and for mean FA, F(4,8) = 82, p < 0.0001, but not for FC, F(4, 9.8) = 0.78, p = 0.56. Given that there were scanner-specific effects in the CT and FA metrics, scanner effects were regressed out of each ROI by building a model incorporating one column per site (thus treating site as a non-linear nominal variable). All further analyses on CT and FA were run on this data with scanner-based effects regressed out, unless otherwise specified.

Fig. 1.

Mean cortical thickness (CT; left), fractional anisotropy (FA; center), and functional connectivity (FC; right) values for every scan, separated by color/shape (for participant ID) and scanner (columns). Significant scanner based differences in the means were present in both CT and FA, but not FC.

3.2. Hierarchical clustering

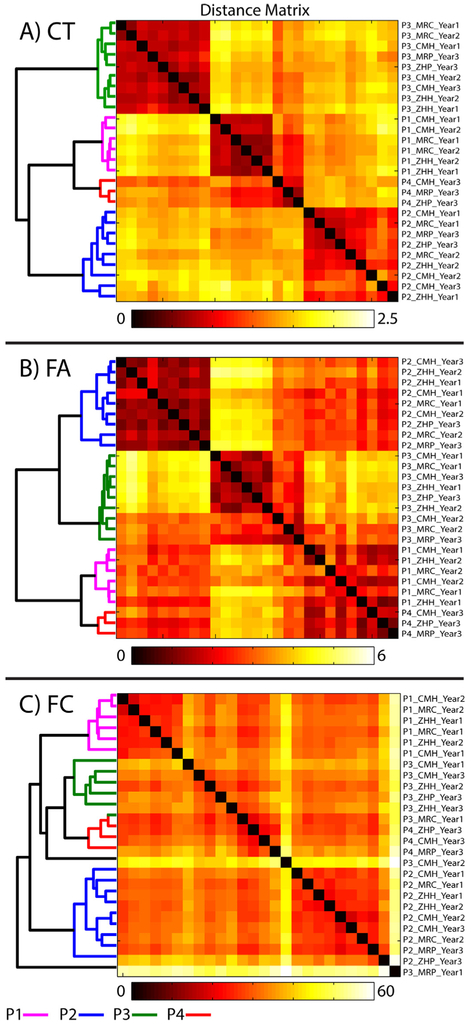
Cluster solutions for CT, FA, and FC are presented in Fig. 2. For both CT and FA, scans clustered by participant ID as opposed to site. In both cases, a four cluster solution resulted in a perfect match with participant ID. In the cluster results for FC, one scan from P3 (Year2 at MRC) was excluded due to excessive motion (only 12 TRs retained after motion censoring). The remaining scans largely clustered by participant ID, with the exception of three scans from P3 (one of which clustered with P4, and two of which formed singular clusters). As one scan from P3 had been removed due to excessive TR censoring, we examined these three misclassified cases. Two of these scans each formed a cluster of size one. Both scans had the majority of TRs censored due to motion (113 and 136, respectively, out of a total of 208 TRs included in the analysis), and can therefore be considered high motion scans which would likely be excluded from most studies. The P3 scan that clustered with P4 had only a single TR removed due to censoring, thus representing a classification error.

Fig. 2.

Results of the hierarchical clustering analysis for: A) cortical thickness (CT); B) fractional anisotropy (FA); C) functional connectivity (FC). The distance matrix shows Euclidean distances between scans (defined as the sum of the squared difference between each ROI for each pair of scans, such that lower distances between scans mean they are more similar). The cluster tree (dendrogram) is shown on the left. Color coding on the dendrogram represents participant ID. Participant ID, scanner, and year for each scan in the distance matrix is shown on the right.

We further explored motion by examining the number of TRs censored in other participants. The average number of censored TRs by participant is presented in Supplemental Table 2. Of the P3 scans which were correctly classified, the highest number of censored TRs is 66. Amongst other participants, the most censored TRs in a single scan is 38. Notably, while P2 had a moderate number of censored TRs (mean 22.1, range 7–33), the scans from that participant were still correctly classified by participant ID. This suggests that resting fMRI may be generally reliable even in the presence of moderate motion, when adequate processing and noise reduction is performed, while emphasizing the need to remove high motion scans.

As scanner effects were regressed from both FA and CT, we ran an additional clustering analysis on those data sets without regressing scanner effects (Supplementary Fig. 1). Despite the fact that there was a significant scanner effect in CT, the scans still clustered by participant, with the exception of P2, who split into two connected smaller clusters (separating MRC and MRP scans from the other sites). For FA, scanner effects were evident in this clustering solution, with the Prisma scanners (MRP and ZHP) forming a distinct cluster. Additionally, clustering on CT was rerun using only regions in the prefrontal cortex (Supplementary Fig. 2), showing accurate clustering by participants with only a smaller set prefrontal ROIs. Clustering with FC was rerun using only nodes in the default mode network (DMN), which resulted in a greater number of classification errors, suggesting single network connectivity was less useful for identifying individuals than whole brain connectivity.

3.3. Evaluating cluster accuracy via ARI

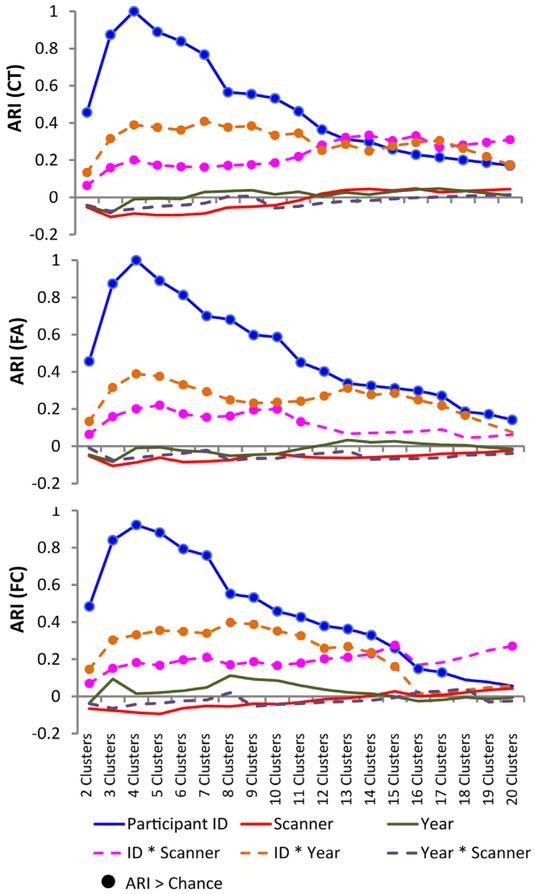
The analysis comparing the ARI for each cluster solution from two to 20 for each metric is presented in Fig. 3. Solutions for which the ARI for each label was above the 99th percentile of the null are flagged with a circle. For both CT and FA, the ARI for participant ID was above the null for all cluster solutions, with an ARI of one for the four cluster solution, indicating a perfect match between participant ID and the cluster solution. The ARI naturally decreased between ID and cluster solutions greater than four, as comparing an increasing number of cluster labels to the four labels in the ID solution will by definition decrease ARI. Year and scanner were near zero and below the null for all solutions for both FA and CT. ARI for ID by scanner and ID by year were above the null for several cluster solutions in CT and FA. However, these ARI values remained relatively low (peaking at ARI < 0.4, as opposed to ARI = 1 for participant IDs).

Fig. 3.

Cluster solutions for cortical thickness (CT; top), fractional anisotropy (FA; middle) and functional connectivity (FC; bottom) for cluster solutions ranging from two to 20 clusters. An analysis was conducted to establish if a given cluster solution was related to the participant ID or scanner. Year was included as a ‘control’ variable. An adjusted Rand index (ARI) was calculated for each cluster solution and scan-related variables, namely participant ID (4 labels; P1, P2, P3, P4), scanner (5 labels; CMH, MRC, MRP, ZHH, ZHP), year (3 labels; Year1, year2, year3), a combination of ID by scan site (16 labels; e.g. P1 at CMH, P1 at MRC, etc.), ID by year (9 labels; e.g. P1 during Year1, P1 during year2, etc.), and year by scanner (9 labels, e.g. CMH at Year1, CMH at year2, etc.). Circles/dots indicate ARI values which are above chance as determined via a null distribution created using a permutation test, suggesting greater than chance overlap between that label and the cluster solution.

ARI analysis for FC was performed with the two high motion scans from P3 removed, as those scans separated to form singleton clusters and will bias the ARI scores. When comparing cluster solutions to participant IDs, the highest ARI was found for a four cluster solution (ARI = 0.922), again showing very close agreement between participant label and cluster labels. When comparing cluster solutions to scanners, ARI for all cluster solutions did not exceed our null distribution threshold. Again, ARI values comparing the cluster solutions for FC to the ID by scanner and ID by year were above the null for several cluster solutions, but were still relatively low (ARIs < 0.4) compared to ID.

3.4. Intraclass correlation coefficients

ICCs were calculated using both the original CT, FA, and FC values (prior to regressing scanner effects from CT and FA), and on CT and FA with scanner effects regressed out. ICC values for participants and scanners are presented in Table 2. For data without regressing scanner effects, ICCs for CT were in the range of 0.89–0.98, for FA were in the range of 0.82–0.97, and for FC were in the range of 0.22–0.39. ICCs were in most cases higher within participant than within scanner. ICCs across scanners were still quite high for CT and FA. Regressing scanner effects from ROIs in CT and FA resulted in a reduction in ICC values. There was a moderate drop in within participant ICCs, save for the scans for P4 which had an ICC near zero. This may be related to the fact that scanner and ID are in fact confounded, in that not all participants had equal data on all scanners. ICC for scanner was negative in all cases when scanner was regressed from the data, suggesting no scan-to-scan reliability across scanners.

Table 2.

ICC values within participant and within scanner.

	P1	P2	P3	P4	CMH	MRC	MRP	ZHH	ZHP
Original values (no regression for scanner effects)
CT	0.98	0.91	0.97	0.90	0.89	0.91	0.89	0.89	0.90
FA	0.97	0.96	0.95	0.82	0.88	0.84	0.85	0.83	0.89
FC	0.37	0.39	0.26	0.39	0.30	0.22	0.27	0.25	0.31
Modified values (after regressing scanner effects)
CT	0.82	0.54	0.75	0.05	−0.13	−0.20	−0.20	−0.50	−0.50
FA	0.90	0.52	0.74	0.00	−0.10	−0.20	−0.17	−0.38	−0.34

4. Discussion

We examined twenty-seven MRI datasets for four individuals collected across three sites, five scanners, and three annual scanning sessions. Scanning parameters were harmonized across sites to minimize inter-site variance. Rather than only assess reliability across scans and time via similarity metrics such as intraclass correlation, we used a hierarchical clustering approach to examine whether results of each neuroimaging measure were more similar within-subject compared to within-scanner. We sought to determine whether this clustering approach could identify an individual from all other participants (Finn et al. 2015). Scanner-based effects were present in both the CT and FA data; these were corrected for by regressing scanner effects from each ROI. Alternate approaches (Chen et al., 2014; Fortin et al., 2017; Mirzaalian et al., 2016) may be more appropriate for group comparisons or multivariate statistical approaches across multiple brain regions simultaneously. Classification accuracy was high across all metrics, with no misclassifications in CT or FA, and only a single individual misclassified based on FC. Critically, the perfect or high classification accuracy (quantified via ARI) across individuals shows that these metrics can be considered reliable indicators of structure and function that are specific to an individual. This provides strong support for the integration of data in multi-center studies, and supports the use of hierarchical clustering to identify individuals across imaging metrics.

While traditional analyses of neuroimaging data have relied upon group statistics, they explicitly assume homogeneity within the samples under investigation. This assumption is dubious even in healthy individuals, where variability in task activity (Miller et al. 2012) and functional architecture (Gordon et al. 2017) appear to be the norm rather than the exception. Data driven approaches may be less limited by heterogeneity compared to case-control designs, and thus may represent an opportunity for discovery, especially within psychiatric populations (Van Horn, Grafton, and Miller 2008). Recent work has highlighted the power of clustering approaches for uncovering new disease and treatment response subtypes respectively (Clementz et al. 2016; Drysdale et al. 2017). We demonstrated that clustering can be used to group scans with similar characteristics, even when site/scanner based effects are present. Furthermore, even when examining the full spectra of information available for a given neuroimaging metric, we were able to achieve high classification accuracy. This supports the use of hierarchical clustering as a tool for discovery to identify groups of participants in a larger dataset with similar brain structure or connectivity. Furthermore, it may be reasonable to do so using data from the entire brain rather than using a data reduction approach or selecting a set of regions a priori. Such data reduction and feature selection practices can have a strong biasing effect on classification, may eliminate important sources of individual variability, and affect reproducibility. The importance of individual neuroanatomical variability (Mueller et al. 2013), even in healthy young adult humans has been shown in a recent study using the large multi-site Human Connectome dataset identifying a subset of participants with atypical patterns of fMRI task activations (Tavor et al. 2016). Approaches such as hierarchical clustering may group together participants with common and relevant atypical activity patterns.

This analysis has an advantage over previous studies examining cross-scanner variability: rather than using measures such as different forms of ICC, we used an unsupervised classification approach which groups data sets (in this case, scans) by similarity. Recent work has emphasized relatively poor scan-to-scan reliability across shorter resting state functional acquisitions (Anderson et al., 2011; Birn et al., 2013; Noble et al., 2017; Shou et al., 2013), and the reliability of functional connectivity may be greater when an individualized as opposed to group parcellation scheme is used (Laumann et al., 2015). However, despite this relatively low reliability for FC as measured by ICC and reduced ICC when scanner effects were regressed from CT and FA, all metrics showed strong clustering by participant. This demonstrates that even in the context of low scan-to-scan reliability the FC data remains individually identifying. As demonstrated in Finn et al. (2015), resting state connectivity can be individually identifying. It is becoming progressively clear that structural and functional patterns within an individual’s brain are consistent to the point that they may be considered a stable and identifying characteristic of that individual, even when measured across scanners. As such, we suggest that the lower reliability in functional metrics should not preclude them as individually and clinically meaningful measurements. When our results and those in the literature are taken together, ICC and clustering approaches provide distinct and potentially complementary metrics: ICC precisely assesses how similar a data series is across points, making it a good measure of reliability, while clustering assesses differences and similarities across individuals, making it useful for identification and classification even in cases where ICC may not be particularly high. It is also worth noting the utility of multivariate ICA approaches (Cannon et al., 2014; Noble et al., 2017; Shou et al., 2013) which may provide more accurate measure of scan-to-scan variance under some circumstances.

We used the ARI as an objective assessment of the relationship between cluster membership and scanner or participant ID. In all cases, ARI related to ID was significantly greater than chance, while ARI related to scanner site was not different from chance. These findings demonstrate that accurate classification is possible based on an individual’s neuroimaging data collected from different scanners across time, particularly when sufficient corrections are applied. It is worth noting that labels of ID by scanner and ID by year also showed significant ARIs across several cluster solutions for all metrics. In this specific set of scans, it is challenging to fully tease apart year and scanner effects from IDs due to the different combinations of scanner and time across participants. As such, these significant ARIs for ID by scanner or ID by year may reflect the unbalanced nature of the design, or represent true effects of unaccounted for differences among scanners and change across years. While we attempted to address the scanner effects by regressing scanner from our metrics of interest, more recent multivariate approaches to scanner variance may do a better job at removing cross-site variance (Chen et al., 2014; Fortin et al., 2017; Mirzaalian et al., 2016).

In terms of limitations, the clustering in FC did fail on two scans that had particularly high motion and a large number of volumes censored during preprocessing. However, clustering was successful when as many as 30% of the TRs were censored. This suggests that functional connectivity remains identifying even in the presence of moderate motion, but high motion scans (which, based on our data, might be defined by scans with around 1/3 of TRs rejected) should be excluded from further analysis. The use of repeated multi-site scans can provide a more objective assessment for defining thresholds for rejecting data from a study. We also focused on whole-brain patterns of activity in our clustering approach, which may have obscured regionally specific scanner effects which may be particularly important for functional localization studies. Relatedly, our F-test for scanner effects considered overall FC (as opposed to mass univariate testing of all edges), and thus may not reveal regional variations of FC which could influence comparisons between participants.