Longitudinal cortical network reorganization in early relapsing–remitting multiple sclerosis

Abstract

Background:

Network science provides powerful access to essential organizational principles of the brain. The aim of this study was to investigate longitudinal evolution of gray matter networks in early relapsing–remitting MS (RRMS) compared with healthy controls (HCs) and contrast network dynamics with conventional atrophy measurements.

Methods:

For our longitudinal study, we investigated structural cortical networks over 1 year derived from 3T MRI in 203 individuals (92 early RRMS patients with mean disease duration of 12.1 ± 14.5 months and 101 HCs). Brain networks were computed based on cortical thickness inter-regional correlations and fed into graph theoretical analysis. Network connectivity measures (modularity, clustering coefficient, local efficiency, and transitivity) were compared between patients and HCs, and between patients with and without disease activity. Moreover, we calculated longitudinal brain volume changes and cortical atrophy patterns.

Results:

Our analyses revealed strengthening of local network properties shown by increased modularity, clustering coefficient, local efficiency, and transitivity over time. These network dynamics were not detectable in the cortex of HCs over the same period and occurred independently of patients’ disease activity. Most notably, the described network reorganization was evident beyond detectable atrophy as characterized by conventional morphometric methods.

Conclusion:

In conclusion, our findings provide evidence for gray matter network reorganization subsequent to clinical disease manifestation in patients with early RRMS. An adaptive cortical response with increased local network characteristics favoring network segregation could play a primordial role for maintaining brain function in response to neuroinflammation.

Introduction

Multiple sclerosis (MS) is a neuroinflammatory disease of the central nervous system that may lead to progressive disability.¹ In particular, gray matter (GM) involvement has been shown to be important for the long-term outcome and is closely related to clinical disability.^2,3 In fact, GM atrophy correlates with disease progression and emerging disability to a greater extent than ‘classical’ T2-hyperintensive lesions.⁴ Furthermore, regional cortical atrophy patterns showed even stronger associations with clinical dysfunction than global cortical atrophy.⁵

Despite continuous GM damage, varying inter-individual rates of atrophy and distinct timespans for evolution from the relapsing–remitting to the progressive phase of the disease are well known.^6,7 In this context, the lack of persistent clinical worsening in the initial phase of relapsing–remitting MS (RRMS) might be explained by the maintenance of structural, in particular cortical, integrity for efficient information transfer across brain regions despite chronic neuroinflammation.

Structural network-based approaches offer new avenues to depict the topological organization of the human brain complementary to conventional volumetric and morphometric measurements, and can reveal general principles about the underlying anatomical connections.^8,9 Recent studies have demonstrated that a robust quantification of structural connectivity can be achieved using diffusion magnetic resonance imaging (MRI) or cortical thickness measurements.^10,11 The latter uses structural covariance measures, i.e. cortical thickness measurements, which allows for the calculation of inter-regional statistical associations at the group level.¹² This approach considers two cortical areas anatomically connected if they show statistically significant correlations in cortical thickness and therefore takes the relationship between cortical regions into consideration.¹³ The resultant inter-regional correlation matrix (containing a set of elements representing the implicit strength of the connections) can be further analyzed in combination with graph theory to quantitatively characterize brain connectivity patterns.¹⁴

In MS, one cross-sectional structural cortical network study of RRMS patients with at least two attacks within the preceding 2 years observed disrupted brain connectivity in the cortex proportional to the white matter (WM) lesion load.¹⁵ In a further multimodal approach, a disruption of structural GM network topology was found to be important to understand concomitant alterations in functional connectivity obtained through magnetoencephalography.¹⁶ A similar pattern towards a globally disconnected topological organization, which has been associated with clinical disability, has also been demonstrated in the WM using diffusion MRI.¹⁷ In a recently published cross-sectional network approach in early RRMS, we could demonstrate that the connectivity profile reconstructed by diffusion MRI with probabilistic tractography is characterized by a modular decomposition and increased local processing,¹⁸ even in comparison with patients with clinically isolated syndrome (CIS).¹⁹ However, little is known about the structural dynamics of the cortical network in the initial phase of RRMS and in particular the impact of overall disease activity on network properties over time.

Here, we investigated the cortical architecture over 1 year at the beginning of the disease using cortical thickness measurements to reconstruct the structural connectivity network in order to identify the initial network response to damage.

We aimed to: (i) assess the topological organization and connectivity profile over time in the cortex of patients with early MS in comparison with healthy controls (HCs); (ii) contrast network dynamics with conventional atrophy measurements; (iii) test whether cortical networks differ between patients with and without disease activity; and (iv) determine the reliability of the network characteristics in a second cohort of MS patients at shorter intervals (trimonthly scans).

Methods

Patients and study design

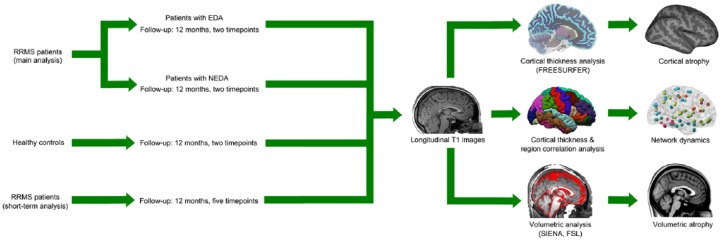
For this prospective study, patients with RRMS were recruited and underwent a standardized MRI protocol.²⁰ For our main analysis we included patients from 2011 to 2016 with disease duration less than 5 years, who were relapse-free for at least 30 days prior to enrolment. The study was approved by the ethics committee of the State Medical Board of Rhineland-Palatine (approval number 837.543.11 (8085); all patients provided written informed consent). Each patient was assessed clinically to determine the Expanded Disability Status Scale (EDSS) score. Ultimately, 92 MS patients (65 female, mean age: 32.9 ± 9.9 years; mean disease duration: 12.1 ± 14.5 months) were included in the main analysis (Figure 1). Furthermore, we included 101 HCs without a history of neurological dysfunction (59 female, mean age: 19.7 ± 0.9 years). HCs and patients were followed up over 1 year. Patients were divided into two groups with either NEDA (no evidence of disease activity) or EDA (evidence of disease activity) over 12 months based on the recently established NEDA-3 criteria.²¹ NEDA was defined as the absence of clinical relapses between the first and second MRI scan, no progress in T2 lesion load, no gadolinium-enhanced lesions in the follow-up MRI and no worsening of the EDSS score. EDSS worsening was defined as an increase of ⩾1 point in the EDSS score for a baseline score of ⩾1.5 or a 1.5 point increase for a baseline score of 0.

Figure 1.

Study analysis design. Left: Classification of the study population. Right: Flow chart for cortical thickness and brain volume measurements and for graph network measures estimation analyses.

In an additional analysis, a separate group of nine RRMS patients (6 female, mean age: 42 ± 12.1 years; mean disease duration: 3.5 ± 6.5 years) was studied every 3 months for 12 months (five consecutive time points) with the same protocol mentioned above. The goal of this analysis was to gain more detailed information on network alterations over short-term intervals and substantiate our results from the main analysis.

Data acquisition

MRI was performed on two identical 3 T MRI scanners (Magnetom Tim Trio, Siemens, Germany) with a 32-channel receive-only head coil in HCs (scanner 1) and RRMS patients (scanner 2). In all patients, imaging was performed using sagittal 3D T1-weighted magnetization-prepared rapid gradient echo (MP-RAGE) sequence [TE/TI/TR = 2.52/900/1900 ms, flip angle = 9°, field of view (FOV) = 256 × 256 mm², matrix size = 256 × 256, slab thickness = 192 mm, voxel size = 1 × 1 × 1 mm³] and sagittal 3D T2-weighted fluid-attenuated inversion recovery (FLAIR) sequence (TE/TI/TR = 388/1800/5000 ms, echo-train length = 848, FOV = 256 × 256 mm², matrix size = 256 × 256, slab thickness = 192 mm, voxel size = 1 × 1 × 1 mm³). The healthy control cohort was scanned with a slightly different scanning protocol using sagittal 3D T1-weighted MP-RAGE sequence (TE/TI/TR = 2.52/900/1900 ms, flip angle = 9°, FOV = 256 × 256 mm², matrix size = 256 × 256, slab thickness = 176 mm, voxel size = 1 × 1 × 1 mm³). Major anatomical abnormalities were excluded by a neuroradiologist based on the subject’s T1-weighted and FLAIR images of the whole brain.

GM analysis

Two established measurement techniques (FreeSurfer and SIENA) were applied to quantify GM and brain atrophy, respectively. The construction of the cortical surface was based on 3D T1 images using the semiautomated stream of FreeSurfer (version 5.3.0). The detailed procedure for surface reconstruction and quantification has been described and validated in previous studies.²² Longitudinal reconstruction was performed to reduce the confounding effects of inter-individual morphological variability, as described previously.²³

Furthermore, we estimated the percentage brain volume change (PBVC), estimated as the shift of the brain parenchyma to the cerebrospinal fluid interface between two time points, based on 3D T1 images using the SIENA package²⁴ embedded in the FSL toolbox (version 5.0.8).²⁵

GM network reconstruction

Individual cortical thickness values were obtained for each region of interest of the AAL Atlas to construct (N × N) connectivity matrices, where N is the number of regions of interest.²⁶ The co-registration from Desikan–Killiany atlas (FreeSurfer output) to AAL atlas was performed by mapping the AAL ROIs [in Montreal Neurological Institute (MNI) 152 space] to the surface and registering each individual subject to it in order to obtain the values in each ROI. The structural correlation matrices (90 × 90) for the group of patients (at each time point) contained the Pearson’s correlation coefficient between the cortical thicknesses of each pair of regions.

To describe the topological organization of the derived structural networks, network measures were obtained using weighted matrices in the BCT toolbox.²⁷

Connectivity measures

Modularity

Brain networks can be separated into modules: groups of regions that have more connections to one another than expected in a randomly sampled group of regions. Thus, modules are densely interconnected regions that have only sparse connections to other regions.²⁸ Higher modularity (Q) reflects an improved capacity of the network to divide itself into communities and thus represents a more efficient network structure. Modularity was defined as the relationship between intra- and inter-module connections and calculated using the Newman algorithm:^28–30

$$Q=\frac{1}{2m}\sum _{ij}\left[A_{ij}-P_{ij}\right]\delta \left(g_i,g_j\right)$$

where A_ij is the actual number of edges falling between a particular pair of vertices i and j; P_ij is the probability that an edge falls between every pair of vertices i, j; g_i is the community to which vertex i belongs; m is the number of edges in the network; and δ(r, s) = 1 if r = s and 0 otherwise.³⁰

Clustering coefficient

The clustering coefficient (C) is a measure of local organization reflecting the number of connections between directly neighboring regions (the topological motif of a triangle), with sparsely interconnected regions showing lower values.³¹ The clustering coefficient was calculated, reflecting the number of connections between the neighbor’s nodes, using the following algorithm:³²

$$C_i=\frac{2t_i}{k_i(k_i-1)},$$

where k_i is the degree of node i and t_i is the number of triangles attached to the node.

Local efficiency

The efficiency of a network primarily reflects how information is exchanged between regions. Local efficiency (E_loc) quantifies a network’s resistance to failure and is defined as the inverse of the shortest path length computed only for the neighborhood of the region.³³ The local efficiency is calculated using the Dijkstra’s algorithm:^32,33

$$E_{loc}(G)=\frac{1}{N}\sum _{i\in G}{E}_{glop}(G_i)$$

Transitivity

The transitivity (T) of the network is a measure of the probability that two regions neighbor each other. The transitivity of a graph is based on the relative number of triangles in the graph, compared with the total number of connected triples of regions,³⁴ and represents a cost-efficient organization principle. The transitivity of a network was defined as³⁴

$$T=\frac{{\sum }_{i\in N}2t_i}{{\sum }_{i\in N}{k}_i(k_i-1)},$$

where $t_i$ is the number of triangles around the node $i$, $N$ is set of all nodes in the network, and $k_i$is the degree of the node $i$.

For the above-described network measures, 21 density intervals (range 0.1–0.6) were applied to threshold the connection matrix with an incremental interval of 0.025. The density range was chosen in such a way that the network was fully connected at the minimum value and fully disconnected at the maximum value.³⁵ Thresholding the constructed association matrices at a minimum network density of both groups (none of the networks are fragmented) and at a range of network densities for comparing the network topologies across that range provides a robust strategy to conduct legitimate statistical inference on the data and to minimize the number of spurious links in each network.^13,36,37 An absolute threshold would influence the network measures and reduce interpretation of between group results.³⁸ Finally, the topological organization of the resultant matrices at each density level was examined for each study group. Creating matrices for each density interval (individual values) allowed us to compare the mean of the groups by employing the following statistical approaches.

Statistical analysis

Statistical evaluation was performed with SPSS software (version 22.0; IBM). Clinical and demographic data of patients with NEDA and EDA were compared using a Student’s t test for continuous variables and Pearson’s chi-squared test for categorical variables. Paired sample t tests were used to compare EDSS values between baseline and 12 months. Unless otherwise indicated, data are expressed as mean ± SD (standard deviation).

For all network measures (clustering coefficient, modularity, local efficiency and transitivity) of the patients and HCs, the Shapiro–Wilk normality test showed that the data were normally distributed between the time points. For the comparison of the network measures between the groups, repeated measures analysis of variance (ANOVA) was used. Mauchly’s test of sphericity, used to validate the repeated measures ANOVA, indicated that the assumption of sphericity had not been violated. Furthermore, applying posterior predictive distribution (Bayesian statistics) we were able to assess model fit and also found with this statistical approach that the observed data are normally distributed (please refer to Supplement Figure 1).

The network measures at baseline and follow up were compared as follows. First, the baseline connectivity value and the connectivity value after 12 months (t₂) were compared with a one-way analysis of variance (ANOVA) for all MS patients and for HCs, separately, as each group was scanned with a different scanning protocol. Next, the longitudinal within-group comparison between MS patients with and without disease activity (EDA versus NEDA) was performed with a two-way ANOVA (all patients were scanned with the same scanning protocol). Here, we not only aimed to assess the main effect of the two independent variables (factor ‘group’ [NEDA versus EDA] and factor ‘time’ [baseline versus 12 months]) but also the interaction between them (‘group’ and ‘time’ interaction). Finally, a one-way ANOVA was performed to assess longitudinal differences for the individual topological measurements over the five time points in our additional analysis. In cases of a significant F value, we performed post hoc t tests Bonferroni-corrected for multiple comparisons (p < 0.05).

For the topological analyses and the representation of clusters, we used the network measures clustering coefficient and only show nodes that were above the 95th percentile of the maximum value to depict areas of maximum cluster formation.

Results

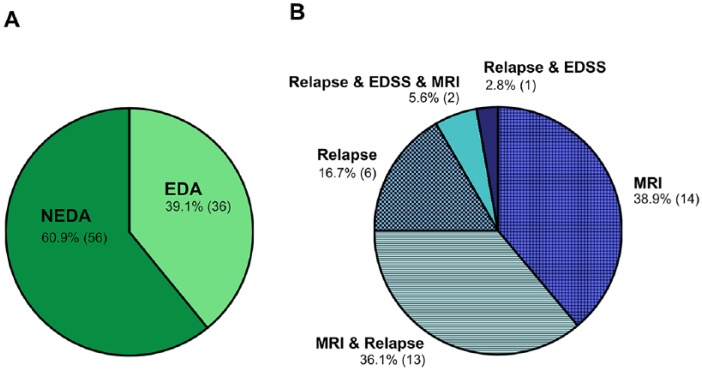
In the main analysis, 92 RRMS patients and 101 HCs were followed-up over 1 year with a median follow up of 12.0 (10.0–14.0) months and 11.5 (10.0–16.0) months, respectively (p = 0.655). Of the MS patients, 56 had NEDA during the study period, while 36 had disease activity (EDA group) (Figure 2). Demographic and clinical data of all MS patients combined and after division into NEDA and EDA groups is presented in Table 1 and Supplementary Tables 1, 2a, and 2b.

Figure 2.

(A) Disease activity distribution. Distribution of 92 patients into patients with disease activity (EDA) and those without disease activity (NEDA). (B) Disease activity composition. Composition of the 36 patients with disease activity (clinical relapse, Expanded Disability Status Scale (EDSS) worsening, or magnetic resonance imaging (MRI) activity) during the 12 month follow-up period.

Table 1.

Demographics of the MS patients. Clinical data of MS patients at baseline (0 months) and after division into NEDA and EDA groups (after 12 months).

	MS patients (n = 92)	HC (n = 101)	NEDA (n = 56)	EDA (n = 36)	p value (NEDA versus EDA)	p value (MS versus HC)
Sex (female/male)	65/27	59/42	39/17	26/10	p = 0.791a	p = 0.076a
Mean (± SD) age at MRI (years)	32.9 ± 9.9	19.7 ± 0.9	34.6 ± 9.0	30.4 ± 10.8	p = 0.052b	p < 0.001b
Mean (± SD) age at diagnosis (years)	31.9 ± 9.8	-	33.2 ± 9.1	29.9 ± 10.7	p = 0.115b	–
Mean (± SD) disease duration (months)	12.1 ± 14.5	-	15.1 ± 15.7	7.4 ± 10.9	p = 0.006b	–
Median (range) follow-up (months)	12.0 (10.0–14.0)	11.5 (10.0–16.0)	12.0 (10.0–14.0)	12.0 (10.0–14.0)	p = 0.163c	p = 0.655c
Median (range) EDSS (at baseline)	1.0 (0–4.0)	–	1.0 (0–4.0)	1.5 (0–3.5)	p = 0.637c	–
Median (range) EDSS (after 12 months)	1.0 (0–4.0)	–	1.0 (0–4.0)	1.0 (0–4.0)	p = 0.268c	–
Median (range) LV at baseline (ml)	1.9 (0.02–33.0)	–	2.3 (0.1–33.0)	1.6 (0.02–24.2)	p = 0.115c	–
DMDd (no/yes)	30/62	–	14/42	16/20	p = 0.052a	–

DMD, disease-modifying drug; EDA, evidence of disease activity; EDSS, Expanded Disability Status Scale; HC, healthy control; LV, lesion volume; MS, multiple sclerosis; NEDA, no evidence of disease activity; SD, standard deviation.

^ap value derived from Pearson’s chi-squared test (sex and disease-modifying treatment).

^bp value derived from Student’s t test (age at MRI, age at diagnosis, and disease duration).

^cp value derived from Mann–Whitney U test (follow-up time, EDSS at baseline, EDSS at follow up, and lesion volume).

^dA detailed list of each DMD (at baseline and at follow up) and the corresponding statistics between NEDA and EDA patients is provided in the Supplementary Tables 2a and 2b.

Overall, the longitudinal cortical network analysis revealed an increase in local and modular connections over 12 months in patients with MS. These longitudinal changes were attested both in patients with NEDA and in patients with EDA, indicating continuous cortical reorganization independent of disease activity. This local and modular cortical reorganization was not detected in HCs over the same period of time. Similar network alterations were seen even at shorter periods of follow up already at a timespan of less than 12 months in an independent patient cohort.

Longitudinal network changes

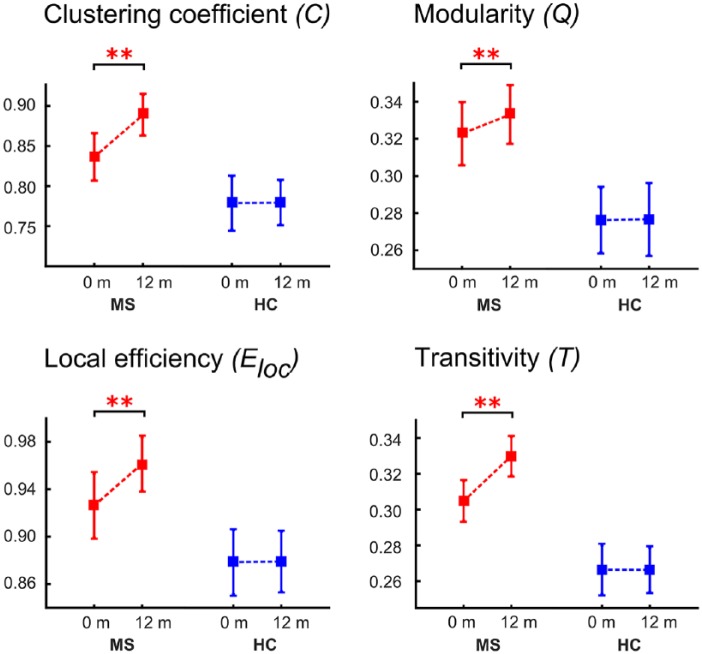
In the case of the local network measures, we found that modularity, clustering coefficient, local efficiency, and transitivity characterizing local connectivity properties (based on 20 density values per group per time point) increased over 1 year in patients (Figure 3).

Figure 3.

Longitudinal network measures of multiple sclerosis (MS) patients and healthy controls.

The plots show the estimated mean and standard deviation values at the two time points for the measures clustering coefficient, modularity, local efficiency, and transitivity for the cortical thickness analyses (**p < 0.001).

Modularity increased between baseline and 12 months in patients (F(1,38) = 8.472, p < 0.001; [post hoc: p < 0.001]), but no significant differences were detected in HCs (F(1,38) = 1.685, p > 0.05). This longitudinal increase suggests cortical reorganization towards a structure with stronger intramodular connections and increased local homogeneity, indicated by more connections within a module than expected by chance.

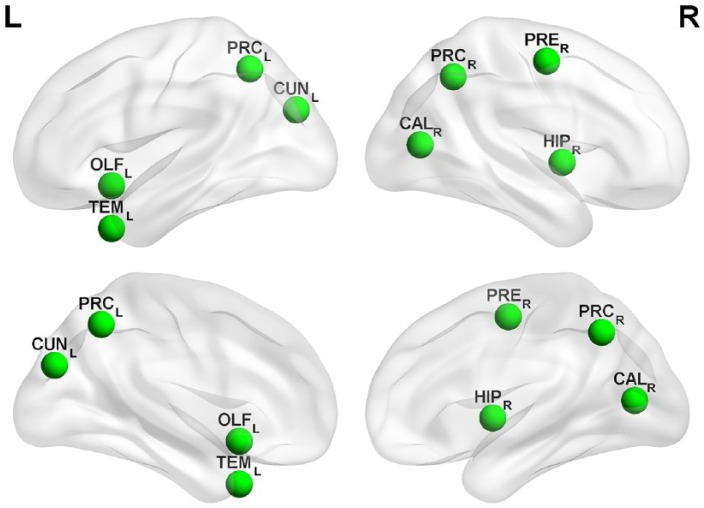
For the network measure clustering coefficient, ANOVA revealed an increase in patients over time (F(1,38) = 6.475, p < 0.001; [post hoc: p < 0.001]), whereas there was no difference in HCs (F(1,8) = 1.378, p > 0.05). Increased clustering coefficient indicates local pathology spreading and homogenization in neighboring regions. This increase in local clusters was seen in the temporal (middle temporal gyrus and hippocampus), occipital (cuneus and calcarine cortex), and parietal (precuneus) lobes. Clusters with the highest increase in clustering coefficient (above the 95th percentile) are shown in Figure 4 and Table 2.

Figure 4.

Topological representation of restructured clusters.

Topological representation of clustering coefficient changes between baseline (0 months) and the last time point (12 months). Regions with the highest clustering coefficient changes over time (only clusters above the 95% confidence interval are shown) as a marker of local reorganization.

CUN_L, cuneus (left); OLF_L, olfactory cortex (left); TEM_L, middle temporal gyrus (left); CAL_R, calcarine cortex (right); HIP_R, hippocampus (right); PRC_L, precuneus (left); PRC_R, precuneus (right); PRE_R, precentral gyrus (right).

Table 2.

Brain regions of restructured clusters. Results of the comparison of clustering coefficient between baseline (0 months) and 12 months from the complete multiple sclerosis patient cohort (eight brain regions with the corresponding p value). Only the cortical regions above the 95% confidence interval of clustering coefficient are shown. The Montreal Neurological Institute (MNI) coordinates (x, y, and z) and p values are given.

Lobe	Brain region	Side	x	y	z	p value
Frontal	Olfactory cortex (OLF)	L	−9	15	−12	0.0002
Central	Precentral gyrus (PRE)	R	40	−8	52	0.0004
Parietal	Precuneus (PRC)	L	−8	−56	48	0.0003
	Precuneus (PRC)	R	9	−56	44	0.0006
Occipital	Cuneus (CUN)	L	−7	−80	27	0.0001
	Calcarine cortex (CAL)	R	15	−73	9	0.0005
Temporal	Middle temporal gyrus (TEM)	L	−37	15	−34	0.0004
	Hippocampus (HIP)	R	28	−20	−10	0.003

The network measures transitivity also increased in patients (F(1,38) = 5.982, p < 0.001; [post hoc: p < 0.001]), and showed no significant differences in HCs (F(1,38) = 1.637, p > 0.05). In addition to clustering coefficient, the increased network measure transitivity indicates the presence of a greater number of triangles in a brain network. It is another representation of proximity as well as a measure of the facilitation of information exchange between network anatomical regions.

Moreover, we detected a longitudinal increase of local efficiency over 12 months in patients (F(1,38) = 6.268, p < 0.001; [post hoc: p < 0.001]) compared with HCs (F(1,38) = 1.743, p > 0.05). Higher values of local efficiency are associated with strengthened short-range connections between neighboring regions that are involved in local information processing. Thus, in addition to enhanced local connectivity patterns, the network capacity for local information transfer between neighboring anatomical regions was strengthened.

Similar cortical reorganization in patients with NEDA and EDA

Comparing patients with NEDA and EDA, we observed that changes in network measures were in accordance with the results of the complete patient cohort. Specifically, modularity, clus-tering coefficient, local efficiency, and transitivity increased significantly over 1 year in both groups (Figure 5).

Figure 5.

Longitudinal network measures of multiple sclerosis (MS) patients without and with disease activity (NEDA versus EDA).

The plots show the estimated mean and standard deviation values at the two time points for the measures clustering coefficient, modularity, local efficiency, and transitivity for the cortical thickness analyses (*p < 0.01).

Precisely, the two-way ANOVA for modularity was not significant for the factor ‘group’ (F(1,78) = 1.245, p > 0.05), but significant for the factor ‘time’ (F(1,78) = 3.547, p < 0.01), and post hoc tests revealed an increase over time for both NEDA (p < 0.01) and EDA patients (p < 0.01).

For clustering coefficient, the ANOVA was not significant for the factor ‘group’ (F(1,78) = 1.213, p > 0.05), but significant for the factor ‘time’ (F(1,78) = 3.647, p < 0.01). Post hoc tests showed an increase over time for NEDA (p < 0.01) as well as for EDA patients (p < 0.01).

For transitivity (factor ‘group’ (F(1,78) = 1.317, p > 0.05) and factor ‘time’ (F(1,78) = 4.214, p < 0.01)) our results also demonstrated an increase over time for NEDA (p < 0.01) and EDA patients (p < 0.01) in post hoc testing.

Finally, ANOVA for local efficiency was not significant for factor ‘group’ (F(1,78) = 1.145, p > 0.05), but significant for factor ‘time’ (F(1,78) = 3.854, p < 0.01). The post hoc results of local efficiency showed an increase over time for NEDA (p < 0.01) and EDA patients (p < 0.01).

For all measures, the interaction (‘group’ × ‘time’) was not significant.

Short-term cortical network reorganization in MS

In our short-term analysis with quarterly MRI scans (all with NEDA) we could replicate the longitudinal cortical reorganization at the local level. Over five consecutive time points we found that modularity (F(4,95) = 2.612, p < 0.01), clustering coefficient (F(4,95) = 3.547, p < 0.001), local efficiency (F(4,95) = 3.0874, p < 0.01), and transitivity (F(4,95) = 3.214, p < 0.01) all increased significantly (Figure 6).

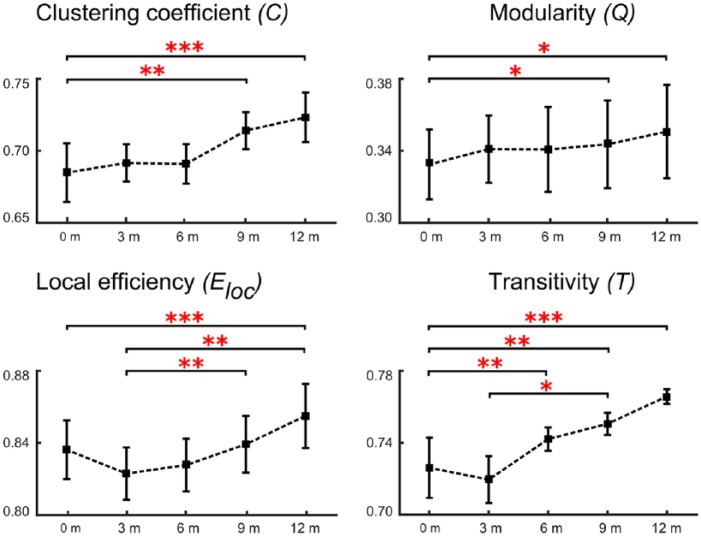
Figure 6.

Longitudinal short-term network measures of multiple sclerosis (MS) patients scanned every 3 months.

The plots show the estimated mean and standard deviation values at the five time points for the measures clustering coefficient, modularity, local efficiency, and transitivity for the cortical thickness analyses. (*p < 0.01; **p < 0.001; ***p < 0.0001).

For clustering coefficient (C) and modularity (Q), post hoc tests revealed a significant increase between baseline (0 months) and 9 months (p < 0.001 for C and p < 0.01 for Q) and between baseline and 12 months (p < 0.0001 for C and p < 0.01 for Q). Furthermore, transitivity showed a similar dynamic with an increase over time, suggesting a higher connection probability of neighboring nodes. Post hoc tests revealed significantly higher values between baseline and 6 months (p < 0.001), between baseline and 9 months (p < 0.001), and between baseline and 12 months (p < 0.0001). Moreover, post hoc tests were significant between the values at 3 and 9 months (p < 0.01). Post hoc tests for local efficiency revealed significant differences between the values at baseline and at 12 months (p < 0.0001). Finally, post hoc testing was significantly different between 3 months and 9 months (p < 0.001) and 12 months (p < 0.001).

No change in cortical thickness and brain volume

Both established methods for investigating whole-brain atrophy and regional changes in cortical integrity (SIENA and FreeSurfer) revealed no longitudinal differences in our early disease cohort over 12 months.

At the examined statistical threshold (p < 0.05 false discovery rate corrected and p < 0.001 uncorrected), there were no significant changes over time in cortical thickness and no significant difference between patients divided according to their inflammatory activity (NEDA versus EDA). Moreover, no regions with longitudinal atrophy over 12 months were attested in HCs.

Likewise, PBVC evaluated using SIENA showed no significant results. The mean PBVC estimate from the 92 MS subjects did not differ significantly from zero (family-wise error correction was applied for multiple comparisons). In addition, there were no significant differences (p > 0.05, family-wise error-corrected) in longitudinal brain volumes of the patients in the NEDA and EDA groups.

Discussion

By assessing the cortical architecture in a patient cohort with not yet measurable GM atrophy, we provide evidence for early structural reorganization towards increased local and modular connectivity. These patterns were detected in the cerebral networks, reconstructed from cortical thickness measurements applying graph theoretical analyses, in both patients with and without disease activity, but were absent in HCs.

Our analysis algorithm depicted cortical reorganization proceeding beyond established measures of brain or cortical atrophy and revealed cortical network changes at even shorter intervals of merely 6 months in a frequently followed-up subanalysis. Increased local connectivity and modularization generally represent an optimized network organization principle of biological systems in response to changing environment reported during brain development and maturation in humans.^39,40 In contrast to this evolutionary modularization, the modular structure is decreased later in life with healthy aging.^41,42 As modular evolution is predominantly detectable in the early lifespan and in maturation,⁴⁰ it is conceivable that the increase in network modularity in this very early RRMS cohort might not depict the mere consequence of damage, but rather an evolving reorganization process in the cortex in order to deal with widespread focal tissue damage.

The applied network approach of depicting the structural connectome of MS patients highlights cortical regions with similar microstructural properties, which is most notably not depicted in cortical thickness measurements alone.^12,43 The observed increase in network measures on the local and community level imply that adjacent cortical regions in particular develop a higher probability to show structural covariance with each other, albeit these anatomical connectivity patterns represent only an indirect degree of inter-regional interactions. Nevertheless, structural covariance networks are replicable, heritable, and representative of disease-related changes in topology.⁴⁴ In addition, several attempts have highlighted a convergence of cortical thickness covariance networks with diffusion MRI connections⁴⁵ as well as functional connectivity,⁴⁶ suggesting that the applied network approach also contains information about correlated intrinsic functional activity. The previously reported partial congruence between cortical thickness reconstructed networks and diffusion MRI as well as functional MRI-derived networks also suggest cellular mechanisms behind structural covariance, e.g. synaptic physiology.⁴⁷ Hence, our data infer that MS disease manifestation seems to induce an increasingly synchronized structural connectivity of cortical near-neighbor regions.

Moreover, we found that while local and modular connectivity increased over 12 months in our cohort, the network connectivity measures did not change in HCs. This not only underscores the methodological reliability of the introduced structural measurements in the test–retest manner, but also demonstrates that no similar cortical reorganization occurs over the same period of time in healthy people. One limitation of this comparison is that HCs and MS patients were not age-matched in our study, however we used age as a covariate in our statistical model considering that cortical thickness covariance networks can be altered across lifespan, at least between young and older adults.⁴²

Recent studies demonstrated long-range disconnection in MS patients.^17,48 This global disruption of structural networks correlated with increased lesion volume¹⁵ and disease duration.¹⁸ Our findings demonstrate increasing local and modular connectivity in early MS over time. Modularization and local connectivity were reported to maintain function and network effectiveness and therefore indicate an organization concept allowing for rapid adaptation.⁴⁹ Thus, in the concept of network science, the role of local connectivity is to efficiently enhance the fault-tolerance ability and to thereby resist external attacks (e.g. neuroinflammatory activity).³³

In line with this, the network reorganization observed here occurred independently of disease activity indicating that continuous strengthening of local connectivity is not hampered by acute inflammatory attacks. More than 80% of our patients with EDA (see Figure 2) had MRI activity, meaning that new or enlarging T2-hyperintensive lesions have appeared on the follow-up MRI. Despite this MRI-visible tissue damage, patients with and without disease activity both experienced cortical network reorganization. This suggests that both active and stable patients underwent continuous microscopic changes within the cortex which were captured by structural covariance networks but not by cortical thickness measurements alone. The simultaneous homogenization of near-neighbor cortical regions (within NEDA and EDA patients) might originate either from direct microscopic rearrangements within in the cortex or from ‘conventional MR-invisible’ changes within the normal-appearing WM,⁵⁰ which might impact the cortical structure through apparently unaffected WM tracts. Taken together, the evidence of network reorganization even in patients with NEDA supports the view that cortical restructuring occurs beyond detectable atrophy and regardless of observable disease activity, even though the sensitivity to detect MS disease activity is already higher when applying a composite such as NEDA rather than single component measures. Owing to the low proportion of patients with EDSS worsening within the EDA cohort (sustained progression within the NEDA composite measure is a characteristic hallmark of the later stages of the disease), we cannot exclude that the observed local network reorganization probably abates when persistent clinical worsening occurs.

We could recently show that the connectivity of WM reconstructed from diffusion MRI with probabilistic tractography is characterized by increased modular and local processing in patients 1 year after disease onset in a cross-sectional approach.¹⁸ These patterns were detectable even in patients with CIS who displayed network measures between those of MS patients and HCs.¹⁹ This suggests that local network reorganization has already emerged at this stage. However, these processes of network reorganization faded out in patients with longer disease duration.¹⁸ Moreover, it was recently demonstrated that the disruption of structural networks is associated with impaired cognition, especially involving attention and executive functions.⁵¹ In this study of structural networks reconstructed through probabilistic tractography, a decline in structural connectivity was depicted by decreased global efficiency and nodal strength in a mixed group of RRMS and secondary progressive MS patients.

Our analyses of atrophy and brain volume loss revealed no longitudinal differences in our early disease patient cohort over 12 months. Several algorithms exist to capture atrophy; the two most robust and established (SIENA and FreeSurfer) have been applied here. However, the short disease duration (less than 5 years), the minor clinical disability of our patients (median EDSS = 1) and the high proportion of patients on disease-modifying drugs (>67%) as well as inter- and intra-subject variations in longitudinal measurements of brain volume^20,52 render these morphometric measurements not sensitive enough to be picked up in our cohort. In contrast, the applied network algorithms revealed quantifiable changes within the cortex architecture during the study period.

In our study, several brain regions more strongly showed increased local connectivity and increased clustering. Cluster formation within the cortex was depicted in the precuneus, cuneus and calcarine cortex, and the hippocampus. These areas are intensively interconnected with widespread cortical regions and are directly involved in higher-order cognitive functions.⁵³ The bilateral anatomical representation with cluster formation in the precuneus underlines the importance of this area for compensation and adaptation for brain function maintenance with disease progression.⁵⁴

In our additional analysis at shorter periods, we found a similar increase in local and modular connectivity patterns. A more in-depth analysis of time intervals shorter than 1 year underlines that the observed cortical processes do not fluctuate over 12 months but rather evolve continuously. The applied algorithms show quantifiable changes in brain architecture at periods of 6 months (local efficiency and transitivity) and 9 months (modularity and clustering coefficient), whereas the morphometric variables (brain and cortical atrophy) remained insensitive.

It should be taken into account that brain or cortical atrophy may prove to be valuable markers to be added to the composite measure of NEDA, which is heavily weighted towards focal inflammatory disease activity and to a lesser extent to neurodegeneration.⁵⁵ However, there is not yet consensus on an MRI-derived atrophy threshold on an individual basis to reliably classify subjects into patients versus HCs.⁷ In addition, our applied algorithms are used to distinguish between groups and are not directly applicable for prediction at the individual level. Recent methodological approaches try to solve this limitation by developing techniques that describe an individual cortex as a network.^56,57 This single-subject GM network approach was lately applied in MS patients and showed that these graphs captured information that is associated with individual cognitive impairment.⁵⁸ However, in our study our ultimate focus was not on individual subjects, but rather on the pathological substrates of disease evolution in the initial phase of the disease.

Conclusion

In conclusion, our findings provide evidence that structural network reorganization processes emerge cortically in the absence of measurable atrophy in the initial phase of MS. Restructuring of the cortical architecture subsequent to clinical disease manifestation suggests a primordial response of the cortex evolving from the onset of the disease, with relevance for the clinical outcome of MS patients. Hence, future studies should evaluate the impact of increased local and modular network properties within the cortex on the long-term disease progression and functional impairment, including cognitive performance. Finally, it is important to determine whether changes in graph theoretical metrics in RRMS are consistent over time compared with other stages of the disease (CIS, secondary or primary progressive MS). How local and modular architecture progresses in patients with initial RRMS before passing over to the progressive form of the disease will be of particular interest.