Prevention: Necessary but Insufficient?

Abstract

We present 1^st-grade, 2^nd-grade, and 3^rd-grade impacts for a 1^st-grade intervention targeting the conceptual and procedural bases that support arithmetic. At-risk students (average age at pretest = 6.5) were randomly assigned to 3 conditions: a control group (n = 224) and 2 variants of the intervention (same conceptual instruction but different forms of practice: speeded [n = 211] vs. non-speeded [n = 204]). Impacts on all 1^st-grade content outcomes were significant and positive, but no follow-up impacts were significant. Many intervention children achieved average mathematics achievement at the end of 3^rd grade, and prior math and reading assessment performance predicted which students will require sustained intervention. Finally, projecting impacts two years later based on non-experimental estimates of effects of 1^st-grade math skills overestimates long-term intervention effects.

Individual differences in mathematical competencies arise early and remain stable over time (Duncan et al., 2007; Fuchs et al., 2016), and are associated with quality of life and financial security in adulthood (Every Child a Chance Trust, 2009; Murnane et al., 2001; Ritchie & Bates, 2013). Given these long-term associations, there is a pressing need for programs that ameliorate the mathematical deficits of at-risk children and that sustain intervention gains throughout schooling and into adulthood. Many interventions produce substantial gains in academic competencies relative to conventional education programs (i.e., the control group or counterfactual condition); yet, follow-up studies of such successful interventions reveal that those effects diminish, or fade out, over time (Li et al., 2017). Here, we assessed the follow-up effects of an effective first-grade mathematics intervention one and two years later and sought to determine if child-level variables moderated fadeout. We begin with discussion of the factors that are thought to sustain intervention effects, and then turn to prior analyses of longitudinal effects of early mathematics interventions, before overviewing the foci and contributions of the present study.

Factors That Support Persistence

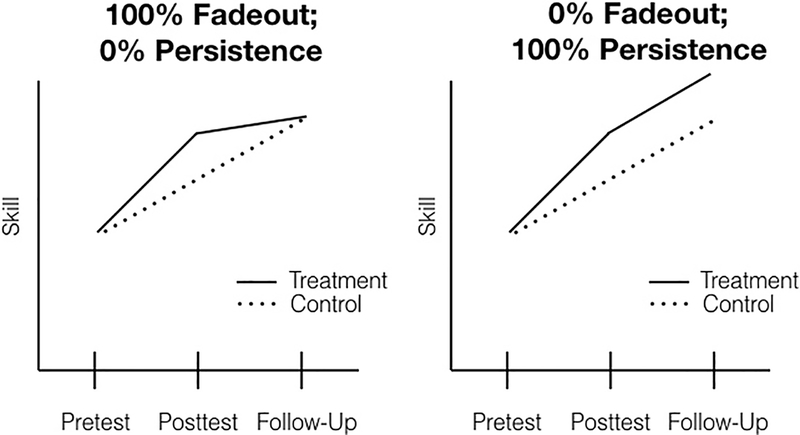
Fadeout is a pattern in which the initial effect of an intervention on treated individuals (relative to individuals randomly assigned to a control group) diminishes after the end of the intervention. For academic interventions, a common finding is that the children assigned to the intervention group do not experience a net skill loss, but the control group catches up in the post-treatment period. A schematic depiction of this pattern is shown in Figure 1, along with a contrast that shows persistent intervention effects.

Figure 1: Schematic of Fadeout and Persistence Patterns in Childhood Interventions.

The left panel depicts full fadeout, while the right panel depicts persistence at 100% of the level of the treatment effect at posttest. Importantly, as is commonly observed in childhood interventions, the treatment group does not experience net skill loss from posttest to follow-up, even when fadeout is complete.

The ubiquity of intervention fadeout requires careful consideration of the factors that might underlie it and consideration of how to best address these factors. Bailey, Duncan, Odgers, and Yu (2017) proposed that three processes can help support the persistence of intervention effects. The first involves building student capacity on “trifecta” skills: those that are malleable, fundamental for future success, and unlikely to develop quickly in the counterfactual. Malleability pertains most directly to immediate intervention effects, without which persistence is not possible (except perhaps with unusual sleeper effects). Boosting academic outcomes of at-risk students, even in the short-term, usually requires an explicit instructional framework (Gersten et al., 2008). This framework differs from business-as-usual classroom instruction by remediating delayed skills (e.g., whole-number knowledge) to consolidate the fundamental knowledge necessary for success on the intervention’s targeted skills (e.g., fractions knowledge); by incorporating instructional design to compensate for at-risk students’ limitations in linguistic, cognitive, or socio-emotional processing (e.g., using clear, direct language; relying on worked examples; increasing motivation, on-task behavior, and persistence in the face of academic challenge); and by providing smaller group size to ensure many opportunities to respond and receive corrective feedback (Fuchs, Fuchs, & Malone, 2017; Gersten et al., 2008). Most classroom instruction lacks these features (Doabler, Fien, Nelson, & Baker, 2012; Sood & Jitendra, 2007), without which the academic progress of at-risk students suffers (Kroesenbergen & Van Luit, 2003).

Whereas malleability pertains to immediate effects, persistence depends on additional factors. In particular, an intervention must target skills that are fundamental for future success. Interventions that result in substantive gains in fundamental skills should position intervention students to more fully benefit from subsequent classroom instruction. The basic idea is to provide an early lift via supplemental intervention, which then helps students to succeed in the regular classroom. Cunha and Heckman (2007) popularized the phrase skill begets skill to describe the processes through which early changes to children’s skills might lead to accumulating subsequent advantages to skill acquisition; Stanovich (1986) used the term Matthew Effect to capture how early competence increases engagement in and success with future education opportunities; and educators sometimes borrow inoculation effect from medicine (e.g., Ramey & Ramey, 1998). By whatever name, preparation for future learning is critical in mathematics, as fundamental skills are transparently reemployed in the service of later curricular targets.

Persistence also depends on the third of the trifecta skills: the unlikelihood that a skill will quickly develop under counterfactual conditions. The counterfactual is an alternative hypothetical scenario in which a child does not receive an intervention. It cannot be directly observed, but can be approximated by randomly assigning children to a control group. These children may receive business-as-usual classroom practices and alternative interventions. At-risk children experience poor arithmetic development in typical classroom settings (Fuchs et al., 2013), even though their not-at-risk peers enjoy rapid development in these same classrooms (Bailey, Littlefield, & Geary, 2012; Fuchs et al., 2013). Thus, first-grade arithmetic may meet the third criterion for status as a trifecta skill, at least for the duration of first-grade. However, under typical conditions, at-risk students do improve in their arithmetic skills in subsequent years (Geary et al., 2012). This potential for catch-up may present a challenge to the maintenance of intervention effects beyond first-grade.

Even in the face of malleability, fundamentality, and slow development for children who do not receive the intervention, fadeout may occur when schools do not provide the first-grade intervention students with explicit instructional support after intervention ends. This need for sustaining environments (e. g., Bailey et al., 2017; Ramey & Ramey, 1998) reflects the possibility that the conditions that created the initial risk (environmental circumstances or child-level variables) interfere with intervention students acquiring novel, more complex mathematical concepts or procedures, even when fundamental skills have been improved by an intervention. This problem may be particularly relevant to mathematics, because the mathematics curriculum includes periodic shifts to dramatically novel content (e.g., from additive to multiplicative concepts; from integers to rational numbers). Without explicit instructional support to navigate these shifts, persistence of intervention effects may be threatened, given at-risk learners’ need for explicit instruction (Gersten et al., 2008; Kroesenbergen & Van Luit, 2003).

A final plausible risk factor for fadeout is that selection for interventions is an ongoing and dynamic process, in which schools select students with weaker mathematics skill for later intervention (Balu et al., 2015). Thus, control students would be more likely to receive intervention in the immediate follow-up period while students who initially received intervention receive fewer follow-up services, on average. This would further account for a control group catch-up effect, not only on the remedial content but also on the material presented in the follow-up period.

Prior Studies on Longitudinal Effects of Math Interventions

In many intervention studies, participants are not followed beyond the end of the program (e.g., Duriak, Weissberg, Dymnicki, Taylor, & Schellinger, 2011; Smit, Verdurmen, Monshouwer, & Smit, 2008). When they are followed, fadeout is common. The typical finding is rapid declines in treatment effects soon after the program has ended and small to no long-term advantages relative to at-risk children who did not receive the intervention (Bailey et al., 2018; Li et al., 2017).

The same pattern emerged in two prior evaluations of early grade-school mathematics interventions that included follow-up testing at least 3 months after the intervention ended. Clarke et al. (2016) evaluated ROOTS, a kindergarten intervention focused on number sense and operations, delivered in 20-min sessions five days per week for approximately 10 weeks. Improvement from pretest to immediately after intervention was significantly stronger for ROOTS students than the control group on four of five measures (ESs = 0.16–0.75); this included a commercial test of early mathematics achievement, where the ES was 0.31. However, in January of first grade, performance on a mathematics achievement test did not differ across conditions (ES=0.00).

Another first-grade intervention with follow-up assessed the effectiveness of Math Recovery, which was designed for daily implementation with 30-min sessions across 12 weeks (Smith, Cobb, Farran, Cordray, & Munter, 2013). Immediately after intervention, ESs (0.15 to 0.30) favored Math Recovery over the control group on arithmetic, concepts and applications, quantitative concepts, and math reasoning. By end of second grade, differences between the conditions were no longer significant (ESs = −0.02 – 0.09). All this suggests that “skills beget skills” and Matthew effects of mathematics intervention are not as strong, at least for the typical treated student, as might reasonably be predicted based on theories of mathematics learning.

Focus and Nature of Present Study’s Intervention and Immediate Effects

In the present analysis, we assessed potential fadeout effects for a first-grade intervention targeting the conceptual and procedural bases that support arithmetic (Fuchs et al., 2013). At-risk students were randomly assigned to three conditions: a control group and two variants of the intervention (same conceptual instruction but different forms of practice). Fuchs et al. reported immediate intervention effects (spring of first grade). We replicated those effects using a different set of statistical procedures and a larger set of pretest controls. Our major focus, however, was longitudinal effects through third grade.

The intervention incorporated several features that, in theory, should produce persistence. The intervention relied on an explicit instructional framework, and results demonstrated skill malleability in the intervention condition as well as inadequate learning in the control group. Immediate effects on arithmetic favored both variants of the intervention over control (ESs = 0.87 and 0.51; Fuchs et al., 2013). Positive effects occurred as well on complex calculations, number knowledge, and word problems. Also, the intervention’s focus, children’s arithmetic skill, is empirically linked with future mathematics success, such as word problems (Fuchs et al., 2006), fractions (Jordan et al., 2013), and algebra (Fuchs et al., 2012; Tolar, Lederberg, & Fletcher, 2009). Arithmetic is also a robust predictor of overall mathematics learning through the end of fifth grade (Geary, 2011) and eventual mastery of high school algebra (National Advisory Mathematics Panel [NMAP], 2008).

At the same time, there were three major threats to persistence in the Fuchs et al. (2013) study. First, without intervention, the skilled use of the basic arithmetic targeted in the intervention develops rapidly. In one longitudinal study, a group of U.S. children increased their use of retrieval on an arithmetic strategy task by about half while improving their accuracy on these trials from approximately 60% to 80% from grade 1 to grade 2 (Bailey et al., 2012). Further, children at risk for persistently low mathematics achievement have been found to improve as much or more as their typically developing peers on some measures of arithmetic skill during this later period (Geary et al., 2012; Jordan et al., 2003). The second is the possibility that schools fail to provide intervention students access to sustained explicit instructional support after the intervention ends. The third is the possibility that schools incorporate multitier systems of support (Balu et al., 2015), in which they select students with weaker mathematics skill for subsequent intervention. Thus, at-risk students who did not receive the initial intervention receive intervention in the immediate follow-up period, while students who initially received intervention do not receive such services. This would contribute to a catch-up effect.

Present Study’s Contributions

With the present analyses, we extended the literature on longitudinal effects of early grade-school mathematics intervention in five ways. First, we examined longer-term (two years after intervention) effects than is typical in this literature. Because arithmetic skills remain important throughout third grade, it stands to reason that boosting first-grade arithmetic skills affects subsequent learning. Second, we relied on a variety of follow-up measures that reflect not just maintenance of first-grade skill but also accumulating effects on second- and third-grade curricular targets.

The third extension is that we incorporated a pretest battery of foundational mathematics competencies, reading performance, and cognitive and linguistic processes, which permitted us to consider moderating effects that potentially qualify the long-term effects of intervention. Relatedly, with the fourth extension, we explored whether and if so which pretest or end-of-intervention child-level variables forecast which children will need ongoing intervention. The first, second, and third extensions may provide insight into the processes by which fadeout effects occur, while the fourth provides insight into the developmental pathways associated with responsiveness versus unresponsiveness to intervention and offers a possible strategy for helping schools identify which students are in need of sustained intervention.

We targeted five potential moderators of long-term intervention effects. Four of these variables were measures of cognitive and linguistic processes associated with individual differences in mathematics development: working memory, listening comprehension, nonverbal reasoning, and processing speed (e.g., Fuchs, Geary, Fuchs, Compton, & Hamlett, 2014; Fuchs, Gilbert, Powell, Cirino, Fuchs, Hamlett, Seethaler, & Tolar; 2015; Geary et al., 2009; Swanson & Beebe-Frankenberger, 2004), factors for which increases in arithmetic fluency could plausibly compensate in children’s subsequent mathematics learning. The fifth variable, word-reading skill, was included given evidence of developmental parallels between early calculation and word reading (Chu, vanMarle, & Geary, 2016; Göbel, Watson, Lervåg, & Hulme, 2014; Koponen, Salmi, Eklund, & Aro, 2013), evidence that students with concurrent math and reading difficulty experience worse outcomes in each area than do peers with difficulty in one domain (Cirino et al., 2015; Willcutt et al., 2013), and prior evidence that such comorbidity is associated with less adequate response to generally effective intervention (Fuchs et al., 2013; Fuchs et al., 2004). We relied on these same five variables to investigate pathways associated with responsiveness versus unresponsiveness to intervention. Moreover, because we were interested in exploring a heuristic by which schools might identify students in need of sustained intervention via this logistic regression approach, we included end-of-first-grade math outcomes (focused on first-grade math content) as additional predictors in the logistic regression.

The fifth extension addressed a methodological issue: the previously documented discrepancy in estimating long-term impact from regression analyses, projected from end-of-intervention effects, versus the observed long-term impact (Bailey, Duncan, Watts, Clements, & Sarama, 2018; Bailey, Watts, Littlefield, & Geary, 2014). A possible explanation for such discrepancies is the lack of detailed sets of baseline control measures available in many longitudinal non-experimental datasets. The present analysis provides an opportunity to extend prior work with a rigorous set of pretest control measures, in a sample with which end-of-treatment impacts projected forward based on regression-derived estimates in the control group can be compared with observed intervention effects.

Method

For detailed information on study methods, see Fuchs et al. (2013) at https://www.ncbi.nlm.nih.gov/pubmed/24065865.

The Vanderbilt University Institutional Review Board approved this study, which conforms to U. S. Federal Policy for the Protection of Human Subjects and the Declaration of Helsinki. Participating teachers and a parent or guardian of each participating child gave their informed consent prior to inclusion in the study; each participating child provided informed assent prior to their participation in the study. Children in 40 schools and 233 first-grade classes (n = 2,806) were screened for risk for poor math outcomes using a latent factor cut-score across math applications, concepts, calculations, and word-reading assessments. (Note that the screening measures did not overlap with, i.e., were distinct from, pretest, posttest, and follow-up measures.) The cut-score corresponds to the 25^th percentile on the Wide Range Achievement Test (WRAT)-Arithmetic (Wilkinson, 1993). Students with standard scores on both subtests of the Wechsler (1999) Abbreviated Intelligence Scale (WASI) <80 (n=59) or whose teachers identified them as non-English speakers (n=359) were excluded.

At-risk students were randomly assigned at the individual level, stratifying by pre-intervention math scores and classrooms, to three conditions: mathematics intervention with speeded practice (n = 211), mathematics intervention with non-speeded practice (n = 204), and a control group (the school’s program; n = 224). Sample size for this analysis differs slightly from Fuchs et al. (2013) because those analyses were restricted to children with complete data on the full study battery.

Intervention sessions occurred for 16 weeks, 3 times per week, for 30 min per session. The first 25 min of each session were identical across intervention conditions: explicit instruction on the conceptual and procedural bases for first-grade arithmetic. The major emphases were numeral identification, quantities, number relations, arithmetic principles, number families, and decomposition of sets. To represent and contextualize mathematical ideas, number lines, manipulatives, games, and story problems were used. Near the end of the program, six lessons focused on place value and 2-digit calculations with and without regrouping. See Table 1 in Fuchs et al. (2013) for an outline of content.

Table 1:

Variable List

Variable type	Variable List
Demographics	Age at pretest, Sex (1=male), Free or reduced price lunch, Special education, Race and ethnicity, English Learner status
Pretests: General Processing	Nonverbal Reasoning, Processing Speed, WM-Listening Recall, WM-Counting Recall, Attentive Behavior, Listening Comprehension
Pretest: Reading	WRAT-Reading
Mathematics: First-Grade Content (only collected in fall and spring of First-Grade)	Arithmetic Combinations, Double-Digit Calculation, Story Problems
Mathematics: First-Grade Content (collected at every wave)	Facts Correctly Retrieved, Number Sets
Mathematics: Cross-Grade Content (collected at every wave)	WRAT-Arithmetic, Number Line, KeyMath-Numeration

Note: For details about scoring, see Supplementary Materials. For variable means by group at all waves, see Tables S1 and S2

In the final 5 min of each session, speeded practice promoted strategic responding to arithmetic problems: retrieval of answers when students felt confident; otherwise, use of the efficient counting strategies taught in the lessons. Children immediately corrected errors via counting strategies. Children had 90 s to respond to flash cards and tried to beat that initial score in two additional trials. With non-speeded practice, children used relations and principles addressed in the first 25 min of lessons to solve arithmetic problems in the context of games, with the tutor immediately correcting errors.

The variables used in the present study are listed in the present report’s Table 1. In spring of first grade, intervention effects were assessed with five measures, each providing broad sampling of first-grade mathematics content. Transfer distance from the intervention differed across measures. In order of proximity, measures were Arithmetic Combinations (Fuchs, Hamlett, & Powell, 2003; adding and subtracting through sets of 12); Double-Digit Calculations (Fuchs, Hamlett, & Powell, 2003; 2-digit adding and subtracting with and without regrouping); Addition Strategy Assessment-Facts Correctly Retrieved (Geary et al., 2007; simple addition problems answered quickly and correctly without indication of counting); Number Sets Test (Geary et al., 2009, Moore, vanMarle, & Geary, 2016; an integrative task of cardinality, subitizing, counting, numeral identification, symbolic and nonsymbolic quantity understanding, number decomposition, arithmetic principles), and Story Problems (Jordan & Hanich, 2000; combine, compare, and change word problems involving simple arithmetic). See Supplemental File for explanation of transfer distance.

To model longitudinal effects, three tasks indexing cross-grade mathematics content, with few relevant items at any one grade level, were administered at all four waves (pre and post in first grade and spring of second and third grade): Wide Range Achievement Test-Arithmetic (Wilkinson, 1993; calculation problems spanning K-12), Number Line Estimation (Siegler & Booth, 2004; accuracy of placing numerals on a 0–100 number line), and KeyMath-Numeration (Connolly, 1998; numeration items spanning K-12). Two of the first-grade measures, Addition Strategy Assessment-Facts Correctly Retrieved (Geary et al., 2007) and Number Sets Test (Geary et al., 2009), were also administered at each wave, because prior work indicates that fluent performance based on retrieval improves across grades 1 and 3 (Bailey et al., 2012). All these measures except Facts Correctly Retrieved were deemed distal to intervention.

To assess covariates and moderators at the start of first grade, teachers completed student demographic forms and the Attentive Behavior Rating Scale (Swanson et al., 2004). The following measures were administered to children: WASI-Matrix Reasoning (Wechsler, 1999); Woodcock-Johnson III Visual Matching (Woodcock, McGrew, & Mather, 2001; a measure of processing speed); Woodcock Diagnostic Reading Battery (WDRB)-Listening Comprehension (Woodcock, 1997); Working Memory Test Battery for Children-Counting Recall (WMTB-C; Pickering & Gathercole, 2001; a working memory span test); and WRAT-Reading (Wilkinson, 1993; a word-reading test). See Supplemental File for description of all measures.

Examiners were trained to criterion at each testing wave. Sessions were audio recorded; a random sample at each wave was coded for accuracy (>99%). Intervention sessions were audio recorded; a random sample at each wave was coded for accuracy (>97%). Testers were blind to students’ experimental conditions.

Results

Group Comparability

On 24 demographic and pretest variables, one group difference was statistically significant: A lower proportion of children in the non-speeded condition qualified for subsidized lunch than in the control group (.80 vs. .88, p = .03); see Supplemental File Table S1 for demographics, pretest performance, and attrition data by condition, along with tests of group differences. Given the lack of other group differences, including pretest math performance, this is likely a Type I error. Attrition was comparable and low across conditions: 4%−6% at grade 1 posttest, 11%−16% by grade 2 follow-up, and 13%−17% by grade 3 follow-up.

Intervention Impacts

The means and standard deviations (SDs) on math performance by wave and condition are in Supplementary Table S2. Few participants had missing data for cognitive pretests (< 1% for each group, for each test, except for attentive behavior; Table S1); models with full controls do not include these observations. We estimated intervention effects on spring-of-first-grade outcome measures using mixed effects regression in the lme4 package in R (Bates, Maechler, Bolker, & Walker, 2015), based on a model that included a large set of pretest controls and nested children in first-grade classrooms (the wide dispersion to second- and third-grade classrooms, along with their possible endogeneity to intervention status, makes clustering at these levels irrelevant). See Supplementary Table S3 for models including only demographic controls (using missing dummy variables for missing demographic observations). Because of the pretest balance across groups, estimates are robust across different sets of covariates, but they are more precisely estimated in the models with full pretest controls. So, we rely on models with full controls (see Table 2 note for a list). Table 2 shows ESs expressed in control group SD units.

Table 2:

Experimental Impacts at Spring of First Grade and Follow-up Waves

	Speeded vs. Control			Non-Speeded vs. Control
Outcomes	Estimate (S.E.)	p	Standardized Estimate	Estimate (S.E.)	p	Standardized Estimate
Spring of Grade 1
First-Grade Content
Arithmetic Combinations	10.50 (.92)	<.001	.90	5.15 (.94)	<.001	.44
Double-Digit Calculations	2.26 (.27)	<.001	.80	1.46 (.27)	<.001	.51
Facts Correctly Retrieved	1.42 (.30)	<.001	.42	.83 (.31)	.007	.24
Number Sets	.40 (.10)	<.001	.33	.25 (.10)	.010	.20
Story Problems	.54 (.19)	.006	.24	.68 (.20)	<.001	.30
Cross-Grade Content
WRAT Arithmetic	4.66 (.95)	<.001	.30	4.53 (.96)	<.001	.29
Number Line	1.00 (.61)	.100	.14	.46 (.62)	.455	.06
KeyMath-Numeration	1.44 (.72)	.046	.14	.60 (.73)	.412	.06
Spring of Grade 2
First-Grade Content
Facts Correctly Retrieved	.62 (.37)	.089	.16	.35 (.37)	.351	.09
Number Sets	.14 (.13)	.282	.09	−.05 (.14)	.708	−.03
Cross-Grade Content
WRAT-Arithmetic	1.16 (1.08)	.283	.08	.08 (1.10)	.868	.01
Number Line	.81 (.63)	.200	.11	.89 (.64)	.167	.12
KeyMath-Numeration	.00 (.75)	.999	.00	−.03 (.77)	.970	.00
Spring of Grade 3
First-Grade Content
Facts Correctly Retrieved	−.03 (.37)	.942	−.01	.13 (.37)	.721	.04
Number Sets	.21 (.15)	.152	.12	.22 (.15)	.140	.12
Cross-Grade Content
WRAT-Arithmetic	.39 (1.25)	.753	.03	1.16 (1.26)	.356	.08
Number Line	−.10 (.53)	.845	−.02	.12 (.53)	.823	.02
KeyMath-Numeration	.83 (.83)	.313	.08	.90 (.83)	.283	.08

Note: Covariates include the same test at pretest, pretest KeyMath-Numeration, WRAT Reading, Matrix Reasoning, Cross Out, Listening Recall, and Counting Recall, along with ethnicity, sex, subsidized lunch status. Missing demographic variables are coded as missing dummy variables. Participants are nested in grade 1 classrooms. Standardized effects are in control group standard deviation units. Number line is reverse coded, so higher scores indicate stronger performance.

At spring of first grade, the speeded practice group significantly outperformed the control group on all five first-grade outcome measures (ES = 0.24 – 0.90) and on two of the three cross-grade outcome measures (ES = 0.14 – 0.30). The non-speeded practice condition significantly outperformed the control group all five first-grade outcomes (ES = 0.20 – 0.51) and on one of the three cross-grade outcomes (ESs = 0.06 – 0.29).

We estimated intervention effects in grades 2 and 3 using the same statistical approach with mixed effects models that included the same set of pretest controls and with children nested in first-grade classrooms. The outcomes were the two first-grade content measures for which continued growth is expected (Facts Correctly Retrieved and Number Sets) and the cross-grade content measures assessed in spring of first grade. At grade 2 and 3 follow-up assessments, none of the 20 effects was significant, although five exceeded 0.10 control group SDs, with Facts Correctly Retrieved registering an ES of 0.16 at end of grade 2. The study was not, however, powered to detect effects of this magnitude in the follow-up waves (note that an ES of 0.14 was statistically significant at posttest, but standard errors are slightly higher at follow-up waves due to modest attrition). Impacts on the five outcomes assessed at both the spring of first grade and the grade 2 follow-up faded to an average of 37% of the spring of grade 1 unstandardized treatment effect in the speeded condition and 34% in the non-speeded condition.

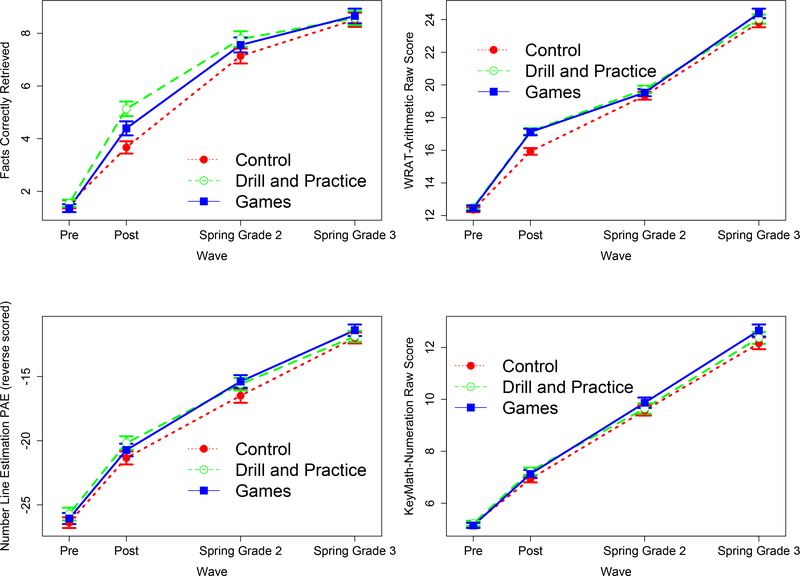
To explore whether diminished intervention gains were characterized better by the intervention groups’ net skill loss or by the control group’s accelerating growth, we plotted raw scores in Figure 2 for four of the five tests administered at all three outcome waves: Facts Correctly Retrieved, WRAT-Arithmetic, Number Line Estimation, and KeyMath-Numeration. (Because the Number Sets Test is scored as within-year standardized hits and false alarms, scores are not comparable across years.)

Figure 2: Raw Score Means across Waves by Group.

Means are unadjusted for covariates; bars are standard errors. PAE = Percent absolute error, which was reverse-scored, with higher number representing stronger performance.

To test for catch-up, we estimated mixed effects regression models between each consecutive pair of time points (pretest, posttest, grade 2, grade 3), with time, treatment group, and the interaction between time and treatment group as predictors. We focused on catchup effects for Facts Correctly Retrieved and WRAT-Arithmetic because group by time interactions for pre- and posttest were significant only for these measures (see slopes and interaction terms in Table S4; power to detect effects is weaker with these difference score analyses, without covariates, than for our main analyses in Table 2).

For Facts Correctly Retrieved, the speeded practice and non-speeded groups grew faster than the control group between pre- and posttest (difference in improvement scores for speeded practice vs. control and for non-speeded practice vs. control, respectively, of 1.4 and 0.9 facts, both p < .01; Table S4). Between posttest and grade 2, the speeded and non-speeded practice groups grew less than the control group, the speeded practice group significantly so (respective difference in improvement scores of −0.8 and −0.3 facts, p = .049 and .457). Yet, between grades 2 and 3, differences in slope were not statistically significant (respective difference in improvement scores of −0.5 and −0.2 facts, p = .207 and .654).

For WRAT-Arithmetic, the pattern was similar. The speeded practice and non-speeded groups grew faster than the control group between pre- and posttest (respective difference in improvement scores between speeded vs. control and non-speeded vs. control of 1.1 and 1.1 items, both p < .001; Tables S2 for means and S4 for inferential statistics). Between posttest and grade 2, the speeded and non-speeded groups grew less than the control group (respective difference in improvement scores of −0.8 and −1.0 items, both p < .01). Yet, between grades 2 and 3, group differences in growth were small and not statistically significant (respective difference in improvement scores of −0.2 and 0.3 items, p = .602 and .472).

Thus, on both measures diminishing intervention effects were related to faster improvement in the control than intervention groups in the first but not the second year following the end of the intervention. Although the treatment impacts in spring of grades 2 and 3 did not reach statistical significance, they were positive on both these measures: At end of grade 2, on Facts Correctly Retrieved, an ES of 0.16 still favored the speeded group over control, and an ES of 0.09 still favored the non-speeded group over control. On WRAT-Arithmetic, an ES of .09 still favored the speeded group over control. At end of grade 3, on WRAT, an ES of .09 still favored the non-speeded group over control.

Moderation Analyses

To investigate moderators of intervention effects indexed at third grade, we added interaction terms (intervention effect × moderator) to the models investigating the main effects of intervention. Each moderator was assessed in a separate model to avoid problems with collinearity. Because the baseline moderators were not randomly assigned, these analyses are not strictly causal, but descriptive of differential impacts of the intervention across baseline child characteristics. Intervention by pretest child competency interaction coefficients appear in Table S5.

We identified one significant interaction: On the third-grade Number Sets Test, children with lower pretest working memory capacity benefitted more from math intervention with non-speeded practice, compared to the control group, than did children with higher performance on these pretest competencies. This interaction is plotted in Figure S1. However, given the large number of moderation tests, this effect should be interpreted cautiously.

Forecasting Grade 3 Learning Difficulties

We next explored whether and if so which pretest or end-of-intervention (spring-of-first-grade) child-level variables forecast which intervention students experience inadequate outcomes at grade 3. We defined adequate response as is often done in response-to-intervention studies (e.g., Frijters, Lovett, Sevcik, & Morris, 2013; Fuchs, Sterba, Fuchs, & Malone, 2016): normalized performance, operationalized as an outcome standard score of 90 or above. We ran these analyses using the third-grade WRAT-Arithmetic as the outcome which, although a transfer measure (indexing forms of calculations not addressed in intervention), more directly requires foundational skill in arithmetic than do the other two norm-referenced longitudinal outcome measures.

We first ran a logistic regression model in which responsiveness status was regressed on posttest arithmetic combinations, number line estimation, and story problems. In a second model, we added pretest arithmetic combinations, listening comprehension, reasoning, processing speed, working memory, and word reading. Then, models were compared using a χ² test to evaluate equality between areas under the receiver operating characteristic curve (AUC, which indexes the model’s correct classification performance; 1.00 = perfect classification). Because students were nested in first-grade classrooms, coefficient standard errors were adjusted accordingly using the vce(cluster classroom) option in Stata’s logit command.

Results from Models 1 and 2 are shown in Table S6. In Model 1, posttest arithmetic combinations and number line accuracy were significant predictors of responsiveness status; AUC was .69. In Model 2, posttest arithmetic combinations, but not number line, remained significant. Word reading was the only significant pretest predictor, when controlling for other variables in the model; AUC was .73. The χ² value comparing AUCs was 4.59 (p-value = .03), indicating that Model 1 fit was significantly worse than Model 2. Thus, pretest word reading added predictive value to posttest arithmetic combinations in determining end-of-grade-3 responsiveness status.

To determine whether the set of significant predictors was comparably good at classifying third-grade status as the whole set of pre- and posttest variables, we ran a third model with only the significant predictors from Model 2. The comparison revealed no difference in the fit of Model 2 and Model 3, χ² = 1.62 (p = .20). Thus, at-risk students who were relatively skilled at solving basic addition and subtraction problems at the end of first grade and who had stronger letter knowledge and word-reading skill at start of first grade were more responsive to intervention, as indicated by a greater likelihood they would score in the average or better range on a broad-based measure of calculation achievement at the end of third grade.

Comparing Regression-Projected versus Observed Longitudinal Effects

We used regression-based methods to estimate the effects of first-grade math skills on third-grade math skills in the control group, and then used these and the first-grade intervention effects to estimate the projected intervention effects at the end of 3^rd grade. If projected and observed intervention effects differ, then the estimated effects of early mathematical skills on later mathematical skills may not be useful for making predictions about the long-term effects of interventions. We first calculated composite scores for arithmetic (Facts Correctly Retrieved at all waves and Arithmetic Combinations at pre- and posttest), calculations (WRAT-Arithmetic at all waves and Double-Digit Calculations at pre- and posttest), word problems (Story Problems at pretest and posttest), and number understanding (Number Sets Test, Number Line Estimation, and KeyMath-Numeration at all waves).

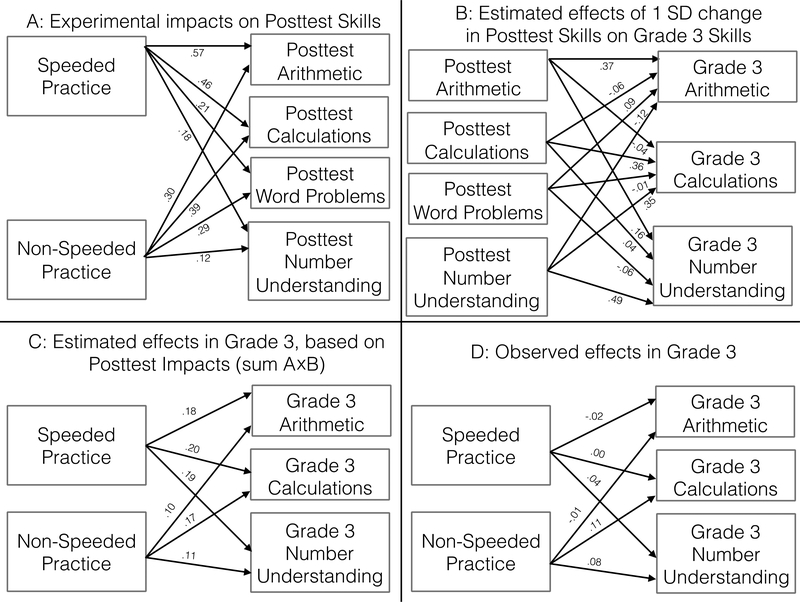
Then, we calculated actual end-of-intervention (spring-of-first-grade) effects (relative to the control group) on each composite score (Figure 3, Panel A) and estimated the causal effect of 1 SD change in first-grade arithmetic, calculations, word problems, and number understanding on composites of third-grade arithmetic, calculations, and number understanding using only the control group (Figure 3, Panel B), controlling for a rich set of pretest covariates (see note on Figure 3). The latter are the predicted long-term advantages of being 1 SD above average on these measures at the end of first grade, controlling for baseline covariates, and without receiving the intervention. So, if an intervention resulted in a 1 SD gain in say arithmetic, then the average intervention student is predicted to have a 0.37 SD advantage over the average control student in arithmetic at the end of 3^rd grade (0.37 is from Figure 3, Panel B), assuming no other indirect effects of the intervention.

Figure 3: Calculation of Projected vs. Observed Effects of Treatments on Grade 3 Follow-up Outcomes.

Panels A and D show effects relative to control group on standardized outcome measures, with full controls from models in Table 2. Effects in Panel B are estimated with full controls using data from the control group only. Projected effects in Panel C are the sum of the products of the effects in Panel A for each treatment and the estimated effects in Panel B. In all models, children are nested in grade 1 classrooms.

Following this logic, we projected intervention effects on children’s grade 3 calculations and number understanding by multiplying the estimates in Figure 3, Panel A by those in Figure 3, Panel B, and summing the estimated indirect effects for each intervention. These projections are shown in Figure 3, Panel C. For example, the projected effect of the speeded practice condition on grade 3 arithmetic was computed by multiplying the effects of speeded practice on grade 1 posttest arithmetic, calculations, word problems, and number understanding (.57, .46, .21, .18; Figure 3, Panel A) by the estimated effects of the same grade 1 outcomes on grade 3 arithmetic (.37, −.06, .09, −.12; Figure 3, Panel B) and then adding these effects together (.21-.03+.02-.02=.18; Figure 3, Panel C).

Based on the observed grade 1 posttest effects and the regression-based estimates of the effects of grade 1 posttest performance on grade 3 outcomes, our analysis projected that students in the speeded intervention condition would outperform the control group by .18 SDs on grade 3 arithmetic; .20 SDs on grade 3 calculations; and .19 SDs on number understanding. The students in the non-speeded intervention condition were projected to score .10 SDs higher than the control group on grade 3 arithmetic; .17 SDs on grade 3 calculations; and .11 SDs on number understanding. Finally, Panel D shows the observed intervention effects on grade 3 arithmetic, calculations, and number understanding were lower than the projected effects in all cases.

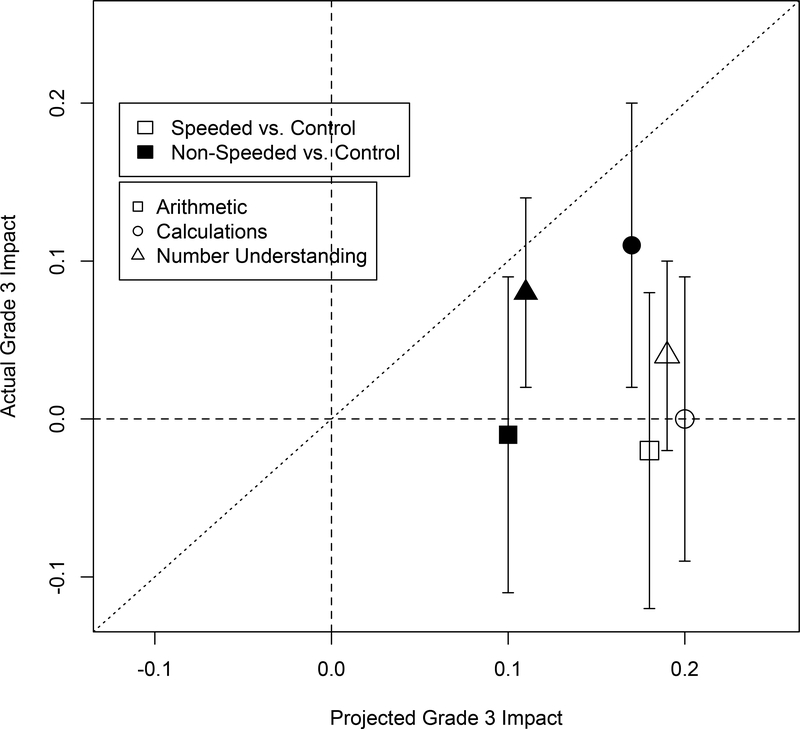
Projected versus actual impacts for each outcome are plotted in Figure 4. Projected impacts appear biased, given that actual effects are smaller than projected effects in every case. Further, estimates are not well calibrated to actual long-term effects: The comparisons with the largest projected effects do not show larger actual effects. The relation between predicted and actual impacts was weak (r = −.10); this correlation is based on only six pairs of projected and actual impacts and is therefore imprecisely estimated.

Figure 4: Scatterplot of Projected by Observed Impacts of Treatments on Grade 3 Follow-up Outcomes.

Projected impacts are from Figure 3, Panel C. Actual impacts are from Figure 3, Panel D. Unbiased prediction would yield similar errors on either side of the line with intercept 0 and slope 1. Calibrated prediction would be indicated by a correlation between predicted and observed effects. Error bars are standard errors.

Discussion

We begin by discussing the immediate and longitudinal impacts of the intervention on tasks of varying transfer distance. We next consider the processes by which fadeout occurs and whether pre- or posttest (end-of-intervention) child-level variables may serve to identify which students will likely require ongoing intervention support. Finally, we address our methodological question concerning whether longitudinal effects of intervention can be predicted on the basis of posttest performance. We close with study limitations and overall conclusions about the persistence of intervention effects.

Immediate and Longitudinal Effects of Intervention

Using a larger set of pretest controls, we replicated and extended the post-intervention effects reported by Fuchs et al. (2013). Significant effects favored intervention over control on all five first-grade math outcomes for both intervention conditions. For the math intervention condition with speeded practice, the ES on arithmetic combinations, the outcome measure closest in proximity to the intervention’s focus was large (0.90). This was also the case for the measure with the next closest proximity, double-digit calculations with and without regrouping (ES = 0.80), even though this content was explicitly addressed in only six intervention lessons. On facts correctly retrieved, the next closest in proximity to the intervention, the ES was a moderate 0.42.

Corresponding figures in the non-speeded condition for these three measures were smaller but significant: on arithmetic, 0.44 (vs. 0.90); on double-digit calculations, 0.51 (vs. 0.80); and on facts correctly retrieved, 0.24 (vs. 0.42). Both practice conditions were designed to support retrieval but in different ways: speeded practice via strategic responding with recall or efficient counting strategies and many opportunities for forming correct associations between problem stems and answers; non-speeded practice by reinforcing relations and principles that serve as the basis of reasoning strategies that support retrieval. The pattern of smaller ESs for the non-speeded versus speeded practice group, largest on arithmetic combinations and double-digit calculations, reproduces Fuchs et al.’s (2013) findings, in which speeded practice significantly outperformed non-speeded practice with respective ESs of 0.51 and 0.21 on the two outcomes.

Number sets was deemed farther transfer because strong performance requires the integration of skills across multiple dimensions of number knowledge and thus was novel (not taught or practiced during intervention). Here, the ES for speeded practice was 0.33 and 0.20 for non-speeded practice. This advantage for speeded practice was unexpected because the sole focus of non-speeded practice was the conceptual and procedural bases for arithmetic. In any event, the similar impacts on the number sets test and addition fact retrieval are consistent with Moore et al.’s (2016) finding that fluency on the number sets test is related to children’s understanding of addition and subtraction. The results here suggest that fluency in these operations facilitates fluency in combining symbolic and nonsymbolic quantities (core skills assessed by the number sets test; Geary et al., 2009), although the results could also emerge because some number-sets items involve comparison of pairs to numerals (e.g., “3 4”) to the target (e.g., “5”). Fast and accurate retrieval of basic facts should facilitate performance on these items and thus boost overall number sets scores. On story problems, the most distal first-grade outcome, ESs were more similar across the two conditions (0.24 and 0.30).

The parent study was designed with additional waves of testing at end of grades 2 and 3, using three tasks tapping cross-grade math content. For longitudinal modeling purposes, the parent study also included these same measures at end of first grade, although first-grade effects on these measures were not expected to differ across conditions. Yet, on WRAT-Arithmetic, which includes approximately six calculation items at the first-grade level but also taps kindergarten number knowledge, effects were significant and of nearly identical magnitude for both intervention conditions: 0.30 and 0.29. On KeyMath-Numeration, which has approximately three items at the first-grade level, effects were significant for the speeded practice condition (ES = 0.14) but not for the non-speeded practice condition (ES = 0.06). This echoes the end-of-first-grade number sets findings already discussed. On number line, effects were nonsignificant for both conditions (ES = 0.14 for the speeded condition; 0.06 for the non-speeded condition), perhaps due to the measure’s focus on double-digit numbers (although we note that the ES of 0.14 was the same as for KeyMath-Numeration, where the effect was significant).

In these ways, the immediate effects of intervention provide the basis for two conclusions. First, explicit instruction on the core ideas, principles, and procedures of simple arithmetic has strong effects on at-risk students’ first-grade math learning, especially on but not limited to arithmetic and calculation outcomes. Second, conceptual math intervention with speeded practice, even for a small amount of intervention time (5 min of each 30 min session), plays a substantial role in improving outcomes over the same conceptual mathematics instruction but with non-speeded practice. This assumes that practice is delivered in the context of instruction on the conceptual bases of arithmetic, as in the Fuchs et al. (2013) study’s intervention.

Yet, despite convincing effects at first grade, there was little evidence that the effects of intervention persisted one or two years after the intervention ended. To index math targets expected for continued development across grades 2–3, follow-up assessments were restricted to two of the five tasks involving first-grade content: Facts Correctly Retrieved and Number Sets, where continued growth through third grade had previously been shown (Geary et al., 2012). At end of second grade, ESs on these respective measures were 0.16 and 0.09 for math intervention with speeded practice and 0.09 and −0.03 for math intervention with non-speeded practice; at end of third grade, −0.01 and 0.12 for the speeded practice condition and 0.04 and 0.12 for non-speeded practice. Some of these ESs may be meaningful for education practice. The p-value of the 0.16 ES was a marginally significant .089 (Table 2), suggesting that effects for math intervention with speeded practice may have persisted one year after intervention ended. By end of grade 3, however, the effect had faded (ES = 0.04, Table 2), with the graphed data (Figure 2) suggesting that performance reached an asymptote on the Facts Correctly Retrieved measure by end of second grade.

On the three follow-up cross-grade tests, WRAT-Arithmetic, Number Line, KeyMath-Numeration, ESs were generally smaller: 0.08, 0.11, and .00 for speeded practice and 0.01, 0.12, and 0.00 for non-speeded practice at end of second grade; 0.03, −0.02, and 0.0 for speeded practice and 0.08, 0.02, and 0.08 for non-speeded practice at end of third grade. For context, the average annual growth on nationally normed mathematics achievement tests declines from approximately 1 SD in the first-grade year to approximately .5 SD by the end of elementary school (Hill, Bloom, Black, & Lipsey, 2008). By comparison, the average of the intervention effects on the two cross-grade standardized mathematics assessments (WRAT-Arithmetic and KeyMath-Numeration) at the grade 2 and 3 follow-up waves was .045 control group SD. Thus, as with prior math intervention studies at kindergarten (Clarke et al., 2016) and at first grade (Smith et al., 2013), interventions that provide at-risk children with a substantial and significant boost at the end of intervention fail to deliver the hoped-for persistence of effects.

Processes by Which Fadeout Occurs

To gain insight into the processes by which fadeout occurs, we return to the notion of trifecta skills needed to support persistence (Bailey et al., 2017). First, the intervention’s main focus, arithmetic, was clearly malleable. With an instructional framework rooted in explicit, systematic instructional design, at-risk intervention students’ arithmetic performance surged, even as arithmetic learning among at-risk first graders receiving the school’s typical program (this study’s control group) was limited. As established in prior work, arithmetic also fulfills the second dimension of trifecta skills, that is, it is foundational to higher-level mathematics (Fuchs et al., 2006; Fuchs et al., 2012; Geary, 2011; Jordan et al., 2013; NMAP, 2008). Still, fadeout occurred for one or several of three possible reasons.

The first is catch up: The at-risk children in the control group showed more rapid gains in arithmetic after the intervention ended then did children who participated in the interventions, consistent with previous studies (Clements et al., 2013; Elango, García, Heckman, & Hojman, 2015). Our results indicated that catch-up primarily occurred during the first year after the intervention ended.

A second potential reason is the possibility that schools fail to provide intervention students access to sustained explicit instructional support after the intervention ends. In other words, the effectiveness of the interventions is related in part to the explicit supports built into the learning activities. If these same types of supports are not available in the regular classroom when intervention ends, then the ease of learning new mathematical material, even with enhanced foundational skills, may be impeded to that seen in the control group. Unfortunately, we did not have information on the types of instructional supports provided in the regular classrooms and thus we cannot directly assess this possibility.

We also assessed whether persistence of intervention effects was moderated by individual differences in students’ cognitive and linguistic processes. Such effects might be expected because children who have cognitive advantages generally show more rapid gains in mathematical achievement than their less apt peers (Bailey et al., 2014; Geary, Nicholas, Li, & Sun, 2017). But this is not what we found, possibly due to range restriction among the at-risk groups. The exception was for the contrast involving the non-speeded intervention versus control on the third-grade number sets outcome; specifically, children with lower pretest working memory capacity outperformed control group students with similar pretest working memory. By contrast, third-grade effects between the non-speeded practice and control conditions were smaller for children with higher performance on pretest working memory.

The pattern of this interaction is similar to that found with a recent effective fractions intervention. There, conceptual fractions practice was particularly helpful for students with extremely limited working memory capacity, whereas speeded fractions practice produced stronger effects for students with more intact working memory resources (Fuchs et al., 2014). However, as previously mentioned, the observed moderator effect should be interpreted cautiously given the large number of moderation tests.

The third threat to the persistence is the possibility that schools incorporate multitier systems of support (MTSS), in which they select students with weaker mathematics skill for subsequent intervention (Balu et al., 2015). Thus, students in the control group would be more likely to receive subsequent intervention than students in the intervention groups. This would contribute to the control group’s second-grade catch-up effect on math fact retrieval and complex calculations. The participating school district did in fact offer MTSS services during this period and based on end-of-first-grade performance would have identified more control group students than intervention students for second-grade MTSS intervention. Although this is a distinct possibility, the present study cannot directly test this hypothesis, because we lack data on school-delivered intervention during the follow-up period.

Child-Level Variables that Forecast Grade 3 Learning Difficulties

The present study adds to a growing body of evidence that intervention effects cannot be expected to persist over time for many children, even when strong and meaningful effects are found when intervention ends. An intervention with strong efficacy does not work for all children, but an intervention that suffers fadeout over time does not mean that all children fail to derive continued benefit. This is the case in the present study, where some children reached normalized performance, while others did not. For example, on the longitudinal WRAT-Arithmetic measure, indexing simple and complex calculations, more than one-third of intervention students across the two conditions met the criterion for adequate response commonly applied in the response-to-intervention literature (Frijters et al., 2013; Fuchs et al., 2016) at end of third grade: normalized performance, with standard score of 90. We note that although dichotomizing continuous data has its drawbacks (Irwin & McClelland, 2003; MacCullum, Zhang, Preacher, & Rucker, 2002), school personnel are regularly called upon to make dichotomous service allocation decisions.

Our logistic regression analyses addressed the question of whether pretest or end-of-intervention child-level variables serve to differentiate students who will and will not require sustained intervention. Two variables demonstrated predictive utility for classifying students who did and did not respond adequately on complex calculations two years later. End-of-intervention arithmetic combinations skill was one of the two variables. In other words, students who demonstrated weaker response to the first-grade intervention were less likely to meet criteria for average or better math achievement at the end of third grade. This suggests that stronger foundational skill begets stronger math achievement. It also suggests the importance of monitoring progress over the course of intervention to designate a subset of children for more differentiated adjustments.

Start-of-first-grade letter knowledge and word reading offered additional predictive value, in line with prior work showing a relation between early literacy skills and later mathematics achievement (Chu et al., 2016; Göbel et al., 2014). Ease of learning words and memorizing basic arithmetic facts tends to co-occur (Geary, 1993; Koponen et al., 2013), potentially because they rely on the same brain and cognitive systems that support symbol and number and arithmetic fact learning (Holloway, Battista, Vogel, & Ansari, 2013; Yeo, Wilkey, & Price, 2017). That start-of-first-grade reading distinguished long-term responders and nonresponders to a strong first-grade mathematics intervention is also noteworthy: It echoes evidence indicating students with concurrent math and reading difficulty experience worse outcomes in each area than do peers with difficulty in one domain (Cirino et al., 2015; Willcutt et al., 2013) and that such comorbidity is associated with less adequate response to intervention (Fuchs et al., 2013; Fuchs et al., 2004).

The best and most parsimonious model classified 73% of students correctly. This value, along with the specific predictors identified in this model should be interpreted tentatively, pending replication. These results do, however, provide an innovative heuristic for using cross-domain child-level performance (e.g., reading and math) at different time points (e.g., before and after intervention) to identify children’s later responsiveness to intervention and to generate hypotheses about and deepen insight the variables that underlie at-risk learners’ post-intervention developmental trajectories.

Estimating Long-Term Impact from Regression Analyses

Finally, our approach addresses a methodological issue related to the usefulness of making predictions about the effects of interventions from non-experimental data; specifically, we focused on the previously documented difficulty in estimating long-term impacts, when estimates are projected via regression analyses using end-of-intervention impacts (Bailey et al., 2018; Bailey et al., 2014). A possible explanation for such discrepancies is the lack of detailed sets of baseline control measures available in many longitudinal, non-experimental studies. The present analysis extends prior work with a rigorous set of pretest control measures, in a sample with which observed impacts can be compared with projections based on end-of-intervention impacts and regression-estimated persistence rates. We found that projected impacts systematically over-estimated observed impacts, replicating Bailey et al. (2018). Thus, given the implausibility of regularly collecting a battery of pretest controls more thorough than those included in the present study, regression control does not appear to provide an effective means for projecting the future benefits of successful interventions.

These findings contrast with quasi-experimental work (i.e., without random assignment to intervention and control groups) that successfully approximated effects of mathematics interventions (Dong & Lipsey, 2018; Shadish, Clark, & Steiner, 2008). A critical difference between these designs may be that participation in a controlled math intervention may be similar whether or not children are randomly assigned, while absolute levels of math skills may have different meanings in children who just received an effective early math intervention versus those who did not (Bailey et al., 2016). In particular, the same level of math skill may reflect greater underlying cognitive, developmental, and contextual advantages in children who did not receive an effective math intervention than in children who did. Models that account for potential differences between within- and between-child variation (for review, see Borsboom, Mellenbergh, & van Heerden, 2003) in math skills may yield more accurate predictions about the long-term patterns of impacts after effective math intervention ends. This problem is worthy of additional attention in cognitive developmental research to increase our ability to make useful predictions about long-term effects of interventions based on longitudinal non-experimental data. Additionally, these quantitative comparisons of experimental and non-experimental estimates of the same effects act as important checks on the validity of common research practices in child development.

Major Study Limitation and Conclusions

As noted, a major limitation is the absence of information on which students received school-delivered intervention during the follow-up period. The design of future intervention studies should include information on these interventions, especially in the year following the end of the intervention. Indeed, if the control group converges with the intervention group because schools are able to allocate more instruction to these children, the intervention’s positive effect would be observed by comparing all of the children in the classroom or school in which only some children received the intervention against similar children in other classrooms or schools. The possibility of universal education interventions generating more persistent effects has been discussed (Bailey et al., 2017; Greenberg & Abenavoli, 2017), although it is notable that fadeout following an effective mathematics intervention has been observed in studies that have randomly assigned children at the classroom (Clarke et al., 2016) and school (Bailey et al., 2018; Clements et al., 2013) levels.

With this caveat in mind, we draw the following conclusions. Diminishing longitudinal effects of effective kindergarten or first-grade math intervention, as revealed in prior work (Clarke et al., 2016; Smith et al., 2013) and in the present study, raise questions about whether early prevention is sufficient to support long-term outcomes in children who manifest substantial math delays early in school.

The present study contained five outcome measures, more than a prior mathematics intervention study with a 6-month follow-up (Clarke et al., 2016) and the same number as in Smith et al. (2013) with a 1-year follow-up. The present study also included content targeted in first grade and across grades. Still, we cannot conclusively rule out the possibility that the intervention led to lasting effects on measures not given at the follow-up waves.

The extent to which these findings generalize to other types of interventions, target skills, and age groups is not well understood. The finding that intervention effects declined to approximately 1/3 their initial size after the first year is similar to findings from prior comparisons of fadeout effects across multiple studies of academic interventions in early childhood and the early school years (Bailey et al., 2018; Li et al., 2017). It is less clear if this pattern generalizes well to interventions targeting older children. We predict that the general finding that pretest academic skills can be used to predict which students need persistent intervention will generalize to other contexts. However, the exact regression weights, proportions of at-risk children in need of persistent intervention based on these criteria, and predictors may be sensitive to how low performance is defined and how participants are screened for eligibility into the intervention.

Our results suggest that although early prevention, in the form of math intervention provided in first grade, is probably necessary, it is not sufficient. Instead, sustained intervention, designed to capitalize on the benefits derived from effective early prevention services, is necessary for a subset of students who receive first-grade intervention. Our analyses indicate this may be the case for nearly two-thirds of children who receive effective first-grade intervention. Therefore, randomized controlled trials are needed to examine whether early intervention combined with sustained intervention produces stronger long-term outcomes than early or later intervention alone. If so, one important challenge is to identify the subset of early intervention students who require sustained intervention, and the present study demonstrates potential for such a post-intervention screening process using post-intervention math scores as well as pre-intervention reading skill. Future work should continue to improve the accuracy and investigate the robustness of such methods for forecasting need for sustained intervention.