Assessing covariate balance when using the generalized propensity score with quantitative or continuous exposures

Abstract

Propensity score methods are increasingly being used to estimate the effects of treatments and exposures when using observational data. The propensity score was initially developed for use with binary exposures (e.g., active treatment vs. control). The generalized propensity score is an extension of the propensity score for use with quantitative exposures (e.g., dose or quantity of medication, income, years of education). A crucial component of any propensity score analysis is that of balance assessment. This entails assessing the degree to which conditioning on the propensity score (via matching, weighting, or stratification) has balanced measured baseline covariates between exposure groups. Methods for balance assessment have been well described and are frequently implemented when using the propensity score with binary exposures. However, there is a paucity of information on how to assess baseline covariate balance when using the generalized propensity score. We describe how methods based on the standardized difference can be adapted for use with quantitative exposures when using the generalized propensity score. We also describe a method based on assessing the correlation between the quantitative exposure and each covariate in the sample when weighted using generalized propensity score -based weights. We conducted a series of Monte Carlo simulations to evaluate the performance of these methods. We also compared two different methods of estimating the generalized propensity score: ordinary least squared regression and the covariate balancing propensity score method. We illustrate the application of these methods using data on patients hospitalized with a heart attack with the quantitative exposure being creatinine level.

1 Introduction

Observational studies are increasingly being used to estimate the effects of treatments, interventions, and exposures. In designing and analyzing such studies, analysts must account for the confounding that occurs when treated subjects differ systematically from control subjects in terms of prognostically important baseline covariates. Statistical methods must be used to remove or minimize the effect of this confounding so that valid inferences on treatment effects can be drawn from observational studies. Statistical methods based on the propensity score are increasingly being used to reduce or minimize the confounding that occurs in observational studies.^1,2

The propensity score was initially developed for use with binary or dichotomous treatments or exposures (e.g., active treatment vs. control).¹ However, propensity score methodology has subsequently been extended to allow analysts to estimate the effect of quantitative treatments or exposures.^3–5 Examples of such quantitative exposures include dose or quantity of medication used, pack-years of cigarettes smoked, income, or years of education. The extension of propensity score methods to quantitative exposures has been referred to as the generalized propensity score (GPS).^5,6 In the current study, we restrict our focus to studies with quantitative exposures and do not consider the case of categorical exposures with more than two exposure levels (e.g., low vs. medium vs. high dose of medication). For the purposes of this paper, we consider the terms quantitative and continuous to be synonymous.

A critical element of any propensity score analysis is balance assessment. This entails assessing whether conditioning on the propensity score (using stratification, matching, weighting, or covariate adjustment) has resulted in the distribution of measured baseline covariates being similar between treated and control subjects. A suite of balance diagnostics have been proposed for use with propensity score matching,^7,8 inverse probability of treatment weighting using the propensity score,⁹ covariate adjustment using the propensity score,¹⁰ and stratification on the propensity score.^11,12 Many of these methods of balance assessment are based on the standardized difference, which is the difference in the mean of a covariate between the treated and control groups, divided by a pooled estimate of the standard deviation of the covariate. While methods of balance assessment are well developed for when the propensity score is used with binary exposures, there is a paucity of information as to how to assess covariate balance when using the GPS with quantitative exposures.

The objective of the current study was to describe methods for balance assessment when using the GPS with quantitative exposures and to evaluate the performance of these methods. The paper is structured as follows: In Section 2, we provide notation, a brief background on the GPS and describe balance diagnostics for use with the GPS. In Section 3, we use Monte Carlo simulations to evaluate the performance of these balance diagnostics. In Section 4, we provide a case study to illustrate the application of the proposed methods using a sample of patients hospitalized with acute myocardial infarction (AMI) when the first measured value of creatinine is the quantitative exposure. Finally, in Section 5, we summarize our findings and place them in the context of the existing literature.

2 Balance diagnostics for use with the GPS

In this section, we introduce the GPS. We then describe two ways in which it can be used to estimate the dose–response function for a quantitative exposure. Finally, we describe balance diagnostics for use with each of these two methods of using the GPS.

2.1 The generalized propensity score

We use the following notation throughout the paper. Let T denote a quantitative variable denoting the level of exposure (e.g., dose or quantity of a medication), and let X denote a vector of measured baseline covariates. Using the terminology of Hirano and Imbens, let $r(t,x)$ denote the conditional density of the quantitative exposure variable given the observed covariates

$$r(t,x)=f_{T|X}(t|x)$$ (1)

Then the GPS is $R=r(T,X)$.⁵ Imai and van Dyk refer to the conditional density function f_T|X as the propensity function.⁴

Robins et al. suggest that one might specify that, given X, the quantitative exposure T is normally distributed with mean ${\beta }^T\text{X}$ and variance ${\sigma }^2$ (the regression parameters β and ${\sigma }^2$ could in practice be estimated using ordinary least squares (OLS) regression).¹³ For a given subject, the conditional density function can be evaluated at the observed value of that subject’s exposure. This is the value of the GPS for that subject. Thus $f_{T|X}(t|x)$ can be estimated by the normal density $\frac{1}{\sqrt{2\pi {\hat{\sigma }}^2}}{e}^{-\frac{(t-{\hat{\mathbf{\beta }}}^T\mathbf{x}{)}^2}{2{\hat{\sigma }}^2}}$. This is a two-step process in which a regression model is first fit to the data. In the second step, one determines the value of the conditional density function at the value of the quantitative exposure. Note that this requires the assumption that the conditional distribution of the exposure given the observed baseline covariates is approximately normal.

Hirano and Imbens⁵ state that the

GPS has a balancing property similar to that of the standard propensity score. Within strata with the same value of r(t,X), the probability that T = t does not depend on the value of X. Loosely speaking, the GPS has the property that $X\perp 1\{T=t\}|r(t,X)$. (p. 75)

An alternative to the use of a parametric model (such as OLS regression) to estimate the distribution of the quantitative exposure conditional on the observed baseline covariates is to use the covariate balancing propensity score (CBPS).¹⁴ When the exposure is binary, Imai and Ratkovic¹⁴ described the CBPS methodology which models treatment assignment while optimizing covariate balance. To do so, they used a generalized method-of-moments or empirical likelihood framework. In doing so, they used “a set of moment conditions that are implied by the covariate balancing property” (p. 244). Fong et al. subsequently extended the CBPS methodology to quantitative exposures.¹⁵ The CBPS estimates the GPS so as to minimize the association between the quantitative exposure variable and baseline covariates. We will use the term CBGPS to refer to the application of this method to quantitative exposures.

2.2 Estimation of the dose–response function using the GPS

The GPS assumes the existence of a set of potential outcomes, $Y_i(t),\text{ for }t\in \Psi ,$ where $Y_i(t)$ denotes the outcome of the ith subject if they received exposure $\text{T}=t$, while Ψ denotes the set of all possible values of the exposure. In the conventional setting with a dichotomous exposure, $\Psi =\{0,1\}.$ The dose–response function is defined as $\mu (t)=\text{E}[Y_i(t)]$. This dose–response function denotes the average response in the population (or sample) if all subjects were to receive $T=t$. By comparing $\mu (t_1)$ with $\mu (t_2)$, one can estimate the mean change in the outcome if all subjects were exposed to $T=t_2$ instead of to $T=t_1$. A variety of methods have been proposed for using the GPS to estimate the dose–response function.^3,5,6,16,17 We will focus on two approaches: covariate adjustment using the GPS and weighting using the inverse of the GPS.

When using covariate adjustment using the GPS, one regresses the outcome on the quantitative treatment and the estimated GPS.^5,6 An appropriate regression model is selected based on the nature of the outcome (e.g., a linear model for continuous outcomes and a logistic model for binary outcomes). Based on the fitted outcomes model, one can then estimate the expected outcome for a given subject if their exposure was set equal to $T=t$ (and if their GPS was evaluated at the given exposure level t, instead of at the observed exposure level. Thus the value of the GPS is $R=r(t,X)$, where t is the specified exposure level). By taking the expectation of this quantity over the study sample, one can estimate the dose–response function: $\mu (t)=\text{E}[Y_i(t)]$.

Imbens,³ Robins et al.,¹³ and Zhang et al.¹⁶ suggested that weights could be derived from the GPS and be used to estimate the dose–response function. Weights can be defined as $\frac{W(T_i)}{r(T_i|X_i)}$, where the numerator is a function that is included to stabilize the weights. It has been suggested that a reasonable choice for W is an estimate of the marginal density function of T.¹⁶ This density function can be determined by calculating the mean and the variance of the quantitative exposure variable in the overall sample (${\mu }_{\text{sample}}$ and ${\sigma }_{\text{sample}}^2$, respectively). Then $W(T_i)=\frac{1}{\sqrt{2\pi {\sigma }_{\text{sample}}^2}}{e}^{-\frac{(T_i-{\mu }_{\text{sample}}{)}^2}{2{\sigma }_{\text{sample}}^2}}$.¹³ Robins et al. note that for quantitative exposures unstabilized weights (i.e., those with W(T_i) = 1) will have infinite variance and should not be used.¹³ Once the GPS-based weights have been estimated, a univariate regression can be conducted in which the outcome is regressed on the quantitative exposure using a weighted regression model that incorporates the GPS-based weights. From the fitted outcomes model, the dose–response function can be estimated by calculating the expected outcome for each subject under each level of exposure.

2.3 Balance diagnostics for use with the GPS

In this section, we describe balance diagnostics for use with the GPS. Our balance diagnostics are motivated by the property described above

$$X\perp 1\{T=t\}|r(t,X)$$ (2)

This property says that for a given a specific level of exposure (t), then in strata of subjects who have the same value of the GPS for that specific level of exposure, the distribution of baseline covariates in subjects with T = t is the same as the distribution in subjects with T ≠ t. Note that in the above definition, we are conditioning on the GPS evaluated at treatment level t, not at the observed level.

We describe two different types of balance diagnostics: blocking-based diagnostics and correlation-based diagnostics. The latter are for use exclusively with weighting using the GPS.

2.3.1 Blocking-based diagnostics

The blocking-based diagnostic method is motivated by a similar approach described by Hirano and Imbens and by Bia and Mattei.^5,6 Both of these two sets of authors suggested that a discretization of the study sample be accomplished using strata defined by the quantitative exposure variable. They described the following steps:

1. The quantitative exposure variable is discretized into K strata. We label these K strata as T₁, T₂,…, T_K. The midpoint of each stratum is computed using either the mean or median of the exposure variable for subjects who lay within the given stratum. Label these midpoints as $t_1,t_{2,}\dots ,t_K$.

2. Choose the jth of the K exposure strata.

3. For each subject in the sample, evaluate the GPS at the midpoint of the jth exposure stratum: $\text{GPS}(t_j,X)=r(t_j,X)$.

4. Block on the quintiles of $\text{GPS}(t_j,X)$, the GPS evaluated at the midpoint of the jth exposure stratum. To do so, divide subjects into five mutually exclusive strata using the quintiles of $\text{GPS}(t_j,X)$. We label these five blocking strata as ${\text{B}}_1^{(j)},{\text{B}}_2^{(j)},\dots ,{\text{B}}_5^{(j)}$. Note that this blocking is critical to the balance assessment. In formula (2) above, we are conditioning on subjects who have the same value of $\text{GPS}(t_j,X)$. As this is a continuous quantity, it is difficult to condition on it directly. Instead, by comparing subjects within quintiles of the this variable, we are creating subsets or strata of subjects who have approximately similar values of $\text{GPS}(t_j,X)$.

5. Define a binary exposure indicator variable according to whether or not a subject’s quantitative exposure variable lies within the jth stratum of the quantitative exposure variable: $Z_j=I(T\in T_j)$, where I is the indicator variable taking the value if the condition is true, and zero otherwise.

6. Given the jth exposure stratum (T_j) and a given baseline covariate, one then computes the difference in the mean of the covariate between subjects with Z_j = 1 and subjects with Z_j = 0 for subjects in the ith blocking stratum within the jth exposure stratum (B_i^(j), as defined in Step 4). One similarly computes the standard error of this difference in means. This is repeated for each of the five blocking strata (i = 1,…, 5).

7. Thus, for the jth exposure stratum (T_j) we have five differences in means (and associated standard errors) for each baseline covariate (one for each of the five blocking strata). For a given covariate and exposure stratum, one then computes a weighted difference in means, in which each of the five differences in means is weighted by the proportion of subjects within the given exposure stratum (T_j) who lie within each of the five blocking strata. From this weighted mean (and standard error), a t-test can be used to compare the mean of the covariate between those subjects in the jth exposure stratum and those subjects in the other exposure strata combined.

8. Steps 2 through 7 are repeated for all K exposure strata, resulting in one t-test for each of the K exposure strata.

The above process uses statistical significance testing to compare the distribution of baseline covariates between subjects in a given exposure stratum and subjects in the remaining exposure strata combined. Imai et al. criticized the use of statistical hypothesis testing for balance assessment.¹⁸ Among their criticisms is that balance is a property of a particular empirical sample and not a property of a hypothetical population from which the sample was drawn. Furthermore, using hypothesis testing to assess balance results in the ability to detect imbalance being confounded with the size of the sample. This can hamper comparison of balance between studies that had different sample sizes.

We propose that the above algorithm be modified to use standardized differences rather than statistical significance testing. This proposed modification reflects the increasing acknowledgment that, in the setting with binary treatments or exposures, the use of standardized differences is preferable to the use of statistical significance testing.^18,19 When used with binary treatments, the standardized difference is defined as

$$d=\frac{({\overline{x}}_{\text{treatment}}-{\overline{x}}_{\text{control}})}{\sqrt{\frac{s_{\text{treatment}}^2+s_{\text{control}}^2}{2}}}$$ (3)

for continuous covariates, where ${\overline{x}}_{\text{treatment}}$ and ${\overline{x}}_{\text{control}}$ denote the sample mean of the covariate in treated and untreated subjects, respectively, while $s_{\text{treatment}}^2$ and $s_{\text{control}}^2$ denote the sample variance of the covariate in treated and untreated subjects, respectively. For binary covariates, the standardized differences is defined as

$$d=\frac{({\hat{p}}_{\text{treatment}}-{\hat{p}}_{\text{control}})}{\sqrt{\frac{{\hat{p}}_{\text{treatment}}(1-{\hat{p}}_{\text{treatment}})+{\hat{p}}_{\text{control}}(1-{\hat{p}}_{\text{control}})}{2}}}$$ (4)

where ${\hat{p}}_{\text{treatment}}$ and ${\hat{p}}_{\text{control}}$ denote the prevalence or mean of the dichotomous variable in treated and untreated subjects, respectively.

We propose that the sixth and seventh steps of the above algorithm be modified as follows. In the sixth step, for a given baseline covariate and for the ith blocking stratum, one computes the mean of the covariate and its standard deviation (not its standard error) in subjects with Z_j = 1. One then repeats this calculation in those subjects with Z_j = 0. Using these calculated statistics, one then computes the standardized difference comparing the mean of the covariate between subjects with Z_j = 1 and subjects with Z_j = 0 within the ith blocking stratum. One then computes the absolute value of this term, to obtain the absolute standardized difference. One thus obtains five absolute standardized differences, one for each of the five blocking stratum. The seventh step in the above algorithm is modified by computing the mean of these five absolute standardized differences. Thus, for a given covariate, one obtains K mean absolute standardized differences, one for each of the K strata of the exposure variable.

2.3.2 Correlation-based diagnostics for use with GPS-based weighting

As stated above, our balance diagnostics are motivated by the property that $X\perp 1\{T=t\}|r(t,X)$.⁵ If two variables are independent of one another then the correlation between these two variables will be zero.²⁰ When using GPS-based weights, Zhu et al. suggested that the weighted correlation between the quantitative exposure variable and a given baseline covariate be used to assess whether weighting with GPS-based weights has produced a weighted sample in which the baseline covariate is independent of the continuous covariate. A similar approach was used by Fong et al. when they extended the CBPS to the setting with quantitative exposures.¹⁵ Zhu et al. suggested that the correlation between each covariate and the quantitative exposure be computed and that authors report the maximum absolute correlation coefficient and the mean absolute correlation coefficient. They also suggested that confounding between the exposure and the outcome is small when the average absolute correlation coefficient is less than 0.1.

3 Monte Carlo simulations of the performance of balance diagnostics for the GPS

We conducted a series of Monte Carlo simulations to examine the performance of balance diagnostics for use with the GPS.

3.1 Methods

3.1.1 Simulating a large super-population

We simulated baseline covariates and a quantitative exposure for a large population consisting of 1,000,000 subjects. Ten baseline covariates ($X_1-X_{10}$) were simulated for each subject from independent standard normal distributions. For each subject, a quantitative exposure variable was generated from the following linear model

$$T_i=0.25x_{1i}+0.50x_{2i}+0.75x_{3i}+1x_{4i}+1.25x_{5i}+1.50x_{6i}+1.75x_{7i}+2x_{8i}+2.5x_{9i}+3x_{10i}+{\varepsilon }_i$$

where ${\varepsilon }_i\sim N(0,{\sigma }^2)$.

Thus, increasing values of all eight of the baseline variables were associated with an increase in the mean exposure. Furthermore, the magnitude of the effect of the covariates on the mean exposure was progressively stronger. The value of ${\sigma }^2$ was chosen so that variation in the 10 baseline covariates would explain a desired proportion of the variation in the quantitative exposure (see below for the selected proportions).

3.1.2 Monte Carlo simulations

From the large super-population, we drew a random sample of 1000 subjects. The primary objective of this paper was to evaluate the performance of balance measures for use with the GPS. However, a secondary objective was to compare the relative balance induced by two different methods of estimating the GPS. Thus, in this random sample, we estimated the GPS using two different approaches. In the first approach, we used the OLS-based method described in Section 2.1 to estimate the GPS. In the first stage of this two-stage process, we used OLS regression to regress the observed quantitative exposure variable on all 10 measured baseline covariates. In the second stage of the two-stage process, we evaluated the conditional normal density function at the value of the exposure. We refer to this first approach as GPS-OLS, to highlight that OLS regression was used to estimate the conditional distribution of the exposure given the baseline covariates. In the second approach, we used the CBGPS method that was originally developed by Imai and Ratkovic¹⁴ for binary and categorical exposures and was subsequently extended by Fong et al. to quantitative exposures.¹⁵

The balance induced by the estimated GPS was determined using the methods described in Section 2. When using the blocking-based methods, the random sample was divided into five strata based on the quintiles of the quantitative exposure variable. Our rationale for using five strata was that this would result in approximately 200 subjects per stratum. Then, when we blocked on the quintiles of the GPS at the midpoint of the given exposure stratum, there would be approximately 40 subjects within each blocking stratum. These 40 subjects would then be divided into those who lay within the given exposure stratum and those who did not. As long as there was moderate overlap, we would have sufficient subjects to estimate stratum-specific means and variances with relatively acceptable precision. Thus, five standardized differences were estimated for each of the 10 covariates (one for each of the quintile-based comparisons). The process of drawing random samples of size 1000 from the super-population was conducted 1000 times. The average covariate balance was assessed by determining the mean standardized difference across the 1000 iterations of the simulation.

When using the correlation-based method with weighting using GPS-based weights, the Spearman correlation coefficient between each of the 10 baseline covariates and the quantitative exposure variable was computed. For each of the 10 covariates, we then determined the mean correlation coefficient across the 1000 iterations of the simulation. We then calculated the maximum and the mean of the absolute value of these mean correlations.

One factor was allowed to vary in the Monte Carlo simulations: the proportion of the variation in the quantitative exposure that was explained by variation in the 10 baseline covariates. We considered five values for this R²: 0.1 to 0.5 in increments of 0.1. We thus constructed five different super-populations. From each super-population we drew 1000 random samples, each of size 1000, and conducted the statistical analyses described above.

3.2 Results

3.2.1 Blocking-based diagnostics

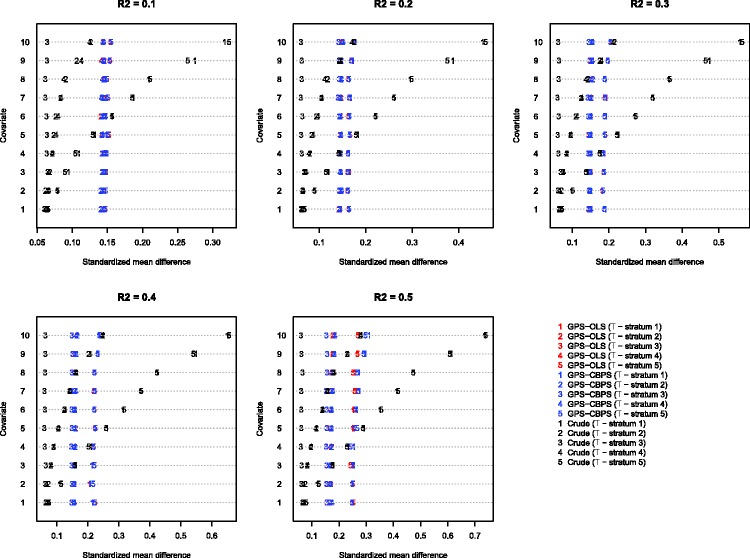
The results of the Monte Carlo simulations when using blocking-based diagnostics are reported in Figure 1. The figure consists of five panels, with one panel for each of the scenarios defined by the proportion of variation in the quantitative exposure that is explained by variation in the baseline covariates. Each panel contains a series of dot charts. Within each panel there is a series of 10 horizontal lines, one for each of the 10 baseline covariates. On a given horizontal line are 15 dots (each represented by a number). There are five dots for the five mean absolute standardized differences resulting from the use of GPS-OLS (one for each of the comparisons in which a given exposure stratum was compared with the other four exposure strata combined). There are five dots for five mean absolute standardized differences resulting from the use of CBGPS. Finally, there are five dots for the mean absolute standardized differences that were produced without incorporating the GPS. These are simply the standardized differences comparing subjects in a given exposure stratum to subjects in the remaining strata combined (these are measures of the initial crude imbalance). The plotting symbols used (“1,” “2,” “3,” “4,” and “5”) denote the stratum of the quantitative exposure that is being compared to the remaining exposure strata combined (“1” denotes the lowest quintile of exposure, while “5” denotes the highest quintile of exposure). In examining the panels, remember that the covariates had an increasingly strong effect on the mean exposure.

Figure 1.

Blocking-based standardized mean differences.

In examining Figure 1, one observes that the method of estimating the propensity function (OLS vs. CBGPS) had minimal impact on balance. As the proportion of variation in the quantitative exposure explained by the covariates increased (i.e., as R² increased), the number of covariates for which there was initial imbalance tended to increase. When initial (or crude) imbalance was observed, it tended to be between subjects in the lowest quintile of exposure compared to subjects in the upper four quintiles combined or between subjects in the highest quintile of exposure compared to subjects in the lower four quintiles combined. As either R² or the magnitude of the covariate on mean exposure increased, we were also more likely to observe imbalance between the second stratum and the remaining strata and between the fourth stratum and the remaining strata. Blocking on the quintiles of the GPS tended to reduce covariate imbalance between subjects in one of the extreme exposure strata and subjects in the remaining four exposure strata combined.

A limitation of blocking-based diagnostics becomes apparent as one examines Figure 1. This is particularly evident when examining the middle exposure stratum (stratum “3”). The initial or crude balance when comparing subjects in this middle exposure stratum to the other four strata combined is almost always minor (standardized differences less than 0.10). This is because differences between the middle stratum and the extreme exposure strata tend to be minimized when these extreme strata are combined. For this specific comparison, the imbalance was amplified when blocking on the GPS strata.

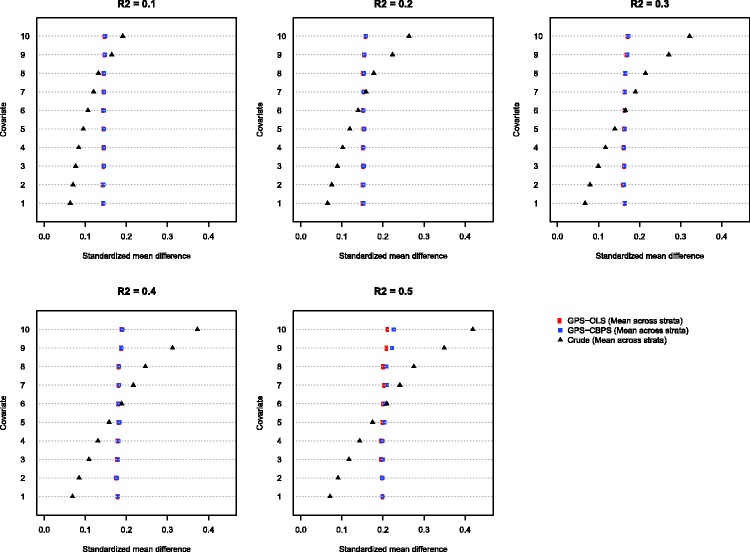
The information presented in Figure 1 is further summarized in Figure 2. Figure 2 is similar in structure to Figure 1, except that the five stratum-based measures of balance for a given method (GPS-OLS, CBGPS, or crude/unadjusted) have been replaced by the mean of these five measures of balance. In this figure, we see that the mean standardized difference across the five exposure strata was approximately 0.15 when blocking on the GPS when the R² was 0.3 or less. It was approximately 0.20 when the R² was equal to 0.50.

Figure 2.

Mean blocking-based standardized mean differences across the five exposure strata.

3.2.2 Correlation-based diagnostics

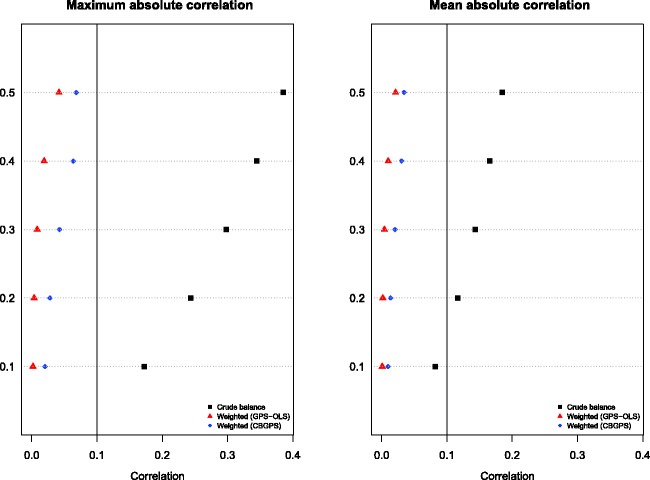
The results for the correlation-based diagnostic methods for use with GPS-based weighting are summarized in Figure 3. The left panel depicts the maximum absolute value of the mean correlation coefficients across the 10 covariates for each of the five scenarios defined by the R² value. The right panel depicts the mean absolute value of the mean correlation coefficients across the 10 covariates for each of the five scenarios. On each panel we have superimposed a vertical line at 0.1, which Zhu et al. suggested could be used as a threshold denoting minimal confounding.²¹ The use of GPS-OLS tended to result in slightly better balance than did the use of CBGPS. However, differences between these two methods were minor. In the figure we have also reported the mean and maximum absolute correlation between the covariate and the quantitative exposure without accounting for the GPS. This provides a measure of the magnitude of the initial degree of confounding between exposure and the baseline covariates prior to adjustment for the GPS. We observe that the use of weighting with the GPS has substantially reduced the magnitude of confounding.

Figure 3.

Maximum and mean absolute correlation across the 10 covariates (GPS-weighted analyses).

4 Case study

We provide an empirical example to illustrate the application of the proposed methods for assessing covariate balance.

4.1 Data and analyses

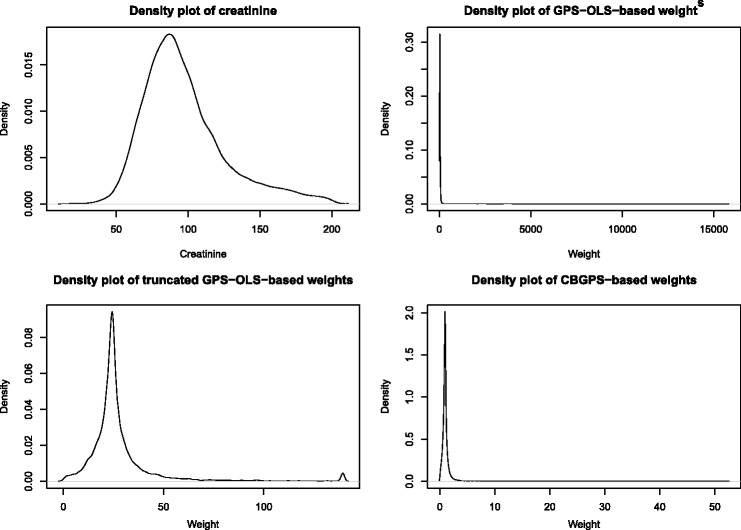
We used data consisting of 10,024 patients hospitalized with an AMI in Ontario, Canada, between April 1999 and March 2001. These data were collected as part of the Enhanced Feedback for Effective Cardiac Treatment (EFFECT) Study.²² We used the value of the patient’s first measured creatinine level as the quantitative exposure. Due a small proportion of subjects with extreme creatinine values, we excluded those subjects whose creatinine values exceeded the 95th percentile of creatinine. The final analytic sample consisted of 9523 subjects. A non-parametric estimate of the distribution of creatinine is described in the top-left panel of Figure 4. The distribution of creatinine was non-normal and was positively skewed.

Figure 4.

Distribution of creatinine and GPS-based weights.

The propensity function was estimated using two different methods. First, it was estimated by regressing average creatinine on a set of 32 baseline covariates using a linear regression model estimated using OLS. Second, it was estimated using the CBGPS method. The 32 baseline covariates included demographic characteristics (age and sex), vital signs on admission (systolic and diastolic blood pressure, respiratory rate, and heart rate), initial laboratory values (white blood count, hemoglobin, sodium, glucose, and potassium), signs and symptoms on presentation (acute congestive heart failure and cardiogenic shock), classic cardiac risk factors (family history of heart disease, current smoker, history of hyperlipidemia, and hypertension), and comorbid conditions (chronic congestive heart failure, diabetes, stroke or transient ischemic attack, angina, cancer, dementia, previous AMI, asthma, depression, hyperthyroidism, peptic ulcer disease, peripheral vascular disease, previous coronary revascularization, history of bleeding, and aortic stenosis). For both estimation approaches, the effect of each continuous covariate was modeled using restricted cubic splines with four knots.²³ To do so, for a given continuous covariate X, one defines t₁, t₂, t₃, and t₄ to be the 0.05, 0.35, 0.65, and 0.95 quantiles of the distribution of X. One then defines three functions of the covariate X

$$\begin{array}{l}{X}_1=X\\ X_2=(X-t_1{)}_{+}^3-(X-t_3{)}_{+}^3(t_4-t_1)/(t_4-t_3)+(X-t_4{)}_{+}^3(t_3-t_1)/(t_4-t_3)\\ X_3=(X-t_2{)}_{+}^3-(X-t_3{)}_{+}^3(t_4-t_2)/(t_4-t_3)+(X-t_4{)}_{+}^3(t_3-t_2)/(t_4-t_3),\\ \text{where }(u{)}_{+}=\{\begin{array}{l}uu>0\\ 0u\le 0\end{array}\end{array}$$

One then includes X₁, X₂, and X₃ in the regression model in place of X. The R² statistic for the linear model estimating using OLS was 0.278, while the adjusted R² statistic was 0.274.

The balance of each of the 32 baseline covariates was assessed using the methods described in Section 2, whose performance was evaluated in Section 3. Due to a few subjects having very large GPS-OLS weights, this set of weights as truncated at the 99th percentile. However, even after truncation, some subjects still had very large weights. In contrast to this, the weights obtained using the CBGPS tended to be better behaved (although 1% of the sample had CBGPS weights that lay between 3.54 and 52.55). Non-parametric estimates of the distribution for the original GPS-OLS weights, the truncated GPS-OLS weights, and the CBGPS-based weights are described in Figure 4. Even with truncation, there were more subjects with larger weights when GPS-OLS was used compared to when the CBGPS was used.

4.2 Results

4.2.1 Blocking-based methods

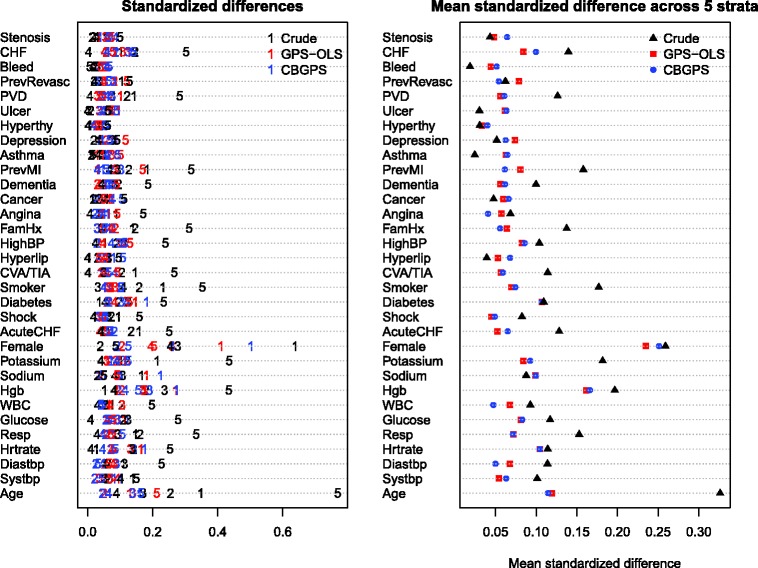
The balance of the 32 baseline covariates that was induced by blocking on the GPS is described in Figure 5. The left panel of the figure has a structure similar to that of Figure 1, while the right panel has a structure similar to that of Figure 2. In each panel, there are 32 horizontal lines, each representing one of the 32 baseline covariates. Initially, several covariates (congestive heart failure, peripheral vascular disease, previous AMI, family history of heart disease, current smoker, sex, potassium, hemoglobin, respiratory rate, and age) displayed evidence of imbalance. For many of these covariates, the mean (or prevalence) of the covariate differed between subjects in the highest quintile of creatinine and subjects in the lower four quintiles. After incorporating the GPS, balance on these variables improved (although the improvements for sex were more minor). In examining the right panel two observations are apparent. First, differences were minimal between GPS-OLS and CBGPS in terms of the balance that was induced. Second, for few covariates (e.g., asthma) mean balance was better prior to adjustment than it was after incorporating the GPS.

Figure 5.

Balance in case study across the strata of creatinine.

4.2.2 Correlation-based methods with GPS-based weighting

To provide an indication of the magnitude of the initial degree of imbalance, we estimated the Spearman correlation coefficient to assess the correlation between creatinine and each of the 32 covariates. The absolute value of crude Spearman correlation coefficients ranged from 0 to 0.29. The median was 0.09, while the 25th and 75th percentiles were 0.04 and 0.12, respectively.

For each of the two methods (use of OLS-based weights and CBGPS-based weights), we estimated 32 correlation coefficients (the weighted Spearman correlation coefficient between creatinine and each of the covariates). When using the GPS-OLS-based weights, the mean and maximum absolute correlation coefficients were 0.02 and 0.06, respectively. The median (25th percentile–75th percentile) was 0.02 (0.01–0.03). When using the CBGPS-based weights, the mean and maximum absolute correlation coefficients were 0.01 and 0.08, respectively. The median (25th percentile–75th percentile) was 0.01 (0–0.02). Both the use of GPS-OLS weights and the use of CBGPS-based weights resulted in a weighted sample in which there was at most a weak correlation between the quantitative exposure and each of the 32 baseline covariates. Based on a paired t-test, the mean absolute Spearman’s correlation coefficient between the covariates and the quantitative exposure did not differ between these two methods (P = 0.07).

5 Discussion

In the current study, we described and evaluated balance diagnostics for use with the GPS. We described two methods: one based on blocking on the GPS and the other based on correlations. The blocking-based method does not require that the GPS be used in a specific way when estimating the dose–response function, while the correlation-based approach is for use with weighting using the GPS. Balance diagnostics play a critical role in any propensity score analysis, as they allow the analyst to assess whether the propensity score model (or the propensity function) has been adequately specified so as to induce balance on measured covariates. While balance diagnostics have been extensively described and are used frequently when using the propensity score with dichotomous treatments or exposures (e.g., treated vs. control), there is a paucity of information as to how to assess covariate balance when using the GPS with quantitative exposures. The methods described in this paper fill this gap in the literature.

Our blocking-based method for balance assessment was motivated by an approach suggested by Hirano and Imbens⁵ and which was subsequently used by Bia and Mattei.⁶ Their approach, described in greater detail in Section 2, was based on blocking on the quintiles of the GPS estimated at the midpoint of strata of the quantitative exposure variable. While this approach provided a motivation for our proposed stratification-based methods, we did not consider this approach in the current study for the reasons provided in Section 2. The use of blocking on the GPS in this approach is crucial and is reminiscent of the use of stratification on the propensity score when used with binary treatments. When stratifying on the propensity score with binary treatments, outcomes between treated and control subjects within strata defined by quantiles of the propensity score are compared. In the initial application of this method, Rosenbaum and Rubin stratified on strata defined by the quintiles of the propensity score.¹¹ By doing so, the analyst is comparing outcomes between subjects with an approximately similar distribution of baseline covariates (because their propensity score lie in the same quintile). Similarly, in the blocking-based approach, one blocks on the quintiles of the GPS, allowing for the comparison of baseline covariates between those who have approximately equal values of the GPS (evaluated at the midpoint of the exposure stratum), thus permitting one to evaluate the condition expression described by formula (2).

Our blocking-based diagnostic method was a modification of an approach suggested by by Hirano and Imbens⁵ and by Bia and Mattei.⁶ As described above, their original approach was based on statistical significance testing to compare covariates between exposure strata after blocking on the GPS. Our modification was informed by Imai et al.’s criticism of the use of statistical hypothesis testing for balance assessment.¹⁸ Our modification of this blocking-based approach employed standardized differences, which do not use statistical hypothesis testing and only make reference to the study sample and not to a hypothetical population. Furthermore, the proposed method is a modification of the conventional standardized difference, which is increasingly being recognized as the preferred method for balance assessment when the propensity score is used with dichotomous exposures.

There are a few limitations to the use of the blocking-based diagnostic method that warrant being highlighted. The first limitation is its reliance on stratification. Indeed two choices about stratification must be made. The first decision is that one must decide into how many strata to stratify subjects based on the quantitative exposure variable. The second decision is that one must decide into how many strata to stratify subjects based on the GPS evaluated at the midpoint of an exposure stratum when blocking on the GPS. We decided to use five strata for each of these two stratifications. However, it must be acknowledged that the choice of the number of strata is relatively arbitrary. We decided to use five strata based on the quintiles of the distribution for both of these stratifications. Our choice of five strata for blocking on the GPS reflects the decision made by previous authors.^5,6 Subsequent research is required to determine the trade-offs between different choices for the number of strata. The second limitation to the blocking-based method is that it is difficult to summarize the balance diagnostics. Figure 1 is relatively difficult to synthesize. Figure 2 permits a succinct summarization of the balance achieved. However, averaging balance across strata can mask imbalance in specific comparisons. The third limitation to the blocking-based method is that creating strata based on the quantitative exposure variable can mask differences in the distribution of covariate between exposure categories. This may be particularly evident when comparing subjects in the middle stratum to subjects in the more extreme strata. Differences between subjects in the lower extreme strata and those in the upper extreme strata may cancel out, resulting in the combination of these strata appearing to be no different from the middle stratum. In comparison to blocking-based balance assessment, the use of weighted correlation is straightforward and requires that fewer decisions be made. Balance can be succinctly summarized by describing the mean and maximum correlation coefficients.

Some of the results of our simulations were, at first glance, surprising. When using the blocking-based balance assessment methods, we observed that the mean blocking-based standardized difference across the five exposure strata tended to range between approximately 0.15 and approximately 0.20 (Figure 2). It bears stressing that when assessing balance we had fit the true propensity score model that had been used to simulate the data. In the setting of a binary treatment, some authors suggest that standardized differences that exceed 0.25 can be classified as “large,”²⁴ while other authors suggest that adequate balance has been achieved when standardized differences are less than 0.10.^7,25 By the former standard, the blocking-based balance diagnostics found that balance was adequate; however, by the latter standard, residual imbalance has been detected. In previous research, we have demonstrated that the ability to induce balance varies across the different propensity score methods.²⁶ In particular, stratification on the propensity score induced poorer balance than did matching or weighting using the propensity score. A similar pattern was observed in our simulations. When using GPS-based weighting, the weighted correlations between the covariates and the quantitative exposure were small (Figure 3), whereas modest imbalance was observed using the stratification-based diagnostics (Figure 2). Our research suggests that, when using the stratification-based diagnostics, a threshold of approximately 0.20 could be used to indicate whether the GPS has been adequately specified.

There are certain limitations to the current study. First, the evaluation of the balance diagnostics was conducted using Monte Carlo simulations and empirical analyses. For pragmatic reasons, we were constrained to examine a limited number of scenarios in our simulations. It is possible that results would differ under different data-generating processes. Second, we did not examine the performance of estimation of the dose–response function when using the GPS. Examination of the accuracy of estimation of the dose–response function (bias, precision, etc.) merits consideration in a paper focused on that topic. The balance diagnostics proposed in the current study can be employed regardless of the nature of the outcome. These balance diagnostics can be used with continuous, binary, and time-to-event outcomes. However, examining the accuracy of the dose–response function would require that each type of outcome be considered separately. We have focused on balance diagnostics as these serve an important role in all propensity score analyses. We refer to reader to a separate paper that examines the performance of methods to use the GPS to estimate the effect of quantitative exposures on binary outcomes.²⁷

We considered two different methods of estimating the GPS: OLS regression and the CBPS algorithm. We found that the method of estimating the GPS had minimal impact on the subsequent balance of the observed covariates.

In summary, balance diagnostics are a critical component of any propensity score analysis. We have described balance diagnostics for use with the GPS. These methods should be a routine part of any study that uses the GPS to estimate the effect of quantitative exposures. When using GPS-based weighting, we suggest that the correlation-based diagnostics be used as they appeared to have better performance and are simpler to summarize and report.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This study was supported by the Institute for Clinical Evaluative Sciences (ICES), which is funded by an annual grant from the Ontario Ministry of Health and Long-Term Care (MOHLTC). This research was supported by an operating grant from the Canadian Institutes of Health Research (CIHR) (MOP 86508). Austin was supported by a Career Investigator award from the Heart and Stroke Foundation. The Enhanced Feedback for Effective Cardiac Treatment (EFFECT) data used in the study was funded by a CIHR Team Grant in Cardiovascular Outcomes Research (grant numbers CTP 79847 and CRT43823).