Solid phantom recipe for diffuse optics in biophotonics applications: a step towards anatomically correct 3D tissue phantoms

Abstract

We present a tissue mimicking optical phantom recipe to create robust well tested solid phantoms. The recipe consists of black silicone pigment (absorber), silica microspheres (scatterer) and silicone rubber (SiliGlass, bulk material). The phantom recipe was characterized over a broadband spectrum (600-1100 nm) for a wide range of optical properties (absorption 0.1-1 cm⁻¹, reduced scattering 5-25 cm⁻¹) that are relevant to human organs. The results of linearity show a proper scaling of optical properties as well as the absence of coupling between the absorber and scatterer at different concentrations. A reproducibility of 4% among different preparations was obtained, with a similar grade of spatial homogeneity. Finally, a 3D non-scattering mock-up phantom of an infant torso made with the same recipe bulk material (SiliGlass) was presented to project the futuristic aspect of our work that is 3D printing human organs of biomedical relevance.

1. Introduction

Tissue-mimicking optical phantoms play a crucial role in characterization, optimization, routine calibration and validation of biophotonics systems [1–3]. The phantoms can be made both in solid or liquid forms, however, solid phantoms have some advantages such as long shelf life, can be molded to realistic organ shapes, stable optical properties (absorption-µ_a, reduced scattering-µ’_s), and easy handling for routine instrument validation. In general, a phantom consists of three main components: bulk material (water, epoxy resin, silicone, agar), absorber (India ink, printer toner, black silicone), and scatterer (intralipid, titanium oxide, aluminum oxide, silica microspheres) [4–8]. The advent of silicone rubber has enabled the phantoms to mimic not only optical but also mechanical properties to some extent [7,9]. Importantly, the advancement of 3D printing technology has enabled the printing of realistic human organs from X-ray CT scans [10]. The recent work of Larsson et al. showed a 3D phantom of the upper body of an infant which includes lung, heart, bones, and muscles. This work used a liquid phantom recipe to obtain realistic optical properties [11]. Taking this technology to solid phantoms was achieved by Dempsey et al. who created a 3D printed brain phantom [12]. The recent work of Kennedy et al. used a room temperature vulcanizing silicone rubber as a bulk material and a special absorber to mimic optical properties of water and lipid absorption [13]. A recent review of tissue-mimicking optical phantoms can be found in Ref [8].

Multiple phantom recipes are thus found in literature, indicating remaining challenges to find a phantom material that is ideal for a wide range of needs in biophotonics. Possible limiting factors for the acceptance of some of the published phantom recipes include that the recipe does not provide a detailed manufacturing procedure or a systematic study of phantom behavior over a wide range of absorber and scatterer concentrations. In addition, liquid phantoms are cumbersome to handle especially for realistic tissue geometries and typically have a short shelf life. An example of a phantom developed for a specific purpose is given by Maughan Jones et al. They proposed an improved method for phantom manufacturing using silica microsphere as a scatterer for OCT applications. This phantom was thereby characterized at a single wavelength only [4]. Similarly, multiple groups have proposed various manufacturing procedures, some proposed complex methods to ensure absorber and scatterer uniformity [14,15], while some simpler recipes are also available [9,13,16]. Yet, all of these methodslack one of the following aspects:

• i) A detailed protocol for the procedure of phantom manufacturing and the phantom recipe.
• ii)A characterization of the behavior of the phantom over a wide range of absorber and scatterer concentrations relevant to the tissue optical properties.
• iii)A broadband (600-1100 nm) optical characterization of the phantoms.
• iv)Characterization of the phantoms in terms of reproducibility, shelf life, and homogeneity.

The first (i) point takes care of robust manufacturing procedure, whereas the second point ensures the phantoms have linear optical behavior over the entire range of absorber and scatterer concentrations. Point (iii) makes sure that point (ii) was tested over a broad wavelength range, while (iv) ensures the phantoms are optically reproducible and homogeneous over the entire phantom volume. In addition, thorough consideration of phantom ingredients is important in order to facilitate the best possible properties. These points form the building block to provide a well-tested, robust solid phantom that could be manufactured by any group interested in optical properties relevant to human organs.

In our opinion there is still a need for a recipe for a good 3D tissue–mimicking phantom that is robust and tested over the wide range of optical properties covering most of the human organs, preferably characterized over the entire therapeutic wavelength range to benefit the wide community in biophotonics. The aim of this work was to fulfill this need. The study was designed to cover optical properties (absorption 0.1-1 cm⁻¹, reduced scattering 5-25 cm⁻¹) relevant to various organs of the human body. The optical characterization was performed using photon time-of-flight diffuse optical spectrometer (pTOFS) which has been validated in various phantom and clinical studies [17]. Time domain measurements can inherently disentangle absorption and scattering properties, providing reliable results of both absorption and scattering properties of the phantoms [18–21]. To the best of our knowledge, this was the first study that covers all the above-mentioned challenges to provide an integrated recipe solution that could provide 3D solid phantoms in biomedical optics. To emphasize the cause, a realistic anatomically correct 3D phantom of an infant's torso was provided in the results section.

2. Materials and methods

2.1 Phantom recipe

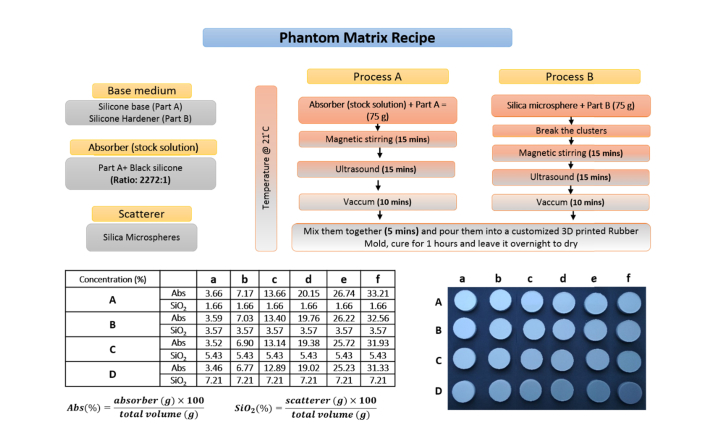
A detailed description of the phantom ingredients, the method to make the phantoms, and the concentration of absorber and scatterer for different optical properties are shown in Fig. 1. The bulk material of the phantom was made of SiliGlass which is a transparent silicone rubber procured from MBFibreglass (PlatSil SiliGlass). SiliGlass is a two-component cured room-temperature-vulcanizing (RTV) silicone. It consists of two liquid parts, part A (base material) and part B (hardener). When the two parts are mixed together in a 1:1 ratio, the mixture cures to a solid at room temperature within 1 hour. Compared to other silicone based rubbers, SiliGlass is a clear medium instead of becoming bluish or turbid on curing. The scattering contribution from the silicone matrix needs to be negligible for better control of scattering properties in the produced phantoms. Also, low scattering regions, such as the cerebrospinal fluid (CSF) in the human head can be accurately modeled. The absorber employed was black silicone pigment (Polycraft Black Silicone Pigment) compatible with silicone and silica microspheres (440345, Sigma-Aldrich) were used to obtain the desired reduced scattering. The pure absorber was highly absorbing hence it was diluted in Part A (silicone base) at a ratio of (2272:1), here onwards whenever the absorber is mentioned it is the diluted (2272:1) stock solution of black silicone pigment in Part A.

Fig. 1.

The key ingredients (top left), the phantom recipe with detailed manufacturing procedure (top right), a picture of the phantom matrix (bottom right) produced and their respective absorber (stock solution) and scatterer percentage concentrations (bottom left).

The phantom preparation includes two parallel processes. One part comprises of mixing part A of the SiliGlass and the absorber (stock solution). The absorption properties of the phantoms were tuned by changing the quantity of absorber (stock solution) and part A with their total sum kept at constant value (75 g). The second process constitutes mixing part B of the SiliGlass with the microspheres. Both processes follow a similar procedure as shown in Fig. 1. Process B includes an extra step where the silica microspheres were disaggregated manually for 15 minutes with a spatula prior to the mixing with a magnetic stirrer (two magnetic beads (25x8 mm), speed-5, VWR VMS-C7). In general, both processes start with magnetic stirring for 15 minutes followed by ultrasonication (power-5, VWR USC500THD, 45 kHz) for 15 minutes. The entire preparation of the phantoms produced in this study was carried out at a controlled temperature (21° C) to avoid temperature-related reactions and extensive bubbling in the vacuum chamber employed for degassing. Following the bubble removal in a vacuum, both parts were mixed together and stirred manually for 5 minutes to ensure uniformity of the phantom mixture. The final step was to pour the mixture in the phantom cast, which for the characterization was a 3D printed cylinder with large diameter (10 cm). Subsequent measurements were performed in transmittance geometry. Therefore, the phantoms were made with large diameter (10 cm) to avoid boundary effects and granting use of a slab model [22]. The thickness of the phantoms was 18 mm. This value was chosen as a good compromise between the validity of the Diffusion equation and the signal level over the entire spectrum. A previous study on the validity of the Diffusion equation for time-resolved measurements at different source detector distances is reported in reference [23]. In total 24 phantoms were created with a matrix combination of 6 absorption values and 4 reduced scattering values as shown in Fig. 1. For a convention we used small alphabets (a, b, c, d, e, f) for the absorption series and capital letters (A, B, C, D) for the scattering series. The exact values of the absorber (stock solution) and scatterer percentage concentrations used for the entire phantom matrix are tabulated in the table of Fig. 1.

2.2 Instrumentation, measurement protocol, data analysis

A time-domain diffuse optical spectrometer was used for the characterization of the phantoms. The spectrometer is described in detail elsewhere [17] and briefly described here. The setup consists of a pulsed supercontinuum laser (SC450, Fianium, UK) coupled to a Pellin Broca prism for wavelength selection. Light between 600 and 1100 nm was wavelength-scanned by rotating the prism and coupled into a 50 µm fiber. Depending on the wavelength, the bandwidth of the laser was varying between 2 - 6 nm. The fiber coupled light was injected into the tissue phantom. The diffused light from the phantom was collected in transmittance geometry using a fiber (core 1 mm, 0.39 NA) set on the opposite side of the phantom on the very same axis. The light transmitted to the other end of the fibre was focused on a silicon photomultiplier (SiPM) [24]. The instrument used in the present study was built by Politecnico di Milano and was a lab version of the portable system described in Ref [17]. The system has since previously been characterized, tested, validated and employed in various phantom design, tissue chromophore characterization and clinical studies [22,25–27]. The use of well-validated time-domain instrument adds reliability to the phantom recipe as it inherently disentangles absorption and reduced scattering, thus avoiding coupling between optical properties.

The measurements of the tissue phantoms were conducted in transmission geometry. The source-detector distance of the phantom was thereby 18 mm. The measurements were repeated 3 times of 1.0 s acquisition for each wavelength over the entire broadband range (600-1100 nm) at steps of 20 nm. All phantoms were measured in the same session to minimize instrument error and the instrument response function (IRF) was taken before and after the measurement session.

The acquired temporal curves were summed over repetitions and were analyzed using the semi-infinite slab model of the diffusion equation with extrapolated boundary conditions [28], [29]. The theoretical curves were convolved with the IRF and a nonlinear Levenberg-Marquardt algorithm was used for residual minimization between the theoretical and experimental data to extract optical properties (µ_a, µ’_s). The curve fitting was performed from 80% of the rising edge to 1% of the falling edge of the acquired temporal curves. A home-made fully automated software was used to automatize the entire fitting procedure over the broadband range for 24 phantoms.

3. Results and discussion

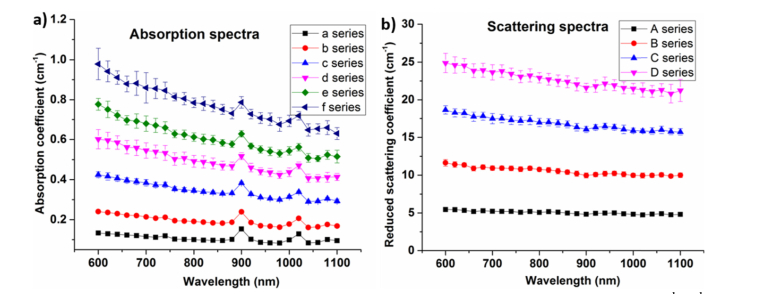
The various results presented in this work followed a protocol similar to the MEDPHOT protocol, well-established and agreed by 21 European laboratories for assessment of time domain diffuse optical instrument performance [1]. This rigorous protocol enabled the phantom recipe to be tested for various parameters like linearity, optical properties coupling, reproducibility and homogeneity. The obtained optical properties of the phantoms are shown in Fig. 2(a) for the absorption series, and Fig. 2(b) for the scattering series of the entire phantom matrix. The optical properties were extracted by the time domain instrument using the method discussed in the previous section. The coefficient of variation (CV) which is defined as the ratio of standard deviation to mean was used to determine the dispersion in the estimated optical properties. The CV of the absorption series was found to be less than 4% which was the expected CV of the time domain instrument used in this study and also partially due to the change in total volume of the phantom due to changing volume of the added scatterers within each series. The silicone peaks at 910 nm and 1020 nm are evident from all absorption spectra. Figure 2(b) shows the reduced scattering coefficient for different scattering series. As expected, the reduced scattering values decrease with increasing wavelength. A slight increase in scattering spectrum at 900 nm was observed which could be caused by some residual absorption-to-scattering coupling due to the model related to the absorption change at 900 nm or to the increased bandwidth effect [22,30] caused by the wider laser bandwidth. The CV of all scattering series was found to be less than 4%.

Fig. 2.

a) Average absorption spectra of all the scattering phantoms with fixed absorption, and b) average reduced scattering spectra of all the absorption phantoms with fixed reduced scattering coefficients. The error bar represents the standard deviation of the spectra in a series.

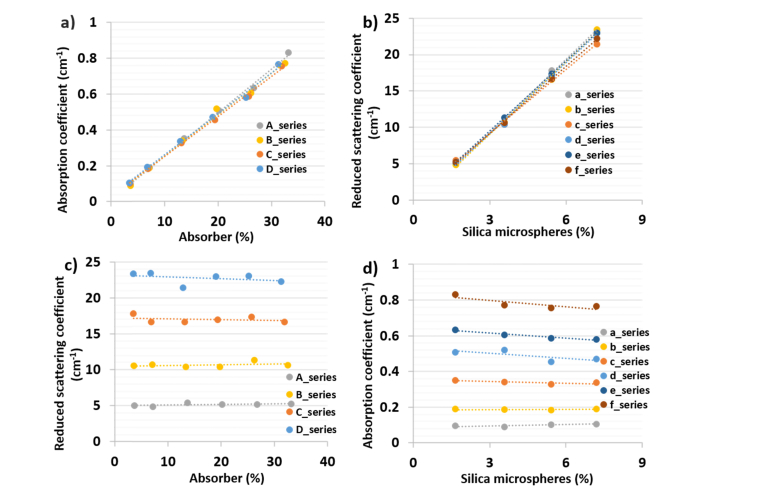
As mentioned in the introduction, one of the novelties of this work is to provide a phantom recipe that is well tested for its linear behavior over the wide range of absorber and scatter concentrations. Figure 3a plots the change in absorption for different concentrations of absorber solution at 820 nm. The absorption scales linearly with increasing absorber concentration. The same plot was repeated for reduced scattering at different scatter concentrations (Fig. 3b) at 820 nm. There was a linear change in optical properties with changing concentration of absorber or scatterer within the limits of the instrument’s CV. The 820 nm was chosen for two reasons: this wavelength lies around the mid-point of the range of observed wavelengths and is one of the key wavelengths in gas in scattering media absorption spectroscopy (GASMAS) technique. GASMAS has been an emerging non-invasive technique to monitor gas concentration in human cavities like sinus, lung, etc [31–33]. One of our main projects for the tissue phantoms developed is to develop a method to measure oxygen in the lung of 3D printed infant phantom using GASMAS [11], [34]. The reference gas, water vapor, has an absorption line at 820 nm, which prompted us to choose this wavelength. In conjunction with the linearity plot at 820 nm (Fig. 3(a), 3(b)), a table containing linearity parameters (slope, y-intercept) for each series over the broadband range is presented (Table 1). This enables the user to fabricate optical phantoms with well characterized deterministic optical properties. The slope and intercept values are characterized over a limited range of optical properties (absorption 0.1-1 cm⁻¹, reduced scattering 5-25 cm⁻¹) relevant to human tissues and caution should be used for values beyond this range that were not characterized in this study. Using Table 1, for a given series, users can compute:

Fig. 3.

Results of linearity tests at 820 nm a) absorption linearity as a function of added absorber b) scattering linearity as a function of added scatterers c) scattering properties of phantoms for different amount of absorber d) absorption properties of phantoms for different amount of added scatterers.

Table 1. Linearity parameters (slope and intercept) of phantom matrix over the broadband range (600-1100 nm).

Wavelength λ (nm)	Parameters	Absorption Linearity				Reduced scattering Linearity
		A	B	C	D	a	b	c	d	e	f
600	slope	0.031	0.028	0.029	0.027	3.70	3.72	3.30	3.44	3.79	3.22
	intercept	0.015	0.041	0.025	0.056	−1.26	−1.57	0.15	−0.53	−0.93	0.47
700	slope	0.028	0.026	0.024	0.024	3.54	3.53	3.11	3.43	3.43	3.01
	intercept	0.016	0.033	0.042	0.053	−1.23	−1.37	0.28	−1.00	−0.56	0.31
800	slope	0.024	0.024	0.023	0.024	3.36	3.34	2.97	3.30	3.26	3.15
	intercept	0.018	0.026	0.029	0.032	−0.81	−1.04	0.33	−0.79	−0.31	−0.37
820	slope	0.024	0.023	0.022	0.023	3.36	3.33	2.93	3.23	3.22	3.08
	intercept	0.011	0.024	0.026	0.033	−0.82	−0.96	0.41	−0.53	−0.15	−0.05
900	slope	0.022	0.021	0.021	0.022	3.05	3.10	2.86	3.16	3.14	2.97
	intercept	0.075	0.094	0.087	0.090	−0.49	−0.77	0.09	−0.93	−0.48	−0.40
1000	slope	0.021	0.019	0.020	0.021	3.06	3.09	2.80	3.02	3.18	2.96
	intercept	0.020	0.041	0.038	0.044	−0.56	−0.87	0.30	−0.47	−0.66	−0.37
1100	slope	0.019	0.018	0.018	0.019	3.02	3.11	2.62	3.01	3.33	2.76
	intercept	0.023	0.044	0.045	0.046	−0.50	−1.02	0.76	−0.43	−1.07	0.12

$$\text{Expected absorption coefficient}({\text{µ}}_{\mathrm{a}})=slope*Absorber (\%)+intercept$$

$$\text{Expected reduced scattering coefficient} ({{\mathrm{\mu }}_{\text{s}}}^{\prime })=slope*Scatter(\%)+intercept$$

Figure 3(c), 3(d) illustrate the dependency of reduced scattering coefficient on absorber concentration and vice versa. The straight lines observed in these plots confirm the absence of any chemical reaction between the scatterer and absorber. The slight coupling of absorption to scatterer concentration observed in Fig. 3(d) (especially for the f-series) relates to the change in total volume of the phantom due to increasing scatterer concentration and may be partly due to no longer fulfilling the assumptions of the diffusion approximation for high absorption (μ_a ≈0.8 cm⁻¹) and low reduced scattering (μ_s’ ≈5 cm⁻¹).

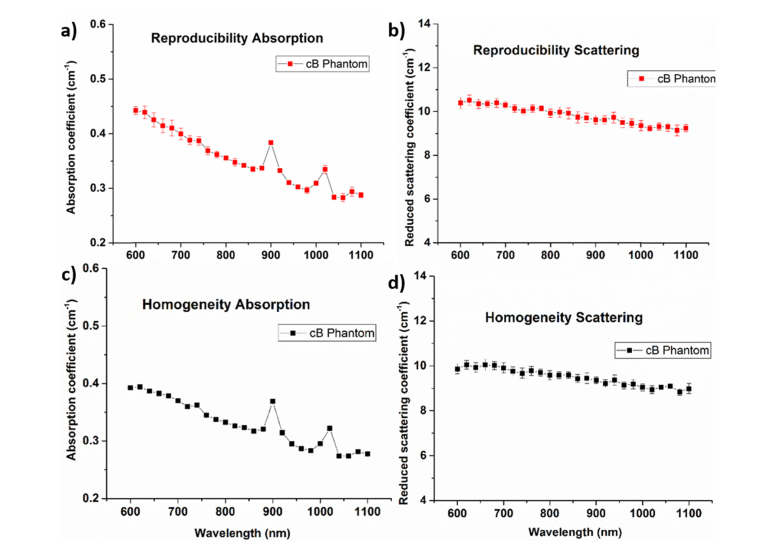
A key feature of a robust recipe is to ensure that the outcome is insensitive to irrelevant parameters like the person who made the phantom, the day it was produced, the batch of raw material used, etc. To this end, a reproducibility test was conducted by manufacturing four phantoms (series code: cB) on different days by different people using a different batch of bulk material. Figure 4(a), 4(b) show the absorption and reduced scattering spectra, respectively, of the same phantom (series code: cB) produced under different conditions. Though the CV was found to be slightly higher in the shorter wavelengths, the overall CV of around 4% reaffirms the robustness of the recipe. Finally, a test to confirm the homogeneity of the phantom (series code: cB) was carried out by measuring optical properties at different points on the same phantom surface. Five points on the phantom surface were chosen, one in the middle and four points were around the midpoint of the phantom top surface (Fig. 4(c) and 4(d)). Similar to the reproducibility test, the CV of the homogeneity test was well below 4%, which confirms the homogenous nature of thek sample. A long term stability of the phantom was performed by measuring phantom (cB) 3 times in the last 5 months and the results showed that the phantom were fairly stable with a CV close to 5% with more variation in the short wavelength range.

Fig. 4.

Reproducibility test a) absorption reproducibility, b) reduced scattering coefficient reproducibility of the cB phantom. Homogeneity test results of absorption (c) and reduced scattering (d) both tests were found to have CV less than 4%.

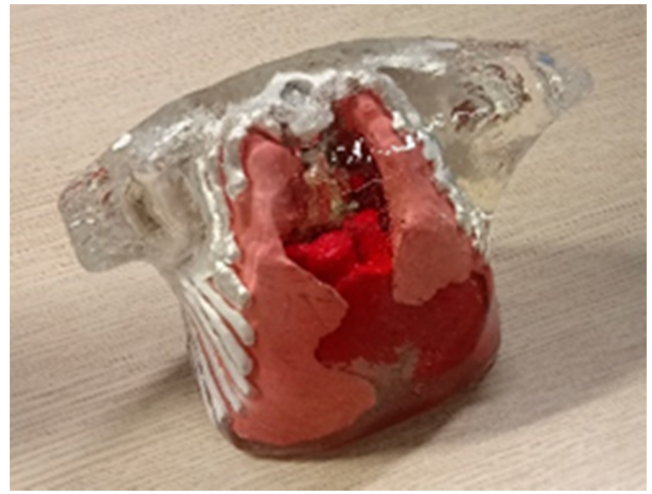
As mentioned in the introduction, one of the key aspects of this study was to provide a robust phantom recipe that can be used to make realistic 3D phantoms of biomedical importance. For example, the present recipe can be used to match all optical properties of various main organs of an infant torso (heart, muscle, lung, bone, fat and skin). An anatomically correct 3D phantom with multiple structures can be built by placing individual organs inside out as shown in the Fig. 5. A CAD design of the phantoms was obtained by segmenting an anonymized DICOM image of computed tomography (CT) scan of a newborn infant with consent from the parents and hospital. The forms of the segmented individual organs in the infant (heart, lung, trachea, thoracic cage, muscles) were cast in resin using the 3D printer (Formlabs Form 2). These forms were subsequently employed to create negative molds of organs which were then used to produce anatomically correct organs in SiliGlass. The fabrication method ensures that no air gaps were present in our phantom assemble, the phantoms were assembled into torso negative mold and liquid phantom mixture was poured to bind them with perfect contact thus simulating an ideal human body conditions. Figure 5 shows the mockup transparent sample that emphasizes the vision that we want to achieve, to make 3D printed phantoms with realistic optical properties.

Fig. 5.

Non-scattering anatomically correct 3D mock-up SiliGlass phantom made using CT scans of a newborn infant.

4. Conclusion

We have presented a robust, broadband (600-1100 nm) characterized, well-tested, and documented phantom recipe. To the best of our knowledge, this is the first study that tackles simultaneously the multiple issues of robust recipe, optical properties, and wavelength range relevant to human organs. The linearity, reproducibility, and homogeneity tests ensured the reliable nature of the phantom recipe. All the tested variables were found to have a CV of less than 4% which is the inherent CV of the time-domain system and a long term stability of CV of 5% was observed. With the technological advancement in 3D printing, we foresee this recipe could play a crucial role in the future of realistic biomedical 3D optical phantoms [11,31].

Funding

Science Foundation Ireland (SFI/15/RP/2828); European Union H2020 project Laserlab Europe (n. 654148).

Disclosures

The authors declare that there are no conflicts of interest related to this article.