Quantitative measurements of cerebral blood flow with near-infrared spectroscopy

Abstract

We propose a new near-infrared spectroscopy (NIRS) method for quantitative measurements of cerebral blood flow (CBF). Because this method uses concepts of coherent hemodynamics spectroscopy (CHS), we identify this new method with the acronym NIRS-CHS. We tested this method on the prefrontal cortex of six healthy human subjects during mean arterial pressure (MAP) transients induced by the rapid deflation of pneumatic thigh cuffs. A comparison of CBF dynamics measured with NIRS-CHS and with diffuse correlation spectroscopy (DCS) showed a good agreement for characteristic times of the CBF transient. We also report absolute measurements of baseline CBF with NIRS-CHS (69 ± 6 ml/100g/min over the six subjects). NIRS-CHS can provide more accurate measurements of CBF with respect to previously reported NIRS surrogates of CBF.

1. Introduction

Maintaining adequate cerebral blood flow (CBF) is critically important for brain function and tissue viability, especially for patients in the neurocritical care unit (NCCU) with conditions such as acute ischemic stroke, traumatic brain injury, and subarachnoid hemorrhage [1,2]. Although multiple factors may contribute to the poor outcome in those patients, a major focus of the intensive care is to prevent delayed ischemia due to low blood supply to the brain tissue [3]. Continuous bedside monitoring of CBF could improve outcome by providing the ability to detect any signs of impaired CBF in the patients and allow for suitable interventions to prevent ischemia before permanent tissue damage occurs.

Conventional imaging techniques, such as oxygen-15 positron emission tomography (PET), single-photon emission computer tomography (SPECT), perfusion magnetic resonance imaging (MRI), and xenon-computed tomography (Xe-CT), can measure CBF accurately, but these techniques are not suited for clinical bedside monitoring because they are costly, unable to provide continuous monitoring, involve major instrumentation, and may require radiation exposure and patient transport [4]. Transcranial Doppler ultrasound (TCD) is more common for clinical practice because this technique can record temporal changes in cerebral blood flow velocity (CBFV) in large arteries noninvasively and continuously. However, TCD cannot probe microvascular blood flow, which limits this technique from monitoring regional ischemic conditions in the brain. Besides, performance of TCD is operator dependent and may not be applicable in 10-15% of patients due to lack of ultrasound transmission windows [5,6].

Optical techniques using near-infrared light are promising for portable, continuous, long-term and noninvasive monitoring of regional CBF at bedside settings. Hemoglobin difference ([HbD]), defined as the difference between the tissue concentrations of oxy-hemoglobin ([HbO₂]) and deoxy-hemoglobin ([Hb]), is a quantity measured by near-infrared spectroscopy (NIRS). [HbD] has been observed to be highly correlated with CBF [7]. However, [HbD] is not solely sensitive to CBF but also to cerebral blood volume (CBV) and cerebral metabolic rate of oxygen (CMRO₂). Furthermore, [HbD] does not take into account the delay, due to the blood transit time in the microvasculature, between tissue concentrations of [HbO₂] and [Hb] and the driving changes in CBF. Diffuse correlation spectroscopy (DCS) is another optical technique that can measure CBF directly based on the decorrelation of the intensity fluctuations of the multiple-scattered light [8–10]. Relative changes in blood flow index (BFI) measured by DCS have been shown to correlate with relative changes in CBF as assessed by standard modalities, such as TCD [11], Xe-CT [12], arterial spin labeling MRI (ASL-MRI) [13], and velocity encoding MRI (VENC-MRI) [14]. However, DCS measurements do not provide absolute CBF, which hampers the capability of DCS to determine when CBF has fallen under critical levels. Recently, we introduced a method, namely coherent hemodynamics spectroscopy (CHS), to characterize cerebral hemodynamics that are coherent with a given physiological quantity and we have described how it may be used to obtain CBF from NIRS measurements [15–18]. This method is based on an analytical model that relates [HbO₂] and [Hb] to perturbations in CBV, CBF, and CMRO₂ [15,19]. CHS improves on the [HbD] estimation of CBF dynamics by correcting for CBV changes and for the blood transit times in the capillary and venous compartments. Quantitative measurements of capillary blood volume and capillary transit time by CHS also provide absolute values of local CBF. The clinical applicability of CHS and its ability to provide absolute CBF at baseline has been reported in our previous work [17,20,21]. Here, we report for the first time dynamic measurements of CBF with NIRS-CHS, their comparison with [HbD] and DCS measurements, and a critical analysis of absolute and relative measurements of CBF with NIRS-CHS.

The scope of this work is to validate the temporal dynamics of microvascular CBF measured with NIRS-CHS in a protocol that involves induced transient changes in mean arterial pressure (MAP). The blood pressure changes were induced by a rapid deflation of a pneumatic cuff applied to both subject’s thighs after 2 minutes of sustained inflation at a super-systolic pressure. Thigh cuff deflation is a well-established method for producing transient changes in arterial blood pressure and in CBF measured by TCD [11,22,23]. We have validated the temporal dynamics of CBF measured with NIRS-CHS by comparison with relative CBF measured concurrently with DCS in the same tissue volume. In addition to the validation of dynamic CBF measurements, we also discuss the sensitivity to model parameters and the effect of model assumptions on NIRS-CHS measurements of CBF.

2. Methods

2.1 Subjects

Six healthy subjects (3 females; 3 males; age range: 22-33 years) participated in this study. The Tufts University Institutional Review Board approved the experimental protocol, and the subjects provided written informed consent prior to the experiment. Experiments were performed in accordance with the Declaration of Helsinki.

2.2 Data acquisition and measurement protocol

Concurrent and co-localized NIRS and DCS measurements were performed. The NIRS instrument is a commercial frequency-domain tissue spectrometer (Imagent, ISS, Inc., Champaign, IL) that operates at wavelengths of 690 and 830 nm and at a modulation frequency of 140 MHz. The DCS instrument is home-built according to the specificiations of previously reported systems [10,13,14]. It uses a long-coherence-length continuous-wave laser (DL785-070-3O, CrystaLaser, Inc., Ren, NV) emitting light at 785 nm, and a bundle of four co-localized few-mode optical fibers (SMF-28-100, NA: 0.14, core: 8.2 μm, single-mode cutoff wavelength at 1260 nm, Thorlabs, Newton, NJ) for collection. The detection fibers were wrapped around a 15-cm diameter cylinder to convert higher-order modes into non-propagating leaky modes. This setup of detection fiber is similar to what have been reported in literature [24], which results in bending-insensitive transport of six modes at 785 nm for the detection fibers. The detected light for DCS is delivered to an avalanche photodiode module (SPCM-AQ4C, Excelitas Technologies Corp., Waltham, MA), which outputs a TTL signal for every detected photon. An eight-channel autocorrelator board (FLEX05-8CH, Correlator.com, Bridgewater, NJ) uses this TTL signal to derive the intensity autocorrelation function, g₂(τ), based on the photon arrival times. To synchronize the NIRS and DCS devices, we used an Arduino microcontroller (Arduino Uno R3) to generate a trigger pulse at the time the DCS acquisition was started. The trigger pulse was transmitted to the NIRS instrument via an auxiliary input channel. Continuous mean arterial blood pressure (MAP) was collected with a beat-to-beat finger plethysmography system (NIBP100D, BIOPAC Systems, Inc., Goleta, CA). During the experiment, two pneumatic cuffs were placed around both thighs of the subject and were connected to an automated inflation device (E-20 Rapid Cuff Inflation System, D. E. Hokanson, Bellevue, WA) and a digital manometer (Series 626 Pressure Transmitter, Dwyer Instruments, Inc., Michigan City, IN) to monitor air pressure in the cuffs. NIRS, MAP, and thigh cuff pressure were collected synchronously at a sampling rate of 9.93 Hz (i.e. every ~0.1 s), while DCS autocorrelation curves were acquired every 1.2 s.

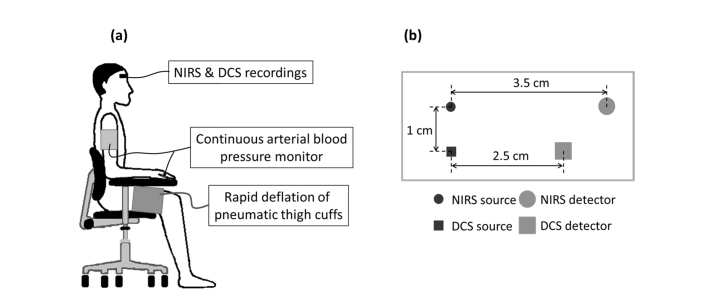
Before starting the experiment, initial baseline optical properties of the brain were recorded from each subject by using a multi-distance optical probe with six source-detector distances (range: 1.6-4.0 cm) connected to the NIRS instrument. The multi-distance probe was secured to the right side of the subject’s forehead for 16 s of data acquisition. Multi-distance baseline measurements allow the quantification of absolute concentration of total hemoglobin, which is a key parameter for estimation of both changes and absolute dynamics of $\text{cbf}(t)$ (see Section 2.3.3). During the experiment, the subject sat upright in a chair with their feet on the floor and with two pneumatic thigh cuffs wrapped around both thighs (Fig. 1(a)). A custom-made optical probe with two source-detector pairs, one for NIRS (source-detector distance: 3.5 cm) and one for DCS (source-detector distance: 2.5 cm) (Fig. 1(b)) was placed on the subject’s forehead at about the same area sensed by the multi-distance probe. The thigh cuffs were inflated to a pressure of 180-200 mmHg for 2 minutes to induce arterial occlusion, and then rapidly deflated to induce a transient decrease in MAP. A 2-min baseline was recorded before and after the thigh-cuff occlusion.

Fig. 1.

(a) Experimental setup. (b) Optical probe for NIRS and DCS data collection from the right side of the subject’s forehead.

2.3 Data analysis

2.3.1 Diffuse correlation spectroscopy

For DCS, normalized intensity autocorrelation curves $g_2(\tau )$ measured at the four co-localized detectors were averaged and then fitted to the model based on the semi-infinite homogeneous medium solution to the correlation diffusion equation. The fit provides a blood flow index (BFI) and $\beta$ (a factor that allows to translate the normalized electric field autocorrelation function into $g_2(\tau )$) [8,25]. We discarded DCS data measured at any detector if the intensity was too low, i.e. if the detected photon count rate was less than 5 kHz. The method assumes the mean squared displacement of the moving scatterers to follow a Brownian motion model [8]. For the fitting procedure, absorption and scattering coefficients (${\mu }_a$and ${\mu }_s\text{'}$) at 785 nm were extrapolated from optical properties measured at 690 and 830 nm with frequency-domain NIRS. While the time-dependent ${\mu }_a$ at 785 nm was estimated from the time traces of [HbO₂] and [Hb], ${\mu }_s\text{'}$ was assumed to be constant and extrapolated from ${\mu }_s\text{'}$ measured at 690 and 830 nm using the power-law dependence ${\mu }_s\text{'}~{(\lambda /{\lambda }_0)}^{-b}$ (where ${\lambda }_0$ = 690 nm). We restricted the fit to the early portion of the $g_2(\tau )$ curve, wherein $g_2(\tau )$ was greater than 1.05, to give more weight to longer photon pathlengths and increase the sensitivity of the BFI signal to cerebral contributions [26]. Then, the relative CBF measured by DCS (${\text{rCBF}}_{DCS}(t)$) is computed as follows:

$${\text{rCBF}}_{DCS}(t)=\frac{\text{BFI}(t)}{{\text{BFI}}_0},$$ (1)

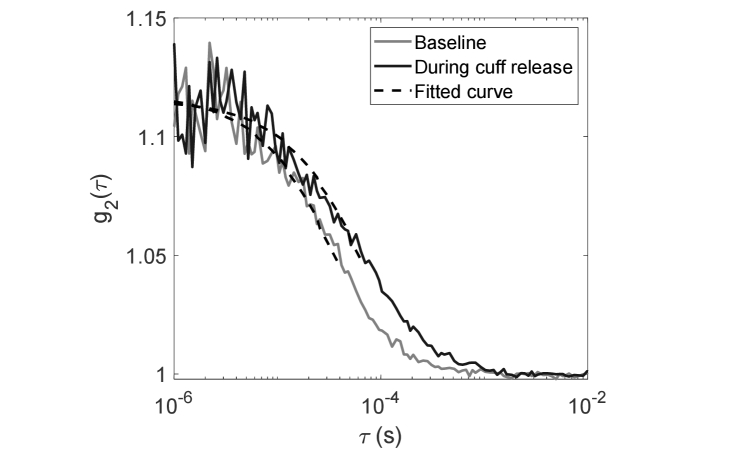
where ${\text{BFI}}_0$ is the average BFI value during baseline. The time traces of ${\text{rCBF}}_{DCS}$ were smoothed via a moving average window size of 3 frames (~3.6 s). Examples of $g_2(\tau )$from one experiment are shown in Fig. 2 during baseline and at 5 s following the cuff release. We note that the steeper slope of $g_2(\tau )$ during baseline compared with the one after cuff release is consistent with higher blood flow during baseline. With the setup of the detection fibers, we initially obtained β = 0.15 ≅ 1/6 as expected for six-mode detection fibers. Here in this study, the correlation factor β = 0.12 is lower than the theoretical prediction. We hypothesize that this could be due to laser instability. However, we note that β is constant during the whole experiment, and since we only care for relative changes in CBF measured by DCS we expect that this low β will not affect the results of this study.

Fig. 2.

Measured intensity autocorrelation curves during baseline and during the cuff-release-induced transient (5 s following the cuff deflation) as a function of delay time $\tau$. The fits to the hemogeneous semi-infinite DCS model are presented in black dashed lines. The fits are constrained to the early delays corresponding to $g_2(\tau )$ ≥ 1.05. BFI value is 3.4 × 10⁻⁹ cm²/s during baseline and 1.9 × 10⁻⁹ cm²/s at 5 s following the cuff release.

2.3.2 Near-infrared spectroscopy

We obtained absolute baseline cerebral concentrations of oxy-hemoglobin ([HbO₂]₀), deoxy-hemoglobin ([Hb]₀), and total hemoglobin ([HbT]₀) from the initial baseline measurement with the multi-distance optical probe by applying diffusion theory for a semi-infinite homogeneous medium. The method to calculate absolute optical properties from multi-distance amplitude (AC) and phase measurements in frequency-domain NIRS is described elsewhere [27]. Optical signal changes collected with the NIRS/DCS probe at a 3.5 cm source-detector distance were translated into relative changes in cerebral hemoglobin concentrations $\Delta [{\text{HbO}}_2]$, $\Delta [\text{Hb}]$, and $\Delta [\text{HbT}]$ by applying the modified Beer-Lambert law [28]. Differential pathlength factors for 690 and 830 nm light were determined from the tissue optical properties measured at baseline [29]. Here, we did not apply corrections that we have previously considered for water contributions to absorption [30] and for the layered structure of the examined tissue [31]. The reason is that these two corrections would modify the cerebral concentrations in opposite directions (water-corrected [HbT] is lower and layer-corrected cerebral [HbT] is greater than uncorrected [HbT]) and would still be associated with assumptions (the volume fraction of water in tissue) and approximations (a tissue structure made of regular layers).

AC amplitudes (rather than average DC intensities) at the two wavelengths were used for the conversion of hemoglobin concentrations via the modified Beer-Lambert law. We found that using AC amplitudes for NIRS and the optical fiber arrangement of the NIRS/DCS probe [Fig. 1(b)], there was negligible crosstalk between the NIRS and DCS measurements. The superposition of the relative changes to the absolute baseline measurements provided temporal dynamic measurements of absolute concentrations [HbO₂], [Hb], and [HbT]. Time traces of hemoglobin concentrations and MAP were low-pass filtered with a cut-off frequency of 0.2 Hz to remove contributions from respiration and cardiac pulsation. For further analysis with the hemodynamic model, we used the dynamic responses of [HbO₂] and [Hb] within 10 s following the thigh cuff deflation, which corresponds to the time frame in which cerebral autoregulation is less confounded by other intervening phenomena like the baroreflex mechanism [32,33].

2.3.3 Hemodynamic model and fitting procedures

The CHS model describes how the time traces of [HbO₂], [Hb], and [HbT] are related to the time-dependent changes in cerebral blood volume (CBV), cerebral blood flow (CBF), and cerebral metabolic rate of oxygen (CMRO₂) [15,16,19]. The key equations are:

$$\begin{array}{l}[{\text{HbO}}_2](t)=\text{ctHb}[S^{(a)}{\text{CBV}}_0^{(a)}(1+{\text{cbv}}^{(a)}(t))+〈S^{(c)}〉{\mathcal{F}}^{(c)}{\text{CBV}}_0^{(c)}+S^{(v)}{\text{CBV}}_0^{(v)}(1+{\text{cbv}}^{(v)}(t))]\\ +\text{ctHb}[\frac{〈S^{(c)}〉}{S^{(v)}}(〈S^{(c)}〉–S^{(v)}){\mathcal{F}}^{(c)}{\text{CBV}}_0^{(c)}{h}_{RC-LP}^{(c)}(t)+(S^{(a)}–S^{(v)}){\text{CBV}}_0^{(v)}{h}_{G-LP}^{(v)}(t)]*[\text{cbf}(t)–{\text{cmro}}_2(t)\text{]},\end{array}$$ (2)

$$\begin{array}{l}[\text{Hb}](t)=\text{ctHb}[\left(1–S^{(a)}\right){\text{CBV}}_0^{(a)}(1+{\text{cbv}}^{(a)}(t))+\left(1–〈S^{(c)}〉\right){\mathcal{F}}^{(c)}{\text{CBV}}_0^{(c)}+\left(1–S^{(v)}\right){\text{CBV}}_0^{(v)}(1+{\text{cbv}}^{(v)}(t))]\\ –\text{ctHb}[\frac{〈S^{(c)}〉}{S^{(v)}}(〈S^{(c)}〉–S^{(v)}){\mathcal{F}}^{(c)}{\text{CBV}}_0^{(c)}{h}_{RC-LP}^{(c)}(t)+(S^{(a)}–S^{(v)}){\text{CBV}}_0^{(v)}{h}_{G-LP}^{(v)}(t)]*[\text{cbf}(t)-{\text{cmro}}_2(t)\text{]},\end{array}$$ (3)

$$[\text{HbT}](t)=\text{ctHb}{\text{CBV}}_0[1+\text{cbv}(t)\text{]},$$ (4)

where * denotes the convolution operator. Lowercase notation denotes normalized relative changes in CBV, CBF, and CMRO₂ with respect to baseline (i.e., $\text{cbv}(t)=\Delta \text{CBV}(t)/{\text{CBV}}_0$, $\text{cbf}(t)=\Delta \text{CBF}(t)/{\text{CBF}}_0$, ${\text{cmro}}_2(t)=\Delta {\text{CMRO}}_2(t)/{\text{CMRO}}_{2|0}$), and ctHb is the concentration of hemoglobin in blood. The superscripts indicate the arterial (a), capillary (c), or venous (v) compartment values of hemoglobin saturation (S), CBV and cbv. ${\mathcal{F}}^{(c)}$is the Fåhraeus factor that accounts for the reduced hematocrit in the capillaries with respect to large blood vessels. The mean capillary and venous saturations depend on arterial satuation (S^(a)) and mean capillary transit time (t^(c)) according to $〈S^{(c)}〉=S^{(a)}(1–e^{–\alpha t^{(c)}})/(\alpha t^{(c)})$ and $S^{(v)}=S^{(a)}{e}^{-\alpha t^{(c)}},$ respectively. The symbol $〈〉$ denotes a spatial average over the average length of one capillary, and α is the rate constant of oxygen diffusion. The impulse response functions associated with the blood transit time in the capillary bed $[h_{RC-LP}^{(c)}(t)]$ and in both capillary and venous compartments $[h_{G-LP}^{(v)}(t)]$ are given by the resistor-capacitor (RC) and Gaussian low-pass filters, respectively, as functions of $t^{(c)}$ and $t^{(v)}$ [16,19]. The baseline cerebral blood volume is defined as:

$${\text{CBV}}_0={\text{CBV}}_0^{(a)}+{\mathcal{F}}^{(c)}{\text{CBV}}_0^{(c)}+{\text{CBV}}_0^{(v)},$$ (5)

or:

$$1=\frac{{\text{CBV}}_0^{(a)}}{{\text{CBV}}_0}+\frac{{\mathcal{F}}^{(c)}{\text{CBV}}_0^{(c)}}{{\text{CBV}}_0}+\frac{{\text{CBV}}_0^{(v)}}{{\text{CBV}}_0}.$$ (6)

To clarify how the retrieval procedure works, we divide the variables/parameters of Eqs. (2)-(4) into three categories: (a) measured, (b) assumed, and (c) fitted, as described below.

• (a) Measured parameters: $[{\text{HbO}}_2](t)$, $[\text{Hb}](t)$ and ${\text{CBV}}_0$. The latter is computed from ${[\text{HbT}]}_0$ measured at baseline as ${\text{CBV}}_0={[\text{HbT}]}_0\text{/ctHb}$ (where the value of ctHb is assumed as specified in point (b) below). cbv(t) is obtained based on Eq. (4): $\text{cbv}(t)=\frac{\Delta \text{CBV}(t)}{{\text{CBV}}_0}=\frac{\Delta [\text{HbT}](t)}{{[\text{HbT}]}_0}$.

• (b) Assumed parameters: S^(a) = 0.98, ctHb = 2.3 mM, α = 0.8 s⁻¹, and ${\text{CBV}}_0^{(a)}{\text{/CBV}}_0=\mathrm{0.3.}$ α was assumed because t^(c) is coupled with α through the product αt^(c) in the expressions for S^(c) and S^(v). ${\text{CBV}}_0^{(a)}{\text{/CBV}}_0$was assumed to avoid crosstalk with the fitted parameter${\mathcal{F}}^{(c)}{\text{CBV}}_0^{(c)}{\text{/CBV}}_0$, and the specific value used (0.3) was based on reported measurements with positron emission tomography in the living human brain [34].

  For the dynamic variables, we assumed cbv^(c)(t) = 0 based on the fact that cerebral capillary recruitment and dilation has been reported to be negligible [35–37]. From this assumption, cbv(t) is then expressed as the weighted sum of cbv^(a)(t) and cbv^(v)(t):

  $$\text{cbv}(t)=\frac{\Delta [\text{HbT}](t)}{{[\text{HbT}]}_0}=\frac{{\text{CBV}}_0^{(a)}}{{\text{CBV}}_0}{\text{cbv}}^{(a)}(t)+\frac{{\text{CBV}}_0^{(v)}}{{\text{CBV}}_0}{\text{cbv}}^{(v)}(t\text{)},$$ (7)
  Recent studies by our group have suggested that cerebral blood volume changes in response to MAP dynamics are dominated by venous contributions in the lower frequency range (f < 0.2 Hz) [38,39]. On the basis of these studies, we partition the total cerebral blood volume changes into 80% venous and 20% arterial. This implies that $\Delta {\text{CBV}}^{(a)}(t)=0.2\Delta \text{CBV}(t)$ and $\Delta {\text{CBV}}^{(v)}(t)=0.8\Delta \text{CBV}(t)$or:

  $${\text{cbv}}^{(a)}(t)=0.2{\left(\frac{{\text{CBV}}_0^{(a)}}{{\text{CBV}}_0}\right)}^{-1}\text{cbv}(t\text{)},$$ (8)

  $${\text{cbv}}^{(v)}(t)=0.8{\left(\frac{{\text{CBV}}_0^{(v)}}{{\text{CBV}}_0}\right)}^{-1}\text{cbv}(t\text{)}.$$ (9)

  Note that in Eq. (8) the coefficient ${\left({\text{CBV}}_0^{(a)}{\text{/CBV}}_0\right)}^{-1}$ is assumed, while in Eq. (9) the coefficient ${\left({\text{CBV}}_0^{(v)}{\text{/CBV}}_0\right)}^{-1}$ is derived from Eq. (6) where ${\mathcal{F}}^{(c)}{\text{CBV}}_0^{(c)}{\text{/CBV}}_0$is one of the fitting parameters. Finally, for the inversion procedure, we considered cbf(t) and cbv(t) to be related by a high-pass impulse response function [$h_{RC-HP}^{(AR)}(t)$] that depends on a cutoff frequency for cerebral autoregulation (f_c^(AR)). This relationship assumes that cbf(t) could be estimated from cbv(t) by an RC high-pass filter relationship $\text{cbf}(t)=k{h}_{RC-HP}^{(AR)}(t)\ast \text{cbv}(t)$, where k is the inverse of the modified Grubb’s exponent [16,33].

• (c) Fitted parameters: t^{( c )}, t^{( v )}, ${\mathcal{F}}^{(c)}{\text{CBV}}_0^{(c)}{\text{/CBV}}_0$, f_c^(AR), and k. They are obtained by fitting the measured [HbO₂](t) and [Hb](t) over the 10 s following the cuff release to Eqs. (2) and (3). The fit was performed using the MATLAB function “fmincon” to minimize the sum of squared differences between the model prediction and the measured data. The parameters were obtained from the fit by setting limits within physiological ranges [16]. We used the MATLAB function “GlobalSearch” that uses a scatter-search mechanism for generating trial points within pre-defined bounds, and finds the best local minimum from those trial points with “fmincon”. To compute the error on each parameter, we applied a bootstrapping technique [40]. We computed the residuals as the difference between the data and the best fit. Then the residuals were randomly sampled and added to the fit to represent a new data set. We performed the fit again on the new data set and repeat this sampling procedure 20 times to obtain a distribution of parameter values. The standard deviation of the 20 results was used to represent the error on the fitting parameters. We found that performing the fit by using “GlobalSearch” and bootstrapping give similar results to using 48 different sets of initial guesses evenly spreaded throughout the range of upper and lower bounds of the five parameters.

  From the fitted parameters, an absolute value of CBF at baseline (CBF₀) is computed as follows in units of milliliters of blood per 100 grams of tissue per minute (ml/100g/min) based on the central volume principle [17]:

  $${\text{CBF}}_0=\frac{1}{{\rho }_b}\frac{{\mathcal{F}}^{(c)}{\text{CBV}}_0^{(c)}}{t^{(c)}}=\frac{1}{{\rho }_b}\frac{{\text{[HbT]}}_0}{\text{ctHb}}\frac{\frac{{\mathcal{F}}^{(c)}{\text{CBV}}_0^{(c)}}{{\text{CBV}}_0}}{t^{(c)}},$$ (10)

  Where ρ_b is the mass density of brain tissue, taken to be 1.04 g/ml.

  Finally, under the assumption of constant CMRO₂(t), the values of t^(c), t^{( v )}, and ${\mathcal{F}}^{(c)}{\text{CBV}}_0^{(c)}{\text{/CBV}}_0$ obtained from the time domain fit were used to compute normalized changes in CBF with respect to baseline (${\text{cbf}}_{NIRS-CHS}\left(t\right)\equiv \Delta {\text{CBF}}_{NIRS-CHS}\left(t\right)/{\text{CBF}}_0$) by taking the inverse Fourier transform of the following equation [16]:

  $${\widetilde{\text{cbf}}}_{NIRS-CHS}(\omega )=\frac{\frac{\Delta [{\widetilde{\text{HbO}}}_2](\omega )-\Delta [\widetilde{\text{Hb}}](\omega )}{{[\text{HbT}]}_0}-(2S^{(a)}-1)\frac{\Delta {\widetilde{\text{CBV}}}^{(a)}(\omega )}{{\text{CBV}}_0}-(2S^{(v)}-1)\frac{\Delta {\widetilde{\text{CBV}}}^{(v)}(\omega )}{{\text{CBV}}_0}}{2\left[\frac{〈S^{(c)}〉}{S^{(v)}}(〈S^{(c)}〉-S^{(v)})\frac{{\mathcal{F}}^{(c)}{\text{CBV}}_0^{(c)}}{{\text{CBV}}_0}{H}_{RC-LP}^{(c)}(\omega )+(S^{(a)}-S^{(v)})\frac{{\text{CBV}}_0^{(v)}}{{\text{CBV}}_0}{H}_{G-LP}^{(v)}(\omega )\right]},$$ (11)

  where the tilde denotes Fourier transformation with angular frequency ω. The complex transfer functions $H_{RC-LP}^{(c)}(\omega )$ and $H_{G-LP}^{(v)}(\omega )$ are the Fourier transforms of the corresponding impulse response functions $h_{RC-LP}^{(c)}(t)$and $h_{G-LP}^{(v)}(t)$. We observe that if CMRO₂ changes cannot be neglected, the left-hand side of Eq. (11) becomes${\widetilde{\text{cbf}}}_{NIRS-CHS}(\omega )–{\widetilde{\text{cmro}}}_2(\omega )$. Similar to the inversion procedure, we also assumed $\Delta {\widetilde{\text{CBV}}}^{(a)}(\omega )=0.2\Delta \widetilde{\text{CBV}}(\omega )$ and$\Delta {\widetilde{\text{CBV}}}^{(v)}(\omega )=0.8\Delta \widetilde{\text{CBV}}(\omega )$. The normalized CBF is ${\text{rCBF}}_{NIRS-CHS}(t)=1+{\text{cbf}}_{NIRS-CHS}(t)$. The absolute dynamic CBF is ${\text{CBF}}_{NIRS-CHS}\left(t\right)={\text{CBF}}_0{\text{rCBF}}_{NIRS-CHS}\left(t\right)$. We note that only three out of the five parameters used for the time domain fit (t^(c), t^(v), and ${\mathcal{F}}^{(c)}{\text{CBV}}_0^{(c)}{\text{/CBV}}_0$) were used for calculating ${\widetilde{\text{cbf}}}_{NIRS-CHS}(\omega )$ in Eq. (11). Specifically, we released the assumption of an RC high pass filter relationship between cbv(t) and cbf(t).

2.4 Statistical analysis

To compare the dynamic responses of [HbD] ([HbO₂] – [Hb]), CBF_NIRS-CHS, and rCBF_DCS, we measured the values of time-to-minimum (t_min) and time-to-half-recovery (t_1/2) (in units of second) for these time traces in the interval of 20 s following the thigh cuff deflation. The minimum value following the cuff release defines the maximum decrease from baseline, and the time interval between the cuff release and the time of the minimum is defined as t_min. We denote with t_1/2 the time needed to recover from the minimum value to half of the maximal decrease. A two-tailed signed-rank test was performed to determine statistically significant differences between t_min and t_1/2 obtained from [HbD], CBF_NIRS-CHS, and rCBF_DCS. Analyses were performed with MATLAB, and statistical significance was associated with p-values < 0.05.

3. Results

3.1 CBF dynamics with NIRS-CHS

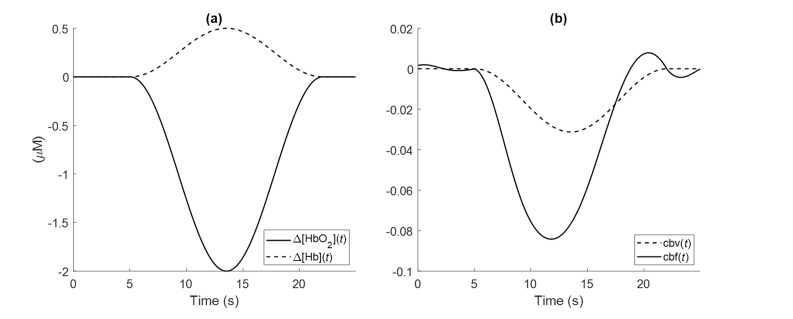
In this section, we study how variations or uncertainties in the CHS parameters and in the relative arterial-to-venous contributions to cerebral blood volume changes affect the amplitude and temporal dynamics of CBF in response to the cuff release. In other words, how the key parameters in Eq. (11) affect the calculation of ${\widetilde{\text{cbf}}}_{NIRS-CHS}(\omega )$ and its inverse Fourier transform which yields its temporal dynamics. Based on the average NIRS measurements from the subjects reported in this paper, we simulated temporal traces of Δ[HbO₂] and Δ[Hb] following the cuff release (Fig. 3(a)), with a maximal decrease of 2 μM for Δ[HbO₂](t) and a maximal increase of 0.5 μM for Δ[Hb](t). We assumed [HbT]₀ = 48 μM. First, we start with a set of initial parameter values: $t^{(c)}=0.7\text{s,}$ $t^{(v)}=5\text{s,}$ ${\mathcal{F}}^{(c)}{\text{CBV}}_0^{(c)}{\text{/CBV}}_0=0.4$and ${{\text{CBV}}_0}^{(a)}{\text{/CBV}}_0=0.3$(i.e.,${{\text{CBV}}_0}^{(v)}{\text{/CBV}}_0=0.3$). By assuming equal arterial and venous contributions to blood volume changes ($\Delta {\text{CBV}}^{(a)}\left(t\right)=\Delta {\text{CBV}}^{(v)}\left(t\right)$), the time trace of cbf(t) could be generated as shown in Fig. 3(b). cbv(t) is generated as the normalized change in Δ[HbT](t) with respect to [HbT]₀.

Fig. 3.

(a) Simulated time traces of Δ[HbO₂] and Δ[Hb] as can be measured with NIRS. (b) The NIRS measurements of panel (a) are converted by CHS into cbv(t) and cbf(t), under the assumption cmro₂(t) = 0, by using the parameter values t^(c) = 0.7 s, t^(ν) = 5 s, $\frac{{\mathcal{F}}^{(c)}{{\text{CBV}}_0}^{(c)}}{{\text{CBV}}_0}=0.4,$ $\frac{{{\text{CBV}}_0}^{(a)}}{{\text{CBV}}_0}=0.3,$ and by assuming $\Delta {\text{CBV}}^{(a)}(t)=\Delta {\text{CBV}}^{(v)}(t).$

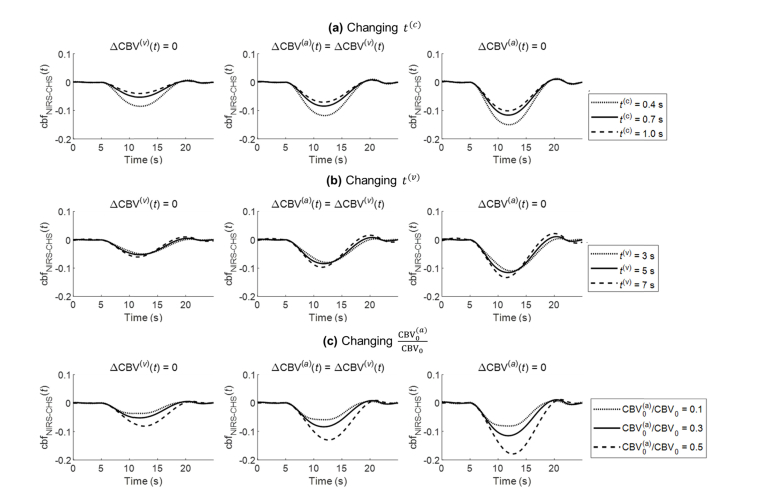
The simulations of Fig. 3 illustrate the approach of CBF dynamic measurements with NIRS-CHS [Eq. (11)] using typical CHS parameters. We now consider the sensitivity of the CBF dynamics generated with NIRS-CHS to some of the choices, assumptions, or measurements of these parameters. We consider three conditions of relative arterial-to-venous contributions to CBV dynamics: only arterial (condition 1: $\Delta {\text{CBV}}^{(v)}(t)=0$, i.e ${\text{cbv}}^{(v)}(t)=0$), equally venous and arterial (condition 2: $\Delta {\text{CBV}}^{(a)}(t)=\Delta {\text{CBV}}^{(v)}(t)$, i.e. ${{\text{CBV}}_0}^{(a)}{\text{cbv}}^{(a)}(t)={{\text{CBV}}_0}^{(v)}{\text{cbv}}^{(v)}(t)$), only venous (condition 3: $\Delta {\text{CBV}}^{(a)}(t)=0$, i.e. ${\text{cbv}}^{(a)}(t)=0$). For each of these conditions, we simulate the dynamic CBF trace obtained for the same parameters used to generate Fig. 3(b), except that we consider three different values for one specific parameter at a time: the capillary transit time (t^(c)), the venous transit time (t^(v)), or the arterial vs. venous baseline cerebral blood volume ratio$\left(\frac{{{\text{CBV}}_0}^{(a)}}{{\text{CBV}}_0}\text{vs}.\frac{{{\text{CBV}}_0}^{(v)}}{{\text{CBV}}_0}\right)$. Figure 4(a) shows cbf(t) traces for three values of the capillary transit time, t^(c) (0.4, 0.7 and 1.0 s). Figure 4(b) shows cbf(t) traces for three values of the venous transit time t^(v) (3, 5 and 7 s). In Fig. 4(c), while fixing $\frac{{\mathcal{F}}^{(c)}{{\text{CBV}}_0}^{(c)}}{{\text{CBV}}_0}=0.4$, cbf(t) traces were obtained for three values of the arterial baseline cerebral blood volume ratio $\frac{{{\text{CBV}}_0}^{(a)}}{{\text{CBV}}_0}$ (0.1, 0.3, 0.5), so that the three sets of values for $\left(\frac{{{\text{CBV}}_0}^{(a)}}{{\text{CBV}}_0},\frac{{\mathcal{F}}^{(c)}{{\text{CBV}}_0}^{(c)}}{{\text{CBV}}_0},\frac{{{\text{CBV}}_0}^{(v)}}{{\text{CBV}}_0}\right)$ in Fig. 4(c) are (0.1, 0.4, 0.5), (0.3, 0.4, 0.3), and (0.5, 0.4, 0.1). Table 1 shows the peak time of cbf(t) with respect to the peak time of cbv(t), and the maximum change of cbf(t) (i.e. its largest negative value) for all the conditions. Note that in Table 1, since cbv(t) peaks later than cbf(t), more negative values for the peak time of cbf(t) with respect to cbv(t) indicate peaks in cbf(t) that occur at earlier times.

Fig. 4.

Sensitivity of cbf_NIRS-CHS(t) to (a) capillary transit time (t^(c)), (b) venous transit time (t^(v)), and (c) the arterial baseline cerebral blood volume ratio $\frac{{{\text{CBV}}_0}^{(a)}}{{\text{CBV}}_0}.$ For each panel, three conditions are illustrated left to right for the relative arterial-to-venous blood volume dynamics: arterial only ($\Delta {\text{CBV}}^{(v)}(t)=0$), equally venous and arterial ($\Delta {\text{CBV}}^{(a)}(t)=\Delta {\text{CBV}}^{(v)}(t)$), and venous only ($\Delta {\text{CBV}}^{(a)}(t)=0$). The cbf(t) traces indicated by solid lines in the middle plots for (a)-(c) are the same with the cbf(t) trace in Fig. 3(b).

Table 1. Sensitivity of the CBF dynamics to CHS parameters (capillary and venous transit times, baseline arterial to venous blood volume, relative arterial-to-venous blood volume changes).

Parameters →		$\text{Any}\frac{\Delta {\text{CBV}}^{(a)}}{\Delta {\text{CBV}}^{(v)}}$	$\frac{\Delta {\text{CBV}}^{(a)}}{\Delta {\text{CBV}}^{(v)}}\gg 1$	$\frac{\Delta {\text{CBV}}^{(a)}}{\Delta {\text{CBV}}^{(v)}}=1$	$\frac{\Delta {\text{CBV}}^{(a)}}{\Delta {\text{CBV}}^{(v)}}\ll 1$
↓		$t_{\min ,\text{CBF}}-t_{\min ,\text{CBV}}(s)$	${\frac{\Delta \text{CBF}}{{\text{CBF}}_0}|}_{\max }$
t(c) (s)	0.4	−1.5	−0.08	−0.11	−0.15
	0.7	−1.7	−0.05	−0.08	−0.12
	1.0	−1.8	−0.04	−0.07	−0.10
t(v) (s)	3	−1.1	−0.05	−0.08	−0.11
	5	−1.7	−0.05	−0.08	−0.12
	7	−2.0	−0.06	−0.10	−0.13
$\frac{{{\text{CBV}}_0}^{(a)}}{{\text{CBV}}_0}$	0.1	−1.5	−0.04	−0.06	−0.08
	0.3	−1.7	−0.05	−0.08	−0.12
	0.5	−0.9	−0.08	−0.13	−0.18

As t^(c) increases from 0.4 to 1.0 s, cbf(t) peaks 0.3 s earlier and decreases 4-5% less. As t^(v) increases from 3 to 7 s, cbf(t) peaks 0.9 s earlier and decreases 1-2% more. The effects of t^(c) and t^(v) are mostly associated with the effects of the two low-pass filters $H_{RC-LP}^{(c)}$ and $H_{G-LP}^{(v)}$ in the denominator of cbf(t) equation (Eq. (11)), which are responsible for the earlier peak time of cbf(t) measured by NIRS-CHS as compared to Δ[HbD]. This is the correction for the delay of Δ[HbD](t) with respect fo cbf(t) due to capillary and venous blood transit times.

As relative arterial-to-venous baseline blood volume increases from 0.1/0.5 = 0.2 to 0.5/0.1 = 5, cbf(t) peaks 0.6 s later and decreases 4-10% more. This latter result can be explained by the fact that changes in CBF do not affect the concentrations of Hb and HbO₂ in the arterial compartment [15], so that a greater sensitivity to the arterial compartment translates given changes in [Hb] and [HbO₂] into greater changes in CBF.

One common effect that one can observe in Fig. 4 is the greater decrease in cbf(t) when the dynamic blood volume changes are venous (right panels of Fig. 4) vs. when they are arterial (left panels of Fig. 4). This effect could be explained mathematically by Eq. (11): as $\Delta {\text{CBV}}^{(v)}(t)$ becomes greater than $\Delta {\text{CBV}}^{(a)}(t)$ (and $\Delta {\widetilde{\text{CBV}}}^{(v)}(\omega )$ becomes greater than$\Delta {\widetilde{\text{CBV}}}^{(a)}(\omega )$), after considering that $(2S^{(a)}-1)>(2S^{(v)}-1)$, one can see that the numerator on the right-hand side of Eq. (11) becomes smaller, since $\frac{\Delta \widetilde{[{\text{HbO}}_2]}(\omega )-\Delta {\widetilde{[\text{Hb}]}}^{(a)}(\omega )}{{[\text{HbT}]}_0}$ is subtracted by a smaller amount.

While the relative sensitivity of optical measurements to the arterial, capillary, and venous compartments is still unclear, in this work we assumed $\frac{{{\text{CBV}}_0}^{(a)}}{{\text{CBV}}_0}=0.3$ based on a PET study [34], and we fitted for $\frac{{\mathcal{F}}^{(c)}{{\text{CBV}}_0}^{(c)}}{{\text{CBV}}_0}$ ($\text{then}\frac{{{\text{CBV}}_0}^{(v)}}{{\text{CBV}}_0}=1-0.3-\frac{{\mathcal{F}}^{(c)}{{\text{CBV}}_0}^{(c)}}{{\text{CBV}}_0}$).

3.2 NIRS-CHS measurements of dynamic CBF transients in human subjects

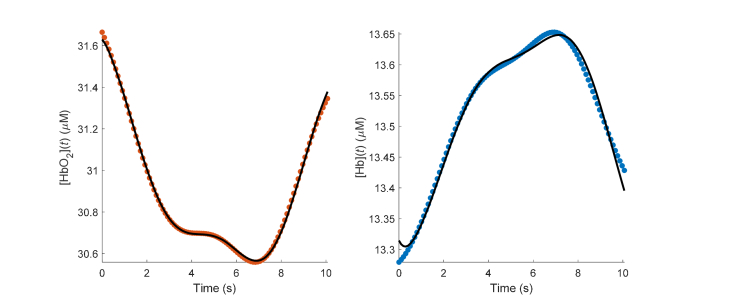
Figure 5 shows a representative case of the model fit to the data over 10 s immediately after the thigh-cuff release. The figure shows the measured absolute hemoglobin traces (symbols) and the model fit (continuous lines) from subject 3.

Fig. 5.

Typical time traces after thigh-cuff release (t = 0; data from subject 3). Symbols show measured hemoglobin concentrations, solid lines depict the model fit obtained from the MATLAB function “GlobalSeach”.

Baseline NIRS measurements yielded the following tissue concentration values (mean ± standard error over six subjects): ${[{\text{HbO}}_2]}_0=39\pm 3\text{μM,}$ ${[\text{Hb}]}_0=11\pm 1\text{μM,}$ and${[\text{HbT}]}_0=51\pm 3\text{μM}.$ The CHS fit to the transient responses of [HbO₂] and [Hb] yielded the following values for the hemodynamic parameters (mean ± standard error over six subjects):$t^{(c)}=0.7\pm 0.1\text{s,}$ $t^{(v)}=5.3\pm 0.8\text{s,}$ and${\mathcal{F}}^{(c)}{{\text{CBV}}_0}^{(c)}{\text{/CBV}}_0=0.41\pm \mathrm{0.02.}$ The value of the transit time in the capillaries, t^(c)~0.7 s, is within the reported range of 0.3 to 1.7 s as measured by fluorescence videography in rats [41]. The transit time in the veins, t^(v) (which here represents the venous drainage time within the banana-shaped optically probed volume), of ~5 s corresponds to an overall length of ~5 mm for the draining venules in the probed volume and a typical speed of blood flow in the venule of 1 mm/s [42]. The capillary compartment contribution to the total baseline blood volume, ${\mathcal{F}}^{(c)}{{\text{CBV}}_0}^{(c)}{\text{/CBV}}_0,$ of 0.41 is within reported physiological values of 0.3 to 0.65 in the human brain cortex [43]. These values of t^(c) and ${\mathcal{F}}^{(c)}{{\text{CBV}}_0}^{(c)}{\text{/CBV}}_0$ are somewhat lower than those reported in a previous study that used the same thigh cuff deflation protocol in eleven healthy human subjects during normal breathing [33]: 1.1 ± 0.1 s for t^(c) and 0.54 ± 0.03 s for${\mathcal{F}}^{(c)}{{\text{CBV}}_0}^{(c)}{\text{/CBV}}_0.$ In that previous study, the change in blood pressure was assumed to be equal to the relative change in arterial blood volume at the cardiac pulsation, and the arterial blood volume fraction ${{\text{CBV}}_0}^{(a)}{\text{/CBV}}_0$ was derived based on this assumption. This procedure led to a much lower value of ${{\text{CBV}}_0}^{(a)}{\text{/CBV}}_0$ (~0.04) compared to the assumed value in this study. Another difference of that study is that it performed a separate fit for α, which is always multiplied by t^(c) in the expressions for capillary and venous saturations [t^(c) appears independently of α only in the microvascular impulse functions of Eqs. (2) and (3)].

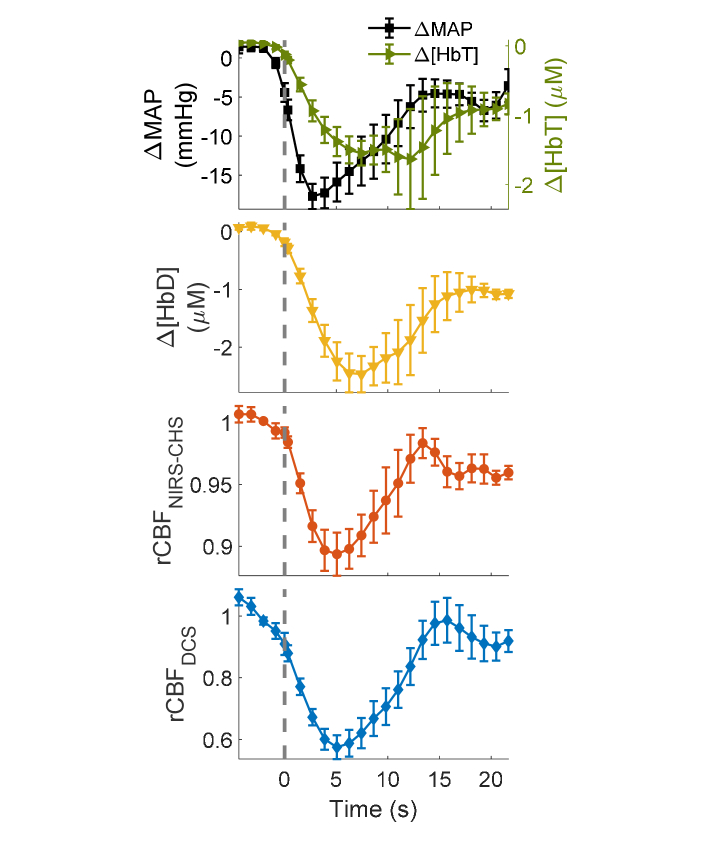
Figure 6 shows the grand averages of ΔMAP (relative change in MAP), Δ[HbT], Δ[HbD], ${\text{rCBF}}_{NIRS-CHS}$, and ${\text{rCBF}}_{DCS}$as mean values (symbols) and standard errors (error bars) across the six subjects. The time axis ranges from 5 s-before to 20 s-after the deflation of thigh cuffs, and the dashed line at t = 0 s indicates the cuff release. For comparison, NIRS and MAP signals were down-sampled to the DCS sampling rate at 0.83 Hz. As shown in Fig. 6, a transient drop in MAP induces transient decreases in [HbT], [HbD], ${\text{CBF}}_{NIRS-CHS}$ and${\text{rCBF}}_{DCS}$. Following the cuff deflation, ${\text{rCBF}}_{NIRS-CHS}$and ${\text{rCBF}}_{DCS}$showed similar temporal dynamics, which lead the delayed temporal dynamics of Δ[HbD]. Specifically, the time to minimum of CBF from the cuff deflation (t_min) was 5.3 ± 0.7 s with NIRS-CHS, 5.5 ± 0.3 s with DCS and 7.9 ± 0.8 s with Δ[HbD], whereas the time to half recovery of (t_1/2) was 9.7 ± 0.9 s for${\text{rCBF}}_{NIRS-CHS}$, 9.9 ± 0.8 s for ${\text{rCBF}}_{DCS}$, and 12 ± 1 s for Δ[HbD]. All values are reported as mean ± standard error over the six subjects.

Fig. 6.

Grand averages of ΔMAP, Δ[HbT], Δ[HbD], ${\text{rCBF}}_{NIRS-CHS}$, and ${\text{rCBF}}_{DCS}$, (all relative to baseline) across six subjects. Symbols represent the mean, and error bars represent standard errors. The dashed vertical line indicates the time of cuff deflation (t = 0).

The difference of t_min for ${\text{rCBF}}_{NIRS-CHS}$ and ${\text{rCBF}}_{DCS}$ was not statistically significant (two-sided non-parametric signed rank test, p = 0.69), whereas the mean difference between t_min for ${\text{rCBF}}_{NIRS-CHS}$ and Δ[HbD] was −2.6 s and significantly different from 0 (two-sided non-parametric signed rank test, p = 0.03). Similarly, the difference of t_1/2 for ${\text{rCBF}}_{NIRS-CHS}$and ${\text{rCBF}}_{DCS}$ was not statistically significant (two-sided non-parametric signed rank test, p = 0.90), whereas the mean difference between t_1/2 for ${\text{rCBF}}_{NIRS-CHS}$ and Δ[HbD] was −2.7 s and significantly different from 0 (two-sided non-parametric signed rank test, p = 0.03).

The maximum reduction in ${\text{CBF}}_{NIRS-CHS}$following the cuff deflation was 10% ± 2%, ranging from 6% to 17%. The corresponding reduction in ${\text{rCBF}}_{DCS}$was 39% ± 5%, ranging from 20% to 54%. Furthermore, we did not observe a meaningful correlation between the amplitudes of the CBF transients measured with NIRS-CHS and with DCS. We will comment on these results for the amplitude of CBF changes in the discussion section.

3.3 Absolute CBF with NIRS-CHS in human subjects

Absolute baseline CBF (CBF₀) values were obtained from the fitted values of t^(c) and${\mathcal{F}}^{(c)}{{\text{CBV}}_0}^{(c)}{\text{/CBV}}_0.$ We found an average CBF₀ of 69 ± 6 ml/100g/min (mean ± standard deviation) over six subjects, with a range of 53-110 ml/100g/min. Table 2 shows CBF₀ values obtained from the fit for every single-step response in each subject. To estimate the uncertainty of CBF₀, we assumed relative errors of 5% in ${[\text{HbT}]}_0$ [44], 10% in ctHb on the basis of healthy ranges in men and women (of course this error may be significantly reduced if ctHb is measured from a blood test on the subject), and 1% in each of t^(c) and ${\mathcal{F}}^{(c)}{{\text{CBV}}_0}^{(c)}{\text{/CBV}}_0,$ based on the results of this work. The uncertainty of CBF₀ obtained from Eq. (10) is then ~11% of the measured value.

Table 2. Baseline CBF₀ measured on the six subjects with NIRS-CHS.

Subject #	CBF0 (ml/100g/min)
1	87 ± 10
2	70 ± 8
3	53 ± 6
4	110 ± 12
5	63 ± 7
6	78 ± 9

It is also important to mention a systematic source of error in CBF₀, which results from the CHS estimate of t^(c). A careful inspection of the CHS equations for [HbO₂] and [Hb] [Eqs. (2) and (3)] shows that t^(c) almost always appears in conjunction with α in the product αt^(c) (α is the rate constant of oxygen diffusion from capillary blood to tissue), through the expressions for <S^(c)> and S^(v). The only exception is the appearance of t^(c) (separate from α) in the capillary and venous impulse response functions [$h_{RC-LP}^{(c)}(t)$and $h_{G-LP}^{(v)}(t)$]. Consequenly, the assumed value of α (which is directly related to the baseline CMRO₂) has a direct impact on the CHS estimate of t^(c), with greater values of α resulting in smaller values of t^(c).

4. Discussion

In this study, we applied the mathematical CHS model to obtain dynamic absolute measurements of CBF from NIRS measurements in six healthy human subjects. This is the first time that NIRS-CHS is compared with another optical technique, DCS, that is applied concurrently and in the same tissue volume. We also showed that NIRS-CHS can generate absolute measurements of CBF that are co-localized with measurements of CBV.

We observe that the blood flow index obtained from DCS is a direct measure of blood flow and is affected by the speed of moving red blood cells in all vascular compartments, while NIRS-CHS provides an indirect measurement of CBF and is sensitive to the effects of blood flow only in the capillary and venous vascular compartments. Specifically, DCS is based on the time scale of intensity decorrelation, which directly depends on the speed of moving scattering centers (i.e., red blood cells in the blood stream) regardless of the blood compartment. Instead, NIRS-CHS is based on dynamic measurements of [HbO₂] and [Hb], which are affected by the oxygen diffusion from blood to tissue and by the speed of blood flow in the microcirculation. A greater blood flow results in a faster intensity decorrelation in DCS and a smaller deoxygenation of hemoglobin in NIRS-CHS (under the assumption of negligible changes in tissue oxygen consumption). Changes of blood flow in the arterial compartment have no effect on the changes in [HbO₂] and [Hb] since there is no oxygen exchange in the arteries. On the contrary, changes of blood flow in the capillary compartment will affect the rate of deoxygenation and the concentrations of both HbO₂ and Hb in tissue. The capillary compartment is actively altering the ratio of [HbO₂] and [Hb], while the venous compartment is passively propagating those changes. Of course, changes in blood flow likely occur in all vascular compartments, but the NIRS-CHS method is specifically sensitive to capillary flow changes.

In terms of temporal dynamics, we have found that CBF measured with NIRS-CHS is in good agreement with CBF measured with DCS, which is not the case for [HbD] (see Fig. 6). Although NIRS studies in the literature have proposed [HbD] as a surrogate for CBF [45–47], validation studies of [HbD] only compared the correlation between amplitude of changes in [HbD] and CBF during perturbations in MAP [7,47]. Instead, the temporal dynamics of [HbD] and CBF were not compared. Equations (2) and (3) show that [HbD] dynamics are determined by temporal changes in CBV, CBF, and CMRO₂. Equation (11), where CMRO₂ dynamics are neglected, shows how CHS measurement of CBF subtract CBV dynamics from [HbD] dynamics [see the numerator of the right-hand-side of Eq. (11)]. Furthermore, the introduction of the transfer functions associated with the blood transit times in the capillary bed $[H_{RC-LP}^{(c)}(\omega )]$ and in the venous compartment $[H_{G-LP}^{(v)}(\omega )]$ in the expression for ${\widetilde{\text{cbf}}}_{NIRS-CHS}(\omega )$ accounts for the time lag between blood flow changes and the associated changes in the cerebral concentrations of HbO₂ and Hb [see the denominator of the right-hand-side of Eq. (11)]. This delay results in a shorter time-to-minimum (t_min) and time-to-half-recovery (t_1/2) values in ${\text{CBF}}_{NIRS-CHS}$as compared to [HbD] (see Fig. 6), and in earlier peaks of ${\text{cbf}}_{NIRS-CHS}(t)$ for longer t^(c) and t^(v) (see Fig. 4 and Table 1). The assumption of negligible changes in CMRO₂ seems reasonable in our protocol, which does not involve brain activation paradigms, and where cerebral hemodynamics are induced by systemic changes in arterial blood pressure. We observe that even during brain activation protocols, the increase of CBF has been reported to be much greater (~30%) than CMRO₂ changes (~5%) [48,49]. We note that when changes in CMRO₂ are not negligible, our approach is still valid but Eq. (11) yields cbf(t) – cmro₂(t) instead of cbf(t). In this case, NIRS-CHS can be used in conjunction with an independent measurement of cbf(t) to yield cmro₂(t).

While we found a good agreement between the characteristic times of the ${\text{rCBF}}_{NIRS-CHS}$ and ${\text{rCBF}}_{DCS}$transients following the thigh cuffs release, their amplitudes of changes were significantly different (about 10% with NIRS-CHS vs. 39% with DCS) and showed no correlation. The reduction in ${\text{CBF}}_{NIRS-CHS}$ of 10%, ranging from 6% to 17%, is in agreement with previous CBF changes measured with TCD, in a similar protocol, which are in the range 10-20% [11,32,50]. This is also in reasonable agreement with the reported changes in rCBF measured with DCS, also in a similar protocol, after correcting for scalp flow contributions (median % decrease of 9.1%, 95% confidence interval of 6.8-11.2%) [11]. These results suggest that the discrepancy in the amplitudes for CBF measured with DCS and NIRS-CHS in this study may reflect different relative sensitivities of the two techniques to blood flow in the scalp and in the brain, which may also result from the different source detector separation used in this study for NIRS (3.5 cm) and DCS (2.5 cm). The unknown blood flow changes in the superficial tissue layers (scalp, skull, etc.) and in deeper brain tissue, and the unknown relative sensitivity to such changes in the NIRS-CHS and DCS techniques, may also account for the lack of correlation between the amplitudes of CBF changes measured with NIRS-CHS and with DCS. The lack of discrimination of extracerebral and cerebral blood flow is a limitation of this study, which will need to be addressed in future work aimed at depth discrimination (through layered models or tomographic reconstruction, or by application of external pressure onto the scalp to suppress scalp hemodynamics [51,52] to identify and correct for extracerebral tissue confounds in NIRS-CHS measurements of CBF.

In addition to relative CBF dynamics, we have described how NIRS-CHS can measure absolute CBF and reported an average value of 69 ± 15 ml/100g/min (mean ± between-subject standard deviation) in six healthy adult human subjects, ranging from 53 to 110 ml/100g/min. In a study of CBF measurement variability, Henriksen et al reported mean values of 50 ± 9, 66 ± 13, and 59 ± 10 ml/100g/min for CBF in the gray matter in 17 healthy young subjects (age range: 20-30 years) as measured with ASL-MRI, diffusion contrast enhanced perfusion (DCE) MRI, and PET, respectively [53]. Grandin et al reported a value of 59 ± 13 ml/100g/min for cortical gray matter blood flow by using MRI bolus tracking and 45 ± 6 ml/100g/min by using PET in 13 healhty male volunteers [54]. Vonken et al reported an average CBF in gray matter of 69 ± 21 ml/100g/min in 41 healthy subjects using dynamic susceptibility contrast MRI [55]. Here, we found comparable or slightly greater CBF values, on average, than reported in literature. It is noted that our absolute CBF measurements using NIRS-CHS depend on various approximations and assumptions in the model, and we need to further study the impact of such assumptions on the accuracy, precision, reliability, and reproducibility of absolute CBF measurements. In particular, we are currently exploring options to minimize the systematic error on t^(c) (and therefore on CBF₀) associated with the assumed value of the oxygen diffusion from capillary blood to tissue (α). It is possible that these assumptions introduce systematic errors on CBF₀ and would possibly have minimal effects on the reproducibility of CBF₀ measurements on a single subject, so that longitudinal studies or cerebral perfusion monitoring on individual subjects may not be negatively impacted. However, the robustness and reliability of absolute baseline CBF measurements with NIRS-CHS needs to be further demonstrated in future studies.

5. Conclusion

In this study, we have presented a new optical approach using NIRS in conjunction with CHS to non-invasively and continuously measure CBF in human subjects. We have reported a first comparison of this technique using concurrent and co-localized diffuse correlation spectroscopy (DCS) measurements of local CBF dynamics during transient changes in mean arterial pressure caused by thigh cuffs release following 2 min of cuff inflation at a super-systolic pressure. The CBF dynamics measured with DCS were in much better agreement with ${\text{CBF}}_{NIRS-CHS}$ than with [HbD], a common NIRS surrogate of blood flow. However, we have found a discrepancy in the amplitude of CBF changes between NIRS-CHS and DCS, which we assign to confounding contributions from scalp blood flow and that will be further investigated in future studies. Even though DCS measurements are directly sensitive to the motion of red blood cells, we note that current models of quantification in DCS (i.e. the diffusion correlation equation) rely on NIRS measurements of the temporal trend of absolute optical properties. Therefore, both techniques will benefit from future comparative studies. If NIRS-CHS measurements of CBF will be further validated, they will leverage the typically high signal-to-noise ratio of NIRS, and provide a strong complement to the NIRS assessment of cerebral blood volume. In fact, the continuous co-registration of local CBV and CBF provides a rich hemodynamic characterization that may correlate with functional, physiological, and pathological states.

Funding

National Institutes of Health (NIH) (R01 NS095334, R21 EB020347).

Disclosures

The authors declare that there are no conflicts of interest related to this article.