Abstract
In tissue engineering, porous biodegradable scaffolds are developed with morphological, chemical and mechanical properties to promote cell response. Therefore, the scaffold characterization at a (sub)micrometer and (bio)molecular level is paramount since cells are sensitive to the chemical signals, the rigidity, and the spatial structuring of their microenvironment. In addition to the analysis at room temperature by conventional quasi-static (0.1–45 Hz) mechanical tests, the ultrasonic (10 MHz) and μ-Brillouin inelastic light scattering (13 GHz) were used in this study to assess the dynamical viscoelastic parameters at different frequencies of elastomeric scaffolds. Time-temperature superposition principle was used to increase the high frequency interval (100 MHz–100 THz) of Brillouin experiments providing a mean to analyse the viscoelastic behavior with the fractional derivative viscoelastic model. Moreover, the μ-Raman analysis carried out simultaneously during the μ-Brillouin experiment, gave the local chemical composition.
1. Introduction
The aim of tissue engineering is to develop porous biodegradable structures (scaffolds) adequate for the migration, the adhesion, the proliferation and the differentiation of cells seeded in the material before the implantation or recruited from the implantation site [1]. It is well known that the scaffold properties, such as surface chemistry, porosity and mechanical properties, affect cells response [2–5]. Indeed, surface chemistry has a huge impact on the local adhesion, the cell spreading and overall biocompatibility [6], while the mechanical properties in relation to the porosity influence the cell form, proliferation, and cortical stiffness [7]. As a consequence, it is of very high importance to be able to deeply characterize scaffolds at (sub)micrometer and (bio)molecular levels. For this purpose, μ-Raman spectroscopy is a technology increasingly used in the field of biomedical research. This technique uses the inelastic scattering of light by matter to give informations related to the (bio)chemical composition of cells, tissues, and scaffolds [8]. Regarding μ-Brillouin spectroscopy, this non-destructive and non-invasive technique has only been considered recently for the biomedical field [9]. Based on the analysis of the frequency spectrum (position and full width at half maximum of the inelastic peaks) of the light scattering induced by the coupling of a bulk acoustic wave with the light propagating in the matter [10], it is possible to quantify locally the viscoelastic properties of cells and biomaterials.
Polyurethane-based scaffolds have been increasingly used in tissue engineering since the elastomeric character offers an alternative to conventional rigid thermoplastic scaffolds [11]. Indeed, elastomeric scaffolds can be used to regenerate soft and dynamic tissues such as skin, tendons, and muscles, since the mismatch of Young moduli is reduced and the material is able to recover large mechanical deformations. CSPBAT has developed biodegradable poly(ester-urethane)-based scaffolds (PCLU) that can support the adhesion of cells [12]. This study shows the potential of the combination use of the nanoindentation tests, the pulse-echo ultrasonic technique and of the μ-Brillouin spectroscopy vs temperature to assess some dynamical viscoelastic parameters of elastomeric scaffolds at very different frequencies (Hz–100 THz). Moreover, the scaffold longitudinal moduli obtained by Brillouin spectroscopy are compared with the experimental data of conventional quasi-static (0.1 Hz) mechanical tests in an uni-axial stress mode of compression, as well as in a tri-axial stress mode of compression to mimic the containment to which the material can be subjected after implantation in cavitary defects. Finally, the scaffold chemical properties were also followed by an original coupled μ-Raman–μ-Brillouin spectroscopies system and compared with the results obtained from infrared spectroscopy.
2. Methods
2.1. Materials
All solvents were purchased from Fisher and used as received. Triol poly(ϵ-caprolactone) oligomers, hexamethylene diisocyanate, Span 80, dibutyltin dilaurate, were purchased from Sigma-Aldrich.
2.2. Elaboration and characterization of PCLU scaffolds
PCLU scaffolds were obtained through a high internal phase emulsion process named polyHIPE, and characterized by determination of their density, porosity and pore inter-connectivity, as previously described [12]. The glass transition temperature was estimated below −80 °C by differential scanning calorimetry.
The scaffold morphology was monitored using an environmental scanning electron microscope (ESEM TM3000 - Hitachi).
The chemical composition of PCLU scaffolds was monitored by Fourier-transformed infrared spectroscopy (FTIR Nicolet 380 - Thermo Scientific) in an attenuated total reflectance mode (ATR - Smart Omni Sampler) within the range 500-4000 with a resolution of 4 , as well as by μ-Raman analysis. Here, we used an original setup that enabled to perform simultaneously, μ-Raman and μ-Brillouin local analysis. Raman spectra were recorded with the same microscope setup from the backscattered light with a Raman spectrometer (Horiba Jobin-Yvon iHR 550, 300 lines grating, 50 μm entrance slit). More details on this setup can be found in Ref. [13].
The number average molecular weight between cross-links of a porous cross-linked structure can be determined through swelling measurement. For this purpose, PCLU scaffolds were immersed in toluene at room temperature up to swelling equilibrium. At the end of the immersion period, PCLU scaffolds were removed from toluene, rapidly wiped to remove solvent excess at the sample surface, and weighted to obtain the wet mass of the scaffold. The apparent polymer volume fraction in the porous system was calculated using Eq. (1) [14]:
| (1) |
where is the mass of the scaffold before swelling, is the mass of the scaffold after swelling, ρs is the density of the swelling agent (toluene), is the density of the non-porous PCLU network prepared in the same conditions compared to the porous scaffold without the addition of water, and is the density of the porous PCLU scaffold.
Thereafter, the actual polymer volume fraction , which is related to the measured apparent polymer volume fraction determined from Eq. (1) and the porosity P of the scaffold, can be expressed by Eq. (2) [14]:
| (2) |
Finally, the number average molecular weight between cross-links is calculated using the Flory-Rehner equation, Eq. (3) [15]:
| (3) |
where Vs is the molar volume of the swelling agent (toluene), is the specific volume of the polymer, χ is the Flory polymer-solvent interaction parameter calculated from the solubility parameters using Bristow and Watson equation, Eq. (4) [15]:
| (4) |
where Vs is the molar volume of the solvent (toluene), R is the universal gas constant, T is the absolute temperature, δs is the solubility parameter of the solvent, and δp is the solubility parameter of the polymer network calculated using the group contribution method based on Van Krevelen’s molar attraction constants [16].
2.3. Compression tests
The mechanical behavior of PCLU scaffolds was determined by compression test carried out in the axial direction to the foam rise with a universal machine. Specimens’ dimensions were 8 mm in height and 18 mm in diameter. Compressive properties were determined in a 500 N force range, a 7 mm displacement range, and a displacement rate of 5 . The stress/strain relation was computer-recorded and processed using Realview 3.0 software. The linear regression procedure was applied for determination of elastic moduli at the beginning of the curve for the porous PCLU scaffold, and at the end of the curve for the non-porous PCLU material. The typical acquisition time of the linear slope (strain increasing of 0.05–0.1) was of ∼10 s corresponding to a 1/10 Hz frequency for this test. The mechanical behavior of confined PCLU scaffolds was also determined in a similar experiment except that the scaffold was confined in a hole of 16 mm in diameter.
2.4. Nanoindentation tests
The mechanical properties of the films were determined from load-displacement curves obtained with a MTS Nanoindenter XP apparatus. Nanoindentation tests with continuous stiffness measurement (CSM) were carried out for indentation modulus EIT measurements. All experiments were performed with a diamond-type Berkovich indenter. The strain rate and the frequency oscillation of the displacement was varied in the range 0.01–0.2 and 1–45 Hz, respectively. The parameters set for the measurement are a depth of 2 μm and an amplitude of 2 nm. Each value was computed as the average of 20 measurements in the range of 0–2000 nm penetration depth by using the Oliver and Pharr method [17].
2.5. Ultrasound echoes
The pulse-echo technique was employed to measure the longitudinal sound velocity VL from the time of flight of the echoes that are traveling forth and back along the length of two PCLU dense samples (3.5 mm and 3.8 mm) of the cylindrical shaped sample with 10 mm in diameter and opposite parallel faces. The travel time of ultrasonic waves propagating through the sample with a 10 MHz frequency was measured using a Sofranel D20 ultrasound device with a measuring time accuracy of 0.5 ns. The accuracy for the sound velocity is about 0.1 %. Acoustic attenuation was not measured.
2.6. μ-Brillouin spectroscopy and time-temperature superposition principle
The longitudinal sound velocity VL was measured locally (laser spot size of a few ) by the μ-Brillouin light scattering technique [8, 9, 13] in the backscattering geometry with a long-working-distance (6 mm) x100 objective (Mitutoyo plan-apo infinity corrected (N.A. 0.7) and an entrance pinhole = 300 μm for the Brillouin spectrometer. More details about the setup and procedure are given in Ref. [13]. We just give here a brief summary. For Brillouin scattering experiments, the incoming light from a single longitudinal mode laser at nm (Coherent Verdi 6) was coupled to the microscope. The intensity was kept below 100 mW at the sample. The light back-scattered into the objective was analyzed with a 2x3-pass tandem Fabry-Perot interferometer (Sandercock TFP-1) to record its Brillouin spectrum. The wavevector modulus k of the probe bulk acoustic wave is defined by:
| (5) |
1.6 ± 0.05 is the refractive index of the PCLU material. From the measurement of the Brillouin frequency shift fB of the inelastic scattered light, the sound velocity VL is calculated by:
| (6) |
The intensity as a function of the frequency shift f was fitted with a damped harmonic oscillator (DHO) function considering a Brillouin frequency shift fB and a full-width at half-maximum ΓB, convoluted with the instrumental response well reproduced by a Gaussian profile (line-width 418 MHz). The dynamical longitudinal viscosity η can be estimated from the natural line-width (ΓB) obtained after deconvolution of the instrumental line-width, by the following relation:
| (7) |
The complex longitudinal modulus , M’ being the storage modulus and M” the loss modulus, is defined by:
| (8) |
The same mechanical characterization (i.e. the longitudinal modulus M) carried out at room temperature (20 °C) by varying the frequency could only be applied for 10 MHz (ultrasound echoes) and 13 GHz (BLS). Nevertheless, an attempt to estimate the high frequency behavior of M is accessible via the time-temperature superposition principle (TTSP) by performing BLS as a function of the temperature. It states that the effect of changing the temperature is the same as applying a multiplication factor to the timescale (frequency), , which is given by the William-Landel-Ferry (WLF) equation [18]:
| (9) |
Tr is the reference temperature (here, 20 °C) at which we calculate the translated frequency with the modulus , in case of a thermo-rheologically simple polymer (i.e. ) [19]. In some cases, for heterogeneous materials with multiple relaxation times, it can be necessary to consider a vertical shift for the modulus. This shift is related to thermal expansion effects, which for most polymers can be neglected. Nevertheless, it can be theoretically evaluated if the thermal expansion of the polymer is known [19], but it is not our case. A direct calculation considering the minimisation of a criterion based on the Kramers-Kronig relations has also been proposed by Rouleau et al. [20]. To partially overcome this difficulty, we considered the closest modulus measured at 10 MHz and room temperature by ultrasounds, as a reference, through which the used viscoelastic model have to go through and as closest as possible to the higher frequency data obtained by BLS. Similar methods in which the shifts coefficients are identified along the parameters of a viscoelastic model have already been proposed [21, 22] This concept works well for amorphous and self-adhesive rubber, as an example, and allows for the construction of master curves of the complex modulus on a broad frequency scale [18, 23].
3. Results and discussions
3.1. Scaffold elaboration and structural characterization
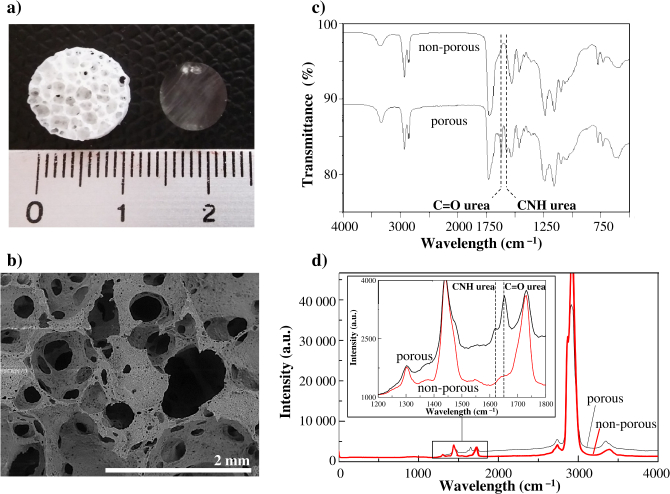
Various elastomeric polymers have been proposed as scaffolds for tissue engineering. Among available biocompatible and biodegradable elastomers, polyurethane, poly(ester-urethane) and poly(ester-urethane-urea) are of much interest since they can be synthesized with various chemical and mechanical properties, as well as with various degradation rates [11]. In this study, poly(ester-urethane)-based scaffolds (PCLU) were elaborated from a high internal phase emulsion in which oligoesters contained in the continuous phase were cross-linked. Depending of the emulsion parameters, various multi-scale and interconnected porosities can be obtained [12]. More specifically here, PCLU scaffolds were designed to present a 85.1% open-porosity that did not contain closed voids, and pore sizes ranging from below 150 to 1800 μm (Fig. 1(a) - left and Fig. 1(b)). A non-porous material, which is transparent, was also prepared in the same conditions compared to the PCLU scaffold without the addition of water (Fig. 1(a) - right).
Fig. 1.
(a) Photography of the porous PCLU scaffold (left) and non-porous material (right); (b) ESEM image of the porous PCLU scaffold; (c) FTIR-ATR analysis of the non-porous material and the porous PCLU scaffold; (d) μ-Raman analysis of the non-porous material and the porous PCLU scaffold. (dotted lines indicate urea functions).
It was demonstrated that during the scaffold elaboration, side reactions with water arose leading to the formation of urea moieties [12]. Thereby, the determination of the scaffold chemical composition is critical as it may affect the degradation behavior, as well as the mechanical properties since urea moieties are known to act as hard segments in poly(ester-urethane-urea) [24]. The FTIR and the μ-Raman analyses of the porous PCLU scaffold and the non-porous material exhibits characteristic bands of poly(ester-urethane)-based material (Fig. 1(c) and 1(d)) [12]. Indeed in the μ-Raman spectrum (Fig. 1(d)), it is possible to identify the following chemical groups for the non-porous material [25, 26]: stretching of urethane NH groups shifted by H-bonding at 3385 , asymmetric and symmetric stretching of groups at 2925, 2870 and 2740 , stretching of urethane and ester free groups at 1731 and hydrogen-bonded groups for the shoulder of the peak at 1639 , bending of urethane NH group and stretching of CN groups at 1544 , bending of groups at 1451 and 1372 , and stretching of CN and CO groups at 1304 . For the porous PCLU scaffold, it was also identified two additional peaks attributed to urea and groups at 1650 and 1620 . μ-Raman spectroscopy is very interesting for further scaffold analysis since the technique allows the enhancement of polyurethane characterization and can be used to follow polyurethane degradation processes at a molecular level [25].
3.2. Determination of the scaffold quasi-static mechanical properties
Due to the presence of additional urea moieties in the structural composition of PCLU scaffolds, it is necessary to confirm the retention of the elastomeric behavior. Therefore, the quasi-static mechanical properties were determined through compression tests. In an uni-axial stress mode of compression, that is to say when the scaffold only developed stresses in the compression direction and expanded freely in the two other directions, a typical compressive stress-strain response of an elastomeric open-cell foam was found (Fig. 2(a)) [27]. At the beginning of the stress-strain curve, the stress depends linearly on the strain and it is possible to determine the effective elasticity modulus of the porous scaffold (Fig. 2(b)). Then, the post-buckling domain is characterized by a long elastic plateau due to pores collapse. Finally, strain increases dramatically when the densification is reached and it is possible to determine the elastic modulus of the related non-porous material () (Fig. 2(a)).
Fig. 2.
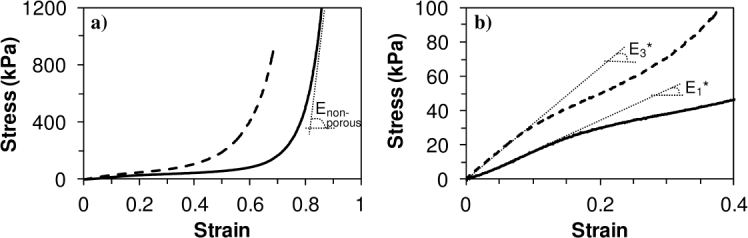
Mechanical behavior of the PCLU scaffold under uni-axial (solid line) and tri-axial (dotted line) stress modes of compression: (a) all strain range; (b) low strain range.
The compression test gave values of 16 ± 2 MPa for and 161 ± 14 kPa for at a frequency 1/10 Hz corresponding to the acquisition time of the linear slope. For comparison, the nanoindentation tests of the non-porous material provided Young modulus of 49 ± 7 MPa, 42 ± 7 MPa and 35 ± 8 MPa, for 45 Hz, 10 Hz and 1 Hz frequencies, respectively, at a fixed strain rate of 0.05 . Typical load and unload force-displacement curves are shown in Fig. 3 and evidence the stiffening as the frequency is increasing.
Fig. 3.
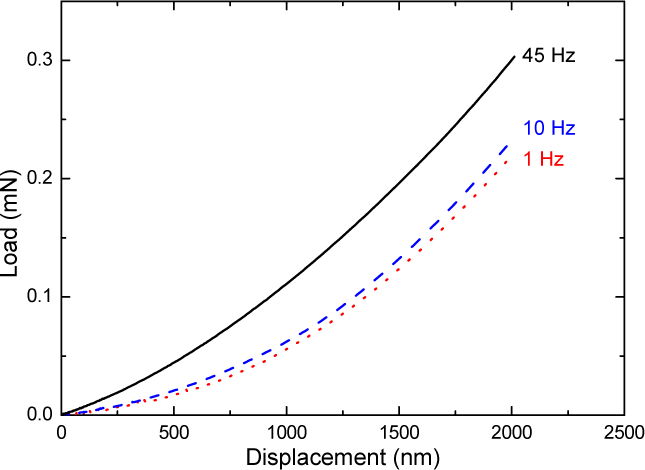
Load-displacement curves of the dense PCLU from nanoindentation tests for three different frequency (1 Hz, 10 Hz and 45 Hz) and a fixed strain rate of 0.05 s−1.
The effective elasticity modulus found for the PLCU scaffold is in good agreement with the expected theoretical value ( = 165 kPa with N = 2.4) evaluated using Eq. (10) [28]:
| (10) |
where P is the porosity of the scaffold (P = 85.1%), and N is an exponent value which varies between 1 and 3 depending on pore shape and orientation.
Moreover, the number average molecular weight between cross-links of the PCLU scaffold can be evaluated according to the theory of the rubber elasticity using using Eq. (11) [29]:
| (11) |
where ρ is the PCLU scaffold density (159 ), R is the universal gas constant, and T is the absolute temperature. The number average molecular weight between cross-links was found to be 7340 which is in good agreement with the value found by the swelling experiments ( = 7930 ± 1600 ).
The mechanical properties of the PLCU scaffold were also studied when confining the scaffold in a hole to mimic the containment to which the material can be subjected after implantation in cavitary defects. Therefore, the scaffold developed stresses in all directions. As expected for the tri-axial stress mode of compression, the stress-strain curve is similar to that under uni-axial stress mode of compression (Fig. 2(a)); but the compressing requires larger stresses. During tri-axial stress mode of compression, the effective elasticity modulus was found to be 321 kPa (Fig. 2(b)), which is in good agreement with the theoretical modulus ( = 308 kPa with N = 2.4 and = 0.425) calculated using Eq.(12) [27]:
| (12) |
where is the elastic modulus of the non-porous material ( = 16 ± 2 MPa), P is the porosity of the scaffold (P = 85.1%), and is the Poisson's ratio of the foam which varies between 0.1 and 0.4 for polymeric foams - it was found for instance to be 0.4 for polyester foams and 0.3-0.5 for polyurethane foams [30, 31]. We used a Poisson ratio ν = 0.425 to convert the Young’s modulus E measured at low frequency (compression and nanoindentation) to the longitudinal storage modulus , in order to compare later to the high frequency ones (ultrasonic and BLS). Finally, it is possible to conclude from the quasi-static mechanical tests that the porous PCLU scaffold behaves as elastomeric foam with appropriate elastic modulus for soft tissue regeneration [32].
3.3. Determination of the scaffold dynamical viscoelastic properties by μ-Brillouin spectroscopy and ultrasound echoes
A typical spectrum obtained at room temperature, is shown in Fig. 4(a) for the non-porous material and the porous PCLU scaffold. Their Brillouin frequency shift fB lies close to 13 GHz while their full line-width at half-maximum are = 2140 MHz and = 1873 MHz, respectively. We measured VL = 2160 ± 110 m/s and the related longitudinal elastic modulus M′ = 4.8 ± 0.4 GPa. The dynamical longitudinal viscosity η defined by Eq. (7), could be estimated from the natural line-width obtained after deconvolution of the instrument line-width, 1.3 mPa.s. It is of the same order of magnitude as for soft glassy polymers [33] in the glassy state.
Fig. 4.
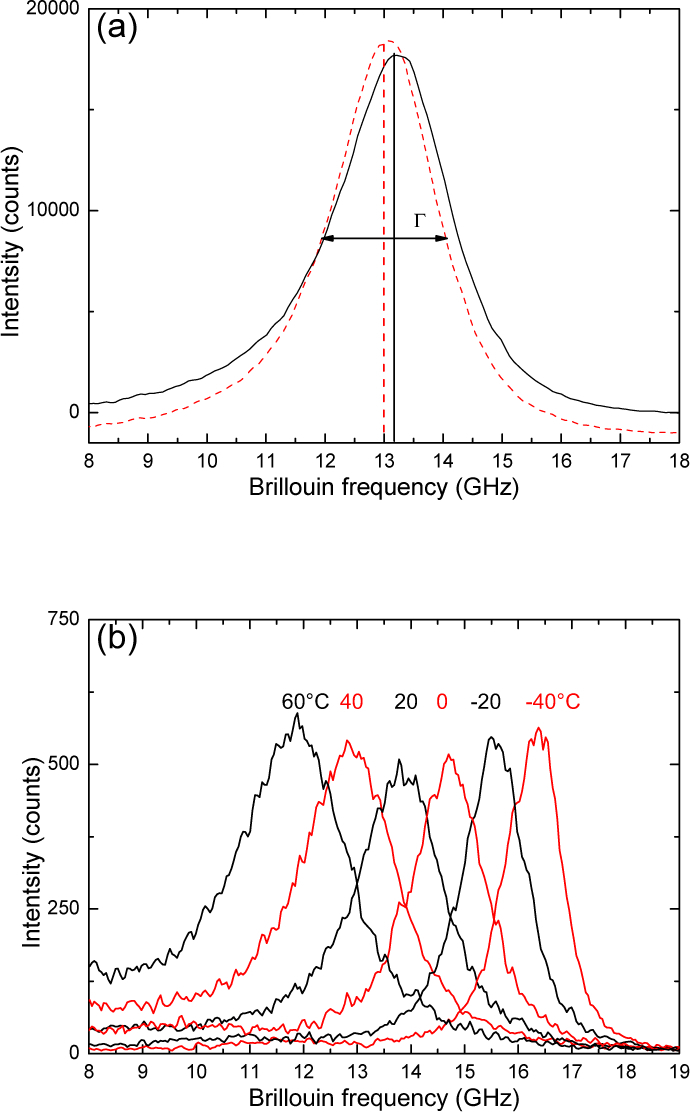
(a) μ-Brillouin light scattering spectra of the non-porous material (dotted line) and the porous PCLU scaffold (solid line) at room temperature (20 °C). The peak is the inelastic scattering of the incident light by the longitudinal bulk acoustic wave with a Brillouin frequency shift fB ~ 13 GHz. (b) μ-Brillouin light scattering spectra of the non-porous material as a function of the temperature (−40 °C, + 60 °C).
These high-frequency results lead to a stiffer material than the ones measured by the ultrasonic pulse-echo method with a 10 MHz longitudinal transducer, VL = 1773 ± 53 m/s and M′ = 3.2 ± 0.15 GPa. We plotted the high frequency longitudinal storage modulus together with the quasi-static results in a log-log scale, as a function of the frequency, in Fig. 5. Finite relaxation time and low compressibility provide a qualitative explanation for the observed large difference in modulus between the ultrasound, Brillouin light scattering and quasi-static mechanical tests.
Fig. 5.
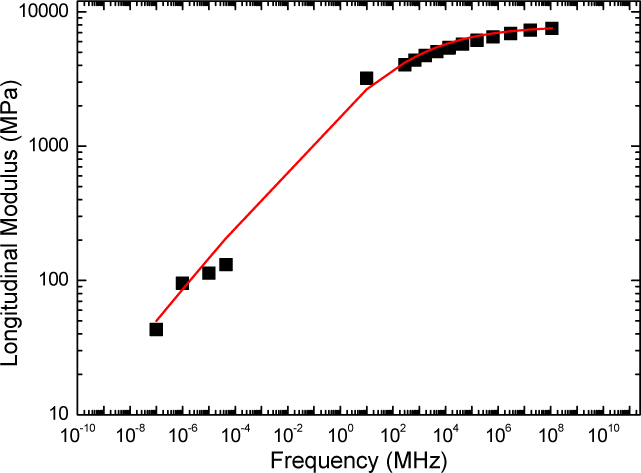
Longitudinal storage modulus M′ as a function of the frequency f (log-log scale) of the PCLU dense polymer. The line (red-color on-line) is a fit using the fractional derivative model described in the text.
Indeed, recent rheological studies have shown that the mechanical modulus (M) of many soft materials follows a power-law dependence on frequency (f):
| (13) |
Here, M0 and f0 are scale factors for stiffness and frequency, respectively, and α is the scaling exponent factor (α = 0 for purely elastic and 0 < α < 1 for viscoelastic materials) [34, 35]. can be related to the “noise temperature” x, introduced in the the soft glassy rheology (SGR) model [36]. Considering the Young modulus measured at low frequency (0.1 Hz–45 Hz), a best-fit provided α = 0.17 and = 2.48. Our α value lies in the range 0.1 - 0.3 measured for several different cells in Ref. [34]. Additional information on the dynamical shear modulus G are needed to determine separately, the scale factors E0 and f0 [37].
For a more complete description of the modulus vs frequency behavior, a viscoelastic model is needed. The Cole-Davidson model [38], the Maxwell model [39] or the fractional derivative model [40] have been successfully employed to reproduce such behavior considering at least one relaxation time. In order to do such analysis, more data were necessary. We applied the time-temperature superposition principle to the temperature BLS results shown in Fig. 4(b) in combination with the employed viscoelastic model, described below. The horizontal translational parameter aT defined by the two constants, K and K (see, Eq. (9)) was reasonably determined, ensuring an overall agreement between the viscoelastic model and the experiments (see Fig. 5).
In order to well interpret the storage modulus M′ variation over the whole frequency range, using only a few number of parameters, we consider a fractional derivative model: the complex modulus reads
| (14) |
With (in fact, ), GPa, and τ = 1 ns, the calculated storage modulus variation frequency fits well the measurements (see Fig.5). According to this model, the modulus tends to the unrelaxed modulus for frequencies much larger than . This could explain the observed slow increase of M′ for higher frequencies. Moreover for frequencies much smaller than , the modulus variation can be fitted by a power law as previously discussed: for and ,
Supplementary information are still necessary, either on the loss-modulus and on the storage longitudinal modulus M′ in the mHz–kHz range, in order to explore with more details the relaxation processes at lower frequency (< 0.1 Hz) and measuring the relaxed modulus M0.
4. Conclusions
We demonstrated that PCLU scaffolds seem to possess the required mechanical features for soft tissue engineering since the quasi-static compression tests provided the effective Young modulus of the porous material, and confirmed the elastomeric behavior. The use of the ultrasonic at room temperature and μ-Brillouin inelastic light scattering as a function of the temperature (- 40 °C, + 60 °C) provided a reasonable insight on the the high-frequency dynamical viscoelastic parameters and the relaxation time. The fractional derivative viscoelastic model with one single relaxation process successfully reproduced the longitudinal modulus evolution as a function of the frequency (0.1 Hz–100 THz). Moreover, combining μ-Raman and μ-Brillouin spectroscopies allowed to assess locally and simultaneously the chemical composition and the viscoelastic properties of the scaffold that does not differ significantly from the dense polymer. Therefore, the coupling of the two techniques should allow to establish relationship between local molecular variations and changes in mechanical properties during scaffold degradation, extra-cellular matrix deposition and cell adhesion.
A typographical correction was made to the author affiliations.
Funding
Institute of Experimental Sciences of Université Paris 13 (BIO-POLYM and BIO-POLYM CELL projects) and PEPS-Mécanobiologie from CNRS (BRIPLASM project).
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References
- 1.Ko I.K., Lee S.J., Atala A., Yoo J.J., “In situ tissue regeneration through host stem cell recruitment,” Exp. & Mol. Medicine 45, e57 (2013). 10.1038/emm.2013.118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Tamada Y., Ykada Y., “Effect of preabsorbed proteins on cell adhesion to polymer surfaces,” J. Colloid Interface Sci. 155, 334–339 (1993). 10.1006/jcis.1993.1044 [DOI] [Google Scholar]
- 3.Melchels F.P.W., Barradas A.M.C., van Blitterswijk C.A., de Boer J., Feijen J., Grijpma D.W., “Effects of the architecture of tissue engineering scaffolds on cell seeding and culturing,” Acta Biomater. 6, 4208–4217 (2010). 10.1016/j.actbio.2010.06.012 [DOI] [PubMed] [Google Scholar]
- 4.Mastrogiacomo M., Scaglione S., Martinetti R., Dolcini L., Beltrame F., Cancedda R., Quarto R., “Role of scaffold internal structure on in vivo bone formation in macroporous calcium phosphate bioceramics,” Biomaterials 27, 3230–3237 (2006). 10.1016/j.biomaterials.2006.01.031 [DOI] [PubMed] [Google Scholar]
- 5.Breuls R.G.M., Jiya T.U., Smit T.H., “Scaffold stiffness influences cell behavior: opportunities for skeletal tissue engineering,” The Open Orthop. J. 2, 103–109 (2008). 10.2174/1874325000802010103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chang H.-I., Wang Y., “Cell responses to surface and architecture of tissue engineering scaffolds,” in “Regenerative medicine and tissue engineering - cells and biomaterials,” Eberli D., ed. (InTech, 2011). 10.5772/21983 [DOI] [Google Scholar]
- 7.Tee S.-Y., Fu J., Chen C.S., Janmey P.A., “Cell shape and substrate rigidity both regulate cell stiffness,” Biophys. J. 100, L25–L27 (2011). 10.1016/j.bpj.2010.12.3744 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ember K.J.I., Hoeve M.A., McAughtrie S.L., Bergholt M.S., Dwyer B.J., Stevens M.M., Faulds K., Forbes S.J., Campbell C.J., “Raman spectroscopy and regenerative medicine: a review,” npj Regen. Medicine 2, 12 (2017). 10.1038/s41536-017-0014-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Antonacci G., Braakman S., “Biomechanics of subcellular structures by non-invasive Brillouin microscopy,” Sci. Reports 6, 37217 (2016). 10.1038/srep37217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Djemia P., “La diffusion Brillouin pour caractériser les propriétés élastiques ou magnétiques de multicouches,” in “Instrumentation, Mesure, Métrologie - Les ondes en instrumentation VOL 9/1–2,” Elmazria O., ed. (Hermes - Lavoisier, 2009). [Google Scholar]
- 11.Chen Q., Liang S., Thouas G.A., “Elastomeric biomaterials for tissue engineering,” Prog. Polym. Sci. 38, 584–671 (2013). 10.1016/j.progpolymsci.2012.05.003 [DOI] [Google Scholar]
- 12.Changotade S., Radu-Bostan G., Consalus A., Poirier F., Peltzer J., Lataillade J.-J., Lutomski D., Rohman G., “Preliminary in vitro assessment of stem cell compatibility with cross-linked poly(ϵ -caprolactone urethane) scaffolds designed through high internal phase emulsions,” Stem Cells Int. 2015, 283796 (2015). 10.1155/2015/283796 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pallares G., Mekki Azouzi M. El, González M.A., Aragones J.L., Abascal J.L.F., Valeriani C., Caupin F., “Anomalies in bulk supercooled water at negative pressure,” Proc. Natl. Acad. Sci. USA 111, 7936 (2014). 10.1073/pnas.1323366111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Brannon-Peppas L., Peppas N.A., “The equilibirum swelling behavior of porous and non-porous hydrogels,” in “Absorbent polymer technology,” Brannon-Peppas L., Harland R.S., eds. (Elsevier Science Publishers, 1990). 10.1016/B978-0-444-88654-5.50009-1 [DOI] [Google Scholar]
- 15.Barikani M., Hepburn C., “Determination of crosslink density by swelling in the castable polyurethane elastomer based on 1/4-cyclohexane diisocyanate and para-phenylene diisocyanate,” Iran. J. Polym. Sci. & Technol. 1(1), 1–5 (1992). [Google Scholar]
- 16.Rohman G., Grande D., Lauprêtre F., Boileau S., Guérin P., “Design of porous polymeric materials from interpenetrating polymer networks (IPNs): poly(DL-lactide)/poly(methyl methacrylate)-based semi-IPN systems,” Macromolecules 38, 7274–7285 (2005). 10.1021/ma0501390 [DOI] [Google Scholar]
- 17.Oliver W.C., Pharr G.M., “Measurement of hardness and elastic modulus by instrumented indentation: advances in understanding and refinements to methodology,” J. Mater. Res. 19, 3–20 (2005). 10.1557/jmr.2004.19.1.3 [DOI] [Google Scholar]
- 18.Ferry J.D., “Viscoelastic Properties of Polymers,” (John Wiley & Sons, New Jersey, USA, 1980). [Google Scholar]
- 19.Dealy J., Plazek D., “Time-Temperature Superposition- a User’s Guide,” Rheol. Bull. 78, 16–31 (2009). [Google Scholar]
- 20.Rouleau L., Deü J. -F., Legay A., Le Lay F., “Application of Kramers-Kronig relations to time-temperature superposition for viscoelastic materials,” Mech. Mater. 65, 66–75 (2013). 10.1016/j.mechmat.2013.06.001 [DOI] [Google Scholar]
- 21.Guedes R. M., “A viscoelastic model for a biomedical ultra-high molecular weight polyethylene using the time-temperature superposition principle,” Polym. testing 30, 294–302 (2011). 10.1016/j.polymertesting.2011.01.006 [DOI] [Google Scholar]
- 22.Madigosky W. M., Lee G. F., Niemiec J. M., “A method for modeling polymer viscoelastic data and the temperature shift function,” J. Acoust. Soc. Am. 119, 3760–3765 (2006). 10.1121/1.2195292 [DOI] [Google Scholar]
- 23.Rouleau L., Pirk R., Pluymers B., Desmet W., “Characterization and Modeling of the Viscoelastic Behavior of a Self-Adhesive Rubber Using Dynamic Mechanical Analysis Tests,” J. Aerosp. Technol. Manag. São José dos Campos 7(2), 200–208 (2015). 10.5028/jatm.v7i2.474 [DOI] [Google Scholar]
- 24.Rosthauser J. W., Haider K. W., Steinlein C., Eisenbach C.D., “Mechanical and dynamic mechanical properties of polyurethane and polyurethane/polyurea elastomers based on 4,4'-diisocyanatodicyclohexyl methane,” J. Appl. Polym. Sci. 64(5), 957–970 (1997). [DOI] [Google Scholar]
- 25.Janik H., Pałys B., Petrovic Z. S., “Multiphase-separated polyurethanes studied by micro-Raman spectroscopy,” Macromol. Rapid Commun. 24(3), 265–268 (2003). 10.1002/marc.200390039 [DOI] [Google Scholar]
- 26.Chollet M., Horgnies M., “Analyses of the surfaces of concrete by Raman and FT-IR spectroscopies: comparative study of hardened samples after demoulding and after organic post-treatment,” Surf. Interface Analysis 43, 714–725 (2011). 10.1002/sia.3548 [DOI] [Google Scholar]
- 27.Ben-Dor G., Mazor G., Cederbaum G., Igra O., “Stress-strain relations for elastomeric foams in uni-, bi- and tri-axial compression modes,” Arch. Appl. Mech. 66, 409–418 (1996). 10.1007/s004190050079 [DOI] [Google Scholar]
- 28.Hou Q., Grijpma D. W., Feijen J., “Porous polymeric structures for tissue engineering prepared by a coagulation, compression moulding and salt leaching technique,” Biomaterials 24, 1937–1947 (2003). 10.1016/S0142-9612(02)00562-8 [DOI] [PubMed] [Google Scholar]
- 29.Yang J., Webb A.R., Pickerill S.J., Hageman G., Ameer G.A., “Synthesis and evaluation of poly(diol citrate) biodegradable elastomers,” Biomaterials 27, 1889–1898 (2006). 10.1016/j.biomaterials.2005.05.106 [DOI] [PubMed] [Google Scholar]
- 30.Lakes R., “Foam structures with a negative Poisson's ratio,” Sciences 235, 1038–1040 (1987). 10.1126/science.235.4792.1038 [DOI] [PubMed] [Google Scholar]
- 31.Widdle Jr R.D., Bajaj A.K., Davies P., “Measurement of the Poisson's ratio of flexible polyurethane foam and its influence on a uniaxial compression model,” Int. J. Eng. Sci. 46, 31–49 (2008). 10.1016/j.ijengsci.2007.09.002 [DOI] [Google Scholar]
- 32.Burdick J. A., Mauck R. L., “ Biomaterials for tissue engineering applications,” (Springer-Verlag, 2011). 10.1007/978-3-7091-0385-2 [DOI] [Google Scholar]
- 33.Fioretto D., Scarponi F., “Dynamics of a glassy polymer studied by Brillouin light scattering,” Mater. Sci. Eng., A 521-522, 243–246 (2009). 10.1016/j.msea.2008.09.095 [DOI] [Google Scholar]
- 34.Fabry B., Maksym G.N., Butler J.P., Glogauer M., Navajas D., Fredberg J.J., “Scaling the microrheology of living cells,” Phys. Rev. Lett. 87, 148102 (2001). 10.1103/PhysRevLett.87.148102 [DOI] [PubMed] [Google Scholar]
- 35.Sollich P., Lequeux F., Hébraud P., Cates M.E., “Rheology of soft glassy materials,” Phys. Rev. Lett. 78, 2020–2023 (1997). 10.1103/PhysRevLett.78.2020 [DOI] [Google Scholar]
- 36.Sollich P., “Rheological constitutive equation for a model of soft glassy materials,” Phys. Rev. E. 58, 738–759 (1998). 10.1103/PhysRevE.58.738 [DOI] [Google Scholar]
- 37.Scarcelli G., Kim P., Yun S. H., “In vivo measurement of age-related stiffening in the crystalline lens by Brillouin optical microscopy,” Biophys. J. 101, 1539–1545 (2011). 10.1016/j.bpj.2011.08.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Davidson D. W., Cole R. H., “Dielectric Relaxation in Glycerine,” J. Chem. Phys. 18, 1417 (1951). 10.1063/1.1747496 [DOI] [Google Scholar]
- 39.Renaud F., Dion J. L., Chevallier G., Tawfiq I., Lemaire R., “A New Identification Method of Viscoelastic Behavior: Application to the Generalized Maxwell Model,” Mech. Syst. Signal Process. 25(3), 991–1010 (2011). 10.1016/j.ymssp.2010.09.002 [DOI] [Google Scholar]
- 40.Pritz T., “Five-Parameter Fractional Derivative Model for Polymeric Damping Materials,” J. Sound Vib. 265(5), 935–952 (2003). 10.1016/S0022-460X(02)01530-4 [DOI] [Google Scholar]