Spatiotemporal optical coherence (STOC) manipulation suppresses coherent cross-talk in full-field swept-source optical coherence tomography

Abstract

Full-field swept-source optical coherence tomography (FF-SS-OCT) provides high-resolution depth-resolved images of the sample by parallel Fourier-domain interferometric detection. Although FF-SS-OCT implements high-speed volumetric imaging, it suffers from the cross-talk-generated noise from spatially coherent lasers. This noise reduces the transversal image resolution, which in turn, limits the wide adaptation of FF-SS-OCT for practical and clinical applications. Here, we introduce the novel spatiotemporal optical coherence (STOC) manipulation. In STOC the time-varying inhomogeneous phase masks are used to modulate the light incident on the sample. By properly adjusting these phase masks, the spatial coherence can be reduced. Consequently, the cross-talk-generated noise is suppressed, the transversal image resolution is improved by the factor of$\sqrt{2}$, and sample features become visible. STOC approach is validated by imaging 1951 USAF resolution test chart covered by the diffuser, scattering phantom and the rat skin ex vivo. In all these cases STOC suppresses the cross-talk-generated noise, and importantly, do not compromise the transversal resolution. Thus, our method provides an enhancement of FF-SS-OCT that can be beneficial for imaging biological samples.

1. Introduction

Full-field optical coherence tomography (FF-OCT) achieves high-resolution volumetric images of the sample with wide-field illumination and parallel, interferometric detection of the backscattered light [1–6]. Contrary to conventional OCT systems [7], FF-OCT does not rely on the transversal scanning of the incident beam. Instead, the sample volume is illuminated at once and the interferometric signal is recorded by a multi-pixel light sensor or imaging spectrometer [8]. Like any other OCT systems, FF-OCT uses light sources with low-temporal coherence to introduce axial sectioning. An additional advantage of such “coherence gating” is the rejection of backscattered light that travels longer than the effective coherence time of the light source [7]. Very recently, FF-OCT was successfully applied for in vivo high-resolution imaging of the human retina [9–12]. Therefore, FF-OCT becomes a promising modality for retinal imaging. Especially for applications that aim at depicting true eye topology [13].

Originally, in FF-OCT, the interference pattern is produced in time-domain by scanning the reference mirror. Hence, FF-OCT can be further advanced to significantly higher speeds with possibly improved signal-to-noise ratio, required for clinical applications, by utilizing the Fourier- (or spectral-) domain detection. In particular, full-field swept-source OCT (FF-SS-OCT) achieves this goal with rapidly tunable lasers [9,14–16]. However, such lasers are highly spatially coherent, which in turn, leads to the cross-talk-generated noise [17], that can significantly reduce the transversal image resolution and hide important sample features. The cross-talk-generated noise is due to the interference of the scattered light (not rejected by temporal coherence gate), propagating in parallel detection channels. The issue of cross-talk-generated noise thus disables a wide adaptation of the FF-OCT for imaging biological samples.

This problem has been tackled by several researchers. Pioneering studies were done by Karamata et al. [17–19], who showed that cross-talk-generated noise can be completely suppressed if spatially incoherent light source (thermal lamp or LED) is employed. Recently, Xiao et al. demonstrated that the point spread function of the FF-OCT with spatially incoherent illumination is almost insensitive to low-order geometrical aberrations, e.g. defocus [20,21]. So, in FF-OCT, the cross-talk-generated noise and low-order geometrical aberrations can be overcome by damping the spatial coherence of the incident light beam. However, thermal lamps and LEDs can suffer from the low power per spatial mode, which limits detection sensitivity [17]. For this reason, it would be preferable to use lasers and control their degree of spatial coherence. As pointed out by Karamata [17], such spatial coherence gating works analogously as the confocal spatial filtering in scanning OCT systems [22,23].

The laser spatial coherence can be suppressed in FF-SS-OCT by placing a rotating ground diffuser before the entrance of the interferometer [24]. This idea was also utilized in scanning OCT system. The so-called speckle-modulating OCT (SM-OCT) has been recently applied to suppress speckles and to improve imaging the mice pinna, mice cornea and the human fingertip skin [25]. SM-OCT was implemented by randomly changing in time the phase of the optical field illuminating the sample. Random phase shifts were induced by either translating or rotating the ground glass diffuser. Though this approach improves the visibility of various sample features in the cross-sectional OCT images, the diffraction-limited transversal resolution was not achieved because of the image blurring from averaging multiple speckle realizations induced by a moving diffuser.

An alternative approach of suppressing the cross-talk-generated noise to improve depth ranging in FF-OCT with spatially coherent illumination was presented in [26,27]. FF-OCT was supplemented by the spatial light modulator (SLM) and a numerical procedure of cumulative time-reversal. SLM sequentially displays the set of rotating variable diffraction gratings. The optical signals at the exit of the interferometer are then used to determine the time-gated reflectance matrix, R. The latter is processed in the k- (CASS microscopy [26]) or in the real-space (smart OCT [27]). Then, numerical filtering splits R into two independent components. One representing singly-scattered light, R_ss, and the other corresponding to multiply scattered light R_ms. Subsequently, the R_ss is used to recover the image of the sample hidden deep inside the scattering medium. CASS microscopy and smart OCT were employed to extend ballistic imaging depths up to 12-13 scattering mean free paths, l_s.

Here, we present a novel method, in which the cross-talk-generated noise in FF-SS-OCT is suppressed by spatiotemporal optical coherence (STOC) manipulation [28]. In STOC, the phase of light in one of the interferometer arms is modulated in time with a set of patterns (phase masks) displayed sequentially on the SLM. The light modulation is synchronized with the light acquisition to effectively control the spatial coherence of the detected light. A term “effectively” means that we do not generate the secondary source with prescribed coherence properties (e.g. spatially incoherent light source). Instead, the idea is to tailor the incident light to constrict the region of high fringe visibility to the spatial extent of the individual detection channel.

Specifically, the active area of the SLM comprises a two-dimensional array of pixels, each of which introduces the programmable phase shift ranging from 0 up to 2$\text{π}$. These pixels are grouped into small blocks of uniform phase shifts (macro pixels). Then, phases of macro pixels are varied in time to modulate the light, which illuminates the sample. By matching the dimensions of the macro pixels to spatial extents of detection channels, we can de-correlate scattered light from each channel. The unwanted interference between channels is washed-out and the cross-talk-generated noise is suppressed helping to improve the transversal image resolution. Consequently, the sample features become visible.

To accomplish this, we first use the second-order optical coherence theory and derive conditions for phase masks, so they will reduce the spatial coherence. We use these phase masks to image a high-resolution 1951 USAF resolution test chart. We show that STOC manipulation suppresses artifacts, typical for spatially coherent illumination and improves spatial resolution by a factor of $\sqrt{2}$ with respect to the unmodulated case. Finally, we apply STOC manipulation to image the sample covered by diffusing and scattering phantoms, and the rat skin ex vivo.

2. Methods

In this section we first recall several aspects of the second-order optical coherence theory (Sec. 2.1), which we then utilize to derive conditions for phase masks, that should be satisfied to suppress the spatial coherence (Sec. 2.2). Subsequently, we show how to apply this approach to FF-SS-OCT (Sec. 2.3). Then we describe experimental implementation (Sec. 2.4) along with signal processing (Sec. 2.5).

2.1 Spatial coherence and the cross-talk-generated noise

Traditionally, the spatial coherence of the complex-valued time-dependent optical field $U(\mathit{r},t)$ is quantified with the mutual intensity function [29,30]:

$$J\left({\mathit{r}}_1,{\mathit{r}}_2\right)={〈U^{*}\left({\mathit{r}}_1,t\right)U\left({\mathit{r}}_2,t\right)〉}_{t }=\underset{T\to \infty }{\text{lim}}\frac{1}{T}{\displaystyle {\int }_{-\raisebox{1ex}{$T$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{\raisebox{1ex}{$T$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{U}^{*}\left({\mathit{r}}_1,t\right)U\left({\mathit{r}}_2,t\right)dt,}$$

where $T$ is the detector integration time, and $\mathit{r}$ denotes the position in a two-dimensional detector plane (pixel location). Function $J\left({\mathit{r}}_1,{\mathit{r}}_2\right)$ quantifies spatial correlations between optical fields at two different locations, ${\mathit{r}}_1$ and ${\mathit{r}}_2.$ By normalizing $J\left({\mathit{r}}_1,{\mathit{r}}_2\right)$ one obtains the complex degree of coherence [31]:

$$j\left({\mathit{r}}_1,{\mathit{r}}_2\right)=\frac{J\left({\mathit{r}}_1,{\mathit{r}}_2\right)}{\sqrt{I\left({\mathit{r}}_1\right)I\left({\mathit{r}}_2\right)}},$$ (1)

where $I\left(\mathit{r}\right)=J\left(\mathit{r},\mathit{r}\right)={〈{\left|U\left(\mathit{r},t\right)\right|}^2〉}_t$ is the time-averaged light intensity recorded at point $\mathit{r}$. The region, in which the magnitude $\left|j\left({\mathit{r}}_1,{\mathit{r}}_2\right)\right|$ is larger than the prescribed threshold, defines the coherence area $A_c$ [31]. In other words, this area is the spatial extent, in which the optical fields are correlated. Since $j\left({\mathit{r}}_1,{\mathit{r}}_2\right),$ and consequently $A_c$, is linked with the mutual intensity function through Eq. (1), the light intensities recorded at various detector pixels are not independent, when $A_c$ is larger than the individual pixel size (in extreme case of a single spatial mode emitted by the light source, all camera pixels are in the area smaller than $A_c$).

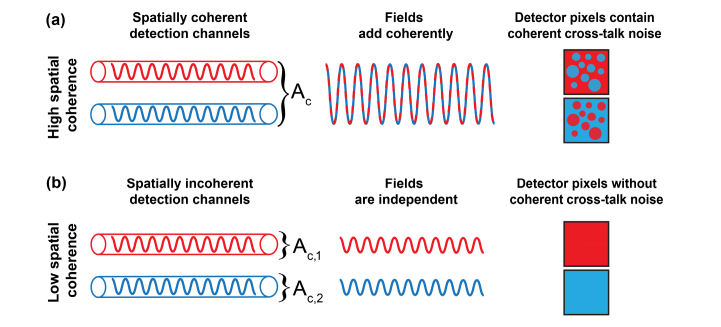
In FF-OCT, the light scattered from the sample is detected on a multi-pixel camera. The whole volume of measured sample is partitioned into subvolumes, determined by the transverse and depth resolutions of the optical system. Light originating from each sample subvolume is imaged on the associated, specific group of camera pixels [17]. This relation between sample subvolume and camera pixels is referred to as the detection channel. Ideally, only light originating from the specific sample subvolume should be detected through the given channel. However, multiple scattering breaks this ideal relation. Consequently pixel intensities are affected by the optical fields from parallel detection channels. The underlying waves propagating in each channel can add coherently leading to the cross-talk-generated noise in the detection plane as schematically drawn in Fig. 1.

Fig. 1.

The cross-talk-generated noise is induced by high spatial coherence. (a) The optical fields from parallel detection channels (drawn schematically as tubes) are within the same coherence area $A_c$. So, as shown in the second column, fields add coherently (red and blue waves produce a wave with larger amplitude), and intensities recorded by detector pixels (squares in the last column) contain cross-talk-generated noise, which is represented here as random spheres. (b) Contrary, for low spatially coherent light, fields from parallel detection channels are independent (each channel is within different coherence area,$A_{c,1}$ and $A_{c,2}$). Thus, optical fields do not interfere, and the cross-talk-generated noise is absent.

Specifically, the intensity of two superposed optical fields is given by the interference equation [31]:

$$\mathcal{I}=I\left({\mathit{r}}_1\right)+I\left({\mathit{r}}_2\right)+2\sqrt{I\left({\mathit{r}}_1\right)I\left({\mathit{r}}_2\right)}\left|j\left({\mathit{r}}_1,{\mathit{r}}_2\right)\right|\cos \left(\alpha \right),$$

where $\alpha =\text{arg}\left[j\left({\mathit{r}}_1,{\mathit{r}}_2\right)\right]$ is the phase of the complex degree of coherence. Assuming equal intensities $I\left({\mathit{r}}_1\right)=I\left({\mathit{r}}_2\right)=I_0$ and fully spatially coherent light $\left(\left|j\left({\mathit{r}}_1,{\mathit{r}}_2\right)\right|=1\right),$ $\mathcal{I}=4I_0\text{cos}\left(\text{α}\right)$. So, pixel intensities are affected by the cross-talk-generated noise [Fig. 1(a)]. Namely, the signal from one detection channel [red wave in Fig. 1(a)] produces noise in the neighboring channel [blue wave in Fig. 1(a)] because fields from parallel detection channels add coherently (they are within the same coherence area), and produce a wave with larger amplitude [dashed curve in second column of Fig. 1(a)]. Contrary, for spatially incoherent light, $\left|j\left({\mathit{r}}_1,{\mathit{r}}_2\right)\right|=0,$ and $\mathcal{I}=2I_0.$ In that case, detection channels are independent (or un-correlated). The coherent cross-term [$\text{cos}\left(\text{α}\right)$] does not exist, so the cross-talk-generated noise is not present. Consequently, red and blue pixels (squares in right column of Fig. 1) do not contain noise from neighboring channels because corresponding fields do not interfere [Fig. 1(b)]. In practice, the detector contains more than just two pixels. To describe the spatial coherence of such a multi-pixel detector we will use the matrix approach, described under Section 2.2.

2.2 Spatial coherence suppression

The particular form of the coherence area is governed by the Van Cittert-Zernike theorem (incoherent sources) or its generalized version (partially coherent sources) [29]. In the special case of uniformly bright spatially incoherent light source, the coherence area is $A_c˜{\lambda }^2/\text{Ω}$, where $\lambda$ is the center wavelength and $\text{Ω}$ is the solid angle subtended by the source from the detection plane. Thus, the standard approach to overcome the cross-talk-generated noise from high spatial coherence is to use light source with small $A_c$. This can be achieved by increasing $\text{Ω}$ through extending the source emission area or angle. Here, we propose a different solution, in which the phase of optical field $U(\mathit{r},t)$ is spatiotemporally modulated using the SLM. By doing so, we obtain the modulated field

$$\tilde{U}\left(\mathit{r},t\right)=U\left(\mathit{r},t\right)\text{exp}\left[i\phi (\mathit{r},t)\right],$$

where $\phi (\mathit{r},t)$ denotes the phase shift induced by the SLM. The corresponding effective mutual intensity $\tilde{J}\left({\mathit{r}}_1,{\mathit{r}}_2\right)$ can be then written as:

$$\tilde{J}\left({\mathit{r}}_1,{\mathit{r}}_2\right)={〈U^{*}\left({\mathit{r}}_1,t\right)U\left({\mathit{r}}_2,t\right)\text{exp}\left\{i\text{Δ}\phi \left({\mathit{r}}_1,{\mathit{r}}_2,t\right)\right\}〉}_t,$$

where $\text{Δ}\phi \left({\mathit{r}}_1,{\mathit{r}}_2,t\right)=\phi \left({\mathit{r}}_2,t\right)-\phi \left({\mathit{r}}_1,t\right)$. Our goal is to adjust phase masks displayed on the SLM such that the above function will reduce to the mutual intensity function of the spatially incoherent light [29]:

$$J\left({\mathit{r}}_1,{\mathit{r}}_2\right)\approx I\left({\mathit{r}}_1\right)\delta \left({\mathit{r}}_1-{\mathit{r}}_2\right),$$ (2)

where $\delta (\mathit{r})$ is the two-dimensional Dirac delta function (because $\mathit{r}$ is the two-component position vector). To achieve this goal $M$ phase masks are displayed on the SLM at discrete times $t_m$ and each phase mask is active for the same fixed duration (in general, this duration allows to adjust the weight of the phase mask). Therefore, $\tilde{J}\left({\mathit{r}}_1,{\mathit{r}}_2\right)$ is given by:

$$\tilde{J}\left({\mathit{r}}_1,{\mathit{r}}_2\right)={〈U^{*}\left({\mathit{r}}_1,t\right)U\left({\mathit{r}}_2,t\right)\frac{1}{M}{\displaystyle {\sum }_{m=1}^M{e}^{i\Delta \phi \left({\mathit{r}}_1,{\mathit{r}}_2,t_m\right)}}〉}_t.$$ (3)

The above equation will reduce to Eq. (2), if the phase masks are adjusted to satisfy the following condition:

$$\frac{1}{M}{\displaystyle {\sum }_{m=1}^M\text{exp}\left\{i\Delta \phi \left({\mathit{r}}_1,{\mathit{r}}_2,t_m\right)\right\}=\delta \left({\mathit{r}}_1-{\mathit{r}}_2\right).}$$ (4)

If so,

$$\tilde{J}\left({\mathit{r}}_1,{\mathit{r}}_2\right)={〈U^{*}\left({\mathit{r}}_1,t\right)U\left({\mathit{r}}_2,t\right)\delta \left({\mathit{r}}_1-{\mathit{r}}_2\right)〉}_t=I\left({\mathit{r}}_1\right)\delta \left({\mathit{r}}_1-{\mathit{r}}_2\right).$$

The above approach considers only two pixels located at ${\mathit{r}}_1$ and ${\mathit{r}}_2.$ To generalize this method for a detector containing $N$ pixels, we first arrange the effective mutual intensity functions in the matrix:

$$G=\left[\begin{array}{ccc}{\tilde{J}}_{11}& {\tilde{J}}_{12}& \begin{array}{cc}\cdots & {\tilde{J}}_{1N}\end{array}\\ {\tilde{J}}_{21}& {\tilde{J}}_{22}& \begin{array}{cc}\cdots & {\tilde{J}}_{2N}\end{array}\\ \begin{array}{c}⋮\\ {\tilde{J}}_{N1}\end{array}& \begin{array}{c}⋮\\ {\tilde{J}}_{N2}\end{array}& \begin{array}{c}\begin{array}{cc}\ddots & ⋮\end{array}\\ \begin{array}{cc}\cdots & {\tilde{J}}_{NN}\end{array}\end{array}\end{array}\right]$$ (5)

where each element ${\tilde{J}}_{kj}\equiv \tilde{J}\left({\mathit{r}}_k,{\mathit{r}}_j\right)$ quantifies correlations between fields sensed by detector pixels located at positions ${\mathit{r}}_k$ and ${\mathit{r}}_j,$ respectively (indices $k$ and $j$ are incremented from $1$ to $N$). Note that the number of detector pixels $N$ is distinguished from the number of phase masks, $M$. Here, $N$ is used to define matrix $G,$ which quantifies spatial coherence between various detector pixels. On the other hand, $M$ indicates how many phase masks were used for STOC manipulation.

Second, we rewrite Eq. (4) in the following form:

$${\displaystyle {\sum }_{m=1}^M\text{exp}\left[i{\phi }_k^{\left(m\right)}\right]\text{exp}\left[-i{\phi }_j^{\left(m\right)}\right]=M{\delta }_{kj},}$$ (6)

where ${\phi }_{k,j}^{(m)}\equiv \phi \left({\mathit{r}}_{k,j},t_m\right).$ If these phase masks are adjusted to satisfy Eq. (6), $G$ will be diagonal (because all terms with ${\mathit{r}}_k\ne {\mathit{r}}_j$ are effectively zero). Moreover, the remaining diagonal terms ${\tilde{J}}_{kk}$ will reduce to the time-averaged light intensities at ${\mathit{r}}_k,$ $I_k=J_{kk}={〈{\left|U\left({\mathit{r}}_k,t\right)\right|}^2〉}_t$. Thus, the matrix $G$ is reduced to:

$$G=\left[\begin{array}{ccc}{I}_1& 0& \begin{array}{cc}\cdots & 0\end{array}\\ 0& I_2& \begin{array}{cc}\cdots & 0\end{array}\\ \begin{array}{c}⋮\\ 0\end{array}& \begin{array}{c}⋮\\ 0\end{array}& \begin{array}{c}\begin{array}{cc}\ddots & ⋮\end{array}\\ \begin{array}{cc}\cdots & I_N\end{array}\end{array}\end{array}\right].$$

In general, the diagonal width is not sharp and spreads to adjacent elements of $G$ (Fig. 2). The extent of this spreading depends on the coherence area, $A_c$. As we will show in Section 3, the value of $A_c$ (proportional to the thickness of the $G$ matrix diagonal) can be controlled by changing the pixel block size on the SLM.

Fig. 2.

Quantification of the spatial coherence with scattering coherency matrix, $G$. (a) When STOC manipulation is disabled, the spatial coherence is unchanged and high (non-diagonal $G$). In practice, blue lines (low values) in matrix $G$ appear, when region used for matrix calculation contains pixels of zero values. (b) After enabling STOC manipulation, the low spatial coherence is synthesized. This is confirmed by a diagonal $G$.

In [32] it has been shown that phase masks, which satisfy condition from Eq. (6), should be determined from rows or columns of the orthogonal matrix of size $M^2\times M^2$. In other words, the phase masks should constitute the basis. This basis is used to decompose the initially spatially correlated optical fields from parallel channels into orthogonal series. By summing intensities of spatially uncorrelated fields, we get an undistorted image of the sample. This summation is equivalent to constructing an image from the diagonal elements of the $G$ matrix (reshaping from vector to matrix), provided that off-diagonal entries were previously suppressed by the STOC manipulation.

To verify this approach, we use two sets of phase masks:

• • Pseudo-randomly generated masks with uniformly distributed phases in the range from 0 to 2$\pi$, referred to as random phase masks.
• • Binary phase patterns derived from the Sylvester-type Hadamard matrix. Phase masks were derived from this matrix as explained in [32]. We call this set of phase masks Hadamard phase masks.

Experimentally we have found that Hadamard phase masks are more effective than random phase masks as they have been proven to be mutually orthogonal [32].

It should be noted that matrix $G$ is not required to obtain the final image of the sample. Instead, this matrix is used to quantify spatial correlations between detector pixels and to derive conditions for phase patterns that suppress spatial coherence.

2.3 STOC manipulation in FF-SS-OCT

In this section, we show that the STOC approach can be straightforwardly applied to FF-SS-OCT. To this end, let us recall that the FF-SS-OCT, like any other Fourier-domain OCT method, measures the spectral density of the form

$$\mathcal{S}\left(\mathit{r},\omega \right)={\mathcal{S}}_{DC}\left(\mathit{r},\omega \right)+2\text{Re}[{\mathcal{W}}_{rs}\left(\mathit{r},\omega \right)],$$

where $\omega$ is the optical frequency, ${\mathcal{S}}_{DC}\left(\mathit{r},\omega \right)$ is the DC component and ${\mathcal{W}}_{rs}\left(\mathit{r},\omega \right)$ denotes the cross-spectral density of the sample, ${\mathcal{U}}_s(\mathit{r},\omega )$ and reference, ${\mathcal{U}}_{\mathit{r}}(\mathit{r},\omega )$ optical fields that are associated with the light propagating in the corresponding interferometer arms. Typically, ${\mathcal{S}}_{DC}\left(\mathit{r},\omega \right)$ is dominated by the reference arm, so it can be suppressed by subtracting the signal acquired with the blocked sample arm. Because of doing this, we end up with $\mathcal{S}\left(\mathit{r},\omega \right)\approx 2\text{Re}[{\mathcal{W}}_{rs}\left(\mathit{r},\omega \right)]$. The latter is then inverse-Fourier transformed to obtain the pair of the Hermitian-conjugated “mirror-terms”:

$$\mathcal{I}\left(\mathit{r},z\right)={\mathcal{F}}^{-1}\left\{\mathcal{S}\left(\mathit{r},\omega \right)\right\}={\text{Γ}}_{rs}\left(\mathit{r},z\right)+{\text{Γ}}_{rs}^{*}(\mathit{r},-z),$$

where $z$, the variable conjugated to $\omega$, denotes the sample depth. Thus, the mutual coherence function ${\text{Γ}}_{\text{rs}}\left(\mathit{r},z\right)={〈U_r^{*}\left(\mathit{r},z\right)U_s\left(\mathit{r},z\right)〉}_t$ approximates the depth-resolved field scattered from the sample. In practice, the interferometer path mismatch is adjusted to reject ${\text{Γ}}_{rs}^{*}(\mathit{r},-z)$. Hence, the FF-SS-OCT signal reduces to $\mathcal{I}\left(\mathit{r},z\right)={\text{Γ}}_{rs}\left(\mathit{r},z\right).$

In STOC manipulation, the light from one of the interferometer arms is tailored using time-varying phase mask $P_m=\text{exp}\left[i\phi \left(\mathit{r},z,t\right)\right].$ Consequently, the FF-SS-OCT signal, after the inverse Fourier transform, takes the following form:

$${\widetilde{\text{Γ}}}_{rs}\left(\mathit{r},z,t\right)={\text{Γ}}_{rs}\left(\mathit{r},z,t\right)\text{exp}[i\phi \left(\mathit{r},z,t\right)].$$

By analogy to the effective mutual intensity function [$\tilde{J}\left({\mathit{r}}_1,{\mathit{r}}_2\right)$, Eq. (3)] we can now quantify spatial correlations of FF-SS-OCT signals, recorded at two different transversal locations, ${\mathit{r}}_1$, ${\mathit{r}}_2$ as follows:

$$\mathcal{J}\left({\mathit{r}}_1,{\mathit{r}}_2\right)={〈{\widetilde{\text{Γ}}}_{rs}^{*}\left({\mathit{r}}_1,z,t\right){\widetilde{\text{Γ}}}_{rs}\left({\mathit{r}}_2,z,t\right)〉}_t={〈{\text{Γ}}_{rs}^{*}\left({\mathit{r}}_1,z,t\right){\text{Γ}}_{rs}\left({\mathit{r}}_2,z,t\right)e^{i\Delta \phi \left({\mathit{r}}_1,{\mathit{r}}_2,z,t\right)}〉}_t$$

If $M$ phase masks are used, the above equation is written as:

$$\mathcal{J}\left({\mathit{r}}_1,{\mathit{r}}_2\right)={〈{\text{Γ}}_{rs}^{*}\left({\mathit{r}}_1,z,t\right){\text{Γ}}_{rs}\left({\mathit{r}}_2,z,t\right)\frac{1}{M}{\displaystyle {\sum }_{m=1}^M{e}^{i\text{Δ}\phi \left({\mathit{r}}_1,{\mathit{r}}_2,z,t_m\right)}}〉}_t.$$

The resulting function $\mathcal{J}\left({\mathit{r}}_1,{\mathit{r}}_2\right)$ is analogous to $\tilde{J}\left({\mathit{r}}_1,{\mathit{r}}_2\right)$ [Eq. (3)] but quantifies spatial correlations of mutual coherence functions, ${\text{Γ}}_{rs}$ (measured by FF-SS-OCT) rather than true optical fields, $U$. So, $\mathcal{J}\left({\mathit{r}}_1,{\mathit{r}}_2\right)$ can be used to define the $N\times N$ matrix. Subsequently, phase masks are adjusted to diagonalize this matrix, and hence, to suppress the cross-talk-generated noise. All further steps proceed the same as in Section 2.2 but with ${\text{Γ}}_{rs}$ replacing $U$. Henceforth, the subscript “rs” will be omitted: ${\text{Γ}}_{rs}=\text{Γ}.$

2.4 Experimental setup

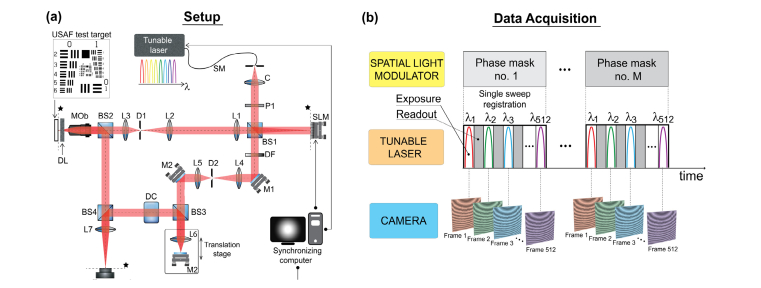
The optical setup used in this study is sketched in Fig. 3(a). A light from the rapidly tunable laser centered at $\lambda =840$ nm (Broadsweeper BS-840-2, Superlum, tuning range: 75 nm, linewidth: 0.12 nm, sweep rate: 2.3 $\mu$m/s, 512 spectral points per sweep) supplied by a single-mode fiber (NA 0.13) is collimated using an achromatic doublet lens, C ($f=50$ mm, Thorlabs). The resulting beam is of diameter 13 mm (at 1/e²) and its polarization is set to 0 degrees (horizontal polarization), in order to match the “working” polarization state of the spatial light modulator, SLM (LCD full HD display, 8 $\mu \text{m}$ pixel size, 30 Hz refresh rate, PLUTO NIR2, HoloEye). The first non-polarized beam splitter (BS1) is used to split the light into the sample and reference arms. In the sample arm light illuminates the SLM, which displays first one out of total $M$ phase masks. The SLM active area is then re-imaged at the sample plane by using a system of lenses L1, L2, L3 ($f=300$ mm, $f=75$ mm, $f=50$ mm, respectively, all achromatic doublets) and the microscope objective. The light back-reflected from the sample is subsequently recombined with the reference optical field and the resulting spectral density (or spectral fringe pattern) is recorded by a two-dimensional detector. Afterward, the second phase pattern is displayed on the SLM and the measurement is repeated. This procedure is continued until the last phase mask is reached [Fig. 3(b)].

Fig. 3.

Full-field swept-source optical coherence tomography supplemented by the STOC manipulation. (a) A light from the rapidly tunable laser ($\lambda =840$ nm) is linearly polarized and split into the object and reference arms. Optical field in the object path is modulated in time by phase masks displayed on the spatial light modulator (SLM). The modulated light illuminates the sample covered by the layer inducing cross-talk-generated noise (Distorting Layer, DL). A light back-reflected from the sample is then recombined with the reference field and the resulting superposition is recorded by a two-dimensional camera. Abbreviations: SM – single mode optical fiber; C – collimator; P1 polarizer (0 degree polarization); BS1, BS2, BS3, BS4 – non-polarizing beam splitters (50:50); SLM – spatial light modulator; L1, L2, L3, L4, L5, L6, L7 – lenses; M1, M2 – flat mirrors; MOb – microscope objective; D1, D2 – diaphragms; DF – density filter; DL – distorting layer, DC – dispersion compensation module; * – conjugated planes. (b) Synchronization of light modulation with data acquisition. A phase mask is displayed on the spatial light modulator (SLM), and modulates the light from a tunable laser at every instantaneous wavelength (${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_{512}$) leading to the corresponding spectral fringe pattern recorded at the 2D camera. The above process is repeated for consecutive phase masks until the last phase mask is reached.

The imaging part of the MZI sample arm, equipped with the microscope objective (20x, NA 0.4, Olympus or 10x, NA 0.25, Olympus), was operated in a double-pass arrangement for illuminating and imaging beam paths (epi-illumination). A high-resolution 1951 USAF test target (up to 645 line pairs per millimeter, Edmund Optics) serves as the sample. A tube lens L7 ($f=200$ mm, achromatic doublet) delivers an image from the exit pupil of the objective and re-images an object onto the camera. Two cameras were used: Mikrotron EoSens mini 2, pixel size: 14 x 14 $\mu$m, 1696 x 1710 px active area, readout area: 256 x 256 px, acquisition speed: 15.9 kFPS or Basler acA2000-340km, pixel size: 5 x 5 $\mu$m, readout area: 1024 x 1024 pixels, acquisition speed 340 FPS. The former camera is much faster (total measurement time 4.5 s) but allows to use relatively low number of $M=128$ due to limited internal memory. The second camera (Basler) does not have this limitation and was used to obtain supporting results for $M=512$ (total measurement time 390 s).

The optical setup sketched in Fig. 3(a) differs from the typical configuration of the dynamic speckle-illumination [33] such that the light modulation is performed in one interferometer arm only, keeping the other arm unmodulated. In this respect, the setup resembles the phase-shifting arrangement used to remove autocorrelation, DC and complex conjugate artifacts in the Fourier-Domain (FD) OCT setups [7,34]. As a consequence, the OCT signal is modulated in a similar way as in the phase-shifting FD OCT. Namely, by changing the phase difference between optical fields in two interferometer arms. The main distinction, however, is that in STOC the phase shifts are non-uniform across the beam. Namely, the phase shift $\phi (\mathit{r},t)$ is inhomogeneous in both spatial variable $\mathit{r}$ and temporal variable, $t$. This important aspect is utilized here to induce decorrelation in the parallel detection channels and to suppress the cross-talk-generated noise.

2.5 Signal processing

The registered, STOC manipulated spectral fringe patterns are processed using the standard OCT methods to obtain complex (amplitude and phase) volumetric (depth-resolved) representations of the sample [7]. Subsequently, the single axial plane representing the layer of interest is extracted, yielding a complex-valued array, ${\text{Γ}}_{ij}(z,t_m),$ where $i,j=1,2,\dots ,\sqrt{N}$ denote the horizontal and vertical image indices and $m=1,2,\dots ,M$ represents the phase mask index. According to Sec. 2.3, ${\text{Γ}}_{ij}\left(z,t_m\right)$ approximates the true optical field scattered from the selected sample layer acquired for the $m$-th mask. Thus, to obtain the time-averaged intensity image, $I_{ij},$ the square magnitudes of ${\text{Γ}}_{ij}^{(m)}\equiv {\text{Γ}}_{ij}(z, t_m)$ must be averaged: $I_{ij}=\frac{1}{M}{\displaystyle {\sum }_{m=1}^M{\left|{\text{Γ}}_{ij}^{\left(m\right)}\right|}^2.}$ Given, the set of ${\text{Γ}}_{ij}^{(m)}$, we determine the scattering coherency matrix, $G$. To this end, each ${\text{Γ}}_{ij}^{(m)}$ is reshaped from $\sqrt{N}\times \sqrt{N}$ matrix into the $1\times N$ vector:

$${\mathit{V}}^{\left(m\right)}=\left[{\text{Γ}}_{11}^{\left(m\right)},{\text{Γ}}_{12}^{\left(m\right)},\dots ,{\text{Γ}}_{1\sqrt{N}}^{\left(m\right)},{\text{Γ}}_{21}^{\left(m\right)},{\text{Γ}}_{22}^{\left(m\right)},\dots ,{\text{Γ}}_{2\sqrt{N}}^{\left(m\right)},\dots ,{\text{Γ}}_{\sqrt{N}\sqrt{N}}^{\left(m\right)}\right].$$

Then, the matrix $G$ of size $N\times N$ is calculated as:

$$G={\displaystyle {\sum }_{m=1}^M{\left({\mathit{V}}^{(m)}\right)}^{†}{\mathit{V}}^{(m)},}$$ (7)

where $†$ denotes Hermitian conjugate.

In practice, to reduce the computation cost, only a selected portion of complex images is used to determine matrix $G$. This follows from the fact that direct computation of matrix $G$ requires to declare an array of $N^2$ elements. This becomes an issue for large images. For instance, for the square detector with $N=256\times 256$ pixels, $G$ contains ${256}^4\approx 4.3\times {10}^9$ elements. Assuming complex double digital representation of each element (16 bytes per element), such a matrix would require nearly 70 Gb of the operating memory.

3. Results

3.1 Spatial coherence suppression

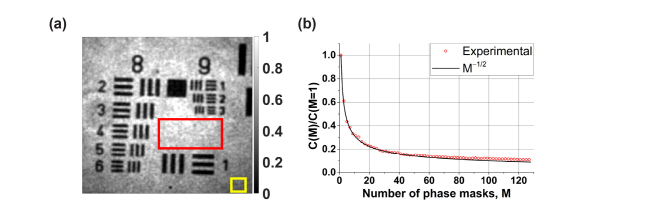
To show the capability of suppressing spatial coherence, an uncovered 1951 USAF resolution test chart was imaged without STOC manipulation. Then, $M=128$ pseudo-randomly generated masks with uniformly distributed phases in the range from 0 to 2$\pi$ with the block size of $1\times 1$ SLM pixels were used to image the sample with STOC manipulation and EoSens mini2 camera. The resulting total measurement time was 4.5 s.

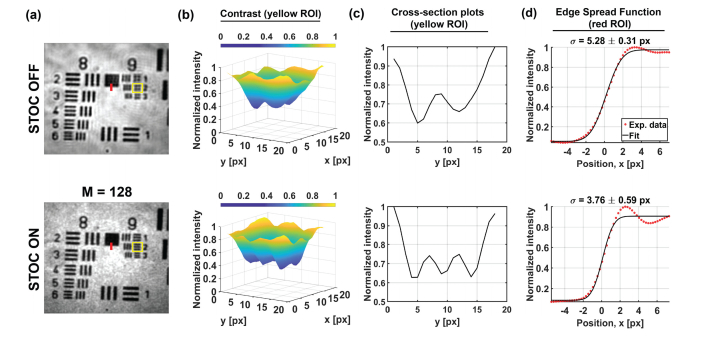
When STOC is disabled, the image of the sample contains artifacts typical for spatially coherent illumination [Fig. 4(a)]. These artifacts, which include various diffraction patterns around the bars and digits, are suppressed after enabling STOC manipulation. Moreover, the STOC helps to improve spatial resolution [Fig. 4(b,c)]. Namely, the bars of the ninth group of the resolution chart become distinguishable, when compared to the unmodulated case [STOC OFF row of Fig. 4(b,c)]. An observed improvement is due to the fact that coherent imaging systems are linear in the complex amplitude, contrary to incoherent systems, which are linear in the intensity [29]. So, from this point of view, the spatial resolution of the STOC-manipulated FF-SS-OCT image should be improved by the factor of $\sqrt{2}$ with respect to the unmodulated, spatially coherent case. This is true, provided analyzed camera pixels are within the same coherence area. In our case this condition is satisfied, which is proven by non-diagonal matrix $G$ (see below).

Fig. 4.

STOC manipulation suppresses the spatial coherence and improves spatial resolution. (a) Intensity images of the high-resolution resolution test chart with two ROIs (red line and yellow rectangle) used for further analysis. (b,c) High spatial frequency bars of the resolution test chart [yellow ROI in (a)] cannot be resolved when STOC is off but become clearly distinguishable after enabling STOC. Cross-sectional plots were obtained by averaging 3D plots from subfigure (b) along the x-direction. (d) The resulting improvement in spatial resolution is quantified with the width, $\sigma$ of the Edge Spread Function [determined from red ROI in (a)]. As shown in figure titles, ESF width is reduced by a factor of $\sqrt{2}$ after enabling STOC manipulation.

To quantify resolution improvement, we use the edge spread function (ESF). Experimental ESF was extracted from the bottom part of the box between eighth and ninth groups of the resolution test chart [marked with the red line in Fig. 4(a)]. The resulting data was then fit with the theoretical ESF:

$$\text{ESF}\left(x\right)=\frac{a}{2}\left[1+\text{Erf}\left(\frac{x-\mu }{\sqrt{2}\sigma }\right)\right],$$

valid for the Gaussian PSF:

$$\text{PSF}\left(x\right)=\frac{1}{\sqrt{2\pi \sigma }}\text{exp}\left[-{\left(\frac{x-\mu }{\sqrt{2}\sigma }\right)}^2\right].$$

In above equations $a$ accounts for the differences between theoretical and experimental intensities, $\text{Erf}\left(x\right)$ is the error function, $x$ stands for position across the edge, and $\mu ,\sigma$ denote the mean (center of the ESF) and the standard deviation (ESF’s width) of the Gaussian distribution, respectively. As shown in Fig. 4(d), the un-modulated ESF is indeed wider (has larger $\sigma$) than ESF of the STOC manipulated FF-SS-OCT data by a factor of 1.4. The obtained value agrees with the theoretical prediction of $\sqrt{2}$, confirming that detected optical signals are effectively spatially incoherent.

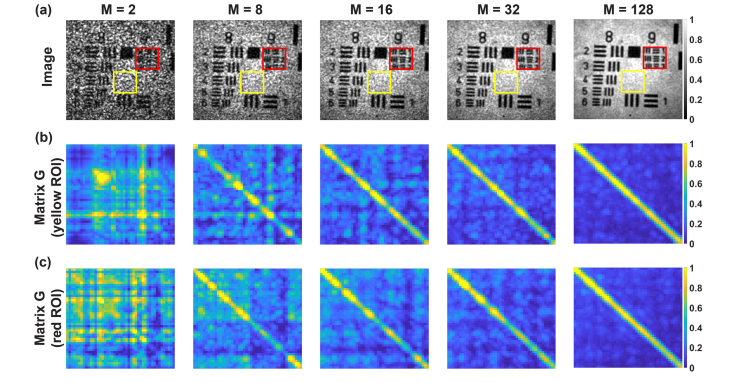
The intensity image of the sample and the scattering coherency matrix, $G$ were then calculated for varying number of phase masks, $M$. According to Sec. 2.5, the intensity image is the average of squared magnitudes calculated from the set of processed complex OCT signals, ${\left\{{\text{Γ}}^{\left(m\right)}\right\}}_{m=1}^M$. To calculate matrix $G$ we first extract the region of interest (ROI) from each ${\text{Γ}}^{(m)}$. The resulting, two-dimensional complex array of dimensions $\sqrt{N_1}\times \sqrt{N_1}$ is reshaped to the $1\times N_1$ vector, ${\mathit{V}}^{(m)}.$ Subsequently, $G$ of size $N_1\times N_1$ is determined using Eq. (7).

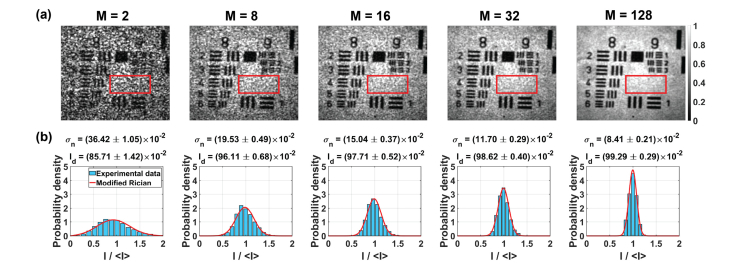
For $M<32$, the intensity image contains the speckle noise (Fig. 5). This noise is due to high spatial coherence, which is manifested as the non-diagonal scattering coherency matrix. In such a case, the optical fields are adding on the amplitude basis and interfere randomly due to nonuniformly distributed phase shifts across the SLM area. These effects change as $M$ increases. For $M=128,$ the matrix $G$ becomes diagonal. Therefore, fields are now independent (spatially incoherent) and are adding on the intensity basis. Thus, the speckle noise is suppressed and the speckle contrast, $C$ decreases proportionally to $M^{-1/2}$ [Fig. 6(b)] as predicted theoretically [29].

Fig. 5.

STOC manipulation controls the degree of spatial coherence by varying the number of phase masks, $M.$ (a) Intensity images with two rectangles showing ROIs used to calculate scattering coherency matrix $G$ (b,c). For $M<32$, the intensity image contains speckle noise. The corresponding matrices $G$ are not diagonal, which indicate the high degree of spatial coherence. For $M\ge 32$ this degree is reduced (diagonal $G$), so the speckle contrast in the corresponding intensity images is diminished.

Fig. 6.

Quantification of the speckle contrast in STOC manipulated FF-SS-OCT for the variable number of phase masks. (a) The intensity image with two ROIs used for calculations (red and yellow rectangles). Pixels from red ROI are used to determine mean signal intensity, $〈I〉.$ Pixels from yellow ROI are used to calculate standard deviation, $\sigma$. (b) $〈I〉$ and $\sigma$ yield $C=\sigma /〈I〉$ for a variable number of phase masks $M$ (red circles). These are compared to theoretical prediction of $C\left(M\right)=C\left(1\right)/\sqrt{M}$ (black solid line).

The speckle contrast was calculated using the standard definition: $C=\sigma /〈I〉,$ where $〈I〉$ is the mean signal intensity [calculated from pixel intensities within the red ROI in Fig. 6(a)] and $\sigma$ is the standard deviation [calculated from the yellow ROI in Fig. 6(b)].

Next, to quantify cross-talk-generated noise we use statistical analysis. The probability density of the FF-SS-OCT intensity $I$ in the presence of the cross-talk-generated noise obeys the modified Rician distribution [18,29,35,36]:

$$p\left(I\right)=\frac{\sqrt{I}}{{\sigma }_n^2}\text{exp}\left\{-\frac{I+I_d}{2{\sigma }_n^2}\right\}{I}_0\left(\frac{\sqrt{I{I}_d}}{{\sigma }_n^2}\right),$$ (8)

where ${\sigma }_n$ is the standard deviation of the cross-talk-generated noise intensity, $I_0$ is the zero-order Bessel function of the first kind, and $I_d$ denotes the intensity of the signal (undistorted by the noise). Equation (8) represents the intensity distribution of the scattered field, which is formed by a coherent addition of the random phasor (from the cross-talk-generated noise) and deterministic phasor (useful signal). So, by fitting $p\left(I\right)$ to experimental data we can estimate ${\sigma }_n$ and $I_d$ from the distribution width and height, respectively.

Figure 7(a) shows the intensity images with red rectangle denoting the ROI, used for statistical analysis. The intensity of each pixel within this area was normalized to ROI mean intensity $〈I〉$. Subsequently, the normalized data was fit by $p\left(I\right)$. The resulting fit, presented over the intensity histograms in Fig. 7(b), yields values of ${\sigma }_n$ and $I_d$. As $M$ increases, the intensity distribution becomes narrow. Specifically, intensities are distributed within the narrow range, centered at $〈I〉$. As a result, ${\sigma }_n$ decreases, while $I_d$ increase. This indicates that the useful signal dominates, and the image of the sample can be clearly seen (compare extreme left and right columns in Fig. 7).

Fig. 7.

Statistical analysis of the STOC-manipulated FF-SS-OCT intensities for the variable number of phase masks, $M$. (a) Images with red rectangle denoting the region used for statistical analysis. (b) Experimentally determined intensity histograms were fit with the modified Rician probability density function to estimate the standard deviation of the cross-talk-generated noise (${\sigma }_n$) and the useful signal intensity ($I_d$). As $M$ increases, the intensity distributions become narrower. Consequently, the noise quantified with ${\sigma }_n$ decreases, while the useful signal intensity, $I_d$ increases.

3.2 Control of the coherence area

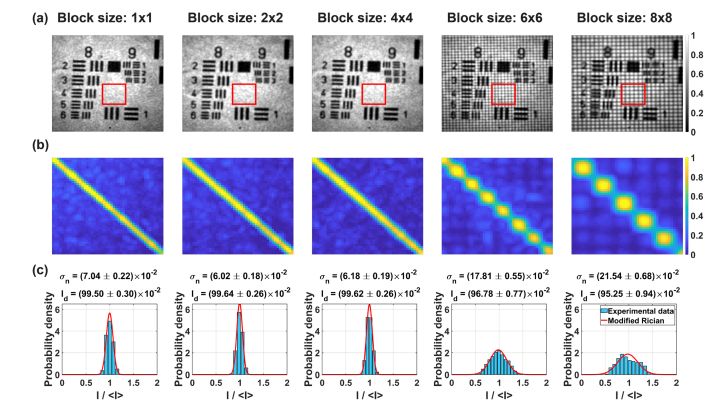
In this subsection, we show that STOC manipulation controls the extent of the coherence area. To this end, we repeated the previous experiment by fixing the number of random phase masks to $M=128$ and we changed the phase mask block size, $R$. Five different block sizes were used: $1\times 1$, $2\times 2$, $4\times 4$, $6\times 6$ and $8\times 8$ SLM pixels. The acquired signals were then processed to determine matrix $G$ and intensity distributions.

Figure 8(b) shows that the width of the $G$ diagonal increase with $R$. This indicates that, the size of the coherence area also increases (the spatial extent, where fields are correlated is larger). The ability to control the coherence area depends on the optical magnification between SLM and camera pixels. So, if the effective size of the SLM pixel is below the detector resolution spot, we do not observe large differences in the coherence area size until $R\le 4\times 4$, which approximately corresponds to the optical layout.

Fig. 8.

STOC manipulation controls the extent of the spatial coherence by varying the SLM block size $R$. (a) For $R\le 4\times 4$, the intensity images do not change significantly. Contrary, for $R>4\times 4$, an additional regular, dark pattern appears. This pattern is due to diffraction from edges of the phase mask blocks. (b) The coherence area, which corresponds to the diagonal thickness of the scattering coherency matrix, starts to increase for $R>4\times 4$ due to larger spatial blocks that are manipulated. Larger blocks reduce the number of controllable degrees of freedom. (c) This behavior is also confirmed through intensity distributions, which become wider for $R=6\times 6$ and $R=8\times 8$. Red rectangles in subfigure (a) denote the region of interest which was used to determine matrix $G$ and intensity distributions.

Phase masks with $R=6\times 6$ and $R=8\times 8$ produce dark areas in the intensity images [Fig. 8(a)]. This effect is due to diffraction from large phase differences between edges of phase blocks. The light intensity is distributed into diffraction orders that are out of the imaging objective’s NA and thus appear as dark regular patterns in the intensity images [37]. These patterns are also manifested as dark areas appearing in the diagonal of matrix $G$.

An increasing coherence area reduces the efficiency of STOC manipulation. This is confirmed by intensity distributions [Fig. 8(c)]. When $R\le 4\times 4$, these distributions are narrow. Cross-talk-generated noise is relatively low $\left({\sigma }_n\approx 0.06-0.07\right),$ so the intensity is dominated by the useful signal ($I_d\approx 0.99$). For $R>4\times 4$ the distributions become wider: ${\sigma }_n\approx 0.17$ ($R=6\times 6$) and ${\sigma }_n\approx 0.21$ $(R=8\times 8)$. Consequently, the useful signal decreases to $I_d\approx 0.97$ and $I_d\approx 0.95$, respectively.

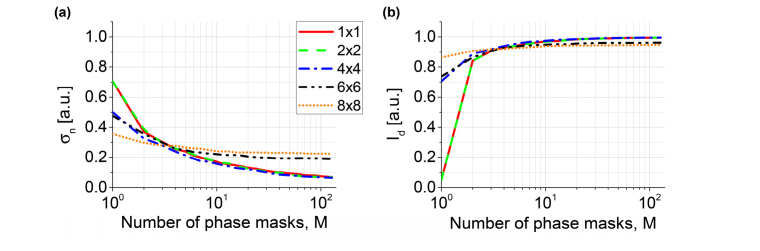
Figure 9 depicts plots of ${\sigma }_n$ and $I_d$ under varying $R$ and number of averaged intensities (or the number of phase masks), $M,$ The standard deviation ${\sigma }_n$ decrease with increasing $M$ [Fig. 9(a)]. Namely, for $R=2\times 2$, the ${\sigma }_n$ is reduced from ${\sigma }_n\approx 0.71$ $(M=1)$ down to ${\sigma }_n\approx 0.06$ $\left(M=128\right)$. A reduction in ${\sigma }_n$ is accompanied by an increase in $I_d$ [Fig. 9(b)], while the sum $I_T=2{\sigma }_n^2+I_d$ (total intensity received by all detection channels within the analyzed ROI) is nearly 1 and almost independent on $M$. A similar behavior is observed for larger block sizes. However, plots for $R=6\times 6$ and $R=8\times 8$ show that corresponding phase masks decrease the noise only to ${\sigma }_n\approx 0.18$ and ${\sigma }_n\approx 0.22$, respectively. Moreover, for $R\ge 4\times 4$, $I_T<1$ due to dark patterns from high order diffraction. Therefore, the STOC manipulation efficiency, measured as the ability to reduce the cross-talk-generated noise, achieves the optimum level for $R\le 4\times 4$.

Fig. 9.

Quantification of the cross-talk-generated noise and useful signal for the variable number of phase masks, $M$ and block size, $R$. The standard deviation of the noise, ${\sigma }_n$ decreases with $M$ (a), while the ratio ${\sigma }_n(M=1)/{\sigma }_n(M=128)$ decrease with $R$ (inset in a). The signal, $I_d$ expresses the opposite behavior and increases with $M$ (b). The total intensity $I_T=2{\sigma }_n^2+I_d$ received by all channels approaches 1 [inset in (b)]. The maximum improvement in $I_d$ is observed for $R\le 4\times 4$. Larger block sizes lead to a decrease in $I_T$.

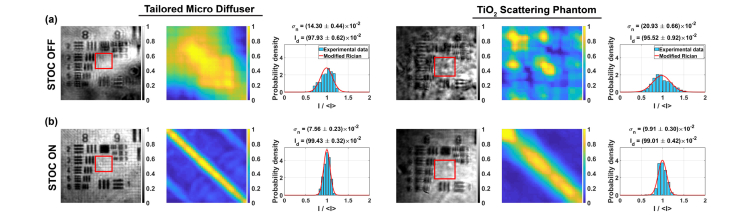
3.3 Imaging through the diffuser and the scattering phantom

After confirming that STOC manipulation controls the spatial coherence, we have fixed the block size to $R=4\times 4$ and used such phase masks to image the 1951 USAF resolution test chart covered by two different distorting layers. The first, tailored micro diffuser (TMD), is the glass diffuser (WaveFront Technology), characterized by 1° range of specular scattering angle. The second layer was fabricated by mixing titanium dioxide (TiO₂) with polydimethylsiloxane (PDMS) to prepare weakly scattering tissue phantom. The concentration of TiO₂ was set to 10 mg/ml and the resulting fluid was cured to form the $140 \text{μm}$ uniform phantom layer on the coverslip glass.

Each diffuser was then placed directly on the 1951 USAF resolution test chart, and the objective lens was refocused. Then, the data was acquired with $M=128$ Hadamard phase masks. The resulting signals were processed to obtain intensity images, matrix $G$ and intensity distributions (Fig. 10). These results are compared to the unmodulated case (labeled as STOC OFF rows in Fig. 10). When the STOC manipulation is disabled, the image of the sample is clearly deformed [first column in Fig. 10(a)] or barely visible [fourth column in Fig. 10(a)]. Consequently, in both cases, the scattering coherency matrix is non-diagonal due to high spatial coherence [second and fifth column in Fig. 10(a)], leading to the cross-talk-generated noise, represented as wide intensity distributions [third and sixth column in Fig. 10(a)]. Importantly this noise can be removed by STOC manipulation (STOC ON rows in Fig. 10). In the case of the TMD, the expected shape of the sample features is restored (bars become straight and resolvable), while in the case of the TiO₂ scattering phantom, bars and digits become visible. At the same time, the scattering coherency matrices are diagonal and intensity distributions are narrow, proving that indeed the cross-talk noise was suppressed by damping the spatial coherence.

Fig. 10.

STOC manipulation in FF-SS-OCT imaging of the sample covered by diffusing and scattering phantoms. (a) The sample image is distorted due to high spatial coherence, which is represented as non-diagonal matrix $G$ and wide intensity distributions. (b) The cross-talk noise is suppressed by STOC manipulation as confirmed by diagonal matrix $G$ and narrow intensity distributions.

Due to limitations of the camera transfer time, the objective lens was refocused without STOC manipulation. This becomes an issue when distorting layer induces significant noise. Such nonoptimal conditions for STOC manipulation can be identified by a non-sharp diagonal of the matrix $G$. Clearly, this problem exists for TiO₂ phantom [the fifth column in Fig. 10(b)]. Nevertheless, as shown in Fig. 6 and Fig. 9, the efficiency of the STOC manipulation can be improved by increasing the number of phase masks $M.$

3.4 Imaging through the diffuser and the scattering phantom: supporting results

In this subsection we present results obtained for $M=512$ pseudo-randomly generated masks with uniformly distributed phases in the range from 0 to 2$\pi$ with the block size of $1\times 1$ SLM pixels and the Basler camera.

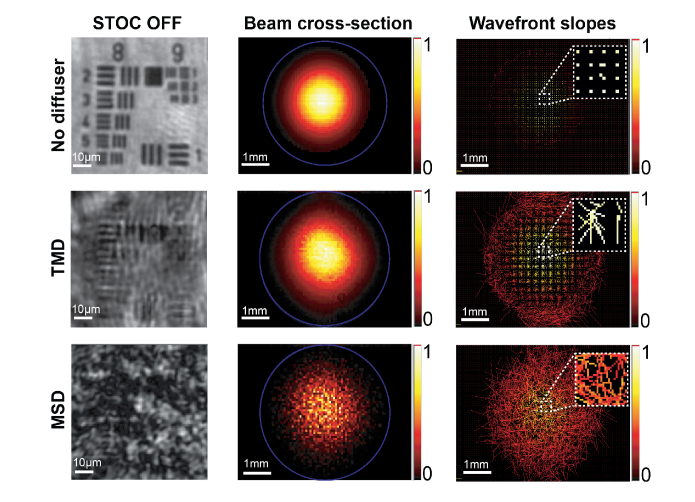
To induce the cross-talk-generated noise we used the same tailored micro diffuser (TMD) as in previous section. To remind, the TMD is the glass diffuser with 1 degree of specular scattering angle. As the scattering phantom, we used the micro-spheres diffuser (MSD). MSD consists of 25 $\mu \text{m}$ thick suspension of 1 $\mu \text{m}$ diameter aluminum spheres (Premasol DA Alumina Suspension, Al₂O₃ powder) solution sandwiched between two cover-slip glasses. Using the collimated transmission method [38], we estimated optical thickness (OT) of the MSD to eight mean free paths ($\text{OT}=8{\mathrm{l}}_{\text{s}}$).

Each diffuser was then placed on the 1951 USAF resolution test chart and imaged with the setup shown in Fig. 3(a) with Basler camera and disabled STOC manipulation. Resulting images are compared to the undistorted case (without diffuser) in Fig. 11 (the first column). Then, both diffusers were analyzed using the commercial Shack-Hartmann (SH) sensor. TMD and MSD were placed in the plane, optically conjugated to SH sensor and illuminated throughout with the parallel beam. The TMD unnoticeably alters the beam profile (second column in Fig. 11) and leads to small wavefront slopes (last column in Fig. 11). On the other hand, the MSD strongly alters the beam profile and leads to the speckle pattern in the sample image (last row in Fig. 11). Speckles are seen by the SH sensor as randomly distributed wavefront slopes (bottom right cell in Fig. 11). This analysis further confirms that the cross-talk-generated noise results from the fact that the optical signal isolated by a micro lens of the SH sensor is affected by signals from neighboring detection channels due to spatial correlations (see insets in the last column of Fig. 11). Optical signals from the given detection channel spreads to neighboring channels, where they randomly interfere.

Fig. 11.

Characterization of wavefront deformations caused by the optical system (the first row), the TMD (second row) and the MSD (the third row).

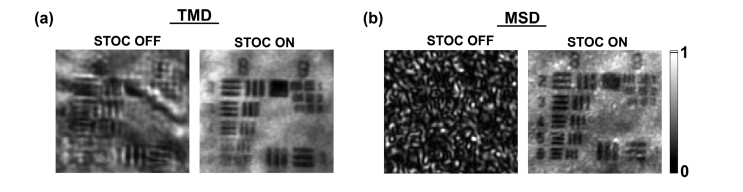
STOC manipulation with $M=512$ random phase masks ($R=1\times 1$) was then applied to suppress the coherent cross-talk noise generated by the TMD and the MSD. As shown in the left part of Fig. 12, the TMD induces image deformations. Namely, bars and digits of the resolution chart are distorted and shifted. Their correct shape and location are restored after enabling STOC manipulation [second column in Fig. 12(a)]. Similarly, the speckle noise generated by the MSD [first column in Fig. 12(b)] is suppressed by STOC manipulation and the high-resolution features of the sample can be seen [second column in Fig. 12(b)].

Fig. 12.

STOC manipulation suppresses the cross-talk-generated noise in FF-SS-OCT (see Visualization 1 ^{(113.1KB, mp4)} and Visualization 2 ^{(69.2KB, mp4)} ). USAF test target covered by two different diffusers [TMD (a) and MSD (b)] was imaged without (STOC OFF) and with STOC manipulation (STOC ON). After enabling STOC manipulation image deformations (TMD) and speckles (MSD) are suppressed without any prior information about the distorting layer.

To qualitatively examine the correction of image deformations from TMD we analyzed the uncropped images of the 1951 USAF resolution test chart. The undistorted (acquired without any diffuser) reference image [first column of Fig. 13(a)] was digitally processed to extract contours of bars and digits [first column of Fig. 13(b)]. This was done using standard contour finding algorithms available in open source image processing tools such as ImageJ. Then, the resulting contours were overlaid on the images obtained with and without STOC manipulation. As shown in the second column of Fig. 13(a), the TMD leads to deformations and displacements of bars and labels in the image of the sample. This is seen as a mismatch between contours, indicating correct shape and position, and the actual locations of elements of the 1951 USAF resolution test chart [second column in Fig. 13(b)]. As shown in the last column of Fig. 13(a), image deformations are suppressed after enabling STOC manipulation. Consequently, bars and labels are shifted back to their “correct” locations. This is confirmed with the contours map, which now matches the corresponding features in the image [last column in Fig. 13(b)]. This correction is best visible in Visualization 1 ^{(113.1KB, mp4)} .

Fig. 13.

Qualitative analysis of the STOC performance for compensating image deformations (see Visualization 1 ^{(113.1KB, mp4)} ). An undistorted reference FF-SS-OCT image of the sample [first column in (a)] was used to extract contours [first column in (b)]. The resulting contour map is overlaid on the distorted image to show that the TMD deforms and displaces sample features from their correct locations (STOC OFF). This effect can be corrected for by STOC manipulation (see STOC ON column).

3.5 Imaging through rat skin ex vivo

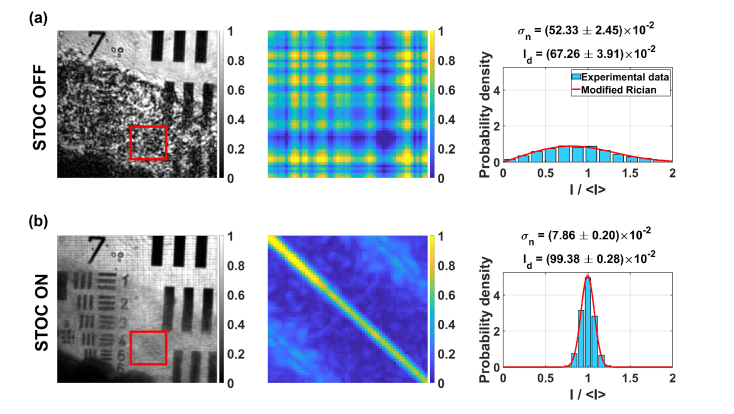
Finally, we present the STOC manipulation performance in ex vivo FF-SS-OCT imaging of biological samples. The rat skin layer of a nominal thickness of 100 $\mu$m was placed on the 1951 USAF resolution test chart and the imaging was performed with $M=128$ Hadamard phase masks of $R=4\times 4$ and 10x imaging objective.

The resulting intensity images, scattering coherency matrices and intensity distributions are depicted in Fig. 14. When the STOC manipulation is disabled, the region of the sample, which is covered by the scattering layer cannot be clearly seen [first column in Fig. 14(a)]. Instead, the resolution test chart features (like bars and digits) are distorted by the cross-talk-generated noise, which is due to high spatial coherence, manifested as non-diagonal matrix $G$ [middle column in Fig. 14(a)]. Intensity distribution, which is shown in the last column of Fig. 14(a), further confirms that the image intensity is dominated by the noise (intensity distribution is wide and low). After enabling STOC manipulation, the sample features become clearly visible [first column in Fig. 14(b)]. In this case, the spatial coherence is suppressed, which is confirmed by diagonal matrix $G$ [middle column in Fig. 14(b)]. Furthermore, the intensity distribution is narrow and high, proving that the useful information now dominates the registered signal [last column in Fig. 14(b)].

Fig. 14.

STOC manipulation suppresses the cross-talk-generated noise in FF-SS-OCT imaging of the high-resolution 1951 USAF resolution chart covered by the 100 $\mu$m-thick rat skin ex vivo. (a) When STOC manipulation is disabled, the sample features hidden by the scattering layer cannot be seen due to cross-talk-generated noise. In that case, the scattering coherency matrix (middle column) is non-diagonal and the intensity distribution is wide (right column). (b) By enabling STOC manipulation we suppress the cross-talk-generated noise, so the previously hidden scrambled fragments of the sample become visible. Scattering coherency matrix is now diagonal (middle column) and the intensity distribution is narrow (right column). Red rectangle denotes the ROI used to determine scattering coherency matrix and intensity distributions.

Intensity images depicted in Fto a igs. 14(a) and 14(b) were extracted from the single axial layer. Thus, in both cases, the coherence gating was implicitly applied. However, when STOC manipulation is disabled, coherence gating is not enough to obtain a high-resolution image of the sample due to cross-talk-generated noise. Consequently, the speckle contrast is high. As a sanity check, we calculated speckle contrast from the red ROI in Fig. 14(a) and obtained $C=0.48$. After enabling STOC manipulation, the spatial coherence is reduced, and the cross-talk-noise is suppressed. So, the high-resolution image of the sample can be obtained [Fig. 14(b)]. Accordingly, the speckle contrast [calculated from red ROI in Fig. 14(b)] is reduced to $C=0.08$.

4. Discussion

The main goal of the STOC manipulation is to modulate the light in one of the interferometer arms with the set of time-varying phase patterns. Therefore, STOC is like phase-shifting used to remove autocorrelation, DC and complex conjugate artifacts in the Fourier-Domain (FD) OCT setups [7,34]. However, the key difference is that, in STOC, the phase masks are spatially inhomogeneous contrary to spatially uniform phase masks utilized in phase-shifting FD-OCT systems. This important difference was used here to suppress the spatial coherence in the full-field swept-source OCT. Namely, the unwanted interference between parallel detection channels was diminished, leading to an improvement in the spatial resolution of the factor of $\sqrt{2}$. This resolution can be further enhanced (to a factor of 2) if the phase masks are adjusted such that the optical fields from parallel channels will only interfere constructively. This is a subject of an ongoing work.

STOC manipulation was also shown to improve the FF-SS-OCT imaging through three different distorting layers made of the tailored micro diffuser, scattering phantom and the rat skin ex vivo. An important advantage of our method with respect to previous developments in this field [25] is that STOC does not sacrifice the transversal resolution.

The presented technique extends the interferometer by the SLM, and thus makes the system slightly more complex than previous approaches, that use spatially incoherent light sources. However, STOC manipulation can reduce the spatial coherence in an arbitrarily selected region of the detection plane [28]. Virtually, any degree of spatial coherence can be synthesized. This advantage can be beneficial for sensing applications that use speckle contrast to infer dynamics in turbid media [39].

When phase modulation patterns contain rapid phase jumps (like in Hadamard phase masks), the image of the sample contains the square grid pattern [Fig. 10(b), Fig. 14(b)]. This is due to the fact that light intensity is distributed into diffraction orders that are out of the imaging objective’s NA [37]. This issue, as shown in Sec. 3.2, can be avoided by reducing the macro pixel size or by smoothing phase differences at the edges of SLM blocks.

The STOC efficiency can be improved if more phase masks are used. In the main text, we utilized fast camera Mikrotron EoSens 2, which allows using a relatively low number of $M=128$ due to limited internal memory. Sec 3.4 contains results achieved with $M=512$ random phase masks and a slower camera. This camera (Basler acA2000-340km) does not have a memory nor data transfer limitation (as in the case of Mikrotron EoSens 2) but leads to much longer acquisition times. In the case of $M=512$, the total measurement time was 390 s.

STOC manipulation should be also compared to CASS microscopy [26] and smart OCT [27]. These approaches use a similar experimental configuration but utilize different phase masks and signal processing approaches. Both, CASS microscopy and smart OCT employ phase masks composed of the rotating, variable diffraction gratings. Then, the amplitude and phase of the scattered optical fields are used to reconstruct the image of the static sample (resolution test chart) hidden inside the scattering medium. The improvement in signal-to-noise ratio (SNR) was found to be proportional to the number of phase masks, $M$.Contrary, the STOC image is achieved by averaging intensities (Sec. 2.5). Thus, the SNR improvement is on the order of $\sqrt{M}$. Consequently, STOC requires more phase masks to achieve similar results as CASS microscopy and smart OCT but is less sensitive to phase instabilities between consecutive volumetric measurements. All methods, however, are equally sensitive to phase instabilities during the wavelength sweep, which can be induced by axial sample motion, and will lead to image artifacts. This issue can be compensated for by numerical phase correction [40,41], while the transversal sample motion can be corrected for by tracking the sample, using, for example, cross-correlation based approaches [42,43].

The speed performance of STOC manipulated FF-SS-OCT is governed by three factors. The laser sweep rate, camera acquisition speed, and SLM refresh rate. It has been already shown that rapidly tunable lasers along with high-speed 2D cameras can be used to implement FF-SS-OCT with A-scan rates reaching nearly 40 MHz, which is an order of magnitude better than scanning OCT systems [9]. In this study, we used very slow liquid crystal SLM with refresh rates up to 30 Hz. Accordingly, our current implementation is not yet suitable for imaging biological samples. However, a faster modulator (e.g. digital micromirror device, DMD) will allow overcoming this limitation. Further performance improvements can be achieved by employing numerical phase correction as it has been already shown to improve FF-SS-OCT imaging of the human retina.

5. Conclusions

In summary, we demonstrated STOC manipulation for suppressing the cross-talk-generated noise in the full-field swept-source optical coherence tomography. We used the second-order coherence theory to find phase masks, which remove the coherent cross-talk noise. This approach allows for ex vivo imaging of the sample covered by various scattering phantoms and the rat skin without degrading the transversal resolution. Our method, when combined with fast spatial light modulators, can possibly open the door for using high-power lasers to implement high sensitivity FF-SS-OCT systems. Thus, solving one of the main issues of this imaging modality. Consequently, such STOC-enhanced FF-SS-OCT could serve as the high-resolution imaging alternative to scanning OCT systems.

Funding

National Science Center (NCN, 2016/22/A/ST2/00313); European Union’s Horizon 2020: research and innovation programme (666295); and the Marie Skłodowska-Curie grant (675512).

Disclosures

The authors declare that there are no conflicts of interest related to this article.