Ultra-coherent nanomechanical resonators via soft clamping and dissipation dilution

Abstract

The small mass and high coherence of nanomechanical resonators render them the ultimate mechanical probe, with applications ranging from protein mass spectrometry and magnetic resonance force microscopy, to quantum optomechanics. A notorious challenge in these experiments is thermomechanical noise related to dissipation through internal or external loss channels. Here, we introduce a novel approach to defining nanomechanical modes, which simultaneously provides strong spatial confinement, full isolation from the substrate, and dilution of the resonator material’s intrinsic dissipation by five orders of magnitude. It is based on a phononic bandgap structure that localises the mode, without imposing the boundary conditions of a rigid clamp. The reduced curvature in the highly tensioned silicon nitride resonator enables mechanical Q > 10⁸ at 1 MHz, yielding the highest mechanical Qf-products (> 10¹⁴ Hz) yet reported at room temperature. The corresponding coherence times approach those of optically trapped dielectric particles. Extrapolation to 4.2 Kelvin predicts ~quanta/ms heating rates, similar to trapped ions.

I. Introduction

Nanomechanical resonators offer exquisite sensitivity in the measurement of mass and force. This has enabled dramatic progress at several frontiers of contemporary physics, such as magnetic sensing of a single spin [1], single-protein mass spectrometry [2] and mechanical measurements of quantum vacuum fields [3]. Essentially, this capability originates from the combination of two features: first a low mass m, so that small external perturbations induce relatively large changes in the motional dynamics. Second, high coherence, quantified by the quality factor Q, implying that random fluctuations masking the effect of the perturbation are small. In practice, a heuristic Q ∝ m^1/3 rule, likely linked to surface losses [4], often forces a compromise, however.

A notable exception to this rule has been reported recently, in the form of highly stressed silicon nitride (SiN) string [5] and membrane [6] resonators, achieving Q ~ 10⁶ at MHz-resonance frequencies f, and nanogram (ng) effective masses m_eff. By now it is understood [7–9] that the pre-stress σ̄ “dilutes” the dissipation intrinsic to the material (or its surfaces), a feat known and applied also in the mirror suspensions of gravitational wave antennae [10]. The resulting exceptional coherence has enabled several landmark demonstration of quantum effects with nanomechanical resonators [11–14] already at moderate cryogenic temperatures.

Systematic investigations [15] of such silicon nitride resonators have identified an upper limit for the product Q⋅f < 6 × 10¹² Hz ≈ k_BT_R/(2πℏ) for the low-mass fundamental modes, insufficient for quantum experiments at room temperature T_R [3]. Better Qf-products have been reported in high-order modes of large resonators, but come at the price of significantly increased mass and intractably dense mode spectrum [16, 17] (SI Figs. S4, S5). Consequently, the revived development of so-called trampoline resonators [18] has received much attention recently [19, 20]. In these devices, four thin, highly tensioned strings suspend a small, light (m_eff ~ ng) central pad. The fundamental oscillation mode of the pad can achieve Q ⋅ f ≳ 6 × 10¹² Hz, provided that radiation losses at the strings’ clamping points are reduced through a mismatched, i. e. very thick, silicon substrate [20].

In this work, we choose a different approach based on phononic engineering [21]. Our approach not only suppresses radiation to the substrate [22] strongly, it also enhances dissipation dilution dramatically. This is because it allows the mode to penetrate, evanescently, into the “soft” clamping region, which exhibits a phononic bandgap around the mode frequency [23]. This strongly reduces the mode’s curvature, whose large value close to a rigid clamp usually dominates dissipation if radiation loss is absent [7–10].

As a result, we obtain Qf-products exceeding 10¹⁴ Hz at MHz frequencies, combined with ng-masses—an ideal combination for experiments in quantum optomechanics and sensing. It allows realising many coherent oscillations, reaching high quantum cooperativities, and helps evade low-frequency technical noise in optomechanics and sensing experiments. Remarkably, to the best of our knowledge, this is the highest room-temperature Qf-product of any mechanical resonator fabricated to date. This includes silicon MEMS devices and bulk quartz resonators, which are fundamentally limited to Qf ≲ 3 × 10¹³ Hz by Akhiezer damping, but also LIGO’s mirror suspensions [24–28].

II. Key Design Features

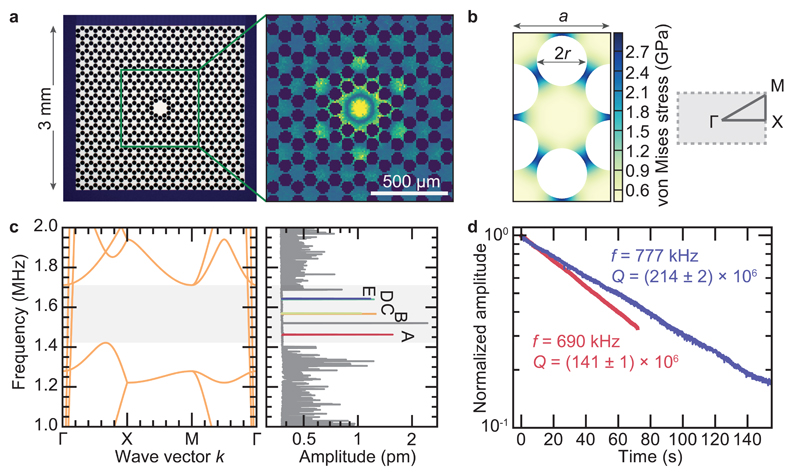
Figure 1 shows the key characteristics of the devices fabricated following this new approach. A thin (thickness h = 35 … 240 nm) silicon nitride film is deposited on a standard silicon wafer with a homogenous in-plane stress of σ ≈ 1.27 GPa. The film is subsequently patterned with a honeycomb lattice (lattice constant a) of air holes over a ~ (19 × 19.5)a² square region, where a = 87 … 346 µm in the batch studied here. Back-etching the silicon substrate releases membranes of a few mm sidelength (Methods). Crucially, the lattice is perturbed by a small number of removed and displaced holes. They form a defect of characteristic dimension ~ a in the centre of the membrane, to which the mechanical modes of interest are confined.

Fig. 1. Device characterisation.

a) Micrograph of a silicon nitride membrane patterned with a phononic crystal structure (left) and measured out-of-plane displacement pattern of the first localised mode “A” (right), of a device with lattice constant a = 160µm. b) Simulation of the stress redistribution in a unit cell of the hexagonal honeycomb lattice (left) and the corresponding first Brillouin zone (right). c) Simulated band diagram of a unit cell (left) and measured Brownian motion in the central part of the device shown in (a). Localised modes A-E are colour-coded, the peak around 1.5 MHz is an injected tone for calibration of the displacement amplitude. d) Ringdown measurements of A (red) and E (blue) modes of two membrane resonators with a = 346µm.

In contrast to earlier optomechanical devices featuring phononic bandgaps [14, 29–31], a full bandgap is not expected [32] here, due to the extreme ratio h/a ≲ 10⁻³. A quasi-bandgap can nonetheless be opened [33, 34], whereby only in-plane modes with high phase velocity persist in the gap (Fig. 1c). Under high tensile stress, a honeycomb lattice achieves a relatively large bandgap—about 20% of the centre frequency 251 m/s ⋅ a⁻¹—with a hole radius r = 0.26a. At the same time, the design allows straightforward definition via photolithography, given that the tether width is still above 5 µm even for the smallest a. Evidently, the phonon dispersion is altered dramatically by the in-plane (d. c.) stress, which relaxes to an anisotropic and inhomogeneous equilibrium distribution that must be simulated (Fig. 1b) or measured [35] beforehand.

We characterise the membranes’ out-of-plane displacements using a home-built laser interferometer, whose sampling spot can be raster-scanned over the membrane surface (Methods and [36]). Figure 1c shows the displacement spectrum obtained when averaging the measurements obtained in a raster scan over a (200 µm)²-square inside the defect, while the (a = 160 µm) membrane is only thermally excited. The spectral region outside ~ 1.41 … 1.68 MHz is characterised by a plethora of unresolved peaks, which can be attributed to modes delocalised over then entire membrane. In stark contrast, within this spectral region, only a few individual mode peaks are observed, a direct evidence for the existence of a bandgap. Its spectral location furthermore agrees with simulations to within 2%.

Extracting the amplitude the first peak at f_A ≈ 235 m/s ⋅ a⁻¹ allows mapping out the (r. m. s.) displacement pattern of the first mode when raster-scanning the probe (Methods). Figure 1a (right) shows an image constructed in this way, zooming on the defect region. The pattern resembles a fundamental mode of the defect, with no azimuthal nodal lines, and its first radial node close to the first ring of holes defining the defect. Outside the defect, the displacement follows the hexagonal lattice symmetry, but decays quickly with increasing distance to the centre. This is expected due to the forbidden wave propagation in the phononic bandgap, and leads to a strong localisation of the mode to the defect.

III. Ultra-High Quality Factors

To assess the mechanical quality of the mode, we subject the defect to a second, amplitude-modulated “excitation” laser beam, and continuously monitor the defect’s motion at the mode frequency, by lock-in detection of the interferometer signal. When the excitation laser is abruptly turned off, we observe the ring-down of the mechanical mode (Methods). Under a sufficiently high vacuum (p ≲ 10⁻⁶ mbar), but at room temperature, the ringdown can last for several minutes at MHz frequencies. Figure 1d shows an example of an E-mode with f = 777 kHz and amplitude ringdown time 2τ = (87.7 ± 0.8)s. This corresponds to Q = 2πfτ = (214 ± 2) × 10⁶ and Q ⋅ f = (1.66 ± 0.02) × 10¹⁴ Hz.

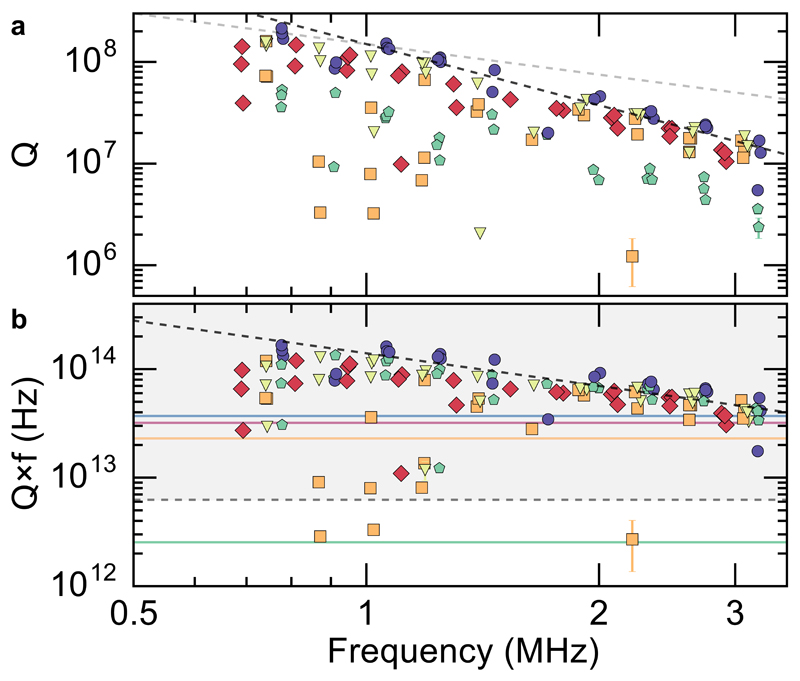
To corroborate and explain this result, we have embarked on a systematic study of more than 400 modes in devices of varying thickness and size (rescaling the entire pattern with a, yet leading the stress redistribution of Fig. 1b unchanged). Figure 2 shows a subset of quality factors and Qf-products measured in 5 different modes of ~ 20 devices with varying size a = 87 … 346 µm but fixed thickness h = 35 nm. Clearly, the Qf-products exceed those of trampoline resonators by more than an order of magnitude, reaching deeply into the region of Q⋅f > 6×10¹² Hz. They also consistently violate the “quantum” (Akhiezer) damping limit of crystalline silicon, quartz and diamond at room temperature, which fundamentally precludes mechanical resonators made from these materials from reaching beyond Q ⋅ f ~ 3 × 10¹³ Hz [24–26, 28].

Fig. 2. Quality factor statistics.

a) Measured Q-factors of A-E defect modes in membranes of h = 35 nm thickness and different size. Black (grey) dashed line is a Q ∝ f⁻² (Q ∝ f⁻¹) guide to the eye. Colours indicate different localised defect modes, as in Fig. 1c. b) Corresponding Qf-products. For reference, solid orange, red and blue lines indicate the “quantum limit” of crystalline silicon, quartz and diamond resonators, respectively [28]. Solid green line shows the expected value for the fundamental mode of a square membrane under σ = 1 GPa stress (4), and dashed grey line indicates Qf = 6 × 10¹² Hz required for room-temperature quantum optomechanics and reached by trampoline resonators [20] at f ≈ 0.2 MHz (not shown).

Our data, in contrast, do not seem to be limited by Akhiezer damping. Indeed a crude estimate following [28] indicates Q_Akhf ~ $𝒪$(10¹⁵ Hz) for silicon nitride. Furthermore, since the phonon relaxation times are much faster than the mechanical oscillation period, we would expect constant Qf, rather than the Q ∝ f⁻² trend discernible in our data. Thermoelastic damping, another notorious dissipation mechanism in micro- and nanomechanical resonators [37], has previously been estimated [6, 17] to allow Q > 10¹¹ at f ~ 1 MHz in highly stressed SiN resonators, and is therefore disregarded.

We expect the phononic crystal to strongly suppress radiation loss [22], due to the > 100-fold suppression of motional amplitude by the phononic crystal (SI Figs. S2, S3). In contrast to standard square [17] or trampoline resonators [20], we thus focus our analysis on internal dissipation. The microscopic nature of this internal dissipation is not known, but evidence is accumulating that it is caused by two-level systems [38, 39] located predominantly in a surface layer [15]. Their effect is well captured by a Zener model [7–9], in which the oscillating strain (ϵ̃(t) = Re[ϵ̃₀e^i2πft]) and stress (σ̃(t) = Re[σ̃₀e^i2πft]) fields acquire a phase lag, σ̃₀ = Eϵ̃₀, from a relaxation mechanism described by a complex-valued Young’s modulus E = E₁ + iE₂. Per oscillation cycle, mechanical work amounting to $\Delta w=\oint \tilde{\sigma }(t)\dot{\widetilde{ϵ}}(t)dt=\pi E_2|{\widetilde{ϵ}}_0{|}^2$ is done in each dissipating volume element. Integrating up the contributions yields the loss per cycle ΔW = ∫ ΔwdV. The comparison with the mode’s total energy W determines its quality factor via

$$Q^{-1}=\frac{\Delta W}{2\pi W}.$$ (1)

In highly stressed strings and membranes, W is dominated by the large pre-stress σ̄, counteracting the membrane’s elongation. In contrast, for small amplitudes, the oscillating strain and thus per-cycle loss is dominated by pure bending. As a result, W and ΔW in eq. (1) depend on different parts of the strain tensor ${\widetilde{ϵ}}_0={\widetilde{ϵ}}_0^{\text{elong}}+{\widetilde{ϵ}}_0^{\text{bend}}$ associated with the mode’s displacement profile. For pure out-of-plane displacement u(x, y) of a clamped membrane, this translates into the imperative to minimise bending-related loss

$$\Delta W\approx {\displaystyle \int \frac{\pi E_2}{1-v^2}{z}^2{\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right)}^{2}dV}$$ (2)

over the tensile energy

$$W\approx {\displaystyle \int \frac{\overline{\sigma }}{2}\left({\left(\frac{\partial u}{\partial x}\right)}^2+{\left(\frac{\partial u}{\partial y}\right)}^2\right)dV,}$$ (3)

where ν is Poisson’s ratio (ν ≈ 0.27 for SiN).

For the fundamental mode of a plain square membrane (marked in the following with index □) of size L, this analysis predicts

$$Q_{\square }^{-1}=\left(2\lambda +2{\pi }^2{\lambda }^2\right)Q_{\text{int}}^{-1}\approx 2\lambda Q_{\text{int}}^{-1},$$ (4)

in very good agreement with available data [9, 15]. Here, $\lambda =\sqrt{E_1/(12\overline{\sigma })}h/L$ quantifies the “dilution” of the intrinsic dissipation $Q_{\text{int}}^{-1}\equiv E_2/E_1$ by the large internal stress σ̄. That is, λ ≪ 1, given the extreme aspect ratio h/L ∼ $𝒪$(10⁻⁴) and the Young’s modulus E₁ = 270 GPa and prestress σ̄ = 1.27 GPa. In an extension of this model [15], extra loss in a δh-thick surface layer $E_2(z)=E_2^{\text{vol}}+E_2^{\text{Surf}}\theta (|z|-(h/2-\delta h))$ can be mapped on a thickness dependent dissipation

$$Q_{\text{int}}^{-1}(h)=Q_{\text{int},\text{Vol}}^{-1}+{(\beta h)}^{-1}.$$ (5)

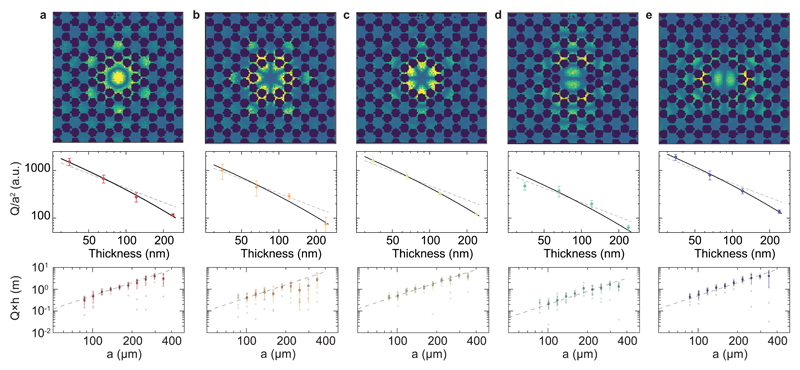
with $\beta =E_1/(6\delta h{E}_2^{\text{Surf}}).$ If the latter dominates, it yields a total scaling $Q_{\square }^{-1}\propto h^0/L^1$ with the geometry of the device. Our devices, however, follow a rather different scaling (Fig. 3), even though they are embedded in square membranes.

Fig. 3. Scaling of quality factors.

(a)-(e) Measured mode shapes of localised defect modes (top) with frequencies {f_A, f_B, f_C, f_D, f_E} = {1.4627, 1.5667, 1.5697, 1.6397, 1.6432} MHz for a device with a = 160µm, as well as characteristic scalings with the membrane thickness h (middle row) and size, parametrized by the lattice constant a (bottom row), when either are varied. Dashed grey lines in the middle row indicate a Q/a² ∝ h⁻¹ scaling, while the solid black lines take into account the additional losses due to the bulk following eq. (5). Dashed grey line in bottom row indicates Q×h ∝ a² scaling. The semi-transparent points correspond to the individual membranes, while the solid points (error bars) indicate their mean value (standard deviation).

In this context, it is important to understand the origin of the two terms in eq. (4): the first, dominating term is associated with bending in the clamping region, while the second arises from the sinusoidal mode shape in the centre of the membrane [9]. The former is necessary to match this sinusoidal shape with the boundary conditions $u({\overrightarrow{r}}_{\text{cl}})=({\overrightarrow{n}}_{\text{cl}}\cdot \overrightarrow{\nabla })u({\overrightarrow{r}}_{\text{cl}})=0,\text{where}{\overrightarrow{r}}_{\text{cl}}=(x_{\text{cl}},y_{\text{cl}})$ are points on, and ${\overrightarrow{n}}_{\text{cl}}$ the corresponding normal vectors to, the membrane boundary. It requires, in particular, that the membrane lie parallel to the substrate directly at the clamp, before it bends upwards supporting the sinusoidal shape in the centre. The extent, and integrated curvature of this clamping region are determined by its bending rigidity.

The boundary conditions in our case are dramatically different,

$$u_{\text{d}}\left({\overrightarrow{r}}_{\text{cl}}\right)-u_{\text{pc}}\left({\overrightarrow{r}}_{\text{cl}}\right)=0$$ (6)

$$\left({\overrightarrow{n}}_{\text{cl}}\cdot \overrightarrow{\nabla }\right)\left(u_{\text{d}}\left({\overrightarrow{r}}_{\text{cl}}\right)-u_{\text{pc}}\left({\overrightarrow{r}}_{\text{cl}}\right)\right)=0,$$ (7)

requiring only the matching of the defect mode u_d with the mode in the patterned part u_pc. If the phononic crystal clamp supports evanescent waves of complex wavenumber k_pc, it stands to reason that this “soft” clamping can be matched to a sinusoidal mode of the defect, characterised by a wavenumber k_d ≈ Re(k_pc) ≫ |Im(k_pc)| without requiring significant extra bending. This eliminates the first term in eq. (4), leaving only the dramatically reduced dissipation

$$Q^{-1}=\eta \frac{E}{\overline{\sigma }}\frac{h^2}{a^2}{Q}_{\text{int}}^{-1}\left(h\right),$$ (8)

dominated by the sinusoidal curvature in the defect (and evanescent waves) $\propto k_{\text{d}}^2\propto 1/a^2,$ whereby the numerical prefactor η depends on the exact mode shape. In the surface damping (thin-membrane) limit, we have again $Q_{\text{int}}^{-1}\left(h\right)\approx {\left(\beta h\right)}^{-1}$ and obtain the overall scaling Q ∝ a²/h. This is indeed the scaling we observe over a wide range of parameters, in all five defect modes, supporting our argumentation (Fig. 3). Overall better agreement is found allowing contributions from volume loss (eq. (5)), which dominates for large thickness. From the fit shown in Fig. 3 we infer equal contributions of volume and surface loss at a thickness of (170 ± 130) nm, in reasonable agreement with Ref. [15].

IV. Simulations

Finite element simulations (Methods) further support the hypothesis of coherence enhancement by soft clamping. Simulating the entire structure, including defect and the finite, periodically patterned phononic crystal clamp, produces only five modes with substantial out-of-plane displacements within the bandgap. Their displacement patterns match the measured ones excellently (SI Fig. S1), and the measured and simulated frequencies agree to within 2%.

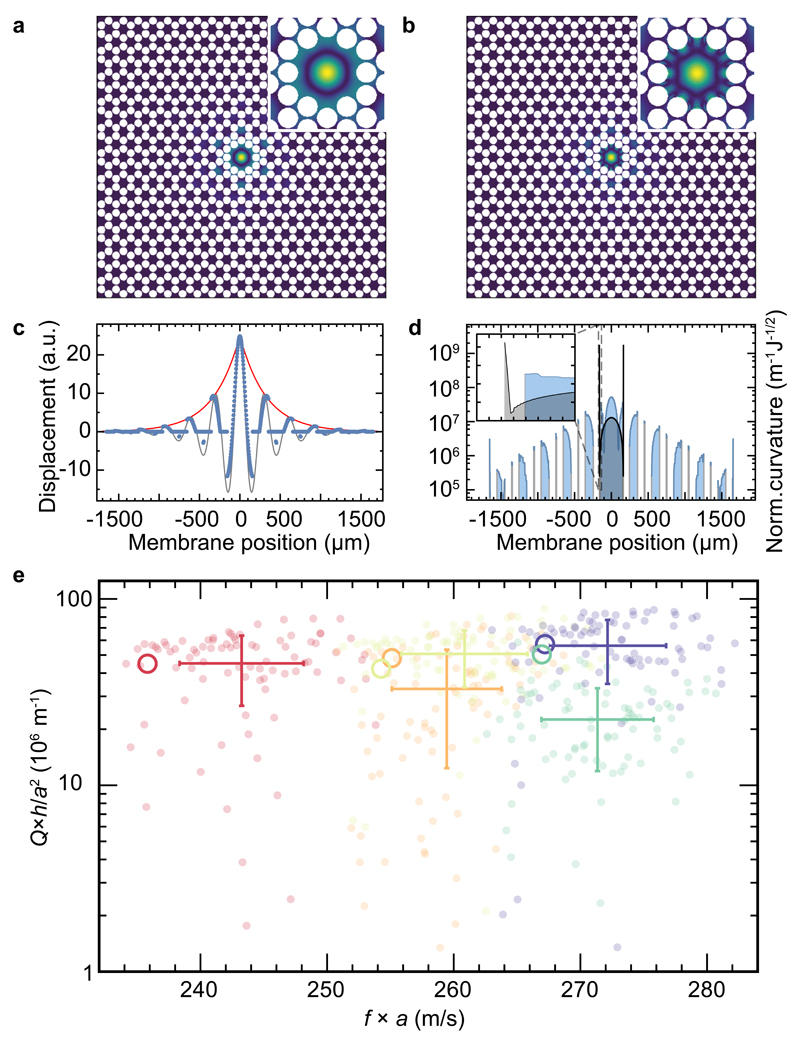
Figure 4 shows the simulated displacement pattern of mode A. It features strong localisation to the defect and a short, evanescent wave tail in the phononic crystal clamp.

Fig. 4. Enhancing dissipation dilution.

a) Simulated displacement field of the fundamental defect modes and zoom on the defect (inset). b) Absolute value of mode curvature and zoom on the defect (inset). c) Simulated displacement along a vertical line through the defect (blue points). The red curve is an exponential function as a guide to the eye, while the grey curve represents a simplistic model of an exponentially decaying sinusoid (see text). d) Absolute value of mode curvature (blue line) along the same section as c). Curvature is normalised to the square-root of the total stored energy in the resonator. Also shown, for comparison, is the normalised curvature of a square membrane with the same frequency (grey line). Inset is a zoom on the membrane clamp, revealing the exceedingly large curvature of a rigidly clamped membrane, which is absent with soft clamping. e) Compilation of measured (transparent markers and errorbars, indicating standard deviations) and simulated (hollow circles) quality factors, normalised to a²/h, consistent with the observed scaling with the corresponding quantities for h = {35 nm, 66 nm, 121 nm}.

Already a simplistic model u(0, y) ∝ Re[exp(ik_pc|y|)], with k_pc = 2π(0.57 + i 0.085)/a reproduces a cross-sectional cut remarkably well (Fig. 4c), supporting the scaling of curvature, and thus damping ∝ 1/a². Note that more accurate modelling of the Bloch waves, their complex dispersion, and interaction with the defect [33, 40], is possible, but, in general, has to take bending rigidity into account to obtain the correct mode shape and curvature.

With the full simulated displacements at hand, we are in a position to evaluate the bending energy (2) and the total stored energy (3) for a prediction of the quality factor (1). For computational efficiency, we use the maximum kinetic energy $W_{\text{kin}}^{\text{max}}={\left(2\pi f\right)}^2{\displaystyle \int \rho u{\left(x,y\right)}^{2}dV/2=W,}$ equivalent to the stored energy (3) (ρ = 3200 kg/m³ is the density of SiN). A comparison of the normalised curvature $\left|\left({\partial }_x^2+{\partial }_y^2\right)u\left(x,y\right)\right|/\sqrt{W}$ reveals the advantage of phononic crystal clamping over the fundamental mode of a square membrane: the latter exhibits a 2-order of magnitude larger curvature in the clamping region (Fig. 4d). The somewhat larger integration domain of the phononic crystal membrane does not overcompensate this, given that the integration is carried out over the mean squared curvature (2). Indeed, carrying out the integrals leads to quality factors in very good agreement with our measured values, much higher than the square membranes’. Figure 4e shows the normalised quality factor Q × h/a² for the five defect modes of more than 30 samples, assuming Q_int(h = 66 nm) = 3750 [15]. Not only are the observed extreme quality factors consistent with simulations, the latter also confirm the trend for the highest Q’s to occur in mode E, apparent (albeit not very significant) in the measurements.

Not all the modes’ measured features are in quantitative agreement with the simulations. Small (< 2%) deviations in the resonance frequency are likely due to small disagreements between the simulated and fabricated devices’ geometry and material parameters, and deemed unproblematic for the purpose of this study. It is noteworthy, however, that mode D exhibits significantly lower measured quality factors than simulated. We attribute this to the insufficient suppression of radiation losses. Indeed simulations indicate that mode D has the largest amplitude at the silicon frame (SI Fig. S2). In experiments, mode D responds most sensitively to the clamping conditions of the sample, further hinting at residual radiation loss.

V. Applications in Optomechanics and Sensing

The ultra-high quality factors enabled by soft clamping offer unique advantages for experiments in quantum optomechanics, as well as mass and force sensing. In quantum optomechanics [3], the presence of a thermal reservoir (temperature T) has the often undesired effect that it leads to decoherence of a low-entropy mechanical quantum state: for example, a phonon from the environment excites the mechanical device out of the quantum ground state. This decoherence occurs at a rate

$$\gamma =\frac{k_{\text{B}}T}{\hslash Q}=1/\tau$$ (9)

and sets the timescale τ over which quantum-coherent evolution of mechanical resonators can be observed. For many experiments—such as cooling to the quantum ground state [41], or probing macroscopic superpositions [42]—it is a basic experimental requirement that this time exceeds the oscillation period, enabling coherent evolution over a number of ~ 2πfτ > 1 mechanical cycles. At room temperature T = 300 K, this translates to Q ⋅ f > 6 × 10¹² Hz, as already discussed above. Our measured devices fulfil this condition with a significant margin.

The more challenging requirement typically is to optically measure and/or prepare the mechanical quantum state within the time τ. Since the measurement rate is proportional to the inverse effective mass, Γ_meas ∝ 1/m_eff, the latter constitutes another important parameter. For a device with a = 160 µm, h = 66 nm, we have measured (Methods) effective masses m_eff of {4.3, 4.7, 4.4, 9.8, 7.2} ⋅ (1 ± 0.11) ng for the five defect modes, which compare very favourably with m_eff,□ = 4.9 ng of a square membrane with the same fundamental frequency f = 1.46 MHz as mode A. In a recent experiment [14], we have realised optical measurements rates close to Γ_meas = 2π × 100 kHz on square membranes with similar mass. Notably, this exceeds γ of the new resonators already at room temperature. In principle, it is thus possible to ground-state cool, or entangle the novel mechanical resonators at room temperature.

The limits in force and mass sensitivity due to thermomechanical noise are also improved by the devices’ enhanced coherence and low mass, given the (double-sided) Langevin force noise power spectral density

$$S_{FF}=2m_{\text{eff}}\frac{2\pi f}{Q}{k}_{\text{B}}T.$$ (10)

Table I gives an overview of the figures of merit that ensue for the best device we have measured at room temperature. It also includes an extrapolation of these parameters to liquid helium (dilution refrigerator) temperatures. Here we conservatively assumed a 2.5-fold (9-fold) reduction of intrinsic dissipation upon cooling, a as observed in cold SiN films [30, 38, 39]. At T = 4.2 K, the expected decoherence rates are about an order of magnitude lower than those of optically trapped dielectric particles [43], and reach those achieved with trapped ions [44]. It combines with the low effective mass to thermomechanical force noise at the $\text{aN}/\sqrt{\text{Hz}}-\text{level},$ attractive for force sensing and -microscopy, such as magnetic resonance force microscopy (MRFM) of electron and nuclear spins [1, 45], as well as mass detection [2].

Table I.

Key parameters and figures of merit of the E-mode in the best (a = 320 µm, h = 35 nm) sample at room temperature, where all measurements were performed, and extrapolated to liquid helium, and dilution refrigerator temperatures.

Temperature T	300	4.2	0.014	K
Frequency f	777			kHz
Effective mass meff	16			ng
Quality factor Q	214	535	2070	106
fQ-product f × Q	166	416	1610	THz
Decoherence rate γ/2π	33,000	175	0.15	Hz
Coherence time τ = 1/γ	0.005	0.91	1060	ms
Number of coh. osc. 2πfτ	23	4400	5.1M	1
Thermal force noise $\sqrt{S_{FF}}$	55	4.1	0.12	$\text{aN}/\sqrt{\text{Hz}}$

Efficient optical and electronic readout techniques are readily available [38, 46], facilitating also applications beyond cavity optomechanics. Further, due to the relatively high mode frequencies, 1/f -type noise, and technical noise, such as laser phase noise, are less relevant. On a different note, due to the relatively low density of holes, it can be expected that the heat conductivity (provided by unaffected high-frequency phonons) is higher than that of trampoline resonators, an advantage in particular in cryogenic environments, and a fundamental difference to dielectric particles trapped in ultra-high vacuum. Finally, the sparse spectrum (SI Fig. S6) of well-defined defect modes provide an ideal platform for multimode quantum optomechanics [14], or may be harnessed for multimode sensing, e. g. for mass imaging [47].

VI. Outlook

Clearly, the devices we have discussed above are just specific examples of soft clamping, and many other designs are possible. Due to the strong suppression of intrinsic dissipation, many other materials can be used to implement high-Q mechanical resonators, including polymers, piezoelectric and crystalline materials, semiconductors, as well as metals. Engineering of defect shape and size will modify the mode spectrum, mass, and dilution properties, and it is evident that our design can be further optimised, depending on the application. For example, larger defects will exhibit a richer multi-mode structure, of interest for multimode optomechanics and mass moment imaging [14, 47]. Small, trampoline-, or string-like defects have a potential to further reduce mass, as desired for force sensing. To illustrate this point, Fig. 5 shows three other examples we have realised in our laboratory, and verified to possess a phononic bandgap enhancing dissipation dilution. Similarly, the phononic crystal clamp can be engineered for stronger confinement, optimised dilution, and/or directional transport. Exploiting these new opportunities, it will be interesting to apply our soft-clamping approach to truly one-dimensional resonators [34], and to explore networks and arrays of defects with ultra-coherent modes with defined couplings.

Fig. 5. Alternative structures.

a) Measured higher-order localised mode of a large defect. b) Micrograph of a trampoline-like resonator, and c) of a string resonator, embedded in a phononic crystal membrane.

For more favourable and robust results, variants of soft-clamped resonators in new geometries or materials should obey a few simple rules of thumb. Sharp geometrical features should be avoided, since the resulting high stress concentration can exceed yield stress and cause rupture. In contrast, too low stress can lead to wrinkling or folding. Smooth, convex geometric shapes are therefore preferable. It is also important to realise an appreciable phononic bandgap. Elementary properties of various lattice structures are known in the phononic literature [21, 32], yet it is crucial to take stress relaxation in the unit cells into account. To estimate performance, the mode’s curvature must be known. To this end, FEM has yielded the most accurate results. Taking the predicted Q (or Q × f) as the objective function, we envision that performance can be further improved via optimisation algorithms such as simulated annealing.

In summary, we have introduced a novel type of mechanical resonator, which combines soft clamping and dissipation dilution. Its extremely weak coupling to any thermal reservoir can, on one hand, be harnessed to relax cooling requirements, and thus allow more complex experiments with long-coherence mechanical devices. On the other hand, if combined with cryogenic cooling, it enables ultra-slow decoherence, which can be overwhelmed even by very weak coherent couplings to other physical degrees of freedom. A wide range of scientific and technical fields can thus benefit from this new development, including, but not limited to cavity optomechancis [3, 14], MRFM [1, 45], mass sensing and imaging [2, 47], hybrid quantum systems [48–50], and fundamental studies of quantum mechanics at mesoscopic mass scales.

Methods

A. Fabrication

The membrane resonators are fabricated by depositing stoichiometric silicon nitride (Si₃N₄) via low-pressure chemical vapor deposition (LPCVD) onto a double-side polished 500 µm single-crystal silicon wafer. A positive photoresist is spin-coated on both sides of the wafer, and patterns are transferred onto both sides of the wafer via UV illumination, corresponding to the phononic crystal patterns on one side and rectangular patterns on the other side of the wafer. After UV exposure and development of the resist the silicon nitride is etched in these regions using reactive ion etching. The photoresist is removed using acetone and oxygen plasma. In order to protect the phononic patterned side of the wafer during the backside potassium hydroxide (KOH) etch, we use a screw-tightened PEEK wafer holder, only allowing the KOH to attack the side with square patterns. Finally, after a 6 hour etch the wafers are cleaned in a piranha solution, thus completing the fabrication process.

B. Characterisation

Optical measurements of the mechanical motion are performed with a Michelson interferometer driven by a laser at a wavelength of 1064 nm. We place a sample at the end of one interferometer arm and spatially overlap the reflected light with a strong local oscillator. The relative phase between the two beams is detected by a high-bandwidth (0 – 75MHz) InGaAs balanced receiver and recorded with a spectrum analyser. In the local oscillator arm a mirror is mounted on a piezoelectric actuator that follows an electronic feedback from the slow monitoring outputs of the receiver, stabilizing the interferometer at the mid fringe position. Furthermore, the piezo generates a peak with a known voltage and frequency. By measuring the full fringe voltage, the power of this peak is converted into a displacement, which is then used to calibrate the spectrum. Using an incident probe power of ~ 1 mW the interferometer enables shot noise limited sensitivity of $\text{10 fm}/\sqrt{\text{Hz}}.$

To image mechanical modes the probe beam is focused down to a spot diameter of 2µm and raster-scanned over the sample surface by means of a motorized 3-axis translation stage with a spatial resolution of 1.25 µm. At each position we extract the amplitude of a few spectral bins around a mechanical peak and thereby construct a 2D displacement map of each mode. The effective masses of mode A-E are extracted from the maximum of the displacement maps after subtracting a background and smoothing. Uncertainties in the mass are based on a 11% error of the above-mentioned displacement calibration.

Quality factor measurements are performed by continuously monitoring the membrane motion at a fixed spot on the sample and optically exciting a given mechanical mode using a laser at a wavelength of 880nm and incident power of 0.5-1 mW, which is amplitude modulated at the mode frequency using an acousto-optic modulator. We use a lock-in amplifier to analyse the driven motion and record mechanical ringdowns.

For our systematic study of more than 400 mechanical modes, we place a 4-inch wafer each with ~ 20 membranes in a high vacuum chamber at a pressure of a few 10⁻⁷mbar and gently clamp down the wafer at its rim. We have verified that the mechanical modes with Qf > 10¹⁴Hz are unaffected by viscous (gas) damping to within 10%.

C. Simulations

We use COMSOL Multiphysics to simulate the phononic crystal patterned membrane resonators. The following material parameters were assumed for the SiN film density ρ = 3200 kg/m³, Youngs modulus E₁ = 270 GPa, Poisson ratio ν = 0.27 and initial stress σ̄ = 1.27 GPa.

The simulations are typically carried out in two steps. First, we perform a stationary study to calculate the stress redistribution due to perforation, assuming a homogeneous initial in-plance stress σ_xx = σ_yy. The redistributed stress is subsequently used in an eigen-frequency analysis, where we either calculate the eigenmodes of an infinite array for different wavevectors $\overrightarrow{k}$ in the first Brillouin zone, or simply simulate the eigenmodes of actual devices.

The mechanical quality factors are extracted by calculating the curvature of a given localised mode, which is obtained from an eigenfrequency simulation, as described above. In order to minimize numerical errors, the geometry is densely meshed. We ensure that increasing the number of mesh elements by a factor of 3 only results in 10% change in the integrated curvature.

Data Availability Statement

The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.

Supplementary Material

Supplementary information is available in the online version of the paper.