Auditory nerve fibre responses in the ferret

Abstract

The ferret (Mustela putorius) is a medium-sized, carnivorous mammal with good low-frequency hearing; it is relatively easy to train, and there is therefore a good body of behavioural data detailing its detection thresholds and localization abilities. However, despite extensive studies of the physiology of the central nervous system of the ferret, even extending to the prefrontal cortex, little is known of the functioning of the auditory periphery. Here, we provide an insight into this peripheral function by detailing responses of single auditory nerve fibres. Our expectation was that the ferret auditory nerve responsiveness would be similar that of its near relative, the cat. However, by comparing a range of variables (the frequency tuning, the variation of rate–level functions with spontaneous rate, and the high-frequency cut-off of phase locking) across several species, we show that the auditory nerve (and hence cochlea) in the ferret is more similar to that of the guinea-pig and chinchilla than to that of the cat. Animal models of hearing are often chosen on the basis of the similarity of their audiogram to that of the human, particularly in the low-frequency region. We show here that whereas the ferret hears well at low frequencies, this is likely to occur via fibres with higher characteristic frequencies. These qualitative differences in response characteristics in auditory nerve fibres are important in interpreting data across all of auditory science, as it has been argued recently that tuning in animals is broader than in humans.

Introduction

The auditory nerve is the route by which all information concerning sound enters the central auditory system, and its activity also provides a way of indirectly estimating cochlear function. This is particularly important at the low frequencies that are important for speech and sound localization, as direct measurements of basilar membrane (BM) responses in this region are particularly challenging. Many issues of cochlear function remain unresolved, for example the nature of non-linearity at low frequencies (Cooper & Rhode, 1992, 1995; Hao & Khanna, 1996; Cooper, 1999; Zinn et al., 2000; Lopez-Poveda et al., 2003; Rosengard et al., 2005; Cooper, 2006; Dong & Cooper, 2006). Even the relative sharpness of tuning within the cochlea is controversial – it has been suggested that the tuning of auditory nerve fibres in humans is narrower than that directly measured in various other mammals (Shera et al., 2002), a claim that has been challenged by other studies (Ruggero & Temchin, 2005). Auditory nerve responses are relatively direct measures of cochlear tuning, and remain pivotal in addressing such questions.

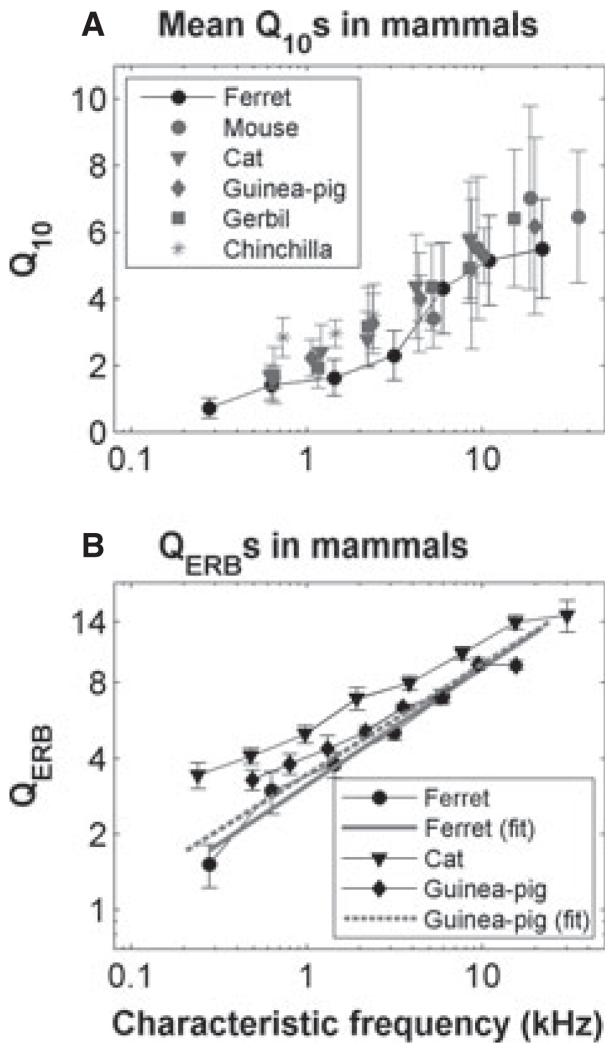
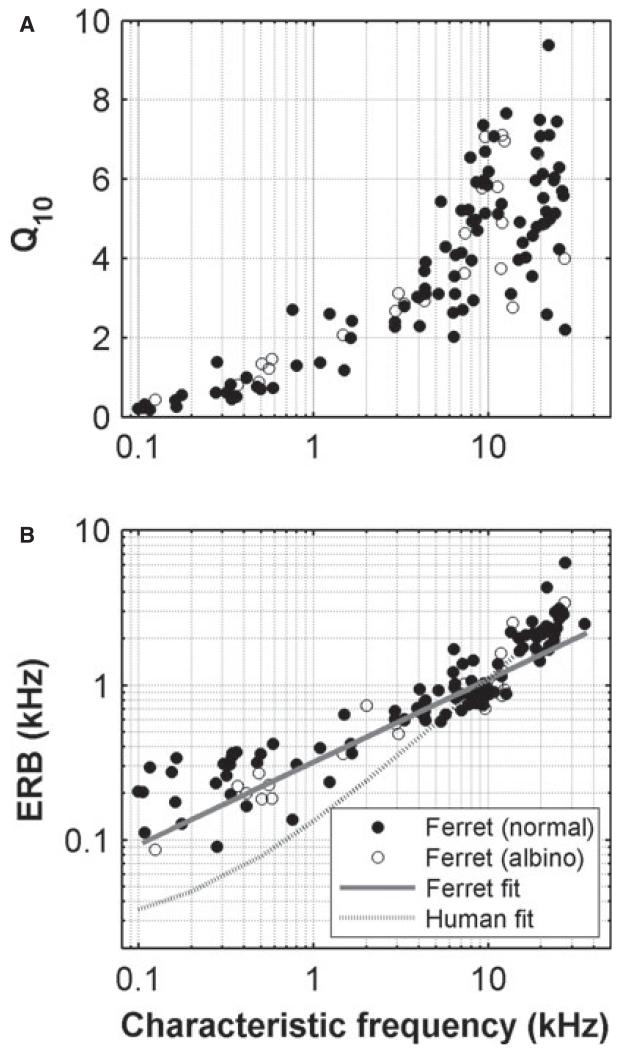
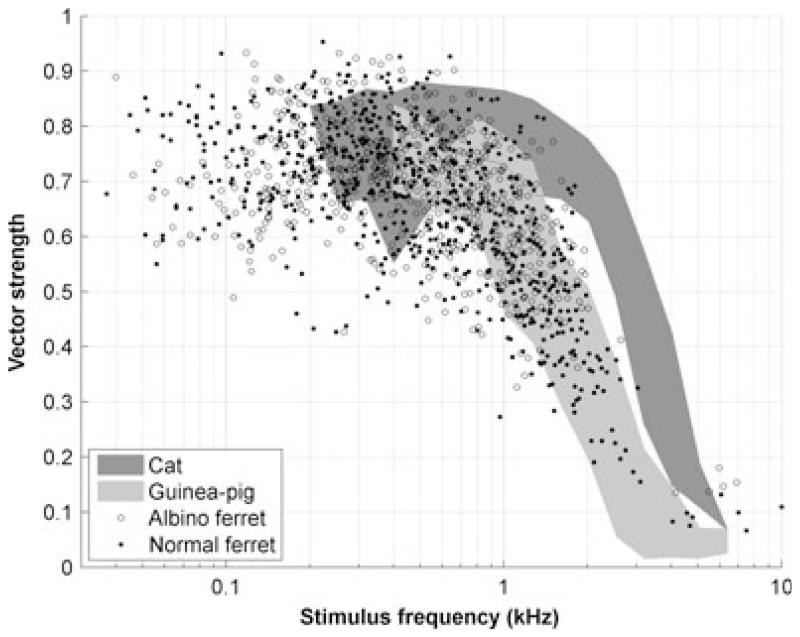
Although different species hear over quite different frequency ranges, their auditory nerve responses are remarkably similar. However, although there is qualitative agreement on the nature of the responses in different animals, there can be considerable quantitative variation. For example, some measures appear to show systematic differences in frequency tuning across non-human mammals – in some accounts, the tuning appears to be broader in the guinea-pig than in the cat (see, for example, fig. 1 in Shera et al., 2002), whereas in others they appear very similar (Ruggero & Temchin, 2005; Taberner & Liberman, 2005) (Fig. 11). Distributions of spontaneous activity (see Taberner & Liberman, 2005) and the dependence of the shape of rate–level functions on spontaneous rates vary across mammals (Liberman M.C., unpublished data; Winter et al., 1990). Even more strikingly, the upper frequency limit of the phase locking in response to low-frequency tonal stimuli is lower in the guinea-pig and chinchilla than in the cat [see comparisons in Palmer & Russell (1986)], which has a cut-off frequency well below that of the barn owl [see comparisons in Hillery & Narins (1984), Smolders & Klinke (1986), and Koppl (1997)].

Fig. 11.

Variation of tuning with CF across species. (A) Variation of Q₁₀ dB with CF for various different species (adapted from Taberner & Liberman, 2005). (B) Variation of Q_ERB with CF for the ferret, guinea-pig, and cat (adapted from Shera et al., 2002). The solid and dashed grey lines are linear regression fits to the ferret and guinea-pig data, respectively.

The ferret is an increasingly used animal model of central auditory processing, and in several studies frequency tuning has been measured (Kelly et al., 1986a; Kowalski et al., 1995; Fritz et al., 2003; Bizley et al., 2005). What is lacking, in this animal, is a description of the tuning and other properties at the input to its central auditory system. Here, we describe the response properties in auditory nerve fibres in the ferret by measuring the frequency tuning properties, rate–level functions, adaptation, spontaneous firing rates (SRs), and phase locking.

Materials and methods

Anaesthesia and surgical preparation

Adult ferrets (male, n = 6, 1000–1994 g; female, n = 5, 786–970 g, two albino), all bred in house, were anaesthetized by intramuscular injection of either a mixture of ketamine (0.08 mL/kg/h) and Domitor (0.04 mg/kg/h) or, in two animals, sodium pentobarbitone (35 mg/kg/h) to maintain areflexia. There were no significant differences between measurements associated with pigmentation or anaesthetic, except where reported in the results. All animals were tracheotomized or intubated, and mounted in a stereotaxic frame with hollow earbars. The animals’ core temperature was maintained at 38 °C with a heating blanket controlled by a rectal thermistor. Endtidal CO₂ was monitored and kept within normal physiological limits by artificially respiring with oxygen, and the electrocardiogram was monitored via a pair of electrodes inserted into the skin on either side of the animal’s thorax.

The skin around the pinna on both sides was separated, and the external auditory meatus was sectioned close to the bony rim. This allowed the animal to be mounted via blunt, hollow earbars in a stereotaxic frame. The front of the animal’s skull was then firmly fixed to the stereotaxic frame with an inflexible mounting rod, which was secured to the animal’s skull with stainless steel screws and dental acrylic. This allowed complete removal and repositioning of the earbars. This was essential because the ferret meatus turns abruptly caudally, and the earbars, when initially inserted, were often completely sealed by the wall of the meatus. The earbars were repositioned with an operating microscope, so that a clear channel towards the eardrum was visible. Petroleum jelly was then applied around the earbar to ensure a seal despite the less firm placement of the earbar.

After a midline incision and retraction of the skin, the temporalis muscle was removed on the left side. The left auditory bulla was exposed, a small hole was made in the posterolateral aspect of the bulla, and it was resealed, including a small-bore nylon tube to allow static pressure equalization while maintaining closed bulla acoustic conditions.

A craniotomy was performed with hand drills and rongeurs, which extended from the midline 8 mm laterally and from below the nuccal ridge 7–8 mm anteriorly. The cerebellum was displaced with a spatula, and micropipettes filled with 2.7 m KCl (starting impedances, 50–150 MΩ) were introduced into the nerve under direct visual control. The craniotomy was filled with 1.5% agar in 0.9% saline to prevent desiccation and to aid stability. For all analyses, the microelectrode signals (recorded with an Axon Instruments Axoprobe 1A) were amplified (×1000) and filtered (300–2000 Hz), and the time of occurrence of the spike was recorded with 1-μs accuracy (using TDT spike conditioner PC1, spike discriminator SD1, and event timer ET1; Tucker-Davis Technologies, Alachua, FL, USA). All procedures were carried out under licence from the UK Home Office, in accordance with the Animals (Scientific Procedures) Act 1986 and in accordance with the European Communities Council Directive of 24 November 1986 (86/609/EEC). This work was also approved by the Medical Research Council and the University of Nottingham.

Sound presentation

Experiments were carried out in a sound-attenuated booth. Stimuli were delivered monaurally via a closed-field system (modified Radioshack 40-1377 tweeters; M. Ravicz, Eaton Peabody Laboratory, Boston, MA, USA) coupled to damped 4-mm-diameter probe tubes, which fitted into the hollow earbars. A probe tube microphone (Brüel and Kjaer 4134 with a calibrated 1-mm probe tube) was used to calibrate the sound system close to the tympanic membrane. Sound levels are expressed in dB SPL (dB re 20 micropascals). The sound system response was flat to within ±10 dB from 100 to 35 000 Hz [see, for examples, Winter & Palmer (1995), Palmer et al. (1996), and Rutkowski et al. (2000)]. All stimuli were generated with an array processor (TDT AP2; Tucker-Davis Technologies), which was housed in a personal computer. The stimuli were output via a digital-to-analogue converter and waveform reconstruction filter at rates of at least 100 kHz (TDT System II). The maximum output level of the system was limited to approximately 100 dB SPL.

All stimuli in this study were pure tones of duration 50 ms and rise–fall time of 2 ms presented every 200 ms. Our search stimulus was mostly a broadband noise (10–50 kHz) at overall levels up to approximately 80 dB SPL RMS. This represented a level of 50–60 dB SPL within the bandwidth of the average fibre, and would thus have been well above threshold (see Fig. 4). However, for low-frequency fibres, this was not an effective search stimulus, and when in the low-frequency part of the nerve we used pure tones varying in frequency and level (up to 90 dB SPL). After audio-visual (AV) estimation of the fibre minimum threshold and characteristic frequency (CF), different data sets were collected, although not generally all for each fibre. In the early experiments, we collected a series of iso-level functions in 1/8-octave and 5-dB steps. However, stability was often not sufficient for completion of data collection, and it was necessary to streamline our data collection, adding in analyses piecemeal as stability allowed, once the initial assessment of frequency tuning was complete. When possible, we measured the full frequency/level response area by using single presentations of tones spanning a 100-dB range of sound level (approximately 0–100 dB SPL in 5-dB steps) and a 4-octave frequency range (3 octaves below and 1 octave above AV CF in 1/8-octave or 1/16-octave steps). We supplemented these data with single iso-level functions (1/8–1/40-octave steps) at +10 and +40 dB above AV threshold and rate–intensity functions (1-dB, 2-dB or 5-dB steps) at CF and below CF (−1.0, −0.5 and −0.3 octaves).

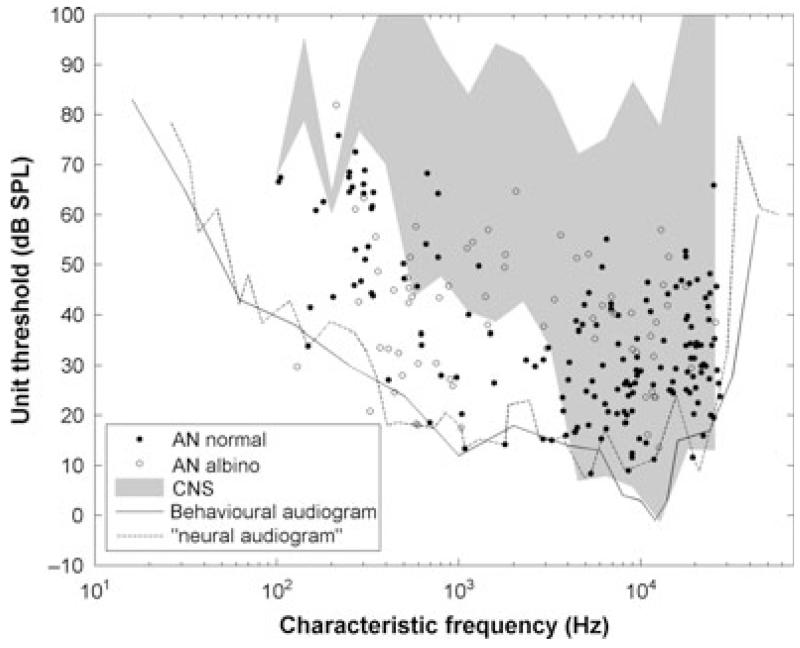
Fig. 4.

Minimum thresholds as a function of CF. The black continuous line is the ferret audiogram (Kelly et al., 1986b). The grey area is the outline of minimum thresholds reported in the inferior colliculus and auditory cortex (Moore et al., 1983; Kelly et al., 1986a; Phillips et al., 1988). The dashed line is the outline when all of the FTCs from all of the fibres are superimposed. AN, auditory nerve; CNS, central nervous system.

Analyses

Quantification of the frequency response areas

Frequency threshold tuning curves were obtained from response areas by finding the minimum sound level at which the spike rate reached 10–20 spikes/s above the spontaneous firing rate. Raw response areas were derived by counting the mean number of spikes per stimulus presentation in the 50-ms window during which the stimulus was presented. Raw response areas were then upsampled by a factor of two in frequency and sound level. These were then smoothed with a two-dimensional filter kernel derived from the matrix multiplication of two triangular windows, each having a ‘half-width’ equal to the resolution of the upsampled response area in frequency and in level. To minimize edge effects, the response areas were padded with extra values (the median of the three nearest neighbours) around their edge.

Owing to the time for which a nerve fibre could be held, response areas were often limited to one stimulus repeat. To improve the contrast of the receptive field for deriving tuning at threshold, we subtracted from the filtered response area a second area, calculated for the 50 ms following the stimulus and processed in the same way as the peristimulus response area. Negative firing rates in the contrast were set to zero. Poststimulus responses for units with significant spontaneous activity were mirror images of the excitatory response during the tones (Harris & Dallos, 1979), so the resulting derived response area had the same bandwidth and greater contrast, and the spontaneous activity was largely removed.

A threshold was automatically defined for each frequency step as the sound level at which the spike count met the criterion of 1.5 spikes per stimulus presentation (in the difference between the 50-ms peristimulus and poststimulus response windows, which is roughly equivalent to the 1 spike per stimulus criterion used elsewhere in this article). This traced out the frequency threshold curve (FTC) for the fibre.

CF, Q₁₀ (CF/bandwidth at 10 dB suprathreshold) and equivalent rectangular bandwidth (ERB) were derived by fitting a rounded exponential function to the FTC, where the upper (ρ_U) and lower (ρ_L) slopes were allowed to vary independently:

$$\begin{array}{cc}\hfill & I\left(g\right)=k(1+{\rho }_U\mid g\mid )\exp (-{\rho }_U\mid g\mid ),\text{for}g⩽0\text{and}\hfill \\ \hfill & I\left(g\right)=k(1+{\rho }_L\mid g\mid )\exp (-{\rho }_L\mid g\mid ),\text{for}g>0\hfill \end{array}$$ (1)

where I is the threshold sound intensity at stimulus frequency f, g = (CF – f)/CF, and k is the threshold sound intensity at CF (g = 0). The ERB is calculated to be the bandwidth of a rectangular filter that would pass the same power as the fitted rounded exponential function. If the overall RMS error (computed across all frequencies) between the measured thresholds and fitted function thresholds was > 6 dB, this unit was excluded from further analysis of tuning.

The bandwidth of tuning was also estimated from iso-intensity functions at 10 dB above AV threshold by fitting the spike counts vs. frequency function with a saturating non-linear function adapted from Sachs et al. (1989):

$$R_{\text{total}}=R_{\text{spontaneous}}+R_{\max }\left(\alpha \mathrm{GN}\right)1.77∕(1+\alpha \mathrm{GN}1.77)$$ (2)

where R_spontaneous, R_max and α determine spontaneous, maximum rate and gain respectively. GN is a Gaussian, normalized to have a maximum value of 1, where the standard deviation determines the ‘bandwidth’, as a function of log₂ frequency, centred on log₂CF. The final bandwidth (and thus Q₁₀) measure was determined from the points at which the fitted function met the criteria of a 1 spike per stimulus (20 spikes/s) increase over the spontaneous activity.

There was no systematic difference between these methods when testing across the entire data set (anova; log CF × Q₁₀ × method, F_1,228 = 1.74, P = 0.19). Where both measurements existed, we took the response area estimate of Q₁₀ for that fibre.

Quantification of rate–level functions

Rate–level functions at CF were fitted with a model originally developed to account for cat auditory nerve fibres (Sachs et al., 1989; Taberner & Liberman, 2005). This assumes a combined linear and compressive gain function, to model the putative response of the BM:

$$P^{\prime }=p∕{[1+{\left(\beta p\right)}^2]}^{1∕3}$$ (3)

where p is sound level in Pascals, and β is a gain parameter determining the level at which the output becomes compressive. The output P′ then forms the input to the function into Eqn (2), in place of GN. From this, a threshold could be determined as the level at which the response was 1 spike over the spontaneous rate. Also, a measure of dynamic range was taken as the range (in dB) over which the response was between 10 and 90% of the driven rate (the difference between the spontaneous and maximum rates).

In a few low-SR (LSR) fibres, we were also able to collect a below-CF rate-level function, which was sigmoidal, with the maximum firing rate equalling or exceeding the maximum firing rate at CF. Following Yates et al. (1990), we estimated a cochlear compression function. This relies on the assumption that, below CF, the mechanical response of the cochlea is linear, and so the non-linear rate–level function reflects post-BM processing that does not vary with stimulus frequency for that fibre. Thus, any difference between the shape of the low-frequency function and the function at CF probably reflects mechanical non-linearity.

Quantification of phase locking

From the spike times, we constructed period histograms locked to the period of the stimulus waveform, and from these we calculated the vector strength (VS) (Goldberg & Brown, 1969). In this article, we report only VS values at the best phase for which the period histogram showed statistically significant (P < 0.001) phase locking (estimated by computing the Rayleigh test of uniformity (Mardia, 1972; Buunen & Rhode, 1978). Using a wide frequency range of tonal stimulation results in large changes in the best phase of phase locking, and when period histograms were constructed, this resulted in the inevitable phase wrapping to within a single cycle.

Phase locking was determined from response areas, iso-intensity functions at 40 dB above threshold, and CF rate–level functions. VS values computed from response area and rate–level function measures were, for each stimulus frequency, computed from a period histogram computed for all levels at 20 dB or more above the calculated threshold at that frequency. For iso-intensity functions, VS was calculated at 40 dB above threshold for each stimulus frequency. In some units, multiple measures yielded multiple estimates of VS. As the measure of interest is the maximum, we took the maximum VS computed in 1/8-octave bins, to yield one number per unit for a given stimulus frequency.

Quantification of peristimulus time histogram (PSTH) shape

PSTH shapes for responses at CF were quantified from CF rate–level function data. Each PSTH was computed by using responses within each 10-dB range (15–24, 25–34, 35–44, and 45–54) above the unit threshold. Thus, each PSTH could include responses from between two (for 5-dB steps) and nine (for 1-dB steps) different sound levels. PSTHs were computed with 0.5-ms bin widths. For fibres with CF > 1.5 kHz, the onset rate was calculated from the bin with the highest firing rate, and the steady-state firing rate was calculated from 30 to 50 ms after stimulus onset (Taberner & Liberman, 2005). For CFs < 1.5 kHz, phase locking complicates this analysis, as the relationship between the onset and the mean steady-state firing rate does not only reflect firing rate adaptation. Instead, we quantified steady-state firing rate as the average peak firing rate in the PSTH for each cycle within the phase-locked response 30–50 ms after stimulus onset.

Results

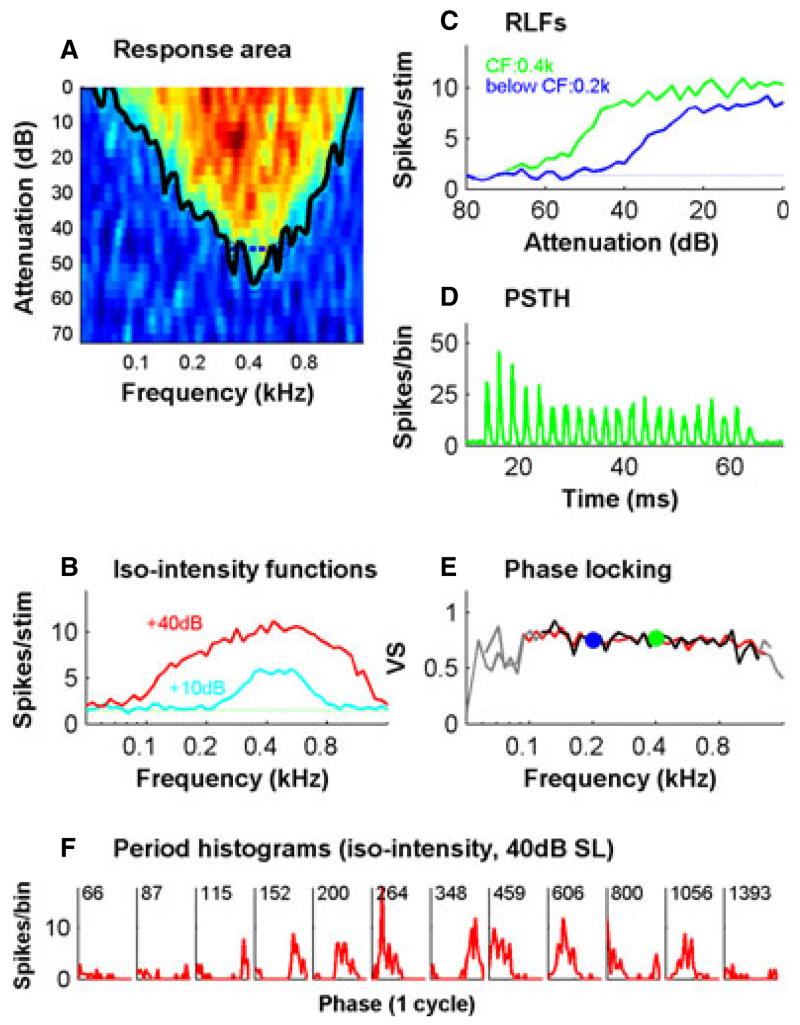
The data presented here are based on recordings from 378 auditory nerve fibres in the anaesthetized ferret. Using a range of stimuli and measures, we quantified many of the basic response characteristics reported in other species. In some fibres, these recordings were comprehensive, as is shown for a low-CF fibre in Fig. 1. We used the response area (Fig. 1A) to derive the FTC (black curve in Fig. 1A), from which we computed the bandwidth at 10 dB suprathreshold. Iso-intensity functions at 10 dB above threshold also yielded rapid estimates of tuning (Fig. 1B). Phase locking (Fig. 1E) was calculated from suprathreshold responses to tones that were part of the response area (Fig. 1A), the iso-intensity function (Fig. 1B) at 40 dB above threshold, or the rate–level functions (Fig. 1C). The rate–level function data, in addition to characterizing the effect of sound level on firing rate and providing estimates of threshold and phase locking, were used to quantify peristimulatory adaptation. An example PSTH obtained from the rate–level function data is shown in Fig. 1D. The tone was always at constant starting phase, and hence, in this low-CF fibre, the PSTH was characterized by peaks at intervals of the tone period, indicating very good phase locking. Phase locking was also evident in the period histograms (locked to the tone period) of Fig. 1F, derived here from the iso-intensity function. Figure 1E demonstrates the correspondence of these different measures of phase locking.

Fig. 1.

The complete set of data collected on a single low-CF (0.4-kHz) auditory nerve fibre. (A) The frequency response area. This was obtained by the presentation of single tones extending in 1/8-octave steps across 2 octaves above and below the CF and 100 dB in level in 5-dB steps. The noisy response area shown here that was obtained with single repeats was smoothed (see Materials and methods), and the FTC was calculated (black line – see Materials and methods); from this, the bandwidths at 10 dB suprathreshold (blue dashed lines) were calculated. (B) Iso-intensity plots at 10 dB (cyan) and 40 dB (red) suprathreshold. SR is shown as the horizontal dotted line. (C) Rate–level functions in response to CF tones (green line) and tones 1 octave below the CF (blue line). (D) Combined PSTH for a CF tone computed from the tones presented during the rate–level function measurement, combined for all suprathreshold levels. (E) Phase locking to tones at different frequencies quantified as the VS (see Materials and methods). Data for this plot were obtained from the +40-dB iso-intensity curve (red) and from the response area (black). The data were obtained from the response area by combining all tone presentations that exceeded 20 dB above threshold at each of the plotted frequencies. Grey indicates non-significant values. VS values derived from the CF (green) and below CF (blue) rate–level functions are also shown. (F) Period histograms as a function of tone frequency (indicated in Hertz) showing phase locking. Data were obtained from the +40-dB iso-intensity function. RLF, rate–level function.

Spontaneous Rates

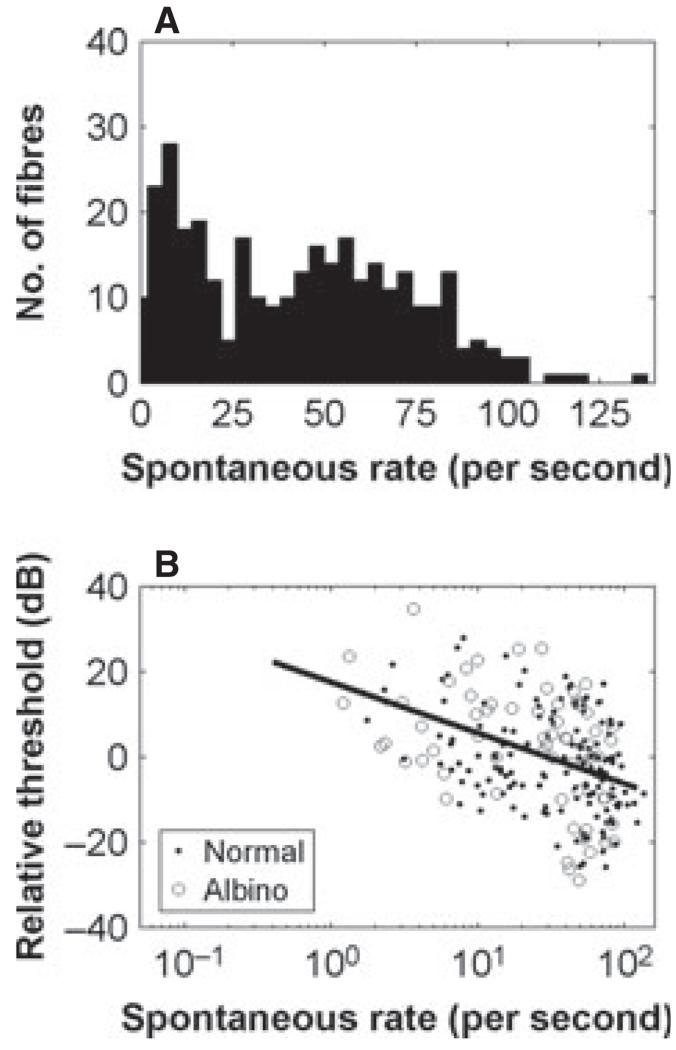
SRs, as in other species, varied by up to ~100 spikes/s. As can be seen in Fig. 2, the SRs were bimodally distributed in the ferret, with a peak at or close to zero and another at ~50 spikes/s. The data show a clear trend for lower-SR fibres to have higher thresholds (P < 0.00001, R = 0.4). Here, thresholds are shown relative to the mean in each octave range, averaged across all the data. SRs were slightly higher in pigmented than in albino ferrets (mean difference, 12 spikes/s, P < 0.01, two-sided Kolmogorov–Smirnov test).

Fig. 2.

Distribution of SRs across all recorded fibres (A) and variation of minimum threshold with SR (B). Thresholds are expressed relative to the mean threshold across all animals, and all fibres in an octave range. The line shows the regression of log SR vs. threshold (R = 0.4, P < 0.00001).

Shape of the frequency response area

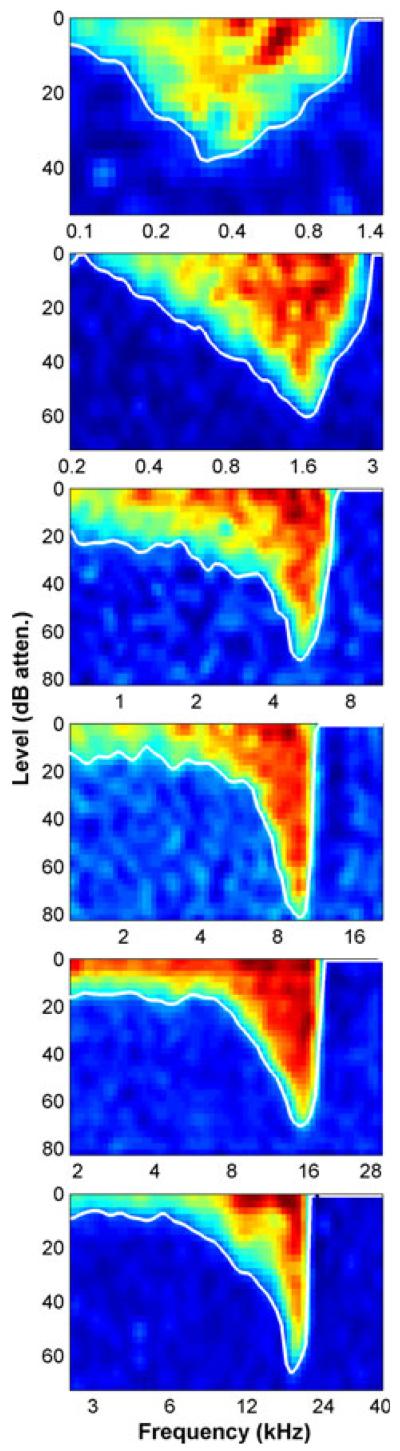
The shape of the response area is dependent on the CF. This is illustrated in Fig. 3 with six examples, all taken from a single animal. Note that the analyses were around each fibre’s CF, so the x-axis of each plot is different. Nevertheless, as the frequency axes are in octaves, an immediate impression can be gained of the relative differences between fibre response areas. High-CF fibre response areas were characteristically asymmetrical, with a greater slope on the high-frequency side of the CF than on the low-frequency side. They also had a low-frequency tail region with an almost constant threshold of ~10–20-dB attenuation (~80–90 dB SPL). The response areas lost their obvious tail and became more symmetrical at or near CFs of 1 kHz.

Fig. 3.

Frequency response areas from six auditory nerve fibres in one animal with CFs ranging from below 0.6 kHz to above 17 kHz. Sound level is expressed in dB attenuation, where 0 dB attenuation is ~100 dB SPL.

Variation of minimum thresholds with CF

In Fig. 4, we show the minimum thresholds as a function of the CF. The thresholds plotted here were either the minimum computed from the frequency response area data or (if this was unavailable) from rate–level functions at the CF. The lowest minimum thresholds generally fell on or near the behavioural audiogram for the ferret (from Kelly et al., 1986b) down to CFs of a few hundred Hertz. Below ~300 Hz, we found rather elevated low-CF fibre thresholds relative to the audiogram, which is consistent with data from the ferret inferior colliculus and auditory cortex (Moore et al., 1983; Kelly et al., 1986a; Phillips et al., 1988). In fact, we measured thresholds as low or lower in this frequency range than previously reported. The slopes of both the high-CF fibres and the very low-CF fibres were finite and are often quite shallow, and when all of the FTCs for our whole population were overplotted [see Taberner & Liberman (2005) for a similar plot in the mouse], the outline of this population tuning curve (which we termed the ‘neural audiogram’) nicely accounted for the ferret behavioural thresholds at both the high-CF and low-CF regions (dashed line in Fig. 4). Here and elsewhere, we have separately plotted the data from two albino animals. Qualitatively, the albinos did not appear to constitute a separable population with respect to this response characteristic. Indeed, in the low-frequency area, thresholds in one of the albinos were among the most sensitive in any animal. However, thresholds in albinos were, on average, 3 dB higher than in pigmented ferrets (t₂₃₁ = −2.6, P < 0.05, t-test on thresholds corrected for CF dependence by subtracting the neural audiogram).

Variation of width of frequency tuning with CF

The tuning width as a function of CF for the ferret is illustrated in Fig. 5. The usual Q₁₀ dB values (see Materials and methods) are plotted in Fig. 5A. The relative tuning was quite wide at low CFs (Q₁₀ values of ≤1) and became narrower from ~1 kHz up to 7–8 kHz, from which point it stayed at approximately the same value (generally below Q₁₀ of 8). When the tuning width was expressed in ERBs (see Materials and methods), the function looked quite linear on a log–log scale. Following Evans (2001) (see also Sayles & Winter, 2010), this was fitted with the function ${\mathrm{ERB}}_{\mathrm{kHz}}=0.31{\mathrm{CF}}_{\mathrm{kHz}}^{0.533}$. Also shown is the human function, derived from psychophysical measurements [ERB_kHz = 0.0247 (0.00437CF_kHz + 1) (Moore & Glasberg, 1983). (Tuning values with other species are compared in the Discussion.) There were no quantitative differences between albino and pigmented ferrets in either tuning measure (anova, CF × pigment × anaesthetic; Q₁₀, F_1,196 = 0.19, P = 0.66; ERB, F_1,121 = 2.36, P = 0.12).

Fig. 5.

Variation of the tuning of auditory nerve fibres with CF. (A) Q₁₀ vs. CF. (B) ERBs vs. CF. The solid line in B shows the fit ERB_kHz = 0.31CF_kHz^0.533. The dashed line shows a fit to human psychophysical data [ERB_kHz = 0.0247 (0.00437CF_kHz + 1)] (Moore & Glasberg, 1983).

Temporal firing patterns

Adaptation

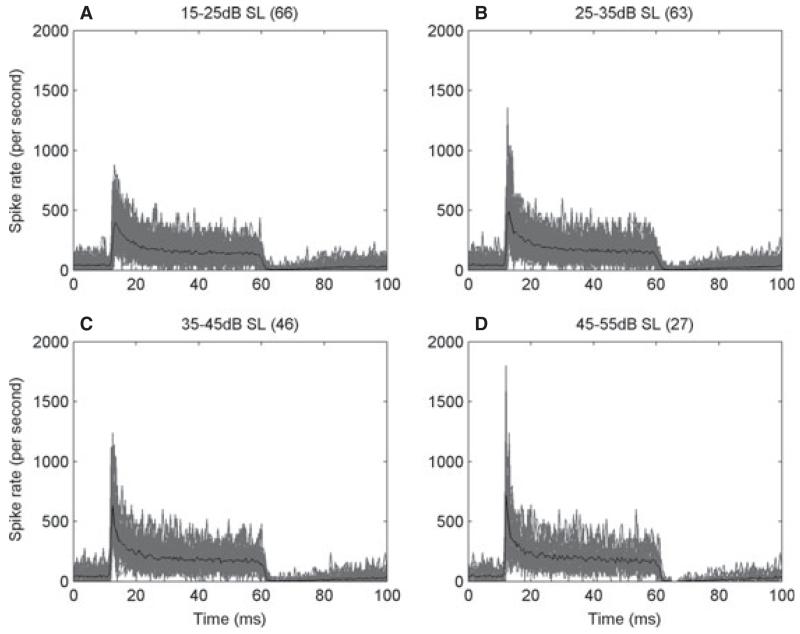
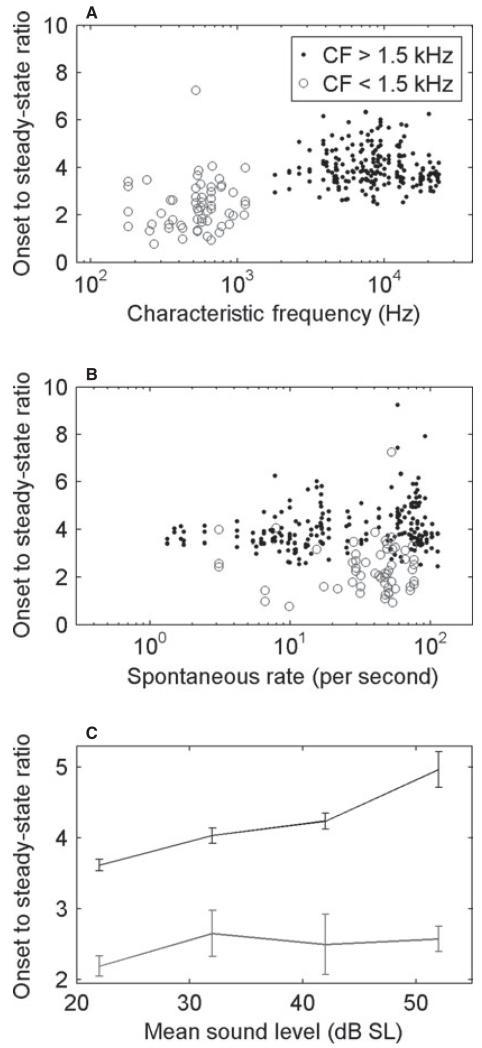
As in all other sensory neurons (Adrian & Zotterman, 1926), auditory nerve fibres in all species show adaptation (Nomoto et al., 1964; Kiang et al., 1965). It takes the form of a higher instantaneous firing rate when a stimulus is switched on, slowing to a lower steady-state rate after a few tens of milliseconds. PSTHs for the short-duration tones that we have used here are illustrated in Fig. 6 (for CFs > 1.5 kHz) for four different ranges of the level of suprathreshold CF tones. The responses, derived from data collected for CF rate–level functions, are shown for a large number of fibres (grey), together with the mean (black). The onset response grew at a higher rate than the steady-state response. We have quantified these adaptation characteristics by computing the ratio of the onset to the steady-state firing rates, and these are shown as a function of CF, SR and sound level in Fig. 7. In high-CF fibres (> 1.5 kHz; black points), this was a simple ratio of spike count at the peak to the steady-state response. In low-CF fibres (> 1.5 kHz; grey circles), the average steady-state firing rate over a fixed time window was strongly influenced by the silent phase in each cycle. Instead, in low-CF fibres, the steady-state response was calculated as the average of the peak in each phase-locked cycle (see Materials and methods). Figure 7A shows that adaptation was stronger in high-CF fibres (t-test, t₂₆₃ = −11.5, P < 0.001), which may be related to the phenomenon of phase locking – the interleaving of ‘silent’ phases reduces the cumulative synaptic depletion thought to underlie adaptation. Although the two measures are not exactly the same, this relationship still holds if the method used to quantify adaptation in low-CF fibres is applied to all units (t-test, t₂₆₃ = −3.58, P < 0.001, data not shown). Adaptation characteristics were essentially independent of SR in our data (Fig. 7B). Adaptation became stronger with sound level in high-CF fibres, but not in low-CF fibres (Fig. 7C). This is attributable to the onset rate increasing at higher levels in high-CF fibres, as seen in Fig. 6, whereas the steady state is largely saturated above 20 dB SL. In low-CF fibres, the onset to steady-state ratios were largely unaffected by sound level. There were no differences in adaptation between albino and pigmented ferrets (three-way anova, CF × pigment × anaesthetic, F_1,216 = 0, P = 0.97). However, adaptation was stronger under pentobarbitol anaesthesia (F_1,216 = 8.64, P < 0.01, mean difference in onset to steady-state ratio of 0.5).

Fig. 6.

Variation in the shape of the PSTH in response to CF tones with sound level above minimum threshold. (A–D) PSTHs at different levels above threshold (shown above the plots) from all fibres (number in parentheses) with CF > 1.5 kHz overplotted (grey). Each individual PSTH is derived by averaging across the levels in a CF rate–level function. The black lines are the mean values.

Fig. 7.

Amount of adaptation measured as the onset to steady-state ratio (see Materials and methods) as a function of CF (A), SR (B), and mean sound level (C). Filled circles and the black line are for CF > 1.5 kHz, and unfilled circles and the grey line are for CF < 1.5 kHz. The data in A and B were obtained over the whole range of sound levels (see Materials and methods for details).

Phase locking

In response to low-frequency tones, auditory nerve fibres are able to signal the shape of the waveform at the ear in the precise timing of their action potentials (see Galambos & Davis, 1943; Kiang et al., 1965; Rose et al., 1967). This is known as phase locking. The ability to phase-lock in response to a stimulus waveform is frequency-dependent, as the hair cell membranes filter out the alternating component of the receptor potential (Palmer & Russell, 1986). This is also shown in the present data in Fig. 8. Here, we have plotted the phase locking quantified as the VS (see Materials and methods). Only significant VS values are shown (P < 0.001, Rayleigh test). It is clear from Fig. 8 that phase locking in ferret auditory nerve fibres fell off from ~1 kHz, and was almost negligible above ~3 kHz. Many of the data points in this figure were obtained from iso-level and response area measures, as well as by use of the usual repeated CF tones. This should not lead to an underestimate of the cut-off frequency, because a direct comparison of the phase locking obtained with these different analyses (not shown) indicated that VS values derived from CF rate–level functions were slightly lower than those derived from either 40-dB SL iso-intensity functions or from response areas (two-way anova, stimulus × CF, F_2,1923 = 8.19, P < 0.001; mean difference, 0.059); that is, our estimate may be slightly higher than would have been obtained only with repeated CF tones.

Fig. 8.

Phase locking as a function of stimulus frequency. Each point represents a significant VS value (see Materials and methods) for a single stimulus frequency in a single fibre. Also shown are the range of values reported by Palmer & Russell (1986) in the guinea-pig (light grey) and Johnson (1980) in the cat (dark grey).

Response as a function of sound level

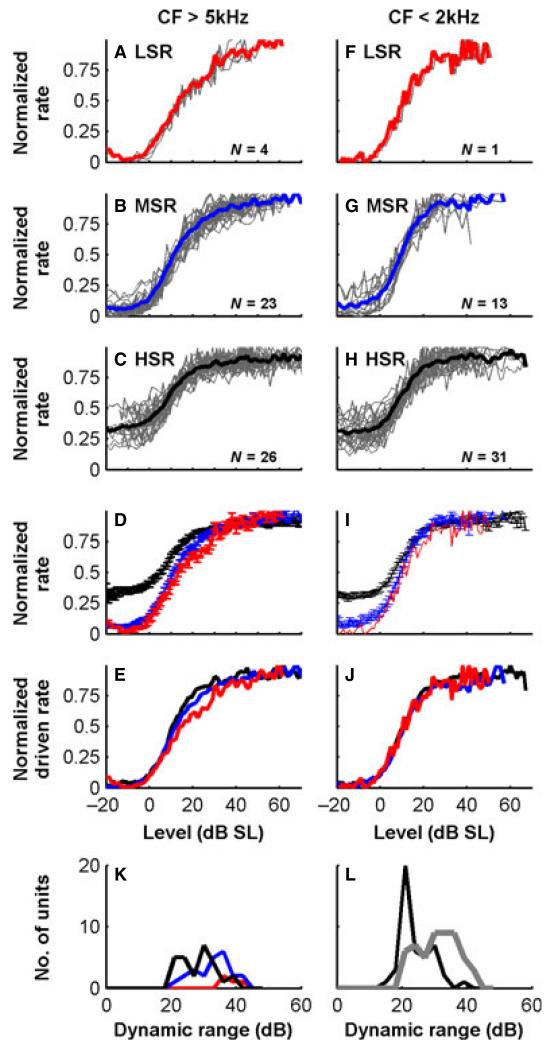
Firing rate functions (normalized to maximum firing rate) for different CFs and different SR fibres are shown in Fig. 9. The LSR fibres showed rate–level functions that did not appear to saturate over the quite wide range of sound levels presented (as shown in Fig. 9, saturation was not complete at 60 dB above threshold). In contrast, the high-SR (HSR) fibres showed sigmoid-shaped rate–level functions that completely saturated. The medium-SR (MSR) fibres showed ‘sloping saturation’ (as in Sachs & Abbas, 1974). These differences were clearly seen in the mean functions for each SR group at high CFs (Fig. 9D), even when they were normalized for SR (Fig. 9E). This pattern was absent in low-CF fibres (Fig. 9F–J). The only differences in low-CF fibres were the vertical offsets below threshold, which reflect the variations in spontaneous activity (Fig. 9I). With normalization for SR (Fig. 9J), the mean driven rate functions for all low-CF fibres overlaid, with no difference in rate–level function shape. Only one low-CF, LSR fibre was held long enough for the rate–level function to be completed. Nevertheless, it was overlaid on the normalized driven rate functions for higher SRs. To quantify these differences further, we fitted model functions to the rate responses in individual fibres (see Materials and methods). The dynamic ranges computed from the fitted functions for fibres with different SRs show that the narrowest dynamic ranges were found in HSR fibres and the widest in LSR fibres, with the MSR fibres spanning the two (Fig. 9K, shown for CFs > 5 kHz). As expected from the observed shapes of functions, we also found a correlation of wider dynamic ranges with higher CFs (Fig. 9L).

Fig. 9.

Rate–level functions for CF tones, for nerve fibres with different SRs and high and low CFs. (A–E) The functions for high-CF fibres (> 5 kHz). (F–J) The functions for low-CF fibres (< 2 kHz). A–C and F–H show individual responses overplotted (grey) and average functions in colour. Sound level is relative to threshold, and rates are normalized to the maximum. (D and I) Mean rate–level functions (± standard error) for HSR (> 25/s, black), MSR (> 3/s, blue) and LSR (< 3/s, red) fibres. (E and J) Mean rate–level functions when also normalized for spontaneous activity, to emphasize the shape of the functions. (K) Dynamic ranges (10–90% range of firing rate) of high-CF ferret auditory nerve fibres with different SRs. (L) Dynamic ranges of high-CF fibres (grey) and low-CF fibres (black).

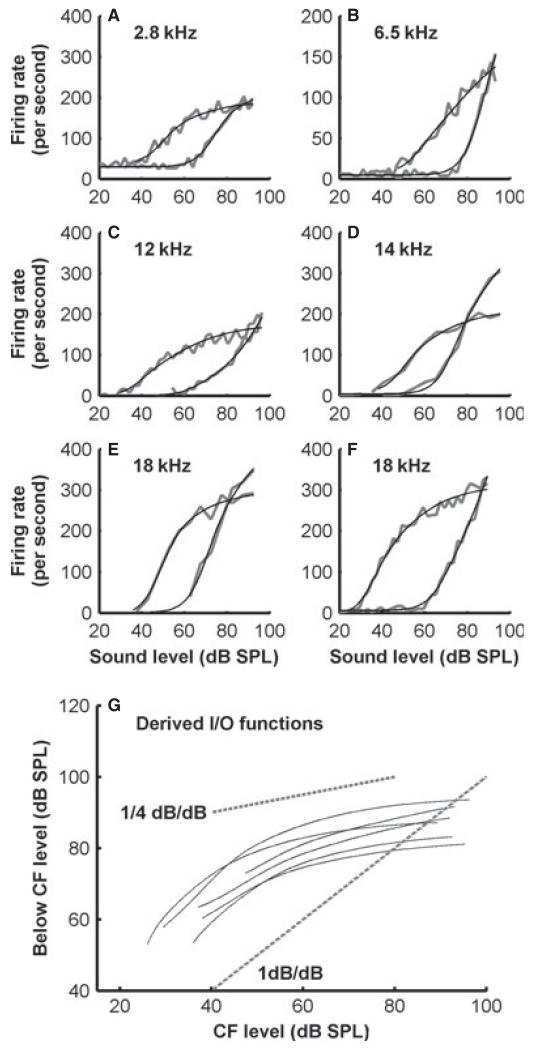
Measuring the rate–level function both at the CF and at lower frequencies in LSR and MSR fibres allows us to estimate the BM input–output characteristics, following the methods of Yates et al. (1990). The results for six auditory nerve fibres with CFs ranging from 2.8 to 18 kHz are shown in Fig. 10. For all of the estimates based on these fibres, the input–output function was nearly linear at low levels and was compressed at higher sound levels (Fig. 10G). The exponent at the high levels was < 0.25 dB/dB.

Fig. 10.

Variation of rate–level functions with CF. (A–F) Un-normalized rate–level functions for MSR and LSR ferret auditory nerve fibres with a range of CFs. In each plot, the raw rate–level function is shown for the CF and for a frequency 1 octave below the CF along with a fitted function. (G) The input–output (I/O) functions for the BM derived from the fitted functions shown for each fibre, calculated by equating firing rates at and below the CF. Dashed lines indicate a linear input–output relationship, and a compressive function of the 0.25-dB/dB slope.

Discussion

Here, we have sought a general characterization of the auditory nerve of the ferret. Using responses to tones in various combinations, we have measured the basic frequency tuning, temporal characteristics and variations in response with sound level.

Shape of the frequency response areas

The variation in the shape of the frequency response areas shown in Fig. 3 has been shown previously in a variety of species, most notably in the large sample from chinchillas reported by (Temchin et al., 2008a,b) and cats (e.g.Kiang & Moxon, 1974). Similar variations in shape are found in most species, although the low-frequency tails in mice appear to have relatively higher thresholds than in other species (Taberner & Liberman, 2005). Frequency response areas in ferret auditory nerve fibres appear to follow very similar trends to those in other mammals of roughly similar size.

Spontaneous rates and thresholds

The range of SRs in the ferret match those in other species, varying from 0 spikes/s to more than 100 spikes/s (for a recent review, see Taberner & Liberman, 2005). However, although we also showed a bimodal distribution of SRs, we appeared to encounter very low-SR fibres less often than reported in other studies (usually ~10%) (Kiang et al., 1965; Liberman, 1978; Evans & Palmer, 1980). Obviously, we cannot rule out a sampling bias, as LSR fibres are thinner (Liberman & Oliver, 1984) and more difficult to record from, but this is unlikely, as the electrodes used here have also been successfully used in the guinea-pig, and are not obviously different from those used in the cat (Palmer & Evans, 1980; Palmer et al., 1995). Recording stability was not obviously poorer in the ferret than in the cat or guinea-pig (personal observation). It is also unlikely that we simply failed to drive them, as our search stimulus was often ~80 dB SPL, which is in the high-frequency area of the ferret, and at least should be well above the minimum thresholds of the vast majority of even LSR fibres. The bimodal distribution of SRs as found in other mammals also argues that there is not a major sampling problem. The relative rarity of LSR fibres has also been found in other studies using ketamine-based anaesthesia (Taberner & Liberman, 2005). We ruled out the possibility that the particular anaestheic regime affected the measured SRs by recording the latter half of the data set under barbiturate anaesthesia, which has been routinely used in a variety of previous studies of auditory nerve activity. The very marked variation in fibre minimum threshold with SR was by no means as obvious in our ferret data, but was demonstrable, and indeed the plot in Fig. 2B looks much like that in the mouse [see fig. 4 of Taberner & Liberman (2005)].

Frequency range of hearing in ferrets

Behavioural audiograms show that ferrets’ hearing extends from a few hundred Hertz up to ~30 kHz (Kelly et al., 1986b). This broad range and relatively good low-frequency response makes them suitable for a wide range of studies, such as low-frequency binaural studies (Hine et al., 1994) or speech (Versnel & Shamma, 1998; Bizley et al., 2010). However, the earliest physiological studies [even from the same laboratory that measured the audiograms (Moore et al., 1983; Kelly et al., 1986a; Phillips et al., 1988)] showed a discrepancy (see Fig. 4) at low frequencies between the audiogram and the minimum thresholds of central auditory neurons. This was also evident in our data, but was attributable, in some measure, to sampling, as later animals, including an albino, reduced the discrepancy somewhat, but did not remove it, at least at the lowest frequencies. Although our sample contains a good number of low-CF fibres, we cannot entirely rule out a sampling bias. However, we demonstrate (Fig. 4, ‘neural audiogram’) that the very low-frequency hearing of the ferret is almost certainly mediated by fibres with somewhat higher estimated CFs, but with quite shallow low-frequency slopes that essentially match the audiogram slope.

Frequency tuning

A particularly important characteristic of auditory processing is the frequency selectivity or bandwidth of receptive fields of individual nerve fibres. We characterized tuning by using two standard measures – Q₁₀ and ERB. The ferret appears to have sharper tuning at low CFs than humans (see Fig. 5), but tuning approximates the human estimates at frequencies above ~5 kHz. Figure 11 further compares these measures across various mammals. Comparisons between species with these measures are complicated by the inconsistent use of standard deviation (Fig. 11A) and standard error (Fig. 11B) for the error bars. Nevertheless, taking the findings at face value, the guinea-pig has broader tuning than the cat, as indicated by the Q_ERB values in Fig. 11B [cat and guinea-pig values taken from Shera et al. (2002)]. The monkey has even narrower tuning (Joris et al., 2011). The ferret is very like the guinea-pig, but, if anything, has slightly broader tuning. However, Fig. 11A suggests that, in terms of the 10-dB bandwidth, the tuning is much more uniform across species. Even here, the ferret measurements that we report are at the low edge, particularly in the frequency range 1–5 kHz. Both measures suggest that tuning in ferret auditory nerve fibres is very similar to that seen in other species, but is on the broad side of this distribution. Perhaps most surprising was that tuning in ferrets closely resembles that in guinea pigs. Although other studies in the ferret have made some estimates of the tuning (Moore et al., 1983; Phillips et al., 1988; Bizley et al., 2005), they are generally too qualitative for accurate comparisons to be drawn, either with our own auditory nerve data, or with data from brain regions where bandwidths are generally more diverse. We found no significant difference between the tuning in pigmented and albino ferrets. Our original expectation had been that frequency tuning in the ferret would be close to that in the more closely related cat (more close than that in the guinea-pig, at least).

Adaptation

Another important aspect of auditory fibre responses is their adaptation, which was again similar to that reported in other species. There were, however, some differences. High SRs are typically associated with more pronounced onsets, and thus greater adaptation. Similarly, onsets are more pronounced in high-frequency fibres (Rhode & Smith, 1985; Muller & Robertson, 1991). We did not observe such a clear relationship between SR and adaptation as has been reported in other species. The relationship with SR here may have been confounded by the rate of stimulus presentation (50-ms tones, five per second), which was slower than in previous studies (25-ms tones presented, ~10 per second) (Rhode & Smith, 1985; Muller & Robertson, 1991). It has been shown that, at very slow stimulus presentation rates (e.g. one every 2 s), the relationship reverses, with LSR fibres showing more pronounced onset responses than HSR fibres (Relkin & Doucet, 1991). Thus, LSR fibres show less adaptation, mainly because they are already adapted at the stimulus presentation rates conventionally used in auditory nerve experiments. It is very likely that the intermediate rate that we employed obscured some of these differences in the population.

The way in which the adaptation characteristics change with sound level is also CF-dependent, the onset response becoming more prominent with level in high-CF fibres, as has also been previously observed in other species (Westerman & Smith, 1984, 1985).

Our data also showed an effect of CF on adaptation, as previously reported in the cat and guinea-pig (Rhode & Smith, 1985; Muller & Robertson, 1991). However, quantitative comparison was difficult, owing to the differences in analysis methods used previously. Previous studies have measured steady-state firing rate over a window of 15–25 ms after stimulus onset, irrespective of CF. In our data, this resulted in measured onset to steady-state ratios that were much higher at low CFs, as the mean was reduced by the silent portions of the response. Despite this, individual PSTHs at low frequencies demonstrated less adaptation as previously reported. Instead, when we used an alternative method, which measured adaptation of the phase-locked peaks, low-frequency fibres showed less adaptation. Clearly, adaptation and phase locking interact at low frequencies. At very low frequencies, phase locking can be asymmetric, presumably reflecting adaptation to individual phases of the signal. What is not clear from this, or other studies, is whether there are intrinsic differences in the adaptation mechanism itself, or whether the apparent differences are entirely attributable to the interaction with phase locking.

Phase locking

The high-frequency cut-off of phase locking is species-dependent (see review in Koppl, 1997). Phase locking in the ferret, like frequency tuning, is a close match for that in the guinea-pig (Palmer & Russell, 1986), and is therefore ~1 octave lower than in the cat (Johnson, 1980). This, again, was unexpected. Phase locking is largely established in the inner hair cell (Palmer & Russell, 1986). The implication, therefore, is that inner hair cell function is limiting phase locking to a similar degree as in guinea-pigs.

Rate–level functions

In most species (Sachs & Abbas, 1974; Winter et al., 1990; Winter & Palmer, 1991), HSR fibres, which are the majority of fibres, have steep rate–level functions and narrow dynamic ranges. At much of the level range of normal hearing, HSR fibres are saturated. This has led to the suggestion that much of the useful information may be carried in the phase-locked responses, which are much more robust to sound level variations (Young & Sachs, 1979). Dynamic range is less limited in MSR and LSR fibres. These fibres tend not to saturate completely even at high sound levels. Thus LSR fibres offer a superior range for rate-coding (Sachs & Young, 1980; Le Prell et al., 1996).

In the cat, the LSR fibres show sloping saturation, HSR fibres show a sigmoid shape, and there are no fibres that fail to saturate (Sachs & Abbas, 1974; Palmer & Evans, 1980). In guinea-pigs, it has been shown, and confirmed in several laboratories, that LSR fibres have a more nearly straight rate–level function, which may not saturate even at the highest sound levels tested (often exceeding 100 dB SPL). We encountered all three types of rate–level function in the ferret, and the shape progression with spontaneous rate (Fig. 9) is more like that in guinea-pigs (Winter et al., 1990; Winter & Palmer, 1991). Although we recorded only small numbers of LSR fibres, they did seem to conform well to the straight functions seen in guinea-pigs. The LSR straight rate–level functions had the largest dynamic range of any fibres in our dataset. Normalizing for SR, the mean driven rate functions all overlie for low-CF fibres, with no difference in rate–level function shape. Low-CF fibres had steep-saturating functions irrespective of SR, as also observed in the guinea-pig (Winter & Palmer, 1991). Overall, it appears that, as with tuning and phase locking, variations of firing rate with sound level in ferret auditory nerve responses closely resemble those in the guinea-pig.

It is noticeable that we were able to fit rate–level functions in our data well (see Fig. 10 for examples) by using the model of Sachs et al. (1989), without changing parameters (the threshold for compression, the compression exponent, and the gradient of the rate–level function for a linear change in input). Fitting of this function to mouse data required modifications to be made. Derived dynamic ranges in ferret auditory nerve fibres also match those in the cat well [see Fig. 14 in Taberner & Liberman (2005)]. This suggests overall that many rate–level functions in the ferret closely match those in the cat.

BM non-linearity

The differences between rate–level functions in mammals are thought to reflect the variation in compression seen in responses on the BM. Briefly, HSR fibres are more excitable, with a high system gain. Thus, they have low thresholds but also saturate at lower sound levels. They are responsive to changes in level at low levels where the BM is very sensitive and its response is largely linear. Less excitable MSR fibres have lower gain and higher thresholds, and so span some of the low sound levels where the BM response is linear, but also the compressive region. Thus, they are often seen to have two distinct regions – a steep region and a slowly saturating region – and a wider overall dynamic range. LSR fibres in guinea-pigs are less sensitive still, and are excitable mainly across the range of levels where the growth of the vibration on the BM is compressive.

At the basal end of the cochlea in particular, compression is limited to near-CF frequencies. The wide tuning tail below the CF is more nearly linear (Nuttall & Dolan, 1996; Ruggero et al., 1997). Taking advantage of this, one can infer cochlear compression from auditory nerve rate–level functions. In a small number of MSR and LSR fibres, we were able to collect below-CF rate–level functions, and thus estimate BM compression in ferrets. These results again yielded estimates that were very similar to those in other species, and suggested that compressive growth in the ferret cochlea is of the order of ~0.25 dB/dB, which compares well with previous estimates in other species (0.2 in the monkey to 0.3 in the guinea-pig) (Rhode, 1971; Patuzzi & Sellick, 1983; Yates et al., 1990).

Hearing in albinos vs. pigmented ferrets

Although it was not a focus of our study, our use of two albinos offered us the opportunity to test whether the peripheral hearing of these animals differed from that of pigmented animals. Hearing in albinos and other spotting mutants is often not entirely normal [see, for example, Strain (2004) for a review of pigment-related deafness in dogs]. In the measurements that we have described here, we found two significant, but small, differences – thresholds were slightly raised and SRs were slightly higher in albinos. No other measurements showed any significant difference. This is consistent with data from the guinea-pig, where cochlear function is generally very little different in coloured and albino strains (Harrison et al., 1984). This suggests that, although the use of albino ferrets is probably not ideal, peripheral function, at least, is only subtly different from that in pigmented ferrets.

Implications for the use of ferrets as an animal model

The ferret is becoming a preferred animal model for auditory processing, for a variety of reasons, not least of which is their trainability, owing to their extreme inquisitiveness. It is clear that ferrets do have good low-frequency hearing, as do humans. However, our data would seem to suggest that this is not because they have fibres that are specifically tuned to very low frequencies (below ~100 Hz), as is certainly the case in other species. The ferret appears to rely on detecting activity below ~100 Hz in higher-frequency channels. For this reason, it may not necessarily be an ideal animal model for the processing that takes place in specifically low-frequency channels. What is also clear from the present data is that the phase-locking limit in the ferret matches that in the guinea-pig, which is by no means as high as in the cat. At present, we have no direct data to indicate which species is more like the human in this respect. In terms of frequency resolution, the range in the ferret is generally somewhat broader than in other mammalian species, but still overlaps with the distribution in tuning measures. However, from Fig. 5 it appears that, as in many other animals, its tuning matches human tuning rather well above 5 kHz.

An interesting question raised by these data is why cochlear function is different between species. A reasonable hypothesis is that variation in the response properties of sensory systems reflects the different needs of the animals – for example, whether the animal is a carnivorous predator, like the cat, or a herbivorous prey animal, like the guinea-pig. It has been suggested that sound localization ability is loosely consistent with such a division, although is actually better predicted by the width of the ‘best’ visual field (Heffner et al., 2008). Consistent with the hypothesis, previous studies of the ferret auditory system have concluded that its tuning properties are very similar to those of cats (Moore et al., 1983; Kelly et al., 1986a; Phillips et al., 1988). Rather surprisingly, we find that the properties that we measure in the carnivorous, predatory ferret are much more like those of the herbivorous, prey guinea-pig than those of the more closely related carnivorous predatory cat.

Abbreviations

AV

audio-visual

BM

basilar membrane

CF

characteristic frequency

ERB

equivalent rectangular bandwidth

FTC

frequency threshold curve

HSR

high-spontaneous firing rate

LSR

low-spontaneous firing rate

MSR

medium-spontaneous firing rate

PSTH

peristimulus time histogram

SR

spontaneous discharge rate

VS

vector strength