Abstract
The CD8 coreceptor modulates the interaction between the T cell antigen receptor (TCR) and peptide-major histocompatibility class I (pMHCI). We present evidence that CD8 not only modifies the affinity of cognate TCR/pMHCI binding by altering both the association rate and the dissociation rate of the TCR/pMHCI interaction, but modulates the sensitivity (triggering threshold) of the TCR as well, by recruiting TCR/pMHCI complexes to membrane microdomains at a rate which depends on the affinity of MHCI/CD8 binding. Mathematical analysis of these modulatory effects indicates that a T cell can alter its functional avidity for its agonists by regulating CD8 expression, and can rearrange the relative potencies of each of its potential agonists. Thus we propose that a T cell can specifically increase its functional avidity for one agonist, while decreasing its functional avidity for other potential ligands. This focussing mechanism means that TCR degeneracy is inherently dynamic, allowing each TCR clonotype to have a wide range of agonists while avoiding autorecognition. The functional diversity of the TCR repertoire would therefore be greatly augmented by coreceptor-mediated ligand focussing.
Keywords: T cell immunity, T cell Antigen Receptor, CD8 coreceptor, tetrameric Major Histocompatibility Complex, cross-reactivity, polyspecificity
1. INTRODUCTION
Activation of cytotoxic T lymphocytes (CTLs) is dependent on recognition of protein antigens presented in the form of peptide fragments on the surface of target cells by class I products of the Major Histocompatibility Complex (MHCI). The peptide-MHCI (pMHCI) complex interacts with the T cell antigen receptor (TCR), with an affinity governed by the TCR’s complementarity-determining regions, which vary highly across the host’s repertoire of TCR clonotypes (Malissen, 2003). The T cell surface glycoprotein CD8 independently interacts with invariable regions of the MHCI molecule (Wyer et al., 1999). Despite the low affinity of the pMHCI/CD8 interaction (Hutchinson et al., 2003), TCR/pMHCI signalling is crucially dependent upon CD8 (Holler and Kranz, 2003), which acts as a coreceptor modulating the productivity of TCR engagement by pMHCI (Janeway, 1992; Luescher et al., 1995; Purbhoo et al., 2001) and thereby the TCR’s functional avidity (Cawthon and Alexander-Miller, 2002).
Various distinct modulatory roles of CD8, possibly acting in concert, have been proposed: (i) promoting the association of TCR and pMHCI (Pecht and Gakamsky, 2005); (ii) stabilizing the TCR/pMHCI interaction (Luescher et al., 1995; Wooldridge et al., 2005), thus prolonging the mean dwell time of the interaction which alters the efficacy of the pMHCI ligand (Kalergis et al., 2001); and (iii) enhancing the rate at which the TCR/CD3 complex attains signalling status (Purbhoo et al., 2001; Holler and Kranz, 2003), by association of TCR/CD3 with protein tyrosine kinases such as p56lck (Arcaro et al., 2001) and adaptor molecules such as LAT (Bosselut et al., 1999) and LIME (Brdičková et al., 2003). The contributions of these various coreceptor roles remain to be fully elucidated. Moreover, the CD8 αβ heterodimer is considerably more potent as a coreceptor than the αα homodimer (Bosselut et al., 2000; Arcaro et al., 2001; Gangadharan and Cheroute, 2004), pointing to the importance of the third function, which is strongly dependent on the presence of the CD8β chain (Bosselut et al., 2000; Arcaro et al., 2000).
In the present paper, we quantify the three CD8 coreceptor functions and evaluate their relative contributions to functional avidity, tying together a wealth of previous and novel data obtained in various experimental systems, using a mathematical theory of TCR avidity and T cell activation (reviewed in Van den Berg and Rand, 2007). We examine TCR binding and functional avidity of both soluble and cell-surface expressed hla a2 molecules that all have faithful interactions with the TCR yet exhibit a large range of CD8 binding affinities. In addition, we analyse data on a system where a suite of altered peptide ligands is available with a range of affinities for a fixed CTL clone.
Our analysis supports the concept that CD8 is a key regulator of TCR degeneracy, Thus, we suggest that variation of CD8 expression allows the T cell to focus on the salient ligand by differentially adjusting its fine sensitivity to potential agonists (cf. Blok et al., 1996; Maile et al., 2005). Such focussing would allow each single T cell to have a wide range of potential agonists (Holler and Kranz, 2004; Wilson et al., 2004), while only one of these is a high-avidity ligand at any given time.
2. MATERIALS & METHODS
2.1. Tetrameric, pMHCI staining, association and dissociation kinetics
Recombinant pMHCI proteins were produced and multimerized as previously described (Wooldridge et al., 2005); gel filtration chromatography showed that >98.5% of the preparation was tetrameric. For tetramer association, 106 ILA1 CTLs were washed and resuspended in 150 μl pbs with phycoerythrin-conjugated MHCI tetramer at a final concentration of 1 μg/ml (with respect to monomer). At the indicated time points, 10 μl aliquots were taken of each sample and diluted to a final volume of 500 μl in pbs prior to flow cytometric analysis. Tetramer concentrations were thus diluted 50-fold, ensuring that further staining after collection did not contribute significantly to the measured mean fluorescence intensity (MFI). Background staining was estimated by labelling ILAl CTLs with non-cognate hla a2 tetramers at room temperature for 30 min. This background value was subtracted from the MFI obtained at each time point. Detailed procedures for the tetramer decay assay have been described elsewhere (Wooldridge et al., 2005). Rate parameters were estimated by non-linear least squares regression.
2.2. Cells
Hmy.2 C1R B (C1R) cells expressing full length hla a*0201 and mutants thereof were produced as previously described (Purbhoo et al., 2001). Cells were cloned and tested with anti-hla a2 fitc (clone BB7.2, Serotec) to ensure that they expressed identical levels of MHCI on their surface. The CTL clone NRT1 is specific for residues 77–85 (SLYNTVAL) of HIV-1 pl7 Gag, presented in association with hla a*0201; NRT1 was generated from a healthy donor by tetramer sorting as previously described (Dunbar et al., 1998). The CTL clone ILAl is specific for residues 540–548 (ILAKFLHWL) of the catalytic sub-unit of the ubiquitous tumour-associated telomerase reverse transcriptase (hTERT), presented in association with hla a2; the monoclonal CTL line ILAl was generated from a healthy donor by limiting dilution culture from a parent cell line which was enriched for hTERT540 –548-specific T cells as previously described (Laugel et al., 2005).
2.3. Functional bioassays
CTLs were washed twice in RPMI/PSG, rested overnight in RPMI/PSG/(2% FCS) and then adjusted to a concentration of 2.5 x 105 CTL/ml in RPMI/PSG/(2% FCS). An aliquot of 106 C1R target cells was pulsed in a 50 μl volume of various concentrations of SLYNTVATL peptide for 90 minutes at 37°C, 5% CO2. After washing twice in RPMI/PSG, target cell concentration was adjusted to 2.5 x 105 cells/ml. An aliquot of 2.5 x 104 CTLs was placed into each well of a 96-U bottomed plate either with or without 2.5 x 104 pulsed C1R target cells in a final volume of 200 μl. Plates were incubated for 4 hours at 37° C. Supernatant was removed and assayed for MIP-1β using a Quantikine elisa kit (R&D systems).
2.4. Analysis of dose-response curves
Let y denote the assay read-out, approaching a maximum value ymax at high peptide pulsing concentrations, with a non-specific background value ymin. The ratio (y − ymin)/(ymax − ymin) can be taken to indicate the proportion of the T cells in the bioassay responding at the given pulsing concentration x. Accordingly, we assume that this proportion denotes the probability that a T cell will register a TCR-derived signal exceeding the cellular threshold for activation (Viola and Lanzavecchia, 1996; Hemmer et al., 1998; Van den Berg and Rand, 2004a) We assume that the TCR signal W is composed of two terms, a background term Wbg due to signalling elicited by ligands other than the relevant agonist and a term due to the agonist, which we analyse as a product of the MHCI copy number (presentation level) Z and the agonist-derived TCR signal w, normalized per pMHCI molecule (Van den Berg et al., 2001). It is standard to assume Langmuir binding for the presentation level: where x denotes the peptide incubation concentration, ξ is a saturation parameter and is the maximum presentation level that can be attained. We assume that ξ is independent of the MHCI α3 mutation. Preliminary simultaneous least-squares fitting of this expression gave an estimate for ξ greater than the greatest pulsing concentration. Therefore we take
We assume that Wact − Wbg follows a lognormal distribution. For the sake of analytic convenience this can be approximated as a loglogistic distribution, with location and scale parameters ω > 0 and α > 0, respectively:
| (1) |
The quantity can be estimated from the experimental data. This compound parameter serves as an index of TCR signal strength per ligand molecule (provided that the quantity has the same value for all ligands under consideration).
2.5. Theory of TCR triggering: TCR/pMHCI kinetics and optimal dwell-time
We briefly review those aspects of the TCR/pMHCI kinetics and TCR triggering that are relevant for the quantification of coreceptor effects (for further mathematical details and arguments, see Van den Berg et al., 2001; Van den Berg et al., 2002; Van den Berg and Rand, 2007; Burroughs and Wedagedera, 2006; Chan et al., 2003). The probability that an interaction between a pMHCI and a TCR molecule results in intracellular signalling is given by the following formula:
| (2) |
Here G(t) denotes the probability that the TCR/CD3 complex and the associated (nascent) signalosome will have attained signalling status t time units after the TCR/pMHCI interaction started, and F(t) is the distribution function of the lifetime of the TCR/pMHCI interaction, i.e. F(t) denotes the probability that the TCR/pMHCI interaction will last for at most t time units. The standard assumption for the dwell-time distribution is that the interaction is characterized by a fixed hazard rate for dissociation, usually called the off-rate. This leads to the exponential distribution for the TCR/pMHCI dwell-time: F(t) = 1 − exp(−vt), where v denotes the off-rate.
The function G reflects the steps involved in the transition to signalling status, the statistics of the weighting times associated with these steps, and their transition diagram (a graph expressing precedence relationships between these steps). It can be shown that the density G' is well-approximated by a weighted series of Dirac pulses, provided that the transition diagram satisfies certain conditions on the number of steps relative to the graph’s complexity. For the simplest member of this family of approximations, let G(t) to be the Heaviside step function with G(t) = 0 for t ≤ TR and G(t) = 1 for t > TR. Here TR is a positive compound parameter which represents the time required for a TCR/pMHCI interaction to last in order to achieve intracellular signalling elicited by that TCR; TR is called the TCR receptor triggering threshold.
On the standard assumption of a time-constant hazard rate v for TCR/pMHCI dissociation, the mean dwell-time of the TCR/pMHCI interaction equals 1/v and the probability that the interaction will be productive works out as Under the assumption that the TCR/pMHCI interaction is MHC-limited (Van den Berg et al., 2002) the rate at which a single pMHCI copy elicits intracellular signals is v exp{−vTR). This is a hump-shaped function of v (Valitutti and Lanzavecchia, 1997; Bongrand and Malissen, 1998; Kalergis et al., 2001), with a maximum at v = 1/TR, i.e. the optimum mean dwell-time equals TR. Every TCR/pMHCI pair is characterized by a specific value for v. For a given TCR, virtually all pMHCI species are null ligands which dissociate very rapidly whereas those ligands that satisfy are precisely the agonists for that TCR clonotype (van den Berg et al., 2001; Lyons et al., 1996; Hudrisier et al., 1998; Matsui et al., 1994; Van den Berg and Rand, 2004b).
A TCR may have one or several ligands such that (Malissen, 2003); such rare heteroclitic agonists are suboptimal under MHC-limited conditions, but not under TCR-limited conditions (Van den Berg et al., 2002). The mean rate at which a single agonist copy elicits TCR triggering events can be identified with the TCR’s functional avidity for that ligand: a clonotype is said to have high avidity for a given epitope if it is able to respond even when the ligand is present at very low levels, whereas a low-avidity clone requires higher presentation levels for activation (Ashton-Rickardt and Tonegawa, 1994; Alexander-Miller, 2000; Gross et al., 2004).
2.6. Derivation of the microdomain recruitment equation
The coreceptor CD8 has been implicated in recruiting engaged TCR to specialized membrane microdomains that are kinase-enriched and/or phosphorylase-depleted. In such domains, phosphorylation and kinase/adaptor-recruitment processes are assumed to proceed more rapidly than outside these domains (Montixi et al., 1998; Janes et al., 1999; Arcaro et al., 2001; Doucey et al., 2001; Cawthon and Alexander-Miller, 2002; Bunnell et al., 2002; Filipp et al., 2003). Let denote the time it takes to attain a fully triggered TCR/CD3/signalosome outside of the microdomains, and let denote the shorter corresponding time in these domains. Also, let Trc denote the time it takes for an engaged TCR to be recruited to one of these domains; this is a random variable. The parameter TR is a function of Trc; the shorter Trc, the faster the TCR/CD3 proceeds through the steps that lead to activation. In particular, if Trc is the time till recruitment, we have
| (3) |
Let ϑrc denote the rate at which a TCR/pMHCI complex is recruited to a microdomain when bound to a CD8 capable of mediating the association with such a domain (Arcaro et al., 2000; Gangadharan and Cheroute, 2004; Gakamsky et al., 2005). The probability that a recruitment event occurs during an association with CD8 equals ϑrc/(ρ + ϑrc) where ρ denotes the pMHCI/CD8 dissociation rate. If pMHCI/CD8 kinetics is fast (Wyer et al., 1999) this probability is very small, which means that the expected time until recruitment can be treated as an exponential variate with mean (1 + ρ/γ)/ϑrc where γ denotes the pMHCI/CD8 association rate (specifically, the moment generating function of Trc is where p = ϑrc/(ρ + ϑrc); this becomes the moment generating function of the exponential distribution upon dropping the term in t2).
Conditioning the triggering probability on the recruitmenttime Trc, we have
| (4) |
The recruitment equation, which appears below as equation (19), is obtained from equation (4) with the definition and the physically reasonable assumptions and
2.7. Kinetic theory of T cell/pMHCI-tetramer association and dissociation
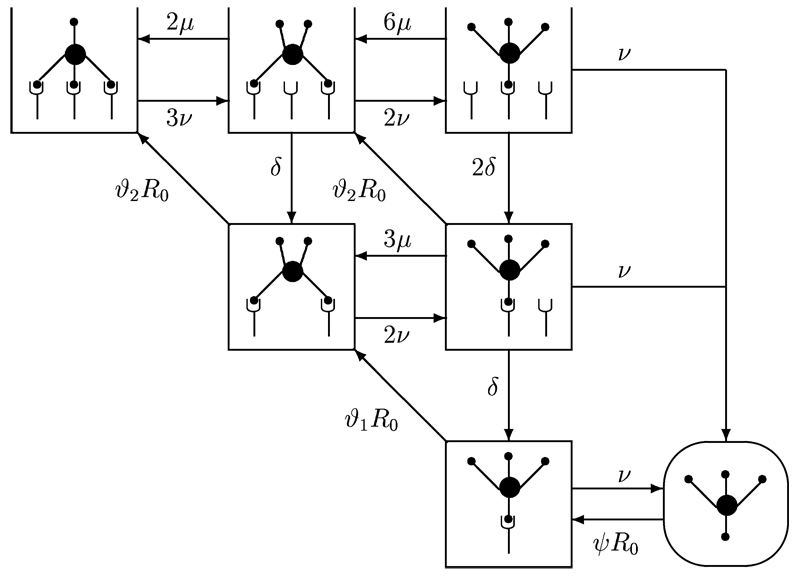
Kinetic constants of the TCR/pMHCI interaction can be inferred from the intensity of fluorescence staining with pMHCI tetramers, as well as the rates at which a T cell acquires and loses the staining in association and dissociation assays. A mathematical model of these association and dissociation kinetics is depicted schematically in Figure 1; the corresponding equations are given in Table 1. Steric considerations suggest that each tetramer can bind at most three TCR molecules. When one of the contacts dissociates, the temporarily unoccupied MHCI site will generally be able to rebind the same TCR before it is able to diffuse away from the reaction radius of the tetramer. Consequently, the tetramer forms a comparatively persistent association with a cluster of TCRs. These associations can outlast the duration of the mean single-site dwell time by several orders of magnitude (Laugel et al., 2005); this avidity effect is most pronounced in triplet TCR clusters (defined by a 3:1 TCR/tetramer stoichiometry), somewhat less marked for duplet TCR clusters (2:1), and absent in TCR singlets (1:1).
Figure 1. Diagram showing the progressive binding of pMHCI-tetramers to TCR singlets, duplets and triplets.
Non-covalent association and dissociation steps are indicated by arrows, which are labelled with the relevant rate constants.
Table 1. Equation of MHCI tetramer/T cell kinetics.
As shown in Figure 1, an MHCI tetramer newly recruited to the T cell surface forms a singlet which needs to recruit two more TCRs to form a triplet cluster. The parameters are: v, the single-site dissociation rate of the TCR/pMHCI interaction; µ, the single-site (re)binding rate within a TCR-cluster (not necessarily identical to the native TCR/pMHCI association rate in a physiological cell:cell conjugate); δ, the rate of loss of an unbound TCR molecule from the cluster; ψR0, the rate at which MHCI tetramers are recruited from the solution, where R0 denotes the density of free TCR molecules on the T cell surface, i.e. TCRs which are not engaged in a tetramer-binding cluster. The ambient solution serves as an infinite reservoir, so that the concentration of MHCI tetramer in solution (to which ψ is proportional) can be taken to be constant. Moreover, ϑ1R0 denotes the rate at which singlet TCR clusters recruit another TCR molecule to form a duplet cluster and ϑ2R0 is the rate at which duplet TCR clusters recruit another TCR molecule to form a triplet cluster. The integer coefficients in Figure 1 reflect the numbers of available sites in the various transitions.
When an MHCI tetramer is released to the ambient solution, the cluster will disband by diffusion, merging into the background of free TCRs. We assume that this break-up is effectively complete before one of the TCRs captures another tetramer from the solution. The only non-linearity in the system arises as a result of the following conservation law:
| (5) |
where RT is the surface density of all TCR molecules and xij denotes the surface density of TCR clusters containing i TCR molecules which are bound to the MHCI tetramer at j sites; we assume that j = 4 is ruled out by steric hindrance. Conjugated with a fluorescent group, the MHCI tetramers can be used as a staining agent. Staining intensity I equals provided that tetramer fluorescent brightness is not affected by the valency of its coupling to TCR.
2.7.1. Derivation of the equilibrium staining equation
The following definitions are introduced for notational convenience:
| (6) |
Assuming we find the following equations characterizing the steady state:
which leads to a system of two equations describing staining intensity:
| (7) |
| (8) |
(the second equation is just the conservation law, equation (5)). Routine analysis yields I → RT/3 as v/μ → 0, which shows that most of the staining involves TCR triplets when rebinding is rapid. Moreover, if we assume that v is proportional to the off-rate of the TCR/pMHCI interaction and that ψ, θ1, θ2 and μ are all proportional to the on-rate of this interaction, we can rewrite these equations in terms of the dissociation constant . In particular, the staining equation becomes
| (9) |
where and the constants KA, KB and KC absorb the various proportionality constants. The sixth-power dependence of the affinity of the TCR/pMHCI interaction is the result of two avidity interactions: one involving the dominance of triply-bound tetramers, as discussed above, and one involving the progression of binding through TCR singlets, duplets and triplets. These results imply a sigmoid dependence of I on In particular, rapid within-cluster rebinding makes the sixth-power term dominant, so that this curve becomes very steep: the transition from background staining to saturated staining is predicted to occur within less than an order of magnitude, as was confirmed by experimental observations (Laugel et al., 2007).
2.7.2. Effective dissociation rate of the tetramer/TCR-triplet complex
In a tetramer dissociation assay, tetramer-treated T cells are placed in a tetramer-free solution which contains antibodies to cap tetramers coming off the T cell surface, precluding their reattachment. If the rebinding rate μ far exceeds the single-site dissociation rate v and most of the MHCI tetramer bound to the surface is bound to TCR triplet clusters, staining intensity decays with apparent rate constant v3. The kinetics of the triplet system {x31, x32, x33} is linear and thus there are two further eigenvalues. A routine exercise in analysis yields the following (approximate) formulae for these two additional eigenvalues:
These two values correspond to equilibration between singly, double and triply bound tetramers in the triplet cluster. Inasmuch as these two rates exceed v3 (since ) by several orders of magnitude, the empirical dissociation curve (as observed on the time scale) will be effectively monophasic. The observed rate constant λeff,off then serves as an estimate for v3.
Inasmuch as μ is unknown, the single-site off-rate v cannot be determined directly from the measured rate λeff,off (i.e. v3). However, ratios of the experimental rates (e.g. between mutant variants) can be used to gauge the effect on v; since v3 ∝ v3 the cube root of the experimental ratio gives the relative change of v. When initial staining is predominantly in the form of duplets, a similar argument applies, but now the rate v2 is determined and a square root has to be extracted.
2.7.3. Analysis of MHCI-tetramer/T cell association kinetics
The association phase of tetramer staining has more complicated dynamics than the decay curves, since it involves a progression through the binding states depicted in Figure 1. When (rapid within-cluster rebinding), fast modes within the triplet and duplet systems rapidly relax the dynamics onto the {R1, R2, R3}-manifold, on which the following dynamics obtains:
| (10) |
| (11) |
| (12) |
which immediately yields the following staining kinetics:
| (13) |
with a time-varying effective rate λeff(t), defined by:
| (14) |
Equation (13) shows that this means that the rate of MHCI tetramer recruitment from solution can be estimated from the initial slope of the association curve. Furthermore, the equilibrium staining equation (9) can be used to calculate the steady-state value of λeff, because the relative magnitudes of the three terms on the right-hand side of equation (9) correspond directly to the relative numbers of singlets (i = 1), duplets (i = 2), and triplets (i = 3) at steady state.
3. RESULTS
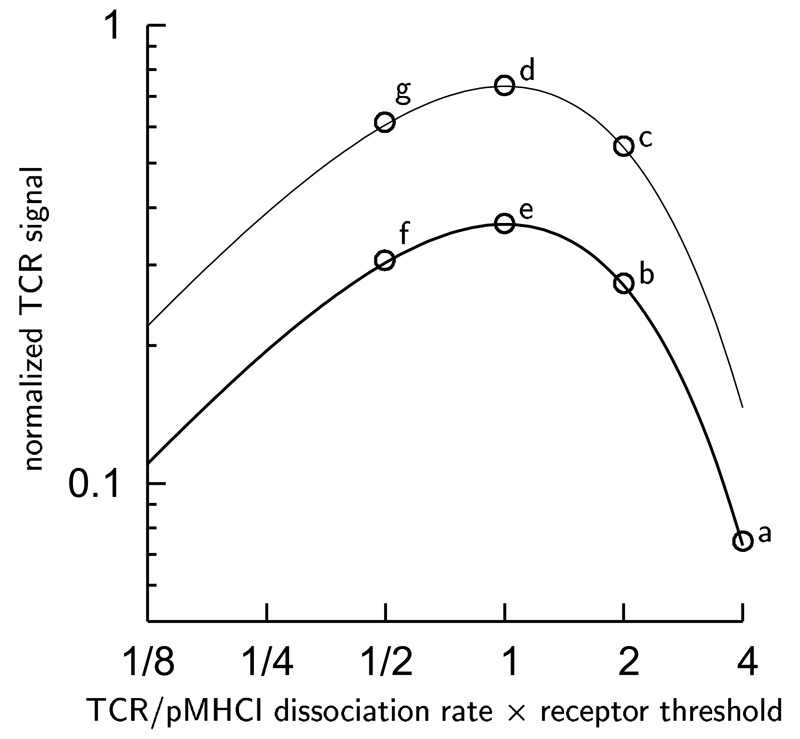
The TCR triggering rate per agonist molecule is given by the formula v exp{–vTR} (Van den Berg et al., 2002), illustrated in Fig. 2, where v is the TCR/pMHCI dissociation rate and TR is the time the TCR/pMHCI docking needs to last to promote intercellular signalling. At least two distinct coreceptor effects are suggested by the formula: modulation of the TCR/pMHCI dissociation rate v (Hutchinson et al., 2003; Wooldridge et al., 2005) and modulation of the receptor triggering threshold time TR by colocalization with kinases, adaptors and linkers (Doucey et al., 2001; Montixi et al., 1998; Bosselut et al., 1999; Brdičková et al., 2003; Filipp et al., 2003). We investigate both types of coreceptor-mediated modulation.
Figure 2. Graph illustrating the scope for coreceptor-mediated modulation of the TCR activation rate per pMHCI molecule.
A reduction of the TCR/pMHCI dissociation rate v by 50% takes the ligand at point a to b. However, the same ligand is taken to point c by a 50% reduction in the receptor threshold TR. The two modulatory effects can act synergistically: when both v and TR are reduced by 50%, the ligand at point a is taken to d. By contrast, the optimal ligand at point e becomes less effective when the TCR/pMHCI dissociation rate is reduced by 50% (e to f) whereas the same ligand is improved by a 50% reduction in the receptor threshold TR (e to g).
3.1. Coreceptor modulation of the mean dwell-time of the TCR/pMHCI interaction
One important effect of the MHCI/CD8 interaction is a reduction of v, the TCR/pMHCI dissociation rate (Table 2; Luescher et al., 1995; Wooldridge et al., 2005). Thus, let vslow denote the dissociation rate when MHCI is bound to CD8, and vfast otherwise. Coreceptor-mediated stabilization of the TCR/pMHC interaction is then expressed by the inequality vfast > vslow. A useful index for the stabilizing effect is vslow/vfast; this ratio is at least 2 (Wooldridge et al., 2005; Laugel et al., 2007). To relate this index to T cell activation, consider first the distribution function F(t). In the presence of CD8, F(t) is given as where the latter two terms satisfy the differential equations,
| (15) |
| (16) |
with initial conditions and Here γ is the rate of MHCI association with CD8, which is proportional to the density of free CD8 molecules on the T cell surface ([CD8]F) and ρ is the MHCI/CD8 dissociation rate. Solving equations (15) and (16), we obtain expressions for F(t), best understood by consideration of two special cases representing the extremes of a range of possibilities.
Table 2. MHCI tetramer staining: dissociation rates.
| ligand | dissociation rate | increase | ||
|---|---|---|---|---|
|
|
||||
| wild-type | CD8-null | triplets | duplets | |
| 3G | 0.123 | 0.462 | 55% | 92% |
| 8Y | 0.203 | 0.587 | 42% | 69% |
| 8T | 0.206 | 0.608 | 43% | 72% |
dissociation rate expressed in min−1
wild-type: hla - a2; CD8-null: hla - a2 DT227/8KA
increase: calculated increase of off-rate in CD8-null
First, in the case where pMHCI/CD8 kinetics is very rapid compared to the TCR/pMHCI interaction we obtain:
| (17) |
The mean dwell-time of the TCR/pMHCI interaction is then found as
On the other hand, when pMHCI/CD8 kinetics is very slow compared to the cognate interaction so that a TCR/pMHCI interaction typically occurs in its entirety with the coreceptor either associated or disassociated, we have
| (18) |
and the mean dwell-time of the TCR/pMHCI interaction is
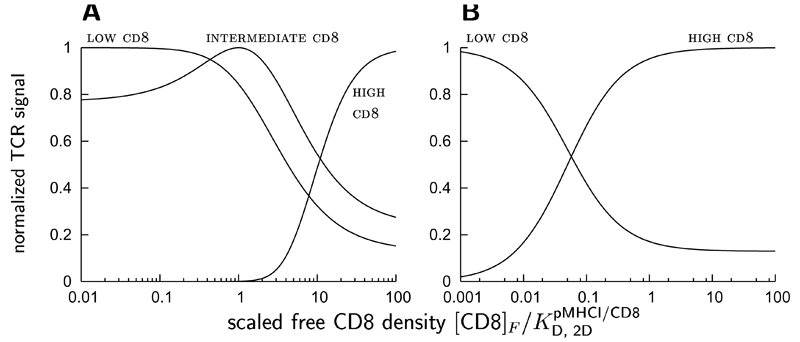
To illustrate how the T cell can differentially modulate its sensitivity to various ligands by altering its surface expression of CD8, the rate of TCR triggering is plotted as a function of the scaled free CD8 density in Fig. 3. The TCR triggering rate is expressed by the probability of productive TCR/pMHCI interaction, divided by mean dwell-time. The curves obtain for hypothetical pMHCI ligands which differ with respect to their TCR/pMHCI dissociation rates (the effect magnitude vslow/vfast is assumed the same for all ligands, for the sake of simplicity). Scaling is with respect to the 2-dimensional dissociation constant of the pMHCI/CD8 interaction. Accordingly, the scaled free CD8 density is the net representation not only of the cell surface expression level of CD8, but also of any physico-chemical properties of CD8 that affect the association and dissociation rates of the pMHCI/CD8 interaction.
Figure 3. Normalized (maximum = 1) rate of TCR triggering dependent on the free CD8 density on the T cell surface (normalized with respect to the dissociation constant) for various ligands, in the case of fast CD8 kinetics, or slow CD8 kinetics,
For all ligands, the magnitude of the CD8 stabilization effect has been set at vslow/vfast = 20 in these graphs, in order to clearly demonstrate the effects. low cd8 denotes a hypothetical ligand that is most potent at low CD8 densities, and similarly for intermediate cd8 and high cd8.
As the scaled free CD8 density increases, the TCR/pMHCI dissociation rate changes over from vfast to vslow. Along with this shift, the potency of a ligand shifts as well: a ligand such that is more potent at low CD8 and becomes less potent as the free CD8 density increases, whereas the opposite is true for a ligand for which These effects are illustrated by the CD8-response curves in Fig. 3. Variation of CD8 surface expression thus equips the T cell with a tuning mechanism that allows a given TCR clonotype to control ligand promiscuity by optimizing responsiveness to the relevant ligand and at the same time reducing responsiveness to other potential agonists (which would be favoured at different CD8 expression levels). In effect, the coreceptor CD8 mediates focussing on a specific ligand chosen from among a larger set of potential agonists.
Such CD8-mediated focussing may also be involved in the maturation of functional responsiveness during an immune response, irrespective of additional maturation mechanisms such as clonal selection or TCR editing. The scope for tuning is somewhat greater when pMHCI/CD8 kinetics are rapid compared to the mean TCR/pMHCI dwell-time (Fig. 3A), where a tuning to intermediate ligands is possible. This may indeed be the case as the available evidence (Wyer et al., 1999) suggests that pMHCI/CD8 kinetics is relatively rapid.
3.2. Coreceptor modulation of the threshold duration of the TCR/pMHCI interaction
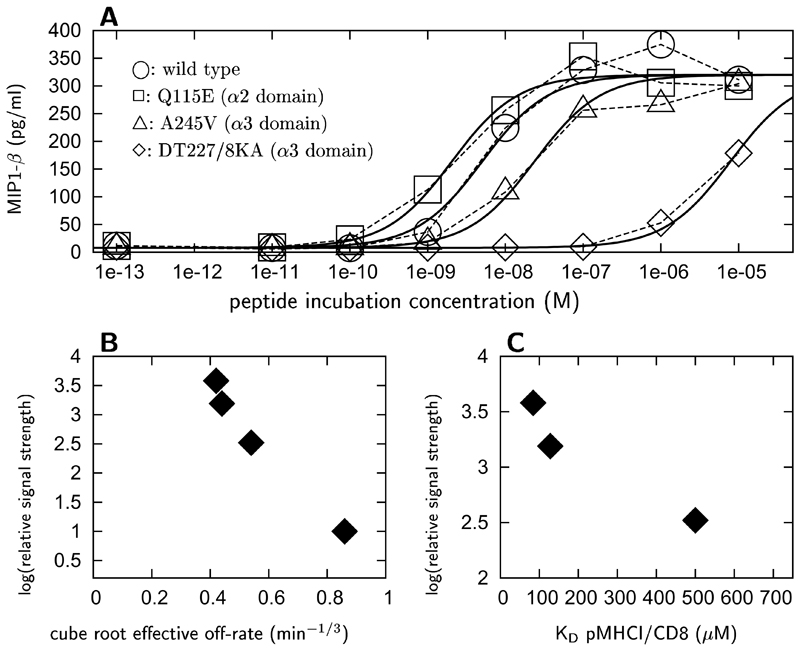
To assess a further CD8 enhancement effect besides dwell-time prolongation, functional response bio-assays were carried out in which CTLs were incubated with antigen-presenting cells (APCs) incubated with agonist peptide at increasing concentrations, and expressing various hla mutants with differing CD8 affinities (Hutchinson et al., 2003; Wooldridge et al., 2005), The response of CTL clones stimulated by APCs incubated with the agonist HIV-1 Gag epitope SLYNTVATL, measured as the concentration of MIP-1β produced after a 4 hour incubation, is shown in Fig. 4A as a function of agonist peptide concentration. To compare the relative strengths of the MHCI-specific TCR triggering rate elicited by these mutants, the MHCI-specific triggering rates estimated from the dose-response curves were normalized with respect to the TCR triggering rate associated with mutant DT227/8KA; the hla a2 heavy chain α3 domain of the latter mutant is incapable of binding to CD8 (Purbhoo et al., 2001). The relative strength of the MHCI-specific TCR triggering rate, thus defined, is shown as a function of the cube root of the effective tetramer decay rate in Fig. 4B, and as a function of in Fig. 4C. The cube root of the effective tetramer decay rate is proportional to the single-site TCR/pMHCI dissociation rate (see Wooldridge et al., 2005 and kinetic theory in Materials & Methods above).
Figure 4. MIP1-β release response of NRT1 CTLs as a function of agonist incubation concentration.
Response is shown (A) for APCs expressing various mutations in hla a2: ○: wild type; □: Q115E (α2 domain); △: A245V (α3 domain); ◊: DT227/8KA (α3 domain). Curves represent the least-squares fit of Eqn. (1), where ymin = 7.9 ± 0.07 pg/ml; ymax − ymin = 312 ± 0.17 pg/ml; α = 1.03 ± 0.05; log(wQ115E/wDT227/8KA) = 3.58 ± 0.06; log(wwild type/wDT227/8KA) = 3.19 ± 0.05; log(wA245V/wDT227/8KA) = 2.52 ± 0.07. Values of log(w./wDT227/8KA) are plotted against the cube root of the effective off-rate in tetramer decay curves (B) and the dissociation constant of the pMHCI/CD8 interaction (B). Cube roots of effective off-rates are as follows: Q115E: 0.42 min−1/3; wild type: 0.44 min−1/3; A245E: 0.54 min−1/3; DT227/8KA: 0.85 min−1/3. (data from Wooldridge et al., 2005).
The trends shown in Fig. 4B and C suggest an involvement of CD8 in the triggering of TCRs, in addition to the dwell-time effect discussed in the previous section. This second coreceptor mode of action would involve interaction with the molecular machinery which assembles the signalosome. The TCR triggering theory represents such modulation via the function G in equation (2), here taken to have the simplest possible form, a Heaviside function with threshold parameter TR. In particular, this putative additional role of CD8 is detailed by the following assumptions: (i) pMHCI/CD8 kinetics is fast relative to TCR/pMHCI kinetics (Wyer et al., 1999; Gakamsky et al., 2005); (ii) the T cell membrane is spatially heterogeneous, with microdomains that favour TCR triggering, being rich in the required kinases (or poor in phosphorylases, or both), versus unfavourable microdomains that are kinase-depleted and/or phosphorylase enriched (Bunnell et al., 2002); (iii) TCRs can be recruited to the favourable domains through interaction with the coreceptor, dependent on the affinity of the CD8:α3 interaction (Doucey et al., 2001; Montixi et al., 1998); (iv) the rate of recruitment is slow relative to the mean-dwell time of the TCR/pMHCI complex; (v) once recruited to these membranes, the TCR/pMHC ternary complex does not require CD8 to remain in the favourable domain.
Letting w denote the MHC-specific TCR triggering rate, the triggering threshold in the unfavourable domains, the threshold in the favourable domains () and krc a recruitment parameter proportional to the surface density of CD8 molecules associated with the favourable domains, we obtain the following equation from assumptions (i)–(v):
| (19) |
The rate at which ternary complexes are recruited to the favourable domains is (it is customary to take the two-dimensional dissociation constant to be proportional to the three-dimensional affinity, for which data are available; the proportionality constant, known as the confinement length, is absorbed in the recruitment parameter.) For the TCR:pMHCI dissociation rate v we have where keff off is the effective dissociation rate as measured in tetramer dissociation experiments (Wooldridge et al., 2005) and C is a correction factor with the dimensions TIME−2/3 Given the estimates on w□/wDT227/8KA for □ = Q115E, wild type, or A245W, equation (19) furnishes three equations in three unknown parameters, one of which is which is how much faster the steps in CD3 activation and signalosome assembly proceed in the favourable domains (steps in signalosome assembly include ITAM phosphorylation and recruitment of kinases and adaptors). The other two parameters are irrelevant nuisance parameters. The best solution of these equations by least-squares yields the estimate While there is considerable uncertainty associated with this estimate, it does indicate that CD3 activation and kinase/adaptor recruitment proceeds faster in the favourable domains.
Since the factor ~ 4.5 occurs in the exponent, its impact on the TCR triggering rate can be huge: for a pMHCI ligand with mean dwell-time ~ the probability that the interaction is productive will be some thirty times greater when the ternary complex is recruited to the favourable domains as compared to the unfavourable domains. On the other hand, for a ligand optimal for the unfavourable domains (i.e. ), the TCR triggering rate will be about twice as large in the unfavourable domains as compared to the favourable domains. Thus, the effect of dwell-time modulation described in the previous section will be strongly magnified whenever the contribution of favourable domains to the overall TCR triggering rate is significant. The enhanced TCR triggering rate is represented by the second term on the right-hand side of equation (19) which is proportional to the surface density of CD8 molecules associated with the favourable domains. In the absence of favourable domain-associated CD8 molecules, optimal ligands are those pMHCI with mean dwell-time whereas at high levels of such CD8s, ligands are optimal if their mean dwell time is near
Thus membrane heterogeneity plus CD8-mediated recruitment provides a second focussing mechanism that allows the clonotype to tune its sensitivity specifically to one pMHCI species from among a range of potentially optimal ligands.
3.3. Coreceptor modulation of TCR/pMHCI affinity
A series of hTERT540–548 altered peptide ligands (APLs) to CTL clone ila1 was used to obtain estimates for the parameters of the staining equation (9) (see also Laugel et al., 2007). Singlet TCRs were found to contribute very little to equilibrium staining, and KA had to be fixed at the value zero; estimated values were KB = 10.8 ± 1.10 µM and KC = 26.6 ± 1.03 µM. These values apply for the wild-type hla a2 molecule; for interactions with hla a2 DT227/8KA, these values have to be divided by a CD8 effect factor estimated at 2.25 ± 0.086. Table 3 shows the proportion of staining clusters that are triplets rather than duplets, calculated from the staining equation, both for wild-type hla and DT227/8KA, in three APLs, 3G, 8Y and 8T. The TCR/pMHCI dissociation constants are listed for comparison; the trend is clearly for lower-affinity APLs to have an increasing proportion of clusters present as duplets; and this trend is emphasized when the pMHCI/CD8 interaction is abrogated.
Table 3. MHCI tetramer staining: TCR triplet clusters.
| ligand | triplet fraction |
||
|---|---|---|---|
| wild-type | CD8-null | ||
| 3G | 0.993 | 0.984 | 3.7 ± 0.28 |
| 8Y | 0.921 | 0.733 | 22.6 ± 2.05 |
| 8T | 0.882 | 0.536 | 27.6 ± 6.71 |
wild-type: hla-a2; CD8-null: hla-a2 DT227/8KA
KD for the TCR/pMHCI interaction
The estimated CD8 affinity effect factor ~ 2.25 absorbs mean-dwell time prolongation (i.e. a decrease of the off-rate v mediated by CD8) as well as a possible effect on the on-rate. Consider the apparent MHCI tetramer staining dissociation rates for wild-type hla and hla DT227/8KA, given in Table 2. The column marked “triplets” shows the estimated percentage increase of the single-site off-rate consequent upon abrogation of the pMHCI/CD8 interaction, based on all-triplet staining (extracting a cube root of the rate ratios) whereas the column marked “duplets” shows the percentages on the basis of all-duplet staining (based on the square root of the rate ratios). The effective dwell-time prolongation thus appears to be about 1.5, indicating that the effect of pMHCI/CD8 on the single-site on-rate is again about 1.5, to make up the total factor of 2.25. Thus, the data suggest that the favourable effect conferred by the coreceptor CD8 is composed of roughly equal contributions of increased on-rate and decreased off-rate.
Further evidence pointing to an on-rate modulatory effect of CD8 is provided by the staining association kinetics of the hTERT540–548 APLs system. The association curves (shown in Laugel et al., 2007) closely fit by a biphasic model:
| (20) |
The estimated values for the empirical rate parameters are listed in Table 4. Numerical simulations of the full kinetic system (Table 1) confirm that such biphasic behaviour is consistent with the much more intricate underlying dynamics. As indicated in Materials & Methods, the initial rate of association is a measure of ψRT, where the parameter ψ absorbs the incubation concentration of MHCI tetramer as well as the rate at which singlet TCRs capture tetramers from solution. For the empirical model, equation (20), the initial rate is given by Combining these quantities for both wild-type hla and hla DT227/8KA, we arrive at an estimated percentage decrease of the single-site tetramer capture rate consequent upon abrogation of the pMHCI/CD8 interaction, shown in the column marked “capture effect” in Table 4. The effects are dramatic, and become more pronounced with lower TCR/pMHCI affinity.
Table 4. MHCI tetramer staining: association rates.
| ligand | λslow (min−1) | λfast (min−1) | capture effect |
λeff(∞) (min−1) | |||
|---|---|---|---|---|---|---|---|
|
|
|
||||||
| wild-type | CD8-null | wild-type | CD8-null | wild-type | CD8-null | ||
| 3G | 0.18 | 0.07 | 3.08 | 4.01 | 61% | 1.53 | 0.76 |
| 8Y | 0.12 | 0.13 | 3.07 | 4.45 | 85% | 1.30 | 1.25 |
| 8T | 0.14 | 0.13 | 8.10 | 7.81 | 90% | 3.11 | 2.34 |
wild-type: hla-a2; CD8-null: hla-a2 DT227/8KA capture effect: calculated decrease of recruitment rate ψ in CD8-null data from Laugel et al. (2007)
The empirical fits also allow the estimation of the time-varying effective rate λeff(t) of staining kinetics, equation (13). This rate relaxes to the equilibrium value λeff(∞) on a time scale ~ 1/λfast. The equilibrium value can be calculated from the empirical parameters, as follows:
| (21) |
(this follows immediately from equation (13)). These estimates, shown in the two final columns of Table 4, indicate that abrogation of the pMHCI/CD8 interaction leads to a decrease in λeff(∞), which is most pronounced in ligand 3G.
4. DISCUSSION
This study attempts to dissect and quantitate the various ways in which CD8 modulates and augments TCR signal transduction. Our analysis suggests that, in addition to its role in recruiting the kinase p56lck to the TCR/CD3 complex, which is essential for virtually all normal syngeneic interactions (Arcaro et al., 2001; Holler and Kranz, 2003; Lyons et al., 2006), the coreceptor CD8 has a number of modulatory effects: CD8 (i) enhances the TCR/pMHCI association rate by 50% or more; (ii) stabilizes the TCR/pMHCI interaction by at least 50%; and (iii) recruits TCR/pMHCI complexes to membrane domains where the steps needed to attain signalling status for the TCR/CD3 complex proceed more than four times faster, equivalent to a thirty-fold increase in productive ligand engagement. These modulatory effects allow the T cell to fine-tune its sensitivity to the salient ligands.
Coreceptor modulation of functional avidity is differential: as illustrated in Figs. 2 and 3, the T cell becomes more responsive to one of its potential agonists while becoming less responsive to another one at the same time. This differential modulation enables genuine focussing, as opposed to merely tuning signal transduction gain, which affects signals from all potential agonists equally (Slifka and Whitton, 2001; Schade and Levine, 2003). On this view, T cells exert active control over which antigen they focus on, by regulating the modulatory actions of the coreceptor in three ways: (i) through the expression level of CD8 (Blok et al., 1996; Maile et al., 2005); (ii) through the ratio of expression between CD8αα and CD8αβ (Cawthon and Alexander-Miller, 2002); and (iii) through the affinity of pMHCI for CD8, which can be modulated by varying the glycosylation of the interacting molecules (Daniels et al., 2001). Manipulation of one or more of these three control parameters should make it possible to reorder the hierarchy of potency among a CTL’s potential agonists in an experimental system; if successful, such experiments would corroborate a central role for coreceptor-mediated fine tuning and focussing of TCR specificity against a background of high degeneracy.
The existence of a focussing mechanism implies that an individual clonotype may have a fairly wide range of ligands, among which, at any given time, only a small subset is potent (i.e. can act as optimal agonist). We thus propose that CD8-modulation of TCR promiscuity endows the TCR repertoire with an additional dimension of diversity, enhancing the capability of a limited number of clonotypes to cover “epitope space” efficiently (Goldrath and Bevan, 1999; Mason, 2001; Nicholson et al., 2000; Holler et al., 2002).
The inherent polyspecificity and crossreactivity of the TCR has been well established (Gavin and Bevan, 1995; Ignatowicz et al., 1996; Kersh and Allen, 1996; Mason, 1998; Holler et al., 2002; Holler and Kranz, 2004; Bankovich et al., 2004; Wilson et al., 2004). Yet such TCR promiscuity needs to be reconciled with the need to distinguish salient antigens (pathogen-related non-self and harmful self) from non-salient ones (harmless self), and the immune system employs various central and peripheral tolerance mechanism acting in unison (Seddon and Mason, 2000; Anderton and Wraith, 2002; Van den Berg and Rand, 2004b; Van den Berg and Molina-París, 2003).
Coreceptor-mediated focussing of TCR degeneracy may be an important additional mechanism. In particular, the concept of focussed modulation of functional avidity strongly complements theories that view degeneracy as a fundamental molecular feature of the TCR, such as the multiple conformer theory which proposes that a single TCR exists in multiple conformations that are in equilibrium (Holler and Kranz, 2004), allowing a single T cell to potentially recognize many different ligands. Moreover, coreceptor-mediated focussing allows autorecognition to be physiological, not pathological: a large proportion of patent repertoire TCR clonotypes can have autoantigens among their potential antigens, but autoimmunity is averted provided the CD8-modulatory system keeps an activated clonotype “trained” on the salient epitope.
The present model postulates the existence of favourable membrane microdomains, to which TCRs can be recruited only when bound to pMHCI. Such domains have been proposed to exist in the form of lipid rafts, membrane areas enriched in cholesterol and glycosphingolipids which serve as the sites of colocalization of TCR/CD3, protein tyrosine kinases, and adaptor molecules (Arcaro et al., 2001; Montixi et al., 1998; Bosselut et al., 1999; Janes et al., 1999; Brdičková et al.,2003). Partitioning of CD8 to lipid rafts is crucially dependent on palmitoylation of the cytoplasmic tail of CD8β (Arcaro et al., 2000, 2001). Therefore, inasmuch as the increased rate of phosphorylation is dependent on recruitment to microdomains (rather than direct recruitment of p56lck by CD8 to the TCR/CD3 complex, which CD8αα could mediate), the main action of CD8αα would be to modulate on- and off-rates. Either type of dimer is able to reduce the TCR/pMHCI dissociation rate since CD8α binds MHCI, (Kern et al., 1998; Wyer et al., 1999). The contrast between points f and g in Fig. 2 illustrates the opposite effects which may be exerted by upregulation of CD8αα, which only affects the mean TCR/pMHCI dwell time and CD8αβ which affects lipid raft colocalization (cf. Cawthon and Alexander-Miller, 2002; Gangadharan and Cheroute, 2004). Thus, a T cell may be able to shift its focus to a distinct subset of its potential agonists by altering the relative expression levels of CD8αα and CD8αβ.
The off-rate measured with hla DT227/8KA depends only on vfast, whereas the off-rate found with the wild-type hla is a mixture of both vfast and vslow, as explained above in the section on mean dwell-time modulation. Thus, the effective dwell-time prolongation of ~ 1.5 as measured with hTERT540–548 APLs is a lower bound to the actual CD8-mediated stabilization factor vfast/vslow. Analysis based on hla a2 mutants with a range of pMHCI/CD8 affinities indicated that stabilization can exceed a factor 2 (Wooldridge et al., 2005; Laugel et al., 2007); in physiological terms, this factor corresponds to the extremes of CD8 expression, i.e. from no expression to MHCI-saturating levels. Similar remarks apply to the enhancement of the on-rate. Thus, the data presented here support the claim that the pMHCI/CD8 interaction prolongs dwell-time by at least a factor 1.5, and also enhances the on-rate by at least a factor 1.5, with the important caveat that this latter figure is derived from two model estimates (the affinity effect in the equilibrium staining curve and the off-rate effect), so that the strength of the on-rate effect may well be much greater or smaller.
Moreover, the on-rate effect may differ among APL variants. The empirical rate λfast in the association experiments estimates how rapidly λeff(t) relaxes to its equilibrium value. The rate which may be expected to dominate the initial rapid phase is ϑ1RT +v; indeed, APL variants 3G and 8Y show that λfast broadly agrees with the off-rate v, and λfast increases upon abrogation of the pMHCI/CD8 interaction, as expected when the rate is dominated by v. For variant 8T, however, the initial rate λfast is much faster, and abrogation of the pMHCI/CD8 interaction acts to decrease this rate somewhat; again this points to a greater role of on-rate effects, as opposed to off-rate effects, in coreceptor modulation for this intermediate affinity ligand.
The dominant (slow) rate in the biphasic association curves arises from an intricate interplay between the various bound forms depicted in Fig. 1. To interpret the rate estimates listed in the final column of Table 4, we must also consider the estimated proportions of triplets, Table 2, and equation (14) for the effective rate. The apparently much more profound effect on APL variant 3G can be understood from the fact that λeff is determined almost exclusively by 3ψ + v3, since the staining is almost entirely in the form of triplets. Since v3 is relatively small, the decrease in ψ due to abrogation of the pMHCI/CD8 interaction (“capture effect”) is the dominant effect on the effective rate of association. For variants 8Y and 8T, the duplet proportions are higher. In the duplet factor, the decrease in the term 2ψ is partially compensated for by the increase in v2.This explains why, for 8Y and 8T, the final two columns of Table 4 show a far less marked reduction of λeff(∞) when the MHCI/CD8 interaction is abrogated.
A second indirect piece of evidence pointing to TCR/pMHC on-rate modulation by CD8 is the marked effect of the abrogation of the pMHCI/CD8 interaction on MHCI tetramer capture (Table 4). The pronounced capture effect we report is consistent with the analysis of Gakamsky et al. (2005), who suggest that CD8 is likely to play a major role in capturing a pMHCI-tetramer from solution. Our analysis points to roughly equal contributions of on-rate and off-rate enhancement on affinity modulation by CD8. However, if the rate of tetramer capture is closely linked to the single-site on-rate in the cell:cell contact environment, the contribution of the on-rate might be much more important, particularly in ligands with relatively high TCR/pMHCI dissociation constants.
In terms of the collision theory of molecular reaction dynamics, the effect of CD8 on the TCR/pMHCI association rate may be viewed as a modulation of either the activation energy or the reactive cross-section, or both, although the former seems less likely since the interaction between CD8 and MHCI is relatively weak (Purbhoo et al., 2001). Modulation of the reactive cross-section can be understood as an increase of the steric factor characterizing TCR/pMHCI collisions, with the CD8 molecule effectively acting as a grappling hook; this picture would be consistent with the finding that favourable entropic forces rather than enthalpic forces play a major role in (at least some) TCR/pMHCI interactions (Ely et al., 2006). Indirect evidence supporting the notion of CD8 promoting the formation of TCR/pMHCI contacts, even with non-cognate peptide presented by MHCI, has recently been put forward by Anikeeva et al. (2006).
The physiological significance of TCR/pMHCI on-rate modulation is rather subtle. The formula v exp{−vTR} for the rate of productive ligand engagement suggests that the single-site off-rate v and the receptor triggering threshold TR are the sole determinants of T cell activation. However, this formula applies only under MHC-limited conditions (Van den Berg et al., 2002); the full formula is where [R] is the surface density of free TCRs. This full formula reduces to the simpler (MHC-limited) expression provided that On-rate enhancement, which leads to a smaller allows this condition to be satisfied at lower TCR-expression levels. The curves in Fig. 2 indicate that there is a clear optimal TCR/pMHCI off-rate; the theory of Van den Berg et al. (2002) predicts that the optimum broadens in the TCR-limited regime, as has recently been confirmed experimentally (Gonzales et al., 2005). Thus, the physiological significance of on-rate modulation (i.e. improvement of affinity through reduction of the TCR/pMHCI dissociation constant) may be to maintain the sharp optimum in the dependence of triggering on off-rate. This effect would be more important for ligands of intermediate to low affinity.
As the foregoing discussion of the fast and slow rates MHCI-tetramer staining kinetics makes clear, these kinetics contains information of duplet/triplet ratios in tetramer/TCR associations. Since tetramers are artificial constructs, such data may seem to have no direct physiological significance. However, therapeutic use of MHCI tetramers has been proposed (Sakita et al., 1996; Maile et al., 2001). MHC oligomers are capable of inducing T cell activation, indicating that TCR-clusters are competent nucleation points for signalosome formation; experiments with MHCII monomers, dimers, trimers and tetramers indicate that both duplet and triplet clusters are competent (Boniface et al., 1998; Cochran et al., 2000). If duplets and triplets are not equally potent, an experimental means of gauging triplet/duplet ratios would be of clinical value.
In summary, we have used pMHCI tetramer-based kinetic analysis, combined with target cells expressing MHCI mutants, to dissect the various modulatory effects through which the coreceptor CD8 differentially modulates TCR sensitivity to its various potential agonists, and thereby modulates TCR specificity in a dynamic, tunable fashion. Taken together, the experimental findings suggest that CD8 has an influence on TCR/pMHCI affinity through modulation of both the on-rate and the off-rate. Furthermore, we have presented evidence that CD8 modulates the TCR triggering threshold by recruiting TCRs to favourable membrane microdomains in which progression to signalling-competent signalosomes proceeds much faster. These effects endow the T cell with an exquisite means of tuning its TCR to the pertinent peptide ligand by adjusting the expression levels of CD8αα and/or CD8αβ. We suggest that at the level of the whole adaptive immune system, CD8-based modulation of TCR specificity vastly amplifies the functional diversity of the finite number of TCR clonotypes present in the T cell repertoire.
Acknowledgments
This work was supported by the Wellcome Trust.
References
- Alexander-Miller MA. Differential expansion and survival of high and low avidity cytotoxic T cell populations during the immune response to a viral infection. Cellular Immunology. 2000;201:58–62. doi: 10.1006/cimm.1999.1632. [DOI] [PubMed] [Google Scholar]
- Anderton SM, Wraith DC. Selection and fine-tuning of the autoimmune T cell repertoire. Nature Rev Immunol. 2002;2:487–497. doi: 10.1038/nri842. [DOI] [PubMed] [Google Scholar]
- Anikeeva N, Lebedeva T, Clapp AR, Goldman ER, Dustin ML, Mattoussi H, Sykulev Y. Quantum dot/peptide-MHC biosensors reveal strong CD8-dependent cooperation between self and viral antigens that augment the T cell response. Proc NatI Acad Sci USA. 2006;103:16846–16851. doi: 10.1073/pnas.0607771103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arcaro A, Grégoire C, Bakker TR, Baldi L, Jordan M, Goffin L, Boucheron N, Wurm F, van der Merwe PA, Malissen B, Luescher IF. CD8β endows CD8 with efficient coreceptor function by coupling T cell receptor/CD3 to raft-associated CD8/p56lck complexes. J Exp Med. 2001;194:1485–1495. doi: 10.1084/jem.194.10.1485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arcaro A, Grégoire C, Boucheron N, Stolz S, Palmer E, Malissen B, Luescher IF. Essential role of CD8 palmitoylation in CD8 coreceptor function. J Immunol. 2000;165:2068–2076. doi: 10.4049/jimmunol.165.4.2068. [DOI] [PubMed] [Google Scholar]
- Ashton-Rickardt PG, Tonegawa S. A differential-avidity model for T-cell selection. Immunol Today. 1994;15:362–366. doi: 10.1016/0167-5699(94)90174-0. [DOI] [PubMed] [Google Scholar]
- Bankovich AJ, Girvin AT, Moesta AK, Garcia KC. Peptide register shifting within the MHC groove: Theory becomes reality. Mol Immunol. 2004;40:1033–1039. doi: 10.1016/j.molimm.2003.11.016. [DOI] [PubMed] [Google Scholar]
- van den Berg HA, Burroughs NJ, Rand DA. Quantifying the strength of ligand antagonism in TCR triggering. Bull Mat Biol. 2002;64:781–808. doi: 10.1006/bulm.2002.0302. [DOI] [PubMed] [Google Scholar]
- van den Berg HA, Molina-París C. Thymic presentation of autoantigens and the efficiency of negative selection. J Theor Med. 2003;5:1–22. [Google Scholar]
- van den Berg HA, Rand DA. Dynamics of T cell activation threshold tuning. J Theor Biol. 2004a;228:397–416. doi: 10.1016/j.jtbi.2004.02.002. [DOI] [PubMed] [Google Scholar]
- van den Berg HA, Rand DA. Foreigness as a matter of degree: The relative immunogenicity of peptide/MHC ligands. J Theor Biol. 2004b;231:535–548. doi: 10.1016/j.jtbi.2004.07.008. [DOI] [PubMed] [Google Scholar]
- van den Berg HA, Rand DA. Quantitative theories of T-cell responsiveness. Immunological Reviews. 2007;216:81–92. doi: 10.1111/j.1600-065X.2006.00491.x. [DOI] [PubMed] [Google Scholar]
- van den Berg HA, Rand DA, Burroughs NJ. A reliable and safe T cell repertoire based on low-affinity T cell receptors. J Theor Biol. 2001;209:465–486. doi: 10.1006/jtbi.2001.2281. [DOI] [PubMed] [Google Scholar]
- Blok R, Margulies DH, Pease L, Ribaudo RK, Schneck J, McCluskey J. CD8 expression alters the fine specificity of an alloreactive MHC class I-specific T hybridoma. International Immunology. 1996;4:455–466. doi: 10.1093/intimm/4.4.455. [DOI] [PubMed] [Google Scholar]
- Bongrand P, Malissen B. Quantitative aspects of T-cell recognition: From within the antigen-presenting cell to within the T cell. BioEssays. 1998;20:412–422. doi: 10.1002/(SICI)1521-1878(199805)20:5<412::AID-BIES8>3.0.CO;2-P. [DOI] [PubMed] [Google Scholar]
- Boniface JJ, Rabinowitz JD, Wülfing C, Hampl J, Reich Z, Altman JD, Kantor RM, Beeson C, McConnell HM, Davis MM. Initiation of signal transduction through T cell receptor requires the peptide multivalent engagement of MHC ligands. Immunity. 1998;9:459–466. doi: 10.1016/s1074-7613(00)80629-9. [DOI] [PubMed] [Google Scholar]
- Bosselut R, Kubo S, Guinter T, Kopacz JL, Altman JD, Feigenbaum L, Singer A. Role of CD8β domains in CD8 coreceptor function: Importance for MHC I binding, signaling, and positive selection of CD8+ T cells in the Thymus. Immunity. 2000;12:409–418. doi: 10.1016/s1074-7613(00)80193-4. [DOI] [PubMed] [Google Scholar]
- Bosselut R, Zhang W, Ashe JM, Kopacz JL, Samuelson LE, Singer A. Association of the adaptor molecule LAT with CD4 and CD8 coreceptors identifies a new coreceptor function in T cell receptor signal transduction. J Exp Med. 1999;190:1517–1525. doi: 10.1084/jem.190.10.1517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brdičková N, Brdička T, Angelisová P, Horváth O, Špiča J, Hilgert I, Pačes J, Simeoni L, Kliche S, Merten C, Schraven B, et al. LIME: A new membrane raft-associated adaptor protein involved in CD4 and CD8 coreceptor signaling. J Exp Med. 2003;198:1453–1462. doi: 10.1084/jem.20031484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bunnell SC, Hong DI, Kardon JR, Yamazaki T, McGlade CJ, Barr VA, Samelson LE. T cell receptor ligation induces the formation of dynamically regulated signaling assemblies. J Cell Biol. 2002;158:1263–1275. doi: 10.1083/jcb.200203043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burroughs N, Wedagedera J. T cell activation: A queueing theory analysis at low agonist density. Biophys J. 2006;91:1604–1618. doi: 10.1529/biophysj.105.066001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cawthon AG, Alexander-Miller MA. Optimal colocalization of TCR and CD8 as a novel mechanism for the control of functional avidity. J Immunol. 2002;169:3492–3498. doi: 10.4049/jimmunol.169.7.3492. [DOI] [PubMed] [Google Scholar]
- Chan C, George AJT, Stark J. T cell sensitivity and specificity — kinetic proofreading revisited. Discrete and Continuous Dynamical Systems—Series B. 2003;3:343–360. [Google Scholar]
- Cochran JR, Cameron TO, Stern LJ. The relationship of MHC-peptide binding and T cell activation probed using chemically defined MHC class II oligomers. Immunity. 2000;12:241–250. doi: 10.1016/s1074-7613(00)80177-6. [DOI] [PubMed] [Google Scholar]
- Daniels MA, Devine L, Miller JD, Moser JM, Lukacher AE, Altman JD, Kavathas P, Hogquist KA, Jameson S. CD8 binding to MHC class I molecules is influenced by T cell maturation and glycosylation. Immunity. 2001;15:1051–1061. doi: 10.1016/s1074-7613(01)00252-7. [DOI] [PubMed] [Google Scholar]
- Doucey M-A, Legler D, Boucheron N, Cerottini J-C, Bron C, Luescher IF. CTL activation is induced by cross-linking of TCR/MHC-peptide-CD8/p56lck adducts in rafts. Eur J Immunol. 2001;31:1561–1570. doi: 10.1002/1521-4141(200105)31:5<1561::AID-IMMU1561>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- Dunbar PR, Ogg GS, Chen J, R NN, van der Bruggen P, Cerundolo V. Direct isolation, phenotyping and cloning of low-frequency antigen-specific cytotoxic T lymphocytes from peripheral blood. Current Biology. 1998;8:413–662. doi: 10.1016/s0960-9822(98)70161-7. [DOI] [PubMed] [Google Scholar]
- Ely LK, Beddoe T, Clements CS, Matthews JM, Purcell AW, Kjer-Nielsen L, McCluskey J, Rossjohn J. Disparate thermodynamics governing T cell receptor-MHC-I interactions implicate extrinsic factors in guiding MHC restriction. Proc Natl Acad Sci USA. 2006;103:6641–6646. doi: 10.1073/pnas.0600743103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filipp D, Zhang J, Leung BL, Shaw A, Levin SD, Veillette A, Julius M. Regulation of Fyn through translocation of activated Lck into lipid rafts. J Exp Med. 2003;197:1221–1227. doi: 10.1084/jem.20022112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gakamsky DM, Luescher IF, Pramanik A, Kopito RB, Lemonnier F, Vogel H, Rigler R, Pecht I. CD8 kinetically promotes ligand binding to the T-cell antigen receptor. Biophys J. 2005;89:2121–2133. doi: 10.1529/biophysj.105.061671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gangadharan D, Cheroute H. The CD8 isoform CD8αα is not a functional homologue of the TCR co-receptor CD8αβ . Current Opinion in Immunology. 2004;16:264–270. doi: 10.1016/j.coi.2004.03.015. [DOI] [PubMed] [Google Scholar]
- Gavin MA, Bevan MJ. Increased peptide promiscuity provides a rationale for the lack of N regions in the neonatal T cell repertoire. Immunity. 1995;3:793–800. doi: 10.1016/1074-7613(95)90068-3. [DOI] [PubMed] [Google Scholar]
- Goldrath AW, Bevan MJ. Selecting and maintaining a diverse T-cell repertoire. Nature. 1999;402:255–262. doi: 10.1038/46218. [DOI] [PubMed] [Google Scholar]
- Gonzales PA, Carreño LJ, Coombs D, Mora JE, Palmeiri E, Goldstein B, Nathenson SG, Kalergis AM. T cell receptor binding kinetics required for T cell activation depend on the density of the cognate ligand of the antigen-presenting cell. Proc Natl Acad Sci USA. 2005;102:4824–4829. doi: 10.1073/pnas.0500922102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross D-A, Graff-Dubois S, Opolon P, Cornet S, Alves P, Bennaceur-Griscelli A, Faure O, Guillaume P, Firat H, Chouaib S, Lemonnier FA, et al. High vaccination efficiency of low-affinity epitopes in antitumor immunotherapy. J Clin Invest. 2004;113:425–433. doi: 10.1172/JCI19418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemmer B, Stefanova I, Vergelli M, Germain RN, Martin R. Relationships among TCR ligand potency, thresholds for effector function elicitation, and the quality of early signaling events in human T cells. J Immunol. 1998;160:5807–5814. [PubMed] [Google Scholar]
- Holler PD, Chlewicki LK, Kranz DM. TCRs with high affinity for foreign pMHC show self-reactivity. Nature Immunol. 2002;4:55–62. doi: 10.1038/ni863. [DOI] [PubMed] [Google Scholar]
- Holler PD, Kranz DM. Quantitative analysis of the contribution of TCR/pepMHC affinity and CD8 to T cell activation. Immunity. 2003;18:255–264. doi: 10.1016/s1074-7613(03)00019-0. [DOI] [PubMed] [Google Scholar]
- Holler PD, Kranz DM. T cell receptors: Affinities, cross-reactivities, and a conformer model. Mol Immunol. 2004;40:1027–1031. doi: 10.1016/j.molimm.2003.11.013. [DOI] [PubMed] [Google Scholar]
- Hudrisier D, Kessler B, Valitutti S, Horvath C, Cerottini J-C, Luescher IF. The efficiency of antigen recognition by CD8+ CTL clones is determined by the frequency of serial TCR engagement. J Immunol. 1998;161:553–562. [PubMed] [Google Scholar]
- Hutchinson SL, Wooldridge L, Tafuro S, Laugel B, Glick M, Boulter JM, Jakobsen BK, Price DA, Sewell AK. The CD8 T cell coreceptor exhibits disproportionate biological activity at extremely low binding affinities. J Biol Chem. 2003;278:24285–24293. doi: 10.1074/jbc.M300633200. [DOI] [PubMed] [Google Scholar]
- Ignatowicz L, Kappler J, Marrack P. The repertoire of T cells shaped by a single MHC/peptide ligand. Cell. 1996;84:521–529. doi: 10.1016/s0092-8674(00)81028-4. [DOI] [PubMed] [Google Scholar]
- Janes PW, Ley SC, Magee AI. Aggregation of lipid rafts accompanies signalling via the T cell antigen receptor. J Cell Biol. 1999;147:447–461. doi: 10.1083/jcb.147.2.447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janeway CA., Jr The T cell receptor as a multicomponent signalling machine: CD4/CD8 coreceptors and CD45 in T cell activation. Annu Rev Immunol. 1992;10:645–674. doi: 10.1146/annurev.iy.10.040192.003241. [DOI] [PubMed] [Google Scholar]
- Kalergis AM, Boucheron N, Doucey M-A, Palmieri E, Goyarts EC, Vegh Z, Luesher IF, Nathenson SG. Efficient T cell activation requires an optimal dwell-time of interaction between the TCR and the pMHC complex. Nature Immunol. 2001;2:229–234. doi: 10.1038/85286. [DOI] [PubMed] [Google Scholar]
- Kern PS, Teng MK, Smolyar A, Liu JH, Liu J, Hussey RE, Spoerl R, Chang HC, Reinherz EL, Wang JH. Structural basis of CD8 coreceptor function revealed by crystallographic analysis of a murine CD8αα ectodomain fragment in complex with H-2Kb. Immunity. 1998;9:519–530. doi: 10.1016/s1074-7613(00)80635-4. [DOI] [PubMed] [Google Scholar]
- Kersh GJ, Allen PM. Structural basis for T cell recognition of altered peptide ligands: A single T cell receptor can productively recognize a large continuum of related ligands. J Exp Med. 1996;184:1259–1268. doi: 10.1084/jem.184.4.1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laugel B, Boulter JM, Lissin N, Vuidepot A, Li Y, Gostick E, Crotty LE, Douek DC, Hemelaar J, Price DA, Jakobsen BK, et al. Design of soluble recombinant T cell receptors for antigen targeting and T cell inhibition. J Biol Chem. 2005;280:1882–1892. doi: 10.1074/jbc.M409427200. [DOI] [PubMed] [Google Scholar]
- Laugel B, van den Berg HA, Gostick E, Cole DK, Wooldridge L, Boulter J, Milicic A, Price DA, Sewell AK. Different T cell receptor affinity thresholds and CD8 coreceptor dependency govern cytotoxic T lymphocye activation and tetramer binding properties. J Biol Chem. 2007;000:0000–00000. doi: 10.1074/jbc.M700976200. [DOI] [PubMed] [Google Scholar]
- Luescher IF, Vivier E, Layer A, Mahiou J, Godeau F, Malissen B, Romero P. CD8 modulation of T-cell antigen receptor-ligand interactions on living cytotoxic T lymphocytes. Nature. 1995;373:353–356. doi: 10.1038/373353a0. [DOI] [PubMed] [Google Scholar]
- Lyons DS, Lieberman SA, Hampl J, Boniface J, Chien Yh, Berg LJ, Davis MM. A TCR binds to antagonist ligands with lower affinities and faster dissociation rates than to agonists. Immunity. 1996;5:53–61. doi: 10.1016/s1074-7613(00)80309-x. [DOI] [PubMed] [Google Scholar]
- Lyons GE, Moore T, Brasic N, Li M, Roszkowski JJ, Nishimura MI. Influence of human CD8 on antigen recognition by T-cell receptor-transduced cells. Cancer Research. 2006;66:11455–11461. doi: 10.1158/0008-5472.CAN-06-2379. [DOI] [PubMed] [Google Scholar]
- Maile R, Siler CA, Kerry SE, Midkiff KE, Collins EJ, Frelinger JA. Peripheral “CD8 tuning” dynamically modulates the size and responsiveness of an antigen-specific T cell pool in vivo. J Immunol. 2005;174:619–627. doi: 10.4049/jimmunol.174.2.619. [DOI] [PubMed] [Google Scholar]
- Maile R, Wang B, Schooler W, Meyer A, Collins EJ, Frelinger JA. Antigen-specific modulation of an immune response by in vivo administration of soluble MHC class I tetramers. J Immunol. 2001;167:3708–3714. doi: 10.4049/jimmunol.167.7.3708. [DOI] [PubMed] [Google Scholar]
- Malissen B. An evolutionary and structural perspective on T cell antigen receptor function. Immunological Reviews. 2003;191:7–27. doi: 10.1034/j.1600-065x.2003.00016.x. [DOI] [PubMed] [Google Scholar]
- Mason D. A very high level of crossreactivity is an essential feature of the T-cell receptor. Immunol Today. 1998;19:395–404. doi: 10.1016/s0167-5699(98)01299-7. [DOI] [PubMed] [Google Scholar]
- Mason D. Some quantitative aspects of T cell repertoire selection: The requirement for regulatory T cells. Immunological Reviews. 2001;182:80–88. doi: 10.1034/j.1600-065x.2001.1820106.x. [DOI] [PubMed] [Google Scholar]
- Matsui K, Boniface JJ, Steffner P, Reay PA, Davis MM. Kinetics of T-cell receptor binding to peptide/I-Ekcomplexes: Correlation of the dissociation rate with T-cell responsiveness. Proc Natl Acad Sci USA. 1994;91:12862–12866. doi: 10.1073/pnas.91.26.12862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montixi C, Langlet C, Bernard A-M, Thimonier J, Dubois C, Wurbel M-A, Chauvin J-P, Pierres M, He H-T. Engagement of T cell receptor triggers its recruitment to low-density membrane domains. The EMBO Journal. 1998;17:5334–5348. doi: 10.1093/emboj/17.18.5334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholson LB, Anderson AC, Kuchroo VK. Tuning T cell activation threshold and effector function with cross-reactive peptide ligands. International Immunology. 2000;12:205–213. doi: 10.1093/intimm/12.2.205. [DOI] [PubMed] [Google Scholar]
- Pecht I, Gakamsky DM. Spatial coordination of CD8 and TCR molecules controls antigen recognition by CD8+ T-cells. FEBS Lett. 2005;579:3336–3341. doi: 10.1016/j.febslet.2005.04.025. [DOI] [PubMed] [Google Scholar]
- Purbhoo MA, Boulter JM, Price DA, Vuidepot A-L, Hourigan CS, Dunbar PR, Olson K, Dawson SJ, Phillips RE, Jakobsen BK, Bell JI, et al. The human CD8 coreceptor effects cytotoxic T cell activation and antigen sensitivity primarily by mediating complete phosphorylation of the T cell receptor ζ chain. J Biol Chem. 2001;276:32786–32792. doi: 10.1074/jbc.M102498200. [DOI] [PubMed] [Google Scholar]
- Sakita I, Hörig H, Rui S, Fuming W, Nathenson SG. In vivo CTL immunity can be elicited by in vitro reconstituted MHC/peptide complex. J Immunol Meth. 1996;192:105–115. doi: 10.1016/0022-1759(96)00027-0. [DOI] [PubMed] [Google Scholar]
- Schade AE, Levine AD. Phosphatases in concert with kinases set the gain for signal transduction through the T cell receptor. Mol Immunol. 2003;40:531–537. doi: 10.1016/s0161-5890(03)00170-6. [DOI] [PubMed] [Google Scholar]
- Seddon B, Mason D. The third function of the thymus. Immunol Today. 2000;21:95–99. doi: 10.1016/s0167-5699(99)01559-5. [DOI] [PubMed] [Google Scholar]
- Slifka MK, Whitton JL. Functional avidity maturation of CD8+ T cells without selection of higher affinity TCR. Nature Immunol. 2001;2:711–717. doi: 10.1038/90650. [DOI] [PubMed] [Google Scholar]
- Valitutti S, Lanzavecchia A. Serial triggering of TCRs: A basis for the sensitivity and specificity of antigen recognition. Immunol Today. 1997;18:299–304. [PubMed] [Google Scholar]
- Viola A, Lanzavecchia A. T cell activation determined by T cell receptor number and tunable thresholds. Science. 1996;273:104–106. doi: 10.1126/science.273.5271.104. [DOI] [PubMed] [Google Scholar]
- Wilson DB, Wilson DH, Schroder K, Pinilla C, Blondelle S, Houghten RA, Garcia KC. Specificity and degeneracy of T cells. Mol Immunol. 2004;40:1047–1055. doi: 10.1016/j.molimm.2003.11.022. [DOI] [PubMed] [Google Scholar]
- Wooldridge L, van den Berg HA, Glick M, Gostick E, Brenchley JM, Douek DC, Price DA, Sewell AK. Interaction between the CD8 coreceptor and MHC class I stabilizes TCR-antigen complexes at the cell surface. J Biol Chem. 2005;280:27491–27501. doi: 10.1074/jbc.M500555200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wyer JR, Willcox BE, Gao GF, Gerth UC, Davis SJ, Bell JI, van der Merwe PA, Jakobsen BK. T cell receptor and co-receptor CD8αα bind peptide-MHC independently and with distinct kinetics. Immunity. 1999;10:219–225. doi: 10.1016/s1074-7613(00)80022-9. [DOI] [PubMed] [Google Scholar]