Force transmission during adhesion-independent migration

Abstract

When cells move using integrin-based focal adhesions, they pull in the direction of motion with large, ~100 Pa, stresses that contract the substrate¹. Integrin-mediated adhesions, however, are not required for in vivo confined migration². During focal adhesion-free migration, the transmission of propelling forces, and their magnitude and orientation, are not understood. Here, we combine theory and experiments to investigate the forces involved in adhesion-free migration. Using a non-adherent blebbing cell line as a model, we show that actin cortex flows drive cell movement via non-specific substrate friction. Strikingly, the forces propelling the cell forward are several orders of magnitude lower than during focal adhesion-based motility. Moreover, the force distribution in adhesion-free migration is inverted: it acts to expand, rather than contract, the substrate in the direction of motion. This fundamentally different mode of force transmission may have implications for cell-cell and cell-substrate interactions during migration in vivo.

Cell migration is essential to many physiological and pathological processes, including embryonic development, wound healing, immune response and cancer metastasis. To migrate, cells must exert forces on their substrate to propel the cell body forward. Classical models of cell migration imply that specific adhesion points transmit intracellular pulling forces from the cytoskeleton to the substrate³. Yet, recent studies indicate that in 3-dimensional confinement, migration can be achieved without specific adhesions^2,4,5. Here we investigated force generation during such adhesion-independent cell migration.

Traction force microscopy measurements have established that in adherent cells single focal adhesions can transmit forces of tens of nN⁶, resulting in force densities on the cell surface of several kPa⁷. In contrast, force transmission during focal adhesion-independent migration has not been investigated experimentally and the origin and magnitude of the forces involved remain unclear. Several theoretical models have been proposed. For example, in smooth three-dimensional (3D) confinement, such as during migration through dense tissues in cancer invasion or in development^8–10, non-specific substrate friction could account for force transmission¹¹. However, a friction-based mechanism has not been demonstrated experimentally, and it is unknown whether friction alone can generate sufficient force to mediate cell body translocation.

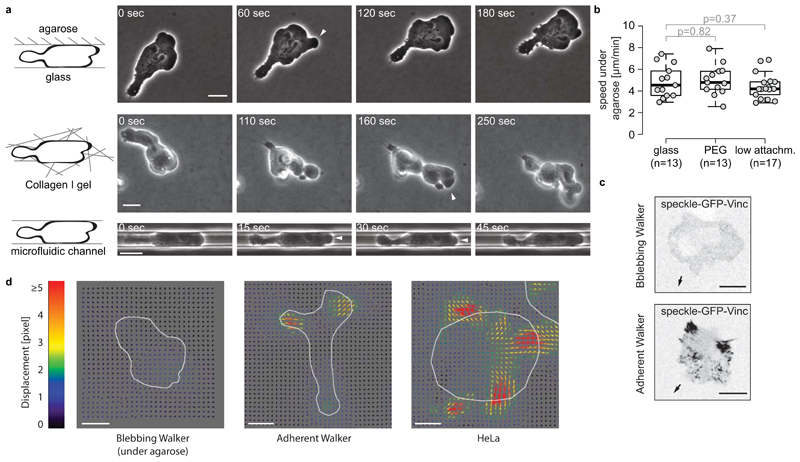
To investigate forces exerted during focal adhesion-independent migration, we used a non-adherent subline of Walker 256 carcinosarcoma (henceforth Walker) cells as a model. Walker cells polarize spontaneously in suspension and form blebs at their leading edge. They are unable to migrate on two-dimensional substrates, but move effectively when confined in 3D¹². We verified that Walker cells migrate in a variety of confined environments, including in confinement between an agarose pad and serum-coated glass, within 3D collagen gels and in PDMS microfluidic channels passivated with bovine serum albumin (BSA) or beta-lactoglobulin to prevent cell adhesion^13,14 (Fig. 1a, Supplementary Fig. 1a,b). Walker cells remained motile when confined between agarose, which is non-adhesive¹⁵, and other non-adhesive surfaces (Fig. 1b, Supplementary Fig. 1d). We therefore hypothesized that Walker cells migrate in confinement without using specific substrate adhesions. To test this directly, we first attempted to localize focal adhesion components in these cells. We found that neither GFP-tagged Focal Adhesion Kinase (FAK) nor speckle-GFP-Vinculin, a low expression construct of Vinculin allowing for detection of faint focal adhesion points¹⁶, formed foci at the basal surface of Walker cells migrating under agarose (Fig. 1c and Supplementary Fig. 1c). Furthermore, Walker cells with reduced Talin expression levels did not display significant changes in migration velocity under agarose (Supplementary Fig. 1e). Finally, Walker cells remained motile in 3D collagen gels upon addition of EDTA, which sequesters Ca²⁺ and Mg²⁺ ions that are essential for the function of most adhesion proteins (Supplementary Video 1). Taken together, our findings show that blebbing Walker cells migrate in confinement without forming specific integrin-mediated focal adhesions.

Figure 1. Specific adhesion-independent migration of blebbing Walker cells in confined environments.

a - Timelapses of migrating blebbing Walker cells under agarose, within a three-dimensional collagen-I gel or in a BSA-coated microfluidic channel. Arrowheads: blebs. b - Instantaneous velocities of migrating blebbing Walker cells under agarose on glass, PEG-coated glass and commercial low attachment surfaces (Corning). Cells were manually tracked for 52 min using Fiji. P-Value: Welch's two-sided T-Test; n: number of cells analyzed in 2 independent experiments. Boxes in boxplots extend from the 25th to 75th percentiles, with a line at the median. Whiskers extend to 1.5x IQR (interquartile range) or the max/min datapoints. c - Representative images (inverted contrast) of Walker cells expressing the focal adhesion component speckle GFP-Vinculin¹⁶. Top: blebbing Walker cell migrating under agarose; no focal adhesions are detected. Bottom: control; clear focal adhesions are formed by adherent Walker cells migrating on glass. Arrows indicate the direction of migration. d - Representative images of in-plane substrate deformations during migration of adherent and non-adherent cells. Non-adherent blebbing Walker cells migrating under agarose on soft (3kPa), elastic PDMS substrates with embedded beads do not elicit substantial bead displacements, while adherent Walker cells and HeLa cells do. Displacement fields caused by the cells were calculated from images of fluorescent beads using a traction force Fiji plugin. Cell outlines are drawn in white. All scale bars: 10 µm.

We then attempted to measure forces exerted during adhesion-independent migration of Walker cells using traction force microscopy. As a control, we plated HeLa cells and an adherent subline of Walker cells¹² on soft PDMS substrates with embedded fluorescent beads. We observed clearly detectable in-plane bead displacements, indicative of strong pulling forces (Fig. 1d). In contrast, we did not observe substantial in-plane bead displacements during blebbing Walker cell migration under agarose (Fig. 1d). This indicates that forces exerted during adhesion-free migration are considerably smaller than those exerted during classical, focal adhesion-based migration.

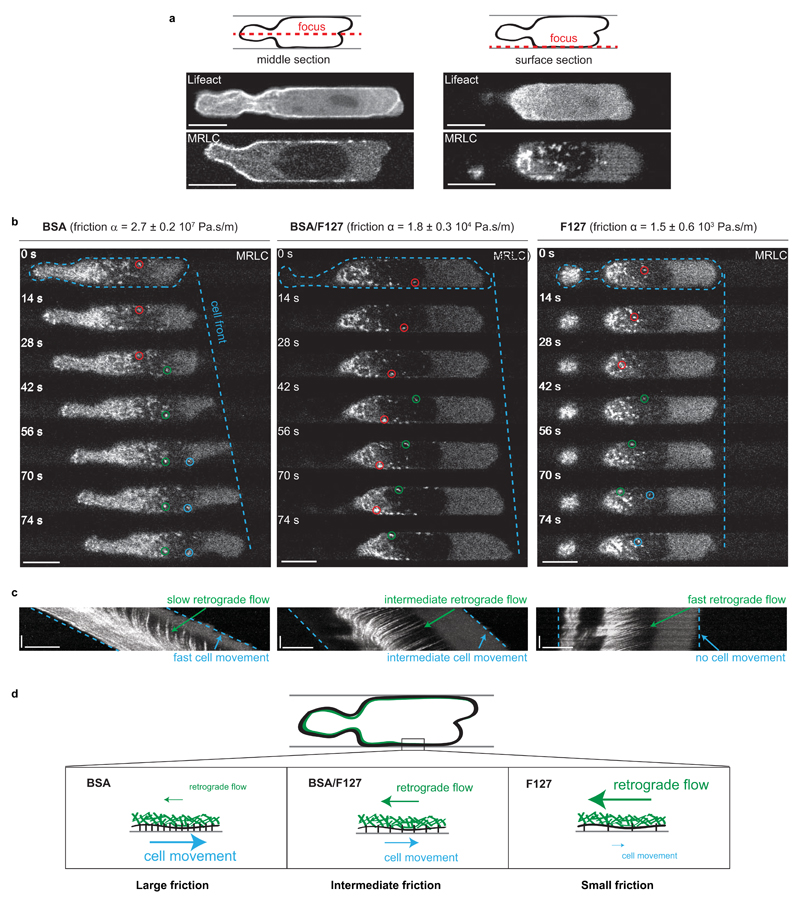
To understand the forces underlying focal adhesion-independent migration, we characterized the actomyosin cytoskeleton, which drives migration in most cell types¹⁷. We focused on Walker cells migrating in microchannels, as the simple channel geometry imposes a well-defined, static cell morphology easily amenable to quantitative analysis (Fig. 2a, Supplementary Video 2). The medium was supplemented with the Arp2/3 inhibitor CK-666, which does not affect blebbing Walker cell behavior but prevents the cells from occasionally switching to an adhesion-based, lamellipodia-driven migration mode¹². Both F-Actin and myosin were enriched at the cell cortex and displayed a strong gradient towards the cell rear (Fig. 2a, Supplementary Fig. 1), suggesting a rearward gradient in contractility. To test whether the rearward actomyosin gradient was essential for migration, we performed laser ablations to relax cortical contractility locally¹⁸. Cortex ablation at the cell rear strongly decreased cell velocity, whereas ablation at the leading edge had no effect (Supplementary Fig. 1f, Supplementary Videos 3 and 4). This suggests that cortical contractility at the rear is necessary for confined migration of Walker cells. We next imaged dynamics of the actomyosin cortex. We found that in BSA-coated channels, both actin and myosin displayed a strong retrograde flow in the reference frame of the cell (Supplementary Videos 5 and 6). These flows appeared tightly coupled to the surface of the microchannel, as myosin foci in the cortex remained almost stationary in the channel reference frame (Fig. 2b,c, Supplementary Video 6). Taken together, our observations suggest a mechanism in which cortex flows resulting from a rearward actomyosin gradient drive Walker cell migration in the absence of specific adhesions.

Figure 2. A minimum friction is required for cortical flow-driven migration of non-adherent Walker cells.

a - F-actin (Lifeact) and Myosin (MRLC) gradients in Walker cells, imaged in the middle cross-section of the cell (left) and within the plane of the actomyosin cortex close to the channel wall (right). Scale bars: 10 µm. b - Timelapses of migrating Walker cells in microchannels with different frictions. The cell substrate friction coefficient α was measured for the 3 different channel coatings (BSA, F127 and BSA/F127-mix) by applying a pressure to the channel entry and measuring the velocity of non-polarized cells (mean ± SEM, see Supplementary Fig. 2 and Materials and Methods for details). Dynamics of the actomyosin cortex in a confocal section at the cell surface were visualized with MRLC-GFP. Colored circles highlight the dynamics of individual myosin foci. Scale bars: 10 µm. c - Kymographs showing the dynamics of the cortex along the long axis of the cell. Scale bars: horizontal: 10 µm, vertical: 50 s. d - Summary of the observed cell behaviors and actomyosin cortex dynamics depending on the friction between the cell and the channel walls.

Retrograde actin flows in the leading edge have been shown to drive cell migration when coupled to the substrate via integrin-based adhesions¹⁷. In the absence of adhesions, non-specific transient interactions between transmembrane proteins and the substrate might generate friction, transmitting flows into cell movement, as suggested by theoretical studies¹¹. To test this hypothesis, we modified the coating of the channel walls to decrease friction-based coupling. We passivated the channel walls with Pluronic F127, an analogue of PEG, which has been suggested to provide low-friction substrates¹⁹. We directly measured friction coefficients on single, unpolarized cells using a microfludic chip and confirmed that this coating resulted in a very low-friction environment compared to BSA coating (Supplementary Fig. 2, Supplementary Video 7). In the low friction F127-coated channels, Walker cells adopted the same polarized morphology as in the high friction BSA-coated channels but were unable to migrate (Supplementary Video 8). Strikingly, retrograde actomyosin flows in the cell reference frame persisted in these channels but, in contrast to BSA-coated channels, were completely uncoupled from the substrate (Fig. 2b,c, Supplementary Video 9). We then coated the channels with a mixture of BSA and F127 to achieve intermediate friction (Supplementary Fig. 2), and observed that blebbing Walker cells could migrate in such channels, but at significantly slower velocities than in high friction BSA channels (V_BSA = 7.6 ± 0.5 µm/min, n=18 cells from 5 independent experiments, vs. V_BSA/F127 = 5.2 ± 0.4 µm/min n=25 cells from 3 independent experiments; error: SEM; p < 0.01, Supplementary Video 10). Furthermore, in contrast to cells in BSA-coated channels, the retrograde cortical flows did not remain stationary in the channel reference frame (Fig. 2b,c), indicating only partial coupling of the cortex to the channel wall. Taken together, these experiments suggest that rearward cortical flows coupled to the substrate via friction drive adhesion-free migration in Walker cells, and that a minimum friction is required to achieve effective force transmission (Fig. 2d).

We then used the measured friction coefficients to obtain an estimate of the forces driving friction-based migration. Assuming that the friction coefficient we measured in unpolarized cells (Supplementary Fig. 2) does not change upon cell polarization, the product of the measured friction coefficient and the cortical flow velocity yields an estimate of the force density (stress) exerted by the cells. We thus estimated average cortical flow velocities in the different friction conditions (Fig. 2c), and found that cells in BSA, BSA/F127, and F127 channels exerted stresses lower than ~1 Pa, 5 mPa and 0.5 mPa, respectively, on the channel walls. These stresses are several orders of magnitude smaller than the hundreds of Pa stresses typically exerted by adhesive cells^6,7, consistent with our traction force microscopy observations (Fig. 1d).

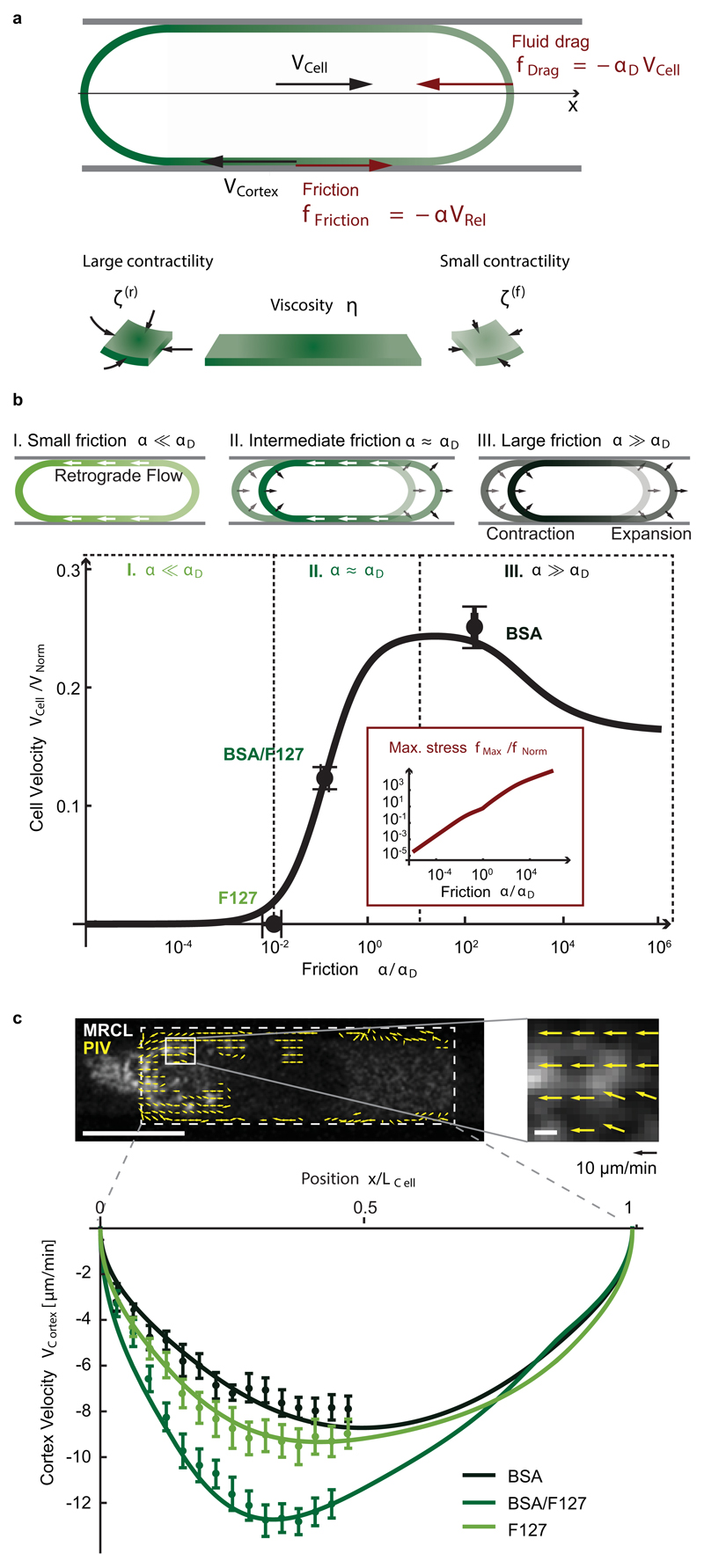
To understand how such small forces can drive cell motion and to obtain the spatial force distribution, we developed a theoretical description of friction-based cell migration. We modeled the actomyosin cortex as an axisymmetric, viscous surface subjected to the following forces: myosin-generated internal contractile stress within the cortical layer, external friction with the channel walls resisting cortical flows, and drag force arising from the displacement of external medium opposing cell motion (Fig. 3a, Supplementary Fig. 3 and Supplementary Note). We did not include internal friction caused by intracellular structures such as the nucleus, as several lines of evidence indicate that it is negligible in our system (Supplementary Note 4.2, Supplementary Fig. 4a-d). Our model predicts that a rearward contractility gradient can drive non-adhesive cell movement in confinement via two complementary mechanisms (Fig. 3b, see Supplementary Note for details): i) frictional forces resisting myosin-driven retrograde cortical flows generate propelling forces, ii) myosin contractility drives contraction at the cell rear, leading to front expansion and net cell movement when friction is sufficient to maintain the cell body in place (Supplementary Video 11). We calculated the cell velocity as a function of the channel friction coefficient, and found that, consistent with our experimental observations, a threshold friction is required for cell motion (Fig. 3b, Supplementary Fig. 3f). This threshold friction is of the order of the external drag resisting cell motion; thus, forces as small as the drag are sufficient to propel the cell forward. Above the threshold friction, cell velocity is roughly constant while friction-generated stresses increase (Fig. 3b inset), highlighting that velocity does not correlate with the amplitude of the stresses exerted in this migration mode but is dictated by the velocity of the actomyosin flow.

Figure 3. The mechanics of specific adhesion-independent migration.

a - Schematic and parameters of the physical description of friction-based cell migration. The cell cortex is represented by an axisymmetric surface with viscosity η, subjected to a myosin-II-dependent contractile active tension ζ (see Supplementary Note). A gradient in active tension along the cell axis induces deformations of the cell poles and retrograde cortical flow of velocity V_Cortex, resulting in cell movement at velocity V_Cell if the generated friction force f_Friction is sufficient to counteract the fluid drag force f_Drag. [V_Rel = V_Cell + V_Cortex] b - Top: Cell translocation is achieved by frictional forces resisting a retrograde cortical flow coupled to contraction of the cell rear and expansion of the leading edge. The relative contribution of the two mechanisms depends on the friction coefficient. Bottom: Cell velocity as a function of friction (dots: experimental data (error: SEM), solid line: fitted theoretical curve). Fluid drag α_D leads to cell stalling below a threshold value of substrate friction α*/ α_D ~ 0.1. The maximum stress exerted on the channel wall (inset) increases for increasing friction, while the cell velocity reaches a plateau. [Normalization: V_Norm = (ζ^(r) - ζ^(f))L/η, f_Norm = α_D V_Norm.] c - Cortical flow profiles in different friction conditions quantified using PIV. Dots: experimental data; lines: fit theoretical curves calculated for measured myosin gradients (Supplementary Fig. 1i and Supplementary Note for details). Scale bars: 10 µm (left panel) and 0.5 µm (right panel). For b/c: n_BSA=33, n_BSA/F127=25, and n_F127=33 cells were analyzed in 5 (BSA), 3 (BSA/F127) and 5 (F127) independent experiments. Data were systematically filtered based on the PIV sample size (error bar: SEM, see Materials and Methods for details).

We then tested if our theoretical description could quantitatively recapitulate observed cell and cortex dynamics in the different friction regimes, and quantified the spatial profile of cortical flows in the different friction conditions (Fig. 3c). We performed a simultaneous fit of the model equations to i) the cortical flow profiles and ii) the cell velocities measured for different frictions. Flow profiles and cell velocities could be fitted accurately with a single set of three fit parameters (Fig. 3b,c), yielding estimates for the mechanical parameters of the model. We found a cortical tension gradient Δζ = 68 ± 7 pN/µm, consistent with reported cortical tension values^12,18 and a two-dimensional cortex viscosity η = 27 ± 3 10^-4 Pa.s.m, consistent with reported values of 3D cortex viscosities²⁰. The drag coefficient was found to be α_D= 208 ± 29 kPa.s/m, corresponding to about 50% of the extracellular medium being pushed forward as the cell migrates, in agreement with direct estimates of medium flows (Supplementary Fig. 4e-h, Supplementary Note). In summary, we could accurately fit both cell and cortex dynamics for all three friction conditions using a single set of three fit parameters. The strong agreement between data and theory suggests that rearward cortical flows coupled to the substrate via unspecific friction are sufficient to drive focal adhesion-independent migration.

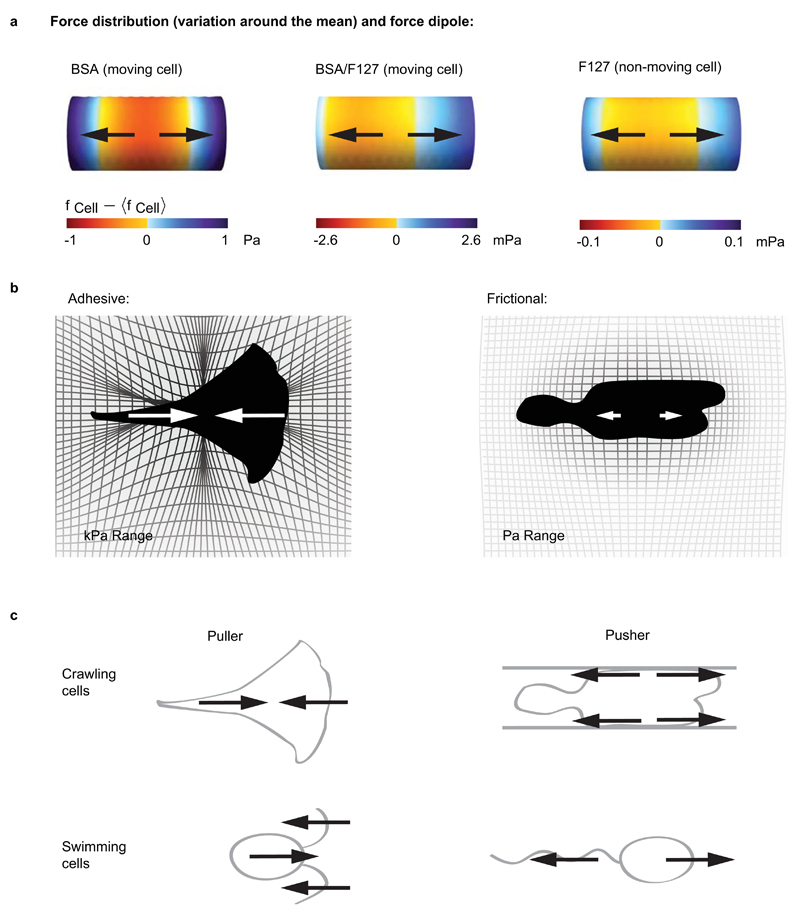
Finally, we used the model and the extracted parameter estimates to compute the spatial distribution of forces exerted on the substrate during adhesion-free migration (Supplementary Note). We found that the total force exerted by migrating Walker cells on the channel walls was a few pN, balancing the drag experienced by cells in microchannels. The spatial force distribution of a migrating cell can be described by a force dipole, a measure of the separation of pushing and pulling forces exerted by the cell (see Supplementary Note for details). A positive force dipole characterizes a cell that pushes itself from the rear, while a negative dipole describes a cell that pulls at the front. The force dipole determines the pattern of substrate deformation and can influence cell orientation and cell-cell interactions [reviewed in¹]. Cells migrating using focal adhesions exert a contractile, negative force dipole, where strong pulling forces on adhesions at the cell leading edge are counterbalanced by contractile forces at the rear^1,21. In striking contrast with adherent cells, we found that in migrating Walker cells, the dipolar moment of the force distribution was positive (Fig. 4a). This indicates that the cells tend to expand rather than contract their substrate, with the propulsive thrust being generated in the cell rear (Fig. 4b). Thus, even though force generation relies on actomyosin driven flows for both migration modes, the force dipoles during adhesion-free and focal adhesion-based migration have opposite orientations.

Figure 4. Force distribution underlying migration in the absence of specific adhesion.

a - Distribution of forces (variation around the mean, see also Supplementary Fig. 4i) exerted by migrating Walker cells on the channel wall. Cell migration direction is to the right, the force is oriented on average in the direction opposite to this motion, and the stress magnitudes are in the mPa-Pa range, considerably smaller than stresses reported for adhesive cellular movement. Propulsive thrust is generated in the rear part of the cells, and cells exert a positive, extensile force dipole on their surrounding environment (ρ_BSA = 7.7 10^-17 N.m, ρ_BSA/F127 = 2.5 10^-18 N.m and ρ_F127 = 4.4 10^-20 N.m). b - Schematic comparison of stresses exerted during adhesive vs. frictional cell migration. Adhesive cells exert large stresses, and induce strong, contractile deformations on their environment; frictional movement relies on small stresses and generates weak, extensile deformations. c - Schematic classification of swimming and crawling cell motion according to the sign of the force dipole.

In summary, our study reveals fundamental differences in force transmission mechanics between focal adhesion-dependent and -independent migration modes (Fig. 4). We find that stresses generated during adhesion-free migration are orders of magnitude smaller than stresses typically exerted during specific adhesion-based motility (Fig. 4b, Supplementary Fig. 4i). Indeed, even cells relying on weak or transient adhesions, such as fast-moving keratocytes or adherent cells with reduced myosin activity, exert forces in the nN/µm² range on their substrate^22,23. We report here that Walker cells exert stresses of ~1 Pa or lower, corresponding to forces on the channel walls in the pN/µm² range. This range of stresses is under the limit of detection using sensitive traction force measurement setups^23–25. Instead, our approach, which relies on friction measurements coupled to fitting of imaging data to a mechanical model of migration, provides a technique to extract forces and cell physical properties from cell shape and cortex dynamics. Such fitting-based measurements are increasingly being used in studies of cell mechanics^26,27. It will be a challenge for future studies to design substrates allowing for a more direct measurement of stresses under 1 Pa during migration in confinement.

Our study suggests that the large forces transmitted by focal adhesions, rather than being essential for motion itself, could function mostly to guide persistent directional migration²⁸ or to probe substrate stiffness^29,30. Furthermore, in integrin-based migration, large forces are required to detach focal adhesions and too strong adhesion prevents migration³¹; in friction-based migration, the detachment forces are minimal and above a threshold friction, cell velocity remains constant, even for very high frictions (Fig. 3b). Mechanisms giving rise to friction, including possible contributions of substrate irregularities in vivo, remain to be investigated. Finally, we show that during friction-driven migration, the force distribution corresponds to a positive force dipole in striking contrast with adhesive migration, where the force dipole is negative (Fig. 4b). A similar distinction exists for microswimmer organisms, which can be divided into two categories, 'pushers', such as Escherichia coli, and 'pullers', such as Chlamydomonas reinhardtii, according to the sign of their force dipoles³² (Fig. 4c). This distinction has important consequences for coupling between swimming cells: side-by-side moving pushers repel each other while pullers attract each other. It will be interesting to investigate how cell-cell interactions differ between crawling 'pushing' and 'pulling' cells migrating in vivo.

Materials and Methods

Reagents and Plasmids

The Arp2/3 complex inhibitor CK-666³³ was purchased from Tocris Bioscience and dissolved in DMSO. BSA, β-Lactoglobulin and Pluronic F127 were purchased from Sigma and dissolved in 1x PBS. pLL-PEG was from Surface SolutionS and diluted in 10~mM HEPES. GFP-FAK was provided by Ekaterina Papusheva/ Carl-Philipp Heisenberg. Speckle GFP-Vinculin was a gift from Alan Rick Horwitz. MRLC-GFP was a gift from Rex Chisholm. siRNAs were Stealth Select RNAi siRNAs from Invitrogen with the following sequences: TLN1 siRNA (RSS320275): 5'-GGGCAUAUCCAUGUCUUCGAGCAAA-3'; TLN2 siRNA (RSS321623): 5'-GAGAGGAGCCGAGAAGCGAAUAUUU-3'. Knockdown efficiency was quantified by Western blotting with antibodies for TLN1 (monoclonal, clone 8d4, Sigma #T3287, 1:2000), TLN2 (GeneTex, #EPR2536(2), 1:1000) and GAPDH (clone 1D4, NovusBiologicals #NB300-221, 1:20000). Representative images of immunoblots are based on at least 2 experiments.

Culture and Transfection of Cells

Walker 256 carcinosarcoma cells were a gift from V. Niggli. Cells were grown in RPMI

1640 supplemented with 10% FCS, 1% penicillin-streptomycin and 2 mM glutamine (allGIBCO, Invitrogen) at 37°C and 5% CO₂. Transient cell transfection was performed with Amaxa Nucleofection systems (Cell Line Nucleofector Kit V or Cell Line 96-well Nucleofector Kit SF, Lonza) using 0.5 to 2 µg plasmid DNA and protocols optimized for HL-60 cells provided by the manufacturer. For MRLC-GFP, a stable cell line was created by transient transfection of WT-cells followed by selection with 500 µg/ml G-418 and clonal separation by FACS (performed at the Wolfson Institute for Biomedical Reseach, London).

Cell migration environments

a). Under agarose assay

Walker cells were placed between a glass surface or a commercially available ultra-low-attachment surface (Corning Life Sciences) and an agarose layer by using the earlier described under-agarose-assay³⁴ one hour prior to the experiment. Cell culture tested agarose with low gelling temperature was used (Sigma). In under-agarose experiments with PEG coated glass substrates, small agarose patches were made and placed onto glass-bottom dishes previously coated with 100 µg/ml pLL-PEG for one hour at room temperature.

b). Micropipettes and 3D collagen

For migration in micropipettes, polarized cells were slowly aspirated in medium-filled glass micropipettes by applying a negative pressure. Once the cell fully entered the pipette, pressure was equilibrated prior to imaging. 3D collagen gels were produced as described earlier³⁵.

c). Microfluidic channels

Microfluidic channels were produced as described earlier³⁶, except that PDMS blocks with channels were not bound to glass but instead onto PDMS-coated glass coverslips. This creates microfluidic channels where all 4 sides are made out of PDMS. Bonding was achieved by partially curing the PDMS on the coverslip as well as the PDMS with the features, then assembling the device followed by final curing step. Microchannels were then coated with 50 µg/ml BSA, 2 mg/ml F127 or a mix of BSA and F127 (50 µg/ml BSA and 30 µg/ml F127, all in 1× PBS) for 30 min at room temperature. After a washing step, channels were filled with cell culture medium (supplemented with 50 µM of the Arp2/3 inhibitor CK-666, to prevent cells from switching to an adhesion-based, lamellipodia-driven migration mode¹²). Cells pretreated with 50 µM CK-666 for 15min were introduced into the channels by applying a gentle pressure with a syringe containing a concentrated cell suspension. At all steps it was ensured that the tubing and the syringes were free of air bubbles, to avoid introducing air into the microfluidic system. After introducing the cells in the channels, the entire chip was covered with medium in order to ensure an equal hydrostatic pressure through the channel.

Traction force substrates

Traction force substrates were prepared as follows: Dow corning Silicone Elastomer CY 52-276 Components were thoroughly mixed in a 1:1 mass ratio (3kPa substrates^37,38), degassed and spin-coated on glass coverslips to create a 30 µm thick layer. After curing for 30min at 70 °C samples were treated for 30min with 10 % (3-Aminopropyl)triethoxysilane (Sigma) in ethanol, followed by several washings with ethanol. Air dried samples where then incubated at 70 °C for 1h. 40 µm fluorescent microspheres (Lifetechnologies) were bound to the surface of the samples by a 1min incubation with a 1×PBS solution containing microspheres and 50 µg/ml 1-Ethyl-3-(3-dimethylaminopropyl)-carbodiimide (EDC) (Sigma). Finally, elastic substrates were coated with a solution containing 50 µg/ml Fibronectin (Lifetechnologies) and 50 µg/ml EDC for 30min before cell seeding. In the case of HeLa cells and adherent Walker cells, substrates were relaxed by adding 0.1% SDS to the medium. For suspension Walker cells, elastic substrates and cells were overlaid with an agarose layer and cells were imaged over time, allowing to observe the bead positions with and without the cell.

Imaging and laser ablation

Fluorescence, DIC and IRM imaging was performed on a scanning confocal microscope (Olympus FV1000 or FV 1200, UPlanSApo 60× NA 1.35 Oil Objective or UPlanSApo 60XS NA 1.3 Silicone Objective) using a 488 nm or a 561 nm laser as light sources. Laser ablation experiments were performed on the same system using a 405~nm picosecond pulsed laser, as described previously^18,27. Phase contrast observations were performed on an inverted Zeiss Axiovert 200M wide-field microscope using a Ph2 Plan Neofluar 40× NA 0.75 or a LD Plan Neofluar 40× NA 0,6 Ph2 Korr objective. Environmental control (37°C, 5 % CO₂) was applied for all imaging setups. Representative images of cells shown are based on ≥2 independent experiments.

Cell Tracking

Analysis of migration of cells under agarose was done by manual tracking of the nuclei of cells using the Manual Tracking Plugin of Fiji. Quantification of cell velocities in microchannels from phase contrast videos was done by producing kymographs along the long axis of the cell followed by calculation of the velocity from the angle of the kymograph.

Quantification of cortical flows (PIV)

To estimate the velocity field in the cell cortex, we analyzed timelapse videos of migrating Walker cells expressing MRLC-GFP in microchannels (height: 6µm, width: 10µm, 2s/frame). In the analysis of cell migration in microchannels with large and intermediate frictions, only actively migrating cells were considered. Cells failing to migrate, or switching direction or dividing during imaging, were excluded. This criterion was pre-established and then applied to all experiments. The videos were taken in the focal plane of the actomyosin cortex close to the cell surface. Videos were first registered using the MultiStackReg Fiji plugin and a gaussian blur filter of height 3 and width 0.9 was applied to all images to reduce noise prior to analysis. The PIV algorithm described in²⁶ was then applied to obtain an estimate of the cortical flow field by computing the cross-correlation between subsequent images. The same set of PIV parameters was used in all analyzes. The ROI for each cell, spanning from the rear to the front excluding the uropod, was selected manually on time-averaged images (see Fig. 3c for example). Assuming axisymmetry and stationarity of the flow field, we averaged the data over the height of the cell and over time. To account for differences in cell length and to average over cells, we binned the data into 33 bins along the cell. In both averaging steps, datapoints were excluded based on the following criteria: for each cell, we included only datapoints that came from a sample of n>300 time- and cell-height-points; and for the cell average flow profile, we used only points coming from a sample larger than the sample size median for each friction condition. We noticed a systematic underestimation of velocities by the PIV algorithm due to the static noisy background. To correct for this, we generated series of artificial test images, where random patterns of blurred spots were shifted in front of middle plane images of the analyzed cells. The intensity of the spots was adjusted to match real myosin foci. The pattern was advanced at a rate of 3 px/frame, in the range of the observed cortical flow. Performing PIV on these artificial cortical flows with known velocity allowed to compute the factor correcting for the bias. We found v_corr = 1.167 v_PIV. The code for the PIV algorithm is available upon request to the corresponding authors.

Quantification of myosin intensity profiles

We estimated the relative fluorescence intensity of cortical myosin from the same images the PIV was performed on. Again, assuming axisymmetry and stationarity of the myosin distribution, we binned the data into 50 bins along the cell and averaged each video over time and cell height. Finally, data was averaged between different cells for each friction condition. We subtracted the background cytoplasmic signal from cortex plane images, using images from the middle section of the cells. All intensities were normalized to the average intensity in a region devoid of myosin spots in the front of the cell.

Friction measurements

The friction device was designed based on previous work^39,40 and assembled and coated in a way identical to the microchannels (see above). After the device was filled with cell culture medium, the 3 entry ports were connected to reservoirs containing medium with 0.2 µm fluorescent microspheres (Invitrogen), medium with cells and plain medium (see Supplementary Fig. 2). Lowering the output reservoir E3 created a pressure difference, leading to flows of beads and cells into and through the device. The relationship between the mean free flow velocities in the analysis channel of the device and the height of reservoir E3 relative to the other reservoirs E1 and E2 (Δh) was determined by imaging and measuring microspheres velocities using a LD Plan NeoFluar 20x NA 0,4 Ph2 Korr objective on a inverted Zeiss Axiovert 200M wide-field microscope equipped with a spinning disc scan head (Andor/ Yokogawa) (Supplementary Fig. 2, Supplementary Video 7). Briefly, in order to extract the mean free flow velocities, kymographs were created along the entire channel width and the mean angle of each kymograph was determined using Fiji's Directionality plugin. As the imaging setup allowed imaging the entire channel height in a single plane, averaging over the channel width gives the mean free flow velocity (see Supplementary Fig. 2). Friction measurements were performed on unpolarised cells, which did not display any motility. Single cells were introduced into the analysis channel and their velocity was recorded for different mean free flow velocities in the device with various coatings (Supplementary Fig. 2).

To estimate the friction, the pressure difference P_applied was first estimated by measuring the average free flow velocity ${\overline{\text{v}}}_{\text{c},\text{free}}$ in the channel without cells, related to the applied pressure through the following relation:

$${\text{P}}_{\text{applied}}={\xi }_{\text{c}}\text{S}{\overline{\text{v}}}_{\text{c},\text{free}}$$ (1)

where ${\xi }_{\text{c}}=\frac{8{\eta }_{\text{c}}{\text{L}}_{\text{c}}}{\left({\text{R}}^{\text{4}}\pi \right)}$ is the hydraulic resistance of the channel, with η_c the viscosity of water and L_c the length of the channel. Once a single cell was introduced into the channel, its velocity U was measured at the same applied pressure P_applied. The cell velocity was then related to the friction coefficient α and to the applied pressure through the following relation

$${\text{P}}_{\text{applied}}=\left[\left(\frac{{\xi }_{\text{c}}}{\xi }+1\right)\frac{2\text{L}\alpha }{\text{R}}+{\xi }_{\text{c}}\text{S}\right]\text{U}$$ (2)

where R is the channel radius and L is the contact length of the cell estimated from the microscopy images. To obtain Eq. 2, we take into account the hydraulic resistance of the cell ξ to estimate the fraction of fluid going through the cell. The applied pressure to the channel can be written as ${\text{P}}_{\text{applied}}=\frac{2\text{L}\alpha }{\text{R}}{\text{U+ξ}}_{\text{c}}\text{S}{\overline{\text{v}}}_{\text{c}},$ where the first term relates the pressure to the resulting displacement of the cell, which is resisted by friction, and the second term describes the relation to the induced fluid flow in the channel. To obtain the resistance of the cell to displacement in the first term, we integrated the friction force density αU over the cell surface, assuming the cell behaves as a solid object. The second term depends on the mean fluid velocity in the channel in the presence of a cell, which is given by ${\overline{\text{v}}}_{\text{c}}=\left(\frac{2\text{Lα}}{{\text{R}}^{\text{3}}\xi \pi }+1\right)\text{U},$ leading to the expression given in Eq. 2. The hydraulic resistance of the cell ξ was estimated self-consistently together with the fitting procedure for cellular retrograde flows (see Supplementary Theory). Using this estimate, we compute the friction coefficients in different conditions from Eq. 2.

Image Processing, Data Analysis, and Statistics

Images were processed using Fiji and Adobe Illustrator. They were cropped, rotated, and their contrast and brightness were manually adjusted.

Data were analyzed, tested for statistical significance, fitted and visualized using R, MATLAB (MathWorks, 2013) and Mathematica (Wolfram Research, 2013) software. In particular, the code used to fit the data to the mechanical model of migration was a custom-made code written in Mathematica. The source code is available upon request to the corresponding authors. No statistical method was used to predetermine sample size. The Shapiro-Wilk-Test or the Kolmogorov-Smirnov test was used to ensure normality of data. Welch's t-test was chosen for statistical testing, which is insensitive to the equality of variances. Boxes in all boxplots extend from the 25th to 75th percentiles, with a line at the median. Whiskers extend to 1.5× IQR (interquartile range) or the max/min datapoints if they fall within 1.5× IQR.