A general time dependent approach to vibronic spectroscopy including Franck-Condon, Herzberg-Teller and Dushinsky effects

Abstract

An effective time-dependent approach to compute vibrationally resolved optical spectra from first principles is presented for the computation of one-photon electronic spectra induced by either electric or magnetic transition dipoles or by their mutual interaction, namely absorption, emission, and circular dichroism. Particular care has been devoted to generality, modularity, and numerical stability including all the effects that play a role at the harmonic level of approximation, namely Franck-Condon, Herzberg-Teller, and Dushinsky (i.e. mode mixing) effects. The implementation shares the same general framework of our previous time-independent (TI) model, thus allowing an effective integration between both approaches with the consequent enhancement of their respective strengths (e.g. spectrum completeness and straightforward account of temperature effects for the TD route versus band resolution and assignment for the TI route) using a single set of starting data. Implementation of both models in the same general computer program allows comprehensive studies using several levels of electronic structure description together with effective account of environmental effects by atomistic and/or continuum models of different sophistication. A few medium-size molecules (furan, phenyl radical, anthracene, dimethyloxirane, coumarin 339) have been studied in order to fully validate the approach.

1. Introduction

Electronic spectroscopy is nowadays among the most powerful tools for the study of chemical systems also thanks to ongoing development of both conventional techniques (one-photon absorption, hereafter OPA, fluorescence, phosphorescence) toward increased resolution together with shorter time scales and of more recent and powerful non-linear approaches (e.g. Resonance Raman, two-photon absorption and emission, etc.) not to speak about chiroptical methods (e.g. electron circular dichroism, ECD).^1–3 However, proper assignment of spectra relies more and more on quantum mechanical (QM) computations for both interpretative and predictive aspects.^4,5 Moving from the current practice of extracting numerical data from experiment to be compared with QM results toward the direct comparison between in vitro and in silico spectra would strongly reduce any arbitrariness and allow a proper account of the information hidden behind both position and shapes of spectral bands. Of course, theory can represent a valuable and robust support to experimental findings only if it is able to couple accuracy and feasibility for systems of current chemical, biological, and/or technological interest. On the one side this has led to the development of electronic structure methods able to deliver accurate results for small rigid systems in the gas phase, which provide also the balanced description of ground and excited states needed for the computation of accurate transition energies.^6–10 On the other side, the development of methods based on the density functional theory (DFT) and its time-dependent extension (TD-DFT) is already allowing a sufficiently accurate treatment of medium- to large-size systems and is constantly increasing the range of possible applications thanks to ongoing efforts to solve some well-known shortcomings (e.g. charge transfer states, double excitations, etc.).^9–11 In particular, the development of effective analytic gradients^12–14 and, very recently, of analytic Hessians^15,16 is allowing a full characterization of excited states.

However, the way in which electronic spectra are simulated is often basic, with a single peak per electronic transition, which is related to the associated moment of the property of interest (e.g. the electronic dipole for one-photon absorption). The band-shape is then obtained by applying a symmetric distribution function. Since this approach neglects the vibrational structure present in experimental spectra, it suffers from various shortcomings: for instance it cannot be used for the interpretation of high-resolution data showing a detailed vibrational structure is visible and is also limited for low-resolution spectra, whose asymmetric peaks cannot be reproduced by a single distribution function.^17–20

This problem has been widely studied and two parallel theories have been developed following time-independent or time-dependent routes, but always relying on a Taylor expansion of the transition moment whose first two contributions (constant and linear) give rise to the so-called Franck-Condon and Herzberg-Teller approximations.

The first general approach is the so-called sum-over-states or time-independent method, where the spectrum is obtained as the ensemble of all transitions between the vibrational initial and final states treated independently from one another. Since it is well known that the whole vibronic spectrum can be expressed in terms of Franck-Condon integrals, several approaches have been developed to compute these terms either by analytic or numerical approaches. Sharp and Rosenstock derived analytic expressions for Franck-Condon integrals up to four simultaneously excited normal modes using the properties of the generation function of Hermite polynomials.^21,22 However this formulation was limited to the Franck-Condon approximation. Baranov and co-workers proposed a generalization to the Herzberg-Teller level taking into account any combination of excited normal modes.^23,24 However, this approach was poorly suited for a general computational implementation of the method since each type of transition has a different expression, hence all needed Franck-Condon integrals had to be known before actual calculations and implemented in order to use the proper formulas. Furthermore, the equations become very cumbersome for more than four excited modes. These difficulties can be overcome using the recursive approach developed by Ruhoff, which relate the Franck-Condon integrals for transition differing at most by two quantum numbers.^25,26 Using these formulas, once the Franck-Condon integral between the two fundamental vibrational levels is known, all the other factors can be derived in terms of some matrices, referred to as the Sharp and Rosenstock matrices. Unlike the approach based on analytic formulas, this one is well-suited for implementation and computerization: in fact, it is based on a reduced number of quite simple formulas that are general for all the transitions. However this method requires also an efficient storage system in order to avoid the redundant calculation of Franck-Condon factors required more than once. At this level, the time-independent formulation of vibronic spectroscopy presents a general limitation: the need of truncating the in principle infinite summations of Franck-Condon integrals to some level, which involves, in turn, the development of general and reliable methods to select the most relevant transitions without actually computing nor storing all the terms (the so-called prescreening). The simplest prescreening approach defines lower and upper bounds for the transition energy and proceeds to calculate all Franck-Condon integrals included between those bounds.^27–29 The method is easy to implement, but becomes quite inefficient when taking into account either temperature effects or large spectral ranges. Nooijen and co-workers have developed a more general procedure to choose the most relevant transitions by analyzing directly the Franck-Condon factors.³⁰ However this procedure has strong limitations because it breaks down the normalization of the integrals and makes impossible the control of the quality of the calculation. Alternative approaches have been proposed, each one with its pros and cons regarding the efficiency, generality, ease of implementation, computational cost^18,31 (see Ref.32 for a more detailed discussion). In our group another prescreening method has been developed, based on the separation of the excitations into different classes labeled by the number of involved vibrational quanta and treated with decreasing levels of precision. Thanks to a number of methodological and technical improvements the latest version of the corresponding computational implementation (a detailed discussion of which can be found in ref.33,34) represents a very effective and general tool for all kinds of one-photon spectra including environmental and temperature effects.

Despite all these developments, time-independent methods still suffer from the fundamental problems related to the huge number of transitions to be taken into account for medium/large-size systems and of the intrinsic arbitrariness of any prescreening algorithm. The alternative time-dependent approach offers a viable route for avoiding these shortcomings since it exploits the properties of the Fourier transform leading to fully converged spectra including also temperature effects, without additional computational cost. As we will show in the next section, the basic idea behind the time-dependent formulation of spectroscopy is to write the Dirac delta function as the Fourier transform of the dipole moment autocorrelation function with the aim of working in the time domain rather than in the frequency one. This approach has been developed since 1950 and applied to many spectroscopic problems. The first studies of time-dependent optical spectroscopy were aimed at deriving spectroscopic properties for crystals starting from a proper definition of a time-dependent expression for the OPA spectrum of a regular crystal.³⁵ However, the validity of this theory was limited to a semiclassical framework and did not take into account the vibrational levels associated to electronic states. Kubo and Toyozawa introduced significant improvements by deriving a general expression for calculating the OPA vibronic spectrum of a crystal under the Franck-Condon approximation neglecting the Duschinsky mixing.³⁶ This theory was also extended to the evaluation of internal conversion rates. Next, the group of Mukamel showed that, starting from the expression for the absorption spectrum as the Fourier transform of the dipole autocorrelation function, the theory can be recast using two different, but equivalent formalisms.³⁷ The first one makes use of the generation function formalism³⁸ and can be related to the theory of stochastic processes leading to Fokker-Plank-type equations. The second approach is based on the quantum Green function’s theory, whose matrix elements can be related to the calculation of an absorption spectrum. Mukamel generalized this latter approach to multi-photon processes and non-linear optical effects, making use of the perturbation theory within the interaction picture.³⁹ At the same time, the group of Heller and co-workers introduced another formulation, namely the doorway-state vector formalism. The doorway-state vector is an auxiliary vector that can be written as a linear combination of the vibrational level of the final state and whose time evolution is obtained by propagation over the final Potential Energy Surface (PES). The absorption spectrum can be thus obtained as the Fourier transform of the overlap between this vector at time 0 and the same vector at time t. The work of Heller and coworkers has been focused on the derivation of a method to evaluate the time evolution of the doorway-state vector, but was limited to a semiclassical model and focused mainly on the description of Raman Spectroscopy starting from the interaction-picture formulation of perturbation theory in QM.⁴⁰ In this framework, analytic formulas for the calculation of Raman spectra have been derived, valid only under the assumption that the propagation occurs over a short time.^41,42 Tannor and Heller have derived a more general expression, whose validity is, however, limited by the assumption that the molecule is initially in the lowest vibrational state.⁴³ As a consequence, this theory cannot be easily generalized to take into account also temperature effects. In the last years this approach has been revised and further developed by Neese and co-workers, by paying particular attention to band-broadening effects and to provide a good numerical stability to the simulation of the spectra.^44,45 However, differences between the normal modes of initial and final electronic states (the so-called Duschinsky effect) are completely neglected and this is also the case for the generalization proposed by Silverstein and Jensen to deal with other multi-photon processes like Hyper-Raman scattering.^46,47

In recent years, the theoretical framework proposed by Mukamel,⁴⁸ based on finding an expression for the dipole moment autocorrelation function, has been extended to other types of problems. Pollak and Tachten used the Green function formalism to analyze the influence of Duschinsky effects on photoinduced cooling.^49,50 Borrelli and Peluso used this theory to calculate the temperature dependence of internal conversion rate of molecules of biological interest.⁵¹ They included in the calculation also a window function with the aim of helping the convergence of the Fourier transform. Similarly, Lin et al. have used the Green function formulation in order to calculate the influence of Duschinsky mixing on the rate of electron transfer.⁵² All those approaches led to the same analytic formula, including Duschinsky rotation but neglecting Herzberg-Teller effects. The generalization of the theory to Herzberg-Teller effects has been analyzed by Peng et al. in their studies of internal conversion rates.^53,54 Unfortunately this approach shows a quite poor numerical stability and the derivation of equations including Herzberg-Teller effects is not clear. Similarly, Borrelli and co-workers have proposed a general time-dependent approach to one-photon absorption spectroscopy,⁵⁵ but also in this case the extension to Herzberg-Teller effect is not straightforward. To summarize, several time-dependent models have been proposed till now, but their implementation in a general and robust code suffers from a number of difficulties including numerical instability, errors in the published equations or lack of significant contributions.⁵² As a consequence we decided to perform a new thorough theoretical derivation starting from the equations of Tang and coworkers and proceeding up to the coding of a general yet effective computer code closely paralleling our previous time-independent implementation. We should mention, for the sake of completeness, that Berger and coworkers have also proposed an alternative formulation using a generating function based on the coherent states including Herzberg-Teller and Duschinsky effects. However, to the best of our knowledge, the complete derivation has not been described as a whole, hindering its implementation.^56,57 Our derivation will not be based on any of the previous works because we will not introduce any further approximation besides the restriction of initial- and final- state PESs at the harmonic level. Furthermore, band broadening has been taken into the proper account, all kind of one photon spectroscopies (absorption, emission and ECD) have been included, and temperature effects have been considered. The implementation of the whole method within the same framework as the previous time-independent approach allows direct comparison between the two approaches under the same conditions and their combined use to couple their advantages and minimize their respective limits. Ease of use (user-friendliness and minimal input), effective inclusion of environmental effects (by both polarizable continuum models and/or polarizable force fields), numerical stability and computational efficiency have been also taken into account during the development also thanks to the inclusion of the whole procedure within a general-purpose QM code.

The paper is organized as follows. The derivation of the time-dependent formulation is discussed in the first section, together with the simulation broadening, and some concluding remarks are made regarding the numeric stability of the calculations. This is followed by a description of the computational details regarding the simulation of time-dependent and time-independent spectra. Then, to illustrate the reliability and accuracy of our time-dependent model, comparison with experimental spectra and the well-tested time-independent version will be done, using anthracene and furan as test studies. Several medium-sized systems, dimethyloxirane, coumarin 339 and the phenyl radical, will serve as examples to show some aspects of the versatility of our procedure, able to easily account for environment effects and to support multiple electronic spectroscopies.

2. Theory

2.1. General theory of vibronic spectroscopy

Following our previous works on time-independent vibronic spectroscopy,^33,34 we present here an extension of the procedure described previously including the time-dependent formulation. In this way, it is possible to use all the existing machinery, in particular the generalized definition for the transition intensity for one-photon absorption (OPA), emission (OPE) and electronic circular dichroism (ECD),

$$I=\alpha {\omega }^{\beta }{\displaystyle \sum _m{\displaystyle \sum _n{\rho }_{\gamma }}}{\mathit{d}}_{mn}^{\text{A}}{\mathit{d}}_{mn}^{\text{B}}{}^{*}\delta \left(\frac{E_n-E_m}{ħ}-\omega \right)$$ (1)

where ω is the frequency of the incident (OPA, ECD) or emitted (OPE) photon, ρ is the Boltzmann population, δ is the Dirac function, and the double summation runs over all the lower- (m) and higher- (n) energy states. I, α, β, γ, ${\mathit{d}}_{mn}^{\text{A}}$ and ${\mathit{d}}_{mn}^{\text{B}}$ depend on the kind of spectroscopy, following the equivalency table below,

$$\begin{array}{l}\text{OPA}:I=ϵ\left(\omega \right),\alpha =\frac{10\pi {𝒩}_A}{3{ϵ}_0\text{ln}\left(10\right)ħc},\beta =1,\gamma =m,{\mathit{d}}_{mn}^{\text{A}}={\mathit{d}}_{mn}^{\text{B}}={\mathit{\mu }}_{mn}\\ \text{OPE}:I=I_{em}/N_n,\alpha =\frac{2{𝒩}_A}{3{ϵ}_0{c}^3},\beta =4,\gamma =n,{\mathit{d}}_{mn}^{\text{A}}={\mathit{d}}_{mn}^{\text{B}}={\mathit{\mu }}_{mn}\\ \text{ECD}:I=\Delta ϵ\left(\omega \right),\alpha =\frac{40{𝒩}_A\pi }{3{ϵ}_0\text{ln}\left(10\right)ħc^2},\beta =1,\gamma =m,{\mathit{d}}_{mn}^{\text{A}}={\mathit{\mu }}_{mn},{\mathit{d}}_{mn}^{\text{B}}=\Im \left({\mathit{m}}_{mn}\right)\end{array}$$

where ϵ(ω) is the molar absorption coefficient for a given angular frequency ω, Δϵ(ω) is the difference (referred to as anisotropy) between the molar absorption coefficients ϵ⁻ and ϵ⁺ relative to the left and right circularly polarized light, respectively, and I_em/N_n is the energy emitted by one mole per second.

${\mathit{d}}_{mn}^{\text{A}}$ and ${\mathit{d}}_{mn}^{\text{B}}$ are respectively the transition moments of d^A and d^B between the lower and higher electronic states. Since d^A and d^B are generic in eq. 1, the following discussion will be done on a symbolic property d^X, which can represent indifferently each of them.

$${\mathit{d}}_{mn}^{\text{X}}=\langle {\Psi }_m|{\mathit{d}}^{\text{X}}|{\Psi }_n\rangle \approx \langle {\chi }_{r(\underset{¯}{m})}|{\mathit{d}}_{e,mn}^{\text{X}}|{\chi }_{s(\underset{¯}{n})}\rangle$$ (2)

where r(m) respresents the vibrational state r associated to the electronic state m for the total lower molecular state m, and s(n) its counterpart for the total higher molecular state n. Ψ and χ are the total and vibrational wave functions, respectively. Finally, ${\mathit{d}}_{e,mn}^{\text{X}}$ is the electronic transition moment, ${\mathit{d}}_{e,mn}^{\text{X}}=\langle {\varphi }_{\underset{¯}{m}}|{\mathit{d}}^{\text{X}}|{\varphi }_{\underset{¯}{n}}\rangle$

The main issue in using equation 1 is that no analytic expression for the electronic transition moment is known. In practice, a Taylor series with respect to the mass-weighted normal coordinates Q about the equilibrium geometry of one of the electronic state is used,

$${\mathit{d}}_{e,mn}^{\text{X}}\left(\mathit{Q}\right)={\mathit{d}}_{e,mn}^{\text{X}}\left({\mathit{Q}}_{\text{eq}}\right)+{\displaystyle \sum _{i=1}^N{\left(\frac{\partial {\mathit{d}}_{e,mn}^{\text{X}}}{\partial Q_i}\right)}_0{Q}_i+\dots }$$ (3)

The development is commonly limited to the first two terms in the rhs, with the zeroth-order term corresponding to the Franck-Condon approximation^58–61 and the first-order correction to the Herzberg-Teller approximation.⁶²

Finally, the simulation of vibronic spectra requires the calculation of the overlap integrals, which depend on both the normal modes of the initial and the final states. To carry out the integration, we will use the linear transformation proposed by Duschinsky⁶³ to express the two set of coordinates with respect to one another,

$$\overline{\mathit{Q}}=\mathit{J}\overline{\overline{\mathit{Q}}}+\mathit{K}$$ (4)

where Q̄ and Q̿ are the normal coordinates of the initial (symbolized by one overline in the following) and final (symbolized by two overlines) states, respectively. J is the Duschinsky matrix and K is the shift vector. The expressions of J and K differ depending on the model used to describe the electronic transition (adiabatic, vertical) and the level of approximation (both potential energy surfaces assumed equal or not). More detailed discussions on these approaches and their impact on the Duschinsky transformation are available in Refs.^32,34 and references therein.

2.2. Time-dependent theory: Franck-Condon approximation

The starting point of the time-dependent theory of vibronic spectroscopy is the sum-over-states formula given in Eq. 1. In the following, we consider the case of a photon absorption (OPA, ECD) between two uncoupled electronic states. In practice, this means that the initial state is the lower-energy one (m), the final state is the higher-energy one (n), and the double summation in eq. 1 is carried out over the vibrational states of each electronic state. For the transition dipole, the part of the subscript indicating the electronic states will be dropped so only the subscript e indicating the electronic transition dipole moment will remain.

The basic idea to switching from the sum-over-states problem to a time-dependent problem is to use the definition of the Dirac distribution function,

$$\delta (\omega )=\frac{1}{2\pi }{\displaystyle {\int }_{-\infty }^{+\infty }{e}^{i\omega t}}dt$$ (5)

By replacing the Dirac delta function in Eq. 1 with the previous expression we obtain:

$$I=\frac{\alpha {\omega }^{\beta }}{Z}{\displaystyle \sum _j{\displaystyle \sum _k{e}^{-\frac{{\overline{\epsilon }}_j}{k_{B}T}}}}\langle {\overline{\chi }}_j|{\mathit{d}}_e^{\text{A}}|{\overline{\overline{\chi }}}_k\rangle \langle {\overline{\overline{\chi }}}_k|{{\mathit{d}}_e^{\text{B}}}^{*}|{\overline{\chi }}_j\rangle {\displaystyle {\int }_{-\infty }^{+\infty }{e}^{i\left[\frac{{\overline{\overline{E}}}_k-{\overline{E}}_j}{ħ}-\omega \right]t}dt}$$ (6)

Ē_j and E̿_k are the total energies of the initial and the final vibrational states, respectively, ε̄_j represents the vibrational energy and Z is the total Boltzmann population of the vibrational levels of the ground states. Under the harmonic approximation, Z can be expressed in the following way:

$$Z={\displaystyle \prod _{j=1}^N{\displaystyle \sum _{n_j=1}^{+\infty }{e}^{-ħ{\overline{\omega }}_j\left(n_j+\frac{1}{2}\right)/k_{B}T}}}$$ (7)

The infinite sum can be carried out thanks to the well-known formula for the sum of a geometric series. The result is the following:

$$Z={\displaystyle \prod _{j=1}^N\frac{e^{-\frac{ħ{\overline{\omega }}_i}{2k_{B}T}}}{1-e^{-\frac{ħ{\overline{\omega }}_i}{k_{B}T}}}}={{\displaystyle \prod _{i=1}^N\left[2\text{sinh}\left(\frac{ħ{\omega }_i}{2k_{B}T}\right)\right]}}^{-1}$$ (8)

Since Z is a constant, we can integrate it in α and will use from now on the constant factor α′ = α/Z.

The difference “E̿_k – Ē_j ” can be rewritten as E_ad + ε̿_k – ε̄_j where E_ad = ħω_ad is the energy gap between the vibrational ground states of the initial and final states.

$$I={\alpha }^{\prime }{\omega }^{\beta }{\displaystyle {\int }_{-\infty }^{+\infty }dt{\displaystyle \sum _{jk}{e}^{-\frac{{\overline{\epsilon }}_j}{k_{B}T}}}}\langle {\overline{\chi }}_j|{\mathit{d}}_e^{\text{A}}|{\overline{\overline{\chi }}}_k\rangle \langle {\overline{\overline{\chi }}}_k|{{\mathit{d}}_e^{\text{B}}}^{*}|{\overline{\chi }}_j\rangle e^{i\frac{{\overline{\overline{\epsilon }}}_k}{ħ}t}{e}^{-\frac{{\overline{\epsilon }}_j}{ħ}t}{e}^{i\left({\omega }_{\text{ad}}-\omega \right)t}$$ (9)

Since ε̄_j and ε̿_k are eigenvalues of their respective vibrational Hamiltonians, the equation can be expressed in terms of exponential operators as follows,

$$I={\alpha }^{\prime }{\omega }^{\beta }{\displaystyle {\int }_{-\infty }^{+\infty }dt{\displaystyle \sum _{jk}\langle {\overline{\chi }}_j|{\mathit{d}}_e^{\text{A}}{e}^{-\overline{\overline{\tau }}\overline{\overline{H}}}|{\overline{\overline{\chi }}}_k\rangle \langle {\overline{\overline{\chi }}}_k|{{\mathit{d}}_e^{\text{B}}}^{*}{e}^{-\overline{\tau }\overline{H}}|{\overline{\chi }}_j\rangle e^{i\left(E_{\text{ad}}-\omega \right)t}}}$$ (10)

where τ̄ and τ̿ are defined as,

$$\begin{array}{ccc}\overline{\tau }=\frac{1}{k_{B}T}-\frac{it}{ħ}& ;& \overline{\overline{\tau }}\end{array}=\frac{it}{ħ}$$

The vibrational eigenstates of the excited electronic states form a complete basis, so the closure relation holds on them:

$${\displaystyle \sum _k|{\overline{\overline{\chi }}}_k\rangle \langle {\overline{\overline{\chi }}}_k|}=1$$

This formula can be used in order to simplify Eq. 10 as follows:

$$I={\alpha }^{\prime }{\omega }^{\beta }{\displaystyle {\int }_{-\infty }^{+\infty }dt{\displaystyle \sum _j\langle {\overline{\chi }}_j|{\mathit{d}}_e^{\text{A}}{e}^{-\overline{\overline{\tau }}\overline{\overline{H}}}{{\mathit{d}}_e^{\text{B}}}^{*}{e}^{-\overline{\tau }\overline{H}}|{\overline{\chi }}_j\rangle e^{i\left({\omega }_{\text{ad}}-\omega \right)t}}}$$ (11)

The eigenstates |χ̄_j) form another orthonormal basis set, so the sum over j can be written as a trace. To summarize, the absorption spectrum can be calculated as a Fourier transform of the trace of the following exponential operator,

$$I={\alpha }^{\prime }{\omega }^{\beta }{\displaystyle {\int }_{-\infty }^{+\infty }dt\text{Tr}\left({\mathit{d}}_e^{\text{A}}{e}^{-\overline{\overline{\tau }}\overline{\overline{H}}}{{\mathit{d}}_e^{\text{B}}}^{*}{e}^{-\overline{\tau }\overline{H}}\right)e^{i\left({\omega }_{\text{ad}}-\omega \right)t}}$$ (12)

$$={\alpha }^{\prime }{\omega }^{\beta }{\displaystyle {\int }_{-\infty }^{+\infty }dt\chi \left(t\right)e^{i\left({\omega }_{\text{ad}}-\omega \right)t}}$$ (13)

In order to calculate the trace, an appropriate basis set must be chosen. By using the continuous basis set formed by the normal coordinates of the initial state (Q̄), χ(t) can be expressed as,

$$\chi \left(t\right)={\displaystyle {\int }_{-\infty }^{+\infty }d\overline{\mathit{Q}}}\langle \overline{\mathit{Q}}|{\mathit{d}}_e^{\text{A}}{e}^{-\overline{\overline{\tau }}\overline{\overline{H}}}{\mathit{d}}_e^{\text{B}}{e}^{-\overline{\tau }\overline{H}}|\overline{\mathit{Q}}\rangle$$ (14)

By introducing Eqs. 5 and 6 in Eq. 14, we obtain,

$$\begin{array}{l}\chi \left(t\right)={\mathit{d}}_{e,if}^A\left({\overline{\overline{\mathbf{\text{Q}}}}}_{eq}\right){\mathit{d}}_{e,if}^B\left({\overline{\overline{\mathbf{\text{Q}}}}}_{eq}\right)+{{\displaystyle \sum _{k=1}^N\left(\frac{\partial {\mathit{d}}_e^{\text{A}}}{\partial {\overline{\overline{\text{Q}}}}_k}\right)}}_0{\mathit{d}}_{e,if}^B\left({\overline{\overline{\mathbf{\text{Q}}}}}_{eq}\right)\langle \overline{\mathit{Q}}|{\overline{\overline{Q}}}_k^{\circ }{e}^{-\overline{\overline{\tau }}\overline{\overline{H}}}{e}^{-\overline{\tau }\overline{H}}|\overline{\mathit{Q}}\rangle \\ +{{\displaystyle \sum _{k=1}^N\left(\frac{\partial {\mathit{d}}_e^{\text{B}}}{\partial {\overline{\overline{\text{Q}}}}_k}\right)}}_0{\mathit{d}}_{e,if}^A\left({\overline{\overline{\mathbf{\text{Q}}}}}_{eq}\right)\langle \overline{\mathit{Q}}|e^{-\overline{\overline{\tau }}\overline{\overline{H}}}{\overline{\overline{Q}}}_k^{\circ }{e}^{-\overline{\tau }\overline{H}}|\overline{\mathit{Q}}\rangle \\ +{{\displaystyle \sum _{kl=1}^N\left(\frac{\partial {\mathit{d}}_e^{\text{A}}}{\partial {\overline{\overline{\text{Q}}}}_k}\right)}}_0{\left(\frac{\partial {\mathit{d}}_e^{\text{B}}}{\partial {\overline{\overline{\text{Q}}}}_l}\right)}_0\langle \overline{\mathit{Q}}|{\overline{\overline{Q}}}_k^{\circ }{e}^{-\overline{\overline{\tau }}\overline{\overline{H}}}{\overline{\overline{Q}}}_l^{\circ }{e}^{-\overline{\tau }\overline{H}}|\overline{\mathit{Q}}\rangle \end{array}$$ (15)

where ${\overline{\overline{Q}}}_k^{\circ }$ is the operator associated to the k-th final-state normal coordinate.

Under the Franck-Condon approximation, only the first term of the previous summation remains. For this case, we will employ the derivation presented by Lin and co-workers⁵² to obtain an analytic expression for χ(t).

In Eq. 15, we introduce an additional set of orthonormal coordinates for the initial state Q̄′ and two of them for the final state Q̿ and Q̿′, which all verify the closure relation

$${\displaystyle {\int }_{-\infty }^{+\infty }d}{\overline{\mathit{Q}}}^{\prime }|{\overline{\mathit{Q}}}^{\prime }\rangle \langle {\overline{\mathit{Q}}}^{\prime }|={\displaystyle {\int }_{-\infty }^{+\infty }d\overline{\overline{\mathit{Q}}}|\overline{\overline{\mathit{Q}}}\rangle \langle \overline{\overline{\mathit{Q}}}|={\displaystyle {\int }_{-\infty }^{+\infty }d{\overline{\overline{\mathit{Q}}}}^{\prime }|}{\overline{\overline{\mathit{Q}}}}^{\prime }\rangle \langle }{\overline{\overline{\mathit{Q}}}}^{\prime }|=1$$ (16)

Using this relationship, Eq. 14 can be rewritten in the following way,

$$\chi \left(t\right)={\displaystyle {\int }_{-\infty }^{+\infty }d\overline{\mathit{Q}}}{\displaystyle {\int }_{-\infty }^{+\infty }d\overline{\overline{\mathit{Q}}}}{\displaystyle {\int }_{-\infty }^{+\infty }d{\overline{\mathit{Q}}}^{\prime }}{\displaystyle {\int }_{-\infty }^{+\infty }d{\overline{\overline{\mathit{Q}}}}^{\prime }}\langle \overline{\mathit{Q}}|\overline{\overline{\mathit{Q}}}\rangle \langle \overline{\overline{\mathit{Q}}}|e^{-\overline{\overline{\tau }}\overline{\overline{H}}}|{\overline{\overline{\mathit{Q}}}}^{\prime }\rangle \langle {\overline{\overline{\mathit{Q}}}}^{\prime }|{\overline{\mathit{Q}}}^{\prime }\rangle \langle {\overline{\mathit{Q}}}^{\prime }|e^{-\overline{\tau }\overline{H}}|\overline{\mathit{Q}}\rangle$$ (17)

Let us introduce the auxiliary matrices a, b, c, d whose elements are defined as,

$$\begin{array}{ll}{\overline{\text{c}}}_{ij}=\frac{{\overline{\omega }}_i}{ħ}\text{coth}\left(\frac{{\overline{\omega }}_iħ\overline{\tau }}{2}\right){\delta }_{ij}\hfill & {\overline{\overline{\text{c}}}}_{ij}=\frac{{\overline{\overline{\omega }}}_i}{ħ}\text{coth}\left(\frac{{\overline{\overline{\omega }}}_iħ\overline{\overline{\tau }}}{2}\right){\delta }_{ij}\hfill \\ {\overline{\text{d}}}_{ij}=\frac{{\overline{\omega }}_i}{ħ}\text{tanh}\left(\frac{{\overline{\omega }}_iħ\overline{\tau }}{2}\right){\delta }_{ij}\hfill & {\overline{\overline{\text{d}}}}_{ij}=\frac{{\overline{\overline{\omega }}}_i}{ħ}\text{tanh}\left(\frac{{\overline{\overline{\omega }}}_iħ\overline{\overline{\tau }}}{2}\right){\delta }_{ij}\hfill \\ \hfill {\overline{\text{a}}}_{ij}=\frac{{\overline{\omega }}_i}{\text{sinh}\left(ħ\overline{\tau }{\overline{\omega }}_i\right)}{\delta }_{ij}\hfill & {\overline{\overline{\text{a}}}}_{ij}=\frac{{\overline{\overline{\omega }}}_i}{\text{sinh}\left(ħ\overline{\overline{\tau }}{\overline{\overline{\omega }}}_i\right)}{\delta }_{ij}\hfill \\ \hfill {\overline{\text{b}}}_{ij}=\frac{{\overline{\omega }}_i}{\text{tanh}\left(ħ\overline{\tau }{\overline{\omega }}_i\right)}{\delta }_{ij}\hfill & {\overline{\overline{\text{b}}}}_{ij}=\frac{{\overline{\overline{\omega }}}_i}{\text{tanh}\left(ħ\overline{\overline{\tau }}{\overline{\overline{\omega }}}_i\right)}{\delta }_{ij}\hfill \end{array}$$

Two supplementary matrices, C and D, will also be used,

$$\mathit{C}=\overline{\overline{\mathit{c}}}+{\mathit{J}}^{\text{T}}\overline{\mathit{c}}\mathit{J}\mathit{D}=\overline{\overline{\mathit{d}}}+{\mathit{J}}^{\text{T}}\overline{\mathit{d}}\mathit{J}$$

The matrix elements of the exponential Hamiltonian operator between two coordinate vectors play a key role in the Feynmann’s path integral formulation of quantum mechanics, and they have been calculated for several hamiltonian operators. One of them is the multidimensional harmonic oscillator hamiltonian H̄_harm:

$$\langle \overline{\mathit{Q}}|e^{-{\overline{H}}_{\text{har}{\text{m}}^{\tau }}}|\overline{\mathit{Q}}\prime \rangle =\sqrt{\frac{\text{det}\left(\overline{\mathit{a}}\right)}{{\left(2\pi ħ\right)}^N}}\text{exp}\left(\frac{i}{ħ}\left[\frac{1}{2}{\overline{\mathit{Q}}}^{\text{T}}\overline{\mathit{b}}\overline{\mathit{Q}}+\frac{1}{2}\overline{\mathit{Q}}{\prime }^{\text{T}}\overline{\mathit{b}}\overline{\mathit{Q}}\prime -\overline{\mathit{Q}}{\prime }^{\text{T}}\overline{\mathit{a}}\overline{\mathit{Q}}\right]\right)$$ (18)

The same relationship holds also for the excited-state normal coordinates.

Since Q̄ and Q̿ are orthonormal, the following equality holds,

$${\displaystyle {\int }_{-\infty }^{+\infty }\langle \overline{\mathit{\text{Q}}}|\overline{\overline{\mathit{\text{Q}}}}\rangle =\delta \left(\overline{\mathit{\text{Q}}}-\mathit{\text{J}}\overline{\overline{\mathit{\text{Q}}}}-\mathit{\text{K}}\right)}$$ (19)

The same equality holds also for the primed coordinates.

Introducing Eq. 18 in Eq. 17, the integration can be carried out over the initial-state normal modes, leading to a new formulation of the autocorrelation function,

$$\begin{array}{l}\chi \left(t\right)=\sqrt{\frac{\text{det}\left(\overline{\mathit{a}}\overline{\overline{\mathit{a}}}\right)}{{\left(2\pi iħ\right)}^{2N}}}{\displaystyle \int d\overline{\overline{\mathit{Q}}}}{\displaystyle \int d{\overline{\overline{\mathit{Q}}}}^{\prime }}\text{exp}\left(\frac{i}{ħ}\left[\frac{1}{2}{\overline{\overline{\mathit{Q}}}}^{\text{T}}\overline{\overline{\mathit{b}}}\overline{\overline{\mathit{Q}}}+\frac{1}{2}{\overline{\overline{\mathit{Q}}}}^{\prime \text{T}}\overline{\overline{\mathit{b}}}{\overline{\overline{\mathit{Q}}}}^{\prime }-{\overline{\overline{\mathit{Q}}}}^{\text{T}}\overline{\overline{\mathit{a}}}{\overline{\overline{\mathit{Q}}}}^{\prime }\right]\right)\\ \times \text{exp}\{\frac{i}{ħ}[\frac{1}{2}\left({\mathit{K}}^{\text{T}}+{\overline{\overline{\mathit{Q}}}}^{\prime \text{T}}{\mathit{J}}^{\text{T}}\right)\overline{\mathit{b}}\left(\mathit{J}{\overline{\overline{\mathit{Q}}}}^{\prime }+\mathit{K}\right)+\frac{1}{2}\left({\mathit{K}}^{\text{T}}+{\overline{\overline{\mathit{Q}}}}^{\text{T}}{\mathit{J}}^{\text{T}}\right)\overline{\mathit{b}}\left(\mathit{J}\overline{\overline{\mathit{Q}}}+\mathit{K}\right)\\ -\left({\mathit{K}}^{\text{T}}+{\overline{\overline{\mathit{Q}}}}^{\text{T}}{\mathit{J}}^{\text{T}}\right)\overline{\mathit{a}}\left(\mathit{J}{\overline{\overline{\mathit{Q}}}}^{\prime }+\mathit{K}\right)]\}\end{array}$$ (20)

The previous equation can be simplified by introducing two new sets of coordinates, U and Z, and by replacing ā, a̿, b̄, b̿ with c̄, c̿, d̄, d̿:

$$\begin{array}{l}\mathit{\text{Z}}=\frac{1}{\sqrt{2}}(\overline{\overline{\mathit{\text{Q}}}}+{\overline{\overline{\mathit{\text{Q}}}}}^{\prime })\\ \mathit{\text{U}}=\frac{1}{\sqrt{2}}(\overline{\overline{\mathit{\text{Q}}}}-{\overline{\overline{\mathit{\text{Q}}}}}^{\prime })\end{array}$$

$$\chi (t)=\sqrt{\frac{\text{det}\left(\overline{\mathit{\text{a}}}\overline{\overline{\mathit{\text{a}}}}\right)}{{\left(2\pi iħ\right)}^{2N}}}\text{exp}\left(-{\mathit{\text{K}}}^{\text{T}}\overline{\mathit{\text{d}}}\mathit{\text{K}}\right){\displaystyle \int d\mathit{\text{U}}}{\displaystyle \int d\mathit{\text{Z}}\text{exp}\left(-\frac{1}{2}{\mathit{\text{Z}}}^{\text{T}}\mathit{\text{D}}\mathit{\text{Z}}-\sqrt{2}{\mathit{\text{υ}}}^{\text{T}}\mathit{\text{Z}}\right)\times \text{exp}\left(-\frac{1}{2}{\mathit{\text{U}}}^{\text{T}}\mathit{\text{C}}\mathit{\text{U}}\right)}$$ (21)

where υ^T = K^Td̄J.

Using the well-known analytic expression for a multidimensional gaussian-type integral,

$${\displaystyle {\int }_{-\infty }^{+\infty }{d}^{N}x{e}^{-x^T\mathit{B}\mathit{x}+{\mathit{\text{υ}}}^T\mathit{x}}=\frac{{\left(\sqrt{\pi }\right)}^N}{{(\det \mathit{\text{B}})}^{1/2}}\text{exp}\left(\frac{1}{4}{\mathit{\text{υ}}}^T{\mathit{B}}^{-1}\mathit{\text{υ}}\right)}$$

it is possible to derive this final expression for the autocorrelation function under the Franck-Condon approximation,

$${\chi }_{FC}(t)=\sqrt{\frac{\det (\overline{\mathit{\text{a}}}\overline{\overline{\mathit{\text{a}}}})}{{(iħ)}^{2N}\det (\mathit{\text{C}}\mathit{\text{D}})}}\times \text{exp}(-{\mathit{\text{K}}}^{\text{T}}\overline{\mathit{\text{d}}}\mathit{\text{K}}+{\mathit{\text{υ}}}^{\text{T}}{\mathit{\text{D}}}^{-1}\mathit{\text{υ}})$$ (22)

2.3. Extension to the Herzberg-Teller case

Let us consider now the more general case including first-order terms in the Taylor expansion of the transition dipole moment. The corresponding autocorrelation function has been given in Eq. 15 and its evaluation requires to make the successive terms in the rhs explicit.

Let us start with the second term in the rhs of Eq. 15, $\langle \overline{\mathit{\text{Q}}}|{\overline{\overline{Q}}}_k^{\circ }{e}^{-\overline{\overline{\tau }}\overline{\overline{H}}}{e}^{-\overline{\tau }\overline{H}}|\overline{\mathit{\text{Q}}}\rangle .$ By using the same technique as for the Franck-Condon approximation this term can be rewritten as,

$${\displaystyle \int d\overline{\mathit{\text{Q}}}}{\displaystyle \int d{\overline{\mathit{\text{Q}}}}^{\prime }{\displaystyle \int d\overline{\overline{\mathit{\text{Q}}}}}}{\displaystyle \int d{\overline{\overline{\mathit{\text{Q}}}}}^{\prime }}\langle \overline{\mathit{\text{Q}}}|\overline{\overline{\mathit{\text{Q}}}}\rangle \langle \overline{\overline{\mathit{\text{Q}}}}|{\overline{\overline{Q}}}_k^{°}{e}^{-\overline{\overline{\tau }}\overline{\overline{H}}}|{\overline{\overline{\mathit{\text{Q}}}}}^{\prime }\rangle \langle {\overline{\overline{\mathit{\text{Q}}}}}^{\prime }|{\overline{\mathit{\text{Q}}}}^{\prime }\rangle \langle {\overline{\mathit{\text{Q}}}}^{\prime }|e^{-\overline{\tau }\overline{H}}|\overline{\mathit{\text{Q}}}\rangle$$ (23)

${\overline{\overline{Q}}}_k^{°}$ can be taken out of the trace since 〈Q̿_k | is an eigenbra of this operator with eigenvalue Q̿_k. As a consequence, the integrand must be simply scaled by a factor Q̿_k. After rewriting this factor in terms of U and Z the integral can be expressed as,

$$\langle \overline{\mathit{Q}}|{\overline{\overline{Q}}}_k{e}^{-\overline{\overline{\tau }}\overline{\overline{H}}}{e}^{-\overline{\tau }\overline{H}}|\overline{\mathit{\text{Q}}}\rangle =\frac{1}{\sqrt{2}}\langle \overline{\mathit{\text{Q}}}|({\text{U}}_k+{\text{Z}}_k)e^{-\overline{\overline{\tau }}\overline{\overline{H}}}{e}^{-\overline{\tau }\overline{H}}|\overline{\mathit{\text{Q}}}\rangle$$ (24)

Let us consider the autocorrelation function at the Franck-Condon level χ_FC¹ given in Eq. 21. By definition of the exponential function, the following equality holds,

$$\frac{{\partial \chi }_{\text{FC}}}{\partial {\text{v}}_k}=-\sqrt{2}\langle \overline{\mathit{\text{Q}}}|{\text{Z}}_k{e}^{-\overline{\overline{\tau }}\overline{\overline{H}}}{e}^{-\overline{\tau }\overline{H}}|\overline{\mathit{\text{Q}}}\rangle$$ (25)

where the derivative is calculated with respect to the k-th element of υ.

The integral containing U_k is null by symmetry since the integrand is odd with respect to U_k. The final result is thus,

$$\langle \overline{\mathit{Q}}|{\overline{\overline{Q}}}_k^{\circ }{e}^{-\overline{\overline{\tau }}\overline{\overline{H}}}{e}^{-\overline{\tau }\overline{H}}|\overline{\mathit{Q}}\rangle =-\frac{1}{2}\frac{\partial {\chi }_{\text{FC}}}{\partial {\text{v}}_k}$$ (26)

The calculation of the third term in the rhs of Eq. 15, $\langle \overline{\mathit{Q}}|e^{-\overline{\overline{\tau }}\overline{\overline{H}}}{\overline{\overline{Q}}}_k^{\circ }{e}^{-\overline{\tau }\overline{H}}|\overline{\mathit{Q}}\rangle ,$ is similar to the previous one. A slight difference is that, after application of the closure relation, ${\overline{\overline{Q}}}_k^{\circ }$ will act on | Q̿′ 〉 instead of 〈 Q̄ | with eigenvalue ${\overline{\overline{Q}}}_k^{\prime },$

$$\langle \overline{\mathit{Q}}|e^{-\overline{\overline{\tau }}\overline{\overline{H}}}{\overline{\overline{Q}}}_k^{\circ }{e}^{-\overline{\tau }\overline{H}}|\overline{\mathit{Q}}\rangle =\frac{1}{\sqrt{2}}\langle \overline{\mathit{Q}}|e^{-\overline{\overline{\tau }}\overline{\overline{H}}}\left({\text{Z}}_k-{\text{U}}_k\right)e^{-\overline{\tau }\overline{H}}|\overline{\mathit{Q}}\rangle$$ (27)

However, the final result is the same as in Eq. 25 because the integral containing U_k is null. The extension of the previous method to the fourth term in the rhs of Eq. 15 is straightforward.

$$\langle \overline{\mathit{\text{Q}}}|{\overline{\overline{Q}}}_k^{\circ }{e}^{-\overline{\overline{\tau }}\overline{\overline{H}}}{\overline{\overline{Q}}}_l^{\circ }{e}^{-\overline{\tau }\overline{H}}|\overline{\mathit{\text{Q}}}\rangle =\frac{1}{2}\langle \overline{\mathit{\text{Q}}}|\left(Z_k+U_k\right)e^{-\overline{\overline{\tau }}\overline{\overline{H}}}\left(Z_l-U_l\right)e^{-\overline{\tau }\overline{H}}|\overline{\mathit{\text{Q}}}\rangle$$ (28)

By taking into account that terms with odd powers of U_k are null by symmetry, Eq. 28 can be rewritten in terms of the derivatives of χ_FC with respect to the elements of υ and C in the following way:

$$\langle \overline{\mathit{\text{Q}}}|{\overline{\overline{Q}}}_k^{\circ }{e}^{-\overline{\overline{\tau }}\overline{\overline{H}}}{\overline{\overline{Q}}}_l^{\circ }{e}^{-\overline{\tau }\overline{\overline{H}}}|\overline{\mathit{\text{Q}}}\rangle =\frac{\partial {\chi }_{\text{FC}}}{\partial {\text{C}}_{kl}}+\frac{1}{4}\frac{{\partial }^2{\chi }_{\text{FC}}}{\partial {\text{v}}_k\partial {\text{v}}_l}$$ (29)

Please note that only the real part of the matrix elements is used in the derivations. For the sake of readibility, the real-part symbol will be omitted, so that ∂χ_FC/∂v_k is intended to be read as ∂χ_FC/∂ℜ(v_k). The same holds for the derivatives with respect to elements of C. The derivatives of χ_FC can be expressed, starting from eq. 22, in the following way: ²

$$\frac{\partial {\chi }_{\text{FC}}}{\partial {\text{v}}_k}={\chi }_{\text{FC}}\left[{\displaystyle \sum _{𝜚=1}^N{{\text{D}}_{k𝜚}}^{-1}{\text{v}}_{𝜚}}+{\displaystyle \sum _{𝜚=1}^N{{\text{D}}_{𝜚k}}^{-1}{\text{v}}_{𝜚}^{*}}\right]$$ (30)

$$\frac{\partial {\chi }_{\text{FC}}}{\partial {\text{C}}_{kl}}=-\frac{1}{2}{\chi }_{\text{FC}}{{\text{C}}_{kl}}^{-1}$$ (31)

$$\begin{array}{l}\frac{{\partial }^2{\chi }_{\text{FC}}}{\partial {\text{v}}_k\partial {\text{v}}_l}={\chi }_{\text{FC}}\left[{\displaystyle \sum _{𝜚=1}^N{{\text{D}}_{k𝜚}}^{-1}{\text{v}}_{𝜚}+{\displaystyle \sum _{𝜚=1}^N{{\text{D}}_{𝜚k}}^{-1}{\text{v}}_{𝜚}^{*}}}\right]\left[{\displaystyle \sum _{𝜚=1}^N{{\text{D}}_{l𝜚}}^{-1}{\text{v}}_{𝜚}}+{\displaystyle \sum _{𝜚=1}^N{{\text{D}}_{𝜚l}}^{-1}{\text{v}}_{𝜚}^{*}}\right]\\ +{\chi }_{\text{FC}}\left({{\text{D}}_{kl}}^{-1}+{{\text{D}}_{lk}}^{-1}\right)\end{array}$$ (32)

2.4. A special case: T=0 K

One of the most important advantages of the time-dependent formulation is the possibility to include automatically temperature effects without any additional computational cost. On the contrary, in the time-independent framework the computational time increases very rapidly because of the large number of overlap integrals to compute.

However, the formulas derived in the previous part suffer from a poor numerical stability in the case of low temperatures related to the Boltzmann factor with a discontinuity for T=0 K. At such temperatures, the vibrational ground state of the initial electronic state is far more populated than the other states, which can be safely neglected. Let us assume that only the vibrational ground state | χ̄₀ 〉 is populated and ρ₀ = 1.

$$I=\alpha {\omega }^{\beta }{\displaystyle {\int }_{-\infty }^{+\infty }dt}{\displaystyle \sum _k\langle {\overline{\chi }}_0|{\mathit{d}}_e^{\text{A}}|{\overline{\overline{\chi }}}_k\rangle \langle {\overline{\overline{\chi }}}_k|{\mathit{d}}_e^{\text{B}*}|{\overline{\chi }}_0\rangle e^{i\frac{{\overline{\overline{\epsilon }}}_k}{ħ}t}{e}^{i({\omega }_{\text{ad}}-\omega )t}}$$ (33)

Similarly to the previous derivation, we introduce the vibrational hamiltonian,

$$I=\alpha {\omega }^{\beta }{\displaystyle {\int }_{-\infty }^{+\infty }dt}{\displaystyle \sum _k\langle {\overline{\chi }}_0|{\mathit{d}}_e^{\text{A}}|{\overline{\overline{\chi }}}_k\rangle \langle {\overline{\overline{\chi }}}_k|e^{\frac{i\overline{\overline{H}}t}{ħ}}{\mathit{d}}_e^{\text{B}*}|{\overline{\chi }}_0\rangle e^{i({\omega }_{\text{ad}}-\omega )t}}$$ (34)

$$=\alpha {\omega }^{\beta }{\displaystyle {\int }_{-\infty }^{+\infty }dt}\langle {\overline{\chi }}_0|{\mathit{d}}_e^{\text{A}}{e}^{\frac{i\overline{\overline{H}}t}{ħ}}{\mathit{d}}_e^{\text{B}*}|{\overline{\chi }}_0\rangle e^{i({\omega }_{\text{ad}}-\omega )t}$$ (35)

In this case, the autocorrelation function can be written as,

$$\mathbf{\chi }(t)=\langle {\overline{\chi }}_0|{\mathit{d}}_e^{\text{A}}{e}^{\frac{i\overline{\overline{H}}t}{ħ}}{\mathit{d}}_e^{\text{B}*}|{\overline{\chi }}_0\rangle$$ (36)

As previously, we introduce Q̿ and Q̿′, two sets of coordinates of the final state,

$$\chi (t)={\displaystyle {\int }_{-\infty }^{+\infty }d\overline{\overline{\mathit{\text{Q}}}}}{\displaystyle {\int }_{-\infty }^{+\infty }d\overline{\mathit{\text{Q}}}}\langle {\overline{\chi }}_0|\overline{\overline{{\mathit{\text{Q}}}^{\prime }}}\rangle \langle \overline{\overline{\mathit{\text{Q}}}}|e^{-\overline{\overline{\tau }}\overline{\overline{H}}}|\overline{\overline{\mathit{\text{Q}}}}\rangle \langle \overline{\overline{\mathit{\text{Q}}}}|{\overline{\chi }}_0\rangle$$ (37)

Using Eq. 18, the autocorrelation function can be expressed as,

$$\begin{array}{l}\chi (t)=\sqrt{\frac{\det \overline{\overline{\mathit{\text{a}}}}}{{(2\pi ħ)}^N}}{\displaystyle {\int }_{-\infty }^{+\infty }d\overline{\overline{\mathit{\text{Q}}}}{\displaystyle {\int }_{-\infty }^{+\infty }d{\overline{\overline{\mathit{\text{Q}}}}}^{\prime }}}\\ \times \langle {\overline{\chi }}_0|{\overline{\overline{\mathit{\text{Q}}}}}^{\prime }\rangle \text{exp}\left(\frac{i}{ħ}\left[\frac{1}{2}{\overline{\overline{\mathit{\text{Q}}}}}^{\prime \text{T}}\overline{\overline{\mathit{b}}}{\overline{\overline{\mathit{\text{Q}}}}}^{\prime }+\frac{1}{2}{\overline{\overline{\mathit{\text{Q}}}}}^{\text{T}}\overline{\overline{\mathit{b}}}\overline{\overline{\mathit{\text{Q}}}}-{\overline{\overline{\mathit{\text{Q}}}}}^{\text{T}}\overline{\overline{\mathit{\text{a}}}}{\overline{\overline{\mathit{\text{Q}}}}}^{\prime }\right]\right)\langle \overline{\overline{\mathit{\text{Q}}}}|{\overline{\chi }}_0\rangle \end{array}$$ (38)

We recall here the form of the harmonic wave function of the vibrational ground state,

$$|{\overline{\chi }}_0\rangle ={{\displaystyle \prod _{i=1}^N\left(\frac{{\overline{\omega }}_i}{\pi ħ}\right)}}^{\frac{1}{4}}\text{exp}\left(-\frac{{\overline{\omega }}_i{{\overline{Q}}_i}^2}{2ħ}\right)=\frac{\det {(\overline{\mathbf{\text{Γ}}})}^{1/2}}{{\pi }^{\frac{N}{4}}}\text{exp}\left(-\frac{{\overline{\mathit{\text{Q}}}}^{\text{T}}\overline{\mathbf{\text{Γ}}}\overline{\mathit{\text{Q}}}}{2}\right)$$ (39)

where Γ̄ is the diagonal matrix of the square root of the reduced frequencies ${\overline{\gamma }}_i=\frac{{\overline{\omega }}_i}{ħ}.$ After introduction of two additional sets of normal coordinates for the initial state, Q̄ and Q̄′, the autocorrelation function can be rewritten as,

$$\chi \left(t\right)={\displaystyle {\int }_{-\infty }^{+\infty }d\overline{\overline{\mathit{Q}}}}{\displaystyle {\int }_{-\infty }^{+\infty }d\overline{\mathit{Q}}{\displaystyle {\int }_{-\infty }^{+\infty }d{\overline{\overline{\mathit{Q}}}}^{\prime }{\displaystyle {\int }_{-\infty }^{+\infty }d{\overline{\mathit{Q}}}^{\prime }\langle {\overline{\chi }}_0|{\overline{\mathit{Q}}}^{\prime }\rangle \langle {\overline{\mathit{Q}}}^{\prime }|{\overline{\overline{\mathit{Q}}}}^{\prime }\rangle \langle {\overline{\overline{\mathit{Q}}}}^{\prime }|e^{-\frac{i\overline{\overline{H}}t}{ħ}}|\overline{\overline{\mathit{Q}}}\rangle }\langle \overline{\overline{\mathit{Q}}}|\overline{\mathit{Q}}\rangle }}\langle \overline{\mathit{Q}}|{\overline{\chi }}_0\rangle$$ (40)

In order to relate this expression to the general formulae used before, the integration is carried out over the final-state coordinates, Q̿ and Q̿′. Using Eq. 39, the autocorrelation function can be written in the following way,

$$\begin{array}{l}\chi \left(t\right)=\frac{\sqrt{\text{det}\overline{\Gamma }}}{{\pi }^{\frac{N}{2}}}\sqrt{\frac{\text{det}\overline{\overline{\mathit{a}}}}{{\left(2\pi ħ\right)}^N}}{\displaystyle {\int }_{-\infty }^{+\infty }d\overline{\overline{\mathit{Q}}}}{\displaystyle {\int }_{-\infty }^{+\infty }d{\overline{\overline{\mathit{Q}}}}^{\prime }\langle \overline{\overline{\mathit{Q}}}|e^{-\frac{i\overline{\overline{H}}t}{ħ}}|{\overline{\overline{\mathit{Q}}}}^{\prime }\rangle }\\ \times \text{exp}\left(-\frac{\left({\mathit{K}}^{\text{T}}+{\overline{\overline{\mathit{Q}}}}^{\prime \text{T}}{\mathit{J}}^{\text{T}}\right)\overline{\mathbf{\Gamma }}\left(\mathit{J}{\overline{\overline{\mathit{Q}}}}^{\prime }+\mathit{K}\right)}{2}\right)\text{exp}\left(-\frac{\left({\mathit{K}}^{\text{T}}+{\overline{\overline{\mathit{Q}}}}^{\prime \text{T}}{\mathit{J}}^{\text{T}}\right)\overline{\mathbf{\Gamma }}\left(\mathit{J}\overline{\overline{\mathit{Q}}}+\mathit{K}\right)}{2}\right)\end{array}$$ (41)

It is interesting to analyze the difference between the previous formula and Eq. 20 in order to derive the expressions for a, b, c and d at T=0 K. The matrix element $\langle \overline{\overline{\mathit{\text{Q}}}}|e^{-\frac{i\overline{\overline{H}}t}{ħ}}|{\overline{\overline{\mathit{\text{Q}}}}}^{\prime }\rangle$ is equal to the first exponential function of Eq. 20. Thus, by direct comparison of the other factors, it is easy to show that b̄ must be replaced by Γ̄ and that ā must be set to zero. As a consequence, also c̄ and d̄ must be replaced by Γ̄. Those results can be easily obtained also with a first-order Taylor approximation of the hyperbolic function. However, it should be underlined that ā in the scaling factor can not be set to zero but must be set equal to Γ̄. In conclusion, the following equivalency table can be built for the values of the variables of eq. 22 at different temperatures.

Table 1.

Equivalency table for the matrices at different temperatures

T=0K	Γ̄	c̿ + Γ̄	c̿ + Γ̄	Γ̄
T≠0K	ā	C̄	D̄	d̄

2.5. Extension to emission spectra

The extension of the previous theory to emission spectroscopy is not straightforward. Since the higher state becomes the initial one and the lower state is the final one, the Boltzmann factor refers to the excited-state vibrational levels, and, in order for ΔE – ω to be null with ω positive, ΔE must be defined as Ē – E̿. Consequently τ̄ and τ̿ must be transformed as,

$$\overline{\tau }=\frac{1}{k_{B}T}+\frac{it}{ħ};\overline{\overline{\tau }}=-\frac{it}{ħ}$$

In practice, there is another difference between absorption and emission in the choice of the state of reference to carry out the Taylor expansion of the transition dipole moment shown in Eq. 3. Indeed, the latter is readily available with respect to the excited state, independently from the nature of the transition we are interested in. Since our development is done with respect to the final state, we need to rewrite the Taylor expansion, assuming that the approximation up to the first-order is exact, that is,

$$\begin{array}{l}{\mathit{\text{d}}}_e^{\text{X}}({\overline{\mathit{\text{Q}}}}_{\text{eq}})+{\displaystyle \sum _{k=1}^N{\left(\frac{\partial {\mathit{\text{d}}}_e^{\text{X}}}{\partial {\overline{\text{Q}}}_k}\right)}_0{\overline{\text{Q}}}_k}\\ ={\mathit{\text{d}}}_e^{\text{X}}({\overline{\overline{\mathit{\text{Q}}}}}_{\text{eq}})+{\displaystyle \sum _{k=1}^N{\left(\frac{\partial {\mathit{\text{d}}}_e^{\text{X}}}{\partial {\overline{\overline{\text{Q}}}}_k}\right)}_0{\overline{\overline{\text{Q}}}}_k}\end{array}$$ (42)

Using the Duschinsky transformation given in Eq. 4, it is possible to express the final-state coordinates in the previous equation with respect to those of the initial, excited state. The relation obtained this way allows us to derive a general formulation holding for both absorption and emission spectra by using the following definition of the electronic transition dipole moment,

$${\mathit{\text{d}}}_e^{\text{X}}\approx 𝓐+{\displaystyle \sum _{i=1}^N{𝓑}_i{\overline{\overline{\text{Q}}}}_i}$$ (43)

The expression of $\mathbf{𝒜}$ and ℬ, as well as for the variables τ̄ and τ̿, are summarized in the following equivalency table:

Table 2.

Equivalency table for the derivatives of the transition dipole moment

	OPA/ECD	OPE
	$\overline{\tau }=\frac{1}{k_{B}T}-\frac{it}{ħ};\overline{\overline{\tau }}=\frac{it}{ħ}$	$\overline{\tau }=\frac{1}{k_{B}T}+\frac{it}{ħ};\overline{\overline{\tau }}=-\frac{it}{ħ}$
$\mathit{𝒜}$	${\mathit{\text{d}}}_e^{\text{x}}\left({\overline{\overline{\mathit{\text{Q}}}}}_{\text{eq}}\right)$	${\mathit{\text{d}}}_e^{\text{X}}\left({\overline{\overline{\mathit{\text{Q}}}}}_{\text{eq}}\right)-{\displaystyle {\sum }_{k=1}^N{\left(\frac{\partial {\mathit{\text{d}}}_e^{\text{X}}}{\partial {\overline{\overline{Q}}}_k}\right)}_{\text{eq}}}{\left({\mathit{\text{J}}}^{-1}\mathit{\text{K}}\right)}_k$
ℬi	${\left(\frac{\partial {\mathit{\text{d}}}_e^{\text{X}}}{\partial {\overline{\overline{Q}}}_i}\right)}_{eq}$	${\displaystyle {\sum }_{k=1}^N{{\text{J}}_{ki}}^{-1}{\left(\frac{\partial {\mathit{\text{d}}}_e^{\text{X}}}{\partial {\overline{\overline{Q}}}_k}\right)}_{eq}}$

Based on the equivalency table, it is possible to generalize Eq. 15 as,

$$\begin{array}{l}\chi (t)={𝓐}^A{𝓐}^B+{\displaystyle \sum _{k=1}^N{𝓑}_k^A{𝓐}^B\langle \overline{\mathit{\text{Q}}}|{\overline{\overline{Q}}}_k^{\circ }{e}^{-\overline{\overline{\tau }}\overline{\overline{H}}}{e}^{-\overline{\tau }\overline{H}}|\overline{\mathit{\text{Q}}}\rangle }+{\displaystyle \sum _{k=1}^N{𝓑}_k^B{𝓐}^A\langle \overline{\mathit{\text{Q}}}|e^{-\overline{\overline{\tau }}\overline{\overline{H}}}{\overline{\overline{Q}}}_k^{\circ }{e}^{-\overline{\tau }\overline{H}}|\overline{\mathit{\text{Q}}}\rangle }\\ +{\displaystyle \sum _{kl=1}^N{𝓑}_k^A{𝓑}_k^A\langle \overline{\mathit{\text{Q}}}|{\overline{\overline{Q}}}_k^{\circ }{e}^{-\overline{\overline{\tau }}\overline{\overline{H}}}{\overline{\overline{Q}}}_l^{\circ }{e}^{-\overline{\tau }\overline{H}}|\overline{\mathit{\text{Q}}}\rangle }\end{array}$$ (44)

where the superscripts A and B refers to the transition dipole ${\mathit{\text{d}}}_e^{\text{A}}$ and ${\mathit{\text{d}}}_e^{\text{B}}$ respectively

2.6. Inclusion of band-broadening effects

In the previous derivation the electronic spectrum has been considered a sum of Dirac delta functions centered on the resonance frequencies. However, bands present in experimental spectra have a non-negligible width due to various broadening effects. In practice, such a broadening can be simulated by replacing the Dirac delta function with one or more distribution functions. Those band-broadening effects can be easily included in the time-dependent framework. In fact, once the inverse Fourier transform g(t) of the distribution function S(ω_if, ω) is known,

$$S({\omega }_{if},\omega )={\displaystyle {\int }_{-\infty }^{+\infty }g(t)e^{({\omega }_{if}-\omega )t}}$$

it can be substituted into Eq. 6

$$I={\alpha }^{\prime }{\omega }^{\beta }{\displaystyle \sum _{jk}{e}^{-\frac{{\overline{\epsilon }}_i}{k_{B}T}}}\langle {\overline{\chi }}_j|{\mathit{\text{d}}}_e^{\text{A}}|{\overline{\overline{\chi }}}_k\rangle \langle {\overline{\overline{\chi }}}_k|{\mathit{\text{d}}}_e^{\text{B}*}|{\overline{\chi }}_j\rangle {\displaystyle {\int }_{-\infty }^{+\infty }g(t)e^{i({\omega }_{if}-\omega )t}dt}$$ (45)

$$={\alpha }^{\prime }{\omega }^{\beta }{\displaystyle {\int }_{-\infty }^{+\infty }dt}{\displaystyle \sum _{jk}{e}^{-\frac{{\overline{\epsilon }}_i}{k_{B}T}}}\langle {\overline{\chi }}_j|{\mathit{\text{d}}}_e^{\text{A}}|{\overline{\overline{\chi }}}_k\rangle \langle {\overline{\overline{\chi }}}_k|{\mathit{\text{d}}}_e^{\text{B}*}|{\overline{\chi }}_j\rangle {\displaystyle {\int }_{-\infty }^{+\infty }g(t)e^{i({\omega }_{if}-\omega )t}}$$ (46)

By comparing Eqs. 11 and 46, we can note that inclusion of broadening only requires the autocorrelation to be multiplied by g(t).

For a Gaussian distribution function, the expression for S(ω_if, ω) is,

$$S({\omega }_{if},\omega )=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{{({\omega }_{if}-\omega )}^2}{2{\sigma }^2}}$$ (47)

where σ is the standard deviation, which can be related to the half-width at half-maximum (HWHM) of the Gaussian function in the frequency domain,

$$\sigma =\frac{\text{HWHM}}{\sqrt{2\text{ln}2}}$$

The Fourier transform of a Gaussian function is another Gaussian function,

$$\frac{1}{2\pi \sigma }{\displaystyle {\int }_{-\infty }^{+\infty }dt}{e}^{-i({\omega }_{if}-\omega )t}{e}^{-\frac{{\sigma }^2{t}^2}{2}}=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{{({\omega }_{if}-\omega )}^2}{2{\sigma }^2}}$$ (48)

Thus the autocorrelation function has to be multiplied by a factor ρ_gau,

$${\rho }_{\text{gau}}=\frac{1}{2\pi \sigma }{e}^{-\frac{t^2{\sigma }^2}{2}}$$ (49)

Let us now consider the case of a Lorentzian distribution function, where the analytic expression for S(ω_if, ω) has the form,

$$\frac{1}{\pi }\frac{\gamma }{{({\omega }_{if}-\omega )}^2+{\gamma }^2}$$ (50)

where 2γ is the half-width at half-maximum of the lorentzian distribution in the frequency domain. The Fourier transform of the Lorentzian function is an exponential,

$$\frac{1}{\pi }\frac{\gamma }{{({\omega }_{if}-\omega )}^2+{\gamma }^2}=\frac{1}{2\pi }{\displaystyle {\int }_{-\infty }^{+\infty }dt}{e}^{-i({\omega }_{if}-\omega )t}{e}^{-\gamma |t|}$$ (51)

In this case, the correlation function is multiplied by the factor ρ_lor

$${\rho }_{\text{lor}}=\frac{1}{2\pi }{e}^{-\gamma |t|}$$ (52)

The time-dependent framework can include both distribution functions, the gaussian-type one and the lorentzian-type one, which represent different kinds of broadening. In fact, the result of the combination of those effects is a Voigt band-shape function, which is the convolution of the product of a gaussian function and a lorentzian function. However, the Fourier transform of the convolution of two functions is the product of Fourier transforms. As a consequence, to consider both effects one must simply multiply the autocorrelation function by an overall factor ρ_gau × ρ_lor.

2.7. Stability of the numerical integration

It should be noted that sometimes the computation of the time-dependent spectrum suffers from numerical instability. Indeed, the integral is computed by means of a discrete Fourier transform, which is a numerical integration procedure. Thus, a certain upper time limit T must be set in order to truncate the integration at some level and the autocorrelation function is sampled in a finite number (N) of points. However, the truncation is valid only if the autocorrelation function goes to zero beyond the upper limit T but this is not always guaranteed. For example, when mode mixing is negligible, as shown by Tannor and Heller,⁴³ the autocorrelation function can present periodic oscillations and thus does not converge to zero; in those cases, the convergence is ensured only if a broadening function is included. In all the following calculations the total time of integration T has been set to 10⁻⁹s. This value guarantees a complete convergence of the autocorrelation function with the values of Half-Width at Half-Maximum, which are usually used (over 10 cm⁻¹). Furthermore, the default value for the number of points in which the function is sampled is set to 2²⁴; several numerical tests have shown that this value is a good compromise between computational time and sampling accuracy.

In order to improve the convergence of the discrete Fourier transform, a window function has been also included. Indeed, it can be mathematically proven that the convergence of the discrete Fourier transform of a function f(t) can be improved by scaling this function by a window function w(t), with an appropriate choice of w(t).⁶⁴ The simplest window function is the rectangular window function, which is equal to one inside the window interval and zero elsewhere. While more elaborated window functions have been developed and applied to the calculation of the Fourier transform of the autocorrelation function,^51,65 our tests have shown that they are often more complex to parametrize in order to get a correct convergence for a broad range of systems. In the perspective of building a robust black-box procedure, a rectangular window function is well-suited since it provides reliable results with very limited parametrization. Indeed, the unique parameter which must be set is the time interval in which the function is non-zero. In order to reduce the noise due to artefacts periodic oscillations and thus increase the signal-noise ratio, it is necessary for the window function to have a range significantly smaller than the time-interval. However, the window function must be large enough not to remove the features of the actual spectrum. On the other hand, increasing the total number of steps in the time interval raises storage issues as the memory required to save the autocorrelation function grows quickly. Our numerical tests have shown that a window function which is 2⁸ times smaller than the whole time-interval of integration provides a complete convergence of the numerical integration in most cases. In practice, and for the default settings, this means that the window function is equal to 1 over 2¹⁶ sampling points, so that χ(t) is non-null over these points and null over the remaining 2⁸ points to ensure the convergence of the discrete Fourier transform.

3. Computational details

Density functional theory (DFT) and its time-dependent extension (TD-DFT) have been used to carry out the electronic structure calculations in the ground and excited states, respectively. The standard B3LYP functional⁶⁶ has been used in conjunction with the double-ζ SNSD⁶⁷ basis set, developed for spectroscopic studies of medium-to-large molecular systems. This basis set has been constructed from the polarized double-ζ N07D basis set^68–71 by consistently including diffuse s functions on all atoms, and one set of diffuse polarized functions (d on heavy atoms and p on hydrogens).

By default, the spectra were simulated using the adiabatic hessian (AH) model, in which both electronic states involved in the transition are treated on the same ground and the harmonic potential energy surface (PES) were calculated about their respective equilibrium geometry (see ref.32 and references therein for more details). When available, first derivatives of the electronic transition moments, ${\mathit{\text{d}}}_{e,\mathit{\text{if}}}^{\text{X}},$ are obtained from TD-DFT calculations by numerical differentiation along the Cartesian coordinates, together with the force constants matrix calculated from the analytic gradients.

All calculations of the electronic structure and the vibronic spectra were done with a locally modified version of the Gaussian suite of quantum chemical programs.⁷² The procedure employed to generate the vibronic spectra follows the same pattern described in Refs.^33,34 Rotation and translation are minimized by superposing the initial- and final-state equilibrium structures, prior to calculating the Duschinsky matrix J and shift vector K using the formulas,

$$\mathit{\text{J}}={\overline{\mathit{\text{L}}}}^T\overline{\overline{\mathit{\text{L}}}};\mathit{\text{K}}={\overline{\mathit{\text{L}}}}^T{\mathit{\text{M}}}^{1/2}\Delta \mathit{X}$$ (53)

where L̄ and L̿ are the transformation matrices from mass-weighted Cartesian to normal coordinates of the initial and final states, respectively, M is the diagonal matrix of atomic masses, and ΔX = X̿–X̄ represents the changes in geometry between the equilibrium structures of the two electronic states. After this step, the time-dependent or time-independent path is taken depending on users’ requests.

The implementation of the time-independent approach has been described in Refs.^33,34 It uses the recursive equations of Ruhoff^25,26 based on the Sharp and Rosenstock matrices^21,22,73 to compute the overlap integrals in the sum-over-states formulation. To limit the number of integrals to take into account, the class-based prescreening proposed by Santoro et al.^74–76 has been employed. It relies on a categorization of the transitions in so-called classes, which correspond to the number of simultaneously excited oscillators in the final state, and if temperature is taken into account, the initial state as well. Class 1 (overtones) and class 2 (2-states combinations) are treated up to a specified number of quanta for each oscillator, $C_1^{\text{max}}$ and $C_2^{\text{max}}$ respectively. Overlap integrals and information related to their calculation from these classes are stored and used for the prescreening to define the maximum number of quanta for each oscillator in order to choose and compute up to $N_{\mathrm{I}}^{\text{max}}$ transitions, evaluated to be the most significant ones, for each class starting from class 3. Extensive details about the prescreening can be found in Refs.^{33,34,74–76} In the present work, if not specified otherwise, sum-over-states spectra were computed with the default settings, that is,

$$C_1^{\text{max}}=20,C_2^{\text{max}}=13,N_I^{\text{max}}={10}^8$$

and up to 7 simultaneously exited modes in the final state have been taken into account (class 7).

Since each time step of the autocorrelation function is independent from the others, it is possible to greatly speed up the calculation of χ(t) by treating the time steps in parallel, as it has been done in our implementation. At this point, the most time-consuming step becomes the Fourier transformation. In order to speed up this process, the implementation was designed so that vendor-specific, highly optimized mathematical library, in particular the AMD Core Math Library (ACML) for AMD processors and the Intel Math Kernel Library (MKL) on Intel processors could be used to perform matrix algebra and Fast Fourier Transformation (FFT) when available, as well as the free software “Fastest Fourier Transform in the West” (FFTW) library.⁷⁷ A serial, robust version, FFTPack 4,⁷⁸ has been also included if no supported library is available and to check the correct interface with the optimized libraries.

In order to improve the accuracy of theoretical spectra, input frequencies obtained at the harmonic level can be replaced by their anharmonic counterparts. In this work, the latter are computed using the second-order vibrational perturbation theory (VPT2).^79–83 The necessary third and semi-diagonal fourth derivatives of the potential energy are obtained by numerical differentiation of the analytic harmonic force constants along the mass-weighted normal coordinates (Q). Gaussian default step has been used, that is δQ = 0.01 Å.^83,84 Due to the unavailability of analytic second derivatives of the potential energy in our TD-DFT calculations, an alternative approach, proposed in Ref.,¹⁹ is available in our procedure to extrapolate the anharmonic frequencies of the excited state from the scaling factors (α′) between the anharmonic (ν′) and harmonic (ω′) frequencies of the electronic ground state, based on the following sequence³,

$$\begin{array}{l}{\alpha }_i^{\prime }={\nu }_i^{\prime }/{\omega }_j^{\prime }\\ {\alpha }_i^{″}={\displaystyle \sum _k{{\text{J}}_{ik}}^2{\alpha }_k^{\prime }}\\ {\nu }_i^{″}={\alpha }_i^{″}{\omega }_j^{″}\end{array}$$

At first glance, the anharmonic correction of the frequency will only correct the band position and marginally the band intensity with respect to the photon energy. Under such conditions, the scaling scheme would have an impact in the simulation of OPA spectra or if temperature effects need to be taken into account, but could be safely neglected for low-temperature OPE spectra, assuming that a correct calculation difference between the zero-point vibrational energies of the initial and final states is not sought.⁸⁵ However, both initial- and final-state frequencies are also directly used in the calculation of the overlap integrals, in χ(t) in TD calculations (see eq. 41) and 〈0̄ | 0̿〉 in TI calculations. In this regard, the general application of the scaling scheme is needed to have a consistent anharmonic correction of the band-shape.

4. Results and Discussions

Figure 1 shows the molecules used in this work to illustrate some capabilities of the procedure with our implementation of the path integral model.

Figure 1.

(1): anthracene, (2): furan, (3): phenyl radical, (4): R,R-dimethyloxirane, (5): coumarin 339

4.1. Anthracene

The rigidity of anthracene (molecule (1) in Figure 1) prevents the distortion of the molecule, so that the Franck-Condon approximation is well-suited to study the S₁ ← S₀ OPA spectrum, and strongly limits the mode-mixing upon the electronic transition, so that full convergence of the spectrum generated by mean of sum-over-states approaches can be easily reached without requiring complex prescreening algorithms. Together with its medium size, such features make the molecule particularly appealing to test and validate implementations of procedures to compute vibrationally-resolved electronic spectra.^{17,18,74,86,87}

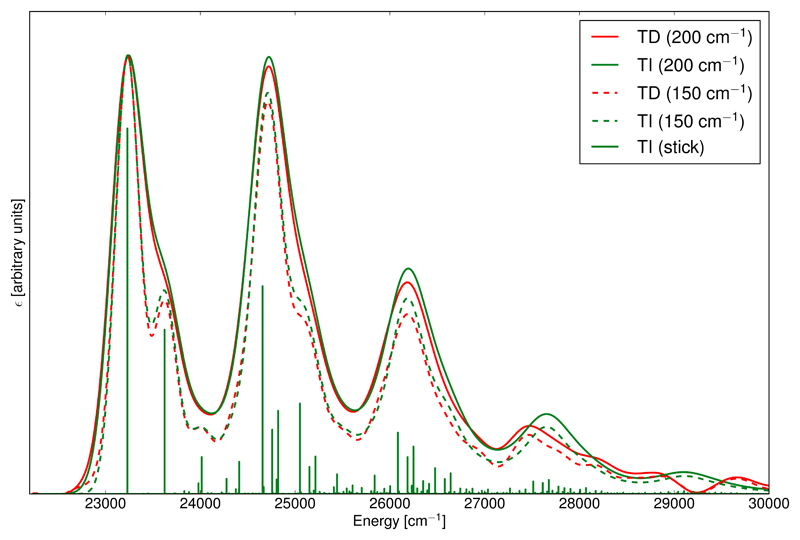
The time-independent (TI) spectrum was simulated at T=0K with the default parameters given in the computational details. The total convergence of the calculated intensity with respect to the analytic intensity based on the sum rules was of 99.9%. The stick spectrum was generated and then convoluted using Gaussian distribution functions with two different half-widths at half-maximum of 150 and 200 cm⁻¹, respectively.

For the time-dependent (TD) spectrum, the total time used for the simulation was 10⁻⁹ s discretized in 2²⁴ steps. The rectangular window function described in the theoretical part was employed with a width 2¹⁶ and the same broadening function as for the time-independent procedure was employed. To match the time-independent spectrum, the autocorrelation function given in section 2 for T=0K was employed.

Comparison of the time-dependent and time-independent spectra is shown in Figure 2 and a comparison of the TD spectrum with its experimental counterpart is reported in supplementary information (Figure S1 of SI). To facilitate the analysis, all spectra were scaled so their highest band or peak had the same height. Focusing first on the spectra with higher resolution (broadening of 150 cm⁻¹), we can note a very good agreement between TD and TI spectra over the most intense bands, below 27000 cm⁻¹. For the higher-energy bands, which are far less intense, larger discrepancies are observed. By increasing the broadening, overlap between the TD and TI band-shapes improves, which hints at the source of discrepancies to be related to some background noise, not fully removed by our window function. However, it should be highlighted that a broadening of 150 cm⁻¹ provides already a rich band-shape of the vibrationally-resolved electronic spectra with several clearly visible bands. When very high resolution is needed,¹⁹ the sum-over-states model, which allows automatically band assignment, is better suited and can be limited to the region of interest defined from the total band-shape generated with the path-integral approach to reduce the computational costs of the complete procedure.⁵⁵ Additionally, analysis of the latter shows that both bands of the convoluted TI spectrum in the higher region stem from a multitude of low-intensity transitions, and that the most intense transitions have an energy below 27000 cm⁻¹.

Figure 2.

S₁ ← S₀ OPA spectrum of anthracene simulated with the path integral (TD, in red) and sum-over-states (TI, in green) approaches. Convoluted band-shapes were obtained by applying Gaussian distribution functions with HWHM=150 cm⁻¹ (dashed line) and 200 cm⁻¹ (solid line), respectively. All spectra were simulated at the AH|FC level at T=0K in vacuum.

4.2. Furan

Furan (molecule (2) in Figure 1) is a five-membered heterocycle, which is used in organic chemistry and biochemistry as a building block for the synthesis of various drugs and biopolymers. The study of its ionic structure is mostly carried out by mean of photoelectron spectroscopy. Due to its chemical interest, furan has been extensively studied, providing a rich set of reference data, which can be used to test new theoretical models to compute vibrationally-resolved electronic spectra (see Ref.88 and references therein for an overview of theoretical and experimental studies on this molecule). Finally, its relatively small size allows the application of accurate albeit expensive computational models.⁸⁹

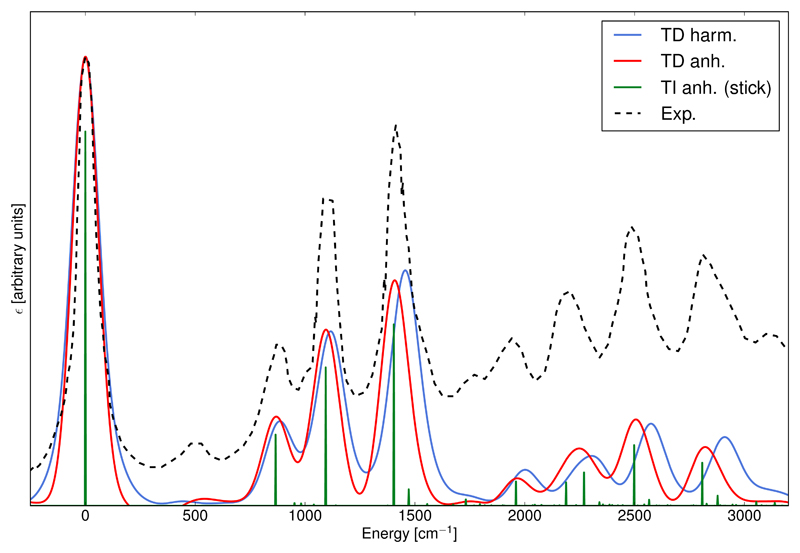
Previous computational studies provide a solid background to ascertain the quality of our electronic structure calculations. Similarly to Luis et al.,⁸⁹ we have focused our attention on the X̃²A₂ ← X̃¹A₁ band in the photoelectron spectrum, associated to the ground states of its cationic and neutral form. Both electronic structure calculations were done at the DFT level, using the B3LYP functional and the SNSD basis set. It should be noted that our calculations do not take into account interactions with the continuum, so that we do not have access to the electronic transition dipole moment corresponding to the photoionization. In such a case, we assume that the transition dipole moment is a unit vector and the Franck-Condon approximation is used. Following previous simulations of the vibronic spectra,^89,90 our time-dependent simulation was done at T=0K, hence ignoring temperature effects. The spectra were simulated over 10⁻⁹ s discretized in steps of 6 · 10⁻¹⁷ s and the window function spanned over 4 · 10⁻¹² s. The broadening was done with a Gaussian distribution function whose full-width at half-maximum was chosen to match experimental data, that is 140 cm⁻¹. The adiabatic ionization energy is underestimated in our calculations with respect to the experimental value measured by Derrick et al.^91,92 by about 0.2 eV. To compare the band-shapes, the most intense bands of each spectrum are superposed and shifted to the origin.

The theoretical and experimental spectra are shown in Figure 3 (temperature effects at T=298K are shown in supplementary information, Figure S2). The theoretical spectrum (TD harm) reproduces fairly well the experimental band-shape and all the strong bands observed experimentally are clearly visible. It is however difficult to estimate the accuracy of the band intensity due to apparent shift of the baseline in the experimental spectrum.

Figure 3.

Experimental and calculated X̃²A₂ ← X̃¹A₁ photoionization spectra of furan. The convoluted spectra were simulated with the path integral (TD) approach using Gaussian distribution functions with HWHM=70 cm⁻¹. The anharmonic spectrum (in red) differs from its harmonic counterpart (in blue) by the use of anharmonic vibrational energies instead of the harmonic ones. The stick spectrum was calculated with the sum-over-states approach using anharmonic frequencies. All computed spectra were done at the AH|FC level at T=0K in vacuum. The experimental spectrum (dashed black line) was taken from Ref.91,92

Anharmonic corrections to the frequencies are included using the procedure described in the computational details. The resulting spectrum (TD anh.) is shown in red. We can note an improvement in the agreement with the experimental spectrum as the band positions are corrected with respect to the purely harmonic spectrum (TD harm.) and most of the bands are clearly recognizable. For the sake of completeness, it should be mentioned that two low-intensity bands in the experimental spectrum are not fully reproduced in both convoluted spectra. The first one, at about 500 cm⁻¹ does not appear also on the stick spectrum, which is in line with previous studies.^89,90 The second one, at about 1770 cm⁻¹ seems shifted to about 1730 cm⁻¹, based on the analysis of the stick spectrum. While the time-dependent band-shapes seem to show a similar trend with a small shoulder about this energy, it is too low for an unambiguous assignment. Overall, it should be noted that the noise remains very low in this example, even with this rather small broadening.

4.3. Phenyl radical

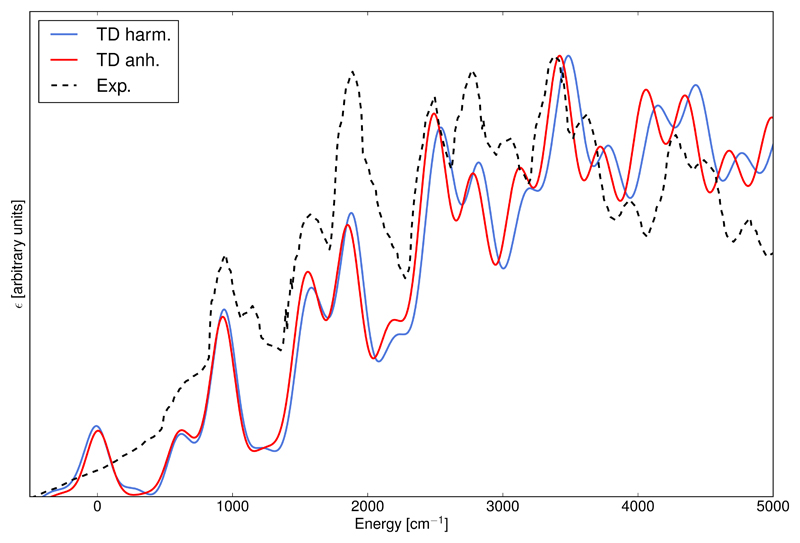
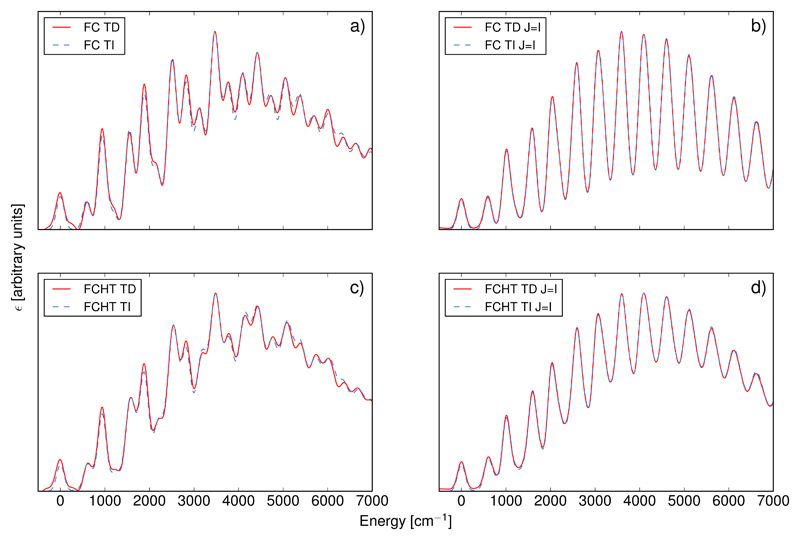
The electronic absorption spectrum of phenyl radical (molecule (3) in Figure 1), and more specifically the A²B₁ ← X̃²A₁ band, has been previously studied by some of us as an illustration of our procedure to compute vibronic spectra within the time-independent framework.⁹³ In addition to its chemical interest for a better understanding of combustion processes, the molecule, being an open-shell system, represents a challenging task for electronic structure calculations. Our previous study followed an earlier analysis of the vibrational structure of the electronic spectrum by Mebel et al.,⁹⁴ who used a sum-over-states approach to compute the vibronic transition intensities at the Franck-Condon level to interpret the band-shape of the electronic spectrum of matrix-isolated phenyl radical reported by Radziszewski⁹⁵ over the 4000–52000 cm⁻¹ energy range. Significant discrepancies between the theoretical spectrum, simulated with a reduced-dimensionality scheme based on symmetry considerations, and its experimental counterpart were observed and ascribed to several sources, including the possible interaction with a neighbor dark state. By adopting a full-dimensionality scheme in the Franck-Condon Herzberg-Teller (FCHT) approximation, we showed that a better agreement with experiment could be reached. The agreement with experiment was further enhanced by using a previously proposed scheme to include in a straightforward way anharmonic effects in our vibronic calculations.¹⁹ Finally, we were able to offer a different interpretation of the band position corresponding to the transition between the vibrational ground states of the two electronic states (0-0 transition).

The same protocol as described in Ref.93 has been used here, but using the SNSD basis set. For all spectra, the broadening was simulated with Gaussian distribution functions having an half-width at half-maximum of 100 cm⁻¹. All time-dependent spectra were simulated over 10⁻⁹ s with the autocorrelation function computed in 2²⁴ points and the window function spanned over 2¹⁶ points. As mentioned before, the FCHT approximation is needed to obtain an accurate band-shape, together with the inclusion of anharmonic effects. The latter are limited to the frequencies, which serve to compute the autocorrelation function, using the same scaling scheme as for furan. The harmonic and anharmonic spectra are displayed in Figure 4. As already observed in Ref.,⁹³ anharmonic corrections improve the agreement with the experimental spectrum, in particular with the higher-energy bands, which superpose better on their experimental counterpart. While the band positions are fairly well reproduced, their relative intensities are less accurate, but still reproduce satisfactorily the general trend of the overall band-shape. Together with the example of furan, this application of the procedure shows two simple schemes to include anharmonic effects and improve the accuracy of the simulation without any increase in the computational cost of the vibronic spectra.

Figure 4.

Experimental and calculated A²B₁ ← X̃²A₁ electronic spectrum of phenyl radical. Both theoretical spectra were simulated with the path integral model (TD) at the AH|FCHT level at T=0K in vacuum. The harmonic spectrum (TD harm., in blue) was simulated using harmonic frequencies, while the anharmonic one (TH anh., in red) was done with anharmonic frequencies using a scaling scheme to include anharmonic correction to the frequencies of the excited state (see text for details). Gaussian distribution functions with HWHM=100 cm⁻¹ were used to convolute the spectra. The experimental spectrum (dashed black line) was taken from Ref.95

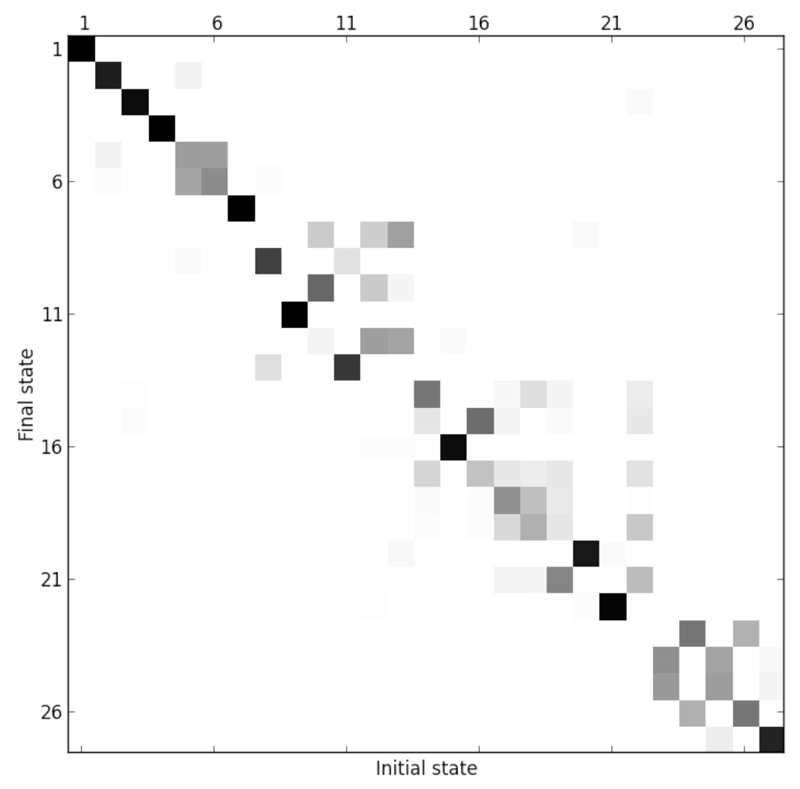
As a final remark on this system, we can observe a marked mode mixing associated to the electronic transition depicted in Figure 5. A common approximation in the simulation of vibronic spectra is to neglect such mixing, so that the Duschinsky matrix corresponds to the identity matrix and simpler equations are obtained for the autocorrelation function. While this approximation can be satisfactory for rigid systems where the mode mixing is small, this can lead to wrong interpretations otherwise. As an illustration, Figure 6 shows the convoluted vibronic spectra of the A²B₁ ← X̃²A₁ band with the same broadening function used as before. This test confirms the very good agreement between the TD and TI procedures. If we restrict ourselves to the Franck-Condon approximation (panels a and b), the neglect of mode mixing results in a strongly altered band-shape and only the upper envelop seems to be in qualitative agreement. As mentioned previously, inclusion of Herzberg-Teller effects has an impact on the band-shape (panels a and c). Again, approximating the Duschinsky matrix to identity (panel d) results in an incorrect band-shape, but the lower and upper envelops are in better agreement than for the Franck-Condon approximation, so that it is likely that the neglect of mode mixing will have a lower impact if larger convolution functions are used. Incidentally, we can observe a better agreement between TI and TD if mode mixing is discarded.

Figure 5.

Duschinsky matrix of the A²B₁ ← X̃²A₁ electronic transition of phenyl radical. The matrix is displayed as follows. The square elements J_ik are calculated and a shade o gray is associated to the element (i, k) in the displayed matrix based on the value (0: white, 1: black). Hence, a mode mixing will be displayed as a block of gray elements.

Figure 6.

Comparison of time-dependent (TD) and time-independent (TI) A²B₁ ← X̃²A₁ electronic spectra of phenyl radical with different approximations. Panel a: Franck-Condon approximation with correct Duschinsky matrix. Panel b: Franck-Condon approximation with Duschinsky matrix assimilated to the identity matrix. Panel c: Franck-Condon Herzberg-Teller approximation with correct Duschinsky matrix. Panel d: Franck-Condon Herzberg-Teller approximation with Duschinsky matrix assimilated to the identity matrix. Gaussian distribution functions with HWHM=100 cm⁻¹ were used to convolute the spectra.

4.4. Dimethyloxirane

The next example regards the application of our path-integral procedure to electronic circular dichroism (ECD). Chiroptical spectroscopies represent methods of choice to study and fully characterize chiral molecular systems, providing information about their configurational and conformational structures. From a methodological point of view, as shown in our development, ECD is very similar to OPA and OPE. However, while the Franck-Condon approximation can be sufficient for OPA and OPE when the transition probability is high, it is often insufficient for ECD as the scalar product μ · ℑ(m) can have a negligible magnitude even in this case.^34,96–98 Furthermore, sign alternance of the band-shape cannot occur at the FC level since this scalar product is only a scaling factor of the Franck-Condon integrals, so the Herzberg-Teller approximation must be included a priori to correctly simulate ECD spectra. Furthermore, Herzberg-Teller terms are usually quite small so that the simulation of ECD spectra is more sensitive to the accuracy of the calculations. Moreover, the presence of significant background oscillations may affect the sign of the ECD spectrum.

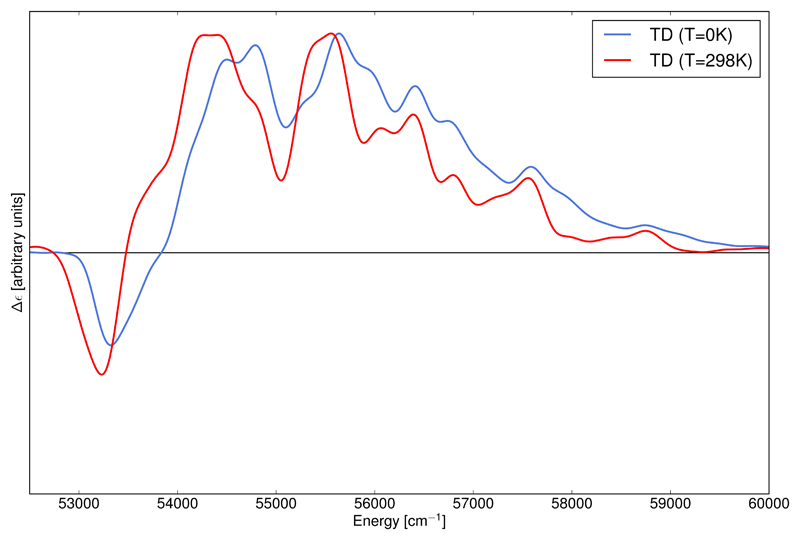
As an illustration of the possibilities of our procedure in the study of chiral systems, the S₃ ← S₀ ECD spectrum of trans-(R,R)-dimethyloxirane (molecule (4) in Figure 1) has been simulated. Its relatively small size makes this derivative of oxirane appealing as a prototypical chiral molecule to test novel theoretical methods or setup reliable protocols to be applied to larger systems.^99–101 The band-shape for the S₃ ← S₀ transition presents a change of sign, which means that the Herzberg-Teller approximation is mandatory to compute the spectra. The simulations were carried out over 10⁻⁹ s at both T=0K and T=298K with the band broadening described by mean of Gaussian distribution functions (HWHM=150 cm⁻¹). The autocorrelation function was computed in 2²⁸ points and the window function spanned over 2¹⁶ points.

The spectra are shown in Figure 7. Temperature effects on the band-shape are clearly visible and the spectrum at T=298K is consistently red-shifted with respect to the one at T=0K. This may have an impact on the analysis of the band-shape when interpreting an experimental spectrum. Indeed, the common practice for this kind of studies is to set the transition between the vibrational ground states of each spectrum to the origin and to define band energies with respect to this reference. While the 0-0 transition energy can be unequivocally defined for the computed spectra, it can be unknown for the experimental counterparts, so that the band-shape superposition has to be done manually by maximizing the overlap of the most intense bands. In the present case, and in the hypothesis that the experimental spectrum would be recorded at room temperature, a visual superposition with a theoretical spectrum computed without taking into account temperature effects is prone to several artefacts. This behavior with respect to temperature is likely to be observed with a sensitive spectroscopy like ECD but also when studying molecules with low vibrational energies, for instance in the case of adsorbates on solid surfaces.

Figure 7.

S₃ ← S₀ electronic circular dichroism (ECD) spectrum of trans-(R,R)-dimethyloxirane computed with the path integral approach at the AH|FC level. Band broadening was simulated at T=0K (in blue) and T=298K (in red) with Gaussian distribution functions with HWHM=150 cm⁻¹.

4.5. Coumarin 339

4-Methyl-6,7,8,9-tetrahydro-2H-pyrano[3,2-g]quinolin-2-one, more commonly known as Coumarin 339 (molecule (5) in Figure 1), is a type of 7-aminocoumarins, an important class of laser dyes in the blue-green region, whose optical properties have been deeply investigated.^20,102–107 Coumarin 339 (C339), which has been previously studied by some of the authors,²⁰ is used here as a test case to illustrate some additional aspects of our computational approach.

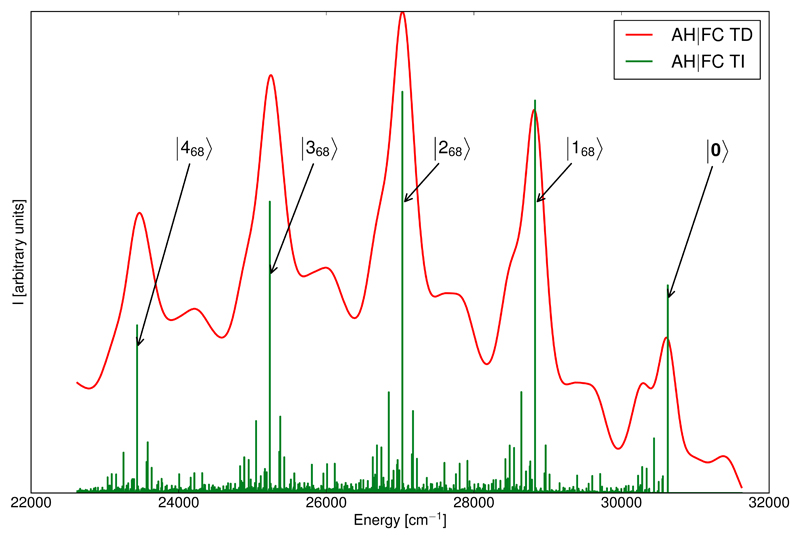
The S₁ → S₀ OPE spectrum of C339 has been simulated at T=0K in vacuum using both path integral (TD) and sum-over-states (TI) models. The TD spectrum was simulated over 10⁻⁹ s using 2²⁴ steps with a window function spanning over 2¹⁶ points. The broadening was obtained with Gaussian distribution functions with HWHM=135 cm⁻¹. For the TI spectrum, the default settings presented in the computational details resulted in recovering 88% of the total intensity. A modification of the parameters $(C_1^{\max }=30,C_2^{\max }=20,N_I^{\max }={10}^9)$ improved the spectrum convergence to 93.3%, but at the expense of significant increase in the computational time. The TI and TD spectra are shown in Figure 8. The convoluted spectrum shows a pattern of regularly spaced intense bands, interspersed with less defined bands partly merged in the former. The stick spectrum provides a deeper insight on the fine structure of the bands, which shows a wealth of low peaks contributing to the lower-intensity convoluted bands. On the other hand, the high-intensity bands can be unequivocally related to the vibrational progression of a single mode, the C=O stretching, except for the leftmost peak, which corresponds to the 0-0 transition. Such an example shows the complementarity of the path integral and sum-over-states models to obtain an accurate and complete analysis of the computed spectra.

Figure 8.

S₁ → S₀ one-photon emission (OPE) spectrum of coumarin 339 in vacuum at the AH|FC level at T=0K. The convoluted spectrum (AH|FC TD, in red) was simulated with the path integral approach using Gaussian distribution functions with HWHM=135 cm⁻¹. The stick spectrum (AH|FC TI, in green) was computed with the sum-over-states model. Since all transitions originate from the initial vibrational ground state, only the vibrational final state is indicated in the assignment. | 0 〉 corresponds to the vibrational ground state, | n_i 〉 means that only mode i is excited with n quanta

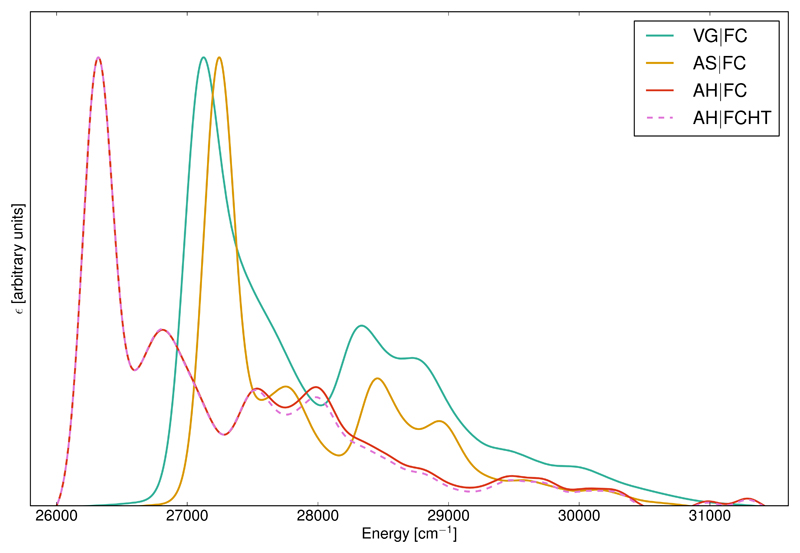
Another example of the features available in our computational procedure is shown in Figure 9 with the S₁ ← S₀ OPA spectrum of C339 in toluene solution. Solvent effects have been accounted for using the conductor-like polarizable continuum model (CPCM).¹⁰⁸ The spectra have been simulated with the path integral approach using the same settings as for the OPE spectrum, including the broadening parameters. It is noteworthy that the OPA spectrum of C339 in toluene is significantly different from the OPE one in vacuum, with the absence of the characteristic vibrational progression observed previously and the strong dominance of the 0-0 transition. Comparison of the spectra computed at the FC (in solid red) and FCHT (in dashed magenta) levels of approximation of the transition dipole moment within the Adiabatic Hessian model shows that AH|FC is sufficient to describe the electronic transition. When considering large systems or in the case of virtual screenings to assess the quantum yield of various chromophores,¹⁰⁹ the cost of computing the frequencies of both electronic states, in particular the excited one at the TD-DFT level, may quickly become prohibitive. An alternative, less expensive approach is to consider that the PES of the final state is the same as the initial one’s except for a shift of the minimum energy geometrical parameter; as a consequence only the frequencies of the initial state must be computed. The Adiabatic Shift (AS, in yellow) is the approximated counterpart of AH and requires only the optimized geometry for the final state. In practice, the shift vector is the same as in AH but the Duschinsky matrix becomes the identity matrix. We can observe an energy shift of the band-shape between AH|FC and AS|FC, which corresponds to the missing account for the difference between the zero-point vibrational energies in the approximated model. Overall, the band-shapes are very similar, with only the second and fourth bands slightly lower in AS|FC than in AH|FC with respect to the first, highest band. Such an agreement hints at a limited mode mixing during the electronic transition. The Vertical Gradient (VG, in cyan) model, also known as the Linear Coupling Model,¹¹⁰ is different as it is an approximated model derived from the vertical approach (see Ref.32 for a more detailed discussion on the various models). The central idea in vertical models is that the correct representation of the strongest features of the vibronic spectra requires an accurate description of the PES in the Franck-Condon region, that is about the equilibrium geometry of the initial state. A practical issue of this concept is that the equilibrium geometry of the final state is not known, so that the shift vector in the Duschinsky transformation must be extrapolated assuming that the PES of the final state is harmonic. Similarly to AS, the PES of the final state is assumed in VG to be the same as the initial state, so that the Duschinsky matrix is the identity matrix. In the VG approximation, the shift vector is,

$$\mathit{K}={\overline{\mathbf{\text{Ω}}}}^{-2}{\overline{\mathit{\text{L}}}}^{\text{T}}{\mathit{\text{M}}}^{1/2}{\overline{\overline{\mathit{\text{g}}}}}_X$$

where $\overline{\mathbf{\Omega }}$ is the diagonal matrix of the initial state’s frequencies, g̿_X is the gradient in the final state at the equilibrium geometry of the initial state expressed in Cartesian coordinates.

Figure 9.

S₁ ← S₀ one-photon absorption (OPA) spectrum of coumarin 339 in toluene solution simulated with the path integral approach at T=0K. Band broadening was obtained by means of Gaussian distribution functions with HWHM=135 cm⁻¹.

As expected, an energy shift is observed between the VG|FC and AH|FC band-shapes due to the lack of zero-point vibrational energies differences in the former model. However, since the exact minimum of the final electronic state is not known in the VG model, its energy is extrapolated on the basis of the harmonic approximation using the force constants and normal modes of the initial state; this leads, of course, to slight differences with respect to the AH|FC band-shape. The most significant difference is the merging of the first two bands observed in both AH|FC and AS|FC in the case of VG|FC.

Depending on the accuracy required for the vibronic structure of the electronic spectrum, the approximated models may be insufficient, thus their reliability should be carefully assessed depending on the needs on sample systems before using them on molecules or groups of molecules of interest. A more detailed analysis of the various transition models is deferred to a future work.

Conclusions

A general time-dependent model allowing the computation of vibronic contributions to different electronic spectra (one-photon absorption, one-photon emission and electronic circular dichroism) in a fully automated manner has been presented. The necessary validations have been performed for a few medium-size, closed- and open-shell, molecular systems. Additionally, the reliability of the results from TD-DFT computations has been assessed through the comparison with their accurate experimental counterparts, showing also that possible discrepancies should be mostly attributed to the underlying vertical excitation energies. These findings are of relevance for the accurate study of larger molecular systems by hybrid models in which excitation energies obtained by accurate many-body approaches are coupled to structures and force fields computed by cheaper DFT and TD-DFT approaches possibly integrated in QM/MM/PCM models.

Furthermore, the time-dependent model introduced in the present work is based on the same general background as our previous time-independent implementation thus allowing integration of both strategies for obtaining at the same time high resolution band assignments and complete spectra at variable temperature. It should be also pointed out that both approaches, implemented in the Gaussian suite of programs, can be applied in conjunction with any quantum mechanical model for which at least analytic gradients are available. This means that, together with isolated molecules, a black-box procedure to evaluate spectroscopic properties at the harmonic level is available also for systems in solution described by the polarizable continuum model. Additionally, an approximate anharmonic treatment allows to take into account simultaneously anharmonic and environmental effects on vibronic spectra even for relatively large molecular systems.

In conclusion, we think that the approach described in this work and its companion time-independent model represent very useful tools for the reliable evaluation and interpretation of band shapes for electronic spectra of medium-to-large semi-rigid molecular systems in the gas phase and in solution whenever non-adiabatic effects can be neglected.

Supplementary Material

Supporting Information Available

Comparison between the experimental and theoretical spectra of anthracene and of the temperature effects on the photoionization spectrum of furan are provided in supplementary information, as well as the listing of the SNSD basis set in the Gaussian Basis Set format. This information is available free of charge via the Internet at http://pubs.acs.org This material is available free of charge via the Internet at http://pubs.acs.org/.