Neurally constrained modeling of speed-accuracy tradeoff during visual search: gated accumulation of modulated evidence

Abstract

Stochastic accumulator models account for response times and errors in perceptual decision making by assuming a noisy accumulation of perceptual evidence to a threshold. Previously, we explained saccade visual search decision making by macaque monkeys with a stochastic multiaccumulator model in which accumulation was driven by a gated feed-forward integration to threshold of spike trains from visually responsive neurons in frontal eye field that signal stimulus salience. This neurally constrained model quantitatively accounted for response times and errors in visual search for a target among varying numbers of distractors and replicated the dynamics of presaccadic movement neurons hypothesized to instantiate evidence accumulation. This modeling framework suggested strategic control over gate or over threshold as two potential mechanisms to accomplish speed-accuracy tradeoff (SAT). Here, we show that our gated accumulator model framework can account for visual search performance under SAT instructions observed in a milestone neurophysiological study of frontal eye field. This framework captured key elements of saccade search performance, through observed modulations of neural input, as well as flexible combinations of gate and threshold parameters necessary to explain differences in SAT strategy across monkeys. However, the trajectories of the model accumulators deviated from the dynamics of most presaccadic movement neurons. These findings demonstrate that traditional theoretical accounts of SAT are incomplete descriptions of the underlying neural adjustments that accomplish SAT, offer a novel mechanistic account of decision-making mechanisms during speed-accuracy tradeoff, and highlight questions regarding the identity of model and neural accumulators.

NEW & NOTEWORTHY A gated accumulator model is used to elucidate neurocomputational mechanisms of speed-accuracy tradeoff. Whereas canonical stochastic accumulators adjust strategy only through variation of an accumulation threshold, we demonstrate that strategic adjustments are accomplished by flexible combinations of both modulation of the evidence representation and adaptation of accumulator gate and threshold. The results indicate how model-based cognitive neuroscience can translate between abstract cognitive models of performance and neural mechanisms of speed-accuracy tradeoff.

INTRODUCTION

Speed-accuracy tradeoff (SAT) is fundamental for adaptive behavior (Heitz 2014). Canonical accumulator models provide a simple account of SAT: perceptual evidence is accumulated over time to a threshold that is adjusted strategically. Higher thresholds generate slower, more accurate decisions; lower thresholds generate faster, less accurate decisions (Bogacz et al. 2006, 2010; Ratcliff and Smith 2004; cf. Rae et al. 2014).

Particular single neurons appear to instantiate an accumulation of evidence to threshold (Ding and Gold 2010; Gold and Shadlen 2007; Schall 2004; but see Latimer et al. 2015), with neural dynamics of saccade-related, movement-related neurons mirroring the dynamics of accumulator models (Hanes and Schall 1996; Ratcliff et al. 2003). In monkeys performing visual search decisions, most visually responsive neurons in frontal eye field (FEF) instantiate a representation of visual search object salience guiding attention and action (Bichot and Schall 1999; Costello et al. 2013; McPeek 2006; Noudoost and Moore 2011; Ramkumar et al. 2016; Schall and Hanes 1993; Zhou and Desimone 2011). Our gated accumulator model (GAM; Purcell et al. 2010, 2012) demonstrated that evidence represented by these visually responsive neurons can drive accumulation of evidence to threshold sufficient to predict saccade response times (RTs) and errors and to replicate dynamics of movement-related neurons.

GAM is a modeling framework generalizing accumulator architectures (Ratcliff and Smith 2004) by allowing for independent race, feedforward, or lateral inhibition (Bogacz et al. 2007; Usher and McClelland 2001), with the novel addition of gated inhibition between the input evidence and accumulators. To test whether visually responsive neurons provide a sufficient representation of evidence driving accumulation, spike trains recorded from these neurons were used as the input to simulated accumulator units. Gated inhibition of spike train inputs was necessary to predict observed search behavior and quantitatively replicate movement neuron dynamics. Further simulations suggested two potential mechanisms in GAM for instantiating SAT (Purcell et al. 2012). Under the assumption of identical GAM inputs between SAT conditions, slower, more accurate responses could be achieved either by elevating threshold, which requires longer accumulation times (consistent with canonical models), or by elevating the gate, which primarily delays the onset of accumulation. The alternative of increasing total accumulation excursion by reducing baseline is not possible in the current GAM framework, as neural firing rate is bounded at 0. Those simulations provided a proof-of-concept that we test here on unique SAT data.

The first single-unit investigation of SAT sampled neurons in the FEF of monkeys revealed multiple mechanisms of control (Heitz and Schall 2012). Two monkeys performed a visual search task with short, interleaved blocks of trials cued to require fast, neutral, or accurate responding. Relative to the fast condition, in the neutral and accurate conditions, visually responsive neurons exhibited lower discharge rates before search array presentation, reduced visual responses, and delayed selection of target from distractors. These findings were recently replicated in a third monkey (Reppert et al. 2018), demonstrating that the representation of the evidence driving accumulation is modulated by SAT.

The influence of SAT on the neural accumulation of evidence to threshold has yielded mixed results. A sample of movement-related neurons from FEF of two monkeys showed smaller excursion, with lower neural activation at RT (A_RT) on accurate relative to neutral and fast conditions (Heitz and Schall 2012). However, the few movement-related neurons sampled from a third monkey showed the opposite pattern (Reppert et al. 2018). It is unclear whether these heterogeneous findings are due to sampling noise or reflect individual differences in SAT strategy. Moreover, in the superior colliculus A_RT of movement neurons was invariant across SAT conditions (Reppert et al. 2018), similar to observations in premotor and motor cortex (Thura and Cisek 2016), as well as posterior parietal cortex (Hanks et al. 2014).

Here, we test computationally the role of gate-and-threshold modulation in neural control of SAT using the GAM framework. Following Purcell et al. (2010, 2012), spike trains recorded from visually responsive neurons drive GAM accumulators to quantitatively predict RTs and errors in visual search under different SAT instructions [behavioral and neural data are from Heitz and Schall (2012) and Reppert et al. (2018)]. Because GAM is a general architecture, we can use it as a theoretical tool to test hypotheses about neurocomputational control over SAT. One possibility is that differences in visually responsive neurons alone are sufficient to explain differences across SAT conditions (hypothesis 1). This hypothesis was not considered by Purcell et al. (2012) because their simulations assumed identical visual neuron inputs across SAT conditions. Other possibilities are that strategic adjustments in gate (hypothesis 2) or threshold (hypothesis 3) are necessary as well. These alternative hypotheses were tested quantitatively in fits to correct and error RTs, as well as error rates across SAT conditions.

MATERIALS AND METHODS

Behavior and Physiology

We modeled behavioral and neurophysiological data previously collected from three macaque monkeys (Q, S, and Da) trained to perform T/L visual search with short blocks of trials (10–20) cued to be fast, neutral, or accurate. Analyses of these data have been reported in previous publications (monkeys Q and S: Heitz and Schall 2012; monkey Da: Reppert et al. 2018). Each trial started with a central fixation point presented for ~1,000 ms. The monkeys were extensively trained to associate the color of the fixation point with a SAT condition (green: fast; black: neutral; red: accurate). The target (T or L, varied across sessions) was presented at one of eight isoeccentric locations, equally spaced around the fixation point at eccentricities ranging from 8° to 12°. Distractors occupied the remaining locations and were oriented randomly among the cardinal directions. A few sessions incorporated homogeneous distractors. This search array variant did not produce any difference of neural modulation or of behavior and was, therefore, not dissociated by our modeling.

RTs were measured as the latency from search array presentation to the initiation of the saccade. Response type (correct or error) was determined by the end point of the saccade with respect to target location. In the accurate condition, monkeys were rewarded if saccades to the target exceeded an implicit response deadline [dynamically fine-tuned such that ~20% of responses were too fast; S: 427 ± 5 ms (means ± SE), Q: 500 ± 0 ms, Da: 437 ± 7 ms]. Incorrect and premature correct saccades were penalized by a 4,000 ms time out. In the neutral condition, correct saccades were rewarded regardless of RT. Incorrect saccades were followed by a 2,000 ms time out. In the fast condition, monkeys were rewarded if saccades to the target preceded an implicit response deadline (dynamically adjusted such that ~20% of responses were too slow; S: 386 ± 7 ms, Q: 364 ± 10 ms, Da: 365 ± 14 ms). Incorrect saccades made within the deadline had no time out to promote quick responding.

Neurons were categorized on the basis of firing rate patterns obtained in a memory-guided saccade task at the start of each session (Bruce and Goldberg 1985). Visually responsive activity was indicated by a significantly elevated firing rate in the interval 75–100 ms after stimulus presentation compared with a 100-ms prestimulus baseline. Presaccadic, movement-related activity was indicated by a significantly elevated firing rate in the 100 ms before saccade initiation compared with a firing rate in the interval 500–400 ms before saccade initiation. Pure visual neurons exhibited visual activity but no presaccadic activity. Visuomovement neurons showed both visual and presaccadic activity. Movement neurons showed presaccadic activity only.

Models

We used a neurally constrained GAM to identify and characterize the neural loci of SAT modulations. We first introduce the general architecture of accumulator models and describe the GAM framework. We next detail our general modeling approach, which consists in 1) driving GAM with spike data from FEF visually responsive neurons and 2) optimizing GAM model parameters to fit observed behavioral data. Unfortunately, we had a small sample of only 16 movement-related neurons in total (S: 8 neurons, Q: 6 neurons, Da: 2 neurons), which precluded a thorough and convincing quantitative analysis and comparison of neural dynamics with accumulator model dynamics—these counts contrast with an order of magnitude more visually responsive neurons driving the accumulation of evidence (S: 72 neurons; Q: 71 neurons; Da: 21 neurons). A brief summary of these analyses is provided in results. The input to GAM for each monkey was restricted to the visual neurons recorded in that monkey.

Accumulator models.

Multialternative accumulator models of decision making are characterized by multiple accumulator units, with one unit associated with each response alternative. Perceptual evidence in favor of a given response is accumulated in the corresponding unit. The unit that first reaches a threshold of accumulated evidence wins the race and determines what response is made (whether correct or error) and when it is made (RT). Different sources of noise (in the physical stimuli, in perceptual processing, intrinsic to each accumulator), both within trials and across trials, make accumulation trajectories stochastic, potentially leading to an incorrect choice, and leading naturally to predicted variability in RT. In the canonical accumulator model framework, SAT is achieved by strategic modulation of threshold. Higher thresholds generate slower but more accurate responses (Bogacz et al. 2006; Ratcliff and Smith 2004).

A complete model of the eight-element visual search task used by Heitz and Schall (2012) and Reppert et al. (2018) would require eight accumulator units (Purcell et al. 2012), each one associated with each potential saccade location in the array. Because search array size was not manipulated in these particular experiments, we followed Purcell et al. (2010) and simplified the modeling by assuming only two accumulator units, one associated with the target location and one associated with the distractor locations. Our past modeling work has revealed that the additional complexity of fully simulating the eight-element arrays buys little additional theoretical insight at the cost of a near order of magnitude longer simulation times.

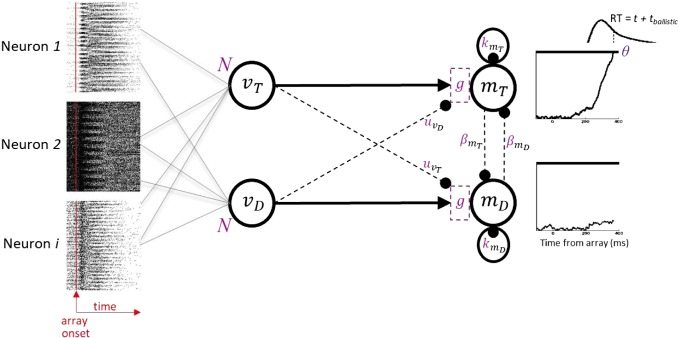
Specifically, we assumed two accumulator units, m_T and m_D, respectively, associated with a correct saccade toward the target versus an error saccade toward a distractor (Fig. 1). Unit m_T accumulates perceptual evidence for the target v_T. Unit m_D accumulates perceptual evidence for distractors v_D. A basic race-to-threshold accumulator architecture can be expanded by incorporating feedforward inhibition u between inputs or lateral inhibition β between accumulators (Ratcliff 1978; Ratcliff and Smith 2004; Usher and McClelland 2001).

Fig. 1.

Gated accumulator model (GAM) framework. Arrows indicate excitatory connectivity, while solid circles indicate inhibition. Accumulator units are driven by spike trains recorded from frontal eye field (FEF) visually responsive neurons, while monkeys performed visual search under speed-accuracy tradeoff (SAT) instructions. On each trial, N spike trains were randomly sampled and averaged to generate the input (v) to each accumulator unit (m). Trials in which the target was located within the neuron’s response field were used to generate input v_T to accumulator m_T (associated with a saccade toward the target). Trials in which a distractor was located within the neuron’s response field were used to generate input v_D to accumulator m_D (associated with a saccade toward a distractor). A simulated saccade is initiated when accumulator unit activity reaches a threshold (θ). GAM generalizes previous accumulator architectures, incorporating independent race, as well as feedforward (µ) or lateral (β) inhibition, with possible leakage (k), and the addition of novel gated inhibition (g) between the input evidence and accumulators. Model parameters (highlighted in purple) were optimized to fit visual search performance in each SAT condition to characterize the loci and mechanisms of SAT modulations.

Gated accumulator model.

GAM is mathematically defined by the following system of stochastic differential equations:

$$d{m}_T=\frac{dt}{\tau }\left[{\left(v_T\left(t\right)-u{v}_D\left(t\right)-g\right)}^{+}-\beta m_D\left(t\right)-k{m}_T\left(t\right)\right]+\sqrt{\frac{dt}{\tau }}\xi$$

$$d{m}_D=\frac{dt}{\tau }\left[{\left(v_D\left(t\right)-u{v}_T\left(t\right)-g\right)}^{+}-\beta m_T\left(t\right)-k{m}_D\left(t\right)\right]+\sqrt{\frac{dt}{\tau }}\xi$$ (1)

(see also Bogacz et al. 2006). The specific parameters in Eq. 1, g, u, β, and k, respectively, correspond to gated inhibition, feedforward inhibition, lateral inhibition, and leakage. The superscript + in the term that includes gate (g) indicates that this quantity is positive-rectified.

The time constant, τ, was set equal to 1 without loss of generality. The stochastic term $\sqrt{\frac{dt}{\tau }}\xi$ represents noise intrinsic to each accumulator unit, with ξ normally distributed with mean 0 and standard deviation σ. The values m_T and m_D accumulate to threshold θ.

As noted earlier, we consider GAM a general modeling framework in that it includes as special cases a number of proposed accumulator model architectures: These include, with u = 0, β = 0, independent race models (e.g., Brown and Heathcote 2008; Logan et al. 2014); with β = 0, u free to vary, feedforward inhibition, diffusion-like models (Mazurek et al. 2003; Ratcliff 1978); and with u = 0, β free to vary, lateral inhibition, competing accumulator models (e.g., Usher and McClelland 2001). Accumulation can be leaky by allowing k > 0. Because we used spike trains from visually responsive neurons (see below) as input to the accumulator, based on the success of past work (Purcell et al. 2010, 2012), all the models we explored allowed gated inhibition, g > 0.

GAM inputs defined by FEF visually-responsive neurons.

Accumulator inputs v_T and v_D were derived from spike trains from both visual and visuomovement neurons that selected the target from distractors (S: 72 neurons; Q: 71 neurons; Da: 21 neurons), following methods described by Purcell et al. (2010, 2012). Visual as well as visuomovement neurons were included because 1) they represent the target evidence used to guide gaze (Sato et al. 2001; Sato and Schall 2003; Thompson et al. 1996) and 2) their presaccadic activity is not involved in motor preparation (Ray et al. 2009). Each spike train was first convolved with a kernel filter y(t) that resembles a postsynaptic potential (Thompson et al. 1996):

$$y\left(t\right)=\left(1-e^{-\frac{t}{{\tau }_g}}\right)\times e^{-\frac{t}{{\tau }_d}}$$ (2)

Time constants for the growth phase (τ_g) and the decay phase (τ_d) were set at 1 ms and 20 ms, respectively, on the basis of measurements of excitatory postsynaptic potentials. The resulting spike density function (SDF) was normalized to the maximum firing rate of the neuron, regardless of condition and response type; this normalization procedure, used by Heitz and Schall (2012), prevented neurons with intrinsically high firing rates and large modulations from dominating model inputs. SDFs were then sorted according to the location of the target with respect to the neuron’s response field (RF), SAT condition (fast versus accurate), and response made (correct versus incorrect) when they were recorded. We only considered data from fast and accurate conditions because the neutral condition was included in only a small subset of sessions for monkeys Q and S, was not included at all for monkey Da.

For each simulated trial in a particular condition, N SDFs associated with that condition were randomly sampled with replacement and averaged to generate the input to a given accumulator; the quantity N is a free parameter in the model that effectively determines the signal-to-noise ratio of the input. Trials in which the target was located within the neuron’s response field (RF) were used to generate input v_T to accumulator m_T. Trials in which a distractor was located in the neuron’s RF were used to generate input v_D to accumulator m_D (Fig. 1). Ambiguous trials in which the target appeared on the irregular border of the neuron’s RF were excluded. We also discarded trials associated with a variation in single-unit isolation. Inconsistent isolation was identified by pronounced variation in discharge rates across trials, beyond that resulting from the SAT conditions, which was associated with marked differences in discharge rates across trial types. Additional criteria included assessment of excessively short interspike intervals (<1 ms). Simulated trials for a given SAT condition used SDFs sampled from that condition. In particular, the number of simulated trials that used SDFs from correct and incorrect trials was determined by the observed proportion of correct and incorrect trials. The rationale behind this procedure was to simulate the model in conditions similar to neurophysiological recordings. Analyses and modeling reported in the results section include only trials in which SAT deadlines were met. By using the same exclusion criteria as Heitz and Schall (2012) and Reppert et al. (2018), this allows the previous work to be compared directly to the present computational modeling results. For the specific data included in this model (considering only those sessions in which visually responsive neurons were recorded), the proportion of trials in which SAT deadlines were missed in the fast and the accurate condition, respectively, was 15.9% and 16.0% for monkey Q, 16.0% and 19.9% for monkey S, and 13.5% and 24.5% for monkey Da. Note that we initially attempted to fit the entire data set, regardless of whether responses met SAT deadlines. Unfortunately, GAM could not capture premature accurate and last fast trials because model inputs from visually responsive neurons were dominated by the large majority of trials in which SAT deadlines were met. Hence, the RTs and associated spike rates used for model fitting were sampled from strictly corresponding sets of trials only when the deadlines were met.

Spikes recorded after saccade initiation cannot contribute to the decision process and were, thus, excluded. To prevent an artifactual increase in variance of model inputs with RT, following Purcell et al. (2010, 2012), we extended each SDF up to 6,000 ms poststimulus as a Poisson process with a rate determined by the mean firing rate in the −50 to −10-ms window before saccade initiation. This was done on a trial-to-trial basis. A relatively large window was chosen to reduce the likelihood of a null firing rate for the Poisson process. As in Purcell et al. (2010, 2012), this procedure has only a minor impact on the models that provide a good fit to data, because the observed and simulated RTs are so similar. But it is necessary to converge on best-fitting parameter estimates.

GAM simulations.

Following Purcell et al. (2010, 2012), GAM was simulated with inputs from 300 ms before the presentation of the search array, until a threshold amount of visual evidence θ was reached. Saccadic RT was defined as the latency between stimulus onset and threshold crossing, plus a residual ballistic motor execution time of 15 ms. The ballistic time corresponds to the time necessary for the brain stem to initiate the gaze shift (Scudder et al. 2002). Because firing rates cannot be negative, accumulators were constrained to be greater than 0. All GAM simulations incorporated a modest amount of noise in the accumulator integration (ξ = 0.05), similar to Purcell et al. (2012). Although pilot explorations showed that GAM could capture search performance without noise in the accumulator units, we incorporated a modest amount of Gaussian noise intrinsic to the accumulator because it is a feature of many sequential sampling models and provides an explanation for the tonic baseline discharge rates of most FEF movement-related neurons (e.g., Bruce and Goldberg 1985; Schall 1991).

Model fitting procedure.

GAM model architectures were fitted to observed errors and correct and error RT distributions for speed and accurate conditions for each monkey. Best-fitting parameters of a particular GAM architecture were estimated with a commonly used quantile-based method (Ratcliff and Smith 2004). For each session, behavioral data were included if and only if visually responsive neurons were recorded (S: 15/18 sessions, Q: 16/20, Da: 8/9). For each condition, the models were simulated to produce RT quantiles (0.1, 0.3, 0.5, 0.7, 0.9) and choice probabilities. These predicted values were compared against observed data using a likelihood-ratio χ² statistic G² (Ratcliff and Smith 2004; Smith and Ratcliff 2009):

$$G^2=2\left({\displaystyle \sum }_{i=1}^2{n}_i{\displaystyle \sum }_{j=1}^{12}{p}_{ij}\text{log}\frac{p_{ij}}{{\pi }_{ij}}\right)$$ (3)

The outer summation over i extends over the two SAT conditions (fast versus accurate). The inner summation over j extends over the 12 bins bounded by RT quantiles (six bins for the distribution of correct responses, and six bins for the distribution of error responses). The quantity n_i corresponds to the total number of trials n per SAT condition i (S: fast = 10,201 trials, accurate = 10,215 trials; Q: fast = 11,217, accurate = 12,028; Da: fast = 4,215, accurate = 3,939). The quantities p_ij and π_ij are the observed and predicted proportions of trials in RT bin j of SAT condition i, respectively. The proportions sum to 1 across each pair of correct and error distributions. This G² statistic characterizes the goodness-of-fit of the model to the correct and error RT distributions and the correct and error choice probabilities simultaneously.

Because the models use Monte Carlo simulations, such as random sampling of observed spike trains as input, they are associated with complex error surfaces making parameter estimation more challenging than it might be for simpler deterministic models. In principle, these challenges could be mitigated by using an infinitely large number of simulated trials, but then parameter estimation would take infinitely long. For any parameter estimation of Monte Carlo models, a balance must be struck between precise parameter estimation and the amount of time allowed for that parameter estimation to converge. Additionally, different parameter estimation toolkits perform better with certain classes of models. During pilot testing, we evaluated the performance of three different optimization routines: Simplex (Nelder and Mead 1965), particle swarm (Kennedy and Eberhart 1995), and differential evolution (Storn and Price 1997). These routines were implemented using the inspyred library for Python (Garrett 2012), and each showed some difficulties in optimizing the fits of models to data.

Simplex generated the smallest G² values when a very large number of starting points (>100) were used. Thus, we employed a two-step simplex optimization procedure. In the first step, we used 150 starting points for each parameter drawn from uniform distributions spanning a wide range of plausible values. Each model was simulated 20,000 times per condition using an integration constant dt = 5 ms. Best-fitting parameters were used to constrain the parameter space during the second optimization step, in which starting points were drawn from uniform distributions with means determined by previous fits and range equal to the mean ± 20%. Each model was simulated 10,000 times per condition using an integration constant dt = 1 ms and 50 Simplex starting points. This method provided relatively stable optimization results. Fitting each model on Vanderbilt’s Advanced Computing Center for Research and Education high-performance computing cluster required several days.

Because model simulations started 300 ms before the onset of the search array, with poorly fitting parameter values, an accumulator could hit the decision threshold before stimulus onset. This behavior was penalized by setting predicted RT = 0 ms, with response type (correct versus error) determined by the winning accumulator. Conversely, the accumulator could meander below the decision threshold, failing to generate a RT. Our extension of SDFs up to 6,000 ms after stimulus onset mitigated this problem. The proportion of trials that failed to converge before the 6,000-ms simulation deadline is reported in results for each model, monkey, and condition (and was very small for the best-fitting models).

Model selection.

For each monkey and GAM model class (race, diffusion-like, and competitive), we first compared the quantitative fit of two model variants: a model in which gate and threshold were constrained to be the same between SAT conditions (referred to as model M_identical), and a model in which gate and threshold were free to vary between SAT conditions (M_{gate,threshold}); all other model parameters were assumed to be the same between SAT conditions. This comparison tested hypothesis 1: if the differences in the visually responsive inputs between SAT conditions are sufficient to account for the behavioral data, then M_identical should not fit significantly worse than M_{gate,threshold}. If M_identical does fit significantly worse than M_{gate,threshold}, then M_{gate,threshold} was compared with alternative models in which only gate (M_gate) or only threshold (M_threshold) was free to vary between SAT conditions. This comparison allowed us to identify whether control over gate (hypothesis 2) or control over threshold (hypothesis 3) is necessary to capture behavior as a function of SAT.

Following standard model comparison practices (Lewandowsky and Farrell 2011), the minimized G² values were converted to Akaike information criterion (AIC) and Bayesian information criterion (BIC) statistics to penalize for model complexity and perform model selection. The AIC and BIC, for binned data, are

$$\text{AIC}=G^2+2m$$

$$\text{BIC}=G^2+m\text{log}N$$ (4)

where m is the number of free parameters and N the number of observations used in the G² computation. The best model is the one associated with the smallest AIC/BIC statistic. However, because we did not use an infinite number of simulated trials, there will be uncertainty in model predictions, and, hence, uncertainty in G², AIC, and BIC values. We do not want to make model comparison decisions based on a point estimate of a somewhat noisy model fit statistic. To circumvent this problem, we simulated each model 1,000 times using best-fitting parameters to obtain a distribution of G², AIC, and BIC (these values roughly approximated a bell-shaped distribution). The 95% central range (range of values between the 2.5 and 97.5 quantiles) of these distributions was then used to guide model selection and was augmented with graphical displays to identify potential misfits. Note that the penalty term offered by AIC and BIC statistics was generally negligible compared with the large variability in G² (see results section). Consequently, model selection must be interpreted with some caution.

Quantification of FEF movement neurons and accumulator dynamics.

Movement-related neurons in FEF are involved in the initiation of saccades (Segraves 1992); these neurons are encountered less frequently than visually responsive neurons (Bruce and Goldberg 1985; Schall 1991). Unfortunately, we had a sample of only 16 movement-related neurons in total (S: 8 neurons, Q: 6 neurons, Da: 2 neurons), which precluded a thorough and convincing quantitative comparison of neural dynamics with accumulator model dynamics. Conclusions based on comparing model versus neural dynamics should be considered secondary.

Spike trains from movement-related neurons were convolved and normalized in the same way as spike trains from visual neurons. Neural dynamics were quantified as described by Woodman et al. (2008) (see also Purcell et al. 2010, 2012): For each monkey and condition, trials in which a saccade was made correctly to a target in the neuron’s movement field (MF) were sorted by RT and grouped into bins of 10 trials. The binning procedure allowed us to increase the signal-to-noise ratio of the movement responses while avoiding distortions generated by averaging trials associated with a wide range of RTs.

In each bin, SDFs were averaged, and five measures of movement neuron dynamics were measured: 1) baseline activity was computed as the mean firing rate in the 200-ms interval before stimulus onset; 2) onset of firing rate increases as computed from the change of firing rate in 30-ms intervals sampled in 1-ms increments from array presentation. Onset was defined as the center of the earliest interval satisfying two criteria: 1) averaged activity was 2 SD above baseline and 2) averaged activity remained 2 SD above baseline when the interval was moved forward for 30 ms. Onset could not be estimated for some bins when, for example, the firing rate did not grow to at least 2 SD above baseline. 3) A_RT was computed from movement responses aligned on saccade initiation and was the average activity in the interval from −20 to −10 ms before the saccade (Hanes and Schall 1996). 4) Rate of growth was estimated by dividing the difference between A_RT and activity at the beginning of the increase by the time elapsed between A_RT and the beginning of the increase. 5) Excursion was the difference between A_RT and baseline activity. We observed cases where measures of growth rate and excursion were negative; we did not remove these negative values from our analyses (their proportion is reported in results).

Neurons were included in these analyses when at least 30 trials (3 bins) were recorded (as in Purcell et al. 2012). To determine how changes in each measure accounted for variation in RT across SAT conditions, each measure was averaged across bins. For each monkey and SAT condition, we report these statistics averaged across neurons, with a 95% confidence interval obtained using a bootstrap procedure (1,000 samples). A confidence interval could not be estimated for monkey Da, because only two movement neurons were recorded.

To measure accumulator dynamics, for each model, we simulated a number of correct trials per SAT condition equal to the average number of correct trials in which the target appeared in the MF of the neuron (S: fast = 120 trials, accurate = 110; Q: fast = 160, accurate = 180; Da: fast = 100; accurate = 90), using parameter values obtained by fitting the model to behavioral data. Simulated trajectories (from the winning accumulator associated with a saccade toward the target) were then rescaled within a plausible range of firing rates. Model trajectories were then converted into Poisson spike trains to approximate the contribution of spiking variance to the data. Simulated model trajectories were then quantified using the exact same algorithms we applied to the observed neural data. For each model and SAT condition, these simulations and analyses were performed 1,000 times, and we report predicted statistics on accumulator dynamics averaged across simulations.

RESULTS

Behavior and Neurophysiology

We modeled behavior and neurophysiology from three macaque monkeys (Q, S, and Da) performing a saccade visual search for a T among L’s or L among T’s with short blocks of trials (10–20) cued for fast or accurate responding (Fig. 2A).

Fig. 2.

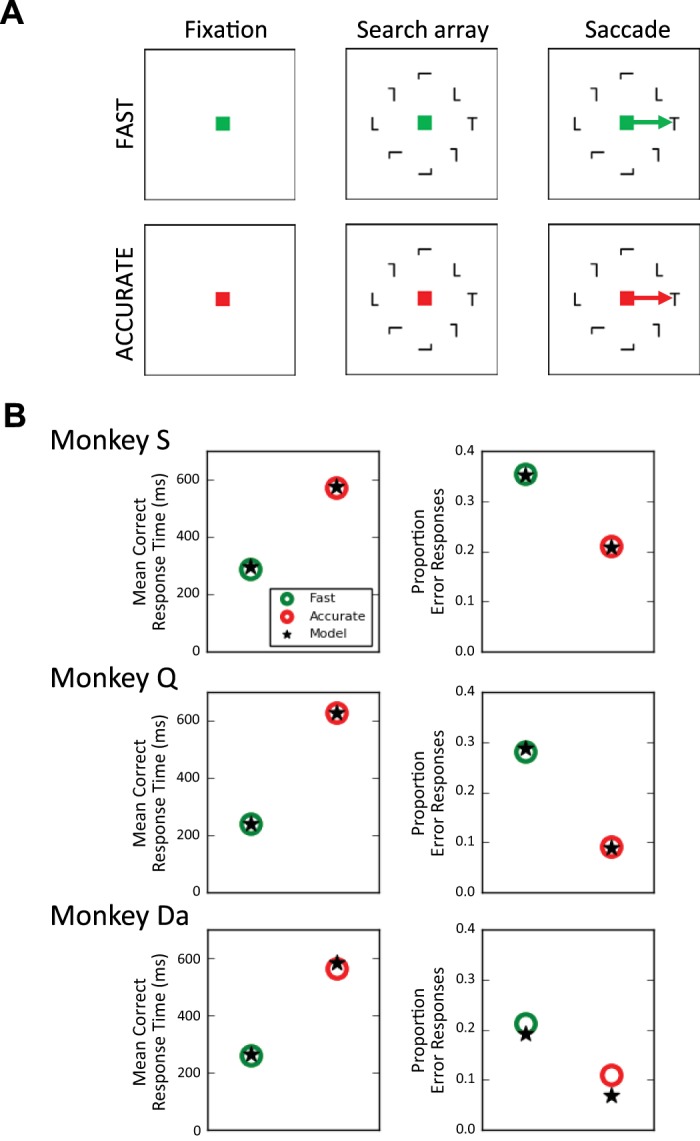
Visual search task and behavioral data. A: monkeys were trained to search for a T (or L) in a circular array of seven randomly oriented, inhomogeneous L (or T). In short blocks of trials, monkeys were cued to be fast (green fixation point) or accurate (red fixation). Reward contingencies and time deadlines enforced performance standards. B: mean response time (left) and error rate (right) for each monkey in fast (green) and accurate (red) conditions aggregated across sessions in which visually responsive neurons were recorded. Stars plot predicted mean response time and error rate from the most flexible gated accumulator model (GAM) class that allowed for variation of both gating inhibition and threshold termination of the accumulation process (monkey S: M_{gate,threshold} diffusion-like; monkey Q: M_{gate,threshold} diffusion-like; monkey Da: M_{gate,threshold} competitive).

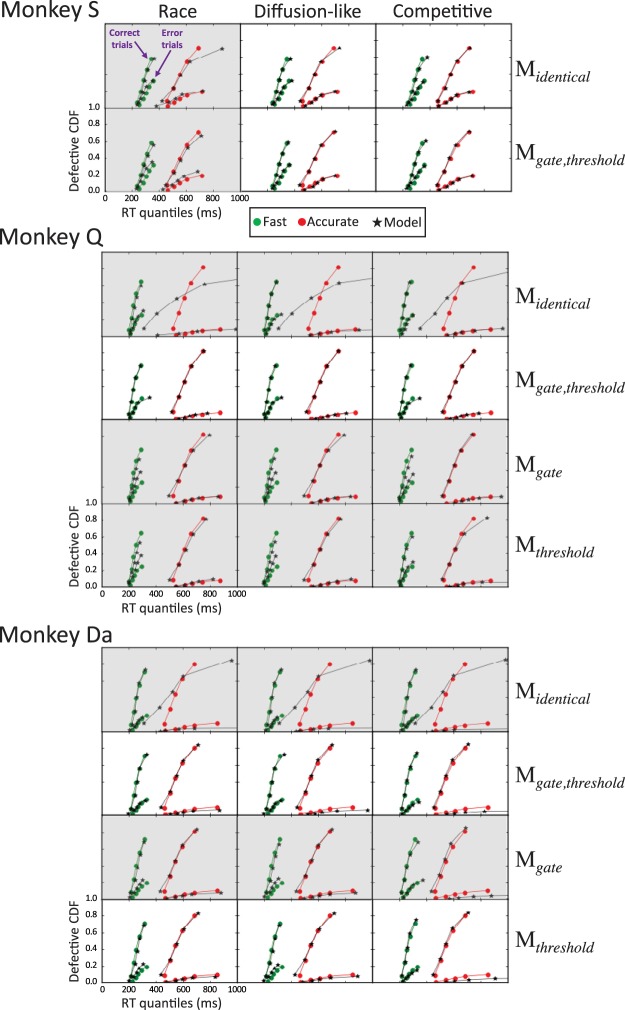
Behavior of each monkey revealed a SAT, characterized by faster mean RT and increased error rate under speed pressure (Fig. 2B). Cumulative RT distributions for each monkey, condition, and response type (correct versus error) are displayed in Fig. 3. To present both the RT distributions and accuracy values on the same graph, RT quantiles (0.1, 0.3, 0.5, 0.7, 0.9) were weighted by their corresponding proportion of correct and error responses. This plot, termed defective cumulative RT distribution, is routinely used in the cognitive modeling literature to depict behavioral data and model fits. For example, the proportion of correct responses from monkey S in the fast condition was 0.65, so weighted RT quantiles from the corresponding defective cumulative RT distribution are (0.1, 0.3, 0.5, 0.7, 0.9) × 0.65 = (0.065, 0.195, 0.325, 0.455, 0.585). Further characterization of performance is available in Reppert et al. (2018).

Fig. 3.

Visual search performance and model predictions. Correct and error response time quantiles from each monkey in the fast (green) and accurate (red) conditions are plotted as defective cumulative response time (RT) distributions in which each distribution asymptotes at the observed proportion of the respective type of trial. Accordingly, the distributions for correct trials asymptote at higher proportions than the distributions of error trials. Values predicted by the indicated gated accumulator model (GAM) architectures are plotted in black. Different architectures are distinguished along a 3 (model class: race, diffusion-like, competitive) × 4 [parameters varying between speed-accuracy tradeoff (SAT) conditions: no parameter (M_identical), gate and threshold (M_{gate,threshold}), gate only (M_gate), threshold only (M_threshold)]. Nonshaded subplots highlight best-fitting models. For monkey S, M_gate, and M_threshold were not fit because M_identical did not fit significantly worse than M_{gate,threshold}. For monkey Q, M_{gate,threshold} provided the best fit. For monkey Da M_{gate,threshold} and M_threshold provided indistinguishable best fits.

Figure 4 shows normalized FEF visually responsive neuron activity averaged across neurons for each monkey, SAT condition, and response type. On correct trials, activity initially increased after the onset of the search array and evolved to discriminate the location of the target. Specifically, activity evoked by a target became larger than activity evoked by a distractor. The reversed pattern was observed on error trials, demonstrating that errors are caused by incorrect representation of a distractor as if it were the target (Heitz et al. 2010; Reppert et al. 2018; Thompson et al. 2005). As a consequence, simulated trials sampled from error trials generally produced an incorrect response.

Fig. 4.

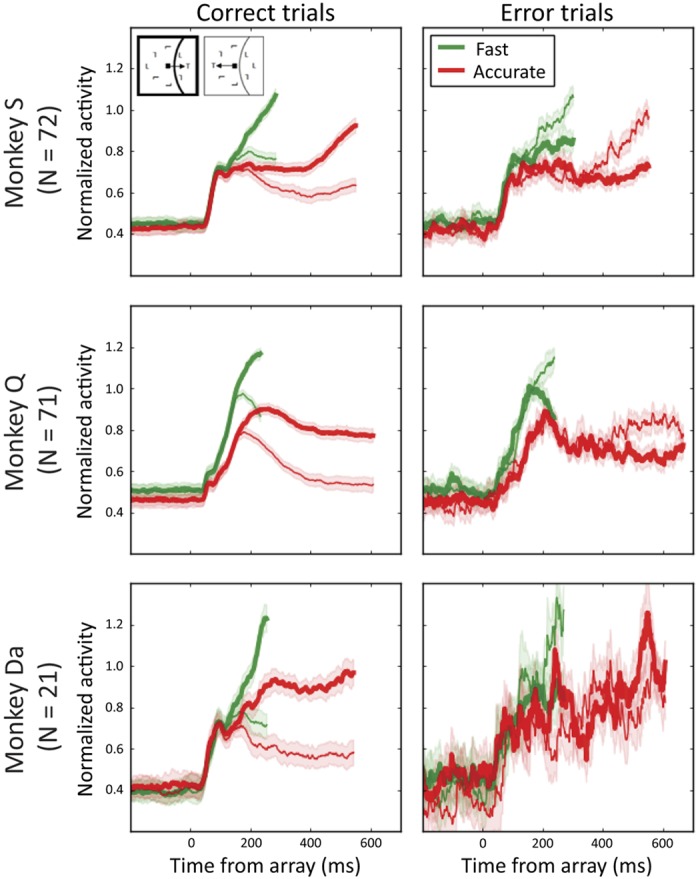
Averaged, normalized discharge rates of frontal eye field visually responsive neuron samples aligned to array presentation when the target (thick) or distractors (thin) appear in the response field on correct (left) and error (right) fast (green) and accurate (red) trials for each monkey. Shaded areas represent means ± SE. For each monkey, search errors occur when the visually responsive neurons treat a distractor as if it were the target.

Previous analyses of visually responsive neuron activity revealed three SAT-related modulations (Heitz and Schall 2012; Reppert et al. 2018). SAT cues induced a modulation of baseline firing rate in ~50% of neurons. For most neurons, baseline firing rate was higher after a fast cue and lower after an accurate cue. The magnitude of visually responsive neuron activity also increased under speed stress, and target selection occurred earlier. SAT is, thus, partly accomplished by pronounced changes in the representation of the evidence by visually responsive neurons in FEF. Our modeling will ask whether these modulations are sufficient by themselves to explain behavioral data during SAT.

Figure 5 shows normalized movement-related neuron activity averaged across neurons for each monkey and SAT condition, when a saccade was correctly made to the target in the neuron’s MF. For monkeys Q and S, Heitz and Schall (2012) reported a baseline shift in 29% of movement neurons. They also reported that the growth rate, A_RT, and excursion between baseline and A_RT were larger on average in the fast condition. However, an analysis of each movement neuron revealed some heterogeneity in A_RT and excursion between SAT conditions. For monkey S, five neurons showed larger A_RT and excursion in the fast condition, and three neurons showed the opposite pattern. For monkey Q, five neurons showed larger A_RT and excursion in the fast condition, and one neuron showed the opposite pattern. The two movement neurons recorded from monkey Da showed larger A_RT and excursion in the accurate condition (Reppert et al. 2018).

Fig. 5.

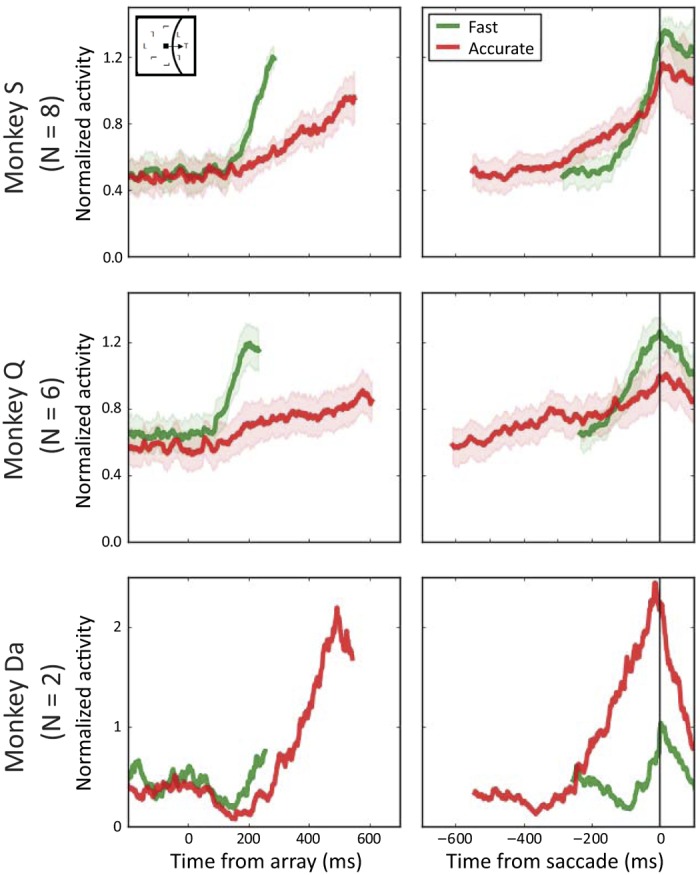
Averaged, normalized discharge rates of frontal eye field movement-related neuron samples aligned to array presentation (left) and saccade initiation (right) when the target appears in the movement field on correct fast (green) and correct accurate (red) trials for each monkey. Shaded areas represent means ± SE. For neurons recorded in monkeys Q and S, the average activation at response time was lower on average for accurate relative to fast trials. The opposite was observed for neurons recorded in monkey Da.

Model Fits to Behavioral Data

We compared fits of specific architectural variants of GAM to the performance data from the three monkeys. Model variants were defined along a 3 (model class: race versus diffusion-like versus competitive) × 4 (parameters allowed to vary between SAT conditions: no parameter [M_identical], gate and threshold [M_{gate,threshold}], gate [M_gate], threshold [M_threshold]) model matrix, constructed to test different hypotheses about the mechanistic locus of SAT.

Best-fitting parameters and fit statistics [95% central range (CR) around G², AIC, and BIC] for each GAM variant are reported in Table 1. The fit quality of each model can further be appreciated in Fig. 3, where data and model predictions are represented as defective cumulative RT distributions. Percentages of simulated trials that hit a threshold before stimulus onset or failed to reach a threshold after 6,000 ms of simulation time are reported in Table 1 for each monkey, model variant, and SAT condition. These percentages were very small for the best-fitting models and will not be further discussed.

Table 1.

GAM fits to behavioral data

		θ	g	N	k	µ	β	G2 95% CR	AIC 95% CR	BIC 95% CR	% Early	% Late
Monkey S
Midentical	R	67	0.346	32	0.0061			2,570–2,996	2,578–3,004	2,610–3036	0*, 0†	0.08*, 4.38†
	D	13	0.345	80	0.0051	0.550		1,109–1,397	1,119–1,407	1,159–1,447	0*, 0†	0.08*, 1.45†
	C	41	0.360	113	0.0074		0.0060	1,278–1,578	1,288–1,588	1,327–1,628	0*, 0†	0*, 0.13†
Mgate,threshold
	R	46*, 117†	0.624*, 0.479†	24	0.0004			1,636–1,734	1,648–1,746	1,696–1,794	0*, 0†	0.01*, 0.01†
	D	19*, 28†	0.276*, 0.268†	73	0.0009	0.626		840–1,090	854–1,104	910–1,160	0.01*, 0†	0*, 0.04†
	C	33*, 36†	0.434*, 0.428†	125	0.0072		0.0079	1,126–1,395	1,140–1,409	1,196–1,465	0*, 0†	0*, 0.01†
Monkey Q
Midentical
	R	30	0.796	23	0.0004			18,308–19,665	18,316–19,673	18,348–19,705	0*, 0†	0.03*, 10.31†
	D	12	0.622	47	0.0004	0.377		17,275–18,573	17,285–18,583	17,325–18,623	0*, 0†	0*, 9.08†
	C	48	0.098	111	0.0130		0.0078	11,331–12,268	11,341–12,278	11,381–12,318	0*, 0†	0*, 6.96†
Mgate,threshold
	R	8*, 160†	1.005*, 0.494†	50	0.0001			740–1,005	752–1,017	800–1,065	0*, 0†	0.01*, 0†
	D	9*, 178†	0.846*, 0.378†	47	0	0.158		708–960	722–974	778–1,030	0*, 0†	0*, 0†
	C	7*, 156†	1.018*, 0.473†	62	0.0003		0.0003	802–1,064	816–1,078	872–1,135	0*, 0†	0.01*, 0†
Mgate
	R	163	0.321*, 0.497†	34	0			3,232–3,818	3,242–3,828	3,282–3,868	0*, 0†	0*, 0†
	D	160	0.279*, 0.450†	35	0	0.082		3,244–3,800	3,256–3,812	3,304–3,860	0*, 0†	0*, 0†
	C	91	0.398*, 0.606†	156	0		0.0041	1,768–2,235	1,780–2,247	1,828–2,296	0*, 0†	0*, 0.05†
Mthreshold
	R	155*, 270†	0.335	26	0.0002			2,557–3,002	2,567–3,012	2,607–3,052	0*, 0†	0*, 0†
	D	156*, 270†	0.191	27	0.0004	0.220		2,531–2,980	2,543–2,992	2,591–3,040	0*, 0†	0*, 0†
	C	36*, 105†	0.571	133	0.0001		0.0144	1,257–1,606	1,269–1,618	1,317–1,666	0*, 0†	0*, 10.87†
Monkey Da
Midentical
	R	8	0.940	38	0.0006			3,109–3,426	3,117–3,434	3,145–3,462	0*, 0†	0.16*, 4.47†
	D	9	0.926	37	0.001	0.002		3,105–3,422	3,115–3,432	3,150–3,467	0*, 0†	0.22*, 6.44†
	C	8	0.924	42	0.0008		0.0302	2,941–3,229	2,951–3,239	2,986–3,275	0*, 0†	0.10*, 4.80†
Mgate,threshold
	R	20*, 126†	0.838*, 0.582†	19	0.0001			713–858	725–858	767–912	0.01*, 0†	0*, 0.03†
	D	10*, 123†	0.834*, 0.458†	23	0.0010	0.124		652–804	666–818	716–867	0*, 0	0.28*, 0.15†
	C	40*, 91†	0.673*, 0.621†	49	0.0003		0.0117	518–722	532–736	581–786	0*, 0†	0*, 0.54†
Mgate
	R	159	0.225*, 0.443†	16	0.0011			883–1,057	893–1,067	928–1,102	0.01*, 0†	0*, 0.23†
	D	167	0.210*, 0.436†	15	0.0008	0.026		863–1,029	875–1,041	917–1,083	0.02*, 0†	0*, 0.09†
	C	53	0.491*, 0.732†	61	0.0002		0.0155	841–1,073	853–1,085	895–1,127	0.0*, 0†	0*, 0.1†
Mthreshold
	R	76*, 167†	0.515	13	0			782–941	792–951	827–986	0.08*, 0†	0*, 0†
	D	73*, 157†	0.447	14	0.0003	0.109		799–958	809–968	844–1,003	0.20*, 0†	0*, 0.01†
	C	38*, 100†	0.593	44	0.0003		0.0101	548–738	560–750	602–792	0*, 0†	0*, 0.44†

^*Parameter values allowed to vary between speed-accuracy tradeoff (SAT) conditions (fast).

^†Parameter values allowed to vary between SAT conditions (accurate).

AIC, Akaike information criterion; BIC, Bayesian information criterion; C, gated competitive model; D, gated diffusion-like model; R, gated race model. Empty cells indicate the parameters were fixed to 0 for a particular architecture. Rows in italics indicate best-fitting models. Note that a few diffusion-like and competitive models failed to produce better fits than their parent race model (e.g., M_{gate, threshold} competitive for monkey Q, M_identical diffusion-like for monkey Da). This failure is indicated by comparable parameter values with the parent race model and strong overlap in 95% central range (CR) intervals. % Early shows the percentage of simulated trials that hit a threshold before array presentation. % Late shows the percentage of simulated trials that failed to reach a threshold after 6,000 ms of simulation time for each SAT condition. N, number of spike trains sampled from frontal eye field (FEF) visually responsive neurons to generate salience input; θ, threshold; g, gate; k, leakage; µ, feedforward inhibition; β, lateral inhibition.

We first compared M_identical and M_{gate,threshold} to test whether the differences in visually responsive neurons alone are sufficient to account for the performance adjustments of SAT (hypothesis 1). Model fits to behavioral data from monkey S were somewhat equivocal. The lowest 95% CR around G², AIC, and BIC statistics was achieved by M_{gate,threshold} diffusion-like, suggesting that the observed modulations of visually responsive inputs are not sufficient to account for SAT behavior. The best-fitting parameters of this model disclosed a higher decision threshold in the accurate than in the fast condition, consistent with the canonical accumulator model account. That said, Fig. 3 shows that both M_identical and M_{gate,threshold} diffusion-like/competitive provide a good fit to the data, with substantial mimicry between models (i.e., no features of the data were captured by one model that could not be captured by another). A detailed look at Table 1 indicates that the 95% CR around AIC and BIC for these models are adjacent or even overlap. Our modeling cannot unequivocally distinguish between these two hypotheses.

A comparison of M_identical and M_{gate,threshold} for monkeys Q and Da revealed considerably lower 95% CR around fit statistics for M_{gate,threshold} than M_identical, whatever the model class (race, diffusion-like, competitive). M_{gate,threshold} provided a good fit to the data, whereas M_identical failed to capture the RT distribution of correct responses in the accurate condition (Fig. 3). Best-fitting parameters for M_{gate,threshold} showed a consistent pattern across the two monkeys and model classes, with a larger threshold and a lower gate in the accurate than in the fast condition. Thus, we explored whether variation in gate (M_gate, hypothesis 2) or threshold (M_threshold, hypothesis 3) alone was sufficient to capture the behavioral data across SAT conditions. For monkey Da, 95% CR around AIC and BIC strongly overlapped for M_{gate,threshold} and M_threshold, suggesting that strategic adjustments in threshold are sufficient to capture the behavioral data. M_threshold competitive provided a slightly better fit performance than M_threshold race, although M_threshold competitive failed to capture the RT distribution of errors in the accurate condition. This failure is not surprising, because the number of visual neurons and trials completed was smaller for monkey Da (see materials and methods), resulting in fewer error trials in the accurate condition. For monkey Q, 95% CR around AIC and BIC were smaller for M_{gate,threshold} than M_gate and M_threshold, suggesting that control over both gate and threshold is necessary to explain the behavioral data. M_{gate,threshold} race, diffusion-like, and competitive provided a good fit to data, with strong mimicry between models and comparable parameter values.

The inferences from our analyses are based on the ability of the model to estimate parameters accurately. The excessive time required to simulate and fit GAM precludes a detailed parameter recovery study (see White et al. 2017), but we did simulate data from the model with the best-fitting parameters and then fit the model to the simulated data. The parameters recovered in the fits to the simulations agreed well with the parameters we used to drive the simulations.

In summary, GAM fits for monkeys Q and Da both show that the pronounced modulations of visually responsive neurons between SAT conditions, when used as input to simulated accumulators, cannot account for the performance adjustments of SAT. For both of these monkeys, while M_identical approximated the differences in median (and mean) RT between fast and accurate conditions, M_identical failed to fit the RT distributions. To fit the complete performance measures, strategic adjustments in threshold (Da) or in both gate and threshold (Q) are necessary. Moreover, the threshold for the accurate condition must exceed that for the fast condition, consistent with the canonical accumulator model explanation of SAT effects. We note that M_gate produced a far closer correspondence between observed data and model predictions than that for M_identical.

In contrast, model fits for monkey S revealed that both M_identical and M_{gate,threshold} fit the data, with slight quantitative superiority for M_{gate,threshold}. While these comparisons were somewhat equivocal, model comparisons for monkey S did reveal that some form of competition between alternatives, via either feedforward (diffusion-like) or lateral (competitive) inhibition, are required to account for the observed data (following Purcell et al. 2010, 2012).

Dynamics of FEF Movement Neuron Activity and GAM Accumulator

Unfortunately, neural recordings yielded a smaller than desired sample of 16 movement-related neurons in total (S: 8 neurons, Q: 6 neurons, Da: 2 neurons), which contrasts by an order of magnitude with the more visually responsive neurons driving the accumulation of evidence (S: 72 neurons; Q: 71 neurons; Da: 21 neurons). Nevertheless, given that further data collection was not possible and that these data are unique, we offer the following analysis with necessary caveats. We focus first on results from monkeys S and Q from which the most movement-related neurons were recorded.

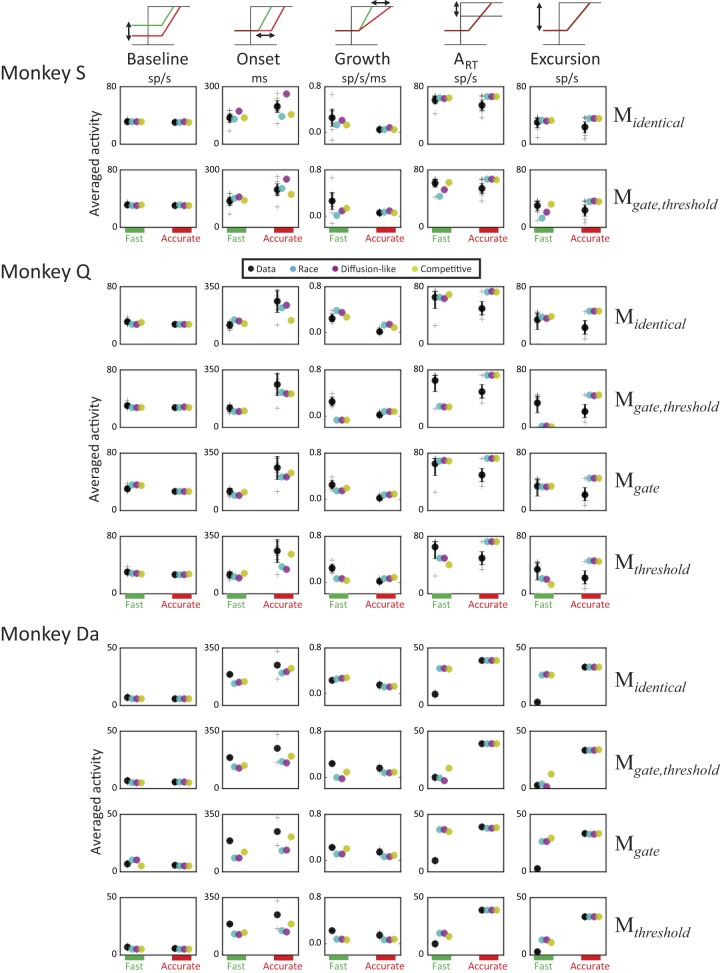
We measured the baseline discharge rate, the onset of accumulation, the growth rate, A_RT, and the excursion between baseline and A_RT. Averaged measures of movement-related neuron activity from trials in which a saccade was made correctly to a target in the neuron’s MF are displayed in Fig. 6 for both monkeys in accurate and fast conditions. Monkeys S and Q showed consistent trends. On average, the onset of activation occurred earlier, and growth rate was larger in the fast condition. Note that growth rate was very small in the accurate condition, especially for monkey Q (Q: 0.02 spikes·s⁻¹·ms⁻¹; S: 0.05 spikes·s⁻¹·ms⁻¹). This phenomenon is partly due to a high percentage of RT bins in which growth rate was negative (47%; see Table 2). Such a high percentage suggests abnormal accumulation dynamics compared with normal trajectories for such neurons. As reported by Heitz and Schall (2012), both A_RT and excursion between baseline and A_RT were larger on average in the fast than in the accurate condition, although as noted earlier, there was some heterogeneity across neurons.

Fig. 6.

Movement neuron modulations and model predictions. Observed neural discharge rates and model accumulator trajectories were characterized by measuring baseline firing rate, onset of activation, growth rate, A_RT, and excursion between baseline and A_RT averaged across response time (RT) bins of trials for fast (left) and accurate (right) speed-accuracy tradeoff (SAT) conditions. Observed (black) and predicted values of each measure for each gated accumulator model (GAM) architecture (cyan: race; magenta: diffusion-like; yellow: competitive) are plotted together. Each plus sign plots the measure from one neuron. Black circles plot data averaged across neurons and are accompanied by a bootstrap 95% confidence interval. Colored circles plot predictions from each GAM architecture averaged across 1,000 simulations with parameter values obtained by fitting the model to behavioral data.

Table 2.

Abnormal measures of FEF movement-related neuron activity and GAM accumulation dynamics

	Failure to Detect Onset of Activation % Bins		Negative Growth Rate % Bins	Negative Excursion % Bins
Monkey S
Data		11*, 21†	9*, 22†	4*, 9†
Midentical	R	5*, 0†	9*, 6†	0*, 0†
	D	24*, 5†	10*, 10†	1*, 0†
	C	5*, 0†	9*, 7†	0*, 0†
Mgate,threshold	R	44*, 1†	51*, 8†	11*, 0†
	D	36*, 3†	29*, 9†	4*, 0†
	C	6*, 0†	11*, 7†	0*, 0†
Monkey Q
Data		18*, 11†	9*, 47†	6*, 6†
Midentical	R	23*, 2†	3*, 2†	0*, 0†
	D	39*, 5†	5*, 2†	0*, 0†
	C	9*, 0†	4*, 1†	0*, 0†
Mgate,threshold	R	71*, 0†	79*, 2†	45*, 0†
	D	72*, 0†	79*, 2†	45*, 0†
	C	72*, 0†	79*, 1†	46*, 0†
Mgate
	R	10*, 0†	12*, 1†	0*, 0†
	D	10*, 0†	13*, 1†	0*, 0†
	C	11*, 0†	10*, 1†	0*, 0†
Mthreshold	R	23*, 0†	29*, 1†	3*, 0†
	D	21*, 0†	31*, 1†	3*, 0†
	C	53*, 0†	44*, 1†	10*, 0†
Monkey Da
Data		80*, 6†	50*, 0†	45*, 0†
Midentical	R	24*, 2†	2*, 1†	0*, 0†
	D	22*, 2†	2*, 1†	0*, 0†
	C	28*, 2†	2*, 1†	0*, 0†
Mgate,threshold	R	52*, 0†	57*, 0†	22*, 0†
	D	60*, 0†	71*, 0†	40*, 0†
	C	19*, 0†	17*, 0†	2*, 0†
Mgate	R	3*, 0†	5*, 0†	0*, 0†
	D	3*, 1†	5*, 0†	0*, 0†
	C	24*, 2†	1*, 0†	1*, 0†
Mthreshold	R	13*, 0†	14*, 0†	1*, 0†
	D	12*, 0†	14*, 0†	1*, 0†
	C	25*, 0†	21*, 0†	3*, 0†

^*Parameter values allowed to vary between speed-accuracy tradeoff (SAT) conditions (fast).

^†Parameter values allowed to vary between SAT conditions (accurate).

Note: The onset of activation is required to compute the rate of growth (see materials and methods). Consequently, the percentage of negative growth rate reported in the table is computed from those response time bins of trials in which the onset of activation could be detected. FEF, frontal eye field; GAM, gated accumulator model. Rows in italics indicate best-fitting models.

Predictions from each GAM architectural variant were obtained by simulating the models 1,000 times per SAT condition, using parameter values that provided the best fit to the behavioral data. Simulated model trajectories were rescaled and converted to simulated spike trains that were analyzed using the same algorithms applied to observed movement neurons. Predictions from each GAM variant averaged over the 1,000 simulations are shown in Fig. 6. Note the slight difference in predicted mean A_RT between SAT conditions for models than do not allow threshold to vary (M_identical and M_gate). These variations reflect the joint influence of four factors: the small and different number of trials per SAT condition in each model simulation (identical to the average number of correct trials in which the target fell in the MF of the neuron; see materials and methods), noise in model predictions, Poisson spike noise, and latency/amplitude distortions introduced by the convolution of spike trains. Abnormal measures of model dynamics (% of bins in which an onset of activation could not be detected, % of bins in which growth rate was negative, and % of bins in which excursion between baseline and A_RT was negative) are reported in Table 2. Four main observations emerge from these results:

1. Predictions from race, diffusion, and competitive models show substantial mimicry within each model variant (M_identical, M_{gate,threshold}, M_gate, M_threshold).

2. M_identical captures all aspects of movement-related neuron dynamics in the fast condition for both monkeys. The majority of predictions fall into the 95% confidence intervals. M_identical also captures several aspects of the movement-related neuron data in the accurate condition, such as the very slight reduction in baseline firing rate, longer onset of activation, and reduction of growth rate. However, this model logically fails to explain the observed variation of A_RT and excursion across SAT conditions.

3. Models that allow threshold to vary between SAT conditions (M_{gate,threshold} and M_threshold) predict a higher threshold and larger excursion in the accurate condition, which was opposite the observed pattern of neural modulation. This disparity is particularly prominent for monkey Q, because the best-fitting GAM threshold was considerably higher in the accurate relative to the fast condition (Table 1). When rescaled into a plausible range of discharge rate, this large parametric variation generates a small difference in discharge rate between baseline and ART in the fast condition and, thus, a high percentage of abnormal measures of model dynamics, at odds with observed data (Table 2).

4. Best-fitting parameters for M_gate (monkey Q) showed lower gating inhibition for the fast than the accurate condition (Table 1). The model, thus, predicts a substantial elevation of baseline and a smaller excursion in the Fast condition, inconsistent with observed neural dynamics.

The two movement-related neurons recorded from monkey Da exhibited higher A_RT and greater excursion in the accurate relative to the fast condition (Reppert et al. 2018), a pattern opposite to that observed on average for monkeys S and Q. Models that allowed threshold to vary between SAT conditions (M_{gate,threshold} and M_threshold) capture these modulations. The models also account for the high percentage of RT bins in which the onset of activation and growth rate could not be detected in the fast condition (Table 2), due the small firing rate difference between baseline and A_RT. The architectures M_identical and M_gate could not capture the large modulations of A_RT and excursion between SAT conditions.

DISCUSSION

This work evaluated alternative hypotheses about neurocomputational control accomplishing SAT using the GAM theoretical framework applied to the first neurophysiological data collected during SAT (Heitz and Schall 2012; see also Reppert et al. 2018). In previous work, simulations of GAM showed that increased gating of the input to the accumulators or increased threshold of evidence accumulation provide two loci for flexible control over SAT (Purcell et al. 2012). Single-unit neurophysiology data from three monkeys revealed systematic modulations of FEF visually responsive neurons across SAT conditions (Heitz and Schall 2012; see also Reppert et al. 2018). Parallel modulations of visually responsive neurons in the superior colliculus has also been found (Reppert et al. 2018). Using the GAM framework, we examined whether these input modulations were alone sufficient to explain performance across SAT conditions. If not, then, were adjustments in gate or threshold necessary as well? To test these alternative hypotheses, we used spike trains from visually responsive neurons that distinguish target from distractors as input to accumulator units in GAM and compared the quantitative fit to behavioral data for different architectural variants. Secondarily, we also examined whether the trajectories of the accumulator units replicated the dynamics of movement neurons, as found in the original GAM implementations (Purcell et al. 2010, 2012).

Model fits showed differences in SAT strategies across monkeys. We found that a higher threshold in the accurate than in the fast condition was necessary to capture search performance for monkeys Q and Da, and a higher level of gating inhibition was also necessary in the fast condition for monkey Q. While a higher threshold also fit the accurate relative to the fast condition for monkey S, a model using only the modulation of the visual inputs explained most of the variability in search performance.

Canonically, SAT is accomplished through adjustment of threshold alone (Bogacz et al. 2006; Ratcliff and Smith 2004; cf. Rae et al. 2014). These findings demonstrate that this approach, while effective in fitting performance data, provide an incomplete account of the neurocomputational mechanisms governing SAT. Modulation of input evidence representations, as well as modulation of decision processes, contributes to SAT. Recent functional MRI (fMRI) and electrophysiological studies in humans indicate an even more complex picture. Modulations have been found along the sensorimotor hierarchy, ranging from early sensory areas (Ho et al. 2012), cortico-striatal circuits (Forstmann et al. 2008; Ivanoff et al. 2008; van Veen et al. 2008), to motor cortex (Osman et al. 2000; Rinkenauer et al. 2004) and differential muscle activation (Reppert et al. 2018; Spieser et al., 2017).

In our previous work, validation of neurally constrained accumulator models was constrained and guided by comparing observed dynamics of movement-related neurons with trajectories of model accumulators (Boucher et al. 2007; Logan et al. 2014; Purcell et al. 2010, 2012; Purcell and Palmeri 2017). The validity of the GAM model approach was reinforced by the quantitative replication of observed movement neuron discharge rates by the trajectories of the model accumulators. Here, we aimed similarly to compare neural dynamics to model dynamics during SAT. Unfortunately, the sample of movement-related neurons in FEF during this SAT task was an order of magnitude smaller than that of visually responsive neurons used to derive accumulator model predictions, and more data cannot be collected. Hence, conclusions drawn from these valuable data must be cautious.

The best-fitting models quantitatively captured many aspects of the movement-related neuron dynamics between SAT conditions such as baseline firing rate, onset of activation, and growth rate. They failed to predict the higher A_RT observed on average in the fast relative to the accurate condition for monkeys S and Q (Heitz and Schall 2012). However, although not emphasized in the original Heitz and Schall study, a reanalysis of these data showed that a few movement neurons exhibited the opposite pattern, consistent with the models. Moreover, the two movement-related neurons recorded from monkey Da showed higher A_RT in the accurate relative to the fast condition (Reppert et al. 2018).

One can also wonder about the quality of fit to performance by models constrained with threshold parameters corresponding to the levels in the neural data. In preliminary work, we explored constraining the GAM threshold θ according to observed variations of A_RT between SAT conditions. For monkey S, this neurally constrained GAM provided a reasonable fit to data, even when the gate was constrained to be fixed across SAT conditions. This should not be surprising given the relatively small amplitude of the A_RT variation across SAT conditions and the good fit of M_identical. For monkey Q, however, the neurally constrained model variant provided a fit as bad as M_identical, with a dramatic misfit of RT distributions in the accurate condition. The conclusions drawn from this analysis must be moderated by the limited sample of movement neurons. Still, the incompatibility of the variation of GAM threshold θ and neural A_RT observed across SAT conditions seems clear.

Further research is needed to determine whether the diversity of movement-related neuron dynamics represents true functional differences or arises only from sampling variability, exacerbated by small sample sizes. Nevertheless, other recent single-unit recordings challenge the canonical assumption of higher threshold in the accurate relative to the fast condition. First, a sample of movement-related neurons in superior colliculus exhibited equivalent A_RT in the accurate and fast conditions (Reppert et al. 2018). Second, two neurophysiological studies showed equivalent A_RT, but lower baseline and build-up firing rates for accurate relative to fast in premotor and motor cortex (Thura and Cisek 2016) and in the lateral intraparietal area (Hanks et al. 2014). This pattern could be interpreted as consistent with the accomplishment of SAT through adjustment of the total excursion of evidence accumulation. In contrast, Heitz and Schall (2012) showed that the magnitude of neural excursion in FEF was insufficient to account for the magnitude of variation RT across SAT conditions. Moreover, the latter two studies interpret SAT in terms of an additional process referred to as urgency, which facilitates response production independent of evidence. Therefore, the pattern of neurophysiological and performance changes observed with SAT are not reconciled by simple changes in total accumulation excursion. Thus, across multiple data sets, the requirement of higher accumulation threshold in the accurate relative to the fast condition is incompatible with the dynamics of movement-related neurons. The implications of this difference will require further empirical work and theoretical consideration. For now, the available evidence raises questions about the transparency of the mapping between model and neural threshold and suggests that the two measures may be incommensurate (see also Zandbelt et al. 2014).

Psychologically inspired accumulator models do not incorporate details of response effectors. However, to understand how FEF movement neuron activity could vary systematically across SAT conditions, while saccade velocity appeared not to vary, Heitz and Schall (2012) introduced an integrated accumulator model. This parametric model assumed that the longer, lower activity of FEF movement neurons on accurate trials and the briefer, higher activity on fast trials were integrated over time by the brain stem saccade generator to produce saccades of matched velocities across SAT conditions. We note here, though, that a reanalysis of the saccade velocity profiles using the more sensitive measure of saccade vigor showed systematic variations with SAT conditions, monkeys, and RT (Reppert et al. 2018). Although these new observations undermine the logic of the integrated accumulator model, the problem remains of understanding the connection between the threshold of psychological models, the discharge rate of neurons, and the dynamics of muscle contractions.

The GAM framework instantiates the main accumulator model architectures, including race, diffusion, and competition, with or without leakage, and with or without gate. An interesting path for future research would be to explore a GAM variant in which the gate is initially set high enough to prevent visual neurons from activating movement neurons and then dropping to 0 or some value g after some time t_g (g and t_g being free parameters). SAT could be accomplished by exerting control over t_g, which would modulate the onset of evidence accumulation. We verified the viability of this model architecture in preliminary analyses. However, this model would necessarily predict an invariance of the baseline activity of FEF movement neurons across SAT conditions, a prediction inconsistent with the baseline shift observed in FEF and SC neurons.

Of course, SAT could entail modulations not instantiated within the GAM framework. For example, Cassey et al. (2014) analyzed some RT distributions from monkeys Q and S and suggested that the monkeys were timing responses relative to the enforced deadline (Heitz 2014; Wickelgren 1977). Such timing mechanisms are not part of standard accumulator models of decision making (but see Finnerty et al. 2015). However, modulation of movement-related neurons may have been influenced by a wide variety of processes outside of GAM, such as working memory (e.g., Murray et al. 2017), time-keeping (Hanks et al. 2011; Jazayeri and Shadlen 2015), urgency (e.g., Thura and Cisek 2016), response set and preparation (e.g., Dorris and Munoz 1998; Lecas et al. 1986; Wise 1985), or top-down control signals (e.g., Lo et al. 2015).

To conclude, this new GAM framework offers the first translation between canonical mechanistic accounts of speed-accuracy tradeoff through adjustment of threshold alone and observed neural mechanisms of SAT. The results provide further evidence that the instantiation of control over speed and accuracy during decision making is more complex than previously envisioned by either cognitive neuroscientists or mathematical psychologists. While the canonical account of evidence accumulation to a flexible bound remains adequate to characterize behavioral performance, understanding how model parameters map onto neural processes will require further application of a model-based cognitive neuroscience approach (Forstmann et al. 2011; Forstmann and Wagenmakers 2015; Palmeri et al. 2017; Turner et al. 2017) that combines the computational insights from mathematical psychology and cognitive modeling with the empirical observations of the brain from cognitive neuroscience and, in particular, neurophysiology.

GRANTS

This work was supported by National Institutes of Health grants NEI R01-EY021833, R01-EY08890, and NEI P30-EY008126; by Robin and Richard Patton through the E. Bronson Ingram Chair in Neuroscience; and by the Temporal Dynamics of Learning Center (NSF SMA-1041755).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

M.S. performed experiments; M.S., G.T., J.D.S., G.D.L., and T.J.P. analyzed data; M.S., G.T., J.D.S., G.D.L., and T.J.P. interpreted results of experiments; M.S. prepared figures; M.S. drafted manuscript; M.S., G.T., J.D.S., G.D.L., and T.J.P. edited and revised manuscript; M.S., G.T., J.D.S., G.D.L., and T.J.P. approved final version of manuscript; J.D.S., G.D.L., and T.J.P. conceived and designed research.