Age-related reweighting of visual and vestibular cues for vertical perception

Abstract

As we age, the acuity of our sensory organs declines, which may affect our lifestyle. Sensory deterioration in the vestibular system is typically bilateral and gradual, and could lead to problems with balance and spatial orientation. To compensate for the sensory deterioration, it has been suggested that the brain reweights the sensory information sources according to their relative noise characteristics. For rehabilitation and training programs, it is important to understand the consequences of this reweighting, preferably at the individual subject level. We psychometrically examined the age-dependent reweighting of visual and vestibular cues used in spatial orientation in a group of 32 subjects (age range: 19–76 yr). We asked subjects to indicate the orientation of a line (clockwise or counterclockwise relative to the gravitational vertical) presented within an oriented square visual frame when seated upright or with their head tilted 30° relative to the body. Results show that subjects’ vertical perception is biased by the orientation of the visual frame. Both the magnitude of this bias and response variability become larger with increasing age. Deducing the underlying sensory noise characteristics, using Bayesian inference, suggests an age-dependent reweighting of sensory information, with an increasing weight of the visual contextual information. Further scrutiny of the model suggests that this shift in sensory weights is the result of an increase in the noise of the vestibular signal. Our approach quantifies how noise properties of visual and vestibular systems change over the life span, which helps to understand the aging process at the neurocomputational level.

NEW & NOTEWORTHY Perception of visual vertical involves a weighted fusion of visual and vestibular tilt cues. Using a Bayesian approach and experimental psychophysics, we quantify how this fusion process changes with age. We show that, with age, the vestibular information is down-weighted whereas the visual weight is increased. This shift in sensory reweighting is primarily due to an age-related increase of the noise of vestibular signals.

INTRODUCTION

With an increasingly aging population, mortality and costs associated with falls and dizziness due to vestibular loss will also increase. Reduction of hair cells has been argued to be the main cause of vestibular loss, irrespective of vestibular diseases (Anson and Jeka 2016; Gleeson and Felix 1987; Lopez et al. 2005; Rosenhall and Rubin 1975; Taylor et al. 2015). Hair cell loss is a chronic degenerative disorder starting from the age of 20 to 40 yr, with more severe loss in semicircular canals (~40%) than otolith organs (~25%) (Gleeson and Felix 1987; Matheson et al. 1999; Merchant et al. 2000).

Recently, Karmali et al. (2018) explained the age-dependent changes in the vestibulo-ocular reflex (Dimitri et al. 2001) by using a Bayesian optimal adaptation model, representing a computational mechanism used by the brain in response to death of motion-sensing hair cells in the canals. Balance disorders due to hair cell loss in the otoliths (Walther and Westhofen 2007) are perhaps due to a reduced sensitivity in processing the gravitational vertical as well as linear acceleration. To compensate for this loss in spatial orientation, the brain may favor more reliable information from other sensory systems, a process called sensory reweighting (Curthoys 2000; Peterka 2002; Peterka and Loughlin 2004).

In support of this hypothesis, behavioral studies have shown that the reliance on visual cues is increased with age in the perception of vertical (Kobayashi et al. 2002; Sun et al. 2014). Recently, we used the rod-and-frame task to quantify instantaneous sensory reweighting of visual frame and vestibular cues in perceiving the orientation of rod (Alberts et al. 2016a). We showed that subjects relied more on visual frame cues when the vestibular information was made less reliable and more on vestibular cues when the visual frame information was made less reliable (see also de Winkel et al. 2018). Also, clinical studies have shown that bilateral vestibular patients are more biased by visual contextual information than healthy controls following a reweighting toward the more reliable visual cue (Alberts et al. 2018; Bronstein et al. 1996; Bronstein 1999; Grabherr et al. 2011; Guerraz et al. 2001; Lopez et al. 2007; see Medendorp et al. 2018 for review). On the basis of these results, one may argue that with the changing vestibular sensitivity, there is sensory reweighting across the life span. However, it is important to realize that the otoliths are not the only sense that becomes less reliable with age. Elderly people also encounter a decline in somatosensory functioning, vision, and hearing (Deveze et al. 2014; Iwasaki and Yamasoba 2015). For rehabilitation and exercise programs, it is important to characterize the remaining function of all sensors, and particularly their reweighting in individual subjects. In this study, using a Bayesian modeling approach and experimental psychophysics, we study the age-dependent reweighting of visual and vestibular cues used in verticality perception.

Participants within a broad age range (19–76 yr) were tested using a psychometric version of the rod-and-frame task both when seated upright and with the head tilted 30° relative to the body. They had to indicate whether the orientation of a briefly flashed rod within a roll-tilted square frame was oriented clockwise (CW) or counterclockwise (CCW) relative to the gravitational vertical. We hypothesized that elderly people rely more on the visual context of the square frame and therefore show larger peak-to-peak biases in the rod-and-frame task because their internal representation of gravity based on somatosensory, proprioceptive, and vestibular information (collectively referred to as vestibular information) has become less precise. Furthermore, our recently developed optimal integration model (Alberts et al. 2016a), combining visual, vestibular, and prior information, was fitted to the responses of each subject. By doing so, we were able to derive the additive (baseline noise when the head is upright) and multiplicative (increase in noise with roll tilt of the head) noise characteristics of the vestibular signals and the tilt-dependent noise characteristics of the contextual visual information. On the basis of these characteristics, we calculated the weighted contributions of visual and vestibular information to the perceived vertical in each individual subject. The contribution of the visual information increases over the life span, whereas the reliance on vestibular information decreases.

MATERIALS AND METHODS

Subjects.

We tested 32 naive healthy subjects (11 men, 21 women; age 19–76 yr) using the rod-and-frame task. All subjects were free of any neurological disorders and had normal or corrected-to-normal vision. Subjects received careful instructions about the experiment and received no feedback about their performance during the experiment. The present study was approved by the Ethics Committee of the Faculty of Social Sciences of the Radboud University, Nijmegen. Every participant gave written informed consent before participating in the experiment.

Setup.

Subjects were seated in front of an OLED television screen (LG 55EA8809, 123 × 69 cm, 1920 × 1080 pixels, refresh rate 60 Hz) such that their line of sight corresponded with the midpoint of the screen. The distance between the cyclopean eye and the center of the screen was 95 cm. An adjustable head cushion was used to comfortably support the head at a 30° tilt angle relative to the body. Head-on-body orientation was monitored several times per session using a digital angle meter. Experiments took place in complete darkness, except for the stimuli. Stimuli were presented in gray (0.23 cd/m²) on a black background, and responses were recorded with a button box.

Experimental paradigm.

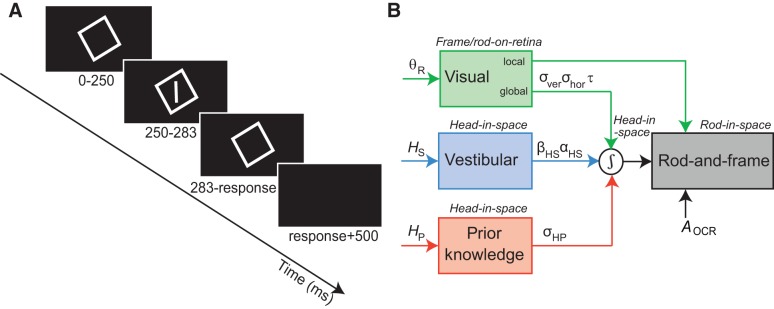
The data for the young adults (n = 10, age 27 ± 6 yr) and older adults (n = 12, age 63 ± 6 yr) were taken from previous studies (Alberts et al. 2016a, 2018). In the current study, we collected novel data of middle-aged adults in the range of 36–55 yr of age (n = 10, age 48 ± 6 yr). We used the same rod-and-frame paradigm as in Alberts et al. (2016a). Figure 1A shows a schematic illustration of the task. At the start of each trial, subjects were presented with a square frame (18.3° × 18.3° visual angle, width 0.2° visual angle). After 250 ms, a luminous rod was briefly flashed (33 ms) in the center of the square frame (angular subtense 12.6°, width 0.2°). We used a set of 18 different frame orientations (−45° to 40° in steps of 5°) and 9 different rod orientations (−12°, −8°, −5°, −2°, 0, 2°, 5°, 8°, and 12° relative to the subjective visual vertical; see below). Subjects were instructed to indicate whether the orientation of the rod was CW or CCW relative to their perceived direction of gravity by pressing the right or left button of a button box, respectively. After the response, the frame disappeared and a black screen was presented for 500 ms. Every combination of frame orientation and rod orientation was tested 10 times in a random order, yielding a total of 1,620 trials per condition.

Fig. 1.

A: experimental procedure of the rod-and-frame task. After presentation of a square frame for 250 ms, a rod is briefly (33 ms) flashed within the frame. When the rod disappears, the square remains visible until the subject responds whether the rod was oriented clockwise or counterclockwise from upright. A 500-ms black screen is presented before the start of a new trial. B: schematic representation of the optimal integration model for verticality perception, integrating global visual frame-on-retina (θ_R), vestibular head-in-space (H_S), and prior knowledge (H_P) information into an optimal head-in-space estimate. All sensory signals are assumed to be accurate but contaminated with Gaussian noise, represented by σ_ver and σ_hor for the visual, α_HS and β_HS for the vestibular, and σ_HP for the prior knowledge information. The optimal head-in-space estimate is then combined with local visual information about the rod-on-retina and eye-in-head information (magnitude A_OCR) to determine the optimal rod-in-space orientation.

Before performing tasks in the rod-and frame condition with 30° head-on-body tilt, subjects performed a subjective visual vertical task without a frame (denoted “dark SVV”), but with their head tilted by 30°. In this task, subjects indicated whether the orientation of a rod presented from a set of 9 different rod orientations (−12°, −8°, −5°, −2°, 0, 2°, 5°, 8°, and 12°) was CW or CCW relative to the perceived gravitational vertical. Each rod orientation was presented 10 times without the presence of a surrounding frame. On the basis of these results, we estimated the point of subject equality (PSE), which reflected the perceived orientation at which the subject responded 50% CW and 50% CCW. The PSE of the dark SVV (which was typically <5° across subjects) was then used as the orientation relative to which the rod orientations were centered in the rod-and-frame condition with 30° head-on-body tilt.

Data analysis.

CW tilted frame orientations and rod orientations were defined as positive. For every combination of frame and rod orientation, the proportion of CW responses was calculated. A cumulative Gaussian was fitted on these data using MATLAB’s fitting routine “fminsearch” (Wichmann and Hill 2001):

$$P\left(\text{CW}\right)=\text{λ}+\left(1-2\text{λ}\right)\frac{1}{\text{σ}\sqrt{2\text{π}}}\underset{-\infty }{\overset{x}{{\displaystyle \int }}}{e}^{-{\left(y-\text{μ}\right)}^2/2{\sigma }^2}\text{d}y,$$ (1)

in which x represents the rod orientation and λ the single lapse rate of a particular subject. The mean µ and standard deviation σ of the Gaussian represent the subjects’ perceived orientation of the gravitational vertical (i.e., the bias) and response variability, respectively.

Model fitting.

To determine the noise characteristics of the individual sensors involved in verticality perception, we fitted a Bayesian optimal integration model to the upright and 30° tilt condition simultaneously. This model was described extensively in Alberts et al. (2016a). Figure 1B shows a schematic representation of the model. To provide an optimal head-in-space orientation estimate, the brain needs to integrate global visual, vestibular, and prior information. The model assumes that the global visual information, as represented by the frame-induced head-in-space orientation, is mainly extracted from the cardinal directions of the frame. This is represented in the model by four von Mises distributions, with one peak at the veridical frame orientation and the others at 90° peak intervals. The variance of this distribution depends on the noise in both the vertical (σ_ver) and horizontal (σ_hor) cardinal directions as well as the rate at which these noise levels increase/decrease, respectively, with rotation of the frame (denoted by parameter τ). This formulation results in σ_hor and σ_ver having the same value when the frame is at 45°.

Following previous work, the vestibular information, which essentially is a combination of body somatosensory, neck proprioceptive, and vestibular information, is assumed to be veridical in coding for the proper head-in-space orientation, but contaminated with tilt-dependent noise (Alberts et al. 2016b; De Vrijer et al. 2008; Tarnutzer et al. 2009). This noise is represented by an additive offset noise component when the head is upright (β_HS) and a multiplicative noise component, which scales linearly with head-tilt angle (α_HS). Because we only tilt the head relative to the body, the body somatosensory and neck proprioceptive noise only have an additive component, whereas the vestibular noise has both an additive and a multiplicative component. Finally, the prior information represents the fact that the head is usually upright (De Vrijer et al. 2008; Eggert 1998; MacNeilage et al. 2007; Vingerhoets et al. 2009). This is modeled by a Gaussian distribution centered at 0° head-in-space orientation, with uncertainty σ_HP. From these three distributions, one can derive the likelihood function for head-in-space orientation. Furthermore, to judge the line orientation based on retinal input, one also needs to the orientation of the eye in the head, due to ocular counterroll (De Vrijer et al. 2009). The part of this counterroll modulation that the brain does not correct for is reflected by the parameter A_OCR, which is used in the reference transformation from line relative to head to line relative to space (Clemens et al. 2011; Palla et al. 2006). For the full mathematics of the model, we refer to Alberts et al. (2016a).

Together, this provides the model with seven free parameters (α_HS, β_HS, σ_HP, σ_ver, σ_hor, τ, and A_OCR). Furthermore, parameter λ denotes the lapse rate (i.e., guess rate), accounting for noninformed responses of the subject, and is another free but not mechanistic parameter of the model. These eight free parameters, also defined in Table 1, had to account for 3,240 stimulus-response pairs (2 conditions × 18 frame orientations × 9 line orientations × 10 repetitions). We fitted the model by maximizing the likelihood of the data in relation to these free parameters using the MATLAB routine “fmincon.” We repeated this routine three times with different initial starting values of the eight parameters to make sure that the fitting procedure found a global minimum rather than a local minimum. Standard deviations of the fitted parameter values were obtained by performing 100 bootstrap runs. For each run, 3,240 (reflecting the size of the data set) stimulus-response pairs were randomly sampled with replacement from the raw data, keeping the number of trials from each condition equal.

Table 1.

Model parameters and their definitions

Model Parameters	Definition
σHP	Width of the head-in-space prior, centered at upright
βHS	Uncertainty of the vestibular signal when head is upright
αHS	Increase in uncertainty of vestibular signal with head tilt
σver	Uncertainty in the vertical cardinal axis of the upright frame
σhor	Uncertainty in the horizontal cardinal axis of the upright frame
τ	Rate of increase/decrease of σver and σhor with frame tilt
λ	Lapse rate, accounting for noninformed responses

Based on the optimized parameters, we can compute the contribution of the contextual visual information, the vestibular information, and prior knowledge (σ_HP) to the estimated vertical. From the parameters we derive the variances of the individual information streams. Especially, σ_context depends on the tilt angle of the frame and σ_vest depends on the head-tilt angle [σ_vest = f(α_HS, β_HS)]. From these variances we can compute the respective weights as follows:

$$w_{\text{context}}=\frac{\frac{1}{{\text{σ}}_{\text{context}}^2}}{\frac{1}{{\text{σ}}_{\text{context}}^2}+\frac{1}{{\text{σ}}_{\text{vest}}^2}+\frac{1}{{\text{σ}}_{\text{prior}}^2}}$$ (2a)

$$w_{\text{vest}}=\frac{\frac{1}{{\text{σ}}_{\text{vest}}^2}}{\frac{1}{{\text{σ}}_{\text{context}}^2}+\frac{1}{{\text{σ}}_{\text{vest}}^2}+\frac{1}{{\text{σ}}_{\text{prior}}^2}}$$ (2b)

$$w_{\text{prior}}=\frac{\frac{1}{{\text{σ}}_{\text{prior}}^2}}{\frac{1}{{\text{σ}}_{\text{context}}^2}+\frac{1}{{\text{σ}}_{\text{vest}}^2}+\frac{1}{{\text{σ}}_{\text{prior}}^2}}$$ (2c)

Statistics.

All analyses were performed offline using MATLAB and SPSS. Between-group differences in parameter values were tested with a two-way paired univariate analysis of variance (ANOVA) with subject as a random factor. Correlations of response measures and model parameters with age were tested using linear regression. For every correlation, an R² value is reported, and t-tests were performed to test for significance.

RESULTS

Psychometric results.

Figure 2 shows the proportion of CW responses plotted against rod orientation for three example frame orientations (20° CCW, upright, and 20° CW) in a representative young, middle-aged, and older adult. When the frame is upright (Fig. 2, middle), all three subjects have high CW probabilities with large CW rod orientations and low CW probabilities with large CCW rod orientations. We fitted a psychometric curve to the responses of the subjects to the different line orientations to quantify the bias and response variability (see methods). The point at which this psychometric curve crosses the 50% CW responses is the PSE at which the subject perceives the rod to be aligned with gravity (dashed lines, µ values). When the frame is upright (Fig. 2, middle), all three representative subjects are accurate in indicating what is vertical (young adult, µ = 0.7°; middle-aged adult, µ = 0.8°; older adult, µ = 0.0°). Response variability, inversely related to the slope of the psychometric curve, is smallest for the middle-aged adult.

Fig. 2.

Probability of clockwise (CW) responses [P(CW)] plotted against rod orientation when the frame is displayed 20° counterclockwise (CCW), upright, or 20° CW for a young adult (green circles), middle-aged adult (blue circles), and older adult (red circles). Solid lines plotted through the data represent the psychometric functions, quantifying the bias (μ; dashed lines) and response variability of the subject.

When the frame is rotated to ±20°, the perceived vertical orientation is shifted in the direction of the frame. Note that these biases are smallest for the young adult (µ = −1.1° and µ = 1.7°), a bit larger for the middle-aged adult (µ = −1.5° and µ = 2.7°), and largest for the older adult (µ = −6.0° and µ = 5.4°). This is an indication that the influence of the visual frame increases with age. Also, note that in the tilted frame orientation, response variability is larger for the older adult, particularly for the 20° CW frame orientation.

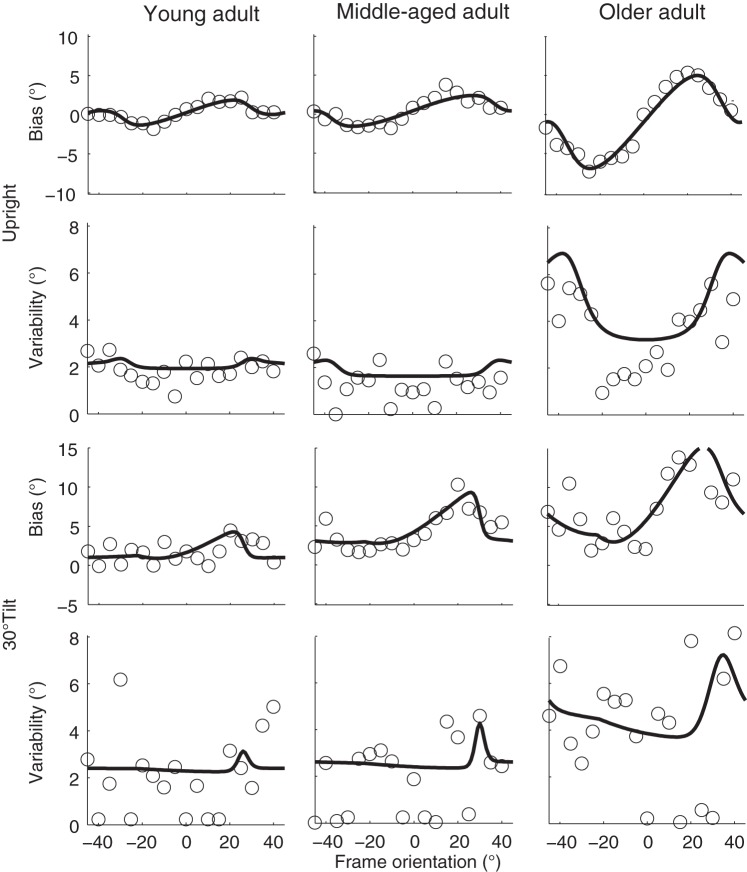
Figure 3 shows the biases and response variabilities of these three representative subjects for all frame orientations. The two top rows of Fig. 3 present the data from the 0° tilt condition in which the subjects were seated upright. In all three subjects, the bias pattern (first row) confirms the shift of perceived orientation of gravity in the direction of the orientation of the frame for frame orientations between 0° and ±45°. The plots also show the increase of the peak-to-peak magnitude from the young adult to the older adult. Response variability (second row) is lowest for the upright orientated frame and increases with increasing frame orientations. Variability is clearly larger for the older adult compared with the middle-aged and young adults.

Fig. 3.

Bias and variability plotted against frame orientation for the 3 representative subjects in the upright (top two rows) and 30° tilt condition (bottom two rows). Solid lines represent the best-fit of the Bayesian optimal integration model of Fig. 1B.

The two bottom rows of Fig. 3 represent the biases and variabilities for the 30° tilt condition. In all three subjects, the bias pattern is shifted toward a more CW (positive) frame orientation, indicating that the perceived vertical without the presence of the frame is already biased toward the 30° head-on-body tilt. In addition, the magnitudes of the biases and response variabilities are larger in the tilted condition than in the upright condition. Again, both the bias and variability patterns show a stronger modulation in the older adult.

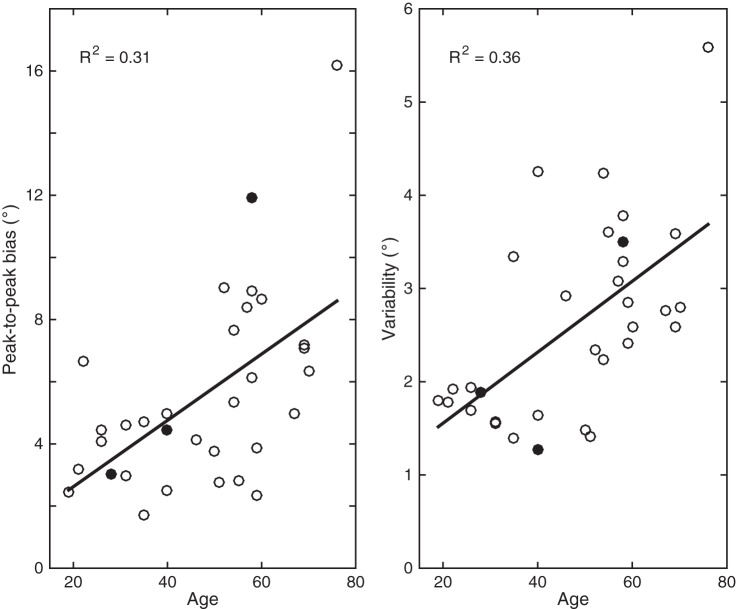
Figure 4 shows the peak-to-peak biases and response variabilities (averaged across frame orientations) plotted against age. Peak-to-peak biases are calculated by fitting a sinusoid function through the bias pattern in the head-upright condition. Regression analyses reveal a significant correlation of peak-to-peak bias with age (R² = 0.31, P < 0.001) and response variability with age (R² = 0.36, P < 0.001). In line with these findings, one would expect an increased peak-to-peak bias and increased response variability if the vestibular reliability were to decrease with age, and subjects would rely more on visual information.

Fig. 4.

Peak-to-peak bias and response variability in the head-upright condition plotted against age. Peak-to-peak biases are calculated by fitting a sinusoid through the bias patterns. Solid lines represent the linear regression analysis, which is reported by the R² correlation measure in each panel. Data points for the 3 exemplar subjects are closed circles.

Model predictions.

The Bayesian optimal integration model allows us to derive the sensory uncertainties that caused the behavioral responses. The solid lines in Fig. 3 represent the best fit of the Bayesian optimal integration model for the individual subjects. The model captures the bias patterns quite well in all three subjects, for both the head-upright (first row) and tilted conditions (third row). Similarly, the model also accounts quite well for the observed increase in response variability with frame orientation in the head-upright condition, especially for the older subject. Note that in the tilted condition (fourth row), the observed response variability is noisier. It appears more difficult for the model to capture the pattern in the data, but based on its architecture it predicts an increase in response variability around a 30° CW frame orientation.

Table 2 lists the best-fit parameters for the individual subjects and their bootstrapped-based SD values, as well as the mean of every age group (representative subjects S6, young adult; S14, middle-aged adult, and S22, older adult). Table 2 also shows the age of the subject and the maximum likelihood estimate (MLE). The latter represents how well the model fits the data, with lower values showing a better fit. Although MLE values are in the same range across the three subject groups, they were slightly but significantly lower in the middle-aged group (P < 0.02), suggesting the model fits were slightly better.

Table 2.

Best-fit parameters and their bootstrapped-based 95% confidence intervals

Subject	Age, yr	MLE	σHP, °	βHS, °	αHS	σver, °	σhor, °	τ	λ
S1	19	839.3	13.1 (9.0–17.2)	2.4 (2.1–3.0)	0.11 (0.08–0.16)	8.4 (7.1–11.7)	>90 (n.a.)	1.00 (0.39–1.00)	0.03 (0.00–0.06)
S2	21	862.1	5.6 (4.0–6.8)	3.4 (2.9–4.4)	0.08 (0.01–0.13)	5.8 (4.5–7.5)	>90 (n.a.)	1.00 (n.a.)	0.04 (0.00–0.08)
S3	22	735.9	6.2 (4.3–7.6)	2.9 (1.8–3.4)	0.01 (0.00–0.05)	4.1 (0.3–6.0)	19.8 (10.0–58.5)	0.82 (0.63–1.00)	0.03 (0.00–0.09)
S4	26	914.7	6.9 (5.9–7.6)	4.6 (4.2–4.9)	0.00 (n.a.)	7.1 (6.2–10.3)	>90 (n.a.)	1.00 (0.66–1.00)	0.00 (0.00–0.03)
S5	26	722.4	4.9 (3.7–6.4)	2.5 (2.1–3.6)	0.06 (0.03–0.09)	4.1 (2.4–6.2)	32.6 (16.3–90.0)	0.75 (0.69–1.00)	0.02 (0.00–0.05)
S6	28	668.2	4.4 (3.2–6.1)	2.3 (1.9–2.8)	0.02 (0.00–0.05)	4.6 (2.7–6.7)	20.0 (16.5–90.0)	1.00 (0.71–1.00)	0.01 (0.00–0.03)
S7	31	643.1	3.4 (2.9–4.2)	2.1 (1.8–2.7)	0.01 (0.00–0.04)	2.4 (0.4–4.2)	25.6 (11.4–50.2)	0.72 (0.67–1.00)	0.02 (0.00–0.04)
S8	31	731.5	6.0 (5.2–7.1)	2.8 (2.4–3.1)	0.00 (n.a.)	2.0 (0.3–4.7)	46.7 (27.2–90.0)	1.00 (n.a.)	0.00 (0.00–0.02)
S9	35	598.7	3.1 (2.7–5.5)	2.2 (1.8–2.7)	0.01 (0.00–0.17)	3.0 (0.5–5.8)	14.3 (7.9–41.6)	0.83 (0.65–1.00)	0.01 (0.00–0.02)
S10	35	729.8	>30 (n.a.)	3.0 (2.6–3.5)	0.10 (0.05–0.14)	11.5 (5.4–11.7)	55.1 (32.9–90.0)	1.00 (0.64–1.00)	0.06 (0.04–0.09)
S11	40	338.4	4.1 (3.2–4.9)	1.8 (1.5–2.3)	0.05 (0.01–0.09)	2.3 (0.3–4.0)	15.2 (8.8–90.0)	0.79 (0.61–1.00)	0.00 (0.00–0.01)
S12	40	404.0	4.2 (3.5–4.7)	3.3 (2.5–4.0)	0.06 (0.02–0.10)	5.1 (2.8–6.6)	15.8 (12.9–45.0)	1.00 (0.68–1.00)	0.00 (0.00–0.01)
S13	40	564.7	6.5 (6.0–7.7)	4.7 (4.4–5.4)	0.00 (n.a.)	3.4 (0.3–11.7)	>90 (n.a.)	0.98 (0.87–1.00)	0.00 (0.00–0.02)
S14	46	641.0	10.8 (8.8–14.6)	3.8 (3.4–4.4)	0.00 (n.a.)	6.0 (4.5–8.3)	89.2 (30.9–90.0)	0.78 (0.70–1.00)	0.01 (0.00–0.03)
S15	50	428.8	5.5 (4.4–6.9)	2.6 (2.1–3.0)	0.05 (0.01–0.07)	1.5 (0.3–3.5)	24.6 (17.9–36.9)	1.00 (0.79–1.00)	0.00 (0.00–0.01)
S16	51	406.1	6.3 (4.8–7.7)	2.0 (1.7–2.3)	0.05 (0.02–0.08)	4.8 (2.4–6.8)	23.7 (16.8–90.0)	0.84 (0.63–1.00)	0.00 (0.00–0.01)
S17	52	596.4	8.2 (7.0–9.3)	3.8 (3.4–4.5)	0.13 (0.07–0.17)	4.3 (3.2–5.5)	42.9 (24.6–90.0)	0.74 (0.70–1.00)	0.00 (0.00–0.01)
S18	54	815.4	>30 (n.a.)	5.0 (4.1–5.8)	0.14 (0.08–0.20)	6.5 (4.6–8.6)	>90 (n.a.)	0.76 (0.68–0.98)	0.01 (0.00–0.06)
S19	54	537.8	7.3 (6.0–9.0)	3.1 (2.6–4.2)	0.06 (0.02–0.09)	3.8 (0.3–5.7)	46.7 (28.2–90.0)	0.77 (0.67–1.00)	0.01 (0.00–0.01)
S20	55	654.3	6.5 (5.5–8.1)	4.4 (3.9–4.8)	0.02 (0.00–0.08)	6.2 (4.1–11.6)	>90 (n.a.)	0.96 (0.81–1.00)	0.02 (0.01–0.05)
S21	57	590.8	7.1 (5.8–8.2)	3.4 (2.8–4.5)	0.13 (0.05–0.19)	3.5 (1.8–6.1)	47.7 (16.0–85.3)	0.73 (0.68–1.00)	0.01 (0.00–0.04)
S22	58	652.2	6.3 (5.4–7.2)	5.0 (4.1–6.2)	0.09 (0.03–0.15)	3.7 (2.4–4.8)	37.0 (26.8–53.3)	0.74 (0.70–0.82)	0.01 (0.00–0.04)
S23	58	680.5	15.9 (12.7–19.5)	4.8 (3.8–5.2)	0.08 (0.03–0.12)	4.4 (1.7–6.5)	89.3 (38.0–90.0)	1.00 (0.74–1.00)	0.00 (0.00–0.01)
S24	58	610.3	12.0 (10.0–14.6)	4.0 (3.6–4.7)	0.14 (0.07–0.21)	5.1 (4.1–7.6)	37.6 (18.5–60.9)	0.78 (0.72–1.00)	0.00 (0.00–0.01)
S25	59	684.6	10.3 (8.0–12.9)	4.7 (3.9–5.5)	0.01 (0.00–0.05)	11.7 (3.9–11.7)	>90 (n.a.)	1.00 (0.87–1.00)	0.01 (0.00–0.04)
S26	59	531.4	8.2 (6.3–9.8)	3.5 (2.6–3.9)	0.05 (0.02–0.09)	2.4 (0.3–7.4)	68.6 (23.0–90.0)	1.00 (0.70–1.00)	0.00 (0.00–0.01)
S27	60	824.0	12.3 (9.7–14.2)	7.6 (6.2–8.1)	0.00 (n.a.)	2.5 (0.3–4.3)	86.4 (48.8–90.0)	1.00 (0.84–1.00)	0.00 (n.a.)
S28	67	513.9	5.0 (4.4–5.7)	3.9 (3.4–4.5)	0.00 (n.a.)	6.1 (5.2–8.7)	26.7 (14.4–90.0)	1.00 (0.71–1.00)	0.01 (0.00–0.02)
S29	69	698.9	10.5 (9.0–13.0)	5.3 (4.5–6.0)	0.09 (0.04–0.17)	5.8 (1.9–7.0)	35.2 (24.1–90)	0.99 (0.85–1.00)	0.00 (0.00–0.01)
S30	69	732.9	24.2 (17.0–30.0)	4.9 (4.1–5.9)	0.06 (0.02–0.11)	5.7 (4.3–6.9)	86.2 (30.8–90.0)	0.85 (0.71–1.00)	0.01 (0.00–0.02)
S31	70	777.8	12.0 (9.8–12.9)	7.2 (6.5–7.7)	0.00 (n.a.)	4.6 (3.3–5.8)	>90 (n.a.)	1.00 (0.85–1.00)	0.00 (n.a.)
S32	76	882.7	11.7 (9.5–16.7)	9.5 (8.2–11.8)	0.00 (n.a.)	5.6 (3.5–7.0)	39.2 (25.9–90.0)	0.93 (0.80–1.00)	0.04 (0.00–0.08)
Group averages
Young	27 ± 6	744.6 ± 100.1	8.4 ± 3.0	2.8 ± 0.7	0.04 ± 0.04	5.3 ± 2.1	48.2 ± 28.6	0.91 ± 0.12	0.02 ± 0.02
Middle	48 ± 6	538.7 ± 146.2	8.9 ± 7.7	3.4 ± 1.1	0.06 ± 0.05	4.4 ± 1.7	52.6 ± 33.1	0.86 ± 0.11	0.01 ± 0.01
Older	63 ± 6	681.7 ± 111.9	11.3 ± 5.1	5.3 ± 1.9	0.05 ± 0.05	5.1 ± 2.4	61.0 ± 25.9	0.92 ± 0.11	0.01 ± 0.01

Values are best-fit parameters (95% confidence intervals) for individual subjects as well as averages for the young, middle-aged, and older groups. Values in italics represent the exemplar subjects S6 (young adult), S14 (middle-aged adult), and S22 (older adult). The imposed fit limit on σ_HP was 30°. The horizontal visual context (σ_hor) was constrained at 90°, indicating that the horizontal visual context tends to show a uniform distribution around the circle. See Table 1 for definitions of parameters.

Sensory weights correlate with age.

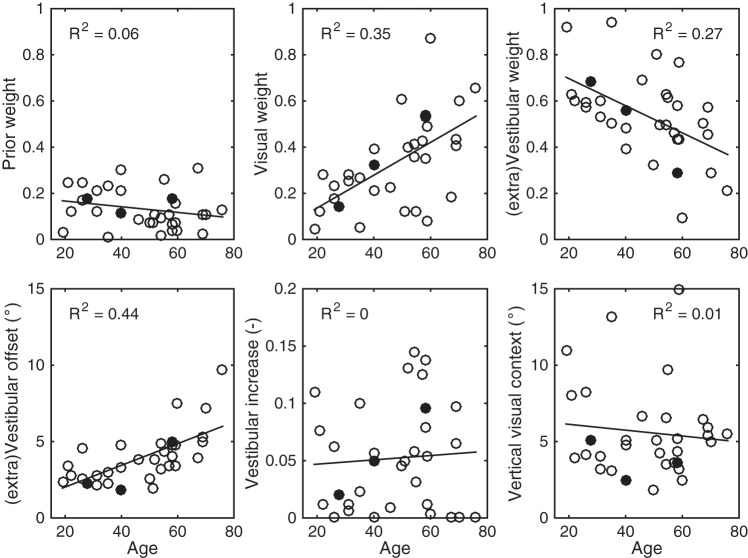
Based on the noise characteristics of the vertical visual context (σ_ver), vestibular information (α_HS, β_HS), and prior knowledge (σ_HP), captured by the parameters in Table 1, the individual weights of each sensory modality can be calculated (see Eq. 2). Figure 5, A–C, shows these sensory weights as a function of age when the subject is seated upright and views an upright square frame. Note that there is a significant positive correlation of the visual contextual weight (R² = 0.35, P < 0.001; Fig. 5B) with age and an accompanying negative correlation of the vestibular weight with age (R² = 0.27, P = 0.002; Fig. 5C). The prior knowledge weight does not show a significant correlation with age (R² = 0.06, P = 0.17; Fig. 5A). This means that older subjects rely more on visual contextual cues for judging verticality, whereas younger subjects rely more on vestibular cues.

Fig. 5.

A–C: for all subjects, prior knowledge (A), visual context (B), and vestibular weights (C) are plotted against age. Solid lines represent the linear regression analysis, which is reported by the R² measure in each panel. D–F: analyses indicating whether the effects shown in A–C are the result of a correlation with age in the additive vestibular offset (D), multiplicative vestibular increase in noise (E), or vertical visual context (F). Data points for the 3 exemplar subjects are closed circles.

This inversely coupled effect of the visual context and vestibular information could be the result of changes in the noise characteristics of the sensory modalities. For example, visual contextual noise could decrease with age, the vestibular information could become noisier, or a combination of both could explain this effect. To investigate this further, these individual parameter values are plotted against age in Fig. 5, D–F. Results show a significant correlation with age for the vestibular offset noise (R² = 0.44, P < 0.0001; Fig. 5D), but not for the proportional increase in vestibular noise (R² = 0.00, P = 1; Fig. 5E) or a reduction in visual contextual noise (R² = 0.01, P = 0.58; Fig. 5F). In conclusion, the increasing additive noise of the vestibular system with age results in a reweighting of the visual and vestibular modalities involved such that elderly subjects rely more on visual contextual cues.

DISCUSSION

Using a rod-and-frame task, we studied the relationship between age and the quality of the sensory systems across the life span. Behavioral measures showed that vertical perception was biased for frame orientations between 0° and ±45°, with increasing biases from true upright with increasing age (Fig. 4). In addition, response variability increased with age. We inferred the noise characteristics of the visual and vestibular systems using a Bayesian optimal integration model. By computing the sensory weights from the noise characteristics, the behavioral effects could be associated with the visual contextual weight correlating significantly positive with age, whereas the vestibular weight showed a significant anticorrelation. This sensory reweighting could be traced down to a change in the additive, not multiplicative, noise component of the vestibular signal, which appeared to increase with age. Our approach of combining psychophysics with Bayesian inference quantifies sensory weights at an individual subject level, which helps us to understand the aging process at a neurocomputational level.

Sensory reweighting with age.

The present findings of larger rod-and-frame biases and increased response variabilities for older subjects are consistent with previous aging (Kobayashi et al. 2002; Sun et al. 2014) and clinical (Bronstein et al. 1996; Bronstein 1999; Grabherr et al. 2011; Guerraz et al. 2001; Lopez et al. 2007) reports on increased visual reliance when vestibular information becomes less reliable. The observations may be the result of a process called sensory reweighting, in which the brain favors more reliable sensory cues rather than vestibular information to determine the direction of vertical (Curthoys 2000; Peterka 2002; Peterka and Loughlin 2004). Our current findings showing increased visual contextual weights over vestibular weights with age confirm this hypothesis.

The cause of this shift in sensory weighting with age could have multiple origins. It has been suggested that elderly people not only have a reduced vestibular functioning but also deteriorate in somatosensory functioning, vision, and hearing (Deveze et al. 2014; Iwasaki and Yamasoba 2015). Here, in the context of a rod-and-frame task, our model suggests that the reweighting for verticality perception is primarily caused by an increase in additive noise of the vestibular signals. Note, however, that in our current model somatosensory and vestibular contributions are lumped together and that the explicit dissociation between the two requires complicated experiments (Alberts et al. 2016b; Clemens et al. 2011).

Age-dependent vestibular noise changes in the brain.

The magnitude of the vestibular additive noise estimated by our Bayesian model is comparable to the perceptual displacement thresholds reported by Lim et al. (2017). They estimated the displacement threshold for static roll tilt at ~2° (see their Fig. 1), which is in the same order as our values (see Table 2). Furthermore, Bermúdez Rey et al. (2016) reported that the displacement threshold for dynamic roll tilt at 0.2 Hz [which is 1/(2f) × velocity threshold] about half of this value, likely due to canal involvement. Interestingly, they found this value to double when comparing older subjects (60–80 yr) to younger subjects (18–40 yr; see their Table 4), which is a pattern consistent with the present observations. Karmali et al. (2017) reported a significant correlation between the roll tilt thresholds, age, and the outcome of the modified Romberg balance test, in which a subject must stand on foam with eyes closed for 30 s. The larger the thresholds, the larger the chance of failing the test, even in individuals reporting no vestibular symptoms and with no evidence of vestibular dysfunction. These findings demonstrate the importance of roll-tilt vestibular cues for balance.

Although previous studies have reported that age-dependent white matter changes are related to changes in balance control (Baezner et al. 2008), not much is known about how neuronal noise changes with age in vestibular processing. Previous model simulations of vestibular afferent processing have shown that an increase of additive noise can be coupled to a reduction in vestibular-ocular reflex (VOR) time constants (Borah et al. 1988; Dimitri et al. 2001; Karmali et al. 2018; Laurens and Droulez 2007; MacNeilage et al. 2008). More specifically, Dimitri et al. (2001) showed that a combination of reduction of peripheral vestibular functioning (increased noise) and a reduction in the VOR time constant was able to classify vestibular patients. More recently, Karmali and colleagues (Karmali and Merfeld 2012; Karmali et al. 2018) used such a Bayesian simulation to show that a linear increase in additive vestibular afferent noise is able to account for the age-dependent reduction of the VOR time constants. These results are in line with our findings.

If increased additive afferent noise is the cause of vestibular symptoms such as nausea and falls, strong stimulation of these afferents in patients with severe peripheral vestibular damage could reduce these symptoms by overpowering the noise levels. The field of vestibular prosthetics makes use of this notion (for overview see Lewis 2015). Recent advances in this field showed that strong electrical stimulation evoked head movements that are close to normal physiological activity (Mitchell et al. 2013), which may be taken to suggest that the increase in additive afferent noise is indeed related to vestibular symptoms.

In support, previous studies have shown that vestibular reweighting already occurs at the first stage of vestibular processing, at the level of the vestibular nuclei (Cullen 2014; Jamali et al. 2014; Sadeghi et al. 2012), making it likely that age-dependent vestibular noise changes occur at the level of the vestibular afferents rather than more downstream in the vestibular pathway (but see Hirvonen et al. 2005). Thus, age-dependent changes in additive noise of vestibular afferents can explain self-motion thresholds and behavior in eye movements as well as responses in the rod-and-frame task, although neural evidence for this increase in additive noise has not yet been shown.

Assumptions about age-dependent hair cell loss.

Loss of vestibular hair cells can be seen as a progressive peripheral vestibular disorder, which is typically bilateral and shows a gradual worsening of vestibular processing. One of the major assumptions in aging is that this hair cell loss is homogenous across the canals/otoliths (Gleeson and Felix 1987; Matheson et al. 1999). This assumption is supported by the present study: we found changes in additive, not multiplicative noise of the vestibular signal.

A further assumption in the present study is that the age-dependent hair cell loss is linearly related to the visual contextual weight and vestibular weights. We tested for this assumption by performing a Durbin-Watson test on the residuals of the regression analysis. Test statistics revealed no significant correlation in the residuals for the different weights (visual contextual weight, P = 0.59; vestibular weight, P = 0.82; vestibular offset noise, P = 0.11), which means that a linear relationship is a valid assumption.

Implications for vestibular function testing and training programs.

Current vestibular assessments are able to test the response and sensitivity of the vestibular system, but they rely on vision-independent stimulations such as head-impulse tests or ocular vestibular-evoked myogenic potentials (Anson and Jeka 2016). We present an alternative psychophysical approach that is based on more naturalistic stimuli: verticality perception in the presence of visual context. By combining this approach with Bayesian inference techniques, we are able to not only test performance but also characterize the individual weight distribution of the subject. In addition to an enhancement in vestibular assessment, this novel approach also has implications for vestibular rehabilitation and training programs. Currently, these programs are tailored toward treating the symptoms of vestibular disorders (Deveze et al. 2014; Lacour and Bernard-Demanze 2015; Tjernström et al. 2016). For example, when subjects experience imbalance. they will receive specific balance training. The present work suggests that by characterizing the sensory reweighting process first, one could promote selective training programs directed at optimizing selective weights of this process. However, it must also be clear that the presented approach can only become a clinical tool if we can reduce the number of trials needed to infer the model parameters, for example, by using adaptive stimulus selection (Cooke et al. 2018).

GRANTS

This work was supported by the European Research Council (EU–ERC 283567) and the Netherlands Organisation for Scientific Research (NWO-VICI: 453-11-001) to W. P. Medendorp.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

B.B.A., L.P.S., and W.P.M. conceived and designed research; B.B.A. performed experiments; B.B.A. analyzed data; B.B.A., L.P.S., and W.P.M. interpreted results of experiments; B.B.A. prepared figures; B.B.A., L.P.S., and W.P.M. drafted manuscript; B.B.A., L.P.S., and W.P.M. edited and revised manuscript; B.B.A., L.P.S., and W.P.M. approved final version of manuscript.