Abstract
What are the neural mechanisms of skill acquisition? Many studies find that long-term practice is associated with a functional reorganization of cortical neural activity. However, the link between these changes in neural activity and the behavioral improvements that occur is not well understood, especially for long-term learning that takes place over several weeks. To probe this link in detail, we leveraged a brain-computer interface (BCI) paradigm in which rhesus monkeys learned to master nonintuitive mappings between neural spiking in primary motor cortex and computer cursor movement. Critically, these BCI mappings were designed to disambiguate several different possible types of neural reorganization. We found that during the initial phase of learning, lasting minutes to hours, rapid changes in neural activity common to all neurons led to a fast suppression of motor error. In parallel, local changes to individual neurons gradually accrued over several weeks of training. This slower timescale cortical reorganization persisted long after the movement errors had decreased to asymptote and was associated with more efficient control of movement. We conclude that long-term practice evokes two distinct neural reorganization processes with vastly different timescales, leading to different aspects of improvement in motor behavior.
NEW & NOTEWORTHY We leveraged a brain-computer interface learning paradigm to track the neural reorganization occurring throughout the full time course of motor skill learning lasting several weeks. We report on two distinct types of neural reorganization that mirror distinct phases of behavioral improvement: a fast phase, in which global reorganization of neural recruitment leads to a quick suppression of motor error, and a slow phase, in which local changes in individual tuning lead to improvements in movement efficiency.
Keywords: brain-computer interface, long-term learning, motor learning, plasticity
INTRODUCTION
Practice makes perfect. When we pick up a new tool for the first time, it creates a perturbation in our arm dynamics: the weight and balance of the tool cause our arm to respond to our motor commands in unexpected ways. Although we quickly adapt to these new dynamics and accomplish our task, it is only with long-term practice that we become an expert, wielding the tool with precision, speed, and efficiency. This learning is presumably accomplished through gradual mechanisms that act on populations of neurons and result in a reorganization of the cortical networks that subserve the task. However, the causal links between neural reorganization and behavioral improvement have been difficult to establish. This is primarily because in most experimental paradigms, the precise link between neural activity and behavior is unknown, making it difficult to interpret the behavioral consequences of any particular observed change in neural activity. A further complication is the timescale of the learning processes involved. Skill acquisition can take place over days or weeks of practice, or even longer (Ganguly and Carmena 2009; Karni et al, 1998; Kargo and Nitz 2003; Shmuelof et al. 2012a; Taylor et al. 2002). Studying the neural mechanisms of skill acquisition thus requires an experimental paradigm in which the causal mechanism between neural activity and behavior is explicit, controlled, and stable over long timescales.
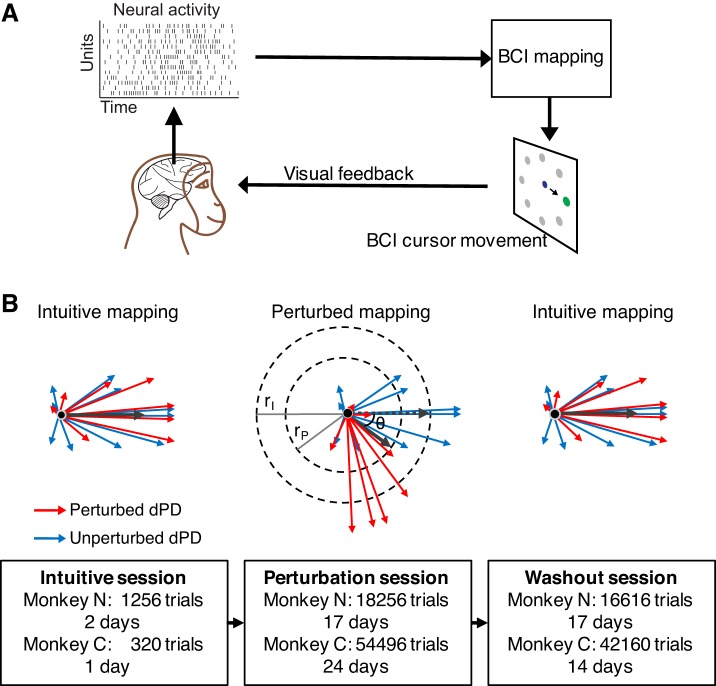
To overcome these limitations, we leveraged a brain-computer interface (BCI) paradigm (Fig. 1A). In a BCI, the causal mapping between neural activity and behavior (in our case, the velocity of a computer cursor) is known exactly and can be specified by the experimenter (Aflalo et al. 2015; Carmena et al. 2003; Gilja et al. 2012; Hochberg et al. 2012; Mulliken et al. 2008; Sadtler et al. 2014; Taylor et al. 2002). This feature makes the BCI framework a powerful tool for studying the neural mechanisms of learning (Golub et al. 2016; Orsborn et al. 2014). We trained two rhesus macaques to perform a center-out cursor movement task using a BCI that linearly maps firing rates of recorded neurons in primary motor cortex to cursor velocity. With these BCI mappings, each neuron can be thought of as “pushing” the cursor in a particular direction (Fig. 1B, left). We then perturbed the subject’s control by rotating the pushing directions of a subset of neurons (Fig. 1B, center). By tracking neurons over time, we were able to provide the same BCI mapping to the animal every day for weeks of practice (Fig. 1B, bottom center). This enabled the animal to develop proficient control of the new mapping and allowed us to characterize the neural reorganization that accompanies long-term learning.
Fig. 1.
Designing a brain-computer interface (BCI) learning experiment. A: schematic of a closed-loop BCI system. Neural activity recorded on a multielectrode Utah array implanted in the primary motor cortex is passed through a BCI mapping and translated into cursor movement on the display shown to the monkey. The monkey controls the cursor to hit targets in an 8-target (monkey N) or 16-target (monkey C) center-out task. B: long-term learning task experiment design. Each subject starts with an intuitive session whose mapping ensures that each neuron pushes the cursor toward its own preferred direction (PD; thin arrows, top left), with the magnitude of the push proportional to the neuron’s firing rate. After at least several hundred trials of practice, a perturbation is applied in which the pushing directions (dPD) of a randomly chosen subset of neurons (red arrows) are rotated relative to their PD (top center). The pushing directions of other neurons are left unchanged (blue arrows). This perturbation results in both a rotation in direction (of θ°) and a reduction in magnitude (from rI to rP) of the cursor velocity. Subjects practice in this perturbation session for multiple weeks. Finally, the BCI mapping is reverted back to its original values during the intuitive session to begin the washout session (top right). This session also lasts multiple weeks.
We found two distinct timescales of behavioral improvement over the course of training that were mirrored by two distinct types of neural reorganization. In the first phase, directional errors decreased to behavioral asymptote within several hundred trials spanning one day. These decreases were accomplished by changes in neural tuning common to all recorded neurons that acted to counter the directional errors caused by the perturbation. In the second phase, movement efficiency increased over the course of tens of thousands of trials spanning multiple weeks. This improvement was accomplished by changes in neuron tuning curves that were specific to individual neurons. In a separate set of experiments, we tested whether these long-term changes in neural tuning were driven to achieve faster cursor speeds, increase accuracy, or increase the overall rate of reward. We found that increases in reward rate were the dominant factor driving neural tuning change. Our experiments demonstrate links between specific neural tuning changes and their associated behavioral improvements throughout the time course of skill acquisition and lend insight into the behavioral drivers of long-term learning.
METHODS
All procedures were performed with the approval of the Institutional Animal Care and Use Committees of both Carnegie Mellon University and the University of Pittsburgh.
Electrophysiological recordings.
Two male rhesus (Macaca mulatta) monkeys were each implanted with a 96-channel multielectrode recording “Utah” array (Blackrock Microsystems, Salt Lake City, UT), visually inserted into the proximal arm area of the primary motor cortex on the caudal convexity of the precentral gyrus at the level of the spur of the arcuate sulcus. Recorded analog voltage signals were amplified (1,000–32,000 times), bandpass filtered (250–8,000 Hz), and digitized using a 96-channel Multichannel Acquisition Processor system (Plexon, Dallas, TX). Waveform data were converted to spiking events by threshold crossing, and waveform snippets that crossed the threshold were sorted online to isolate units for BCI decoding. Both spike times and waveforms were stored to disk for offline analyses. Recorded units were a combination of well-isolated single units and groups of two or more cells that could not be easily isolated from one another but were nevertheless tuned to intended movement direction as a group.
Brain-computer interface decoding.
Once the array was chronically implanted into the subject’s motor cortex, we trained the subject to perform the center-out target acquisition task in two dimensions (2D) in brain-control using a population vector algorithm (PVA) decoder (Chase et al. 2009; Georgopoulos et al. 1986; Taylor 2002). The monkeys’ forearms were lightly restrained during the brain-control experiment, and they exhibited minimal overt arm or hand movements when performing the task.
To implement the PVA decoder, we first fit cosine tuning functions describing how each neuron’s firing rate r tunes for intended cursor velocity d = [dx, dy],
where b0 represents the neuron’s baseline firing rate, and bx and by represent tuning coefficients found through linear regression. We computed the dynamic range of tuning m as the magnitude of the tuning vector b = [bx, by], and the preferred direction (PD) p as b/m. We performed decoding as follows. Spikes from each of the N recorded units were binned into 33-ms intervals, converted to firing rates by dividing by the sampling interval, normalized by first subtracting the baseline firing rate (b0) and then dividing by the dynamic range of tuning (m), and finally smoothed with a boxcar filter over the previous five time bins. The smoothed and normalized firing rates ri(t) were converted to cursor velocity cv(t) using the equation
where ks represents a speed factor set by the experimenter to convert the magnitude of the population vector from a normalized range to a physical speed, and δ is the number of control dimensions (2 in our case). In previous work we have found ks values of ~75 mm/s to yield good control (Chase et al. 2009, 2012). Finally, represents the decoding pushing direction (dPD) of unit i in the population of N units. For standard control during the intuitive session, the dPD of each unit was set equal to its PD as estimated from the calibration session. The cursor position fed back to the subject was obtained by integrating velocity over time. Before these experiments, each subject had received extensive training (years) on various BCI tasks, and their performance on intuitive mappings was consistently high. In these experiments, we ensured that intuitive performance was high (>97% success rate and ≤1-s target acquisition time) before they were exposed to a perturbed mapping.
Brain-computer interface learning paradigm.
Each experiment proceeded as follows (Fig. 1B). First, a calibration session was run to estimate decoding parameters. Next, an intuitive session was run with an intuitive BCI mapping between neural activity and cursor movement. This was followed by a perturbation session using a perturbed BCI mapping for multiple days to weeks and, finally, by a washout session in which the intuitive BCI mapping was again used for several days to weeks. We discuss the calibration session, construction of the intuitive mapping, construction of the perturbed mapping, and the 2D center-out task below.
Decoding parameters were obtained through a calibration session using a coadaptive procedure (Chase et al. 2012) that proceeded as follows. Decoding parameters were initialized to random values and large (40 Hz) modulation depths. Targets for the center-out task were then presented one at a time in random order and were left on the screen until a movement period of 1 s expired. The large modulation depths ensure that the cursor shows little movement during the first trial to each target. After an entire cycle of 8 (for monkey N) or 16 (for monkey C) targets in 2D was presented, the recorded firing rates for each trial were regressed against target direction (relative to center) to compute estimates of the cosine tuning curves. Decoding parameters were then set equal to these estimated values. Another cycle of targets was then presented, and the cursor velocity was decoded from the firing rates. Over the first three to four cycles of target presentation, the velocity component perpendicular to the target direction was scaled gradually and systematically from zero to full decoded value, decreasing the amount of “help” given to the subject’s control. The process repeated until the subject was able to complete the center-out task independently and reliably. In our experiment, four to five cycles of data (~2 min of data collection) were required to achieve good estimation of the decoding parameters and reliable control of the cursor movement by the subject (Brandman et al. 2018).
In each experiment, a certain number of (single or multiple neuron) units were placed into a left-out group whose activity was recorded but not used for online control. We used this group of “indirect” units to identify signatures of adaptive responses that globally affected units in the motor cortex as opposed to units used for direct cursor control. Once the calibration session was complete, the intuitive BCI mapping was defined using the direct units by setting the decoding parameters equal to the parameters estimated from the calibration session. To perturb the BCI mapping, the dPDs of a randomly chosen 50% of direct units were rotated (in a consistent 75° clockwise or counterclockwise direction) from their values obtained during the calibration session, whereas the unperturbed neurons were not adjusted. All other parameters remained the same as in the intuitive session.
In the experiments with the constant-speed BCI mapping, the only variation to the decoding procedure described above was that the cursor velocity cv(t) was normalized to a vector of unit length and then multiplied by a fixed speed factor of 100 mm/s.
Monkeys completed either an 8-target (monkey N) or 16-target (monkey C) center-out task in the 2D plane. The targets were presented in a pseudorandom order such that the monkey had to successfully reach every target in the current cycle exactly once before proceeding to the next cycle. Both the cursor and target radii were set to 8 mm, and the center-to-target distance was 85 mm. A trial started with the cursor automatically placed at the center. After a brief hold period (50 ms), a peripheral target would appear. The monkey then had 3 s to move the cursor to reach the target. When the cursor touched the target for 50 ms, the trial was deemed successful. If the monkey failed any of these timing requirements, the trial was terminated. Each trial was followed by a 500-ms pause before the next trial began.
For monkey N, every successful trial was followed by a water reward. For monkey C, a probabilistic reward paradigm was used from day 16 through day 38 such that each successful trial had a 70% probability of being rewarded. The purpose of adopting a probabilistic reward paradigm was to keep the monkey motivated and slightly challenged. Additionally, catch trials were used in the experiment for monkey C where the perturbation was removed briefly (every 1 in 16 trials during the perturbation session).
Tracking recorded units.
To track units across days, we first sorted spikes on each individual electrode to different units using spike voltage waveforms and principal component distributions. Units were separated only if they were sufficiently distinct from each other and the noise background. If multiple units were clearly distinct from noise but not reliably separable from one another, they were grouped and treated as a single unit for subsequent analyses.
We quantified the similarity of two sorted units recorded on separate experiment days using an approach similar to the methods described in Fraser and Schwartz (2012). Specifically, we compared the mean voltage waveforms (Supplemental Fig. S1; all supplementary figures are available at https://doi.org/10.5281/zenodo.2438372) and pairwise cross-correlograms of each unit between days. To compare mean spike waveform shapes, we calculated the Pearson correlation coefficient between average spike voltage vectors from separate sessions. This correlation value was then Fisher-transformed to make it more normally distributed. Similarity between pairwise cross-correlograms, which was found to be one of the more informative features by Fraser and Schwartz (2012), was calculated by taking the Fisher-transformed correlation between cross-correlograms from separate sessions. Because each unit results in the construction of several pairwise cross-correlograms, a single similarity score was computed for each unit by computing an average across all pairwise comparisons.
Using these similarity scores, we developed a binary classifier that identifies stable units. A key step when performing classification is the selection of an appropriate threshold. Although we cannot compute similarity scores between known same units across separate sessions, it is possible to generate a null distribution of similarity scores between known different units by computing the correlation between two units from separate sessions recorded from different channels on the multielectrode array (Fraser and Schwartz 2012). Using this null distribution, we computed a threshold that produces a 5% false positive rate in the classification. We used an iterative classification approach that proceeded as follows. We computed the similarity scores of all units in the population. If the smallest similarity score was below threshold, it was removed (i.e., deemed not to be tracked), and the pairwise cross-correlation similarity of each remaining unit was recomputed as the average of the cross-correlations over all other remaining units. This procedure repeated until all units remaining had similarity scores above the threshold. To be tracked across multiple days, a unit had to pass this threshold on every day boundary independently.
The performance of this classifier was tested using receiver operator characteristic (ROC) curve analysis on simulated data generated by dividing recordings from individual sessions into two halves and shuffling a subset of units during the second half of the session. When tested on these single-session data sets, the classifier was able to successfully track stable units with 99.96 ± 0.16% accuracy when using the mean spike waveform similarity metric and 98.68 ± 1.58% accuracy when using the pairwise cross-correlogram similarity metric. For analyzing data from monkey N, we used a 2D classifier using both waveform and cross-correlogram information. Using data from a single session, we created a null and known-same distribution and computed the decision boundary using Fishers linear discriminant analysis. The performance of this 2D classifier was similar to using the mean waveforms alone. For data from monkey C, we used only the cross-correlogram classifier. In general, these classification methods tolerate overall changes in spike magnitude associated with the tightness and the resistance of the Cereport connector, as well as mild shifts in time related to the displacement of online sorting thresholds.
Computing behavioral metrics.
To assess the directional errors induced by the perturbation and the subsequent adaptation, we first found the position where the cursor first crossed the circle with a radius of half the distance between the center and the target (dashed circle in Figs. 2A and 7A). We then computed the angular error as the signed angle between the vector from the center to that halfway cursor position and the vector from the center to the target of the current trial. We used the halfway cursor position because it is easy to detect and leads to robust error measures. In prior work comparing learning with full visual feedback of the BCI cursor to learning when the cursor was occluded for slightly more than the first half of the trial, we found little difference in angular errors measured at the halfway point (Chase et al. 2012).
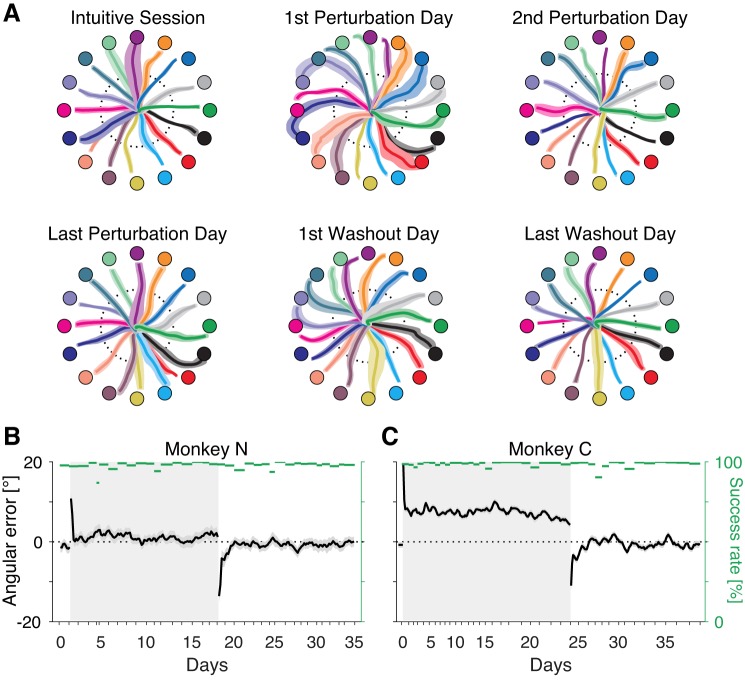
Fig. 2.
Angular errors decrease rapidly on exposure to the perturbed brain-computer interface (BCI) mapping. A: cursor trajectories of the first 5 trials to each target on a particular day for monkey C. Colored circles represent the target locations. Solid curves and shaded areas indicate the mean and SD of the trajectories to each target. Dotted circles represent the halfway point where angular errors are assessed. B and C: angular errors (black) and success rates (green) of all trials for monkeys N and C, respectively. Shaded areas around black lines represent SE. Each data point represents the average of 20 trials to each target, subsequently smoothed with a 5-step sliding window. Gray rectangle background indicates the perturbation session.
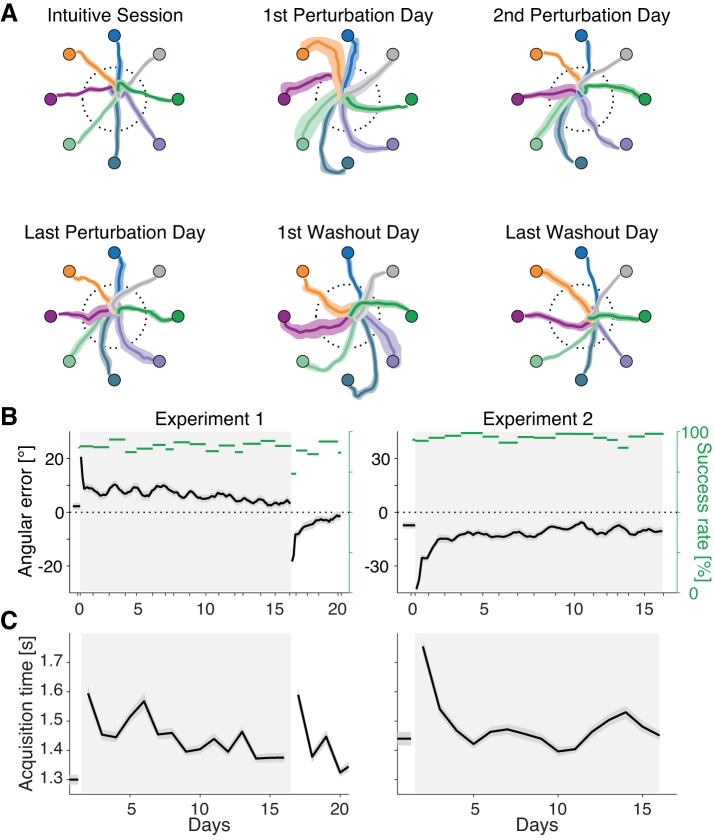
Fig. 7.
Subjects improve with extended practice on a constant-speed credit assignment rotation perturbation (csCARP) mapping. A: cursor trajectories of the first 5 trials to each target on a particular day for monkey N during experiment 1. Colored circles represent the target locations. Solid curves and shaded areas indicate the mean and SD of the trajectories to each target. Dotted circles represent the halfway point where angular errors are assessed. B: angular error and success rate across the multi-day training for experiments 1 (left) and 2 (right). Shaded areas around black lines represent SE. Each data point represents the average of 20 trials to each target, subsequently smoothed with a 5-step sliding window. Gray rectangle background indicates the perturbation session. C: average target acquisition time across days for experiments 1 (left) and 2 (right). Each data point represents the mean of the first 480 trials on each day; shaded area denotes SE.
To measure the amount of time it took the subject to control the cursor to complete a trial, we computed target acquisition time for each trial as the time from when the center hold period ended, indicating the displaying of a peripheral target, to when the target hold period began, indicating the cursor acquiring the target. This same time window was used for computing trajectory length, integrated deviation, and average speed.
Trajectory length was computed for each trial as the length of the path traveled by the cursor during the target acquisition time. The discrete positions along the cursor path were generated online at 30 Hz using the cursor velocity from the PVA decoder. With the trajectory length and target acquisition time computed, the average cursor speed was obtained for each trial as the trajectory length divided by the target acquisition time.
Integrated deviation was computed as the area circumscribed by the cursor path and the straight line between the center and the target in the current trial. This area was unsigned: deviations of the cursor in any direction from a straight line to target resulted in positive accumulation of area.
RESULTS
Two rhesus macaques were trained to perform a center-out target acquisition task under BCI control, using a PVA decoder (Fig. 1A; see methods for details). The cursor was controlled by a small number of hand-picked neurons (10 neurons for monkey C and 12 neurons for monkey N) whose waveforms had been judged to be stable over the last several days to weeks (Supplemental Fig. S1). On the first day, each neuron was fitted with a directional “cosine” tuning curve centered on its PD during a calibration session lasting ~5 min. In the PVA decoder, every neuron can be thought of as pushing the cursor in a particular direction (known as its decoding pushing direction, or dPD), with the magnitude of the push proportional to the neuron’s firing rate (Fig. 1B, top left). After the calibration session was completed, the dPD of each neuron was set to its PD to enable intuitive control of the cursor. The subjects then practiced with this intuitive mapping for at least a few hundred trials (Fig. 1B, bottom left) to establish baseline performance metrics. Both subjects performed well during the intuitive session (Fig. 2). A trial was deemed successful if the subject could move the cursor to hit the target within 3 s. Success rates during the Intuitive session were high (99.7% for monkey C and 97.8% for monkey N), with average movement times on successful trials substantially less than the 3-s cutoff (0.94 ± 0.01 s for monkey C and 1.05 ± 0.01 s for monkey N; means ± SE).
After the intuitive session, the mapping between neural activity and cursor movement was changed to induce learning. This was accomplished by rotating the dPDs of a randomly chosen 50% of “perturbed” neurons in a consistent direction by 75° (Fig. 1B, top center). The dPDs of the other “unperturbed” neurons were left at the values they had in the intuitive session. We call this mapping the credit assignment rotation perturbation (CARP) mapping, and it has two global effects on cursor movements: cursors move at an angle relative to the intended direction, and cursors move more slowly due to a dispersion in the individual pushing vectors (Fig. 1B). The CARP mapping is designed to test whether subjects can use these global error signals and solve the credit assignment problem, i.e., identify and selectively change the perturbed subgroup of neurons responsible for creating the errors (Jarosiewicz et al. 2008). After weeks of training, the CARP was removed and the BCI mapping was restored to the original, intuitive mapping in a washout session lasting multiple weeks.
Distinct phases of behavioral improvement.
We noted two distinct phases of behavioral improvement during practice with the CARP. The first phase was characterized by a rapid reduction in movement error (Fig. 2, B and C). Movement error was characterized as the angular deviation of the initial cursor movement from the straight-line movement to the target (see methods). These errors were small during the intuitive session (0.8 ± 0.70° for monkey C and −1.3 ± 0.46° for monkey N), increased substantially with introduction of the CARP (30.0 ±3.0° for monkey C and 25.9 ± 6.1° for monkey N, averaged over the first 16 trials), and decreased rapidly to behavioral asymptote with practice, with exponential decay time constants of 666 trials (monkey C) and 129 trials (monkey N). Note that the angular error asymptote was substantially larger for monkey C than for monkey N. This is most likely due to a difference in the experimental design for the two subjects. For monkey C, catch trials, in which the perturbation was removed for a randomly chosen single movement, were given during the perturbation session at a rate of 1 in 16 trials (see Supplemental Fig. S2). For monkey N, catch trials were not used. Even though angular errors were only assessed on trials in which the perturbation was on, the catch trials likely induced an unlearning effect (Focke et al. 2013; Overduin et al. 2006; Shadmehr and Holcomb 1997). It is interesting that the use of catch trials made it so that angular errors did not fully disappear, even after tens of thousands of trials lasting several weeks (van der Kooij et al. 2016; Vaswani et al. 2015).
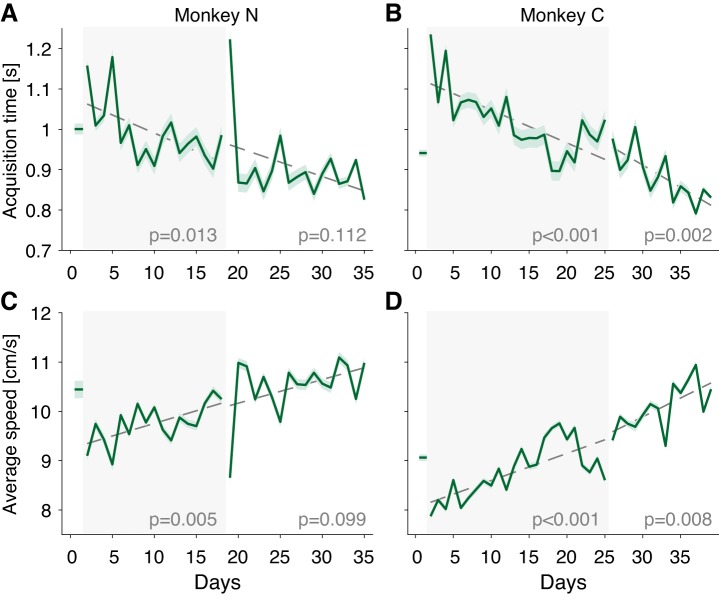
The second phase of behavioral performance was characterized by a very slow improvement in the speed of movement execution. To quantify this, we measured the target acquisition time and the cursor speed. Because of the inherent dependence of these measures on reward satiety, we computed the average of each measure over the first 480 trials each day, when the animal was motivated and focused on the task. Cursor speed was relatively fast during the intuitive session for each subject (10.4 ± 0.2 cm/s for monkey N and 9.1 ± 0.1 cm/s for monkey C; Fig. 3, C and D). On introduction of the CARP, cursor speeds decreased for each subject (to 9.1 ± 0.1 cm/s for monkey N and 7.9 ± 0.1 cm/s for monkey C) but then improved significantly over the weeks of training to final values on the last day of training of 10.3 ± 0.1 cm/s for monkey N (P < 0.001, t-test) and 8.6 ± 0.06 cm/s for monkey C (P < 0.001). Target acquisition time showed a similar effect (Fig. 3, A and B): acquisition time started near 1 s for each subject, experienced an abrupt increase at the onset of the perturbation, and then gradually recovered over the course of training, achieving a final decrease from the first to the last day of training of 0.17 ± 0.02s for monkey N (P < 0.001) and 0.21 ± 0.02 s for monkey C (P < 0.001).
Fig. 3.
Efficiency in cursor movement increases gradually with practice. A and B: target acquisition time across days for monkeys N and C, respectively. Each data point represents the mean of the first 480 trials on each day; shaded area denotes SE. Dashed lines represent a linear regression fit as a function of time within each session, with the P values shown at bottom of the plot. C and D: average cursor speed of each trial across days for monkeys N and C, respectively. Data are from the same trials used in A and B.
Similar effects were seen on transition to the washout session. After weeks of training, the CARP was removed by returning the dPDs of all neurons back to their original values from the intuitive session. Aftereffects were immediately observed in the cursor trajectories during the first washout day, which showed consistent counterclockwise angular errors of similar magnitude to those observed when the monkey initially encountered the perturbation, but of opposite sign. As in the perturbation session, angular errors during washout decreased rapidly, with exponential time constants of 2,210 and 474 trials for monkeys C and N, respectively. Note that these time constants are significantly longer than the initial learning rates (P < 0.001 for both monkeys), suggesting that unlearning proceeded more slowly than learning. Cursor speed continued to improve in one subject (monkey C) during washout but had nonsignificant increases in the other subject (monkey N), driven primarily by a dramatic improvement between the first two days of washout. Notice that target acquisition time was significantly shorter at the end of washout compared with that during the intuitive session for both subjects (acquisition time decrease of 0.33 ± 0.02 and 0.40 ± 0.02 s for monkeys N and C, respectively; P < 0.001 for both). Average cursor speed was also significantly higher by the end of washout (speed increase of 1.9 ± 0.1 cm/s, P = 0.006 for monkey N, and 2.6 ± 0.1 cm/s, P < 0.001 for monkey C, t-test). Although we cannot rule out the possibility that performance had not plateaued before the perturbation was applied, it is also possible that the training resulted in a persistent increase in performance over baseline control levels, as has been observed in human skill learning (Hasson et al. 2016).
Distinct types of neural reorganization.
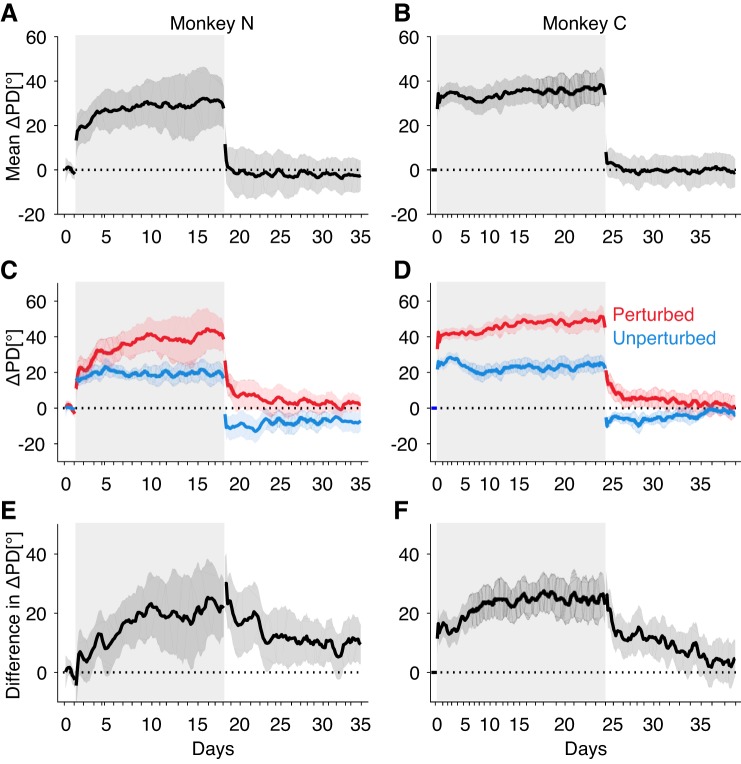
Each phase of behavioral improvement was accompanied by a distinct type of neural reorganization. We measured the change in PD (ΔPD) of each neuron from its baseline value in the intuitive session. We analyzed these ΔPD values separately for the perturbed and unperturbed groups of neurons. This allowed us to assess whether the neural reorganization was specific to the randomly selected subset of neurons we perturbed, or whether it was common to all neurons.
Immediately after the onset of the perturbation, the PDs of all neurons rotated in the direction opposite the applied perturbation (Fig. 4, A and B). This rotation likely reflects a “re-aiming” strategy (Chase et al. 2012; Jarosiewicz et al. 2008) in which the subject aims at a virtual target located counterclockwise to the actual target, thus countering the clockwise rotational effect of the perturbation. This short-timescale change is best seen in the mean ΔPD for all neurons (Fig. 4, A and B), which showed a rapid rise to asymptote after perturbation onset. This change was not specific to neurons directly driving cursor movements. Indirect neurons (neurons that were recorded during the experiment but not used in the BCI mapping to directly drive the cursor) also shifted their PDs, highlighting the global nature of this strategy (Supplemental Fig. S3).
Fig. 4.
Directional tuning changes reflect both fast and slow components of learning. A and B: average changes in preferred direction (ΔPD) of both the perturbed and unperturbed groups for monkeys N and C, respectively. C and D: ΔPD for the perturbed (red) and unperturbed (blue) groups of neurons. E and F: difference in ΔPD of the perturbed and unperturbed groups (perturbed − unperturbed). Shaded areas around lines represent SE. Gray rectangle background indicates the perturbation session.
In addition to the global change in PD shared by all neurons, we noted an initially small differential change in PD between the perturbed and unperturbed groups of neurons that gradually accumulated over the weeks of training (Fig. 4, E and F). As a result, the perturbed subgroup of neurons showed substantially more change in PD (23.0 ± 1.1° for both monkeys combined) than the unperturbed subgroup (P < 0.001; Fig. 4, C and D; also see Supplemental Figs. S4 and S5). This differential response between the perturbed and unperturbed subgroups of neurons likely reflects a credit assignment process (Chase et al. 2012; Jarosiewicz et al. 2008) specific to individual cells. The result of this process is to bring the PDs of the neurons closer to their pushing directions through the CARP mapping, which will ultimately allow for faster movements of the cursor. This credit assignment effect did not approach asymptote until roughly 10–15 days of practice.
Removal of the CARP reversed both types of neural reorganization. At the start of the washout session, there was a large change in the PD averaged across all neurons that completed within the first few hundreds of trials (Fig. 4, A and B), indicating a reversal of the re-aiming strategy. This change is also evident in the group of indirect neurons (Supplemental Fig. S3). In contrast, the differential change in PD between the perturbed and unperturbed subgroups of neurons decayed slowly over thousands of trials spanning days to weeks. In fact, in monkey N, the ΔPD values never actually returned to their pre-perturbation values over the 2 weeks, raising the intriguing possibility that they might be permanent.
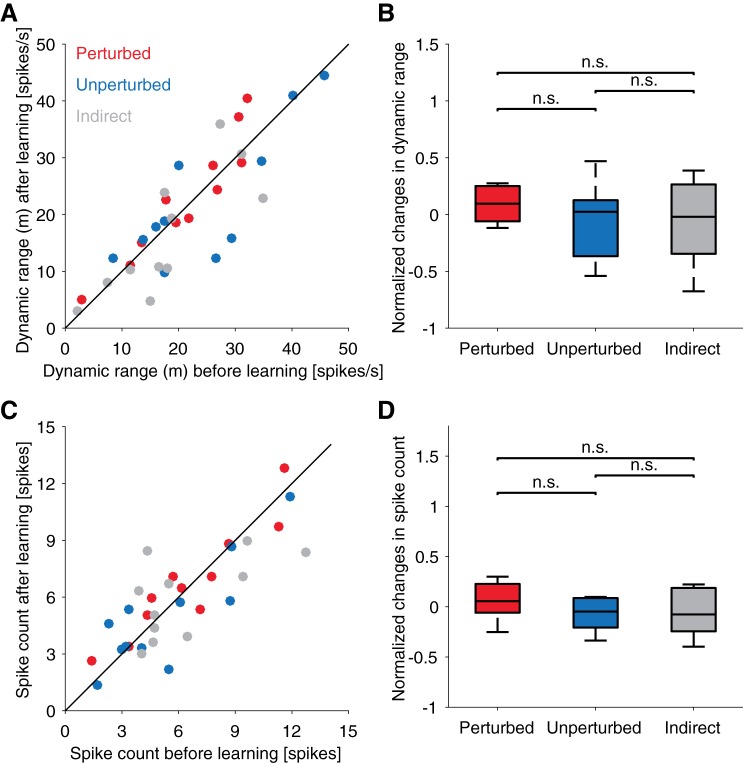
The PD of a cosine fit is just one feature of a neuron’s tuning to intended direction. To assess if other features of tuning changed in a way that might drive behavioral improvement, we also measured changes in the dynamic range of tuning and average firing rate (Fig. 5). In contrast to the marked changes in PD measured in all recorded units, we noted no consistent changes in either the dynamic range of tuning (Fig. 5, A and B) or average firing rate (Fig. 5, C and D). Although individual neurons occasionally showed changes in dynamic tuning range or average firing rate (tuning curve fits of every neuron are shown in Supplemental Figs. S4 and S5), there were no significant differences in any pairwise comparison of the three groups (Fig. 5, B and D). Taken together, our results indicate that long-term practice on this task consistently impacts only the PD of directional tuning curves, and not other tuning parameters.
Fig. 5.
Dynamic range of neural tuning and mean firing rate do not change with long-term practice. A: dynamic range of tuning before and after learning for all tracked neurons. Each point represents the dynamic tuning range fit from the first 40 trials to each target on the first and last days of the perturbation session. Data are combined for both monkeys. The unity line is shown as a reference. B: comparison of the distributions of changes in dynamic tuning range between the 3 groups of neurons. To account for the wide range of dynamic tuning across neurons, changes in dynamic range of tuning were normalized as (DRafter − DRbefore)/DRbefore. Horizontal lines within boxes represent the medians. Upper and lower boundaries of boxes represent the 75% and 25% quantiles of the data, respectively. Upper and lower whiskers represent the 95% and 5% quantiles in a normal distribution fitted on the data, respectively. C and D: same as A and B, but with the average number of spikes emitted by each neuron during every trial before and after learning. Spike counts were taken in a 200-ms window centered at the point when the cursor was halfway from the center to the target. n.s., Not significant.
Drivers of long-timescale neural reorganization.
What drives long-timescale neural reorganization? Motor skill learning has been associated with a decrease in motor variability over the course of training (Athalye et al. 2017; Cohen and Sternad 2009; Müller and Sternad 2004). It is also associated with an increase in motor acuity, characterized by a shift in the speed–accuracy trade-off curve (Shmuelof et al. 2012b). Reward and motivation doubtless play a role. We sought to determine which behavioral signals might be responsible for driving the credit assignment process that leads to long-lasting differential changes in the PDs of the perturbed and unperturbed groups.
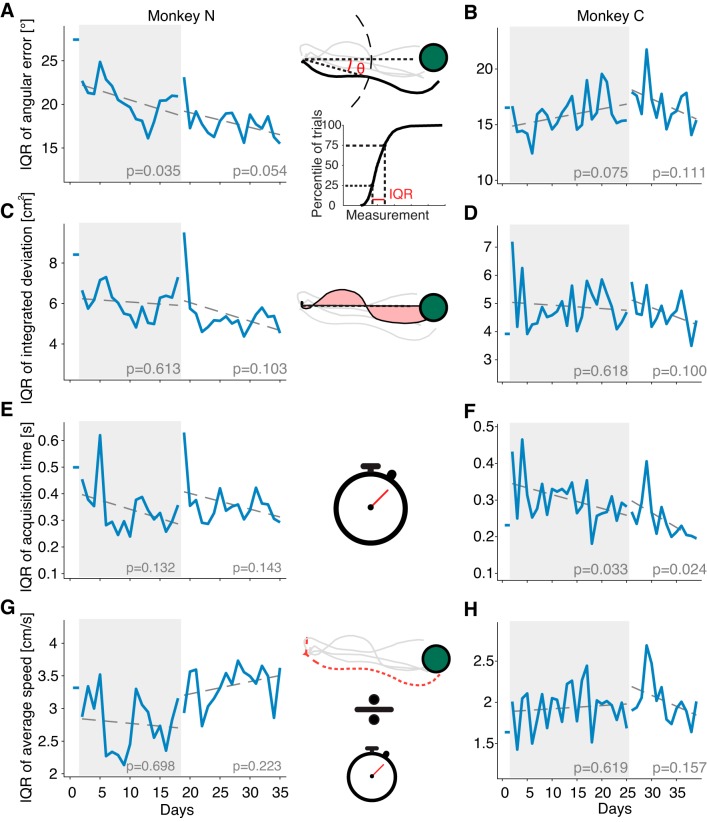
We first assessed whether long-term BCI training led to decreases in cursor movement variability. We assessed motor variability by computing the interquartile ranges (IQRs) of four different behavioral measurements (angular error, integrated deviation from straight movement, target acquisition time, and average cursor speed) reflecting multiple aspects of task performance (Fig. 6). The IQRs were computed from the first 480 trials on each day. If the extended training on either the perturbed mapping or the washout mapping helped to improve behavioral performance by reducing the variability in cursor movement, we should see a decrease in IQRs with extended practice.
Fig. 6.
Cursor movement variability does not decrease appreciably with long-term training. Insets (middle) illustrate the procedures for computing the various behavioral measurements. A–H: graphs show the interquartile ranges (IQRs) computed for the respective behavioral measurement over the first 480 trials on each day of training. Dashed lines indicate a linear regression fit as a function of time within each session, with the P values shown at bottom of the plot. A and B: IQR of angular error across days. Angular errors were computed as angle θ in the inset. C and D: IQR of integrated deviation, computed as the area circumscribed by the cursor trajectory and the straight line between center and target, shown as the pink shaded area in the inset. E and F: IQR of target acquisition time across days. Target acquisition time for each trial was computed as the time spent between the cursor leaving the center target and the cursor reaching the peripheral target. G and H: IQR of average cursor speed in each trial. The average speed in each trial was obtained by dividing the trajectory length by the target acquisition time, illustrated in the inset as the length of the red cursor trajectory divided by target acquisition time.
Movement variability did not show a strong decline with practice. We fit linear regressions to the IQRs as a function of time for all four behavioral measurements, separately for the perturbation and the washout sessions. For monkey N, none of these regressions were significant (at the α = 0.05 level) during the washout session (Fig. 6, A, C, and G), and only one (the IQR for angular error, Fig. 6A) was significant during the perturbation session. Similarly, for monkey C, whereas the IQRs for acquisition time had a significant decrease during both perturbation and washout (Fig. 6F), none of the other regressions showed significant decreases (Fig. 6, B, D, and H). Although 13 of 16 regression slopes were negative for both monkeys, indicating a trend in the direction of decreased variability over time, the effect was not strong.
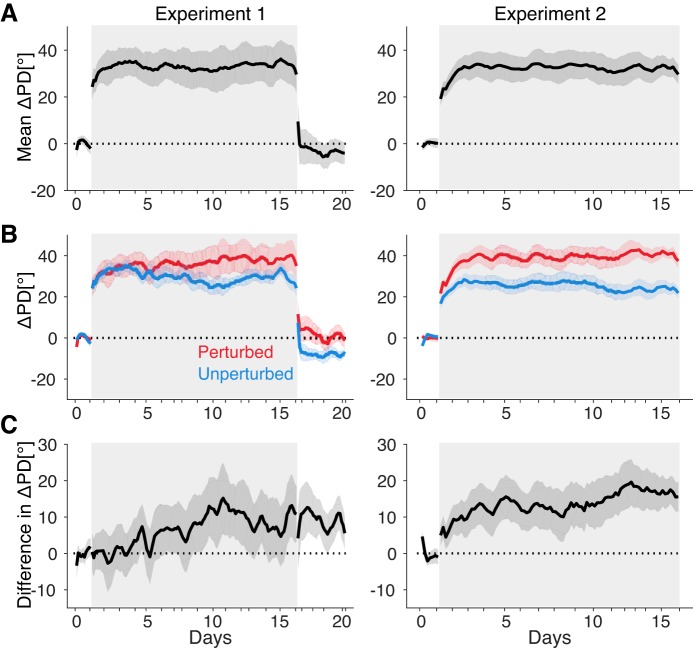
We have already noted that long-timescale neural reorganization is associated with both increases in cursor speed and increases in reward rate (as noted by a decrease in target acquisition time, Fig. 3, A and B). We next tested whether these effects could be dissociated, and investigated whether credit assignment effects are driven to increase cursor speed per se, or to increase reward rate. To disambiguate these measures, we conducted a separate set of experiments with monkey N using a constant-speed BCI mapping, where the subject controlled only cursor direction. Every other facet of the experimental design was the same (i.e., the monkey used a PVA decoder, and the dPDs of a randomly chosen 50% of neurons were rotated counterclockwise in experiment 1 and clockwise in experiment 2 by 75°), but the speed of the cursor movement was set to a constant value at the start of the trial and was independent of neural activity (see methods). We termed this mapping the constant-speed CARP (csCARP). These csCARP experiments allowed us to test whether credit assignment occurs when cursor speed increases are not possible.
We ran the constant speed experiment twice with one animal (Fig. 7). As in the CARP experiments, the subject improved with extended practice on the csCARP, as noted by decreases in angular error (Fig. 7B) and target acquisition time (Fig. 7C). Because cursor speed was a constant, the decrease in acquisition time was driven entirely by straighter cursor movements. Neural tuning changes during extended csCARP practice looked qualitatively similar to the changes observed during extended CARP practice (Fig. 8). PDs of all neurons rotated quickly in the direction counter to the perturbation (Fig. 8A), indicative of re-aiming. These changes quickly reverted in the washout session. The PDs of the perturbed group of neurons gradually rotated more than the PDs of the unperturbed group (Fig. 8B). This credit assignment effect built up slowly over days of training, indicating that credit assignment can proceed even without any changes in overall cursor speed. However, quantitatively, the effect was significantly smaller than in the CARP experiments. When days 10–15 during the perturbation sessions of the CARP experiments (Fig. 4C) were compared with the csCARP experiments (Fig. 8C), the differential change in PD between the perturbed and unperturbed subgroups of neurons was 11.1 ± 1.4° larger for CARP than for csCARP (P < 0.001, t-test). Thus credit assignment can proceed in a constant speed BCI mapping, although the effect is larger when changes in cursor speed are possible.
Fig. 8.
The slow component of learning reflected in differentiable tuning changes still occurs when cursor speed increases are not possible. A: average changes in preferred direction (ΔPD) of neurons from both the perturbed and unperturbed groups of neurons for monkey N in experiments 1 (left) and 2 (right). B: ΔPD for the perturbed (red) and unperturbed (blue) groups of neurons. Note that the signs for experiment 2 were reversed to make easier visualization and comparison. There were 6 neurons in each group in experiment 1, and 5 in each group in experiment 2. C: difference in ΔPD of the perturbed and unperturbed groups (perturbed − unperturbed). Shaded areas around lines represent SE. Gray rectangle background indicates the perturbation session.
In summary, we find that the credit assignment effect does not correlate strongly with reductions in behavioral variability and can proceed in the absence of changes in overt movement speed. Rather, the effect correlates best with increases in movement efficiency: those aspects of movements that cause increases in overall reward rate.
DISCUSSION
Our experimental design allows us to address a long-standing question in the motor learning field: how specific is neural reorganization? By rotating the pushing directions of only a subset of neurons, we can assess whether the neural reorganization that occurs during learning is specific to those perturbed neurons or whether it more globally affects all neurons engaged in the task. In previous work, we identified two types of adaptive responses to short exposures (lasting ~300 trials, or tens of minutes) to this type of perturbation: a global re-aiming response that impacts the activity of all neurons equally, and a local credit assignment and re-tuning of neural response differentially selective to the perturbed subset of neurons (Jarosiewicz et al. 2008). However, it was subsequently discovered that the global re-aiming response dominated the adaptive response that occurs within the first several hundred trials, accounting for ~85% of the overall error reduction, whereas credit assignment and fine-tuning of neural response accounted for only 15% of the response (Chase et al. 2012). In this study, we found that the two distinct adaptive changes in neural activity operate at different timescales during the entire course of learning. On introduction of the perturbation, rapid changes in neural activity common to all neurons led to a fast reduction in movement error. In parallel, local changes differentially selective to the subset of neurons directly contributing to the initial movement errors gradually built up over several weeks of practice. This slower functional reorganization of neural activity persisted long after the movement errors had decreased to asymptote and was associated with more efficient control of movement. Taken together, these findings suggest that skill acquisition is a two-stage process, in which rapid global changes in neural activity acting to reduce movement error are followed by gradual local changes in neural tuning acting to increase efficiency.
Our findings bridge two distinct bodies of work on BCI learning. In one line of research, Sadtler et al. (2014) found that the existing correlation structure of a neural population constrains its short-term learning: monkeys more readily learned BCI mappings that were consistent with the natural correlation structure than those that did not. To learn the mappings that preserved the natural correlation structure, subjects employed a suboptimal strategy of “neural reassociation” (Golub et al. 2018), in which a fixed repertoire of neural activity patterns was repurposed to learn the perturbed mapping. In this study, we found that short-timescale neural reorganization shared common features across the population of neurons indicative of a global re-aiming strategy. Because re-aiming would preserve the natural correlation patterns within the population and rely on existing population activity patterns, our results are entirely consistent with this work. In a second line of research, Ganguly and Carmena (2009) found that a monkey could learn to control a BCI mapping with an arbitrarily scrambled relationship between neurons and movements, but doing so took several days. These mappings likely require neural tuning changes that are specific to individual neurons, consistent with the long-timescale neural reorganization we see in the CARP task. Our work demonstrates how the different types of neural reorganization might complement each other over the entire time course of learning.
Our work also connects to a larger body of work investigating the psychophysical correlates of learning during reaching. The majority of these studies have focused on motor adaptation, the improvement in performance that follows a perturbation away from baseline performance (Shadmehr et al. 2010). Adaptation proceeds quickly (often, within hours) and typically engages strong aftereffects during washout (Shadmehr and Mussa-Ivaldi 1994). The fast component of learning that we observed in our BCI experiments has all the hallmarks of adaptation and likely involves some of the same neural mechanisms. As an example, our results are consistent with findings that rapid visuomotor learning involves changes in the upstream inputs to dorsal premotor cortex and M1 (Perich et al. 2018). In contrast, motor acuity, defined by the speed–accuracy trade-off for a task, improves slowly with training (Shmuelof et al. 2012b, 2014). The slow component of learning we observed is consistent with this process: we found continued decreases in the target acquisition time (Fig. 3), indicating each trial was being performed faster and faster. Although we found slight trends toward a decrease in trial-by-trial variability as expected from previous studies (Mandelblat-Cerf et al. 2009, 2011), the effects were not strong. Thus long-term BCI training appears to improve the speed–accuracy trade-off by emphasizing increases in speed over increases in accuracy. It is worth noting that speed here is not solely cursor speed. Even with decoders in which cursor speed is fixed, as in the csCARP experiments, target acquisition time decreases with practice, due to a progressive straightening of cursor movements over time. We suspect that it is reward rate, more than any other factor, that dictates the selective changes in neural tuning with practice (Legenstein et al. 2010).
Of course, we should always be aware that the BCI paradigm employed in these experiments has several differences from natural arm control. Perhaps the most salient distinction is that the monkeys do not move their arms. Natural reaching adaptation invokes changes to both feedforward and feedback motor commands (Kasuga et al. 2015; Maeda et al. 2018; Wagner and Smith 2008). The feedback changes likely impact how both visual and proprioceptive feedback signals are processed for online, corrective movements. Obviously, we would not expect to elicit changes in proprioceptive feedback processing with our BCI perturbation. Another salient difference is that our perturbation changes only the way some of the neurons push the cursor; other neurons are left unperturbed. Although the movement errors experienced by the monkey are equivalent to a global visuomotor distortion, the particular implementation is more akin to a muscle “reattachment” experiment (Berger et al. 2013; de Rugy et al. 2012; Radhakrishnan et al. 2008). Even so, the adaptive responses we observe are robust and proceed with timescales quite similar to those for learning in natural reaching experiments. Furthermore, visuomotor rotation learning in a BCI context has been found to transfer to natural reaching (Vyas et al. 2018). We speculate that although the perturbation and paradigm we used may not be natural, the adaptive response we see is a general feature of natural motor learning.
One surprising feature of our results is that neural tuning changes were limited to changes in PD: neither strength of tuning nor overall firing rate showed any systematic difference across the three groups of perturbed, unperturbed, and indirect neurons. The absence of change in overall firing rates may have been attributable to the design of the BCI mapping. Each neuron’s firing rate was normalized by subtracting its observed firing rate from its baseline rate as established during calibration before its pushing contribution to cursor velocity was calculated (see methods). Thus a net change in the average firing rate of a single neuron would result in a constant directional bias of the cursor velocity, likely detracting from performance. Although a coordinated change in average firing rates across all neurons would be possible to avoid a bias, these changes would need to be constrained to counterbalance each other. More surprising is that we did not note a systematic decline in the tuning strength of neurons not directly engaged in cursor control, as might be expected from previous work (Ganguly et al. 2011). This may be because, at the time of these experiments, our subjects had been training on tasks using similarly intuitive BCI mappings and were experts at BCI control. Thus overall tuning strength might have been at its physiological limit at the start. It is possible that only increases in tuning strength, observed when less skilled subjects train, are specific to neurons directly in control of the BCI (Koralek et al. 2012); if neurons are at their physiological limit, these increases may not be observed. That indirect neurons did not decrease their tuning strength suggests that there may not have been sufficient behavioral drive to do so, or that these neurons may play a role in balancing plasticity for learning and stability for consolidation (Driscoll et al. 2017). Decreases in indirect tuning strength are predicted by optimal control theories that assume neural spiking is energetically costly (Huang et al. 2012; Thoroughman and Shadmehr 1999). However, on short timescales we have found that spiking energetic constraints do not play a large role in determining neural recruitment during BCI tasks (Hennig et al. 2018). The present results suggest that this may also hold true even over weeks of practice with a particular mapping. It may also be the case that to reorganize the neural activity in order to disengage the indirect neurons from the task is more energetically costly than it is to maintain their natural spiking patterns. It will be interesting to pursue what factors might enable selective recruitment or suppression of neural activity.
One potential concern with the current study is the small number of units used to directly control the BCI (10 units for monkey C and 12 for monkey N). The decision to limit the total number of direct units was made to increase the probability of successfully tracking these units across days. Nevertheless, a reasonable question is whether the results we report would have been the same with a larger number of direct neurons. The nature of the decoder makes these results unlikely to be affected by population size. The PVA computes an average movement vector from all direct neurons. To affect a 10° rotation of the cursor movement, all of the neurons could rotate their PDs by 10°, or half could rotate by 20°, or a third by 30°, etc. However, this is true regardless of the number of direct neurons. One thing that might make a difference is the percentage of the total number of neurons that are perturbed. We have found in prior work that when only 25% of the direct cells are rotated, there is a slight decrease in the modulation depth of those neurons with respect to the unperturbed neurons (Chase et al. 2012). This is not observed when 50% of the direct cells are rotated, as was done in these experiments. A good question for future investigation is whether the gradual credit assignment affects depends on the total percentage of perturbed cells.
It remains an open question what neural mechanisms underlie the different types of neural reorganization we found during long-term learning. In traditional sensorimotor learning paradigms, learning can happen at multiple stages within the feedback control loop. In a BCI learning paradigm, changes in neural activity patterns have to happen in the motor cortical neurons that we record from in order for learning to take place and to improve output behavior (Golub et al. 2016). This reorganization of neural activity can be a result of direct changes in M1 neurons or changes to the input received by M1 neurons. The gradual burn-in of tuning changes during learning and slow burn-out during washout we observed in this study suggests that the neural reorganization that is differentiable between subsets of neurons represents incremental changes in the M1 network itself rather than the more readily modifiable input to M1. Future studies will be needed to further disambiguate any cortical, subcortical, or cerebellar drive of the learning-related neural reorganization (Shadmehr and Krakauer 2008).
GRANTS
This work was supported by National Science Foundation Grants IOS1553252 and BCS1533672 (to S. M. Chase), Pennsylvania Department of Health Research Formula Grant SAP 4100077048 (to S. M. Chase), a Philip and Masha Dowd Fellowship (to X. Zhou), and National Institutes of Health Grant 2R01 HD071686 (to S. M. Chase).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
X.Z., R.N.T., and S.M.C. conceived and designed research; X.Z. and R.N.T. performed experiments; X.Z., S.R., and S.M.C. analyzed data; X.Z., R.N.T., S.R., and S.M.C. interpreted results of experiments; X.Z. and S.M.C. prepared figures; X.Z., S.R., and S.M.C. drafted manuscript; X.Z., R.N.T., S.R., and S.M.C. edited and revised manuscript; X.Z., R.N.T., S.R., and S.M.C. approved final version of manuscript.
REFERENCES
- Aflalo T, Kellis S, Klaes C, Lee B, Shi Y, Pejsa K, Shanfield K, Hayes-Jackson S, Aisen M, Heck C, Liu C, Andersen RA. Neurophysiology. Decoding motor imagery from the posterior parietal cortex of a tetraplegic human. Science 348: 906–910, 2015. doi: 10.1126/science.aaa5417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Athalye VR, Ganguly K, Costa RM, Carmena JM. Emergence of coordinated neural dynamics underlies neuroprosthetic learning and skillful control. Neuron 93: 955–970.e5, 2017. doi: 10.1016/j.neuron.2017.01.016. [DOI] [PubMed] [Google Scholar]
- Berger DJ, Gentner R, Edmunds T, Pai DK, d’Avella A. Differences in adaptation rates after virtual surgeries provide direct evidence for modularity. J Neurosci 33: 12384–12394, 2013. doi: 10.1523/JNEUROSCI.0122-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandman DM, Hosman T, Saab J, Burkhart MC, Shanahan BE, Ciancibello JG, Sarma AA, Milstein DJ, Vargas-Irwin CE, Franco B, Kelemen J, Blabe C, Murphy BA, Young DR, Willett FR, Pandarinath C, Stavisky SD, Kirsch RF, Walter BL, Bolu Ajiboye A, Cash SS, Eskandar EN, Miller JP, Sweet JA, Shenoy KV, Henderson JM, Jarosiewicz B, Harrison MT, Simeral JD, Hochberg LR. Rapid calibration of an intracortical brain-computer interface for people with tetraplegia. J Neural Eng 15: 026007, 2018. doi: 10.1088/1741-2552/aa9ee7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carmena JM, Lebedev MA, Crist RE, O’Doherty JE, Santucci DM, Dimitrov DF, Patil PG, Henriquez CS, Nicolelis MA. Learning to control a brain-machine interface for reaching and grasping by primates. PLoS Biol 1: E42, 2003. doi: 10.1371/journal.pbio.0000042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chase SM, Kass RE, Schwartz AB. Behavioral and neural correlates of visuomotor adaptation observed through a brain-computer interface in primary motor cortex. J Neurophysiol 108: 624–644, 2012. doi: 10.1152/jn.00371.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chase SM, Schwartz AB, Kass RE. Bias, optimal linear estimation, and the differences between open-loop simulation and closed-loop performance of spiking-based brain-computer interface algorithms. Neural Netw 22: 1203–1213, 2009. doi: 10.1016/j.neunet.2009.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen RG, Sternad D. Variability in motor learning: relocating, channeling and reducing noise. Exp Brain Res 193: 69–83, 2009. doi: 10.1007/s00221-008-1596-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Rugy A, Loeb GE, Carroll TJ. Muscle coordination is habitual rather than optimal. J Neurosci 32: 7384–7391, 2012. doi: 10.1523/JNEUROSCI.5792-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Driscoll LN, Pettit NL, Minderer M, Chettih SN, Harvey CD. Dynamic reorganization of neuronal activity patterns in parietal cortex. Cell 170: 986–999.e16, 2017. doi: 10.1016/j.cell.2017.07.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Focke A, Stockinger C, Diepold C, Taubert M, Stein T. The influence of catch trials on the consolidation of motor memory in force field adaptation tasks. Front Psychol 4: 479, 2013. doi: 10.3389/fpsyg.2013.00479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser GW, Schwartz AB. Recording from the same neurons chronically in motor cortex. J Neurophysiol 107: 1970–1978, 2012. doi: 10.1152/jn.01012.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganguly K, Carmena JM. Emergence of a stable cortical map for neuroprosthetic control. PLoS Biol 7: e1000153, 2009. doi: 10.1371/journal.pbio.1000153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganguly K, Dimitrov DF, Wallis JD, Carmena JM. Reversible large-scale modification of cortical networks during neuroprosthetic control. Nat Neurosci 14: 662–667, 2011. doi: 10.1038/nn.2797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgopoulos AP, Schwartz AB, Kettner RE. Neuronal population coding of movement direction. Science 233: 1416–1419, 1986. doi: 10.1126/science.3749885. [DOI] [PubMed] [Google Scholar]
- Gilja V, Nuyujukian P, Chestek CA, Cunningham JP, Yu BM, Fan JM, Churchland MM, Kaufman MT, Kao JC, Ryu SI, Shenoy KV. A high-performance neural prosthesis enabled by control algorithm design. Nat Neurosci 15: 1752–1757, 2012. doi: 10.1038/nn.3265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golub MD, Chase SM, Batista AP, Yu BM. Brain-computer interfaces for dissecting cognitive processes underlying sensorimotor control. Curr Opin Neurobiol 37: 53–58, 2016. doi: 10.1016/j.conb.2015.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golub MD, Sadtler PT, Oby ER, Quick KM, Ryu SI, Tyler-Kabara EC, Batista AP, Chase SM, Yu BM. Learning by neural reassociation. Nat Neurosci 21: 607–616, 2018. [Erratum in Nat Neurosci 21: 1138, 2018.] doi: 10.1038/s41593-018-0095-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasson CJ, Zhang Z, Abe MO, Sternad D. Neuromotor noise is malleable by amplifying perceived errors. PLoS Comput Biol 12: e1005044, 2016. doi: 10.1371/journal.pcbi.1005044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hennig JA, Golub MD, Lund PJ, Sadtler PT, Oby ER, Quick KM, Ryu SI, Tyler-Kabara EC, Batista AP, Yu BM, Chase SM. Constraints on neural redundancy. eLife 7: e36774, 2018. doi: 10.7554/eLife.36774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hochberg LR, Bacher D, Jarosiewicz B, Masse NY, Simeral JD, Vogel J, Haddadin S, Liu J, Cash SS, van der Smagt P, Donoghue JP. Reach and grasp by people with tetraplegia using a neurally controlled robotic arm. Nature 485: 372–375, 2012. doi: 10.1038/nature11076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang HJ, Kram R, Ahmed AA. Reduction of metabolic cost during motor learning of arm reaching dynamics. J Neurosci 32: 2182–2190, 2012. doi: 10.1523/JNEUROSCI.4003-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarosiewicz B, Chase SM, Fraser GW, Velliste M, Kass RE, Schwartz AB. Functional network reorganization during learning in a brain-computer interface paradigm. Proc Natl Acad Sci USA 105: 19486–19491, 2008. doi: 10.1073/pnas.0808113105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kargo WJ, Nitz DA. Early skill learning is expressed through selection and tuning of cortically represented muscle synergies. J Neurosci 23: 11255–11269, 2003. doi: 10.1523/JNEUROSCI.23-35-11255.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karni A, Meyer G, Rey-Hipolito C, Jezzard P, Adams MM, Turner R, Ungerleider LG. The acquisition of skilled motor performance: fast and slow experience-driven changes in primary motor cortex. Proc Natl Acad Sci USA 95: 861–868, 1998. doi: 10.1073/pnas.95.3.861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasuga S, Telgen S, Ushiba J, Nozaki D, Diedrichsen J. Learning feedback and feedforward control in a mirror-reversed visual environment. J Neurophysiol 114: 2187–2193, 2015. doi: 10.1152/jn.00096.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koralek AC, Jin X, Long JD 2nd, Costa RM, Carmena JM. Corticostriatal plasticity is necessary for learning intentional neuroprosthetic skills. Nature 483: 331–335, 2012. doi: 10.1038/nature10845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legenstein R, Chase SM, Schwartz AB, Maass W. A reward-modulated Hebbian learning rule can explain experimentally observed network reorganization in a brain control task. J Neurosci 30: 8400–8410, 2010. doi: 10.1523/JNEUROSCI.4284-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maeda RS, Cluff T, Gribble PL, Pruszynski JA. Feedforward and feedback control share an internal model of the arm’s dynamics. J Neurosci 38: 10505–10514, 2018. doi: 10.1523/JNEUROSCI.1709-18.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandelblat-Cerf Y, Novick I, Paz R, Link Y, Freeman S, Vaadia E. The neuronal basis of long-term sensorimotor learning. J Neurosci 31: 300–313, 2011. doi: 10.1523/JNEUROSCI.4055-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandelblat-Cerf Y, Paz R, Vaadia E. Trial-to-trial variability of single cells in motor cortices is dynamically modified during visuomotor adaptation. J Neurosci 29: 15053–15062, 2009. doi: 10.1523/JNEUROSCI.3011-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller H, Sternad D. Decomposition of variability in the execution of goal-oriented tasks: three components of skill improvement. J Exp Psychol Hum Percept Perform 30: 212–233, 2004. doi: 10.1037/0096-1523.30.1.212. [DOI] [PubMed] [Google Scholar]
- Mulliken GH, Musallam S, Andersen RA. Decoding trajectories from posterior parietal cortex ensembles. J Neurosci 28: 12913–12926, 2008. doi: 10.1523/JNEUROSCI.1463-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orsborn AL, Moorman HG, Overduin SA, Shanechi MM, Dimitrov DF, Carmena JM. Closed-loop decoder adaptation shapes neural plasticity for skillful neuroprosthetic control. Neuron 82: 1380–1393, 2014. doi: 10.1016/j.neuron.2014.04.048. [DOI] [PubMed] [Google Scholar]
- Overduin SA, Richardson AG, Lane CE, Bizzi E, Press DZ. Intermittent practice facilitates stable motor memories. J Neurosci 26: 11888–11892, 2006. doi: 10.1523/JNEUROSCI.1320-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perich MG, Gallego JA, Miller LE. A neural population mechanism for rapid learning. Neuron 100: 964–976.e7, 2018. doi: 10.1016/j.neuron.2018.09.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radhakrishnan SM, Baker SN, Jackson A. Learning a novel myoelectric-controlled interface task. J Neurophysiol 100: 2397–2408, 2008. doi: 10.1152/jn.90614.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadtler PT, Quick KM, Golub MD, Chase SM, Ryu SI, Tyler-Kabara EC, Yu BM, Batista AP. Neural constraints on learning. Nature 512: 423–426, 2014. doi: 10.1038/nature13665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadmehr R, Holcomb HH. Neural correlates of motor memory consolidation. Science 277: 821–825, 1997. doi: 10.1126/science.277.5327.821. [DOI] [PubMed] [Google Scholar]
- Shadmehr R, Krakauer JW. A computational neuroanatomy for motor control. Exp Brain Res 185: 359–381, 2008. doi: 10.1007/s00221-008-1280-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadmehr R, Mussa-Ivaldi FA. Adaptive representation of dynamics during learning of a motor task. J Neurosci 14: 3208–3224, 1994. doi: 10.1523/JNEUROSCI.14-05-03208.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadmehr R, Smith MA, Krakauer JW. Error correction, sensory prediction, and adaptation in motor control. Annu Rev Neurosci 33: 89–108, 2010. doi: 10.1146/annurev-neuro-060909-153135. [DOI] [PubMed] [Google Scholar]
- Shmuelof L, Huang VS, Haith AM, Delnicki RJ, Mazzoni P, Krakauer JW. Overcoming motor “forgetting” through reinforcement of learned actions. J Neurosci 32: 14617–14621, 2012a. doi: 10.1523/JNEUROSCI.2184-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shmuelof L, Krakauer JW, Mazzoni P. How is a motor skill learned? Change and invariance at the levels of task success and trajectory control. J Neurophysiol 108: 578–594, 2012b. doi: 10.1152/jn.00856.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shmuelof L, Yang J, Caffo B, Mazzoni P, Krakauer JW. The neural correlates of learned motor acuity. J Neurophysiol 112: 971–980, 2014. doi: 10.1152/jn.00897.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor DM, Tillery SI, Schwartz AB. Direct cortical control of 3D neuroprosthetic devices. Science 296: 1829–1832, 2002. doi: 10.1126/science.1070291. [DOI] [PubMed] [Google Scholar]
- Thoroughman KA, Shadmehr R. Electromyographic correlates of learning an internal model of reaching movements. J Neurosci 19: 8573–8588, 1999. doi: 10.1523/JNEUROSCI.19-19-08573.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Kooij K, Overvliet KE, Smeets JB. Temporally stable adaptation is robust, incomplete and specific. Eur J Neurosci 44: 2708–2715, 2016. doi: 10.1111/ejn.13355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaswani PA, Shmuelof L, Haith AM, Delnicki RJ, Huang VS, Mazzoni P, Shadmehr R, Krakauer JW. Persistent residual errors in motor adaptation tasks: reversion to baseline and exploratory escape. J Neurosci 35: 6969–6977, 2015. doi: 10.1523/JNEUROSCI.2656-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vyas S, Even-Chen N, Stavisky SD, Ryu SI, Nuyujukian P, Shenoy KV. Neural population dynamics underlying motor learning transfer. Neuron 97: 1177–1186.e3, 2018. doi: 10.1016/j.neuron.2018.01.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner MJ, Smith MA. Shared internal models for feedforward and feedback control. J Neurosci 28: 10663–10673, 2008. doi: 10.1523/JNEUROSCI.5479-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]