Fluid heterogeneity detection based on the asymptotic distribution of the time-averaged mean squared displacement in single particle tracking experiments

Abstract

A tracer particle is called anomalously diffusive if its mean squared displacement grows approximately as σ²t^α as a function of time t for some constant σ², where the diffusion exponent satisfies α ≠ 1. In this article, we use recent results on the asymptotic distribution of the time-averaged mean squared displacement [20] to construct statistical tests for detecting physical heterogeneity in viscoelastic fluid samples starting from one or multiple observed anomalously diffusive paths. The methods are asymptotically valid for the range 0 < α < 3/2 and involve a mathematical characterization of time-averaged mean squared displacement bias and the effect of correlated disturbance errors. The assumptions on particle motion cover a broad family of fractional Gaussian processes, including fractional Brownian motion and many fractional instances of the generalized Langevin equation framework. We apply the proposed methods in experimental data from treated P. aeruginosa biofilms generated by the collaboration of the Hill and Schoenfisch Labs at UNC-Chapel Hill.

1. Introduction

In this paper, we start from the asymptotic distribution of the time-averaged mean squared displacement of nanometric tracer particles [20] to construct statistical protocols for detecting physical fluid heterogeneity. The assumptions on particle motion cover a broad family of fractional Gaussian processes, including fractional Brownian motion and many instances of the generalized Langevin equation framework. The testing protocols allowed providing more accurate quantitative analysis of experimental data from the Hill and Schoenfisch Labs (UNC-Chapel Hill), and the results reported in [73] were generally confirmed.

Improvements in light microscopy, fluorescence techniques, nanoparticle synthesis and high-speed video have ushered in a flurry of experimental activity [81]. Single particle tracking has become a common tool in many scientific areas, such as colloid physics [34], the microrheology of complex fluids [53, 83, 54, 45, 35] and the study of nanobiophysical systems, both in vivo and in vitro [2, 12]. This includes the diffusion of single molecules, e.g., proteins, on biopolymers such as DNA or microtubules, on surfaces or in lipid membranes, inside in vivo cells and in actin solutions [84, 26, 32, 89, 33, 61, 82, 95, 46, 67, 80, 4, 30], as well as two-dimensional biological membranes [58] and heterogeneuous tracer diffusion and first passage characteristics in two-dimensional crowded environments [23].

Of primary concern in the analysis of particle path data is the ensemble mean squared displacement (MSD), where X is the tracer particle’s position. A basic dynamic characterization of the latter is given by the relation

$$\langle X^2(t)\rangle =\mathbb{E}{X}^2(t)\propto {\sigma }^2{t}^{\alpha },{\sigma }^2,\alpha >0,t\ge 0,\mathit{\xi }:=\left(\log {\sigma }^2,\alpha \right).$$ (1)

In (1), α is the diffusion exponent and σ² = 2D, where D is the diffusivity constant. The parameter value α = 1 corresponds to classical diffusion. If α ≠ 1, the stochastic process X is said to be anomalously diffusive, more specifically sub- or superdiffusive depending on whether α < 1 or > 1, respectively. Anomalous diffusion may emerge, for example, as a consequence of binding-unbinding events, of geometrical constraints on the particle’s movement, or of fluid viscoelasticity [57, 77, 76, 49].

The dominant statistical technique in the biophysical literature for estimating the parameters σ² and α is based on the so-named time-averaged mean squared displacement (TAMSD). Suppose that a single particle experiment generates a tracer bead sample path with observations X(j), j = 1, …, N. The pathwise statistic

$$M_N(\tau ):=\frac{1}{N-\tau }\sum _{j=1}^{N-\tau }\{X(j+\tau )-X(j){\}}^2$$ (2)

is the TAMSD at lag value τ, i.e., the statistical counterpart of the MSD 〈X²(τ)〉. One generates an estimator of ξ = (log σ², α) by means of the linear regression

$$\log M_N\left({\tau }_k\right)=\log {\sigma }^2+\alpha \log {\tau }_k+{\epsilon }_k,k=1,\dots ,m,$$ (3)

possibly over several independent particle paths, where m is the number of lag values used and {ε_k}_k=1,…,m is a random vector with an unspecified distribution and correlated entries (see (7) and (22)). Plots of TAMSD curves as a function of the lag value τ, often on a log-log scale, are widely reported as part of anomalous diffusion data analysis (e.g., [90, 50]). The choice of lag values τ₁, …, τ_m reflects the analyst’s visual perception of the range where the slope of the TAMSD curves stabilize and thus indicate the true diffusive regime and power law.

The potential heterogeneity of fluid samples in fields such as microrheology implies that estimating ξ from single trajectories is of great interest [9, 11, 93, 51]. However, the experimental and statistical difficulties involved in estimating ξ based on the regression system (3) have been pointed out by many authors. A non-exhaustive list of issues includes limited fluorophore life-times, proteins diffusing out of the field of view, finite-resolution imaging and motion blurring due to camera integration times, measurement errors, the presence of drifts and intra-path correlation [71, 3, 60, 40, 93, 10, 56, 8, 36]. Such difficulties call for a deeper understanding of the stochastic behavior of the TAMSD and, accordingly, a wealth of literature on the subject has developed. Starting from an underlying fractional stochastic process, several properties of the TAMSD such as ergodicity were established [17, 59, 39, 13, 75, 6, 38]. In particular, finite sample exact characterizations and mathematically convenient approximations to the distribution of the TAMSD under Gaussianity are provided in [71, 27, 28, 6, 1, 65, 7, 29, 79, 22]. In [79], assuming an observed fractional Brownian motion (see Example 2.2), it is shown that the standard TAMSD-based estimator is consistent, with vanishing bias and variance.

We say that a cumulative distribution function (c.d.f.) F gives the asymptotic distribution of a sequence of random variables {W_N}_N∈ℕ if the c.d.f. F_N(x) of W_N converges to F(x) at every x ∈ ℝ where F is continuous. Results on convergence in distribution such as the classical central limit theorem (CLT; see Example 2.1) have a number of interesting statistical consequences. Typically, statements are robust, i.e., they hold for a multitude of models. Moreover, they naturally lead to useful data analysis protocols such as confidence intervals and hypothesis tests with error margins that are quantifiable and whose accuracy provably increases at an explicit rate (e.g., $\sqrt{N}$ for the CLT). In the probability literature, the study of the asymptotic distribution of sums of functions of Gaussian random variables has been carried out over many decades now (see [74, 85, 86, 21, 52, 24, 31, 25, 69] for just a few references). In the context of anomalous diffusion modeling, in turn, the related asymptotic distribution of the TAMSD was established in [20] for a broad class of Gaussian fractional stochastic processes. It was shown that the convergence in distribution of the TAMSD occurs at different rates, and that the limiting distribution may be Gaussian or non-Gaussian, all depending on the value of the diffusion exponent α. This made it possible, for example, to construct asymptotically valid confidence intervals for the anomalous diffusion parameters starting from a single observed particle path.

In this paper, we propose particle path-based statistical protocols for detecting fluid heterogeneity that builds upon the TAMSD’s asymptotic distribution. The protocols test fluid heterogeneity in two different experimental situations, namely,

1. assuming local physical homogeneity, whether different regions of the fluid are heterogeneous;

2. assuming global physical homogeneity of each fluid sample, whether two samples from each fluid are heterogeneous.

Hereinafter, these two senses are referred to as intra- and interfluid heterogeneity, respectively. The testing methodology is based on an improved single-path TAMSD-based estimation technique. To construct the latter, we tackle two of the main issues involved in TAMSD-based estimation, namely: (a) the presence of bias in log-TAMSD-based methods; and (b) the effect of correlated disturbances {ε_k}_k=1,…,m in (3). Starting from a concentration inequality [5], we address these issues by providing mathematical characterizations of the bias and finite sample estimation variance which are by themselves of interest, as well as by introducing procedures for bias-correction and nearly optimal estimation under intra-path correlation. Motivated by applications in viscoelastic diffusion, the single-path estimation and heterogeneity testing protocols are mathematically established for 0 < α < 3/2, which covers all the subdiffusive range and part of the superdiffusive regime, and are asymptotically valid. For the sake of completeness, we also discuss and provide computational studies on the strong superdiffusivity range 3/2 ≤ α < 2 (see Remark 3.2 on the difficulties involved in dealing with the possibly non-Gaussian asymptotic distribution of the TAMSD). To guide experimental practice under common technical constraints such as limited camera recording time, we also apply the proposed tools in investigating the difference between observing longer particle paths and using a larger number of particle paths of given length. To illustrate the use of the protocols in physical practice, we make inferences on fluid viscoelasticity with data from the Hill and Schoenfisch Labs (UNC-Chapel Hill) on biofilm eradication, as first reported and described in [73].

The paper is organized as follows. In Section 2, we summarize the key mathematical results on the asymptotic distribution of the TAMSD. In Section 3, assuming a single observed path of realistic length, we characterize the bias and the variance in TAMSD-based estimation to construct the improved single-path estimator and compare it with the standard TAMSD-based estimator in terms of statistical performance. In Section 4, assuming multiple observed paths, we use the estimator developed in Section 3 to construct statistical testing protocols for intra- and interfluid heterogeneity detection. In Section 5, we model and test fluid heterogeneity through experimental data. For the reader’s convenience, Section A of the Appendix contains mathematically accurate statements of the results in Section 2 and [20]. Sections B, C and D contain all new mathematical results and their proofs. Newly designed Matlab routines containing the estimation and testing protocols will be made available on the authors’ websites at the time of publication.

2. Background

Before we revisit the results in [20] on the asymptotic behavior of the TAMSD, for the sake of exposition we consider some classical results from probability theory.

Example 2.1

Consider independent and identically distributed random variables X₁, …, X_N, each with mean 〈X₁〉 = μ and finite variance $\mathrm{Var}{X}_1:=\langle X_1^2\rangle -{\langle X_1\rangle }^2={\phi }^2>0$. If ${\overline{X}}_N=N^{-1}{\sum }_{i=1}^N{X}_i$ denotes the sample mean, then the celebrated central limit theorem states that, for large N, the distribution of the standardized sample mean approaches that of a standard normal, i.e.,

$$\sqrt{N}\frac{\left({\overline{X}}_N-\mu \right)}{\phi }\stackrel{d}{\to }\mathcal{N}(0,1),N\to \infty .$$ (4)

Apart from naturally leading to confidence intervals and hypothesis tests, the convergence (4) also implies that ${\overline{X}}_N$ is a consistent estimator of μ, namely, it converges in probability to μ. This is so because

$${\overline{X}}_N-\mu =\left(\frac{\phi }{\sqrt{N}}\right)\sqrt{N}\frac{\left({\overline{X}}_N-\mu \right)}{\phi }\stackrel{P}{\to }0,N\to \infty .$$ (5)

The zero limit in probability in (5) stems from the fact that the vanishing term $\phi /\sqrt{N}\to 0$ multiplies a standardized sample mean that converges in distribution (4) (see [78]).

Apart from distinct assumptions on the observations, the claims in [20] on the asymptotic behavior of the TAMSD are reminiscent of the classical statements (4) and (5), with two differences: (i) the rate of convergence is not typically $\sqrt{N}$ in biophysical modeling; (ii) the asymptotic distribution of the TAMSD is not necessarily Gaussian.

So, consider the random vector

$$\left(M_N\left({\tau }_1\right),\dots ,M_N\left({\tau }_m\right)\right),$$ (6)

namely, a vector of TAMSD terms (2) at m different lag values, obtained from one path of a Gaussian, stationary increment process. Fitting (3) and (6) by means of ordinary least squares (OLS) regression is the most intuitive way of constructing an estimator of the diffusion parameter vector ξ = (log σ², α). This corresponds to the common practice in the biophysical literature, both in experimental and methodological work (e.g., [90, 50, 11, 51] among many references). Throughout this paper,

$${\mathit{E}}_{\text{stand}}=\left(L_{\text{stand}},A_{\text{stand}}\right)$$ (7)

denotes this standard estimator (see (22) for a precise expression). In this framework, we need to make the lag sizes τ₁, …, τ_m themselves go to infinity, though no faster than the sample size N. This mathematically expresses the practical analysis of anomalous diffusion data: the lag size has to be

• ($\mathcal{L}1$) large enough for the TAMSD regime to become log-linear;

• ($\mathcal{L}2$) but, at the same time, not too large because of the increased variance of the TAMSD.

For a generic lag value τ, we can model this idea by writing

$$\infty \leftarrow \tau \ll N.$$ (8)

The limit and inequality in (8) express $(\mathcal{L}1)$ and $(\mathcal{L}2)$, respectively (the accurate mathematical statements are given by condition (53); see also Figure 1).

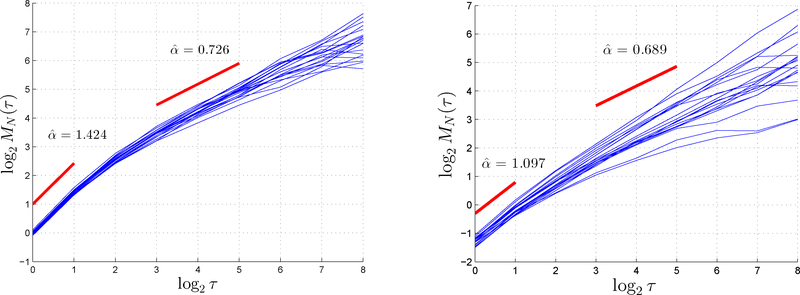
Figure 1: Bias and inconsistency over small scales τ vs vanishing bias and consistency as τ → ∞.

In general, taking the double limit τ,N → ∞ (see (8)) is necessary. Over fixed (“small”) lag values τ, TAMSD-based estimation is biased and, for most anomalous diffusion models other than fBm, inconsistent. As mathematically characterized by expansion (17), estimation bias is fundamentally a consequence of the fact that 〈log ·〉 ≠ log〈·〉 and of the presence of the small scale factor O(τ^−δ), whereas, in turn, inconsistency generally appears as a consequence of this same factor. The left and right plots show, respectively, 20 independent ifOU paths (length 2¹¹, α = 0.6) and 20 particle paths (length 1800) from P. aeruginosa biofilm after COS2-NO treatment at concentration level 8 mg ml⁻¹. The first and second red lines in each plot indicate, respectively, the fitted slope over small (τ = 1, 2) and large (τ = 8, 32) lag values. Based on the former lag values, A = 1.42 and 1.10 (evidence of superdiffusivity) for simulated and experimental data, respectively, whereas, by contrast, A = 0.70 and 0.69 (evidence of subdiffusivity) based on the latter. This illustrates the fact that bias and inconsistency vanish when τ (and N) becomes large.

The asymptotic distribution of the TAMSD random vector (6) after centering is briefly described in Table 1. This leads to the asymptotic behavior of the standard estimator (7), which is summarized in Table 2 in terms of convergence rate, asymptotic distribution and consistency. In both cases, the value of α determines the convergence rate and the nature of the asymptotic distribution. In particular, over almost the whole strong superdiffusivity range (i.e., over 3/2 < α < 2), the asymptotic distribution is non-Gaussian (Rosenblatt-type; see Theorem A.1 and [74, 85, 88, 91]). For any instance, by an argument analogous to (5), the standard estimator is consistent, i.e.,

$${\mathit{E}}_{\text{stand}}\stackrel{P}{\to }\mathit{\xi }.$$ (9)

Table 1:

Asymptotic behavior of the TAMSD random vector (6) (see Theorem A.1).

parameter range	rate of convergence	asymptotic distribution
0 < α < 3/2	$\sqrt{\frac{N}{\tau }}\frac{1}{{\tau }^{\alpha }}$	Gaussian
α = 3/2	$\sqrt{\frac{N}{\log N}}\frac{1}{{\tau }^2}$	Gaussian
3/2 < α < 2	$\frac{N^{2-\alpha }}{{\tau }^2}$	2 non-Gaussian

Table 2:

Asymptotic behavior of the standard TAMSD-based estimator (7) (see Corollary A.1).

parameter range	rate of convergence		joint asymptotic distribution	consistency
	Lstand	Astand
0 < α < 3/2	$\sqrt{\frac{N}{\tau }}\frac{1}{{\tau }^{\alpha }}\frac{1}{\log \tau }$	$\sqrt{\frac{N}{\tau }}\frac{1}{{\tau }^{\alpha }}$	Gaussian	Yes
α = 3/2	$\sqrt{\frac{N}{\log N}}\frac{1}{{\tau }^2}\frac{1}{\log \tau }$	$\sqrt{\frac{N}{\log N}}\frac{1}{{\tau }^2}$	Gaussian	Yes
3/2 < α < 2	$\frac{N^{2-\alpha }}{{\tau }^2}\frac{1}{\log \tau }$	$\frac{N^2-\alpha }{{\tau }^2}$	2 non-Gaussian	Yes

The family of stochastic processes for which the limits in distribution in Tables 1 and 2 hold is broad and contains a number of popular models. Three examples are fractional Brownian motion (fBm), fractional instances of the generalized Langevin equation (GLE) and the (integrated) fractional Ornstein-Uhlenbeck process (ifOU).

Example 2.2

Together with the continuous time random walk, fBm is one of the most popular models of anomalous diffusion [87, 2]. For some value of the so-named Hurst parameter H ∈ (0, 1) and a variance parameter D > 0, a fBm B_H(t) is the only Gaussian, stationary increment process with covariance function

$$\langle B_H(s)B_H(t)\rangle =D\left\{|t{|}^{2H}+|s{|}^{2H}-|t-s{|}^{2H}\right\},s,t\in ℝ.$$ (10)

The particular parameter value H = 1/2 corresponds to the ordinary Brownian motion (Wiener process). In view of (10), which implies exact self-similarity, for fBm the MSD scaling relation (1) holds as an equality, i.e.,

$$\langle B_H^2(t)\rangle ={\sigma }^2{t}^{\alpha },t\in ℝ,$$ (11)

where

$${\sigma }^2=2D,\alpha =2H.$$ (12)

Example 2.3

The GLE has been used as a universal model of anomalous diffusion in the biophysical field of microrheology [53, 96, 68, 66]. A subclass of interest of the GLE framework is the fractional GLE family [44, 43, 18], which is obtained almost surely as the solution of the stochastic differential equation

$$mdV(t)=-\lambda {\int }_{-\infty }^t\mathrm{\Gamma }(t-s)V(s)dsdt+d{B}_H(t),1/2<H<1.$$ (13)

In (13), m, λ > 0 and the memory kernel has the form Γ(t) = 2H(2H −1)|t|^2H−2, t ≠ 0, which is a consequence of invoking the fluctuation-dissipation relation [19, 51]. The integrated fractional generalized Langevin process (ifGL) is given by $X(t)={\int }_0^{t}V(s)ds$, t > 0, where {V (t)}_t≥0 is a solution of the fractional GLE. For the ifGL, relation (1) holds with α = 2(1 − H) (subdiffusive) as t → ∞.

Example 2.4

The ifOU is given by $X(t)={\int }_0^{t}V(s)ds$, t > 0, where the so-named fractional Ornstein-Uhlenbeck process {V (t)}_t≥0 is the almost surely continuous solution to the fBm-driven Langevin equation

$$dV(t)=-\lambda V(t)dt+\phi d{B}_H(t),t\ge 0,\lambda >0,0<H<1$$ (14)

(see [14, 70]). The ifOU process is a mathematically convenient model of anomalous diffusion. In the subdiffusive range, it displays a similar correlation structure to that of the ifGL process. For the ifOU, relation (1) holds with (12) as t → ∞.

Remark 2.1

The results in [20] do not cover some important anomalous diffusion models such as continuous time random walks. For the latter family of models, limit theorems typically involve distinct nonstandard asymptotic distributions depending on the assumptions (see, for instance, [55, 41] and references therein; for general guidelines on the use of the TAMSD, see [42]).

3. Improved TAMSD-based estimation

The standard estimator E_stand = (L_stand, A_stand) in (7) has at least two significant shortcomings: finite sample bias and suboptimal performance in the presence of correlation among the regression disturbance terms {ε_k}_k=1,…,N. We propose a single-path improved estimation protocol that addresses these issues. Accordingly, it involves two components, which we describe next. These two components involve asymptotically valid mathematical expressions for finite-sample bias and variance. Hereinafter, different lag values are expressed as

$${\tau }_k=w_k\tau ,w_1<\dots <w_k,$$ (15)

for fixed constants w., where τ = τ(N) grows as function of N.

(a) Bias correction

In TAMSD-based scaling analysis, there at least two sources of bias. First, bias appears if the particle movement is not exactly self-similar (not a fBm), i.e.,

$$\langle X^2(t)\rangle \ne {\sigma }^2{t}^{\alpha }\text{over}\text{a}\text{range}\text{of}t.$$

In fact, the deviation of the MSD from exact self-similarity or power scaling is generally controlled by the relation

$$\left|\frac{\langle X^2(t)\rangle }{{\sigma }^2{t}^{\alpha }}-1\right|\le \frac{C}{t^{\delta }}\text{for}\text{large}t,$$ (16)

for some constant σ² > 0, where the deviation parameter δ > 0 mostly depends on the high frequency behavior of the particle motion (see Proposition A.1). Second, even under self-similarity, bias stems from the elementary fact that the logarithm of the ensemble average and the ensemble average of the logarithm are distinct (e.g., [92, 63, 62, 64]). In the context of (3), this means that

$$\langle \log M_N(\tau )\rangle \ne \log \langle M_N(\tau )\rangle =\alpha \log \tau +\log {\sigma }^2,\tau \in \mathbb{N}.$$

So, by reinterpreting log M_N(τ) itself as an estimator of α log τ + log σ², we can express the bias involved in TAMSD-based estimation as

$$\langle \log M_N(\tau )\rangle -\left(\alpha \log \tau +\log {\sigma }^2\right)=-\frac{\tau }{N}{\beta }_N(\alpha ,\tau )+O\left(\frac{1}{{\tau }^{\delta }}\right)+O\left(\frac{\tau }{N}\right)$$ (17)

for the same δ > 0 as in (16) (for 0 < α < 3/2 – see Theorem C.1; see also Remark 3.2 on the range 3/2 ≤ α < 2). The term of order O(τ^−δ), then, is mostly determined by the high frequency behavior of the anomalously diffusive particle (see Figure 1 and expressions (52), (54)). In (17), the main bias factor is given by the function

$${\beta }_N(\alpha ,\tau )=\frac{1}{4\tau }\sum _{i=-N+1}^{N-1}\left(1-\frac{\left|i\right|}{N}\right){\left\{{\left|\frac{i}{\tau }+1\right|}^{\alpha }-2{\left|\frac{i}{\tau }\right|}^{\alpha }+{\left|\frac{i}{\tau }-1\right|}^{\alpha }\right\}}^2.$$ (18)

Note that (18) depends on the unknown parameter α. So we use A_stand and (18) to define an estimator of the bias vector by

$${\left({\beta }_N\left(A_{\text{stand}},{\tau }_k\right)\right)}_{k=1,\dots ,m}.$$ (19)

(b) Accounting for disturbance correlation

In linear estimation theory, the method for dealing with correlated random errors is called generalized least squares (GLS). In fact, the resulting GLS estimator is the best linear unbiased estimator, since it outperforms its OLS counterpart in terms of mean squared error (MSE) (see [15]).

In the context of TAMSD-based estimation, to better understand the difference between the standard, OLS-based estimator and the related GLS-based estimator, recast the vector system (3) as the regression model

$$\mathbf{z}=X\mathit{\xi }+\epsilon .$$ (20)

In (20), the term ξ is as in (1), and the dependent variable and the regressor are given by, respectively,

$$\mathbf{z}={\left(\log M_N\left({\tau }_k\right)\right)}_{k=1,\dots ,m},X=\left(\begin{array}{cc}1& \log {\tau }_1\\ ⋮& ⋮\\ 1& \log {\tau }_m\end{array}\right).$$ (21)

It is well known that the expression

$${\mathit{E}}_{\text{stand}}:={\left(X^{T}X\right)}^{-1}{X}^T\mathbf{z}={\left(L_{\text{stand}},A_{\text{stand}}\right)}^T$$ (22)

gives the standard estimator (7) generated by the OLS solution to the system (20). By contrast, let

$$\mathrm{{\rm Y}}(\mathit{\xi })={\left(v_{k_1,k_2}(\mathit{\xi })\right)}_{k_1,k_2=1,\dots ,m},$$ (23)

be the finite sample covariance matrix of the vector z as in (21). The GLS solution is given by

$${\left(X^T\mathrm{{\rm Y}}{(\mathit{\xi })}^{-1}X\right)}^{-1}{X}^T\mathrm{{\rm Y}}{(\mathit{\xi })}^{-1}\mathbf{z},$$ (24)

which involves the unknown matrix (23). In practice, then, one needs to estimate such matrix. For this purpose, we first establish the entrywise expansion

$$v_{k_1,k_2}(\mathit{\xi })=\frac{\tau }{N}{\zeta }_N\left(\alpha ,{\tau }_{k_1},{\tau }_{k_2}\right)+O\left(\frac{{\tau }^{1-\delta }}{N}\right)+o\left(\frac{\tau }{N}\right),k_1,k_2=1,\dots ,m$$ (25)

(for 0 < α < 3/2 – see Theorem C.2; see also Remark 3.2 on the range 3/2 ≤ α < 2). In (25), the main variance factor is given by

$$\begin{gathered} {\varsigma }_N\left(\alpha ,{\tau }_{k_1},{\tau }_{k_2}\right)=\frac{1}{2\tau }\sum _{i=-N+1}^{N-1}\left(1-\frac{\left|i\right|}{N}\right)\{\left|\frac{i}{\sqrt{{\tau }_{k_1}{\tau }_{k_2}}}+{\sqrt{\frac{{\tau }_{k_1}}{{\tau }_{k_2}}|}}^{\alpha }-\right|\frac{i}{\sqrt{{\tau }_{k_1}{\tau }_{k_2}}}+{\sqrt{\frac{{\tau }_{k_2}}{{\tau }_{k_2}}}-\sqrt{\frac{{\tau }_{k_2}}{{\tau }_{k_1}}}|}^{\alpha } \\ {-{\left|\frac{i}{\sqrt{{\tau }_{k_1}{\tau }_{k_2}}}\right|}^{\alpha }+{\left|\frac{i}{\sqrt{{\tau }_{k_1}{\tau }_{k_2}}}-\sqrt{\frac{{\tau }_{k_2}}{{\tau }_{k_1}}}\right|}^{\alpha }\}}^2. \end{gathered}$$ (26)

Note that expression (26) does not involve the constant σ², but it is still a function of the unknown parameter α. Second, and in view of this, we can use A_stand and (26) to define an estimator of the covariance matrix by

$$\mathrm{{\rm Y}}\left(A_{\text{stand}}\right):={\left(\frac{\tau }{N}{\zeta }_N\left(A_{\text{stand}},{\tau }_{k_1},{\tau }_{k_2}\right)\right)}_{k_1,k_2=1,\dots ,m}.$$ (27)

Drawing upon (a) and (b), we can further construct an improved estimator of ξ by a quasi-GLS procedure based on the estimator Υ(A_stand) and by replacing (3) with the bias-corrected regression system

$$\log M_N\left({\tau }_k\right)+\frac{{\tau }_k}{N}{\beta }_N\left(A_{\text{stand}},{\tau }_k\right)=\log {\sigma }^2+\alpha \log {\tau }_k+{\epsilon }_k,k=1,\dots ,m.$$ (28)

The resulting estimator can be expressed as

$$\mathit{E}=(L,A)={\left(X^T{\mathrm{{\rm Y}}}^{-1}\left(A_{\text{stand}}\right)X\right)}^{-1}{X}^T{\mathrm{{\rm Y}}}^{-1}\left(A_{\text{stand}}\right)\mathbf{y},$$ (29)

where X is again as in (21) and

$$\mathbf{y}=\left(\begin{array}{c}\log M_N\left({\tau }_1\right)+\frac{{\tau }_1}{N}{\beta }_N\left(A_{\text{stand}},{\tau }_1\right)\\ ⋮\\ \log M_N\left({\tau }_m\right)+\frac{{\tau }_m}{N}{\beta }_N\left(A_{\text{stand}},{\tau }_m\right)\end{array}\right).$$ (30)

For the reader’s convenience, the construction of the estimator E is summarized in the form of pseudocode in Appendix D.

To compare the performances of E and E_stand, we generated 1000 independent paths of length 2¹⁰ and estimated the diffusion exponent based on the two methods. Figure 2 displays the results in terms of Monte Carlo bias, standard deviation and square root MSE. The improved estimator E outperforms the usual estimator E_stand by any of the three criteria for different values of α.

Figure 2: Comparative analysis of bias, standard deviation and MSE.

of the estimators E (see (29)) and E_stand (see (7)) as a function of diffusion exponents α (x-axis). Left plot: estimation of α. Right plot: estimation of log σ². Solid and dashed lines represent E and E_stand, respectively. For any parameter value α, the proposed estimator E has smaller bias, standard deviation and square root MSE than E_stand. The total number of Monte Carlo runs is 1000 based on paths of length 2¹⁰.

Remark 3.1

Note that the main bias and variance factors β_N(α, τ) and ${\varsigma }_N\left(\alpha ,{\tau }_{k_1},{\tau }_{k_2}\right)$ in (18) and (26), respectively, converge as N → ∞ (see Lemma C.1). Moreover, after standardization, the estimator (29) is provably asymptotically normal and consistent for 0 < α < 3/2 (see (35) in Section 4 and Proposition C.1). See also Remark 3.2 on the range 3/2 ≤ α < 2.

Remark 3.2

Although we do not provide proofs in this paper, the methods developed in this section and also in Section 4 can be extended to the strongly superdiffusive range 3/2 ≤ α < 2. For example, due to nonstandard convergence rates, expressions (17) and (25) hold after replacing $O(\frac{\tau }{N})$ with $O((\frac{\tau \log N}{N}))$ (for α = 3/2) or $O({(\frac{\tau }{N})}^{4-2\alpha })$ (for 3/2 < α < 2). Likewise, the asymptotic non-Gaussian distribution of the estimator (35) in Section 4, with nonstandard convergence rates, can be established. However, inference involving the nonstandard limiting distribution can be cumbersome, and the computational studies in this section and in Section 4 show that the methods in the proposed format work reasonably well for realistic path lengths. See also [20], Remark 2, on how to construct asymptotically valid confidence intervals for ξ based on the standard estimator E_stand assuming prior knowledge that 3/2 < α < 2.

4. Testing heterogeneity

Single particle tracking experiments with viscoelastic diffusion often generate data in the form of multiple particle paths. As discussed in the Introduction, fluid heterogeneity can be tested in the intra- and interfluid senses. The pathwise framework constructed in Section 3 can be used in new testing protocols with good finite sample and asymptotic properties. We remind the reader that the mathematical statements cover the diffusion exponent range 0 < α < 3/2 (subdiffusive and mildly superdiffusive range), though we also include computational experiments for the strongly superdiffusive range 3/2 ≤ α < 2.

Tables 3 and 4 display the proposed framework. For each type of fluid heterogeneity, they show the appropriate hypotheses and testing procedures, respectively. In the remainder of this section, we provide a detailed description of the protocols. To set the notation, we recall that, for a given a hypothesis test, the conditional probability

$$\mathbb{P}\left(H_0\text{is}\text{rejected}|\mathit{\xi }\text{satisfies}{H}_0\right)=:ϵ\in [0,1]$$ (31)

is called the size (or significance level) of the test, whereas the function

$$\mathit{\xi }\mapsto \mathbb{P}\left(H_0\text{is}\text{rejected}|\mathit{\xi }\text{satisfies}{H}_1\right)\in [0,1]$$ (32)

is called the power of the test.

Table 3:

Hypotheses

heterogeneity	H0	Ha
intrafluid	ξ1 = ··· = ξν	ξi ≠ ξj for some 1 ≤ i,j ≤ ν
interfluid	ξI = ξII	ξI ≠ ξII

Table 4:

Tests

heterogeneity	rejection region	test statistic	number of paths
intrafluid	Rintra (see (38))	$S_1^2$, $S_2^2$ (see (37))	ν
interfluid	Rinter (see (46))	T1, T2 (see (45))	νI, νII

Intrafluid heterogeneity

Suppose ν ∈ ℕ bead diffusion paths of length N from a single fluid sample are available. If the fluid is physically homogeneous, it is expected to generate particle paths with nearly identical parameter values ξ. The alternative is that ξ_i ≠ ξ_j for some pair i, j, namely, their anomalous diffusion parameters differ. These two possibilities, labeled H₀ and H_a, respectively, are listed on the row “intrafluid” in Table 3.

Starting from the ν particle paths, let

$${\mathit{E}}_i,i=1,\dots ,\nu ,$$ (33)

be vector-valued estimators as in (29). For the purpose of constructing a test statistic, we need a normalized (standardized) estimator. Note that the variance of the GLS-type solution (24) is given by

$${\left(X^T{\mathrm{{\rm Y}}}^{-1}(\mathit{\xi })X\right)}^{-1}$$ (34)

(cf. [15]). So, define a standardized estimator by

$${\mathit{Z}}_i=\left(\begin{array}{c}{Z}_{i,1}\\ Z_{i,2}\end{array}\right)={\mathrm{\Lambda }}^{-1/2}(A_{\text{stand},i}){\mathit{E}}_i,i=1,\dots ,\nu ,$$ (35)

where

$$\mathrm{\Lambda }\left(A_{\text{stand},i}\right):={\left(X^T{\mathrm{{\rm Y}}}^{-1}\left(A_{\text{stand},i}\right)X\right)}^{-1}$$ (36)

and the variance estimator Υ(A_stand,i) is given by (27). Then, (35) converges in distribution to ν independent and identically distributed normal random vectors with uncorrelated entries (see Proposition C.1). So, for ${\overline{Z}}_j={\nu }^{-1}{\sum }_{i=1}^{\nu }{Z}_{i,j}$, let

$$S_j^2=\frac{1}{\nu -1}\sum _{i=1}^{\nu }{\left(Z_{i,j}-{\overline{Z}}_j\right)}^2,j=1,2,$$ (37)

be the normalized and decorrelated sample variances of {Z_i,j}_i=1,…,ν, j = 1, 2, as in (35). Then, under H₀,

$$\left((\nu -1)S_1^2,(\nu -1)S_2^2\right)\stackrel{d}{\to }\left({\mathcal{X}}_1,{\mathcal{X}}_2\right),{\mathcal{X}}_j\sim {\chi }_{\nu -1}^2,j=1,2,$$

as N → ∞, where ${\mathcal{X}}_1$ and ${\mathcal{X}}_2$ are independent random variables. To test heterogeneity at significance level ϵ, we can use Bonferroni-type correction (e.g., [15], section 5.3) and reject the null hypothesis H₀ if

$$R_{\text{intra}}:(\nu -1)S_1^2>{\chi }_{\nu -1,ϵ/2}^2\text{or}(\nu -1)S_2^2>{\chi }_{\nu -1,ϵ/2}^2,$$ (38)

where ${\chi }_{\nu -1,ϵ/2}^2$ is a chi-square quantile (c.f. Table 4, “intrafluid” rows).

To check the size of the test (38) over finite samples, we conducted a Monte Carlo study with 50 simulated paths of length 2¹² and recorded whether or not the null hypothesis H₀ is rejected at ϵ = 0.05 significance level. This procedure was repeated 2000 times. Since each outcome is a Bernoulli trial (reject or not H₀), the simulation rejection rate follows a binomial distribution with n = 2000 and p = 0.05. Thus, a normal approximation to the 95% confidence interval of the rejection rate gives (0.040, 0.060). As shown in Figure 3, left plot, the observed simulation rejection rate was around 0.05 and within the 95% confidence interval (for 0 < α < 3/2), as expected. Unreported computational experiments for different significance levels lead to analogous conclusions.

Figure 3: Intra- and interfluid heterogeneity: test sizes.

Monte Carlo sizes of the intrafluid test (left plot; see (38)) and interfluid test (right plot; see (46)) as a function of the diffusion exponent α (x-axis). For every value of α, each of 2000 Monte Carlo runs consisted of generating 50 independent paths of length 2¹² and conducting a test at ϵ = 0.05 (see (31)) or, equivalently, 95% confidence level. The Monte Carlo rejection rate is very close to the theoretical value of ϵ = 0.05 for almost all values of α.

Figure 4 displays Monte Carlo power curves for the intrafluid test. The study was conducted with a total of ν = ν₁ + ν₂ paths, where ν₁ and ν₂ have diffusion exponents α₁ = 1 and α₂, respectively, and α₂ = 0.8 (left plot) or α₂ = 0.7 (right plot). In each plot, the x-axis represents the proportion of paths

$$\frac{{\nu }_2}{{\nu }_1+{\nu }_2}$$ (39)

with diffusion exponent α = α₂. The power curves quickly converge to 1 as a function of the ratio (39), especially for the more distinguishable value α₂ = 0.7 < 1 = α₁.

Figure 4: Intrafluid heterogeneity: test power.

Simulations were conducted with a total of ν = ν₁ +ν₂ paths, where ν₁ and ν₂ of them displayed diffusion exponents α = α₁ = 1 and α = α₂, respectively. In each plot, the y-axis represents the observed test power, or rejection rates (see (32)), and the x-axis is the proportion of paths with α = α₂ (see (39)), starting at 0.02. The total number of Monte Carlo runs is 2000. Left plot: α₂ = 0.8. Right plot: α₂ = 0.7.

When α > 3/2, under H₀ the estimators (33) converge in distribution to ν independent and identically distributed non-Gaussian random vectors. Hence, so do the estimators (35). In this case, the marginal distributions of the decorrelated vector $\left((\nu -1)S_1^2,(\nu -1)S_2^2\right)$ do not approach chi-squared distributions. In computational experiments, the size of the intrafluid test (38) did not significantly deviate from the 0.05 target for α = 1.6, indicating that the nonstandard asymptotic behavior is not a concern for paths of length 2¹². Deviation was significant for the extreme value α = 1.8, suggesting that approximating the test size by simulation may be generally recommendable for greater accuracy (see Figure 3, left plot).

Interfluid heterogeneity

Now suppose ν_I and ν_II paths,

$${\nu }_{\text{I}},{\nu }_{\text{II}}\in \mathbb{N},$$ (40)

are obtained from two physically homogeneous fluid samples I and II, respectively. We are interested in testing whether the samples I and II are homogeneous, namely, whether or not particle diffusion in the fluid samples displays the same underlying parameter value ξ. These two possibilities, labeled H₀ and H_a, respectively, are described on the row “interfluid” in Table 3.

Since multiple (independent) particle paths are assumed available for each fluid sample, we can construct an estimator involving all available TAMSD terms. In fact, first define the overall average mean squared displacement over ν TAMSD terms (AMSD) by

$$M_N^{*}(\tau )=\frac{1}{\nu }\sum _{\ell =1}^{\nu }{M}_N{(\tau )}_{\ell }.$$ (41)

By independence,

$$\langle M_N^{*}(\tau )\rangle =\langle M_N(\tau )\rangle =\langle X^2(\tau )\rangle ,\mathrm{Var}{M}_N^{*}(\tau )=\frac{1}{\nu }\mathrm{Var}{M}_N(\tau ).$$ (42)

Then, AMSD-type estimators

$${\mathit{E}}^{*}=\left(L^{*},A^{*}\right)$$ (43)

can be obtained by applying the pseudocode in Appendix D after replacing TAMSD terms M_N(τ_k) with their AMSD counterparts $M_N^{*}\left({\tau }_k\right)$, k = 1, …, m. Given two fluid samples I and II, let ${\mathit{E}}_{\text{I}}^{*}$ and ${\mathit{E}}_{\text{II}}^{*}$ be their respective AMSD-type estimators. Their finite sample covariance matrices are given by ${\nu }_{\text{I}}^{-1}\mathrm{\Lambda }\left({\mathit{\xi }}_{\text{I}}\right)$ and ${\nu }_{\text{II}}^{-1}\mathrm{\Lambda }\left({\mathit{\xi }}_{\text{II}}\right)$, respectively (cf. (34)). By analogy with (25) and (36), we can define their AMSD-type estimators

$$\frac{1}{{\nu }_{\text{I}}}\mathrm{\Lambda }\left(A_{\text{I}}^{*}\right),\frac{1}{{\nu }_{\text{II}}}\mathrm{\Lambda }\left(A_{\text{II}}^{*}\right).$$ (44)

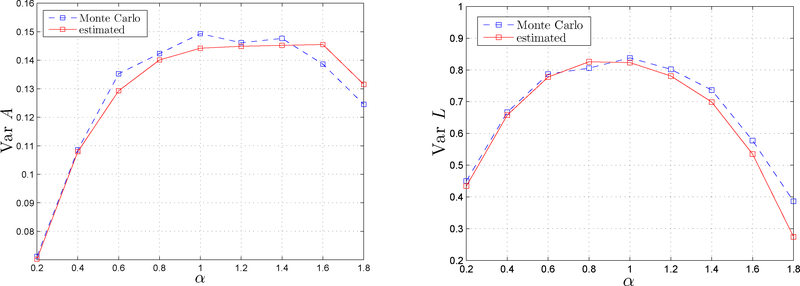
Figure 5 displays a study of the accuracy of $\mathrm{\Lambda }\left(A_{•}^{*}\right)$ as an estimator. It plots Monte Carlo variances of the estimator E as well as their estimates $\mathrm{\Lambda }\left(A_{•}^{*}\right)$ for several values of the parameter α. The latter nearly perfectly match the former in the subdiffusive range. A slight deviation appears in the strongly superdiffusive range, but still within an acceptable margin.

Figure 5: Comparative analysis.

of the standard error of the estimator E = (L, A) (dashed line; see (29)) and its AMSD-type estimator Λ(A*) (solid line; see (44)) as a function of the diffusion exponent α. The latter closely matches the former, especially in the subdiffusive range α < 1. The number of Monte Carlo runs is 1000 based on particle paths of length 2¹⁰.

Hence, we define the standardized estimators

$${\mathit{Z}}_j^{*}=\left(\begin{array}{c}{Z}_{j,1}^{*}\\ Z_{j,2}^{*}\end{array}\right)=\sqrt{{\nu }_j}{\mathrm{\Lambda }}^{-1/2}(A_j^{*}){\mathit{E}}_j^{*},j=\text{I},\text{II}.$$

In view of Proposition C.1, these estimators are also asymptotically normal for 0 < α < 3/2. Hence, let

$$T_1=\frac{Z_{\text{I},1}^{*}-Z_{\text{II},1}^{*}}{\sqrt{2}},T_2=\frac{Z_{\text{I},2}^{*}-Z_{\text{II},2}^{*}}{\sqrt{2}}$$ (45)

be the associated test statistics. The rejection region is given by

$$R_{\text{inter}}:\left|T_1\right|>z_{ϵ/4}\text{or}\left|T_2\right|>z_{ϵ/4},$$ (46)

where z_ϵ/4 is a standard Normal quantile (c.f. Table 4, row “interfluid”). In (46), the probability ϵ/4 stems, first, from applying a Bonferroni-type correction to a double testing region (hence yielding ϵ/2 significance level in each), and second, from the fact that in each region the test statistic distribution is two-sided.

To check the test’s size over finite samples, we produced a 2000-run Monte Carlo study based on two sets of 50 paths with the same diffusion exponent, where tests were conducted at significance level ϵ = 0.05. As shown in Figure 3, right plot, the rejection rate was close to 0.05, as expected.

In Figure 6, we investigate the interfluid test power as a function of the path lengths and number of paths. The x-axis represents the difference between the diffusion exponents from two fluids, namely,

$${\delta }_{\alpha }=\left|{\alpha }_{\text{I}}-{\alpha }_{\text{II}}\right|,$$ (47)

whereas the y-axis is the test power at ϵ = 0.05. From top to bottom, the three plots correspond to α_min = min{α_I, α_II} = 0.2, 1.0, 1.8, respectively, for various combinations of realistic values of N and ν = ν_I = ν_II. In all cases, the power curves start at around 0.05, as expected, and quickly approach 1 as a function of δ_α as defined in (47). Larger path lengths, larger number of particle paths as well as not very large values of α_min are associated with faster convergence of power curves to 1.

Figure 6: Interfluid heterogeneity: test power.

For various values of N (see (2)) and ν = ν_I = ν_II (see (40)), we plot test power (y-axis; see (32)) as a function of δ_α (x-axis; see (47)). The parameter values are given by α_min := min{α_I, α_II} in the range α_min = 0.2, 1.0, 1.8 (top, middle and bottom, respectively).

Interfluid heterogeneity: more or longer paths under technical–experimental constraints?

Figure 6 also illustrates the following phenomenon. For the subdiffusive and diffusive cases, there is no visible difference between doubling the path lengths or the number of paths. However, in the strongly superdiffusive range, doubling the number of paths increases the test power more than doubling the path lengths.

In real world lab conditions, conducting single particle experiments involves coping with technical restrictions. For example, there may be limited camera recording time, tracer particles may slip out of the field of view or there may be a limit on the total number of tracer particles per fluid sample while still assuming that particles diffuse independently. So, assuming technical– experimental restrictions are in place, it is relevant to ask: what is the difference between

• Method I : recording the movement of a larger number of particles (ν) over a fixed period of time (hence, keeping constant the average sample path length N); and

• Method II : recording the same number of particles ν over a longer period of time (hence, yielding a larger average N)?

We answer this question in the framework of interfluid heterogeneity testing.

In the regimes of Methods I and II, we investigate the performance of the AMSD-type estimator (43) in terms of bias, standard deviation and square root MSE. Bearing in mind expression (42), by a similar reasoning to the one leading to expression (17) for a single observed path, the bias of ${\log }_2{M}_N^{*}(\tau )$ as an estimator of α log τ + log σ² is given by

$$O\left({\tau }^{-\delta }\right)-\langle \frac{{\left(M_N^{*}(\tau )-\langle X^2(\tau )\rangle \right)}^2}{2{\langle X^2(\tau )\rangle }^2}\rangle =O\left({\tau }^{-\delta }\right)-\frac{1}{\nu }\langle \frac{{\left(M_N(\tau )-\langle X^2(\tau )\rangle \right)}^2}{2{\langle X^2(\tau )\rangle }^2}\rangle .$$ (48)

Moreover, by the independence of particle paths, we can approximate the variance of ${\log }_2{M}_N^{*}(\tau )$ by

$$\mathrm{Var}\left(\log M_N^{*}(\tau )\right)\approx \frac{\mathrm{Var}{M}_N(\tau )}{\nu {\langle X^2(\tau )\rangle }^4}.$$ (49)

The performance of the estimator (43) in the two regimes depends on the interplay between the bias and variance components (48) and (49), respectively. In a computational experiment, we applied the following procedure.

1. Start out in the same setting: 2⁴ paths of length 2⁸ for each method, run 500 Monte Carlo simulations to get the bias, standard deviation and square root MSE of A for Method I and II;

2. for Method I, fix the path length and at each step generate 2⁴ times the previous number of paths and redo the Monte Carlos experiments;

3. for Method II, fix the number of paths and at each step generate paths of length 2⁴ times the previous length, multiply all lags by 2 and redo the Monte Carlos experiments;

4. repeat 2. and 3. three times.

For ease of comparison, Table 5 displays the multiple instances generated. Note that, at each step, the total number of points recorded

$$\nu \times N$$ (50)

is identical for the two methods.

Table 5:

Methods I and II.

	Method I			Method II
step	N	ν	ν × N	N	ν	ν × N
1	28	24	212	28	24	212
2	28	28	216	212	24	216
3	28	212	220	216	24	220
4	28	216	224	220	24	224

We compare the results in Figure 7, top and middle plots, where the diffusion exponent is set to α = 0.6 and 1.0, respectively. Method II has smaller bias and square root MSE. The reason is that, when ν is large enough, the term O(τ^−δ) dominates the bias. Thus, increasing the number of paths ν does not reduce the bias. However, increasing the path length N means that the TAMSD terms M_N(τ) with larger lag values τ can be used in the regression procedure. This implies a reduction in magnitude of the term O(τ^−δ), and hence, smaller bias. Method I displays smaller standard deviation because a 16-fold increase in ν reduces the standard error by a factor of 1/4. Meanwhile, noting that 〈X²(τ)〉 ~ σ²τ^α, expression (55) implies that for Method II the standard deviation is proportional to $\sqrt{\tau /N}$. By multiplying N by 16 and τ by 2, the standard error is reduced by a factor of $1/2\sqrt{2}$.

Figure 7: Bias, standard deviation, and square root MSE for Methods I (blue) and II (red).

The x-axis denotes the total number of recorded data points (see (50)). Top: α = 0.6. Middle: α = 1.0. Bottom: α = 1.8.

In Figure 7, bottom plot, we set α = 1.8. For this parameter value, the convergence rate of the TAMSD-based estimators is slower than $\frac{1}{\sqrt{N}}$. Method II still shows a smaller bias by comparison to Method I, as expected. However, since δ increases as a function of α (see expression (54)), then O(τ^−δ) shrinks with α. Therefore, the component O(τ^−δ) carries less weight in the estimator’s bias for the superdiffusive case than for the subdiffusive case. Since α > 3/2, again by expression (55) (see also Remark 3.2) the standard deviation for Method II is proportional to (τ/N)^2−α = (τ/N)^0.2. Thus, again assuming a 16-fold increase in N and a 2-fold increase in τ, the standard error is reduced by a factor of 1/8^0.2, which is much slower than the standard error reduction factor of $1/2\sqrt{2}$ for Method I. These are the two reasons why Method I displays smaller square root MSE than Method II.

5. Analysis of experimental data: heterogeneity of treated P. aeruginosa biofilms

The Hill and Schoenfisch Labs at UNC-Chapel Hill produced data from experiments on disruption and eradication of P. aeruginosa biofilms using nitric oxide-releasing chitosan oligosaccharides [73]. For the reader’s convenience, we provide a brief description of the experiments.

Cystic fibrosis (CF) lung disease is caused by defective chloride transport, resulting in thickened, dehydrated mucus. The latter restricts bacterial motility and promotes P. aeruginosa biofilm formation. Inhaled tobramycin is currently the only antibiotic recommended for the treatment of both initial and chronic P. aeruginosa infections in patients with CF. While inhaled tobramycin is effective at eradicating bacteria within biofilms, it fails to physically remove the structural remnants of the biofilm from the airways. This may lead to biofilm regrowth and the development of antibiotic-resistant infections. Therefore, an ideal anti-biofilm therapeutic for CF would both eradicate bacteria and physically degrade the biofilm, facilitating clearance from the airways.

On the other hand, nitric oxide (NO) is an endogenously produced diatomic free radical with significant antibacterial activity against P. aeruginosa biofilms. Atomic force microscopy revealed that NO exposure causes structural damage to the membranes of planktonic Gram-negative bacteria, including P. aeruginosa. The interest lies in the utility of NO-releasing chitosan oligosaccharides to both eradicate and physically alter P. aeruginosa biofilms and in comparing its effect with tobramycin. In order to measure the physical changes to bacterial biofilms caused by NO-releasing chitosan oligosaccharides, movements of fluorescent tracer particles embedded in P. aeruginosa biofilms were imaged at 60 frames per second for 30 seconds on an inverted microscope at 40× magnification. The tracer particle displacement as a function of time was quantified using Video Spot Tracker software (Center for Computer Integrated Systems for Microscopy and Manipulation, University of North Carolina at Chapel Hill); see [73] for more details.

Fluid heterogeneity has been correlated with increased viscoelasticity for complex biological materials such as sputum [16]. In the experiments we describe, the effect of antibacterial treatment on biofilm heterogeneity was thus evaluated at different concentrations based on tracer particle displacement data. In Table 6, we use the data to test the intrafluid heterogeneity of P. aeruginosa biofilms after tobramycin treatments at concentrations levels 25, 50, 100, 200, and 400 μg ml⁻¹. From each of these fluid samples, we randomly select 100 paths of length N = 1800. An application of the intrafluid test (38) produces strong evidence (negligible p-values) of intrafluid heterogeneity in every sample. This conclusion matches those reported in [73]. Since no homogeneous fluid samples are detected from any of these five samples, we do not perform the interfluid heterogeneity test (46).

Table 6:

Intrafluid biofilm heterogeneity testing after treatment with tobramycin at concentration levels 25, 50, 100, 200, 400 μg ml⁻¹. 100 independent paths of length 1800 were randomly selected for each concentration level.

Tobramycin (μg ml−1)	p-value
25	< 10−16
50	< 10−16
100	< 10−16
200	< 10−16
400	< 10−16

In Table 7, we apply (38) in the testing of intrafluid heterogeneity of P. aeruginosa biofilms after COS2-NO treatment at concentration levels 1, 2, 4, 8, and 16 mg ml⁻¹. COS2 releases NO, which cause the physical disruption and eradication of biofilms [73], and also reduces the viscoelastic properties of mucus [72]. As before, 100 paths of length 1800 were randomly selected for each concentration level. At concentrations 1 or 2 mg ml⁻¹, the p-values are still less than machine error, which indicates strongly significant heterogeneity. As the concentration level increases to 4 and 8 mg ml⁻¹, the p-values also increase. At concentration level 16 mg ml⁻¹, the p-value reaches 0.18. Hence, we fail to reject the null hypothesis of intrafluid homogeneity. This provides evidence that the COS2-NO treatment is effective at eradicating P. aeruginosa biofilms. Once again, this analysis confirms the conclusions reported in [73]. In Table 8, by applying (46), we test the interfluid heterogeneity of P. aeruginosa biofilms after COS2-NO treatment at concentration level 16 mg ml⁻¹. From each fluid sample (A, B and C), we selected 100 paths of length 1800 and conducted the test. It turns out that there is no evidence whatsoever of heterogeneity among fluid samples A, B and C.

Table 7:

Intrafluid biofilm heterogeneity testing after treatment with COS2-NO at concentration levels 1, 2, 4, 8, 16 mg ml⁻¹. 100 independent paths of length 1800 were randomly selected for each concentration level.

COS2-NO (mg ml−1)	p-value
1	< 10−16
2	< 10−16
4	2 × 10−13
8	3 × 10−9
16	0.18

Table 8:

Interfluid biofilm heterogeneity testing after treatment with COS2-NO at concentration level 16 mg ml⁻¹. 100 independent paths of length 1800 were randomly selected for each group.

COS2-NO 16 mg ml−1	p-value
Group A vs Group B	0.9996
Group A vs Group C	0.9998
Group B vs Group C	0.9999

6. Conclusion

Motivated by applications in viscoelastic diffusion, in this paper we start from the TAMSD’s asymptotic distribution for a broad class of Gaussian fractional stochastic processes [20] to propose statistical protocols that make use of single-particle tracking data in the detection of fluid heterogeneity.

The testing methodology is based on an improved TAMSD-type estimator. To construct this estimator, we tackle two of the main issues involved in TAMSD-based estimation, namely, we mathematically characterize: (a) the finite-sample bias in log-TAMSD-based methods; and (b) the effect of disturbance correlation. The theoretical results on (a) and (b) allow us to propose a nearly optimal estimator by combining a bias-correction procedure and a generalized least squares-type regression solution. The improved TAMSD-based estimator (29) is asymptotically normal for 0 < α < 3/2, and computational experiments show that the new estimator outperforms the standard TAMSD-based estimator both in terms of bias and square root MSE for values of α over the whole parameter range (0, 2).

The estimator (29) is used in the construction of protocols for fluid heterogeneity detection in two different experimental situations, namely, when testing: (i) whether different regions of the same fluid are heterogeneous (intrafluid heterogeneity); or (ii) whether two samples from each homogenous fluid are heterogeneous (interfluid heterogeneity). Reflecting the asymptotic behavior of (29), for 0 < α < 3/2 the test statistics (37) and (45) for intra- and interfluid heterogeneity are asymptotically chi-square and asymptotically normally distributed, respectively. This ensures the tests and associated quantiles are asymptotically valid. Computational experiments confirm that the tests’ significance levels are accurate over finite samples, and that the tests display high power even for relatively small deviations from the null hypotheses.

In all cases, for the sake of completeness, we discuss and provide computational studies on the strong superdiffusivity range 3/2 ≤ α < 2. Although this may not affect physical areas of application where subdiffusion is prevalent, this research points to one difficulty involved in TAMSD-based modeling, namely, a potentially non-Gaussian (Rosenblatt-type) limiting distribution with an intricate cumulant structure (cf. expression (60)).

The constructed framework helps to shed light on the effect of common technical experimental constraints such as limited camera recording time: we characterize the difference between observing longer particle paths and using a larger number of particle paths of given length.

We apply the protocols in physical practice by making inferences on fluid viscoelasticity with data from the Hill and Schoenfisch Labs (UNC-Chapel Hill), as first reported and described in [73]. The testing protocols reveal that COS2-NO treatment is effective in eradicating P. aeruginosa biofilms, since greater concentration levels of the treatment clearly lead to greater fluid homogeneity as detected by tracer particle displacement data.

The research contained in this paper points to a number of interesting questions. From a modeling standpoint, it would be convenient to construct a heterogeneity testing framework for single particle experiments that, unlike TAMSD-based methods, mathematically covers the full anomalous diffusion parametric range 0 < α < 2 under the same limit parametric family of distributions. Moreover, ideally a heterogeneity testing framework should be robust with respect to nuisance trends and added experimental noise. In another research direction, the same questions can be asked for classes of anomalous diffusion models not covered by the results in [20] such as, for example, continuous time random walks and related stochastic processes.

A. The asymptotic distribution of the TAMSD

In Theorem A.1, we provide the asymptotic distribution of the TAMSD random vector after centering, which in Corollary A.1 allows developing the asymptotic distribution of the OLS estimator (7) of the diffusivity coefficient and diffusion exponent.

Theorem A.1

(Didier and Zhang [20], Theorem 1) Suppose the particle motion is a Gaussian, stationary increment process whose covariance function admits the harmonizable (Fourier domain) representation

$$\langle X(s)X(t)\rangle =C_{\alpha }^2{\int }_{ℝ}\frac{\left(e^{isx}-1\right)\left(e^{-itx}-1\right)}{x^2}f(x)dx,\alpha \in (0,2),C_{\alpha }\ne 0.$$ (51)

In (51), the spectral density has the generic form $f(x)=\frac{s(x)}{|x{|}^{\alpha /2-1/2}}$, where the ℂ-valued high frequency function s(x) is bounded and satisfies the relations

$$|s(0){|}^2=1,||s{(x)|}^2-1\left|\le C_0\right|{x|}^{{\delta }_0},x\in \left(-{\epsilon }_0,{\epsilon }_0\right),$$ (52)

for constants C₀, δ₀, ε₀ > 0. Suppose the growth of the lag value term τ = τ(N) ∈ ℕ as in (15) with respect to the sample size N is given by

$$\frac{\tau (N){\log }^2(N)}{N}+\frac{N}{\tau {(N)}^{1+\delta /2}}\to 0,N\to \infty ,$$ (53)

where

$$\delta =\min \left\{\alpha /2,{\delta }_0/2\right\}.$$ (54)

Also consider the rates of convergence

$$\{\begin{array}{cc}0<\alpha <3/2:& \eta (N)=\sqrt{N},\zeta (\tau )={\tau }^{\alpha +1/2};\\ \alpha =3/2:& \eta (N)=\sqrt{N\log (N)},\zeta (\tau )={\tau }^2;\\ 3/2<\alpha <2:& \eta (N)=N^{\alpha -1},\zeta (\tau )={\tau }^2.\end{array}$$ (55)

Then, as N → ∞,

$${\left(\frac{N_k}{\eta \left(N_k\right)\zeta \left({\tau }_k\right)}\left(M_N\left({\tau }_k\right)-\langle X^2\left({\tau }_k\right)\rangle \right)\right)}_{k=1,\dots ,m}\stackrel{d}{\to }\mathbf{Z},$$ (56)

where, for k = 1, …, m, N_k = N − τ_k is the number of available terms in each TAMSD sum (2) and τ_k is given by (15). In (56), the distribution of the random vector Z can be described as follows.

1. If 0 < α < 3/2, then $\mathbf{Z}\sim \mathcal{N}(0,\mathrm{\Sigma })$ (a m-variate Gaussian distribution), where the entry k₁, k₂ of the matrix Σ = Σ(α) is given by

   $${\mathrm{\Sigma }}_{k_1,k_2}=2w_{k_1}^{-\alpha -1/2}{w}_{k_2}^{-\alpha -1/2}{\left(\frac{C_{\alpha }}{C_H}\right)}^4{\Vert \widehat{G}\left(y;w_{k_1},w_{k_2}\right)\Vert }_{L^2(ℝ)}^2,$$ (57)

   k₁, k₂ = 1, …, m. In (57), we define

   $$C_H=\sqrt{{\pi }^{-1}H\mathrm{\Gamma }(2H)\sin (H\pi )}$$

   and

   $$\widehat{G}\left(y;w_{k_1},w_{k_2}\right)=C_H^2\frac{\left(e^{i{w}_{k_1}y}-1\right)\left(e^{-i{w}_{k_2}y}-1\right)}{|y{|}^{\alpha +1}};$$ (58)
2. if α = 3/2, then $\mathbf{Z}\sim \mathcal{N}(0,\mathrm{\Sigma })$, where the entry k₁, k₂ of the matrix Σ = Σ(α) is given by

   $${\mathrm{\Sigma }}_{k_1,k_2}=4{\vartheta }^2,k_1,k_2=1,\dots ,m,$$ (59)

   and

   $$\vartheta ={\left(\frac{C_{\alpha }}{C_H}\right)}^2\frac{\alpha (\alpha -1)}{2};$$
3. if 3/2 < α < 2, Z follows a multivariate Rosenblatt-type distribution whose characteristic function is given by

   $${\varphi }_{\mathbf{Z}}(\mathbf{t})=\exp \left\{\frac{1}{2}\sum _{s=2}^{\infty }\frac{{\left[2i\vartheta {\sum }_{k=1}^m{t}_k\right]}^s}{s}{c}_s(\alpha )\right\}$$ (60)

   around the origin. In (60), for s ≥ 2, c_s(α) is given by

   $${\int }_{{[0,1]}^s}{\left|x_1-x_2\right|}^{\alpha -2}{\left|x_2-x_3\right|}^{\alpha -2}\cdots {\left|x_s-x_1\right|}^{\alpha -2}d{x}_1\cdots d{x}_s.$$ (61)

Consider again the regression system (20) and recall that expression (22) gives the standard estimator generated by the OLS solution to the system (20). The following corollary describes the asymptotic distribution of the standard estimator (22).

Corollary A.1

(Didier and Zhang [20], Corollary 1) Suppose the assumptions of Theorem A.1 hold. Then, as N → ∞,

$$\frac{N{\tau }^{\alpha }}{\eta (N)\zeta (\tau )}\left(\begin{array}{c}\frac{1}{\log \tau }\left(L_{\text{stand}}-\log {\sigma }^2\right)\\ A_{\text{stand}}-\alpha \end{array}\right)\stackrel{d}{\to }\left(\begin{array}{c}{U}^T\\ -U^T\end{array}\right)A\mathbf{Z}.$$ (62)

In (62),

$$A=A\left({\sigma }^2,\alpha \right)=\mathrm{diag}\left(\zeta \left(w_1\right)/\left({\sigma }^2{w}_1^{\alpha }\right),\dots ,\zeta \left(w_m\right)/\left({\sigma }^2{w}_m^{\alpha }\right)\right),$$ (63)

η(·), ζ(·) and Z are as in Theorem A.1, and

$$U^T=\frac{1}{c_w}\left(\sum _{k=1}^m\log \left(w_k/w_1\right),\dots ,\sum _{k=1}^m\log \left(w_k/w_m\right)\right)$$ (64)

with constant

$$c_w=m\sum _{k=1}^m{\log }^2\left(w_k\right)-{\left(\sum _{k=1}^m\log \left(w_k\right)\right)}^2.$$ (65)

In particular, the standard estimator (22) is consistent, namely, relation (9) holds.

Proposition A.1

(Didier and Zhang [20], Proposition 1, (i)) Under the assumptions of Theorem A.1, there is a constant σ² > 0 such that (16) holds for some C > 0, where δ > 0 is given by (54).

B. Some lemmas

In this section, we present some lemmas that are used to prove Theorems C.1 and C.2 in Section C. Throughout this section, we assume 0 < α < 3/2 and the conditions of Theorem A.1. In proofs, whenever convenient C denotes a constant that may change from one line to the next.

In light of (56), define the standardized statistic

$$\varpi (\tau )=\frac{M_N(\tau )}{\langle X^2(\tau )\rangle }.$$ (66)

In particular,

$$\varpi (\tau )\stackrel{P}{\to }1,N\to \infty ,$$ (67)

so that a Taylor expansion can be applied to $\log \varpi (\tau )$ around 1. Meanwhile, we define the standardized increment

$$W_j(\tau )=\frac{X(j+\tau )-X(j)}{\sqrt{\langle X^2(\tau )\rangle }}.$$ (68)

We will use the following results in our proofs. The first one is the classical Isserlis theorem, which reduces the higher moments of a multivariate normal vector to its second moments. The second one is a concentration inequality that will allow us to establish sharp bounds on the tails of centered quadratic forms.

Theorem B.1

(Isserlis, [37]). Let (Z₁, Z₂, …, Z_2N) be a zero mean, multivariate normal random vector. Then,

$$\langle Z_1{Z}_2\dots Z_{2N}\rangle =\sum \prod \langle Z_i{Z}_j\rangle ,$$

where the notation $\sum \prod$ stands for summing over all distinct ways of partitioning Z₁, …, Z_2N into pairs Z_i, Z_j and each summand is a product of these N pairs.

Theorem B.2

[47, 5] Let $Z_1,\dots ,Z_N\stackrel{\text{i}.\text{i}.\text{d}}{\sim }\mathcal{N}(0,1)$ and consider constants η₁, …, η_N ≥ 0, not all zero. Let ∥η∥₂ and ∥η∥_∞ be the Euclidean square and sup norms of the vector η = (η₁, …, η_N)^T.

Also, define the random variable $X={\sum }_{i=1}^N{\eta }_{i,N}\left(Z_i^2-1\right)$. Then, for every x > 0,

$$\mathbb{P}\left(X\ge 2\Vert \eta {\Vert }_2\sqrt{x}+2\Vert \eta {\Vert }_{\infty }x\right)\le \exp (-x),$$

$$\mathbb{P}\left(X\le -2\Vert \eta {\Vert }_2\sqrt{x}\right)\le \exp (-x).$$

The following lemma describes some basic properties of the central moments of (66).

Lemma B.1

As N → ∞,

$$\langle {(\varpi (\tau )-1)}^2\rangle =O\left(\frac{\tau }{N}\right).$$ (69)

Moreover, any moment of $\varpi (\tau )-1$ is bounded in N, i.e.,

$$\left|\langle {(\varpi (\tau )-1)}^{\kappa }\rangle \right|=O(1),\kappa \in \mathbb{N}.$$ (70)

Proof. Expression (70) (for κ ≥ 3) can be proved by adapting the argument for establishing expression (C.24) in [94], while making use of the bound (76) and Lemma B.2 (expressions (73) and (74)). So, for the reader’s convenience, we establish (69) (for κ = 2). The left-hand side of (69) can be rewritten as

$$\begin{gathered} \frac{1}{N^2}\langle \sum _{k_1=1}^N\sum _{k_2=1}^N\left(\frac{{\left(X\left(\tau +k_1\right)-X\left(k_1\right)\right)}^2}{\langle X^2(\tau )\rangle }-1\right)\left(\frac{{\left(X\left(\tau +k_1\right)-X\left(k_2\right)\right)}^2}{\langle X^2(\tau )\rangle }-1\right)\rangle \\ =\frac{1}{N^2}\langle \sum _{k_1=1}^N\sum _{k_2=1}^N(W_{k_1}^2(\tau )-1)(W_{k_2}^2(\tau )-1)\rangle . \end{gathered}$$ (71)

By applying the Isserlis theorem (Theorem B.1),

$$\begin{gathered} \langle (W_{k_1}^2(\tau )-1)(W_{k_2}^2(\tau )-1)\rangle =\langle W_{k_1}^2(\tau )W_{k_2}^2(\tau )\rangle -\langle W_{k_1}^2(\tau )\rangle -\langle W_{k_2}^2(\tau )\rangle +1 \\ =2{\langle W_{k_1}(\tau )W_{k_2}(\tau )\rangle }^2=\frac{2}{{\langle X^2(\tau )\rangle }^2}{\gamma }_{\tau }^2\left(k_1-k_2\right), \end{gathered}$$

where

$${\gamma }_h\left(k_1-k_2\right)=\langle \left(X\left(k_1+h\right)-X\left(k_1\right)\right)\left(X\left(k_2+h\right)-X\left(k_2\right)\right)\rangle .$$

Thus, (71) can be recast as

$$\frac{2}{N^2{\langle X^2(\tau )\rangle }^2}\sum _{k_1,k_2=1}^N{\gamma }_{\tau }^2\left(k_1-k_2\right),$$ (72)

Note that

$$\frac{2}{N^2{\langle X^2(\tau )\rangle }^2}=O\left(\frac{1}{N^2{\tau }^{2\alpha }}\right)=O\left(\frac{\tau }{N}{\zeta }^{-2}(\tau ){\eta }^{-2}(N)\right),$$

where ζ(τ), η(N) are defined by (55). Then, by (72), Lemmas C.1 – C.4 in [20], expression (71) is of the order $O\left(\frac{\tau }{N}\right)$, as claimed. □

The next lemma draws upon Theorem B.2 and Lemma B.1 to construct a concentration inequality for (66) (see also [22]).

Lemma B.2

Fix −∞ < r < 1/2 < 3/2 < rˊ. Then, for any 0 < ξ < 1/2 and some C > 0,

$$\mathbb{P}(\varpi (\tau )\le r)\le \exp \left\{-C{\left(\frac{N}{\tau }\right)}^{\xi }\right\}$$ (73)

and

$$\mathbb{P}\left(\varpi (\tau )\ge r^{\prime }\right)\ge \exp \left\{-C{\left(\frac{N}{\tau }\right)}^{\xi }\right\}.$$ (74)

Proof. Let W_j(τ), j = 1, …, N be as in (68). Then, for $\varpi (\tau )$ as in (67), we can write

$$\varpi (\tau )=\frac{1}{N}\sum _{j=1}^N{W}_j^2(\tau )=\frac{1}{N}{\mathbf{W}}_N^T{\mathbf{W}}_N,$$

where W_N = (W₁(τ), …, W_N(τ))^T is a multivariate normal vector with covariance matrix Γ. Consider the spectral decomposition QΛQ^T = Γ, where Q is a N × N orthogonal matrix and Λ = diag{λ₁, …, λ_N} is a N × N diagonal matrix. Then, ${\mathbf{W}}_N\stackrel{d}{=}Q{\mathrm{\Lambda }}^{1/2}{\mathbf{Z}}_N$, where ${\mathbf{Z}}_N={\left(Z_1,\dots ,Z_N\right)}^T\sim \mathcal{N}\left(0,I_N\right)$, I_N is the N×N identity matrix, and $\stackrel{d}{=}$ denotes equality in distribution. Therefore,

$$\varpi (\tau )\stackrel{d}{=}\frac{1}{N}{\left(Q{\mathrm{\Lambda }}^{1/2}{\mathbf{Z}}_N\right)}^{T}Q{\mathrm{\Lambda }}^{1/2}{\mathbf{Z}}_N=\frac{1}{N}{\mathbf{Z}}_N^T\mathrm{\Lambda }{\mathbf{Z}}_N=\sum _{j=1}^N{\eta }_{j,N}{Z}_j^2,$$ (75)

where ${\eta }_{j,N}=\frac{{\lambda }_j}{N}$. Let η_N = (η_i,N)_i=1,…,N be the vector of coefficients η·,N. By expression (69) in Lemma B.1,

$${\Vert {\eta }_N\Vert }_{\infty }^2\le {\Vert {\eta }_N\Vert }_2^2=\mathrm{Var}\varpi (\tau )=\langle {(\varpi (\tau )-1)}^2\rangle =O\left(\frac{\tau }{N}\right).$$ (76)

By Theorem B.2, by using the same argument as in the proof of Lemma C.3 in [94], and applying the bound (76),

$$\mathbb{P}(\varpi (\tau )\le r)=\mathbb{P}\left(\sum _{j=1}^N{\eta }_{j,N}(Z_j^2-1)\le r-1\right)\le \exp \left\{-\frac{C}{{\Vert {\eta }_N\Vert }_2^2}\right\}\le \exp \left\{-C\frac{N}{\tau }\right\}$$

for some C > 0. Thus, (73) follows. To show (74), it suffices to adapt the proof of expression (C.34) in [94]. In fact, by (76), 0 < ξ < 1/2 and Theorem B.2,

$$\begin{gathered} \mathbb{P}\left(\varpi (\tau )\ge r^{\prime }\right)=\mathbb{P}\left(\sum _{j=1}^N{\eta }_{j,N}(Z_j^2-1)\ge r^{\prime }-1\right) \\ \le \mathbb{P}\left(\sum _{j=1}^N{\eta }_{j,N}(Z_j^2-1)\ge 2{\Vert {\eta }_N\Vert }_2{\left(\frac{N}{\tau }\right)}^{\frac{\xi }{2}}+2{\Vert {\eta }_N\Vert }_{\infty }{\left(\frac{N}{\tau }\right)}^{\xi }\right)\le \exp \left\{-C{\left(\frac{N}{\tau }\right)}^{\xi }\right\}. \end{gathered}$$

□

The following lemma is used in the proof of Lemma B.6.

Lemma B.3

Let p ≥ 1, there is a constant K_p only depending on p such that

$$\langle |\log \varpi (\tau ){|}^p\rangle \le K_p$$ (77)

Proof. By (75), $\varpi (\tau )$ is a nonnegative weighted sum of independent chi-squared random variables, where not all weights are zero. Then, relation (77) is a consequence of expression (96) in [63], p. 184. □

The following lemma can be shown based on Lemma B.2 and an adaptation of the proof of expressions (C.38) and (C.39) in [94], which pertains to higher order (cross)moments of wavelet variance terms.

Lemma B.4

Let κ₁, κ₂ ∈ ℕ ∪ {0}, κ₁ + κ₂ ≥ 3, and fix 0 < r < 1/2. Then, as N → ∞,

$$\langle {\left(\varpi \left({\tau }_1\right)-1\right)}^{{\kappa }_1}{\left(\varpi \left({\tau }_2\right)-1\right)}^{{\kappa }_2}\rangle =O\left[{\left(\frac{\tau }{N}\right)}^2\right].$$

$$\langle {\left(\varpi \left({\tau }_1\right)-1\right)}^{{\kappa }_1}{\left(\varpi \left({\tau }_2\right)-1\right)}^{{\kappa }_2}{1}_{\left\{\min \left\{\varpi \left({\tau }_1\right),\varpi \left({\tau }_2\right)\right\}>r\right\}}\rangle =O\left[{\left(\frac{\tau }{N}\right)}^2\right].$$ (78)

Lemmas B.5, B.6 and B.7, stated and shown next, are used in the proofs of Theorems C.1 and C.2. The lemmas provide expressions for (cross)moments and (cross)moments of logarithms of the random variables (66) at different lag values.

Lemma B.5

$$\begin{gathered} \langle \left(\varpi \left({\tau }_{k_1}\right)-1\right)\left(\varpi \left({\tau }_{k_2}\right)-1\right)\rangle =\frac{1}{2n}\sum _{i=-N+1}^{N-1}\left(1-\frac{\left|i\right|}{N}\right)\times \\ \times \left\{\right|\frac{i}{\sqrt{{\tau }_{k_1}{\tau }_{k_2}}}+{\sqrt{\frac{{\tau }_{k_1}}{{\tau }_{k_2}}}|}^{\alpha }-{\left|\frac{i}{\sqrt{{\tau }_{k_1}{\tau }_{k_2}}}+\sqrt{\frac{{\tau }_{k_1}}{{\tau }_{k_2}}}-\sqrt{\frac{{\tau }_{k_2}}{{\tau }_{k_1}}}\right|}^{\alpha }- \\ -{\left|\frac{i}{\sqrt{{\tau }_{k_1}{\tau }_{k_2}}}\right|}^{\alpha }{+{\left|\frac{i}{\sqrt{{\tau }_{k_1}{\tau }_{k_2}}}-\sqrt{\frac{{\tau }_{k_2}}{{\tau }_{k_1}}}\right|}^{\alpha }\}}^2\left(1+O\left({\tau }^{-\delta }\right)\right). \end{gathered}$$ (79)

Proof. For notational simplicity, assume k₁ =1 and k₂ = 2. By (68), the left-hand side of (79) can be rewritten as

$$\frac{1}{N^2}\sum _{j_1,j_2=1}^N\langle (W_{j_1}^2\left({\tau }_1\right)-1)(W_{j_2}^2\left({\tau }_2\right)-1)\rangle =\frac{1}{N^2}\sum _{j_1,j_2=1}^N\langle W_{j_1}^2\left({\tau }_1\right)W_{j_2}^2\left({\tau }_2\right)\rangle -1.$$ (80)

By Theorem B.1 (Isserlis),

$$\begin{gathered} \langle W_{j_1}^2\left({\tau }_1\right)W_{j_2}^2\left({\tau }_2\right)\rangle =\langle W_{j_1}^2\left({\tau }_1\right)\rangle \langle W_{j_2}^2\left({\tau }_2\right)\rangle +2{\langle W_{j_1}\left({\tau }_1\right)W_{j_2}\left({\tau }_2\right)\rangle }^2 \\ =1+2{\langle W_{j_1}\left({\tau }_1\right)W_{j_2}\left({\tau }_2\right)\rangle }^2. \end{gathered}$$ (81)

By Lemma A.1 in [20],

$$\begin{gathered} \langle \frac{\left(X\left(j_1+{\tau }_1\right)-X\left(j_1\right)\right)\left(X\left(j_2+{\tau }_2\right)-X\left(j_2\right)\right)}{\sqrt{\langle X^2\left({\tau }_1\right)\rangle }\sqrt{\langle X^2\left({\tau }_2\right)\rangle }}\rangle \\ =\langle \frac{\left(B_H\left(j_1+{\tau }_1\right)-B_H\left(j_1\right)\right)\left(B_H\left(j_2+{\tau }_2\right)-B_H\left(j_2\right)\right)}{\sqrt{\langle B_H^2\left({\tau }_1\right)\rangle }\sqrt{\langle B_H^2\left({\tau }_2\right)\rangle }}\rangle \left(1+O\left({\tau }^{-\delta }\right)\right), \end{gathered}$$ (82)

where B_H is a standard fBm with Hurst parameter given by the relation (12). By (68), (82) and expression (10) for the covariance function of fBm,

$$\begin{gathered} \langle W_{j_1}\left({\tau }_1\right)W_{j_2}\left({\tau }_2\right)\rangle =\frac{1}{2}\{{\left|\frac{j_1-j_2}{\sqrt{{\tau }_1{\tau }_2}}+\sqrt{\frac{{\tau }_1}{{\tau }_2}}\right|}^{\alpha }-{\left|\frac{j_1-j_2}{\sqrt{{\tau }_1{\tau }_2}}+\sqrt{\frac{{\tau }_1}{{\tau }_2}}-\sqrt{\frac{{\tau }_2}{{\tau }_1}}\right|}^{\alpha }- \\ -{\left|\frac{j_1-j_2}{\sqrt{{\tau }_1{\tau }_2}}\right|}^{\alpha }+{\left|\frac{j_1-j_2}{\sqrt{{\tau }_1{\tau }_2}}-\sqrt{\frac{{\tau }_2}{{\tau }_1}}\right|}^{\alpha }\}\left(1+O\left({\tau }^{-\delta }\right)\right). \end{gathered}$$ (83)

Since 〈W_j1 (τ₁)W_j2 (τ₂)〉 = 〈W_j1+k (τ₁)W_j2+k (τ₂)〉, then by expression (81) we can rewrite (80) as

$$\frac{1}{2N}\sum _{i=-N+1}^{N-1}\frac{1}{N}\sum _{j_1-j_2=i,j_1,j_2=1}^N{\left(2\langle W_{j_1}\left({\tau }_1\right)W_{j_2}\left({\tau }_2\right)\rangle \right)}^2.$$ (84)

Relation (79) is now a consequence of (83) and (84). □

Lemma B.6

$$\langle \log \varpi \left({\tau }_{k_1}\right)\log \varpi \left({\tau }_{k_2}\right)\rangle =\langle \left(\varpi \left({\tau }_{k_1}\right)-1\right)\left(\varpi \left({\tau }_{k_2}\right)-1\right)\rangle +o\left(\frac{\tau }{N}\right).$$ (85)

Proof. For notational simplicity, assume k₁ = 1 and k₂ = 2. Let

$$\begin{gathered} S_1=\langle \log \varpi \left({\tau }_1\right)\log \varpi \left({\tau }_2\right)\rangle -\langle \log \varpi \left({\tau }_1\right)\log \varpi \left({\tau }_2\right)1_{\left\{\min \left\{\varpi \left({\tau }_1\right),\varpi \left({\tau }_2\right)\right\}>r\right\}}\rangle , \\ {S}_2=\langle \log \varpi \left({\tau }_1\right)\log \varpi \left({\tau }_2\right)1_{\left\{\min \left\{\varpi \left({\tau }_1\right),\varpi \left({\tau }_2\right)\right\}>r\right\}}\rangle - \\ -\langle \left(\varpi \left({\tau }_1\right)-1\right)\left(\varpi \left({\tau }_2\right)-1\right)1_{\left\{\min \left\{\varpi \left({\tau }_1\right),\varpi \left({\tau }_2\right)\right\}>r\right\}}\rangle , \\ {S}_3=\langle \left(\varpi \left({\tau }_1\right)-1\right)\left(\varpi \left({\tau }_2\right)-1\right)1_{\left\{\min \left\{\varpi \left({\tau }_1\right),\varpi \left({\tau }_2\right)\right\}>r\right\}}\rangle -\langle \left(\varpi \left({\tau }_1\right)-1\right)\left(\varpi \left({\tau }_2\right)-1\right)\rangle . \end{gathered}$$

Note that

$$\langle \log \varpi \left({\tau }_1\right)\log \varpi \left({\tau }_2\right)\rangle =S_1+S_2+S_3.$$

Therefore, establishing (85) is equivalent to showing that $S_1+S_2+S_3=o\left(\frac{\tau }{N}\right)$. It suffices to show that

$$\max \left\{\left|S_1\right|,\left|S_2\right|,\left|S_3\right|\right\}=o\left(\frac{\tau }{N}\right).$$ (86)

Let 0 < r < 1/2. We start off with S₂ by writing out the almost sure Taylor expansion

$$\log \varpi (\tau )1_{\{\varpi (\tau )>r\}}=\left\{(\varpi (\tau )-1)-\frac{1}{2}{\left(\frac{\varpi (\tau )-1}{{\sigma }_{+}^2(\varpi (\tau ))}\right)}^2\right\}{1}_{\{\varpi (\tau )>r\}},$$ (87)

where ${\sigma }_{+}^2(\varpi (\tau ))\in [\min \{\varpi (\tau ),1\},\max \{\varpi (\tau ),1\}]$. Then,

$$\begin{gathered} \langle \log \varpi \left({\tau }_1\right)\log \varpi \left({\tau }_2\right)1_{\left\{\min \left\{\varpi \left({\tau }_1\right),\varpi \left({\tau }_2\right)\right\}>r\right\}}\rangle \\ =\langle \left(\varpi \left({\tau }_1\right)-1\right)\left(\varpi \left({\tau }_2\right)-1\right)1_{\left\{\min \left\{\varpi \left({\tau }_1\right),\varpi \left({\tau }_2\right)\right\}>r\right\}}\rangle \\ -\frac{1}{2}\langle \left(\varpi \left({\tau }_1\right)-1\right){\left(\frac{\varpi \left({\tau }_2\right)-1}{{\sigma }_{+}^2\left(\varpi \left({\tau }_2\right)\right)}\right)}^2{1}_{\left\{\min \left\{\varpi \left({\tau }_1\right),\varpi \left({\tau }_2\right)\right\}>r\right\}}\rangle \\ -\frac{1}{2}\langle {\left(\frac{\varpi \left({\tau }_1\right)-1}{{\sigma }_{+}^2\left(\varpi \left({\tau }_1\right)\right)}\right)}^2\left(\varpi \left({\tau }_2\right)-1\right)1_{\left\{\min \left\{\varpi \left({\tau }_1\right),\varpi \left({\tau }_2\right)\right\}>r\right\}}\rangle \\ +\frac{1}{4}\langle {\left(\frac{\varpi \left({\tau }_1\right)-1}{{\sigma }_{+}^2\left(\varpi \left({\tau }_1\right)\right)}\right)}^2{\left(\frac{\varpi \left({\tau }_2\right)-1}{{\sigma }_{+}^2\left(\varpi \left({\tau }_2\right)\right)}\right)}^2{1}_{\left\{\min \left\{\varpi \left({\tau }_1\right),\varpi \left({\tau }_2\right)\right\}>r\right\}}\rangle \cdot \end{gathered}$$ (88)

The second, third and fourth terms can be bounded by a similar argument, so we only develop the latter. Recast

$$\begin{gathered} {\left(\frac{\varpi (\tau )-1}{{\sigma }_{+}^2(\varpi (\tau ))}\right)}^2{1}_{\{\varpi (\tau )>r\}}={\left(\frac{\varpi (\tau )-1}{{\sigma }_{+}^2(\varpi (\tau ))}\right)}^2\left(1_{\{1/2>\varpi (\tau )>r\}}+1_{\{\varpi (\tau )\ge 1/2\}}\right) \\ \le {\left(\frac{\varpi (\tau )-1}{r}\right)}^2{1}_{\{1/2>\varpi (\tau )>r\}}+{\left(\frac{\varpi (\tau )-1}{1/2}\right)}^2{1}_{\{\varpi (\tau )\ge 1/2\}}. \end{gathered}$$ (89)

Therefore, we can rewrite the fourth term in (88) as

$$\begin{gathered} \langle {\left(\frac{\varpi \left({\tau }_1\right)-1}{{\sigma }_{+}^2\left(\varpi \left({\tau }_1\right)\right)}\right)}^2{\left(\frac{\varpi \left({\tau }_2\right)-1}{{\sigma }_{+}^2\left(\varpi \left({\tau }_2\right)\right)}\right)}^2{1}_{\left\{\min \left\{\varpi \left({\tau }_1\right),\varpi \left({\tau }_2\right)\right\}>r\right\}}\rangle \\ \le \frac{1}{r^4}\langle {\left(\varpi \left({\tau }_1\right)-1\right)}^2{1}_{\left\{1/2>\varpi \left({\tau }_1\right)>r\right\}}{\left(\varpi \left({\tau }_2\right)-1\right)}^2{1}_{\left\{1/2>\varpi \left({\tau }_2\right)>r\right\}}\rangle \\ +\frac{1}{{(r/2)}^2}\langle {\left(\varpi \left({\tau }_1\right)-1\right)}^2{1}_{\left\{\varpi \left({\tau }_1\right)\ge 1/2\right\}}{\left(\varpi \left({\tau }_2\right)-1\right)}^2{1}_{\left\{1/2>\varpi \left({\tau }_2\right)>r\right\}}\rangle \\ +\frac{1}{{(r/2)}^2}\langle {\left(\varpi \left({\tau }_1\right)-1\right)}^2{1}_{\left\{1/2>\varpi \left({\tau }_2\right)>r\right\}}{\left(\varpi \left({\tau }_2\right)-1\right)}^2{1}_{\left\{\varpi \left({\tau }_2\right)\ge 1/2\right\}}\rangle \\ +\frac{1}{{(1/2)}^4}\langle {\left(\varpi \left({\tau }_1\right)-1\right)}^2{1}_{\left\{\varpi \left({\tau }_2\right)\ge 1/2\right\}}{\left(\varpi \left({\tau }_2\right)-1\right)}^2{1}_{\left\{\varpi \left({\tau }_2\right)\ge 1/2\right\}}\rangle \end{gathered}$$ (90)

By (78), the fourth term in (90) is bounded by

$$O\left[{\left(\frac{\tau }{N}\right)}^2\right].$$ (91)

By the Cauchy-Schwarz inequality, (73) and (78), the first term in the sum (90) is bounded by

$$\begin{gathered} \frac{1}{r^4}\sqrt{\langle {\left(\varpi \left({\tau }_1\right)-1\right)}^4{\left(\varpi \left({\tau }_1\right)-1\right)}^4\rangle }\sqrt{\langle 1_{\left\{1/2>\varpi \left({\tau }_1\right)>r\right\}}{1}_{\left\{1/2>\varpi \left({\tau }_2\right)>r\right\}}\rangle } \\ \le \frac{1}{r^4}O\left(\frac{\tau }{N}\right)\sqrt{\mathbb{P}\left(1/2>\varpi \left({\tau }_1\right)>r\right)\mathbb{P}\left(1/2>\varpi \left({\tau }_2\right)>r\right)} \\ \le \frac{1}{r^4}O\left(\frac{\tau }{N}\right)\exp \left\{-C{\left(\frac{N}{\tau }\right)}^{1-\mathit{\xi }}\right\}=o\left(\frac{\tau }{N}\right). \end{gathered}$$ (92)

Again by the Cauchy-Schwarz inequality, (73) and (78), the second term in the sum (90) is bounded by

$$\begin{gathered} \frac{4}{r^2}\sqrt{\langle {\left(\varpi \left({\tau }_1\right)-1\right)}^4{\left(\varpi \left({\tau }_1\right)-1\right)}^4\rangle }\sqrt{\langle 1_{\left\{\varpi \left({\tau }_1\right)\ge 1/2\right\}}{1}_{\left\{1/2>\varpi \left({\tau }_2\right)>r\right\}}\rangle } \\ \le \frac{4}{r^2}O\left(\frac{\tau }{N}\right)\sqrt{\mathbb{P}\left(\varpi \left({\tau }_1\right)\ge 1/2\right)\mathbb{P}\left(1/2>\varpi \left({\tau }_2\right)>r\right)} \\ \le \frac{4}{r^2}O\left(\frac{\tau }{N}\right)\exp \left\{-C{\left(\frac{N}{\tau }\right)}^{1-\mathit{\xi }}\right\}=o\left(\frac{\tau }{N}\right). \end{gathered}$$ (93)

An analogous bound holds for the third term in the sum (90). Therefore, |S₂| is bounded by the right-hand side of (86). To tackle S₃, rewrite it as

$$\begin{gathered} -\langle \left(\varpi \left({\tau }_1\right)-1\right)\left(\varpi \left({\tau }_2\right)-1\right)(1_{\left\{\varpi \left({\tau }_1\right)>r\right\}}{1}_{\left\{\varpi \left({\tau }_2\right)\le r\right\}} \\ +1_{\left\{\varpi \left({\tau }_1\right)\le r\right\}}{1}_{\left\{\varpi \left({\tau }_2\right)>r\right\}}+1_{\left\{\varpi \left({\tau }_1\right)\le r\right\}}{1}_{\left\{\varpi \left({\tau }_2\right)\le r\right\}})\rangle . \end{gathered}$$ (94)

By the Cauchy-Schwarz inequality, (73) and (78), the first term on the right-hand side of (94) is bounded by

$$\begin{gathered} \sqrt{\langle {\left(\varpi \left({\tau }_1\right)-1\right)}^2{\left(\varpi \left({\tau }_2\right)-1\right)}^2\rangle }\sqrt{\mathbb{P}\left(\varpi \left({\tau }_2\right)\le r\right)} \\ \le O\left(\frac{\tau }{N}\right)\exp \left\{-C{\left(\frac{N}{\tau }\right)}^{1-\xi }\right\}=o\left(\frac{\tau }{N}\right). \end{gathered}$$

Similar bounds hold for the remaining terms on the right-hand side of (94). Therefore, |S₃| is also bounded by the right-hand side of (86). As for S₁, it can be reexpressed as

$$\langle \log \varpi \left({\tau }_1\right)\log \varpi \left({\tau }_2\right)\left(1_{\left\{\varpi \left({\tau }_1\right)>r\right\}}{1}_{\left\{\varpi \left({\tau }_2\right)\le r\right\}}+1_{\left\{\varpi \left({\tau }_1\right)\le r\right\}}{1}_{\left\{\varpi \left({\tau }_2\right)>r\right\}}+1_{\left\{\varpi \left({\tau }_1\right)\le r\right\}}{1}_{\left\{\varpi \left({\tau }_2\right)\le r\right\}}\right)\rangle .$$ (95)

Note that, by Lemma B.3, $\langle {\log }^4\varpi (\tau )\rangle$ is bounded. Then, by applying the Cauchy-Schwarz inequality twice, the first term on the right-hand side of (95) is bounded by

$$\begin{gathered} \sqrt{\langle {\log }^2\varpi \left({\tau }_1\right){\log }^2\varpi \left({\tau }_2\right)\rangle }\sqrt{\mathbb{P}\left(\varpi \left({\tau }_2\right)\le r\right)} \\ \le {\left(\langle {\log }^4\varpi \left({\tau }_1\right)\rangle \langle {\log }^4\varpi \left({\tau }_2\right)\rangle \right)}^{1/4}\exp \left\{-C{\left(\frac{N}{\tau }\right)}^{1-\xi }\right\}=o\left(\frac{\tau }{N}\right). \end{gathered}$$

Similar bounds hold for the remaining terms on the right-hand side of (95). Therefore, |S₁| is bounded by the right-hand side of (86). This shows (85). □

Lemma B.7

$$\langle \log \varpi (\tau )\rangle +\frac{1}{2}\langle {(\varpi (\tau )-1)}^2\rangle =O\left(\frac{\tau }{N}\right).$$ (96)

Proof. Fix 0 < r < 1/2. Let

$$\begin{gathered} T_1=\langle \log \varpi (\tau )\rangle -\langle \log \varpi (\tau )1_{\{\varpi (\tau )>r\}}\rangle , \\ {T}_2=\langle \log \varpi (\tau )1_{\{\varpi (\tau )>r\}}\rangle +\frac{1}{2}\langle {(\varpi (\tau )-1)}^2{1}_{\{\varpi (\tau )>r\}}\rangle , \\ {T}_3=\frac{1}{2}\langle {(\varpi (\tau )-1)}^2\rangle -\frac{1}{2}\langle {(\varpi (\tau )-1)}^2{1}_{\{\varpi (\tau )>r\}}\rangle . \end{gathered}$$

Recall that, by Lemma B.3, $\langle {\log }^2\varpi (\tau )\rangle$ is bounded. Thus, by the Cauchy-Schwarz inequality and by Lemma B.2,

$$\begin{gathered} T_1=\langle \log \varpi (\tau )1_{\{\varpi (\tau )\le r\}}\rangle \le \sqrt{\langle {\log }^2\varpi (\tau )\rangle }\sqrt{\mathbb{P}(\varpi (\tau )\le r)} \\ \le \sqrt{\langle {\log }^2\varpi (\tau )\rangle }\exp \left\{-C{\left(\frac{N}{\tau }\right)}^{1-\xi }\right\}=o\left(\frac{\tau }{N}\right). \end{gathered}$$ (97)

By a similar reasoning, we can further prove that

$$T_3=o\left(\frac{\tau }{N}\right).$$ (98)

Now, we turn to T₂. By an almost sure Taylor expansion,

$$\log \varpi (\tau )1_{\{\varpi (\tau )>r\}}=\left\{(\varpi (\tau )-1)-\frac{1}{2}{(\varpi (\tau )-1)}^2+\frac{1}{3}{\left(\frac{\varpi -1}{{\sigma }_{+}^2(\varpi )}\right)}^3\right\}{1}_{\{\varpi (\tau )>r\}},$$

where ${\sigma }_{+}^2(\varpi (\tau ))\in [\min \{\varpi (\tau ),1\},\max \{\varpi (\tau ),1\}]$. Then, T₂ is bounded by

$$\left|\langle (\varpi (\tau )-1)1_{\{\varpi (\tau )>r\}}\rangle \right|+\frac{1}{3}\left|\langle {\left(\frac{\varpi -1}{{\sigma }_{+}^2(\varpi )}\right)}^3{1}_{\{\varpi (\tau )>r\}}\rangle \right|.$$ (99)

Since $\langle \varpi (\tau )-1\rangle =0$, by the Cauchy-Schwarz inequality and Lemmas B.1 and B.2, the first term in (99) can be bounded by

$$\begin{gathered} |\langle \varpi (\tau )-1)1_{\{\varpi (\tau )>r\}}\rangle |=|\langle (\varpi (\tau )-1)1_{\{\varpi (\tau )>r\}}\rangle -\langle \varpi (\tau )-1\rangle | \\ =\left|\langle (\varpi (\tau )-1)1_{\{\varpi (\tau )\le r\}}\rangle \right|\le \sqrt{\langle {(\varpi (\tau )-1)}^2\rangle }\sqrt{\mathbb{P}(\varpi (\tau )\le r)}=o\left(\frac{\tau }{N}\right). \end{gathered}$$

Meanwhile, by the Cauchy-Schwarz inequality and Lemmas B.2 and B.4, the second term in (99) is bounded by

$$\frac{1}{3r^3}\left|\langle {(\varpi -1)}^3{1}_{\{1/2>\varpi (\tau )>r\}}\rangle \right|+\frac{1}{3{(1/2)}^3}\left|\langle {(\varpi -1)}^3{1}_{\{\varpi (\tau )\ge 1/2\}}\rangle \right|\le O\left(\frac{\tau }{N}\right)$$ (100)

Thus,

$$T_2=O\left(\frac{\tau }{N}\right).$$ (101)

Relations (97), (98) and (101) imply (96). □

C. Bias and variance of E_stand and the asymptotic distribution of E

We are now in a position to prove Theorems C.1 and C.2 and Proposition C.1, which give, respectively, asymptotically valid characterizations of the bias and variance involved in TAMSD-based estimation, and the asymptotic distribution of the standardized estimator (35).

The proof of Theorem C.1 is a consequence of a Taylor expansion, followed by using estimates of the decay of TAMSD moments. Constructing the latter requires using a concentration inequality (e.g., [48, 5]), which was done in Section B.

Theorem C.1

For 0 < α < 3/2, under the assumptions of Theorem A.1, (17) holds.

Proof. The left-hand side of (17) can be rewritten as

$$\langle \log \frac{M_N(\tau )}{\langle X^2(\tau )\rangle }\rangle +\log \frac{\langle X^2(\tau )\rangle }{{\sigma }^2{\tau }^{\alpha }}=\langle \log \varpi (\tau )\rangle +\log \frac{\langle X^2(\tau )\rangle }{{\sigma }^2{\tau }^{\alpha }}.$$ (102)

By Proposition 1 in [20], we can rewrite the second sum term on the right-hand side of (102) as

$$\log \left(1+O\left({\tau }^{-\delta }\right)\right)=O\left({\tau }^{-\delta }\right),N\to \infty .$$

By Lemmas B.5 and B.7, we can recast the first sum term on the right-hand side of (102) as

$$\begin{gathered} -\frac{1}{2}\langle {(\varpi (\tau )-1)}^2\rangle +O\left(\frac{\tau }{N}\right) \\ =-\frac{1}{4N}\sum _{i=-N+1}^{N-1}\left(1-\frac{\left|i\right|}{N}\right){\left\{{\left|\frac{i}{\tau }+1\right|}^{\alpha }-2{\left|\frac{i}{\tau }\right|}^{\alpha }+{\left|\frac{i}{\tau }-1\right|}^{\alpha }\right\}}^2+O\left({\tau }^{-\delta }\right)+O\left(\frac{\tau }{N}\right). \end{gathered}$$

Thus, (17) follows. □

Next, the proof of Theorem C.2 relies on Taylor expansions of the moments of the logarithm of the TAMSD.

Theorem C.2

For 0 < α < 3/2, under the assumptions of Theorem A.1, expression (25) holds. Proof. For k₁, k₂ = 1, …, m, rewrite

$$\begin{gathered} v_{k_1,k_2}=\mathrm{Cov}\left(\log M_N\left({\tau }_{k_1}\right),\log M_N\left({\tau }_{k_2}\right)\right) \\ =\langle \left[\log M_N\left({\tau }_{k_1}\right)-\langle \log M_N\left({\tau }_{k_1}\right)\rangle \right][\log M_N\left({\tau }_{k_1}\right)-\langle \log M_N\left({\tau }_{k_1}\right)\rangle ]\rangle \\ =\langle \left[\log \varpi \left({\tau }_{k_1}\right)-\langle \log \varpi \left({\tau }_{k_1}\right)\rangle \right]\left[\log \varpi \left({\tau }_{k_2}\right)-\langle \log \varpi \left({\tau }_{k_2}\right)\rangle \right]\rangle \\ =\langle \log \varpi \left({\tau }_{k_1}\right)\log \varpi \left({\tau }_{k_2}\right)\rangle -\langle \log \varpi \left({\tau }_{k_1}\right)\rangle \langle \log \varpi \left({\tau }_{k_2}\right)\rangle . \end{gathered}$$ (103)

By Lemmas B.1 and B.7,

$$\langle \log \varpi \left({\tau }_{k_1}\right)\rangle =O\left(\frac{\tau }{N}\right).$$

Therefore, (103) can be reexpressed as

$$\langle \log \varpi \left({\tau }_{k_1}\right)\log \varpi \left({\tau }_{k_2}\right)\rangle +o\left(\frac{\tau }{N}\right).$$ (104)

By Lemmas B.5, B.6 and C.1 (expression (121)), expression (25) holds. □

The proof of Proposition C.1 builds upon Taylor expansions and characterizing the asymptotic behavior of the standardization term in the definition of the estimator (35).

Proposition C.1

Under the assumptions of Theorem A.1, suppose 0 < α < 3/2. Then, the estimator (35) satisfies

$${\mathrm{\Lambda }}^{-1/2}\left(A_{\text{stand}}\right)(\mathit{E}-\mathit{\xi })\stackrel{d}{\to }\mathcal{N}(0,I),N\to \infty ,$$ (105)

where the vector ξ is given by (1). In particular, the estimator is consistent, i.e,

$$\mathit{E}\stackrel{P}{\to }\mathit{\xi }.$$

Proof. Recast the estimator (35) as

$$\mathit{Z}={\left(X^T{\mathrm{{\rm Y}}}^{-1}\left(A_{\text{stand}}\right)X\right)}^{1/2}{\left(X^T{\mathrm{{\rm Y}}}^{-1}\left(A_{\text{stand}}\right)X\right)}^{-1}{X}^T{\mathrm{{\rm Y}}}^{-1}\left(A_{\text{stand}}\right)\mathbf{y}.$$ (106)

Rewrite Υ(α) = Υ(α, N) as to express the dependence of the latter matrix on N. Define

$${\left(\frac{N}{\tau }\mathrm{{\rm Y}}\left(A_{\text{stand}},N\right)\right)}^{-1}=:S\left(A_{\text{stand}},N\right)={\left(s_{k_1,k_2}\left(A_{\text{stand}},N\right)\right)}_{k_1,k_2=1,\dots ,m},$$ (107)

$$s_N\left(A_{\text{stand}}\right)=\sum _{k_1=1}^m\sum _{k_2=1}^m{s}_{k_1,k_2}\left(A_{\text{stand}},N\right)\in ℝ.$$

By (23), (25) and (121), we can write

$$S\left(A_{\text{stand}},N\right)\stackrel{P}{\to }S(\alpha )={\left(s_{k_1,k_2}(\alpha )\right)}_{k_1,k_2=1,\dots ,m},N\to \infty ,$$ (108)

and

$$s(\alpha ):=\sum _{k_1=1}^m\sum _{k_2=1}^m{s}_{k_1,k_2}(\alpha )\in ℝ$$ (109)

for some constant matrix S(α). For notational simplicity, write s_N = s_N(A_stand, N) and $s_{k_1,k_2}(N)=s_{k_1,k_2}\left(A_{\text{stand}},N\right)$. Then,

$$X^{T}S(\mathit{\xi })X=\left(\begin{array}{cc}{s}_N& {\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\left(\log {\tau }_{k_1}\right)s_{k_1,k_2}(N)\\ {\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\left(\log {\tau }_{k_1}\right)s_{k_1,k_2}(N)& {\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\left(\log {\tau }_{k_1}\log {\tau }_{k_2}\right)s_{k_1,k_2}(N)\end{array}\right).$$

By a simple calculation and relation (108),

$$\begin{gathered} c_w(N):=\det (X^{T}S(A_{\mathrm{stand}},N)X) \\ =s_N\sum _{k_1=1}^m\sum _{k_2=1}^m\log w_{k_1}\log w_{k_2}{s}_{k_1,k_2}(N)-{\left(\sum _{k_1=1}^m\sum _{k_2=1}^m\log w_{k_1}{s}_{k_1,k_2}(N)\right)}^2 \\ \stackrel{P}{\to }s(\alpha )\sum _{k_1=1}^m\sum _{k_2=1}^m\log w_{k_1}\log w_{k_2}{s}_{k_1,k_2}(\alpha )-{\left(\sum _{k_1=1}^m\sum _{k_2=1}^m\log w_{k_1}{s}_{k_1,k_2}(\alpha )\right)}^2=c_w(\alpha ). \end{gathered}$$

Moreover, by (107),

$${\left(X^T{\mathrm{{\rm Y}}}^{-1}\left(A_{\text{stand}},N\right)X\right)}^{-1}{X}^T{\mathrm{{\rm Y}}}^{-1}\left(A_{\text{stand}},N\right)={\left(X^{T}S\left(A_{\text{stand}},N\right)X\right)}^{-1}{X}^{T}S\left(A_{\text{stand}},N\right)$$ (110)

$$\begin{gathered} =\frac{1}{c_w(N)}{\left(\begin{array}{c}\log \tau \left\{{\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\log w_{k_1}{s}_{k_1,k_2}(N)\left({\sum }_{k=1}^m{s}_{k,j}(N)\right)-s_N{\sum }_{k=1}^m\log w_k{s}_{k,j}(N)\right\}\\ +({\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\log w_{k_1}\log w_{k_2}{s}_{k_1,k_2}(N){\sum }_{k=1}^m{s}_{k,j}(N)\\ -{\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\log w_{k_1}{s}_{k_1,k_2}(N){\sum }_{k=1}^m\log w_k{s}_{k,j}(N))\\ s_N{\sum }_{k=1}^m\log w_k{s}_{k,j}(N)-{\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\log w_{k_1}{s}_{k_1,k_2}(N)\left({\sum }_{k=1}^m{s}_{k,j}(N)\right)\end{array}\right)}_{j=1,\dots ,m} \\ =:{\left(\begin{array}{c}\log \tau a_{n,j}+b_{n,j}\\ -a_{n,j}\end{array}\right)}_{j=1,\dots ,m}, \end{gathered}$$ (111)

where the sequences of constants {a_n,j}_N∈ℕ and {b_n,j}_N∈ℕ, converge to constants a_j and b_j, respectively, for j = 1, …, m.

Recall that, for a symmetric positive definite matrix

$$M=\left(\begin{array}{cc}{m}_{11}& m_{12}\\ m_{12}& m_{22}\end{array}\right),$$

we can write its square root in closed form as

$$M^{1/2}=\frac{1}{\sqrt{\mathrm{tr}(M)+2\sqrt{\det (M)}}}\left(\begin{array}{cc}{m}_{11}+\sqrt{\det (M)}& m_{12}\\ m_{12}& m_{22}+\sqrt{\det (M)}\end{array}\right).$$

Therefore,

$$\begin{gathered} {\left(X^{T}S\left(A_{\text{stand}}\right)X\right)}^{1/2}=\frac{1}{\sqrt{\mathrm{tr}\left(X^{T}S\left(A_{\text{stand}}\right)X\right)+2\sqrt{c_w(N)}}} \\ (\begin{array}{cc}{s}_N+\sqrt{c_w(N)}& {\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\left(\log {\tau }_{k_1}\right)s_{k_1,k_2}(N)\\ {\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\left(\log {\tau }_{k_1}\right)s_{k_1,k_2}(N)& {\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\left(\log {\tau }_{k_1}\log {\tau }_{k_2}\right)s_{k_1,k_2}(N)+\sqrt{c_w(N)}\end{array}). \end{gathered}$$ (112)

Note that

$$\mathrm{tr}\left(X^{T}S\left(A_{\text{stand}}\right)X\right)+2\sqrt{c_w(N)}\sim {\log }^2\tau s_N.$$ (113)

By expressions (108), (109), (111), (112) and (113),

$$\begin{gathered} {\left(X^T{\mathrm{{\rm Y}}}^{-1}\left(A_{\text{stand}},N\right)X\right)}^{1/2}{\left(X^T{\mathrm{{\rm Y}}}^{-1}\left(A_{\text{stand}},N\right)X\right)}^{-1}{X}^T{\mathrm{{\rm Y}}}^{-1}\left(A_{\text{stand}},N\right) \\ =\sqrt{\frac{N}{\tau }}{\left(X^{T}S\left(A_{\text{stand}},N\right)X\right)}^{1/2}{\left(X^{T}S\left(A_{\text{stand}},N\right)X\right)}^{-1}{X}^{T}S\left(A_{\text{stand}},N\right) \\ =\sqrt{\frac{N}{\tau }}\frac{1}{\sqrt{\mathrm{tr}\left(X^{T}S\left(A_{\text{stand}},N\right)X\right)+2\sqrt{c_w(N)}}}\frac{1}{c_w(N)} \\ {\left(\begin{array}{c}{a}_{n,j}[(\log \tau )\left(s_N+\sqrt{c_w(N)}\right)-{\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\left(\log {\tau }_{k_1}\right)s_{k_1{k}_2}(N)]+b_{n,j}\left(s_N+\sqrt{c_w(N)}\right)\\ a_{n,j}[(\log \tau ){\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\left(\log {\tau }_{k_1}\right)s_{k_1{k}_2}(N)\\ -{\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\left(\log {\tau }_{k_1}\log {\tau }_{k_2}\right)s_{k_1{k}_2}(N)-\sqrt{c_w(N)}]\\ +b_{n,j}\left[{\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\left(\log {\tau }_{k_1}\right)s_{k_1{k}_2}(N)\right]\end{array}\right)}_{j=1,\dots ,m} \\ =\sqrt{\frac{N}{\tau }}\frac{1}{\sqrt{\mathrm{tr}\left(X^{T}S\left(A_{\text{stand}},N\right)X\right)+2\sqrt{c_w(N)}}}\frac{1}{c_w(N)} \\ {\left(\begin{array}{c}{a}_{n,j}\left[(\log \tau )\sqrt{c_w(N)}-{\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\left(\log w_{k_1}\right)s_{k_1{k}_2}(N)\right]+b_{n,j}\left(s_N+\sqrt{c_w(N)}\right)\\ a_{n,j}[-(\log \tau ){\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\left(\log w_{k_1}\right)s_{k_1{k}_2}(N)-{\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\left(\log w_{k_1}\log w_{k_2}\right)s_{k_1{k}_2}(N)\\ -\sqrt{c_w(N)}]+b_{n,j}\left[(\log \tau )s_N+{\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\left(\log w_{k_1}\right)s_{k_1{k}_2}(N)\right]\end{array}\right)}_{j=1,\dots ,m} \\ \stackrel{P}{\sim }\sqrt{\frac{N}{\tau }}\frac{1}{s(\alpha )}\frac{1}{c_w(\alpha )}{\left(\begin{array}{c}{a}_j\sqrt{c_w(\alpha )}\\ b_{j}s(\alpha )-a_j\left[{\sum }_{k_1=1}^m{\sum }_{k_2=1}^m\left(\log w_{k_1}\right)s_{k_1{k}_2}(\alpha )\right]\end{array}\right)}_{j=1,\dots ,m} \\ =:\sqrt{\frac{N}{\tau }}\mathrm{\Psi }\in {ℝ}^{2\times m}, \end{gathered}$$ (114)

as N → ∞. For y and X as in (30), rewrite the left-hand side of expression (105) as

$$\begin{gathered} {\left(X^T{\mathrm{{\rm Y}}}^{-1}\left(A_{\text{stand}},N\right)X\right)}^{1/2}(\mathit{E}-\mathit{\xi }) \\ ={\left(X^T{\mathrm{{\rm Y}}}^{-1}\left(A_{\text{stand}},N\right)X\right)}^{1/2}{\left(X^T{\mathrm{{\rm Y}}}^{-1}\left(A_{\text{stand}},N\right)X\right)}^{-1}{X}^T{\mathrm{{\rm Y}}}^{-1}\left(A_{\text{stand}},N\right)(\mathbf{y}-X\mathit{\xi }). \end{gathered}$$ (115)

Recast

$$\mathbf{y}={\left(\log [M_N\left({\tau }_k\right)e^{\frac{{\tau }_k}{N}{\beta }_N\left(A_{\text{stand}},{\tau }_k\right)}]\right)}_{k=1,\dots ,m}.$$

By entrywise first order Taylor expansions,

$$\begin{gathered} \text{y}-X\mathit{\xi }={\left(\log \left(\frac{M_N\left({\tau }_k\right)e^{\frac{{\tau }_k}{N}{\beta }_N\left(A_{\text{stand}},{\tau }_k\right)}}{{\sigma }^2{\tau }_k^{\alpha }}\right)\right)}_{k=1,\dots ,m} \\ ={\left(\frac{M_N\left({\tau }_k\right)e^{\frac{\tau }{N}{\beta }_N\left(A_{\text{stand}},{\tau }_k\right)}}{{\sigma }^2{\tau }_k^{\alpha }}-1\right)}_{k=1,\dots ,m}+{\left(O{\left(\frac{M_N\left({\tau }_k\right)e^{\frac{\tau }{N}{\beta }_N\left(A_{\text{stand}}{\tau }_k\right)}}{{\sigma }^2{\tau }_k^{\alpha }}-1\right)}^2\right)}_{k=1,\dots ,m} \end{gathered}$$ (116)

However, for k = 1, …, m, the first term on the right-hand side of (116) can be reexpressed as

$$\frac{M_N\left({\tau }_k\right)}{{\sigma }^2{\tau }_k^{\alpha }}\left(e^{\frac{{\tau }_k}{N}{\beta }_N\left(A_{\text{stand}},{\tau }_k\right)}-1\right)+\frac{M_N\left({\tau }_k\right)}{{\sigma }^2{\tau }_k^{\alpha }}-1.$$ (117)

Again by a first order Taylor expansion,

$$e^{\frac{{\tau }_k}{N}{\beta }_N\left(A_{\text{stand}},{\tau }_k\right)}-1=\frac{{\tau }_k}{N}{\beta }_N\left(A_{\text{stand}},{\tau }_k\right)+o_P\left(\frac{{\tau }_k}{N}\right).$$ (118)

Therefore, by (114), (117) and (118), we can rewrite relation (115) as

$$\left(\mathrm{\Psi }+o_P(1)\right)\sqrt{\frac{N}{\tau }}{\left(\frac{M_N\left({\tau }_k\right)}{{\sigma }^2{\tau }_k^{\alpha }}-1\right)}_{k=1,\dots ,m}+o_P\left(\sqrt{\frac{\tau }{N}}\right).$$ (119)

Expression (105) is a consequence of (119) and Theorem A.1, where the estimator (106) is asymptotically standardized. □

The following lemma establishes the convergence of the main bias and variance factors and is used in the proofs of Proposition C.1 and Theorem C.2.

Lemma C.1

For 0 < α < 3/2, consider the main bias and variance factors (18) and (26), respectively, under the assumptions of Theorem A.1. Then, there are functions β(α,·) > 0 and ς(α,·,·) > 0 such that

$${\beta }_N\left(A_{\text{stand}},{\tau }_k\right)\stackrel{P}{\to }{\left(\beta \left(\alpha ,{\tau }_k\right)\right)}_{k=1,\dots ,m},$$ (120)

$${\left({\zeta }_N\left(A_{\text{stand}},{\tau }_{k_1},{\tau }_{k_2}\right)\right)}_{k_1,k_2=1,\dots ,m}\stackrel{P}{\to }{\left(\zeta \left(\alpha ,k_1,k_2\right)\right)}_{k_1,k_2=1,\dots ,m},$$ (121)

as N → ∞.

Proof. From expression (25) for the variance term $v_{k_1,k_2}(\mathit{\xi })$, recast

$$\begin{gathered} {\zeta }_N\left(\alpha ,{\tau }_{k_1},{\tau }_{k_2}\right)=\frac{1}{2}\left\{\sum _{\left|i\right|\le \tau }+\sum _{\tau +1\le \left|i\right|\le N-1}\right\}\left(1-\frac{\left|i\right|}{N}\right)\{{\left|\frac{i}{\tau \sqrt{w_{k_1}{w}_{k_2}}}+\sqrt{\frac{w_{k_1}}{w_{k_2}}}\right|}^{\alpha } \\ -{\left|\frac{i}{\tau \sqrt{w_{k_1}{w}_{k_2}}}+\sqrt{\frac{w_{k_1}}{w_{k_2}}}-\sqrt{\frac{w_{k_2}}{w_{k_1}}}\right|}^{\alpha }-{\left|\frac{i}{\tau \sqrt{w_{k_1}{w}_{k_2}}}\right|}^{\alpha }+{\left|\frac{i}{\tau \sqrt{w_{k_1}{w}_{k_2}}}-\sqrt{\frac{w_{k_2}}{w_{k_1}}}\right|}^{\alpha }{\}}^2\frac{1}{\tau }. \end{gathered}$$ (122)

The second sum term on the right-hand side of (122) is bounded by

$$\begin{gathered} \frac{1}{2}\left(1-\frac{\tau }{N}\right)\sum _{\tau +1\le \left|i\right|\le N-1}\{{\left|\frac{i}{\tau \sqrt{w_{k_1}{w}_{k_2}}}+\sqrt{\frac{w_{k_1}}{w_{k_2}}}\right|}^{\alpha } \\ -{\left|\frac{i}{\tau \sqrt{w_{k_1}{w}_{k_2}}}+\sqrt{\frac{w_{k_1}}{w_{k_2}}}-\sqrt{\frac{w_{k_2}}{w_{k_1}}}\right|}^{\alpha }-{\left|\frac{i}{\tau \sqrt{w_{k_1}{w}_{k_2}}}\right|}^{\alpha }{+{\left|\frac{i}{\tau \sqrt{w_{k_1}{w}_{k_2}}}-\sqrt{\frac{w_{k_2}}{w_{k_1}}}\right|}^{\alpha }\}}^2\frac{1}{\tau }. \\ \sim \frac{1}{2}\left(1-\frac{\tau }{N}\right){\int }_{\tau +1\le \left|y\right|\le n}{\left\{{\left|\frac{y}{\sqrt{w_{k_1}{w}_{k_2}}}+\sqrt{\frac{w_{k_1}}{w_{k_2}}}\right|}^{\alpha } \\ -{\left|\frac{y}{\sqrt{w_{k_1}{w}_{k_2}}}+\sqrt{\frac{w_{k_1}}{w_{k_2}}}-\sqrt{\frac{w_{k_2}}{w_{k_1}}}\right|}^{\alpha }-{\left|\frac{y}{\sqrt{w_{k_1}{w}_{k_2}}}\right|}^{\alpha }+{\left|\frac{y}{\sqrt{w_{k_1}{w}_{k_2}}}-\sqrt{\frac{w_{k_2}}{w_{k_1}}}\right|}^{\alpha }\right\}}^{2}dy\to 0, \end{gathered}$$ (123)

as N → ∞. On the other hand, by condition (53) and the dominated convergence theorem, the first sum term on the right-hand side of (122) converges to

$$\begin{gathered} \zeta \left(\alpha ,k_1,k_2\right):=\frac{1}{2}{\int }_{-1}^1\{{\left|\frac{y}{\sqrt{w_{k_1}{w}_{k_2}}}+\sqrt{\frac{w_{k_1}}{w_{k_2}}}\right|}^{\alpha }-{\left|\frac{y}{\sqrt{w_{k_1}{w}_{k_2}}}+\sqrt{\frac{w_{k_1}}{w_{k_2}}}-\sqrt{\frac{w_{k_2}}{w_{k_1}}}\right|}^{\alpha } \\ -{\left|\frac{y}{\sqrt{w_{k_1}{w}_{k_2}}}\right|}^{\alpha }+{\left|\frac{y}{\sqrt{w_{k_1}{w}_{k_2}}}-\sqrt{\frac{w_{k_2}}{w_{k_1}}}\right|}^{\alpha }{\}}^{2}dy>0. \end{gathered}$$ (124)

Moreover, by Corollary A.1, $A_{\text{stand}}\stackrel{P}{\to }\alpha$. So, pick a small enough ϵ₀ such that α ∈ (ϵ₀, 3/2 − ϵ₀). Let $A=\left\{\omega :A_{\text{stand}}(\omega )\in \left(\alpha -\frac{{ϵ}_0}{2},\alpha +\frac{{ϵ}_0}{2}\right)\right\}$. In the set A, by a simple adaptation of the argument leading to (123) and the convergence to (124),

$${\zeta }_N\left(A_{\text{stand}},{\tau }_{k_1},{\tau }_{k_2}\right)\to \zeta \left(\alpha ,k_1,k_2\right),N\to \infty ,$$ (125)

where ℙ(A) → 1. This shows (121). A similar argument can be used to show (120). □

D. Pseudocode for generating the improved TAMSD-based estimator E

Generating the improved pathwise estimator E (see (29))
Input:
• one observed particle path {X1, X2, …, XN}N∈ℕ of length N; • regression lag values τk, k = 1, …, m (typically, τk = τwk, w1 < … < wm, τ ≪ N); • the expression for the asymptotic covariance matrix Υ(α) as a function of α;
Step 1: obtain the standard estimator Astand over the chosen lag values;
Step 2: estimate the asymptotic covariance matrix Υ(ξ) by means of Υ(Astand) (see (27));
Step 3: use Astand and the estimator (19) of the bias vector to produce the bias-corrected regression system (28);
Step 4: obtain the estimator E by means of Υ(Astand)-based GLS on the bias-corrected regression system (28).