Anticooperative Binding Governs the Mechanics of Ethidium-Complexed DNA

Abstract

DNA intercalators bind nucleic acids by stacking between adjacent basepairs. This causes a considerable elongation of the DNA backbone as well as untwisting of the double helix. In the past few years, single-molecule mechanical experiments have become a common tool to characterize these deformations and to quantify important parameters of the intercalation process. Parameter extraction typically relies on the neighbor-exclusion model, in which a bound intercalator prevents intercalation into adjacent sites. Here, we challenge the neighbor-exclusion model by carefully quantifying and modeling the force-extension and twisting behavior of single ethidium-complexed DNA molecules. We show that only an anticooperative ethidium binding that allows for a disfavored but nonetheless possible intercalation into nearest-neighbor sites can consistently describe the mechanical behavior of intercalator-bound DNA. At high ethidium concentrations and elevated mechanical stress, this causes an almost complete occupation of nearest-neighbor sites and almost a doubling of the DNA contour length. We furthermore show that intercalation into nearest-neighbor sites needs to be considered when estimating intercalator parameters from zero-stress elongation and twisting data. We think that the proposed anticooperative binding mechanism may also be applicable to other intercalating molecules.

Introduction

DNA intercalators constitute an important class of small DNA-binding molecules with a variety of applications ranging from pharmacology (1) to fluorescent nucleic acid stains in nano- and biotechnology (2, 3) as well as single-molecule imaging (4, 5, 6). Intercalators have a planar structure and are able to stack themselves in between two adjacent basepairs, which increases the interbasepair distance per intercalating moiety by ∼0.34 nm (7, 8). To accommodate this extreme local stretching, the DNA helix gets almost fully untwisted, and the ribose rings adopt a distorted conformation, called repuckering (7, 8). The structural distortions affect the possible backbone conformations of the neighboring basepair stacks such that intercalation into a nearest-neighbor site is thought to be excluded.

Because of the significant structural changes that the DNA helix undergoes during intercalation, mechanical single-molecule experiments became, since their original development, a routinely used tool to characterize important intercalation properties (9, 10, 11). In particular, this methodology provides structural parameters of the intercalated molecule such as the DNA length increase (12), the degree of untwisting (13, 14, 15), and the binding site size (12, 14). Furthermore, affinity constants (12, 15), different binding modes (11, 16, 17, 18), and the kinetics of association and dissociation (19, 20, 21, 22) can be evaluated.

For deriving the main parameters of the intercalation process from mechanical measurements, the contour length increase at zero force is typically obtained from DNA force-extension measurements. Interpolation to zero force requires, in this case, the correct estimation of the mechanical properties of the DNA, particularly the persistence length p, the stretch rigidity S, and in the case of twisting experiments, the twist rigidity C. Given that the interpretation of the mechanical experiments crucially depends on these parameters, it is quite surprising to see that diverging parameter values have been reported. The persistence length was reported variously to not be affected (14, 21, 23) or to be reduced by intercalation (11, 15, 24). Stretch and torsional rigidities were found to be three- to fourfold lower than for bare double-stranded DNA (12, 25). However, unchanged (22) or even increased stretch rigidities were also reported (21). Notably, typical measurements were done in the presence of free intercalator, i.e., within a pool of unbound molecules (10). It is well known that external mechanical stresses directly affect the thermodynamic equilibrium of a chemical reaction if it is coupled to a conformational change along the stress direction (26, 27). Because intercalator binding elongates DNA, an applied stretching force will thus shift the equilibrium toward the elongated, intercalated state (12). Similarly, the DNA untwisting upon intercalator binding leads to facilitated intercalation when the DNA is untwisted (negatively supercoiled). Recent work has started to consider changes of the intercalation equilibrium during DNA stretching (22) to explain some of the observed discrepancies. However, a comprehensive picture that allows for a consistent, bias-free interpretation of DNA stretch and twist experiments over a large range of applicable conditions is still lacking.

Here, we investigate the binding of the intercalator ethidium bromide (EtBr) on single DNA molecules subjected to force and twist and model the obtained data by accounting for the stress-dependent mechanical equilibrium. We show that the change in equilibrium can describe the previously observed large reduction of the apparent stretch as well as the torsional rigidity that already occurs at very low intercalator coverages. By simultaneously subjecting DNA to high EtBr concentrations and high force or twist, we furthermore demonstrate that intercalation significantly violates the neighbor-exclusion model that forbids intercalation into every second basepair stack. Instead, practically every basepair stack can be occupied, resulting in an almost twofold DNA elongation. This behavior can be modeled by considering anticooperative intercalator binding. With this, we provide an improved procedure to reliably extract intercalator properties from single-molecule mechanical experiments. We note that our interpretation is similar to a very recently proposed “hyperstretched” DNA form (28), for which an anticooperative binding isotherm provides a simpler and more easily applicable model.

Materials and Methods

DNA construct

A 10,929 bp linear DNA fragment was excised from a custom-made 11.3 kbp plasmid by digestion with the restriction enzymes PciI and SacI. Biotin- or digoxigenin-modified attachment handles were produced by digesting 1.2 kbp biotin- and a digoxigenin dUTP-labeled PCR fragments (29) from plasmid pBluescript II SK+ (Stratagene, La Jolla, CA) with PciI and SacI (New England Biolabs, Ipswich, MA), respectively, approximately in the middle of the fragments. The labeled fragments were subsequently ligated to the 10,929 bp fragment for 12 h at 16°C using T4 ligase (New England Biolabs) and purified from an agarose gel, avoiding exposure to EtBr or ultraviolet light (29).

Magnetic tweezers

Our magnetic tweezers setup has been described previously (30, 31). It consists of a home-built inverted microscope equipped with a 100× objective (numerical aperture of 1.25; Olympus, Tokyo, Japan). The bead sample was mounted onto a piezo-actuated nanopositioning stage (P-517.3CD, PI; Physik Instrumente, Karlsruhe, Germany). The sample was illuminated using a LED emitting around 625 nm (CR5111AWY; Roithner Lasertechnik, Vienna, Austria). Imaging was carried out with a TM1067 CL camera (Pulnix, Alzenau, Germany). Two permanent NeFeB magnets (W-05-N50-G; Supermagnete, Gottmadingen, Germany) mounted onto a motorized stage above the sample were used to generate the magnetic field gradient for the magnetic tweezers experiments. Bead images were recorded at 120 Hz, streamed to a computer (Dell Precision T7500 work station; Round Rock, TX) equipped with an image acquisition card (NI PCIe 1428; National Instruments, Austin, TX) and a fast graphics processing unit (GeForce GTX 480; Nvidia, Santa Clara, CA), and analyzed in real time (30). DNA length changes, corresponding to changes of the bead position in axial direction, could be determined with an error of <10 nm. Forces were calibrated using the bead fluctuations along the “long-pendulum” direction and a power-spectral-density analysis, providing a relative force error of <5% at a given force (32).

Sample preparation

Fluidic cells for the magnetic tweezers experiments were built from two cover slides and a cut parafilm spacer that formed the final chamber. The bottom cover slide was spin-coated on the inside with polystyrene before cell assembly. 3 μm carboxylated polystyrene beads (Invitrogen, Carlsbad, CA) in 1 M NaCl were added and incubated for at least 1 h to ensure adherence to the polystyrene film. The fluidic cell was incubated with 50 μg/mL anti-digoxigenin in phosphate-buffered saline for 1 h. Afterwards, it was incubated for 1 h with 10 mg/mL bovine serum albumin to prevent nonspecific binding to the bottom of the cell. DNA constructs were bound to streptavidin-coated superparamagnetic microspheres with nominal radii of 0.52 or 1.4 μm (respectively, MyOne or M-280 beads; Invitrogen, for measurements at standard and at high forces, respectively) and flushed into the fluidic cell. The mechanical measurements were performed at room temperature in the presence of varying concentrations of EtBr and two buffers differing in ionic strength. In particular, either phosphate-buffered saline (10 mM phosphate buffer (pH 7.4) and 138 mM NaCl; Sigma Aldrich, St. Louis, MO) supplemented with 0.1 mg/mL bovine serum albumin or a high-salt buffer containing 20 mM Tris-HCl (pH 7.5), 2 M NaCl, 5 mM EDTA, and 1 mM EGTA was used. Because the fluidic cell contained only few tethered DNA molecules, the free EtBr concentration during the experiment was practically equal to the EtBr concentration added.

Data analysis

Numerical solutions of the equations described in the text and corresponding curve fitting were programmed in and carried out in Labview (National Instruments). Errors for the fractional extensions and stretch rigidities were obtained from the errors of the force-extension fits. The centers and width of the supercoiling curves were obtained by fitting a curve comprising three linear segments to the data. These segments described the two plectonemic regions and the tilted plateau phase. As center of the supercoiling curve, the center position of the plateau was taken. For a symmetric apparent twist rigidity, the torque at the plateau center is zero. The fractional untwisting was obtained by normalizing the center position by the number of helical turns in absence of intercalator. The latter was calculated from the measured DNA contour length and the known DNA twist. The errors of the fractional untwisting and the width of the supercoiling curve were estimated from the SD of repeat measurements.

Results

Force-extension measurements in the presence of EtBr

To study intercalator-complexed DNA molecules subjected to force and twist, we used magnetic tweezers (Fig. 1). A 10.9 kbp DNA molecule was bound via specific attachment handles at one end to a magnetic bead and at the other end to the bottom surface of a fluidic cell. A pair of permanent magnets placed above the fluidic cell was used to apply controlled forces onto the bead (32) and thus to stretch the DNA. The DNA length was measured in real time using video microscopy combined with automated analysis of the recorded images (30). Rotating the magnets allowed to twist the DNA, i.e., to introduce positive or negative supercoils. Using magnetic tweezers, we recorded extension curves using nicked DNA molecules for forces between 0.1 and 8 pN and EtBr concentrations between 0 and 2.5 mM in the presence of 140 NaCl (Figs. 2 a and S1 a). A similar data set was taken in presence of 2000 mM NaCl (Fig. S1 c). The curves were measured in two successive runs of monotonically increasing and decreasing force. The absence of hysteresis indicated equilibrium conditions for the ethidium binding to DNA.

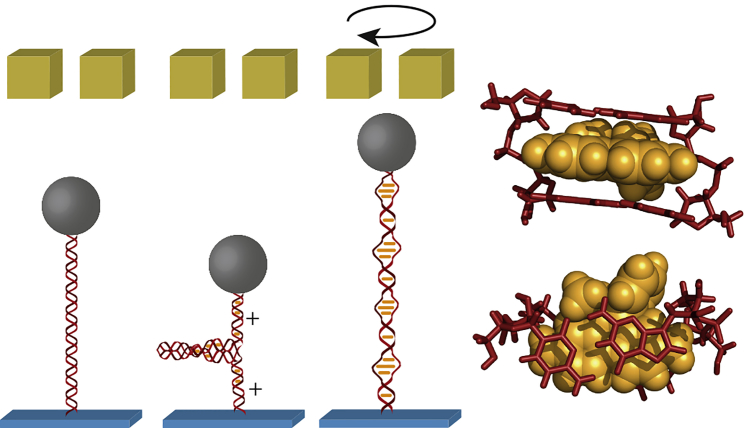
Figure 1.

DNA elongation and untwisting by ethidium measured with magnetic tweezers using a surface-tethered DNA with an attached magnetic bead at its other end. A pair of permanent magnets allows us to stretch and to twist the DNA. Intercalation of ethidium between two adjacent basepairs increases the basepair distance by 0.33 nm and almost completely untwists the DNA double helix by an angle of ∼26° (7, 8). In magnetic tweezers, ethidium intercalation is seen on torsionally relaxed molecules as a DNA length increase (right versus left tweezers sketch). On torsionally constrained DNA molecules, ethidium intercalation locally removes part of the helical turns. This causes positive DNA supercoiling and a DNA length reduction (central tweezers sketch). When negative supercoiling is applied, the DNA can be torsionally relaxed (right tweezers sketch). This allows us to quantify the extent of ethidium-induced DNA untwisting. The structure shown at the right side represents the ethidium-CG/GC complex from (7) (Cambridge Crystallographic Data Center: ETCYGU10).

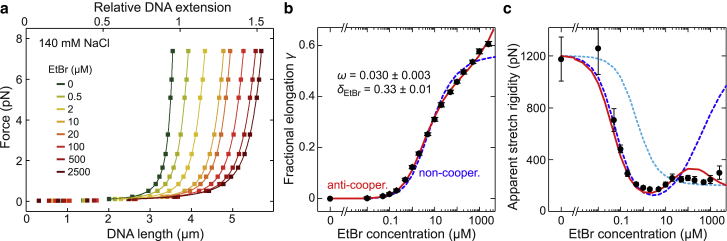
Figure 2.

DNA elongation and decreased stretch rigidity due to ethidium intercalation. (a) Force-extension curves (colored squares) recorded for EtBr concentrations from 0 to 500 μM in the presence of 140 mM NaCl. From fitting an extensible WLC model to the data (solid lines), the zero-force DNA contour length and the apparent stretch rigidity were obtained. (b) Fractional elongation of the DNA contour length at zero force as a function of the EtBr concentration (black circles) obtained from the force-extension data. Fits to the data using a noncooperative and an anticooperative binding model are shown as dashed blue and solid red lines, respectively. Best-fit parameters are given for the anticooperative model. (c) Apparent DNA stretch rigidity as function of the EtBr concentration (black circles) obtained from the force-extension data. Predictions from modeling force-induced intercalation using the noncooperative and the anticooperative binding model are shown as dashed blue and solid red lines, respectively. The prediction of a serial combination of rigid bare and soft ethidium-complexed DNA segments is shown as a dotted cyan line.

The measured curves were fitted (32) with an extensible WLC (33, 34, 35), which includes entropic and Hookean elasticity. This provided values for the contour length L_Eth at zero force, the persistence length p, and the apparent stretch rigidity S. From L_Eth the fractional elongation γ = (L_Eth − L₀)/L₀ at zero force was calculated. It represents the relative increase of the contour length of the ethidium-complexed DNA (L_Eth) compared to bare DNA (L₀). The fractional elongation increased monotonically without a clear saturation even at the highest EtBr concentrations for both tested concentrations of monovalent ions (see Fig. 2 b for low and Fig. S2 a for high salt data). The persistence length decreased slightly but significantly (∼1.5-fold) in an approximately linear fashion with the fractional elongation (Fig. S3). A potential external binding of ethidium to the DNA (36) that changes the persistence length but not L_Eth (or the DNA untwisting) (17) could thus not be discerned. The apparent stretch rigidity exhibited a large reduction upon ethidium intercalation from ∼1200 pN down to 200–300 pN (Figs. 2 c and S2 b) in agreement with previous work (12). Interestingly, the sudden drop of the stretch rigidity occurred at EtBr concentrations at which no significant change of the fractional elongation was yet observed (0.1 μM EtBr for 140 mM NaCl and 1 μM EtBr for 2 M NaCl).

Modeling force-extension data in the absence of mutual ligand interactions

The large reduction of the apparent stretch rigidity in the absence of noticeable intercalation at zero force suggested that force-induced intercalation at elevated tension may lead to an additional DNA lengthening and thus to an apparent softening of the DNA (22). To validate this, we modeled force-extension curves including force-induced intercalation. We first described the DNA elongation at zero force using the noncooperative McGhee-von Hippel binding isotherm (37). It describes the binding of ligands to a linear lattice of binding sites in which each bound ligand occupies n binding sites. Each ligand excludes other ligands from binding to the occupied sites but does not interact with the neighboring ligands. The fractional occupancy ν, i.e., the number of ligands bound per number of binding sites, is in this case provided by

$$\nu =\frac{c_{dye}}{K_d}\frac{{\left(1-n\nu \right)}^{\text{n}}}{{\left(1-\left(n-1\right)\nu \right)}^{n-1}}$$ (1)

where K_d is the dissociation constant of the ligand-lattice interaction. With ν, the fractional elongation of the ethidium-complexed DNA can be expressed as

$$\gamma =\nu \times {\delta }_{Eth}/{\delta }_{bp}$$ (2)

where δ_bp is the contribution of a single basepair to the DNA contour length and δ_Eth is the contour length increase per intercalated dye. When inserting Eq. 1 into Eq. 2, one obtains an expression that relates γ to the EtBr concentration. When fitting the measured fractional elongations using this expression, δ_Eth had to be fixed (15) because the experimental elongations—deviating from theory—did not saturate (see blue dashed lines in Figs. 2 a and S2 b). Setting δ_Eth = 0.34 nm according to crystallographic data (7, 8) provided a binding site size n of 1.8 ± 0.1 and zero-force dissociation constants K_d,0 of 8.4 ± 1.1 and 50 ± 2 μM for 140 and 2000 mM NaCl, respectively (see Table 1). A binding site size close to 2 has been found in previous force-based studies of ethidium intercalation (15) and is in agreement with the neighbor exclusion of ethidium binding, i.e., with binding to every other site in the DNA (38).

Table 1.

Best-Fit Parameters and Reduced χ² of the Fits to the Fractional Elongation or the Fractional Untwisting at Zero Force or Zero Torque, Respectively

cNaCl (mM)	Model	Kd,0 (μM)	δEth (nm)	φEth	n	ω	Reduced χ2
140	noncooperative	8.4 ± 1.1	(0.34)	–	1.8 ± 0.1	–	13.0
		8.4 ± 1.2	–	26.5 ± 0.6°	(1.8)	–	9.2
	anticooperative	5.8 ± 0.4	0.33 ± 0.01	–	(1)	0.030 ± 0.003	1.4
		6.1 ± 0.6	–	25.9 ± 0.6°	(1)	0.025 ± 0.004	1.8
2000	noncooperative	61 ± 4	(0.34)	–	1.8 ± 0.1	–	9.3
		50 ± 2	–	28.3 ± 0.2°	(1.8)	–	6.7
	anticooperative	51 ± 2	0.34 ± 0.01	–	(1)	0.035 ± 0.004	0.71
		50 ± 2	–	30.6 ± 0.4°	(1)	0.010 ± 0.002	1.3

Errors were obtained from the covariance matrix of the corresponding fit. Best-fit curves are shown in Figs. 2b and 3b as well as Figs. S2a and S6a. Parameters in brackets were taken as fixed values.

Using the best-fit parameters for the fractional elongation at zero force, we modeled the DNA force-extension behavior in the presence of EtBr by considering a force-dependent dissociation constant K_d(F). It is obtained by correcting the standard free energy of ethidium intercalation for the mechanical work associated with the DNA elongation during intercalation along the applied force (12, 27):

$$K_d\left(F\right)=K_{d,0}{e}^{-F{\delta }_{Eth}\times z_r\left(F\right)/k_{B}T}$$ (3)

z_r(F) is the relative DNA extension, i.e., the actual extension of the ethidium-complexed DNA at force F normalized by its contour length as provided by the extensible worm-like chain (WLC) model (33, 34, 35). Combining Eqs. 1, 2, and 3 provides the fractional DNA elongation and thus the contour length of the ethidium-complexed DNA as a function of force. Using the measured dependence of the persistence length on the fractional elongation (Fig. S3) and a constant stretch rigidity of 1200 pN, we calculated the expected fractional elongation z_r(F). Multiplication of z_r(F) with the force-dependent contour length then provided the expected DNA extension as a function of force, i.e., a modeled force-extension curve, for the given EtBr concentration. The modeled force-extension curves were at low and intermediate EtBr concentrations in very good agreement with the measured data (Fig. S1 a). Fitting the modeled curves with the extensible WLC model (with constant contour length and apparent stretch rigidity) provided parameters that reproduced the values for the fractional extensions at zero force and the persistence length used in the modeling (see Fig. S4). Thus, the zero-force contour length and persistence length can be reliably extracted from force-extension measurements in the low- to medium-force regime using the extensible WLC model (see also Supporting Materials and Methods and Fig. S4 as well as Fig. S5, in which an independent global fit of the measured force-extension curves with the modeled curves was carried out). Furthermore, the extensible WLC fit provided the apparent stretch rigidity of the model curves. Importantly, the stretch rigidity from the model curves reproduced the drop of the measured stretch rigidity at concentrations with negligible ethidium intercalation down to the observed values of 200–300 pN (Fig. 2 c). This indicates a significant contribution from force-induced intercalation even at the low applied forces because a much higher stretch rigidity of 1200 pN was used for all modeled curves. In contrast, a simple model (see Eq. S3) in which the ethidium-bound DNA consists of a serial combination of bare DNA sections and ethidium-complexed sections with stretch rigidities of 1200 and 200 pN, respectively, could not describe the data (see cyan dotted lines in Figs. 2 c and S2 b). Thus, the observed apparent stretch rigidity in the experiment was dominated by force-induced intercalation and was effectively masking real changes in the stretch elasticity of the ethidium-complexed DNA.

Modeling force-extension data for anticooperative ligand binding

The consideration of force-induced intercalation explains well the measured apparent stretch rigidities at low and intermediate EtBr concentrations. However, in contradiction to the data, it predicts a considerable increase of the apparent stretch rigidity at high EtBr concentrations at which the saturation of the DNA with intercalator should impede additional intercalation (Fig. 2 c). To resolve this discrepancy, we considered the possibility of intercalation occurring without nearest-neighbor exclusion at all binding sites. This is supported by 1) the absence of a clear saturation for the fractional elongation data and 2) a binding site size of 1.8 ± 0.1, suggesting the occupation of more than every second basepair stack (12).

Fits of the fractional extension data were, however, not in agreement with a binding site size of 1, indicating that binding at a neighboring position of a bound intercalator must be to some extend hindered. Such a hindrance can be described by assuming (anti)cooperativity, i.e., by introducing an additional free-energy gain or penalty for the interaction of the ligand with each of its nearest ligand neighbors. This in turn provides an altered dissociation constant of K_d/ω or K_d/ω² for a ligand that has one or two nearest neighbors, respectively (37). ω represents the cooperativity factor with ω > 1 in case of an attractive, i.e., favorably cooperative, and ω < 1 in case of a repulsive, i.e., anticooperative, ligand-ligand interaction. (Anti)cooperative ligand binding to a linear lattice can be described by the cooperative McGhee-von Hippel isotherm (37, 39):

$$\nu =\frac{c_{dye}}{K_d}\left(1-n\nu \right){\left[\frac{\left(2\omega -1\right)\left(1-n\nu \right)+\nu -R}{2\left(\omega -1\right)\left(1-n\nu \right)}\right]}^{n-1}{\left(\frac{1-\left(n+1\right)\nu +R}{2\left(1-n\nu \right)}\right)}^2$$ (4)

with R given by

$$R=\sqrt{{\left[1-\left(n+1\right)\nu \right]}^2+4\omega \nu \left(1-n\nu \right)}$$

Inserting Eq. 4 into Eq. 2 provides an expression for the fractional extension at zero force in case of ligand-ligand interactions and was used to fit the experimental data. To this end, the binding site size was set to 1 to allow binding at each basepair stack. The fits provided salt-dependent dissociation constants K_d,0 (see Table 1) as well as δ_Eth = 0.34 ± 0.01 nm for the contour length increase per dye and ω ≈ 0.03 for the cooperativity factor. This indicates that intercalation just next to a bound ligand is anticooperative, i.e., disfavored, in general agreement with the neighbor-exclusion model. The model is therefore, in the following, called the anticooperative (binding) model. It described the DNA elongation at zero force significantly better because it supports further intercalation at the disfavored nearest-neighbor sites at high EtBr concentrations (Fig. 2 c). Consistently, modeled force-extension curves using the anticooperative binding model reproduced the experimental data at high forces much better (Fig. S1 b). An additional global fit of modeled force-extension curves to the experimental data provided, within error, the same best-fit parameters as fitting the fractional elongation at zero force (Fig. S5). Again, the anticooperative model described the force-extension data better at high EtBr concentrations. This is due to the low apparent stretch rigidity that the anticooperative model correctly predicts at high EtBr concentrations (Fig. 2 c) because of force-induced intercalation at the disfavored sites.

Thus, an anticooperative binding isotherm that allows for an occupation of nearest-neighbor sites provides an improved description of the force-extension data and correctly reproduces the drop of the apparent stretch rigidity over the full concentration range.

DNA untwisting in the presence of EtBr

To further test an anticooperative ethidium intercalation mechanism, we carried out DNA supercoiling experiments. These allow us to probe the DNA untwisting by ethidium and thus to independently monitor the intercalation process (14, 15). To this end, the DNA molecules were held at a constant force of 0.4 pN, and twist was induced by rotating the magnets of the tweezers system. In the absence of intercalator, the DNA length remained initially constant for DNA overwinding (positive applied turns) as well as for DNA unwinding (negative applied turns), thus forming a narrow plateau (Fig. 3 a, green curve). In this phase, the torque in the molecule builds up linearly with the number of applied turns (40, 41). When a critical torque is reached, the molecule buckles and extrudes a plectoneme, i.e., a superhelix in which the DNA wraps around itself. Further induced turns are absorbed by linearly increasing the plectoneme length at constant torque. This translates into a linear decrease of the DNA length such that a characteristic symmetric supercoiling curve is observed that is centered around zero turns and zero torque.

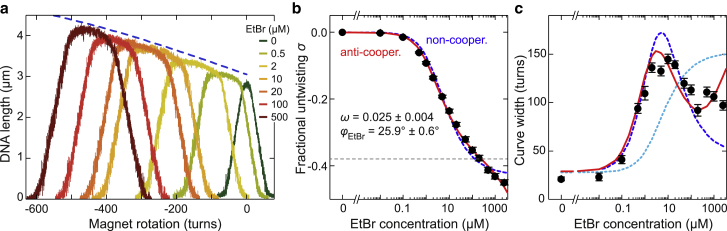
Figure 3.

DNA untwisting and torsional softening due to ethidium intercalation. (a) DNA supercoiling curves recorded for EtBr concentrations from 0 to 500 μM in the presence of 140 mM NaCl. DNA untwisting by the intercalation of ethidium shifts the curves to negative turns. The predicted DNA length at zero torque as function of the untwisting is shown as a blue dashed line (curve shifted to larger length for clarity). (b) Fractional untwisting of the DNA at zero torque as a function of the EtBr concentration (black circles) from the centers of the supercoiling curves. Fits to the data using a noncooperative and an anticooperative binding model are shown as dashed blue and solid red lines, respectively. Best-fit parameters are given for the anticooperative model. The expected untwisting for binding at every second basepair stack is shown as a gray dashed line. (c) Plateau width of the measured supercoiling curves as a function of the EtBr concentration (black circles). Predictions from modeling torque-induced intercalation using the noncooperative and the anticooperative binding model are shown as dashed blue and solid red lines, respectively. The prediction for a serial combination of torsionally rigid bare and soft ethidium-complexed DNA segments is shown as a dotted cyan line.

In the presence of intercalator, the supercoiling curve was shifted toward negative turns, and its plateau was markedly broadened (13, 14, 15, 25) (see Fig. 3 a). Furthermore, although the length decrease in the plectonemic regime was symmetric with respect to positive and negative supercoiling, the prebuckling plateau appeared to be tilted such that the DNA length increased toward negative turns. To understand the behavior of supercoiled ethidium-complexed DNA, we first analyzed the shift of the supercoiling curve center (see Materials and Methods). The curve shift increased with increasing EtBr concentration without showing a clear saturation similar to the elongation data (Figs. 3 b and S6 a). Let ΔN be the number of turns added to the DNA with respect to zero torque in the absence of bound intercalator (also called linking number change). In the presence of intercalator, from the ΔN turns added to a nonbuckled molecule, ΔN_Eth turns are absorbed by helix unwinding from the intercalation, whereas the remaining turns cause a DNA twist (i.e., a helix over- or underwinding) of N_tw. One can thus write

$$\Delta N=N_{tw}+\Delta N_{Eth}$$ (5)

ΔN_Eth is given from the product of the degree of untwisting per ethidium molecule φ_Eth, the fractional occupancy of a binding site and the total number of binding sites given by L₀/δ_bp:

$$2\pi \times \Delta N_{Eth}=-{\phi }_{Eth}\times \nu \times \frac{L_0}{{\delta }_{bp}}$$ (6)

The negative sign in the equation is due to ethidium absorbing negative turns because it untwists the DNA helix. The center of the supercoiling curve being approximately at zero torque/twist (N_tw = 0) is thus located in the presence of ethidium at

$$\Delta N\left(N_{tw}=0\right)=-\frac{{\phi }_{Eth}}{2\pi }\times \nu \times \frac{L_0}{{\delta }_{bp}}$$ (7)

The fractional DNA (un)twisting σ is obtained by normalizing the shift of the supercoiling curve ΔN(N_tw = 0) by the number of helical turns of the bare DNA N_DNA = φ_DNA/2π × L₀/δ_DNA, where φ_DNA is the twist angle per bp:

$$\sigma =-\frac{{\phi }_{Eth}}{{\phi }_{DNA}}\times \nu$$ (8)

Combining this equation with the McGhee-von Hippel isotherms (Eqs. 1 or 4) provides expressions for the fractional DNA untwisting in case of noncooperative or anticooperative ethidium binding, respectively.

We first fitted the measured fractional untwisting as function of the EtBr concentration using the simple, noncooperative model and the previously determined binding site size of 1.8 (Fig. 3 b, dashed lines). This provided similar K_d values as obtained for the elongation data as well as the degree of untwisting per intercalated molecule of φ_Eth = 26.5 ± 0.6° and 28.3 ± 0.2° for 140 and 2000 mM NaCl, respectively. The fit curves did not reproduce the absence of a clear saturation at high EtBr concentrations (particularly for 140 mM NaCl). We therefore carried out a fit with the anticooperative model with a binding site of 1 that provided a better description of the data also at these concentrations (Fig. 3 b). An otherwise unconstrained fit provided consistent values for the K_d values and the degree of untwisting of φ_Eth = 25.9 ± 0.6° and 30.6 ± 0.4°, as well as cooperativity factors of 0.025 ± 0.004 and 0.010 ± 0.002 for 140 and 2000 mM NaCl, respectively (see Table 1). The obtained angles were in excellent agreement with the 26° untwisting determined by crystallography and bulk solution measurements (7, 8, 42) as well as the 27° found in single-molecule measurements (15). The obtained cooperativity factors again supported an anticooperative binding mechanism.

Modeling supercoiling curves in the presence of intercalator

We next tried to understand the broadening of the supercoiling curves. Assuming that the critical buckling torque is not affected by the intercalation, the broadening can be explained by a decrease of the apparent torsional rigidity of the ethidium-complexed DNA (25). In this case, mechanically induced intercalation should also contribute to the apparent DNA softening: induced negative or positive twist will promote ethidium intercalation or dissociation, respectively. In turn, this reduces the magnitude of the applied twist in agreement with l’Chatelier’s principle. To account for this, we modeled supercoiling curves while considering the additional dependence of the dissociation constant on the acting torque Γ according to

$$K_D\left(F\right)=K_{D,0}{e}^{-\left(F{\delta }_{Eth}\times z_r\left(F\right)-\Gamma {\phi }_{Eth}\right)/k_{B}T}$$ (9)

The torque is determined from the DNA twist and the torsional modulus C_s of the DNA, which is corrected for writhe fluctuations (43). Combining Eqs. 2, 5, and 6, an expression for Γ as a function of the applied turns ΔN and the fractional occupancy ν can be obtained:

$$\Gamma =\frac{C_s}{L_{Eth}}2\pi \times N_{Tw}=\frac{C_s}{L_0\left(1+\nu \times {\delta }_{Eth}/{\delta }_{bp}\right)}\left(2\pi \times \Delta N+{\phi }_{Eth}\times \nu \times \frac{L_0}{{\delta }_{bp}}\right)$$ (10)

Inserting Eq. 10 into Eq. 9 and further inserting the result into Eqs. 1 or 5 provides a closed expression that connects the fractional occupancy and the applied turns for noncooperative or anticooperative ethidium intercalation, respectively. Using the obtained best-fit parameters of the fractional untwisting data, we could thus obtain a prediction for the fractional occupancy ν and (by further insertion into Eq. 10) for the resulting torque at a given ΔN. These equations hold if the molecule has not buckled yet. In this state, the relative extension of the molecule can be approximated by (43)

$$z_{pre}\left(F,\Gamma \right)=1-\frac{1}{2}{\left[\frac{p\times F}{k_{B}T}-{\left(\frac{\Gamma }{2k_{B}T}\right)}^2-\frac{1}{32}\right]}^{-\frac{1}{2}}$$ (11)

from which the DNA extension

$$h\left(F,\mathit{\Gamma },c_{EtBr},\mathit{\Delta }N\right)=L_0\left(1+\nu \times {\delta }_{Eth}/{\delta }_{bp}\right)\times z_{pre}\left(F,\mathit{\Gamma }\right)$$ (12)

can be calculated. Using this expression, we modeled supercoiling curves using the best-fit parameters from fitting the fractional untwisting at zero torque. Furthermore, we assumed that the critical torque of about ±7 pN nm and the torsional modulus C_s = 70 k_BT nm at the applied force (0.4 pN) and salt concentrations (41, 43) remained unaffected by the intercalation. An unchanged critical torque is supported by direct torque measurements (25). Supercoiling curves were calculated according to Eq. 12 for absolute torque values below the critical torque. Once the critical torque was reached, the DNA extension was linearly decreased with the applied turns using the experimentally measured slopes of the supercoiling curves. Although both the noncooperative and the anticooperative model reproduced the experimental supercoiling curves at low and moderate EtBr concentrations, only the anticooperative model described the data at high EtBr concentrations (Fig. S7). Particularly, the anticooperative model could reproduce 1) the extreme broadening of the curves including the sudden increase in curve width at concentrations with negligible ethidium intercalation (Figs. 3 c and S6 b), 2) a maximal curve width at EtBr concentrations around the respective K_d, and 3) the only moderate decrease of the curve width at high EtBr concentrations. Remarkably, the tilt of the curve plateaus could also be reproduced (Fig. S7). The overall slope of the plateaus corresponded roughly to the slope of the curve connecting all supercoiling curve centers, where Γ = 0 (blue dashed line in Fig. 3 a). The latter curve arises from the stringent coupling between DNA elongation and untwisting during intercalation. It is thus determined by the ratio between the elongation and the untwisting per intercalated molecule corrected for the relative elongation (see Eq. S10). The fact that the plateau slope matches the slope of the line connecting the rotation curve centers over a large range indicates that upon twisting ethidium-complexed DNA, the induced turns are almost completely absorbed by torque-induced intercalation rather than by increasing the DNA twist. Consistently, the apparent torsional modulus determined from the modeled curves dropped by a factor of 3 to 4 compared to bare double-stranded DNA (Fig. S8), in agreement with previous measurements (25).

We also tested a simple model (see Eq. S5) in which the ethidium-bound DNA consists of a serial combination of bare DNA sections and softer ethidium-complexed sections with twist rigidities of 70 and 20 k_BT nm, respectively. The serial model could neither describe the curve broadening at negligible ethidium intercalation nor the pronounced maximum of the curve width (cyan curves in Figs. 3 c and S6 b). Therefore, a reduced molecular torsional rigidity of EtBr-complexed DNA seems to have a negligible influence on the apparent torsional rigidity. Taken together, these findings demonstrate that anticooperative torque-induced intercalation best describes the observed DNA untwisting and the large reduction in DNA twist rigidity, which fully supports the findings obtained from modeling the force-extension data.

Intercalation into nearest-neighbor sites at elevated forces

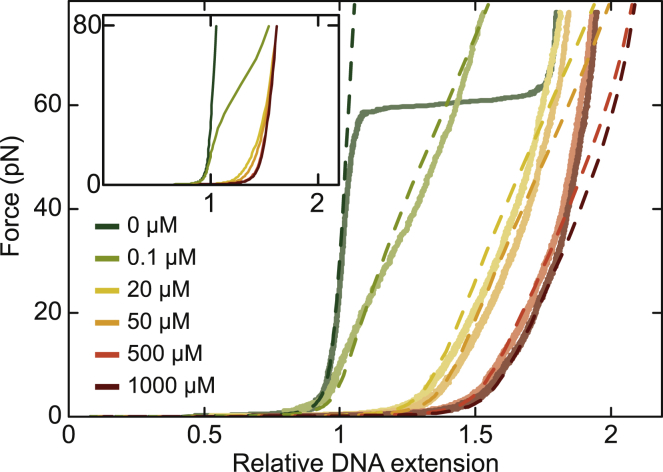
The introduced anticooperative binding model demands that with increasing EtBr concentration and force, all nearest-neighbor sites, i.e., all basepair stacks, become occupied by ethidium. To test this prediction, we recorded force-extension data up to forces of 80 pN for EtBr concentrations ranging from 0.1 to 100 μM. At the highest concentrations, the relative DNA extension reached a value of almost 2, significantly exceeding the extension of bare overstretched DNA (Fig. 4). Notably, even at the highest force, the extension of the ethidium-complexed DNA was strongly dependent on the EtBr concentration. Noncooperative intercalation that is described by a single dissociation constant cannot explain this behavior because according to Eq. 3, the dissociation constant at zero force would be decreased 760-fold from 5.8 μM to 7 nM. Even at the lowest concentration, the ethidium binding would be close to saturation such that all force-extension curves should converge at the high force limit in contradiction to the data (see Fig. 4, inset). Modeling anticooperative intercalation based on the parameters from the low-force measurements, one obtains, however, a concentration-dependent extension also at the high forces (Fig. 4). Intuitively, one can understand this by considering that a cooperativity factor ω of 0.03 defines three zero-force dissociation constants of 5.8 μM, 190 μM, and 6.4 mM for zero, one, and two nearest ligand neighbors, respectively. At 80 pN, these dissociations constants define a range of 7.7 nM–8.4 μM such that saturation is only expected for the highest applied EtBr concentrations. Although for low EtBr concentrations, the anticooperative model describes the DNA extension well even at the highest forces, deviations occurred for high EtBr concentrations (Fig. 4). We attribute these deviations either to a sequence dependence of the ethidium intercalation into nearest-neighbor sites (28) or to an increase in the DNA stretch rigidity because the molecule reaches extensions exceeding the contour length of single-stranded DNA (see Discussion below).

Figure 4.

High-force stretching experiments of ethidium-complexed DNA. Measured force-extension data are shown as solid lines. Predictions from the anticooperative model using the best-fit parameters of the low-force experiments are shown as dashed lines. The inset shows the prediction of the noncooperative binding model. For modeling, a constant stretch rigidity of 1200 pN was used.

Intercalation into nearest-neighbor sites at elevated torque

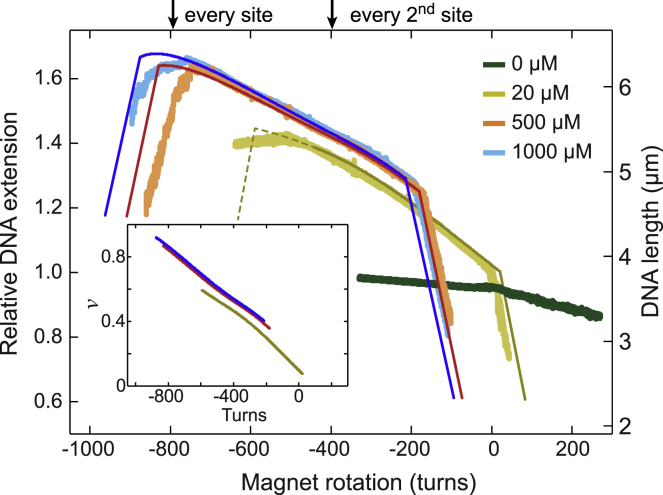
At elevated forces, it is difficult to fully attribute the shape of the force-extension curves to ongoing intercalation or changes of the stretch rigidity in force-extension measurements. To seek independent evidence for intercalation into nearest-neighbor sites, we carried out supercoiling measurements at elevated torque, i.e., when applying an elevated force of 6.4 pN during the twisting measurements (Fig. S6). In the absence of intercalator, neither a clear buckling nor a large DNA length decrease upon twisting—indicative of the formation of a plectonemic superhelix—was visible in the supercoiling curves. This is due to torque-induced structural transitions, in particular DNA melting at negative and formation of Pauling-like DNA at positive supercoiling (44). Intercalation of ethidium stabilizes the basepairing such that Pauling-like DNA formation is suppressed, similarly to DNA overstretching. Therefore, in the presence of intercalator, plectoneme formation, i.e., DNA shortening, could be observed at moderate concentrations for positive supercoiling and at high concentrations also for negative supercoiling (Fig. 5) (15). The prebuckling plateau extended over ∼600 turns because of the larger critical torque compared to the previous measurements. It covered turn numbers that were much larger than the DNA untwisting expected for intercalation into every second site and almost reached the untwisting expected for intercalation into every basepair stack (see arrows on top of Fig. 5). Most importantly, the plateau was tilted over the entire range (Fig. 5). We modeled torque-induced intercalation at this force using the previously obtained best-fit parameters and a critical torque of ±37 pN nm (41). Modeling based on anticooperative ethidium binding reproduced the plateau phase precisely and also described the buckling positions toward positive supercoiling (Fig. 5). Some deviations were observed for the buckling positions toward negative supercoiling, in part due to the absent plectonemic phase at moderate EtBr concentrations. In contrast, the noncooperative binding model could not describe the measured plateaus because it yielded extensions that were too small at elevated negative turns (Fig. S9). This is due to the binding site size of 1.8 such that intercalation saturated at significantly reduced occupancies and turn numbers.

Figure 5.

DNA untwisting in the presence of ethidium at an elevated force of 6.4 pN. Measured supercoiling curves are shown in lighter colors compared to predictions from the anticooperative model, which are shown in darker colors of the same tone. The inset provides the fractional occupancy of the DNA with ethidium for the modeled supercoiling curves. Arrows on top of the plot indicate the expected DNA untwisting if intercalation occurred into every second or every basepair stack. Part of the prediction for 20 μM EtBr is shown as a dashed line because it does not comprise the absence of plectoneme formation.

Thus, ongoing anticooperative ethidium binding also governs the supercoil mechanics at large negative twist. Notably, the fractional occupancies that were obtained within the anticooperative binding model reached 0.9 at the largest negative turn numbers (see Fig. 5, inset). This demonstrates that the intercalator occupies a large fraction (∼80%) of the nearest-neighbor sites under these conditions.

Discussion

In this study, we systematically probed the stretch and the twist mechanics of ethidium-complexed DNA. When adding increasing concentrations of EtBr, both the apparent stretch and the twist rigidities (the latter being approximately proportional to the inverse of the plateau width), experienced a sudden three- to fivefold reduction at EtBr concentrations at which intercalation was still negligible. This behavior could be clearly attributed to stress-induced intercalation in which further ethidium binding causing additional DNA lengthening and untwisting is favored by the applied forces or torques. Previous studies that investigated the stretch (12) and twist rigidities (25) of ethidium-complexed DNA neglected such a process. Rather, the strong reduction of the apparent rigidities was attributed to altered mechanical properties of the ethidium-complexed DNA itself. An altered mechanics alone is, however, inconsistent with the onset of the rigidity reduction at low EtBr concentrations (Figs. 2 c, 3 c, S2 b, and S6 b).

Stress-induced intercalation alone sufficed to describe the full extent of the rigidity reduction as well as the position of the minimal apparent rigidity at EtBr concentrations around the corresponding K_d (Figs. 2 c, 3 c, S2 b, and S6 b). Notably, no free parameters were used for modeling the force-extension and supercoiling data; rather, only the previously determined parameters from the zero-force or -torque data were taken (see Table 1). Thus, the zero-stress binding parameters consistently determine the elastic response of the molecule in agreement with recent force-extension measurements (22). The mechanical response of the ethidium-complexed DNA itself appeared to be effectively masked by the conformational changes from the stress-induced intercalation. Thus, it remains unresolved whether ethidium intercalation leads to a stiffening or a softening of the DNA. An ethidium molecule can only be accommodated between two basepairs by increasing the basepair distance with the help of helix untwisting and repuckering of the ribose rings of the backbone (7, 8). The backbone between the basepairs is therefore in a highly stretched state, whereas it is in its normal conformation for a neighboring unoccupied basepair stack. The highly stretched backbone at an ethidium intercalation site should rather exhibit an increased stretch rigidity because it has limited options to undergo a tensile deformation. The stretch rigidity of ethidium-complexed DNA may therefore be dominated by the undisturbed unoccupied basepair stacks and be only slightly higher than that of bare DNA at moderate fractional occupancies. This idea is consistent with stretch rigidities measured for slowly dissociating intercalators, for which unchanged (22) or increased (21) stretch rigidities were reported.

Full understanding of the performed mechanical measurements required the application of an anticooperative binding model for ethidium intercalation. Within this model, binding at nearest-neighbor sites is allowed but energetically disfavored. Such a binding was evident from 1) the absence of a clear saturation at high EtBr concentrations (Figs. 2 b and 3 b), 2) binding site sizes obtained from the noncooperative model being smaller than 2 (12), 3) the correct prediction of the stretch and twist rigidities even at high EtBr concentrations, and 4) the extraction of correct structural parameters from fits without applying additional constraints. Furthermore, nonsaturated ethidium binding (up to the highest concentrations tested) was essential to explain the concentration dependence of the DNA extensions at high force and the tilted supercoiling plateaus at conditions for extreme negative twist. In particular, the tilt of the supercoiling plateau that is reproduced by our model shows that the typical coupling between DNA elongation and untwisting for intercalators is preserved under these conditions. We therefore attribute the anticooperative binding mode to intercalation into nearest-neighbor sites despite a lacking structural basis (see discussion below). Notably, at high negative twist, intercalation occurs at a considerable fraction of nearest-neighbor sites (ν exceeding 0.8). At even higher EtBr concentrations or mechanical stress, intercalation into all sites can be expected. We note that intercalation into nearest-neighbor sites occurs only at elevated EtBr concentrations because of an elevated K_d at these sites (see above). The noncooperative binding can therefore well describe ethidium intercalation at low concentrations at which nearest-neighbor intercalation does not occur. At higher concentrations or in the presence of external mechanical stress, the noncooperative model fails to correctly describe the points listed above. Because noninteger binding site sizes cannot be rationalized from a structural perspective, we therefore recommend the usage of the anticooperative model instead.

A disfavored binding at nearest-neighbor sites can be readily understood from the structure of the ethidium-complexed basepair stack. The DNA backbone stretching at the intercalation site, including repuckering of the ribose, cannot be translated structurally to the neighboring site but requires a backbone extension with a B-DNA basepair stack (7, 8). Intercalation into a neighboring basepair stack must thus induce a different and potentially energetically more costly backbone perturbation, whose structure has yet to be determined.

An almost complete occupation of the nearest-neighbor sites has been proposed before (45) but was disregarded later because of estimated binding site sizes being considerably larger than 1.0 (12). Only very recently has an independent study of the intercalator YO-PRO reached a similar conclusion as drawn here, calling the fully occupied DNA “hyperstretched DNA” (28). Using careful physics-based modeling, we demonstrated in this study that intercalation into nearest-neighbor sites occurs not only for DNA stretching but can also be introduced by DNA untwisting. We furthermore showed that nearest-neighbor intercalation needs to be considered when fitting zero-force elongation and untwisting data because a clear saturation at the highest applied EtBr concentrations was not observed. Modeling such data with an anticooperative binding isotherm provides an improved description of the observed behavior and constituted a convenient and simple method for considering nearest-neighbor intercalation under the conditions explored here.

The cooperativity factor—in analogy to any equilibrium constant—is related to an energetic penalty ΔΔG⁰_nn that needs to be paid for intercalation adjacent to an occupied rather than unoccupied binding site:

$$\mathit{\Delta \Delta }{G}_{nn}^0=-k_{B}T\times \ln \omega$$ (14)

For the cooperativity factors determined in this study (see Table 1), we obtain a mean neighbor penalty of ΔΔG⁰_nn = 3.7 ± 0.3 k_BT. Within error, this is equal to the value determined from the more complex statistical mechanics model that additionally includes S-DNA formation (28). Thus, both approaches provide consistent results.

Though anticooperative binding can describe the majority of our experimental observations, some deviations remain. For example, the stretch and twist rigidities do not exhibit a clear second minimum at high EtBr concentrations (Figs. 2 c and 3 c), and the measured extension at high force and high EtBr concentrations are smaller than predicted (Fig. 4). Part of these deviations should arise from the known sequence dependence of ethidium intercalation (46) or an even more pronounced sequence dependence for the nearest-neighbor intercalation (28). The binding may thus be described by a sequence-determined distribution of dissociation constants and/or cooperativity factors. This may lead to a preferential occupation of favorable nearest-neighbor sites and thus cause the observed deviations.

Conclusions

In summary, we established a consistent and comprehensive model based on an anticooperative binding mechanism that fully describes force-extension and DNA twisting experiments of ethidium-complexed DNA. The anticooperativity allows for a disfavored but nonetheless possible intercalation into nearest-neighbor sites. Although contour and persistence length could be readily obtained from extensible WLC fits of low force-extension data, the large apparent stretch and twist softening of ethidium-complexed DNA was found to be governed by stress-induced intercalation throughout the applied concentration range. Importantly, we showed that even zero-stress elongation and untwisting data need to be described by an anticooperative binding isotherm. Only such a model allows for a correct estimation of the intercalator parameters without using additional constraints. It furthermore provides the (anti)cooperativity factor and thus the energetic penalty for intercalation into nearest-neighbor sites. Given that intercalation into nearest-neighbor sites has been recently concluded for the intercalator YO-PRO, we think that an anticooperative binding mechanism allowing for intercalation into nearest-neighbor sites may also be applicable to a number of other intercalating molecules.

Author Contributions

R.S. designed the study and developed analysis software. J.D. carried out the measurements and analyzed the data. R.S. wrote the manuscript.

Editor: Keir Neuman.