Subdiffusive Dynamics Lead to Depleted Particle Densities near Cellular Borders

Abstract

It has long been known that the complex cellular environment leads to anomalous motion of intracellular particles. At a gross level, this is characterized by mean-squared displacements that deviate from the standard linear profile. Statistical analysis of particle trajectories has helped further elucidate how different characteristics of the cellular environment can introduce different types of anomalousness. A significant majority of this literature has, however, focused on characterizing the properties of trajectories that do not interact with cell borders (e.g., cell membrane or nucleus). Numerous biological processes ranging from protein activation to exocytosis, however, require particles to be near a membrane. This study investigates the consequences of a canonical type of subdiffusive motion, fractional Brownian motion, and its physical analog, generalized Langevin equation dynamics, on the spatial localization of particles near reflecting boundaries. Results show that this type of subdiffusive motion leads to the formation of significant zones of depleted particle density near boundaries and that this effect is independent of the specific model details encoding those dynamics. Rather, these depletion layers are a natural and robust consequence of the anticorrelated nature of motion increments that is at the core of fractional Brownian motion (or alternatively generalized Langevin equation) dynamics. If such depletion zones are present, it would be of profound importance given the wide array of signaling and transport processes that occur near membranes. If not, that would suggest our understanding of this type of anomalous motion may be flawed. Either way, this result points to the need to further investigate the consequences of anomalous particle motions near cell borders from both theoretical and experimental perspectives.

Introduction

Molecular diffusion is a fundamental process impacting almost every area of cell biology, from transport to gene regulation (as well as fields ranging from superconductor physics to finance (1, 2, 3)). But the cellular environment (cytoplasm, membrane, etc.) is a complicated and crowded place. A consequence of these environmental complexities is that proteins, messenger RNA, vesicles, and other diffusing entities exhibit a range of different exotic and anomalous types of random motion (see (4) for an extensive review). But how do these interactions between particles and their environment influence spatial densities? This article discusses a surprising and potentially important consequence of one particular form of subdiffusion, fractional Brownian motion (FBM), and its physical analog, generalized Langevin equation (GLE) dynamics, on the spatial distribution of particles near cellular boundaries.

Normal diffusion, one of the most basic nonequilibrium phenomena in nature, is well characterized by a linear mean-squared displacement relationship $\langle x^2\rangle =kt$ (where k depends on the particle and environment). It is well known, however, that in the complex, crowded, colloidal environment of the cytoplasm (or the cell membrane), motions of particles instead exhibit subdiffusion¹ where $\langle x^2\rangle =k{t}^{\alpha }$ with α < 1. This raises the well-studied questions 1) what features of the cellular environment give rise to this anomalousness, 2) how can it be accounted for in stochastic models of particle motions, and 3) what are its consequences? Here, I focus on the latter question and consider the consequences of FBM or GLE dynamics in cellular domains.

Although macromolecular crowding has been proposed as one possible mechanism of anomalous motion (5, 6), alternative evidence has suggested simple crowding effects would reduce the speed of normal diffusion rather than introduce anomalousness (7). Instead, some additional environmental factor is likely responsible. From a theoretical perspective, there are a number of possible sources of subdiffusion. The theory of continuous-time random walks (CTRWs) (8), which is typically associated with the transient caging or trapping of particles (by microtubules, for example) in the filamentous cellular environment, hypothesizes that random steps are broadly distributed in time. Alternatively, FBM (9), which is usually associated with the crowded or viscoelastic nature of the cellular environment, assumes the incremental steps taken by a particle are negatively correlated because of the viscoelastic environment. Diffusion on fractals (10) also exhibits subdiffusive characteristics, which could be particularly relevant to transport on actin or microtubule polymer networks.

Fortunately, these types of motion can be distinguished from each other statistically. Motions of chromosome loci (11) and messenger RNA (12) were found to obey an FBM-type dynamic as opposed to CTRW. Similarly, motions of tracer particles in an in vitro dextran solution were found to exhibit an FBM-type dynamic (13). Motions of tracer particles in an actin network, on the other hand, exhibit CTRW characteristics (14). Although these types of motions are distinct and distinguishable, they are not mutually exclusive of each other (15, 16). Insulin granules, for example, were found to exhibit characteristics of both (17). This article will focus on the impact of FBM-type motion on spatial densities near cellular boundaries (membrane, nucleus, etc.).

Although there is a vast amount of literature on this topic, the majority of it has sought to infer the source of anomalous motions by analyzing the statistical properties (time-averaged mean-squared displacement, p-variation (18, 19), turning angle distributions, moments (20), or mean first passage time (10, 21)) of particle paths. Furthermore, most experimental studies have been limited to observing particles distant from cellular boundaries, and most theoretical studies have followed suit. Some studies (22, 23, 24) have investigated the influence of confinement on anomalous motions. They have again, however, focused primarily on the statistical analysis of particle paths to investigate, for example, the effects of confinement on ergodicity. A more recent investigation (25) has shown confinement of particles undergoing FBM can have significant consequences on their spatial distribution. This study, however, focused on transient rather than steady-state dynamics and studied those dynamics on an unbounded domain (half line).

This article investigates the influence of anomalous motions on steady-state particle distributions in bounded, confined domains (e.g., cells). Results show that 1) FBM or GLE dynamics lead to a significant depletion of particles near cellular boundaries; 2) these depletion effects are likely significant enough in both magnitude and spatial extent to be observed experimentally (if, in fact, this theory is an appropriate description of subdiffusive dynamics); and 3) the inherent memory dependence (i.e., increment correlations) of particle motions that are intrinsic to the basic physical hypothesis of this type of motion is responsible for this effect. This raises an important question that could be readily investigated with current super-resolution microscopy techniques: do these depletion zones exist near borders in either cellular or in vitro systems? If so, this would be of profound importance given the wide range of biological processes that rely on interactions with a boundary (trafficking and binding, for example). If not, it may point to a significant flaw in our understanding of this form of subdiffusive motion, both in cellular environments and more generally.

Results

The effect of FBM-type dynamics on the spatial localization of particles near confining borders is investigated here. The goal, however, is not to investigate FBM itself but rather the underlying physical assumptions that are typically associated with it. At the most basic level, FBM is a statistical model that describes antipersistent particle motions as resulting from anticorrelated increments of motion. This inherently introduces a type of history dependence into motion. Although FBM accurately captures (26, 27, 28) many aspects of particle dynamics, it is not inherently a physics-based model. More recently, the GLE (29), which is a well-established generalization of the standard Langevin equation, has been proposed as a more physically grounded model with similar properties to FBM.

Both FBM and GLE dynamics will thus be investigated using simulations. Additionally, a third toy model of anticorrelated, memory-dependent particle motions will be considered. This third model is considered primarily to strip out many of the complexities of the FBM and GLE models while retaining the inherent assumption of anticorrelated increments central to these models. Thus, three distinct but related models encoding the same basic assumptions are used here. This multipronged approach will be used to study, in a model-independent way, how the presence of antipersistent particle motions, and the inherent memory dependence that comes along with them, influences particle densities near confining boundaries.

Models

A brief overview of the models used is given here. For additional details about the models themselves or the numerical implementation details, see the relevant Materials and Methods. As a brief note, all simulations of all models herein are initialized from a uniform initial distribution of particles on the relevant domain. Also, in all figures provided, densities are quoted in units of either particles/micron or particles/micron².

FBM

FBM is a generalization of Brownian motion in which step increments are not independent. Let B^H(t) denote the FBM with mean-squared displacement characterized (in one dimension) by 2Dt^2H, where H is the Hurst exponent and D is the generalized diffusion coefficient (H < 1/2 corresponds to subdiffusion). The FBM process can be generated by a fractional Gaussian noise process (FGN), given by

$$\frac{d{x}^H}{dt}={\xi }^H,$$ (1)

where x^H(t) denotes the trajectory of a particle and ξ^H are correlated increments with $\langle {\xi }^H\left(t\right)\rangle =0$ and covariance

$$\langle {\xi }^H\left(t_1\right){\xi }^H\left(t_2\right)\rangle =2DH\left(2H-1\right){\left|t_1-t_2\right|}^{2H-2}$$ (2)

Thus, FBM is a statistical model that, for H < 1/2, encodes the negative correlation between increments of a particle’s motion. It is this negative correlation that gives rise to antipersistent, subdiffusive dynamics. This model of particle dynamics will be simulated using MATLAB’s (The MathWorks, Natick, MA) wfbm package (part of the wavelet toolbox) for generating FBM. In a confined domain, standard reflecting boundary conditions will be used.

GLE motion

The GLE is a generalization of the canonical Langevin equation that can be derived from basic physical considerations of how a particle interacts with a heat bath (30). It takes the form

$$m\frac{dv}{dt}=-F^{\alpha }+\eta {\xi }^H,\text{where}{F}^{\alpha }\left(T\right)=\gamma \underset{0}{\overset{T}{\int }}{\left(T-s\right)}^{-\alpha }v\left(s\right)ds,$$ (3)

and the fluctuation-dissipation theorem (31) dictates that

$$\eta =\sqrt{\frac{k_{B}T\gamma }{2D_{H}H\left(2H-1\right)}}.$$ (4)

Here, F^α denotes a history-dependent, generalized drag term; ξ^H is the FGN defined above; η is the magnitude of that noise; and γ is the generalized friction coefficient. In this case, the asymptotic dynamics obey $\langle x^2\left(t\right)\rangle \sim t^{\alpha }$, provided the Hurst exponent is H = 1 − α/2. Because the Reynolds number of a typical 100 kDa diffusing protein is Re < 0.05 (32), inertial effects will be neglected, and the m → 0 limit of the GLE will be considered. Simulations of this model for the range γ = 10⁻¹⁰ − 10⁻⁹ will be performed. This yields mean-squared displacements at 60 s in the range 4–40 μm². Smaller values become too computationally cumbersome because of the smaller required time steps and the large number of particles needed to get adequate density estimates. For further discussion of the properties of the GLE, see (28).

For completeness, two methods of simulating this model will be used that provide two qualitatively different interpretations of GLE dynamics. The first is a lattice-free predictor corrector scheme developed in (28) and briefly described in the Materials and Methods. Alternatively, the method of (33) will be used, which views GLE dynamics as a biased random walk in which at each step, a bias due to the particle’s history is introduced by subjecting it to the force F^α (see Numerical Simulation of the Kinetic Monte Carlo Interpretation of the GLE and (33) for implementation details). Standard energetic or Boltzmann statistics arguments can then be used to prescribe the probability of stepping in different directions under the influence of this force. As will be shown, both methods yield similar qualitative conclusions, though they differ in their quantitative predictions of the magnitude of boundary-induced effects. It is important to note here, however, that although the lattice and lattice-free methods here are related models, they are not precisely solving the same underlying model. Specifically, randomness is injected into the lattice method through the sampling of normal random numbers, whereas the lattice-free GLE simulations incorporate an FBM noise source. Although this is a subtle difference, it is an important one and could be the source of this discrepancy.

Antipersistent lattice random-walk model-toy model

Analysis of the FBM and GLE results indicates that the history dependence inherent in the two models is vitally important to the observed results. However, both models have numerous complexities and assumptions embedded in them. To assess the influence of this memory dependence on spatial localization of particles near boundaries, a simple lattice random-walk model is developed (see Antipersistent Lattice Random-Walk Model-Toy Model: Additional Details) in which the probability of right or left steps depend on the number of right or left steps taken over the previous T_m steps. For example, if most of the walker’s steps were to the right, a leftward bias is introduced, and vice versa. The parameter T_m encodes how long into the past this memory process remembers, and an additional bias parameter is included that incorporates the strength of the history-dependent bias. In a sense, this is akin to the kinetic Monte Carlo implementation of the GLE (33) in which the power-law memory kernel is replaced with a uniform kernel with support [t − T_m, t]. This model will be used to determine the influence of memory, and the length of that memory, on spatial distributions.

Modeling results

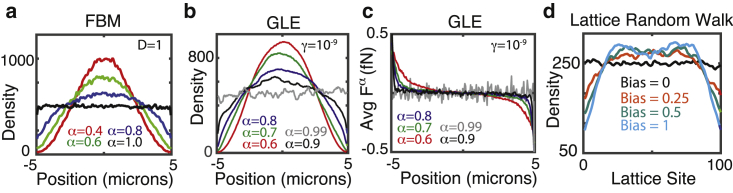
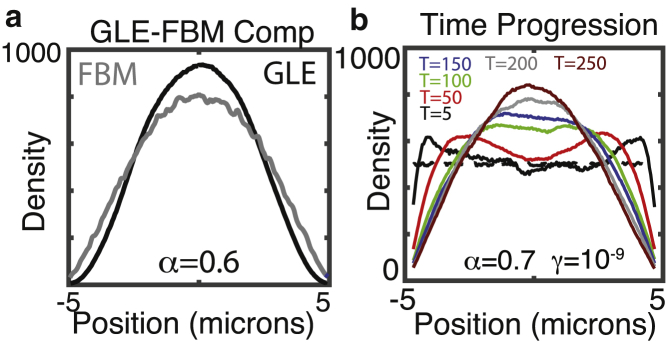
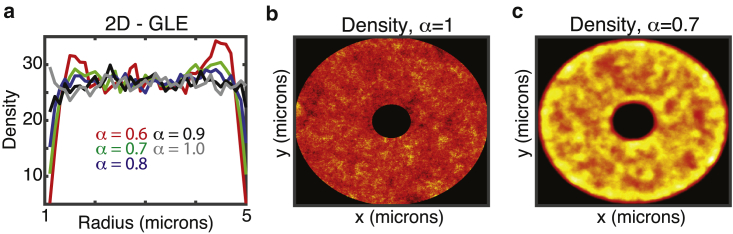
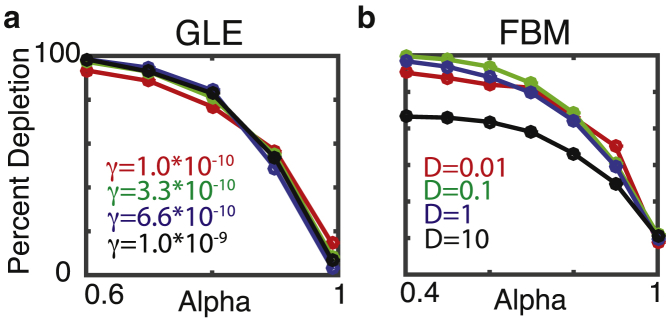
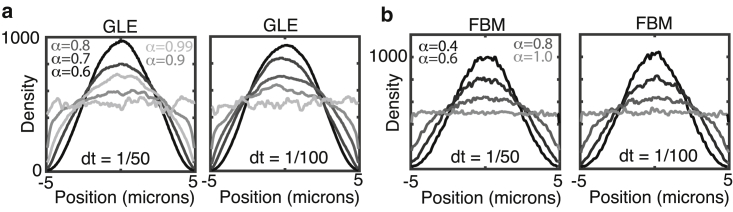
First, simulations of spatial particle densities at steady state were performed for different values of α for both FBM and the GLE. They demonstrate a surprising result: when particle motions are sufficiently anomalous, a substantial depletion zone in the steady-state distribution appears near the cellular border (Fig. 1, a and b). Snapshots of the density distribution at different times (Fig. 2 b) confirm that an initially uniform distribution evolves to this final distribution by steadily pushing mass from the peripheral to the interior regions of the domain. Importantly, this is observed in both the FBM and the GLE. Furthermore, the lattice Monte-Carlo-based GLE simulations in both two dimensions (Fig. 3) and one dimension (Fig. 4 b) show similar results, and the simple antipersistent lattice random-walk model also gives rise to depletion zones (Fig. 1 d). This effect is most prominent when the anomalous exponent (α) is well below one as shown in Fig. 5 (or, in the toy model case, when the bias is sufficiently strong). In all cases, when the exponent approaches α = 1, these depletion zones shrink, and the expected uniform densities appear again. In conclusion, the formation of these zones is universal among these models incorporating memory-dependent antipersistence and is not simply a numerical artifact.

Figure 1.

Anomalous motions lead to depletion of densities near boundaries in a model-independent fashion. (a) A simulated density profile for the FBM with 5000 particles and varying values of α at a fixed value of D = 1 is shown. Densities were calculated after T = 6000 s with a time step of 0.01 s. (b) A simulated density profile (in one dimension, measured in particles per micron) for the GLE with 5000 particles and varying values of α at a fixed value of γ = 10⁻⁹ is shown. Densities were calculated after T = 250 s with a time step of 0.01 s. (c) The spatial profile of the friction force F^α for the simulations in (b) is shown. The force profile is averaged over all particles and all times in the interval T ∈ [240, 250]. The units fN refer to femto-Newtons. (d) A simulated density profile for the toy model with different biasing strengths is shown. 20,000 particles were simulated on a lattice with 100 sites for 20,000 time steps. To see this figure in color, go online.

Figure 2.

(a) Comparison of spatial profiles for the GLE and FBM. The GLE curve is the red curve from Fig. 1b. For the GLE, γ = 10⁻⁹ was used, and for the FBM, D = 0.3 was used. For these values, the MSD curves have the same scaling, and the MSD was comparable after 60 s in an unconfined domain. (b) The simulated time progression from an initially homogeneous density state (dashed line) for the α = 0.7, γ = 10⁻⁹ case from Fig. 1b is shown. To see this figure in color, go online.

Figure 3.

Verification of results in two dimensions with a lattice random-walk implementation of GLE dynamics. (a) Simulated GLE on a two-dimensional annulus using the lattice-based method is shown, demonstrating dependence of depletion layers on α. Plots show density as a function of radius where r = 1 denotes the nuclear membrane and r = 5 the cell membrane. Simulations were calibrated to insulin-granule motility data from (36) so that the MSD after 4 min is ∼1 μm² for α = 0.7. 20,000 particles were simulated for 1000 s with dt = 0.01 s. (b and c) A two-dimensional spatial density map at the end of these simulations is shown, illustrating depletion near the nuclear and cell border for α = 0.7. Red and yellow indicate low and high density, respectively. To see this figure in color, go online.

Figure 4.

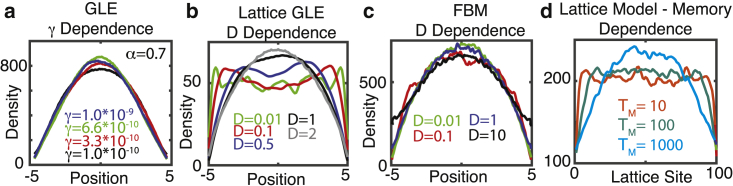
Increasing particle mobility either enhances or has little influence on boundary-depletion effects. (a) Simulated dependence of depletion layers on particle mobility for the GLE (in one dimension) is shown, using the method from (28), and simulation specifics are the same as in Fig. 1a. (b) Simulated dependence of depletion layers on particle mobility for the 1D GLE using the lattice-based method is shown. D is a proxy for the generalized diffusion coefficient in this method, and these values produce MSDs after 1 min that range from 0.04 to 7 μm². 5000 particles were simulated for 500 s with a time step of dt = 0.0025. (c) Dependence of depletion layers on mobility for 1D FBM is shown, using α = 0.7 and similar simulation details as Fig. 1c. (d) Dependence of depletion layers for the toy lattice model on the length of the memory process (e.g., T_m) is shown. To see this figure in color, go online.

Figure 5.

Quantifying depletion as a function of anomalousness (α) and mobility (D, γ). (a) and (b) show the percent depletion at the border relative to the interior as a function of parameters. This is quantified by running simulations with N = 5000 particles to steady state and counting the number of particles in the left half micron [−5, −4.5] and the number in the middle half micron [−0.25, −0.25]. The percent depletion is then (1 − Left/Middle) × 100. Thus, a number close to 100 is a large depletion effect, whereas a number close to 0 represents no significant depletion. To see this figure in color, go online.

Next, the influence of particle mobility on the presence of these zones was assessed. For the GLE, the depletion effect becomes more pronounced for smaller α but appears to be insensitive to varying γ (Fig. 5 a). For FBM, the spatial profile appears to be nearly unaffected by four orders of magnitude variation in D (Fig. 5 b). However, when particles diffuse very quickly, there is a slight reduction in the depletion effect, though it remains significant. In this case, however, the reduced depletion only occurs when particle motions are very fast, i.e., the D = 10, α = 0.6 case corresponds to a mean squared displacement (MSD) of ∼110–120 microns after 60 s. This reduction thus appears to occur only for very fast particles. In conclusion, this depletion effect persists over a range of particle mobilities, and so increasing particle mobility would not abrogate the effect, as might be expected given the homogenizing tendency of diffusion.

Finally, the influence of “memory length” on these boundary-depletion effects was assessed. Simulations of the antipersistent lattice random-walk model with different memory lengths (Fig. 4 d) show that the longer the memory, the larger the steady-state depletion effect. Note that this model does not explicitly encode any spatial or temporal scale, and there is no explicit α encoding the level of anomalousness. The only aspect of this model capable of producing heterogeneity is the antipersistent memory incorporated into it.

There is an important caveat to these results. As shown in Fig. 2 a, the FBM and GLE predict different steady-state distributions, even when the two models are calibrated to have similar MSD scaling. The same α values are used for the FBM and GLE here, and the values of γ and D were chosen so that the two models have the same MSD after 60 s. Thus, in the absence of confinement, both simulations produce the same MSD behavior. However, under confinement, each produces a different spatial distribution. It is not clear what is causing this at the moment, and this discrepancy will be the subject of future investigation. Despite this discrepancy, both, along with the lattice Monte Carlo implementation of the GLE and the toy lattice model, produce the same qualitative pattern of depletion near reflecting domain boundaries. Furthermore, when the time step is increased by a factor of two in the GLE and FBM, the spatial densities and depletion zones are quantitatively similar (Fig. 6). Thus, although this numerical discrepancy must be resolved before the quantitative size of these depletion zones can be predicted, their presence is robust and independent of the specific model being used.

Figure 6.

Verifying depletion effects with different time step. (a) and (b), respectively, demonstrate consistency of results with a larger value of the time step dt for both the GLE and FBM. Throughout the article, dt = 0.01 is used. However, spatial densities are unchanged (up to stochastic variations) when a value of dt = 0.02 is used.

Explanation of boundary-depletion effects in the GLE

This depletion effect is inherently a result of the anticorrelated nature of motion increments built into the FBM, GLE, and toy models analyzed here. This is most clearly seen in the toy model. Consider a particle in this simplified model that is currently observed near the right boundary. This particle will necessarily have a biased history; it will have taken more rightward steps then leftward steps. Given this biased history and the anticorrelated nature of motion increments that is designed into this toy model, this particle near the right boundary will be biased to take a leftward step on the next increment. More generally, this history-dependent anticorrelation will cause particles near boundaries to be biased to move away from them. Furthermore, the closer to the boundary a particle is, the stronger that bias will become.

Although this history-dependent stepping bias was designed into this toy model for illustration purposes, the same fundamental mechanism generates similar depletion effects in the FBM and the GLE. Anticorrelation of motion increments is one of the defining features of subdiffusive FBM. Although there is no directly prescribed statistical association between motion increments in the physics-based GLE, the generalized friction term F^α nonetheless encodes a history-dependent bias of particle’s motion. That is, a particle that moves in a particular direction will be subjected to a restoring friction force pointing in the opposing direction. A direct prediction of this hypothesis is that near a reflecting boundary, the generalized friction force will be, on average, nonzero and point away from that boundary.

To test this, F^α was computed and averaged over every particle over a 10 s timeframe to produce a force map (Fig. 1 c). This is not the force any particular particle is subject to, but rather the expected force (averaged over all simulated past histories that reach that point) that a particle at that location would be expected to feel. The resulting force profile (Fig. 1 c) is heterogeneous (at steady state) as predicted. Away from the boundaries, there is no net friction force when averaged over all particles. There is, however, a net positive (respectively negative) force near the left (respectively right) boundary. Thus, a particle near the left boundary experiences (on average) a generalized friction force pushing it toward the right (and vice versa for the right boundary). This is consistent with the toy model results, suggesting that the simple fact that a particle observed near a boundary necessarily has a biased history will introduce these depletion effects. Furthermore, it suggests that superdiffusion, in which motion increments are positively correlated, would be expected to introduce a commensurate boundary enrichment, as observed in (25) for FBM on the half line.

In conclusion, the antipersistent “memory” of these processes leads to the formation of depleted density zones near cell boundaries. This effect appears to be relatively insensitive to particle mobility, and its magnitude increases as the memory length increases. It is also independent of the specific model encoding these dynamics or numerical method used for simulation. Thus, it is not the detailed statistical or physical assumptions of these models that are responsible for this observation. Rather, it is the antipersistent memory, which is at the very heart of FBM or GLE-type subdiffusion, that is responsible.

Discussion

Results here indicate that FBM or GLE dynamics interact with confining boundaries to produce significant density-depletion zones near those boundaries. This effect is significant when the subdiffusive exponent is α < 0.8, which is a relevant range for the motion of numerous biomolecules (α ∼ 0.7 has been commonly observed; see (4)). Furthermore, this effect is present in multiple models that encode the basic underlying assumptions of FBM (e.g., anticorrelated increments) and is not simply a simulation artifact.

This is of potentially profound importance. How proteins, vesicles, and other molecules localize near various boundaries in the cell is vital to numerous cellular processes. Transport of transcription factors across the nuclear membrane is vital to gene regulation (34, 35). Localization of vesicles near the cell membrane is a precursor to insulin secretion in β cells (17, 36). Cycling of proteins on and off of the membrane is critical to numerous regulatory processes (cell polarity and wound healing, for example) (37, 38, 39, 40, 41). Thus, it is of vital importance to understand how motions of particles in the complex cellular environment influence localization near these boundaries.

These results raise a number of important questions. Do these depletion zones exist near borders in either cellular or in vitro systems? If so, this effect could fundamentally alter the dynamics of any process that requires the localization of substances near such a border. Alternatively, if such effects are not present, what does that say about our understanding of this form of anomalous motion (FBM or GLE-type subdiffusion)? Is the incorporation of history dependence into particle dynamics fundamentally flawed from a biophysical perspective? Or is this simply the result of some unknown technicality associated with boundary conditions? Answering these questions may have wide-ranging implications to our understanding of the microrheology of cellular environments (42) and how anomalous particle motility is influenced by the viscoelastic cellular environment.

Fortunately, the experimental techniques necessary to address these questions are readily available. Existing super-resolution microscopy should be adequate to either measure the spatial densities of tracer particles in confined domains or alternatively look for deviations in the properties of paths of particles (motion biases, for example) close to versus far from confining boundaries. Initially, in vitro systems such as tracer particles in dextran (e.g., (13) or similar) may be a more promising starting point because of the numerous biophysical complexities associated with cellular membranes.

Additional theoretical and computational work is also needed. Although all simulation studies shown here demonstrate this memory-dependent depletion effect, different models and numerical methods predict different sizes of this depletion effect. Given that the magnitude of this potential effect may influence how one looks for it experimentally, it is necessary to resolve this numerical discrepancy to more accurately predict the depth and breadth of the depletion zones in these models. Alternatively, it would be useful to analyze the GLE in scenarios in which inertia is non-negligible. A complementary approach to study this issue is using the continuum fractional Fokker-Planck (43, 44) framework rather than stochastic simulation. Alternatively, recent theories that supersede FBM or GLE, such as diffusing diffusivity (45) or the linear Langevin model with time-varying parameters (46), have been developed. What are the predictions of these models or other models in which increments are non-Gaussian in confined, cellular domains?

In conclusion, this article demonstrates a significant effect of reflecting boundaries (e.g., cellular membranes) on the steady-state spatial distribution of subdiffusive particles obeying FBM or GLE dynamics. This depletion effect is a theoretically robust and experimentally testable prediction that is an intrinsic feature of the underlying FBM or GLE theory. The questions that remain are how significant is this effect, and, more importantly, is it truly present in relevant systems? Regardless of the answer to these questions, this robust consequence of FBM or GLE dynamics may provide an alternative, nonstatistical means of testing the biological validity of the fundamental assumptions underlying those dynamics.

Materials and Methods

Brief overview of simulating the GLE

Here, we give a brief overview of the method (from (28)) used to simulate the GLE. See (28) for more details. After transforming the GLE into a Volterra integral and discretizing the resulting integral equation, temporal updating of stochastic particle location (y_n) is performed using a predictor corrector scheme in which

$$y_{n+1}=y_n+\frac{dt}{2}\left(v_n+v_{n+1}^p\right),$$ (5)

where dt is the size of the time step, n indicates time increment index, v_n is the velocity at time t_n, and $v_{n+1}^p$ is a prediction of the velocity at time t_{n + 1}. The predicted velocity is then given by

$$v_{n+1}^p=\left(\frac{2H\left(2H+1\right)m}{2H\left(2H+1\right)m+d{t}^{2H}\gamma }\right)\left(v_0-\frac{\gamma d{t}^{2H}}{2H\left(2H+1\right)m}\sum _{j=0}^n{a}_{j,n+1}{v}_n+\frac{\eta }{m}{B}^H\left(t_{n+1}\right)\right),$$ (6)

where B^H is the FBM generated by the FGN ξ^H and the velocity-weighting kernel is

$$a_{j,n+1}=\{\begin{array}{ll}{n}^{2H+1}-\left(n-2H\right){\left(n+1\right)}^{2H}\hfill & \text{if}j=0,\hfill \\ {\left(n-j+2\right)}^{2H+1}+{\left(n-j\right)}^{2H+1}-2{\left(n-j+1\right)}^{2H+1}\hfill & \text{if}1\le j\le n\hfill \end{array}.$$ (7)

Given that inertia is typically negligible for diffusing biological particles (the Reynolds number for a typical 100 kDa protein, for example, is <0.05) (32), the mass is set to m = 0 (e.g., the overdamped limit). It is simple to show that in the m → 0 limit, the expression for the predicted velocity becomes

$$v_{n+1}^p=-\sum _{j=0}^n{a}_{j,n+1}{v}_n+\frac{\eta }{\gamma }\frac{2H\left(2H+1\right)}{d{t}^{2H}}{B}^H\left(t_{n+1}\right).$$ (8)

For this study, we simulate the GLE on a fixed, bounded domain y ∈ [−L, L], where L = 5 microns. To account for boundaries, this scheme is augmented with a standard reflecting boundary so that y_n → y_n − 2|y_n − sgn(y_n)L| if |y_n| > L, where sgn(y_n) indicates the sign of the particle’s position.

Numerical simulation of the kinetic Monte Carlo interpretation of the GLE

Here, we follow the approach of (33). This is a lattice-based approach to simulating subdiffusive dynamics governed by the GLE. The key to this approach is to treat subdiffusion motion as a biased lattice random walk in which the bias at any point in time is determined by the particle’s trajectory history. Full details can be found in (33), but I briefly describe the approach.

Consider a one-dimensional (1D) scenario in which Δx represents the spacing of the lattice grid points. Suppose at time t_n, the particle is at location y_n with a past trajectory history ${\left\{y_i\right\}}_{i=1,\dots ,n}$. Given this trajectory, the particle will be subjected to the viscoelastic restoring force F^α (Eq. 3). Define P_n,± to be the probabilities of taking a step to the right (+) or left (−) on this lattice. Then, Boltzmann statistics dictate that

$$P_{n,\pm }=\frac{1}{1+\text{exp}\left(\mp {\mathit{\epsilon }}_n\right)},\text{where}{\mathrm{\epsilon }}_n=\frac{\mathit{\Delta }x{F}^{\alpha }}{k_{B}T},$$ (9)

and F^α is suitably evaluated over the particle’s history. In this way, the force F^α is creating an effective force that the particle must fight, and the P_n,± utilizes Boltzmann statistics and the work required to move against that force to calculate dynamically changing stepping probabilities. For full implementation details, see (33).

Once again, particle trajectories are simulated on a fixed, bounded domain y ∈ [−L, L], where L = 5 microns. Standard reflecting boundary conditions are once again implemented so that any step that attempts to take a particle onto the domain’s border is aborted, and the particle is replaced at its original location for that time step. This method can easily be extended to two spatial dimensions as well. At each time step, a random number is drawn to determine which spatial dimension a step will be attempted in (each dimension has equal probability). The 1D method previously described is then used to determine the direction of the step in that dimension.

I will make one brief note regarding the use of this scheme to generate the simulations in Fig. 3. There, a value of D was used that is based on the observed diffusivity of insulin granules in β cells (36). Insulin granules are very slow-diffusing, and thus it is likely that that these particular simulations have not reached steady state. Given the quadratic dependence on computational time on simulated time and the necessity of storing the full history of many particle trajectories, 1000 s was the longest possible. Because of this, the enriched densities 0.75 microns from domain borders for the red curves in Fig. 3 a are likely transients. Results in Fig. 2 b show a similar result for early times that later resolves as that enriched region of density moves toward the center of the domain over time.

Antipersistent lattice random-walk model-toy model: Additional details

Here, a highly simplified toy model of viscoelastic subdiffusive motion is constructed that incorporates the characteristics of the GLE without the complexities of the fluctuation-dissipation theorem or Boltzmann statistics that are necessary for a more physically grounded model.

The most basic assumption embedded into the viscoelastic theory of subdiffusive motion is that a particle’s environment endows it with a kind of antipersistent memory. That is, the longer a particle moves in a particular direction, the less likely it is to continue moving in that direction in the near future. Here, a toy model of a lattice random walk is constructed with this, and only this, feature.

Consider a 1D lattice random walk on a lattice with sites i = 1…N (N = 100 for specific simulations). Define the position of the random walker to be y_n and define the sign of each step to be s_n = y_n − y_{n − 1}. That is, s_n = ±1 depending on whether the previous step was to the right or left. Now, define the probability of taking a step in the positive direction at time n + 1 to be

$$P_{n+1}^{+}=\frac{1}{2}-B\frac{1}{\text{min}\left(n,n-T_m\right)}\sum _{i=\text{max}\left(1,n-T_m\right)}^n{s}_i,$$ (10)

where T_m denotes the memory length of the process and B > 0 is the strength of the memory-induced bias. Note that when B = 0, this prescribes a pure diffusion process. The probability of stepping to the left will be $P_{n+1}^{-}=1-P_{n+1}^{+}$. Thus, if T_m = 100, this summation will average s_i over the previous 100 steps. This function averages over the previous T_m steps to produce a history-dependent probability of stepping to the right. Consider the three following possible particle histories in the simple case in which B = 0.5. If all possible steps were to the right, then $P_{n+1}^{+}=0$. If all possible steps were to the left, then $P_{n+1}^{+}=1$. If half of all steps were to the right or left, then $P_{n+1}^{+}=0.5$. This is a simple way to incorporate the antipersistence inherent in the GLE without its additional complications. A standard reflecting boundary condition is once again used. Any attempt to step off of the bounded lattice is aborted, and the particle is replaced at its original position.

This is not intended to be a replacement model of viscoelastic subdiffusion. Rather, it is a toy model that will be used to assess the influence of antipersistent particle memory and the length of that memory.

Author Contributions

W.R.H. performed all aspects of this work.

Editor: Ruth Baker.