Cholesterol Depletion by MβCD Enhances Cell Membrane Tension and Its Variations-Reducing Integrity

Abstract

Cholesterol depletion by methyl-β-cyclodextrin (MβCD) remodels the plasma membrane’s mechanics in cells and its interactions with the underlying cytoskeleton, whereas in red blood cells, it is also known to cause lysis. Currently it’s unclear if MβCD alters membrane tension or only enhances membrane-cytoskeleton interactions—and how this relates to cell lysis. We map membrane height fluctuations in single cells and observe that MβCD reduces temporal fluctuations robustly but flattens spatial membrane undulations only slightly. Utilizing models explicitly incorporating membrane confinement besides other viscoelastic factors, we estimate membrane mechanical parameters from the fluctuations’ frequency spectrum. This helps us conclude that MβCD enhances membrane tension and does so even on ATP-depleted cell membranes where this occurs despite reduction in confinement. Additionally, on cholesterol depletion, cell membranes display higher intracellular heterogeneity in the amplitude of spatial undulations and membrane tension. MβCD also has a strong impact on the cell membrane’s tenacity to mechanical stress, making cells strongly prone to rupture on hypo-osmotic shock with larger rupture diameters—an effect not hindered by actomyosin perturbations. Our study thus demonstrates that cholesterol depletion increases membrane tension and its variability, making cells prone to rupture independent of the cytoskeletal state of the cell.

Introduction

Cholesterol is one of the key components of cell membranes in mammalian cells (1, 2) and is implicated in several cellular functions (3, 4, 5, 6, 7, 8), including the formation of membrane structures essential for cellular integrity (9, 10, 11, 12) during stress. Although cholesterol-sensitive structures like caveolae are important (9, 13, 14) for tension regulation during stress in some cell types, red blood cells (RBCs), devoid of caveolae, are known to rupture solely by cholesterol depletion (15). Cholesterol is believed to be a critical factor in cell membrane tension regulation (16) because it can impact the different physical mechanisms used for membrane homeostasis (17). In model membranes, cholesterol content not only alters the basic mechanical parameters like bending rigidity (18) and elastic modulus (19), it also changes the resistance to rupturing on stress (increasing the line tension (19, 20)). We therefore ask how cholesterol depletion in cells affects the membrane topology and dynamics, membrane tension and interaction with cytoskeleton, and cellular integrity on stress.

Cholesterol is depleted by methyl-β-cyclodextrin (MβCD), which encapsulates hydrophobic entities of the plasma membrane in its inner hydrophobic cavity (21) and extracts cholesterol from the outer leaflet continuously (22). Cholesterol extraction by MβCD is widely used in cell biology research (22), and cyclodextrins are proposed drug carriers in anticancer therapies (23). Although cholesterol enrichment in artificial lipid bilayers shows decreased membrane fluidity (19) and membrane viscosity, enrichment on endothelial cell membranes has been reported to cause a decrease in membrane surface viscosity (7) and a weakening of the membrane-cytoskeleton adhesion (3, 7, 24, 25). Studies report cholesterol depletion suppressing lateral diffusion of lipid analogs in the cell membranes (7) while increasing membrane-cytoskeleton attachments and stiffening the cell membrane in aortic endothelial cells (3, 7). These differences may arise because of the different membrane compositions between bilayers and cells or because of the effect of the underlying cytoskeleton in live cells (26). Therefore, the current understanding of the effect of cholesterol on membrane mechanics in cells lacks a clear understanding—unlike in model membrane systems (19)—and needs experimental measurements that can probe the altered membrane tension as well as the altered attachment to cytoskeleton.

Recent studies lay down models (27) that can be used to explain fluctuation spectra that have a contribution of membrane’s attachment to the cytoskeleton via linkers. This is consistent with the incorporation of membrane confinement (net effect of membrane-cytoskeleton attachments and membrane-substrate hydrodynamic interactions (28)) and helps measure the membrane’s tension as well as its degree of membrane confinement in systems ranging from RBCs (29) to nucleated cells (27) and neurons (30). Despite this distinction, it may be noted that fluctuations spectroscopy yields the “membrane mechanical tension” as opposed to “intrinsic bilayer tension” (31). In this study, we have used interference reflection microscopy (IRM) (32, 33, 34, 35, 36, 37) to map spatiotemporal membrane fluctuations. Membrane topology (37), spatial (correlation lengths) and temporal (correlation timescales, PSD, SD of fluctuations, and spatial heterogeneity of fluctuations) parameters of fluctuations (38), and membrane dynamics are captured and calculated from images of live untreated and MβCD-treated cells. To measure membrane tension, we use models that include membrane confinement besides other viscoelastic parameters—so that the effect of membrane-cytoskeleton adhesion energy doesn’t directly get incorporated in the estimated membrane tension.

Besides altering the membrane tension, cholesterol content can change the lysis tension in model membranes (39). Does this also happen in cells? The ability to resist lysis is an important property of lipid membranes in cells (40). However, stresses generated or received by organs (flow of fluid on endothelial cells, flow of RBCs, continuous stretching and relaxation of muscles, etc.) can generate physiological ruptures (41). Cells rupture when a critical tension (lysis tension) is overcome, and the area strain on lipids crosses a threshold. Theoretical studies indicate that whereas pores of sizes below a critical radius rapidly reseal by line tension, larger pores make the membrane unstable (40, 42). Thus, pores that are responsible for rupturing reach a critical radius when the critical tension is attained. Membrane ruptures have so far been studied either by electroporation (40, 42) or photoinduced membrane ablation (43). Unlike these techniques that apply local stresses at specific locations on membranes, physiological stresses are global stresses. The impact of cholesterol depletion on cell membrane integrity is also addressed in this study—by applying global mechanical stress (hypo-osmotic shock) on cells. Measurements of the percentage of ruptured cells and kinetics of the decay of trapped fluorophores in HeLa cells and RBCs are analyzed—the former representing cells with endomembrane and caveolae, whereas the latter lacks both. Comparing our results with known models of the lysis tension, line tension, and rupture/pore diameter (40, 42, 44), we draw inferences about the possible effects of cholesterol depletion on line and lysis tension.

Methods

Cell culture

Mammalian cells (HeLa, CHO-K1, and C2C12) are grown in Dulbecco’s modified essential medium (DMEM) (Gibco, Life Technologies), supplemented with 10% fetal bovine serum (FBS) (Gibco), and 1% Anti-Anti (Gibco) at 37°C, 95% humidity, and 5% CO₂.

Preparation of RBCs

Human RBCs are prepared freshly before each experiment by pricking the finger of a healthy human donor (according to the Institute Ethics Committee approval). Blood (<100 μL collected) is centrifuged at 1000 × g at 4°C for 10 min (45). The supernatant (consisting of plasma, white blood cells, and platelets) is carefully removed. The pellet containing the RBCs is resuspended in 1× Hank’s balance salt solution ((+Calcium Chloride, +Magnesium Chloride) Gibco). 150 μL of this resuspended solution is plated on fibronectin (25 μg/mL)-coated coverslips and incubated at 37°C for 3 h.

Filipin III staining

Cells are fixed with 4% paraformaldehyde (Sigma) for 15 min and incubated with 0.05 mg/mL Filipin III (Santa Cruz Biotechnology) in the dark for 2 h.

Pharmacological treatments

Cells are incubated with 10 mM MβCD (Sigma) in FBS-free DMEM for 50 min (10) to deplete cholesterol. 10 mM sodium azide (Sigma) and 10 mM 2-deoxy D-glucose (Sigma) are added in M1 Imaging medium (150 mM NaCl (Sigma), 1 mM MgCl₂ (Merck), and 20 mM HEPES (Sigma)) for 60 min (46) for ATP depletion. Cells are incubated with 5 μM cytochalasin D (Cyto D) )Sigma) for 60 min to inhibit the polymerization of actin filaments (47). To check the effect of MβCD on ATP-depleted cells, cells atop an onstage microscope incubator in M1 medium are incubated with ATP-depleting reagents for 30 min and then with MβCD for 30 min (without medium replacement). This treatment is termed as ATP dep.+MβCD. To check the role of actomyosin on membrane ruptures, cells in FBS-free DMEM are treated with Cyto D for 60 min and then with MβCD for 50 min without replacing the medium (Cyto D + MβCD). The reverse order of treatments is denoted as MβCD + Cyto D in the study. All the incubations are done at 37°C.

IRM imaging

For IRM imaging (32, 33, 34, 35, 36, 37), cells are imaged in an onstage 37°C incubator (Tokai Hit, Japan) atop a Nikon Eclipse Ti-E motorized inverted microscope (Nikon, Japan) equipped with adjustable field and aperture diaphragms, 60× Plan Apo (numerical aperture (NA) 1.22, water immersion), a 1.5× external magnification, and an electron-multiplying charge-coupled device (Evolve 512 Delta; Photometrics). For IRM, an additional 100 W mercury arc lamp, an interference filter (546 ± 12 nm), and a 50-50 beam splitter is used (38), and images are recorded at electron-multiplying gain 30 and exposure time 50 ms for 102 s at 19.91 frames/s (2048 frames).

Fluorescence imaging

Filipin III-stained cells are imaged using the 4′,6-diamidino-2-phenylindole filter on the microscope, objective, and camera used previously. Images are captured at 300 ms.

Calculation of spatiotemporal fluctuations parameters

MATLAB (The MathWorks, Natick, MA) is used to calculate the relative height of the basal plasma membrane of the cell from the intensities in each pixel of an IRM image by comparing with IRM images of beads (60-μm diameter polystyrene beads; Bangs Laboratories) imaged on the same day (38). In brief, we use a bead-based calibration system to find the intensity to height conversion factor, and then we identify pixels in images of cells in which this calibration holds true.

For calibration, beads stuck on glass are imaged with different exposure times to generate images of interference fringes with varying contrast. Radial intensity profiles yield the conversion factor from intensity difference (ΔI) to height difference (Δh) for the region falling between the first minima and the first maxima. Because this is the first branch of the periodic intensity profile, pixels with intensities falling in this regime are called first branch regions (FBRs). Next, cells are imaged at a preset exposure time and electron-multiplying gain. Minimal, maximal, and background intensities from the cell images are extracted. Bead images with S (maxima + minima) matching the cell’s background and having similar D (maxima − minima) are identified from the already collated list, and the corresponding conversion factor is used for intensity to height conversion.

This way of intensity-height conversion works because the difference in “reflectivity” between the bead and the cell is taken care of by imaging beads at different exposure times (38). It must be noted that the refractive index of the external medium is very important for the correct calibration (38), and hence, beads and cells are always imaged in the same external medium. It is also known that in cases of multiple reflections, the ΔI to Δh conversion will remain similar (38).

Parameters of temporal fluctuations and spatial undulations are measured only for those pixels that qualify as FBRs in cells. Such pixels are identified by first noting pixels with minimal and maximal intensities in the cell. We invoke the fact that those pixels that are spatially contiguous with “minima” pixels without having any “maxima” pixels in between must be those in which the membrane must be at a height less than that at which the first maxima occurs (38). These pixels are termed FBRs in the cell. The height of the membrane in these regions are <∼100 nm and lie in the first branch of the interference pattern. We further limit our analysis to areas of 12 × 12 pixels (also referred to as 144 pixels herein), 2.16 × 2.16 μm² for consistency (38).

The parameters of spatial undulations (Table S1) include SD_space and correlation length, λ. SD_space is calculated from the SD of relative heights across 144 pixels within an FBR and averaged over 20 frames. λ is calculated from three-term exponential fits of spatial autocorrelation functions (ACFs) of heights across 35 × 10 pixels, averaged over 200 frames. The parameters of temporal fluctuations comprise of mean relative height, SD_time, $\overline{\sigma \left(0.01Hz,0.1Hz\right)},$ $\overline{\sigma \left(0.1Hz,1Hz\right)}$, and correlation time, τ. The mean and SD of relative heights calculated in each pixel over 2048 frames and averaged across 144 pixels are termed as mean relative height and SD_time, respectively. To see the frequency dependence of the amplitude of fluctuations, power spectra are plotted. $\overline{\sigma }$ is calculated as the root of the total area under the power-spectral density (PSD) curve between the mentioned frequencies. The slope of log(PSD) versus log(frequency) at frequency band −0.04 to 0.4 Hz is computed to understand the effect of damping in our systems and termed as exponent. We also plot f (ratio of background subtracted PSD of treated to that of control) with frequency to check for frequency-dependent altered fluctuations. τ is calculated from three-term exponential fits of temporal ACFs of heights across 2048 frames, averaged over 2 × 2 pixels.

Mechanical parameters’ (Table S2) active temperature (A), effective cytoplasmic viscosity (η_eff), confinement (γ), and membrane tension (σ) are computed from fitting the PSDs of FBRs to $PSD\left(f\right)=4{\eta }_{eff}A{k}_{B}T/\pi {\int }_{q_{min}}^{q_{max}}dq/\left({\left(4{\eta }_{eff}\left(2\pi f\right)\right)}^2+{\left[\kappa q^3+\sigma q+\left(\gamma /q\right)\right]}^2\right)$ (27, 38, 48). We have fixed the value of bending rigidity (κ) at 15 k_BT (49). Maps of all mechanical parameters are generated by extracting those from fitting PSDs of every pixel to the theoretical model.

Intra-FBR heterogeneity (SD (SD_time)) is calculated from SD of SD_time of pixels over 2048 frames and across 144 pixels. To compute long-range variability within cells, the SD_time of all 144 pixels in an FBR is statistically compared to those in every possible FBR in pairs, and the p value from a one-way analysis of variance is calculated. The number of FBR pairs having dissimilar SD (p < 0.001) is found out, and the ratio of this value to the total number of possible FBR pairs is termed as dissimilar FBR pairs. We use this as a measure of intracellular long-range heterogeneity. Intracellular heterogeneity is also calculated by calculating the SD of all values of SD_time, SD_space, and σ across all FBRs in each cell (Table S1).

Hypo-osmotic shock-induced rupture experiments

Cells are incubated with 2.5 μM Calcein AM (Invitrogen) at 37°C for 30 min, washed well before, and fresh medium (with/without drugs) added for further experiments. Images are acquired with at 10× Plan Apo objective (NA 0.45) with a 1.5× external magnification with 100 ms exposures and at 0.5 frames/s for 5 min. For hypo-osmotic shock, DMEM diluted in deionized water (1/20× for 95% shock) is used. For RBCs, the hypo-osmotic shock is 67%, and the acquisition rate is 2 frames/s. To calculate rupture propensity, cells are scanned 15–30 min after the hypo-osmotic shock. Multiple fields are captured in the differential interference contrast (DIC) and epifluorescence. From DIC, the total number of cells (N_t) present in each field is counted, and from epifluorescence, the total number of fluorescent (hence, not ruptured) cells (N_nr) in the same fields is counted. Rupture propensity (R_P) in that field is calculated as: $R_p=\left(N_t-N_{nr}\right)/N_t$.

Estimation of rupture diameter

Calcein AM fluoresces on permeating live cells (43, 50). The trapped fluorescent Calcein moves out of the cell only if it ruptures and results in a sudden drop in its fluorescence. A model based on simple diffusion (assuming Calcein moves out of the cell by diffusion through the rupture site) is used to estimate rupture diameter (43). The time series of normalized mean intensity (normalized with first frame) of a region inside each cell is plotted, and the ones showing ruptures fitted with $f\left(t\right)=A{e}^{-\left(t/{\tau }_r\right)}+C{e}^{-\left(t/{\tau }_p\right)}$, where τ_r is used as the timescale, whereas τ_p arises from photobleaching, if any. Assuming the radius (R) of a typical HeLa cell is 20 μm (and $V=4\pi R^3/3$ and V = 100 μm³ for RBCs), $l$ is 7 nm, and D is 330 μm²/s, rupture diameter, $r_D$ is calculated from: $r_D=2\sqrt{Vl/\pi {\tau }_{r}D}$.

Statistical analysis

Calibration of IRM with beads and control experiment with cells without any treatment are performed with each IRM experiment. At least 10 cells are imaged for each condition and ∼20–40 FBRs analyzed for each cell. In most cases, analysis is collated over at least three sets of experiments performed on different days. Mann-Whitney U test is performed to determine the statistical significance (^∗p < 0.05, ^∗∗p < 0.001).

Results

MβCD treatment decreases temporal fluctuations and flattens out spatial undulations

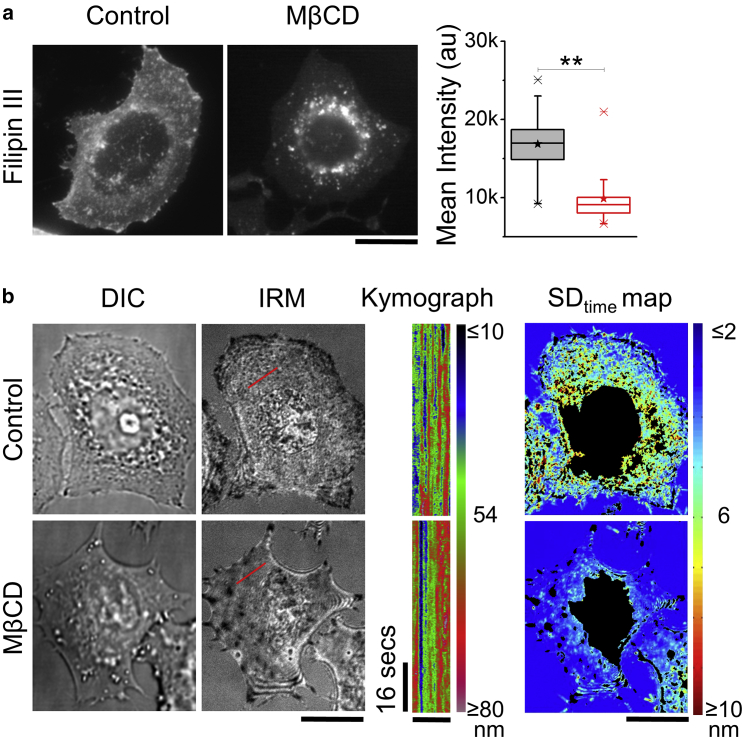
HeLa cells are depleted of cholesterol by MβCD and stained with Filipin III to check for cholesterol depletion (Fig. 1 a, left). As seen in earlier reports (51), images show Filipin III staining at the plasma membrane in control cells, which is lost on MβCD treatment, thereby increasing the contrast of the intracellular vesicles. A quantification of mean Filipin III fluorescence at the membrane shows a ∼40% (N = 30 cells) decrease on cholesterol depletion (Fig. 1 a, right). In Fig. 1 b and Video S1, IRM imaging reveals the altered membrane topology and slower z-movements (seen as intensity variations) of the basal plasma membrane on MβCD treatment. The reduced intensity variations are better visualized by the color-coded kymographs (Fig. 1 b). For quantification, we convert intensity in the images to relative heights (38) as described in the methods and calculate different spatiotemporal parameters (Table S1). The most robustly affected parameter of the height fluctuations is the root mean-squared amplitude of the time variation of membrane height at any pixels (SD_time). The reduction of SD_time on MβCD treatment is evident from SD_time maps (Figs. 1 b and S1 a), from single cell statistics in which the average SD_time for each cell (Fig. S1 b) is plotted and from single FBR statistics obtained from ∼1500 FBRs across ∼70 cells per condition (Fig. S1 c). The relative height (reference zero same for both control and MβCD) is seen to increase on cholesterol depletion.

Figure 1.

Effect of MβCD-mediated cholesterol depletion on membrane topology. (a) Left: representative fluorescence images of Filipin III-stained control and MβCD-treated HeLa cells are shown. Right: shown is a box plot of mean intensity of Filipin III in cells in mentioned conditions (N = 30 cells each). Center lines of boxes show the medians; stars show the means; box limits indicate the 25th and 75th percentiles; and whiskers extend 1.5 times the interquartile range from the 25th to 75th percentiles. ^∗∗p < 0.001, Mann-Whitney U test. (b) Shown are representative DIC (first), IRM (second) images, kymographs of regions overlaid on the images in red (third, scale bars in y, 16 s, scale bars in x, 5 μm) and corresponding SD_time maps of control versus MβCD-treated cells (non-FBRs blacked out). Scale bars, 10 μm. See Table S3 for statistics. To see this figure in color, go online.

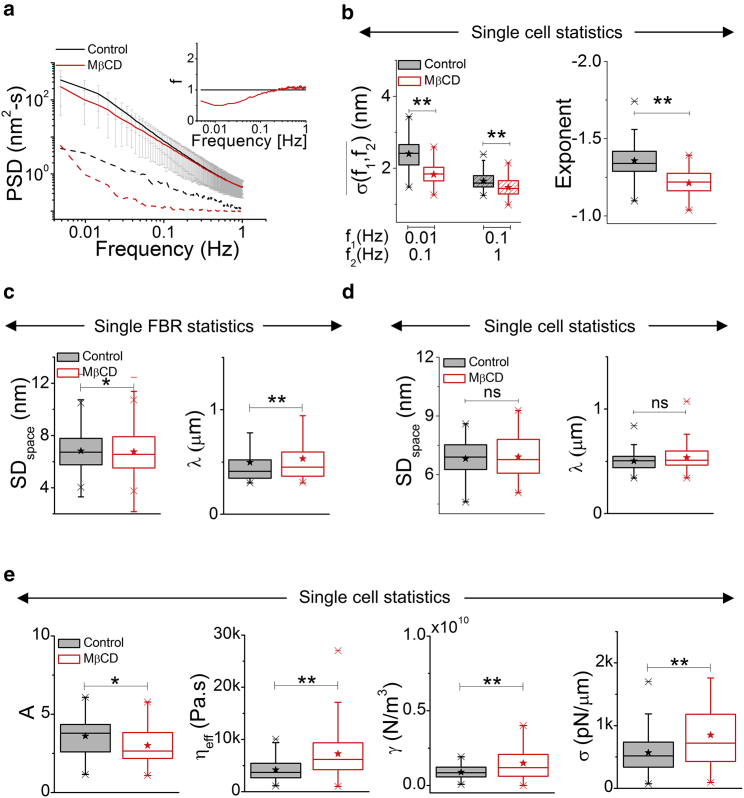
In Fig. 2 a, we plot the PSD for the two conditions. PSD is lowered by MβCD—the effect being more prominent at lower frequencies (∼0.01–0.1 Hz) (Fig. 2 a, inset). Calculated amplitudes ($\overline{\sigma }$) at both frequency bands—0.01–0.1 Hz and 0.1–1 Hz—show a significant reduction on cholesterol depletion (Fig. 2 b). The PSD’s power-law dependence on frequency, captured by the exponent, increases (from −4/3 to −1) on MβCD treatment (Figs. 2 b and S1 c), implying increased confinement (52, 53). All these temporal parameters are significantly affected and captured both in single FBR (Fig. S1 c) as well as single cell statistics (Figs. 2, a and b and S1 b).

Figure 2.

Cholesterol depletion by MβCD reduces temporal fluctuations and enhances membrane tension. (a) Shown are averaged PSDs of FBRs in MβCD-treated cells and their controls (solid lines) with their backgrounds (dashed lines); inset shows f (ratio of background subtracted PSDs). (b) Left: Shown are box plots of $\overline{\sigma \left(f_1,f_2\right)}$ in two different frequency regimes. Right: exponent in the two conditions is shown. N = 70 cells each. (c) Left: single FBR statistics of SD_space in control and cholesterol-depleted cells. n_control = 1683 FBRs, n_MβCD = 1471 FBRs, and N = 70 cell each. Right: correlation lengths are shown. (d) Single cell statistics of SD_space (left) and correlation lengths (right) in the two conditions are shown. N = 70 cell each. (e) Shown are box plots of mechanical parameters A, η_eff, γ, and σ in control and MβCD-treated cells. N = 70 cell each. ^∗p < 0.05, ^∗∗p < 0.001, Mann-Whitney U test. See Fig. S1 and Document S1. Supporting Discussion, Figs. S1–S10, and Tables S1–S2, Table S3. Statistical Parameters for Data Presented in Main Figures for statistics. To see this figure in color, go online.

MβCD leads to a small decrease in the root mean-square amplitude obtained from snapshots of local height profiles (2.16 × 2.16 μm) (SD_space) for the same sets of cells (Fig. S1 c). In parallel, a slight flattening of the spatial ACF (Fig. S1 d) is also obtained from snapshots of local height profiles (6.3 × 1.8 μm), leading to a slight (8%: from 0.49 ± 0.27 μm to 0.53 ± 0.28 μm) increase in the spatial correlation length scale (λ) (Fig. 2 c). However, in all these spatial parameters, the difference is significant only in single FBR statistics but not in single cell statistics, possibly because of the spatial intracellular nonuniformity.

Cholesterol depletion by MβCD increases membrane tension

We next compute membrane mechanical properties by fitting the PSDs with a theoretical model (38) to further characterize the effect of cholesterol depletion. The model is based on Helfrich Hamiltonian (48), which predicts the PSD (31, 54) of a membrane of defined tension (σ), bending rigidity (κ) in a viscous surrounding (of effective viscosity, η_eff). We include adaptations as used in past theoretical (27, 55) and experimental studies (29, 30, 56) that also consider the effect of γ confinement (27, 29, 55). Further, we use the notion of “active temperature” to capture the effect of random active forces on the membrane. Herein, temperature is increased by a factor of “A” (52, 57). Note that these models have been used in both liposomes (54) as well as blebs on cells (56) and cells (29, 30, 38, 58).

On fitting with κ fixed at 15 k_BT (49), although varying the other four, single cell statistics demonstrates that cholesterol depletion leads to a significant decrease in A and a significant increase in η_eff, γ, and σ (Fig. 2 e; Table S3). We note that the change in η_eff and σ persists in single FBR statistics; however, change in γ is found to be insignificant (Fig. S1 e; Table S4).

The values obtained for the four unknown mechanical parameters for control cells are close to numbers found in past reports. Specifically, A ranges ∼1–10 (57), η_eff ranges ∼1–10⁶ Pa s (59, 60), γ ranges ∼0–1 × 10¹⁰ N/m³ (27, 52), and σ ranges ∼10–450 pN/μm (56, 61). Confinement, thus accounted, may originate from the membrane’s interactions with the cytoskeleton (27) or substrate (53). A high η_eff may originate from effective viscosity of the underlying actomyosin gel or from molecular pins impeding membrane flow (60, 62, 63, 64, 65). This range of numbers has been both predicted for actomyosin gels (60) as well as experimentally observed (59).

We show that fits to the PSD are sensitive to each parameter for typical fits (Fig. S2 a). We also plot expected PSDs on varying each of the parameters around the value used in fits (ranges chosen from known values (Table S2)) displaying the frequency range affected by each parameter (Fig. S2 b). A alters the complete PSD as a multiplicative factor, η_eff changes the shape of the PSD, hence altering the lower to higher frequency ratio, γ alters only the lower frequency regime, and σ affects both lower and higher frequencies.

To understand which parameter drives the effect of MβCD on the PSD, we simulate PSDs by using fit parameters (control set) and by switching one parameter at a time of the control set to that for MβCD-treated cells. We then calculate SD from these simulations, plot the expected change in SD (SD_{control set}/SD_simulated), and see that changes in σ results in the most significant reduction of SD (Fig. S2 c). We also check the values and patterns of all mechanical parameters by keeping one or more parameters constant. It is seen that fixing confinement or tension decreases fitting efficiency stronger than fixing other parameters (Fig. S2 d). It needs to be noted that shear modulus arising because of the cytoskeleton’s connection with the membrane, which past studies have included in their model (29), when incorporated in our fitting model resulted in values contributing to the PSD ∼100 times lesser than σ and hence not considered in the final fits (Fig. S2 e). These set of checks underscore the robustness of the effect of MβCD on membrane tension (Fig. S2 e).

Active signatures retained on MβCD treatment

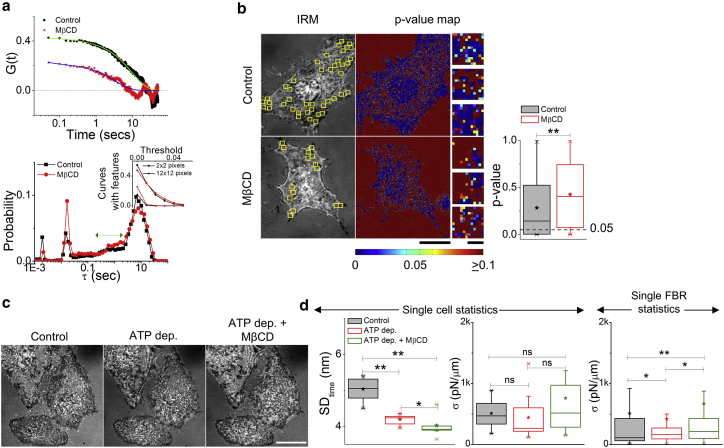
We next ask how cholesterol depletion affects the contribution of activity-driven processes to the observed fluctuations. Temporal ACFs and the distribution of correlation timescales (τ) (Fig. 3 a) and Gaussian-ness of fluctuations are calculated toward this (Fig. 3 b). ACFs reflect reduced correlation strengths on MβCD treatment (Fig. 3 a, top). The distribution of correlation timescales, however, retains the peak in the 0.2–2 s range among other peaks (Fig. 3 a, bottom). This range is usually under-represented when ATP-dependent metabolic activity is hampered by ATP depletion or when fluctuations of plasma membrane spheres are evaluated (38). The other signature of active fluctuations is the presence of “bumps” (local peak-like features) in ACFs (proposed to be caused by correlated kicks on the membrane), which are known to be reduced in ATP-depleted cells (29, 38) and in plasma membrane spheres (38). Herein, we find that similar proportions of ACFs have “bumps” (Fig. 3 a, bottom inset) and there is a drop in this fraction (like that of control) on increasing the region of averaging from 2 × 2 pixels (0.36 × 0.36 μm) to 12 × 12 pixels (2.16 × 2.16 μm). Thus, despite the decrease in correlation strength, the fraction of curves with bumps are not affected by cholesterol depletion. Is the level of “Gaussian-ness” of fluctuations in these cells also retained? We map the p values of Kolmogorov-Smirnov hypothesis testing to quantify the similarity of the temporal fluctuations at each pixel with Gaussian distributions—in which higher p values indicate greater similarity to Gaussian fluctuations (Fig. 3 b, left). We find that the p values increase significantly on MβCD treatment (Fig. 3 b, right). Such an increase may either result from the loss of ATP-dependent fluctuations (38, 66) or may be a result of a reduction in the strength of fluctuations. On analyzing data for mitotic cells, in which fluctuation strength reduces with respect to interphase cells, we find an increase in Gaussian-ness. These cells are expected to retain ATP-dependent activities as also corroborated by the existence of correlation timescales at 0.2–2 s. Herein, the level of Gaussian-ness is thus determined more by the strength of the fluctuations than by the relative contribution of ATP-dependent fluctuations—consistent with studies describing nonequilibrium fluctuations retaining their Gaussian nature (67). On MβCD treatment, although the relative contribution of ATP-dependent fluctuations persists, fluctuations reduce and are less autocorrelated. Does MβCD treatment, therefore, physically affect the membrane irrespective of the cell’s metabolic state?

Figure 3.

MβCD treatment does not abrogate signatures of activity. (a) Top: shown are the typical temporal ACFs of single 2 × 2 pixels FBRs in control and MβCD-treated cells, along with their fits to a three-term exponential function. Bottom: shown is the weighted distribution of correlation timescales (τ) obtained from the temporal ACFs. The green arrow marks the timescales for active fluctuations. Inset shows a plot of the fraction of curves with features versus threshold used to detect the features (n_control = 2890 fits, n_MβCD = 3071 fits, and N = 21 cells each). (b) Shown are FBRs overlaid in yellow on IRM images and their corresponding whole cell (Scale bars, 10 μm) and FBR (Scale bars, 1 μm) p value maps (Kolmogorov-Smirnov hypothesis testing). Right: Shown is the p value for FBRs in control versus cholesterol-depleted cells. n_control = 53,568 pixels, and n_MβCD = 42,480 pixels. (c) Shown are the representative IRM images of control, ATP dep., and ATP dep. + MβCD cells. Scale bars, 10 μm. (d) Box plot for SD_time (left) and σ (middle) for these conditions. N = 10 cells. Right: Shown are single FBR statistics of σ in the three conditions. nc_ontrol = 305 FBRs, n_ATPdep. = 207 FBRs, n_{ATPdep.+MβCD} = 229 FBRs, and N = 10 cells each. ^∗p < 0.05, ^∗∗p < 0.001, ns p > 0.05, Mann-Whitney U test. See Fig. S3 and Document S1. Supporting Discussion, Figs. S1–S10, and Tables S1–S2, Table S3. Statistical Parameters for Data Presented in Main Figures for statistics. To see this figure in color, go online.

MβCD treatment also affects ATP-depleted cells

We use ATP-depleted cells to test the effect of MβCD and once again find reduced temporal fluctuations (Figs. 3, c and d and S3, a and b)—significant both in single cell and single FBR (>250 FBRs in each condition, Fig. S3 c) statistics. Though we do not see enhanced tension in the single cell statistics (N = 10), single FBR statistics show that tension is enhanced on MβCD treatment of ATP-depleted cells. We do not see a significant change in SD_space when MβCD is treated on ATP-depleted cells (Fig. S3 d). Note that although the changes in the mechanical parameters are nonsignificant in single cell statistics, we find decreased γ, decreased A, and enhanced η_eff in single FBR statistics (Fig. S3 e). Hence, MβCD reduces temporal fluctuations robustly, but the effect of increasing tension is less pronounced and, although evident at subcellular length scales, becomes less significant on being averaged.

MβCD enhances intracellular mechanical heterogeneity

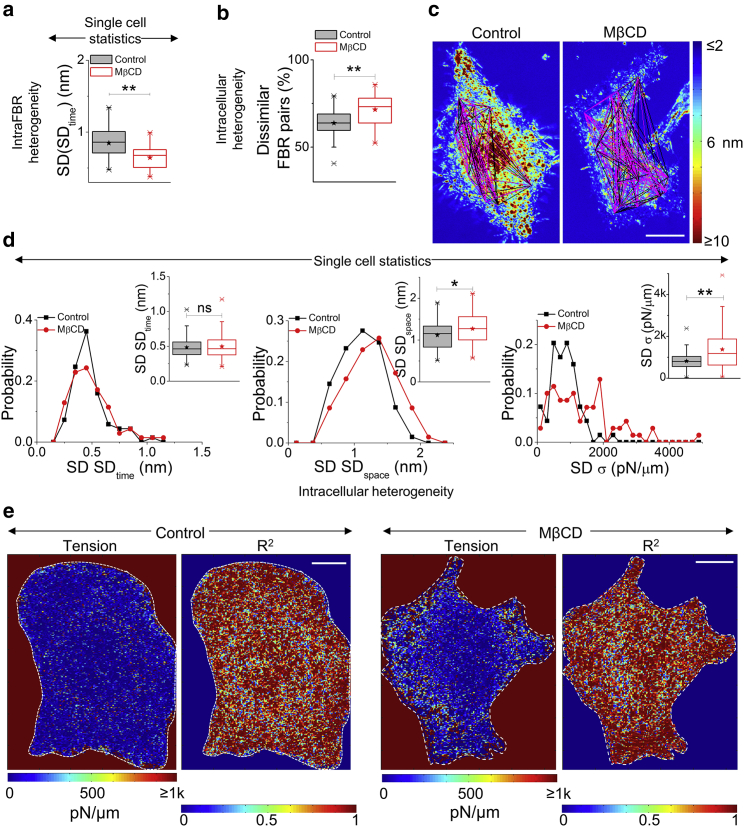
We next seek to understand the effect of cholesterol depletion on the spatial heterogeneity and characterize both short- (inside an FBR, <2.16 μm) and long-range heterogeneity (distances ranging from 2.16 to 54 μm). To compute short-range or local heterogeneity, we calculate the intra-FBR variation in amplitude of temporal fluctuations as the SD (SD_time) and find a reduction in this quantity (even after the averaging of each cell and using single cell statistics) on MβCD treatment (Figs. 4 a and S1 c). Long-range heterogeneity is first quantified by comparing all possible pairs of FBRs in cells and obtaining the p values (of SD_times) to segregate similar (p > 0.001) and dissimilar (p < 0.001) FBR pairs. The percentage of dissimilar FBR pairs increases on cholesterol depletion (Fig. 4, b and c). Next, we quantify the intracellular variability of SD_time, SD_space, and σ by calculating the SD of these parameters from measurements done at every FBR for any cell. Such single FBR statistics show that intracellular variation of SD_time is not affected by cholesterol depletion but that of SD_space and σ are significantly enhanced (Fig. 4 d). This is in line with weaker statistical changes for both SD_space and σ on cholesterol depletion when evaluated by single cell statistics than single FBR statistics. On mapping mechanical parameters, we find a visual proof of enhanced intracellular heterogeneity in σ on MβCD treatment (Figs. 4 e and S4).

Figure 4.

Enhanced spatial and mechanical intracellular heterogeneity on MβCD treatment. (a) Intra-FBR fluctuations heterogeneity measured by SD (SD_time) for the two conditions are shown. (b) Shown are intracellular long-range fluctuations heterogeneity measured by box plots of the number of dissimilar FBR pairs. Dissimilarity is evaluated by comparing SD_time. N = 70 cells each. (c) Lines in magenta and black connect FBRs that are dissimilar and similar in SD values, respectively. The lines are overlaid on the SD_time maps in representative control and MβCD-treated cells. Each node in the maps represents the center of an FBR. Scale bars, 10 μm. (d) Shown are histograms and box plots of intracellular heterogeneity of cell averaged SD_time, SD_space, and σ in the two conditions. N = 70 cells each. (e) Representative single pixel maps of tension (σ) and goodness of fit (R²) for a control and MβCD-treated cell are shown. The white dashed line marks the boundary of the cell. Fitting was performed for pixels inside this boundary. Scale bars, 10 μm. ^∗p < 0.05, ^∗∗p < 0.001, ns p > 0.05, Mann-Whitney U test. See Figs. S1 and S4 and Document S1. Supporting Discussion, Figs. S1–S10, and Tables S1–S2, Table S3. Statistical Parameters for Data Presented in Main Figures for statistics. To see this figure in color, go online.

We further investigate the generality of this effect by testing the impact of MβCD on another epithelial cell line CHO and a mouse myoblast cell line C2C12. CHO, unlike HeLa, has a robust CLIC/GEEC (CG) endocytosis pathway (68), making the possible active mechanisms for its tension regulation different from that of HeLa.

Multiple cell lines display enhanced tension on cholesterol depletion

In Fig. S5 a, we show parameters pertaining to fluctuations measured in CHO and C2C12 on MβCD-mediated cholesterol depletion. We see that temporal fluctuations are always reduced after MβCD treatment in both CHO and C2C12 like in HeLa (Fig. S5, b–d). In CHO, we report a decrease in intra-FBR variations SD (SD_time) (Fig. S6 a), whereas the changes in the spatial parameters of undulations or long-range heterogeneity are not seen to significantly alter upon cholesterol depletion (Fig. S6 b). It is noteworthy that MβCD leads to an increase in σ (single cell and single FBR statistics) and η_eff (single FBR statistics) (Fig. S6, c and d) as in HeLa. C2C12 cells, however, do not show a significant change in the short-range heterogeneity in cholesterol-depleted C2C12 cells or tension (Fig. S6, a and d)—however, they do show an enhanced correlation length scale (Fig. S5 d) and η_eff (Fig. S6 d).

Although γ values increased on MβCD treatment in single cell statistics in HeLa cells, we remind that no significant change was found in single FBR statistics. Also, ATP-depleted cells showed a reduction in γ on MβCD treatment (based on single FBR statistics). In CHO and C2C12 cells, γ is either not significantly altered in single cell statistics while reduced in single FBR statistics on MβCD treatment. It must be noted that γ has both the contribution of interaction of the membrane with the cytoskeleton as well as substrate—and emerges to be less robustly affected than tension.

Therefore, the most robust effect of MβCD on membrane mechanics in single cells is to reduce temporal fluctuations, increase the membrane tension and its spatial heterogeneity, and increase η_eff. In the next section, we address how MβCD treatment alters the rupture propensity and affects the lysis tension in cells.

Cholesterol depletion increases membrane rupturing propensity and diameter on hypo-osmotic shock

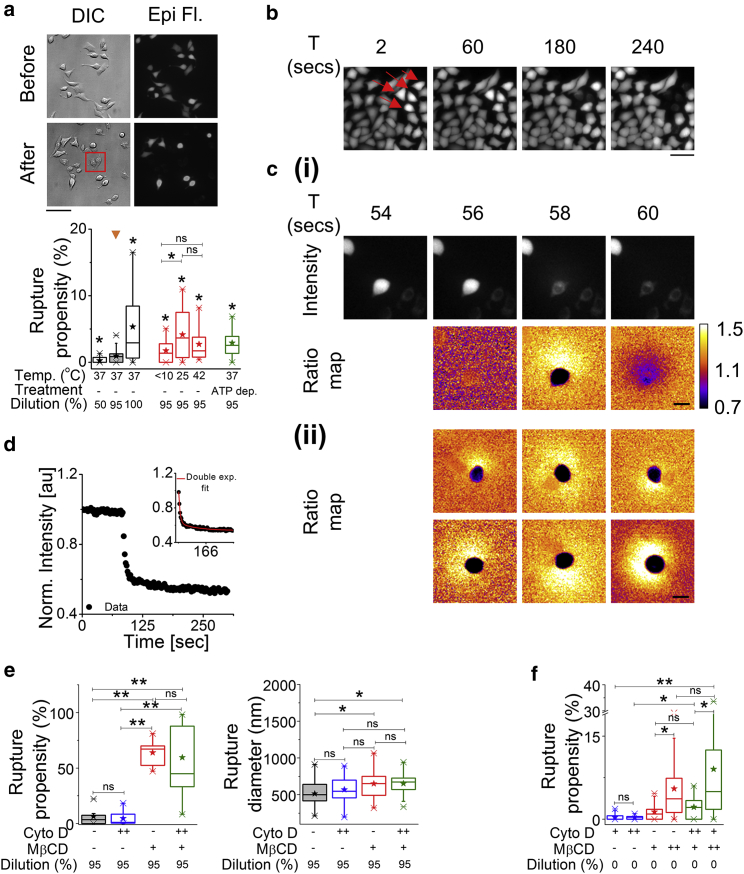
We use hypo-osmotic shock to impart global mechanical stress (Videos S2 and S3) on cell membranes and assess its propensity to rupture. HeLa cells are loaded with Calcein AM and analyzed before and at least 15 min after hypo-osmotic shock. Cells with a ruptured membrane lose the internal Calcein AM and are hence identified by comparing their absence in fluorescence images to their presence in DIC images (Fig. 5 a). Rupture propensity is defined as the percentage of cells that undergo rupturing, and it increases the strength of the hypo-osmotic shock (Fig. 5 a, bottom). Rupture propensity also increases when the temperature is decreased from 37°C (0.9% ruptures) to <10°C (1.7% ruptures) or 25°C (4.2% ruptures) or increased to 42°C (2.7% ruptures). ATP depletion too increases rupture propensity but only to 5–10% (Fig. 5 a, bottom). We find that RBCs (Fig. S7 a), in general, have a much higher rupture propensity than HeLa cells. In addition to calculating rupture propensity, we also follow the Calcein AM-loaded cells (HeLa and RBCs) after hypo-osmotic shock and find that rupturing events lead to a sudden loss in internal mean intensity (Figs. 5 b and S7 b). Ratio maps (Fig. 5 c) between consecutive images show that the rupturing is marked by fluorescence loss from the whole cell and by a simultaneous and sudden increase of fluorescence in the surrounding medium that is often asymmetric (Figs. 5 c and S7 c). This indicates that the loss of intensity is due to a single-point rupture and is also seen in RBCs (Fig. S7 c, left). Fitting the temporal intensity profile (Figs. 5 d and S7 c, right) with exponential decay functions yields a time constant that is used to estimate the rupture diameter based on a simple model that assumes fluorescence loss from the lesion by pure diffusion.

Figure 5.

Membrane rupture induced by hypo-osmotic/iso-osmotic medium in the presence of MβCD. (a) Top: shown are DIC and epifluorescent images of Calcein AM-labeled HeLa cells before and after the administration of a 95% hypo-osmotic shock (Scale bars, 100 μm). Among others, the cells in the box are representatives of membrane rupture. Bottom: shown is a box plot of rupture propensity of cells due to change in hypo-osmotic stress, change in temperature, and ATP depletion (N = 3 experiments each). (b) Top: shown are time lapse images of Calcein AM-loaded HeLa cells undergoing rupture (arrowheads in red) (Scale bars, 50 μm). (c) (i) Shown is the intensity and ratio $\left(Intensityofframe/Intensityofprevio\text{us}\text{frame}\right)$ map of a rupturing cell followed in time to show single point rupture. (ii) Shown are representative ratio maps of six different cells showing an asymmetric spread of fluorescence after rupture (Scale bars, 30 μm). (d) A time profile of normalized mean intensity of a ruptured cell is shown; inset shows the double exponential fit to the profile. (e) Shown are box plots of rupture propensity (left) and rupture diameter (right) of 95% hypo-osmotic shock administered HeLa cells under control, Cyto D (2 h post-treatment), MβCD (50 min post-treatment), and Cyto D + MβCD conditions (N = 3 experiments each). (f) Shown are box plots of rupture propensity of cells under Cyto D, MβCD, and dual drug treatments (N = at least three experiments each) in the absence of hypo-osmotic shock. “+” denotes 60 min treatment (for Cyto D) and 50 min (for MβCD), and “++” denotes 120 min treatment. ^∗p < 0.05, ^∗∗p < 0.001, ns p > 0.05, Mann-Whitney U test. See Fig. S7 and Table S3 for statistics. To see this figure in color, go online.

MβCD treatment results in an enhanced rupture propensity and an increased rupture diameter on hypo-osmotic shock (Fig. 5 e). As reported earlier (15), we too see that RBCs and a small percentage of HeLa cells rupture in isotonic media when treated with MβCD (Figs. 5 f and S7 e). We also find that increasing MβCD concentration enhances rupture propensity in RBCs, whereas the rupture diameter matches that with hypo-osmotically shocked control cells (Fig. S7, d and e).

To understand the role of the cytoskeleton in the measured effect, we perform experiments in which cells are first treated with Cyto D before MβCD treatment and then a hypo-osmotic shock is administered. We find that Cyto D on its own does not alter the rupture propensity or rupture diameter on hypo-osmotic shock (Fig. 5 e). Similar values of rupture propensity and rupture diameter in MβCD-treated cells as well as Cyto D + MβCD cells on hypo-osmotic shock show that the effect of MβCD is not abrogated by Cyto D. This indicates that the cytoskeleton is not essential for the effect of MβCD on membrane integrity. This effect is also seen in MβCD-pretreated cells (Fig. 5 f) and is found to be more pronounced in RBCs (Fig. S7 e; Video S4).

Thus, cholesterol depletion by MβCD alters membrane mechanics by increasing the membrane tension and its heterogeneity and enhances the rupturing propensity of the membrane with or without external stress. These effects are not mediated through the enhanced membrane-cytoskeleton interactions and found to be also true in RBCs.

Discussion

In this article, we use interference-based membrane fluctuation maps to quantify the effect of MβCD-mediated cholesterol depletion on cell membranes and their integrity. Our study also evaluates the intracellular variability of measured fluctuations and estimated mechanical parameters—to the best of our knowledge, unaddressed in previous studies. The most robust statistic pertains to the reduction of temporal fluctuations—a plausible consequence of the continued loss of an abundant membrane component, cholesterol, and observed in three different cell lines (HeLa, CHO, C2C12) as well as in ATP-depleted HeLa cells. Concomitantly, we observe a statistically significant increase in membrane tension in HeLa and CHO cells—although their tension regulation mechanisms may differ (68). The existence of the active regulation of membrane tension (17) raises the possibility that the observed tension increase may primarily originate from cholesterol’s involvement in diverse membrane trafficking processes. However, we find that active signatures persist on cholesterol depletion, although signal strengths reduce. Although it indicates that MβCD may not affect cells only through cholesterol’s role in active processes, it doesn’t establish if cholesterol depletion also directly affects the membrane and its tension. Our data on MβCD’s effect on ATP-depleted cells, however, addresses this point and firmly concludes that having a metabolically active cell is not essential for the manifestation of MβCD’s impact of reduced fluctuations and enhanced tension on the plasma membrane.

Alteration to the mechanical state is assessed at three length scales. The first comprises using pixel-wise information to calculate local (2.16 × 2.16 μm² regions) variation of height termed SD_space and that of temporal variation termed SD_time. Correlation lengths (0.2–10 μm) also portray length scales of this level. In the second level, averaging is performed over single FBRs, and the pool from all FBRs (from all cells) are termed as single FBR analysis. Finally, single cell statistics entails averaging data from all FBRs for cells, and pooling data (mean and SD for each cell) for all cells in each condition. The SD calculated for each cell captures the intracellular variability. Therefore, we treat regions inside cells to be possibly distinct. We comment both on how overall cell states get affected as well as how the overall median alters, and thus, we include both cell-based and FBR-based statistics for most comparisons.

Such quantifications of intracellular variability of SD_time, SD_space, and σ demonstrate that different regions in a cell may be affected to different degrees by MβCD. Although intracellular variations of SD_time don’t significantly enhance, there are more region pairs that are statistically dissimilar on comparing their SD_time map. This contrasts with the effect of other treatments reported by us in the past by evaluating the number of statistically dissimilar FBR pairs, like ATP depletion, Cyto D treatment, etc. (38). Long-range intracellular heterogeneity is higher for SD_space as well as σ on MβCD treatment. Thus, besides changing mean values, MβCD also creates a more heterogeneous mechanical state.

Our next part shows the undesirability of mechanical conditions created by MβCD. Corresponding to its enhancement of dissimilar regions, MβCD distinctly enhances rupture propensity on hyposhock. Altering temperature, depleting ATP, or disrupting the cytoskeleton do not increase rupture propensity as strongly. We find a finite pool of cholesterol-depleted cells rupturing even without hyposhock—as also seen for RBCs. Our data suggests this to be independent of its effect on the cytoskeleton because the effect of MβCD enhancing rupturing propensity persists in cells pretreated with Cyto D. What drives membrane destabilization? Is it due to the enhanced tension, or is it due to the enhanced heterogeneity in tension?

Although membrane tension can be enhanced by ATP depletion, it marginally increases (to 5%) rupturing propensity compared to MβCD (to 50%). Because cell membranes can show slower timescales of flow of local membrane perturbations compared to model membranes (14), our data suggests that mechanical heterogeneity created by cholesterol depletion might be weak regions that cannot be equilibrated quickly and hence rupture in the advent of global cell swelling by hypo-osmotic shock. Note that ATP depletion, in fact, reduces intracellular heterogeneity of SD_space, something that is amplified by MβCD.

Can enhanced membrane tension alone explain the increase in rupture propensity and radius by MβCD? We undertake estimations wherein we invoke the dependence of the critical rupture size on the membrane’s line to surface tension (r = γ/Σ) during lysis (Supporting Discussion). Estimations show that the energy (40, 42) required to open the pore ($\mathit{\Delta }E=\pi {\gamma }^2/\text{Σ}=\pi \gamma r$ ∼12 k_BT (for RBCs), 200 k_BT (for HeLa), assuming a lower limit γ ∼1 pN and using observed radii of rupture, 15 and 250 nm, for RBC and HeLa cells, respectively) is too high and contrasts the observed probability of rupture (expected (exp (−ΔE/k_BT)): 6 × 10⁻⁶; observed: 0.092, for RBCs without hypo-osmotic shock and in the presence of MβCD). Although this already implies that the ruptures might be induced by local defects in the membrane, we believe lowered line tension (as observed in giant unilamellar vesicles (20)) and lysis tension can also lead to the observations of an enhanced propensity with similar or enhanced rupture diameter on cholesterol depletion (Supporting Discussion; Fig. S8). It is therefore not possible to conclude on the mechanism by which MβCD enhances membrane rupturing in cells.

How does this study address the issue of separating MβCD’s effect on membrane-cytoskeleton attachment from its effect on membrane tension? First, we emphasize that although the cytoskeleton affects membrane fluctuations, incorporating confinement parameter in the model describing PSD, $PSD\left(f\right)=4{\eta }_{eff}A{k}_{B}T/\pi {\int }_{q_{min}}^{q_{max}}dq/\left({\left(4{\eta }_{eff}\left(2\pi f\right)\right)}^2+{\left[\kappa q^3+\sigma q+\left(\gamma /q\right)\right]}^2\right)$, allows us to estimate both the confinement (has contribution from substrate as well as an attachment to the cytoskeleton by linker (27)) as well as the mechanical tension felt by the membrane (31). Restricting the confinement of a fixed value overestimates the effect of MβCD (Fig. S2), underscoring the importance of confinement. Having assessed both parameters, our analysis shows that the tension increase is robust and persists even when ATP-depleted cells are used for MβCD treatment. Alterations in γ by MβCD, however, is less robust, and although maps show a close correspondence between heterogenous tension and that of confinement (Figs. 4 e and S4), statistics show that tension is increased even when confinement is not significantly affected (Fig. S1 e) or reduced (Fig. S3 f).

Finally, we would like to remind the reader about the potential limitations of this study and how they were addressed. At first, IRM as a technique has been extensively used in model membranes and RBCs but less so in adherent cells for membrane height measurement. To get proper measurements, we have performed checks (Fig. S9) to show that in FBRs, local actin density (marked fluorescently) doesn’t strongly alter reflectivity as also evident in studies using IRM showing actin localizing but affecting an IRM image only by pushing the membrane later (33). Similarly, in regions chosen for analysis (FBRs), we do not find a nonrandom correlation of movement of internal membranous structure (marked fluorescently) with IRM intensity fluctuations (Fig. S10). Any correlation found in both cases were still present on choosing random noncorresponding sets. The other important part of the study is the fitting of PSDs to a known model for extracting mechanical parameters. We emphasize that any trend in mechanical parameters reported herein was rigorously checked in multiple ways (Supporting Discussion) and observed even on changing the number (4–6) of fitting parameters. Furthermore, to verify if enhanced spatial heterogeneity in mechanical parameters is also visually distinguishable, we calculate values for each pixel and present the maps (Figs. 4 e and S4). Maps beautifully depict a uniform, although noisy, state of membrane tension in control cells. Pockets emerge in MβCD-treated cells in line with the intracellular heterogeneity evaluated by using averaged PSDs. Although the fitting is not perfect for each pixel as evident from the map of R² and mapping was extended beyond FBR pixels, these maps capture the central essence of this article and provide further support of the use of four-parameter fits. Interestingly, the factor “A” (implying active temperature) has a similar pattern as that of a Gaussian-ness map.

In conclusion, we show that under cholesterol depletion by MβCD, cells have altered fluctuations (enhanced flattening of spatial undulations and damping of temporal fluctuations) and show a clear increase in membrane tension. This work extends our understanding about the effect of MβCD on cells by demonstrating that it creates long-range heterogeneity or intracellular variability in membrane tension and enhances rupture rates and rupture diameter.

Author Contributions

Conceptualization, B.S.; Methodology, B.S., A.B., T.S., S.D., and P.K.; Software, B.S. and A.B.; Validation, A.B. and B.S.; Investigation, A.B., P.K., S.D., and T.S.; Formal Analysis, A.B. and P.K.; Data Curation: A.B.; Writing—Original Draft, B.S. and A.B.; Writing—Review & Editing, T.S. and P.K.; Visualization, A.B.; Supervision, B.S.; and Funding Acquisition, B.S.

Editor: Dimitrios Stamou.