Abstract
Currently, clinical determination of pathologic fracture risk in the hip is conducted using measures of defect size and shape in the stance loading condition. However, these measures often do not consider how changing lesion locations or how various loading conditions impact bone strength. The goal of this study was to determine the impact of defect location on bone strength parameters in both the sideways fall and stance-loading conditions. We recruited 20 female subjects aged 48-77 years for this study and performed MRI of the proximal femur. Using these images, we simulated 10-mm pathologic defects in greater trochanter, superior, middle, and inferior femoral head, superior, middle, and inferior femoral neck, and lateral, middle, and medial proximal diaphysis to determine the effect of defect location on change in bone strength by performing finite element analysis. We compared the effect of each osteolytic lesion on bone stiffness, strength, resilience, and toughness. For the sideways fall loading, defects in the inferior femoral head (12.21%) and in the greater trochanter (6.43%) resulted in the greatest overall reduction in bone strength. For the stance loading, defects in the mid femoral head (−7.91%) and superior femoral head (−7.82%) resulted in the greatest overall reduction in bone strength. Changes in stiffness, yield force, ultimate force, resilience, and toughness were not found to be significantly correlated between the sideways fall and stance-loading for the majority of defect locations, suggesting that calculations based on the stance-loading condition are not predictive of the change in bone strength experienced in the sideways fall condition. While stiffness was significantly related to yield force (R2 > 0.82), overall force (R2 > 0.59), and resilience (R2 > 0.55), in both, the stance-loading and sideways fall conditions for most defect locations, stiffness was not significantly related to toughness. Therefore, structure-dependent measure such as stiffness may not fully explain the post-yield measures, which depend on material failure properties. The data showed that MRI-based models have the sensitivity to determine the effect of pathologic lesions on bone strength.
Keywords: Sideways Fall, Stance, Lesion Location, Proximal Femur, Strength, Stiffness
INTRODUCTION
A pathologic fracture has been defined as a fracture caused by the weakening of bone structure by a diseased or disordered condition, such as cancer, which can result in increased bone fragility and fracture with minimal forces applied, such as those forces and mechanical environment of daily activity [1]. Of the million new cases of cancer each year, 7% to 27% of patients are likely to experience a metastatic bone defect which can increase the risk of pathologic fracture [2]. In such patients, bone strength reductions caused by pathologic fractures have severe consequences on morbidity and quality of life.
Certain bone pathologies, such as cancer, may result in lesions applied to different parts of the bone [3]. These pathologies can be particularly dangerous in the femur, where high loads are placed during activities of daily movement. The femur, particularly the proximal end supports a significant amount of weight at the regions contacting the hip joint [4]. Femoral forces on the proximal femur range from 3.5 times body weight during the mid-stance phase of gait, to 7.7 times body weight for stair climbing [5, 6]. Additional osteolytic lesions can severely reduce bone strength, and thus, patient mobility which can contribute to increasing patient mortality [7]. Past studies have found that high-risk, osteolytic lesions produced in cadaveric proximal femurs may decrease bone strength up to 50% [8].
Depending on the size and location of the lesion, bone strength may be impacted differently based on load distribution [9, 10]. Understanding the relationship between bone strength and lesion location may aid in determination of risk of femoral fracture [11]. Long-held guidelines to determine high risk pathologic fractures include a defect 2.5 cm in dimension and (2) >50% cortical destruction as an indication for prophylactic stabilization. In vitro studies suggest that these current clinical guidelines of a 2.5-cm defect and 50% cortical destruction are associated with large errors in estimation of the load-bearing capacity of a bone [1]. Sixty to over ninety percent reductions in load-bearing capacity can be observed with the commonly cited 50% cortical involvement. This large variation in strength reduction, when combined with radiographic defect size measurement errors as large as 100% is the major reason clinical studies have failed to produce a consistent and objective radiographic guideline for predicting pathologic fracture [12]. While metastatic disease to bone is common in many types of cancers (renal, thyroid, breast), it is sometimes not clear if the patient would benefit from a surgical intervention compared to a non-surgical approach.
To predict the risk of pathologic fracture, Mirels developed a scoring system based on radiographic criteria (location (upper limb, lower limb, or trochanteric region), degree of cortical involvement (< 33.3%, 33.3% to 66.6%, and > 66.6%), nature of lesion (lytic, blastic, mixed)), and degree of pain (mild, moderate, functional) [13]. However, the Mirels criteria lacks specificity and does not account for other properties of bone that can influence its strength [14]. While dual-energy X-ray absorptiometry (DXA) has been used for predicting osteoporotic fracture, it has not been useful in the setting of pathologic fractures [15].. To better determine bone strength and calculate fracture risk, researchers and physicians have validated quantitative computed tomography (CT) in place of DXA imaging [16-20]. While there is evidence that CT is more accurate than the Mirels criteria, CT exposes the subject to increased ionizing radiation while also not providing microstructural bone information [21, 22]. Focusing on bone microstructure and lesion location in the proximal femur using high-resolution magnetic resonance imaging (MRI) and finite element analysis (FEA) [23-25], which does not expose patients to any ionizing radiation and obtains more data about bone microstructure, rather than bone macrostructure, may provide valuable information for clinical assessment of treatment and preventing pathologic fracture [26].
The primary goal of this study was to investigate how the site of bone pathology influences the reduction in bone strength at the proximal femur when trabecular and cortical bone microstructural information is incorporated using high-resolution MRI and FEA, which ultimately can provide a general model for longitudinal noninvasive patient monitoring and a potential means of future individualized bone strength profiling. The secondary goal of this study was to mimic and analyze the degree of influence that varying bone pathology sites have on the bone strength of patients during conditions of normal weight-bearing and traumatic impact. The third goal of this study was to determine the predictive value of stiffness, a simple linear calculative parameter to assess bone strength, to determine more nonlinear parameters such as bone resilience, yield force, ultimate force, and toughness.
2. MATERIALS AND METHODS
2.1. Study Population
This HIPAA compliant study was approved by the institutional review board and obtained written informed consent from all subjects. Twenty female subjects were recruited (mean age = 62.15 ± 7.78 years, age range= 48-77 years) from our institution with total hip dual-energy X-ray absorptiometry (DXA) results spanning osteopenia and osteoporosis (mean total hip BMD T-score = −2.025 ± 0.597, range= −1.2 to −2.7) and body mass index (BMI) of approximately normal (mean BMI= 21.72 ± 3.23) without a history of fragility fractures.
2.2. MRI Scanning and Image Pre-Processing
For all subjects, the nondominant hip was imaged with a 3-T whole-body MR imaging unit. In vivo high-resolution MRI images of the hip were obtained using a 26-element receive-coil set up, in which 18 elements from a body matrix coil anteriorly and eight elements from a spine coil posteriorly, with a coil wrapped and secured around the hip [23, 24, 27, 28]. All 20 subjects were scanned using a 3-Dimensional Fast Low-Angle Shot Sequence (FLASH), with scan parameters consisting of: a repetition time (TR) of 37ms, an echo time (TE) of 4.92ms, 0.234mm × 0.234mm, 60 coronal slices, a slice thickness of 1.5mm, a bandwidth of 200 Hz/pixel, a parallel acceleration (generalized auto calibrating partially parallel acquisition) factor of 2, and an acquisition time of 15 minutes 18 seconds [23].
Freely available Firevoxel software was used to segment all 3-dimensional image data sets for the periosteal border of the whole proximal femur and the acetabulum [24]. To account for partial volume effects and distinguish between red marrow and fatty marrow, which possess varying signal intensities, grayscale values were linearly scaled from 0% for minimum values of pure marrow and bone intensity to 100% for maximum values of pure marrow and bone intensity [23]. A bone volume fraction (BVF) map was then generated, consisting of a 3-D array representing the fractional occupancy of bone at each voxel location [23, 24].
2.3. Nonlinear FEA
Femur strength was estimated by constructing a microlevel finite element model of each femur from BVF maps. Each voxel in the bone volume fraction map was modeled as a hexahedral finite-element with dimensions equal to the three-dimensional voxel resolution and tissue modulus of elasticity set proportionally to greyscale intensity range. The 100% intensity was assigned a value of 15 GPa for bone tissue and Poisson’s ratio was set at 0.3 [24], there by modulating each finite element’s tissue properties based on local bone volume fraction. The first of the two mechanical behavior simulations performed in this study mimicked the force exerted by the acetabular contact region of the femoral head and the constraint of the greater trochanter (opposite the loading surface) during a “lateral” or “sideways” fall. The second condition mimicked the weight-bearing conditions on the femur similar to “standing” or “stance”. A kernel with heterogeneous isotropic tissue modulus, yield strength, and post-yield properties was used to describe a nonlinear stress-strain relationship in each voxel, and 3-dimensional strain (Figure 1) [24].
Figure 1:
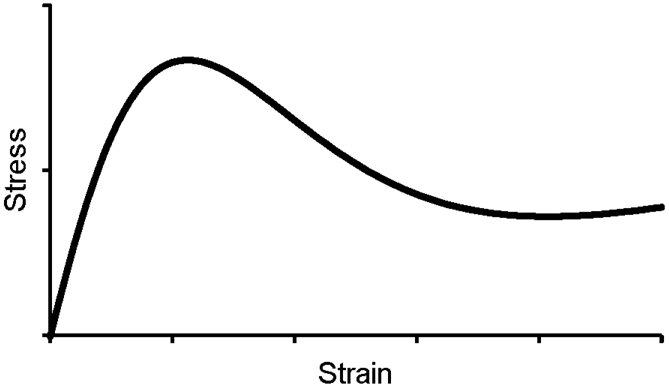
The element level nonlinear stress-strain relationship used for finite element modeling.
2.4. Pathology Simulation
After performing these simulations as a control, a 10-mm diameter cylindrical region in the trabecular bone compartment was artificially removed from the 3D-reconstructed femur model to mimic osteolytic bone lesions. The location of artificial bone removal (lesion) was varied to ten different sites, three in the femoral head (superior, middle, inferior), three in the femoral neck (superior, middle, inferior), three in the proximal diaphysis (lateral, middle, medial), and one in the greater trochanter (Figure 2). Independent finite element analyses were then performed for each subject for stiffness, yield force, ultimate force, resilience, and toughness in a standing and sideways-fall loading configuration and compared against the pathology-free bone simulations. The fitted load-deformation curve was used to determine the following: stiffness (slope of the linear-elastic region), yield point (i.e., the point at which plastic deformation begins to occur, defined using the 0.2% offset rule [24, 29, 30]), ultimate point (i.e., ‘fracture’ strength, the point at which the force is maximum), resilience (i.e., elastic work, defined as area under the curve from zero to the yield point), toughness (i.e., work-to-fracture, defined as the area under the curve from zero to the ultimate point). Three-dimensional strain maps provided visual representation of changes in strain distribution at a microstructure level due to simulated lesions. ‘Element’ strain was calculated as √(2 × U/E) where U is the strain-energy density and E is the tissue modulus at each element.
Figure 2:
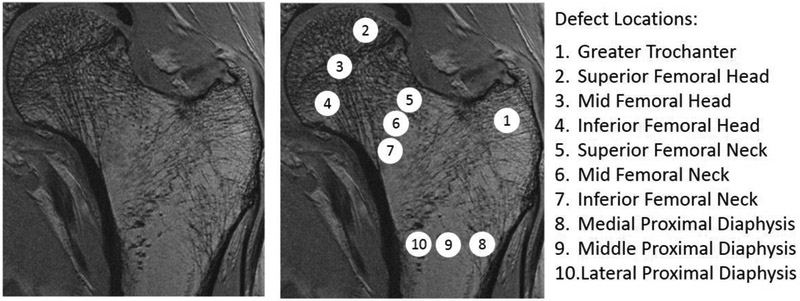
High-Resolution MRI and simulated defect locations
2.5. Statistical Analysis
After checking for normality of distributions using Shapiro-Wilk W test, paired t-tests were used to determine significance and to assess the effect of the two loading conditions before and after artificial lesion creation. The differences among the defect locations were tested for statistical significance using ANOVA. To assess the predictive value of the standing condition to the sideways fall condition, the significance of change in stiffness, resilience, yield force, ultimate force, and toughness before and after lesion creation was assessed between the standing condition and the sideways fall condition by using the correlation coefficient to calculate p value, where any p value less than 0.05 was considered to be significant in this study. To assess the predictive value of the stiffness parameter to bone resilience, yield force, ultimate force, and toughness, the significance of change in stiffness was assessed in comparison to the aforementioned parameters in both, the standing condition and the sideways fall condition by using the correlation coefficient to calculate p value.
3. RESULTS
3.1. Sideways Fall Loading Simulation
Under loading conditions similar to a sideways fall, a pathologic lesion in the inferior femoral head resulted in the greatest overall reduction in strength (12.21% ± 0.58 [p < 0.0001]) (Figure 3). There was a reduction of 11.28% ±.73 (p < 0.0001) in bone stiffness, 14.04% ± 1.12 (p < 0.0001) in yield force, 14.93% ± 1.56 (p < 0.0001) in resilience, and 8.11% ± 2.47 (p < 0.004) when the artificial pathology was placed in the inferior femoral head. Destruction within the greater trochanter showed a similar reduction of 6.43% ± 0.96 (p < 0.0001) in overall hip strength. Additionally, there were reductions of 9.12% ± 1.45 (p < 0.0001) in stiffness, 8.53% ± 1.08 (p < 0.0001) in yield force, and 8.61% ± 1.26 (p < 0.0001) in resilience in the hip. Overall, significant differences were seen in changes at different defect locations, with proximal diaphysis showing the least change and inferior femoral head showing the greatest change (p < 0.0001). Baseline DXA total hip BMD T-scores did not show any significant correlation with the changes in parameters due to lesions at any site.
Figure 3:
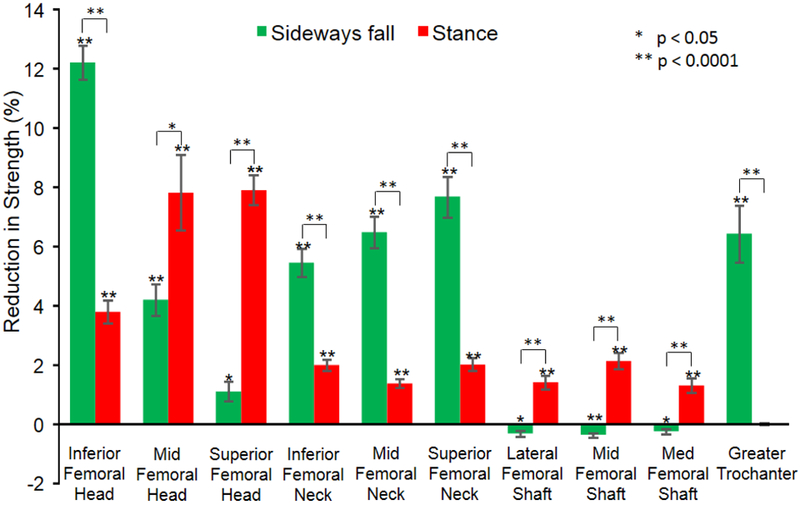
Reduction in strength due to defects at each location. The percent reduction in strength is calculated as (strength without lesion – strength with lesion) * 100 / (strength without lesion).
3.2. Stance Loading Simulation
The simulation of weight bearing that mimics standing in conjunction with the artificial bone pathology caused the most significant decrease in overall strength when the pathologic lesion was located in the mid and superior femoral head; −7.91% ± 0.5 (p < 0.0001) with a pathologic lesion located in the superior femoral head and −7.82% ± 1.3 (p < 0.0001) when located in the mid femoral head (Figure 4). Bone stiffness decreased by 7.29% ± 2 (p < 0.0001) when the pathology was in the femoral head and neck. Yield force decreased 8.39% ± 1.5 (p < 0.0001) with pathology located in the medial femoral head and 7.45% ± 0.4 (p < 0.0001) when in the superior femoral head. Resilience decreased by 9.22% ± 1.4 (p < 0.0001) with the destruction of the mid femoral head and by 8.21 ± 0.9 (p < 0.0001) when located in the superior femoral head. In addition, toughness decreased 13.83% ± 3.0 (p < 0.0002) with a pathologic lesion in the superior femoral head. Overall, significant differences were seen in changes at different defect locations, with greater trochanter showing the least change and middle and superior femoral head showing the greatest change (p < 0.0001). Baseline DXA total hip BMD T-scores did not show any significant correlation with the changes in parameters due to lesions at any site.
Figure 4:
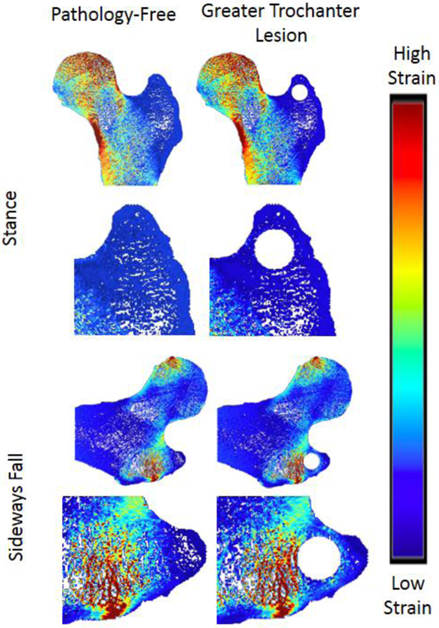
Strain Distribution of Greater Trochanter Lesion
3.3. Changes in Internal Strain Distribution due to Simulated Defects
In the greater trochanter, there were no visible differences in the strain distribution before and after the addition of defects in the stance loading condition, but there were slight noticeable increases in strain in the sideways fall loading condition (Figure 4). In the proximal diaphysis, visible increases in strain in comparison to the pathology-free simulation were noted in the mid proximal diaphysis, and medial proximal diaphysis lesion simulations for the stance loading conditions, but no differences were noted in the sideways fall condition (Figure 5). In the femoral neck, visible increases in strain in comparison to the pathology-free simulation were noted in the mid femoral neck, and superior femoral neck lesion simulations for the stance loading condition, and the superior femoral neck lesion simulation in the sideways fall loading condition (Figure 6). In the femoral head, visible increases in strain in comparison to the pathology-free simulation were noted in all three of the lesion simulation stance loading conditions, and in the inferior femoral head lesion simulation in the sideways fall loading condition (Figure 7).
Figure 5:
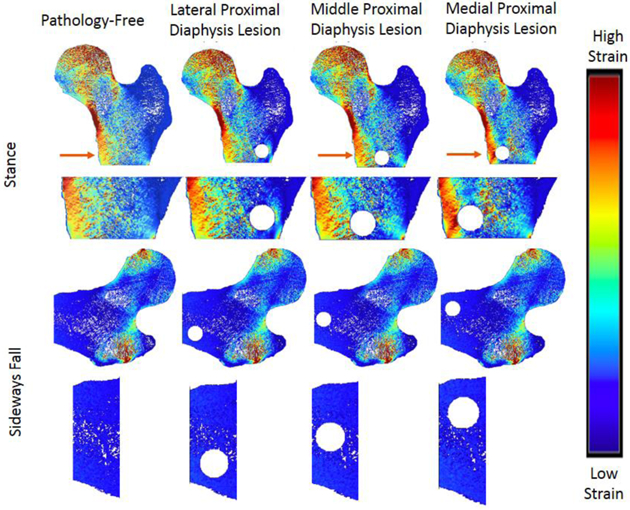
Strain Distribution of Proximal Diaphysis Lesions. Arrows point to visible differences in strain.
Figure 6:
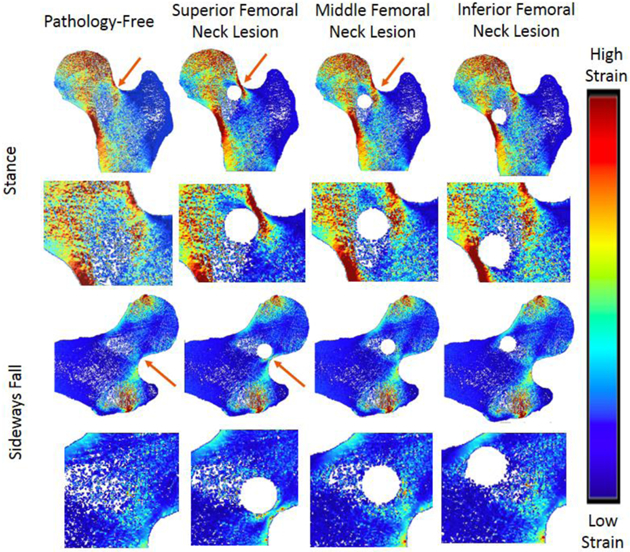
Strain Distribution of femoral neck lesions. Arrows point to visible differences in strain.
Figure 7:
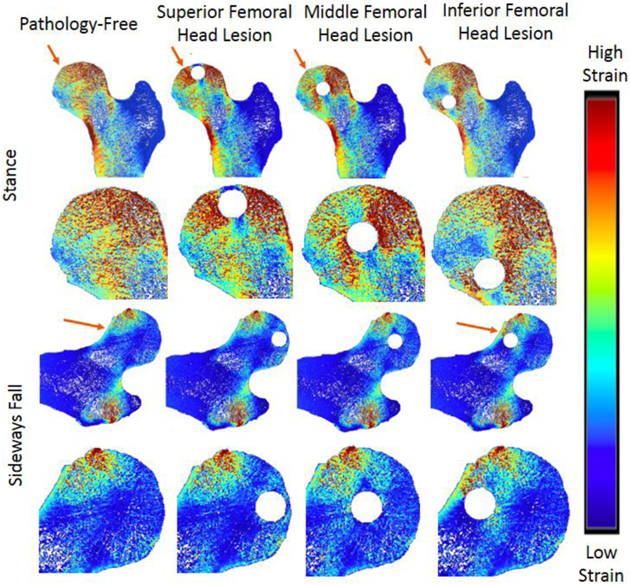
Strain Distribution of femoral head lesions. Arrows point to visible differences in strain.
3.4. Stiffness as a Predictor of Nonlinear Behavior in Stance Loading Simulation
Change in yield force was highly correlated to change in stiffness in the stance loading condition for all artificial lesion locations; in the greater trochanter (R2 = 0.82; p < 0.0001), superior femoral head (R2 = 0.91; p < 0.0001), middle femoral head (R2 = 0.99; p < 0.0001), inferior femoral head (R2 = 0.95; p < 0.0001), superior femoral neck (R2 = 0.96; p < 0.0001), middle femoral neck (R2 = 0.94; p < 0.0001), inferior femoral neck (R2 = 0.91; p < 0.0001), lateral proximal diaphysis (R2 = 0.99; p < 0.0001), middle proximal diaphysis (R2 = 0.98; p < 0.0001), and medial proximal diaphysis. (R2 = 0.98; p < 0.0001). (Table 1) Change in ultimate force was highly correlated to change in stiffness in the stance loading position for artificial lesions in the greater trochanter (R2 = 0.84; p < 0.0001), middle femoral head (R2 = 0.93; p < 0.0001), lateral proximal diaphysis (R2 = 0.87; p < 0.0001), middle proximal diaphysis (R2 = 0.86; p < 0.0001), and medial proximal diaphysis (R2 = 0.81; p < 0.0001) but had no significant trend for artificial lesions in the superior femoral head and inferior femoral head in the stance loading condition Change in resilience was highly correlated to change in stiffness for artificial lesions located in the greater trochanter (R2 = 0.97; p < 0.0001), middle femoral head (R2 = 0.80; p < 0.0001), inferior femoral head (R2 = 0.80; p < 0.0001), superior femoral neck (R2 = 1.00; p < 0.0001), middle femoral neck (R2 = 1.00; p < 0.0001), lateral proximal diaphysis (R2 = 1.00; p < 0.0001), and middle proximal diaphysis (R2 = 1.00; p < 0.0001). No significant trends were found for changes in resilience and change in stiffness for the superior femoral head in the stance loading condition. No significant trends were found for the association of stiffness to toughness in the stance loading condition for all pathologic lesion locations.
Table 1:
Change in Stiffness vs. Change in Parameter Correlations for Standing Position.
| R values | Stiffness Correlations Standing Position | |||
|---|---|---|---|---|
| Yield Force | Ultimate Force | Resilience | Toughness | |
| Greater Trochanter | 0.82**** | 0.84**** | 0.97**** | −0.11 |
| Superior Femoral Head | 0.91 **** | 0.45 | 0.43 | −0.04 |
| Middle Femoral Head | 0.99**** | 0.93**** | 0.80**** | 0.11 |
| Inferior Femoral Head | 0.95**** | 0.20 | 0.80**** | 0.20 |
| Superior Femoral Neck | 0.96**** | 0.70*** | 1.00**** | 0.37 |
| Middle Femoral Neck | 0.94**** | 0.70*** | 1.00**** | 0.26 |
| Inferior Femoral Neck | 0.91 **** | 0.59** | 0.63** | 0.42 |
| Lateral Proximal Diaphysis | 0.99**** | 0.87**** | 1.00**** | 0.12 |
| Middle Proximal Diaphysis | 0.98**** | 0.86**** | 1.00**** | 0.33 |
| Medial Proximal Diaphysis | 0.98**** | 0.81 **** | 0.55* | 0.26 |
3.5. Stiffness as a Predictor of Nonlinear Behavior in Sideways Fall Simulation
Change in yield force was highly correlated to change in stiffness in the stance loading condition for all artificial lesion locations in the sideways fall loading condition; in the greater trochanter (R2 = 0.96; p < 0.0001), in the superior femoral head (R2 = 0.96; p < 0.0001), in the middle femoral head (R2 = 0.87; p < 0.0001), in the inferior femoral head (R2 = 0.91; p < 0.0001), in the superior femoral neck (R2 = 0.90; p < 0.0001), in the middle femoral neck (R2 = 0.84; p < 0.0001), in the inferior femoral neck (R2 = 0.84; p < 0.0001), in the lateral proximal diaphysis (R2 = 0.87; p < 0.0001), in the middle proximal diaphysis (R2 = 0.93;p < 0.0001), and in the medial proximal diaphysis (R2 = 0.87;p < 0.0001). (Table 2) Change in ultimate force was highly correlated to change in stiffness in the sideways fall loading condition for artificial lesions in the greater trochanter (R2 = 0.84; p < 0.0001), middle femoral head (R2 = 0.88; p < 0.0001), middle proximal diaphysis (R2 = 0.80; p < 0.0001), and medial proximal diaphysis (R2 = 0.89; p < 0.0001) had no significant trend for artificial lesions in the superior femoral head in the sideways fall loading condition. Change in resilience was highly correlated to change in stiffness for artificial lesions located in the lateral proximal diaphysis (R2 = 0.99; p < 0.0001), middle proximal diaphysis (R2 = 0.98; p < 0.0001), and medial proximal diaphysis (R2 = 0.99; p < 0.0001). No significant trends were found for changes in resilience and change in stiffness for the superior femoral head in the sideways fall loading condition. No significant trends were found for the association of stiffness to toughness in the sideways fall loading condition for all pathologic lesion locations except for one slight correlation observed between change in toughness and change in stiffness in the sideways fall loading condition in artificial lesions created in the middle proximal diaphysis (R2 = 0.46; p < 0.05).
Table 2:
Change in Stiffness vs. Change in Parameter Correlations for Sideways Fall Position.
| R values | Stiffness Correlations Sideways Fall Position | |||
|---|---|---|---|---|
| Yield Force | Ultimate Force | Resilience | Toughness | |
| Greater Trochanter | 0.96**** | 0.84**** | 0.61** | 0.32 |
| Superior Femoral Head | 0.96**** | 0.20 | 0.44 | −0.21 |
| Middle Femoral Head | 0.87**** | 0.88**** | 0.46* | 0.45 |
| Inferior Femoral Head | 0.91 **** | 0.52* | 0.72*** | −0.21 |
| Superior Femoral Neck | 0.90**** | 0.77*** | 0.73*** | 0.18 |
| Middle Femoral Neck | 0.84**** | 0.77*** | 0.69** | 0.27 |
| Inferior Femoral Neck | 0.84**** | 0.70*** | 0.62** | 0.21 |
| Lateral Proximal Diaphysis | 0.87**** | 0.74*** | 0.99**** | 0.20 |
| Middle Proximal Diaphysis | 0.93**** | 0.80**** | 0.98**** | 0.46* |
| Medial Proximal Diaphysis | 0.87**** | 0.89**** | 0.99**** | 0.13 |
3.6. Association between Stance and Sideways Fall Measures
Changes in stiffness between the stance and sideways fall loading conditions were highly correlated for artificial lesions located in the superior femoral neck (R2 = 0.80; p < 0.0001), middle femoral neck (R2 = 0.92; p < 0.0001), and inferior femoral neck (R2 = 0.90; p < 0.0001). (Table 3) No significant trends were found for changes in stiffness between the stance and sideways fall loading conditions when artificial lesions were created in the greater trochanter, middle femoral head, lateral proximal diaphysis, middle proximal diaphysis, and medial proximal diaphysis. No significant trends were found for changes in yield force between the stance and sideways fall loading conditions when artificial lesions were created in the greater trochanter, superior femoral head, middle femoral head, inferior femoral head, superior femoral neck, inferior femoral neck, lateral proximal diaphysis, middle proximal diaphysis, and medial proximal diaphysis. No significant trends were found for changes in ultimate force between the stance and sideways fall loading conditions when artificial lesions were created in the greater trochanter, superior femoral head, middle femoral head, inferior femoral head, superior femoral neck, middle femoral neck, inferior femoral neck, middle proximal diaphysis, and medial proximal diaphysis. No significant trends were found for changes in resilience between the stance and sideways fall loading conditions when artificial lesions were created in the greater trochanter, superior femoral head, middle femoral head, inferior femoral neck, lateral proximal diaphysis, middle proximal diaphysis, and medial proximal diaphysis. No significant trends were found for changes in toughness between the stance and sideways fall loading conditions when artificial lesions were created in the greater trochanter, middle femoral head, inferior femoral head, superior femoral neck, middle femoral neck, inferior femoral neck, lateral proximal diaphysis, middle proximal diaphysis, and medial proximal diaphysis.
Table 3:
Standing position vs Sideways Fall Position Correlations
| R values | Standing vs Sideways Fall Correlations | ||||
|---|---|---|---|---|---|
| Stiffness | Yield Force |
Ultimate Force |
Resilience | Toughness | |
| Greater Trochanter | 0.08 | 0.01 | −0.21 | −0.15 | −0.05 |
| Superior Femoral Head | 0.67** | 0.33 | 0.23 | −0.20 | 0.49* |
| Middle Femoral Head | −0.05 | 0.30 | 0.25 | −0.24 | −0.37 |
| Inferior Femoral Head | −0.57* | −0.30 | 0.05 | −0.57* | −0.12 |
| Superior Femoral Neck | 0.80*** | 0.47 | 0.25 | 0.64** | −0.09 |
| Middle Femoral Neck | 0.92*** | 0.45* | 0.19 | 0.66** | 0.32 |
| Inferior Femoral Neck | 0.90*** | 0.36 | 0.10 | 0.34 | 0.28 |
| Lateral Proximal Diaphysis | 0.15 | 0.44 | 0.54* | 0.13 | −0.07 |
| Middle Proximal Diaphysis | 0.23 | 0.10 | 0.40 | 0.26 | 0.03 |
| Medial Proximal Diaphysis | 0.31 | 0.33 | 0.42 | −0.07 | −0.21 |
5. DISCUSSION
Our study showed that recently developed imaging and computational tools can effectively quantify the effect of various bone pathologies on hip quality and overall strength. This approach accounts for the contribution of an individual’s bone microstructure, especially in the case of osteolytic bone lesions in the proximal femur. Since osteolytic cancers create lesions in various parts of the bone, it is necessary to account for the effect of such lesions on the ability of bone to support the load of a patient under different load-bearing conditions and regions- specifically in high load-bearing regions, such as the proximal femoral head [31].
For most lesion locations, the bone strength reduction in a sideways fall is much greater than the bone strength reduction in the standing position for the same location [32]. The femoral-acetabular joint is primarily made to support load under stance loading conditions [5]. During falling conditions, especially the sideways fall condition, which has the greatest impact on increase in fracture risk [33], the femoral-acetabular joint cannot effectively serve to support patient load. When the proximal femur is weakened via same-sized osteolytic lesions in various locations, as in the case of bone pathologies such as cancer, bone strength is impacted differently based on the normal load distribution throughout the proximal femur for each scenario. Load distribution changes during standing versus sideways fall conditions [34]. Therefore, a lesion in one location of the femoral head may impact the ability of the bone to support a sideways fall more than it may impact the ability of the bone to support standing conditions. Thus, when considering pathologic bone strength reduction in patients to calculate fracture risk, bone strength reduction under both loading conditions must be considered [9].
Simply relying on data regarding osteolytic lesions in the standing configuration may not accurately predict the ability of the proximal femoral micro structure to support the weight of the patient under common falling conditions. Previous studies have determined the effect of osteolytic lesion location on bone strength reduction in the femoral neck [34] and subtrochanteric [35] regions, but our work bridges the gap between osteolytic bone lesion strength reduction and hip fracture risk calculation by expanding this study to include the effect of osteolytic lesions throughout the proximal femur under varying loading conditions.
Bone quality properties appear to decrease during defect simulation based on load distribution during those simulated loading conditions [9]. This may suggest that although small defects in the inferior or greater trochanter may not cause as great of a decrease in bone strength in the stance loading condition, they should still be of great concern to physicians upon determining fracture risk due to their impact on bone strength in the sideways fall loading condition.
Assessment of post-yield measures require substantial amount of computational power and memory compared to calculation of bone stiffness. Our data show that, using a simpler linear-elastic parameter, such as stiffness, to serve as a predictor of overall bone quality may have limited usefulness to clinicians who want to determine the fracture risk and further treatment options in patients with osteolytic bone lesions in the proximal femur. Similar to other studies, our study found that stiffness is highly correlated to the nonlinear parameter yield force and has no significant relationship to bone toughness in both, the stance and sideways fall loading conditions for all simulated defect locations [30, 36]. We also found that although stiffness is correlated with ultimate force and resilience in most artificial defect locations in both the stance loading and sideways fall conditions, except for defects in the inferior femoral head for the stance loading condition only, it seems to be a poor predictor for those parameters when a defect is placed in the superior femoral head. This may possibly suggest that due to the high load placed on the superior femoral head in both loading conditions, an osteolytic defect in the superior femoral head induces dramatic effects in the strength properties of the bone that cannot be explained simply by the linear parameter stiffness [9, 24].
Current clinical parameters for prediction of fracture risk are based on those measurements taken during a stance loading condition. However, the sideways fall condition can greatly contribute to increasing fracture risk in most patients. Our study calculated correlations between the changes in linear and nonlinear parameters in bone between the stance and sideways fall loading conditions for each simulated defect region. Strong correlations were found between the stance and sideways fall loading condition for all artificial lesions located in the femoral neck for the stiffness parameter and for artificial lesions located in the superior and middle femoral neck for resilience, suggesting that the stance loading condition may be a good predictor for few bone quality parameters in the sideways fall loading condition. Poor correlations were found for changes in all calculated bone strength parameters between stance and sideways fall loading condition when artificial lesions were simulated in the greater trochanter, middle femoral head, middle proximal diaphysis, and medial proximal diaphysis. This suggests that when clinically determining fracture risk, the sideways fall condition must also be considered prior to determination of fracture risk for most parameters, as data from the stance loading condition alone is not a strong predictor of pathologic fracture risk in the sideways fall condition [37].
Strain mapping data could aid physicians in their determination of whether or not surgery is a preferable option. This analysis could also help predict the most effective method for intervention, as different strategies, such as different lesion sizes, shapes, and configurations, can be simulated and compared. This simulation is especially notable for circumstances in which a lesion causes a significantly larger increase in strain in a non-stance loading condition, such as the sideways fall, and can revel potential dangers and limitations that would not be revealed through the traditional standing-only method.
Future studies may be required to address several limitations of this study. Our study simulated small, uniform osteolytic defects throughout varying locations in the proximal femur. These simulated defects were much smaller and more uniform than clinically observed defects. Future studies could also include the effect of changes in defect size or shape in both stance and sideways fall loading conditions to determine the extent of bone strength reduction. In reality, sideways fall conditions may not be as uniform as simulated in this study. Variations in weight, hip impact velocity, amount of support by other limbs during the fall, and height of fall may impact the load placed on the hip during fall, and thus change how the bone will respond to parameters such as stiffness, yield force, ultimate force, resilience, and toughness [38]. Furthermore, we did not specifically assess the location of fracture in our simulations, which might be useful to compare against clinical observation in future studies. While we observed significant correlations between stiffness and post-yield measures, such associations might be a result of the assumed constitutive model and material properties, which has to be confirmed using direct mechanical testing of cadaveric femurs in future studies. Finally, in the future, it will also be important to compare the performance of MRI (which incorporates microstructural information without administering ionizing radiation) with that of CT (which incorporates macrostructural information and BMD while administering ionizing radiation) for the prediction of pathologic fracture. It will also be important to compare MRI with the Mirels criteria for prediction of pathologic fracture. We note that in this study, none of the 10 lesions involved the cortex and only one involved the greater trochanter; therefore, the Mirels system would not been unable to account for the reductions in bone strength related to the majority of the pathologic lesions in this study.
In conclusion, osteolytic defects have the greatest impact on bone strength parameters based on the dependence of that region of the bone depending on the bone loading condition. Different bone loading conditions, such as stance and sideways fall loading conditions, must be independently assessed for fracture risk due to their low correlational values. To quantity this change in bone strength, linear parameters, such as stiffness, may serve as a good predictor of nonlinear parameters, such as yield force, ultimate force, and resilience, but not toughness. Further studies will be needed to assess the clinical utility of the MRI-based FEA and if this approach could improve current standard of care regarding whether or not to do prophylactic surgery when there is a bone lesion. Finally, it is important for future studies to compare the nonlinear constitutive model to other failure criteria, commonly used in CT-based FEA studies to predict the risk of pathological fracture.
HIGHLIGHTS.
MRI-based finite-element analysis (FEA) can detect the influence of bone lesions on bone strength measures
MRI-based FEA can identify sites of osteolysis that increase risk of fracture
Inferior femoral head lesions most impacted strength in sideways fall condition
Mid and superior femoral head lesions most impacted strength in stance-loading
Stance-loading measures are not correlated to sideways fall loading
Stiffness was correlated with yield force, ultimate force, and resilience
ACKNOWLEDGEMENTS:
This study was supported by the National Institutes of Health R01 AR 066008, R01 AR 070131 and R01 AR 068382.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- 1.Hipp JA, Springfield DS, and Hayes WC, Predicting pathologic fracture risk in the management of metastatic bone defects. Clin Orthop Relat Res, 1995(312): p. 120–35. [PubMed] [Google Scholar]
- 2.Hipp JA, et al. , Trabecular bone morphology from micro-magnetic resonance imaging. J Bone Miner Res, 1996. 11(2): p. 286–97. [DOI] [PubMed] [Google Scholar]
- 3.Toomey A and Friedman L, Mortality in cancer patients after a fall-related injury: The impact of cancer spread and type. Injury, 2014. 45(11): p. 1710–6. [DOI] [PubMed] [Google Scholar]
- 4.Crowninshield RD, et al. , A biomechanical investigation of the human hip. J Biomech, 197811(1-2): p. 75–85. [DOI] [PubMed] [Google Scholar]
- 5.Lotz JC, Cheal EJ, and Hayes WC, Stress distributions within the proximal femur during gait and falls: implications for osteoporotic fracture. Osteoporos Int, 1995. 5(4): p. 252–61. [DOI] [PubMed] [Google Scholar]
- 6.Patriarco AG, et al. , An evaluation of the approaches of optimization models in the prediction of muscle forces during human gait. J Biomech, 198114(8): p. 513–25. [DOI] [PubMed] [Google Scholar]
- 7.Zhou Y, et al. , The effect of pathological fractures on the prognosis of patients with osteosarcoma: a meta-analysis of 14 studies. Oncotarget, 2017. 8(42): p. 73037–73049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Alexander GE 3rd, et al. , Biomechanical model of a high risk impending pathologic fracture of the femur: lesion creation based on clinically implemented scoring systems. Clin Biomech (Bristol, Avon), 2013. 28(4): p. 408–14. [DOI] [PubMed] [Google Scholar]
- 9.Zani L, et al. , Strain distribution in the proximal Human femur during in vitro simulated sideways fall. J Biomech, 2015. 48(10): p. 2130–43. [DOI] [PubMed] [Google Scholar]
- 10.Caypinar B, et al. , Biomechanical determination of the relationship between femoral neck lesion size and the risk of pathological fracture. Hip International, 2016. 26(2): p. 158–163. [DOI] [PubMed] [Google Scholar]
- 11.Roodman GD, Mechanisms of bone metastasis. N Engl J Med, 2004. 350(16): p. 1655–64. [DOI] [PubMed] [Google Scholar]
- 12.Benca E, et al. , The insufficiencies of risk analysis of impending pathological fractures in patients with femoral metastases: A literature review. Bone Rep, 2016. 5: p. 51–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mirels H, Metastatic disease in long bones. A proposed scoring system for diagnosing impending pathologic fractures. Clin Orthop Relat Res, 1989(249): p. 256–64. [PubMed] [Google Scholar]
- 14.Jawad MU and Scully SP, In brief: classifications in brief: Mirels' classification: metastatic disease in long bones and impending pathologic fracture. Clin Orthop Relat Res, 2010. 468(10): p. 2825–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Macintyre NJ and Lorbergs AL, Imaging-Based Methods for Non-invasive Assessment of Bone Properties Influenced by Mechanical Loading. Physiother Can, 2012. 64(2): p. 202–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Link TM, Osteoporosis imaging: state of the art and advanced imaging. Radiology, 2012. 263(1): p. 3–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kawabata Y, et al. , The risk assessment of pathological fracture in the proximal femur using a CT-based finite element method. Journal of Orthopaedic Science, 2017. 22(5): p. 931–937. [DOI] [PubMed] [Google Scholar]
- 18.Yosibash Z, et al. , Predicting the stiffness and strength of human femurs with real metastatic tumors. Bone, 2014. 69: p. 180–90. [DOI] [PubMed] [Google Scholar]
- 19.Sternheim A, et al. , Pathological fracture risk assessment in patients with femoral metastases using CT-based finite element methods. A retrospective clinical study. Bone, 2018110: p. 215–220. [DOI] [PubMed] [Google Scholar]
- 20.Anez-Bustillos L, et al. , Finite element analysis and CT-based structural rigidity analysis to assess failure load in bones with simulated lytic defects. Bone, 2014. 58: p. 160–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Oei L, et al. , Quantitative imaging methods in osteoporosis. Quant Imaging Med Surg, 2016. 6(6): p. 680–698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Damron TA, et al. , CT-based Structural Rigidity Analysis Is More Accurate Than Mirels Scoring for Fracture Prediction in Metastatic Femoral Lesions. Clin Orthop Relat Res, 2016. 474(3): p. 643–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chang G, et al. , Measurement reproducibility of magnetic resonance imaging-based finite element analysis of proximal femur microarchitecture for in vivo assessment of bone strength. MAGMA, 2015. 28(4): p. 407–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rajapakse CS, et al. , Patient-specific Hip Fracture Strength Assessment with Microstructural MR Imaging-based Finite Element Modeling. Radiology, 2017. 283(3): p. 854–861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rajapakse CS, et al. , Accuracy of MRI-based finite element assessment of distal tibia compared to mechanical testing. Bone, 2018. 108: p. 71–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.de Bakker CMJ, et al. , Clinical Evaluation of Bone Strength and Fracture Risk. Curr Osteoporos Rep, 201715(1): p. 32–42. [DOI] [PubMed] [Google Scholar]
- 27.Chang G, et al. , Finite Element Analysis Applied to 3-T MR Imaging of Proximal Femur Microarchitecture: Lower Bone Strength in Patients with Fragility Fractures Compared with Control Subjects. Radiology, 2014. 272(2): p. 464–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chang G, et al. , Feasibility of three-dimensional MRI of proximal femur microarchitecture at 3 tesla using 26 receive elements without and with parallel imaging. J Magn Reson Imaging, 2014. 40(1): p. 229–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Niebur GL, et al. , High-resolution finite element models with tissue strength asymmetry accurately predict failure of trabecular bone. J Biomech, 2000. 33(12): p. 1575–83. [DOI] [PubMed] [Google Scholar]
- 30.Zhang N, et al. , Potential of in vivo MRI-based nonlinear finite-element analysis for the assessment of trabecular bone post-yield properties. Med Phys, 2013. 40(5): p. 052303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gnudi S, Sitta E, and Pignotti E, Prediction of incident hip fracture by femoral neck bone mineral density and neck-shaft angle: a 5-year longitudinal study in post-menopausal females. Br J Radiol, 2012. 85(1016): p. e467–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Robinovitch SN, Hayes WC, and McMahon TA, Prediction of femoral impact forces in falls on the hip. J Biomech Eng, 1991. 113(4): p. 366–74. [DOI] [PubMed] [Google Scholar]
- 33.Tanck E, et al. , Pathological fracture prediction in patients with metastatic lesions can be improved with quantitative computed tomography based computer models. Bone, 2009. 45(4): p. 777–83. [DOI] [PubMed] [Google Scholar]
- 34.Kaneko TS, Skinner HB, and Keyak JH, Lytic lesions in the femoral neck: Importance of location and evaluation of a novel minimally invasive repair technique. J Orthop Res, 2008. 26(8): p. 1127–32. [DOI] [PubMed] [Google Scholar]
- 35.Sivasundaram R, et al. , The biomechanical effect of proximal tumor defect location on femur pathological fractures. J Orthop Trauma, 2013. 27(8): p. e174–80. [DOI] [PubMed] [Google Scholar]
- 36.Miura M, et al. , Prediction of fracture load and stiffness of the proximal femur by CT-based specimen specific finite element analysis: cadaveric validation study. BMC Musculoskelet Disord, 2017. 18(1): p. 536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sarvi MN and Luo Y, Sideways fall-induced impact force and its effect on hip fracture risk: a review. Osteoporosis International, 2017. 28(10): p. 2759–2780. [DOI] [PubMed] [Google Scholar]
- 38.Majumder S, Roychowdhury A, and Pal S, Simulation of hip fracture in sideways fall using a 3D finite element model of pelvis–femur–soft tissue complex with simplified representation of whole body. Medical Engineering & Physics, 2007. 29(10): p. 1167–1178. [DOI] [PubMed] [Google Scholar]


