Pore condensation and freezing is responsible for ice formation below water saturation for porous particles

Significance

The formation of ice at relative humidity below 100% is assumed to proceed without the presence of liquid water. However, it has been shown that liquid water can exist well below water saturation in narrow cracks and pores. Here we show that the barrier for deposition nucleation of ice directly from the vapor is insurmountable in experiments; liquid water is involved in ice formation on porous particles, regardless of the ambient humidity. Thus, our results render deposition nucleation unlikely for the formation of ice clouds in the atmosphere.

Abstract

Ice nucleation in the atmosphere influences cloud properties, altering precipitation and the radiative balance, ultimately regulating Earth’s climate. An accepted ice nucleation pathway, known as deposition nucleation, assumes a direct transition of water from the vapor to the ice phase, without an intermediate liquid phase. However, studies have shown that nucleation occurs through a liquid phase in porous particles with narrow cracks or surface imperfections where the condensation of liquid below water saturation can occur, questioning the validity of deposition nucleation. We show that deposition nucleation cannot explain the strongly enhanced ice nucleation efficiency of porous compared with nonporous particles at temperatures below −40 °C and the absence of ice nucleation below water saturation at −35 °C. Using classical nucleation theory (CNT) and molecular dynamics simulations (MDS), we show that a network of closely spaced pores is necessary to overcome the barrier for macroscopic ice-crystal growth from narrow cylindrical pores. In the absence of pores, CNT predicts that the nucleation barrier is insurmountable, consistent with the absence of ice formation in MDS. Our results confirm that pore condensation and freezing (PCF), i.e., a mechanism of ice formation that proceeds via liquid water condensation in pores, is a dominant pathway for atmospheric ice nucleation below water saturation. We conclude that the ice nucleation activity of particles in the cirrus regime is determined by the porosity and wettability of pores. PCF represents a mechanism by which porous particles like dust could impact cloud radiative forcing and, thus, the climate via ice cloud formation.

Small volumes (∼10⁻¹¹ cm³) of pure water freeze at the homogeneous nucleation temperature (HNT, Fig. 1) of about −38 °C (e.g., ref. 1). Heterogeneous ice nucleation must be invoked to explain ice formation at higher temperatures. In heterogeneous nucleation, an interface provided by an ice nucleating particle reduces the nucleation barrier, allowing the phase transition from liquid, or vapor, to ice (2). Cirrus clouds, composed entirely of ice, play a pertinent role in regulating the amount of long-wave radiation being emitted to space, necessitating a detailed understanding of the mechanisms responsible for cirrus cloud formation (3, 4). In situ studies investigating upper-level cirrus clouds over North and Central America and the Pacific found that heterogeneous nucleation dominates over homogeneous nucleation, and the observed ice formation was mainly attributed to deposition nucleation (Fig. 1) on mineral dust particles (5). Based on such observations, laboratory-based parameterizations of deposition nucleation have been incorporated in global climate models to predict ice-crystal number concentrations (6, 7), which influence Earth’s radiative balance and ultimately future climate projections. However, laboratory experiments exposing atmospherically relevant dust particles to conditions below water saturation show a steep increase in the frozen particle fractions (i.e., activated fraction, AF) when the temperature falls below the HNT (8, 9), suggesting that the liquid phase is involved in the nucleation of ice (9). This dependence led to the hypothesis that ice formation attributed to deposition nucleation is actually pore condensation and freezing (PCF) (10) (Fig. 1). PCF is defined as the condensation of liquid water in pores, cracks, steps, or capillaries (hereafter referred to as “pores”) in humid air below water saturation by the inverse Kelvin effect (See SI Appendix, section 2.1), followed by homogeneous or heterogeneous freezing. Additionally, classical nucleation theory (CNT) predicts that ice embryos need to reach a critical size for macroscopic growth to occur. Thus, PCF is limited to the range of pore sizes large enough to accommodate a critical ice embryo, and narrow enough for condensation of liquid water to occur. Once pore ice is present, it has been proposed that ice can grow out of the pore as long as the ice-filled pore is large enough to accommodate the base of the critical embryo to nucleate ice from the vapor phase (11). The size of the pore required to sustain a nucleus that can grow directly from the vapor at atmospherically relevant conditions, however, is too large to permit condensation of water in the pore below water saturation (SI Appendix, sections 2.1 and 2.2), theoretically limiting the relevance of PCF. However, experiments investigating preactivation, or the ability of materials to nucleate ice more efficiently after being precooled below the HNT, found a dependence on the materials’ porosity and pore-size distribution (12, 13). This suggests that ice can form homogeneously in pores and subsequently trigger ice growth out of the porous material at warmer temperatures. Furthermore, recent studies have shown that organic (14, 15) and water (16) vapors crystallize via the liquid phase condensed in wedge-shaped pockets, suggesting a PCF mechanism being responsible. Regardless, the generally accepted mechanism for ice nucleation below water saturation is currently deposition nucleation. Here we provide further evidence of the PCF mechanism by comparing the ice nucleation ability of synthesized porous and nonporous particles composed of the same material, in combination with CNT and molecular dynamics simulations.

Fig. 1.

Scheme of the pathways for pore condensation and freezing (Upper Left), deposition nucleation (Lower Left), and homogeneous nucleation of pure water droplets (Right), followed by ice-crystal growth. The vertical dashed lines indicate ice saturation (Left) and water saturation (Right).

Results

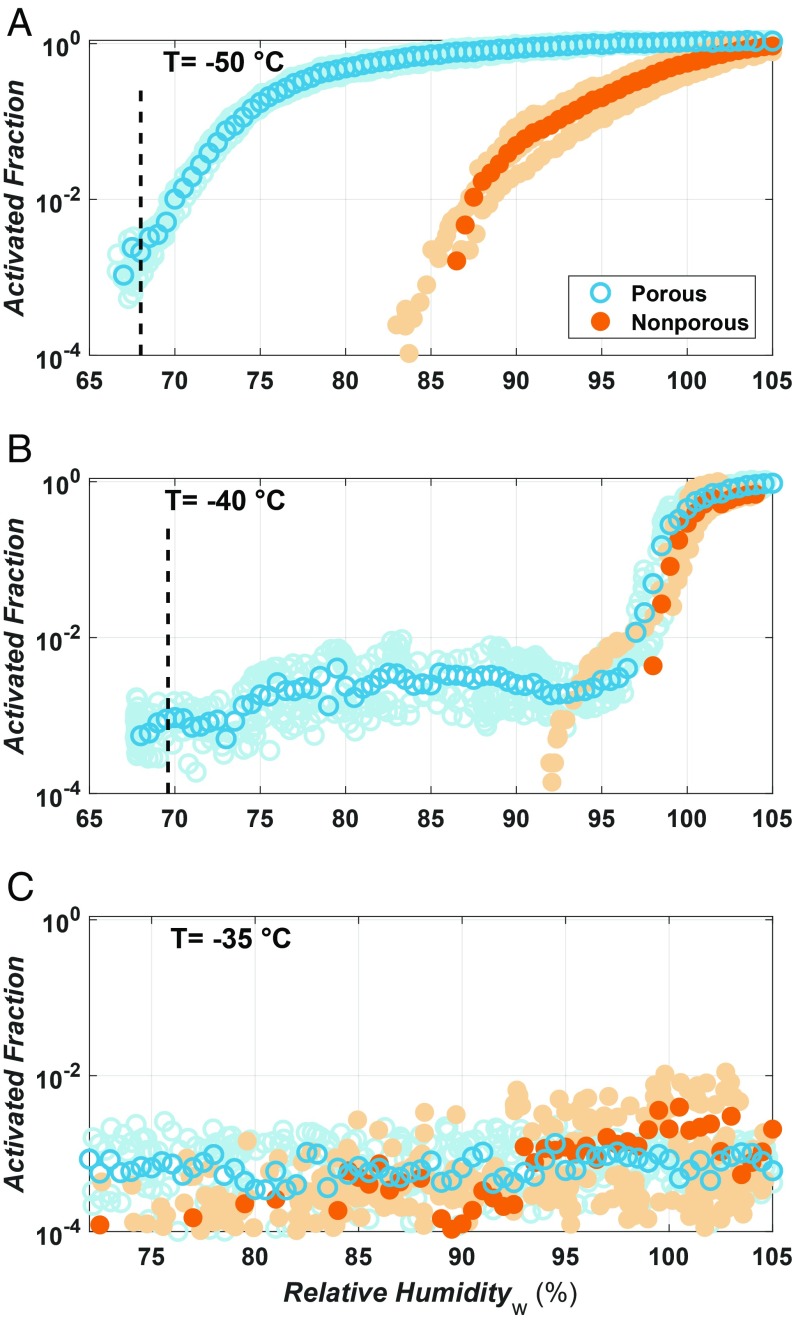
Advances in material sciences have allowed for the synthesis of porous silica (significant component of atmospheric mineral dust) with well-defined pore diameters and morphologies (17). This allowed testing the so-called deposition nucleation with silica particles that have uniformly distributed 3.8-nm pores, as well as with nonporous silica particles (Methods). The ice nucleation ability of silica particles exposed to varying temperatures and ice supersaturations in the Zurich Ice Nucleation Chamber (ZINC) (18), shows a strong dependence on the presence of pores (Fig. 2). In Fig. 2A, the silica samples with monodispersed pore diameters of 3.8 nm (open symbols) show an increase in activated fraction at a much lower relative humidity with respect to water (RH_w) than the nonporous samples (filled symbols) for −50 °C. Due to the inverse Kelvin effect, the 3.8-nm pores should be full at RH_w = 67% (dashed line in Fig. 2A; see SI Appendix, section 2.1), which corresponds to the RH_w at which the porous samples start to nucleate ice. It is important to note that this RH_w is also close to the required RH for ice crystals to grow to a detectable size in ZINC (SI Appendix, section 3.1). The observation of ice crystals at this RH_w, in combination with the ability of pores of this size to nucleate ice homogeneously (10, 19, 20), is strong evidence that the enhanced freezing ability of the porous samples is due to pore filling and subsequent homogeneous freezing of the pore water at or near the predicted RH_w for pore filling.

Fig. 2.

Activated fraction of 400-nm porous (3.8-nm pore diameter; blue open circles) and nonporous (orange filled circles) silica particles at −50 °C (A), −40 °C (B), and −35 °C (C) as a function of RH_w above ice saturation. The darker shaded symbols represent the mean of three experiments (lightly shaded symbols) averaged into 1% RH_w bins. The dashed vertical line indicates the RH_w required for a 3.8-nm pore to fill as predicted using the inverse Kelvin effect with a silica–water contact angle of 62°(SI Appendix). No vertical line appears at −35 °C (C) as the pores are expected to be full below ice saturation (71% RH_w). The points at low activated fractions which remain relatively constant are due to particles larger than 1 μm making it into the chamber (Methods).

The ability of the nonporous silica particles to nucleate ice below water saturation (Fig. 2A) might suggest the concurrent presence of a deposition nucleation mechanism. However, applying CNT to the porous and nonporous particles we find that the barrier for deposition nucleation on nonporous silica is 8,000 times the thermal energy, rendering the barrier for deposition nucleation insurmountable on the timescales relevant to clouds or laboratory experiments (SI Appendix, section 3.4). Furthermore, high-resolution scanning electron and atomic force microscopy images (SI Appendix, Fig. S1) reveal the presence of imperfections and steps on the surface of the nonporous silica particles, which provide pore-like features for PCF to occur, albeit at higher RH_w than the truly porous samples. Therefore, the observed freezing on the nonporous particles suggests a PCF mechanism occurring due to the presence of surface imperfections.

At −40 °C, freezing for both porous and nonporous samples shifts to water saturation (Fig. 2B). The absence of ice nucleation activity of the porous sample is explained by considering the nucleation rate for homogeneous freezing of water inside the pores as predicted by CNT. Using experimental homogeneous nucleation rate coefficients between 10¹⁰ and 10¹¹ cm^−3·s⁻¹ at −40 °C (21–23), CNT predicts that the particles would require a residence time of 3–4 orders of magnitude longer than that in ZINC (∼10 s) for pore water to freeze. Although our measurements show no evidence of ice nucleation below water saturation at −40 °C within the residence time of ZINC, aerosol residence times in regions of ice supersaturation in the atmosphere can exceed several hours, thus providing sufficient time for PCF. At temperatures above the HNT the porous and nonporous silica samples are unable to nucleate ice, even above water saturation (Fig. 2C). This further supports a freezing mechanism that involves homogeneous nucleation of liquid water in pores. It is important to note that although the freezing in the silica pores proceeds homogeneously, active sites in other sample types (24, 25) can trigger heterogeneous freezing and extend PCF to temperatures above the homogeneous freezing temperature, as previously reported (10) and shown on illite NX (Arginotec), a surrogate for natural mineral dust (SI Appendix, Figs. S3 and S4). Therefore, PCF can explain the ice nucleation on illite particles for humidity conditions that are subsaturated with respect to water. Indeed, PCF is not needed to explain ice nucleation within an immersed droplet.

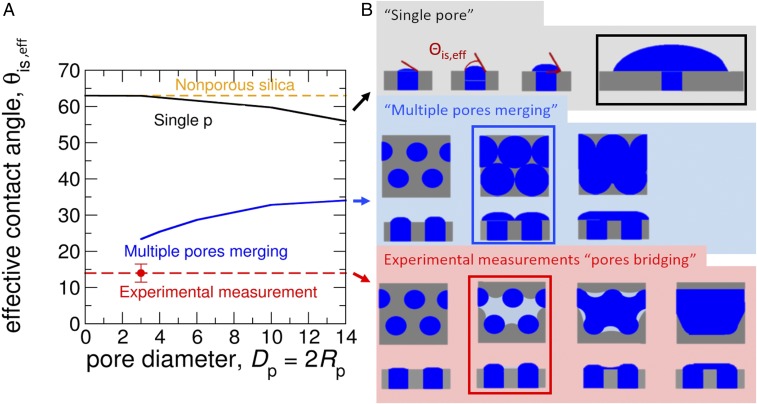
The freezing characteristics of the porous and nonporous silica particles at −50, −40, and −35 °C are in agreement with PCF. However, CNT predicts an energy barrier that limits the ability of ice to grow out of pores (SI Appendix) (11, 14). The homogeneous nucleation temperature of water in 3.8-nm pores is −43 °C (19). The contribution of freezing within the pore is, therefore, not the limiting barrier in our experiments at −45 and −50 °C. Rather, the second process of ice growing out of the pores into the unconfined vapor region is the step that limits PCF to yield bulk ice crystals. We therefore focus on investigating the ice growth out of ice-filled pores. To that end, we conducted grand canonical molecular dynamics simulations of vapor deposition with the monatomic water model (mW) (26, 27), which reproduces the structure and thermodynamics of melting and nucleation of ice in bulk, in pores, and on surfaces (20, 27–31). We expose three different models for silica surfaces to supersaturated mW water vapor: a nonporous slab, a porous slab with a single 3-nm ice-filled pore, and a model of the porous silica used in this study with a triangular array of 3-nm ice-filled pores separated by 1-nm-wide walls, same as in the porous silica particles used in the experiments (32–34; see Methods and SI Appendix, section 3.4). Ice was unable to form on the nonporous silica slab (Fig. 3A), and grew extremely slowly from the single ice-filled pore as a spherical cap that expands onto the silica surface with a constant contact angle until bulk ice forms (Fig. 3B and SI Appendix, section 3.4). However, ice grew rapidly out of the array of pores of the porous silica model surface, producing bulk ice (Fig. 3C). Using CNT with experimental properties of water, we calculated the effective contact angle between ice and the silica surface for nonporous silica, a single pore, and an array of pores as shown in Fig. 4A (SI Appendix, section 3.4). In the presence of an array of pores, bulk ice can either form through the merging of neighboring spherical ice caps (Fig. 4B) or from the bridging of growing ice caps due to capillary condensation of water and subsequent freezing of the water between them (Fig. 4B). The latter pathway has the lowest energy barrier (SI Appendix, Fig. S8) and thus a lower effective contact angle (Fig. 4A). We calculate the barriers (from which we derive the effective contact angle; see SI Appendix, section 3.4) along the minimum free-energy path for the nucleation and growth of ice out of the pore, accounting for the change in volume as the ice caps emerge from neighbor pores. We conclude that arrays of narrow, closely spaced pores are key for producing low ice nucleation barriers in porous silica. The narrow width of the pores is needed for capillary condensation and freezing, while the close spacing of the pores results in ice bridging that leads to fast nucleation out of the pores (Fig. 4 and SI Appendix, section 3.4). The area of the array of pores needs not be macroscopic, only larger than the size of the critical ice embryo with respect to the vapor. The molecular simulations and the theoretical analysis of nucleation pathways (SI Appendix, section 3.4) support that ice formation below water saturation proceeds through a PCF mechanism, which is boosted when pores are closely spaced. Furthermore, the lack of freezing in the molecular dynamics simulations on the nonporous silica slab, together with the insurmountable ice nucleation barriers determined from CNT (SI Appendix, section 3.4), indicates that ice nucleation cannot proceed via deposition nucleation. Instead, ice nucleation occurs via PCF below water saturation. We note that for pores with large openings, bridging ice growth out of narrowly spaced pores may not be necessary, as has been demonstrated for wedge-shaped pockets (16).

Fig. 3.

Configurations from grand canonical molecular dynamics simulations of ice growth from vapor starting from a (A) nonporous silica slab, (B) single 3-nm-diameter ice-filled pore, and (C) multiple 3-nm-diameter ice-filled pores separated by 1-nm walls. The vapor uptake is performed at −81 °C with RH_i = 250%. Water in ice is shown with blue sticks, disordered water with red spheres, and silica of the pore with gray balls. We note that the molecular model of this study reproduces the experimental size dependence of the melting temperature of ice in pores, the Gibbs–Thomson coefficient for water, and the width of the premelted layer in contact with the silica pore (20, 28, 29). Recent experiments (59) quantitatively confirm the simulations prediction (30) of the fraction of water that is premelted in silica pores as a function of temperature. We have demonstrated, using thermodynamics and nucleation theory, that surfaces that induce premelting (as is the case of silica) cannot heterogeneously nucleate ice from the liquid phase (31).

Fig. 4.

Effective contact angle between ice and the silica surface as a function of pore size for nonporous silica (yellow), a single pore (black), multiple pores merging (blue), and multiple pores bridging (red) is shown in A. The silica walls between the pores are taken to be 1 nm wide, irrespective of pore diameter. SI Appendix, Fig. S8 presents the same kinetic information in terms of the ratio of the barriers for heterogeneous nucleation for each mechanism and the homogeneous nucleation pathway. (B) Sketches for ice growth for different scenarios. (Top) For a single pore, increase of contact angle at constant radius followed by increase of radius at constant contact angle, the black square marks the critical size. (Middle) For multiple pores merging scenario, the critical size is reached when the ice nuclei start to merge (indicated by blue square). (Bottom) For multiple pores bridging, condensation of liquid water between emerging ice nuclei is followed by crystallization of the liquid. Growth continues by freezing of condensed liquid water. Silica is pictured in gray, ice in blue, and liquid water in light blue.

In view of these results, we investigated the susceptibility of atmospheric mineral dust to PCF. The contribution of various desert dusts to ice nucleation via the PCF mechanism depends on their transported airborne fraction together with their pore-size distribution (SI Appendix, section 1.1). To assess the relevance of PCF for irregular pore structures occurring in natural mineral dust particles, we chose the clay mineral illite due to its important contribution to airborne dust (35) (44%) and its established porosity in the range from 2 to 5 nm (36–38).

Ice nucleation experiments in ZINC with submicrometer illite NX particles are very similar to that of the porous silica with 3.8-nm pores (SI Appendix, Fig. S2) and yield similar ice nucleation results (SI Appendix, Fig. S2). This is true even over a wide range of particle sizes (SI Appendix, Fig. S3), suggesting that even the smallest illite particles exhibit narrow pore structures and confirming the suitability of PCF to predict ice nucleation on atmospherically relevant dust types. Other clay minerals have typical pore sizes that are narrower (montmorillonite) or wider (kaolinite) than illite (36, 38), also making them susceptible to PCF. Indeed, ice nucleation on kaolinite particles has been found to occur at the particle edges with a high density of trenches (25).

Based on the fraction of transported clay mineral particles and their porosity, we present a parameterization (SI Appendix, section 1.1 and Fig. S2) for climate models that can utilize an AF as a function of humidity (6, 39, 40), by incorporating experimental results from ZINC on illite NX and nonporous silica (SI Appendix, Fig. S2). This parameterization discriminates between accumulation and coarse-mode particles. The parameterization of accumulation mode particles is based on the AFs observed for illite NX, assuming that 60% of the transported accumulation mode particles are clays (35, 41), containing pore-size distributions similar to the sample used in this study and 40% of the particles are nonporous. All coarse-mode particles are assumed to exhibit pores and, therefore, nucleate ice below water saturation. Unlike conventional deposition nucleation parameterizations, which are temperature dependent (6, 42), the PCF-based parameterization applies to all temperatures below −38 °C. This is consistent with results from previous experiments on natural dusts that have shown little dependence of the onset RH_w required for ice nucleation at temperatures below −38 °C (8, 9, 43), supporting the occurrence of PCF rather than deposition nucleation. In the atmosphere, airborne dust particles may acquire a coating with atmospheric aging, potentially leading to a deactivation of pores when they are completely filled (13). However, in our parameterization we assume PCF does not depend on aging time, since single-particle mass spectrometry of ice crystal residuals from cirrus clouds found dust particles to be predominantly uncoated (5, 44, 45).

Our findings suggest that at conditions subsaturated with respect to liquid water, the ice nucleating ability of the most common components of airborne mineral dust is determined by their porosity. This, in combination with experiments with synthetic particles, molecular dynamics simulations, and nucleation theory, confirms that PCF should be considered as an important mechanism for ice formation below water saturation. Due to the large radiative impact of cirrus clouds on climate (3, 4), conventional ice formation parameterizations, which rely on deposition nucleation, should be replaced with schemes that incorporate PCF in cirrus cloud models (6, 7). In the presence of heterogeneous ice-nucleating pore surfaces, the PCF mechanism should remain active above the HNT for humidity conditions subsaturated with respect to water, making deposition nucleation less likely at warmer temperatures as well. We anticipate that other atmospherically relevant porous particles nucleate ice via the PCF mechanism (46), potentially further increasing the contribution of PCF to anthropogenic climate change.

Methods

Particle Synthesis.

The porous silica particles (MCM-41) were synthesized adapting the procedure in ref. 47 by dissolving 1.74 g cetyltrimethylammonium bromide (C₁₆TMABr; 99%, Acros Organics) in a mixture of 122 mL aqueous ammonia (28%, Aldrich), 300 mL distilled water, and 500 mL ethanol (99.8%, Aldrich). The mixture was stirred for 15 min before 4.5 mL of tetraethyl orthosilicate (TEOS, 99%; Aldrich) were added within 3 s. After 2 h of reaction time, the silica particles were extracted from the solution using a filter (Grade 939, Sartorious) and subsequently dried at 80 °C. The particles were then ground in methanol (99.9%, Aldrich) and dried again before being calcined at 550 °C (4.5-h ramp to 550 °C) for 12 h. Pores larger than 3.0 nm were obtained by aging the suspended silica particles in distilled water for 24 h at 120 °C before grinding in methanol. Verification of pore size was obtained using nitrogen adsorption and desorption isotherms combined with nonlinear density-functional theory (SI Appendix, Fig. S5).

Nonporous silica particles were synthesized applying the procedure described in ref. 48 with adjusted ratios of ammonia, distilled water, and ethanol in the initial solution to achieve the desired particle diameters. Namely, 44 mL of TEOS were added to a vigorously stirred solution composed of 66 mL ammonia (28%, Aldrich), 133 mL distilled water, and 217 mL ethanol (99.8%, Aldrich). After a 4-h reaction time, the particles were extracted and washed twice with water by centrifugation (1,864 × g, Hettich Rotofix 32). The drying and calcination procedure was the same as for the porous particles.

Particle Characterization.

Particle-size distributions were created by measuring at least 100 particle diameters with ImageJ on SEM (Quanta, FEG 250; see SI Appendix, Fig. S1) images. The nitrogen adsorption and desorption isotherms at −196 °C (77 K) were measured using a Quantachrome Nova 3000e system. The sample was pretreated at 80 °C overnight in air and the pore-size distributions were obtained by nonlinear density-functional theory (NLDFT) calculations. NLDFT provides an accurate method to determine pore-size distributions (49) using theoretical isotherms to predict the pore-size distribution through a comparison with previous experimental data (50). As can be seen in SI Appendix, Fig. S5, a very narrow pore-size distribution is achieved with the synthesis method used in this study. The total surface area was obtained using the standard Brunauer–Emmett–Teller method for adsorption data in a relative pressure range from 0.05 to 0.30. The surface roughness of the nonporous particles was measured with atomic force microscopy (AFM; NT-MDT, SOLVER PRO). Before sampling in the AFM, dry nonporous particles were suspended in a hydrochloric acid suspension [pH = 2–3, ω(SiO₂) = 1%] and then incubated on a glass slide overnight. The microscope was run in the noncontact mode and the particle curvature was fitted with a second-order polynomial to obtain a flat surface (SI Appendix, Fig. S1). Transmission electron microscopy [JEOL-JEM 1400 run with SlightX Viewer (JEOL)] was performed on the porous particles to ensure the spherical nature of the porous particles (SI Appendix, Fig. S1). The illite NX particles were not imaged in this study but have previously been examined in refs. 51 and 52.

Ice Nucleation Experiments.

The particles used in this study were aerosolized using a rotating brush generator (Palas, RBG 1000) and then passed through a cyclone with a 1-μm cut size (URG-2000–30EHB) before entering a 2.7-m³ stainless-steel tank (53). The particles were then size selected to produce a quasi-monodisperse aerosol of 400 nm using a polonium source neutralizer and a differential mobility analyzer (Long DMA, model 3081; TSI Inc.) column before entering the continuous flow diffusion chamber, ZINC (18). However, due to multiple charging in the neutralizer, aggregates of particles larger than 1 μm can pass through the DMA and enter ZINC where they are misidentified as ice (Fig. 2). The porous particles were observed to have a higher fraction of aggregates than the nonporous particles and this explains the difference in the AF curves in Fig. 2 B and C before an increase in AF is observed. The size distribution of size-selected aerosols is presented in SI Appendix, Fig. S5. The secondary peaks at 200 and 300 nm are due to 400-nm particles being multiply charged. Further evidence that the peaks at these sizes are artifacts and not representative of the samples can be seen in SI Appendix, Fig. S1D, displaying an SEM image presenting the uniform size of the silica particles. In ZINC, the aerosol particles are layered between two-particle free-sheath flows of 4.5 L min⁻¹ each on either side of the 1 L min⁻¹ aerosol layer for a total flow rate of 10 L min⁻¹ (ref. 18). With a flow rate of 10 L min⁻¹, the residence time in ZINC is ∼10 s but varies with increasing ice supersaturation and temperature due to buoyancy effects in the chamber (18). To determine the ice nucleating ability of the samples tested in this study, particles were exposed to increasing RH_i at a rate of 2% per minute for a selected temperature. The RH_i where ice begins to form is determined by distinguishing larger ice crystals (1 μm) from the smaller (400 nm) unactivated particles by an optical particle counter (OPC, Lighthouse, Remote 5104) at the bottom of the chamber. The activated fraction of the aerosol was calculated as the ratio of ice crystals (i.e., particles larger than 1 μm) detected by the OPC at the bottom of the chamber to the total number of aerosols entering the chamber determined by a water-based condensation particle counter (model 3787, TSI Inc.).

Molecular Simulations of Ice Growth out of Nanopores Under Controlled Supersaturation.

To study the growth of ice on nonporous amorphous silica and porous silica we run molecular dynamics simulations in the grand canonical (μVT) ensemble (GCMD) (54), coded into the MDS software LAMMPS (55). The dimensions of the periodic simulation cells are 8 nm × 8 nm × 10 nm, containing a 5-nm-wide silica-like slab with either (i) no pores, (ii) a single pore of 3-nm diameter, or (iii) a triangular array of 3-nm-diameter pores separated by 1-nm silica walls. The latter corresponds to the arrangement of pores in the porous silica used in this work (32–34). The pores in (ii) and (iii) are filled with hexagonal ice exposing the primary prismatic face to vapor. Water is represented with the mW model (26). We consider two sets of parameters from ref. (54) for the interaction between the silica-like (s) walls and water (w): (i) a more hydrophilic silica (contact angle with water θ = 0°), with a characteristic interaction energy of ε_ws = 6.19 kcal mol⁻¹, a characteristic interaction size is σ_ws = 0.2392 nm, and a measure of the tetrahedrality of the potential of λ = 23.15 which at 25 °C reproduces (54) the experimental pressure of capillary condensation of pores in silica (56), and (ii) a less hydrophilic surface (contact angle with water θ = 64°), which at 25 °C has a pressure of capillary condensation that is 6.7 times higher than in the experiment, is modeled with ε_ws = 0.45 kcal mol⁻¹, σ_ws = 0.356 nm, and λ = 0 (54). We consider the first set to be more representative of actual silica.

We evolve the GCMD simulations at controlled supersaturation with respect to ice S_i = 2.5 and 3.0 with respect to the vapor pressure of a slab of ice at −81 °C, the temperature of maximum crystallization rate for mW water in the 3-nm-wide pore (20). Previous studies have shown that the mW water model reproduces the experimental supersaturations at a given temperature (54, 57).

The equations of motion are integrated with the Velocity Verlet algorithm with a time step of 5 fs. Temperature is controlled by Nosé–Hoover thermostat with a relaxation time constant of 0.5 ps. A number of attempts to insert or delete molecules are realized every time step to control the chemical potential of the system, and this relation is called GC/MD ratio. In this work we use a ratio of 20, which has been shown to give accurate supersaturations for mW water (54). We run the GCMD simulations at each S_i for about 200 ns. Ice is identified with the CHILL+ algorithm (58).