Effect of deforestation on access to clean drinking water

Significance

In the existing literature on forest science and hydrology, the consensus is that deforestation increases water yield. In this study, instead of focusing on water yield, we directly examine the effect of deforestation on households’ access to clean drinking water in Malawi while controlling various other factors. Our empirical results show that a 1.0-percentage-point increase in deforestation decreases access to clean drinking water by 0.93 percentage points. With this estimated impact, deforestation in the last decade in Malawi (14%) has had the same magnitude of effect on access to clean drinking water as that of a 9% decrease in rainfall. This suggests that the effect of deforestation on access to clean drinking water is not trivial.

Abstract

Using satellite data on deforestation and weather in Malawi and linking those datasets with household survey datasets, we estimate the causal effect of deforestation on access to clean drinking water. In the existing literature on forest science and hydrology, the consensus is that deforestation increases water yield. In this study, we directly examine the causal effect of deforestation on households’ access to clean drinking water. Results of the two-stage least-squares (2SLS) with cluster and time fixed-effect estimations illustrate strong empirical evidence that deforestation decreases access to clean drinking water. Falsification tests show that the possibility of our instrumental variable picking up an unobserved time trend is very unlikely. We find that a 1.0-percentage-point increase in deforestation decreases access to clean drinking water by 0.93 percentage points. With this estimated impact, deforestation in the last decade in Malawi (14%) has had the same magnitude of effect on access to clean drinking water as that of a 9% decrease in rainfall.

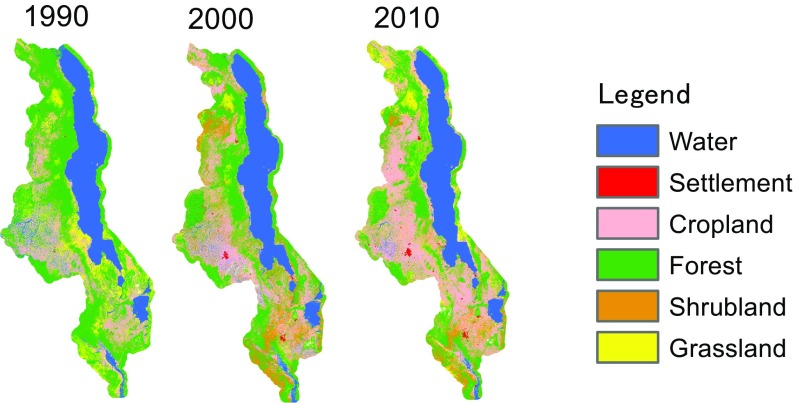
Sub-Saharan Africa has experienced rapid deforestation of about 3.4 million ha/y between 2000 and 2010 (1). Malawi has the highest deforestation rate in sub-Saharan Africa. In 2016, the Malawian government started to deploy military soldiers to combat illegal tree cutting. The government of Malawi estimated that the annual rate of deforestation in Malawi is 1.0–2.8% (2), and our estimation shows that from 1990 to 2010, the ratio of forest area decreased from 51% to 33% (Fig. 1 and SI Appendix, Table S3).

Fig. 1.

Deforestation of Malawi based on satellite images during 1990–2010.

Such deforestation can affect the welfare of people in several dimensions. Recently, there has been increasing international interest in the concept that deforestation has a direct negative impact on access to clean drinking water. In the 2030 Agenda of Sustainable Development Goals (SDGs), the topic “forests and water” gained more prominence in the political agenda (3). Protection and restoration of forests were included among the targets required to achieve the United Nations Sustainable Development Goals (SDG 6: Clean Water and Sanitation). SDG 15 explicitly indicates the value of forests with reference to the attainment of clean drinking water. In rural areas of Malawi, where 85% of the households are located, only 11% had access to community- or individual-level piped water, and 35% used unprotected wells or stream water as a source of drinking water. Thus, the SDGs’ agenda of protection and reforestation of forest area for access to clean drinking water has an important implication for policymakers.

On the other hand, literature on the effect of deforestation on water in forest science and hydrology is contrary to the general perception (4). Reviewing 94 studies, Bosch and Hewlett (5) summarize that an increase in forest area decreases the quantity of water in the streamflow. Reviewing 137 cases, Andréassian (6) summarizes that deforestation results in an increase in water yield, and reforestation results in a decrease. Reviewing 308 study cases, Filoso et al. (7) summarize that reforestation decreases the total annual water yield in 80% of the cases. These counterintuitive results of deforestation increasing the annual water yield are explained in the literature by the fact that trees themselves consume water, which is evaporated in the air, resulting in a decrease in the streamflow.

However, an increase in the quantity of water in the streamflow is not equal to the increased availability of water for human consumption. Deforestation decreases soil infiltration of water (7) and increases soil erosion (8, 9). A lower level of soil infiltration and a higher level of soil erosion cause higher flux of sediment and a higher level of turbidity. This results in lower water quality (10–14) and an increase in the cost of drinking-water treatment (15–17), which imposes a serious constraint on the installation and maintenance of a water system for local communities in low-income countries such as Malawi. Thus, whether or not deforestation decreases access to clean drinking water is an open question.

Given the potential importance of the effect of deforestation on access to clean drinking water as well as the lack of studies on this topic, in this study, we directly examine the causal effect of deforestation on access to clean drinking water (such as water from piped water) in lieu of less clean water (such as water from unprotected wells and unprotected streams) in the rural areas of Malawi from 2000 to 2010, using satellite images, microsurvey data, population data, and weather data.

We believe that we contribute to the previous literature in two aspects. First, this study directly examines the effect of deforestation on households’ access to clean drinking water in lieu of less clean water. Given the importance of access to clean drinking water in improving living standards in developing countries, our study has first-order policy importance. Second, our study analyzes the causal effect of deforestation on access to clean drinking water.

Our paper is related to several other studies. First, a large body of literature documents several potential sources of deforestation in developing countries, including Malawi, such as the expansion of cropland; food and land shortages, which are highly associated with a high population growth rate; fuelwood dependency; and weak tenure security of forestland (18–22). Second, a growing body of recent economics literature has started to analyze the environment’s effect on health in developing countries (23–26). Our study indicates a possible pathway from deforestation to health outcomes.

Results

Main Results.

Table 1 describes various sources of drinking water in Malawi’s rural areas where 85% of the population lives. SI Appendix, Background explains how the water system is maintained in these areas. In our satellite dataset, the ratio of forest area decreased from 39% to 33.4% or by 14.3% (= 5.6/39) at the national level (SI Appendix, Table S3).

Table 1.

Share of each rural population’s source of drinking water in Malawi

Water source	1998, %	2008, %
Clean drinking water
Piped inside dwelling unit	0.62	0.67
Piped outside dwelling unit	2.91	1.54
Communal stand pipe	8.08	6.69
Protected well	11.89	6.39
Borehole	29.71	53.94
Spring	1.29	0.59
Unsafe drinking water
Unprotected well	28.69	20.21
Stream/river	14.86	7.85
Pond/lake/dam	1.70	0.79
Others	0.24	1.32
Total	100.00	100.00

Data from refs. 34 and 35; calculated by the authors.

SI Appendix, Table S4 shows the summary statistics of the main variables used in our analysis. The dataset indicates that 38% of households used unsafe water as their source of drinking water in 2000. In 2010, this percentage decreased to 17%. At clusters that are used for the analysis, the ratio of forest area decreased from 27.7% in 2000 to 22.2% in 2010. SI Appendix, Fig. S2 shows a histogram of changes in the ratio of forest area from 2000 to 2010. Although the mean of changes in the ratio of forest area is just 5.5 percentage points, there is a huge variation in the changes in this ratio.

Table 2 presents the results of our two-stage least-squares (2SLS) estimation with the cluster and time fixed effects. Top and middle sections in Table 2 show the first- and second-stage estimation results, respectively. Our instrumental variable is the latitude $\times$ time dummy. Bottom section lists the control variables that apply to both the first- and second-stage estimations. All columns include the cluster fixed effect, time fixed effect, log of rainfall, (cluster-level) ratio of forest area in the 1990 $\times$ time dummy, and cluster-level average of the floor material dummy in the 2000 $\times$ time dummy as control variables. Bottom section lists other control variables that apply to both first- and second-stage estimations. Temperature is the temperature in July and November. Demographic characteristics include the size of each household, year of schooling, and gender of the head of the household. Household wealth includes information on the floor material and bicycle and radio ownership.

Table 2.

Effect of the ratio of forest area (7.5-km radius) on access to clean drinking water (two-stage least-square estimation)

Regression stage	1	2	3	4
First-stage regression
Dependent variable	Ratio of forest area
Latitude $\times$ time dummy	0.0297*** (0.00441)	0.0305*** (0.00445)	0.0305*** (0.00444)	0.0305*** (0.00444)
Log of rainfall	−0.0987** (0.0421)	−0.0919** (0.0419)	−0.0922** (0.0419)	−âĹŠ0.0925** (0.0418)
Kleibergen–Paap	45.45	46.95	47.16	47.23
$R^2$	0.948	0.949	0.949	0.949
Second-stage regression
Dependent variable	Clean drinking water dummy
Ratio of forest area	1.063** (0.494)	0.959** (0.465)	0.922** (0.455)	0.932** (0.453)
Log of rainfall	0.610*** (0.169)	0.569*** (0.163)	0.577*** (0.160)	0.566*** (0.159)
$R^2$	0.252	0.256	0.263	0.266
Control variables
Log of population		Yes	Yes	Yes
Temperature		Yes	Yes	Yes
Demographic characteristics			Yes	Yes
Household wealth				Yes
N	9,682	9,682	9,682	9,682

The clustering robust standard errors are in parentheses, assuming that the error terms are correlated within each cluster × year cell. The endogenous variable is the ratio of forest area and is instrumented by the latitude × time dummy. Top and middle sections display the results of the first- and second-stage regressions, respectively. All columns in top and middle sections include the cluster fixed effect, time fixed effect, log of rainfall, and cluster-level initial values×time dummy as control variables. Bottom section displays the specification of additional control variables. * indicates significant at 10%; ** indicates significant at 5%; *** indicates significant at 1%.

The Kleibergen–Paap rank in Table 2 indicates the Kleibergen–Paap rank Wald statistics, and it examines whether our instrumental variable is weak. The Kleibergen–Paap rank Wald statistics show that our instrumental variable is not weak even after the inclusion of many covariates as well as cluster-level initial values $\times$ time dummy as control variables. Note that our instrumental variable is the latitude $\times$ time dummy, and a cluster in the northern region has lower latitude than a cluster in the southern region because Malawi is in the southern hemisphere. Top section of Table 2 shows that a cluster with higher latitude (southern region) has a time trend of reforestation. Thus, a cluster with lower latitude (northern region) has a time trend of deforestation, which is consistent with the past pattern of deforestation (SI Appendix, Tables S1 and S3) and our prediction. In Table 2, top section, column 1 shows that if a cluster’s location is 1° more north, the forest area decreases further by 3 percentage points over time than other clusters. In Table 2, columns 2–4 show that the inclusion of other control variables does not affect the first-stage results.

Table 2, middle section shows our main results regarding the causal effect of the ratio of forest area on access to clean drinking water. Column 1 shows that a 1-percentage-point increase in the forest ratio increases the probability of access to clean drinking water by 1.06 percentage points, and a 1% increase in the amount of rainfall increases the probability of access to clean drinking water by 0.61 percentage points. Columns 2–4 show that the estimated coefficients of the ratio of forest area are quite stable with the inclusion of these control variables. Including all control variables, Table 2, middle section, column 4 shows that a 1-percentage-point increase in the forest ratio increases the probability of access to clean drinking water by about 0.93 percentage points, and a 1% increase in rainfall increases the probability of access to clean drinking water by 0.57 percentage points. The estimated coefficient of log of rainfall measures the total effect of log of rainfall on access to clean drinking water, including the effect of a change of the quality of water at watersheds. A statistically and economically significant estimated coefficient of log of rainfall suggests that local weather conditions matter for access to clean drinking water.

SI Appendix, Table S6 shows the results of the reduced-form estimation, which displays the estimated coefficient of our instrumental variable (latitude $\times$ time dummy). The estimated coefficients are stable with different specifications. SI Appendix, Table S6 shows that a cluster located 1° south has a 2.8 percentage points higher time trend on the probability of accessing clean drinking water than other clusters. On the other hand, the first-stage regression shows that such a cluster has a 3 percentage points higher time trend of the forest area ratio. Thus, a 1-percentage-point higher forest area ratio leads to about 0.93 (= 2.8/3) percentage points higher probability of accessing clean drinking water.

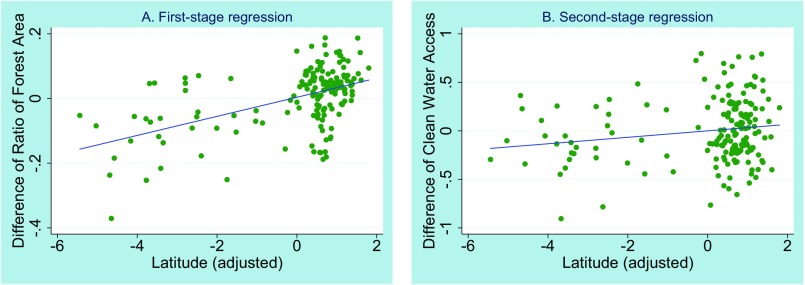
Fig. 2 shows the graphical relationship between the first-stage estimation (Fig. 2A) and the reduced-form estimation (Fig. 2B). In Fig. 2A, the vertical axis measures the adjusted difference of the ratio of forest area, and the horizontal axis is the adjusted latitude. In Fig. 2B, the vertical axis is the adjusted difference of the average of the clean drinking-water access dummy between 2000 and 2010. The adjusted latitude is the residual from the regression of the latitude on the difference of the log of the amount of rainfall. The vertical axes are measured in a similar way.

Fig. 2.

(A and B) Graphical presentation of the (A) first-stage regression and (B) reduced-form regression, after controlling for the effect of control variables. A and B show positive relationships between the adjusted latitude and adjusted difference of the forest area during the period 2000–2010 and the adjusted latitude and adjusted difference of the cluster-level average access to clean drinking water during the period 2000–2010. Note that slopes of the two fitted lines (0.03 and 0.028) are quite similar, although they look different due to the difference in the range of the vertical axes in A and B. In A and B, the axes range from −0.4 to 0.2 and from −1 to 1, respectively. Also note that higher variance of B is due to the nature of the reduced form. The error term of the reduced form includes the error term of the first-stage equation.

SI Appendix, Table S5 shows the estimation results of the ordinary least-squares estimation. The estimated coefficients in SI Appendix, Table S5 are 1/10th of the estimated coefficients of Table 2, and they are statistically insignificant. The exogeneity test rejects the null hypothesis that the ratio of forest is exogenous. Thus, SI Appendix, Table S5 shows the importance of controlling the endogeneity of the ratio of forest area.

SI Appendix, Tables S7 and S8 examine the sensitivity of our results by controlling the ratio of cropland, cropland intensity, and the ratio of the wetland. SI Appendix, Tables S7 and S8 show that the estimated coefficients of the ratio of forest area increase slightly, and the results of Table 2 are strengthened. SI Appendix, Table S9 examines whether our results are sensitive to the exclusion of the initial cluster-level characteristics. SI Appendix, Table S9 shows that our results are not sensitive to the initial cluster-level characteristics. In SI Appendix, Table S10, we make a circle with a radius of 12.5 km, instead of 7.5 km, at each cluster; calculate the forest area ratio; and conduct a 2SLS estimation. SI Appendix, Table S10 shows that the estimated coefficients are quite similar to the estimated coefficients in Table 2, which demonstrates the robustness of the results in Table 2.

Mechanism.

In this study, as we discussed in the Introduction, we hypothesize that deforestation decreases the capacity of soil infiltration of water, increases soil erosion, and decreases the quality of water at the source. We justify this hypothesis based on the fact that most water systems in rural areas of Malawi are developed and maintained by local communities. Thus, we should expect that when deforestation progresses, the use of piped water will decrease and the use of unprotected wells, rivers, and ponds will increase, because a local piped water system needs high-quality water sources, whereas an unprotected well, river, or pond does not.

Table 3 shows the effect of the ratio of forest area on access to each source of drinking water in the 2SLS estimation. In Table 3, each row shows the estimation result of a 2SLS regression with a different dependent variable. Each dependent variable is a dummy variable indicating the source of drinking water. For example, the row of piped water at public tap presents the estimation result when the dependent variable is a dummy variable indicating whether the household uses piped water at a public tap as the source of drinking water. The column for the estimated coefficient shows the estimated coefficient of the forest area ratio in the 2SLS regression. Table 3 shows when the ratio of the forest area increases by 1 percentage point, access to piped water at public taps increases by 0.93 percentage points, and the use of unprotected wells as the source of drinking water decreases by about 0.59 percentage points. The effects on the use of the river/pond/lake/dam and unprotected springs are negative as the hypothesis predicted, although they are statistically insignificant. Table 3 is consistent with the idea that when the ratio of forest area increases, the quality of the source of a piped water system that connects to a public tap improves; as a result, people can use piped water at a public tap instead of an unprotected well as the source of drinking water.

Table 3.

Effect of the ratio of forest area on access to each source of drinking water

Dependent variable	Estimate (SE)	$R^2$	N
Clean water
Piped water into dwelling	0.0313 (0.0329)	0.114	9,682
Piped water into yard	$-$0.131 (0.0828)	0.156	9,682
Piped water at public tap	0.934*** (0.300)	0.321	9,682
Protected well/tube	0.101 (0.431)	0.279	9,682
Less clean water
Unprotected well	$-$0.585** (0.228)	0.243	9,682
River/pond/lake/dam	$-$0.321 (0.420)	0.193	9,682
Unprotected spring	$-$0.0342 (0.0642)	0.056	9,682

Details are in Table 2 legend. The dependent variable in each row is a dummy variable indicating whether a household uses the corresponding source of water as drinking water. The column of the estimated coefficient shows the estimated coefficient of the ratio of forest area and its SE in the two-stage least-squares regression. All specifications include all control variables (cluster fixed effect, time fixed effect, log of rainfall, log of population, temperature in July, temperature in November, demographic characteristics, household wealth, and the cluster-level initial value × time dummy). * indicates significant at 10%; ** indicates significant at 5%; *** indicates significant at 1%.

Discussion.

Studies in forest science and hydrology often indicate that the relationship between land use and the quality of water is complex (4, 7, 27). Thus, readers might argue that many factors that are not included in our model are correlated with both the ratio of forest area and the accessibility to clean drinking water and that our estimated coefficients of the ratio of forest area are biased. However, our model includes the time fixed effect and the cluster fixed effect. Thus, the national-level time trend and the effect of time-invariant cluster-specific variables are already controlled. By applying 2SLS, we also prevent the possibility that the (time-variant) error term, the effect of time-variant variables that are not modeled in Eq. 1, is correlated with the ratio of the forest area and that our estimated coefficients of the ratio of forest area are biased.

Note that the instrumental variable in our 2SLS is the latitude $\times$ time dummy and we include the cluster-level initial values $\times$ time dummy as control variables. Thus, essentially in our 2SLS estimation, we compare clusters with different latitudes but the same initial characteristics, assuming that those clusters have the same time trend on access to clean drinking water if the rates of deforestation are the same.

However, some might argue that a cluster with higher latitude, that is, a cluster in the southern areas, has a time trend of higher infrastructure development, even after controlling the initial cluster-level characteristics and other covariates. In such a case, our 2SLS estimation might pick up not only the effect of the ratio of forest area but also the fact that a cluster with higher latitude has a time trend of higher infrastructure development.

To determine whether a cluster with higher latitude has a time trend of higher infrastructure development, we conduct a falsification test based on the reduced-form regression. In this test, we pick up a variable that is strongly correlated with development but is not directly affected by the forest ratio. Then, we regress this variable on the instrumental variable and control variables. The estimated coefficient of the instrumental variable showing a significant positive sign indicates that, in Table 2, our instrumental variable picks up the effect of urban development since the ratio of forest area should not affect such a variable. For the first falsification test, we use a dummy variable indicating access to electricity as a dependent variable because the ratio of forest area should not directly affect the use of electricity. For the second and third tests, we use the radio ownership and the quality of the respondent’s home as dependent variables. SI Appendix, Data Sets discusses how we measure the quality of a home. We exclude information on household wealth from the control variables in this falsification test, since the dependent variables are related to wealth.

SI Appendix, Table S11A shows the estimated coefficients of the instrumental variable in our first falsification test. In SI Appendix, Table S11A, the absolute value of the estimated coefficient of the instrumental variable is 1/10th of the estimated coefficient of the effect of the instrumental variable on access to clean drinking water (SI Appendix, Table S6). The sign of the estimated coefficients is the opposite of the signs in SI Appendix, Table S6, and the estimated coefficients are statistically insignificant. Thus, it is unlikely that our instrumental variable is picking up the higher time trend of development in clusters with higher latitude. SI Appendix, Table S11B, which uses the radio ownership as a dependent variable, shows a similar pattern.

SI Appendix, Table S11C shows that the effect of the instrumental variable is again negative and statistically insignificant. SI Appendix, Table S11A–C suggests that it is unlikely that the southern region has a time trend of higher development. We can thus safely conclude that it is unlikely that a positive effect of the forest ratio on access to clean drinking water in our 2SLS estimation is the consequence of the southern region having a higher time trend of development.

In summary, all robustness checks and falsification tests show that our estimated results are robust and consistent. Thus, it is very unlikely that the estimated coefficients of the ratio of forest area in our 2SLS pick up other unobserved effects.

Conclusion

In this study, we directly examine the causal relationship between deforestation and access to clean drinking water using the deforestation and household-level water access data in Malawi. We find that a 1-percentage-point decrease in the forest area in a local area decreases the probability of households’ access to clean drinking water in lieu of less clean drinking water by 0.93 percentage points.

Our analysis has two implications. First, it shows that protecting the forest area and fighting against illegal tree cutting will benefit local communities. Since the local residents often earn income by selling charcoal during the off-harvest season and the forest area is quite diverse, the community’s understanding of the merit of forest protection as well as participation in protecting the forest is essential. Our study shows the benefit of forest protection for local residents in Malawi.

Second, during 2000–2010, the ratio of forest area in Malawi decreased by 14% or by 5.6 percentage points (SI Appendix, Table S3). This implies that the probability of accessing clean drinking water decreases by 5.2 (= 5.6 $\times$ 0.93) percentage points. On the other hand, our regression shows that a 1% decrease in rainfall decreases access to clean drinking water by 0.57 percentage points. Thus, to compensate for a 5.6-percentage-point decrease in the forest ratio, Malawi needs about a 9 (= 5.2/0.57)% increase in rainfall. In other words, when the amount of rainfall decreases by about 9% due to a change in the weather pattern, this effect can be offset, for example, by preventing a 5.6-percentage-point decrease in the forest area. This calculation shows that the effect of deforestation on access to clean drinking water is not trivial and has important policy implications, for example, to prepare for a possible change of weather patterns in the future.

Materials and Methods

Datasets.

This study uses satellite data of the land cover and land use of 2000 and 2010, data of the Demographic Health Survey (DHS) of 2000 (28) and 2010 (29) with GPS location information, weather data, and population data.

The DHS datasets report geographical coordinates of the primary sampling unit, called a cluster. Each cluster is defined based on the census enumeration areas. To apply the panel data analysis at the cluster level, we match clusters in DHS 2000 to clusters in DHS 2010, such that the distance between a cluster in DHS 2000 and a matched cluster in DHS 2010 is less than 5 km. Among the matched pairs of clusters, we select cluster pairs in which a cluster at year 2000 is in a rural area. After matching and selection, 171 pairs of clusters are selected. The 171 clusters in DHS 2000 have 4,378 households, and the 171 clusters in DHS 2010 have 5,304 households.

The forest ratio in each cluster is obtained from satellite images of land use and land cover maps from the Ministry of Natural Resources, Energy and Mining in Malawi. We create circles with 7.5-km radius using the cluster’s GPS coordinate as the center of each circle and calculate the share of the forest area using the 2000 and 2010 satellite images. For robustness checks, we create circles with 12.5-km radius and calculate the ratio of forest area in each circle. After calculating this ratio, we conduct the same regression for robustness checks.

Regarding information on access to clean drinking water, the DHS datasets have information on a household’s source of drinking water. The DHS’s final report classifies the sources of drinking water into improved water sources and unimproved water sources. Following this DHS definition, we classify the sources of drinking water as clean drinking water or unsafe water if they are classified in the DHS as improved or unimproved, respectively. In SI Appendix, Data Sets, we explain how each source of water is classified. For the population, temperature, and rainfall datasets, we use the Gridded Population of the World (GPW) v4 [Center for International Earth Science Information Network (CIESIN)] (30), WorldClim (31), and Climate Hazards Group InfraRed Precipitation with Station data 2.0 (32), respectively. SI Appendix, Data Sets describes how each variable is constructed. All datasets and Stata code used in this study are available at ref. 33.

Estimation Model and Identification Strategy.

To estimate the causal effect of deforestation on access to clean drinking water, we estimate the equation

$$\begin{array}{ccc}\hfill {\text{Water}}_{ijt}& =\hfill & {\beta }_0+{\beta }_1{\text{RatioForest}}_{jt}+{\beta }_{2}X{1}_{ijt}\hfill \\ \hfill & \hfill & +\hspace{0.17em}{\beta }_{3}X{2}_{j0}\times D_t+{\alpha }_{2t}+{\alpha }_{2j}+u_{ijt},\hfill \end{array}$$ [1]

where ${\text{Water}}_{ijt}$ is a dummy variable indicating whether household $i$ in cluster $j$ at time $t$ has access to clean drinking water. ${\text{RatioForest}}_{jt}$ is the ratio of the area covered by the forest to the total area of the DHS cluster $j$ at time $t$. ${\alpha }_{2t}$ is a time fixed effect, and ${\alpha }_{2j}$ is a cluster fixed effect. $X{1}_{ijt}$ is a vector of control variables that directly affects access to clean drinking water. At the household level, $X{1}_{ijt}$ includes the household assets, educational level of the head of the household, number of household members, and gender of the head of the household. At the cluster level, $X{1}_{ijt}$ includes the log of annual rainfall, average temperatures of the hottest and coldest months, and log of the population in each cluster. $X{2}_{j0}$ is a vector of the cluster-level values at the initial period, and $D_t$ is a time dummy. $X{2}_{j0}\times D_t$ allow clusters with different initial values to have different time trends. $u_{ijt}$ is the error term that explains the variation of ${\text{Water}}_{ijt}$ that cannot be explained by the listed explanatory variables of Eq. 1. The model needs the error term because there are many factors that are not observable to researchers but affect the access to clean drinking water. When this error term is correlated with ${\text{RatioForest}}_{jt}$ through omitted variables or other confounders, we have the endogeneity problem.

To solve the endogeneity problem of ${\text{RatioForest}}_{jt}$, we use a 2SLS estimation. As the first-stage equation of the 2SLS estimation of Eq. 1, we estimate the following first-stage equation,

$$\begin{array}{ccc}\hfill {\text{RatioForest}}_{jt}& =\hfill & {\gamma }_0+{\gamma }_1{\text{Latitude}}_j\times D_t\hfill \\ +\hspace{0.17em}{\gamma }_{3}X{1}_{ijt}+{\gamma }_{4}X{2}_{j0}\times D_t+{\alpha }_{1t}+{\alpha }_{1j}+{\epsilon }_{ijt},\hfill \end{array}$$ [2]

where ${\alpha }_{1t}$ is a time-fixed effect, and ${\alpha }_{1j}$ is a cluster-fixed effect. $D_t$ is a time dummy and ${\epsilon }_{ijt}$ is the error term. The excluded instrumental variable is the latitude $\times$ the time dummy, ${\text{Latitude}}_j\times D_t$. We assume that this instrumental variable is uncorrelated with $u_{ijt}$. This is the key identifying assumption of our 2SLS.

This key identifying assumption implies that, after controlling the effect of covariates, clusters with different latitudes have the same time trend regarding access to clean drinking water if changes in forest areas are the same in those different clusters (SI Appendix, Eqs. S3 and S4). To be fully flexible in our estimation, we include the cluster-level initial value such as the 1990s level of the forest ratio and the cluster-level average of the good floor material dummy in 2000 $\times$ time dummy as additional control variables. Inclusion of these variables allows us to assume that different clusters with the same latitude have different time trends if those initial values are different in those clusters. In this estimation strategy, we essentially compare the change in access to clean drinking water of different clusters with different latitudes that have the same initial characteristics, such as (cluster-level) population, the 1990s forest area ratio, and wealth level in the initial year.

Historically, in Malawi, the northern region has a higher deforestation rate, as is shown in SI Appendix, Table S1 and Fig. 1, despite the fact that only about 10% of the population lives in this region, as indicated in SI Appendix, Table S2. This regional difference in deforestation results from the fact that monitoring and preventing illegal tree cutting in the northern region is not easy because of the small population density, whereas a higher population density in the southern and central regions makes illegal tree cutting more difficult. Furthermore, historically, before the independence of Malawi, the majority of the population lived in the southern region, and easily accessible forests were already cut in that region before 1970. Given the deforestation trend in Malawi during 1972–1992, it is reasonable to assume that such a pattern persisted during 2000–2010. SI Appendix, Table S3 supports this assumption and shows that this is indeed the case. In addition, the first-stage regression results of the top section in Table 2 show that there is a strong relationship between the latitude and the rate of deforestation.

Regarding the SE calculation, we apply the clustering robust SEs while assuming that the error terms are correlated within each cluster $\times$ year cell. SI Appendix, Standard Error Calculation discusses the appropriateness of this SE calculation.