Significance
There is a large gap between the number of protein complex structures currently solved and the number of functionally relevant structures. Mass spectrometry-based approaches for biomacromolecule structural characterization are growing, are beginning to fill critical gaps, and complement other structural biology tools. We have shown for several examples that collision of protein complex ions with a surface yields products that are reflective of substructure. We present here a computational model that predicts the relative appearance energy at which a globular protein complex dissociates. This appearance energy prediction can provide structural information when a high-resolution structure has not or cannot be obtained and in the future has potential to be used to select the best-fit candidate computational models, dramatically increasing the structural information obtained.
Keywords: protein complex, native mass spectrometry, protein interactions, structural biology, surface-induced dissociation
Abstract
To fulfill their biological functions, proteins must interact with their specific binding partners and often function as large assemblies composed of multiple proteins or proteins plus other biomolecules. Structural characterization of these complexes, including identification of all binding partners, their relative binding affinities, and complex topology, is integral for understanding function. Understanding how proteins assemble and how subunits in a complex interact is a cornerstone of structural biology. Here we report a native mass spectrometry (MS)-based method to characterize subunit interactions in globular protein complexes. We demonstrate that dissociation of protein complexes by surface collisions, at the lower end of the typical surface-induced dissociation (SID) collision energy range, consistently cleaves the weakest protein:protein interfaces, producing products that are reflective of the known structure. We present here combined results for multiple complexes as a training set, two validation cases, and four computational models. We show that SID appearance energies can be predicted from structures via a computationally derived expression containing three terms (number of residues in a given interface, unsatisfied hydrogen bonds, and a rigidity factor).
Native mass spectrometry (MS) has emerged as a powerful structural biology tool. By using “soft” ionization techniques such as nanoelectrospray ionization, noncovalent interactions can be retained, enabling the study of intact protein:protein, protein:ligand, and protein:RNA complexes in the gas phase (1–4). Native MS overcomes many of the barriers associated with traditional protein characterization methods; it requires low sample volumes (3–10 μL) and micromolar or lower concentrations, while also having a broad mass range for analysis, allowing study of small monomeric proteins up to large megadalton assemblies (1, 5).
Typical MS experiments to study subunit interactions of protein complexes involve first preparing the sample in an aqueous solution at near neutral pH, typically 100–200 mM ammonium acetate. The complex is then introduced intact into the mass spectrometer to measure the mass of the native complex. To obtain subunit connectivity information on the sample, the complex can be disrupted in solution, typically either with small volumes of organic solvent or through alteration of the ionic strength; this destabilizes the protein:protein interfaces and allows measurement of stable subcomplexes (6, 7). This approach, however, targets all species present in solution and can therefore be problematic for heterogeneous samples where it may not be possible to decipher which subcomplex came from which precursor. Alternatively, the complex can be isolated and then dissociated in the gas phase. The most commonly used dissociation method for such studies is collision-induced dissociation (CID). In CID protein ions are accelerated into a bath gas with which they undergo multiple collisions. CID proceeds via an unfolding mechanism and therefore typically produces an unfolded monomer (which typically carries half the charge of the precursor ion) and the corresponding (n − 1) multimer (which retains the other half of the charge) (8–10). CID is a very effective tool for confirming stoichiometry; however, due to the unfolding mechanism it often provides limited information on assembly.
An alternative activation/dissociation method for protein complexes is surface-induced dissociation (SID). In SID ions are accelerated toward and collide against a surface. This is a fast, high-energy deposition process which enables faster, more structurally informative dissociation pathways to outcompete the slower multistep activation unfolding and rearrangement pathways typically observed for CID (11, 12). We have previously shown that SID produces fragments in which the charge is more symmetrically partitioned than it is in CID and that products can remain compact (13–15). In addition, we have demonstrated that SID disassembly pathways are consistent with the known protein assembly pathways and hence can provide structural information on known and unknown structures (16–18). To expand upon these previous studies and to more fully characterize SID and its utility in structural biology studies, we chose a set of globular protein complexes with different oligomeric orders and of known structure to determine whether SID consistently produces subcomplexes reflective of the solved structure. We coupled our experimental studies with computational approaches to discern which structural factors of the protein complex determine the appearance energy for fragmentation. In future studies this would then allow the SID pattern and energy requirements to predict the overall topology of a complex of unknown structure and to position the complex in the periodic table of protein complexes (19).
Results and Discussion
SID Patterns for Oligomers of Different Structures.
All protein complexes (Fig. 1) were studied under native-like conditions. Complexes were studied under charge-reducing conditions, afforded by preparing the protein in ammonium acetate and triethylammonium acetate, to keep the proteins more compact and native-like (20). Under these conditions, CID proceeds via the typical unfolding mechanism, producing unfolded, highly charged monomers, providing no direct information on subunit connectivities (SI Appendix, Figs. S1–S5, Left). In contrast, SID produces a wide range of different subcomplexes.
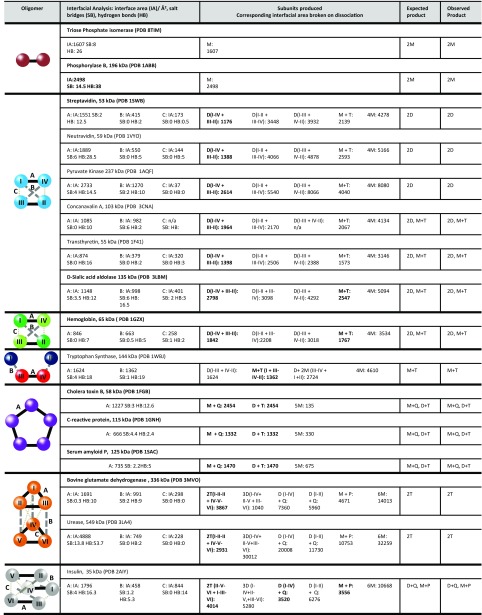
Fig. 1.
Interfacial information for the proteins studied, in addition to the predicted and observed SID products. Proteins highlighted in boldface type were used for the computational modeling. Only proteins for which a crystal or NMR structure for the complex exists (as opposed to a PISA predicted structure) were used for modeling. Interfacial analysis was performed with PISA analysis and is reported in the form of interface area (IA)/Å2, salt bridges (SB), and hydrogen bonds (HB). The largest interface in each complex is represented by a solid black line, the second largest interface in each complex is represented by a gray dashed line, and the smallest interface is represented by a gray dotted line. For products: D, dimer; H, hexamer; M, monomer; P, pentamer; Q, tetramer; T, trimer. For representative SID spectra see SI Appendix. For phosphorylase B the crystal structure is a tetramer; dimer interfaces were predicted from PISA.
Dimers can only fragment to monomers or fragment covalently along the backbone, and we first consider the homodimers triose phosphate isomerase and phosphorylase B (SI Appendix, Fig. S1). The main differences in CID and SID for dimers are that the monomers produced by CID often show the typical asymmetric charge partitioning while SID typically produces symmetrically charged species. As the oligomeric order of protein complexes increases, the range of products that can be produced also increases. We next considered the homotetrameric proteins streptavidin, neutravidin, and pyruvate kinase, for which low-energy SID primarily produces dimers (SI Appendix, Fig. S2 D–F) and in some cases lower-intensity monomers (in contrast to forming primarily monomers by CID; SI Appendix, Fig. S2 A–C). These tetramers are all dimers of dimers and have D2 symmetry. We performed preliminary structural analysis using Proteins, Interfaces, Structures, and Assemblies (PISA) interfacial prediction (21) (Fig. 1). PISA can predict the interfacial area, the number of salt bridges, and the number of hydrogen bonds at the interface between protein subunits. PISA reveals that the interface between the two monomers forming the dimer (interface A) is much stronger than the other two interfaces present (B and C) for these three homotetrameric complexes. Therefore, the theoretically most favorable dissociation pathway is dissociation from tetramers to dimers, based upon cleaving the smallest total interfacial area (IA) and correspondingly cleaving fewer predicted intermolecular interactions, salt bridges (SBs), and hydrogen bonds (HBs). For example, for streptavidin to produce dimers (cleaving two C and two B interfaces) an IA of 1,176 Å2 would be cleaved whereas to produce a monomer and a trimer (cleaving one A, one C, and one B interface) an IA of 2,139 Å2 would be cleaved (16). The dissociation pathway to produce dimers is, therefore, predicted to be more favorable (by ∼1,000 Å2) and is consistent with our SID results.
In contrast, for the D2 tetramers transthyretin, Con A, d-sialic acid aldolase, and hemoglobin, PISA predicts that the three interfaces present in these complexes are more similar, with respect to interfacial area, than in the previous set of tetramers. Therefore, the IAs that would have to be broken to produce the different products (namely dimer + dimer vs. monomer + trimer) are more similar than in the previous set of tetramers. For example, for transthyretin to dissociate from the tetramer to produce dimers (cleaving two C and two B interfaces) a total IA of 1,398 Å2 has to be cleaved whereas to produce a monomer and a trimer (cleaving one A, one C, and one B interface) a total interfacial area of 1,573 Å2 would be cleaved. These two dissociation pathways are closer in relative interfacial area cleaved (differing by only 175 Å2), and hence both might be expected to occur with low-energy SID. Indeed, for transthyretin, Con A, d-sialic acid aldolase, and hemoglobin both pathways (production of dimers and production of monomer and trimer) are observed in the low-energy SID spectrum (SI Appendix, Fig. S3 E–H). A significantly higher proportion of monomer is observed here (SI Appendix, Fig. S3 E–H) compared with the previous tetramers (SI Appendix, Fig. S2 D–F).
Finally, we considered the heterotetramer tryptophan synthase, which is composed of a β dimer flanked by two α subunits in a linear arrangement. PISA interfacial prediction highlights that tryptophan synthase has a stronger interface between the two β subunits than between the α and β subunits. Correspondingly, in low-energy SID the formation of an α monomer and the complementary ββα trimer is observed (22).
We next present the cyclic pentamers cholera toxin B, C-reactive protein, and serum amyloid P, all of which have equal interfaces between subunits (Fig. 1). With equal interfaces between all subunits it is predicted that cleavage will occur at any two interfaces, forming both monomer and tetramer, plus dimer and trimer. The PISA interfacial predictions are entirely consistent with experimental SID (SI Appendix, Fig. S4 D–F), demonstrating that SID can produce subcomplexes consistent with the solved structure for complexes of different oligomeric orders and with varied subunit arrangements.
To further expand this approach we also examined homohexameric complexes. Glutamate dehydrogenase (GDH) and urease are both dimers of trimers, which have strong A interfaces between the monomers forming the trimer and weaker B and C interfaces, bringing the two trimers together to form the hexamer. For both of these hexamers, cleaving the lowest interfacial area would produce trimers as observed experimentally by SID (SI Appendix, Fig. S5C, bovine GDH) as previously reported (23). We also considered insulin which can be considered to be a trimer of dimers; it has more equal interfaces between the subunits and hence is predicted to dissociate to dimer and tetramer, monomer and pentamer, plus trimer and trimer. Experimentally all pathways are indeed observed in low-energy SID (SI Appendix, Fig. S5D). This set of hexamers demonstrates that SID can distinguish between different subunit connectivities and provide insight into structure.
Finally, we studied the dodecamer glutamine synthetase, which is composed of two stacked hexameric rings. PISA interfacial prediction identifies the strongest interface as an interring interface (SI Appendix, Fig. S6A), followed by an intraring interface (SI Appendix, Fig. S6B) and another weaker interring interface (SI Appendix, Fig. S6C). Producing dimer and undecamer, tetramer and octamer, and two hexamers involves breaking the lowest IA (6,494 Å2) with only a slightly higher IA having to be broken to produce the monomer and 11-mer (6,958 Å2) (SI Appendix, Table S1). Interfacial prediction is again consistent with our experimental SID results (SI Appendix, Fig. S7). For all complexes studied here, from tetramer to dodecamer, SID cleaves the weakest protein:protein interfaces, producing the products predicted from the interfacial analysis.
Computational Modeling to Predict SID Appearance Energies.
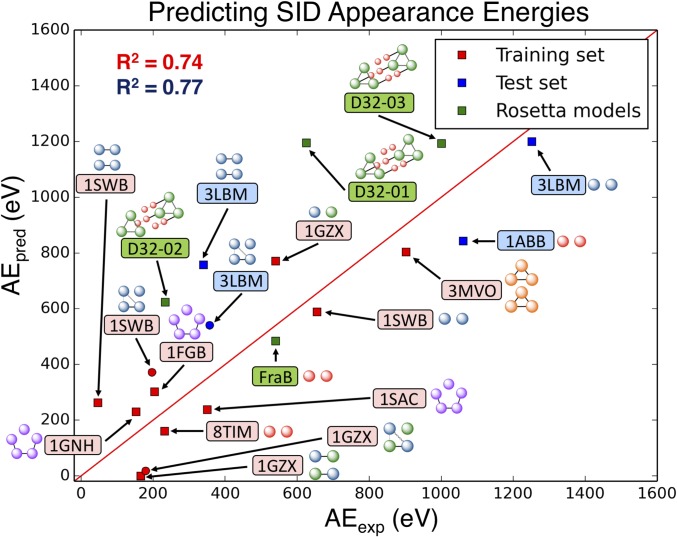
We have demonstrated that the subcomplexes produced from SID of a range of different complexes with different known oligomeric states and connectivities can be predicted from the known structure of the complex. This is consistent with our previous work where we have used SID subcomplex products to predict connectivity for complexes of unknown structure (17). The utility of SID as a structural biology tool could be increased if the appearance energy required to produce the subcomplex could also be related to the structure. The potential to predict SID appearance energies (AEs), defined here as 10% fragmentation, based on structural features of protein:protein interfaces (PPIs) was also investigated. For this analysis, initially a subset of seven globular complexes was chosen that have a complete complex structure deposited in the Protein Data Bank as opposed to a structure assembled in PISA. SID energy-resolved MS (ERMS) plots were generated for each protein complex studied (SI Appendix, Figs. S8–S10). For the tetramers (1SWB, 1GZX, 3LBM), we were able to extract AEs for multiple interfaces. In addition to the dimer–dimer interfaces, we also calculated an AE for the monomer–monomer interface of the dissociated dimers. For example, 1SWB (homotetramer) first dissociated into dimers, resulting in an appearance energy of 184 eV for the dimer–dimer interface. At higher acceleration energies, 1SWB dissociated into monomers, which could have appeared from the tetramer directly (resulting in monomer + trimer) or from the dimers. To calculate the appearance energy from the dimer complex, we subtracted the trimer curve from the monomer curve, which indicates monomers that dissociated from dimers since the number of monomers from trimers should be equal to the number of trimers, resulting in an appearance energy of 655 eV for the interface in the dimer subcomplex. We used similar methodology to calculate appearance energies of subcomplexes for the remaining tetramers. For the SID dataset, Rosetta’s InterfaceAnalyzer (24) was used to calculate several interface features (such as IA, HB, SB, etc.) to analyze correlation to SID AE. While some of the calculated interface features individually showed a correlation to AE (SI Appendix, Fig. S11) (number of interface residues, R2 = 0.52; interface surface area, R2 = 0.40; interface hydrophobic surface area, R2 = 0.32; Rosetta interface ΔG, R2 = 0.17), a model that combined several interfacial features allowed more accurate AE prediction (Fig. 2). We also considered correlation to molecular weight only, which showed poorer correlation than the model combining several interfacial features (SI Appendix, Fig. S12). The model vastly improved when information about the rigidity of individual subunits was included, using a metric called the rigidity factor (RF). The RF is based on the density of intrasubunit SB, HB, and disulfide bonds. We hypothesize that this term accounts for any partial unfolding upon surface collision, reflecting entropic contributions. Although SID typically produces compact species, with compact collision cross-sections measured from ion mobility, and with ligand retention (25, 26), it is possible that flexible species can partially unfold or rearrange as the energy is redistributed throughout the system after surface collision and before dissociation. The best predictive model for estimating appearance energies from structure, using the computed parameters and shown in Eq. 1, contained nonzero weights (w) for the number of interacting residues (NRs) at the interface, the number of unsatisfied HBs (UHBs) at the interface, and the RF. The weights were optimized to maximize prediction power, i.e., minimizing χ2 between predicted and experimental values. The model suggests that larger interfaces (higher NR) have higher AE, interfaces with a larger number of UHBs have lower AE, and interfaces with more rigid subunits (RF) have lower AE. Fig. 2 shows the strong correlation (R2 = 0.74) between the predicted AE (AEpred) and the experimental AE (AEexp) for the training set, shown in red. Because of concern about error associated with calculation of the AE for secondary dissociation of dimers to monomers (subtraction of the trimer curve, with trimer possibly discriminated against experimentally), we also extracted the trimer–monomer interface AEs by using the 10% monomer onset and plotted those points on the plot in Fig. 2 (red circles) and found that they fit well to the model, changing the R2 to 0.70.
| [1] |
The majority of the complexes chosen to build this model had similar experimental and predicted AE but there was a clear lack of model complexes with AE > 1,000 eV. To further validate the model and expand the approach, we selected two additional protein complexes that have solved structures and that the model predicted to have higher AE. We found that the experimental AE and predicted AE have good agreement using the model developed with the training set (two known validation complexes shown in blue in Fig. 2), with the R2 improving slightly after inclusion of the additional complexes (R2 = 0.77). Finally, we further tested this approach for complexes with no experimentally determined, solved structure. We chose three computationally designed dodecamers, which have been previously studied using SID (27), and a protein complex which has a computational homology model. The predicted and experimental AEs for the four Rosetta models (shown in green in Fig. 2) show good correlation using this approach. The correlation for these models is not as high as in the training and validation sets, which is expected, given that we do not have solved structures for these complexes and there may be some variations in interface strength between the computational or homology model and the experimental structure. However, a greater correlation between experimental and predicted AE is achieved when using this model as opposed to using molecular weight alone. It is important to note that all experiments were performed using charge-reducing conditions, gentle instrumental settings, and no disruptive organic solution additives to keep the complexes compact and native-like. The correlation shown in Fig. 2 suggests that the native conditions chosen maintain the interfaces of these complexes intact until SID occurs. For a set of dimers not included here, we have seen that AE varies very little, for SID of normal and reduced charge species, suggesting that the interfaces remain intact in those cases and that any change in charging is the result of changes on noninterfacial regions of the complex. If complexes are activated or denatured (e.g., through the addition of organic solvents), the interfaces could be disrupted, affecting the relationship between experimental and predicted appearance energy. We have previously reported that AE can change if structure is disrupted (e.g., by in-source CID) (28). The form of Eq. 1 may also change when not just appearance energy, but the ability to select among candidate structural models is the goal.
Fig. 2.
Optimized model for predicting SID AE. Eq. 1 contains the following parameters: NR, number of residues at the interface; RF, rigidity factor; UHB, number of unsatisfied hydrogen bonds at the surface. There is a strong correlation between predicted and experimental AE for the training set (R2 = 0.74, red), and the test set (R2 = 0.77, blue). Tetramers dissociating to monomer–trimer are shown as red circles. Four proteins for which Rosetta models exist were also tested (green) and also show good correlation [three computationally designed dodecamers (D32-01 to -03) (27) and Salmonella FraB deglycase (FraB)]. A simplest model structure of each complex is included to show interface cleavages associated with low AE. PDB codes for each protein in the training and test sets are given in red rounded rectangles.
Conclusions
We have demonstrated that low-energy SID consistently cleaves the weakest interfaces in globular protein complexes in a manner concordant with their known structures, under charge-reducing conditions. In cases where the difference in total cleaved interfacial area for two competing pathways is small, both pathways are detected near the onset. Furthermore, we have constructed a model that can predict the AE for subcomplex formation based on protein complex structural features. The potential to utilize subunit interactions, connectivities, and agreement between experimental and predicted appearance energies for the selection of candidate structural models in a direct MS/MS experiment is promising with the potential to enhance future MS-based structural biology approaches.
Materials and Methods
Synthesis of the Perfluorodecylethanethiol (FC12).
The CF3(CF2)9CH2CH2SH for self-assembled monolayer surfaces was synthesized following multiple significant improvements to a previously published protocol (29). The material was characterized by melting-point analysis, IR spectroscopy, and NMR. Full details on the synthesis and characterization can be found in the SI Appendix
Preparation of the Self-Assembled Monolayer Surfaces.
A 17-mm × 13-mm × 0.5-mm gold surface slide, 1,000 Å of Au on 50 Å of Ti on glass (EMF Corp.), was cleaned for 15 min in a UV cleaner (Model 135500; Boekel Scientific). The cleaned surface was then incubated in ∼3 mL of 1-mM solution of FC12 in ethanol for at least 12 h in the dark. Following incubation, the surface was cleaned by sonicating in ∼3 mL of ethanol for 1 min; this process was repeated six times with fresh aliquots of ethanol.
Modification of Synapt G2 and G2S for Surface-Induced Dissociation.
All SID experiments were performed on in-house–modified Synapt G2 or G2S instruments (Waters). The instrument was modified as previously described (13); however, in this case the SID device was placed before the ion mobility (IM) cell and hence referred to as Trap-SID. In brief, the Trap t-wave region was truncated by 3 cm without damaging critical electrical parts to accommodate the SID device which was voluntarily machined and provided by Waters Corporation, as a copy of the previous Wysocki group design but with improved mounting brackets. In the current design, the connections for the 10 lenses in the SID device (SI Appendix, Fig. S13) are supplied through a Fischer connection through a modified Triwave chamber cover and supplied using an external power supply (Ardara Technologies).
Surface-Induced Dissociation Ion Mobility-Mass Spectrometry.
All proteins were introduced into the mass spectrometer using nanoelectrospray ionization in positive ionization mode. Nanoelectrospray tips were made in house using thin-walled glass capillaries (i.d. 0.8 mm), using a Flaming/Brown micropipette puller (Sutter Instrument Company). The ionization potential (typically 1–1.4 kV) was applied using a thin (0.368 mm) platinum wire (Alfa Aesar). The instrument was operated in ion mobility, sensitivity mode. For MS and Trap-CID experiments the SID device was tuned for “fly through” mode, so the ion beam would pass through the device without hitting the surface. A Trap gas flow rate of 4 mL/min and a Trap DC bias of 45 V are applied and the SID device is tuned to give a 1- to 5-V difference between the Trap exit and the entrance lens of the SID device and a 5- to 10-V difference between the exit lens of the SID device and the helium cell entrance.
To perform SID, operating in “Trap-SID mode” meaning the SID device is before the IM cell, the lenses on the device have to be tuned to direct the ion beam toward the surface and will depend on the system under study. The SID acceleration potential is defined as the difference between the exit of the Trap T-wave region and the surface. The SID voltage is tuned to higher or lower voltage via changing the dc bias on the Trap, which will enable the SID acceleration potential to be tuned from 10 V to 200 V. In SID mode, entrance lenses 1 and 2 are tuned to focus the beam before contact with the surface, typically 10–100 V between the two with entrance lens 1 set to 1–7 V below the exit of the Trap T-wave region while entrance lens 2 is held at approximately the same voltage as the surface. The front deflector is tuned with the top deflector 10–100 V more negative than the surface and the bottom deflector more positive than the surface. The surface is offset by 30–50 V from the helium cell dc, and the middle bottom deflector typically is 10–90 V less positive than the surface. The back deflector is tuned to focus the beam of ions after collision with the surface, the top deflector is typically 10–90 V more negative, and the bottom deflector is typically 5–90 V more negative the surface. The exit lenses are typically tuned to be 10–30 V more negative than the entrance to the helium cell. Example voltages for SID of 50 V in a Waters Synapt G2 instrument are given in SI Appendix, Table S2. When changing the SID acceleration potential, the Trap T-wave dc potential, entrance lens 1, and the front bottom deflector are all raised by the same potential. For SID experiments, a Trap gas flow rate of 2 mL/min is used; lowering the gas flow in this region decreases the likelihood of CID (collision with the argon trap gas) occurring alongside SID.
Preparation of the Protein Complexes.
Streptavidin and neutravidin were purchased from Thermo Scientific Pierce Biotechnology, C-reactive protein and serum amyloid P were purchased from CalBioChem (EMD Biosciences, Inc.). Transthyretin, triose phosphate isomerase, insulin, cholera toxin B, phosphorylase B, d-silac acid aldolase, Con A, pyruvate kinase, hemoglobin, tryptophan synthase, urease, bovine GDH, and glutamine synthetase were all purchased from Sigma-Aldrich. All samples were analyzed at ∼10 µM complex concentration in 80 mM ammonium acetate (Sigma-Aldrich) plus 20 mM triethyl ammonium acetate (TEAA) (Sigma-Aldrich), except d-silac acid aldolase which was prepared at 160 mM AmAc and 40 mM TEAA. We used TEAA to produce “charge-reducing” conditions, which are thought to keep the complex more compact and native-like (20, 30, 31). Residual salt impurities were removed by buffer exchanging using micro-Spin 6 columns (Bio-Rad), as required.
Interfacial Analysis of Protein Complexes Using PISA.
In initial SID predictions PISA, available at www.ebi.ac.uk/pdbe/pisa, was used (21). PISA can assemble protein complex structures from the Protein Data Bank (PDB) files and is used to estimate the strength of the interfaces between subunits in each complex. PISA provides the interfacial area, as well as the average number of potential hydrogen bonds and salt bridges between the subunits based upon the solved structure. From this interfacial analysis, predicted dissociation pathways were generated with the most favorable dissociation pathway being cleavage of the lowest interfacial area. The number of potential interactions broken was also noted. While this approach can be used to estimate the interface strength and hence predict the first interfaces to break, more in-depth computational analysis was required to predict the SID AE required to break the interfaces.
Computational Protein Structure Analysis and SID Prediction.
ERMS plots from SID were used to determine how the individual subunits dissociated from the complex (SI Appendix, Figs. S8–S10). This information was then used to identify possible protein:protein interfaces that fragmented during the collision. For each of the possible fragmented interfaces, AE, which was arbitrarily defined as the acceleration energy needed to reach 10% intensity with respect to the intensity of the native complex, was determined. The experimental AEs were subsequently normalized by the number of intersubunit protein:protein contacts. For example, the homotetramer shown in SI Appendix, Fig. S14 dissociated into the dimers of I/II and III/IV, so there were four intersubunit protein–protein contacts (2B and 2C). Next, Rosetta’s InterfaceAnalyzer (24) was used to calculate the following structural features (also normalized by number of intersubunit protein:protein contacts) of the native crystal structure complexes of the identified dissociating interfaces: change in Rosetta energy when subunits interact, change in Rosetta energy when subunits interact per area of interface, Rosetta energy of interface residues, Rosetta energy per residue for the interface, hydrophilic/hydrophobic/polar/total surface area of interface, salt bridges at interface, hydrogen bonds at interface, unsatisfied hydrogen bonds at interface, hydrogen bond Rosetta energy at interface, and number of interface residues. We used experimental AE to determine which possible quantities correlated strongly with stronger interfaces (high AE). SI Appendix, Fig. S11 shows correlation to AEexp for the Rosetta interface ΔG (dG_separated), the hydrophobic interface surface area (dSASA_hphobic), the interface surface area (dSASA_int), and the number of interface residues (nres_int), respectively.
Even though subunit unfolding is minimized in SID compared with CID (32), precursor or subunit unfolding during the SID collision is possible. To account for this effect, RF, a measure of protein rigidity was developed, to quantify the rigidity of the subunits involved in the interface. A set of 11,060 nonredundant structures (12,591 total unique subunits) from the Protein Data Bank, obtained using PISCES (33), was analyzed. Extracting all unique subunits from complexes, we calculated the number of intramolecular SBs, HBs, and disulfide bonds (DSs), all normalized by the number of residues, using an in-house Rosetta application. The individual distributions of SBs, HBs, and DSs per residue are shown in SI Appendix, Fig. S15 A–C. Next, intrasubunit energy (Eintra), shown in Eq. 2, was calculated to approximately account for the relative strengths of SBs (34), HBs (35), and DSs (36). Next, we examined the distribution of the Eintra values, shown in SI Appendix, Fig. S15D. Ultimately, the RF was defined to be zero if Eintra was more than 2 SDs below the mean, the RF was defined to be one if Eintra was more than 2 SDs above the mean, and linear extrapolation was used if Eintra was within 2 SDs. As a consequence, the RF was bounded between zero (minimum rigidity, maximum possible unfolding during SID collision) and one (maximum rigidity, minimum possible unfolding during SID collision):
| [2] |
A model was devised to predict experimental dissociation energy for given interfaces using a linear combination of the RF and the Rosetta Interface Analyzer interface parameters as shown in Eq. 1. To optimize the model, we iteratively searched through possible combinations of parameters and optimized the weights to minimize the χ2 between predicted and experimental AE using Python’s simplex algorithm (37). The weights (w) were optimized using the training set of seven complexes and tested on a set of two complexes with known structure and four complexes for which Rosetta models exist (27).
Supplementary Material
Acknowledgments
We thank Sumudu Leelananda for advice regarding interface property evaluations and Florian Busch for advice regarding additional proteins to study. We also thank Venkat Gopalan and Jikang Wu for the FraB data used in model development. We thank the Ohio Supercomputer Center for computational resources. We acknowledge financial support from the National Institutes of Health Grants R01GM113658 (to V.H.W.) (experimental SID-MS studies) and P41 GM128577 (to V.H.W. and S.L.) (computational modeling studies).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1817632116/-/DCSupplemental.
References
- 1.Uetrecht C, Barbu IM, Shoemaker GK, van Duijn E, Heck AJ. Interrogating viral capsid assembly with ion mobility-mass spectrometry. Nat Chem. 2011;3:126–132. doi: 10.1038/nchem.947. [DOI] [PubMed] [Google Scholar]
- 2.Konijnenberg A, Butterer A, Sobott F. Native ion mobility-mass spectrometry and related methods in structural biology. Biochim Biophys Acta. 2013;1834:1239–1256. doi: 10.1016/j.bbapap.2012.11.013. [DOI] [PubMed] [Google Scholar]
- 3.Allison TM, et al. Quantifying the stabilizing effects of protein-ligand interactions in the gas phase. Nat Commun. 2015;6:8551. doi: 10.1038/ncomms9551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ma X, et al. Uncovering the stoichiometry of Pyrococcus furiosus RNase P, a multi-subunit catalytic ribonucleoprotein complex, by surface-induced dissociation and ion mobility mass spectrometry. Angew Chem Int Ed Engl. 2014;53:11483–11487. doi: 10.1002/anie.201405362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.van Berkel WJH, van den Heuvel RHH, Versluis C, Heck AJR. Detection of intact megaDalton protein assemblies of vanillyl-alcohol oxidase by mass spectrometry. Protein Sci. 2000;9:435–439. doi: 10.1110/ps.9.3.435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Levy ED, Boeri Erba E, Robinson CV, Teichmann SA. Assembly reflects evolution of protein complexes. Nature. 2008;453:1262–1265. doi: 10.1038/nature06942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Marsh JA, et al. Protein complexes are under evolutionary selection to assemble via ordered pathways. Cell. 2013;153:461–470. doi: 10.1016/j.cell.2013.02.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Beardsley RL, Jones CM, Galhena AS, Wysocki VH. Noncovalent protein tetramers and pentamers with “n” charges yield monomers with n/4 and n/5 charges. Anal Chem. 2009;81:1347–1356. doi: 10.1021/ac801883k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Benesch JLP, Aquilina JA, Ruotolo BT, Sobott F, Robinson CV. Tandem mass spectrometry reveals the quaternary organization of macromolecular assemblies. Chem Biol. 2006;13:597–605. doi: 10.1016/j.chembiol.2006.04.006. [DOI] [PubMed] [Google Scholar]
- 10.Hall Z, Hernández H, Marsh JA, Teichmann SA, Robinson CV. The role of salt bridges, charge density, and subunit flexibility in determining disassembly routes of protein complexes. Structure. 2013;21:1325–1337. doi: 10.1016/j.str.2013.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Blackwell AE, Dodds ED, Bandarian V, Wysocki VH. Revealing the quaternary structure of a heterogeneous noncovalent protein complex through surface-induced dissociation. Anal Chem. 2011;83:2862–2865. doi: 10.1021/ac200452b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhou M, Jones CM, Wysocki VH. Dissecting the large noncovalent protein complex GroEL with surface-induced dissociation and ion mobility-mass spectrometry. Anal Chem. 2013;85:8262–8267. doi: 10.1021/ac401497c. [DOI] [PubMed] [Google Scholar]
- 13.Zhou M, Huang C, Wysocki VH. Surface-induced dissociation of ion mobility-separated noncovalent complexes in a quadrupole/time-of-flight mass spectrometer. Anal Chem. 2012;84:6016–6023. doi: 10.1021/ac300810u. [DOI] [PubMed] [Google Scholar]
- 14.Jones CM, et al. Symmetrical gas-phase dissociation of noncovalent protein complexes via surface collisions. J Am Chem Soc. 2006;128:15044–15045. doi: 10.1021/ja064586m. [DOI] [PubMed] [Google Scholar]
- 15.Zhou M, Dagan S, Wysocki VH. Protein subunits released by surface collisions of noncovalent complexes: Nativelike compact structures revealed by ion mobility mass spectrometry. Angew Chem Int Ed Engl. 2012;51:4336–4339. doi: 10.1002/anie.201108700. [DOI] [PubMed] [Google Scholar]
- 16.Quintyn RS, Yan J, Wysocki VH. Surface-induced dissociation of homotetramers with D2 symmetry yields their assembly pathways and characterizes the effect of ligand binding. Chem Biol. 2015;22:583–592. doi: 10.1016/j.chembiol.2015.03.019. [DOI] [PubMed] [Google Scholar]
- 17.Song Y, Nelp MT, Bandarian V, Wysocki VH. Refining the structural model of a heterohexameric protein complex: Surface induced dissociation and ion mobility provide key connectivity and topology information. ACS Cent Sci. 2015;1:477–487. doi: 10.1021/acscentsci.5b00251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Romano CA, et al. Biogenic manganese oxide nanoparticle formation by a multimeric multicopper oxidase Mnx. Nat Commun. 2017;8:746. doi: 10.1038/s41467-017-00896-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ahnert SE, Marsh JA, Hernández H, Robinson CV, Teichmann SA. Principles of assembly reveal a periodic table of protein complexes. Science. 2015;350:aaa2245. doi: 10.1126/science.aaa2245. [DOI] [PubMed] [Google Scholar]
- 20.Hall Z, Politis A, Bush MF, Smith LJ, Robinson CV. Charge-state dependent compaction and dissociation of protein complexes: Insights from ion mobility and molecular dynamics. J Am Chem Soc. 2012;134:3429–3438. doi: 10.1021/ja2096859. [DOI] [PubMed] [Google Scholar]
- 21.Krissinel E, Henrick K. Inference of macromolecular assemblies from crystalline state. J Mol Biol. 2007;372:774–797. doi: 10.1016/j.jmb.2007.05.022. [DOI] [PubMed] [Google Scholar]
- 22.Quintyn RS, Zhou M, Dagan S, Finke J, Wysocki VH. Ligand binding and unfolding of tryptophan synthase revealed by ion mobility-tandem mass spectrometry employing collision and surface induced dissociation. Int J Ion Mobil Spec. 2013;16:133–143. [Google Scholar]
- 23.Ma X. 2014. Mass spectrometry dissociation studies of protein-protein and protein-nucleic acid complexes and 13C flux of amino acids. PhD dissertation (Ohio State Univ, Columbus, OH)
- 24.Lewis SM, Kuhlman BA. Anchored design of protein-protein interfaces. PLoS One. 2011;6:e20872. doi: 10.1371/journal.pone.0020872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Harvey SR, Liu Y, Liu W, Wysocki VH, Laganowsky A. Surface induced dissociation as a tool to study membrane protein complexes. Chem Commun (Camb) 2017;53:3106–3109. doi: 10.1039/c6cc09606a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Busch F, et al. Localization of protein complex bound ligands by surface-induced dissociation high-resolution mass spectrometry. Anal Chem. 2018;90:12796–12801. doi: 10.1021/acs.analchem.8b03263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sahasrabuddhe A, et al. Confirmation of intersubunit connectivity and topology of designed protein complexes by native MS. Proc Natl Acad Sci USA. 2018;115:1268–1273. doi: 10.1073/pnas.1713646115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Quintyn RS, Zhou M, Yan J, Wysocki VH. Surface-induced dissociation mass spectra as a tool for distinguishing different structural forms of gas-phase multimeric protein complexes. Anal Chem. 2015;87:11879–11886. doi: 10.1021/acs.analchem.5b03441. [DOI] [PubMed] [Google Scholar]
- 29.Naud C, Calas P, Blancou H, Commeyras A. Synthesis of terminally perfluorinated long-chain alkanethiols, sulfides and disulfides from the corresponding halides. J Fluor Chem. 2000;104:173–183. [Google Scholar]
- 30.Pagel K, Hyung S-J, Ruotolo BT, Robinson CV. Alternate dissociation pathways identified in charge-reduced protein complex ions. Anal Chem. 2010;82:5363–5372. doi: 10.1021/ac101121r. [DOI] [PubMed] [Google Scholar]
- 31.Zhou M, Dagan S, Wysocki VH. Impact of charge state on gas-phase behaviors of noncovalent protein complexes in collision induced dissociation and surface induced dissociation. Analyst (Lond) 2013;138:1353–1362. doi: 10.1039/c2an36525a. [DOI] [PubMed] [Google Scholar]
- 32.Zhou M, Wysocki VH. Surface induced dissociation: Dissecting noncovalent protein complexes in the gas phase. Acc Chem Res. 2014;47:1010–1018. doi: 10.1021/ar400223t. [DOI] [PubMed] [Google Scholar]
- 33.Wang G, Dunbrack RL., Jr PISCES: A protein sequence culling server. Bioinformatics. 2003;19:1589–1591. doi: 10.1093/bioinformatics/btg224. [DOI] [PubMed] [Google Scholar]
- 34.Waldburger CD, Schildbach JF, Sauer RT. Are buried salt bridges important for protein stability and conformational specificity? Nat Struct Biol. 1995;2:122–128. doi: 10.1038/nsb0295-122. [DOI] [PubMed] [Google Scholar]
- 35.Steiner T. The hydrogen bond in the solid state. Angew Chem Int Ed Engl. 2002;41:49–76. doi: 10.1002/1521-3773(20020104)41:1<48::aid-anie48>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
- 36.Cremlyn RJW. An Introduction to Organosulfur Chemistry. Wiley; Hoboken, NJ: 1996. [Google Scholar]
- 37.Kiusalaas J. Numerical Methods in Engineering with Python 3. Cambridge Univ Press; Cambridge, UK: 2013. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.