Biased competition in the absence of input bias revealed through corticostriatal computation

Significance

The canonical model of the basal ganglia is based on competing direct (GO) vs. indirect (NO-GO) pathways. However, how is either of the two pathways activated if they receive the same corticostriatal inputs as experimental evidence suggests? Also, in the context of rule-based decisions, how is a specific action selected among competing GO pathways? We introduce a neural circuit model that identifies three alternative mechanisms flexibly supporting preferential processing between GO and NO-GO alternatives under balanced input. Only one of these mechanisms, however, is capable of enabling action selection by reinforcing, in the striatum, the rule-based rhythmic biases reported in prefrontal cortex.

Abstract

Classical accounts of biased competition require an input bias to resolve the competition between neuronal ensembles driving downstream processing. However, flexible and reliable selection of behaviorally relevant ensembles can occur with unbiased stimulation: striatal D1 and D2 spiny projection neurons (SPNs) receive balanced cortical input, yet their activity determines the choice between GO and NO-GO pathways in the basal ganglia. We here present a corticostriatal model identifying three mechanisms that rely on physiological asymmetries to effect rate- and time-coded biased competition in the presence of balanced inputs. First, tonic input strength determines which one of the two SPN phenotypes exhibits a higher mean firing rate. Second, low-strength oscillatory inputs induce higher firing rate in D2 SPNs but higher coherence between D1 SPNs. Third, high-strength inputs oscillating at distinct frequencies can preferentially activate D1 or D2 SPN populations. Of these mechanisms, only the latter accommodates observed rhythmic activity supporting rule-based decision making in prefrontal cortex.

Biasing the competition between neuronal ensembles is essential for preferential processing of relevant visual information (1). Two computational principles underlie biased competition as currently understood. First, stimulus-driven neuronal ensembles having distinct stimulus selectivity suppress each other’s activity via mutual inhibition. Second, an external input preferentially targets one of the competing ensembles, breaking the symmetry of the system. Computational models of biased competition implementing these principles can differ in considering either an asynchronous (2–5) or a rhythmic (6) input bias as well as in the impact of the bias on neural circuit dynamics, which may increase firing rate (FR) (2, 3), coherence (4, 5), or both (6).

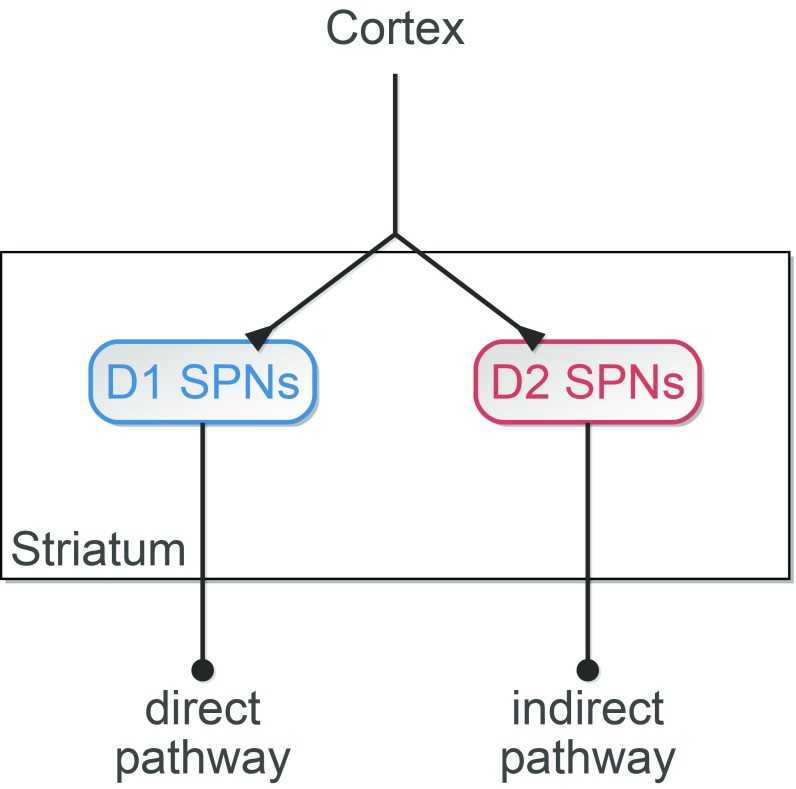
In this work, we introduce an entirely different set of computational principles for biased competition. In the absence of externally imposed (i.e., input) biases, we will show that biased competition, robust against activity fluctuations, emerges between neuronal ensembles endowed with distinct physiological properties. We use corticostriatal processing as a model system for biased competition in the absence of input bias (Fig. 1), denoted from here as internal biased competition, because striatal input–output processing is mediated by competition between two distinct GABAergic populations of spiny projection neurons (SPNs) expressing either D1 or D2 dopamine receptors (7–9) that receive balanced cortical stimulation (10).

Fig. 1.

Corticostriatal circuit model. The model is composed of D1 and D2 SPNs according to expressed dopamine receptor. Both phenotypes receive the same cortical input. D1 and D2 SPNs represent the first stage of the GO and NO-GO pathways, respectively, of the basal ganglia.

The differences between D1 and D2 SPNs span anatomical (11), network (12), and intrinsic properties (13), and the two inhibitory populations interact in complex and asymmetrical ways. Thus, it is difficult to predict a priori which physiological asymmetries enable biased competition and under which conditions. Consequently, we addressed this question in a neural circuit model of corticostriatal processing (Fig. 1).

Functionally, D1 and D2 SPNs represent the first relay of the direct (GO) and indirect (NO-GO) pathways of the basal ganglia. GO and NO-GO pathways compete with each other to either execute or hold an action (14). Coactivation of D1 and D2 SPNs during action initiation (15) imposes a limitation on winner-take-all competition in the striatum (16). Recent modeling work proves, however, that even weak activity biases strongly influence downstream attractor dynamics subserving routing and decision making (17). Our corticostriatal model builds on this view. Thus, we think of and refer to D1 and D2 SPNs in the model as neuronal ensembles representing execution (GO) or hold (NO-GO), respectively, of an action (Fig. 1). While the time course of a selected action may depend on complex interactions among distinct basal ganglia nuclei (16, 18), we hypothesize that a significant bias in the activity of D1 SPNs with respect to that of D2 SPNs or vice versa specifies the selection.

More generally, goal-directed behavior, as in rule-based decision tasks, requires selecting an action from multiple alternatives. Neural activity selective for rules, categories, and specific stimuli have been reported in prefrontal cortex (PFC) (19–22) and striatum (23, 24), with coactivation of competing ensembles in PFC, coactivating, in turn, competing pathways in the basal ganglia (25). Furthermore, recent experimental evidence in rule-based decisions highlights the central role of temporal dynamics (26), which challenges connectionist and rate models, omitting rhythms in their accounts for rule biases (17, 27, 28). Specifically, rhythmic activity at high beta frequencies is observed in the interaction between PFC and striatum during category learning (29) as well as within PFC while performing a rule-based decision task (26), where beta phase locking was higher for the neuronal ensemble encoding relevant information than for its irrelevant competitors. In the same rule-based decision task, alpha-band prefrontal activity emerged in ensembles processing the dominant sensory motor responses during nondominant trials (i.e., when these representations were irrelevant) (26), suggesting a link between alpha rhythms and inhibitory control.

Based on this evidence, we hypothesize that corticostriatal processing and internal biased competition in particular may be strongly implicated in rule-based preferential processing.

Results

D1 and D2 SPNs receive balanced cortical stimulation (10) (Fig. 1). How can balanced input enable a flexible biasing of neuronal ensembles (i.e., one that allows the selection of either ensemble through variation in the properties of their common input)? We hypothesize that biased competition is possible, because D1 and D2 SPNs are neuronal ensembles endowed with distinct physiological properties.

D1 and D2 SPNs Possess Different Physiological Properties.

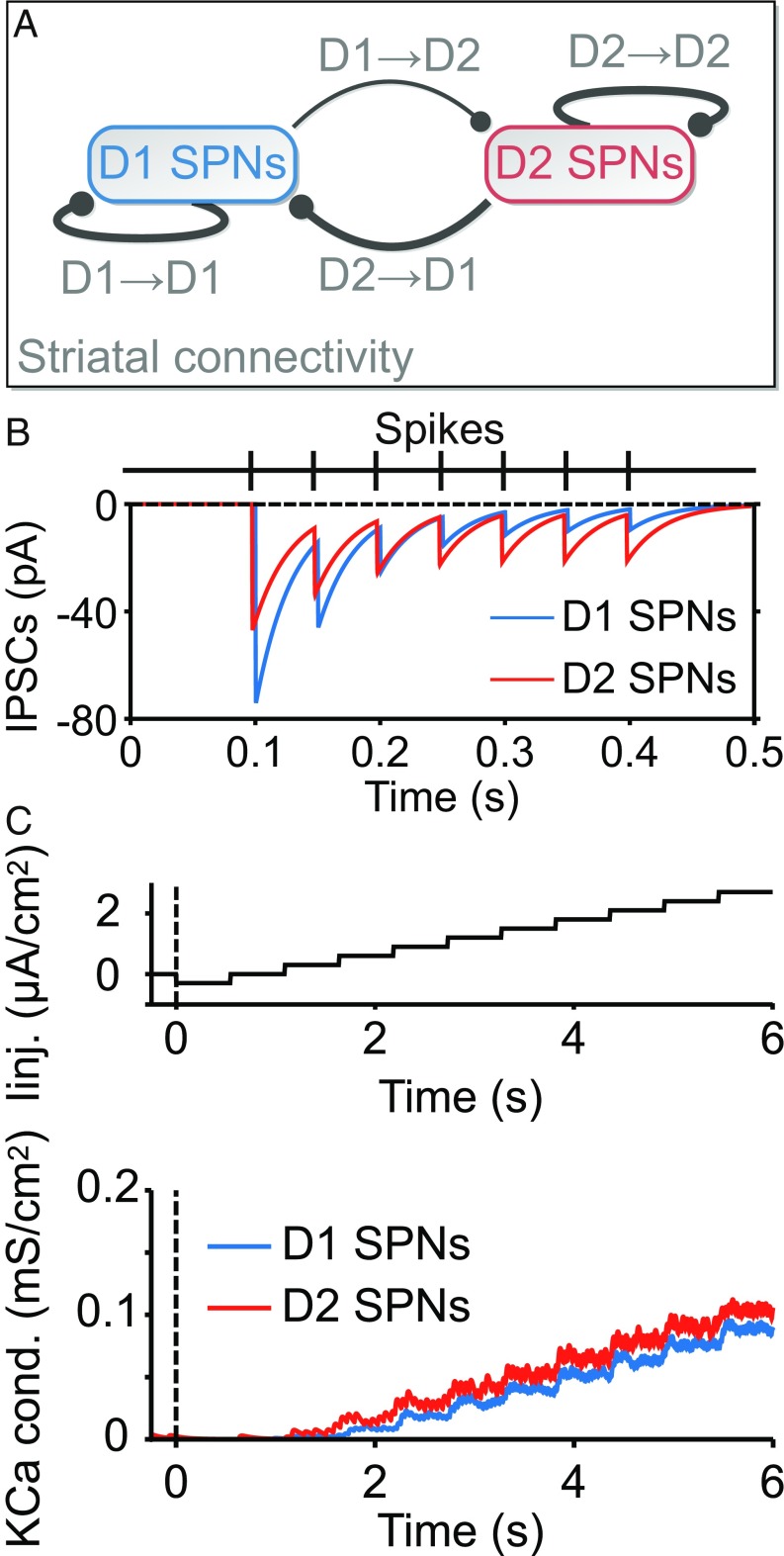
D1 and D2 SPN phenotypes exhibit three main experimentally observed physiological differences (Fig. 2): (i) an asymmetry in the sparse connectivity profile (Fig. 2A), in which there are about five times more connections from D2 to D1 SPNs than vice versa (11); (ii) distinct GABAergic dynamics (Fig. 2B), with efferent synapses from D1 SPNs having higher maximum conductance but more rapid depression than those from D2 SPNs (12); and (iii) distinct intrinsic properties (Fig. 2C) such that outward calcium-dependent potassium currents are activated earlier and more strongly in D2 SPNs (13).

Fig. 2.

D1 and D2 SPNs possess distinct physiological properties. (A) Asymmetric connectivity between D1 and D2 SPNs. About 5% of D1 SPNs target D2 SPNs, whereas other synaptic connections vary within the 25–35% range. (B) Distinct GABAergic dynamics in D1 and D2 SPNs. Synapses emerging from D1 SPNs have higher GABAergic conductance [see the difference in amplitude of the first inhibitory postsynaptic current (IPSC)], but they are depressed more rapidly (see the evolution of IPSC amplitudes). (C) Higher activation of outward calcium-dependent potassium currents in D2 SPNs. Upper shows the protocol of injected current that is applied to D1 and D2 SPNs in the model. Lower shows earlier and stronger activation of the channel in D2 SPNs.

Given that physiological differences between D1 and D2 SPNs exist (Fig. 2), the question arises about whether these physiological properties can be combined so that flexible biased competition emerges and if so, how.

Types of Biases Under Balanced Input: Tonic Excitability and Oscillatory Resonance.

There are two main ways to mediate internal biased competition, each exploiting a neural code based on either mean FR or precise spike timing (coherence).

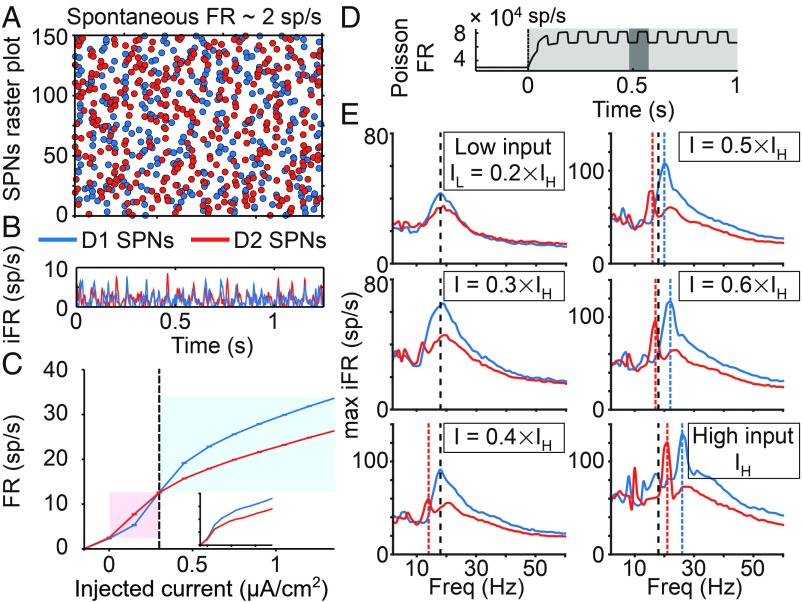
First, tonic input strength is able to induce a flexible mean FR bias, due to which each neuronal ensemble is preferentially activated by inputs within a characteristic range of intensities (Fig. 3C). This bias occurs, although the spontaneous activity of the two ensembles fluctuates around the same baseline level (Fig. 3 A and B). The fact that the two ensembles are differentially activated by high- and low-intensity inputs results from a tradeoff between inhibition and activity-dependent hyperpolarization: higher GABAergic inhibition targeting D1 SPNs predominates at lower input strengths, leading to higher FR in D2 SPNs, whereas higher outward calcium-dependent potassium currents in D2 SPNs reverse this bias at higher input strengths (Fig. 2C). This turning point in relative excitability fits with a confidence-based action selection interpretation of corticostriatal computation: lower input strengths represent low signal-to-noise ratios, for which triggering NO-GO actions may be behaviorally advantageous. Thus, the NO-GO pathway is favored at low confidence levels (i.e., when SPNs receive asynchronous inputs of lower strength), whereas the GO pathway is favored at high confidence levels (i.e., when SPNs receive asynchronous inputs of higher strength). This mechanism for producing a bias is only apparent at the population level when a sufficiently large proportion of cells is stimulated by the input. In contrast, the turning point disappears under single-cell stimulation (Fig. 3C, Inset), because single-cell stimulation barely affects the GABAergic dynamics of the network.

Fig. 3.

D1 and D2 SPNs respond differently to the same input. (A) Raster plot of the spontaneous activity of SPNs. (B) Instantaneous firing rate (iFR; average firing of the population varying in time) of SPNs. (C) Averaged f–I curve of each neuronal ensemble (input–output transfer function between injected current, as in Fig. 2C, Upper, and time-averaged population FR). The higher excitability of D2 SPNs is shaded in red. The higher excitability of D1 SPNs is shaded in blue. (Inset) The f–I curve when the injected current is applied only to a single cell of each population. (D) Rate of the Poisson process underlying the stochastic oscillatory input to the striatal circuit: when the stimulus is on (shaded in light gray), the rate increases and oscillates at a given frequency (inverse of the period, which appears shaded in dark gray). (E) Resonance of SPNs for different inputs strengths. The resonance in each panel is quantified in terms of maximum iFR, a measure of local population synchronization: across input frequencies (x axis), the average of the peak iFR through all cycles is computed (y axis). Resonant frequencies are highlighted by vertical lines. Black dashed lines represent the resonance of D1 and D2 SPNs at low input strength. Blue and red dashed lines represent shifts in resonance for D1 and D2 SPNs, respectively.

Second, an oscillatory input can induce a coherence bias by preferentially activating the resonant properties of a specific neuronal ensemble. In fact, by varying the frequency of a rhythmic cortical input (Fig. 3D), our model reveals two ways in which the resonances of the two SPN ensembles are distinguished from each other. At the low input strength (Fig. 3E, low input), D1 and D2 SPN populations both resonate at the same beta frequency, but D1 SPNs are more strongly synchronized by rhythmic input, despite their lower mean FRs (8.4 vs. 8.9 sp/s for D1 and D2 SPNs, respectively). This divergence between rate and coherence relies on synaptic inhibition. Higher inhibition decreases the overall FR but enhances spiking coherence, since cells are pushed closer to baseline by inhibition, and thus, they exhibit a more uniform state when inhibition wears off (30). At the high input strength (Fig. 3E, high input), the resonant frequencies of D1 and D2 SPN populations both increase and separate from each other. For D1 SPNs, the increase in resonant frequency (Fig. 3E, Right) occurs, because the external input drives SPNs faster (19, 21, and 26 sp/s, respectively) than their network frequency (centered around 18 Hz). This is not the case when the external input drives SPNs more slowly (Fig. 3E, Left) (8.4, 13, and 16 sp/s, respectively). Interestingly, D2 SPNs do not need to be driven faster than their resonant frequency at low input strength to shift their resonance. While under low input strengths, D2 SPNs inherit their resonance from that of D1 SPNs (Fig. 3E, Top Left and Middle Left) (overall FR: 8.9 and 12 sp/s, respectively, which represent a mismatch with respect to their resonant frequency), and higher external inputs allow D2 SPNs to coordinate their own firing irrespective of D1 SPNs (Fig. 3E, Bottom Left and Bottom Right) (13, 16, 17, and 21 sp/s, respectively, which closely match their resonant frequency), presumably by triggering more recurrent inhibition and hence, increasing the release of GABA neurotransmitter in D2 SPNs.

The signal-to-noise ratio of an input can be enhanced by increasing its strength (assuming that the fluctuations stay the same) but also, by increasing its temporal structure. For inputs of modest strength, favoring the NO-GO pathway by default seems behaviorally advantageous, yet reliable GO selections may still be accomplished if rhythmic inputs match the resonant dynamics of SPNs. In addition, our model suggests that highly reliable selections (in terms of high signal-to-noise ratio) of GO and NO-GO actions occur under rhythmic inputs of higher strength when the frequency of the input specifically matches the resonant frequency of either D1 or D2 SPNs.

In summary, Fig. 3 reveals three ways by which balanced inputs can bias the competition between D1 and D2 SPNs, and two of those are supported by the resonant properties of SPNs. The next section addresses how these biases can be used to flexibly and reliably bias between the GO and NO-GO action selection.

Flexibly Biasing Between the GO and the NO-GO Pathways.

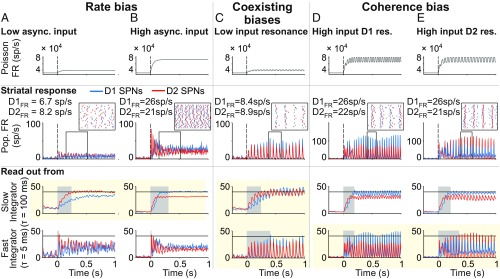
Fig. 4 illustrates how preferential processing, built on tonic excitability and oscillatory resonance of SPNs, is flexible according to input properties: (i) in terms of a rate bias regulated by the high- vs. low-strength input (Fig. 4 A and B) and (ii) in terms of a coherence bias regulated by the high-strength input oscillating at distinct beta bands (Fig. 4 D and E).

Fig. 4.

Three mechanisms flexibly and reliably bias the striatal circuit under balanced input: rate, coherence, and coexisting biases. Rate bias: A vs. B. (A and B) Biasing between GO and NO-GO pathways depends on the overall strength of the balanced cortical input. (Top) Rate of the Poisson process underlying the stochastic asynchronous input to the striatum. (Middle) Population FR [instantaneous firing rate (iFR)]. (Inset) Raster activity of (n = 20) D1 and D2 SPNs (the time window is indicated by the black frame in Middle). (Bottom) Downstream readout of the activity of SPNs using distinct integration timescales. Only slow timescale integration shows flexibility in biasing GO and NO-GO actions (highlighted with the yellow background). Response time is shaded in light gray. Response threshold is at 40 sp/s (solid horizontal lines). (C) Coexisting biases. Biasing between GO and NO-GO pathways under balanced inputs of low strength depends on resonant properties of SPNs and a dynamic tuning of readout timescale. (Top) Rate of the Poisson process underlying the stochastic oscillatory input to the striatal circuit that matches the resonant frequency of SPNs. (Middle) Population FR (iFR; amplitude of which is a measure of local population synchronization). (Inset) Raster activity of (n = 20) D1 and D2 SPNs (the time window i0s indicated by the black frame in Middle). (Bottom) Downstream readout of the activity of SPNs using a distinct integration timescale. On-the-fly tuning of the readout timescale (details are in the text) allows for flexibility in biasing between GO and NO-GO actions (highlighted with the yellow background). Response time is shaded in light gray. Response threshold is at 40 sp/s (solid horizontal lines). Coherence bias: D vs. E. (D and E) Biasing between GO and NO-GO pathways under balanced inputs of high strength depends on resonant properties of SPNs and the spectral content of the cortical input. (Top) Rate of the Poisson process underlying the stochastic oscillatory input to the striatal circuit that matches the resonant frequency of either SPN type. (Middle) Population FR (iFR; the amplitude of which is a measure of local population synchronization; note the higher scale of D and E compared with A–C). (Inset) Raster activity of (n = 20) D1 and D2 SPNs (the time window is indicated by the black frame in Middle). (Bottom) Downstream readout of the activity of SPNs using a distinct integration timescale. Only fast timescale integration shows flexibility in biasing GO and NO-GO actions (highlighted with the yellow background). Response time is shaded in light gray. Response threshold is at 40 sp/s (solid horizontal lines).

In addition to those, our model also reveals flexible preferential processing between SPNs (iii) in terms of coexisting rate and coherence biases for rhythmic inputs of low-intensity oscillating at SPN resonance (Fig. 4C). Coexisting biases can occur simultaneously only because the rate bias favors the activity of D2 SPNs, whereas the coherence bias favors the activity of D1 SPNs.

We next investigated how reliable each of these mechanisms is at driving downstream action selection. To address this question, we ran the model output through two readout decoders of striatal activity. The first decoder was a spiking activity accumulator with a slow integration timescale ($\tau$ = 100 ms). The second decoder was a coincidence detector with a fast integration timescale ($\tau$ = 5 ms). Our results show that the nature of the striatal bias must fit the timescale of the decoder to guarantee reliable downstream selection (Fig. 4). Thus, only the activity accumulator reliably selects either the GO or NO-GO pathway from the FR bias between D1 and D2 SPNs (Fig. 4 A, Bottom and B, Bottom), while only the coincidence detector flexibly selects either the GO or NO-GO pathway from the coherence bias between D1 and D2 SPNs (Fig. 4 D, Bottom and E, Bottom). When rate and coherence biases coexist, the selection between GO and NO-GO pathways depends on the integration timescale of the decoder. Thus, a coincidence detector reads out the coherence bias of D1 SPNs, whereas an activity accumulator reads out the rate bias of D2 SPNs. Flexible action selection in this case requires adjusting the decoder integration timescale, and therefore, it behaves as a coincidence detector or as an activity accumulator. A way to accomplish this may be by adjusting the amount of balanced inhibition in the decoder, which has been shown to regulate temporal precision (31).

These mechanisms impose predictions that can be tested experimentally. According to the rate bias mechanism, action release must functionally correlate with higher mean FR of D1 over D2 SPNs (Fig. 4B). According to the coherence bias mechanism, action release must functionally correlate with a peak in spike-field coherence at either higher (Fig. 4D) or lower (Fig. 4C) beta frequencies. Note that mean rate and coherence biases may both be present at once (Fig. 4D). A contrast between correct and error trials and/or between short and long response time trials may help to identify the ultimate mechanism supporting internal biased competition. For instance, in the context of Fig. 4D, we expect that spike-field coherence is more strongly correlated with behavior than the mean rate difference between D1 and D2 SPNs.

Internal Biased Competition Supporting Rule-Based Decisions.

We focused so far on the situation in which D1 and D2 SPN ensembles compete for the power to trigger or hold isolated actions, but goal-directed behaviors, such as rule-based decisions, require selecting a proper action from multiple alternatives.

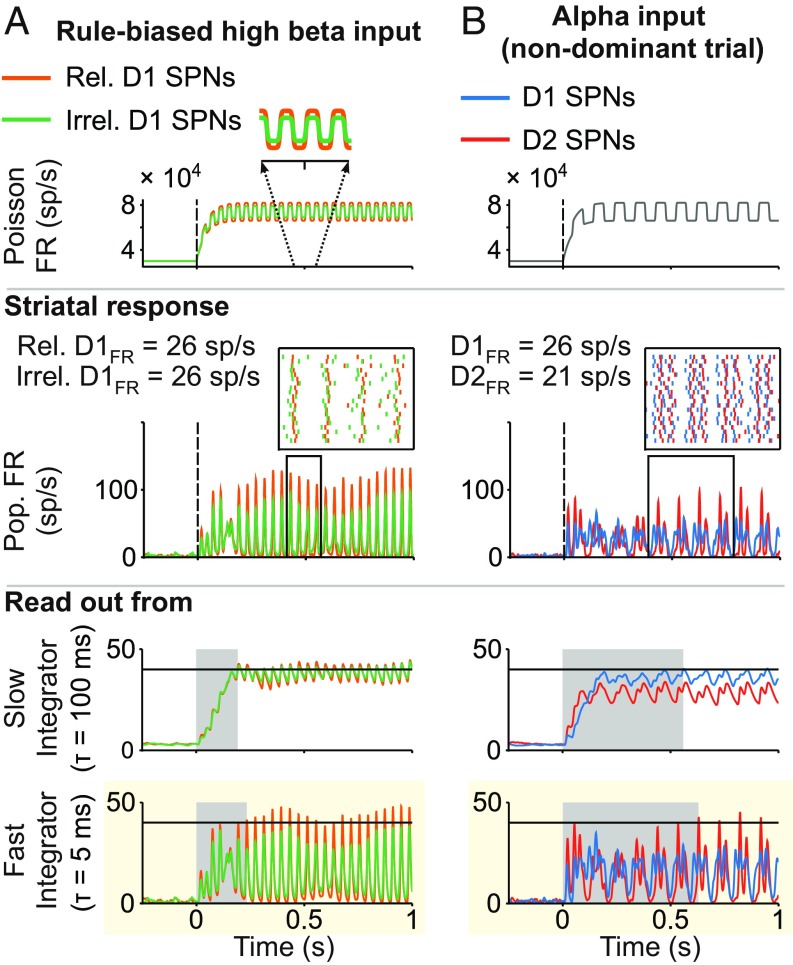
Our model sheds light on how rule-based high beta and alpha rhythms in PFC may affect downstream processing in the striatum via the coherence bias mechanism. Based on experimental evidence, we assume that (i) D1 and D2 SPN ensembles representing the same categorical action receive balanced input (10), whereas (ii) SPNs representing relevant categorical actions receive more synchronized input at high beta frequency than SPNs representing irrelevant categorical actions (26) (Fig. 5A, Top). The model omits any potential bias in terms of input strength, since experimental support is currently lacking. Under these conditions, higher input synchrony produces more coherent striatal firing (Fig. 5A, Middle), a bias that can be reliably read out by a coincidence detector but not by an activity accumulator, because the mean FR is assumed to be the same for relevant and irrelevant SPN ensembles (Fig. 5A, Middle and Bottom). Thus, higher beta coherence in PFC is able to bias relevant over irrelevant GO pathways in the basal ganglia. The other two internal biased competition mechanisms failed to favor the relevant GO pathway under these conditions (SI Appendix, Fig. S3B and SI Text).

Fig. 5.

Striatal processing of rhythmic cortical inputs involved in rule-based decisions. (A) Rule-based biased competition between GO pathways: stimulus-driven high beta rhythmic input from PFC biases action selection. (Top) Rate of the Poisson process underlying the stochastic high beta oscillatory input to the striatal circuit. The frequency (high beta) and distinct amplitude of the oscillatory input to SPNs (higher for relevant SPNs; in Inset) are constrained by reported synchronous activity in PFC (details are in the text). The same input targets D1 and D2 SPNs. (Middle) Population FR [instantaneous firing rate (iFR), the amplitude of which is a measure of local population synchronization]. (Inset) Raster activity of (n = 20) relevant and irrelevant D1 SPNs (the time window is indicated by the black frame in Middle). (Bottom) Downstream readout of the activity of D1 SPNs using the distinct integration timescale. Only fast timescale integration shows a reliable bias in favor of the relevant GO action (highlighted with the yellow background). Response time is shaded in light gray. Response threshold is at 40 sp/s (solid horizontal lines). (B) Striatal dynamics toward the NO-GO pathway favored by alpha oscillatory inputs (present in PFC ensembles in nondominant trials; details are in the text). (Top) Rate of the Poisson process underlying the stochastic alpha oscillatory input to the striatal circuit. (Middle) Population FR (iFR). (Inset) Raster activity of (n = 20) D1 and D2 SPNs (the time window is indicated by the black frame in Middle). (Bottom) Downstream readout of the activity of SPNs using the distinct integration timescale. For the alpha rhythm to mediate inhibitory control, an NO-GO bias should prevail. This is only the case through the fast integration timescale (highlighted with the yellow background). Response time is shaded in light gray. Response threshold is at 40 sp/s (solid horizontal lines).

In the striatum, inhibitory control is mediated favoring the NO-GO pathway. For an alpha rhythm in PFC to play a role in downstream inhibitory control, it needs to bias the activity of D2 over D1 SPNs. This is the case for the coherence bias mechanism: the balanced cortical input of high strength, oscillating at alpha frequencies (Fig. 5B, Top), leads to more coherent firing in D2 SPNs (Figs. 3E, high-input panel, and 5B, Middle), which can be reliably read out by a coincidence detector (Fig. 5B, Bottom). An activity accumulator, on the contrary, does not support an alpha oscillatory input as an inhibitory control mechanism, since it reads out the higher mean FR of D1 SPNs (Fig. 5B, Bottom). Thus, our model suggests a manner by which cortical inputs oscillating at alpha frequencies synchronize the activity of D2 SPNs more strongly than that of D1 SPNs, hence favoring the selection of the NO-GO pathway. The other two internal biased competition mechanisms failed to favor the NO-GO pathway (SI Appendix, Fig. S3A and SI Text).

Discussion

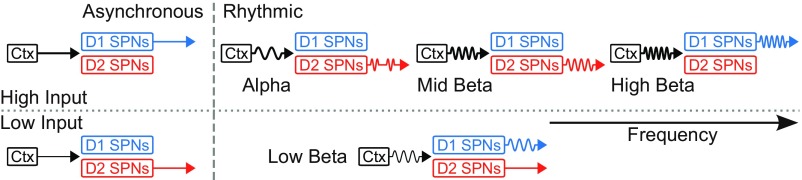
The results reported in this work, summarized in Fig. 6, reveal computational principles underlying preferential processing in support of goal-directed behaviors, such as action selection in the striatum. These mechanisms extend previous approaches that considered unbalanced inputs as the source of the bias between competing neuronal ensembles. Such an approach in the context of corticostriatal processing (32) seems to be challenged by the experimental evidence of balanced cortical input to SPNs (10) [but note the caveat that plasticity biases between cortical synapses targeting D1 vs. D2 SPNs, shaped (for instance) by learning, were not explicitly considered]. In contrast, our model predicts that flexibly biasing basal ganglia dynamics toward activation of either the GO or NO-GO pathway can be accomplished by tuning either the strength or the spectral properties of a balanced cortical input (SI Appendix, SI Text has a detailed comparison between our model and that in ref. 32). Of the alternative mechanisms supporting internal biased competition, only the coherence bias mechanism is consistent with observed rhythmic activity in PFC in the context of rule-based decisions (26). In fact, our model of corticostriatal processing suggests a mechanistic explanation for how alpha and high beta rhythms in PFC support inhibitory control and rule-based action selection, respectively, in the basal ganglia.

Fig. 6.

Schematic representation of input–output computation between cortex (Ctx) and striatum. Only the biases between D1 and D2 SPNs are represented as striatal output, and they are determined by the properties of the cortical input: strength (low vs. high; vertical axis) and frequency (asynchronous vs. synchronous; horizontal axis). Note the coexistence of biases for the low strength input oscillating at low beta frequency.

An attractive, if speculative, hypothesis is that the three internal biased competition mechanisms (Fig. 4) play a role at different learning stages. Dopamine release increases the FR of rule-selective neural ensembles in the PFC (33), and these very same ensembles synchronize at high beta frequency (26, 34), which is expected to build up through training. Based on these observations, we suggest that corticostriatal inputs grow in signal-to-noise ratio, both in strength and coherence, through practice. Thus, at early learning stages, cortical inputs are presumably of weak intensity, for which NO-GO activation may be the default mode (Fig. 4A). Only when the signal-to-noise ratio is slightly higher, either by a modest increase in overall strength (Fig. 3C) or by enhanced temporal coordination at beta frequency (Fig. 4C), may a GO selection be effectively prioritized. Through continuous learning, cortical inputs are expected to grow in mean drive, biasing the preferential selection toward the GO pathway further and further (Fig. 3C). Soon thereafter, cortical inputs are strong enough to dissociate the resonant frequency of SPNs (Figs. 3E and 4D vs. Fig. 4E). Starting at this learning stage, alpha vs. high beta inputs may be able to reliably activate top down-triggered inhibitory control (Fig. 5B) vs. rule-based action selection (Fig. 5A) downstream in the striatum.

The validity of these computational principles may extend beyond corticostriatal processing. Thus, a rate bias may arise wherever a difference in relative excitability exists between competing neuronal ensembles (35, 36), and a coherence bias may be induced whenever competing neuronal ensembles resonate at distinct frequencies (37). For the two biases to exist simultaneously, there must be a tradeoff between FR and coherence. In our model, this tradeoff relies on competing neuronal ensembles receiving different amounts of inhibition internally generated within the striatal microcircuit, despite balanced cortical input. We suspect that the FR–coherence tradeoff may also be present (for instance, in cortex) when the competing ensembles possess different AMPA-to-NMDA conductance ratios, resulting in different synaptic decay timescales: while more AMPA excitation may enhance coherent dynamics (6), less NMDA excitation reduces the overall excitability and hence, decreases the overall FR.

We analyzed biased competition between distinct neuronal ensembles receiving the same input, the inverse condition of “classical” biased competition, where identical ensembles receive unbalanced inputs. In general, biased competition may occur between competing neuronal ensembles that differ both physiologically and in their input. While this situation is more complex (e.g., cooperation vs. competition between internal and external biased competition mechanisms), it may be ubiquitous in the brain and likely dynamically modulated by learning; hence, it is important to consider systematically. Our work provides a foundation on which to address this challenge.

Materials and Methods

The model’s architecture appears in Fig. 1. Main differences between D1 and D2 SPNs are specified in Fig. 2. The model was implemented in DynaSim (38), a free open source MATLAB- and GNU Octave-compatible toolbox for simulating dynamical systems. Additional text, equations, and parameter values of the model as well as computation of population activity and formulation of readout decoders are fully described in SI Appendix.