Abstract
Based on the coarse-grained UNRES and NARES-2P models of proteins and nucleic acids, respectively, developed in our laboratory, in this work we have developed a coarse-grained model of systems containing proteins and nucleic acids. The UNRES and NARES-2P effective energy functions have been applied to the protein and nucleic-acid components of a system, respectively, while protein – nucleic-acid interactions have been described by the respective coarse-grained potentials developed in our recent work [Yin et al., J. Chem Theory Comput., 2015, 11, 1792–1808]. The Debye-Hückel screening has been applied to the electrostatic-interaction energy between the phosphate groups and charged amino-acid side chains. The model has been integrated into the UNRES package for coarse-grained molecular dynamics simulations of proteins and the implementation has been tested for energy conservation in microcanonical molecular dynamics runs and for temperature conservation in canonical molecular dynamics runs. Two case studies were performed: (i) the dynamics of the Ku protein heterodimer bound to DNA, for which it was found that the Ku70/Ku80 protein complex plays an active role in DNA repairing and (ii) conformational changes of the multiple antibiotic resistance (MarA) protein occurring during DNA binding, for which the functionally-important motions occurring during this process were identified.
Keywords: Protein-nucleic acid interactions, Coarse graining, UNRES, NARES-2P, Molecular dynamics
Graphical Abstract

Illustration of the coarse-grained representation of protein – nucleic-acid systems implemented in this work with the example of the multiple antibiotic resistance (MarA) protein – DNA complex. Left: the DNA fragment in NARES-2P representation, right: the protein fragment in UNRES representation. The virtual bonds are shown as sticks, united side chains and nucleic-acid bases are shown as ellipsoids of revolution, united peptide groups are shown as light-blue spheres and united phosphate groups are shown as light-red spheres.
INTRODUCTION
Modeling the structure and dynamics of biological macromolecules and molecular assemblies is nowadays of utmost importance in the quest for the understanding of the functioning of the machinery of life. Owing to the use of world-distributed computing (the FOLDING@HOME project)1 the development of very efficient load-balanced parallel codes such as GROMACS2, NAMD3, or DESMOND4, the implementation of all-atom molecular dynamics (MD) programs on graphical processor units (GPUs)5, and the construction of dedicated machines6,7, enormous progress has been achieved in the field of all-atom molecular simulations in the last two decades. Nevertheless, the biological size- and time-scale is still beyond reach with the all-atom approach.
Coarse graining, which is a procedure to reduce the representation of a system under study from atomistic-detailed to a less detailed one, provides an intermediate resolution at which it is possible to handle large systems8–11. In the last two decades, we have been developing the physics-based UNited RESidue (UNRES) model for the simulations of the structure and dynamics of proteins12,13 and, quite recently, the NARES-2P model of nucleic acids13–15. The effective energy functions of UNRES and NARES-2P originate from the potential of mean force of the system under study, in which the degrees of freedom not present in the model (secondary degrees of freedom) are integrated out8,16,17, which is further split into the Kubo cluster-cumulant functions18. The cluster-cumulant functions can be identified with particular components of the effective energy and are, finally, expanded into the generalized cumulant series18, this enabling us to obtain analytical expressions for the effective energy terms, including the very important multibody terms16,17. Owing to the application of this rigorous methodology, the number of interaction sites in UNRES and NARES-2P is only 2 per residue, while successful unrestrained simulations of the structure and dynamics of proteins and nucleic acids are successful with these models13,19.
UNRES has proved to be a successful tool for protein structure prediction, as assessed in the Community Wide Experiments on the Critical Assessment of Techniques for Protein Structure Prediction (CASP)20,21, and has been a useful tool for studying protein complexes22,23. NARES-2P13–15 can treat both DNA and RNA systems14. The NARES-2P model was able to reproduce many biologically-relevant properties of double-helix B-DNA, such as duplex formation, breathing motions, melting temperatures14,15, and mechanical stability17.
Although the structure, dynamics, and thermodynamics of proteins and nucleic acids can be modeled reliably with UNRES and NARES-2P, until now, these two models did not cover systems containing both kinds of these biological macromolecules. Interactions between proteins and nucleic acids are essential for proper cell functioning24, DNA replication25, transcription activation26 and regulation27, recombination process28,29, DNA repairing29,30, etc. Therefore, in this work, we combined the UNRES and NARES-2P models to handle protein – nucleic-acid systems. We used the coarse-grained potentials for the interactions between the protein and nucleic-acid components that we developed in our earlier work31. We integrated the UNRES and NARES-2P models and the protein – nucleic-acid interaction potentials into the newest UNRES package written in FORTRAN 9032. As for UNRES33,34 and NARES-2P14, we implemented molecular dynamics (MD) as the main conformational-search engine33–35. After testing the implementation for energy and temperature conservation in microcanonical and canonical MD runs, respectively, we applied the newly developed model to study the initial stage of DNA-repair mechanism by the Ku70/Ku80 protein heterodimer30 and found that the heterodimer is actively involved in DNA unwinding. We also applied the model to study conformational changes upon DNA - protein association with the example of multiple antibiotic resistance protein (MarA)36. We found that domain closing and major grove binding loop re-adjustment are the most important moves during DNA binding.
METHODS
Structure of the coarse-grained model of protein – nucleic-acid systems
In the model of protein – nucleic-acid systems developed in this work, the UNRES12,13,16,37–40 representation is used for the protein part of a protein – nucleic acid-system, while the NARES-2P13,14 representation is used for the nucleic-acid part. As in UNRES and NARES-2P, the solvent is implicit in the model and is accounted for in the effective potentials of interactions between the coarse-grained sites. The effective energy function consists of the UNRES and the NARES-2P energies of the protein and the nucleic-acid parts, respectively, and the effective energy of interactions between these parts (Uprot−nucl), as expressed by eq. (1). It should be noted that both the protein and the nucleic-acid parts usually consist of multiple chains.
| (1) |
The UNRES and NARES-2P models and the pertinent effective energy functions are summarized in sections “UNRES model of polypeptide chains” and “NARES-2P model of the polynucleotide chains”, respectively, while the effective potentials of protein – nucleic-acid interactions are discussed in section “Effective potentials for the polypeptide-nucleic acid interactions”.
UNRES model of polypeptide chains
In the UNRES model12,13,16,37–40, a polypeptide chain is represented by a sequence of α-carbon (Cα) atoms, with united peptide groups (p) placed halfway between the two consecutive Cα atoms, and united side chains (SC) attached to the Cαs. Only the SC and p centers are interaction sites, while the Cα atoms serve only to define the geometry of a polypeptide chain (Figure 1A).
Figure 1.

(A) UNRES model of polypeptide chains. The interaction sites are united peptide groups (p) represented by light-blue spheres, which are located halfway between the consecutive α-carbon atoms (shown as small white spheres), and united side chains attached to the α-carbon atoms (SC), represented by spheroids with different colors and dimensions. Backbone geometry of the simplified polypeptide chain is defined by the Cα · · · Cα · · · Cα virtual-bond angles θ (θi has the vertex at Cα) and the Cα · · · Cα · · · Cα · · · Cα virtual-bond-dihedral angles γ (γi has the axis passing through and ). The local geometry of the ith side-chain center is defined by the zenith angle αi (the angle between the bisector of the respective angle θi and the vector) and the azimuthal angle βi (the angle of counter-clockwise rotation of the vector about the bisector from the plane, starting from ). For illustration, the bonds of the all-atom chains, except for those to the hydrogen atoms connected with the carbon atoms, are superposed on the coarse-grained picture. (B) NARES-2P model of polynucleotide chains. The interaction sites are united phosphate groups (P), represented by yellow circles, which are located halfway between the centers of the consecutive sugar rings (S; shown as small red spheres), and united sugar-base groups (B), represented by light-blue spheroids. The united sugar centers serve only to define chain-backbone geometry. The meaning of angles, θ, γ, α, and β is as in panel A.
The UNRES force field originates from the potential of mean force of a protein in aqueous environment, which has been expanded into a cluster-cumulant series to give an implementable effective energy function16,17. This energy function is given by eq. 2.
| (2) |
where the U′s are energy terms, θi is the backbone virtual-bond angle between the , and , atoms, γi is the backbone virtual-bond-dihedral angle, defined by the , , , and , atoms, αi and βi are the angles defining the location of the center of the united side chain of residue i (Figure 1A) with respect to the frame defined by the , and atoms, di is the length of the ith virtual bond, which is either a Cα · · · Cα or a Cα · · · SC virtual bond, and the angles τ(1) – τ(3) are the SC· · · Cα · · · Cα · · · Cα (τ(1)), Cα · · · Cα · · · Cα · · · SC (τ(2)), and SC· · · Cα · · · Cα · · · SC (τ(3)), respectively. Each energy term is multiplied by the appropriate weight, wx, and the terms corresponding to factors of order higher than 1 are additionally multiplied by the respective temperature factors which were introduced in our earlier work39 and which reflect the dependence of the first generalized-cumulant term in those factors on temperature, as discussed in refs 39 and 41. The factors fn are defined by eq. (3).
| (3) |
where T◦=300 K.
The terms represent the mean free energy of the hydrophobic (hydrophilic) interactions between the side chains, which implicitly contain the contributions from the interactions of the side chains with the solvent. The terms denote the excluded-volume potentials of the side-chain – peptide-group interactions. The peptide-group interaction potentials are split into two parts: the Lennard-Jones terms and the average peptide-group-dipole interaction terms ; the second of these terms accounts for the tendency to form backbone hydrogen bonds between peptide groups pi and pj. The terms Utor, Utord, Ub, Urot, and Ubond are the virtual-bond-dihedral angle torsional terms, virtual-bond dihedral angle double-torsional terms, virtual-bond angle bending terms, side-chain rotamer, and virtual-bond-deformation terms; these terms account for the local properties of the polypeptide chain. The terms represent correlation or multibody contributions from the coupling between backbone-local and backbone-electrostatic interactions, and the terms are correlation contributions that involve m consecutive peptide groups; they are, therefore, termed turn contributions. The multibody terms are indispensable for reproduction of regular α-helical and β-sheet structures16,42,43. The USC−corr terms are side-chain backbone correlation potentials44,45 introduced to the UNRES force field, which improved loop structures and secondary structure recognition of the UNRES force field.
The energy-term weights have been determined and other force-field parameters have been refined by calibrating the force field with a set of seven proteins that belong to different structural classes46.
NARES-2P model of the polynucleotide chains
In the NARES-2P model13,14, a polynucleotide chain is represented by a sequence of deoxyribose (for DNA) or ribose (for RNA) ring centers (S) with united sugar – nucleic-acid-base (B) centers attached to them and united phosphate groups (P) located in the middle between the consecutive sugar-ring centers (Fig. 1B). As the Cαs in UNRES, the sugar centers serve only to define the virtual-chain geometry, while the B and P centers are the interaction sites. The effective energy function of the NARES model14 is expressed by eq. (4).
| (4) |
where and denote the Gay-Berne and mean field dipole-dipole interaction potentials of the sugar-base sites, respectively, and denote the phosphate-phosphate and phosphate – sugar-base interaction potentials, respectively, Ubond, Uang, Utor and Urot denote virtual-bond-stretching, virtual-bond-angle-bending, torsional, and sugar-base-rotamer potentials, respectively, and f2(T) is defined by eq. (3) with n = 2. Each term is multiplied by the appropriate weight (wx); the weights have been determined by force-field calibration with small DNA molecules14,15.
This energy function was implemented in the new FORTRAN 90 UNRES package32.
Effective potentials for the polypeptide-nucleic acid interactions
The energy function for DNA-nucleic acid interactions (Uprot−nucl) is based on the potentials determined in our earlier work31 and is expressed by eq. (5):
| (5) |
where , , and are protein side-chain – nucleic acid sugar-base, protein peptide-group – nucleic acid phosphate group, protein peptide-group – nucleic acid sugar-base, and protein side-chain – nucleic acid phosphate group effective interaction potentials, respectively, which are expressed by eqs. (S1-S53) of the Supporting Information of ref 31. Each term is multiplied by the appropriate weight (wx). Currently, all weights are set at 1. In order to determine the energy-term weights and fine-tune the other parameters of the force field calibration should be carried out15,46 with a set of model small protein-DNA systems. This task requires a lot of effort and, therefore, we defer it to our further work. Nevertheless, as the two examples presented in the Results section suggest, even the present force field can give reliable results regarding the DNA-binding mode and functionally important motions of protein-DNA complexes.
Because we have found that charged side chains interact with the phosphate groups too strongly, the expressions for the electrostatic-interaction energies of the Asp-P, Glu-P, Lys-P, and Arg-P pairs have been modified in this work to introduce a Debye screening factor, as expressed by eq. (6). The other parameters of these potentials have been taken from our earlier work31.
| (6) |
with
| (7) |
where qi = ±1 is the charge of a side-chain headgroup, qj = −1 is the charge of the phosphate group, Rij is the distance between the side-chain headgroup and the phosphate-group center, ϵin is the effective dielectric constant, which was one of the fitted parameters in deriving the potentials31, κ is the Debye screening constant, and σi is the thickness of the solvation shell of site i [see eq. (S27) of the Supporting Information of ref 31 and eq. (17) of ref 47]. Another modification was to reduce the distances of the polar head groups of the His and Asn residues from the side-chain centers to 1.74 Å and 1.01 Å, respectively because the distances obtained by PMF fitting were too long (4.62 Å and 6.04 Å, respectively; see Table S24 of the Supporting Information of ref 31).
The protein-DNA energy function described above was implemented in the new FOR-TRAN 90 package32.
Tests of coarse-grained molecular dynamics
To verify the stability of MD runs with the new potentials for protein – nucleic-acid interactions, energy conservation in microcanonical MD simulations were checked first with the example of the MarA protein bound to DNA (PDB code: 1BL0)36. The system was energy-minimized before performing simulations, and 1,000,000 MD steps with 0.498 fs time step were subsequently run.
Temperature conservation with the new potentials was verified by running canonical simulations with the Langevin34 and then Berendsen48 thermostats implemented with UNRES34. The system was energy-minimized before performing simulations, and 1,000,000 MD steps with 4.98 fs time step were subsequently run. Both Langevin- and Berendsen-thermostat runs were performed at T=300 K. For the Berendsen thermostat48, the coupling parameter τ = 48.9 fs was used and water friction was scaled by the factor of 0.01 in Langevin simulations to speed up the calculations, as in our earlier work34.
Dynamics of the Ku heterodimer bound to DNA
To study the initial stage of the DNA repair mechanism, MD simulations were carried out with the Ku heterodimer bound to damaged DNA (with mismatched base pairs). The starting structure was the crystal structure of the Ku70/Ku80 heterodimer bound to damaged DNA (PDB code:1JEY)30. Because two protein loops are missing in the crystal structure, MODELLER49 was used to add these missing sections of the structure. A series of five Langevin dynamics simulations at T = 300 K, 180,000 MD steps with 0.498 fs step length each, were carried out. These simulations were run with a small time step in order to capture all important events that take place during DNA repair by the Ku protein. It should be kept in mind that the time scale of coarse-grained simulations is at least 1,000 times wider than that of all-atom simulations34,50 and, consequently, processes occur much faster at the coarse-grained level. This time-scale extension results from the high reduction of the number of explicitly treated degrees of freedom (only 6 virtual-bond-vector coordinates per residue34) and smoothing the free energy landscape. Because of this time-scale distortion, the simulation settings correspond to approximately 90 ns of an all-atom simulation. Snapshots were collected every 1000 steps (a total of 900 snapshots from all trajectories). To select a representative structure, a set composed of the last structures from all trajectories was created first. The structure with the lowest maximum root-mean-square deviation (RMSD) from all other structures was then selected as a representative structure. This representative structure was subsequently superposed on the experimental structure and the deviations of the consecutive residues of the protein and DNA parts from their experimental counterparts were calculated and plotted in residue index. Subsequently, the structures from all 900 snapshots were subjected to Principal Component Analysis (PCA)51–53 to determine the most important motions that characterize the initial stages of the DNA-repair mechanism.
Dynamics of multiple antibiotic resistance protein (MarA) during DNA binding
To study the conformational changes of the MarA protein during the DNA binding, the crystal structure of the MarA – DNA complex was energy-minimized first. The protein and DNA chains were subsequently separated from each other by shifting to the distance of 5 Å and by 8 Å to produce the starting structure. Two series of 16 Langevin dynamics trajectories and 200,000 steps per trajectory each were run. The simulations of the first series were started with the initial configuration in which the DNA molecule was separated by 5 Å from the protein; the time step in these series of simulations was set at 0.489 fs, this corresponding to a total of 100 ns all-atom-simulation time (given an approximately 1000-fold time-scale extension34). In the second series of simulations, DNA was initially at a larger, 8 Å, distance from the protein and the simulations were carried out with the time step of 4.89 fs, which corresponded to approximately 100 ns simulation time per trajectory. Each simulation was run in the NVT mode at the temperature of T = 300 K. The time step was reduced to 0.498 fs in the first simulation series, because the binding of DNA to MarA occurred very fast in the coarse-grained model at such a small initial separation of the components, and setting a larger time step lead to omission of important events that occur upon binding. Snapshots were collected every 1,000 steps (a total of 3,200 snapshots from all trajectories). For each series of simulations, a representative structure was selected as described in section “Dynamics of the Ku heterodimer bound to DNA”.
In order to get better insight into the DNA-protein binding pattern, contact maps were calculated for both series of simulations. For each series of simulations, the distances between the Cα atoms of the protein and the C5′ atoms of the DNA were calculated. For a given Cα · · · C5′ pair, a score of 1 was assigned if the respective distance was 8 Å or less, 0, if it was 10 Å or greater, while the score decreased linearly from 1 to 0 for distances between 8 Å and 10 Å. Then the scores were averaged over 10 last snapshots (a total of 160 snapshot for each simulation series). The last structures from all trajectories were compared with each other. The structure with the lowest maximum root-mean-square deviation (RMSD) from all the others selected structures was selected as a representative structure. The results of the simulation in which the initial separation of the protein and DNA molecules was 5 Å were used in the analysis and in the principal component analysis described in the next section. Residue-wise deviations of the protein and DNA parts of the representative structure from the experimental structure after optimal superposition were calculated and the corresponding residue-wise plots were constructed. Subsequently, all 3,200 snapshot structures were subjected to PCA51–53 to determine the most important motions that occur during DNA-protein association.
Principal component analysis
PCA is an implementation of the Normal Mode Analysis (NMA) and is an efficient method to identify all collective motions of a molecular system51–53. A key concept of NMA is that the displacements of atom/site coordinates of the molecular system from those of the average structure are expressed as a linear combination of normal mode coordinates. The normal modes are obtained as eigenvectors of the variance-covariance matrix of coordinates C defined by eq. (8),
| (8) |
where qik is the mass-scaled x, y or z coordinate of the respective atom/site of the kth snapshot defined by eq. (9), ⟨qi⟩ is the respective average coordinate (the coordinates are averaged after all structures are superposed on a selected structure of the trajectory), N is the number of snapshots and n is the total number of atoms/sites in the system.
| (9) |
where mi is the mass of the ith atom/site. The eigenvectors of of the matrix C, denoted as V1, V2,…, V3n, respectively, and termed the principal components, are arranged according to the descending order of the corresponding eigenvalues, χi, i = 1, 2, … 3n, so that χ1 ≥ χ2 ≥ … ≥ χ3n. The top-ranked PC modes describe global motions of the system, while the low ranked PC modes describe the local motions. The eigenvalues normalized to the sum of 1 are termed loadings. The ProDy interface of the Normal mode visualization and comparative analysis (NMWiz) plug-in of the Visual Molecular Dynamics (VMD) software was used to run PCA54,55.
RESULTS
Tests of MD behavior in microcanonical and canonical runs
Variation of the total energy with MD simulation time for the MarA-DNA system is shown in Figure 2A. As can be seen from the Figure, the total energy fluctuates only about the average value, the variations amounting to 0.008 kcal/mol, this proving symplectic behavior of the simulation.
Figure 2.
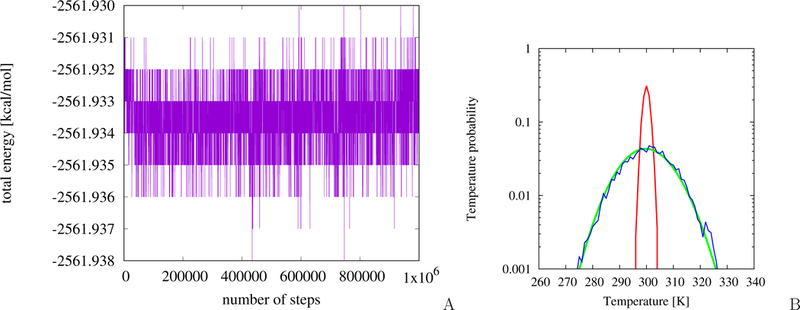
(A) Plot of the total energy changes as a function of time. Simulations were performed in micro-canonical mode for the MarA protein bound to DNA. (B) Temperature probability distribution plot (shown in logarithmic scale) for the Berendsen thermostat (red) and Langevin thermostat (blue) compared with theoretical distribution (green) given by the equation , where g is the number of the degrees of freedom, Tb is the thermal-bath temperature, and A is the normalization constant.
The plots of temperature distribution for the Langevin and Berendsen run are shown in Figure 2B. It can be seen that, for the Langevin run, the distribution resulting from the simulations matches the theoretical distribution for the respective number of degrees of freedom, while the Berendsen thermostat produces too narrow a distribution, as found in earlier work56,57. Nevertheless, the mean temperature is very close to the bath temperature for both simulations.
Dynamics of Ku heterodimer bound to DNA
The structure of the Ku heterodimer bound to DNA after simulations is compared with the experimental structure in Figure 3. As can be seen from the Figure, the most significant changes occurred at the wrongly paired fragment of damaged DNA. The pairing was broken and one of the DNA chains moved towards the protein. The conformational changes are also visualized in Figure 4, where the residue-wise deviations from the experimental structure are shown. As can be seen from Figure 4B, large deviations are observed for the shorter DNA chain at the C3′ end and at the C5′ end, and in the loop region of the longer chain. The RMSD of the representative final structure from the experimental structure is 5.19 Å whereas, for the DNA part, the RMSD is 6.71 Å after superposing the DNA fragments of the system. For the Ku protein, the largest fluctuations are observed in the β-sheet of Ku70 that “grabs” the DNA strands and in the C-terminal fragment of Ku70.
Figure 3.
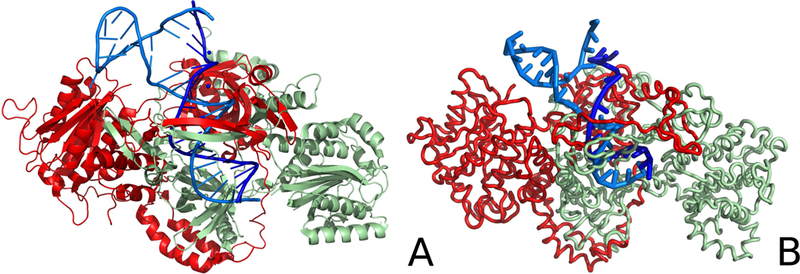
Comparison of the crystal structure of the Ku heterodimer bound to DNA (A) with the representative structure of this system obtained after coarse-grained MD simulation (B). The Ku70 (chain A) and Ku80 (chain B) monomers are colored pale-green and red, respectively, DNA chains C and D are colored dark blue and light blue, respectively. The chains are labeled as in the 1JEY experimental structure of the Ku protein.
Figure 4.

Deviations of the positions of the Cα and C5′ atoms of the representative structure obtained in coarse-grained MD simulations of the DNA-Ku heterodimer from their positions in the experimental structure of the Ku protein (PDB code: 1JEY) as functions of residue index (A) and the respective deviations of the DNA bound to the Ku heterodimer (B). Red color: the Ku70 monomer (chain A) and DNA chain C, black color: the Ku80 monomer (chain B) and DNA chain D.
The loadings (normalized eigenvalues) corresponding to the protein, the nucleic-acid and the protein – nucleic-acid-complex are plotted in Figure S1 of the Supporting Information, while the principal components, together with the plots of the fluctuations of the Cα atoms along the principal components, are shown in Figure 5 and Figures S2 and S3 of the Supporting Information. The results of PCA enable us to conclude that the most important motions of the protein consist of (i) reorganization of the loops (residues 289–295 and 304–312 of Ku70, and residues 280–287 and 298–304 of Ku80) in the vicinity of the the β-sheet (Figure 5D), which is composed of one strand from Ku70 (residues 289–297) and one from Ku80 (residues 296–303), (ii) “grabbing” the damaged DNA by the β-sheet (Figure 5A), this motion corresponding to the PC mode with the largest loading, (iii) opening the wrongly-paired DNA by the C-terminal fragment of Ku70 and the N-terminal part of Ku80 (Figure 5C), and (iv) global motion of the protein domains (Figure 5B and E). The most important DNA motions (Supplementary Figures S3) are those corresponding to the wrongly formed loop and wrongly paired DNA-fragment. When this system is analyzed as a whole (Figure 5) it is found that the most important motions are well coordinated and both chains act in harmony in the DNA-repair process.
Figure 5.

Illustration of the first five principal components (panel A-E) obtained by doing the PCA of the snapshots of the Ku heterodimer bound to DNA collected from the coarsegrained MD simulations. The principal components are represented by arrows colored green (A), red (B), orange (C), blue (D), and purple (E), respectively. The structure displayed in a given panel has been obtained by adding the respective eigenvector coordinates to the site coordinates; the deviations from the average structure are marked by coloring the respective parts of the system from blue (low deviations) to deep red (high deviations). On the right side of each panels, the the squares of Cα-atom the fluctuations corresponding to a given component are plotted.
To confirm the motion pattern detected by coarse-grained simulations, we have also carried all-atom MD simulations of the Ku/DNA system with the AMBER force field58,59. The simulations were carried out in the NPT regime, at a temperature of T = 298 K and pressure of p = 1 atm, in a periodic-water box with initial dimensions 100×105×130 Å containing 40,000 TIP3P water molecules and 12 Na+ counter-ions to zero out the net charge. Four independent trajectories, 5 ns each were run. All data were used in principal component analysis. The resulting principal components, together with the plots of the fluctuations of the Cα atoms along the principal components, are visualized in Figure 6. It can be seen that the components corresponding to grabbing (panels A and B) and opening (panel C) the damaged DNA section are similar to their counterparts from coarse-grained simulations (Figure 5). However, the motion of the loops at residues 289–295 and 304–312 of Ku70, and residues 280–287 and 298–304 of Ku80 are less pronounced probably because the motion of the crowded section of the system is facilitated in coarse-grained representation in which the effective energy surface is smoother. Additionally, the α-helix at residues 140–152 moves, which motion is not seen in the coarse-grained dynamics.
Figure 6.

Illustration of the first two principal components (panels A-E) obtained by doing the PCA of the snapshots of the Ku heterodimer bound to DNA collected from the all-atom MD simulations. The principal components are represented by arrows colored green (A), red (B), orange (C), blue (D), and purple (E), respectively. The structure displayed in a given panel has been obtained by adding the respective eigenvector coordinates to the site coordinates; the deviations from the average structure are marked by coloring the respective parts of the system from blue (low deviations) to deep red (high deviations). On the right side of each panels, the the squares of Cα-atom the fluctuations corresponding to a given component are plotted.
Our results suggest that the Ku complex is actively involved in the unwinding of wrongly paired DNA fragments. These results are consistent with the experimentally determined active role of this complex60.
Dynamics of multiple antibiotic resistance protein (MarA) during the DNA binding
As mentioned in Methods, two series of simulations, one started from initial protein-DNA separation of 5 Å and one from the separation of 8 Å were carried out. The DNA-protein complex was formed in all 16 trajectories for both series of simulations. The crystal and the representative structure from the end of the simulations starting from 5 Å separation of the MarA-DNA complex are shown in panels A and B of Figure 7, respectively. It can be seen from the Figure that the protein is bound to DNA in a manner similar to that of the crystal structure36. The RMSD between the representative structure and the crystal structure is 6.68 Å. The RMSD of the protein part is 4.78 Å, while that of the nucleic-acid part is 7.57 Å. It should be noted that, because of a larger dimension of a nucleotide than that of an amino-acid residue, the RMSD of 7.57 Å for the nucleic-acid part means that the structure superposes quite well on its experimental counterpart. On the other hand, the components are packed too tightly in the simulated complex (Figure 7B).
Figure 7.

Comparison of the crystal structure of multiple antibiotic resistance protein (MarA) bound to DNA (A, PDB code: 1BL0) with the representative structure obtained in the coarse-grained MD simulation (B). Each chain is colored in a rainbow style from blue (for the N-terminus and the C5′ end) to red (for the C-terminus and the C3′ end).
In order to get better insight into the binding mode of DNA to MarA, we analyzed the contacts between its component in the experimental structure36 and average contacts in the simulated structure. The respective contact maps are shown in Figure 8A–C. From the analysis of the contacts in the experimental structure (Figure 8A), it can be seen that residues 35–55 and 80–100, which correspond to the loop regions of MarA, are the most important for DNA binding; these residues bind to the major grove of the DNA molecule. The averaged contact maps obtained from simulations indicate the same general binding pattern (Figure 8B and C); however, the contacts are more diffuse and additional contacts involving the residues engaged in the native contacts and the neighboring residues are formed. The contacts corresponding to the simulations in which the MarA and DNA molecules were initially separated by 8 Å are even more diffuse and the contact scores are lower; however, the binding follows the native mode (Figure 8C). These results suggest that that the binding process is dynamic.
Figure 8.
Contact map for MarA DNA interaction (A) crystal structure, (B) last 10 structures from simulations which started from 5Å separation, (C) last 10 structures from simulations which started from 8Å separation
The residue-wise deviations of the representative final simulated structure from the experimental structure (Figure 9) indicate that the greatest deviations occur in the C5′ fragment of both DNA chains and slightly smaller deviations at the C3′ end. The middle part of DNA is stable. For the protein, the most significant changes occur at the major grove binding loop (residues 20–45, 29–54 according to residue numbering in the PDB file).
Figure 9.

Plot of the deviations of the Cα atoms and the C5′ atoms of the representative structure of the MarA-DNA system obtained in coarse-grained MD simulations from the experimental structure of MarA (PDB code: 1BL0) as a function of residue index (A) and of the DNA bound to MarA (DNA chain B: red, DNA chain C: black) (B).
The loadings of the normal modes for the protein, nucleic-acid and the complex are plotted in Figure S4 of the Supporting Information, while the principal components are visualized in Figure 10 and Figures S5 and S6 of the Supporting Information. The principal components indicate that the most important motions during protein-DNA association are (i) the motion of DNA towards the protein (Figure 10A), (ii) protein domain closing (Figure 10B) and (iii) the motion that corresponds to the binding of parts of the protein to the major grove (Figure 10C and D). These motions are well separated probably because DNA was separated from the protein in the starting structure.
Figure 10.
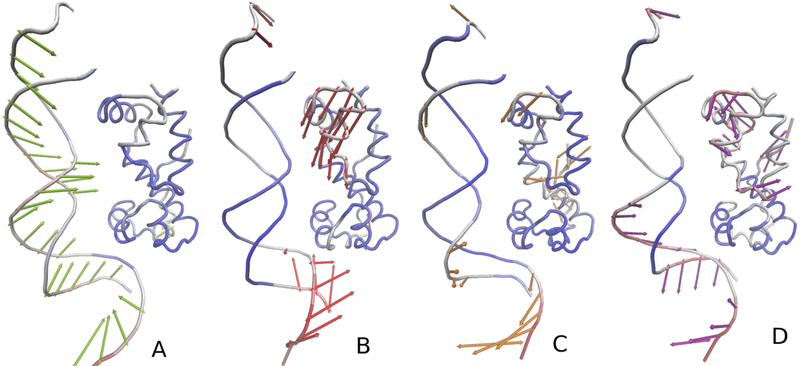
Illustration of the first four principal components (panels A-D) obtained by doing the PCA of the snapshots of the coarse-grained MD simulations of MarA binding to DNA. The principal components are represented by arrows colored green (A), red (B), orange (C), and blue (D), respectively. The structure displayed in a given panel has been obtained by adding the respective eigenvector coordinates to the site coordinates; the deviations from the average structure are marked by coloring the respective parts of the system from blue (low deviations) to deep red (high deviations).
CONCLUSIONS
In this work, we developed a coarse-grained model of protein-DNA systems, which combines UNRES and NARES-2P, as well as the recently determined coarse-grained potentials for protein – nucleic-acid interactions31. The model was integrated into the UNRES software package for coarse-grained molecular dynamics32. The enhanced software run on model protein-DNA systems passed the energy-conservation tests in microcanonical simulations and also produced correct temperature distribution in test Langevin simulations and correct mean temperature in the Berendsen-thermostat simulations.
As the first applications of the coarse-grained model of proteins and nucleic acid systems developed in this work, we simulated the initial stage of the repair of damaged DNA by investigating the dynamics of the complex of the Ku protein heterodimer with damaged DNA and DNA binding to the MarA protein. We found that the initial stage of the repairing of damaged DNA involves breaking the wrong base pairing because of interactions with the Ku heterodimer. Additionally, we found that the DNA bulge also undergoes major structure reorganization. We also found that, in the simulated binding of DNA to MarA, the motions corresponding to binding the protein to the DNA are well separated from DNA association motions.
Supplementary Material
ACKNOWLEDGMENTS
This work was supported by the National Science Center (Poland) Sonata UMO-2015/17/D/ST4/00509 (to AKS) and UMO-2012/06/A/ST4/00376 (to AL) and by NIH grant GM-14312 (to HAS, YY, YH). Computational resources were also provided by (a) the supercomputer resources at the Informatics Center of the Metropolitan Academic Network (IC MAN) in Gdańsk, and (b) computational resources at Interdisciplinary Center for Mathematical and Computer Modeling in Warsaw (ICM), grant GA71–21 (c) Polish Grid Infrastructure (PL-GRID) (d) our 682-processor Beowulf cluster at the Faculty of Chemistry, University of Gdańsk (e) the 624-processor Beowulf cluster at the Baker Laboratory of Chemistry, Cornell University, U.S.A.
References
- 1.Pande VS, Baker I, Chapman J, Elmer S, Kaliq S, Larson SM, Rhee YM, Shirts MR, Snow CD, Sorin EJ, et al. , Biopolymers 68, 91 (2003). [DOI] [PubMed] [Google Scholar]
- 2.Hess B, Kutzner C, van der Spoel D, and Lindahl E, J. Chem. Theory Comput 4, 435 (2008). [DOI] [PubMed] [Google Scholar]
- 3.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kalé L, and Schulten K, J. Comput. Chem 26, 1781 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bowers KJ, Chow E, Xu H, Dror RO, Eastwood MP, Gregersen BA, Klepeis JL, Kolossvary I, Moraes MA, Sacerdoti FD, et al. , ACM/IEEE SC 2006 Conference (SC.06) pp. 43–43 (2006). [Google Scholar]
- 5.Friedrichs MS, Eastman P, Vaidyanathan V, Houston M, Legrand S, Beberg AL, Ensign DL, Bruns CM, and Pande VS, J. Comput. Chem 30, 864 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lindorff-Larsen K, Piana S, Dror RO, and Shaw DE, Science 334, 517 (2011). [DOI] [PubMed] [Google Scholar]
- 7.Dror RO, Dirks RM, Grossman JP, Xu H, and Shaw DE, Annu. Rev. Biophys 41, 429 (2012). [DOI] [PubMed] [Google Scholar]
- 8.Ayton GS, Noid WG, and Voth GA, Curr. Opinion Struct. Biol 17, 192 (2007). [DOI] [PubMed] [Google Scholar]
- 9.Czaplewski C, Liwo A, Makowski M, Ołdziej S, and Scheraga HA, in Multiscale Approaches to Protein Modeling, edited by Koliński A (Springer, 2010), chap. 3, pp. 35–83. [Google Scholar]
- 10.Marrink SJ and Tieleman DP, Chem. Soc. Rev 42, 6801 (2013). [DOI] [PubMed] [Google Scholar]
- 11.Kmiecik S, Gront D, Kolinski M, Wieteska L, Dawid A, and Koliński A, Chem. Rev 116, 7898 (2016). [DOI] [PubMed] [Google Scholar]
- 12.Liwo A, Czaplewski C, Ołdziej S, Rojas AV, Kaźmierkiewicz R, Makowski M, Murarka RK, and Scheraga HA, in Coarse-Graining of Condensed Phase and Biomolecular Systems, edited by Voth G (CRC Press, 2008), chap. 8, pp. 1391–1411. [Google Scholar]
- 13.Liwo A, Baranowski M, Czaplewski C, Gołaś E, He Y, Jagiea D, Krupa P, Maciejczyk M, Makowski M, Mozolewska MA, et al. , J. Mol. Model 20, 2306 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.He Y, Maciejczyk M, Ołdziej S, Scheraga HA, and Liwo A, Phys. Rev. Lett 110, 098101 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.He Y, Liwo A, and Scheraga HA, J. Chem. Phys 143, 243111 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Liwo A, Czaplewski C, Pillardy J, and Scheraga HA, J. Chem. Phys 115, 2323 (2001). [Google Scholar]
- 17.Sieradzan AK, Krupa P, and Wales DJ, J. Phys. Chem. B 121, 2207 (2017). [DOI] [PubMed] [Google Scholar]
- 18.Kubo R, J. Phys. Soc. Japan 17, 1100 (1962). [Google Scholar]
- 19.Baranowski M, Czaplewski C, Gołaś EI, He Y, Jagieła D, Krupa P, Liwo A, Maisuradze GG, Makowski M, Mozolewska MA, et al. , in Coarse-Grained Modeling of Biomolecules, edited by Papoian GA (CRC Press, 2017), chap. 3, pp. 67–120. [Google Scholar]
- 20.He Y, Mozolewska MA, Krupa P, Sieradzan AK, Wirecki TK, Liwo A, Kachlishvili K, Rackovsky S, Jagiea D, Ślusarz R, et al. , Proc. Nat. Acad. Sci. U.S.A 110, 14936 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Krupa P, Mozolewska MA, Wiśniewska M, Yin Y, He Y, Sieradzan AK, Ganzynkowicz R, Lipska AG, Karczyńska A, Ślusarz M, et al. , Bioinformatics 32, 3270 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sieradzan AK, Liwo A, and Hansmann UHE, J. Chem. Theory Comput 8, 3416 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mozolewska M, Krupa P, Scheraga H, and Liwo A, Proteins: Struct., Funct., Bioinf 83, 1414 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Roos WP and Kaina B, Trends Mol. Med 12, 440 (2006). [DOI] [PubMed] [Google Scholar]
- 25.Fumasoni M, Zwicky K, Vanoli F, Lopes M, and Branzei D, Molecular Cell 57, 812 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Baeuerle PA, Biochim. Biophys. Acta 1072, 63 (1991). [DOI] [PubMed] [Google Scholar]
- 27.Jones PL, Veenstra GCJ, Wade PA, Vermaak D, Kass SU, Landsberger N, Strouboulis J, and Wolffe AP, Nature Gen 19, 187 (1998). [DOI] [PubMed] [Google Scholar]
- 28.Longhese MP, Plevani P, and Lucchini G, Mol. Cell. Biol 14, 7884 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wold MS, Annu. Rev. Biochem 66, 61 (1997). [DOI] [PubMed] [Google Scholar]
- 30.Walker JR, Corpina RA, and Goldberg J, Nature 412, 607 (2001). [DOI] [PubMed] [Google Scholar]
- 31.Yin Y, Sieradzan AK, Liwo A, He Y, and Scheraga HA, J. Chem. Theory Comput 11, 1792 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lubecka E and Liwo A, TASK Quart 20, 399 (2016). [Google Scholar]
- 33.Khalili M, Liwo A, Rakowski F, Grochowski P, and Scheraga HA, J. Phys. Chem. B 109, 13785 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Khalili M, Liwo A, Jagielska A, and Scheraga HA, J. Phys. Chem. B 109, 13798 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rakowski F, Grochowski P, Lesyng B, Liwo A, and Scheraga HA, J. Chem. Phys 125, 204107 (2006). [DOI] [PubMed] [Google Scholar]
- 36.Rhee S, Martin RG, Rosner JL, and Davies DR, Proc. Natl. Acad. Sci. U. S. A 95, 10413 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Liwo A, Pincus MR, Wawak RJ, Rackovsky S, and Scheraga HA, Protein Sci 2, 1715 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Liwo A, Ołdziej S, Czaplewski C, Koz-lowska U, and Scheraga HA, J. Phys. Chem. B 108, 9421 (2004). [Google Scholar]
- 39.Liwo A, Khalili M, Czaplewski C, Kalinowski S, Ołdziej S, Wachucik K, and Scheraga H, J. Phys. Chem. B 111, 260 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Liwo A, He Y, and Scheraga HA, Phys. Chem. Chem. Phys 13, 16890 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Shen H, Liwo A, and Scheraga HA, J. Phys. Chem. B 113, 8738 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kolinski A and Skolnick J, J. Chem. Phys 97, 9412 (1992). [Google Scholar]
- 43.Liwo A, Kaźmierkiewicz R, Czaplewski C, Groth M, Ołdziej S, Wawak RJ, Rackovsky S, Pincus MR, and Scheraga HA, J. Comput. Chem 19, 259 (1998). [Google Scholar]
- 44.Krupa P, Sieradzan AK, Rackovsky S, Baranowski M, Ołdziej S, Scheraga HA, Liwo A, and Czaplewski C, J. Chem. Theory Comput 9, 4620 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sieradzan AK, Krupa P, Scheraga HA, Liwo A, and Czaplewski C, J. Chem. Theory Comput 11, 817 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Krupa P, Hałabis A, Żmudzińska W, Ołdziej S, Scheraga HA, and Liwo A, J. Chem. Inf. Model 57, 2364 (2017). [DOI] [PubMed] [Google Scholar]
- 47.Makowski M, Liwo A, and Scheraga HA, J. Phys. Chem. B 115, 6130 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A, and Haak JR, J. Chem. Phys 81, 3684 (1984). [Google Scholar]
- 49.Webb B and Sali A, Methods Mol. Biol 1137, 1 (2014). [DOI] [PubMed] [Google Scholar]
- 50.Sieradzan AK, Scheraga HA, and Liwo A, J. Chem. Theor. Comput 8, 1334 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Cui Q and Bahar I, Normal mode analysis: theory and applications to biological and chemical systems (CRC press, 2005). [Google Scholar]
- 52.Maisuradze GG and Leitner DM, Proteins: Struct. Func. Bioinfo pp. 569–578 (2007). [DOI] [PubMed]
- 53.Yang L-W, Eyal E, Bahar I, and Kitao A, Bioinformatics 25, 606 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Humphrey W, Dalke A, and Schulten K, J. Mol. Graph 14, 33 (1996). [DOI] [PubMed] [Google Scholar]
- 55.Bakan A, Meireles LM, and Bahar I, Bioinformatics 27, 1575 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.D’Alessandro M, Tenenbaum A, and Amadei A, J. Phys. Chem. B 106, 5050 (2002). [Google Scholar]
- 57.Sieradzan AK, J. Comput. Chem 36, 940 (2015). [DOI] [PubMed] [Google Scholar]
- 58.Pearlman D, Case D, Caldwell J, Ross W, Cheatham T III, DeBolt S, Ferguson D, Seibel G, and Kollman P, Comp. Phys. Commun 91, 1 (1995). [Google Scholar]
- 59.Case DA, Darden TA, Cheatham TE, Simmerling CL, Wang J, Duke RE, Luo R, Walker RC, Zhang W, Merz KM, et al. , Amber 12 (2012), University of California: San Francisco. [Google Scholar]
- 60.Ramsden DA and Gellert M, EMBO J 17, 609 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



