Abstract

Interactions of nanoparticles (NPs) with their environment may have a pronounced effect on their structure and shape as well as on their functionality in applications such as catalysis. It is therefore crucial to disentangle the particle–adsorbate and particle–support interaction effects on the particle shape, its local structure, atomic dynamics, and its possible anisotropies. In order to gain insight into the support effect, we carried out an X-ray absorption fine-structure spectroscopy (XAFS) investigation of adsorbate- and ligand-free size-selected Pt NPs deposited on two different supports in ultrahigh vacuum. Polarization-dependent XAFS measurements, neural network-based analysis of X-ray absorption near-edge structure data, and reverse Monte Carlo (RMC) simulations of extended X-ray absorption fine structure (EXAFS) were used to resolve the 3D shape of the NPs and details of their local structure. A synergetic combination of advanced in situ XAFS analysis with atomic force microscopy and scanning tunneling microscopy (STM) imaging provides uniquely detailed information about the particle–support interactions and the NP/support buried interface, not accessible to any experimental technique, when considered alone. In particular, our combined approach reveals differences in the structure of Pt NPs deposited on TiO2(110) and SiO2/Si(111). Pt NPs on SiO2 assume a spherical-like 3D shape and weakly interact with the support. In contrast, the effective shape of analogously synthesized Pt NPs on TiO2(110) after annealing at 600 °C is found to be a truncated octahedron with (100) top and interfacial facets that are encapsulated by the TiO2 support. Modeling disorder effects in these NPs using an RMC approach reveals differences in bond-length distributions for NPs on different supports and allows us to analyze their anisotropy, which may be crucial for the interpretation of support-dependent atomic dynamics and can have an impact on the understanding of the catalytic properties of these NPs.
1. Introduction
Metal nanoparticles (NPs) supported on oxides have tremendous applications in the field of heterogeneous catalysis. Numerous studies have been dedicated to explore the parameters affecting the catalytic performance of nanocatalysts such as their particle size, shape, oxidation state, and interaction with the support.1−12 Nevertheless, in many cases it is hard to isolate the respective contribution of these parameters. For example, it was shown that the NP shape can be affected by the size, adsorbates, ligands, and support, while the NP/support interaction itself is also influenced by the NP size,1,3,13 all of which could subsequently affect the NPs activity and selectivity.14−18 For understanding structure–properties relationship in heterogeneous catalysts and for the rational design of novel catalyst materials, it is necessary to disentangle these many degrees of freedom. For this purpose, studies of well-defined model systems are useful, since they allow us to single out the importance of each of these catalyst characteristics. Here, we focus on particle–support interactions and their effect on particle shape and local structure.
The NP support can affect the NP structure by (i) changing the electronic structure of the NPs,19−21 (ii) inducing strain in the NP lattice due to interfacial mismatch,22,23 and (iii) encapsulating the NP and changing the surface energy.24−26 Interactions with the support may have an impact also on atomic dynamics, especially for smaller NPs,27 resulting in non-bulk-like distributions of interatomic distances, which, again, can result in unique functionality.5 The presence of particle–support interactions introduces naturally also the anisotropy in the NP structure, which may manifest itself in unusual vibrational properties and strain distributions.27
To rationalize the importance of these factors, tools are needed to extract detailed information about the geometry and internal structure of NPs on different supports and under different experimental conditions. For this purpose, different microscopy techniques can be used, including scanning tunneling microscopy (STM), atomic force microscopy (AFM), and transmission electron microscopy (TEM).3,28−31 These techniques can provide insight into the shape of individual NPs and their local arrangement on relatively small substrate areas (hundreds of μm2). Nonetheless, when applied to small NPs, tip-convolution effects in some of these methods can obscure the real NP structure and the amount of quantitative information that can be extracted is limited. On the other hand, complementary spectroscopic techniques such as grazing incidence small-angle X-ray scattering and X-ray absorption fine-structure spectroscopy (XAFS) can provide information about the average NP size, shape, and structure.4,32−36 An important advantage of these spectroscopic techniques is their ability to resolve transformations of nanocatalysts in situ and under operando reaction conditions, including high temperatures and elevated gas pressures. Nevertheless, due to ensemble-averaging, the latter techniques provide the most meaningful answers when they are applied to model systems with narrow particle size, shape, and compositional distributions (as verified by microscopy techniques). When these conditions are not met, extreme care needs to be taken in the interpretation of the obtained results, since the analysis will yield only an effective, ensemble-averaged particle 3D structure. In some cases, such an effective NP model can, nevertheless, be successfully correlated with sample functionality.37
Among the different structure-sensitive techniques, extended X-ray absorption fine-structure (EXAFS) analysis stands out as an element-specific method that is very sensitive to the local structure around the absorbing atom.38 For samples containing monodispersed NPs, EXAFS analysis allows the extraction of very detailed information about the NP size, shape, and structure.39−42 For example, we previously reported the possibility to determine the shape of size-selected Pt NPs supported on nanocrystalline Al2O3 powders by combining the information on the first to fourth coordination numbers (CNs) extracted from multiple-scattering (MS) EXAFS analysis, with the knowledge of the NP diameter determined by TEM.4,16,34 Note, however, that our previous studies were conducted under H2-atmosphere to prevent NP oxidation, and therefore, the NP shapes observed might have been affected by interactions with adsorbed hydrogen.43 It is well known that adsorbates can affect the stability of the otherwise more thermodynamically favorable NP shapes.43−45 Furthermore, on the nanocrystalline supports that were previously employed, epitaxial relationships between the NPs and the support could not be ensured. Since the NPs were oriented randomly on the support surface, possible anisotropies in the NP shape and structure could not be resolved. In the present study, we have used similarly synthesized ensembles of well-defined metal NPs but have deposited them on planar single crystals to unveil, in the absence of adsorbates [in an ultrahigh vacuum (UHV) measurement environment], the role of the support. Furthermore, by employing X-ray polarization-dependent XAFS measurements, we are now able to extract information on the differences in the metal–metal bonds within NPs along different directions (parallel and perpendicular to the support surface) and also to single out the contribution of the bonds between the NPs and the support.46,47 These data allowed us to estimate the most favorable structural configuration for our NPs deposited on a strongly interacting support (TiO2) versus a weak one (SiO2).
The interpretation of in situ polarized XAFS data using conventional approaches is challenging, especially in cases like the present one, where the low metal loading results in limited EXAFS data quality. Reliable MS EXAFS analysis of distant coordination shell contributions that is necessary to resolve NPs shape is not possible in this case. Instead, we have applied recently developed advanced XAFS analysis methods based on the neural network (NN) approach to extract the NP structural information from the experimental X-ray absorption near-edge structure (XANES) data, which have much better signal to noise ratio.48−50 CNs extracted from XANES are then used to construct a 3D structural model. Its agreement with available EXAFS data is further validated using reverse Monte Carlo (RMC) simulations.48,51 RMC–EXAFS analysis allowed us also to extract the entire bond-length distribution function [radial distribution function (RDF)] that encodes information about the variations in bond lengths due to static and dynamic thermal disorder effects.49,52 Here, we employ for the first time the RMC analysis for the interpretation of polarization-dependent EXAFS data. By combining polarization-dependent XAFS measurements of NPs on single crystal supports with the RMC–EXAFS simulation method, we extracted information about the possible anisotropy of RDFs and obtained accurate interatomic distance distributions. In particular, the RMC simulations yielded non-Gaussian, support-dependent shapes for the RDF peaks that indicate the presence of strong particle surface- and support-induced disorder and/or essentially anharmonic atomic dynamics,48,53,54 which could have an impact on the catalytic properties of these NPs. In addition, we were able to analyze separately the bond length distributions for the bonds that are parallel and perpendicular to the substrate surface. Therefore, we were able to probe directly the effect of particle–support interactions on the anisotropy of the particle structure and dynamics. Such detailed insight into the interactions between nanometer-sized particles and the underlying support, including insight into buried interfaces, was enabled by a synergistic combination of scanning-probe microscopy and spectroscopic techniques and advanced data analysis.
2. Methods
2.1. Sample Preparation and Experimental Details
Size-selected Pt NPs were synthesized using inverse micelle encapsulation.55,56 A commercial diblock copolymer poly(styrene)-block-poly(2-vinylpyridine)[PS(26000)-P2VP(4800)] was dissolved in toluene to form the micelles. Subsequently, H2PtCl6·6H2O with a metal/P2VP ratio of 0.18 was added to the solution to create the metal NPs. A monolayer thick film of NPs was achieved after dip coating the TiO2(110) crystal and natively oxidized SiO2/Si(111) substrate into the micellar solution. In situ O2-plasma treatment at 5 × 10–6 mbar for 100 min was performed to remove the polymers. To stabilize the Pt NPs on TiO2, the sample was stepwise annealed in vacuum from 300 up to 900 °C in 100 °C intervals.
To get information about the morphology of the as-prepared samples, AFM images were acquired using a Veeco multimode microscope (Digital Instruments, Nanoscope IIIa). All STM images were acquired at room temperature using an Aarhus 150 HT STM microscope (SPECS GmbH). An electrochemically etched tungsten tip was used for the STM measurements. Due to tip-convolution effects, the NP height (and not the diameter) was used as the representative NP size descriptor. In order to confirm the complete removal of the ligands, X-ray photoelectron spectroscopy measurements were conducted using a monochromatic Al Kα X-ray source (1486.6 eV) and a Phoibos (SPECS) electron energy analyzer.
XAFS measurements were performed at the 12-BM beamline of the Argonne National Laboratory, which is equipped with a UHV chamber compatible with XAFS measurements. The experiments were conducted in fluorescence mode at the Pt L3-edge (11 562 eV) at room temperature. The ex situ synthesized samples were first transferred into UHV and annealed in O2 at 450 °C for 30 min in order to remove adventitious carbon from the NPs. Subsequently, the samples were reduced in vacuum at 600 °C. To get the information about the anisotropic structure of the NPs, in the case of Pt/TiO2(110), EXAFS measurements were carried out with the X-ray polarization in three different orientations, from which two were parallel to the substrate surface and one was perpendicular to the substrate. The two parallel measurements were done along (i) TiO2(110)[001] (denoted as ∥-1) and (ii) TiO2(110)[11̅0] (denoted as ∥-2) directions. Since no well-defined crystalline orientations were available at the native SiO2/Si(111) interface, on this substrate no polarization-dependent measurements were performed, and we collected XAFS data with only one X-ray polarization.
The Athena and FEFFIT programs were used for XAFS data normalization, background subtraction, and conventional nonlinear least-square fitting of the experimental EXAFS data.57 Fitting of the first-shell EXAFS data was done over a range of 3–10.5 Å–1 in k-space and 1.0–3.4 Å in R-space. EXAFS data from Pt/TiO2 were fitted with three components corresponding to Pt–Pt (∼2.7 Å), Pt–Ti (∼2.7 Å), and Pt–O (∼2.0 Å) bonds, while for Pt/SiO2 only Pt–Pt and Pt–O were considered. Due to limited k-range and R-range, available for the analysis and the large number of fitting parameters, multiple constraints were employed: correction to photoelectron reference energy ΔE0 = 1.8 ± 0.7 eV was fixed to be the same for all the samples (this constrain is motivated by the similarity of the obtained XANES spectra for different samples), Debye–Waller factors σ2 and interatomic distances R for Pt–Pt, Pt–O, and Pt–Ti bonds were fixed to be the same for all three spectra, corresponding to the Pt/TiO2 system. The passive electron reduction factor (S02) was estimated to be 0.87 by fitting the EXAFS spectrum of platinum foil. For calculations of the theoretical scattering amplitudes and phase shifts used in the fits, the FEFF8 ab initio code has been employed,38,58 using fcc Pt structure to simulate the Pt–Pt scattering path, PtO2 structure to simulate the Pt–O scattering path, and TiO2 structure with embedded Pt atom to simulate the Pt–Ti scattering path.
2.2. XAFS Data Interpretation
The sub-monolayer sample coverage with widely spaced small NPs employed in this study resulted in low metal concentration in the samples, and thus XAFS data quality is not adequate to conduct reliable conventional MS EXAFS analysis of contributions beyond the first coordination shell. Additional information is therefore necessary to resolve the NP shape. Such additional information can be extracted by considering the polarization of the X-rays in EXAFS measurements. We employ here the fact that the contribution of different interatomic bonds to the total spectrum depends on the relative orientation of the bond with respect to the X-ray polarization vector.59 For K-absorption edges, one can introduce a simple relation between the effective CN (ECN), that is, the number of bonds per absorbing atom that contribute to the X-ray absorption for a specific polarization direction, and the angle between the bond direction and the X-ray polarization60,61
| 1 |
where Nat is the number of absorbing atoms in the particle and θj is the angle between the jth bond direction and the electric field vector of the incident X-ray. This simple relation, however, is not accurate for L2 and L3 absorption edges.62 The effect of X-ray polarization on ECN for these absorption edges can be assessed numerically, using codes like FEFF,63 which treat polarization effects explicitly. As demonstrated in the Supporting Information, Figure S1, for the Pt L3-edge, the shape of the ECN(θ) dependence qualitatively still resembles a cos2(θ) function, but the effect of the polarization is less pronounced than for the K-edge. This means that we can still use eq 1 at least for qualitative analysis of L3-edge XAFS data. As demonstrated in Figure S1, the error in ECN that we introduce in this case is around 15%. In this study, the ECNs extracted from polarized EXAFS data were compared to those obtained from particle structure modeling to extract information on the shape of Pt NPs.
For unambiguous determination of the NP shape, information about CNs in more distant coordination shells is necessary.39,42,64 For this purpose, we employ here NN-based XANES analysis, which yields CNs from distant coordination shells even in the cases when the low data quality does not allow us to use MS EXAFS analysis. Our approach for the analysis of XANES data using NNs is explained in detail in ref (50) and we use here the same NN. Briefly, a large set of ab-initio calculated XANES spectra is constructed for particle models with different sizes and shapes using FEFF63 and FDMNES65 codes. For each of the used structure models, we calculate also the corresponding CNs for the first few coordination shells. The constructed database of calculated XANES spectra and corresponding CNs values is then used to train a NN, which maps the relationship between XANES features and CNs. The trained NN then can be used to determine CNs from experimental XANES spectra. Importantly, our NN was trained on structure models of completely metallic particles only; thus, it cannot recognize and quantify the interactions of the particle with the support (bonding, charge transfer, etc). For example, it cannot give any answers regarding Pt–O and Pt–Ti bonds for Pt particles on the TiO2 support. Nevertheless, our previous studies have shown that if the contribution of these bonds is small, as it is expected at least for the Pt/SiO2 system, our NN can still provide reasonably reliable results about the Pt–Pt CNs that can be used complimentary with CN values extracted from the traditional EXAFS data fitting.
The knowledge of CNs from EXAFS and NN-XANES analysis allows us to determine the NP size and shape. In addition to that, EXAFS data contain also the details about the distribution of bond lengths, which can be characterized by RDF and contains key information about the static structure strain and atomic dynamics.48,51 To extract this information, and also to additionally validate the NP structural models obtained from conventional EXAFS and NN-XANES analysis, we employ the RMC method. In RMC simulations, the aforementioned structure model (which includes Pt NP model as well as support atoms, when applicable) is further optimized, by proposing small and random displacements to all atoms in the model to account for disorder effects. Ab-initio EXAFS calculations are then carried out, and the obtained spectrum is compared with the experimental data. For comparison of theoretical and calculated spectra, we use wavelet transform (WT).66,67 Depending on the agreement, the proposed structure modification is either accepted or discarded. The process is repeated, until after several thousands of iterations a good agreement between experimental and theoretical EXAFS spectra is achieved. Importantly, since only small atomic displacements are allowed, the overall size and shape of the NP do not change during the RMC optimization.
In this work, for RMC–EXAFS analysis we rely on the EvAX code.68 Calculations for Pt NPs on SiO2 are carried out as in ref (50). To benefit from the sensitivity of EXAFS spectra to polarization effects, and to obtain a more unambiguous structure model for Pt NPs on TiO2, we have modified the EvAX code, so that polarization effects on EXAFS spectra can now be modeled explicitly. Note that the calculations of polarized EXAFS spectra are carried out accurately in the EvAX program (which uses FEFF code for EXAFS calculations). In this particular case, at each RMC iteration three theoretical EXAFS spectra are calculated (χ1teor(k), χ2(k), and χ3teor(k)), corresponding to the same structure model, but three different X-ray polarizations (perpendicular to substrate surface and parallel to TiO2(110)[001] (denoted further as ∥-1) and TiO2(110)[11̅0] (denoted further as ∥-2) directions), and all three are compared independently with the corresponding experimental EXAFS spectra (χ1(k), χ2exp(k) and χ3(k)). The residual that characterizes the goodness of current RMC atomic configuration is then calculated as
| 2 |
here, WT[ ] denotes Morlet WT and || ||—Euclidean norm. Thus, at the end of the RMC run, we get a single atomic configuration, which agrees with the EXAFS data collected for the three different X-ray polarizations. Other technical details of the RMC simulations are given in ref (50).
3. Results and Discussion
3.1. Microscopic Morphological Characterization (AFM/STM)
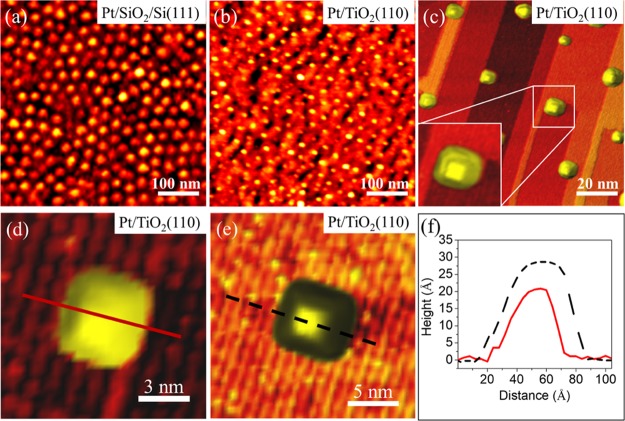
AFM images of the as-prepared micellar Pt NPs supported on SiO2 and TiO2(110) are shown in Figure 1a,b, respectively. According to the AFM data, the average NP heights in these samples are ∼1.8 ± 0.8 and ∼1.9 ± 0.6 nm, respectively (the apparent difference in the NP diameter seen in the images is due to the fact that both samples were measured with tips of different end radius). Height histograms are shown in the Supporting Information, Figure S2. The NPs are distributed with a hexagonal ordering and homogenous interparticle distance (∼40 ± 10 nm) on both substrates. An STM image of the Pt NPs supported on TiO2(110) acquired after annealing in vacuum at a temperature of 1100 °C is shown in Figure 1c. Note that since the SiO2 substrate has a wide band gap, STM measurements are not feasible for this sample unless it is highly doped, which was not the present case. A homogenous interparticle distance has been observed after the high temperature annealing, indicating the high stability and low mobility of the NPs on TiO2. The high-resolution STM images in Figure 1d,e reveal the flat NP top, which can be attributed to truncated octahedron NPs with (100) top and interfacial facets. The corresponding line profiles are shown in Figure 1f. It should be noted that due to the tip convolution effect, the lateral size of the NPs is overestimated in STM and AFM measurements. However, the height of the NPs (Figure S2) is less affected by the tip apex artifact and can be used as a reliable measure of the particle size.
Figure 1.
(1 × 1 μm) AFM images of the as-prepared Pt NPs supported on (a) SiO2/Si(111) and (b) TiO2(110). (c–e) STM images of polymer-free Pt NPs on TiO2(110) acquired at 25 °C after annealing in vacuum at 1100 °C. The inset in (c) and the high-resolution images in (d,e) display truncated octahedron Pt NPs on TiO2(110) with (100) top and interfacial facets. (f) Line profiles of the Pt NPs, shown in (d,e).
3.2. Spectroscopic Structural Characterization (EXAFS/XANES)
3.2.1. XANES Data
Experimental XANES spectra of our Pt NPs measured at room temperature in UHV on SiO2 and TiO2(110) are shown in Figure 2. In all cases, the spectra resemble strongly the spectrum of the Pt foil (also shown in Figure 2), confirming that Pt is mostly metallic in these samples, and no significant oxidation takes place under our UHV measurement environment. One can note that XANES oscillations are broadened and have lower amplitudes for all NPs samples, in comparison to those of bulk Pt, which can be attributed to particle size-effects.50 Also, a minor shift of spectra to higher energies can be detected for all spectra for Pt NPs, which can be due to the interaction with the support. The differences between the spectra for NPs on different supports are rather subtle, suggesting that the particle size and structure are similar in samples on both supports. XANES spectra for Pt on TiO2, acquired with different X-ray polarizations, are also quite close. For Pt NPs on SiO2, we did not perform polarization-dependent measurements because no well-defined crystalline orientations were available at the native SiO2/Si(111) interface. For Pt NPs on TiO2, spectra, acquired with both substrate-parallel X-ray polarizations, overlap completely. The intensity of the white line in the spectrum, acquired with X-ray polarization, perpendicular to sample surface, is slightly lower, suggesting some anisotropy in particle structure and/or particle–support interactions. This difference, however, is much smaller than the one observed in a similar study of raft-like (and, hence, very anisotropic) Pt clusters on α-Al2O3.46
Figure 2.
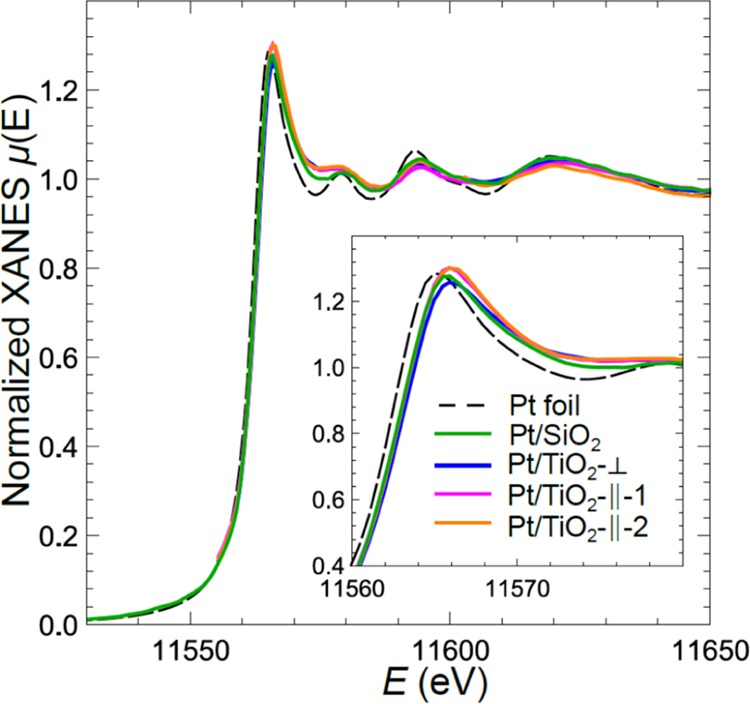
Experimental Pt L3-edge XANES spectra measured at 25 °C in UHV corresponding to Pt NPs supported on SiO2 and TiO2(110). The data on TiO2 were acquired in three different X-ray polarizations, two parallel to the support surface and one perpendicular. Data from Pt foil are also shown for reference.
3.2.2. Analysis of EXAFS Data (Nonlinear Least Square Fitting)
Figure 3 shows k2-weighted EXAFS spectra in k-space (a) and their Fourier-transforms (FT) (b), extracted from the analysis of Pt L3-edge data for NPs on two different supports. Clear differences can be observed. In particular, the amplitude of the EXAFS oscillations is slightly larger for Pt on SiO2 support. In addition, the shoulder in the FT-EXAFS data between 1 and 2 Å that can be attributed to a contribution from low-Z elements is absent in the data for Pt NPs on SiO2. Note that since the same NP solution was used to synthesize the NPs deposited on TiO2 and SiO2, the resulting NPs are expected to have the same average number of atoms in both samples. Therefore, the observed differences can be attributed to the differences in particle shape and/or bonding with the support.
Figure 3.
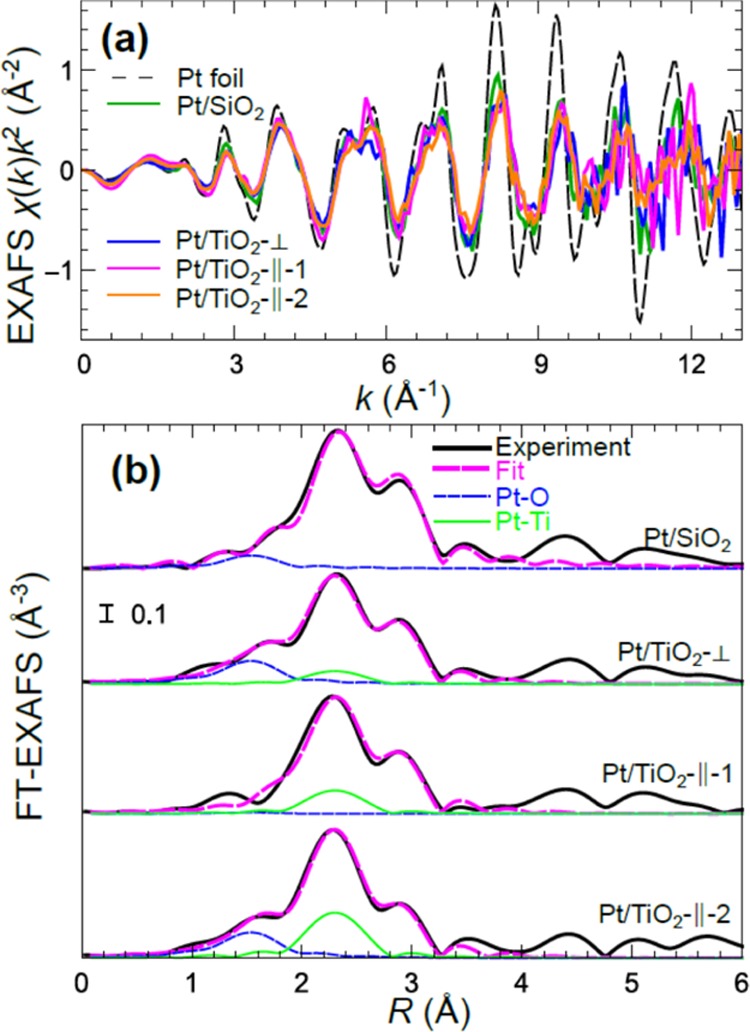
k-space k2-weighted Pt L3-ege EXAFS data (a) and Fourier-transformed EXAFS data (b) for Pt NPs on SiO2 and TiO2(110). Fitted spectra considering Pt–Pt and Pt–O bonds for NPs on SiO2/Si(111), and Pt–Pt, Pt–O, and Pt–Ti bonds for NPs on TiO2(110) are also shown. For clarity, spectra are shifted vertically in (b).
Polarization effects in EXAFS data for Pt NPs on TiO2 are also shown in Figure 3. First of all, note the significant difference between spectra for substrate-perpendicular X-ray polarization and X-ray polarization along [001] direction (∥-1 direction). The FT-EXAFS data for the former one contain a pronounced shoulder between 1 and 2 Å due to a contribution from low-Z elements, which can interpreted as an evidence of Pt bonding with the oxygen atoms in the support. Due to the dependence of contributions of different bonds on the angle between bond orientation and X-ray polarization direction (eq 1), these bonds are not expected to contribute significantly to the spectra with substrate-parallel X-ray polarization, which explains the lack of this contribution in ∥-1 spectrum.
However, in contrast to the ∥-1 spectrum the contribution of low-Z elements is clearly visible in the EXAFS spectrum collected with X-ray polarization in another substrate-parallel direction ([11̅0] or ∥-2 direction). Since substrate-perpendicular Pt–O bonds cannot contribute significantly to this spectrum, this observation suggests the presence of some oxygen atoms also on the side-surfaces of the Pt NP, which can be interpreted as a partial encapsulation of the Pt particle by the TiO2 substrate and/or presence of adsorbed oxygen on side facets of Pt particle. Note that encapsulation of Pt NPs by TiO2 has been observed, for example, through STM studies.25,31 The difference between results for ∥-1 and ∥-2 directions in this case can be explained by an anisotropy of the TiO2(110) surface. This anisotropy and its effect on interactions with Pt clusters have also been acknowledged previously.24,31,69
For quantitative analysis, we perform nonlinear least-square EXAFS fitting. The results of such fitting are shown in R-space in Figure 3, while k-space data are shown in the Supporting Information, Figure S3. The contributions of the individual scattering components are also plotted in R-space (Fourier-transformed) in Figure 3. Corresponding values of structure parameters are reported in Tables 1 and S1 in the Supporting Information. Our strongly constrained fitting model that accounts for the presence of Pt–Pt, Pt–O, and Pt–Ti bonds can fit experimental data quite accurately, and all the values of interatomic distances and Debye–Waller factors seem to be physically reasonable, giving us confidence in the obtained values of structure parameters. It is worth mentioning that an alternative fitting model with an extra Pt–O bond (ca. 2.7 Å) instead of Pt–Ti bond also resulted in a reasonable fit. However, the obtained Pt–Pt structure parameters were similar in both cases.
Table 1. ECNs for Pt NPs on TiO2(110) Obtained for Different X-ray Polarizations with Respect to the Support Surface (Two In-Plane Orientations Parallel to the TiO2(110)[001] (∥-1) and TiO2(110)[11̅0] (∥-2) Support Directions and One Perpendicular). The Results Have Been Extracted from the Analysis of EXAFS Dataa.
| sample/X-ray polarization | NPt–Pt | NPt–O | NPt–Ti |
|---|---|---|---|
| Pt/TiO2 (110)-∥-1 | 7.3(9) | 0.1(2) | 0.5(3) |
| Pt/TiO2 (110)-∥-2 | 6.4(8) | 0.6(2) | 1.0(4) |
| Pt/TiO2 (110)-⊥ | 7.3(9) | 0.6(2) | 0.3(2) |
| Pt/SiO2 | 8.3(3) | 0.2(1) |
CNs from EXAFS data for Pt on SiO2 are also shown. Uncertainties in the last digit are given in parentheses.
In the case of Pt NPs on SiO2, higher Pt–Pt and lower Pt–O CNs (as compared to those for NPs on the TiO2 substrate) are obtained. Since the number of atoms per particle should be close in both samples, the higher Pt–Pt CNs obtained for Pt/SiO2 can be interpreted as an evidence for more spherical particle shape, which is in an agreement with our earlier TEM study showing nearly spherical Pt NPs supported on SiO2 after annealing at 727 °C.55 Low Pt–O CN for Pt on SiO2 is in agreement with the results of visual examination of EXAFS data above and suggests relatively weak particle–support interaction for this system.
Pt–Pt CNs obtained for Pt NPs on TiO2 with different X-ray polarizations are relatively close, suggesting that NPs on this support are also rather three-dimensional (as opposed to flat, raft-like structures, reported elsewhere for small Pt NPs with very strong particle–support interactions).4,16,34 Similarity of Pt–Pt CNs in ∥-1 and ∥-2 directions also suggests the lack of noticeable elongation of Pt NPs in the TiO2(110) plane, reported in the literature24,31 for physical vapor deposition (PVD) NPs. This discrepancy can be explained based on the differences in the synthesis methods employed and in the size of the NPs used. In our study, the NPs were prepared by colloidal chemistry and therefore originally had a spherical shape, while in the other studies (e.g., by Dulub et al., ref (31)) the NPs were directly grown on the substrate. The shape of the NPs evaporated on a substrate is impacted by the growth kinetics such as possible ad-atom diffusion asymmetries. In addition, while our NPs were smaller than 2 nm in size, the PVD-grown NPs in the mentioned study had a lateral size of around 20 nm. Since the strain and the support interactions depend on the NP size, the stress build-up in a larger NP (such as PVD-grown NPs1,70) may facilitate an asymmetrical growth of the NPs.
The main difference between XAFS results for different X-ray polarizations thus lies in the difference in Pt–O and Pt–Ti CNs. In particular, the contribution of Pt–O bonds is significantly lower for ∥-1 spectrum than for other two spectra, confirming the presence of anisotropic particle–support interactions in this system.
3.2.3. NN-Based Analysis of XANES Data
Quantitative interpretation of EXAFS spectra is always complicated by the correlations between different structural parameters. These correlations especially hinder the analysis of strongly overlapping contributions beyond the first coordination shell for data with limited k-range and poor signal-to-noise ratio. Therefore, here we complement EXAFS analysis with the NN-based analysis of XANES data. Experimental XANES data for Pt NPs are shown in Figure 2. These spectra were used as input for NN analysis,50 and the obtained CNs for the first four coordination shells are given in Table 2.
Table 2. Pt–Pt ECNs for the First, Second, Third, and Fourth Coordination Shells (N1, N2, N3, and N4, Correspondingly) Extracted by NN Analysis from Experimental XANES Dataa.
| sample/X-ray polarization | N1 | N2 | N3 | N4 |
|---|---|---|---|---|
| Pt/TiO2 (110)-∥-1 | 6.2(3) | 3.5(3) | 5(2) | 4(2) |
| Pt/TiO2 (110)-∥-2 | 6.0(4) | 3.7(3) | 7(1) | 4(1) |
| Pt/TiO2 (110)-⊥ | 6.1(4) | 3.6(2) | 5(2) | 3(1) |
| Pt/SiO2 | 7.9(4) | 4.0(4) | 7(2) | 5(1) |
Uncertainties in the last digit are given in parentheses.
According to the EXAFS analysis, bonding with the support is the weakest for the sample on SiO2, thus in this case the results, obtained by NN that is trained on metallic particles only, should be the most reliable. Indeed, the first shell CN obtained from XANES analysis for this sample (7.9 ± 0.4) is in an excellent agreement with the results of conventional EXAFS data fitting (8.3 ± 0.3). This agreement shows the power of NN-based analysis of XANES data, which could be a very useful method in the cases where high-quality EXAFS spectra cannot be achieved (e.g., for diluted samples, time-dependent studies, measurements in liquid or high-pressure gas environments due to attenuation of beam).
The applicability of NN-XANES method for the samples on TiO2 is less certain due to a larger contribution of bonds with the support. Interpretation of the CNs values, obtained from NN-XANES analysis, should be done with caution in this case. However, one can note that at least for the first coordination shell the results from NN-XANES analysis (Table 2) agree reasonably with the independently obtained results of EXAFS analysis (Table 1), giving us some confidence that the contribution of Pt–O and Pt–Ti bonds is sufficiently low in this case for NN-XANES method to work and that also the CNs for the second, third, and fourth coordination shells are determined reliably. In addition, perhaps, the most important conclusion from NN-XANES analysis, which should not be affected by the presence of any systematic errors, is that all four CNs for three different polarization directions are similar, suggesting, again, a rather three-dimensional shape of the Pt NPs and the lack of significant elongations along any specific direction.
3.2.4. Resolving the Structure of Pt NPs
A MATLAB code was written to generate a database of Pt NP structure models to match the CNs extracted through the analysis of EXAFS and NN-based analysis of XANES. Different NP shapes were obtained by truncating a bulk Pt fcc structure along three different planes (111), (110), and (100) to generate NPs with sizes ranging from 0.8 to 3 nm. This database includes a variety of NP shapes such as cuboctahedron, truncated octahedron, and hexahedron. For each shape, the corresponding ECNs were calculated by considering different X-ray polarization directions (eq 1). Subsequently, the ECNs and particle sizes for the NPs models were compared with the experimental results extracted from NN-based analysis of XANES data, the first shell conventional EXAFS data analysis, and AFM and STM measurements. Figure 4a shows the particle model for the Pt/SiO2 system with the best agreement with the experimental results (AFM-determined average NP height and CNs from XAFS analysis): all four CNs, obtained from the experimental XAFS data, agree well with those for a cuboctahedral particle with 55 atoms (corresponding CNs for the model are reported in Table 3). The size and shape of this particle model also agree well with the available TEM data for analogously synthesized NPs.55
Figure 4.

NP shapes that are in the best agreement with the experimental AFM average NP height and CNs extracted from experimental EXAFS and NN-XANES analysis of data for Pt NP supported on (a) SiO2/Si(111) and (b,c) TiO2(110). The interface between Pt particle and TiO2 in (b,c) is shown in this figure for illustrative purposes only and does not reflect the actual positions of Pt and Ti/O atoms.
Table 3. Pt–Pt ECNs for the First, Second, Third, and Fourth Coordination Shells (N1, N2, N3, and N4, Correspondingly) for Particle Models, Shown in Figure 4.
| sample/X-ray polarization | N1 | N2 | N3 | N4 |
|---|---|---|---|---|
| Pt/TiO2 (110)-∥-1 | 7.6 | 3.5 | 7.9 | 4.2 |
| Pt/TiO2 (110)-∥-2 | 7.6 | 3.5 | 7.9 | 4.2 |
| Pt/TiO2 (110)-⊥ | 6.0 | 1.1 | 5.8 | 2.2 |
| Pt/SiO2 | 7.9 | 3.3 | 9.6 | 4.1 |
In the case of Pt/TiO2, the determination of particle shape is possible only by combining insights from different techniques, since by its own neither EXAFS, nor XANES, nor microscopy result is conclusive for this complex system, and can be biased by significant systematic errors. To determine the most likely NP shape, we use the first shell CNs from EXAFS analysis and the first four CNs from XANES analysis for each polarization direction. We use also insights from STM and AFM data (Figure 1) regarding possible particle size and shape. Furthermore, we exploit the observation that the total number of atoms in the particles on TiO2 should be close to the number of atoms in the particle on SiO2.55 The NP model that gives the best agreement with these data is shown in Figure 4b,c: a truncated octahedron with Pt(100) top and interfacial facet and with 50 atoms. Corresponding CNs for this model particle are reported in Table 3 and agree well with the results of XAFS data analysis. It is worth mentioning that the first CN (N1) of ca. 7 has been estimated to correspond to a NP with ca. 1 nm in diameter.39,71 Similar shapes have been observed in our earlier STM study of larger Pt NPs (<3000 atoms) supported on TiO2 (110), see example in Figure 1c–e.3,17 However, we have to mention that while STM studies are inherently limited to a very small area and very few NPs can be analyzed, here by relying on spectroscopy methods, the effective NP shape is extracted for a very large ensemble of NPs of similar size. Additionally, information on smaller NPs of 3D shape, for which scanning probe methods will fail due to tip-convolution effects, can also be extracted.
3.2.5. RMC Simulations of EXAFS Data
The structure models obtained from XAFS and AFM analysis can further be refined using RMC–EXAFS simulations.48,50 Calculations for Pt NPs on SiO2 are carried out as in ref (50). For Pt NPs on TiO2, we fit simultaneously experimental data obtained with three different X-ray polarizations to obtain a more unambiguous structure model. In addition, due to the presence of significant Pt–O and Pt–Ti contribution (as evidenced by conventional EXAFS analysis), we need to include support atoms in the RMC model and consider possible NP encapsulation by TiOx species. From the conventional first shell analysis, it is not possible to get much detail about the interface between Pt NPs and TiO2; therefore, it is not possible to tell unambiguously how exactly the particle is positioned with respect to the support. Therefore, we have tried out different models, starting with the model, where the Pt NP is sitting on top of the TiO2(110) surface, ending up with the model, where the NP is completely encapsulated by Ti and O atoms (see the insets in Figure 5). In all cases to model support atoms and the atoms that encapsulate the NP, we started with a large enough slab of TiO2 (rutile), where all atoms are at their ideal equilibrium positions, and carved it to insert the Pt NP. Thus, all Ti and O atoms (both in the support and in the thin layer that encapsulates the particle) are initially at the positions that correspond to coordinates of Ti and O atoms in an ideal rutile structure. During the RMC optimization, coordinates of all Pt atoms and coordinates of Ti and O atoms that are sufficiently close to Pt atoms are optimized to ensure as good as possible agreement with the experimental EXAFS data.
Figure 5.
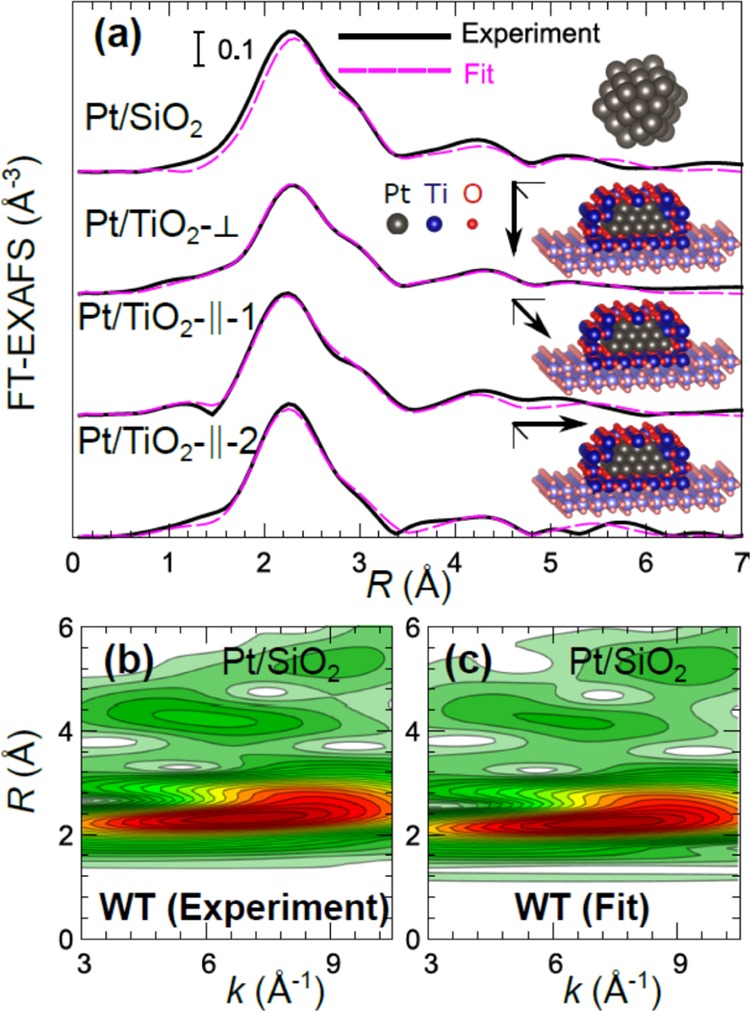
Experimental Pt L3-edge FT-EXAFS moduli (a) and the corresponding fits achieved through RMC simulations of EXAFS spectra (spectra are shifted vertically for clarity). Moduli of the corresponding WT for experimental (b) and for theoretical spectra (c) of Pt/SiO2. Model structures with the best agreement to experimental data are shown as the insets with the corresponding direction of X-ray polarization indicated with an arrow for Pt/TiO2(110). For clarity, Ti and O atoms encapsulating facets located at the front of the NP are not shown. Pt (gray), Ti (dark blue), and O (dark red) atoms were included in the RMC optimization. Lighter blue (Ti) and lighter red (O) atoms are shown for visualization purposes only and are not included in the actual RMC simulation because they are too far away from the absorbing Pt atoms and do not contribute to the EXAFS spectra.
The latter model, where the particle is completely encapsulated by TiOx, gave much better agreement with all available EXAFS data after RMC optimization (see Figure 5), while in the models with only partial encapsulation, the observed Pt–O/Ti contribution was not sufficiently strong to explain all the features in experimental EXAFS data. Thus, we used a model with a fully encapsulated Pt NP for further analysis. Note that despite the fact that the Pt particle is completely surrounded by Ti and O atoms in this model, due to the anisotropy of the TiO2 rutile structure the contribution of shorter Pt–O and Pt–Ti bonds along the [001] direction (∥-1 direction) is significantly lower than the contribution of such bonds along the [11̅0] direction (∥-2 direction) and in the substrate-perpendicular direction, in agreement with the observed trends in EXAFS data collected with different X-ray polarizations and results of conventional EXAFS analysis. Note also that we do not claim that our simple model is able to reproduce accurately the whole complexity of particle–support interactions and the true structure of the encapsulating TiOx layer, since there is not enough information in the EXAFS data available in this case concerning the Pt–O and Pt–Ti bonds. Nevertheless, as shown in Figure 5, this model allows us to obtain a good fit to experimental Pt L3-edge EXAFS data, and, thus, to analyze the local structure and distributions of Pt–Pt bond lengths within the metal NP. It is worth mentioning that this result shows an advantage of resolving the structure of NPs using X-ray absorption spectroscopy over scanning probe methods, since the latter cannot provide information about the encapsulation of NPs by Ti and O for very small 3D NPs (e.g., <3 nm), where atomic resolution on the NP facets cannot likely be achieved.
As shown in Figure 5 and in the Supporting Information, Figure S4, a good agreement between simulated and experimental EXAFS was obtained both for SiO2 and TiO2 supports and for all considered X-ray polarization directions. Importantly, it should be noted that RMC is able to ensure good fit to experimental data not only for the first, but also for more distant coordination shells, as evidenced by the good agreement between experiment and simulations in the R range between 3 and 6 Å in Figure 5. This good agreement gives us additional confidence in the chosen particle structural models.
From the atomic coordinates obtained in RMC simulations, it is straightforward to calculate RDF that characterizes the distribution of atoms around the absorbing atom and contains complete information on bond-lengths and their variations. The partial RDFs (for Pt–O, Pt–Ti and Pt–Pt pairs) for Pt NPs on TiO2 are shown in Figure 6. Both Pt–O and Pt–Ti contributions are disordered, which is expected for interfacial bonds. RDF peaks for Pt–Pt bonds, in turn, are relatively narrow, suggesting that the NP has a well-defined ordered structure. At the same time, all peaks have remarkably non-Gaussian shapes. To investigate the distributions of bond-lengths in more detail, we have analyzed separately the contributions of Pt–Pt bonds with different orientation with respect to the substrate surface (see schematic in Figure 6b). As shown in Figure 6c, the widths of the corresponding bond-length distributions are similar. Distribution of bond lengths along [001] direction (orange bonds in Figure 6b) seems to be more disordered and even bimodal, although this could also be an artifact of our procedure due to a short k-range (up to 10.5 Å–1) available for the analysis, which limits the resolution of our method in R-space. Overall, our results indicate that despite the strong and anisotropic interactions with the support, the local structure of Pt NP on TiO2 remains approximately the same along different directions.
Figure 6.
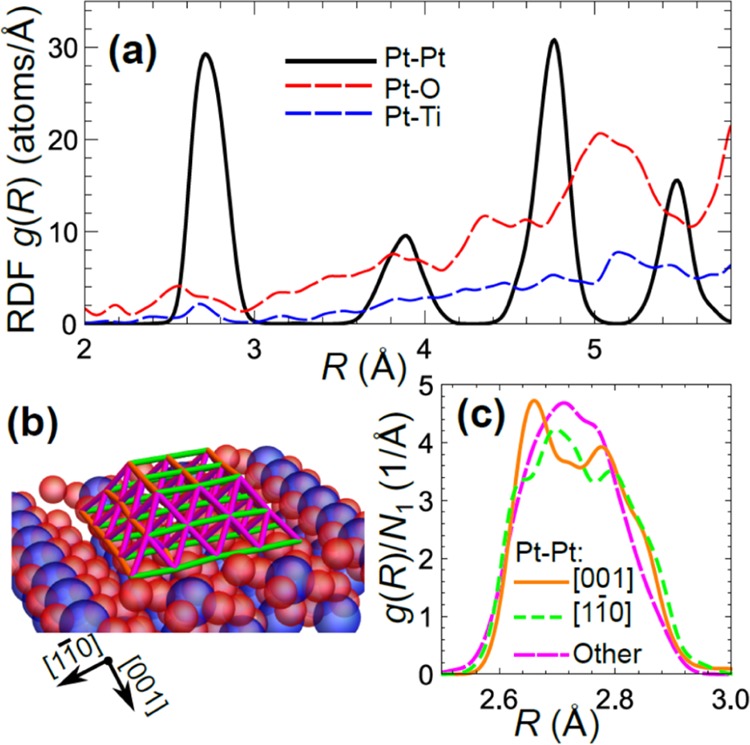
Partial RDFs (for Pt–Pt, Pt–O, and Pt–Ti bonds) for Pt NPs on TiO2(110), obtained in RMC simulations with three different X-ray polarizations data analyzed simultaneously (a). In case of Pt–Pt bonds, one can distinguish between Pt–Pt bonds aligned parallel to substrate and its [11̅0] direction (green), aligned parallel to [001] direction (orange) and other bonds oriented at 60° to the substrate (magenta) (scheme in (b)). Corresponding bond-length distributions are shown separately in (c). For better comparison, bond-length distributions are normalized by the corresponding CN in (c).
For comparison, the obtained RDF for Pt NPs on SiO2 (where one expects weaker particle–support interactions) is shown in Figure 7. Average Pt–Pt bond distances (positions of RDF peaks) in all coordination shells are similar for both substrates, but the Pt–Pt bond is slightly longer in the case of Pt/SiO2 as compared to Pt/TiO2. This trend can also be seen in the results of conventional EXAFS data fitting, see Supporting Information, Table S1, where the average Pt–Pt distance for Pt/SiO2 (2.740 ± 0.006 Å) is larger and closer to the Pt–Pt distance in bulk Pt (ca 2.76 Å) than that of Pt/TiO2 (2.728 ± 0.005 Å). At the same time, while also for Pt NPs on SiO2 the distribution of bond lengths has a non-Gaussian shape, RDF peaks are sharper, and the bond length disorder is less pronounced for this sample, implying more ordered structure. This difference demonstrates that the interactions with the support can compress the interatomic distances and introduce additional stress in the structure of Pt NPs on TiO2, and thus the type of support may have a pronounced effect on the local structure and distributions of interatomic distances in metallic NPs. As a side note, let us emphasize here that the presence of substrate- or surface-induced asymmetries and non-Gaussian effects in the bond-length distributions may have a profound effect on the accurate NP structure determination in conventional EXAFS fitting. It is known that conventional approaches to EXAFS data analysis are inadequate if the distribution of bond-lengths is asymmetric,72,73 resulting in inaccurate (typically—underestimated) CNs, interatomic distances, and Debye–Waller factors. By complementing conventional EXAFS analysis with such advanced techniques as NN-XANES analysis (which is less affected by disorder effects) and RMC simulations (that allow treatment of non-Gaussian RDF shapes), this problem can be avoided. Future experimental work and data analysis will be directed toward understanding how the distribution of bond lengths changes with temperature, to separate the static disorder effects from dynamics effects (atomic thermal motion), and to explore the role of particle–support interactions in such intriguing nanoscale phenomena such as negative thermal expansion effect44 and enhanced catalytic activity.4−6
Figure 7.
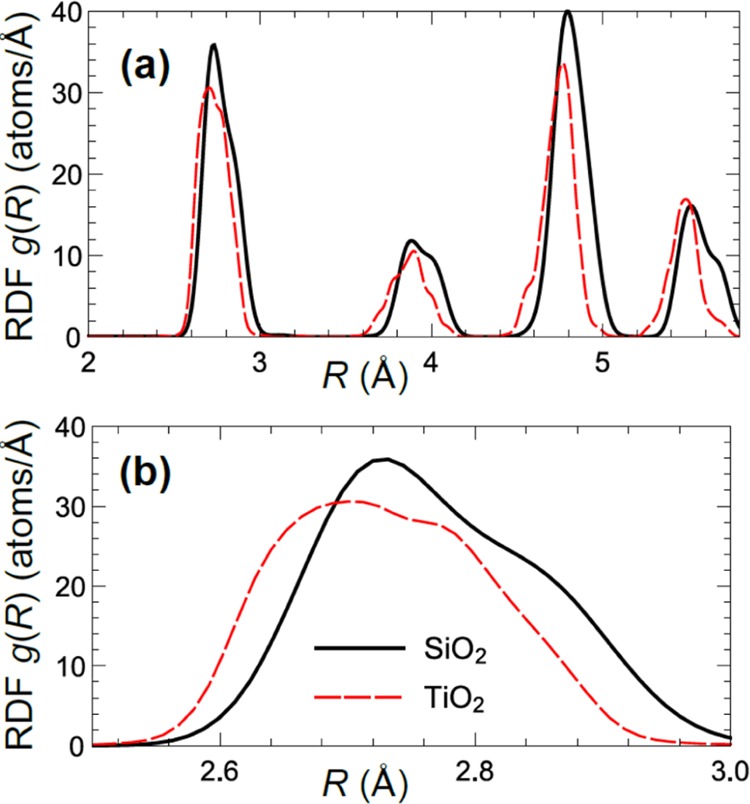
Pt–Pt RDF for Pt NPs on SiO2 and TiO2, obtained from RMC simulations.
4. Conclusions
We have introduced a new approach to resolve the morphology of NPs supported on single-crystal substrates to gain insight into the role of the support material on the NPs shape and structure anisotropy. We have found that polarized XAFS measurements carried out for adsorbate-free size-selected NPs are a very useful tool for this purpose, especially when coupled with advanced data analysis approaches. In particular, NN-based analysis of in situ XANES spectra could be used to extract CNs for the first few coordination shells, which, in combination with microscopy data, can be used to construct an unambiguous 3D NP model. Disorder effects and the details of anisotropic bond-length distributions can then be modeled via the RMC–EXAFS approach. Using this set of techniques, we have shown that well-defined faceted truncated octahedron Pt NPs can be grown on TiO2(110) after annealing at 600 °C in vacuum, while similarly synthesized NPs on SiO2/Si(111) assumed a more spherical 3D morphology. Interactions with the support have a profound effect also on the distribution of bond-lengths. In particular, significant differences were found in the contribution of Pt–O interatomic distances for Pt NPs on two different supports, as well as for different bond directions in Pt NPs on TiO2. By analyzing polarization-dependent XAFS data, we have found evidences that Pt on TiO2 is encapsulated by Ti and O from the support, with significantly anisotropic Pt/TiO2 interfaces along different directions. Our study thus revealed that the shape and distribution of static strain, which are both known to affect the functionality of metal NPs, can be controlled through tuning their interaction with the support.
Acknowledgments
This work was funded by the European Research Council (ERC-725915, OPERANDOCAT) and the US National Science Foundation (NSF-CHEM-1213182 and NSF-DMR-1207065). The authors are grateful to Dr. H. Mistry, Dr. L. R. Merte, and Dr. J. Matos for assistance during the in situ EXAFS measurements. RMC–EXAFS simulations were performed on the LASC cluster-type computer at the Institute of Solid State Physics of the University of Latvia.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.9b00945.
Calculated polarization dependence of the ECNs for K- and L3-absorption edges; particle height histograms extracted from AFM data; values of interatomic distances and disorder factors from EXAFS data fitting; results from the EXAFS data fitting in k-space; and a comparison of WTs for experimental EXAFS data for Pt on TiO2 and for theoretical spectra, obtained in RMC simulations (PDF)
Author Contributions
§ Equally contributing authors.
The authors declare no competing financial interest.
Supplementary Material
References
- Ahmadi M.; Behafarid F.; Roldan Cuenya B. Size-Dependent Adhesion Energy of Shape-Selected Pd and Pt Nanoparticles. Nanoscale 2016, 8, 11635–11641. 10.1039/c6nr02166b. [DOI] [PubMed] [Google Scholar]
- Merte L. R.; Ahmadi M.; Behafarid F.; Ono L. K.; Lira E.; Matos J.; Li L.; Yang J. C.; Roldan Cuenya B. Correlating Catalytic Methanol Oxidation with the Structure and Oxidation State of Size-Selected Pt Nanoparticles. ACS Catal. 2013, 3, 1460–1468. 10.1021/cs400234h. [DOI] [Google Scholar]
- Ahmadi M.; Behafarid F.; Holse C.; Nielsen J. H.; Roldan Cuenya B. Shape-Selection of Thermodynamically Stabilized Colloidal Pd and Pt Nanoparticles Controlled via Support Effects. J. Phys. Chem. C 2015, 119, 29178–29185. 10.1021/acs.jpcc.5b09980. [DOI] [Google Scholar]
- Mostafa S.; Behafarid F.; Croy J. R.; Ono L. K.; Li L.; Yang J. C.; Frenkel A. I.; Roldan Cuenya B. Shape-Dependent Catalytic Properties of Pt Nanoparticles. J. Am. Chem. Soc. 2010, 132, 15714–15719. 10.1021/ja106679z. [DOI] [PubMed] [Google Scholar]
- Ahmadi M.; Mistry H.; Roldan Cuenya B. Tailoring the Catalytic Properties of Metal Nanoparticles via Support Interactions. J. Phy. Chem. Let. 2016, 7, 3519–3533. 10.1021/acs.jpclett.6b01198. [DOI] [PubMed] [Google Scholar]
- Roldan Cuenya B.; Behafarid F. Nanocatalysis: Size- and Shape-Dependent Chemisorption and Catalytic Reactivity. Surf. Sci. Rep. 2015, 70, 135–187. 10.1016/j.surfrep.2015.01.001. [DOI] [Google Scholar]
- Bruix A.; Rodriguez J. A.; Ramírez P. J.; Senanayake S. D.; Evans J.; Park J. B.; Stacchiola D.; Liu P.; Hrbek J.; Illas F. A New Type of Strong Metal-Support Interaction and the Production of H2 through the Transformation of Water on Pt/CeO2(111) and Pt/CeOx/TiO2(110) Catalysts. J. Am. Chem. Soc. 2012, 134, 8968–8974. 10.1021/ja302070k. [DOI] [PubMed] [Google Scholar]
- Lustemberg P. G.; Palomino R. M.; Gutiérrez R. A.; Grinter D. C.; Vorokhta M.; Liu Z.; Ramírez P. J.; Matolín V.; Ganduglia-Pirovano M. V.; Senanayake S. D.; Rodriguez J. A. Direct Conversion of Methane to Methanol on Ni-Ceria Surfaces: Metal-Support Interactions and Water-Enabled Catalytic Conversion by Site Blocking. J. Am. Chem. Soc. 2018, 140, 7681–7687. 10.1021/jacs.8b03809. [DOI] [PubMed] [Google Scholar]
- Narayanan R.; El-Sayed M. A. Shape-Dependent Catalytic Activity of Platinum Nanoparticles in Colloidal Solution. Nano Lett. 2004, 4, 1343–1348. 10.1021/nl0495256. [DOI] [Google Scholar]
- Qian J.; Shen M.; Zhou S.; Lee C.-T.; Zhao M.; Lyu Z.; Hood Z. D.; Vara M.; Gilroy K. D.; Wang K.; Xia Y. Synthesis of Pt Nanocrystals with Different Shapes Using the Same Protocol to Optimize Their Catalytic Activity Toward Oxygen Reduction. Mater. Today 2018, 21, 834–844. 10.1016/j.mattod.2018.08.005. [DOI] [Google Scholar]
- Liu J.; Jiang L.; Zhang B.; Jin J.; Su D. S.; Wang S.; Sun G. Controllable Synthesis of Cobalt Monoxide Nanoparticles and the Size-Dependent Activity for Oxygen Reduction Reaction. ACS Catal. 2014, 4, 2998–3001. 10.1021/cs500741s. [DOI] [Google Scholar]
- Cao S.; Tao F.; Tang Y.; Li Y. Size- and shape-dependent catalytic performances of oxidation and reduction reactions on nanocatalysts. Chem. Soc. Rev. 2016, 45, 4747–4765. 10.1039/c6cs00094k. [DOI] [PubMed] [Google Scholar]
- Giorgio S.; Chapon C.; Henry C. R.; Nihoul G.; Penisson J. M. High-resolution transmission electron microscopy study of gold particles (greater than 1 nm), epitaxially grown on clean MgO microcubes. Philos. Mag. A 1991, 64, 87–96. 10.1080/01418619108206128. [DOI] [Google Scholar]
- Xu R.; Wang D.; Zhang J.; Li Y. Shape-Dependent Catalytic Activity of Silver Nanoparticles for the Oxidation of Styrene. Chem.—Asian J. 2006, 1, 888–893. 10.1002/asia.200600260. [DOI] [PubMed] [Google Scholar]
- Tian N.; Zhou Z.-Y.; Sun S.-G.; Ding Y.; Wang Z. L. Synthesis of Tetrahexahedral Platinum Nanocrystals with High-Index Facets and High Electro-Oxidation Activity. Science 2007, 316, 732–735. 10.1126/science.1140484. [DOI] [PubMed] [Google Scholar]
- Mistry H.; Behafarid F.; Zhou E.; Ono L. K.; Zhang L.; Roldan Cuenya B. Shape-Dependent Catalytic Oxidation of 2-Butanol over Pt Nanoparticles Supported on γ-Al2O3. ACS Catal. 2014, 4, 109–115. 10.1021/cs400888n. [DOI] [Google Scholar]
- Behafarid F.; Roldan Cuenya B. Nanoepitaxy Using Micellar Nanoparticles. Nano Lett. 2011, 11, 5290–5296. 10.1021/nl2027525. [DOI] [PubMed] [Google Scholar]
- Henry C. R. Morphology of Supported Nanoparticles. Prog. Surf. Sci. 2005, 80, 92–116. 10.1016/j.progsurf.2005.09.004. [DOI] [Google Scholar]
- Tauster S. J.; Fung S. C.; Baker R. T. K.; Horsley J. A. Strong Interactions in Supported-Metal Catalysts. Science 1981, 211, 1121–1125. 10.1126/science.211.4487.1121. [DOI] [PubMed] [Google Scholar]
- Vayssilov G. N.; Lykhach Y.; Migani A.; Staudt T.; Petrova G. P.; Tsud N.; Skála T.; Bruix A.; Illas F.; Prince K. C.; Matolín V. r.; Neyman K. M.; Libuda J. Support Nanostructure Boosts Oxygen Transfer to Catalytically Active Platinum Nanoparticles. Nat. Mater. 2011, 10, 310–315. 10.1038/nmat2976. [DOI] [PubMed] [Google Scholar]
- Mason M. G. Electronic Structure of Supported Small Metal Clusters. Phys. Rev. B: Condens. Matter Mater. Phys. 1983, 27, 748–762. 10.1103/physrevb.27.748. [DOI] [Google Scholar]
- Nilsson Pingel T.; Jorgensen M.; Yankovich A. B.; Gronbeck H.; Olsson E. Influence of Atomic Site-Specific Strain on Catalytic Activity of Supported Nanoparticles. Nat. Commun. 2018, 9, 2722. 10.1038/s41467-018-05055-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walsh M. J.; Yoshida K.; Kuwabara A.; Pay M. L.; Gai P. L.; Boyes E. D. On the Structural Origin of the Catalytic Properties of Inherently Strained Ultrasmall Decahedral Gold Nanoparticles. Nano Lett. 2012, 12, 2027–2031. 10.1021/nl300067q. [DOI] [PubMed] [Google Scholar]
- Kibsgaard J.; Clausen B. S.; Topsøe H.; Lægsgaard E.; Lauritsen J. V.; Besenbacher F. Scanning tunneling microscopy studies of TiO2-supported hydrotreating catalysts: Anisotropic particle shapes by edge-specific MoS2-support bonding. J. Catal. 2009, 263, 98–103. 10.1016/j.jcat.2009.01.016. [DOI] [Google Scholar]
- Tauster S. J. Strong Metal-Support Interactions. Acc. Chem. Res. 1987, 20, 389–394. 10.1021/ar00143a001. [DOI] [Google Scholar]
- Fu Q.; Wagner T.; Olliges S.; Carstanjen H.-D. Metal–Oxide Interfacial Reactions: Encapsulation of Pd on TiO2(110). J. Phys. Chem. B 2005, 109, 944–951. 10.1021/jp046091u. [DOI] [PubMed] [Google Scholar]
- Vila F.; Rehr J. J.; Kas J.; Nuzzo R. G.; Frenkel A. I. Dynamic Structure in Supported Pt Nanoclusters: Real-Time Density Functional Theory and X-ray Spectroscopy Simulations. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 78, 121404. 10.1103/physrevb.78.121404. [DOI] [Google Scholar]
- Silly F.; Castell M. R. Selecting the Shape of Supported Metal Nanocrystals: Pd Huts, Hexagons, or Pyramids on SrTiO3(001). Phys. Rev. Lett. 2005, 94, 046103. 10.1103/physrevlett.94.046103. [DOI] [PubMed] [Google Scholar]
- Graoui H.; Giorgio S.; Enry C. R. Effect of The Interface Structure on The High-Temperature Morphology of Supported Metal Clusters. Philos. Mag. B 2001, 81, 1649–1658. 10.1080/13642810108223109. [DOI] [Google Scholar]
- Hansen K. H.; Worren T.; Stempel S.; Lægsgaard E.; Bäumer M.; Freund H.-J.; Besenbacher F.; Stensgaard I. Palladium Nanocrystals on Al2O3: Structure and Adhesion Energy. Phys. Rev. Lett. 1999, 83, 4120–4123. 10.1103/physrevlett.83.4120. [DOI] [Google Scholar]
- Dulub O.; Hebenstreit W.; Diebold U. Imaging Cluster Surfaces with Atomic Resolution: The Strong Metal-Support Interaction State of Pt Supported on TiO2(110). Phys. Rev. Lett. 2000, 84, 3646–3649. 10.1103/physrevlett.84.3646. [DOI] [PubMed] [Google Scholar]
- Renaud G. Real-Time Monitoring of Growing Nanoparticles. Science 2003, 300, 1416–1419. 10.1126/science.1082146. [DOI] [PubMed] [Google Scholar]
- Nolte P.; Stierle A.; Jin-Phillipp N. Y.; Kasper N.; Schulli T. U.; Dosch H. Shape Changes of Supported Rh Nanoparticles During Oxidation and Reduction Cycles. Science 2008, 321, 1654–1658. 10.1126/science.1160845. [DOI] [PubMed] [Google Scholar]
- Roldan Cuenya B.; Croy J. R.; Mostafa S.; Behafarid F.; Li L.; Zhang Z.; Yang J. C.; Wang Q.; Frenkel A. I. Solving the Structure of Size-Selected Pt Nanocatalysts Synthesized by Inverse Micelle Encapsulation. J. Am. Chem. Soc. 2010, 132, 8747–8756. 10.1021/ja101997z. [DOI] [PubMed] [Google Scholar]
- Lagarde P. Surface X-ray absorption spectroscopy principles and some examples of applications. Ultramicroscopy 2001, 86, 255–263. 10.1016/s0304-3991(00)00117-0. [DOI] [PubMed] [Google Scholar]
- Gordon R. A.; Crozier E. D.; Jiang D.-T.; Budnik P. S.; Monchesky T. L.; Heinrich B. In situ XAFS study of Fe epitaxially grown by MBE on GaAs(001)-4×6. Surf. Sci. 2005, 581, 47–57. 10.1016/j.susc.2005.02.031. [DOI] [Google Scholar]
- Petkov V.; Shastri S.; Kim J. W.; Shan S.; Luo J.; Wu J.; Zhong C. J. Application of Differential Resonant High-Energy X-ray Diffraction to Three-Dimensional Structure Studies of Nanosized Materials: A Case Study of Pt-Pd Nanoalloy Catalysts. Acta Crystallogr., Sect. A: Found. Adv. 2018, 74, 553–566. 10.1107/s2053273318009282. [DOI] [PubMed] [Google Scholar]
- Rehr J. J.; Albers R. C. Theoretical Approaches to X-ray Absorption Fine Structure. Rev. Mod. Phys. 2000, 72, 621–654. 10.1103/revmodphys.72.621. [DOI] [Google Scholar]
- Jentys A. Estimation of Mean Size and Shape of Small Metal Particles by EXAFS. Phys. Chem. Chem. Phys. 1999, 1, 4059–4063. 10.1039/a904654b. [DOI] [Google Scholar]
- Frenkel A. I.; Yevick A.; Cooper C.; Vasic R. Modeling the Structure and Composition of Nanoparticles by Extended X-ray Absorption Fine-Structure Spectroscopy. Annu. Rev. Anal. Chem. 2011, 4, 23–39. 10.1146/annurev-anchem-061010-113906. [DOI] [PubMed] [Google Scholar]
- Frenkel A. I. Applications of Extended X-ray Absorption Fine-Structure Spectroscopy to Studies of Bimetallic Nanoparticle Catalysts. Chem. Soc. Rev. 2012, 41, 8163–8178. 10.1039/c2cs35174a. [DOI] [PubMed] [Google Scholar]
- Frenkel A. I.; Hills C. W.; Nuzzo R. G. A View from the Inside: Complexity in the Atomic Scale Ordering of Supported Metal Nanoparticles. J. Phys. Chem. B 2001, 105, 12689–12703. 10.1021/jp012769j. [DOI] [Google Scholar]
- Mistry H.; Behafarid F.; Bare S. R.; Roldan Cuenya B. Pressure-Dependent Effect of Hydrogen Adsorption on Structural and Electronic Properties of Pt/γ-Al2O3 Nanoparticles. ChemCatChem 2014, 6, 348–352. 10.1002/cctc.201300783. [DOI] [Google Scholar]
- Sanchez S. I.; Menard L. D.; Bram A.; Kang J. H.; Small M. W.; Nuzzo R. G.; Frenkel A. I. The Emergence of Nonbulk Properties in Supported Metal Clusters: Negative Thermal Expansion and Atomic Disorder in Pt Nanoclusters Supported on γ-Al2O3. J. Am. Chem. Soc. 2009, 131, 7040–7054. 10.1021/ja809182v. [DOI] [PubMed] [Google Scholar]
- Mager-Maury C.; Bonnard G.; Chizallet C.; Sautet P.; Raybaud P. H2-Induced Reconstruction of Supported Pt Clusters: Metal-Support Interaction versus Surface Hydride. ChemCatChem 2011, 3, 200–207. 10.1002/cctc.201000324. [DOI] [Google Scholar]
- Asakura K.; Chun W.-J.; Shirai M.; Tomishige K.; Iwasawa Y. In-Situ Polarization-Dependent Total-Reflection Fluorescence XAFS Studies on the Structure Transformation of Pt Clusters on α-Al2O3(0001). J. Phys. Chem. B 1997, 101, 5549–5556. 10.1021/jp970394p. [DOI] [Google Scholar]
- Ankudinov A. L.; Rehr J. J.; Low J. J.; Bare S. R. Sensitivity of Pt X-ray Absorption Near Edge Structure to the Morphology of Small Pt Clusters. J. Chem. Phys. 2002, 116, 1911–1919. 10.1063/1.1432688. [DOI] [Google Scholar]
- Timoshenko J.; Frenkel A. I. Probing Structural Relaxation in Nanosized Catalysts by Combining EXAFS and Reverse Monte Carlo Methods. Catal. Today 2017, 280, 274–282. 10.1016/j.cattod.2016.05.049. [DOI] [Google Scholar]
- Timoshenko J.; Anspoks A.; Cintins A.; Kuzmin A.; Purans J.; Frenkel A. I. Neural Network Approach for Characterizing Structural Transformations by X-Ray Absorption Fine Structure Spectroscopy. Phys. Rev. Lett. 2018, 120, 225502. 10.1103/physrevlett.120.225502. [DOI] [PubMed] [Google Scholar]
- Timoshenko J.; Lu D.; Lin Y.; Frenkel A. I. Supervised Machine-Learning-Based Determination of Three-Dimensional Structure of Metallic Nanoparticles. J. Phys. Chem. Lett. 2017, 8, 5091–5098. 10.1021/acs.jpclett.7b02364. [DOI] [PubMed] [Google Scholar]
- Gurman S. J.; Mcgreevy R. L. Reverse Monte Carlo simulation for the analysis of EXAFS data. J. Phys. Cond. Matt. 1990, 2, 9463–9473. 10.1088/0953-8984/2/48/001. [DOI] [Google Scholar]
- Timoshenko J.; Wrasman C. J.; Luneau M.; Shirman T.; Cargnello M.; Bare S. R.; Aizenberg J.; Friend C. M.; Frenkel A. I. Probing Atomic Distributions in Mono- and Bimetallic Nanoparticles by Supervised Machine Learning. Nano Lett. 2019, 19, 520–529. 10.1021/acs.nanolett.8b04461. [DOI] [PubMed] [Google Scholar]
- Yevick A.; Frenkel A. I. Effects of Surface Disorder on EXAFS Modeling of Metallic Clusters. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 81, 115451. 10.1103/physrevb.81.115451. [DOI] [Google Scholar]
- Price S. W. T.; Zonias N.; Skylaris C. K.; Hyde T. I.; Ravel B.; Russell A. E. Fitting EXAFS Data Using Molecular Dynamics Outputs and a Histogram Approach. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 85, 075439. 10.1103/physrevb.85.075439. [DOI] [Google Scholar]
- Ono L. K.; Yuan B.; Heinrich H.; Roldan Cuenya B. Formation and Thermal Stability of Platinum Oxides on Size-Selected Platinum Nanoparticles: Support Effects. J. Phys. Chem. C 2010, 114, 22119–22133. 10.1021/jp1086703. [DOI] [Google Scholar]
- Kästle G.; Boyen H.-G.; Weigl F.; Lengl G.; Herzog T.; Ziemann P.; Riethmüller S.; Mayer O.; Hartmann C.; Spatz J. P.; Möller M.; Ozawa M.; Banhart F.; Garnier M. G.; Oelhafen P. Micellar Nanoreactors-Preparation and Characterization of Hexagonally Ordered Arrays of Metallic Nanodots. Adv. Funct. Mater. 2003, 13, 853–861. 10.1002/adfm.200304332. [DOI] [Google Scholar]
- Ravel B.; Newville M. ATHENA, ARTEMIS, HEPHAESTUS: data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron Radiat. 2005, 12, 537–541. 10.1107/s0909049505012719. [DOI] [PubMed] [Google Scholar]
- Ankudinov A. L.; Bouldin C. E.; Rehr J. J.; Sims J.; Hung H. Parallel Calculation of Electron Multiple Scattering Using Lanczos Algorithms. Phys. Rev. B: Condens. Matter Mater. Phys. 2002, 65, 104107. 10.1103/physrevb.65.104107. [DOI] [Google Scholar]
- Benfatto M.; Natoli C. R.; Brouder C.; Pettifer R. F.; Lopez M. F. R. Polarized Curved-Wave Extended X-ray-Absorption Fine Structure: Theory and Application. Phys. Rev. B: Condens. Matter Mater. Phys. 1989, 39, 1936. 10.1103/physrevb.39.1936. [DOI] [PubMed] [Google Scholar]
- Shirai M. Polarized Total-Reflection Fluorescence EXAFS Study of Anisotropic Structure Analysis for Co Oxides on α-Al2O3 (0001) as Model Surfaces for Active Oxidation Catalysts. J. Catal. 1994, 145, 159–165. 10.1006/jcat.1994.1018. [DOI] [Google Scholar]
- Manceau A.; Chateigner D.; Gates W. P. Polarized EXAFS, Distance-Valence Least-Squares Modeling (DVLS), and Quantitative Texture Analysis Approaches to the Structural Refinement of Garfield Nontronite. Phys. Chem. Min. 1998, 25, 347–365. 10.1007/s002690050125. [DOI] [Google Scholar]
- Heald S. M. Anisotropic X-ray Absorption in Layered Compounds. Phys. Rev. B: Solid State 1977, 16, 5549–5559. 10.1103/physrevb.16.5549. [DOI] [Google Scholar]
- Rehr J. J.; Kas J. J.; Vila F. D.; Prange M. P.; Jorissen K. Parameter-free Calculations of X-ray Spectra with FEFF9. Phys. Chem. Chem. Phys. 2010, 12, 5503–5513. 10.1039/b926434e. [DOI] [PubMed] [Google Scholar]
- Glasner D.; Frenkel A. I.. Geometrical Characteristics of Regular Polyhedra: Application to EXAFS Studies of Nanoclusters. AIP Conference Proceedings, 2007; Vol. 882, pp 746–748.
- Bunău O.; Joly Y. Self-Consistent Aspects of X-ray Absorption Calculations. J. Phys. Condens. Matter. 2009, 21, 345501. 10.1088/0953-8984/21/34/345501. [DOI] [PubMed] [Google Scholar]
- Timoshenko J. Wavelet Data Analysis of EXAFS Spectra. Comput. Phys. Commun. 2009, 180, 920–925. 10.1016/j.cpc.2008.12.020. [DOI] [Google Scholar]
- Kuzmin J.; Kuzmin J. Reverse Monte Carlo Modeling of Thermal Disorder in Crystalline Materials from EXAFS Spectra. Comput. Phys. Commun. 2012, 183, 1237–1245. 10.1016/j.cpc.2012.02.002. [DOI] [Google Scholar]
- Timoshenko J.; Kuzmin J. EXAFS study of hydrogen intercalation into ReO3 using the evolutionary algorithm. J. Phys. Condens. Matter. 2014, 26, 055401. 10.1088/0953-8984/26/5/055401. [DOI] [PubMed] [Google Scholar]
- Iddir H.; Browning N. D.; Disko M. M. Adsorption and Diffusion of Pt and Au on the Stoichiometric and Reduced TiO2 Rutile (110) Surfaces. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 72, 081407. 10.1103/physrevb.72.081407. [DOI] [Google Scholar]
- Iddir H.; Komanicky V.; Öǧüt S.; You H.; Zapol P. Shape of Platinum Nanoparticles Supported on SrTiO3: Experiment and Theory. J. Phys. Chem. C 2007, 111, 14782–14789. 10.1021/jp073041r. [DOI] [Google Scholar]
- Frenkel A. I.; Yevick C.; Vasic R. Modeling the Structure and Composition of Nanoparticles by Extended X-Ray Absorption Fine-Structure Spectroscopy. Annu. Rev. Anal. Chem. 2011, 4, 23–39. 10.1146/annurev-anchem-061010-113906. [DOI] [PubMed] [Google Scholar]
- Chill S. T.; Anderson R. M.; Yancey D. F.; Frenkel A. I.; Crooks R. M.; Henkelman G. Probing the Limits of Conventional Extended X-ray Absorption Fine Structure Analysis Using Thiolated Gold Nanoparticles. ACS Nano 2015, 9, 4036–4042. 10.1021/acsnano.5b00090. [DOI] [PubMed] [Google Scholar]
- Yevick A.; Frenkel A. I. Effects of Surface Disorder on EXAFS Modeling of Metallic Clusters. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 81, 115451. 10.1103/physrevb.81.115451. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.