Designing Electrostatic Interactions via Polyelectrolyte Monomer Sequence

Abstract

Charged polymers are ubiquitous in biological systems because electrostatic interactions can drive complicated structure formation and respond to environmental parameters such as ionic strength and pH. In these systems, function emerges from sophisticated molecular design; for example, intrinsically disordered proteins leverage specific sequences of monomeric charges to control the formation and function of intracellular compartments known as membraneless organelles. The role of a charged monomer sequence in dictating the strength of electrostatic interactions remains poorly understood despite extensive evidence that sequence is a powerful tool biology uses to tune soft materials. In this article, we use a combination of theory, experiment, and simulation to establish the physical principles governing sequence-driven control of electrostatic interactions. We predict how arbitrary sequences of charge give rise to drastic changes in electrostatic interactions and correspondingly phase behavior. We generalize a transfer matrix formalism that describes a phase separation phenomenon known as “complex coacervation” and provide a theoretical framework to predict the phase behavior of charge sequences. This work thus provides insights into both how charge sequence is used in biology and how it could be used to engineer properties of synthetic polymer systems.

Short abstract

Theory, simulation, and experiment demonstrate how the precise sequence of charged monomers along a polymer chain can be designed to tune the strength of polyelectrolyte interactions.

Introduction

Understanding the role of monomer sequence on the physical properties of long-chain macromolecules remains a grand challenge in the field of polymer science,^1,2 due to the utility of sequence as a tool to store information and drive structure formation in biological polymers such as proteins, RNA, and DNA.³ This takes place in a number of ways; for example, molecular storage of genomic data is encoded in DNA via a sequence of four different base pairs which can then be read by the protein machinery of the cell. Proteins leverage sequences incorporating any number of roughly 20 amino acids, that then often undergo hierarchical assembly into highly complex and precise three-dimensional structures. A subclass of proteins known as intrinsically disordered proteins (IDPs) are subtly different, in that they tend not form secondary or higher-order structures; however, IDPs remain crucial to biological structure and function.^4,5 Despite this lack of hierarchical order, recent work has shown that the precise sequence of charged amino acids still plays a defining role in the structure and function of IDPs.⁶⁻¹³ This suggests that the physical effects of charged monomer sequences are generally relevant for a broad range of polymeric materials, not limited to biological molecules; however, the underlying physics of these sequence-dependent electrostatic interactions is not well understood.

Many recent efforts to understand sequence-dependent polymers have focused on biological systems, in particular, intracellular structures known as membraneless organelles or biomolecular condensates.^9,14−20 Membraneless organelles are intracellular compartments that consist largely of IDPs^{9,14−16,18,19,21} and are often driven by interactions with oppositely charged polymers such as RNA.^7,22−24 A flurry of recent simulation and theory work has begun to model this class of biomacromolecular systems, mostly focusing on uncovering correlations between physical quantities over a vast and complex amino acid parameter space.^6,10,25−31 Despite this progress, there remains a need to develop bottom-up theory and simulation that can elucidate the physics of sequence-dependent phase behavior and to do so generally enough that the promise of sequence-defined polymers can be realized in nonbiological systems.³²⁻⁴²

In this spirit of understanding sequence-dependent interactions in nonbiological systems, we turn to a class of polyelectrolyte solutions known as polymeric complex coacervates, which are considered analogous to membraneless organelles. Coacervates consist of oppositely charged polymers (a polycation and a polyanion) in an aqueous salt solution.⁴³⁻⁴⁵ The charge-driven association between the polyelectrolytes drives a phase separation process, forming a polymer-dense coacervate phase and a polymer-dilute supernatant phase (Figure 1a inset). This phase behavior is commonly plotted on a salt concentration versus polymer concentration phase diagram (Figure 1a),⁴⁶⁻⁴⁸ with coacervation occurring in a two-phase region at low salt and polymer concentrations. A tie line in this region connects the polymer-dense coacervate (Figure 1a, α) to the polymer-dilute supernatant phase (Figure 1a, β).^47,49−51

Figure 1.

(a) Example coacervate phase diagram, calculated from the transfer matrix theory of Lytle and Sing⁹⁰ described in eq 1. The area in the bottom left half of the plot is a two-phase (2Φ) region where coacervation occurs along tie lines that connect the polymer-dense coacervate phase (α) to a polymer-dilute supernatant phase (β). The negative slope of the tie line reflects the preferential partitioning of salt to the supernatant phase. The inset shows an optical micrograph of this phase separation, formed from sequence-controlled peptides of poly(lysine-co-glycine) and poly(glutamate) with the coacervate α and supernatant β phases indicated. (b) Simulation snapshot of coacervation, showing the polymer-dense coacervate phase α and polymer-dilute supernatant phase β, at concentrations that reflect the indicated tie line in (a). (c) Schematic of a coacervate phase, showing a test polycation (orange). The transfer matrix theory in this paper is concerned with the adsorption of oppositely charged species to this chain, as shown in the simplified representation shown at the bottom. (d) The sequences used in this paper (A–P), along with the homo-polyanion (blue) that is partnered with the polycation sequences. Sequences can be characterized by parameters such as charge fraction f_C and average “run” length ⟨n_r⟩; however, sequences are not uniquely characterized by these two parameters.

Sequence effects similar to those found in IDPs and membraneless organelles are indeed observed in coacervate-forming systems.⁵² The effects of sequence on coacervation were explored using mixtures of a homo-polyanion with different sequence-specific polycations containing a 50% mixture of charged and uncharged monomers.⁵² Regular polycation sequences, ranging from fully alternating to “blocky” copolymers exhibited significant differences in phase behavior and thermodynamics as determined by both experiment and simulation.⁵² This established a clear connection between charged monomer sequence and coacervate thermodynamics, but prior work has only explored a very limited area of sequence space;⁵² there is a need to develop predictive tools to connect arbitrary sequences to the strength of electrostatic interactions.

Theory is an ideal tool to rapidly explore and understand this sequence space; however, historical efforts to theoretically describe complex coacervation are not well-suited to understanding or predicting the effect of charged monomer sequence. The original coacervation theory developed by Voorn and Overbeek accounted for charged interactions only through the Debye–Hückel attraction that arises in unconnected, dilute electrolytes.^46−48,53 Increasingly sophisticated field theoretic methods have since made an effort to address these shortcomings,⁵⁴⁻⁶⁰ with parallel efforts using liquid state theory,⁶¹⁻⁶³ blob arguments,⁶⁴⁻⁶⁷ and other related theoretical⁶⁸⁻⁷⁰ and computational⁷¹⁻⁷³ methods. While these assorted theoretical efforts have all contributed to the basic understanding of experimental results on coacervates,^46,74−87 they struggle to resolve monomer-level details important for considering monomer to monomer sequence in coacervation.

We have demonstrated the sensitivity of coacervation to monomer-level structure in previous studies,^50,88,89 which show how polymer charge spacing, stiffness, and architecture can play a marked role in determining phase behavior (example snapshot in Figure 1b). Informed by our simulation results, we have developed a new transfer matrix approach that predicts coacervation in a way that reflects these important molecular features.^51,88,90 This model keeps track of the oppositely charged ions and polyelectrolytes surrounding a test polyelectrolyte, by mapping to an adsorption model; here, the test polyelectrolyte is a series of monomeric adsorption sites to which the oppositely charged species bind (see schematic in Figure 1c).⁹⁰ The resulting free energy expression for coacervation is thus:⁹⁰

1

This expression is comprised of three terms; the first term is the translational entropy of all the species i, the second term is the transfer matrix expression for the interactions between charged polymers and their surroundings, and the final term is a phenomenological expression for the nonpairwise excluded volume. The subscript i = P, S, W denotes the polyelectrolyte, salt ion, and water species, respectively. A plus (“+”) or minus “–”) may be necessary to distinguish positively or negatively charged species, if these are asymmetric. ϕ_i is the volume fraction of species i, N_i is the degree of polymerization, and Λ_i is a correction factor for the effective excluded volume. ζ is a phenomenological constant to account for the nonpairwise excluded volume. The transfer matrix M₀ is comprised of the Boltzmann factors related to the adsorption of the various charged species (Figure 1c), counterions C, the initial oppositely charged monomers P′, and subsequent monomers along the same chain P, and unpaired sites 0. By distinguishing P and P′, we take into account the possibility of oppositely charged polyelectrolytes adsorbing sequentially along the test chain. In this way we can write the grand canonical partition function for the polyelectrolyte interaction with its surroundings, , which is the term in the interaction term of 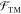. The form of this matrix has been previously derived,^51,88,90 and we denote it with a subscript 0 to indicate that this is for an unpatterned, homo-polyelectrolyte test chain:

2

Here, the first version of the matrix shows the pair of sequences that the matrix element represents (i.e., a C after a P′ would be the CP′ element). D = e^–ϵ accounts for the electrostatic energy penalty when charges along the test chain are “unpaired”. The vector ψ₁ = [C, P, P′, 0]^T = [A₀ϕ_S, 0, B₀ϕ_P, D]^T is the set of Boltzmann factors for the very first monomer on a chain, and ψ₀ is a vector of ones. The form of the terms A₀ϕ_S and B₀ϕ_P are described in our previous work.^51,88,90

In this paper, we show how this approach can be generalized to account for coacervates formed from monodisperse but arbitrary sequences. We compare transfer matrix results directly with experiment and simulation, and observe qualitative agreement for a wide variety of test sequences. Subtle changes in monomer sequence can affect the strength of electrostatic interactions between oppositely charged polyelectrolytes and the resulting phase behavior.

Results and Discussion

Polycation Sequence Space

We show in Figure 1d a schematic of the total range of polycation sequences we use in this paper, along with the fully charged homo-polyanion that was paired with the polycations in each coacervate. Experimentally, these sequences were prepared using solid phase synthesis of poly(lysine-co-glycine) and poly(glutamate) (see Supporting Information for details). All of these sequences have between 48 and 50 monomers, with a variety of charge fractions f_C and an average length “run” of charged monomers ⟨n_r⟩, indicated on Figure 1d. We note that these types of averaged variables do not uniquely define a sequence; for example, sequences C, L, M, and N have the same total number and type of runs, only spaced out with different combinations of neutral monomer runs or “spacers”. Therefore, to identify the different sequences, we assign a letter to them in Figure 1d that will be used to denote points associated with a given sequence later in the paper. We do point out a few sequence-based trends that we will focus on: (Blockiness) we change the periodicity of sequence polymers with the same number of charged, neutral monomers in runs (A–D). This trend was the basis of our prior work.⁵² (Constant Runs) we examine a constant set six runs of four adjacent, charged monomers and change how the neutral spacer monomers are distributed in-between (C, K–M, D). (Constant Spacers) we keep a constant set of six runs of four neutral monomer spacers and change how the charged monomers are distributed in-between (C, N–P, D). Finally, (Constant Runs, Constant Number of Charges) we keep a constant set of runs of four adjacent, charged monomers and change the number of neutral monomer spacers while keeping the overall number of charges per chain constant (not included in Figure 1d, but represented later). We note that, for this manuscript, all polymers are monodisperse in size and sequence in both theory and simulation, and have very low polydispersity in experiments.

Simulation and Experiment Exhibit Sequence-Dependent Coacervation

In looking to understand the nuanced effects of chemical sequence, we first performed a direct comparison between simulation and experiment. Coacervate phase diagrams were calculated using thermodynamic integration of Monte Carlo simulations⁹¹ using a combination of box size-changes^92,93 and Widom insertion^91,94 to calculate the excess free energy along both the polymer (polyanion and sequenced polycation) and salt species respectively (see Supporting Information for details). This approach uses the same simulation model as reported previously.^50−52,88 This model uses a bead–rod representation of charged polymers in an implicit solvent, which is a standard coarse-grained approach that highlights the physical effects due primarily to electrostatics and is agnostic to any specific chemistry. We can qualitatively compare the binodal phase diagrams resulting from these simulations to experimentally determined measures of the phase behavior (Figure 2).

Figure 2.

(a) Salt concentration c_S versus polymer concentration c_P phase diagram of coacervation measured from simulation (points) and transfer matrix theory (lines) for polycations with sequences A–D, F, and H interacting with a homo-polyanion. An example set of tie lines are shown for sequence A (dashed line, simulation and dotted line, theory), with both exhibiting a small negative slope consistent with prior literature.^50,73 Simulation tie lines are also shown for other sequences at concentrations outside the binodal of sequence A, demonstrating that sequence does not alter the sign of the slope. The critical salt concentration as measured by theory c_S⁰ is measured at the largest concentration of salt observed in the supernatant phase for each sequence. (b) Simulation snapshots representative of the points in (a) for sequences H, A, D, and F. The polycation is orange, the polyanion is blue, the cation is purple, and the anion is red. Neutral beads for the polycation are shown with smaller beads connected by rods. (c) Simulation and theory values for salt resistance (left axis, c_S) qualitatively compare well with experimentally measured values of c_S,E⁰ obtained at 1 mM polymer for sequences A–D, showing that we can use theory and simulation to capture sequence variations described by an increase in charge block size (Blockiness). (d) Schematic highlighting counterion localization for two different sequences. For a sequence with a large ⟨n_r⟩ (D), the counterions are locally confined near the charged blocks. In contrast, counterions are more uniformly localized along the chain for sequences with a small ⟨n_r⟩ (B). The red circle represents the cutoff radius, r_C. If a salt ion is within this r_C of a monomer, the salt ion is considered localized.

The phase boundaries in Figure 2a exhibit the same trend observed by Chang et al.,⁵² with minor differences due to the different methods for calculating phase diagrams (see discussion in the Supporting Information). Our results highlight that an increase in blockiness ⟨n_r⟩ and charge fraction f_C generally leads to a marked increase in the two-phase region of the phase diagram, indicating that phase separation is enhanced by stronger electrostatic attractions. Figure 2b shows characteristic snapshots from simulations performed at a constant number of charged monomers for sequences H, A, D, and F, visually highlighting how an increased value of c_S⁰ leads to stronger phase separation and a denser coacervate phase.

Further analysis of simulation results also suggested that electrostatic cooperativity resulting from an increase in ⟨n_r⟩ enhances the localization of counterions at high charge-density locations along the polyelectrolyte chain (Figure 2d). An important consequence of this increase in counterion confinement is a commensurate increase in the entropy resulting from the release of these bound counterions upon complexation with an oppositely charged polymer.⁵²

Because of the correlation between increases in the strength of the electrostatic attraction, counterion localization, and the size of the two-phase region, we can use the highest salt concentration where we observe phase separation, c_S⁰, as a simple descriptor of the system (Figure 2a). This parameter also allows for comparison with experimental data, via the “salt resistance” c_S,E which is the salt concentration at which miscibility is observed for a fixed overall polymer concentration c_P = 1 mM. c_S⁰ and c_S,E represent different parts of the phase diagram and thus have different numerical values; however we show in the Supporting Information that they are highly correlated and can be used to compare qualitative trends. The reasoning for using these different quantities is discussed in the Supporting Information, along with the demonstration that direct comparison of simulation and experimental values of the same metric (c_S,E⁰) indeed yields similar numerical results. Figure 2c demonstrates that the size of the two-phase region, as measured by either the salt resistance c_S,E from experiments or c_S⁰ from simulations, systematically increased with increasing blockiness ⟨n_r⟩ for constant charge fraction f_C, (i.e., sequences A–D).

The results in Figure 2a also include example tie lines connecting coexisting coacervate and supernatant phases. It is noteworthy that we observe tie lines with a negative slope, indicating that the coacervate phase has a lower salt concentration than the supernatant.^{50,51,73,88,90,95} This preferential partitioning of salt out of the dense, polymer-rich coacervate phase has been previously attributed to the excluded volume of the polyelectrolyte species,^{50,51,73,88,90,95} and has been confirmed experimentally.^50,73

Theory of Monomer Sequence in Polymeric Complex Coacervation

Results from simulations suggested that we can capture the relevant physics dictating the effects of charge sequence on coacervate phase behavior by considering how counterions interact with a single polymer chain. Therefore, we extend the transfer matrix theory of complex coacervation to include the effects of charged monomer sequence.^51,88,90 This method is particularly applicable because, for most coacervates, the concentration of charged species is sufficiently high that standard Debye–Hückel or Poisson–Boltzmann electrostatics are no longer applicable,^50,53,96 and correlations are primarily due to charge connectivity and nearest-neighbor pairing.^50,97

To extend the transfer matrix formalism to describe sequence effects in coacervation, the electrostatic association strength ϵ becomes a function of the specific monomer position along the test polycation chain. This accounts for the variation in local electrostatic environment, and specifically the energetic penalty for an unpaired ion, for a particular monomer sequence.^51,90 Thus, the D_homo = D₀ exp(−ϵ₀) that in the homo-polyelectrolyte theory contains a constant ϵ₀, now is written with a contribution ϵ₁ that depends on the monomer index s, D_pattern = D_homo exp(−ϵ₁(s)).

To calculate the value of ϵ₁(s), we use Monte Carlo simulations of single polyelectrolytes in a dilute salt solution to determine the adsorption characteristics of a test polyelectrolyte it in a reservoir of salt ions (see the Supporting Information for simulation details). The localization of salt ions near charged polycation blocks, and thus the local strength of electrostatic interactions, is calculated by defining a region around the chain defined by a cutoff radius r_C (Figure 2d).⁹⁸ This charge localization is energetically favorable due to electrostatic attractions,⁹⁸⁻¹⁰⁰ and there is thus an increased number density n_C(s) of opposite charges within r_C at a given chain monomer s.⁵² We define an electrostatic energy that accounts for this increase in local correlations as the aforementioned ϵ = ϵ₀ + ϵ₁(s). We demonstrate that ϵ(s) can be determined from simulation using the relationship ϵ(s) = −ln n_C(s)/n_C,0(s) (see Supporting Information), where n_C,0(s) is the number density of opposite charges within r_C in the absence of electrostatic interactions. This method thus only requires two single-chain simulations (one with electrostatics and one without) at low (but nonzero) salt concentrations, and we show in the Supporting Information that the value of ϵ(s) is independent of the choice of salt concentration in this limit. Figure 3a shows typical landscapes (ϵ(s)) for patterns A–D, as well as the homo-polyanion, where we denote charged monomers with closed symbols and neutral monomers with open symbols. We take D₀ = 1 and ϵ₀ = 0, in agreement with the theory for homo-polyelectrolyte coacervates.⁹⁰

Figure 3.

(a) Monomer-dependent energy ϵ(s) as a function of the chain index, measured by single-polyelectrolyte simulations in dilute salt solution. Variations in ϵ(s) reflect the different electrostatic environments associated with monomers in different positions along the chain. ϵ(s) is plotted here for sequences A–D, which reflects variation in sequence periodicity ranging from alternating charged/uncharged monomers (A) to blocks of eight charged/uncharged monomers (D). Filled symbols represent charged monomers in the sequence, and open symbols represent neutral monomers. The homo-polyanion is also plotted as the dark red line in each graph. We note that, for the blockiest polycation sequences, ϵ(s) approaches the homo-polyanion behavior in the center of the block. (b) Schematic illustrating how the variation in ϵ(s) is incorporated into the transfer matrix theory. Ξ_seq^int is the grand canonical partition function associated with polymer–polymer interactions. It is composed of products of “runs” of charge, as shown explicitly in the expression given below the schematic; here, the colors are associated with the indicated charged monomer runs: 1 (purple), 5–8 (red), and 10–11 (blue).

As expected, there is a large variation in electrostatic attraction along the contour of the chain due to the precise sequence of monomers. For the sequences plotted in Figure 3a, sequence D exhibits the most marked variations in ϵ(s). In this case, long runs of adjacent, charged monomers (e.g., s = 16–23 and s = 32–39) have a value of ϵ(s) that is similar to ϵ₀ for a homopolymer. As the sequence transitions from a charged run to a neutral spacer (e.g., s = 22–26), there is a concomitant increase in ϵ(s) that we attribute to the weakening of the driving force for charge localization. ϵ(s) decreases once more as the neutral spacer transitions back to a charged run (e.g., s = 30 to 34). In contrast, short runs of charge or isolated, charged monomers (such as in sequences A or B) show weak localization. This is indicated by a larger value of ϵ(s) with weaker oscillations. These energy landscapes ϵ(s) inform our model of sequence effects in complex coacervation.

We define a new transfer matrix, that now depends on the monomer index via the sequence-dependent epsilon:

3

This transfer matrix is specifically for monomers that contain a charge, in contrast to neutral monomers along the chain. We consider neutral monomers to only affect the free energy of coacervation through (1) excluded volume of the monomer units and (2) through their spacing of charges and its effect on ϵ(s) for those monomers. Neutral monomers are otherwise not required to “pair” with an opposite charge, and their contribution to the transfer matrix calculation is as an identity matrix M_n = I. We can use this set of matrices to write a new grand canonical partition function 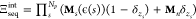. This can be simplified, since when 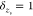for neutral monomers, the product is simply an identity matrix. This means that the system can be divided into a product over a series of charge “runs”, or adjacent charges, of length n_r.

4

We schematically show how this calculation is carried out in Figure 3b. The new interaction free energy contribution for a patterned polymer (in this case, a polycation) is 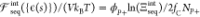. We thus use the free energy for the overall system:

5

Here, the sequence-dependence is almost completely contained within the interaction term for the polycation, while the homo-polyanion is treated as in the previous transfer matrix theory.⁹⁰ In this paper we use the parameters A₀ = 35.0, B₀ = 11.5, 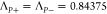, and ζ = 16.0; these are similar to values in prior work^51,90 but with small changes reflecting slight differences in how we model Λ. The same parameters are used for all sequences considered in this paper.

Sequence-Based Transfer Matrix Theory Can Match Experimental and Computational Phase Behaviors

Full theoretical phase diagrams are calculated for the polyelectrolyte patterns. These demonstrate excellent, nearly quantitative matching with the full simulation phase diagrams shown in Figure 2a. In particular, we can capture how the phase diagram changes with increasing blockiness for the constant f_C = 0.5 sequences (A–D) in simulation, experiment, and theory. This is shown in Figure 2c. In particular, this matching includes the significant jumps in c_S⁰ from B to C and C to D, concomitant with the emergence of significant variations in ϵ(s) in Figure 3a.

We showed this charge blockiness effect in simulation in Chang et al.,⁵² which was attributed to the one-dimensional confinement of charges localized along the backbone. This emerges from our theory because the energetic parameter ϵ(s) (Figure 3a) corresponds to a local one-dimensional confinement potential for counterions along the chain.

We extend this matching to the entire set of sequences considered in Figure 1d. In Figure 4a, we plot the experimental c_S,E⁰ as a function of the overall charge fraction f_C for sequences A–J, for coacervates formed in a NaCl salt solution from sequence-controlled polymers of poly(lysine-co-glycine) in complex with a homopoly(glutamate). We observe large variations in c_S,E, ranging from 160 to 580 mM NaCl, showing that charge patterns can significantly alter the strength of electrostatic interactions. We obtain the values of c_S⁰ from simulation and theory for this same, extended set of sequences (full phase diagrams included in the Supporting Information) and also plotted versus f_C in Figure 4b. Both simulation and theory results exhibit nearly quantitative matching and exhibit qualitative matching with the experimental values observed in Figure 4a.

Figure 4.

(a) Experimental salt resistance c_S,E⁰ as a function of charge fraction f_C for sequences A–J, prepared using systems of poly(lysine-co-glycine) in complex with poly(glutamate) in a NaCl salt solution (inset), and also a homo-polyelectrolyte coacervate f_C = 1. We note that experimental data for sequence E is not included, because only solid precipitation is observed and thus c_S,E is not accessible. (b) Theoretical (black circles) and simulation (red triangles) salt resistance c_S⁰ as a function of charge fraction f_C for sequences A–J. We note that simulation and theory are in nearly quantitative agreement, and both qualitatively agree with the experimental trends in (a).

Experiment, theory, and simulation all exhibit the same trends. Broadly speaking, high values of f_C lead to larger values of c_S,E⁰ (experiment) and c_S (theory and simulation), corresponding to higher strengths of electrostatic interactions. This is expected, given that there are more charges per chain and thus more electrostatic attraction to the oppositely charged polymeric species. Nevertheless, we note that even among the same charged fraction there can be a wide variation in c_S,E⁰ and c_S, as apparent in the blockiness trend at f_C = 0.5. The opposite situation is also true, with similar values of c_S⁰ being observed for different values of f_C. For example, we note that the trio D, I, and F or the pair G and A show a similar value of c_S,E despite having different charge fractions. These particular cases generally represent a trade-off between blockiness and charge fraction, with less f_C needed if the sequences have longer blocks. We are able to accurately capture this effect of precise charge sequence on the phase behavior of complex coacervates with both theory and simulation because our theory considers the particular charge sequence rather than average sequence metrics such as charge fraction f_C or blockiness ⟨n_r⟩.

Sequence-Based Trends

Having looked at the effect of blockiness, we tested the ability of this theory to capture nonregular sequences. In particular, we show this by keeping the total charge fraction f_C = 0.5 constant and maintaining constant runs of four charges while varying neutral spacers (sequences C, K–M, and D, i.e., constant runs). These systematically shrink the length of one neutral spacer while increasing the length of another (see schematic in Figure 5a). We do this for charge runs of length n_r = 4, which represents a transition between ⟨n_r⟩ = 4 and ⟨n_r⟩ = 8 (sequences C and D) at the extremes. Despite controlling for both f_C and ⟨n_r⟩, this variation results in a marked change in the values of c_S⁰ and c_S,E for theory and experiment. This is plotted in Figure 5a (circular symbols) as a function of the larger neutral linker length ν and demonstrates that there is a transition from C to D where intermediate values of c_S⁰ are observed. We attribute this change to the proximity of charge runs, which still affect each other even when separated by a few neutral monomers, a cooperative effect that decreases with increasing length of the neutral spacer. Indeed, this is observed in both experiment (open, black points, c_S,E) and theory (filled, red points, c_S⁰).

Figure 5.

(a) Salt resistance c_S⁰ for f_C = 0.5 with varying length neutral spacers, denoted by v and 8 – v, between runs of four charges (circles) and with varying length charge blocks, denoted by v and 8 – v, separated by spacers of four neutral monomers (triangles). Experiment (black), using sequence-controlled poly(lysine-co-glycine) in complex with a homo-poly(glutamate) and theory (red) exhibit qualitative matching, showing the complicated interplay between charge block separation and length. (b) Salt resistance for polycations with 24 total charged monomers, separated by increasingly long neutral spacers, denoted by v.

The next set of sequences we highlight are C, N–P, and D. This example of a constant spacers series is the inverse of the constant run trend and is characterized by constant spacer length (four neutral monomers) with variation in charged runs at a constant ⟨n_r⟩ = 4 and f_C = 0.5. Here we observe a similar transition between the limiting sequences C and D, plotted in Figure 5a as triangular symbols.

We note for both the constant run and constant spacer series, the increase in c_S,E⁰ and c_S is more abrupt as the longer charge-run length ν is increased from ν = 7 to ν = 8, which is again observed in both experiment and theory. This demonstrates that there is a large differential effect of moving an isolated charged (P to D) or neutral monomer (M to D) in a larger run of the other monomer type. This is especially apparent in the P to D transition, which we attribute to the lack of electrostatic cooperativity of the isolated charged monomer with respect to its neighbors in P; upon “promoting” that monomer to be in the long, charged block in D it gains the cooperative electrostatic attractions associated with these blocks.

We consider a final constant runs, constant number of charges series, where runs of four adjacent charges along the polycation have differing numbers of neutral monomers, only now the chain length N_P+ is increased to have a constant number of charged positive charges along the polycation. This runs from two to eight monomers between groupings of four charged monomers. We plot c_S,E⁰ and c_S for these sequences in Figure 5b and show that they decrease with the number of neutral monomers ν for both the experiment and theory values. This further clarifies that the values of n_r and the total number of charges per chain do not, by themselves, dictate the strength of electrostatic interactions. The neutral spacers, despite not being directly involved with the electrostatic interactions, affect the local charge correlations sufficiently to cause significant changes in c_S⁰ and correspondingly the strength of the electrostatic attractions between the oppositely charged polyelectrolytes.

Safety Statement

No unexpected or unusually high safety hazards were encountered.

Conclusion

We have developed a theoretical framework for understanding the role of polyelectrolyte charge sequence in complex coacervates. This framework builds on a transfer matrix approach⁹⁰ that explicitly accounts for the local electrostatic environment along a sequenced polyelectrolyte via an effective energy ϵ(i). We can capture the effects of sequence in complex coacervates, including charge fraction and charge blockiness, as well as the more subtle variations in charge associated with nonregular sequences. Furthermore, we show close matching between experiment, simulation, and theory for the wide range of sequences considered. The emerging physical picture is that there is a trade-off between the number of charges per chain and the blockiness of the sequence; however, the relative position of these blocks also plays a significant role in determining phase behavior.

This computational, experimental, and theoretical effort provides the foundation to study a whole range of polyelectrolytes and bio-polyelectrolytes with charge sequence. The next step is to incorporate other molecular interactions, such as hydrogen bonding, short-range χ-interactions and hydrophobicity, and ion-π interactions, into this theoretical framework. This is particularly relevant to biological systems such as IDPs, which are known to form phase-separated structures in the cell that are sensitive to sequence. However, this may also open the door to engineering charge sequence in synthetic polymers and to inform the self-assembly or phase behavior of soft materials.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.9b00087.

• Experimental procedures, simulation methods, full sets of simulation/theoretical phase diagrams, and description of theoretical details (PDF)

The authors declare no competing financial interest.