Incorporating genome-wide association into eco-physiological simulation to identify markers for improving rice yields

We test abilities of a crop model parameterized with a single experiment to predict genotype×environment interactions. We show that merging the model with GWAS helps prioritize markers for improved yields.

Abstract

We explored the use of the eco-physiological crop model GECROS to identify markers for improved rice yield under well-watered (control) and water deficit conditions. Eight model parameters were measured from the control in one season for 267 indica genotypes. The model accounted for 58% of yield variation among genotypes under control and 40% under water deficit conditions. Using 213 randomly selected genotypes as the training set, 90 single nucleotide polymorphism (SNP) loci were identified using a genome-wide association study (GWAS), explaining 42–77% of crop model parameter variation. SNP-based parameter values estimated from the additive loci effects were fed into the model. For the training set, the SNP-based model accounted for 37% (control) and 29% (water deficit) of yield variation, less than the 78% explained by a statistical genomic prediction (GP) model for the control treatment. Both models failed in predicting yields of the 54 testing genotypes. However, compared with the GP model, the SNP-based crop model was advantageous when simulating yields under either control or water stress conditions in an independent season. Crop model sensitivity analysis ranked the SNP loci for their relative importance in accounting for yield variation, and the rank differed greatly between control and water deficit environments. Crop models have the potential to use single-environment information for predicting phenotypes under different environments.

Introduction

Genomic information provides opportunities for detecting genes and quantitative trait loci (QTLs) associated with various morphological, physiological, and agronomic traits. Rice breeding exploits these genes and QTLs to improve grain yield potential and yield stability of rice cultivars when exposed to different abiotic stresses (Singh et al., 2009; Zhang et al., 2009; Vikram et al., 2011; Ali et al., 2013). The advent of high-throughput and cost-effective genome sequencing technologies has made it possible to conduct in-depth genome analyses of thousands of individual genotypes. For example, complete genome sequencing was carried out on 3000 diverse genotypes of rice (Oryza sativa), and this allowed detection of many mutations (Li et al., 2014) and explaining the diversity at the genome level in the form of single nucleotide polymorphisms (SNPs). Despite advances in rice genetics, several scientific and technical challenges need to be overcome to exploit this information to improve grain yield further. Grain yield is a complex trait with low heritability and strong response to environment [genotype×environment interaction (G×E)]. To improve grain yield further, a deeper understanding of the morphological and physiological traits contributing to grain yield, and the interaction between genes or QTLs regulating these traits with the environment is required.

Quantification of G×E for predicting traits usually involves the build-up of a model based on information generated by phenotyping many genotypes in several characterized environments. The model application can be illustrated in an approach using observed information to predict the phenotypic performance of: (i) genotypes phenotyped in new environments; (ii) new genotypes in characterized environments; and (iii) new genotypes in new environments (Bustos-Korts et al., 2016). The latter aspects have evolved into the so-called ‘genomic prediction’ (GP) to support marker-assisted breeding for quantitative traits (Zhang et al., 2016). While these approaches were proposed largely from the viewpoint of statistical modelling, they can also be applied to eco-physiological modelling of G×E using dynamic process-based eco-physiological crop simulation models (‘eco-physiological models’ hereafter).

Eco-physiological modelling has been widely used to resolve the complexity of grain yield under different environments (Soltani et al., 1999; Yin and Struik, 2010; Martre et al., 2011), by dissecting grain yield into its component traits or parameters. Most parameters in the model may be controlled genetically; therefore, eco-physiological models are believed to be able to quantify genotype–phenotype relationships for complex traits (Hammer et al., 2006; Bertin et al., 2010; Génard et al., 2016), using dynamic simulation on a daily or even shorter time-step basis. Unlike statistical approaches that require a large number of experiments (although on a single trait) to create a prediction model (Bustos-Korts et al., 2016), eco-physiological modelling can, in principle, rely on one or a few experiments for model parameterization because the prediction is made largely based on eco-physiological principles as captured by the models.

However, parameters of eco-physiological models are commonly measured or estimated from phenotyping experiments, and their genetic basis is largely unknown (Kromdijk et al., 2014). Several studies have therefore tried to link crop modelling with QTL analysis (see review by Yin et al., 2016). Using such an approach, grain yield was first predicted in barley (Yin et al., 2000), later followed by studies for simpler traits (e.g. Reymond et al., 2003; Nakagawa et al., 2005) and rice grain yield under water deficit conditions (Gu et al., 2014). Such QTL-based crop modelling also supports marker-assisted selection to accelerate traditional breeding (Gu et al., 2014; Hammer et al., 2016; Xu and Buck-Sorlin, 2016; Yin et al., 2016).

Most studies linking eco-physiological modelling with genetics were conducted on bi-parental mapping populations representing only a small part of the available genetic diversity (Yin et al., 2000, 2005; Nakagawa et al., 2005; Quilot et al., 2005; Laperche et al., 2006; Uptmoor et al., 2008). Genome-wide association studies (GWAS) have become increasingly popular to dissect the genetic architecture of complex traits, using wider genetic diversity in crops (Remington et al., 2001). To the best of our knowledge only a few recent studies were conducted on linking GWAS with eco-physiological modelling (Rebolledo et al., 2015; Dingkuhn et al., 2017a, b; Mangin et al., 2017). Mangin et al. (2017) showed that crop models can be used to develop ‘stress indicators’ that explain yield variation across multiple environments, facilitating GWAS application to identify relevant QTLs for yield in response to environmental stresses. Rebolledo et al. (2015) and Dingkuhn et al. (2017a, b) have shown that eco-physiological models can dissect early vigour, phenology, and spikelet sterility, respectively, into their components, thereby strengthening the phenotyping and GWAS analysis of these traits. These studies demonstrated how GWAS analysis can benefit from crop modelling. However, whether the genetic approach for GWAS can facilitate the application of crop modelling in predicting the G×E effect on crop yields has hardly been demonstrated.

The objective of the current study is to explore the potential of using GWAS to enhance the application of eco-physiological modelling in supporting marker-assisted breeding. We applied the GECROS (Genotype-by-Environment interaction on CROp growth Simulator) model (Yin and Van Laar, 2005; Yin and Struik, 2017) to a rice association mapping panel as a case study. This eco-physiological approach was compared with a simplified statistical GP approach, to investigate any advantage of eco-physiological models in using a single experiment to predict the performance of genotypes in a GWAS panel under different environmental conditions.

Materials and methods

We modified the methodology of Gu et al. (2014), who applied it to a bi-parental population (Supplementary Fig. S1 at JXB online). The model was first parameterized from one environment. Then GWAS was performed on model input parameters to identify SNP markers, and the SNP-based eco-physiological model predictions were compared with the statistical genomic predictions of grain yields across different environments. Eco-physiological model-based sensitivity analysis was further used to rank the identified SNP markers for their importance in determining grain yield. Each step is explained in the following sections.

Association mapping panel and field phenotyping

An association mapping panel of indica rice genotypes was developed and assembled at the International Rice Research Institute (IRRI), Philippines (http://ricephenonetwork.irri.org). This population has been extensively used to study the genetic architecture of many phenotypic traits (Al-Tamimi et al., 2016; Rebolledo et al., 2016; Kadam et al., 2017; Kikuchi et al., 2017). We phenotyped this population (296 genotypes) for grain yield and its component traits under well-watered (control) conditions throughout the crop cycle and under water deficit conditions during the reproductive stage (flowering stage) (Kadam et al., 2018). Two field experiments were executed at the upland farm of IRRI (14°11´N, 121°15´E, 21 m asl) during the dry seasons (DS) of 2013 and 2014. The experiments were laid out in a group block design with three replications (four rows per replicate) for each genotype in each treatment. A systematic staggered sowing and transplanting scheme was followed to synchronize flowering, and thereby the phenological timing of the water deficit stress, for the entire panel. Due to poor germination or early flowering and/or maturity before stress, we collected data for 291 genotypes in 2013 and 288 genotypes in 2014 (Kadam et al., 2018). Here, we used only 267 genotypes, which were common across the years and were uniformly exposed to stress at the reproductive stage. The GECROS model requires weather data on daily radiation, maximum and minimum temperature, vapour pressure, rainfall, and wind speed, and these were taken from an on-site weather station. Further details of the experimental set-up are given by Kadam et al. (2018).

The GECROS model and its modification

The GECROS model, first described by Yin and Van Laar (2005) and recently updated by Yin and Struik (2017), runs on a daily time step, but with subroutines for photosynthesis, transpiration, and phenology running on shorter time steps. The model simulates yield by considering physiological processes involving carbon–nitrogen interaction, functional balance between shoot and root activities, and the interplay between source supply and sink demand.

The number of spikelets m^–2 in the model is assumed to be proportional to the amounts of either carbon or nitrogen (depending on which is more limiting) accumulated until flowering. Gu et al. (2014) showed that this approach overestimated yield of rice genotypes under drought, and this was confirmed in pre-simulations with our GWAS panel (Supplementary Fig. S2). It is now known that when stress occurs during the flowering phase, the percentage of filled spikelets, or grain set, depends more on the panicle temperature during the flowering time window in a day, ~08.00–13.00 h (Jagadish et al., 2007; Julia and Dingkuhn, 2013). Therefore, we modified the GECROS model to account for the direct effect of panicle temperature on sink size. The simulation of panicle temperature was done using the same algorithms in GECROS (Yin and Struik, 2017) for simulating leaf surface energy balance, based on a coupled conductance–photosynthesis–transpiration routine, whereby panicles were treated as a photosynthesizing organ and its conductance was calculated using a semi-empirical leaf conductance model. Because the panicle temperature only within the flowering time window is most crucial in determining the spikelet sterility (Julia and Dingkuhn, 2013), upscaling instantaneous photosynthesis and transpiration to daily total was changed from the five-point Gaussian integration in GECROS to computation of 24 times from sunrise to sunset. A factor for reduction induced by any high panicle temperature at flowering hours under stress, relative to the control, was introduced to simulate the actual spikelet fertility under stress, based on the linear relationship between sterility and panicle temperature reported by Julia and Dingkuhn (2013) for rice. The grain set in control was herein called ‘the baseline grain set’.

Measurement of model input parameters, model calibration, and testing

The GECROS model was designed in such a way that most of its input parameters can be directly determined from measurements without recourse to an optimization procedure (Yin and Van Laar, 2005). The latter procedure requires many experiments to be performed and may not be suitable for parameterization of sophisticated crop models such as GECROS that have different time steps for different subprocesses. The set of genotype-specific phenological, morphological, and physiological input parameters used in this study to simulate grain yield are listed in Table 1. Parameter values for each genotype of the GWAS rice panel were determined from the control treatment of the 2013 DS experiment. The exception was the photoperiod sensitivity parameter δ that was estimated using pre-flowering phenology data collected from the 2013 DS as well as an additional 2012 wet season phenology experiment (Kadam et al., 2018), because at least two photoperiods are required in order to estimate δ. Functions of the phenological response to temperature and photoperiod in the GECROS model were used to calculate the parameters m_V and δ using the measured flowering times, and m_R using the harvest time, based on daily photoperiod and hourly temperature generated from daily maximum and minimum temperatures (Yin et al., 2005). Values of H_max, S_w, and g_set were determined directly from the experimental measurements. The value of n_so was measured using the micro-Kjeldahl method. N_max is not an input parameter in the default GECROS model, and is used here as a genotype-specific parameter to avoid the confounding effect of the inherent inaccuracy in simulating nitrogen availability from soil. The value of N_max was assessed based on dry weight and nitrogen concentration in the various plant organs, assuming that the straw nitrogen concentration was 0.463% (Singh et al., 1998) and nitrogen accumulation in the roots was 5% of N_max (Yin and Van Laar, 2005). Values of other parameters, which are possibly also genotype specific but were not assessed experimentally, were kept for the whole panel at model default values for rice as given by Yin and Van Laar (2005).

Table 1.

Details of genotype-specific GECROS model input parameters classified into three categories

Parameters	Description	Unit
(A) Phenological
m V	Pre-flowering period	Thermal day
m R	Post-flowering period	Thermal day
δ	Photoperiod sensitivity	h–1
(B) Morphological
H max	Maximum plant height	m
S w	Single-grain weight	g
(C) Physiological
g set	Baseline grain set	%
n so	Grain nitrogen concentration	g N g–1 DM
N max	Total crop nitrogen uptake at maturity	g N m–2

‘Thermal day’ is calculated using the bell-shaped temperature response equation as used in GECROS, based on hourly temperatures generated from weather data on daily maximum and minimum temperatures; a thermal day is equivalent to an actual day only if temperature at each hour of the day equals the optimum temperature for phenological development. So, m_V and m_R in thermal days are lower than their values in actual days for expressing the growth duration. DM=dry matter; N=nitrogen.

The GECROS model, calibrated as described above, was then used to simulate values of grain yield of the genotypes in the water deficit condition of 2013, as well as in 2014 environments under both control and water deficit conditions. Relative root mean square error (rRMSE) was used to inspect the quality of model simulation (Brun et al., 2006), and the R² coefficient of the linear regression of simulated versus observed values of grain yield was used to show the percentage of phenotypic yield variation accounted for by the model.

GWAS analysis of model input parameters and grain yield, and estimating SNP-based values of these traits

The rice population of 267 genotypes was randomly divided into a training (213 genotypes; 80% of the population) and a testing (54 genotypes; 20% of the population) set. This random separation of the population had a minimal effect on the population structure as the testing data sets represented the structure of the training sets (Supplementary Fig. S3).

Using the training data set, the single-locus GWAS analysis was performed on model input parameters and grain yield using a 46K SNP data set (8.75% missing imputation) by a compressed mixed linear model (CMLM) in the Genomic Association and Prediction Integrated Tool (GAPIT). The detailed protocol was explained by Kadam et al. (2017, 2018). Using this protocol, we selected the top 10 significant markers with the lowest P-values after excluding the redundant markers within the linkage disequilibrium (LD) of ~55–65 kb reported for this population (Kadam et al., 2017). Similarly, we conducted a multilocus GWAS analysis that in addition to correcting the confounding effect of population structure and family relatedness, corrected for the confounding effect of background loci present due to LD in the genome. We ran the complete model with stepwise forward inclusion of the lowest P-value marker as a cofactor until the heritability reached a value close to zero, followed by backward elimination of the least significant markers from the model (Segura et al., 2012). With this protocol, all significant SNP markers associated with the trait were incorporated as a cofactor in the model. As multilocus analysis also corrects the confounding effect of genome LD (Segura et al., 2012), significant SNP markers associated with traits identified through multilocus analysis were not within the LD region of ~55–65 kb reported for this population (Kadam et al., 2017).

All significant SNPs identified in the above step were fed into a multiple linear regression (MLR) using the lm() function in R with Equation 1:

$${\displaystyle \begin{array}{l}{\displaystyle Y_k=\mathrm{\mu }+{\displaystyle \underset{n=1}{{\displaystyle \sum ^N}}}{a}_n{M}_{k,n}}\end{array}}$$ (1)

where Y_k is a response variable (eco-physiological model parameter or yield) of the kth individual genotype, μ=intercept, a_n=additive effect of the n marker, and M_k,n=genetic score of the kth genotype at the position of the nth marker, taking the value either –1 (homozygous for the major allele) or 1 (homozygous for the minor allele). This analysis identified the non-significant markers due to collinearity of markers, and these markers were removed. We then performed one more round of MLR analysis to remove the markers with cut-off threshold P-value <0.01, and the R² of Equation 1 at this final round MLR was taken as the phenotypic percentage explained by the identified markers. This analysis was performed for each model input parameter and for grain yield.

We also used Equation 1, with estimated additive effects of the individual markers and marker allelic data, to generate SNP marker-based model input parameter values for each genotype in the whole panel. These SNP marker-based model input parameter values were fed into the GECROS model, allowing eco-physiological model predictions of grain yield using the SNP information for training and testing sets grown under different environmental conditions.

Statistical genomic prediction model

We compared the accuracy of the eco-physiological modelling with a direct GP modelling of grain yield. For the latter approach, we used the partial least square (PLS) regression model (Abdi, 2003). A PLS regression is particularly adapted in the case of high-dimensional data to avoid the multicollinearity problems. This regression model is a dimension reduction method that seeks to find the latent components. These latent components maximize the variability of predictors that best explain the variance of the response variable (grain yield). The optimum number of latent components minimizing the RMSE of prediction were selected by a 10-fold cross-validation in the training data set. These optimum numbers of latent components identified in training data sets were then used to make the prediction. To compare with the eco-physiological modelling, rice genotypes and data for training or testing data sets were kept exactly the same as defined earlier, and the predictors used in the PLS regression were those 90 SNPs identified for eco-physiological model input parameters (see the Results). A PLS regression modelling analysis was implemented in R studio using the package ‘PLS’ (Mevik and Wehrens, 2007) with 1000 iterations. The obtained training GP model was used to assess the prediction accuracy in both training and testing data sets across years and treaments.

Sensitivity analysis to rank the relative importance of individual SNP markers

Sensitivity analysis was performed using the GECROS model to test the effect of individual SNP markers on grain yield simulation. Simulated grain yields for 267 genotypes in the earlier step using genotype-specific allelic values of all identified SNPs were first taken to obtain the percentage of yield variation explained by the baseline simulation. Then, we fixed one marker to zero (i.e. excluding the effect of this marker in the analysis). This is equivalent to assuming that all individual genotypes of the GWAS panel carry an identical allele at that SNP locus. We then simulated grain yield using the model with input parameter values estimated from fixing that SNP marker. We performed such an analysis on all significant SNP markers, one marker at a time, and assessed by what percentage the explained variation in grain yield decreased in comparison with the explained percentage of the baseline simulation. Using this protocol, we ranked the relative importance of the markers in determining grain yield variation.

Results

Genotypic variation in model input parameters and their relative contribution to yield

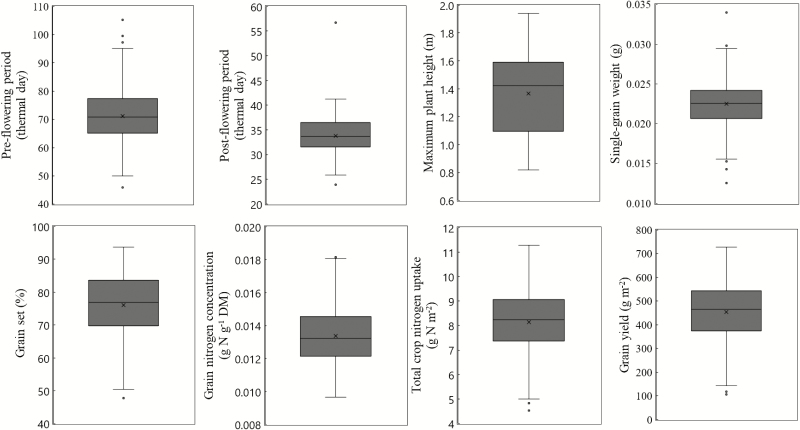
We used the control conditions of the 2013 experiment to parameterize GECROS. Obtained model input parameters (Table 1) showed a strong genotypic variation (Fig. 1). We conducted regression analysis to test whether each of these parameters significantly correlated with grain yield. The total crop nitrogen uptake (N_max) accounted for the highest percentage of the grain yield variation in the whole panel (72.43%) (Table 2). Therefore, multiple linear regression analysis was performed with N_max as a cofactor in the model. Grain yield was significantly correlated with four other input parameters: post-flowering period (m_R), maximum plant height (H_max), grain set (g_set), and grain nitrogen concentration (n_so). However, it was not correlated with pre-flowering period (m_V), photoperiod sensitivity (δ), or single-grain weight (S_w) (Table 2).

Fig. 1.

Phenotypic distribution of model input parameters and grain yield in 267 genotypes of a rice genome-wide association mapping panel under control conditions of the 2013 experiment.

Table 2.

Linear regression of grain yield (Y in g m^–2) with total crop nitrogen uptake (N_max in g N m^–2), and other individual model input parameters (Table 1) of the whole panel in 2013 control conditions

Equation	μ	a1	a2	R 2 (%)
Y=μ+a1Nmax	–207.29	81.28***		72.43
Y=μ+a1Nmax+a2mV	–202.74	81.38***	–0.08NS	72.43
Y=μ+a1Nmax+a2mR	–301.61	79.93***	3.11**	73.39
Y=μ+a1Nmax+a2δ	–211.24	82.28***	–102.65NS	72.79
Y=μ+a1Nmax+a2Hmax	–9.60	83.23***	–156.79***	85.05
Y=μ+a1Nmax+a2Sw	–266.67	81.14***	2688.87NS	72.85
Y=μ+a1Nmax+a2gset	–355.65	66.87***	349.30***	77.92
Y=μ+a1Nmax+a2nso	134.63	76.88***	–22 861.21***	82.00

Performance of the model simulation using original parameter values

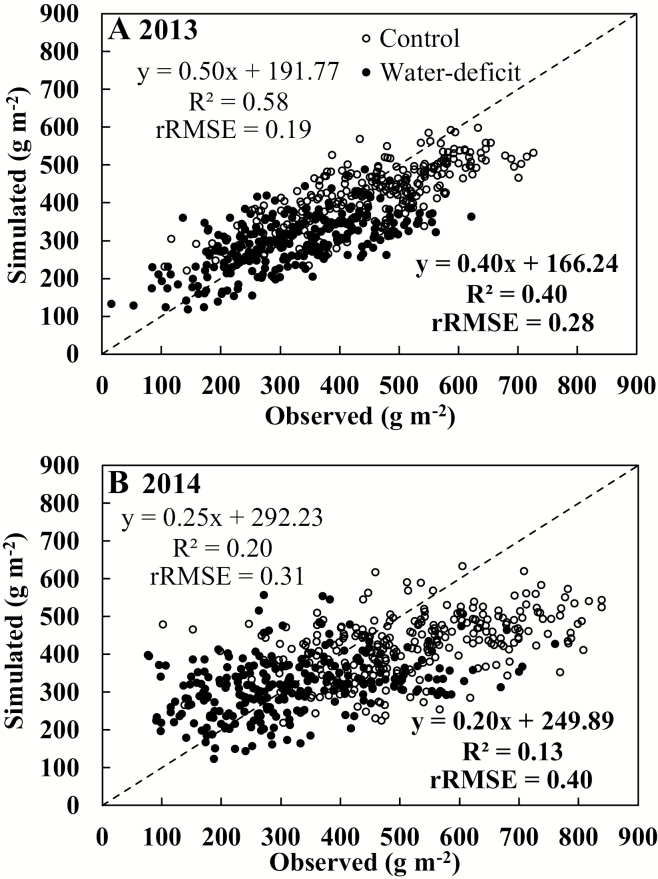
The GECROS model input parameters were estimated from control conditions in the 2013 experiment. For this 2013 control treatment, the model accounted for 58% of the total variation in grain yield with an rRMSE value of 0.19 in the whole panel (Fig. 2A). Using the same input parameter values to simulate the situation under water deficit stress of 2013, the model accounted for 40% of the yield variation with an rRMSE value of 0.28 (Fig. 2A).

Fig. 2.

Relationship between simulated and observed values of grain yield in 267 genotypes of a rice genome-wide association mapping population under control (open symbols, statistical indicators not in bold) and water deficit (filled symbols, statistical indicators in bold) conditions in the 2013 (A) and 2014 (B) experiments.

Model input parameter values from the 2013 control condition were also used to run GECROS to simulate grain yield in the 2014 experiment. The model only accounted for 20% and 13% of the variation in grain yield under control and water deficit conditions with rRMSE values of 0.31 and 0.40, respectively (Fig. 2B). The model tended to underestimate grain yield in control conditions for most genotypes. For water deficit conditions, the model overestimated yield at the lower tail, and underestimated yield at the upper tail, of the observed values.

Identifying SNP markers for model input parameters and for grain yield

Using a single-locus and a multilocus GWAS performed on the 213 genotypes of the training data set from 2013 control conditions, we identified 104 SNP markers associated with model input parameters (Table 3), and the equivalent Manhattan plots are given in Supplementary Figs S4–S6. In the next step, we selected the final set of 90 out of 104 SNP markers for model input parameters with cut-off threshold P-values <0.01 using the MLR Equation 1 (Supplementary Table S1). The combined phenotypic variation explained by the final set of SNPs detected for individual model input parameters ranged from 42.2% (g_set) to 77.0% (H_max; Supplementary Table S1). In comparison, we also detected 12 SNP markers for grain yield, which together explained 44.4% of the total variation in grain yield (Table 3). No common SNP markers were found among model input parameters. Two markers on chromosomes 8 (2341829) and 5 (658940) for N_max, however, were also associated with grain yield.

Table 3.

Total number of significant SNPs detected through multiple linear regression (MLR) for eight GECROS model input parameters and grain yield of the rice training population (n=213) under control conditions in the 2013 experiment

Parameters	Significant SNPs	R 2 (%)
(A) Phenological
m V	16 (20)	74.2
m R	9 (9)	51.6
δ	9 (9)	65.1
(B) Morphological
H max	13 (17)	77.0
S w	8 (9)	47.3
(C) Physiological
g set	6 (6)	42.2
n SO	16 (19)	70.0
N max	13 (15)	66.8
Total SNPs	90 (104)
Grain yield	12	44.3

Percentage of phenotypic variations (R²) explained by significant SNPs of model parameters and yield are derived from MLR (Equation 1). The numbers in parentheses refer to the number of significant SNP markers originally detected through the genome-wide association mapping study before putting them into the MLR analysis (for more details, see the Materials and methods). Coefficients of Equation 1 and the additive effect of each significant SNP for model input parameters and grain yield are given in Supplementary Table S1.

Performance of SNP-based GECROS simulations

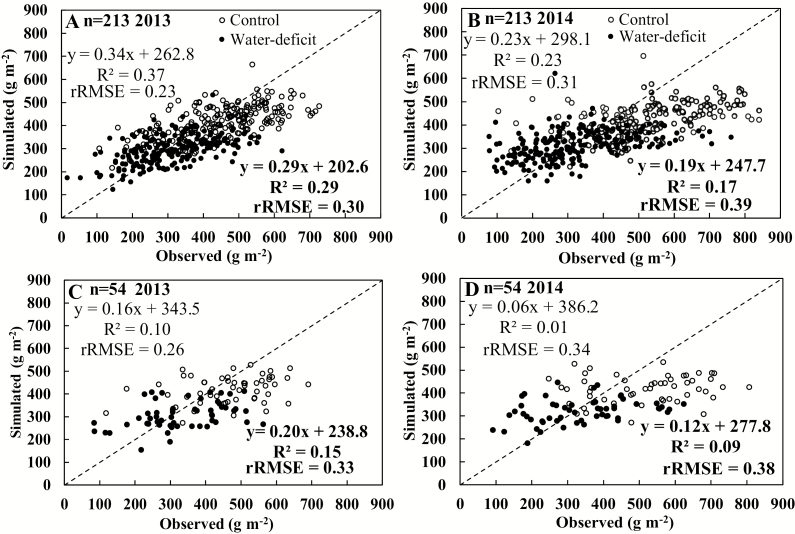
In the next step, an SNP-based GECROS model was created by using parameter values for each genotype calculated from the additive effect of the SNPs on model input parameters by the MLR analysis (Equation 1), and allelic data of each SNP for the whole panel. In training data sets, the SNP-based model accounted for 37% and 29% of variation in grain yield under control and water deficit conditions with rRMSE values of 0.23 and 0.30, respectively, for the 2013 experiment (Fig. 3). However, model simulation on testing data sets accounted only for 10% of yield variation under control conditions (rRMSE=0.26), and 15% of yield variation under water deficit conditions (rRMSE=0.33) in 2013 (Fig. 3).

Fig. 3.

Relationship between SNP-based simulated and observed grain yields in training (A, B) and testing (C, D) populations of rice under control (open circle, statistical indicators not in bold) or water deficit (filled circle, statistical indicators in bold) conditions during 2013 (A, C) and 2014 (B, D) experiments.

For the 2014 experiment, the SNP-based GECROS model accounted for only 23% and 17% of variation in grain yield of the training sets under control and water deficit conditions, respectively (Fig. 3). For the testing data sets, this percentage was only 1% and 9% for the two conditions, respectively (Fig. 3). Across both years and treatments, the model overestimated the lower end, and underestimated the upper end, of observed grain yields (Fig. 3).

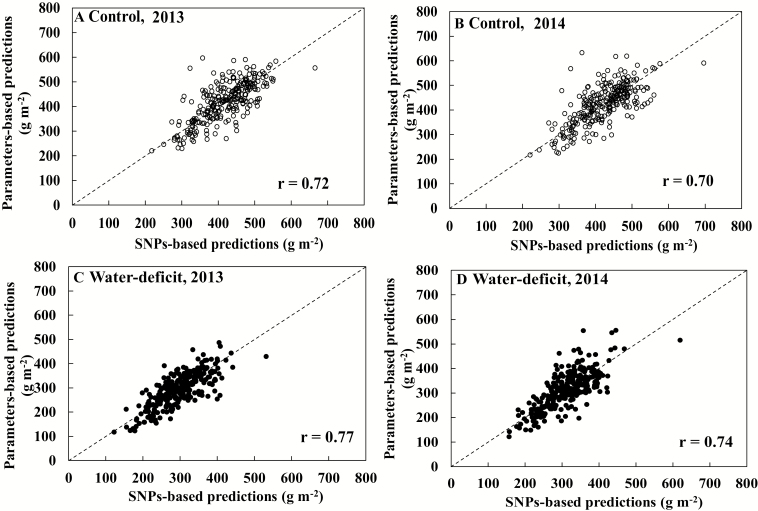
We correlated the original parameter-based simulations with SNP-based simulations, for the whole panel. The SNP-based simulations were well correlated with original parameter-based simulations under control conditions (2013, r=0.72; and 2014, r=0.70) and water deficit conditions (2013, r=0.77; and 2014, r=0.74) (Fig. 4).

Fig. 4.

Correlations between grain yields predicted using phenotypic model input parameter values and those predicted using SNP-based model parameters for 267 rice genotypes under control (open circles, A and B) or water deficit (filled circles, C and D) conditions during 2013 (A, C) and 2014 (B, D) experiments.

Performance of statistical genomic prediction

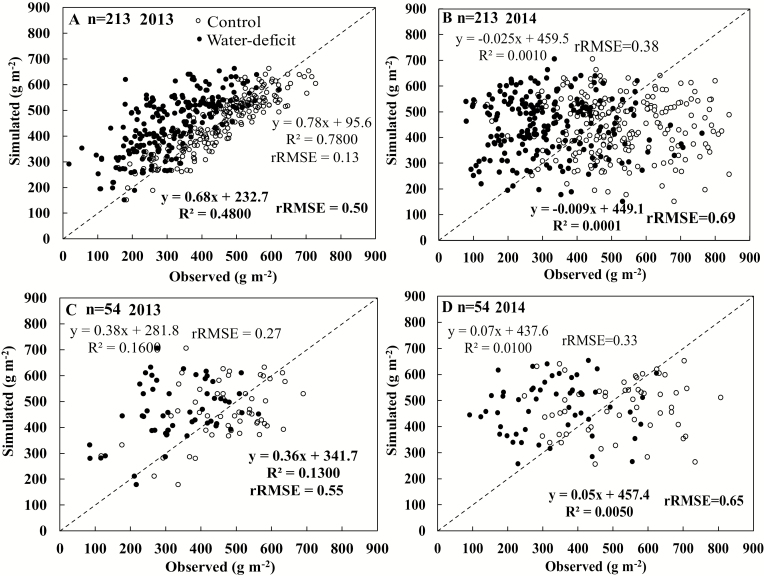
The same 90 SNPs markers identified for GECROS parameters (Supplementary Table S1) were used to develop the GP model, using the grain yield data of the 2013 control conditions for the same training population (n=213). In the 2013 experiment, the GP model accounted for 78% (rRMSE=0.13) of yield variation of the training population under control; but its performance for water deficit stress was poorer with rRMSE=0.50, despite explaining 48% of yield variation (Fig. 5A). Similar to the eco-physiological modelling, the GP model was not effective in the 2013 testing data set, accounting for only 16% (rRMSE=0.27) of yield variation in control and 13% (rRMSE=0.55) of yield variation under water deficit (Fig. 5). When also validated on the 2014 experiment, the GP model was extremely poor in prediction, accounting for ≤1% grain yield variation in training and testing data sets across treatments (Fig. 5). In fact, the GP model overestimated the grain yield under water deficit for all cases (Fig. 5).

Fig. 5.

Relationship between grain yields predicted by the genomic prediction model and the observed values for training (A, B) and testing (C, D) populations of rice under control (open circle, statistical indicators not in bold) or water deficit (filled circle, statistical indicators in bold) conditions during 2013 (A, C) and 2014 (B, D) experiments.

Sensitivity analysis to rank the relative importance of SNP markers in determining yield

To determine the relative importance of the 90 significant SNP markers, a sensitivity analysis was run with GECROS by fixing these markers one at a time. This involved a total of 180 (90 in control and 90 in water deficit) simulations based on the 2013 experiment.

For control conditions, the top four SNP markers on chromosome 6 (1360962; rank 1), 7 (23760855; rank 2), 12 (6720935; rank 3), and 1 (1360962; rank 4) contributing to variation in grain yield were all detected for N_max (Supplementary Table S2). For example, fixing the top ranked SNP on chromosome 6 (1360962), the phenotypic variation accounted for by GECROS decreased from 31.6% to 25.9% in control conditions (Supplementary Table S2). These results are supported by the linear regression results showing that N_max explained most of the variation in grain yield (Table 2).

For water deficit conditions, the top three SNP markers on chromosome 4 (19591930; rank 1), 1 (9243669; rank 2), and 2 (4390533; rank 3) contributing most to grain yield were for m_V (Supplementary Table S2). The phenotypic variation accounted for by the model for yield in water deficit decreased from 26.1% to 14.9% if the top ranked SNP on chromosome 4 (19591930) was fixed. Likewise, the fourth ranked SNP marker under water deficit was on chromosome 7 (58252) detected for H_max.

These results demonstrate that pre-flowering phenology played a major role in influencing grain yield under stress, while N_max predominantly influenced grain yield in control conditions. Nevertheless, the SNP marker on chromosome 6 (1360962; rank 6) influencing N_max and the marker on chromosome 3 (16529108; rank 7) influencing n_SO also had significant effects on grain yield under water deficit (Supplementary Table S2). In addition, we noticed that excluding the effect of some markers did not change the variation in grain yield explained by the model, while in another situation it increased the explained variation. For instance, excluding one of the SNPs on chromosome 9 for m_R increased the explained variation in grain yield in control from 31.6% (baseline simulations) to 33.5% (Supplementary Table S2).

Discussion

In this study, we incorporated SNP markers identified through GWAS into the eco-physiological model GECROS to simulate variation in grain yield among different rice genotypes in an association panel. Key findings are discussed below in detail.

Modelling genotypic differences of yield under stress conditions remains a challenge to eco-physiological models

Models are often adapted empirically to diverse data for an improved prediction. In contrast, GECROS minimizes the use of empirical algorithms and input parameters, and simulates crop yield by capturing the principles of physiological interaction and feedback (Yin and Van Laar, 2005; Yin and Struik, 2010, 2017; Yin, 2013). This model was used to simulate grain yield and biomass differences in a bi-parental segregating population of rice (Gu et al., 2014). For our study, we implemented the simulation procedure in the strictest possible manner: the model was calibrated for only eight parameters (Table 1), which were estimated from measurements in a single environment, namely under well-watered conditions of the 2013 experiment. This model explained 58% of the observed differences in grain yield among the rice association panel in the 2013 experiment (Fig. 2A). The variation accounted for was lower than in a previous study with a bi-parental population of introgression lines (Gu et al., 2014). This was probably because the GWAS panel used in our study contained more diverse genotypes (n=267), while individuals derived from a bi-parental cross in the case of Gu et al. (2014) were fewer (n=96) and more related to each other. The model showed poor simulation accuracy of variation in grain yield in new environments, the 2013 water deficit condition (Fig. 2A), and both control and water deficit conditions in the 2014 experiment (Fig. 2B). These results suggest that the eight GECROS model input parameters chosen in the present study (Table 1) are not sufficient in characterizing yield differences. We previously observed variations in many morpho-physiological traits in our GWAS panel (see Kadam et al., 2017). These traits are potentially important for yield determination, but most of them are not yet accounted for by the model.

Water deficit reduces transpiration cooling and increases tissue and organ temperature leading to higher spikelet sterility in rice (Jagadish et al., 2007). Potential seed number was determined by carbon and nitrogen accumulation during the vegetative phase in an earlier version of GECROS. Hence, the model originally did not have the ability to account for the effect of organ temperature on spikelet sterility and, therefore, generally overestimated grain yields in the panel under stress conditions (Supplementary Fig. S2). In the present study, we introduced the GECROS leaf surface energy balance algorithms to simulate panicle temperature under stress conditions. We need to further evaluate this approach because it is hypothesized that panicles may not have functional stomata and hence do not behave similarly to leaves (Lawas et al., 2018). Also, predicting organ temperature may require a detailed modelling of crop microclimate. Nevertheless, our simple approach allowed us to simulate 40% and 13% of the grain yield variation in the association panel under stress conditions during the 2013 and 2014 experiments, respectively (Fig. 2). The decreased simulated yield for the stress condition was due to an increased spikelet sterility because of simulated warmer panicle temperature by ~2 °C (results not shown). Such an extent of panicle warming was in line with measurements of canopy temperature in the same experiment (G. Melandri, personal communiction). Individual genotypes may differ in: (i) their panicle temperature response to water deficit (Lawas et al., 2018); (ii) the time window of their flowering hours (Bheemanahallia et al., 2017); and (iii) their sensitivity of spikelet fertility to panicle temperature. However, we did not have sufficient data on these possible differences; so uniform sensitivity parameter values were applied to all genotypes, based on the recent report of Julia and Dingkuhn (2013). In addition to the response via panicle temperature, there may be a direct response of spikelet sterility to panicle water deficit, which is extremely hard to model. All these may contribute to why only marginal benefit was obtained after introducing temperature effects on spikelet fertility under stress (Fig. 2A versus Supplementary Fig. S2). Modelling genotypic differences of spikelet fertility remains a major challenge in applying eco-physiological models to stress conditions.

SNP-based eco-physiological prediction was less accurate in training sets but advantageous in new environments, compared with statistical genomic prediction

The SNP-based eco-physiological model was created by replacing the orginal parameter values with those estimated from additive effects of loci identified by GWAS. To evaluate the predictive quality of the SNP-based model, special validation schemes were used, in which the genotypes were randomly subdivided into a training set and a testing set. The SNP-based model showed some potential to quantify the grain yield variation in the training set under 2013 control and new environments (Fig. 3A, B). However, the model had lower accuracy for grain yield, compared with the GP model in the training data set under the 2013 control environment (Fig. 5A). This could be due partly to the fact that SNPs for model input parameters explained only 42–77% of their phenotype variation (Table 3; Supplementary Table S1) and partly to the fact that GECROS does not yet use a full set of yield-determining traits as its input parameters (see discussion earlier). On the other hand, compared with the GECROS model (Fig. 3B), the GP model showed extremely poor predicition accuracy for yield in training data sets across treatments in the 2014 experiment (Fig. 5B). This indicates that the GP model developed in one environment cannot be extrapolated to other environments, particularly not to stress environments where the GP model overpredicted yields (Fig. 5A, B). To some extent, the eco-physiological model had a better ability to be extrapolated to other environments based on physiological principles captured by the model. A GP model could include environmental factors as covariates in analysing multienvironment data; but this is not comparable with our eco-physiological modelling scheme, nor is it feasible within our available data sets.

In validation, both the SNP-based eco-physiological model (Fig. 3C, D) and the GP model (Fig. 5C, D) showed a poor prediction in testing data sets across years and treatments. The GWAS analysis explores the phenotypic variance that is determined by how the two allelic variants differ in their phenotypic effect and their allelic frequency in the population sample. Hence, the lower simulation accuracy for the testing set suggests that excluding the 54 testing genotypes in the GWAS analysis might change the balance of the allelic frequency of a given SNP in the population. This change can influence the phenotypic variance and reduce the prediction accuracy (Isidro et al., 2015). Although the testing set did not represent a very different population structure compared with the training set (Supplementary Fig. 3), it may be important to optimize the population structure using marker and trait data while designing the training and testing sets to maximize the prediction accuracy (Rincent et al., 2012). Unfortunately, it was not possible to implement such a procedure in our analysis because we have different model input parameters and such an approach may result in different training and testing sets for different input parameters.

SNP-based modelling enhances the role of an eco-physiological approach in improving the efficiency of marker-assisted selection

Eco-physiological models have been expected to be a useful tool in supporting plant breeding (Bertin et al., 2010; Hammer et al., 2016). However, the fact that the genetic basis of model input parameters is largely unknown has prevented eco-physiological modelling from achieving its potential in assisting breeding (Kromdijk et al., 2014). Using QTL analysis to overcome this problem has been done in several studies based on traditional linkage analysis with bi-parental populations (see review by Yin et al., 2016). In this study, we explored the use of the GWAS approach with a diverse rice panel, and incorporated the identified effects of multiple SNPs into an eco-physiological model. We then used this SNP-based modelling approach to rank the relative importance of markers identified for various model input parameters. This enabled us to identify the most important markers that breeders can prioritize to improve the efficiency of marker-assisted selection for an improved yield in specific environments.

The relative performance of the detected markers differed totally for control and water deficit conditions: markers for N_max were most important for yield only under control conditions, whereas those for m_V were important for stress conditions (Supplementary Table S2). The importance of m_V markers for yield is because flowering is not only an essential part of reproductive processes but also a critical stage sensitive to various abiotic stresses (e.g. drought and heat) causing the highest grain yield losses (O’Toole, 1982; Barnabás et al., 2008). It is evident that altering the flowering time is a strategy adopted by crops to maximize the fitness under reproductive stage stresses (Kazan and Lyons, 2016). However, the SNP markers for flowering time did not have a strong effect on yield under control conditions (Supplementary Table S2). Hence, the marker-based modelling can help to understand how environmental variables affect the relative importance of phenotypic components and genotypic markers for complex traits. This type of analysis with an improved model can greatly enhance the selection efficiency for future genetic manipulation of crops in the face of changing climatic conditions.

Eco-physiological modelling helps to elucidate the genetic control of grain yield by identifying SNPs for model input parameters

A deeper understanding of how individual processes contribute to grain yield is a prerequisite for designing the plant type for improved grain yields (Peng et al., 2008). Crop models have been used to dissect yield into its physiological components (Yin et al., 2004; Chenu et al., 2008; Hammer et al., 2010). This is the basis of using crop modelling to enhance phenotyping—what Dingkuhn et al. (2017a, b) called ‘the heuristic phenotyping’ of complex traits.

In our study, the model dissected grain yield into eight model input parameters (Table 2). The number of QTLs identified for a single trait is always inadequate (Yin et al., 2002); however, model-based dissection allows detection of more markers than grain yield per se (Table 3; see also Gu et al., 2014; Amelong et al., 2015). Despite this advantage of model-based dissection over analysing grain yield per se, the latter approach cannot be replaced completely. Grain yield analysis identified SNP markers that were not detected by the model-based dissection, except two SNP markers for N_max which co-localized with grain yield. This could be due to the fact that markers detected for grain yield might have less impact on component traits (Yin et al., 2002). Another possibility could be, as stated earlier, that some of the yield-determining mechanisms are not incorporated in the current GECROS model.

Further, we could not find any common SNP markers between model input parameters. This result is in line with that of Dingkuhn et al. (2017a, b) for a rice association panel, but in contrast to a previous report on a bi-parental population of introgression lines (Gu et al., 2014). Such contrasting results could be due to the fact that in a bi-parental population of introgression lines with one or two major segregating genes, QTLs might have a strong influence on multiple phenotypic traits (Yin et al., 2016). However, QTLs detected through GWAS analysis had smaller effects on the main traits. In addition, their effect on other traits might also be too small, and therefore not detectable by the current GWAS threshold P-value.

Challenges in linking the eco-physiological model with genomic approaches

Our study highlighted several problems when combining eco-physiological modelling with GWAS. First, the model calibrated from single-environment data only moderately accounted for the genotypic variation in grain yield across treatments in tested environments, and poorly performed under a new environment. Eight genotype-specific model input parameters (Table 1), which could be estimated from the data available in the present study, were not enough to realize a reasonably good yield prediction in diverse rice genotypes under different environmental conditions. Some of the eight traits did not even contribute much to yield (Table 2, as confirmed by the later marker-ranking analysis in Supplementary Table S2). Hence, the current GECROS model needs to be further upgraded in terms of both model structure and model input parameters, to capture more physiological mechanisms and genotype-specific morphological processes. Earlier discussed responses of spikelet numbers to stress should be urgently attended to, and the design of model parameters should consider using high-throughput phenotyping platforms for characterizing genotypic differences. Secondly, in contrast to a bi-parental QTL analysis (Onogi et al., 2016), identification and estimation of QTL effects in a GWAS analysis indeed need to account for the population structure and genetic relatedness. We have considered both population structure and genetic relatedness in the phase of identifying the QTLs using GWAS. Yet, later, when using Equation 1 to derive model parameter values from the identified QTLs, population structure and genetic relatedness were ignored. To what extent the estimates of additive effect of QTLs on model parameters using Equation 1 could affect the accuracy of the crop model would need further analysis.

Recently, the introduction of GP as a statistical tool has become increasingly popular over GWAS for predicting the quantitative traits, and this GP approach has been integrated with eco-physiological models for different applications (Heslot et al., 2014; Technow et al., 2015; Cooper et al., 2016; Onogi et al., 2016). Onogi et al. (2016) directly linked an eco-physiological model for rice heading date with the GP model, and simultaneously inferred the eco-physiological model parameters and whole-genome marker effects on the parameters in a one-step framework. As such, genetic relatedness among individual genotypes is taken into account in the optimization. They showed that, compared with the two-step method as in our study that applied GWAS or GP to pre-estimated eco-physiological parameters, their one-step method had greater accuracy in prediction in all cross-validation schemes. It is a great challenge to apply this one-step method also to a full crop-yield model such as GECROS, which consists of many physiological subprocesses being simulated possibly with different time steps.

In our analysis, we assumed that the effects of multiple SNPs identified by GWAS are additive. However, as major dominant QTLs were rare (Supplementary Table S1), the individual effects of minor QTLs were probably indirect and thus might involve interactions with those of other, smaller QTLs, and their effects could in many cases neutralize each other. For this reason, a standard GP approach considers very large numbers of markers, where focus is not on individual QTL effects but on the entirety of a whole-genome pattern, thereby providing a fingerprint signature that can be highly predictive of phenotype. This raises the question of whether eco-physiological and genomic integration in modelling should take the selective path of major QTLs (standing for a distinct mechanism of control), or of whole-genome marker patterns, or of something in between (e.g. gene network statistics based on GWAS results and existing databases). Further analyses would be needed to identify the most appropriate path for phenotype prediction using the integrated eco-physiological and genomic approach. Once the eco-physiological model is proven successful, our approach could target whole-genome-based selection, whereby the eco-physiological model would serve to improve predictability of phenotype beyond the training environment, with which standard GP models have problems.

Supplementary data

Supplementary data are available at JXB online.

Fig. S1. The stepwise methodology to combine GWAS with an eco-physiological crop model.

Fig. S2. Relationship between observed and simulated values of grain yield for the water deficit stress treatment of the 2013 experiment, using the GECROS model without introducing the direct effect of panicle temperature on spikelet fertility.

Fig. S3. Principal component analysis (PCA) with the first two principal components showing the population structure of training and testing set genotypes.

Figs S4–S6. The Manhattan plot showing the results of GWAS through the single-locus compressed mixed linear model (CMLM) for various model input parameters.

Table S1. Regression analysis of SNPs against model parameters and yield.

Table S2. Ranking of SNP markers by eco-physiological model simulation for their relative importance in determining grain yield under control and water deficit conditions.