Epistasis in a fitness landscape defined by antibody-antigen binding free energy

Summary

Epistasis is the phenomenon by which the effect of a mutation depends on its genetic background. While it is usually defined in terms of organismal fitness, for single proteins it must reflect physical interactions among residues. Here, we systematically extract the specific contribution pairwise epistasis makes to the physical affinity of antibody-antigen binding relevant to affinity maturation, a process of accelerated Darwinian evolution. We find that, among competing definitions of affinity, the binding free energy is the most appropriate to describe epistasis. We show that epistasis is pervasive, accounting for 25–35% of variability, of which a large fraction is beneficial. This work suggests that epistasis both constrains, through negative epistasis, and enlarges, through positive epistasis, the set of possible evolutionary paths that can produce high-affinity sequences during repeated rounds of mutation and selection.

To ensure a reliable response and to neutralize foreign pathogens, the adaptive immune system relies on affinity maturation. In this process, antibody receptors expressed by B cells undergo an accelerated Darwinian evolution through random mutations and selection for affinity against foreign epitopes (Cobey et al., 2015). Mature antibodies can accumulate up to 20% hypermutations from their germline sequence (Marcou et al., 2018), leading to up to a 10,000 fold improvement in binding affinity (Eisen and Siskind, 1964). Affinity maturation also produces broadly neutralizing antibodies that target conserved regions of the pathogen, of particular importance for vaccine design against fast evolving viruses (Corti and Lanzavecchia, 2013). Despite extensive experimental and theoretical work, the key determinants of antibody specificity and evolvability are still poorly understood, mainly because the sequence-to-affinity relationship is difficult to measure comprehensively or to predict computationally (Esmaielbeiki et al., 2016).

A major confounding factor in characterizing the sequence dependence of any protein function, including affinity, is the pervasiveness of epistasis, the phenomenon by which different mutations interact with each other (Phillips, 2008). Theory (Carter et al., 2005; Good and Desai, 2015; Paixão and Barton, 2016) and genomic data (Breen et al., 2012) suggest that inter- and intragenic epistasis plays a major role in molecular evolution, by constraining the set of accessible evolutionary trajectories towards adapted phenotypes (Weinreich et al., 2006; Poelwijk et al., 2007; Gong et al., 2013; Anderson et al., 2015; Podgornaia and Laub, 2015), enhancing evolvability through stabilizing mutations (Bloom et al., 2006, 2010), or slowing down adaptation by the law of diminishing returns (Chou et al., 2011; Kryazhimskiy et al., 2014). Evidence for epistasis in antibody affinity include direct observations of cooperativity between mutations (Midelfort et al., 2004; Koenig et al., 2015), the dependence of mutational effects on sequence background (Boyer et al., 2016), and statistical co-variation of residues in large sequence datasets (Mora et al., 2010; Asti et al., 2016).

Intragenic epistasis has mostly been studied either by measuring the fitness of all possible mutational intermediates between two variants (Weinreich et al., 2006; Schenk et al., 2013; Szendro et al., 2013; de Visser and Krug, 2014), or by comparing the effect of mutations in different backgrounds (Jacquier et al., 2013; Bank et al., 2015; Boyer et al., 2016). Many such studies rely on a particular measure of fitness rather than a well-defined physical phenotype. Deep mutational scans (DMS) (Fowler and Fields, 2014; Sarkisyan et al., 2016) can comprehensively map out the epistatic landscape of many genetic variants (Araya et al., 2012; Olson et al., 2014; Podgornaia and Laub, 2015). However, most DMS methods do not measure the biophysical quantity of interest directly (Vodnik et al., 2011), introducing both nonlinearities and noise that could be misinterpreted as epistasis.

Here we analyze the detailed epistatic landscape of an antibody’s binding free energy, which we define as the logarithm of the Tite-Seq measurement of the dissociation constant, to its cognate antigen (the 4-4-20 antibody fragment against fluorescein), using data previously obtained by Tite-Seq, a recently introduced DMS variant that accurately measures protein binding affinity in physical units of molarity (Adams et al., 2016). By comparing to a simple additive model of mutations on the binding free energy, and carefully controlling for measurement noise and nonlinearities, we find that epistasis significantly contributes to the antibody’s affinity. This epistasis is not uniformly distributed, but instead favors certain residue pairs across the protein. We use our results to analyze how epistasis both constrains and enlarges the set of possible evolutionary paths leading to high-affinity sequences.

Results

Position Weight Matrix model of affinity

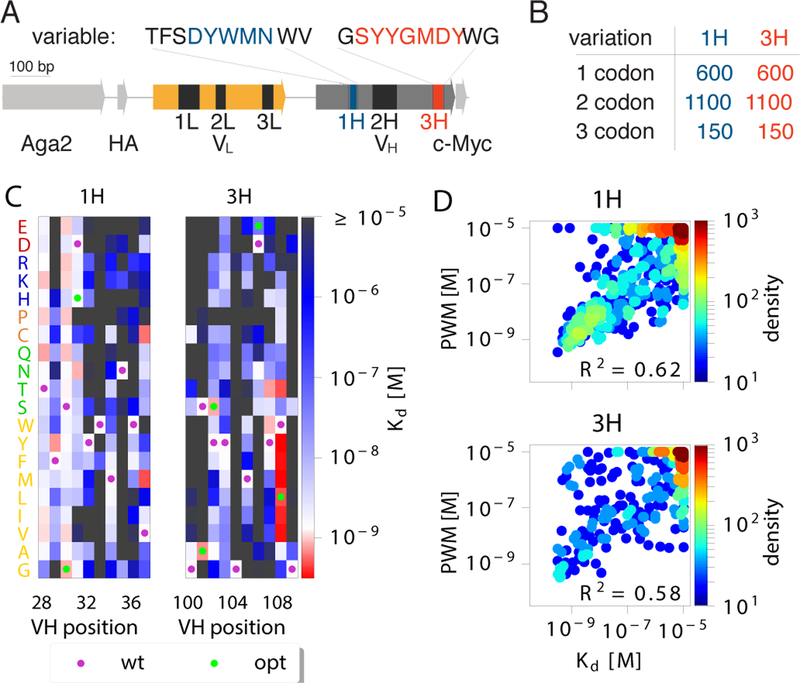
We analyzed data from (Adams et al., 2016) (https://github.com/jbkinney/16_titeseq), where Tite-Seq was applied to measure the binding affinities of variants of the 4-4-20 fluorescein-binding scFv antibody, hence-forth called ‘wildtype’. Libraries were generated by introducing mutations to either the CDR1H or CDR3H domains restricted to 10 amino acid stretches called 1H and 3H (Fig. 1A). All single amino acid mutants, 1100 random double amino acid mutants, and 150 triple amino acid mutants were generated in multiple synonymous variants and measured, (Fig. 1B). Using a combination of yeast display and high-throughput sequencing at various antigen concentrations, Tite-Seq yielded the binding dissociation constant K_d (in M or mol/L) of each variant with the fluorescein antigen.

Figure 1. Additive model of binding affinity.

(A) 4–4-20 scFv antibody sequence. Six complementarity determining regions (CDR: 1L, 2L, 3L, 1H, 2H, 3H) are particularly important for antibody binding affinity. A library of antibody sequences with mutations in 10 amino-acid regions around the CDR1H and CDR3H domains were expressed using yeast display. (B) Using Tite-Seq, the binding constants K_d of all 600 single codon mutants, 1100 random double codon mutants, and 150 random triple codon mutants, were measured. (C) The K_d of single mutants for 1H and 3H domains were used to create position weight matrices (PWMs) to predict the affinity of double and triple mutants. K_d measurements were restricted to the reliable measurements interval of 10^−9.5 – 10⁻⁵ M. WT sequences are marked with purple dots, optimized 4m5.3 mutations are marked in green dots. (D) Comparison between the PWM prediction and the measurement of K_d on double and triple mutants. PWM predictions outside of our reliable readout interval (10^−9.5 – 10⁻⁵ M) were evaluated at the interval boundaries. The PWMs explained a significant portion of the variance, as quantified by the explained variance R² (p < 10⁻⁶¹ for CDR1H, p < 10⁻⁴⁸ for CDR3H, F-test for reduction in variance due to PWM). PWMs trained from the binding free energy, F = ln(K_d/c₀), outperformed PWM trained from K_d (Fig. S3) as well as models without boundaries (Fig. S4).

We first tried to predict the K_d of double and triple mutants from single mutant measurements. Mutations are expected to act on the binding free energy in an approximately additive way (Wells, 1990; Olson et al., 2014). One may thus write the free energy of binding, F = ln(K_d/c₀) (defined up to constant in units of k_BT ), as a sum over mutations in the mutagenized region, s = (s₁, …, s_ℓ):

$$F\left(\mathbf{\text{s}}\right)\approx F_{\text{PWM}}\left(\mathbf{\text{s}}\right)=F_{\text{WT}}+\sum _{i=1}^{\ell }{h}_i\left(s_i\right),$$ (1)

where F_WT is the wildtype sequence energy, and h_i(s_i) is the effect of a mutation at position i to residue s_i. The elements of the Position-Weight Matrix (PWM) h_i(s) are obtained from the K_d of single mutants shown in Fig. 1C. Since Tite-Seq measurements are limited to values of K_d ranging from 10^−9.5 to 10⁻⁵, for consistency PWM predictions outside this range were set to the boundary values. The PWM was a fair predictor of double and triple mutants (Fig 1D), accounting for 62% (p < 10⁻⁶¹, F-test) of the variance for 1H mutants and 58% (p < 10⁻⁴⁸, F-test) of the variance of 3H mutants. In contrast, a simple model based on BLOSUM62 scores (ᴌuksza et al., 2017) achieved far lower R² scores of 22 and 3% for the CDR-1H and 3H domains, respectively (see Fig. S1).

The unexplained variance missed by the PWM model may have four origins: convolution with expression, nonlinear effects, measurement noise, epistasis. Tite-seq was developed specifically to separate the measurement K_D and expression. From Pearson’s correlation between expression and log(K_d), we find that expression explains 6 and 12% of the R² for CDR1H and CDR3H, respectively (Fig. S2). Furthermore, the residual from the PWM prediction, F F_PWM, had almost no correlation with expression (R² < 0.1% for 1H, R² = 0.2% for 3H, see Fig. S2). Log transformed expression values yielded similar but smaller contributions. The second “nonlinear effects” case corresponds to the hypothesis of additivity not being valid for F = ln(K_d/c₀), but for some other nonlinear transformation of F. Such a nonlinearity, also called “scale,” can lead to spurious epistasis (Fisher, 1918; Phillips, 2008). We first checked that additivity did not apply to the untransformed dissociation constant, K_d: a PWM model learned from K_d instead of F could only explain 34% of the variance of all 1H and 3H multiple mutants, down from 62% when learning from F (Fig. S3). Refitting Tite-seq values with no boundary constraints yielded much worse PWM models, largely attributable to poor estimates of poorly binding antibodies (Fig. S4). We then looked for the non-linear transformation E(F ) that would give the PWM model with the best predictive power (Methods and Fig. S5). This optimization yielded only a modest improvement to 65% of the explained variance. In addition, the optimal function E was very close to the logarithm (R² = 97%, Fig. S6). Since nonlinear effects do not play a significant role, henceforth we only consider the PWM model defined on the free energy.

Epistasis affects affinity

To identify epistasis, we estimated the difference between the measured binding free energies of double and triple mutants, F (s), and the PWM prediction, F_PWM(s) (Fig. 2A). However, these small differences can be confounded by measurement noise (see Fig. S7), which can be mistaken for epistasis. To control for this noise, we defined Z-scores between two estimates of the free energy, F_a and F_b, as $Z=\left(F_a-F_b\right)/\sqrt{{\sigma }_a^2+{\sigma }_b^2}$, where ${\sigma }_a^2$ and ${\sigma }_b^2$ are their estimates of uncertainty. Uncertainty was either measured as variance from replicate measurements and synonymous mutations, or as the sum of variances from additive PWM contributions depending on context. We first computed Z-scores between independent estimates of the same free energy using synonymous variants (Z_error, Methods). Excluding mutants at the reliable readout boundary (10^−9.5M ≤ K_d ≤ 10⁻⁵M ), we found that the distribution of Z_error was normal with variance ≈ 1 (Fig. 2B, orange line), as expected from Gaussian measurement noise. A comparison between Tite-seq measurements and clones K_d measured from flow cytometry was also approximately normal with variance ≈ 1 (Fig. S8), meaning that Tite-Seq introduced no systematic errors in addition to those estimated from replicates.

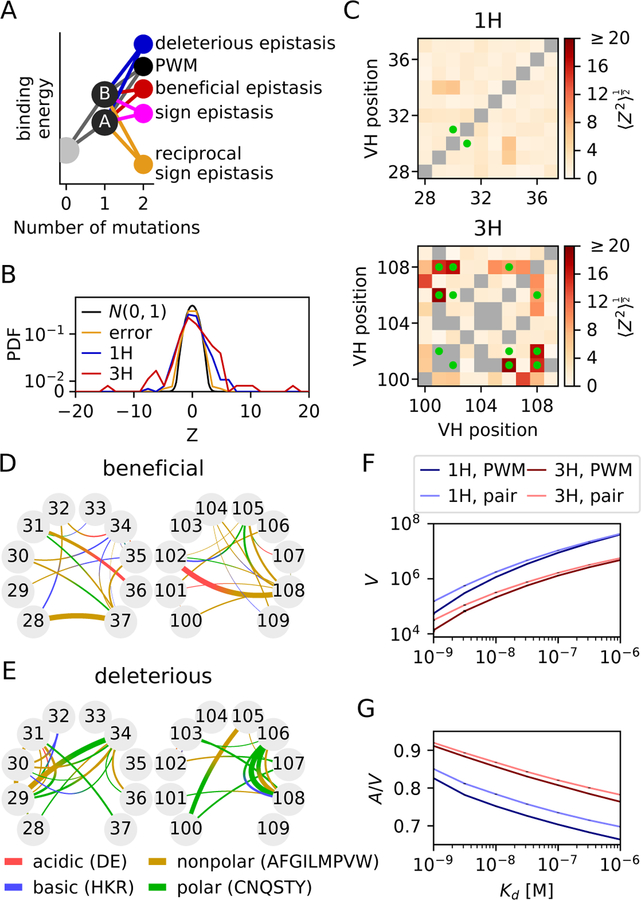
Figure 2. Quantification of epistasis.

A) Epistasis is defined as deviation from the PWM model, which assumes an additive effect of single mutations on the binding free energy F = ln(K_d/c₀) expressed in units of k_BT. Deleterious epistasis occurs when the measured energy exceeds the PWM prediction, beneficial epistasis occurs when the energy is less than the PWM prediction. Sign and reciprocal sign epistasis examples are shown for a beneficial interaction. (B) Distribution of Z-scores, defined as the normalized deviation from the PWM prediction, $Z_{\text{epi}}=\left(F_{\text{PWM}}-F\right)/\sqrt{{\sigma }^2+{\sigma }_{\text{PWM}}^2}$ where σ² and ${\sigma }_{\text{PWM}}^2$ are the estimated errors on F and F_PWM. K_d at boundaries are removed. Positive Z-scores indicate epistasis increased affinity. The Z score standard deviation was much higher than expected from measurement errors (Z_error) for CDR1H (1.78, p < 10⁻¹⁶, Levene’s test) and CDR3H (3.18, p < 10⁻⁴⁸), meaning that the discrepancy between the PWM and measurement is mainly due to true epistasis. (C) Standard Z-score deviation for each pair of positions along the sequence. This deviation is higher at pairs of positions mutated in the super-optimized 4m5.3 antibody (green dots) in 3H (p = 0.005, Mann-Whitney), but not in 1H (p = 0.36). (D-E) A model of biochemical epistatic interactions between polar, nonpolar, acidic, and basic residues was fitted to the data using LASSO regularization and tested by cross-validation, yielding D) 34 beneficial and E) 32 deleterious interaction terms. Line width denotes interaction strength. (F) Number V of amino-acid sequences of the 1H (blue) and 3H (red) regions with dissociation constant below K_d, as estimated by the PWM model (dark color) or the epistatic model (light color). Epistasis enlarges the number of variants with good affinity for both 1H and 3H. (G) Mutational flux A (defined as the average number of random mutation events from all possible sequences to cause the dissociation constant to cross K_d), normalized by V, showing that epistasis also increases the accessibility of the region of good binders in sequence space. Differences between the PWM and epistatic models were robust to errors in the estimate of the interaction parameters (p < 10⁻⁵, Jackknife analysis).

We then estimated the effect of epistasis by calculating Z-scores (Z_epi) from the difference between the PWM prediction, F_PWM (Eq. 1), and the measured F. The resulting distributions of Z-scores (Fig. 2A, blue and red lines) had much larger variances than expected from measurement noise (standard deviation 1.76 for 1H, and 3.18 for 3H), indicating strong epistasis. These epistatic effects were on average slightly beneficial (positive Z): 18% of double mutants inside the reliable readout boundaries (10^−9.5M ≤ K_d ≤ 10⁻⁵M ) showed significant beneficial epistasis (Z_epi > 1.64, corresponding to p < 0.05 in a one-sided Z-test), and 12% significant deleterious epistasis (Z_epi < −1.64). Comparing the variance of Z_epi with that of Z_error gives a large fraction of the unexplained variance that is attributable to epistasis, 1−Var(Z_error)/Var(Z_epi) = 60% for 1H, and 88% for 3H. While clones at the reliable readout boundaries under-estimated measurement error, their inclusion yielded more extreme results (Fig. S9). PWMs trained from optimal transformations had almost no effect on epistasis estimates (Fig. S10).

To determine whether certain positions along the sequence concentrated epistatic effects, we computed the mean squared Z-score for all double mutations at each pair of positions (excluding median boundary values), revealing a complex and heterogeneous landscape of epistasis (Fig. 2C, see Fig. S11 for the epistasis magnitude superimposed on the wildtype’s crystal structure). CDR3H, which interacts directly with the antigen, is observed to have more epistatically interacting sites than CDR1H. Interestingly, the three most epistatic pairs in 3H — between positions 101, 106 and 108 — are mutated in the previously described super-optimized 4m5.3 antibody (Boder et al., 2000) (mutations shown in green in Fig. 1B), consistent with previous suggestions that positions 101 and 106 interact together and with position 108 via hydrogen bonds (Midelfort et al., 2004; Adams et al., 2016). Epistasis is usually expected between residues that are in contact in the protein structure (Romero et al., 2013; Morcos et al., 2011; McLaughlin et al., 2012; Zhang et al., 2013; Melamed et al., 2013), as for instance between positions 101 and 106. However, the mean squared Z-score is only weakly correlated with residue distance (r = −0.13, p = 0.22 for 1H, r = −0.27, p = 0.022 for 3H, Fig. S12). Additionally, while distance to antigen have been shown to predict how strongly mutations affect binding affinity (Brenke et al., 2012; Kepler et al., 2014), we did not detect a strong relationship between epistatic contributions and distance to antigen (r = −0.24, p = 0.511 for 1H, r = 0.19, p = 0.603 for 3H, Fig. S12F). This may be due in part to this study’s mutated region being too close to the antigen to detect an association: 12 out of the 20 mutated residues are within 10 Å of the antigen, and all 20 are within 16 Å.

We next looked for evidence of “sign epistasis,” where one mutation reverses the sign of the effect of another mutation (Fig. 2A). Sign epistasis can constrain evolution by blocking paths to fit sequences (Weinreich et al., 2006; Poelwijk et al., 2011; Weinreich et al., 2005). We defined a Z-score for a single mutation A quantifying the beneficial effect of that mutation relative to the noise, Z_A = (F_WT − F_A)/σ_A, where F_WT and F_A are the wildtype and mutant free energies, and σ is the measurement error estimated as before. Since we are only interested in the sign of the effect, we kept single mutants at the reliable readout boundary. An equivalent Z-score was defined for a mutation A in the background of an existing mutation $Z_{A\left|B\right.}=\left(F_B-F_{AB}\right)/\sqrt{{\sigma }_A^2+{\sigma }_{AB}^2}$, where F_AB is the free energy of the double mutant AB. Significant sign epistasis was defined by $Z_{A\left|B\right.}{Z}_A<0$ and $\left|Z_{A\left|B\right.}\right|,\left|Z_A\right|>1.64$, and reciprocal sign epistasis by the additional symmetric condition A ↔ B.

With a 5% false discovery rate (Benjamin Hochberg procedure) we found 52 significant sign epistasis examples. These are listed in S1_table_sign_epistasis.csv and summarized in Tables S1 and S2. Deleterious sign epistasis was exceptional, with 3 instances in 1H and 6 in 3H. These cases, as well as the four most significant cases of benefecial sign epistasis are depicted in Fig. S13. These mutants represent evolutionary trajectories blocked due to the poor binding affinity of their single mutations. Among cases where both single mutations were deleterious, we found 4% (p < 10⁻¹⁵, Binomial test) of mutants in 1H and 0.8% (p < 10⁻⁷, Binomial test) in 3H with significant beneficial epistasis, versus 0.06% expected by chance (the null expectation, which takes into account the constraint that $Z_A+Z_{B\left|A\right.}=Z_B+Z_{A\left|B\right.}$, is defined in the Methods); 1% (p < 10⁻¹⁵, Binomial test) were reciprocal in 1H, and 0.4% (p < 10⁻¹⁰, Binomial test) in 3H, versus 0.01% expected by chance. To evaluate how these epistatic interactions may affect affinity maturation, we estimated how often “viable” double mutants were separated from the wildtype by nonviable single mutants, where viability is defined by K_d < 10⁻⁶M (Batista and Neuberger, 1998; Foote and Eisen, 1995; Roost et al., 1995), forming possible roadblocks to affinity maturation. This strong instance of “rescue” epistasis occurred in roughly half of the mutants with beneficial sign epistasis (Table S1 and S2).

Modeling epistasis and its impact on affinity maturation

To integrate the observed epistatic interactions into a predictive model of affinity, we introduced a model of binding free energy as:

$$F\left(\mathbf{\text{s}}\right)\approx F_{\text{pairwise}}\left(\mathbf{\text{s}}\right)=F_{\text{PWM}}\left(\mathbf{\text{s}}\right)+\sum _{i<j}{J}_{ij}\left(s_i,s_j\right),$$ (2)

where J_ij is the interaction strength between residues at positions i and j. To avoid overfitting and allow for independent validation (in the absence of a sufficient number of triple mutants), we grouped residues into 4 biochemical categories (Voet and Voet, 2011) (polar, nonpolar, acidic, basic, see Methods) and let the entries of J only depend on that category.

We trained the model on the 1208 1H or 1216 3H double and triple mutants, using a Lasso penalty to control for overfitting. The optimal penalty was set by 10 fold cross-validation, i.e. by maximizing the explained variance of a subset comprising 1/10 of the mutants by using a model trained on the remaining 9/10, averaged over the 10 subsets (Fig. S14A and Methods). Interacting pairs with posterior probabilities > 0.95 as determined by Bayesian Lasso (Park and Casella, 2008) are shown in Figs. 2D and E.

Out of the 360 possible terms, 52 1H and 45 3H interaction terms were identified by this method. Although these interactions, whose number is limited by the number of measured variants, only modestly improved the explained variance relative to the PWM in all multiple mutants (from 62% to 64% for 1H and from 58% to 60% for 3H), it substantially improved the affinity prediction of the mutants with significant epistasis (R² from 27% to 50% in 1H, from 13% to 44% for 3H, Fig. S14B-C). In contrast, a null linear regression model based on the Miyazawa-Jernigen matrix had negligible improvement on R² (see Fig. S15) (George et al., 2017) Notably, two mutations of the super-optimized 4m5.3 antibody are predicted by the model to have epistatic interactions: a slightly deleterious effect between A₁₀₁ and L₁₀₈, and a strongly beneficial one between S₁₀₂ and L₁₀₈. While these results show some generalizability of biochemical properties, the corresponding model only accounts for a small faction of the variance explainable by epistasis. A more sophisticated approach may be warranted for fully predicting epistatic contributions.

Next we used our models to estimate the diversity, or “degeneracy”, of antibodies with good binding affinity. Specifically, we evaluated the degeneracy volume V of high-affinity sequences as the number of sequences with K_d < B, using either the PWM (Eq. 1) or pairwise (Eq. 2) models, using a combination of exhaustive and Monte-Carlo sampling (Methods). Compared to the coarse-grained pairwise model trained previously, the interaction strength J was learned directly for each residue pair, without grouping by biochemical category and with no Lasso penalty. The volume of 1H mutants was larger than that of 3H mutants (Fig. 2F), in agreement with the fact that CDR3H plays a more important role in binding affinity. Epistasis increased the recognition volume for both domains, consistent with the previous observation that epistatic effects are, on average, more beneficial than deleterious. To explore the diversity of evolutionary paths leading to recognition, we computed the neutral mutational flux A in and out of the high-affinity region as the probability that a random mutation in a high-affinity sequence (K_d < B) causes loss of recognition (K_d > B), summed over all high-affinity sequences (Methods). Again, our models show increased mutational flux due to epistasis, even after normalizing by volume, A/V (Fig. 2G). The effect is small, but only reflects the impact of epistasis from the limited, randomly chosen set of double mutations that we measured, which comprises only ~ 7% of all possible double mutations of a 10 amino acid sequence (1058 for CDR1H, and 1066 for CDR3H, out of 16245). We speculate that differences in flux arising from all epistatic interactions may be up to 15 fold stronger. Adding explicit selection to the mutational model would also affect the results, but would require to make additional assumptions about how binding affinity and selection are linked. The neutral mutational flux analysis allows for comparisons that do not depend on such an explicit model of selection.

We checked that these differences were robust to sampling noise and over-fitting by performing a jackknife analysis (p < 10⁻⁵ for the difference in A and V between the PWM and pairwise models, see Methods), and verified that similar conclusions were obtained based on the optimized non-linear transformation (Fig. S16).

Discussion

By analyzing massively parallel affinity measurements obtained by Tite-Seq, we obtained a detailed picture of epistasis in a well-defined physical phenotype — the binding free energy of an antibody to an antigen. Here we define the free energy as the logarithm of the dissociation constant as measured by Tite-Seq and the yeast display assay. While our analysis of epistasis strictly applies to that measured phenotype and not directly to the free energy, these two quantities are believed to be equivalent (Van Antwerp and Wittrup, 2000). We showed that antibody sequences contain many epistatic interactions, and that many of these interactions increase affinity. Our approach involves first training an additive (PWM) model as a baseline, and identifying departures from that model as epistasis. In this comparison, a crucial step was to correct for the two issues of scale and measurement noise. The first issue, identified by Fisher (Fisher, 1918) and also called uni-dimensional epistasis (Szendro et al., 2013), is the idea that an epistatic trait becomes additive upon a different parametrization (Sailer and Harms, 2017a). For instance, protein stability, which often determines fitness, is a nonlinear function of the folding free energy difference, which is expected to be roughly additive (Bloom et al., 2005; Bershtein et al., 2006; Jacquier et al., 2013; Gong et al., 2013; Serohijos and Shakhnovich, 2014; Bank et al., 2015; Sarkisyan et al., 2016). This leads to both a law of diminishing returns (Bank et al., 2015) and robustness to mutations when the protein is very stable (Bloom et al., 2005). To disentangle these potential artifacts, we defined our PWM on the binding free energy, which we expect to be additive in sequence content, and we checked that this parametrization was close to minimizing epistasis.

To tackle the second and perhaps more important issue of noise, especially in the context of deep mutational scans where many variants are tested (Araya et al., 2012), we developed a robust methodology based on Z-scores to identify epistatic interactions as significant outliers. This analysis showed that the variability in binding free energy consists of ~ 60% of additive effects, ~ 25–35% of epistatic effects, and the rest of experimental noise, making the epistatic contribution to the phenotype substantial compared to that of single mutations. A large fraction of that epistasis was beneficial, in contrast with previous reports of mostly negative epistasis owing to the concavity of the scale (Bershtein et al., 2006; Schenk et al., 2013; Bank et al., 2015), which we here circumvent by directly considering the free energy.

Epistasis is key to understanding the predictability and reproducibility of evolutionary paths (Lässig et al., 2017; Kryazhimskiy et al., 2014). Previous studies have shown that much of the unexplained phenotypic variance could be explained by second-order epistatic terms, although specific evolutionary trajectories may be sensitive to higher order epistatic terms (Sailer and Harms, 2017b; Poelwijk et al., 2017). Our results show how second-order epistasis could constrain the space of possible hypermutation trajectories during affinity maturation, with important consequences for antibody and vaccine design, as the importance of eliciting responses of antibodies that are not just strongly binding but also evolvable is being increasingly recognized (Wang et al., 2015). Targeting epistatic interactions may provide an alternative strategy for optimizing antibody affinity: among the 2 epistatic hotspots in CDR1H and 11 in CDR3H that we identified $({\langle Z_{\text{epi}}^2\rangle }^{\frac{1}{2}}>3)$, 4 involved positions mutated in the super-optimized 4m5.3 antibody sequence, with a higher epistatic contribution than expected by chance. This is consistent with a previous study where an antibody with multiple conformations acquired mutations that stabilized the antibody structure, resulting in a single conformation (Wedemayer et al., 1997). We also identified 3 cases of beneficial sign epistasis, in which the double mutant was fit despite the single mutant being deleterious. For instance, the D108E mutations in 4m5.3 is deleterious by itself but is rescued beyond the wildtype value by the S101A mutation (Midelfort et al., 2004), which occurred first in the directed evolution process (Boder et al., 2000). We report 15 extreme cases of viable (K_d < 10⁻⁶ M) double mutants whose single-mutant intermediates are non-viable, possibly blocking affinity maturation. However, our analysis of the volume and mutational flux of the region of low binding free energies in sequence space suggests that epistasis facilitates the evolution of high-affinity antibodies (Fig. 2F,G). Therefore, we speculate that interactions with the non-mutated parts of the sequence and evolution of the antigen binding partner can either add further constraints or open up additional paths.

Antibodies pose unique questions about the evolvability of evolution (Wagner and Altenberg, 1996). What sort of sequence space would favor quick accessibility while maintaining a small number of viable sequences (Perelson and Oster, 1979)? A landscape could contain small, permeable, easily evolvable recognition spaces, or could contain large, hard to access, and robust sequences depending on the prevalent epistatic contributions (Carter et al., 2005). Such a bias could suggest that the tradeoff of an epistatic landscape would include fast initial evolution, followed by slow incremental evolution (Good and Desai, 2014). Our observations, deviating around a viable antibody variant, support a model where epistasis plays a lesser role in determining binding affinity than PWM terms, but could still have far ranging impacts. These impacts would include fast initial/slow long term evolution, the blocking of paths to beneficial mutations, while paradoxically an increase in the accessibility of antigen recognizing sequences.

Taken together, our results show the importance of taking into account epistasis when predicting antibody evolution and guiding vaccine design. We note that, while the yeast display system we studied is highly correlated to alternative measures of affinity (Gai and Wittrup, 2007), antibodies could behave differently under alternative environments. Specifically, a soluble antibody may experience different interactions with the environment and be subject to different constraints than an antibody expressed on a cellular surface. Nevertheless, our systematic approach for identifying and quantifying epistasis, which controls for scale and noise, can be used by other investigators to analyze deep mutational scans of protein function in a wide variety of biological contexts.