Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Apr 5;10(8):2017–2022. doi: 10.1021/acs.jpclett.9b00623

Aromaticity and Antiaromaticity in the Excited States of Porphyrin Nanorings

Martin D Peeks †,*, Juliane Q Gong ‡, Kirstie McLoughlin §, Takayuki Kobatake †, Renée Haver †, Laura M Herz ‡, Harry L Anderson †,*
PMCID: PMC6488184  PMID: 30951313

Abstract

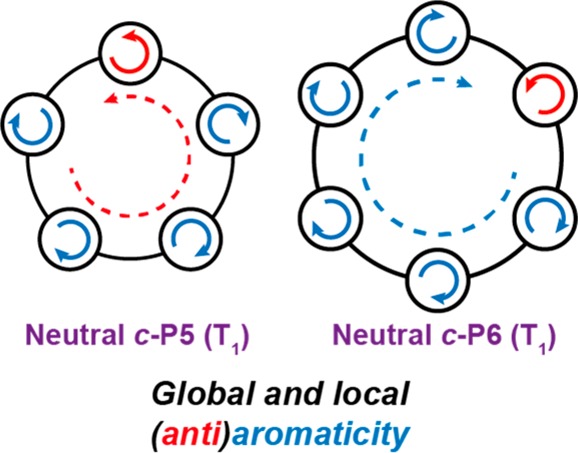
graphic file with name jz-2019-006232_0006.jpg

Aromaticity can be a useful concept for predicting the behavior of excited states. Here we show that π-conjugated porphyrin nanorings exhibit size-dependent excited-state global aromaticity and antiaromaticity for rings containing up to eight porphyrin subunits, although they have no significant global aromaticity in their neutral singlet ground states. Applying Baird’s rule, even rings ([4n] π-electrons) are aromatic in their lowest excited states, whereas the lowest excited states of odd rings ([4n + 2] π-electrons) are antiaromatic. These predictions are borne out by density functional theory (DFT) studies of the nucleus-independent chemical shift (NICS) in the T1 triplet state of each ring, which reveal the critical importance of the triplet delocalization to the emergence of excited-state aromaticity. The singlet excited states (S1) are explored by measurements of the radiative rate and fluorescence peak wavelength, revealing a subtle odd–even alternation as a function of ring size, consistent with symmetry breaking in antiaromatic excited states.

Carbocyclic π-systems with circuits of [4n + 2] and [4n] π-electrons are expected to be aromatic and antiaromatic, respectively, according to modern formulations of Hückel’s rule.1 Introduction of a twist into the π-system reverses the mnemonic, and [4n] π-electron systems become “Möbius aromatic”.2,3 In 1972, Baird predicted a further case in which Hückel’s rule would be reversed: in the lowest triplet state (T1) of a molecule, giving rise to excited-state aromaticity and antiaromaticity for annulenes with [4n] and [4n + 2] π-electrons, respectively.4 Several experimental examples of T1 aromaticity have been presented, and the predictive power of Baird’s rule has been extended to the S1 excited state.5−7 The theory of excited-state aromaticity has been used to rationalize photochemical reactivity.5,8−10 More recently, it has been used to provide design principles for photoswitches11 and molecular motors,12 for energy-level tuning in fulvenes,13 and to explain photoinduced structural changes in a liquid crystal.14

The three main computational methods for investigating (anti)aromaticity involve calculating: (1) bond length alternation using the harmonic oscillator model (HOMA); (2) the aromatic stabilization energy (ASE); and (3) the magnetic effects of (anti)aromaticity using the nucleus-independent chemical shift (NICS).15−17 It is generally accepted that the magnetic criterion is the least ambiguous, particularly for large molecules comprising several potential (anti)aromatic electron pathways, for which the HOMA and ASE can be unsuitable. Experimentally, aromatic character is most convincingly assessed by NMR measurements, which reveal the presence of a ring current. Excited-state (anti)aromaticity is more difficult to evaluate experimentally because NMR is not practical for S1 or T1 excited states.

Kim and co-workers assigned excited-state (anti)aromaticity on the basis of the shape of the excited-state absorption spectrum.6 They found that the antiaromatic excited (triplet) states of hexaphyrins and other expanded porphyrins exhibit broad and featureless absorption spectra, whereas the aromatic excited-state spectra are sharper and more structured, qualitatively resembling the ground-state absorption spectra of ground-state aromatic analogues. However, recent theoretical work shows that antiaromatic expanded porphyrins can also exhibit sharp, intense spectra.18 Kim’s group recently employed time-resolved infrared spectroscopy (TR-IR) to assess aromaticity in singlet excited states, on the basis that aromatic molecules are more symmetric (thus have fewer IR-active vibrations) than antiaromatic ones.19

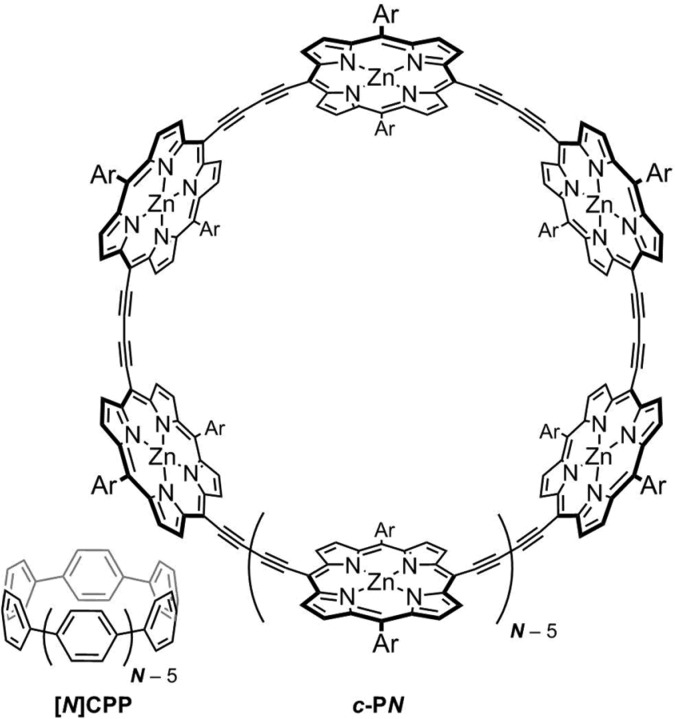
Despite a recent surge of studies into excited-state aromaticity,14,19−27 the effect has rarely been investigated in macrocycles that can sustain multiple aromatic pathways.20,21 A prime example of a system with local (monomer-bound) and global ring currents is given by the series of cyclo-para-phenylenes ([N]CPP, Figure 1).28 In their electronically neutral ground states, these molecules exhibit no global aromaticity (the peripheral electron circuit would contain [4N] π-electrons), and instead, the local aromaticity of each 6π-electron benzene circuit is apparent. However, when such rings are oxidized to the 2+ state, they exhibit global aromaticity about their circumference, determined by calculations, NMR, and magnetic circular dichroism (MCD).29,30 We reported a similar effect in a [6]-porphyrin nanoring (c-P6, Figure 1).31,32 In its neutral state, this molecule has [4n] π-electrons but exhibits no global ring current; instead, the 18π-electron circuit of each porphyrin only contributes to local aromaticity. However, when the ring is oxidized by removal of 4 or 6 π-electrons, global antiaromaticity (80π) and aromaticity (78π), respectively, result (Figure 2).32 This global aromaticity is demonstrated by characteristic NMR chemical shifts and by DFT calculations of magnetic shielding.

Figure 1.

Figure 1

Open in a new tab

Examples of macrocyclic π-conjugated molecules that exhibit no ground-state global aromaticity in their neutral ground states, only local aromaticity: cyclo-para-phenylenes ([N]CPP) and porphyrin nanorings (c-PN).

Figure 2.

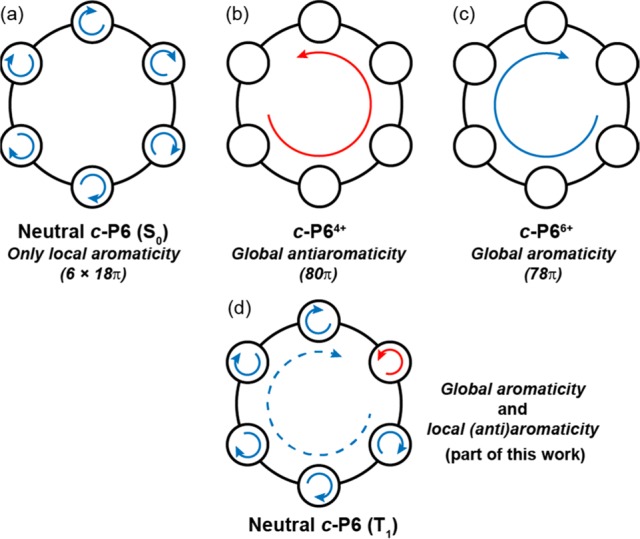
Figure 2

Open in a new tab

Porphyrin nanoring c-P6 contains both a global conjugated circuit (84 π-electrons) and six local porphyrin aromatic circuits (6 × 18π). (a) In its ground state, local circuits dominate and there is no global aromaticity. (b,c) In the 4+ and 6+ oxidation states, local aromaticity is lost and global antiaromaticity and aromaticity, respectively, arise. (d) In part of this work, we show that the T1 state exhibits global excited-state aromaticity in addition to local (anti)aromaticity.

We have previously investigated electronic delocalization in the singlet and triplet excited states of linear butadiyne-linked porphyrin oligomers, the nanoring c-P6, and, for singlet excited states, much larger rings (c-PN up to N = 40). The singlet excited state delocalizes around the entire nanoring within 200 fs for nanorings up to c-P24.33,34c-P6 emits from a delocalized singlet state, whereas partial localization probably occurs prior to emission in c-P10 and larger nanorings, as indicated by an increase in the radiative rate.34 EPR measurements of triplet states indicate uniform triplet delocalization (or fast hopping, at 20 K, on the time scale of the EPR hyperfine coupling, ca. 100 ns) for c-P6 and show that the spin density is mainly localized over 2–3 units in linear oligomers,35 which is consistent with the presence of a coherent triplet exciton extended over at least six units.36 With most functionals, our DFT results do not predict uniform delocalization of the triplet state of the nanorings (vide infra), resulting in different spin densities on each porphyrin subunit.

Here we present DFT results predicting excited-state (T1) aromaticity and antiaromaticity in small porphyrin nanorings, consistent with Baird’s rule. We then present experimental measurements of fluorescence quantum yields, emission spectra, and radiative rates, which indicate the presence of excited-state aromaticity in the S1 states of small porphyrin nanorings (c-P5 to c-P9). Experimental measurements of the triplet-state lifetimes were not possible due to the low triplet yields of porphyrin nanorings, as also encountered for longer linear oligomers.35,37

We used DFT to calculate NICS values in the S0 and T1 states of nanorings from c-P5 to c-P8. Larger nanorings are computationally intractable owing to their size and the loss of symmetry in excited states. The NICS value gives NMR shielding at a point in space, from which the presence and nature of (anti)aromatic ring currents can be readily deduced. The parenthetical number (d in NICS(d)) corresponds to the distance above the molecular plane at which the NICS probe atom is placed, in Å. The NICS(0) value is the most suitable for these systems; use of NICS(1) is not justified because there is no spurious electron density (such as from σ-bonds in the case of benzene) at the center of the nanorings. A negative NICS value inside of the ring indicates aromaticity; positive indicates antiaromaticity. We calculated NICS(0) values across a grid of points through each nanoring in their S0 and T1 states at the B3LYP/6-31G* level of theory38−42 using Gaussian16/A.0343 and Gaussian09/D.01.44 Here we report two NICS values: the isotropic NICS (NICS(0)iso) and the zz component of the shielding tensor (NICS(0)zz), where the z axis is the N-fold rotation axis of the c-PN nanoring. The latter is more sensitive to global aromatic ring current effects, whereas the former is more analogous to chemical shieldings measured through solution NMR chemical shifts. The NICS(0)zz values in the S0 states were approximately zero for all rings (Table 1 and Figure S1), confirming their ground-state global nonaromaticity, whereas NICS(0)iso depicts shielding above and below the plane of each porphyrin subunit, consistent with local aromaticity. The NICS(0)iso and NICS(0)zz for each ring in the T1 state (Figure 3, Table 1, and Figure S2) reveal an alternation between aromaticity and antiaromaticity as a function of ring size, consistent with Baird’s rule and the π-electron count. Each monomer subunit in the nanorings contributes 14 π-electrons; thus c-P5 has 70 π-electrons [4n + 2], c-P6 has 84 [4n], c-P7 has 98 [4n + 2], and c-P8 has 112 [4n]. The NICS values indicate the presence of substantial global aromatic and antiaromatic ring currents in the triplet states of c-P6 and c-P5, respectively, whereas the effect is more subtle in c-P7 and c-P8. The NICS(0)zz for triplet c-P6 is −12.2 ppm, which is approximately a factor of 4 smaller than that for the closed-shell aromatic c-P66+ (−41 ppm at the same level of theory).32

Table 1. NICS(0)iso and NICS(0)zz (all units ppm) at the Centers of Porphyrin Nanorings in Their S0 and T1 States at the B3LYP/6-31G* Level of Theory.

  S0 ground state
 T1 excited state
  iso zz iso zz
c-P5 –2.5 –0.1 1.6 10.3
c-P6 –1.4 1.1 –5.4 –12.2
c-P7 –1.2 0.5 0.4 2.1
c-P8 –0.9 0.5 –1.3 –1.5
Open in a new tab

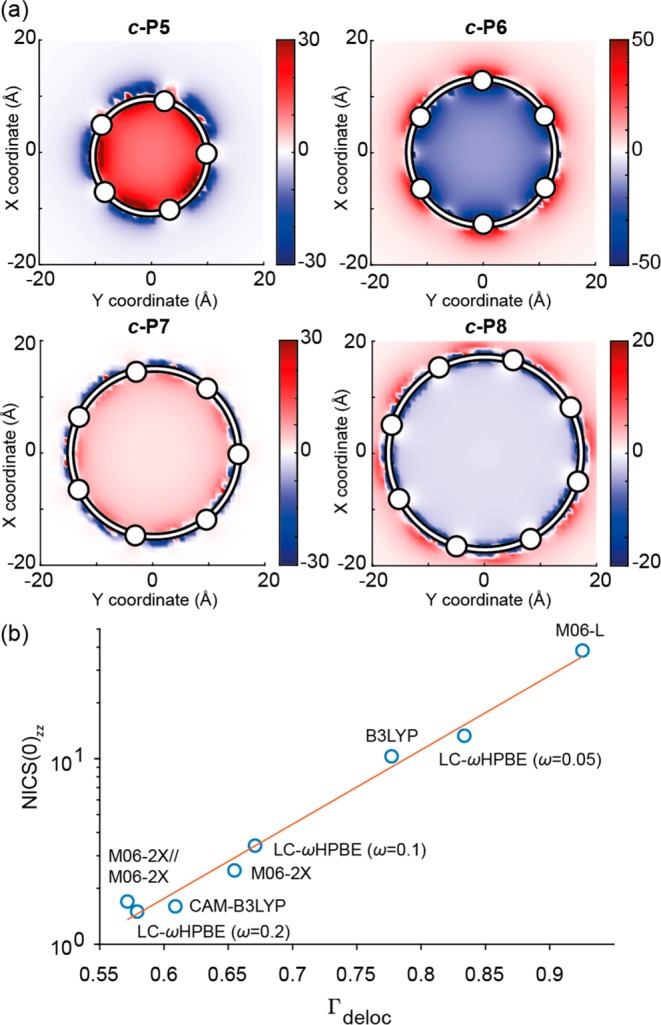
Figure 3.

Figure 3

Open in a new tab

(a) NICS(0)zz grids for the T1 states of c-P5–c-P8 calculated at the B3LYP/6-31G* level of theory, viewed along the z axis. The grids are located in the transverse plane (xy) of the molecules. White circles indicate the locations of Zn atoms. (b) NICS(0)zz vs spin delocalization in c-P5 for a range of different DFT functionals. Γdeloc ranges from 0 (fully localized) to Inline graphic (1.41, fully delocalized); see the SI for further details.

In our previous studies of c-P6 in its oxidized states, we found that oxidation to the 4+ or 6+ state results in loss of local porphyrin aromaticity and emergence of a global ring current.32 Surprisingly, the NICS(0)iso calculations (Figures 4 and S2) suggest that the local aromaticity of each porphyrin subunit persists in the triplet states (cf. negative NICS above and below each porphyrin), except in the case of the porphyrin unit with the greatest spin density. For this porphyrin, the NICS(0)iso is consistent with weak local antiaromaticity. This change is paralleled in the NICS of reduced porphyrin monomers (P1–•), where addition of an electron changes the ring from aromatic to antiaromatic (Figure S6). Analogously, porphyrin monomer dications and dianions are antiaromatic, with 16 π-electrons and 20 π-electrons, respectively.45,46

Figure 4.

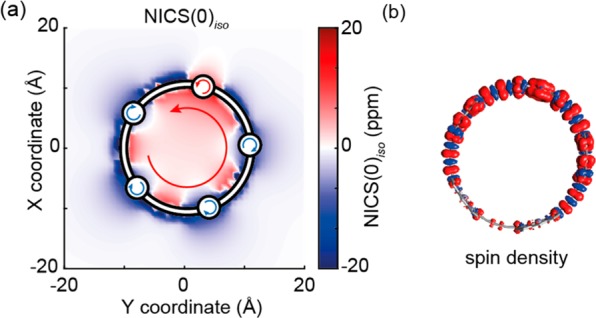
Figure 4

Open in a new tab

(a) NICS(0)iso for c-P5 in its T1 excited state; (b) spin density distribution for c-P5 in its T1 excited state, in the same orientation, both calculated at the B3LYP/6-31G* level of theory. Arrows in part (a) use the same convention as in Figure 2: red arrows correspond to antiaromatic (paratropic) ring currents; blue arrows to aromatic (diatropic). The porphyrin bearing the most spin density (calc. 1.26 spins) has a mildly antiaromatic local ring current.

For the larger c-P7 and c-P8 rings, the magnitude of NICS(0)zz in the T1 state is significantly reduced compared to that for c-P5 and c-P6 (∼2 vs ∼10 ppm; Table 1), indicating that the larger rings are essentially nonaromatic at the B3LYP/6-31G* level of theory, perhaps as a consequence of the finite delocalization of the triplet state (over 5–6 porphyrin units).

The predicted triplet delocalization is strongly affected by the choice of density functional. We decided to compare the choice of functional with the degree of triplet delocalization and the consequential effect on NICS values for c-P5 and c-P6. We used the following functionals: M06-L, M06-2X, CAM-B3LYP, and LC-ωHPBE (ω = 0.05, 0.1, 0.2).47−50 The B3LYP/6-31G* geometry was used in all cases. The results (Figure 3b, Tables S2 and S3, and Figures S3 and S4) show that the NICS(0)zz value is extremely sensitive to the degree of triplet delocalization: those functionals that tend to exhibit enhanced delocalization, such as M06-L and B3LYP, afford a larger NICS than those that tend to delocalize less. The effect shown in Figure 3 would probably be even more pronounced if geometries were optimized in each functional. Most calculations of excited-state aromaticity, to date, have employed B3LYP. As the molecules of interest become larger, it becomes important to carefully consider whether the chosen DFT functional accurately describes the electron delocalization. For c-P6, the triplet state is believed to be either fully delocalized around the ring or hopping rapidly on the EPR spectroscopic time scale.35,36 Our B3LYP calculations are consistent with delocalization of spin density over all six porphyrin units in triplet c-P6, albeit not evenly. Previous B3LYP calculations of triplet density in linear oligomers were consistent with those determined by ENDOR measurements.35

Singlet excited states are generally more delocalized than triplet states.51,52 As mentioned above, Kim and co-workers have employed TR-IR to assess the (anti)aromatic character of singlet excited states on the basis that an antiaromatic state will undergo a pseudo-Jahn–Teller distortion, thus adopting a lower-symmetry excited state and therefore exhibiting more IR-active bands than an analogous aromatic excited state of high symmetry.6,19 We reasoned that this effect should also result in perturbation of the emission properties of porphyrin nanorings, leading to an enhanced quantum yield in Baird antiaromatic states following excited-state symmetry breaking.

Emission quantum yields for small porphyrin nanorings are low (<5%) due to the dipole-forbidden nature of the S1 → S0 transition.53 The reason is best explained by reference to c-P6: in the point-dipole approximation, the transition dipole moments of the six porphyrin monomers around the ring (directed along the butadiyne axis of each monomer) cancel, leaving no net transition dipole moment. A similar S0 → S1 forbiddenness has been reported in small cyclo-para-phenylenes,54 where introduction of a symmetry-breaking element to the molecular structure leads to enhanced emission.55 For both the c-PN and [N]CPP series, the fluorescence quantum yield increases with ring size as a consequence of increased structural flexibility and the loss of excited-state symmetry.34,54

For rings with [4n + 2] π-electrons and excited-state antiaromaticity, pseudo-Jahn–Teller distortion in the excited state would lead to reduced excited-state symmetry and thus an increase in emission quantum yield. In contrast, emission from rings with [4n] π-electrons with excited-state aromaticity should remain largely dipole-forbidden, owing to the high excited-state symmetry.

We measured the radiative rates (Figure 5) and fluorescence quantum yields (ΦF, Figure S11) of c-P5 to c-P16 (see the SI for experimental details). Radiative rates were recovered from measurements of the total excited-state lifetimes by time-correlated single-photon counting (TCSPC). The results show that as the ring size increases the radiative rate and ΦF also increase, from 0.05 ns–1/1% for c-P6 to 0.4 ns–1/20% for c-P16, consistent with previous reports on larger rings.33,34 For the smaller rings (c-P5 to c-P9), there is a subtle odd–even variation in radiative rate: odd rings tend to have a higher radiative rate, and even rings lower. We used a linear model to determine whether the data are best described by a model based on only oligomer length (model A) or a model also incorporating the odd/even porphyrin count of the ring, taking account of the extra degree of freedom (model B; see the SI for full details). For the full data set (c-P5 to c-P16), model A describes the data better than model B. However, for the data set including only c-P5 to c-P9, model B provides a better description of the data (see Figure S12). Analysis of ΦF gives similar results (see Figure S13 and Table S4). Thus, we conclude that there is an odd–even effect in the ΦF and radiative rates of small porphyrin nanorings, consistent with excited-state symmetry breaking in Baird antiaromatic odd-numbered rings. A similar effect is apparent in the photoluminescence peak energy (Figures 5b, S10, S11, and S14, Table S4), which is consistent with a slight odd–even alternation of the HOMO–LUMO gaps as a function of ring size (Figure S7).

Figure 5.

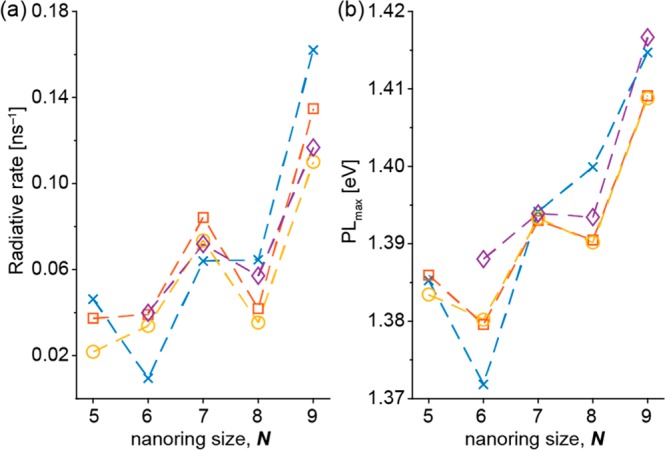
Figure 5

Open in a new tab

(a) Radiative rates and (b) energy of the photoluminescence peak maximum, measured in toluene containing 1% pyridine, referenced to l-P6 (1.47 eV) as a function of ring size N for c-P5–c-P9. Lines connect measurements from the same experimental replicate. λex = 500 nm. See Figure S11 for the full range.

In conclusion, DFT predicts that porphyrin nanorings will exhibit excited-state aromaticity in their triplet (T1) states, though the computational result is very sensitive to the extent of triplet delocalization and thus to the choice of DFT functional. We also present spectroscopic evidence for singlet excited-state (S1) (anti)aromaticity in nanorings containing 5–9 porphyrin subunits, comprising 70–126 π-electrons, consistent with Baird’s rule based on their π-electron counts.

Acknowledgments

We thank the Oxford Advanced Research Computing facility56 for computational support and the EPSRC (Grants EP/M016110/1 and EP/J007161/1) and ERC (Grant 320969) for funding. M.D.P. additionally thanks Exeter College, Oxford for support (Additional Research Grant). T.K. thanks Nippon Shokubai Ltd. for funding.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.9b00623.

  • Details of computational, synthetic, photophysical, and statistical methods, Cartesian coordinates for calculated geometries, and supplementary results figures (PDF)

  • Cartesian coordinates for calculated geometries (ZIP)

The authors declare no competing financial interest.

Supplementary Material

jz9b00623_si_001.pdf (1.8MB, pdf)
jz9b00623_si_002.zip (36.7KB, zip)

References

  1. Gleiter R.; Haberhauer G.. Aromaticity and Other Conjugation Effects; Wiley-VCH, 2012. [Google Scholar]
  2. Heilbronner E. Hückel Molecular Orbitals of Möbius-Type Conformations of Annulenes. Tetrahedron Lett. 1964, 5, 1923–1928. 10.1016/S0040-4039(01)89474-0. [DOI] [Google Scholar]
  3. Ajami D.; Oeckler O.; Simon A.; Herges R. Synthesis of a Möbius Aromatic Hydrocarbon. Nature 2003, 426, 819–821. 10.1038/nature02224. [DOI] [PubMed] [Google Scholar]
  4. Baird N. C. Quantum Organic Photochemistry. II. Resonance and Aromaticity in the Lowest 3.Pi..Pi.* State of Cyclic Hydrocarbons. J. Am. Chem. Soc. 1972, 94, 4941–4948. 10.1021/ja00769a025. [DOI] [Google Scholar]
  5. Rosenberg M.; Dahlstrand C.; Kilså K.; Ottosson H. Excited State Aromaticity and Antiaromaticity: Opportunities for Photophysical and Photochemical Rationalizations. Chem. Rev. 2014, 114, 5379–5425. 10.1021/cr300471v. [DOI] [PubMed] [Google Scholar]
  6. Oh J.; Sung Y. M.; Hong Y.; Kim D. Spectroscopic Diagnosis of Excited-State Aromaticity: Capturing Electronic Structures and Conformations upon Aromaticity Reversal. Acc. Chem. Res. 2018, 51, 1349–1358. 10.1021/acs.accounts.7b00629. [DOI] [PubMed] [Google Scholar]
  7. Sung Y. M.; Yoon M.-C.; Lim J. M.; Rath H.; Naoda K.; Osuka A.; Kim D. Reversal of Hückel (Anti)Aromaticity in the Lowest Triplet States of Hexaphyrins and Spectroscopic Evidence for Baird’s Rule. Nat. Chem. 2015, 7, 418–422. 10.1038/nchem.2233. [DOI] [PubMed] [Google Scholar]
  8. Aihara J.-I. Aromaticity-Based Theory of Pericyclic Reactions. Bull. Chem. Soc. Jpn. 1978, 51, 1788–1792. 10.1246/bcsj.51.1788. [DOI] [Google Scholar]
  9. Shukla D.; Wan P. Evidence for a Planar Cyclically Conjugated 8.Pi. System in the Excited State: Large Stokes Shift Observed for Dibenz[b,f]Oxepin Fluorescence. J. Am. Chem. Soc. 1993, 115, 2990–2991. 10.1021/ja00060a063. [DOI] [Google Scholar]
  10. Wan P.; Krogh E. Evidence for the Generation of Aromatic Cationic Systems in the Excited State. Photochemical Solvolysis of Fluoren-9-Ol. J. Chem. Soc., Chem. Commun. 1985, 1207. 10.1039/c39850001207. [DOI] [Google Scholar]
  11. Durbeej B.; Wang J.; Oruganti B. Molecular Photoswitching Aided by Excited-State Aromaticity. ChemPlusChem 2018, 83, 958–967. 10.1002/cplu.201800307. [DOI] [PubMed] [Google Scholar]
  12. Oruganti B.; Wang J.; Durbeej B. Excited-State Aromaticity Improves Molecular Motors: A Computational Analysis. Org. Lett. 2017, 19, 4818–4821. 10.1021/acs.orglett.7b02257. [DOI] [PubMed] [Google Scholar]
  13. Ottosson H.; Kilså K.; Chajara K.; Piqueras M. C.; Crespo R.; Kato H.; Muthas D. Scope and Limitations of Baird’s Theory on Triplet State Aromaticity: Application to the Tuning of Singlet–Triplet Energy Gaps in Fulvenes. Chem. - Eur. J. 2007, 13, 6998–7005. 10.1002/chem.200700362. [DOI] [PubMed] [Google Scholar]
  14. Hada M.; Saito S.; Tanaka S.; Sato R.; Yoshimura M.; Mouri K.; Matsuo K.; Yamaguchi S.; Hara M.; Hayashi Y.; et al. Structural Monitoring of the Onset of Excited-State Aromaticity in a Liquid Crystal Phase. J. Am. Chem. Soc. 2017, 139, 15792–15800. 10.1021/jacs.7b08021. [DOI] [PubMed] [Google Scholar]
  15. Krygowski T. M.; Cyrañski M. K.; Czarnocki Z.; Häfelinger G.; Katritzky A. R. Aromaticity: A Theoretical Concept of Immense Practical Importance. Tetrahedron 2000, 56, 1783–1796. 10.1016/S0040-4020(99)00979-5. [DOI] [Google Scholar]
  16. Chen Z.; Wannere C. S.; Corminboeuf C.; Puchta R.; Schleyer P. v. R. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. 10.1021/cr030088+. [DOI] [PubMed] [Google Scholar]
  17. Schleyer P. v. R.; Pühlhofer F. Recommendations for the Evaluation of Aromatic Stabilization Energies. Org. Lett. 2002, 4, 2873–2876. 10.1021/ol0261332. [DOI] [PubMed] [Google Scholar]
  18. Woller T.; Geerlings P.; De Proft F.; Champagne B.; Alonso M. Fingerprint of Aromaticity and Molecular Topology on the Photophysical Properties of Octaphyrins. J. Phys. Chem. C 2019, 123, 7318–7335. 10.1021/acs.jpcc.8b10908. [DOI] [Google Scholar]
  19. Sung Y. M.; Oh J.; Naoda K.; Lee T.; Kim W.; Lim M.; Osuka A.; Kim D. A Description of Vibrational Modes in Hexaphyrins: Understanding the Aromaticity Reversal in the Lowest Triplet State. Angew. Chem., Int. Ed. 2016, 55, 11930–11934. 10.1002/anie.201603631. [DOI] [PubMed] [Google Scholar]
  20. Cha W.-Y. Y.; Kim T.; Ghosh A.; Zhang Z.; Ke X.-S. S.; Ali R.; Lynch V. M.; Jung J.; Kim W.; Lee S.; et al. Bicyclic Baird-Type Aromaticity. Nat. Chem. 2017, 9, 1243–1248. 10.1038/nchem.2834. [DOI] [PubMed] [Google Scholar]
  21. Liu C.; Sandoval-Salinas M. E.; Hong Y.; Gopalakrishna T. Y.; Phan H.; Aratani N.; Herng T. S.; Ding J.; Yamada H.; Kim D.; et al. Macrocyclic Polyradicaloids with Unusual Super-Ring Structure and Global Aromaticity. Chem. 2018, 4, 1586–1595. 10.1016/j.chempr.2018.03.020. [DOI] [Google Scholar]
  22. Valiev R. R.; Fliegl H.; Sundholm D. Bicycloaromaticity and Baird-Type Bicycloaromaticity of Dithienothiophene-Bridged [34]Octaphyrins. Phys. Chem. Chem. Phys. 2018, 20, 17705–17713. 10.1039/C8CP03112F. [DOI] [PubMed] [Google Scholar]
  23. Ema F.; Tanabe M.; Saito S.; Yoneda T.; Sugisaki K.; Tachikawa T.; Akimoto S.; Yamauchi S.; Sato K.; Osuka A.; et al. Charge-Transfer Character Drives Möbius Antiaromaticity in the Excited Triplet State of Twisted [28]Hexaphyrin. J. Phys. Chem. Lett. 2018, 9, 2685–2690. 10.1021/acs.jpclett.8b00740. [DOI] [PubMed] [Google Scholar]
  24. Ayub R.; Jorner K.; Ottosson H. The Silacyclobutene Ring: An Indicator of Triplet State Baird-Aromaticity. Inorganics 2017, 5, 91. 10.3390/inorganics5040091. [DOI] [Google Scholar]
  25. Oh J.; Sung Y. M.; Kim W.; Mori S.; Osuka A.; Kim D. Aromaticity Reversal in the Lowest Excited Triplet State of Archetypical Möbius Heteroannulenic Systems. Angew. Chem., Int. Ed. 2016, 55, 6487–6491. 10.1002/anie.201602083. [DOI] [PubMed] [Google Scholar]
  26. Hong Y.; Oh J.; Sung Y. M.; Tanaka Y.; Osuka A.; Kim D. The Extension of Baird’s Rule to Twisted Heteroannulenes: Aromaticity Reversal of Singly and Doubly Twisted Molecular Systems in the Lowest Triplet State. Angew. Chem., Int. Ed. 2017, 56, 2932–2936. 10.1002/anie.201611431. [DOI] [PubMed] [Google Scholar]
  27. Sun H.; An K.; Zhu J. Triplet State Aromaticity: NICS Criterion, Hyperconjugation, and Charge Effects. Chem. - Asian J. 2016, 11, 234–240. 10.1002/asia.201500897. [DOI] [PubMed] [Google Scholar]
  28. Lewis S. E. Cycloparaphenylenes and Related Nanohoops. Chem. Soc. Rev. 2015, 44, 2221–2304. 10.1039/C4CS00366G. [DOI] [PubMed] [Google Scholar]
  29. Kayahara E.; Kouyama T.; Kato T.; Yamago S. Synthesis and Characterization of [n]CPP (n = 5, 6, 8, 10, and 12) Radical Cation and Dications: Size-Dependent Absorption, Spin, and Charge Delocalization. J. Am. Chem. Soc. 2016, 138, 338–344. 10.1021/jacs.5b10855. [DOI] [PubMed] [Google Scholar]
  30. Toriumi N.; Muranaka A.; Kayahara E.; Yamago S.; Uchiyama M. In-Plane Aromaticity in Cycloparaphenylene Dications: A Magnetic Circular Dichroism and Theoretical Study. J. Am. Chem. Soc. 2015, 137, 82–85. 10.1021/ja511320f. [DOI] [PubMed] [Google Scholar]
  31. Hoffmann M.; Kärnbratt J.; Chang M.-H.; Herz L. M.; Albinsson B.; Anderson H. L. Enhanced Pi Conjugation around a Porphyrin[6] Nanoring. Angew. Chem., Int. Ed. 2008, 47, 4993–4996. 10.1002/anie.200801188. [DOI] [PubMed] [Google Scholar]
  32. Peeks M. D.; Claridge T. D. W.; Anderson H. L. Aromatic and Antiaromatic Ring Currents in a Molecular Nanoring. Nature 2017, 541, 200–203. 10.1038/nature20798. [DOI] [PubMed] [Google Scholar]
  33. Yong C.-K.; Parkinson P.; Kondratuk D. V.; Chen W.-H.; Stannard A.; Summerfield A.; Sprafke J. K.; O’Sullivan M. C.; Beton P. H.; Anderson H. L.; et al. Ultrafast Delocalization of Excitation in Synthetic Light-Harvesting Nanorings. Chem. Sci. 2015, 6, 181–189. 10.1039/C4SC02424A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Parkinson P.; Kondratuk D. V.; Menelaou C.; Gong J. Q.; Anderson H. L.; Herz L. M. Chromophores in Molecular Nanorings: When Is a Ring a Ring?. J. Phys. Chem. Lett. 2014, 5, 4356–4361. 10.1021/jz5022153. [DOI] [PubMed] [Google Scholar]
  35. Tait C. E.; Neuhaus P.; Peeks M. D.; Anderson H. L.; Timmel C. R. Transient EPR Reveals Triplet State Delocalization in a Series of Cyclic and Linear π-Conjugated Porphyrin Oligomers. J. Am. Chem. Soc. 2015, 137, 8284–8293. 10.1021/jacs.5b04511. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Hintze C.; Korf P.; Degen F.; Schütze F.; Mecking S.; Steiner U. E.; Drescher M. Delocalization of Coherent Triplet Excitons in Linear Rigid Rod Conjugated Oligomers. J. Phys. Chem. Lett. 2017, 8, 690–695. 10.1021/acs.jpclett.6b02869. [DOI] [PubMed] [Google Scholar]
  37. Kuimova M. K.; Hoffmann M.; Winters M. U.; Eng M.; Balaz M.; Clark I. P.; Collins H. A.; Tavender S. M.; Wilson C. J.; Albinsson B.; et al. Determination of the Triplet State Energies of a Series of Conjugated Porphyrin Oligomers. Photochem. Photobiol. Sci. 2007, 6, 675. 10.1039/b700557a. [DOI] [PubMed] [Google Scholar]
  38. Becke A. D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648. 10.1063/1.464913. [DOI] [Google Scholar]
  39. Hehre W. J.; Ditchfield R.; Pople J. A. Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. 10.1063/1.1677527. [DOI] [Google Scholar]
  40. Rassolov V. A.; Pople J. A.; Ratner M. A.; Windus T. L. 6-31G* Basis Set for Atoms K through Zn. J. Chem. Phys. 1998, 109, 1223–1229. 10.1063/1.476673. [DOI] [Google Scholar]
  41. Ditchfield R.; Hehre W. J.; Pople J. A. Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. 10.1063/1.1674902. [DOI] [Google Scholar]
  42. Hariharan P. C.; Pople J. A. The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies. Theor. Chim. Acta 1973, 28, 213–222. 10.1007/BF00533485. [DOI] [Google Scholar]
  43. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; et al. Gaussian 16, revision A.03; Gaussian Inc.: Wallingford, CT, 2016.
  44. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; et al. Gaussian 09, revision D.01; Gaussian Inc.: Wallingford, CT, 2009.
  45. Cissell J. A.; Vaid T. P.; Yap G. P. A. The Doubly Oxidized, Antiaromatic Tetraphenylporphyrin Complex [Li(TPP)][BF 4]. Org. Lett. 2006, 8, 2401–2404. 10.1021/ol060772l. [DOI] [PubMed] [Google Scholar]
  46. Vaid T. P. A Porphyrin with a C=C Unit at Its Center. J. Am. Chem. Soc. 2011, 133, 15838–15841. 10.1021/ja205738z. [DOI] [PubMed] [Google Scholar]
  47. Zhao Y.; Truhlar D. G. Assessment of Density Functionals for Pi Systems: Energy Differences between Cumulenes and Poly-Ynes; Proton Affinities, Bond Length Alternation, and Torsional Potentials of Conjugated Polyenes; and Proton Affinities of Conjugated Shiff Bases. J. Phys. Chem. A 2006, 110, 10478–10486. 10.1021/jp0630626. [DOI] [PubMed] [Google Scholar]
  48. Zhao Y.; Truhlar D. G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Function. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
  49. Henderson T. M.; Izmaylov A. F.; Scalmani G.; Scuseria G. E. Can Short-Range Hybrids Describe Long-Range-Dependent Properties?. J. Chem. Phys. 2009, 131, 044108. 10.1063/1.3185673. [DOI] [PubMed] [Google Scholar]
  50. Yanai T.; Tew D. P.; Handy N. C. A New Hybrid Exchange-Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
  51. Beljonne D.; Shuai Z.; Friend R. H.; Brédas J. L. Theoretical Investigation of the Lowest Singlet and Triplet States in Poly(Paraphenylene Vinylene)Oligomers. J. Chem. Phys. 1995, 102, 2042–2049. 10.1063/1.468726. [DOI] [Google Scholar]
  52. Beljonne D.; Cornil J.; Friend R. H.; Janssen R. A. J.; Brédas J. L. Influence of Chain Length and Derivatization on the Lowest Singlet and Triplet States and Intersystem Crossing in Oligothiophenes. J. Am. Chem. Soc. 1996, 118, 6453–6461. 10.1021/ja9531135. [DOI] [Google Scholar]
  53. Sprafke J. K.; Kondratuk D. V.; Wykes M.; Thompson A. L.; Hoffmann M.; Drevinskas R.; Chen W.; Yong C. K.; Kärnbratt J.; Bullock J. E.; et al. Belt-Shaped π-Systems: Relating Geometry to Electronic Structure in a Six-Porphyrin Nanoring. J. Am. Chem. Soc. 2011, 133, 17262–17273. 10.1021/ja2045919. [DOI] [PubMed] [Google Scholar]
  54. Adamska L.; Nayyar I.; Chen H.; Swan A. K.; Oldani N.; Fernandez-Alberti S.; Golder M. R.; Jasti R.; Doorn S. K.; Tretiak S. Self-Trapping of Excitons, Violation of Condon Approximation, and Efficient Fluorescence in Conjugated Cycloparaphenylenes. Nano Lett. 2014, 14, 6539–6546. 10.1021/nl503133e. [DOI] [PubMed] [Google Scholar]
  55. Lovell T. C.; Colwell C. E.; Zakharov L. N.; Jasti R. Symmetry Breaking and the Turn-On Fluorescence of Small, Highly Strained Carbon Nanohoops. Chem. Sci. 2019, 10, 3786. 10.1039/C9SC00169G. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Richards A.University of Oxford Advanced Research Computing; Zenodo, 2015; 10.5281/zenodo.22558. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz9b00623_si_001.pdf (1.8MB, pdf)
jz9b00623_si_002.zip (36.7KB, zip)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES